AIS-Based Multiple Vessel Collision and Grounding Risk Identification based on Adaptive Safety Domain

Abstract

The continuous growth in maritime traffic and recent developments towards autonomous navigation have directed increasing attention to navigational safety in which new tools are required to identify real-time risk and complex navigation situations. These tools are of paramount importance to avoid potentially disastrous consequences of accidents and promote safe navigation at sea. In this study, an adaptive ship-safety-domain is proposed with spatial risk functions to identify both collision and grounding risk based on motion and maneuverability conditions for all vessels. The algorithm is designed and validated through extensive amounts of Automatic Identification System (AIS) data for decision support over a large area, while the integration of the algorithm with other navigational systems will increase effectiveness and ensure reliability. Since a successful evacuation of a potential vessel-to-vessel collision, or a vessel grounding situation, is highly dependent on the nearby maneuvering limitations and other possible accident situations, multi-vessel collision and grounding risk is considered in this work to identify real-time risk. The presented algorithm utilizes and exploits dynamic AIS information, vessel registry and high-resolution maps and it is robust to inaccuracies of position, course and speed over ground records. The computation-efficient algorithm allows for real-time situation risk identification at a large-scale monitored map up to country level and up to several years of operation with a very high accuracy.

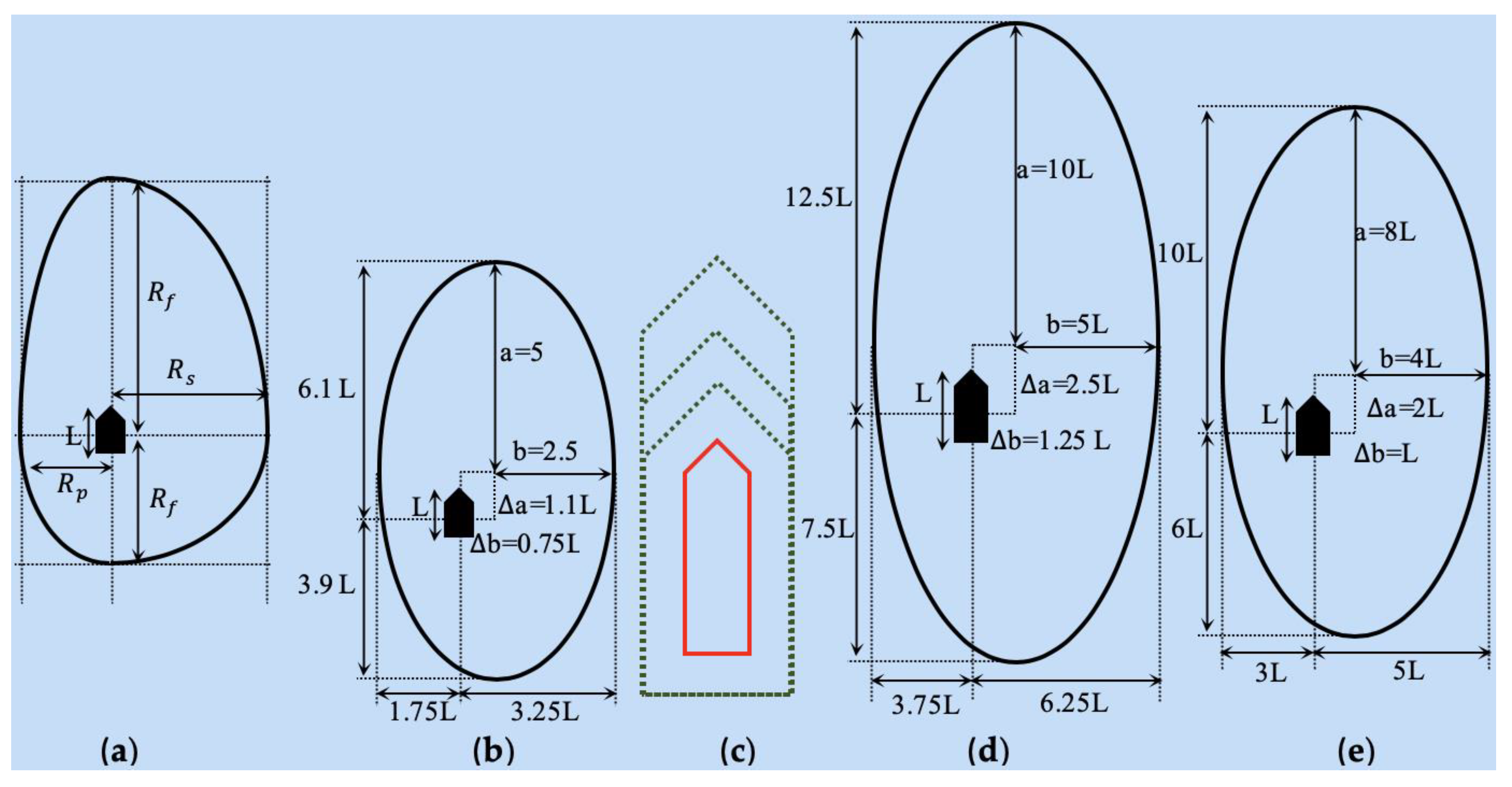
1. Introduction

Maritime transport activities shape a new type of economic sector considered as the blue economy [1]. Since about 90% of the world’s merchandise are transported by sea [2], maritime transport plays a central and potential role in economy nowadays. In parallel, safety requirements are continuously improved to avoid hazardous accidents and ensure a sustainable growth in maritime operations. According to the recent annual review of marine casualties and incidents in 2018 [3] by the European maritime safety agency, more than 20,000 marine casualties and incidents have been reported at the European level in 2011–2017 only. Together, these accidents caused more than 680 fatalities and over 6800 injuries. Navigational accidents represent 53.1% of all casualties with ships as a combination of: grounding (16.6%), contact (16.3%) and collision (23.2%). 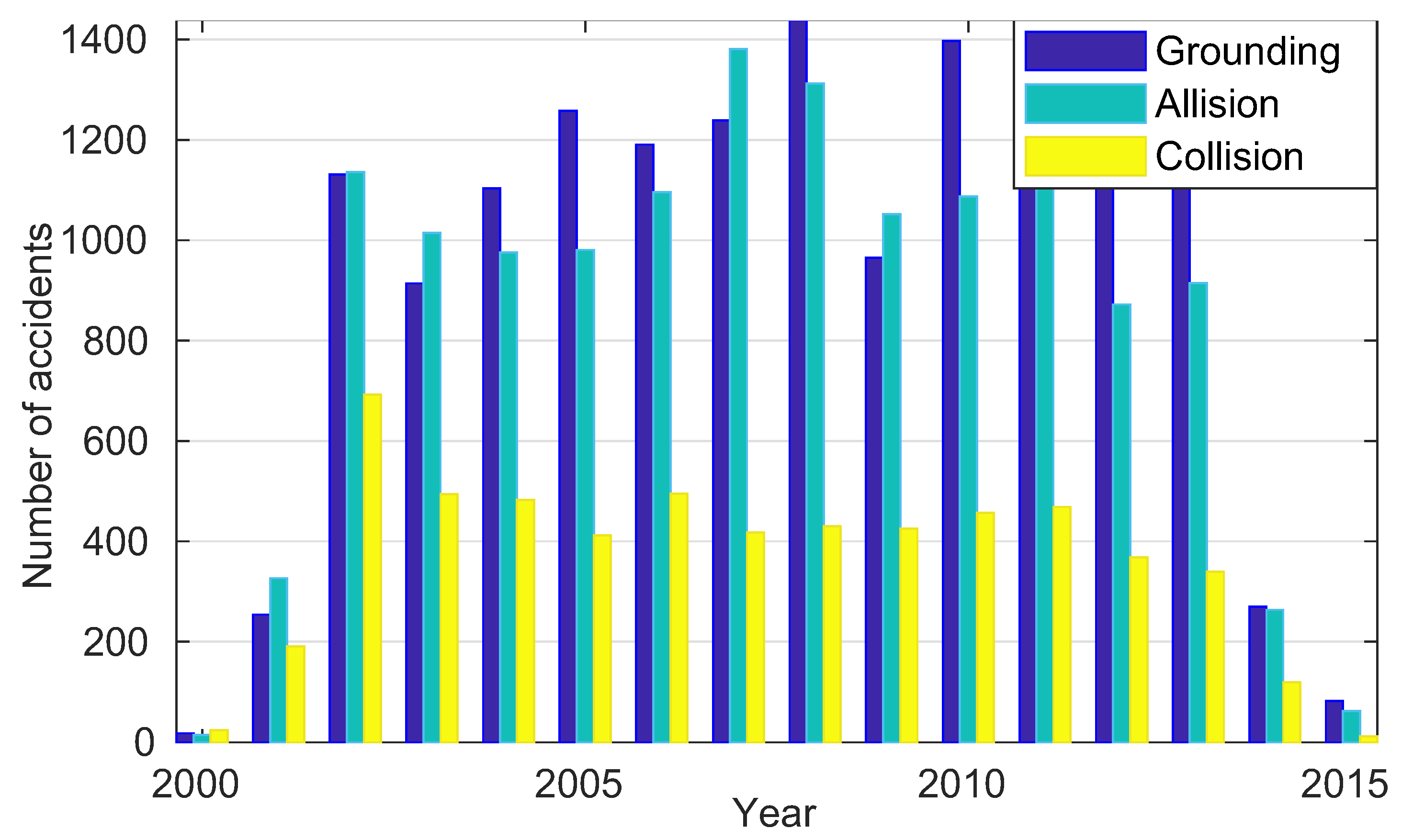Despite being slightly different, the rates of maritime navigation accidents are still tragically high according to marine casualty and pollution database collected by United States Coast Guard (USCG) and provided in July 2015 (not all 2014–2015 accidents reported) by marine information and safety and law reinforcement [4]. In a total of 34,540 reported and fully investigated navigation accidents between 2000 and mid 2015, around 43.5% of the accidents were groundings, 39.6% were allisions with a static object and 16.9% were collisions as demonstrated in Figure 1. A high-level risk analysis on passenger ship collisions presented in Reference [5] suggested that risk control options related to navigation should be considered to reduce the overall risk of collision and that navigational aspects are important.

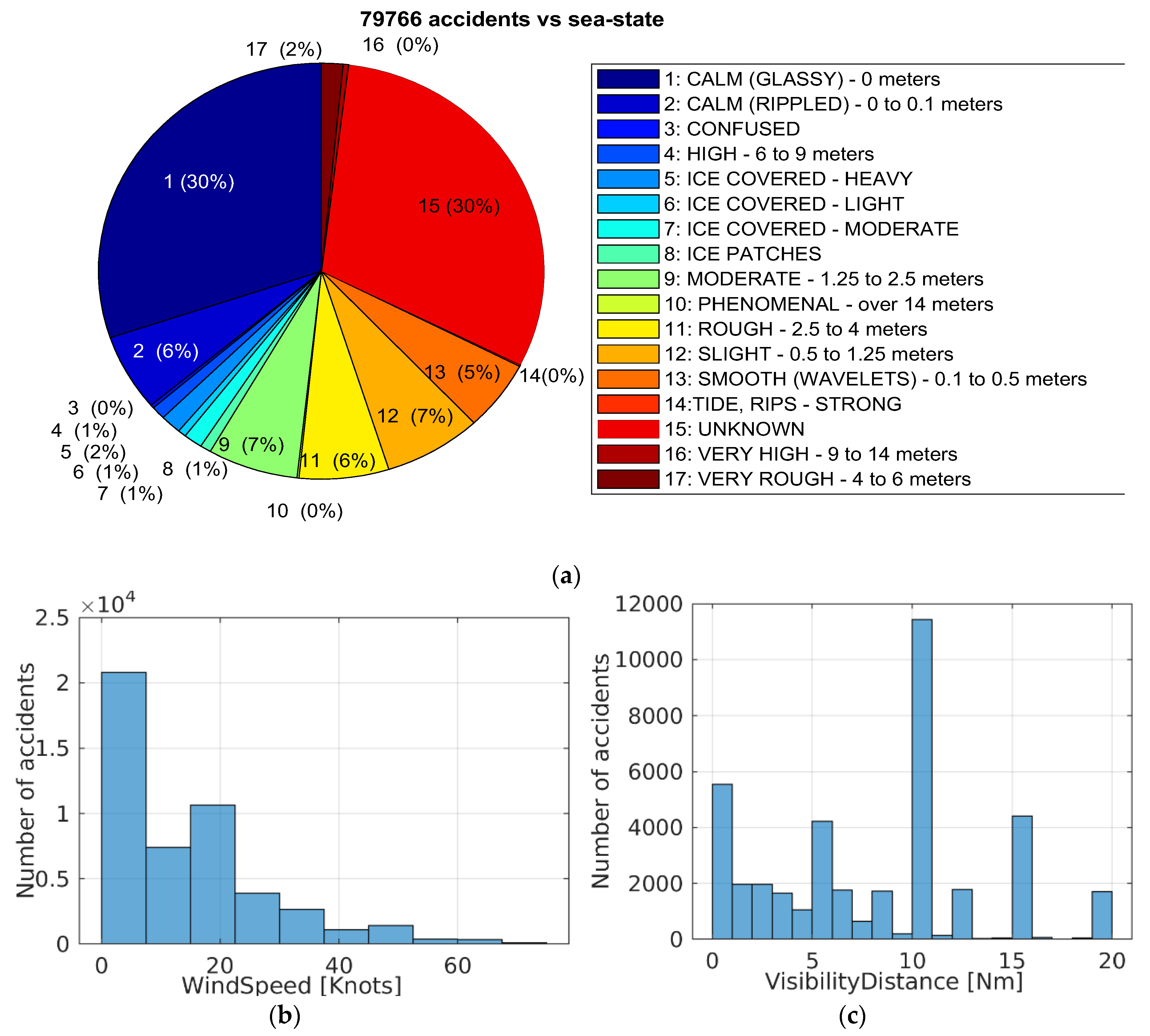
The consequences of maritime accidents can be fairly high as reported by transportation safety board of Canada [6] where the provided data tables include the complete investigations into marine transportation occurrences in 2013–2019. From the reported 79,000 accidents, 80.8% caused damage, 9.86% caused a confirmed pollution, 7.99% caused minor injuries, 4.39% caused serious injuries, while 4.01% of the accidents caused fatalities. The reported accidents also occurred during various environmental conditions as depicted in Figure 2, in which wind speed, visibility condition and sea state have weak effects as accident factors. A full literature review on research in maritime accidents is provided in Reference [7] which lists different research methods and data sources in this context. To help reduce the occurrence rates of such accidents, qualitative research methods were deployed to understand the root causes such as maritime navigation risk indicators [8] with explanatory variables such as vessel type as well as flag of convenience and visibility conditions, human and organizational factors [9] and including decision errors due to conditions of operators and personnel factors and socio-technical factors [10] such as the interactions between ship operators. The qualitative approach is however not very precise as Figure 2 shows since most accidents occurred during good conditions. Moreover, taking into account the traffic densities during each condition and its frequencies, the correlations between sea/wind/visibility conditions and the numbers of accidents are very weak as found in Reference [8]. Alternatively, the authors of Reference [11] demonstrated that the general maritime safety approach is reactive and that accidents cannot be predicted. 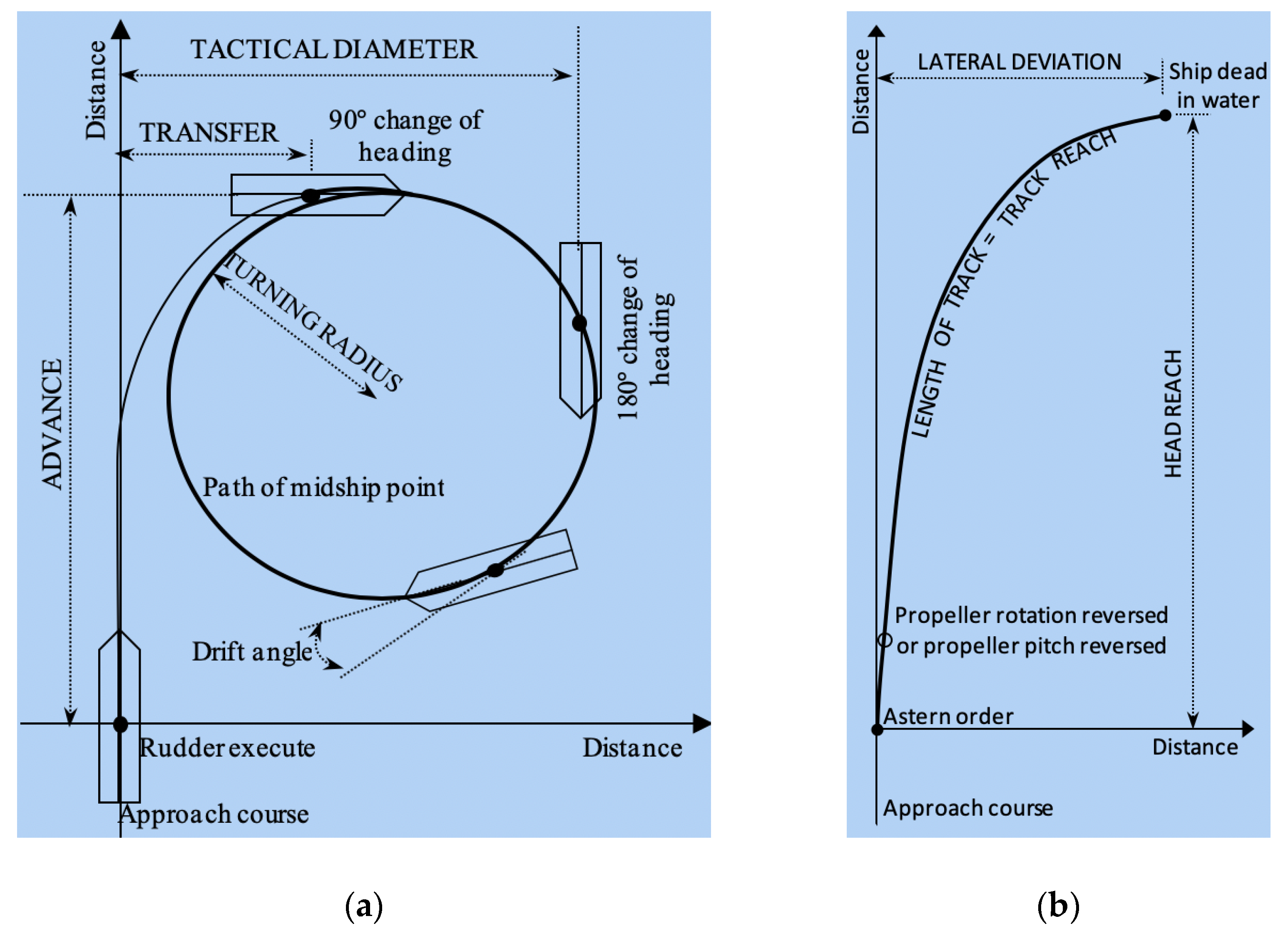In real time, collision and grounding risk depends on the traffic configuration represented by the number of sailing vessels and their locations, relative speed and course to each other and to near objects and their maneuverability such as the stopping distance [12] as well as the tactical diameter, maximum advance and track reach defined by the International Maritime Organization (IMO). These aspects are described in the following and they are incorporated in the design of the proposed risk identification method.

In addition to such severe impact of navigation accidents, the recent developments are continuously increasing the traffic capacity and leading to new emerging technologies and vessels characteristics. This consequently introduces new challenges for fast and early risk identification methods which are crucial to the safety and efficiency of maritime operations, especially in complex navigation situations. To avoid collision and grounding accidents and reduce their occurrence rates, automatic risk identification and analysis tools are receiving a growing attention in theoretical and practical applications. Decision support systems [13] are vital in collision situations at sea and they are proved useful for collision avoidance and safety intervention [14] or extended to intelligent route planning [15] and autonomous navigation algorithms. These methods need to perceive all risky situations in their first stage which is very important for navigation safety. Risk identification was considered in Reference [16] based on Automatic Identification System (AIS) data and the Closest Point of Approach (CPA) [17] as well as distance at CPA and time to CPA parameters. These are typically based on assumptions of linear tracks, constant speed and course and neglect vessel dimensions and maneuverability. Another method for ship collision candidate detection was proposed in Reference [18] based on a velocity obstacle approach. AIS information was also used for risk identification for vessel contact with fixed offshore platforms [19]. Full reviews on individual ship-ship collision risk analysis and assessment are respectively given in Reference [20,21] where a considerable number of research items addressed individual collision risk detection and collision avoidance methods designed and validated using AIS data.

A critical shortcoming in the existing maritime navigation risk identification and evaluation methods is the neglection of vessel maneuverability which is a key factor that varies across different vessels and determines the risk in case of close-quarters situations. Moreover, the existing methods in the literature focus on individual risk while ignoring combinations of multiple collisions and ground situations and their interactions which limits the set of possible evasive actions and increase navigational complexity and confliction with navigation rules. In this work, a vessel maneuverability-based safety domain is designed within an adaptive framework based on navigation situations to identify both collision and grounding risk situations in a fast and computation-efficient approach. This algorithm is designed and validated through extensive amounts of AIS data (as it is the only sufficiently available data), hence the method is not considered as the basic risk identification tool. This was a worth-mentioning aspect for most AIS-based anti-collision methods published so far and it is supported by resolution A.1106(29) [22] issued by IMO including guidelines on potential use of AIS but also its limits in this regard. Those guidelines recognize and recommend the use of AIS for anti-collision assistance but advise cautions that all safety-relevant information must be used and that AIS does not replace other systems. However, the implementation of this algorithm, with sufficient computational resources and access to online AIS information over a large monitored area, does not only detect but also identify navigation risk when available and yields a powerful tool for warnings and decision support, especially when multiple collisions and groundings situations starts developing. In addition, the implementation of this algorithm onboard vessels with access to information from all navigational systems will grant it an increased effectiveness. Compared to the existing methods in the literature, the actual navigation risk is introduced as a combination of interactions of multiple collision and/or grounding candidates. This work considers all types of navigation risk and their combinations over a large monitored area, the objective is to design and validate a computationally efficient algorithm for accurate and automatic risk identification from big historical AIS data. The successful identification of risky situations plays a leading role for decision support and smart navigation to assist the crew and avoid navigational hazards. Moreover, the analysis of huge historical data allows the extraction of a large set of risky situations with their probability of occurrence, this set is invaluable for simulating and verifying the trustworthiness of remote control and autonomous navigation functions.

The rest of this article is organized as follows, Section 2 introduces the proposed method, starting from basic maneuverability aspects involved in the construction of a polygonal safety domain and its efficient approximation, followed by the designed collision and grounding spatial risk functions and the overall risk evaluation methods. Section 3 then describes some data samples used for this application and the main results with a few examples and their discussions. This paper is then concluded in Section 4 where important conclusions are drawn in addition to a summary of the major findings and potential applications of the presented method and suggestions for future work.

2. Risk Identification Methodology

The minimum distance to avoid accidents in a navigation scenario depends on the maneuverability and real navigation conditions and configuration of the involved vessels in addition to the situation complexity. Maritime navigation is dominated by the Convention on the International Regulations for Preventing Collisions at Sea (COLREG) [23]. Different COLREG rules apply for different close quarter situations and therefore the safe navigation distance is generalized to the concept of blocking areas which together define a vessel safety domain with varying parameters based on vessel maneuverability and encounter situation. The simplified polygonal maneuverability-dependent adaptive safety domain outperforms state-of-the-art approaches in terms of risk identification effectiveness and computation efficiency and extends to large temporal and spatial scales in realistic applications. Individual vessel-to-vessel collision risk and vessel grounding risk are evaluated based on a spatial risk function over the region of safety domain violations. The overall risk is a combination of several collision and grounding candidate situations all faced at the same time for one or several interacting vessels.

2.1. Vessel Maneuverability

The vessel maneuverability measures the vessel’s ability of stopping, accelerating, varying its course and maintaining a desired trajectory. There are therefore various types of maneuvers a ship needs to execute to satisfy navigation safety conditions. The vessel stopping ability, for example, measures its capacity to stop within a certain distance (the track reach) when full engine astern is applied for a vessel sailing at its full test speed. The maneuverability aspects are therefore tested to ensure that the vessel can safely navigate under worst case scenarios. Full-scale tests are then used to evaluate the ship’s maneuvering performance, which must satisfy IMO standards [24] for ship maneuverability.

In full-scale trials, the test speed $V_{test}$ corresponds to at least 90% of the speed at 85% of the maximum engine output. At the test speed, the turning circle maneuver test measures the turning ability and it is performed with 35° rudder angle (or maximum permissible angle) to both starboard and port sides following a steady approach with zero yaw rate as demonstrated in Figure 3a.

In this trial, the turning ability is measured in terms of tactical diameter, advance (and maximum advance) and time to change heading 90 degrees and 180 degrees. In addition, the zig-zag test evaluates the ship performance for maintaining a trajectory and the full astern stopping test determines the track reach until a ship is stopped dead in the water after a full astern is given as depicted in Figure 3b.

According to IMO resolution MSC.137(76) [23], the advance ($A_D$) in a turning circle maneuver must not exceed 4.5 ship lengths (L) $A_D\le 4.5 \mathrm{L}$ and the track reach ($S_T$) should not exceed 15 ship lengths in a full astern stopping test $S_T\le 15 \mathrm{L}$ (20 ship lengths in other situations). The maneuverability aspects determine the ability of a vessel to avoid accidents, however, the maneuverability parameters are speed-dependent and need to be estimated for the prevailing navigation conditions which are different from those in the full-scale trials. The authors of Reference [25] derived a mathematical model to estimate the stopping ability of vessels fitted with a screw propulsion or a waterjet propulsion system. Assuming a straight contour track and a thrust changing linearly in time from forward thrust $T_F$ to aft-ward thrust $T_A$ during time $t_r$ to reverse the thrust, the motion equation for the displacement $\Delta$ for a vessel moving at speed $U$ is split into two parts: time since the full astern order is applied ($t=0$) until the time the thrust is fully reversed $\left(t=t_r\right)$ as given by Equation (1) and time after that, $t>t_r$, until the vessel is stopped dead-in-water as given in Equation (2). Hence from Reference [25] we have

$$\frac{\Delta \left(1+k_1\right)}{g}U\frac{dU}{ds}=-\left(T_A+T_F\right)\frac{t}{t_r}-R{\left(\frac{U}{U_0}\right)}^{2}for0<t\le t_r,$$

(1)

$$\frac{\Delta \left(1+k_1\right)}{g}U\frac{dU}{ds}=-T_A-R{\left(\frac{U}{U_0}\right)}^{2}fort>t_r,$$

(2)

where $k_1$ is the longitudinal added mass coefficient, $s$ is the travelled distance along the track and $g$ is the gravity acceleration. $R$ is the ahead vessel resistance at speed $U$ and $R_0$ is the resistance at approach speed $U_0$. Solving the previous equations, the track reach $S_T$ is presented as

$$S_T=\left[\frac{\Delta \left(1+k_1\right)U_0{}^2}{2g{R}_0}ln\left(1+\frac{R_0}{T_A}\right)\right]+0.5U_0{t}_r.$$

(3)

The authors of Reference [26] demonstrated that the track reach depends on the propeller diameter, vessel resistance coefficient, ratio of the astern to the ahead power, quasi-propulsive coefficient and many other parameters. Their results indicate that the track reach is within 4 to 16 ship lengths $L$ for different thrust reverse time $t_r$ and astern to ahead power ratio. In the same context, a free-running model is presented in Reference [27] for the estimation of full-scale stopping ability in which the experimental validation results are in accordance with those obtained by Reference [26].

2.2. Vessel Safety Domains

In a close quarter situation, actions taken by only one vessel will not be enough to avoid risk of collision. The safe passing distance hence depends on the approach rate and directions as well as the speed and maneuverability of both vessels. According to the type of encounter between two approaching vessels, four blocking areas are defined as safety regions that must not be violated by one another. The areas are modelled in Reference [28] as a combination of ellipses having the following radii

$$\{\begin{array}{l}{R}_f=\left(1+1.34\sqrt{k_{AD}{}^2+{\left(\frac{k_{DT}}{2}\right)}^2}\right)L\\ R_a=\left(1+0.67\sqrt{k_{AD}{}^2+{\left(\frac{k_{DT}}{2}\right)}^2}\right)L\\ R_s=\left(0.2+k_{DT}\right)L\\ R_p=\left(0.2+0.75k_{DT}\right)L\end{array},$$

(4)

where $R_f$ and $R_a$ are respectively the longitudinal radii in fore and aft directions; $R_s$ and $R_p$ are the lateral radii in starboard and port sides, respectively as shown in Figure 4. These parameters are estimated based on the vessel speed $V$ and the previously explained vessel maneuverability aspects of advance $A_D$ and tactical diameters $D_T$ as well as their respective gains $k_{AD}$ and $k_{DT}$ which are estimated according to the vessel’s speed over ground ($SOG$) as

$$\{\begin{array}{l}{k}_{AD}=\frac{A_D}{L}={10}^{0.3591{log}_{10}\left(SOG\right)+0.0952}\\ k_{DT}=\frac{D_T}{L}={10}^{0.5441{log}_{10}\left(SOG\right)-0.0795}\end{array}.$$

(5)

These dimensions are adopted by many researchers to identify close quarter situations and hence collision risk [29,30,31] based on a maneuverability-dependent safety domain.

Figure 4. Safety domains: (a) Blocking area versus fixed domains (b–e) with dimensions proposed by [32,33,34,35], respectively ((b–e) are reproduced respectively from [32,33,34,35] with permissions from Cambridge University Press 2009, Cambridge University Press 2013, Elsevier 2016, and Elsevier 2018, respectively).

Figure 4. Safety domains: (a) Blocking area versus fixed domains (b–e) with dimensions proposed by [32,33,34,35], respectively ((b–e) are reproduced respectively from [32,33,34,35] with permissions from Cambridge University Press 2009, Cambridge University Press 2013, Elsevier 2016, and Elsevier 2018, respectively).

It is worth mentioning that this type of domain combines the dimension, maneuverability and real speed-over-ground for each vessel. These extensions present a remarkable advantage over the conventional safety domains [32,33,34,35] which are only length-dependent as shown in Figure 5. The domains presented by References [32,34,35] correspond respectively to major axes of $10\mathrm{L}$, $20\mathrm{L}$ and $16\mathrm{L}$, such dimensions are inappropriate at low speed and those domains need to be adapted for particular situations and for practical applications [33].

2.3. Corrected Efficient Polygonal Domain

A statistical analysis of AIS data in Reference [36] has shown that around 10% of all normal safe situations were performed with a ship-ship passing distance of less than $2\mathrm{L}$. Considering only near collision situations, this rate is much higher. This implies that the fixed $10\mathrm{L}$, $20\mathrm{L}$ and $16\mathrm{L}$ ship domains are oversized, especially for large vessels and cases of low speed. In this work, a 5-vertices polygonal domain is proposed as demonstrated in Figure 5 for accurate approximation of blocking areas and for cost-efficient computations in regard of large area analysis and big AIS data.

To measure the collision and/or grounding risk associated with an individual close quarter situation, grounding and collision risk factors are added to the presented domain for each vessel through a special risk evaluation function as Figure 6 demonstrates.

Figure 6 also presents some comparisons with the quaternion domain [29] and an elliptic domain defined by the blocking area radii [28]. The detailed derivation and correction of the domain and the special risk functions are presented below. In the following, the index/subscript $i$ refers to any vessel at a particular time $t$, both indices are sometimes dropped for simplicity. The domain is defined for any vessel at a particular time though its maneuverability, speed over ground (SOG), course over ground (COG) angle in degrees in clockwise direction with respect to the north pole and {A, B, C, D, L = A + B} dimensions, (see Figure 5). Notice in Equation (4) that the vessel’s breadth is approximated by $0.4\mathrm{L}$, the domain size is $2\mathrm{L}\times 0.4\mathrm{L}$ at very low speed ($SOG\approx 0$) which it is not correct and position errors in data are not considered. First, the blocking area radii in Equation (4) are corrected in Equation (6) based on the accurate vessel dimensions (shown in Figure 5) so that the constructed domain applies with accuracy to low speed situations and tolerate inaccuracies of measured position as well. Compared to the traditional concepts of Figure 4, the proposed fore and aft direction radii of Equation (6) vary respectively in [A, 8 L] and [B, 4.23 L] for the whole range of practical speed [0, 40 knots]. This reflects that the mentioned theoretical proposals do not suit real applications, especially at low speed.

$$\{\begin{array}{l}{R}_{i,f}=A+\left(1.34\sqrt{k_{AD}{}^2+{\left(\frac{k_{DT}}{2}\right)}^2}\right)L+{\Delta }_{er}\\ R_{i,a}=B+\left(0.67\sqrt{k_{AD}{}^2+{\left(\frac{k_{DT}}{2}\right)}^2}\right)L+{\Delta }_{er}\\ R_{i,s}=C+\left(0.2+k_{DT}\right)L+{\Delta }_{er}\\ R_{i,p}=D+\left(0.2+0.75k_{DT}\right)L+{\Delta }_{er}\end{array},$$

(6)

where ${\Delta }_{er}$ is the combined error due to the limited resolution of GPS location accuracy and the precision of which format the AIS (longitude, latitude) location is transferred and stored: it is generally in the level of ${10}^{-4}$ in decimal degrees. This error is constant in time but its meters-equivalent (converted) value is varying according to the latitude

$${\Delta }_{er}=cos\left(Lat\right)\times 2\pi \times 6378137\times \frac{er}{360}.$$

(7)

As shown in Figure 5, the proposed vessel safety domain is characterized by its 5 dimensions

$$\{\begin{array}{l}{D}_1=0.9R_{i,s}\\ D_2=-0.9R_{i,p}\\ D_3=-0.9R_{i,a}\\ D_4=0.75R_{i,f}-0.25R_{i,a}\\ D_5=1.1R_{i,f}\end{array},$$

(8)

which makes a better approximation to the blocking areas [28] compared to the quaternion domain [29], as indicated in Figure 4. A vessel $i$ at time $t$ located at longitude $x=Lon$ and latitude $y=Lat$ sailing at speed $SOG$ and course $COG$ has a safety domain $P_i\left(t\right)$ defined by its five vertices (points)

$$P_i\left(t\right)\equiv \left\{P_{i,1}\left(t\right),P_{i,2}\left(t\right),P_{i,3}\left(t\right),P_{i,4}\left(t\right),P_{i,5}\left(t\right)\right\},$$

(9)

in which their $\left(x,y\right)$ coordinates are obtained as

$$\{\begin{array}{l}{P}_{i,1}=\left(p{1}_x,p{1}_y\right)\\ P_{i,2}=\left(p{2}_x,p{2}_y\right)\\ P_{i,3}=\left(p{3}_x,p{3}_y\right)\\ P_{i,4}=\left(p{4}_x,p{4}_y\right)\\ P_{i,5}=\left(p{5}_x,p{5}_y\right)\end{array},$$

(10)

such that

$$\left[\begin{array}{c}\begin{array}{cc}p{1}_x& p{1}_y\end{array}\\ \begin{array}{cc}p{2}_x& p{2}_y\end{array}\\ \begin{array}{cc}p{3}_x& p{3}_y\end{array}\\ \begin{array}{cc}p{4}_x& p{4}_y\end{array}\\ \begin{array}{cc}p{5}_x& p{5}_y\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{cc}{D}_1& D_3\end{array}\\ \begin{array}{cc}{D}_1& D_4\end{array}\\ \begin{array}{cc}0& D_5\end{array}\\ \begin{array}{cc}{D}_2& D_4\end{array}\\ \begin{array}{cc}{D}_2& D_3\end{array}\end{array}\right]\times \left[\begin{array}{cc}cos\left(COG\right)& sin\left(COG\right)\\ \\ -sin\left(COG\right)& cos\left(COG\right)\end{array}\right]+\left[\begin{array}{cc}{x}_i& yi\\ x_i& yi\\ x_i& yi\\ x_i& yi\\ x_i& y_i\end{array}\right]$$

(11)

Given a particular AIS data set, where $N$ vessels are present at the same time over a given location, there could be up to $\frac{N\left(N-1\right)}{2}$ vessel to vessel close quarter situations and $N$ vessels in grounding situations to be verified for safety domain violation. The key advantage of the proposed approach compared to the oversized domains and the considered uncertainties will be highlighted in the discussion of results from realistic data and application.

2.4. Risk Evaluation Functions

Instead of binary evaluation of risky and risk-free situations, the proposed vessel safety domain is further combined with a risk scoring function that scores the risky situations depending on the type of encounter (crossing, head-on, overtaking), amount of domain violation (intersection of two domains or domain with land shapes) and more importantly, how unsafe is the encounter as indicated in Figure 6. An exponential risk function is adopted which evaluates to a relative risk factor $r=1$ at the actual vessel region and decays exponentially to a relatively small risk factor $r_0=0.1$ at the borders of the vessel’s domain as illustrated in Figure 7. The risk functions are not symmetrical and decay at different rates in different directions. Risk functions are therefore tuned with the parameter $r_0$ (given in $\alpha$ in Equation (12)) and controlled with the four blocking area radii given by Equation (6) and shown in Figure 4a. Risk functions depend on the encounter type defined by positive or negative projections $\left(x_p,y_p\right)$ shown in Figure 5, Section 2.5 will introduce how to calculate the projections and how to evaluate the risk functions, this section only describes the selected longitudinal/lateral/spatial risk functions for collision/grounding at positive/negative sides. The so many combinations are reduced with the sign function.

Collision and grounding risk functions are then defined in longitudinal and lateral directions of the vessel as well as the overall spatial risk functions. The longitudinal collision risk function $C{R}_{Lon}\left(y_p\right)$ is defined through the parameter $\alpha$ as

$$\alpha ={\left(ln\left(\frac{1}{r_0}\right)\right)}^{\frac{1}{3}},$$

(12)

$$C{R}_{Lon}\left(y_p\right)=e^{-{\left(\frac{2y_p\alpha }{\left(1+sign\left(y_p\right)\right)R_{i,f}-\left(1-sign\left(y_p\right)\right)R_{i,a}}\right)}^3},$$

(13)

where $y_p$ is the projection on the longitudinal direction of the vessel track defined by its $COG$ and reference point as indicated in Figure 5 and $sign\left(x\right)$ is the sign function

$$sign\left(x\right)=\{\begin{array}{l}1ifx\ge 0\\ -1ifx<0\end{array},$$

(14)

Hence the longitudinal risk function $C{R}_{Lon}\left(y_p\right)$ of Equation (13) is asymmetrical, it will pass with fore radii $R_{i,f}$ in case of a front encounter $y_p\ge 0;$ and with the aft radii $R_{i,a}$ in case of an encounter from the back $y_p<0$. $R_{i,f}$ or $R_{i,a}$ is the parameter that controls the decaying rate of $C{R}_{Lon}\left(y_p\right)$.

$$C{R}_{Lon}\left(y_p\right)=e^{-{\left(\frac{y_p{\left(ln\left(\frac{1}{r_0}\right)\right)}^{\frac{1}{3}}}{R_{i,f}}\right)}^3}for{y}_p\ge 0;andC{R}_{Lon}\left(y_p\right)=e^{{\left(\frac{y_p{\left(ln\left(\frac{1}{r_0}\right)\right)}^{\frac{1}{3}}}{R_{i,a}}\right)}^3}for{y}_p<0.$$

(15)

Recall Figure 5 where $\left(x_p,y_p\right)$ are projections on the vessel track and $\left(x_p,y_p\right)=\left(0,0\right)$ is the reference point onboard the ship. The longitudinal risk function $C{R}_{Lon}\left(y_p\right)$ is shown in the top-left of Figure 7. The function evaluates to relative risk $r=1$ at the reference point and at the physical ship around $y_p\approx 0$ (due to the power ^3). The function decays at different rates in front of and behind the ship to a smaller risk factor $r_0=0.1$ at $y_p=R_{i,f}\approx 5 \mathrm{L}$ and at $y_p=-R_{i,a}\approx 3 \mathrm{L}$, respectively. Notice that $C{R}_{Lon}\left(2 \mathrm{L}\right)>0.8$ but $C{R}_{Lon}\left(-2 \mathrm{L}\right)<0.4$, this is logical because the same critical passing distance (e.g., $2 \mathrm{L}$) between a target ship and own ship implies more danger in case of front passing than in case of passing behind.

In the same manner, the lateral collision risk function is defined as

$$C{R}_{Lat}\left(x_p\right)=e^{-{\left(\frac{2x_p\alpha }{\left(1+sign\left(x_p\right)\right)R_{i,s}-\left(1-sign\left(x_p\right)\right)R_{i,p}}\right)}^3},$$

(16)

where $x_p$ is the lateral projection on the vessel track as shown in Figure 5. The spatial collision risk function for a vessel $i$ is then given over the defined domain as

$$\begin{array}{c}CR{s}_i\left(x_p,y_p\right)=C{R}_{Lon}\left(y_p\right)\times C{R}_{Lat}\left(x_p\right)\\ =e^{-\left({\left(\frac{2y_p\alpha }{\left(1+sign\left(y_p\right)\right)R_{i,f}-\left(1-sign\left(y_p\right)\right)R_{i,a}}\right)}^3+{\left(\frac{2x_p\alpha }{\left(1+sign\left(x_p\right)\right)R_{i,s}-\left(1-sign\left(x_p\right)\right)R_{i,p}}\right)}^3\right)}.\end{array}$$

(17)

The grounding risk function $G{R}_i\left(x_p,y_p\right)$ for the $i\mathrm{th}$ vessel is defined through the same manner of $CR{s}_i$, as depicted in Figure 8, in which the risk factor decays at the same rate in the forward direction but at twice the rate in the remaining three directions

$$GR{s}_i\left(x_p,y_p\right)=e^{-\left({\left(\frac{2y_p\alpha }{\left(1+sign\left(y_p\right)\right)R_{i,f}-2\left(1-sign\left(y_p\right)\right)R_{i,a}}\right)}^3+{\left(\frac{x_p\alpha }{\left(1+sign\left(x_p\right)\right)R_{i,s}-\left(1-sign\left(x_p\right)\right)R_{i,p}}\right)}^3\right)}.$$

(18)

The longitudinal, lateral and spatial risk functions for collision and grounding, respectively, are shown in Figure 7. Notice that the same vessel domain (Figure 5) and risk evaluation parameters Equation (6) are used for collision and grounding risk evaluation, however, with different spatial functions (Equations (16) and (17) and Figure 7). The main advantage here is to ensure memory-efficiency such that each AIS message in combination with vessel dimensions is mapped into 14 single-precision floating-point numbers (vertices’ x-y coordinates defined by Equation (11) and four parameters of Equation (6)).

2.5. Collision and Grounding Risk Evaluation

The collision risk (CR) in a vessel to vessel encounter situation is defined through the violation of the safety domains and the spatial collision risk functions of both vessels. Consider two vessels $i$ and $j$, the two vessels have different maneuverability, dimensions and SOG and therefore different safety domains $P_i\left(t\right)$ and $P_j\left(t\right)$ respectively. The close quarter situation is in different perspectives for the two vessels; First, the region in which the two domains intersect is defined as

$$C_{i\cap j}\left(t\right)=P_i\left(t\right)\cap P_j\left(t\right)=C_{j\cap i}\left(t\right).$$

(19)

This intersection zone can easily be obtained for the two 5-vertices polygonal shapes and this operation is computationally advantageous compared to elliptical domains. The resulting intersection region is also a polygonal shape in which the calculation of collision risk is feasible. The collision risk is non-zero if this region is not empty and the risk is evaluated as the integration of the multiplication of the two projected CR functions over the region of intersect

$$C{R}_{i,j}={∯}_{C_{i\cap j}}CR{s}_i\left(x_{pi},y_{pi}\right)\times CR{s}_j\left(x_{pj},y_{pj}\right)dxdy,$$

(20)

where $x_{pi}$, $x_{pj}$, $y_{pi}$ and $y_{pj}$ are the lateral and longitudinal projections on the tracks of vessel $i$ and $j$ respectively. This computation is not feasible and it is approximated based on the area $A{p}_{i,j}$ and the centroid $\left(Cx,Cy\right)$ of the intersection region $P_{i,j}$ (assumed small) as

$$\{\begin{array}{l}A{c}_{i,j}=Area\left(C_{i\cap j}\right)\\ \left(Cx,Cy\right)=Centroid\left(C_{i\cap j}\right)\end{array},$$

(21)

$$C{R}_{i,j}=C{R}_{j,i}=A{c}_{i,j}\times CR{s}_i\left(C{x}_{pi},C{y}_{pi}\right)\times CR{s}_j\left(C{x}_{pj},C{y}_{pj}\right),$$

(22)

where

$$\left[\begin{array}{c}C{x}_{pi}\\ C{y}_{pi}\end{array}\right]=\left[\begin{array}{cc}cos\left(CO{G}_i\right)& -sin\left(CO{G}_i\right)\\ sin\left(CO{G}_i\right)& cos\left(CO{G}_i\right)\end{array}\right]\left(\left[\begin{array}{c}Cx\\ Cy\end{array}\right]-\left[\begin{array}{c}{x}_i\\ y_i\end{array}\right]\right),$$

(23)

$$\left[\begin{array}{c}C{x}_{pj}\\ C{y}_{pj}\end{array}\right]=\left[\begin{array}{cc}cos\left(CO{G}_j\right)& -sin\left(CO{G}_j\right)\\ sin\left(CO{G}_j\right)& cos\left(CO{G}_j\right)\end{array}\right]\left(\left[\begin{array}{c}Cx\\ Cy\end{array}\right]-\left[\begin{array}{c}{x}_j\\ y_j\end{array}\right]\right).$$

(24)

The overall risk of immediate collision for a vessel $i$ is identified as the cumulative risk for multiple close quarter situations (see for example Figure 8) in which the vessel is involved, hence

$$C{R}_i={\sum }_{j}C{R}_{i,j},\forall js.t.C{R}_{i,j}>0,$$

(25)

The grounding risk of vessel $i$ is calculated based on the intersection of the vessel safety domain with land shapes represented by a possibly large set of shoreline polygons $\mathit{S}\mathit{P}$. This intersection would result in multiple nonempty grounding risk regions ${\mathit{G}}_{\mathit{i}}$

$${\mathit{G}}_{\mathit{i}}=P_i\left(t\right)\cap \mathit{S}\mathit{P}=\left\{G_{i,1},G_{i,2},\dots ,G_{i,n}\right\}.$$

(26)

The area and the centroid’s coordinates of the $k\mathrm{th}$ grounding risk region of the $i\mathrm{th}$ vessel are

$$\{\begin{array}{c}A{G}_{i,k}=Area\left(G_{i,k}\right)\\ \left(G{x}_{i,k},G{y}_{i,k}\right)=Centroid\left(G_{i,k}\right)\end{array}.$$

(27)

for $k=1,\dots ,n$. The grounding risk for the $i\mathrm{th}$ vessel is then evaluated as

$$G{R}_i={\sum }_{k=1}^{n}A{G}_{i,k}\times GR{s}_i\left(Gx{p}_{i,k},Gy{p}_{i,k}\right).$$

(28)

where $Gx{p}_{i,k}$ and $Gy{p}_{i,k}$ are respectively the projection of $k\mathrm{th}$ grounding-risky region on the track of the $i\mathrm{th}$ vessel

$$\left[\begin{array}{c}Gx{p}_{i,k}\\ Gy{p}_{i,k}\end{array}\right]=\left[\begin{array}{cc}cos\left(CO{G}_i\right)& -sin\left(CO{G}_i\right)\\ sin\left(CO{G}_i\right)& cos\left(CO{G}_i\right)\end{array}\right]\left(\left[\begin{array}{c}G{x}_{i,k}\\ G{y}_{i,k}\end{array}\right]-\left[\begin{array}{c}{x}_i\\ y_i\end{array}\right]\right).$$

(29)

The relative risk score of the immediate danger of a navigation accident (collision or grounding) for a certain navigation scenario depends on all the near risky situations and unsafe maneuvers, it is given as

$$R={\sum }_{i}C{R}_i+\beta G{R}_i,$$

(30)

where $\beta$ is a constant that can be set to specify the relative importance of collisions compared to grounding accidents. When the algorithm outlined above is applied to a large dataset of AIS data, it will identify and extract critical navigational scenarios based on the value of the risk score; situations with a high value will typically be navigationally complex and can be used to define risky navigational scenarios.

3. Applications and Discussion

The algorithms for identifying risky navigational situations outlined above have been applied to a large set of AIS data and have identified a number of challenging navigational situations accordingly. Some of the extracted situations will be described in the following examples.

3.1. Data Description and Set-up

The experimental validation data in this paper consists of two large sets of AIS data over a continuous full year as indicated in

Table 1. Description of raw $8.3\times {10}^7$ automatic identification system (AIS) data records for validation.

Time			Space	Vessels
Time Period	Resolution	Lo. Range	La. Range	Resolution	Length	Breadth	Number	Speed
03-Jan-2018 to 02-Jan-2019	0 to 270 sMAYDAYMedian = 225s	3.942°	2.5°	${10}^{-4}°$	15 m to 400 m	2 m to 61.9 m	17836	0 to 53.1
		1.072°	0.669°

.

AIS information from all vessels is interpolated and synchronized to 1 min in this work and all service vessels are ignored for risk identification. These include: Crew boats, pilot vessels, supply tenders, work and repair vessels, search and rescue vessels and salvage ships as well as mooring/towing/pushing/tugging vessels. These vessels are generally small and agile and are intended to perform their operations in contact with other bigger vessels so they are assumed neutral in this work.

Notice that, for simplicity, the time parameter $t$ was dropped in the previous risk functions as well as the actual collision, grounding and overall risk of each situation. In real applications, AIS data is first synchronized to similar time points at which the blocking area radii are updated as given by Equations (6) and (7) for each vessel ($i$) and their safety domains as in Equations (8)–(11) at each time $t$. All safety domain violations are then identified for all relevant vessel to vessel (Equation (19)) and vessel to ground (Equation (26)) combinations. Collision risk CR is determined through Equations (21)–(25) and similarly the grounding risk (Equations (27)–(29)) and the situation risk by Equation (30).

The AIS data is interpolated and synchronized in this work to 1 min intervals

$$z_i\left(t\right)=z_i\left(t_o\right)+\left(z_i\left(t_f\right)-z_i\left(t_o\right)\right)\frac{t-t_o}{t_f-t_o},$$

(31)

for $t=0,1,2,\cdots$, where $t_o$ is the most recent time vessel $i$ sent AIS records before $t$ and $t_f$ is the first time after that. This equation applies to all dynamic navigation parameters in which $z_i$ stands for either of { $Lo{n}_i$, $La{t}_i$, $SO{G}_i$, $CO{G}_i$} for each vessel $i$. Information about the vessel, such as its type and actual dimensions, are obtained from vessel registry. High-resolution digital maps are also used in the identification of grounding risk.

3.2. Obtained Results and Discussion

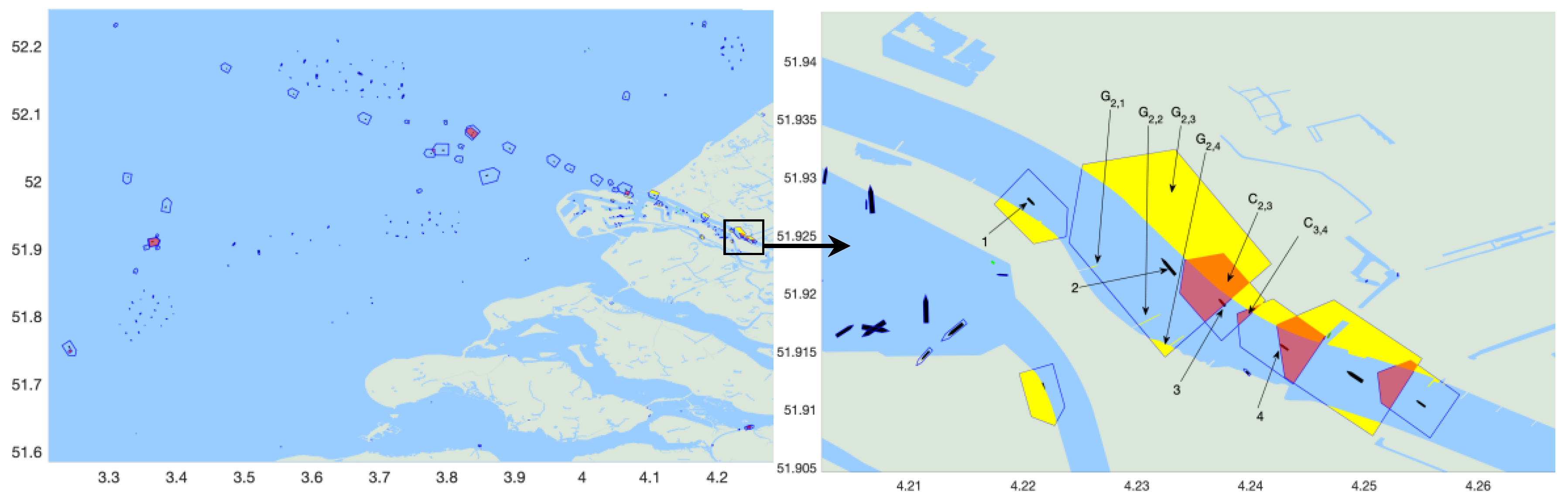
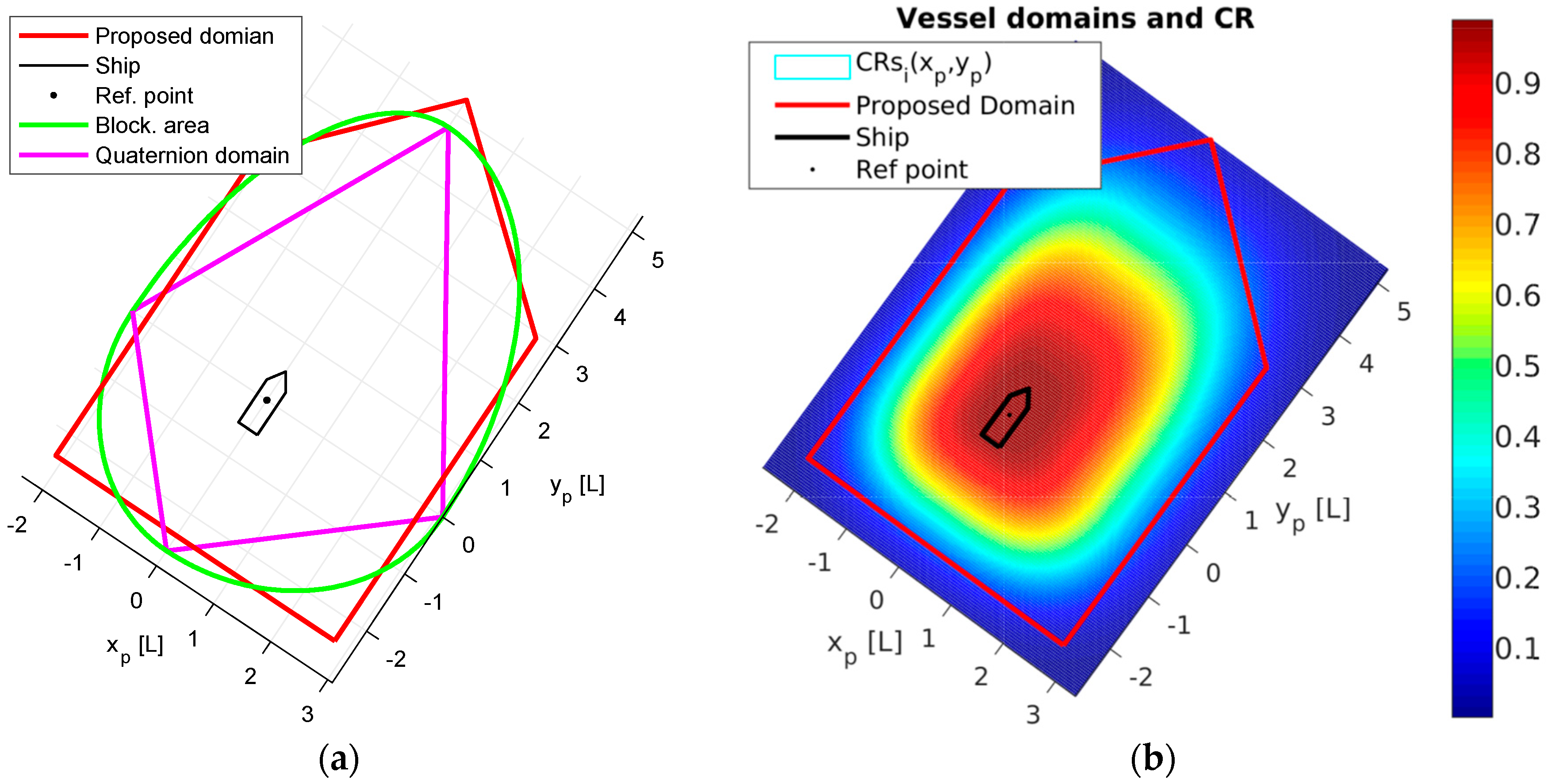
A navigation risk example is demonstrated in Figure 8 in which all vessels are indicated in black surface, their safety domains in blue lines, collision regions in red and grounding regions in yellow. The vessel domain is updated based on the vessel length and maneuverability depending on its speed for which static vessels have a small domain that accounts only for GPS inaccuracy and imprecision, this is a remarkable advantage compared to theoretical fixed L-dependent domains of Figure 4 which are oversized. Since moored vessels usually transmit inaccurate $COG$ records, they are ignored for grounding risk identification without the loss of generality. In this illustration example, vessel 2 encounters four grounding obstacles that need to be avoided ${\mathit{G}}_{\mathbf{2}}=\left\{G_{2,1},G_{2,2},G_{2,3},G_{2,4}\right\}$ and vessel 3 is navigating under two potential collision candidates $C_{2\cap 3}$ and $C_{3\cap 2}$ Figure 8 reflects some types of position uncertainties which have been introduced in Section 2.3 as well as unreliable COG for moored vessels and negligible interpolation errors. Indeed, introducing time to Figure 8 and verifying the situation over a few successive instances reflects many vessels were just about one minute to collision for many times.

In the next timestamp (after one minute), vessels 1 and 2 will be in a close quarter situation of head on collision and both vessels must alter their course to starboard side according to COLREG rule 14 to avoid accident. This cannot be achieved easily since both vessels are in risk of grounding on their starboard side and both vessels must proceed carefully at safe speed to avoid collision or grounding. Vessel 3 on the other hands cannot overtake vessel 2 on the right side due to limited maneuvering area and the danger of grounding for which it must decrease its speed. However, vessel 3 in this case will impede the route of vessel 4, this action is not allowed by COLREG rule 13. Hence, this situation is navigationally complex and associated with considerable navigational risk and can be identified from a large set of AIS data.

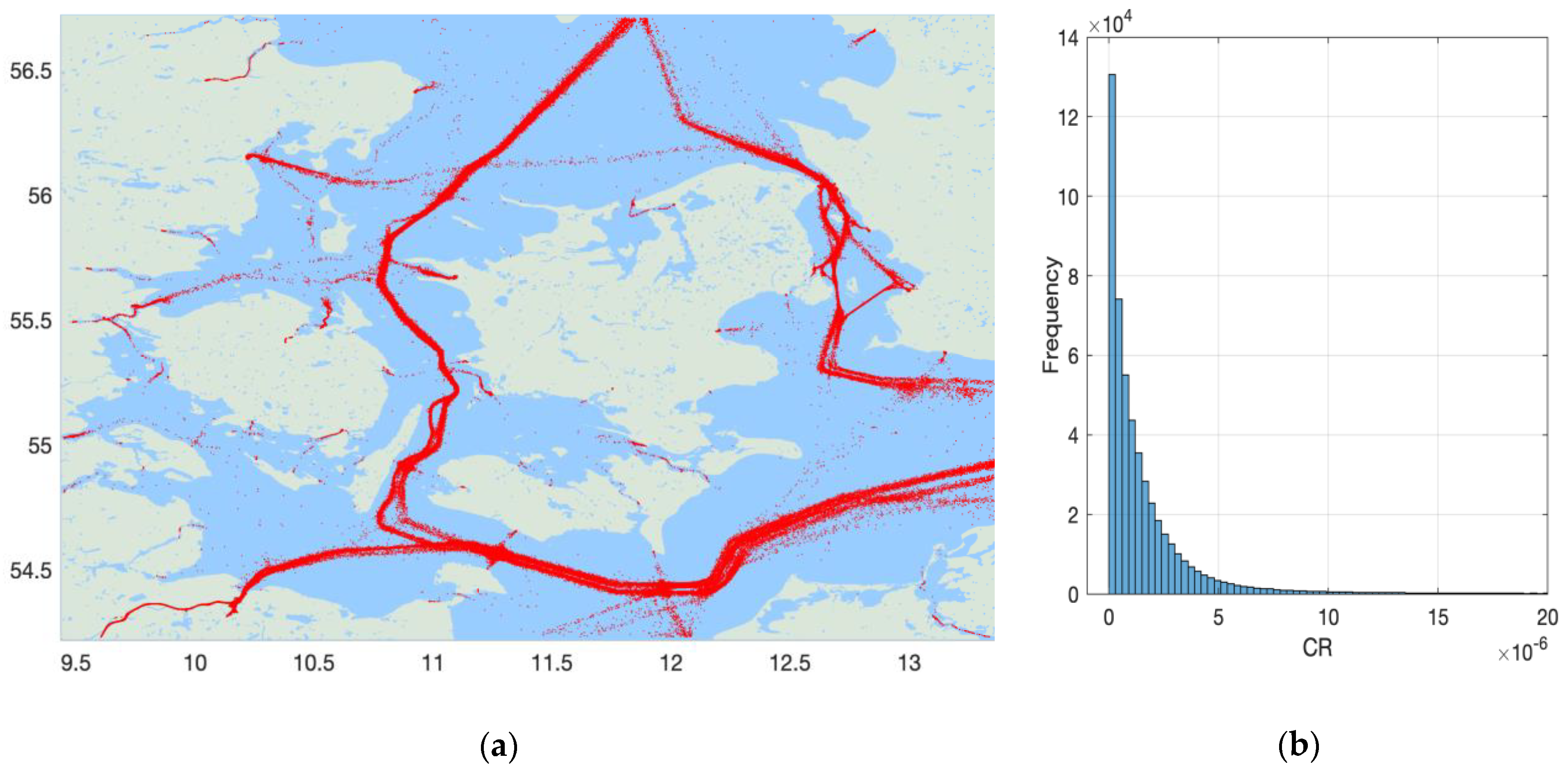
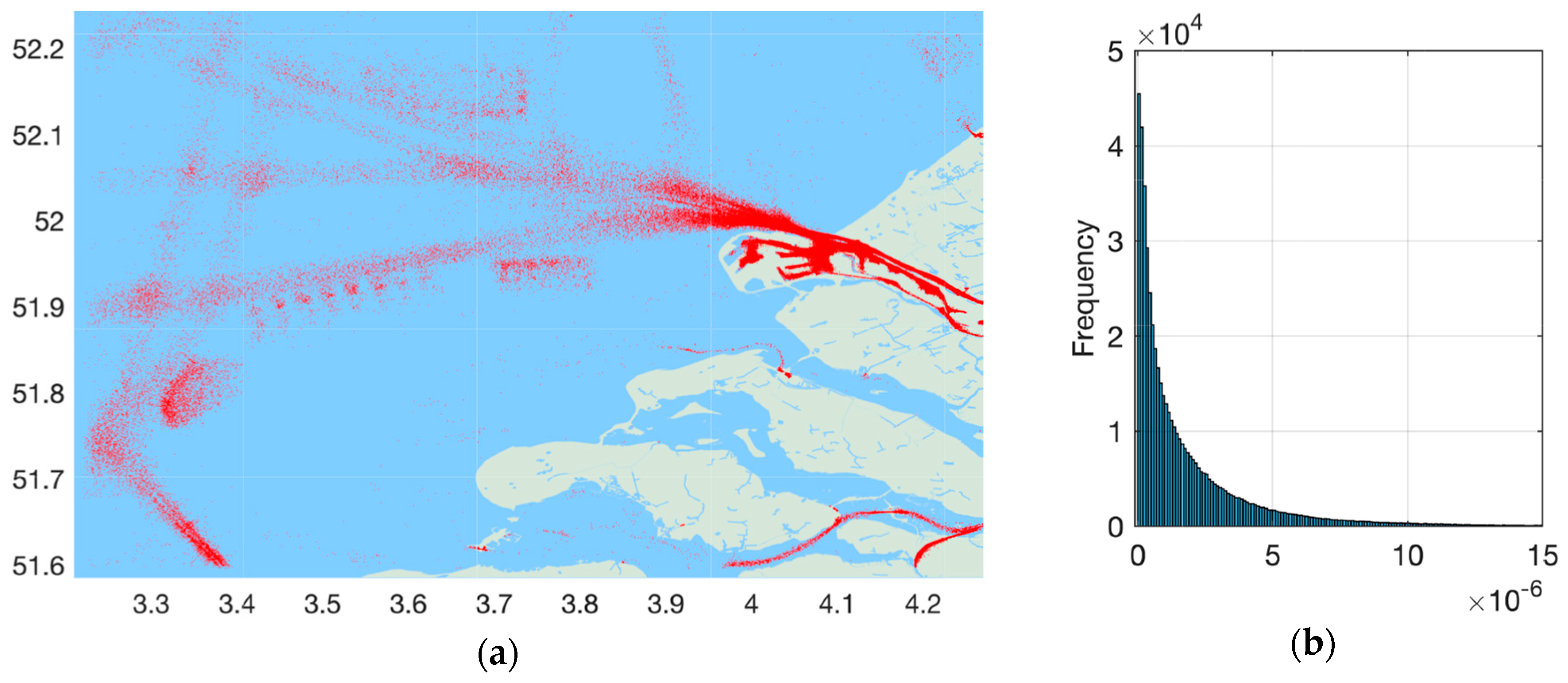
Given the one-year AIS data for the two sample areas described in Table 1, results of all the identified risky situations are demonstrated in Figure 9, Figure 10 and Figure 11. Figure 9a and Figure 10a describe the spatial locations of the identified vessel to vessel collision risks for two different areas and their respective risk distributions are demonstrated in Figure 9b and Figure 10b. Variations of both collision and grounding risk over the two areas are both shown in Figure 11 for the year 2018.

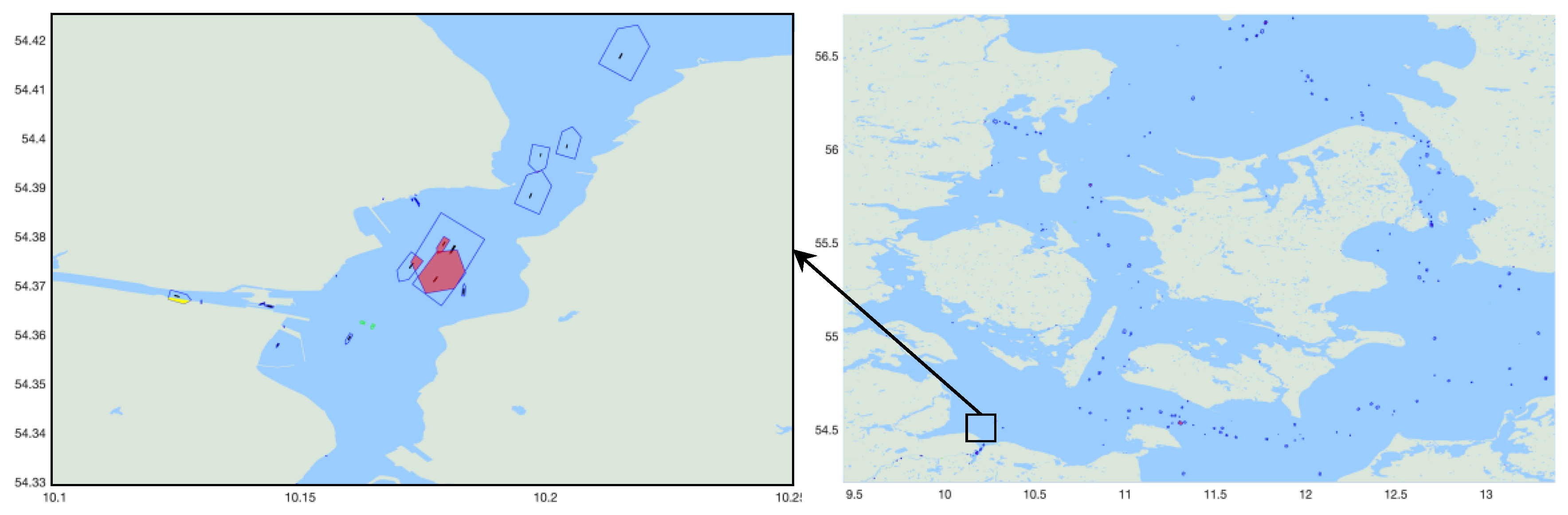
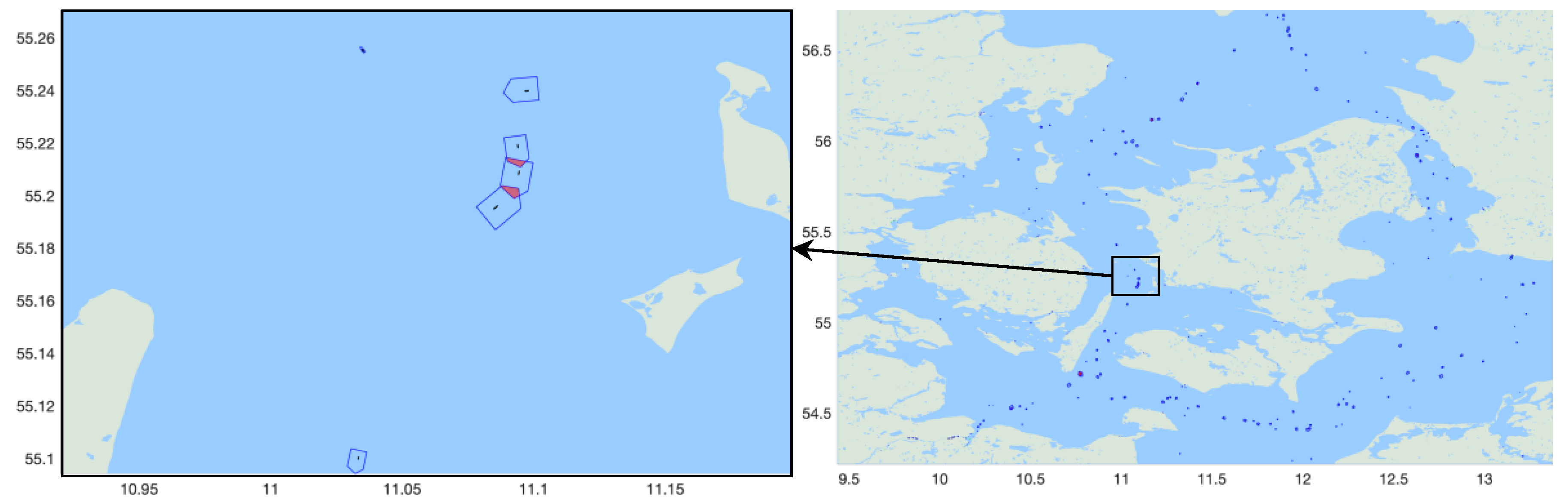
Examples of some risky situations are also illustrated in Figure 12, Figure 13 and Figure 14. Figure 12 represent a collision-risky situation due to a combination of conflicting overtaking and head-on encounter COLREG rules, the largest vessel is involved in three possible collision situations in which the avoidance of head-on collision (alter course to starboard according to rule 14) would result in a collision with the other two vessels for which this vessel must not impede their routes. This situation can be solved if all the vessels keep their track and speed except the vessel moving northward that must take actions alone to avoid collision. These actions highly depend on its maneuverability. Figure 13 also describes another situation involving a combination of head on, overtaking and grounding where the avoidance of one accident may result in another accident.

A combination of conflicting navigation maneuvers (crossing and overtaking) is demonstrated in Figure 14 in which one vessel is in immediate danger of collision with a crossing vessel and an overtaking vessel. This vessel must give way to the vessel crossing on its starboard side according to COLREG rule 15, the later vessel has right of way and is in stand-on maneuver but may take action to avoid collision (rule 17). The first vessel must take substantial action (rule 16) and must not pass in from of the crossing vessel, however, this may result in collision with the overtaking vessel (rule 13).

4. Conclusions

A practical method was presented in this article for the automatic identification of maritime navigation risk in realistic and large-scale applications. The proposed solution has paramount advantages in terms of effectiveness and computational efficiency and plays a crucial role as a warning input for smart navigation and decision support tools as well as in remote control and autonomous navigation technologies. Individual grounding and collision risks were evaluated through an accurate adaptive vessel safety domain that considers the actual navigation parameters as well as vessel dimensions and maneuverability. This approach is based on a correction of blocking area radii in which close quarter situations are addressed through a five-vertices polygonal safety domain. Depending on the type of encounter and danger of collision and/or grounding situations, individual risk was evaluated through a spatial risk function. In this paper, real navigational risk is identified through the combination of multiple candidates of groundings and collisions for a set of interacting vessels over any area and period of time.

The overall method is fast and computation-efficient and exhibits a remarkable possibility to address large-scale navigation monitoring and risk identification. The presented algorithm is supported by a thorough analysis of two large sets of AIS data, each spans one year and covers a large geographical area and are combined with vessel registry and high-resolution digital maps. In addition to high efficiency, the obtained results demonstrate potential applications and illustrate the reliability of the developed methods to identify accurately various aspects of navigation risk. The presented procedure also supports significant future extensions to non-immediate navigation risk identification and prediction to determine safe situations that my cause navigation risk in a while. Another important feature that may be investigated in the future is a deeper analysis of complexity in navigation scenarios regarding COLREGs and special rules while considering weather conditions, visibility, wind, sea state, water depth and tides.

The main limitation of the presented work is in fact a data limitation with the utilization of AIS data only, which limits the applications to decision support rather than the basic tool for collision avoidance. However, the main advantages of the algorithm are its effectiveness and computation-efficiency to analyze big amounts of data for anti-collision support over a large area in a finite time and resources. The algorithm can easily integrate with other navigational systems and access data from more sources for enhanced performance.