Non-Hydrostatic Modeling of Waves Generated by Landslides with Different Mobility
Abstract
1. Introduction
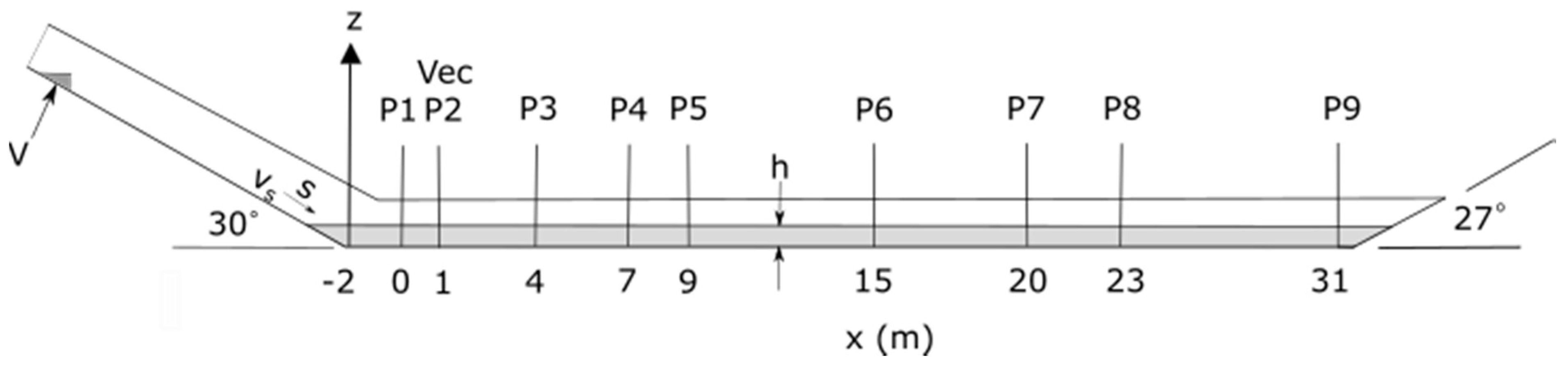
2. Laboratory Experiments
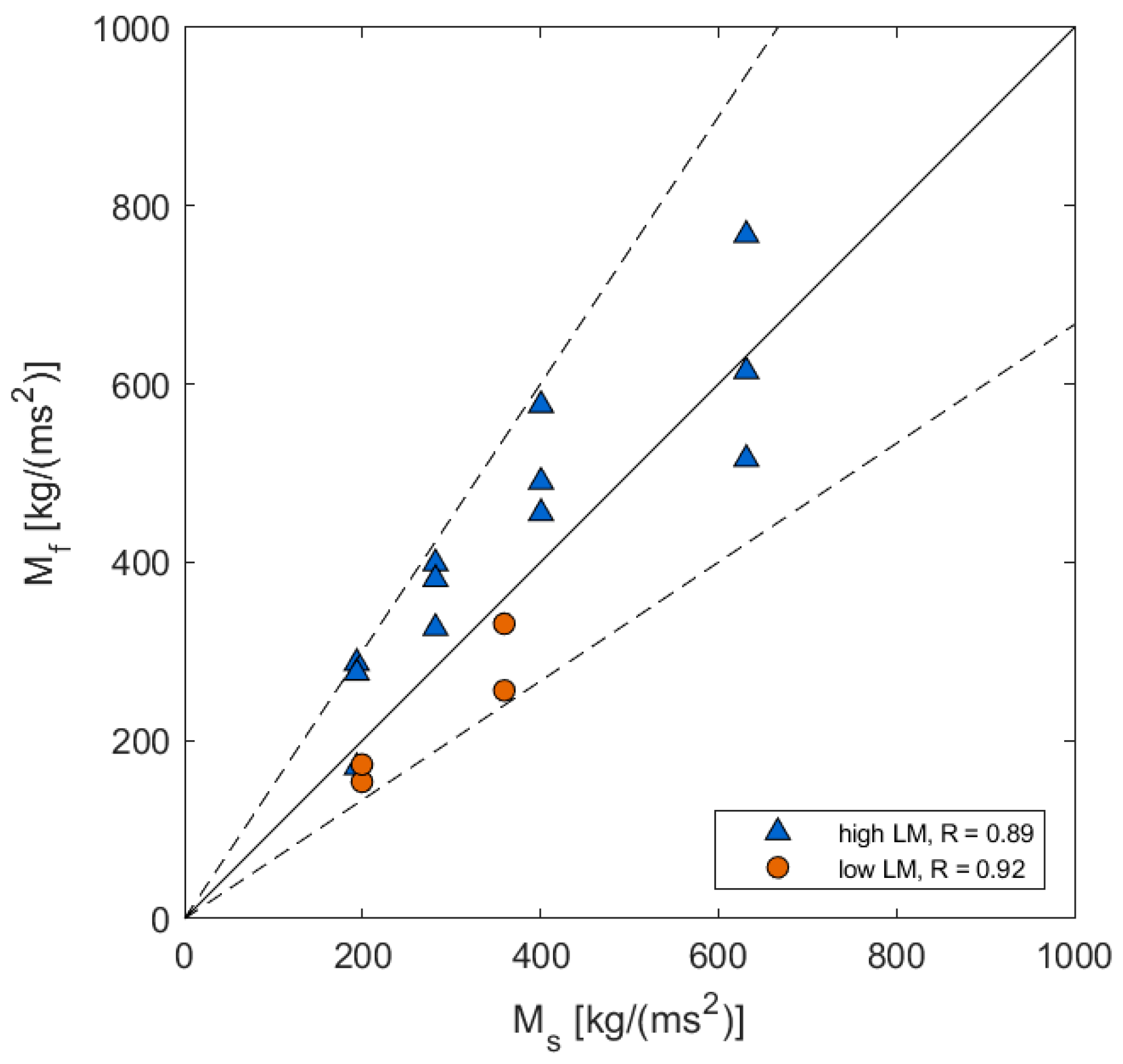
3. Theoretical Momentum Balance
4. Numerical Modelling
4.1. Model Set-up
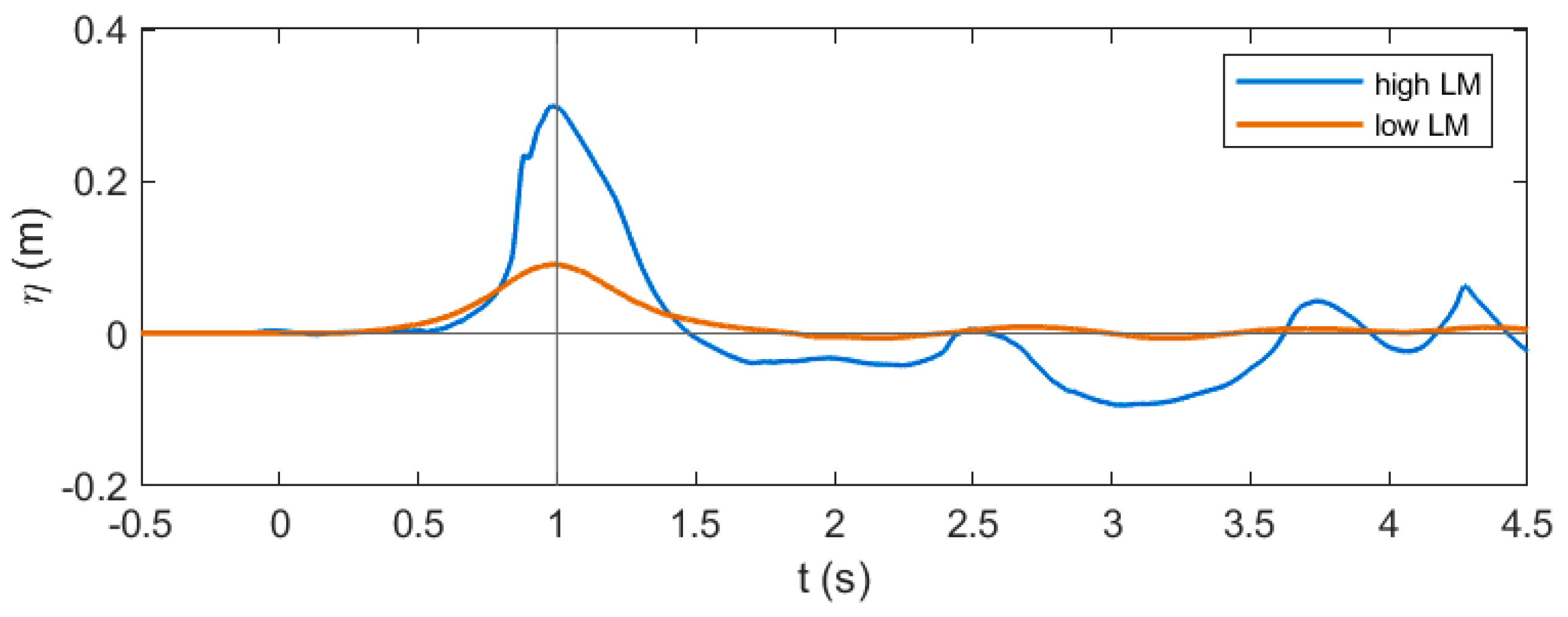
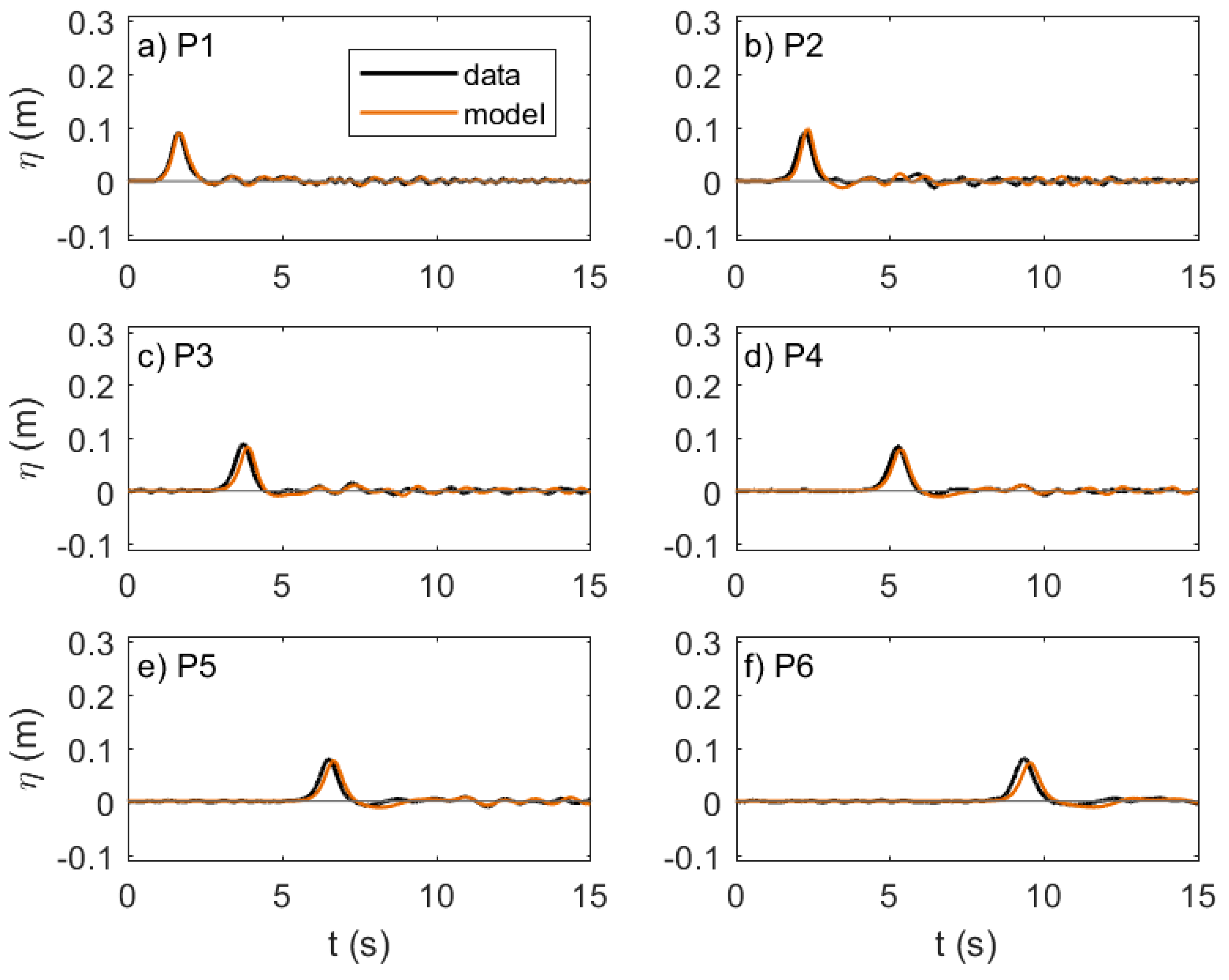
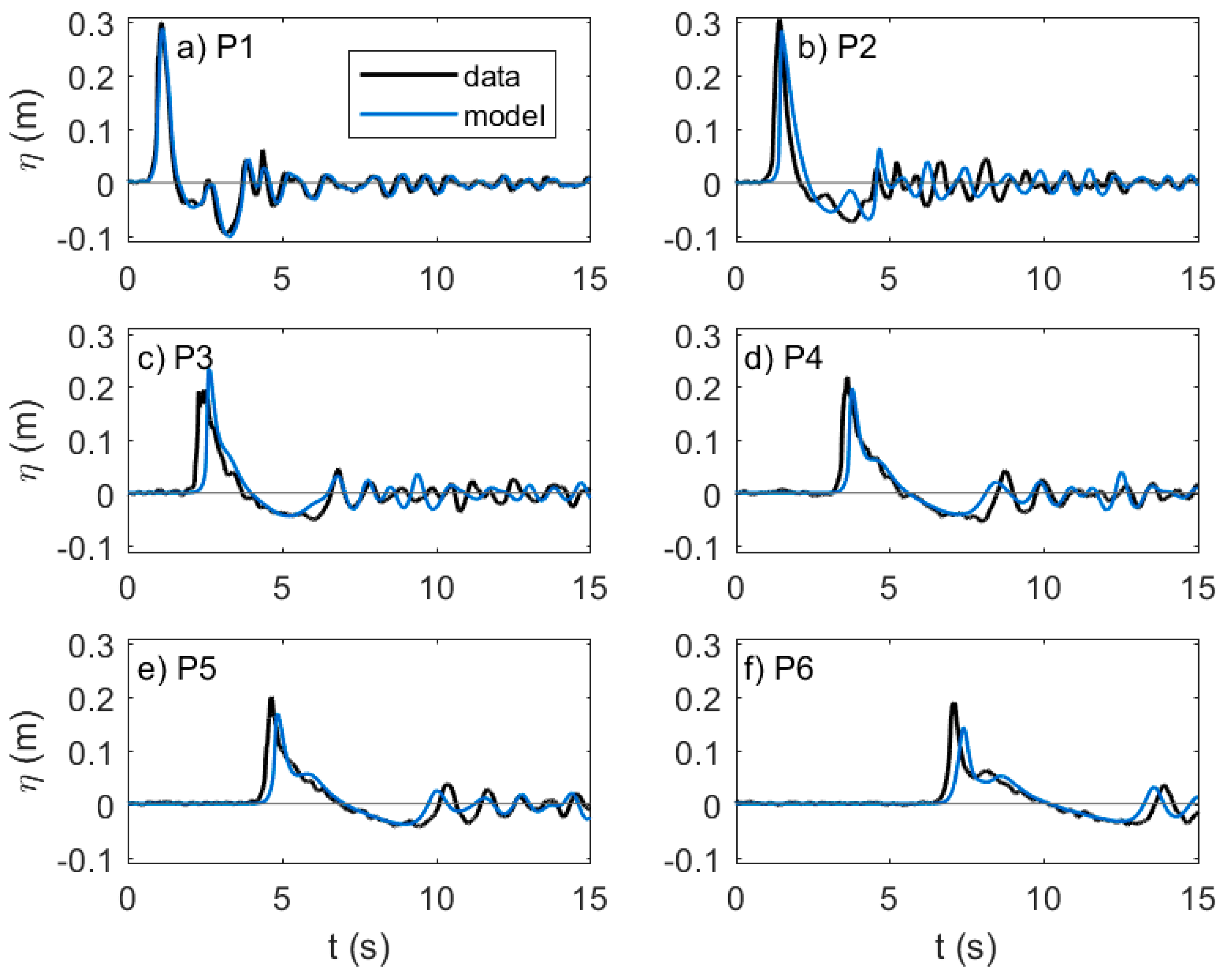
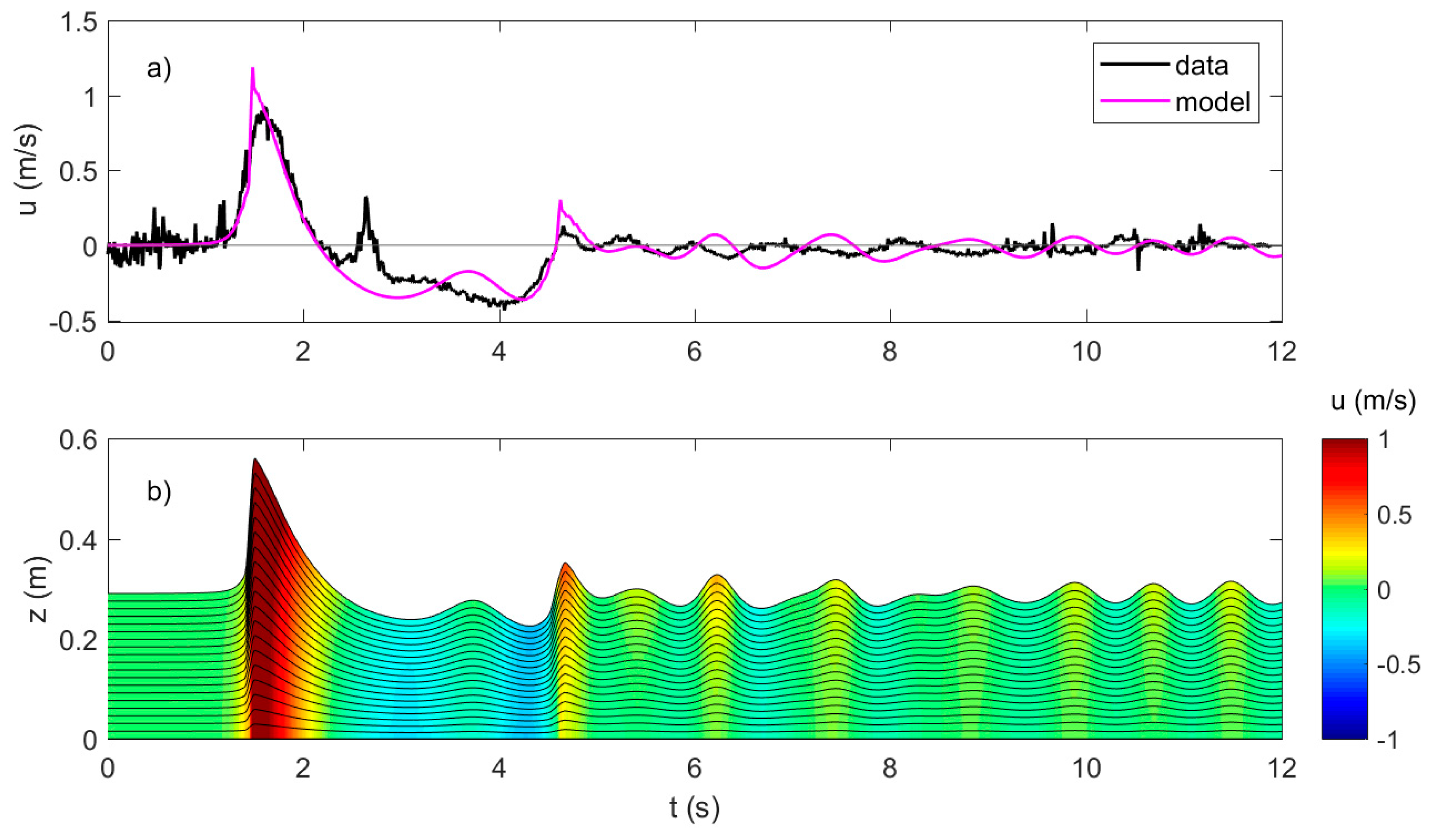
4.2. Model Results
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Legros, F. The mobility of long-runout landslides. Eng. Geol. 2002, 63, 301–331. [Google Scholar] [CrossRef]
- Mulligan, R.P.; Take, W.A. On the transfer of momentum from a granular landslide to a water wave. Coast. Eng. 2017, 125, 16–22. [Google Scholar] [CrossRef]
- Tanioka, Y.; Satake, K. Tsunami generation by horizontal displacement of ocean bottom. Geophys. Res. Lett. 1996, 23, 861–864. [Google Scholar] [CrossRef]
- Fujiwara, T.; Kodaira, S.; No, T.; Kaiho, Y.; Takahashi, N.; Kaneda, Y. The 2011 Tohoku-Oki earthquake: Displacement reaching the trench axis. Science 2011, 334, 1240. [Google Scholar] [CrossRef] [PubMed]
- Zweifel, A.; Hager, W.H.; Minor, H.-E. Plane impulse waves in reservoirs. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 358–368. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Wave types of landslide generated impulse waves. Ocean Eng. 2011, 38, 630–640. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.E. Near field characteristics of landslide generated impulse waves. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Nik-Khah, A. Impulsive waves caused by subaerial landslides. Environ. Fluid Mech. 2008, 8, 263–280. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S.; et al. Landslide mobility and hazards: Implications of the 2014 Oso disaster. Earth Planet. Sci. Lett. 2015, 412, 197–208. [Google Scholar] [CrossRef]
- Zitti, G.; Ancey, C.; Postacchini, M.; Brocchini, M. Impulse waves generated by snow avalanches falling into lakes. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- Lindstrøm, E.K. Waves generated by subaerial slides with various porosities. Coast. Eng. 2016, 116, 170–179. [Google Scholar] [CrossRef]
- Miller, G.S.; Take, W.A.; Mulligan, R.P. Tsunamis generated by long and thin granular landslides in a large flume. J. Geophys. Res. Oceans 2017, 122, 653–668. [Google Scholar] [CrossRef]
- Bullard, G.K. Wave Characteristics of Tsunamis Generated by Landslides of Varying Size and Mobility. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2018; 145p. [Google Scholar]
- Bullard, G.K.; Mulligan, R.P.; Take, W.A. An enhanced framework to quantify the shape of impulse waves using asymmetry. J. Geophys. Res. Oceans 2019, 124. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P.B. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Rijnsdorp, D.P.; Smit, P.B.; Zijlema, M. Non-hydrostatic modelling of infragravity waves under laboratory conditions. Coast. Eng. 2014, 85, 30–42. [Google Scholar] [CrossRef]
- Gomes, E.R.; Mulligan, R.P.; Brodie, K.L.; McNinch, J.E. Bathymetric control on the spatial distribution of wave breaking in the surf zone of a natural beach. Coast. Eng. 2016, 116, 180–194. [Google Scholar] [CrossRef]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Smit, P.; Janssen, T.; Holthuijsen, L.; Smith, J. Non-hydrostatic modeling of surf zone wave dynamics. Coast. Eng. 2014, 83, 36–48. [Google Scholar] [CrossRef]
- Mulligan, R.P.; Take, W.A.; Miller, G.S. Propagation and runup of tsunamis generated by gravitationally accelerated granular landslides. In Proceedings of the Coastlab16, Ottawa, ON, Canada, 10–13 May 2016. [Google Scholar]

| Mobility | V (m3) | s (m) | h (m) | am (m) | ||
|---|---|---|---|---|---|---|
| low LM (granular) | 1400 | 0.34 | 4.00 | 0.040 | 0.30 | 0.09 |
| high LM (water) | 1000 | 0.30 | 5.38 | 0.043 | 0.31 | 0.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulligan, R.P.; Take, W.A.; Bullard, G.K. Non-Hydrostatic Modeling of Waves Generated by Landslides with Different Mobility. J. Mar. Sci. Eng. 2019, 7, 266. https://doi.org/10.3390/jmse7080266
Mulligan RP, Take WA, Bullard GK. Non-Hydrostatic Modeling of Waves Generated by Landslides with Different Mobility. Journal of Marine Science and Engineering. 2019; 7(8):266. https://doi.org/10.3390/jmse7080266
Chicago/Turabian StyleMulligan, Ryan P., W. Andy Take, and Gemma K. Bullard. 2019. "Non-Hydrostatic Modeling of Waves Generated by Landslides with Different Mobility" Journal of Marine Science and Engineering 7, no. 8: 266. https://doi.org/10.3390/jmse7080266
APA StyleMulligan, R. P., Take, W. A., & Bullard, G. K. (2019). Non-Hydrostatic Modeling of Waves Generated by Landslides with Different Mobility. Journal of Marine Science and Engineering, 7(8), 266. https://doi.org/10.3390/jmse7080266





