A Fuzzy-Based Decision-Making Model for Improving the Carrying Capacity of Ship Locks: A Three Gorges Dam Case

Abstract

This paper develops a decision-making model to assist the improvement of the carrying capacity of ship locks by combing fuzzy logic, the analytic hierarchy process (AHP) method, and the technique for order preference by similarity to an ideal solution (TOPSIS). A three-level hierarchical structure is constructed to identify the key factors influencing the carrying capacity of ship locks from the aspects of ship locks, vessels, environment, and administration. On this basis, a series of targeted strategies have been put forward to improve the carrying capacity of ship locks, and the TOPSIS method is applied to rank these strategies in terms of their performance. A case study of the five-stage dual-track ship lock of the Three Gorges Dam in China has been conducted to demonstrate the feasibility and rationality of the proposed model, and correlation analysis is conducted to verify the identified influencing factors in order to eliminate potential bias which may be generated from using AHP. The results obtained from the proposed methods are consistent with the real-life situation to a certain extent, indicating that the proposed method can provide a useful reference for improving the carrying capacity of ship locks.

1. Introduction

Maritime transportation is at the core of international trade due to its outstanding advantages compared to other transport modes, accounting for around 80% of the volume of goods transported around the globe, and this share is estimated to be even higher for most developing countries [1]. As shown in Figure 1, global containerized trade continued to expand after 2009, and reached an expansion rate of nearly 5% in 2017, with volumes attaining an estimated 145 million 20-foot equivalent units (TEUs) [2].

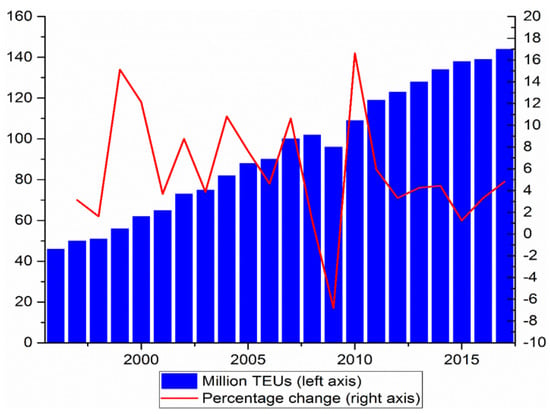
Figure 1. Global containerized trade in recent two decades (Millions TEUs and annual percentage change). Sources: By author based on the data from the Review of Maritime Transport 2017.

In response to the rapid development of maritime transportation, a series of studies have been conducted to develop innovative models in order to improve the effectiveness of maritime transportation, including berth planning [3,4,5,6,7] and vessel scheduling [8,9], to name but a few. As an important complement to the global maritime transportation system, inland waterway transportation provides a crucial linkage between domestic and international shipping markets, and the boom of inland shipping in recent years further highlights the strategic position of inland waterways such as the Yangtze River—the longest inland river in China [10].

The Three Gorges hydro-junction is located at the Xiling Gorge section of the Three Gorges. It is a key backbone for using the waterway resource of the Yangtze River, which plays an important role in promoting the circulation of nationwide cargos as well as the development of the regional economy [11]. However, the constantly increasing gap between the limited carrying capacity of the Three Gorges Ship Locks and the vigorous transportation demand of ships passing through it is becoming increasingly prominent. Many vessels detained in the lock areas, putting great pressure on the operational management of ship locks. On the other hand, the crowed ships in the lock areas also increase the safety and security risks [12]. Therefore, it is both significant and urgent to solve the problem of ship detention in ship locks. In view of this, this study identifies the factors that influence the carrying capacity of ship locks and the measures their weights according to their impact levels. Some countermeasures are developed to improve the carrying capacity of ship locks, and they are ranked with respect to their effects on the control of each influencing factors. The contributions of this study are two-fold. Firstly, analyzing the reasons for ship detention in ship lock areas is helpful for administrative officers on actively responding to similar situations. Secondly, the proposed countermeasures, as well as the flexible approaches presented in this paper, can be tailored and used to achieve congestion risk reduction in other ship locks to improve the transportation safety and efficiency [13,14].

The rest of this paper is organized as follows. Section 2 reviews the previous studies conducted on carrying capacity improvement of ship locks, and the research related to multiple-criteria decision-making (MCDM) problems to disclose the advantages and explore the applicability of the hybrid method in this study. Section 3 describes the research steps and proposed methods to select suitable countermeasures for ship lock carrying capacity improvement. The feasibility of the proposed approach method is analyzed using a real case study of the ship locks in Three Gorges Dam in Section 4. The findings are discussed in Section 5, and this paper is concluded in Section 6.

2. Literature Review

In this section, the previous studies relating to the carrying capacity of ship locks are reviewed, followed by the introduction of the features and applications of the TOPSIS method.

2.1. Safety and Carrying Capacity of Ship Locks

There were some early studies on guaranteeing the operational safety of ship locks and the emergency response schemes to unexpected incidents, which have been done in Germany, Austria, and other countries in Europe. In Germany, navigational accidents were classified into three categories, namely general, abnormal, and important ones according to the different risk levels. The labors assigned to each type of accident were different according to different accident levels [15]. Normally, two sets of emergency plans would be set, which were internal and external emergency plans, aiming at addressing different aspects of accidents [16]. Taking the safety management of ship locks as an example, external emergency specified tasks such as the rescue measures, the rescue of the persons in charge of the accident, and the communication with rescuers. Meanwhile, the internal emergency plans were mainly used to guide the escape of staff of the ship once an accident occurs [17]. In Austria, management departments keep track of the operational risk status of ship locks and conduct early-warning analysis and risk assessment regularly. Advanced scientific and technological approaches were adopted to adjust emergency response measures according to the actual situation, and targeted measures are taken to reduce operational risks of ship locks [18]. There was also some research related to the safety of the ship locks of the Three Gorges Dam. However, most the current research only put forward some countermeasures to enlarge the carrying capacity of the Three Gorges ship locks in a general level, without assessing the usefulness of different countermeasure, let along the quantitative evaluations [19].

Regarding the carrying capacity of ship locks, two main branches of research can be concluded in previous studies. One branch focused on the operational condition of ship locks and measures the carrying capacity of ship locks by using the calculation model from a macroscopic perspective. They were referred to as quantity-oriented research branch. Whereas, another branch paid more attention to the service quality of ship lock operations. They try to develop the simulation model of ships going through ship locks by using operational data of ship locks, and thus they were regarded as quality-oriented research branch.

In quantity-oriented research, comprehensive influencing factors were generalized to facilitate the calculation of ship lock carrying capacity [20]. The average daily number of times that ships went through ship locks was used to characterize the technical factors and the average lockage tonnage was used to characterize the ship types and their navigating behaviors. Then, the ideal carrying capacity could be calculated as the sum of the product of the average lockage number and the average lockage tonnage. The quality-oriented research emphasized on the service quality of ship locks. In their research, the ship locks were innovatively regarded as one or more service windows, and the whole system was viewed as a queuing system. The waiting time of ships for lockage could then be predicted by using queuing models. In recent years, some researchers realized that the two research branches should not be isolated. On the contrary, both the actual operating conditions of the ship locks and the associated service quality should be considered together from a systematic perspective, taking into account the interests of different stakeholders such as shipping companies and transport management authorities [21,22,23].

2.2. Multiple-Criteria Decision-Making Methods

MCDM plays a critical role in practice, as this kind of problems are frequently encountered in almost every aspect of real life. MCDM methods can be defined as structured frameworks that deal with the process of making decisions in the presence of multiple objectives. They are the methods that used to find the best opinion from all the feasible alternatives in the presence of multiple, usually conflicting, decision criteria. Various methods have been developed to solve MCDM problems, such as analytic hierarchy process (AHP), Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), and Elimination Et Choice Translating Reality (ELECTRE), to name but a few.

TOPSIS has been applied in various fields including the risk management of waterway congestion, maritime risk analysis [24], and evaluation of supply chain performance [25]. With respect to its application related to the inland waterway transportation, Wan [26] proposed a set of risk control options according to the current development of the Yangtze River and comparatively analyzed the performance of each risk control option under different cost-benefit ratios in order to choose the best one. In the research of [27], an entropy-TOPSIS method is applied to select the railway express freight train service sites and group them into different classes.

In this study, the TOPSIS method is applied to assist the selection of the most suitable carrying capacity improvement (CCI) countermeasures of ship locks due to the following reasons [28]. Firstly, differing from AHP or simple weighted sum methods, TOPSIS prioritize the selections considering two distances. This could be, for instance, the case when the decision-makers seek not only for the maximum effectiveness of carrying capacity improvement of ship locks but above all for the minimum cost to achieve the goal. Secondly, the method is intuitive, as well as easy to be applied in practice. It can also reduce the effect of the decision maker’s subjective point of view. This important to an industrial implementation by ship lock management authorities. Thirdly, it can manage each kind of variables and each type of criteria, to address the rank reversal issue.

Taking all the above into consideration, the limitations of the current research are obvious. Firstly, there are quite a few studies considering the features of traffic flows when analyzing the factors influencing the carrying capacity of ship locks. Besides, there is a lack of quantitative analysis when identifying key factors influencing the carrying capacity of ship locks and proposing relevant countermeasures. Therefore, based one statistical analysis methods, both the identification of key factors and the proposition of CCI schemes are achieved in this study, and the performance of CCI schemes are further evaluated to ensure their effectiveness.

3. Methodology

3.1. Research Framework

In view of the present situation and common problems faced by ship locks, the ship traffic flow characteristics of ship locks are analyzed, especially the characteristics of inland ship traffic flow between ship locks. Moreover, the factors affecting the carrying capacity of the ship locks are systematically studied in a quantitative way. Finally, a real-world case of the Three Gorges Dam is conducted to illustrate the capability of the proposed model. The main steps developed to support the selection of CCI countermeasures are described as below:

Step 1: Identification of the key factors influencing the carrying capacity of ship locks

A hierarchical model will be developed to identify the possible factors that affect the carrying capacity of ship locks. Based on that, historical operational data and expert opinions will be collected to investigate the factors that influence most the working status of ship locks by using a fuzzy-AHP judgment matrix. The weight of each factor within each level will be calculated level by level, and then the global weight of every factor can be obtained.

Step 2: Proposition of CCI countermeasures

According to the identified key influencing factors, some countermeasures for improving the carrying capacity of ship locks are put forward and sorted into different groups.

Step 3: Performance evaluation of each CCI countermeasure

An expert survey is conducted to measure the positive effect of each countermeasure on the improvement of carrying capacity of ship locks. Four criteria are cost, expected benefit, implementation difficulty, and project cycle. A triangle fuzzy function is further applied to transform subjective judgments into fuzzy numbers.

Step 4: Ranking of the CCI countermeasures

The Positive Ideal Reference Point (PIRP) and Negative Ideal Reference Point (NIRP) are determined, and the distances from each CCI countermeasure to PIRP and NIRP are calculated. The closeness coefficient of each CCI countermeasure is calculated, and CCI countermeasures are ranked according to their closeness coefficients.

The research framework of the fuzzy-based decision-making model is shown in Figure 2.

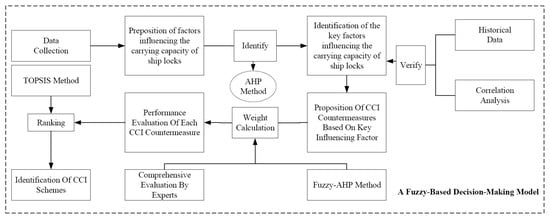
Figure 2. Research framework of the fuzzy-based decision-making model.

3.2. Comprehensive Evaluation by Experts

The comprehensive evaluation by experts is achieved based on experts’ knowledge and long-term working experience in the field [29]. This method is more suitable, especially when there is a lack of statistical data. This method relies much on the design of questionnaires and the selection of experts. As the capability of each expert may vary, each expert will be assigned different weights according to the importance of their judgments when merging their opinions.

In this study, the evaluation of the carrying capacity improvement of ship locks is represented by D, the importance coefficient of each factor is represented by I, and the improved value of ship locks’ carrying capacity is represented by A. They all can be obtained by weighting average the results of questionnaires, and their relations are expressed as follows:

$$D_k=I_k\times A_k$$

(1)

where $D_k$ is the assessed value of ship locks carrying capacity improvement by the $k$th factor considering its importance, $I_k$ is evaluation coefficient of the importance of $k$th factor, and $A_k$ is the assessed value of ship locks carrying capacity improvement by the $k$th factor. They can be calculated as follows:

$$I_k=\frac{1}{n}\sum _{m=1}^n{w}_m{i}_{\mathit{km}}=\frac{1}{n}\left(w_{\mathit{1}}{i}_{k\mathit{1}}+w_{\mathit{2}}{i}_{k\mathit{2}}+\cdots +w_m{i}_{\mathit{km}}\right)$$

(2)

where $n$ is the total number of valid questionnaires; $m$ indicates the $m$th questionnaire; $k$ represents the $k$th influencing factor; $w$ is the weight of the questionnaire. Similarly, the following equation can be used to calculate the score of the $k$th influencing factor in terms of capacity improvement of ship locks.

$$A_k=\frac{1}{n}\sum _{m=1}^n{w}_m{\alpha }_{\mathit{km}}=\frac{1}{n}\left(w_{\mathit{1}}{\alpha }_{k\mathit{1}}+w_{\mathit{2}}{\alpha }_{k\mathit{2}}+\cdots +w_m{\alpha }_{\mathit{km}}\right)$$

(3)

3.3. Fuzzy-AHP Method

Although traditional AHP needs few quantitative data when providing solutions for multi-objective and multi-criterion problems, it still shows some inherent drawbacks. For example, only an integer of a certain scale can be assigned when constructing a judgment matrix, which cannot reflect the real situation accurately. Meanwhile, the judgment matrix constructed by this method usually has limitations [30,31]. Therefore, in this paper, a fuzzy-AHP judgment matrix will be constructed by using triangular fuzzy numbers (TFNs). In this way, the fuzziness between the attributes and human knowledge can be better reflected to minimize the impact of participants’ bias on outcomes.

In a fuzzy-AHP judgment matrix, the comparative importance of two factors can be represented with a 9-scale of importance, as shown in Table 1.

Table 1. The relational scale for pairwise comparisons with TFNs.

Scale of Importance	Interpretation	TFN (${\mathit{l}}_{\mathit{i}}$,${\mathit{m}}_{\mathit{i}}$,${\mathit{u}}_{\mathit{i}}$)
1	Equal importance of two elements	(1,1,1)
3	Former is slightly more important than the latter.	(2,3,4)
5	Former is clearly more important than the latter.	(4,5,6)
7	Former is strongly more important than the latter.	(6,7,8)
9	Former is absolutely more important than the latter.	(8,9,9)
2, 4, 6, 8	The middle value of the above judgment.	(1,2,3), (3,4,5), (5,6,7), (7,8,9)
Reciprocal	If the importance ratio between elements $i$ and $j$ is $a_{\mathit{ij}}$, then the importance ratio between elements $j$ and $i$ is $a_{\mathit{ji}}=1/a_{\mathit{ij}}$.	($1/u_i$, $1/m_i$, $1/{\mathit{l}}_i$ )

According to Table 1, the results of pairwise comparisons are used to construct the fuzzy-AHP judgment matrix for each level of factors as follows. Assuming that there are $n$ factors in a certain level of the hierarchical model, and ${\tilde{a}}_{\mathit{ij}}$ represents the pairwise comparisons for the importance of the $i$th factor with respect of the jth one. The judgment matrix $\tilde{\mathrm{A}}$ of each level can be represented by a $n\times n$ matrix.

$$\tilde{\mathrm{A}}={\left({\tilde{a}}_{\mathit{ij}}\right)}_{n*n}=\left[\begin{array}{cccc}(1,1,1)& {\tilde{a}}_{\mathit{12}}& \cdots & {\tilde{a}}_{\mathit{1}n}\\ 1/{\tilde{a}}_{\mathit{12}}& (1,1,1)& \cdots & {\tilde{a}}_{\mathit{2}n}\\ ⋮& ⋮& \ddots & ⋮\\ 1/{\tilde{a}}_{\mathit{1}n}& 1/{\tilde{a}}_{\mathit{2}n}& \cdots & (1,1,1)\end{array}\right]i,j=1,\dots ,n,i<j$$

(4)

The following equation is the expansion of fuzzy judgment matrix $\tilde{\mathrm{A}}$.

$$\tilde{\mathrm{A}}={\left({\tilde{a}}_{\mathit{ij}}\right)}_{n*n}=\left[\begin{array}{cccc}(1,1,1)& \left({\mathit{l}}_{\mathit{12}},m_{\mathit{12}},u_{\mathit{12}}\right)& \cdots & \left({\mathit{l}}_{\mathit{1}n},m_{\mathit{1}n},u_{\mathit{1}n}\right)\\ \left(\frac{1}{u_{\mathit{12}}},\frac{1}{m_{\mathit{12}}},\frac{1}{{\mathit{l}}_{\mathit{12}}}\right)& (1,1,1)& \cdots & \left({\mathit{l}}_{\mathit{2}n},m_{\mathit{2}n},u_{\mathit{2}n}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \left(\frac{1}{u_{\mathit{1}n}},\frac{1}{m_{\mathit{1}n}},\frac{1}{{\mathit{l}}_{\mathit{1}n}}\right)& \left(\frac{1}{u_{\mathit{2}n}},\frac{1}{m_{\mathit{2}n}},\frac{1}{{\mathit{l}}_{\mathit{2}n}}\right)& \cdots & (1,1,1)\end{array}\right]$$

(5)

Support two TFNs are $M_{\mathit{1}}=\left({\mathit{l}}_{\mathit{1}},m_{\mathit{1}},u_{\mathit{1}}\right)$ and $M_{\mathit{2}}=\left({\mathit{l}}_{\mathit{2}},m_{\mathit{2}},u_{\mathit{2}}\right)$, then the operations with these fuzzy numbers are defined as follows.

$$\left({\mathit{l}}_{\mathit{1}},m_{\mathit{1}},u_{\mathit{1}}\right)\oplus \left({\mathit{l}}_{\mathit{2}},m_{\mathit{2}},u_{\mathit{2}}\right)=\left({\mathit{l}}_{\mathit{1}}+{\mathit{l}}_{\mathit{2}},m_{\mathit{1}}+m_{\mathit{2}},u_{\mathit{1}}+u_{\mathit{2}}\right)$$

(6)

$$\left({\mathit{l}}_{\mathit{1}},m_{\mathit{1}},u_{\mathit{1}}\right)\odot \left({\mathit{l}}_{\mathit{2}},m_{\mathit{2}},u_{\mathit{2}}\right)=\left({\mathit{1}}_{\mathit{1}}{\mathit{l}}_{\mathit{2}},m_{\mathit{1}}{m}_{\mathit{2}},u_{\mathit{1}}{u}_{\mathit{2}}\right)$$

(7)

$$(\lambda ,\lambda ,\lambda )\odot \left({\mathit{l}}_{\mathit{2}},m_{\mathit{2}},u_{\mathit{2}}\right)=\left(\lambda {\mathit{l}}_{\mathit{2}},\lambda m_{\mathit{2}},\lambda u_{\mathit{2}}\right),\lambda >0,\lambda \in R$$

(8)

$${\left({\mathit{l}}_{\mathit{1}},m_{\mathit{1}},u_{\mathit{1}}\right)}^{-1}\approx \left(1/u_{\mathit{1}},1/m_{\mathit{1}},1/{\mathit{l}}_{\mathit{1}}\right)$$

(9)

According to the proposed TFNs, the sum of the column vectors of the fuzzy judgment matrix $\tilde{\mathrm{A}}$ can be calculated as:

$${\mathrm{RS}}_i=\sum _{j=1}^{\mathrm{n}}{\tilde{a}}_{\mathit{ij}}=\left(\sum _{j=1}^n{\mathit{l}}_{\mathit{ij}},\sum _{j=1}^n{m}_{\mathit{ij}},\sum _{j=1}^n{u}_{\mathit{ij}}\right),i=1,\dots ,n$$

(10)

The normalization of matrix $\tilde{\mathrm{A}}$ can be realized by the following equation.

$$\begin{array}{c}\hfill {\tilde{S}}_i=\frac{R{S}_i}{{\sum }_{j=1}^n{\mathrm{RS}}_j}=\left(\frac{{\sum }_{j=1}^n{\mathit{l}}_{\mathit{ij}}}{{\sum }_{j=1}^n{\mathit{l}}_{\mathit{ij}}+{\sum }_{k=1,k\ne i}^n{\sum }_{j=1}^n{u}_{\mathit{kj}}},\frac{{\sum }_{j=1}^n{m}_{\mathit{ij}}}{{\sum }_{k=1}^n{\sum }_{j=1}^n{m}_{\mathit{kj}}},\frac{{\sum }_{j=1}^n{u}_{\mathit{ij}}}{{\sum }_{j=1}^n{u}_{\mathit{ij}}+{\sum }_{k=1,k\ne i}^n{\sum }_{j=1}^n{\mathit{l}}_{\mathit{kj}}}\right),\\ \hfill i=1,\cdots ,n.\end{array}$$

(11)

where ${\tilde{S}}_i$ represents the weight of TFNs of the $i$th index in judgment matrix $\tilde{A}$, and ${\left({\tilde{S}}_{\mathit{1}},\dots ,{\tilde{S}}_n\right)}^T$ consists of the eigenvectors of fuzzy judgment matrix $\tilde{A}$. When numerous pairwise comparisons are evaluated, their consistency must be checked before a convincing result can be achieved, which can be achieved as follows.

$$CR=\frac{CI}{RI}$$

(12)

where $CR$ is the consistency ratio and $RI$ is the random index for the matrix size. $CI$ is the consistency index that can be obtained from Equation (13).

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(13)

where ${\lambda }_{max}$ is the maximum weighting value of a $n\times n$ comparison matrix $\tilde{\mathrm{A}}$. The comparisons will be considered reasonable only if the consistency ratio is equal to or less than 0.10.

3.4. TOPSIS Method

The TOPSIS method is used for identifying solutions from a finite set of alternatives, with a basic principle that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution. As a useful method in dealing with multi-attribute or multi-criterion decision-making problems in the real world, TOPSIS has been successfully applied to various aspects such as human-resource management, transportation and manufacturing [32,33]. The TOPSIS method can be expressed in the following steps:

(1) Establish a decision matrix

When conducting TOPSIS, it is required that a decision problem be well structured and represented in the form of decision matrix D with m rows, each representing the alternatives under consideration and n columns, each representing the evaluation criterion. Matrix D consists of various original information is shown as Equation (14).

$$D=\left[\begin{array}{cccc}{x}_{\mathit{11}}& x_{\mathit{12}}& \cdots & x_{\mathit{1}n}\\ x_{\mathit{21}}& x_{\mathit{22}}& \cdots & x_{\mathit{2}n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{m\mathit{1}}& x_{m\mathit{2}}& \cdots & x_{\mathit{mn}}\end{array}\right]$$

(14)

Each variable $x_{\mathit{ij}}$ in matrix D describes the performance of alternative $O_i(i=1,2,\cdots ,m)$ with respect to the criterion $C_j(j=1,2,\cdots ,n)$.

(2) Normalize the decision matrix

It is essential to normalize the data to transform it into a dimensionless matrix, which allows the comparison of the criteria from different sources. Normalized value $r_{ij}$ of each variable $x_{ij}$ is calculated through Equation (15).

$$r_{\mathit{ij}}=x_{\mathit{ij}}/\sqrt{\sum _{i=1}^m{x}_{\mathit{ij}}^2},j=1,2,\dots ,n$$

(15)

(3) Obtain the weighted normalized decision matrix

Then, the weighted normalized decision matrix ($V_{ij}$) can be obtained by multiplying the normalized decision matrix by its associated weights with Equation (16).

$$v_{\mathit{ij}}=w_j·r_{\mathit{ij}},i=1,2,\dots ,m,j=1,2,\dots ,n$$

(16)

where $w_j$ is the weight of $j$th criteria.

(4) Identify the positive ideal solutions (PIS) and negative ideal solutions (NIS)

In a TOPSIS, the PIS ($A^{+}$) and NIS ($A^{-}$) are defined as Equation (17).

$$\begin{array}{c}{A}^{+}=\left(v_{\mathit{1}}^{+},v_{\mathit{2}}^{+},\dots ,v_n^{+}\right)=\left\{\left(\underset{i}{max}\left\{v_{\mathit{ij}}\right\}|j\in J_{\mathit{1}}\right),\left(\underset{i}{min}\left\{v_{\mathit{ij}}\right\}\right)|j\in J_{\mathit{2}}\right\};\hfill \\ A^{-}=\left(v_{\mathit{1}}^{-},v_{\mathit{2}}^{-},\dots ,v_n^{-}\right)=\left\{\left(\underset{i}{min}\left\{v_{\mathit{ij}}\right\}|j\in {\mathrm{J}}_{\mathit{1}}\right),\left(\underset{i}{max}\left\{v_{\mathit{ij}}\right\}\right)|j\in J_{\mathit{2}}\right\}\hfill \end{array}$$

(17)

where $J_{\mathit{1}}$ and $J_{\mathit{2}}$ represent the criteria benefit and cost, respectively.

(5) Calculate separation measures

The Euclidean distances from the PIS ($d_j^{+}$) and the NIS ($d_j^{-}$) of each alternative $O_i$ can be calculated as:

$$\begin{array}{c}{d}_i^{+}=\sqrt{{\sum }_{j=1}^n{\left(v_{\mathit{ij}}-v_{\mathrm{j}}^{+}\right)}^2},i=1,2,\dots ,m;\hfill \\ d_i^{-}=\sqrt{{\sum }_{j=1}^n{\left(v_{\mathit{ij}}-v_j^{-}\right)}^2},i=1,2,\dots ,m\hfill \end{array}$$

(18)

(6) Calculate the relative closeness to the ideal solution

The relative closeness $S_j$ for each alterative with respect to PIS is calculated using Equation (10).

$$S_j=\frac{d_j^{-}}{d_j^{+}+d_j^{-}},j=1,2,\dots ,m$$

(19)

where $0⩽S_j⩽1$.

(7) Rank the alternatives

As the distance to both PIS and NIS are considered in the last step, the larger value of result $S_j$ represents a better alternative $O_j$ that is close to positive ideal and far from a negative ideal solution. In addition, therefore, the solution with the largest $S_j$ should be ranked at the top when choosing the preferable alternative.

4. A Case Study of the Ship Locks of the Three Gorges Dam

The Three Gorges Dam locates on the Yangtze River (west of the city of Yichang in Hubei province, China). It is a straight-crested concrete gravity structure with 2335 m long and a maximum height of 185 m. The five-stage ship lock of Three Gorges Dam, the biggest ship lock in the world, acts as an elevator which raises and lowers ships to cross the Three Gorges Dam. It can lift a cargo ship of 14,000 tons to a height of 113 m [34]. In total, it will take about half an hour to cross Three Gorges Dam. Due to its significant role in the world, the ship locks of the Three Gorges Dam are believed to be representative for the case study.

Statistics of all types of ships passing through the Three Gorges Dam area are shown in Figure 3. During the flood season in 2016, the detention of ships reached 941 ship times [35]. Moreover, the ships detained due to Three Gorges ship lock suspension in one day are usually cleared up in a week or even half a month. In special periods such as bad weathers (e.g., strong wind and heavy fog), navigation limit between two dams in flood season, suspension due to exceeding design flow, and ship lock maintenance, the detention of ships in the Three Gorges Dam area will become more serious [36].

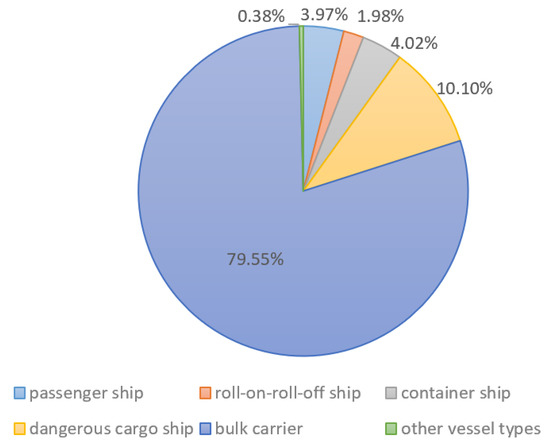
Figure 3. Type of ships in the Three Gorges Dam in 2016.

To obtain a complete overview of the results, individuals that have an explicit and recognizable role in relevant domains are chosen as experts in this survey. These experts have rich working experience in their respective organizations and are familiar with the operation and management of ship locks of the Three Gorges Dam. The number of experts of different types is listed in Table 2.

Table 2. Number of experts of different types.

Type of Experts	Number of Response
Senior research fellows from enterprises	2
Management staff	3
Project manager	2
Dispatcher	4
Maintenance staff	3
Testing staff	4
On-site staff	10
Professor from universities	3

4.1. Identification of Factors Influencing the Carrying Capacity of Ship Locks

There are multiple factors simultaneously affecting the carrying capacity of the ship locks of the Three Gorges water area. In this study, literature review, expert survey, and field investigations are adapted to identify and analyze the risk factors influencing the carrying capacity of ship locks of the Three Gorges Dam from different aspects. Altogether, there are 12 factors are identified, and the identified factors are finally categorized into the ship, ship lock, environment, and administrative classes with 12 sub-indices, as listed in Table 3.

Table 3. The factors influencing the carrying capacity of the Three Gorges Dam.

Target Level	Level I Index	Level II Index	Remarks
Factors Influencing the carrying capacity	Ship lock	Limited design carrying capacity	Representing the ultimate capacity of ship locks
		Overhaul of ship lock and facilities	Caused by ship lock maintenance
		Ship lock malfunctions	Operation barred by ship lock failure
	Vessel	Different types of ship	The poor use rate of the lock chamber area
		Waterway traffic accident	Backlogs caused by safety accidents
		A sudden increase of ship traffic flow	Too large traffic density
	Environment	Strong wind	Affecting ship voyage
		Heavy fog
		Flood season
		Dry season
	Management	Management level	Ineffective management systems
		Traffic control	Management measures due to special circumstances

The hierarchical structure model of influencing factors for Three Gorges Dam carrying capacity is established, as shown in Figure 4.

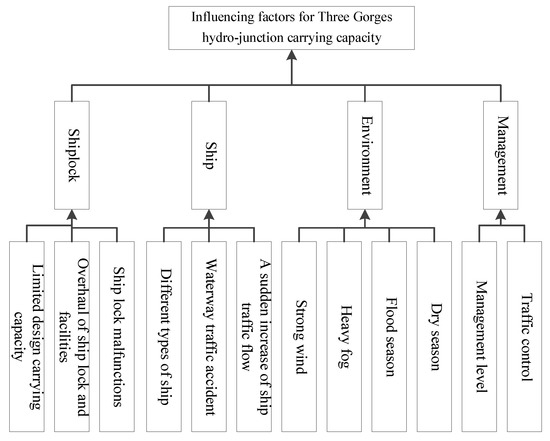
Figure 4. Hierarchical structure of influencing factors.

It is clear from the above AHP that four major factors are in the target layer, each layer with several sub-index factors, as shown in Table 4. To ensure the appropriate data processing, the collected expert questionnaires should be first calculated and then weight-averaged.

Table 4. Index system of influencing factors.

Target Level	Level I Index	Level II Index
Influencing factors of carrying capacity C	Ship lock C1	Limited design carrying capacity C11
		Overhaul of ship lock and facilities C12
		Ship lock malfunctions C13
	Ship C2	Waterway traffic accident C21
		Different types of ships C22
		A sudden increase of ship traffic flow C23
	Environment C3	Flood season C31
		Strong wind C32
		Dry season C33
		Heavy fog C34
	Management C4	Management Level C41
		Traffic control C42

According to the hierarchical structure in Section 4.1, the weight of each factor is calculated according to the method in Section 3.2. By calculating the factor weights of the index on each level, the weights of Level II indices and corresponding Level I indices were multiplied, resulting in the synthetic weight value of each index, as shown in Table 5.

Table 5. Local weights of influencing factors.

Factors	Local Weight	Order
Limited design carrying capacity	0.2649	1
Overhaul of ship lock and facilities	0.1458	3
Ship lock malfunctions	0.0802	4
Waterway traffic accident	0.0694	7
Different types of ships	0.0232	10
A sudden increase of ship traffic flow	0.1556	2
Flood season	0.0701	6
Strong wind	0.0361	9
Dry season	0.0209	11
Heavy fog	0.0474	8
Management level	0.0719	5
Traffic control	0.0144	12

To ensure the appropriate data processing, the opinion results of experts are averaged, generating the final results shown in Table 6.

Table 6. Final weights of influencing factors.

Factors	Weight	Order
Limited design carrying capacity	0.2254	1
Overhaul of ship lock and facilities	0.1789	2
Ship lock malfunctions	0.1420	3
Waterway traffic accident	0.1084	4
A sudden increase of ship traffic flow	0.1006	5
Different types of ships	0.0698	6
Flood season	0.0553	7
Strong wind	0.0374	8
Dry season	0.0285	9
Heavy fog	0.0233	10
Management level	0.0165	11
Traffic control	0.0140	12

4.2. Selections of Measures to Improve the Carrying Capacity of Ship Locks

According to the recognition of risk factors, using field research methods, and combining opinions of experts and personnel of the Three Gorges ship lock and anchorage, the relevant optimization scheme was set up, as listed in Table 7.

Table 7. CCI schemes related to ship locks of the Three Gorges Dam.

Code	Effect	CCI Scheme
A	Increase the carrying capacity of ship locks	Ship type standardization [A1], Optimization of lock chamber use[A2], Organizational scheduling optimization [A3], Ship lock capacity expansion [A4], Usage of ship lift [A5], Pipeline transportation [A6]
B	Reduce the repair time of ship lock and facilities	Maintenance at off-season [B1], Overhaul of two ship lock chambers at one time [B2], Overhaul process optimization [B3]
C	Reduce ship lock failure rate	Testing regularly [C1], On-site inspection [C2], Monitoring and alarming [C3]
D	Alleviate the effects of waterway traffic accidents	Early warning [D1], Ship scheduling [D2], Improve crew quality [D3], Ship safety management [D4]
E	Diversion of traffic flows	Diversion at dam areas [E1], Transshipment over dam [E2], Diversion at source [E3]
F	Lower the impact of a sudden increase of ship traffic flow	Restrict navigation [F1]
G	Reduce the influence of high flow during flood season	Reduce flood discharge [G1], Restrict navigation [G2], Navigational priority for full loaded ships [G3]
H	Reduce the influence of bad weathers	Weather forecast [H1], Scheduling optimization [H2]
I	Reduce the influence of dry season	Increase flood discharge [I1]
J	Improve management level	Establish a scheduling performance assessment system [J1], Electronic patrol [J2], Management officer training [J3]
K	Traffic control	Estimation of control system [K1], Improve management efficiency [K2], Develop management plan [K3]
L	Develop New channels	New channels of the Gezhouba Dam [L1], New channels of Three Gorges [L2]

For each scheme and corresponding optimization factors, an AHP model is established. Taking Scheme A as an example, the structure of the model is shown in Figure 5.

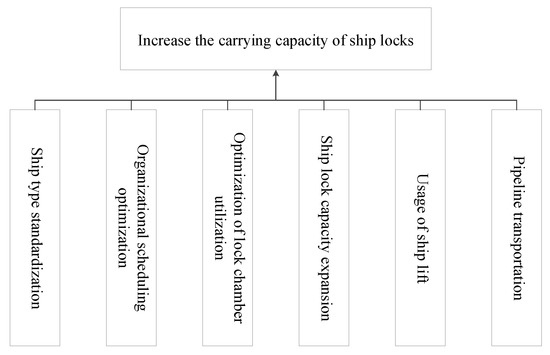
Figure 5. The AHP model of scheme A.

According to the methods introduced in Section 3.2, the weights were assigned based on the influencing degree of each factor in each scheme on capacity improvement. However, since the numbers of optimization factors in different schemes were different, the factors in Table 7 should be normalized, resulting in the normalized weights of 32 factors, listed in Table 8.

Table 8. Normalized results of factors.

CCI Scheme	Normalized Weight	CCI Scheme	Normalized Weight
Ship type standardization [A1]	0.4043	Optimization of lock chamber use [A2]	0.0740
Usage of ship lift [A5]	0.1469	Pipeline transportation [A6]	0.0567
Overhaul process optimization [B3]	0.104	Testing regularly [C1]	0.251
Early warning [D1]	0.100	Ship scheduling [D2]	0.1687
Diversion at dam areas [E1]	0.2355	Transshipment over dam [E2]	0.1155
Reduce flood discharge [G1]	0.2355	Restrict navigation [G2]	0.1155
Scheduling optimization [H2]	0.1355	Increase flood discharge [I1]	0.217
Management officer training [J3]	0.2185	Estimation of control system [K1]	0.1165
New channels of the Gezhouba Dam [L1]	0.181	New channels of Three Gorges [L2]	0.152
Organizational scheduling optimization [A3]	0.1705	Ship lock capacity expansion [A4]	0.1476
Maintenance at off-season [B1]	0.2105	Overhaul of two ship lock chambers at one time [B2]	0.1855
On-site inspection [C2]	0.1155	Monitoring and alarming [C3]	0.1335
Improve crew quality [D3]	0.2873	Ship safety management [D4]	0.110
Diversion at source [E3]	0.0667	Restrict navigation [F1]	0.1667
Navigational priority for full loaded ships [G3]	0.149	Weather forecast [H1]	0.1667
Establish a scheduling performance system [J1]	0.1475	Electronic patrol [J2]	0.1165
Improve management efficiency [K2]	0.2185	Develop management plan [K3]	0.165

Based on risk factor identification and the factors of each scheme, according to the weights of each scheme in capacity improvement, the optimization ability index of each factor in each scheme can be quantized in the capacity optimization system. Results sorted according to optimization performance are listed in Table 9.

Table 9. Ranking of CCI schemes according to the weights.

Order	CCI Scheme	Weight	Order	CCI Scheme	Weight
1	Ship type standardization [A1]	0.1071	18	Ship scheduling [D2]	0.0117
2	Organizational scheduling optimization [A3]	0.0452	19	Scheduling optimization [H2]	0.0113
3	Ship lock capacity expansion [A4]	0.0391	20	Monitoring and alarming [C3]	0.0107
4	Usage of ship lift [A5]	0.0389	21	Establish a scheduling performance assessment system [J1]	0.0106
5	Maintenance at off-season [B1]	0.0307	22	Navigational priority for full loaded ships [G3]	0.0104
6	Overhaul of two ship lock chambers at one time [B2]	0.0270	23	On-site inspection [C2]	0.0093
7	Restrict navigation [F1]	0.0259	24	Electronic patrol [J2]	0.0084
8	Testing regularly [C1]	0.0201	25	Restrict navigation [G2]	0.0081
9	Improve crew quality [D3]	0.0199	26	Ship safety management [D4]	0.0076
10	Optimization of lock chamber use [A2]	0.0196	27	Early warning [D1]	0.0069
11	New channels of the Gezhouba Dam [L1]	0.0181	28	Diversion at dam areas [E1]	0.0055
12	Reduce flood discharge [G1]	0.0165	29	Increase flood discharge [I1]	0.0045
13	Management officer training [J3]	0.0157	30	Improve management efficiency [K2]	0.0031
14	New channels of Three Gorges [L2]	0.0152	31	Transshipment over dam [E2]	0.0027
15	Overhaul process optimization [B3]	0.0151	32	Develop management plan [K3]	0.0024
16	Pipeline transportation [A6]	0.0150	33	Estimation of control system [K1]	0.0017
17	Weather forecast [H1]	0.0139	34	Diversion at source [E3]	0.0015

4.3. Quantification of Optimization Factors’ Improving Effect

For each optimization factor, the evaluation was made in terms of cost, expected benefit, implementation difficulty, and project cycle. The factors for the above four evaluation indices were quantized according to the scores of the experts for each factor. The average values of the evaluation indices of all experts were used as the scores of the economic inputs of implementation, expected effect after implementation, the ease of realization, implementation cycle, with maximum and minimum scores being 9 and 0. Finally, sorting was made according to the optimization effect. The emerged judgments from experts are listed in Table 10.

Table 10. Performance of CCI schemes of different criteria.

CCI Scheme	Cost	Expected Benefit	Implementation Difficulty	Project Cycle
Organizational scheduling optimization [A3]	8	3	6	8
Optimization of lock chamber use [A2]	8	3	5	8
Increase flood discharge [I1]	8	4	3	8
Diversion at source [E3]	7	2	7	8
Early warning [D1]	6	5	5	6
Scheduling optimization [H2]	8	3	6	8
On-site inspection [C2]	8	2	7	8
Restrict ship navigation [G2]	7	5	6	8
Restrict navigation [F1]	6	6	5	8
Estimation of control system [K1]	8	2	8	8
Weather forecast [H1]	7	3	5	8
Improve management efficiency [K2]	8	2	6	8
Improve crew quality [D3]	6	4	3	5
Overhaul of two ship lock chambers at one time [B2]	6	7	6	5
Usage of ship lift [A5]	5	7	5	6
Navigational priority for full loaded ships [G3]	8	2	6	8
New channels of the Gezhouba Dam [L1]	1	9	3	1
Establish a scheduling performance assessment system [J1]	8	2	7	8
Develop management plan [K3]	8	3	7	8
Reduce flood discharge [G1]	8	4	2	8
Overhaul process optimization [B3]	9	5	3	7
Testing regularly [C1]	7	2	7	7
Monitoring and alarming [C3]	7	3	6	7
Management officer training [J3]	7	3	7	6
Pipeline transportation [A6]	3	6	4	4
Ship lock capacity expansion [A4]	5	6	6	5
Transshipment over dam [E2]	6	5	6	7
Electronic patrol [J2]	6	4	5	7
Maintenance at off-season [B1]	7	4	7	7
Ship safety management [D4]	7	4	6	7
Ship type standardization [A1]	5	7	3	3
Ship scheduling [D2]	8	3	7	8
Diversion at dam areas [E1]	7	5	6	7
New channels of Three Gorges [L2]	2	7	4	2

4.4. Evaluation of the Performance of CCI Schemes on the Three Gorges Dam

On the basis of selecting risk factors and optimization ability in Section 4.2 and Section 4.3, calculate the sum of the Euclidean distance between the optimization scheme to the positive and negative ideal schemes, as shown in Table 11, and calculate the closeness between the Three Gorges carrying capacity optimization scheme and the positive ideal scheme, with the closeness score of each factor shown in Table 12 according to the TOPSIS method in Section 3.3.

Table 11. Performance of CCI schemes of different criteria.

CCI Scheme	${\mathit{d}}_{+}$	${\mathit{d}}_{-}$	CCI Scheme	${\mathit{d}}_{+}$	${\mathit{d}}_{-}$
Organizational scheduling optimization [A3]	0.1706	0.1287	Establish a scheduling performance assessment system [J1]	0.2643	0.0575
Optimization of lock chamber use [A2]	0.2401	0.0679	Develop management plan [K3]	0.2863	0.0521
Increase flood discharge [I1]	0.2816	0.0451	Reduce flood discharge [G1]	0.2500	0.0600
Diversion at source [E3]	0.2890	0.0473	Overhaul process optimization [B3]	0.2526	0.0624
Early warning [D1]	0.2745	0.0397	Testing regularly [C1]	0.2387	0.0690
Scheduling optimization [H2]	0.2622	0.0559	Monitoring and alarming [C3]	0.2641	0.0504
On-site inspection [C2]	0.2679	0.0560	Management officer training [J3]	0.2503	0.0605
Restrict ship navigation [G2]	0.2707	0.0487	Pipeline transportation [A6]	0.2548	0.0429
Restrict navigation [F1]	0.2228	0.0771	Ship lock capacity expansion [A4]	0.1876	0.1086
Estimation of control system [K1]	0.2884	0.0552	Transshipment over dam [E2]	0.2858	0.0404
Weather forecast [H1]	0.2557	0.0535	Electronic patrol [J2]	0.2708	0.0410
Improve management efficiency [K2]	0.2847	0.0492	Maintenance at off-season [B1]	0.2094	0.0925
Improve crew quality [D3]	0.2406	0.0594	Ship safety management [D4]	0.2722	0.0472
Overhaul of two ship lock chambers at one time [B2]	0.2194	0.0811	Ship type standardization [A1]	0.0387	0.2893
Usage of ship lift [A5]	0.1883	0.1077	Ship scheduling [D2]	0.2610	0.0589
Navigational priority for full loaded ships [G3]	0.2649	0.0547	Diversion at dam areas [E1]	0.2779	0.0461
New channels of the Gezhouba Dam [L1]	0.2569	0.0447	New channels of Three Gorges [L2]	0.2475	0.0500

Table 12. Performance of CCI schemes of different criteria.

CCI Scheme	Closeness	CCI Scheme	Closeness
Ship type standardization [A1]	0.5819	Transshipment over dam [E2]	0.2238
Maintenance at off-season [B1]	0.5063	Optimization of lock chamber use [A2]	0.2205
Ship scheduling [D2]	0.4842	Improve crew quality [D3]	0.1979
Electronic patrol [J2]	0.4315	Scheduling optimization [H2]	0.1757
Organizational scheduling optimization [A3]	0.43	On-site inspection [C2]	0.1729
Usage of ship lift [A5]	0.4139	Navigational priority for full loaded ships [G3]	0.1711
Management officer training [J3]	0.3947	Estimation of control system [K1]	0.1607
Establish a scheduling performance assessment system [J1]	0.3787	Monitoring and alarming [C3]	0.1602
New channels of Three Gorges [L2]	0.3681	Restrict ship navigation [G2]	0.1524
Ship lock capacity expansion [A4]	0.3667	Ship safety management [D4]	0.1477
Develop management plan [K3]	0.3539	Improve management efficiency [K2]	0.1474
New channels of the Gezhouba Dam [L1]	0.3482	Diversion at dam areas [E1]	0.1422
Pipeline transportation [A6]	0.344	Diversion at source [E3]	0.1406
Overhaul process optimization [B3]	0.298	Increase flood discharge [I1]	0.1379
Overhaul of two ship lock chambers at one time [B2]	0.2699	Early warning [D1]	0.1263
Restrict navigation [F1]	0.257	Reduce flood discharge [G1]	0.1135
Testing regularly [C1]	0.2243	Weather forecast [H1]	0.0916

It can be concluded that ship type standardization [A1], maintenance at off-season [B1], ship scheduling [D2], electronic patrol [J2], organizational scheduling optimization [A3], and usage of ship lift [A5] have greater impacts on improving the carrying capacity of ship locks in the Three Gorges Dam.

5. Discussion

Since the use of AHP method may bring bias, the analysis results in the previous section need to be verified using correlation analysis to ensure the accuracy of the obtained results. Correlation analysis is a mathematical method which discovers whether there is dependence among different factors and how strong it is. Without the loss of generality, taking the correlation analysis of two groups of data as an example, correlation coefficient $\mathrm{r}$ is used to describe the correlation degree between them, and it can be either positive or negative [37]. Given two groups of variables $X$ and $Y$, and then the correlation coefficient can be calculated as follows.

$$r=\frac{{\sum }_{i=1}^n\left(x_i-\overline{X}\right)\left(y_i-\overline{Y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(x_i-\overline{X}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{Y}\right)}^2}}$$

(20)

where $\overline{X}=\frac{1}{n}{\sum }_{i=1}^n{X}_i$ and $\overline{Y}=\frac{1}{n}{\sum }_{i=1}^n{Y}_i$ represents the mathematic expectation of variables $X$ and $Y$, respectively; $\sqrt{{\sum }_{i=1}^n{\left(x_i-\overline{X}\right)}^2},\sqrt{{\sum }_{i=1}^{\mathrm{n}}{\left(y_i-\overline{Y}\right)}^2}$ represents the standard deviation of $X$ and $Y$; ${\sum }_{i=1}^n\left(x_i-\overline{X}\right)\left(y_i-\overline{Y}\right)$ represents the covariance of $X$ and $Y$.

Generally, an absolute value of $r$ that is larger than 0.95 indicates a significant correlation between variables $X$ and $Y$. An absolute value of $r$ that is larger than 0.8 indicates that $X$ and $Y$ are highly correlated. If $0.5\le \left|r\right|<0.8$, $X$ and $Y$ are moderately correlated. If $0.3\le |$r$|<0.5$, $X$ and $Y$ have low correlation. If |r$|<0.3$, the correlation between $X$ and $Y$ is very weak, or they are irrelevant. The results of correlation analysis are presented in Table 13.

Table 13. Analysis of correlations between ship backlog and key factors.

Number	The Object of Correlation Analysis		Data Source	Correlation Coefficient
1	Ship detention capacity	Ship lock maintenance	Statistics from 2010 to 2016	0.823
2		Gale		0.487
3		Fog		0.512
4		Flood season		0.682

It can be seen from Table 13 that the correlation between ship lock maintenance and ship detention capacity is the highest, while the correlations between the ship detention capacity and high flow during flood season, fog weather, and gale weather respectively show a decreasing trend, which indicates that the influence of ship lock maintenance is more significant than that of other three factors.

Based on the statistics for the Three Gorges in ship lock maintenance period from 2010 to 2016, the average navigation delay time of Three Gorges ship lock caused by routine maintenance, overhaul, and malfunctions were 167.58 h, 81.75 h, 124.43 h, 121.65 h, respectively. It is clear that ship lock maintenance and malfunction are the key factors influencing carrying capacity.

In the flood season of 2016, The Three Gorges received the largest flood since the opening of the Three Gorges ship lock, with large numbers of flood peaks and large peak value, the maximum flow being 71,200 $m_3/s$. The flood dramatically affected the ship navigation in the Three Gorges river segment, causing the detention of large numbers of ships, with a maximum number of detained ships being 941. Therefore, the large flow of flood season in Three Gorges has a large influence on ship detention in the dam area, and the larger the flow is, the more ships are detained. Therefore, it can be concluded that the results are consistent with the analyses results obtained from this research.

This paper develops a decision-making model to assist the improvement of the carrying capacity of ship locks by combing the fuzzy logic, the AHP method, and the TOPSIS. A three-level hierarchical structure is constructed to identify the key factors influencing the carrying capacity of ship locks from the aspects of ship locks, vessels, environment, and administration.

A decision-making model to assist the improvement of the carrying capacity of ship locks by combing the fuzzy logic, AHP, and TOPSIS is proposed, and the results obtained from the proposed methods are consistent with the real-life situation to a certain extent, indicating that the proposed method can provide a good reference for improving the carrying capacity of ship locks. The uncertainties on the conclusions will be taken in consideration as follows: Inaccuracies in data, assumptions in model and modelling procedures are conditions or choices which may affect the conclusions. Various uncertainty assessment methods have been proposed [38]. The simple approach is applied in the research, which is suggested by Flage and Aven [39].

The navigational records of Three Gorges Dam contain detailed information including the summary and statistics, general description of ships, external conditions, navigational environment, and so on, which can facilitate the influencing factors identification. Though the number of the navigational records is not so many years, the qualitative risk identification carried in this research is further complemented with expert knowledge. The uncertainty assessment for the proposed method is shown in Table 14.

Table 14. The uncertainty assessment for the proposed method.

Model Element	Uncertainty	Justification
Navigational records of the Three Gorges Dam	Low	The navigational records of Three Gorges Dam are presented by Three Gorges Navigation Administration usually present valuable and detailed information, which contain the summary and statistics, general description of ships, external conditions, navigational environment, and so on. This allows defining that the uncertainty assessment for accident reports can be considered good.
Expert knowledge	Medium	The experts have experience to identify and classify the influencing factors under icebreaker assistance. The certainty of the expert’s knowledge is medium which will be described regarding the influence of influencing factors identification and optimization ability on the results.
Models and assumptions	Low	Other factors outside the analysis framework, which could affect the results, new navigation systems which may affect the soundness of the analysis. However, A decision-making model is used to assist the improvement of the carrying capacity of ship locks using combing the fuzzy logic, AHP, and TOPSIS based on the navigational records of Three Gorges Dam and expert knowledge. Thus, this allows defining that the uncertainty assessment for models and assumptions can be considered low.

In brief, this may question the reliability of the navigational records when used to determine the influencing factors in assisting the improvement of the carrying capacity of ship locks. Besides, the research involves uncertainties. The research relies on navigational records formulated in a specific format, where a larger number of navigational records would reduce the uncertainty of the collision risk factors. We will improve the research in the terms of uncertainty analysis in the future. The proposed method for improving the carrying capacity of ship locks has also some potential benefits to the analysis of traffic flow in Three Gorges Dam.

6. Conclusions

In this paper, AHP method and correlation analysis method are synthetically used to effectively quantify the influencing factors of Three Gorges carrying capacity. In view of traffic engineering, correlation analysis is carried out combining ship traffic flow characteristics. The Three Gorges navigation optimization system was established in aspects of optimization capability, economy, expected effect, ease of realization, period. TOPSIS decision method is adopted to obtain the optimization factors of Three Gorges carrying capacity, avoiding the drawback in most studies that only corresponding optimization schemes were proposed without re-evaluation for the proposed schemes.

The five most significant factors influencing the Three Gorges Dam carrying capacity are “limited design carrying capacity”, “overhaul of ship lock and facilities”, “ship lock malfunctions”, “waterway traffic accidents”, and “a sudden increase of ship traffic flow”. Based on that some CCI schemes are proposed, and their performance is compared with respect to the cost, expected benefit, implementation difficulty, and project cycle. It is found that CCI schemes such as organizational scheduling optimization, establish a scheduling performance assessment system, management officer training, ship type standardization, usage of ship lift, ship scheduling, new channel of the Gezhouba Dam, new channel of the Three Gorges are among the ones that improve the carrying capacity of the ship locks of the Three Gorges the most.

Since the sample data were difficult to collect, in this study, experts’ judgment is involved, which may inevitably bring some bias. Therefore, under certain conditions where more statistical data is available, more quantitative analysis can be conducted to improve the accuracy of the performance evaluation results of the proposed CCI schemes, and these schemes will be further compared to the real situation in the Three Gorges Dam area.