Numerical and Experimental Modelling of a Wave Energy Converter Pitching in Close Proximity to a Fixed Structure
Abstract
:1. Introduction
2. Research Question
3. Numerical Model Description
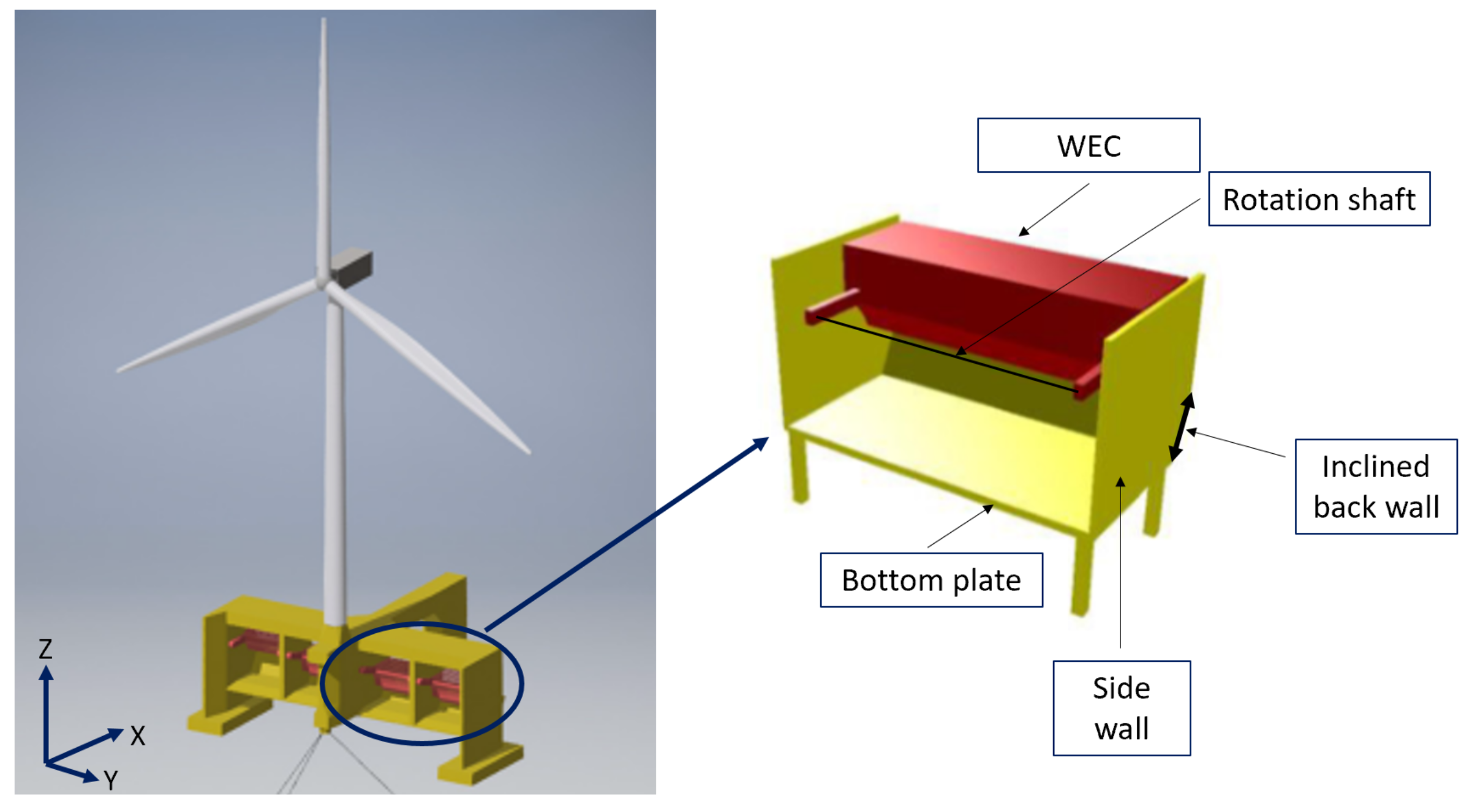
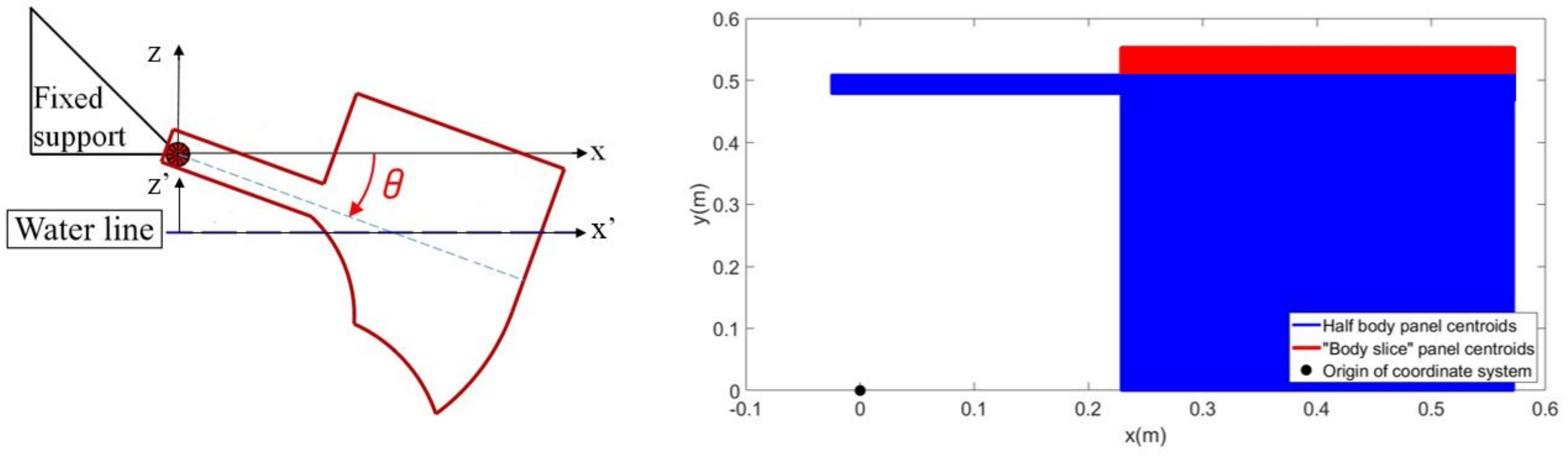
3.1. Geometry Definition
3.2. Equation of Motion
3.3. Model Versions
3.3.1. Water Surface Elevation:
3.3.2. Radiation Moment:
3.3.3. Hydrostatic Moment:
Linear Hydrostatic Moment
Gravity Moment, :
Buoyancy Moment, :
3.3.4. Excitation Moment:
Froude-Krylov, :
Scattering Moment:, :
Implementation of Measured Water Surface Elevation
3.3.5. Quadratic Drag Moment:
- (a)
- Exact formulation of quadratic drag forcesThe quadratic force opposes the velocity of the WEC. To select which submerged panels contribute to the quadratic drag force the condition that has to be met is that the angle defined by the panel normal vector and the panel velocity vector is less than 90 degrees. A quadratic drag force in the translational modes can be implemented as follows,where is the drag coefficient, the vector of projected areas, the velocity vector and the undisturbed fluid velocity vector in the directions at the centroid of the jth panel. is the total number of contributing submerged panels. Further details can be found in Reference [27].At , the angles of inclination of the WEC are known at and at the previous time step . These angles are used to calculate the instantaneous location of the centroids of the panels (see Section 3.1) at and . The cartesian coordinates defining these positions are used to calculate the translational panel velocities using the following equation.For heading waves the fluid velocity in the y direction is , and the horizontal and vertical velocity components are given by:The corresponding moments in roll, pitch and yaw arewhere are the cartesian coordinates of the jth panel and × represents cross product.
- (b)
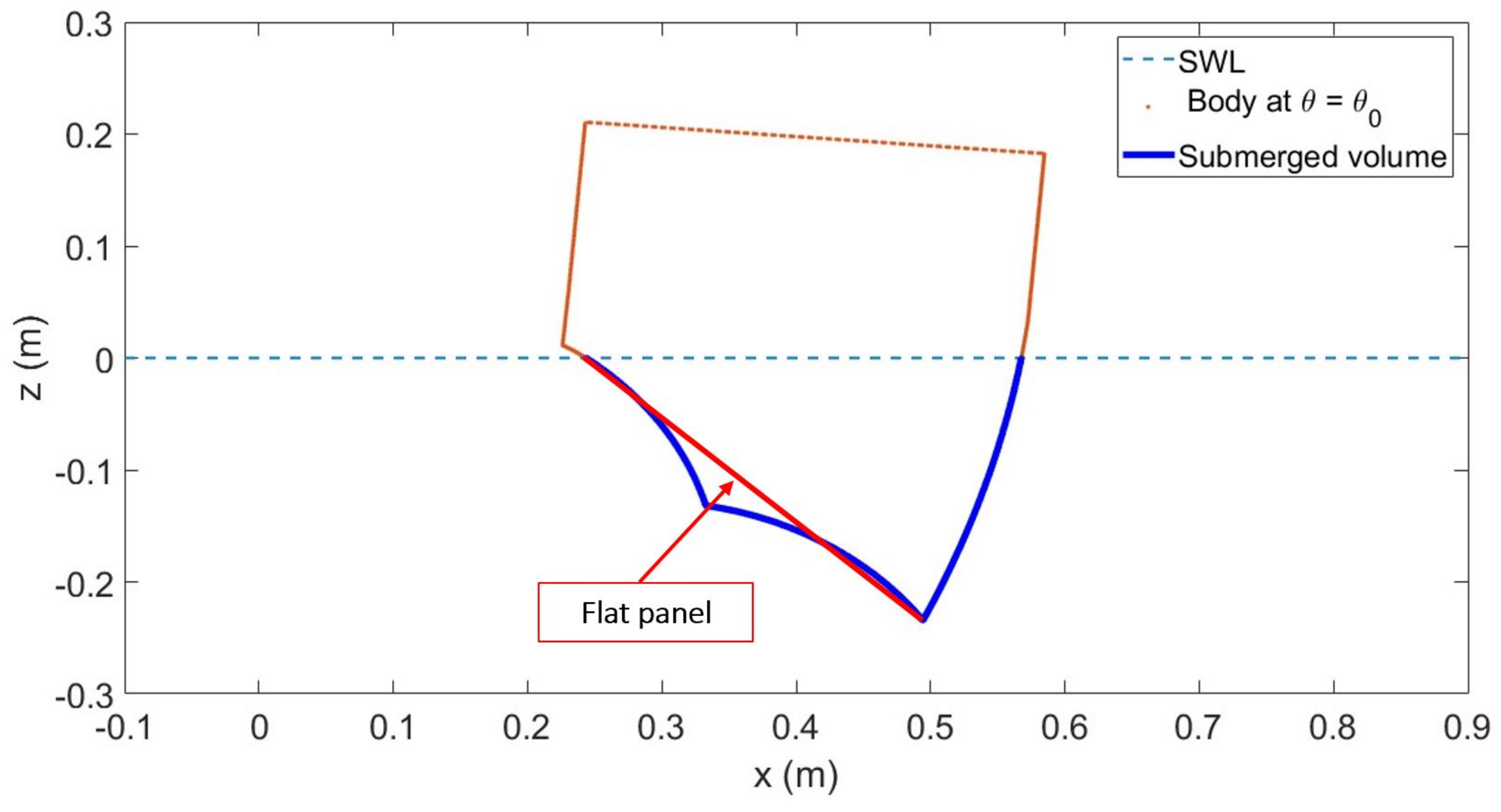
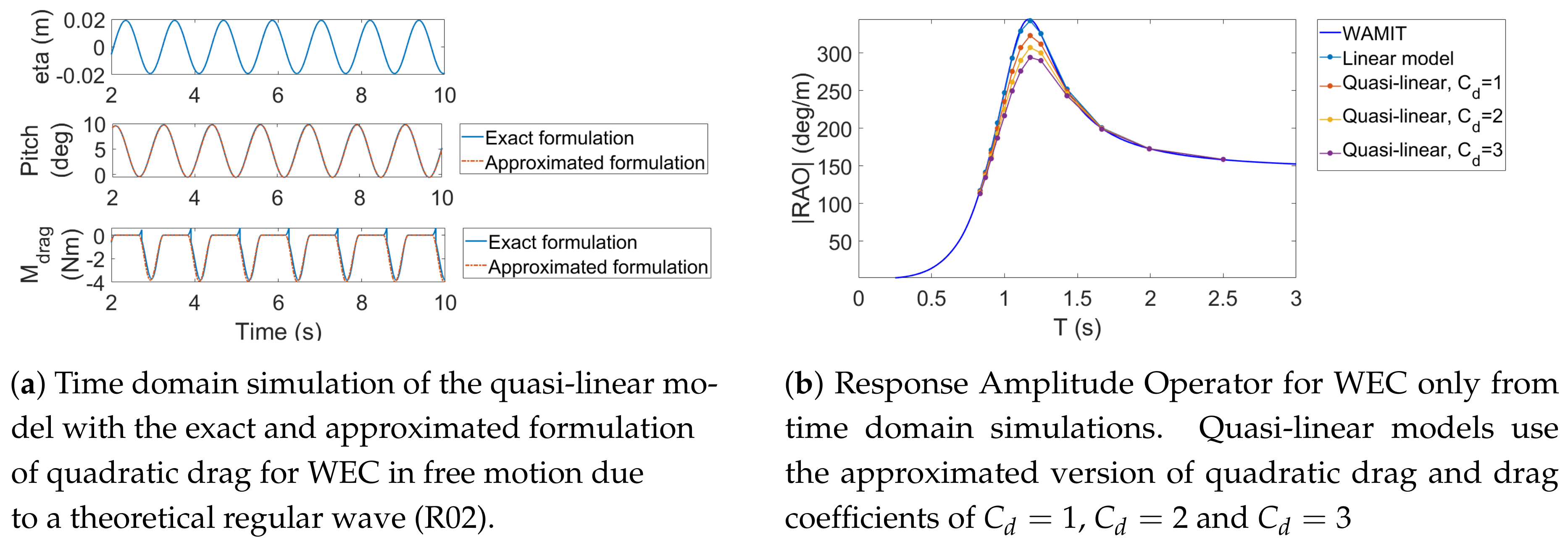
- Approximated formulation of quadratic drag forcesIn order to simplify and improve the computational efficiency, three simplifications to Equation (22) are applied. The first simplification is that the instantaneous submerged body surface area is approximated by single flat panel (Figure 4). The second simplification is that the fluid velocity is neglected. The third simplification is that the drag forces are only computed when the WEC is pitching clockwise (when the WEC rotates in the opposite direction the projected area is small hence the quadratic drag forces can be neglected).Applying these three simplifications, Equation (22) reduces to,where represents translational velocity of the centroid of the single panel in the directions and is the projected surface area of the flat panel.
3.3.6. Friction in the Bearings,
3.3.7. Numerical Model Solver
4. Wave Basin Experiments
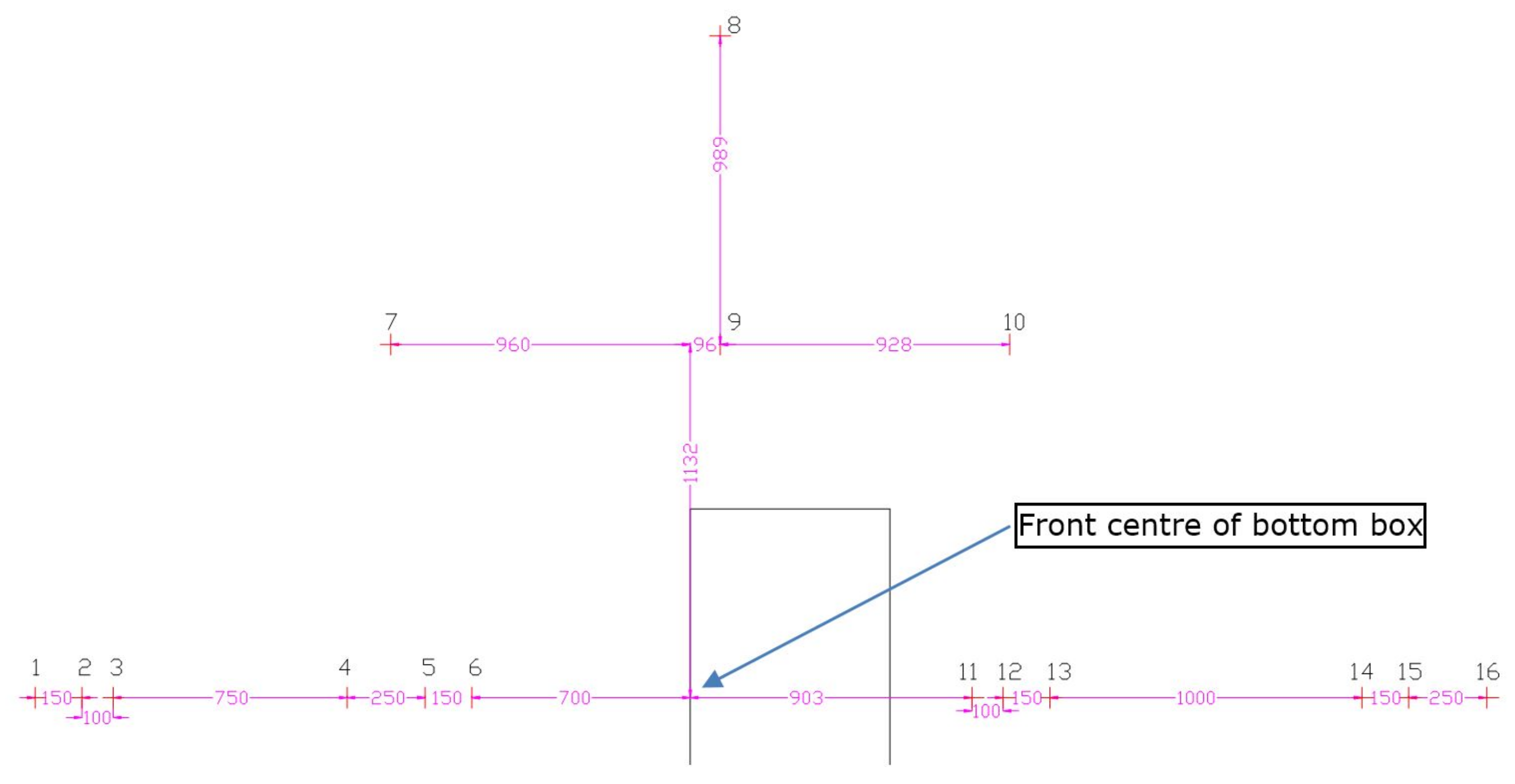
4.1. Laboratory Setup
4.2. Wave Basin Experimental Data
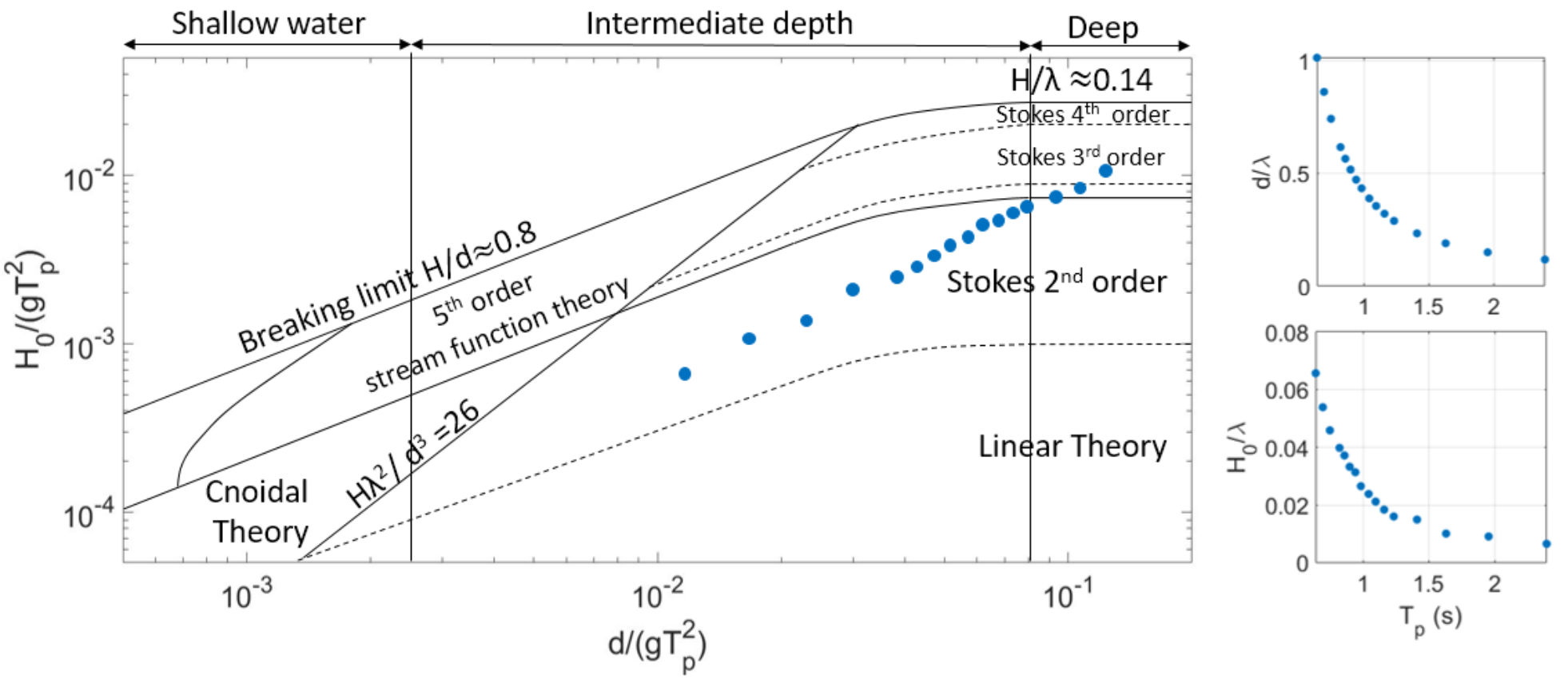
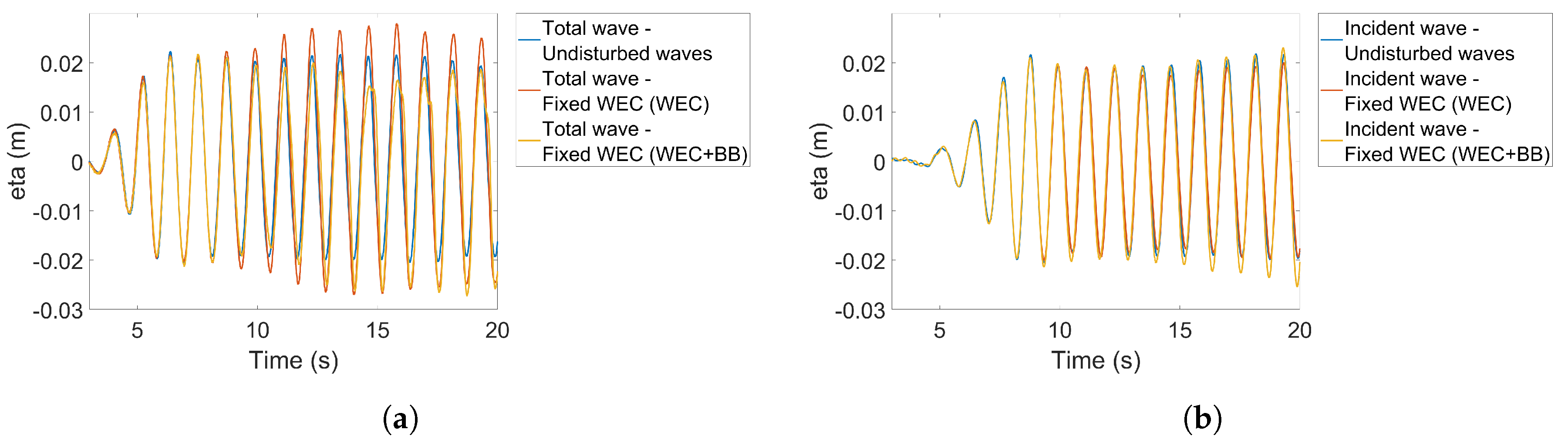
4.2.1. Undisturbed Waves
- Waves are generated and measured in the basin without the WEC in place (undisturbed waves) using the software “Awasys” from Aalborg University, including active absorption.
- A non-linear wave analysis is performed to separate incident and reflected waves using the software “WaveLab” from Aalborg University [28]. WaveLab takes into account the propagation speed of the waves in a non-linear manner.
- The same waves are then repeated with the device in position.
4.2.2. Slow-Motion Experiments
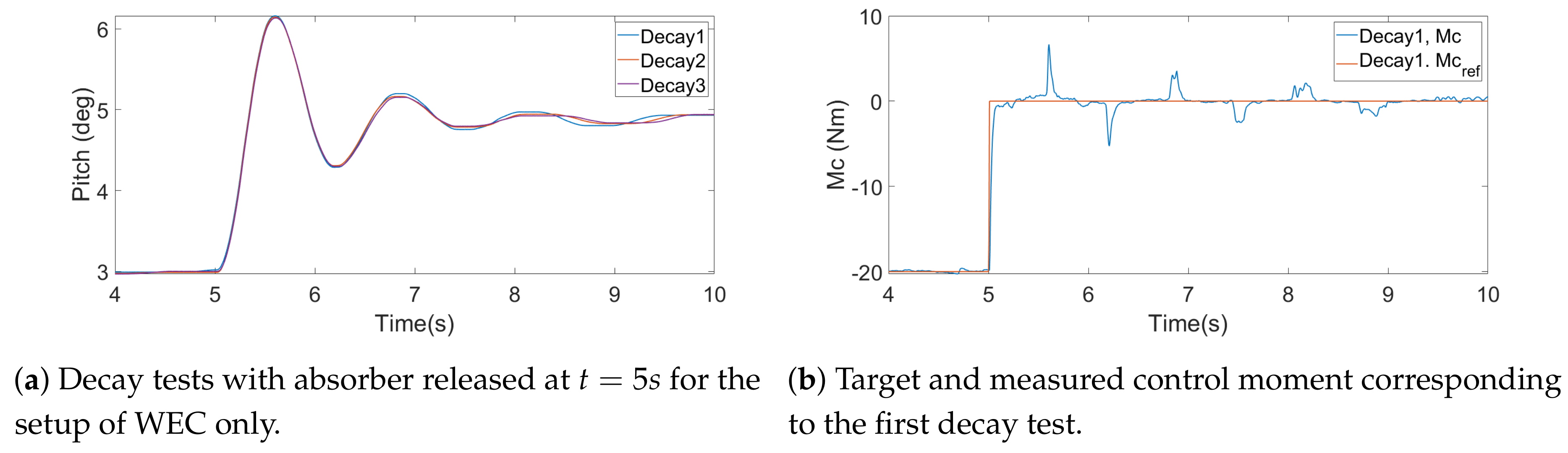
4.2.3. Decay Tests
4.2.4. Fixed WEC Experiments
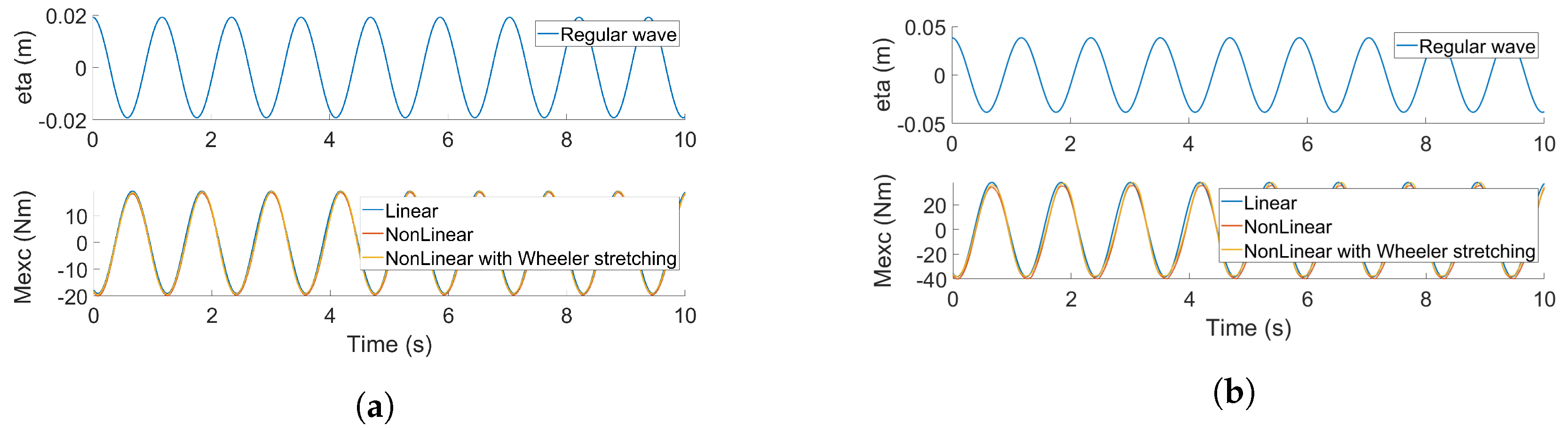
4.2.5. Regular Waves
4.2.6. Free Motion in Regular Waves
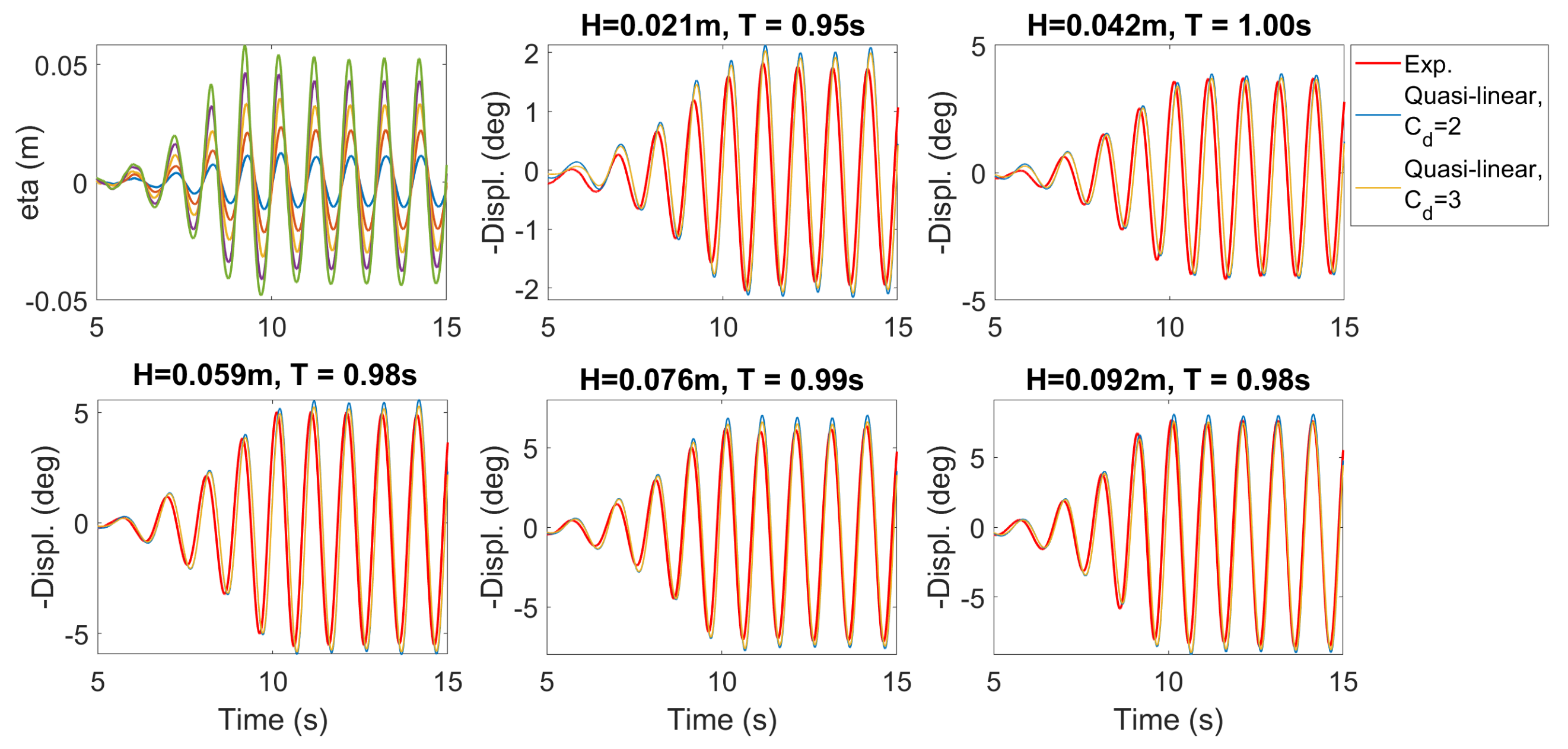
4.2.7. Quadratic Drag Moment
5. Results
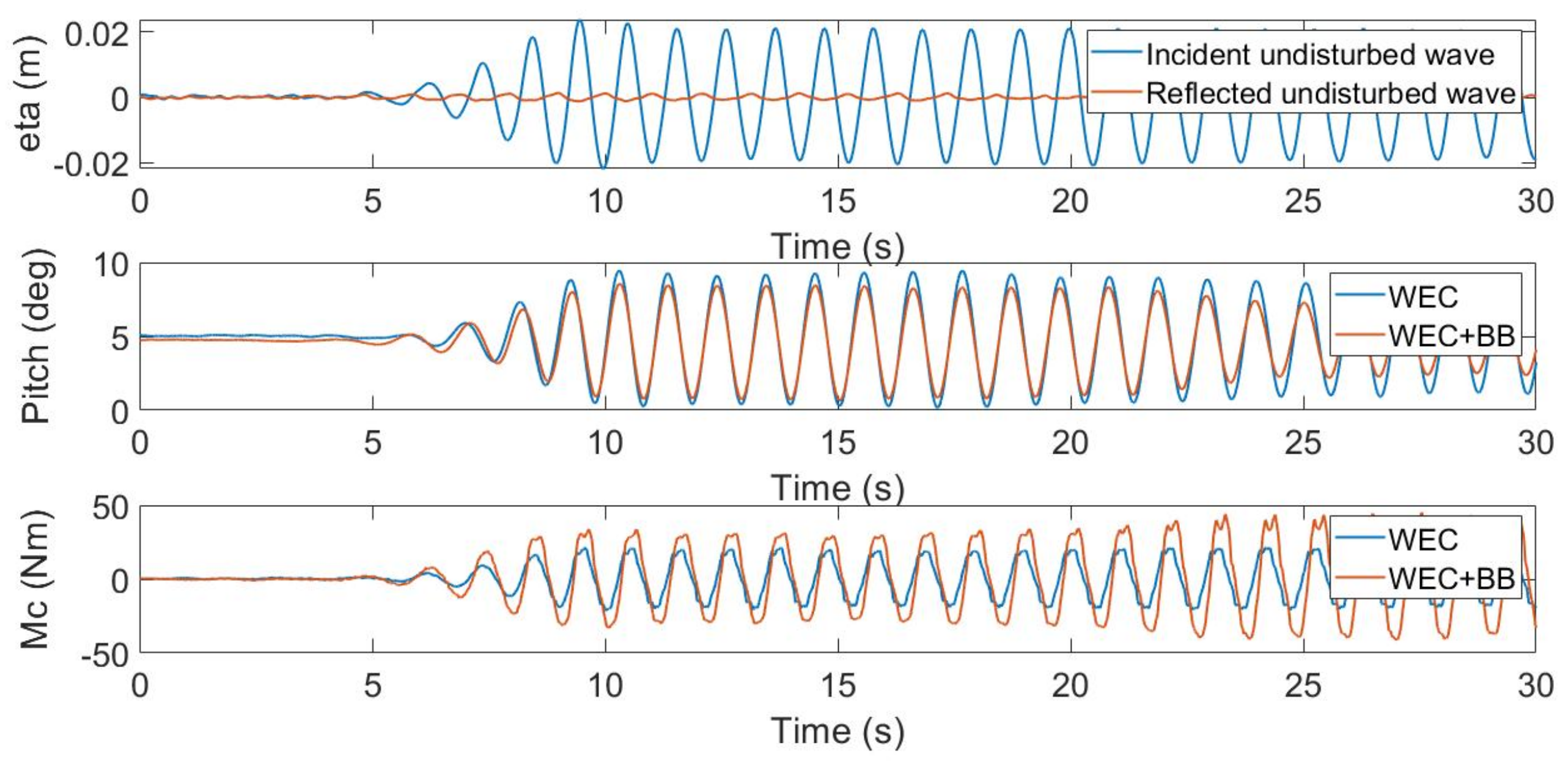
5.1. Wave Reflections and Repeatability
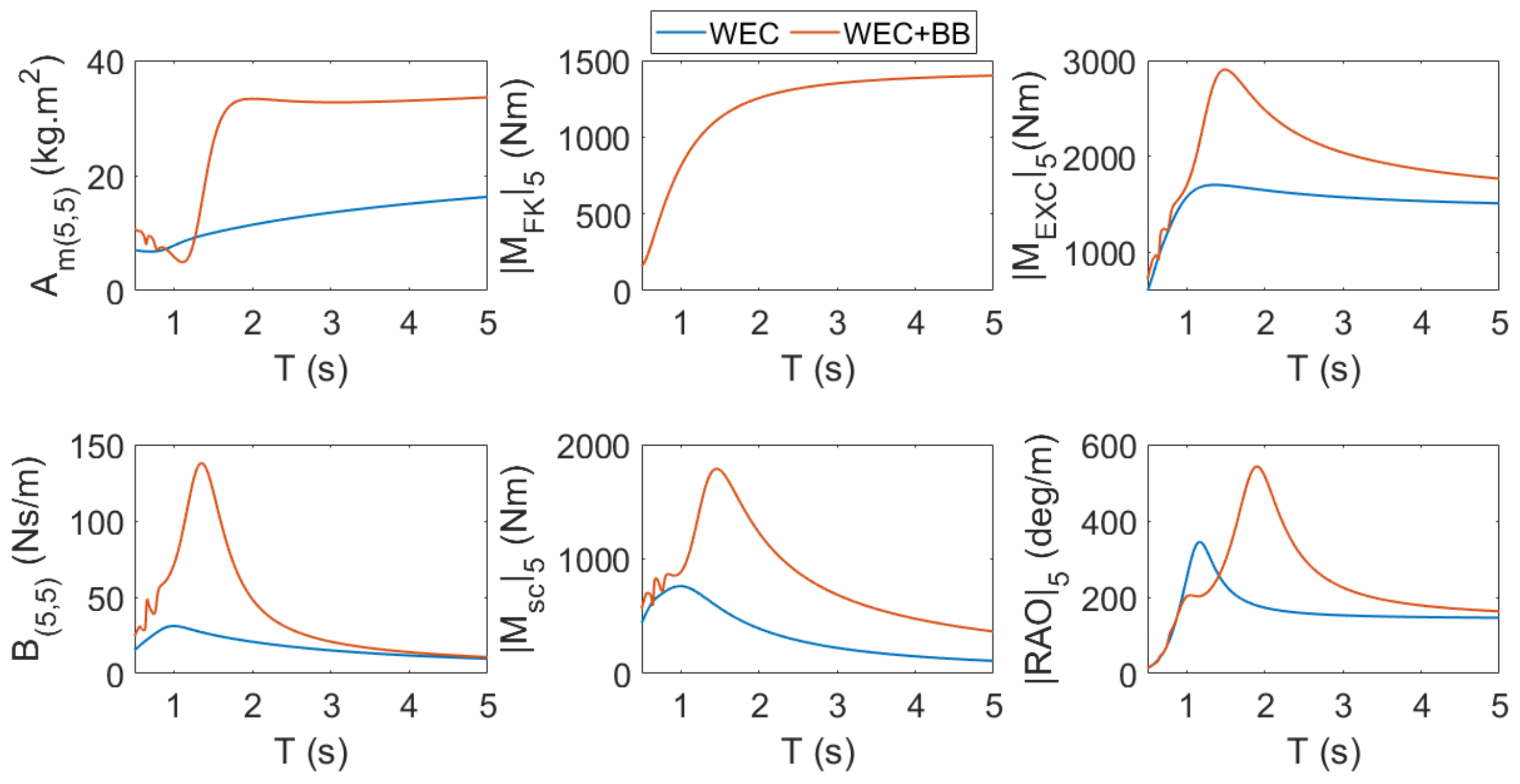
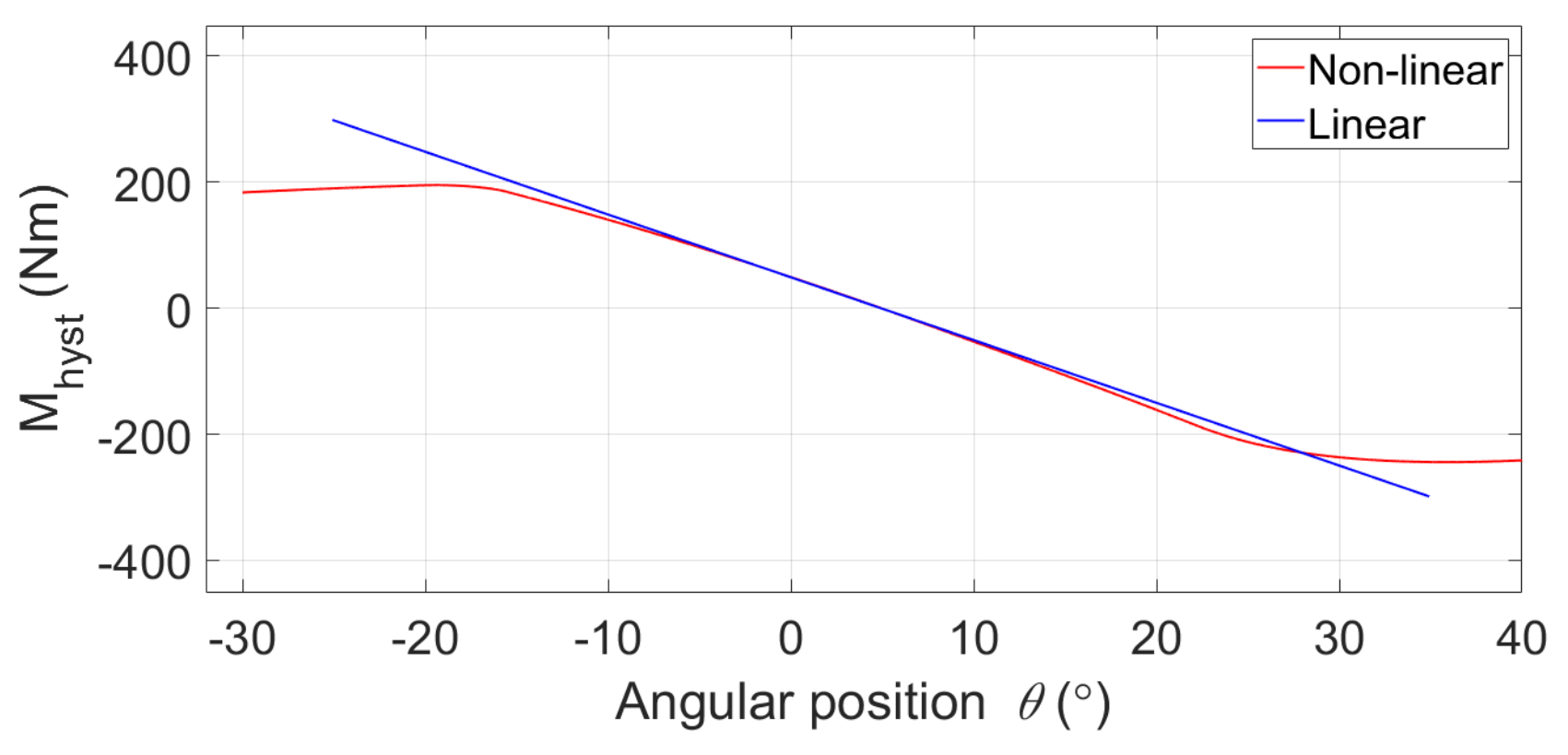
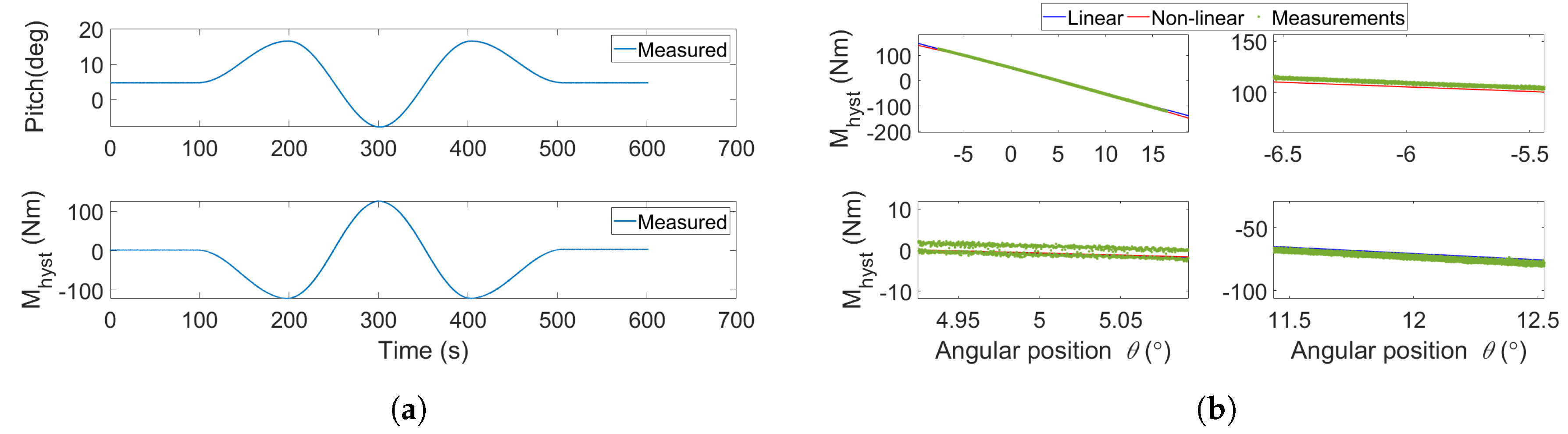
5.2. Modelling of Hydrostatics and Friction
5.3. Decay Tests Simulations
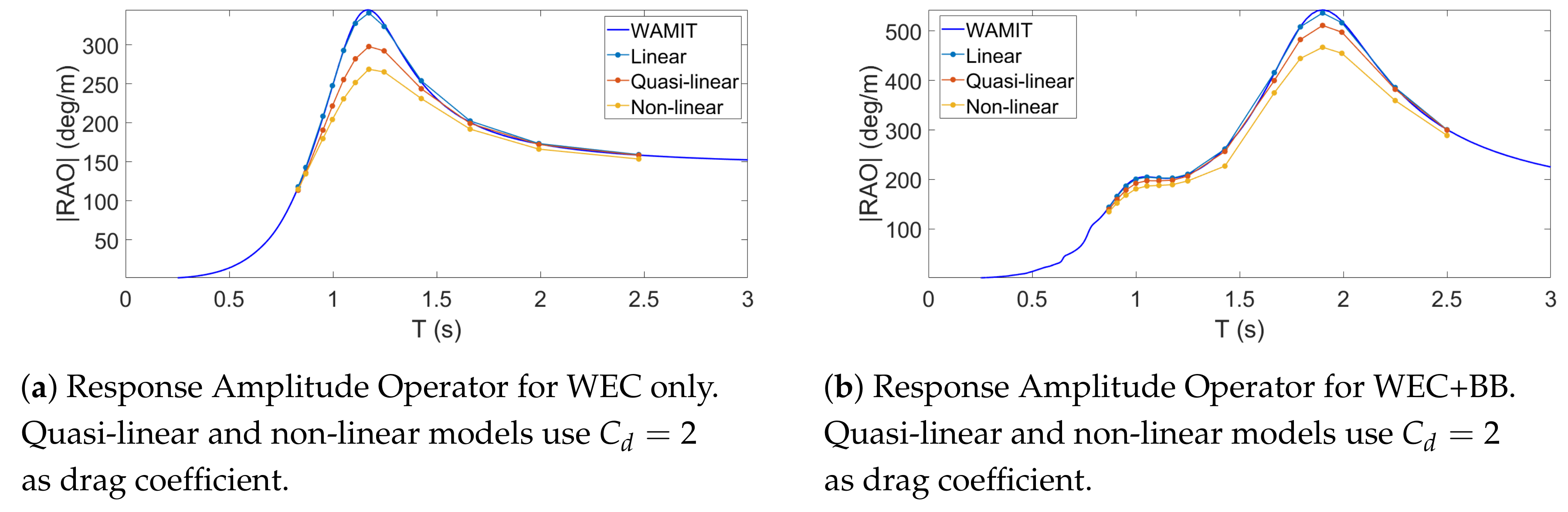
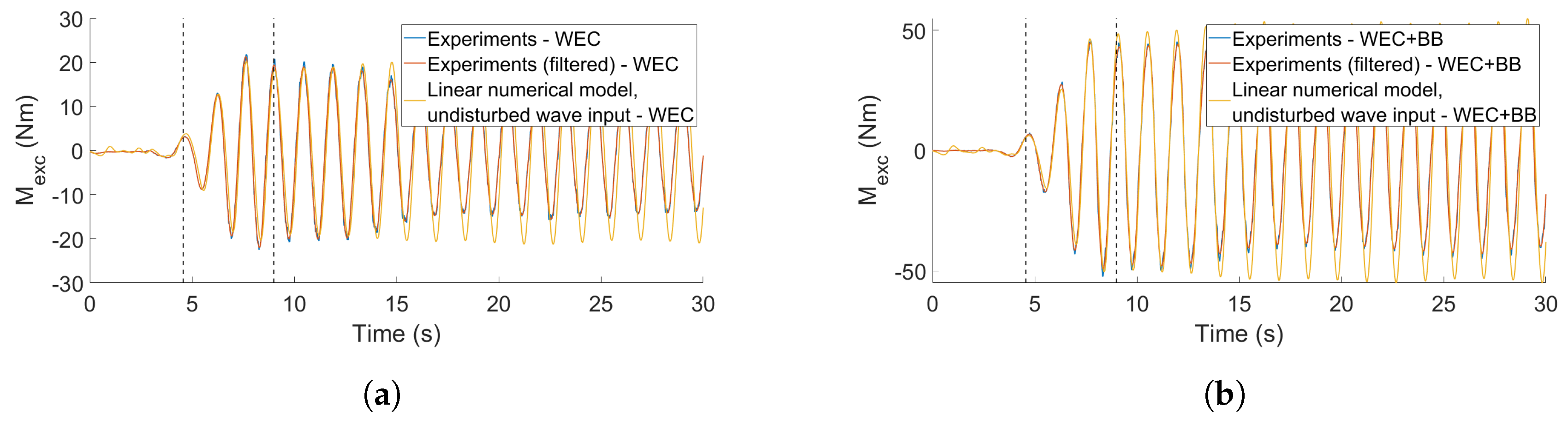
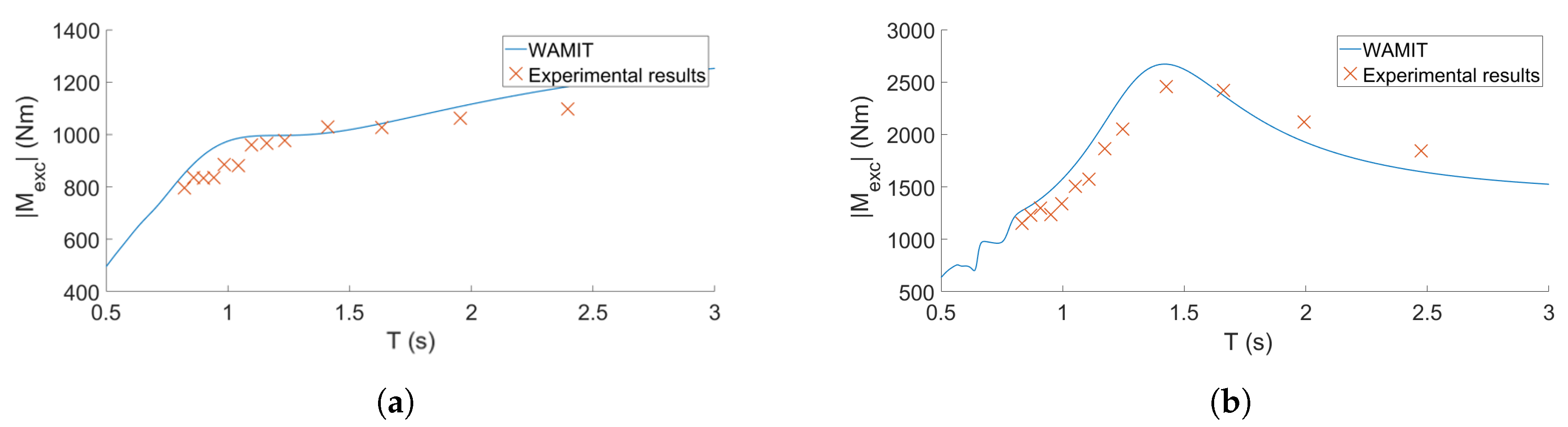
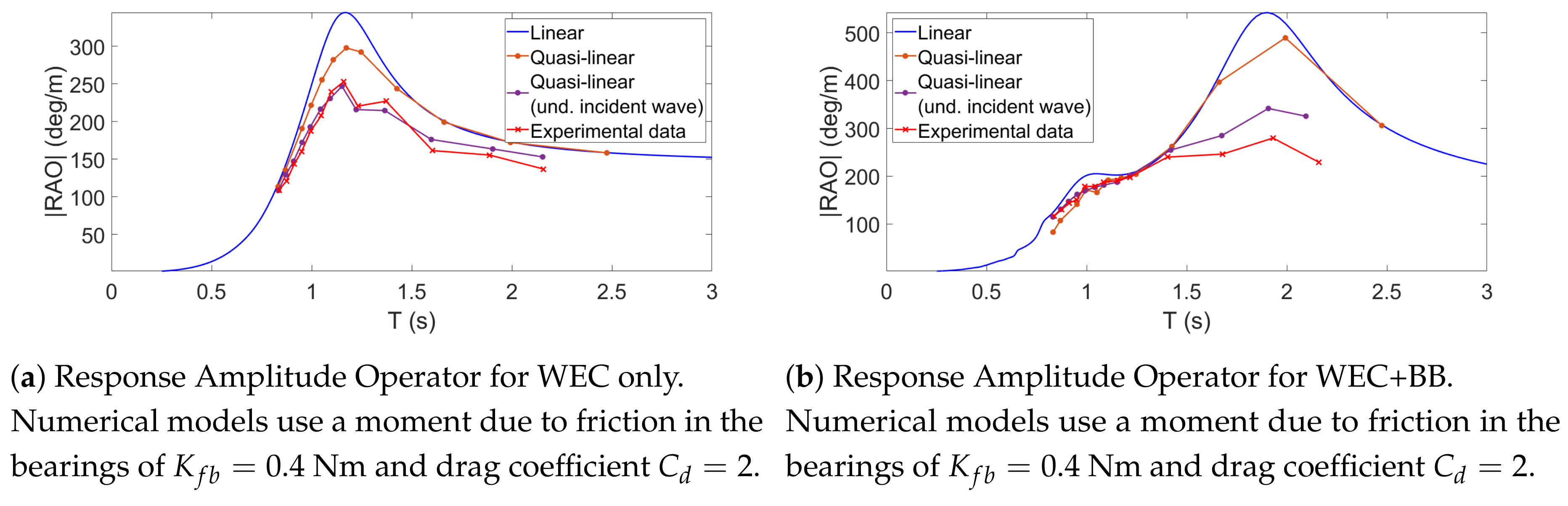
5.4. Wave Excitation
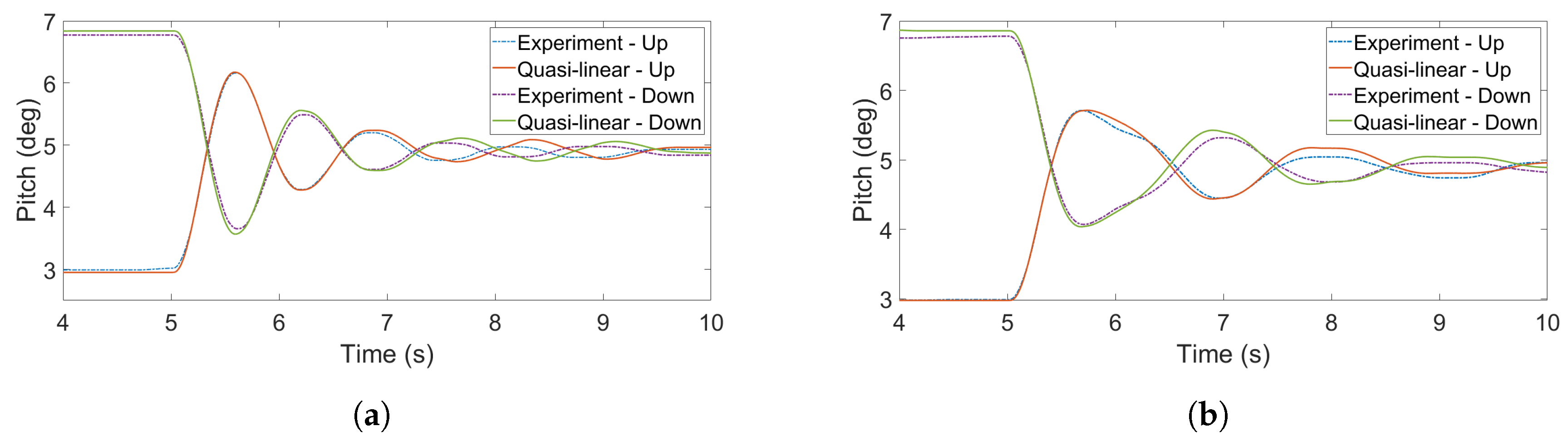
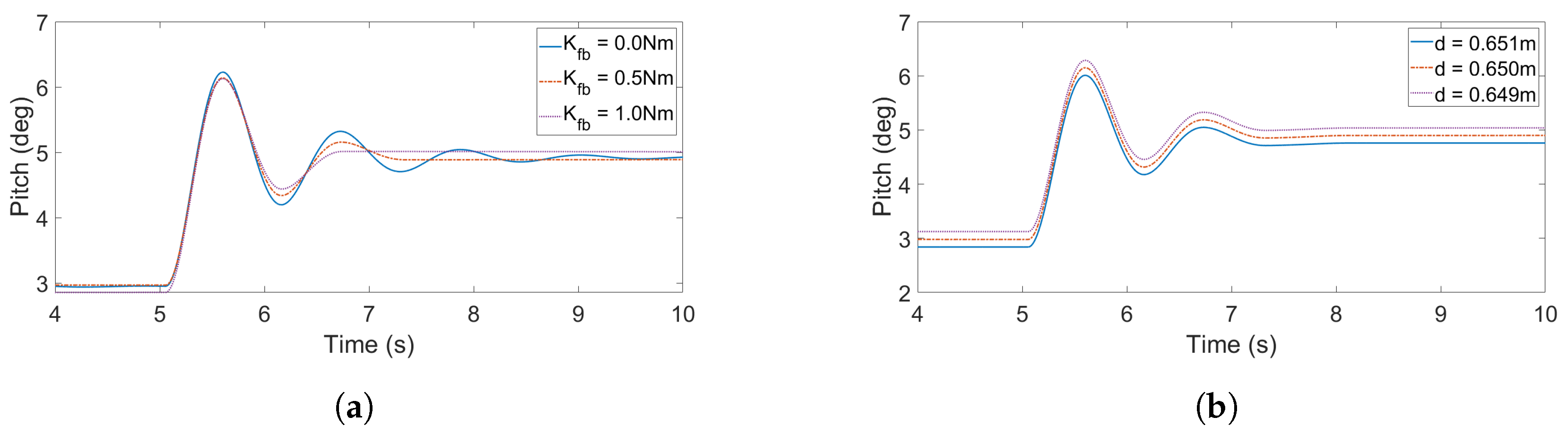
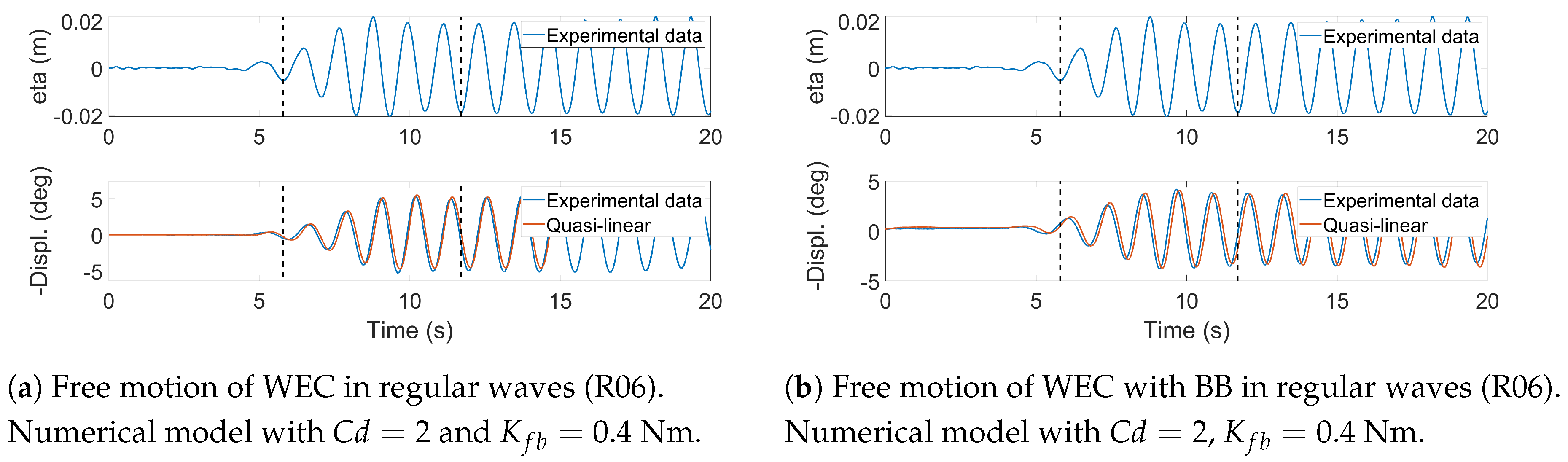
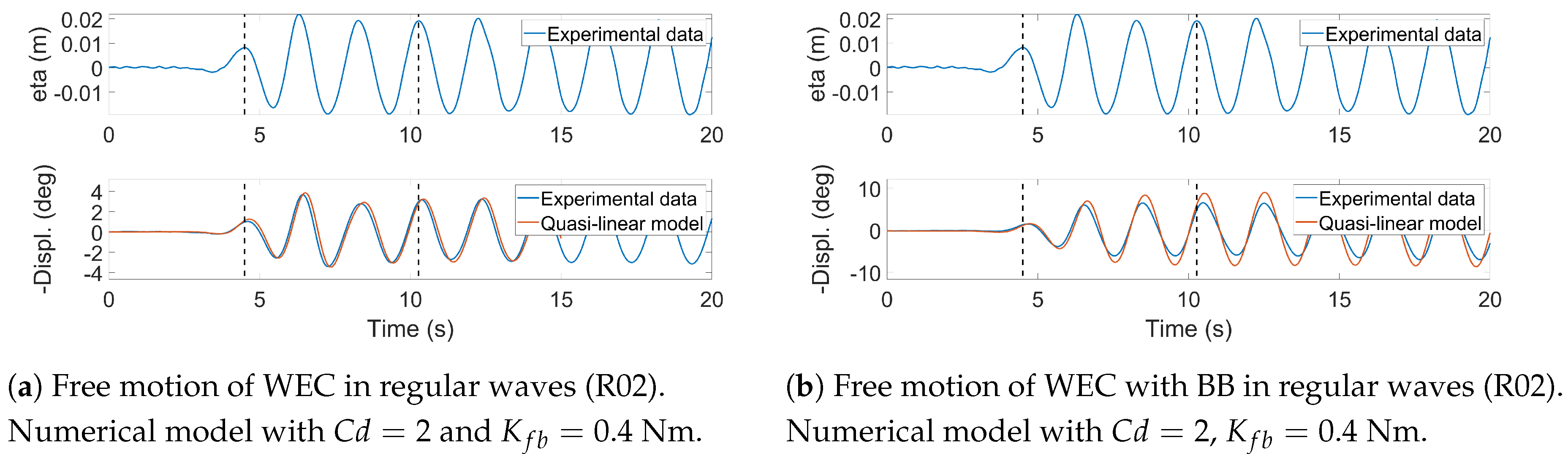
5.5. Free motion in Regular Waves
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weber, J. WEC technology readiness and performance matrix—Finding the best research technology development trajectory. In Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012. [Google Scholar]
- Falnes, J. Principles for Capture of Energy from Ocean Waves. Phase Control and Optimum Oscillation; Department of Physics, NTNU, N-7034: Trondheim, Norway, 1997. [Google Scholar]
- Salter, S.H. Wave power. Nature 1974, 249, 720–724. [Google Scholar] [CrossRef]
- Pecher, A.F.S.; Kofoed, J.P. (Eds.) Handbook of Ocean Wave Energy; (Ocean Engineering and Oceanography series, Vol. 7); Springer: Cham, Switzerland, 2017; 287p. [Google Scholar]
- Floating Power Plant. Available online: http://floatingpowerplant.com/ (accessed on 10 January 2019).
- Bellew, S.; Yde, A.; Verelst, D.R. Application of the aero-hydro-elastic model hawc2-wamit, to offshore data from floating power plants hybrid wind and wave energy test platform p37. In Proceedings of the 5th International Conference on Ocean Energy (ICOE), Halifax, NS, Canada, 4–6 November 2014. [Google Scholar]
- Yde, A.; Larsen, J.; Hansen, A.M.; Fernandez, M.; Bellew, S. Comparison of simulations and offshore measurement data of a combined floating wind and wave energy demonstration platform. J. Ocean. Wind. Energy 2015, 2, 129–137. [Google Scholar] [CrossRef]
- OES Task 10: Wave Energy Converters Modelling Verification and Validation. Available online: https://bit.ly/2zv0ebb (accessed on 10 January 2019).
- Wendt, F.F.; Yu, Y.H.; Nielsen, K.; Ruehl, K.; Bunnik, T.; Touzon, I.; Nam, B.W.; Kim, J.S.; Janson, C.E.; Jakobsen, K.R.; et al. International Energy Agency Ocean Energy Systems Task 10 Wave Energy Converter Modeling Verification and Validation. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1st September 2017. [Google Scholar]
- Folley, M. Numerical Modelling of Wave Energy Converters: State-of-the Art Techniques for Single WEC and Converter Arrays; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-803210-7. [Google Scholar]
- Babarit, A.; Mouslim, H.; Clément, A.; Laporte Weywada, P. On the Numerical Modelling of the Non Linear Behaviour of a Wave Energy Converter. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar] [CrossRef]
- Wolgamot, H.A.; Fitzgerald, C.J. Nonlinear hydrodynamic and real fluid effects on wave energy converters. Proc. Inst. Mech. Eng. Part J. Power Energy 2015, 229, 772–794. [Google Scholar] [CrossRef]
- Giorgi, G. Nonlinear Hydrodynamic Modelling of Wave Energy Converters under Controlled Conditions. Ph.D. Thesis, National University of Ireland Maynooth, Maynooth, Ireland, 2018. [Google Scholar]
- Ruehl, K.; Michelen, C.; Yu, Y.-H.; Lawson, M. Update on WEC-Sim Validation Testing and Code Development. In Proceedings of the 4th Marine Energy Technology Symposium, METS 2016, Washington, DC, USA, 25–27 April 2016. [Google Scholar]
- Combourieu, A.; Lawson, M.; Babarit, A.; Ruehl, K.; Roy, A.; Costello, R.; Laporte Weywada, P.; Bailey, H. WEC 3: Wave Energy Converter Code Comparison Project Preprint. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Ruehl, K.; Michelen, C.; Bosma, B.; Yu, Y.-H. WEC-Sim Phase 1 Validation Testing—Numerical Modeling of Experiments. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2016, Busan, Korea, 19–24 June 2016. [Google Scholar]
- WAMIT Software Information. Available online: https://www.wamit.com/ (accessed on 10 January 2019).
- Triangle Area. Available online: http://mathworld.wolfram.com/TriangleArea.html (accessed on 3 December 2018).
- Angle between Vectors Given Cross and Dot Product. Available online: https://math.stackexchange.com/questions/2041099/angle-between-vectors-given-cross-and-dot-product (accessed on 3 December 2018).
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, 3rd ed.; Addison Wesley: Reading, MA, USA, 2002; ISBN 978-0-201-65702-9. [Google Scholar]
- Heras, P.; Thomas, S.; Kramer, M.M. Validation of Hydrodynamic Numerical Model of a Pitching Wave Energy Converter. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC), Cork, Ireland, 27 August–1st September 2017. [Google Scholar]
- De Backer, G. Hydrodynamic Design Optimization of Wave Energy Converters Consisting of Heaving Point Absorbers. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2009. [Google Scholar]
- Datta, R.; Guedes Soares, C.; Rodrigues, J.M. A time domain panel method for the prediction of nonlinear hydrodynamic forces. In Proceedings of the 11th International Conference on Hydrodynamics—ICHD, Singapore, 19–24 October 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Giorgi, G.; Ringwood, J. Computationally efficient nonlinear Froude–Krylov force calculations for heaving axisymmetric wave energy point absorbers. J. Ocean Eng. Mar. Energy 2016, 3, 21–33. [Google Scholar] [CrossRef]
- Retes, M.P.; Mérigaud, A.; Gilloteaux, J.C.; Ringwood, J. Nonlinear Froude-Krylov force modelling for two heaving wave energy point absorbers. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Housseine, C.; Monroy, C.; de Hauteclocque, G. Stochastic Linearization of the Morison Equation Applied to an Offshore Wind Turbine. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; Volume 9. [Google Scholar] [CrossRef]
- Frigaard, P.; Andersen, T.L. Analysis of Waves: Technical Documentation for WaveLab 3. Aalborg; DCE Lecture notes, No. 33; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2014. [Google Scholar]
- Kramer, M. WEC experiments and the equations of motion. Presented at the 2017 Maynooth Wave Energy Workshop, Maynooth, Ireland, 20 January 2017. [Google Scholar]
- Le Mehaute, B. An introduction to Hydrodynamics and Water Waves; Springer Science & Business Media: New York, NY, USA, 1976. [Google Scholar]
- López, M.D.P.H.; Thomas, S.; Kramer, M.M. Validation of a Quasi-Linear Numerical Model of a Pitching Wave Energy Converter in Close Proximity to a Fixed Structure. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Artic Engineering: OMAE2017: Volume 10: Ocean Renewable Energy. Vol. 10 American Society of Mechanical Engineers, Trondheim, Norway, 25–30 June 2017; p. V010T09A020. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Bricktown, NJ, USA, 1965. [Google Scholar]
- Lawson, M.; Yu, Y.H.; Nelessen, A.; Ruehl, K.; Michelen, C. Implementing nonlinear buoyancy and excitation fordes in the WEC-Sim wave energy converter modelling tool (Preprint). Presented at the 33rd International Conference on Ocean Offshore and Artic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Newman, J.N. Wave effects on multiple bodies. In Hydrodynamics in Ship and Ocean Engineering; Kashiwagi, M., Ed.; RIAM, Kyushu University: Fukuoka, Japan, 2001; pp. 3–26. [Google Scholar]
- Zhao, W.; Taylor, P.H.; Wolgamot, H.A.; Taylor, R.E. Linear viscous damping in random wave excited gap resonance at laboratory scale—NewWave analysis and reciprocity. J. Fluids Struct. 2018, 80, 59–76. [Google Scholar] [CrossRef]



| Semisubmersible | WEC | WEC Scale Model | |||||
|---|---|---|---|---|---|---|---|
| Length main body | 86.5 m | Length main body | 10.8 m | Length main body | 343.5 mm | ||
| Length hinged arms | 99.3 m | Width | 18.3 m | Width | 1105.0 mm | ||
| Width | 36.0 m | Height | 11.0 m | Height | 423.0 mm | ||
| Height | 25.0 m | Length hinged arms | 6.2 m | Length hinged arms | 228.5 mm | ||
| Water depth | >45.0 m | Water depth | 650.0 mm |
| Wave condition | R01 | R02 | R03 | R04 | R05 | R06 | R07 | R08 |
| (s) | 2.500 | 2.000 | 1.667 | 1.429 | 1.250 | 1.176 | 1.111 | 1.053 |
| (m) | 0.019 | 0.020 | 0.019 | 0.019 | 0.019 | 0.019 | 0.020 | 0.021 |
| Wave condition | R09 | R10 | R11 | R12 | R13 | R14 | R15 | R16 |
| (s) | 1.000 | 0.952 | 0.909 | 0.870 | 0.833 | 0.769 | 0.714 | 0.667 |
| (m) | 0.021 | 0.023 | 0.021 | 0.022 | 0.021 | 0.021 | 0.023 | 0.023 |
| Wave condition | R09 | R17 | R18 | R19 | R20 |
| (s) | 1.00 | 0.95 | 0.98 | 0.99 | 0.98 |
| (m) | 0.042 | 0.020 | 0.059 | 0.076 | 0.092 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heras, P.; Thomas, S.; Kramer, M.; Kofoed, J.P. Numerical and Experimental Modelling of a Wave Energy Converter Pitching in Close Proximity to a Fixed Structure. J. Mar. Sci. Eng. 2019, 7, 218. https://doi.org/10.3390/jmse7070218
Heras P, Thomas S, Kramer M, Kofoed JP. Numerical and Experimental Modelling of a Wave Energy Converter Pitching in Close Proximity to a Fixed Structure. Journal of Marine Science and Engineering. 2019; 7(7):218. https://doi.org/10.3390/jmse7070218
Chicago/Turabian StyleHeras, Pilar, Sarah Thomas, Morten Kramer, and Jens Peter Kofoed. 2019. "Numerical and Experimental Modelling of a Wave Energy Converter Pitching in Close Proximity to a Fixed Structure" Journal of Marine Science and Engineering 7, no. 7: 218. https://doi.org/10.3390/jmse7070218






