Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics
Abstract
1. Introduction
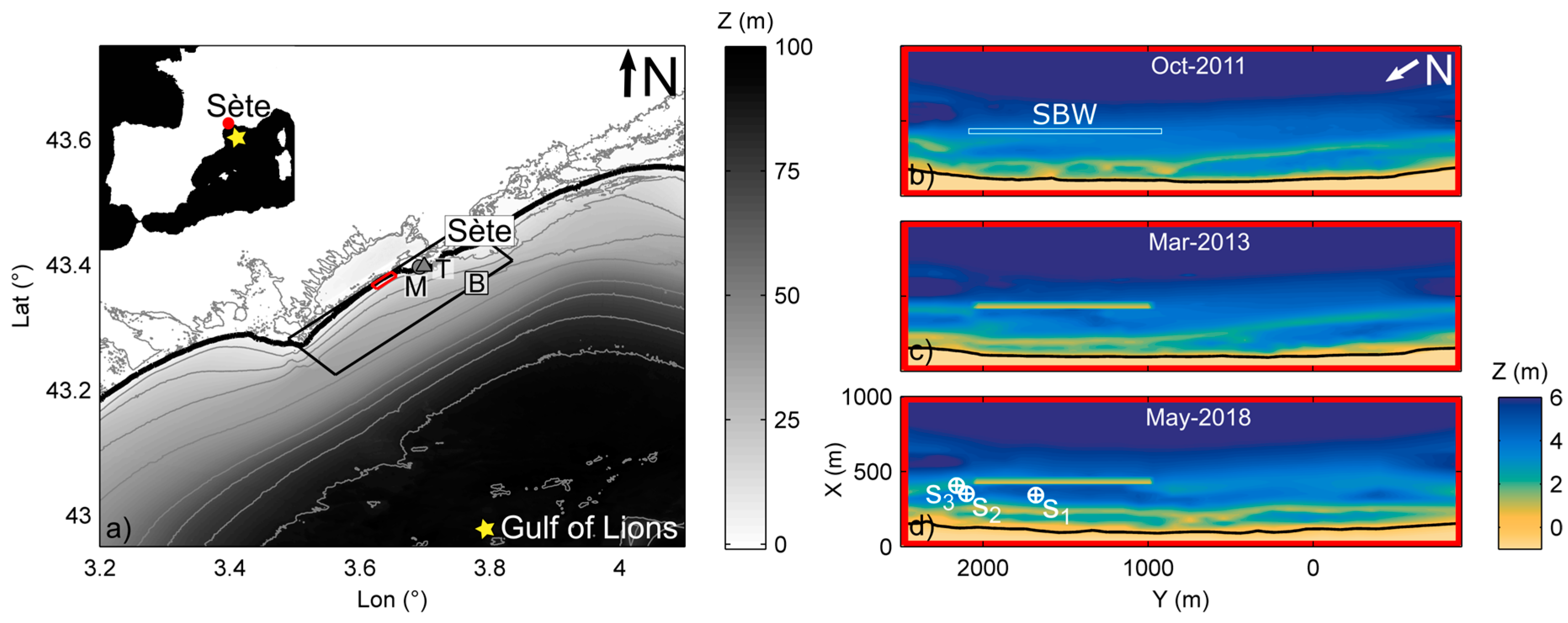
2. Study Area
3. Data & Methods
3.1. Field Measurements (April–May 2018 Field Campaign)
3.2. Model and Simulation Setup
3.2.1. Numerical Morphodynamic Model
3.2.2. Model Setup
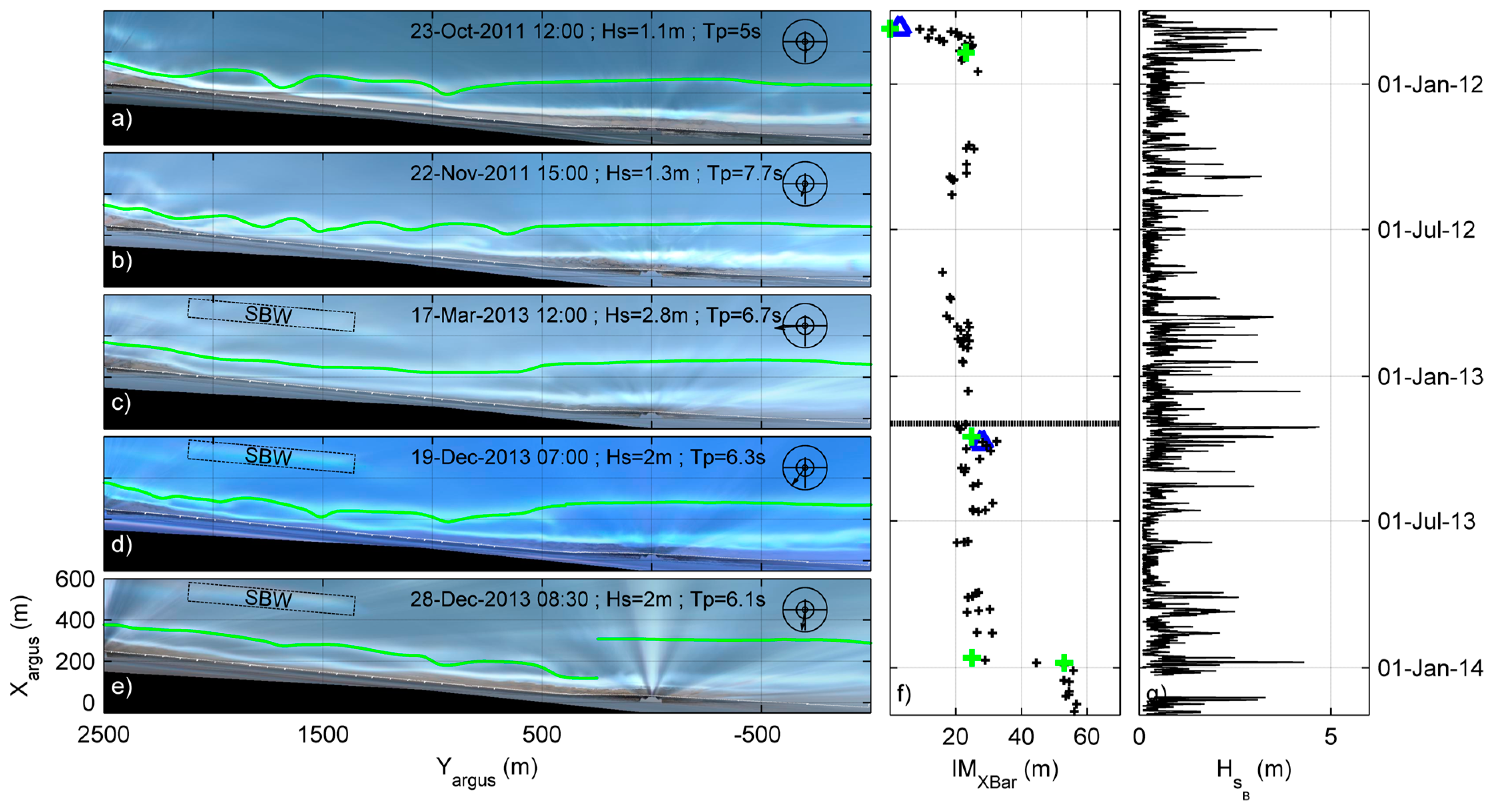
3.3. Video Data and Historical Storm Events Scenario
3.4. Residual and Vorticity Forcing
4. Results
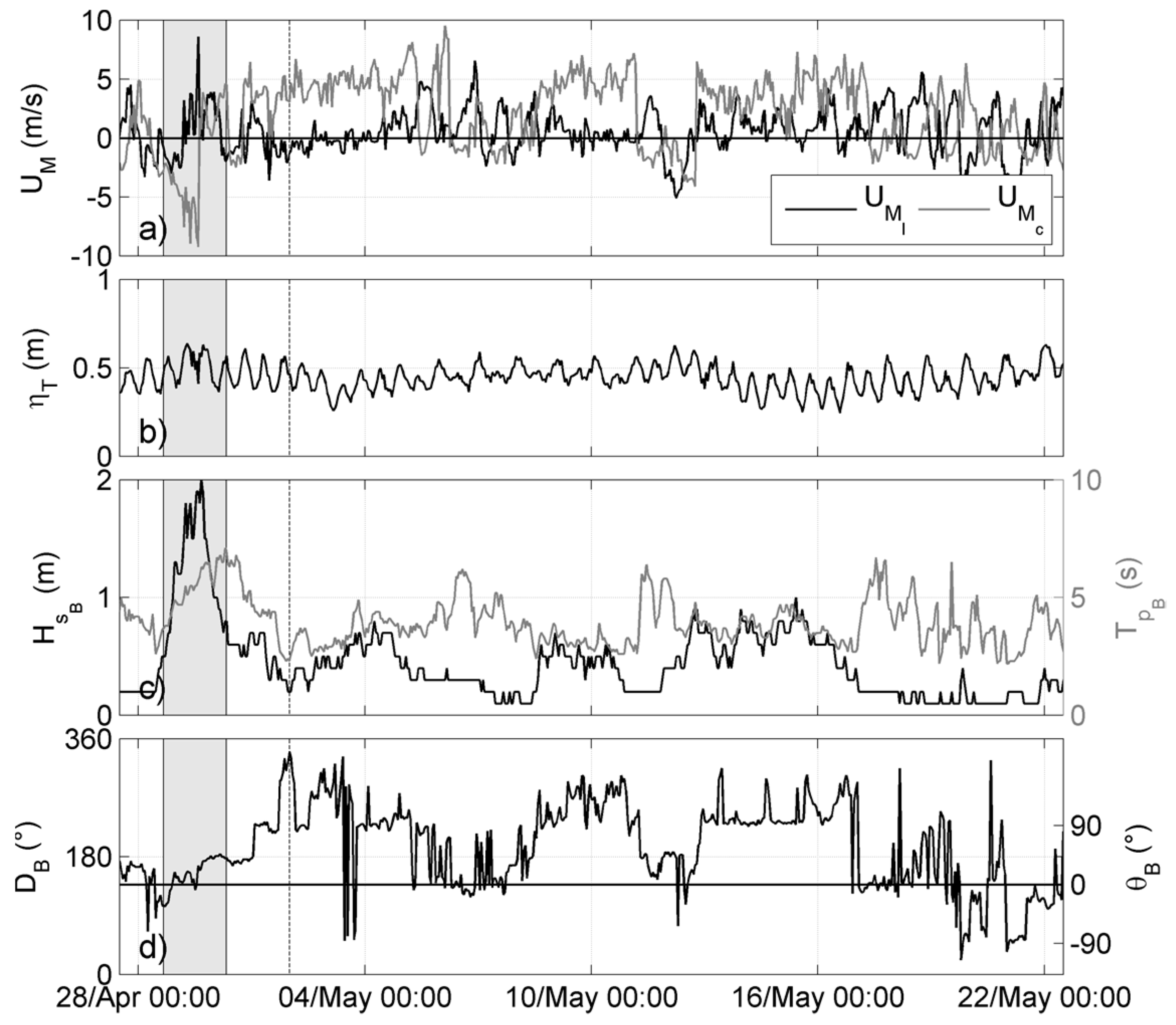
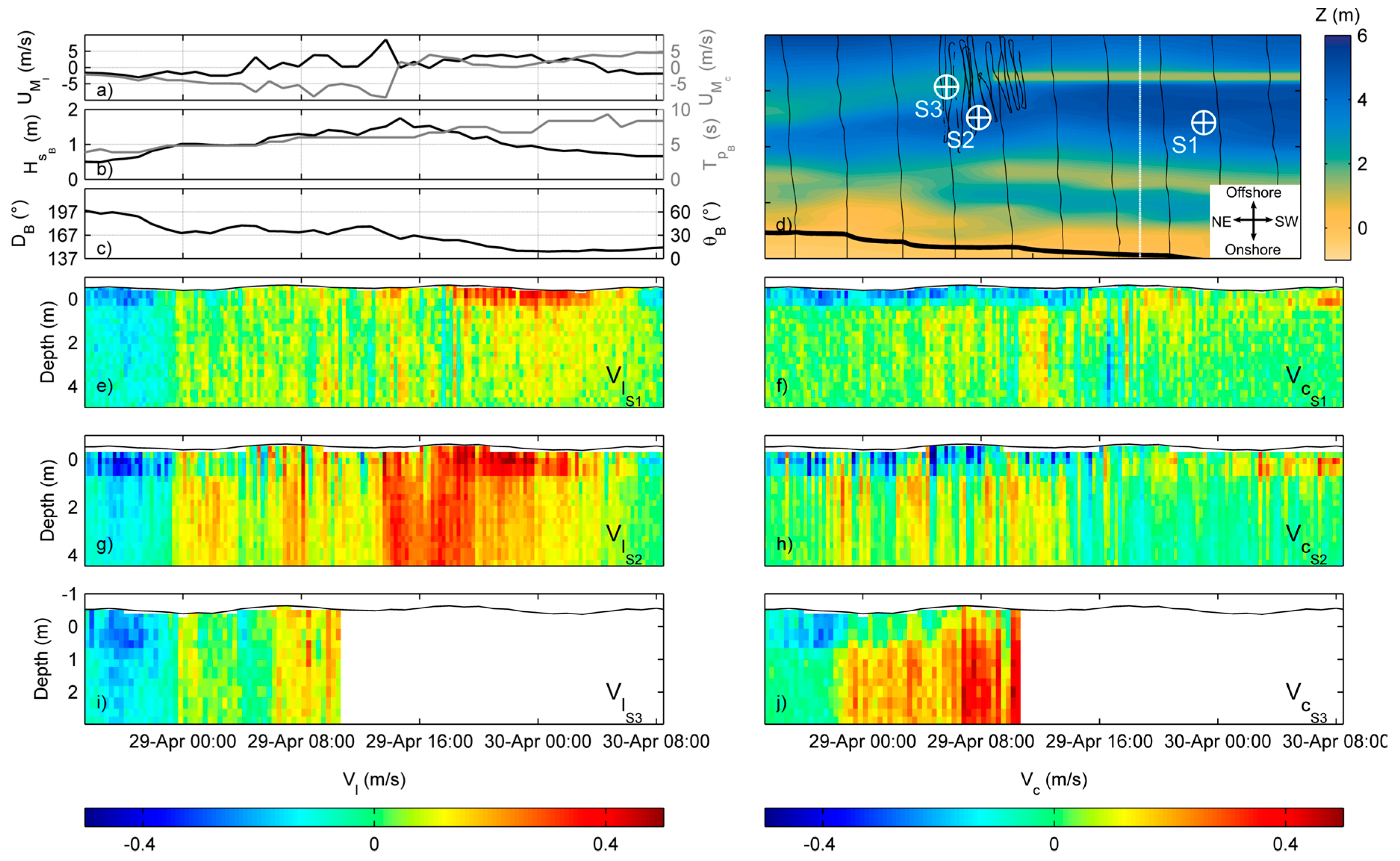
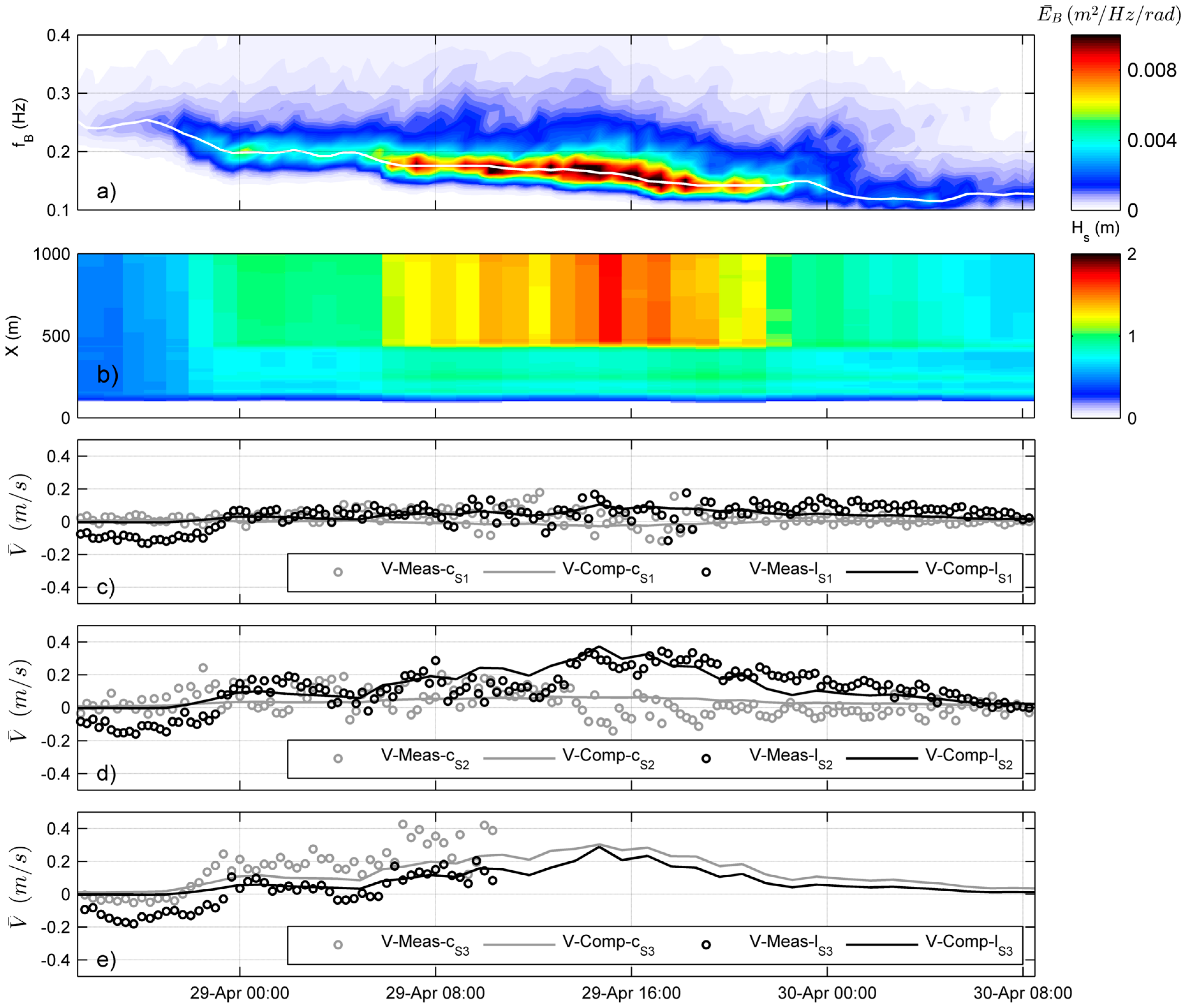
4.1. Wave-Driven Circulation Measurements
4.2. Model Calibration/Validation
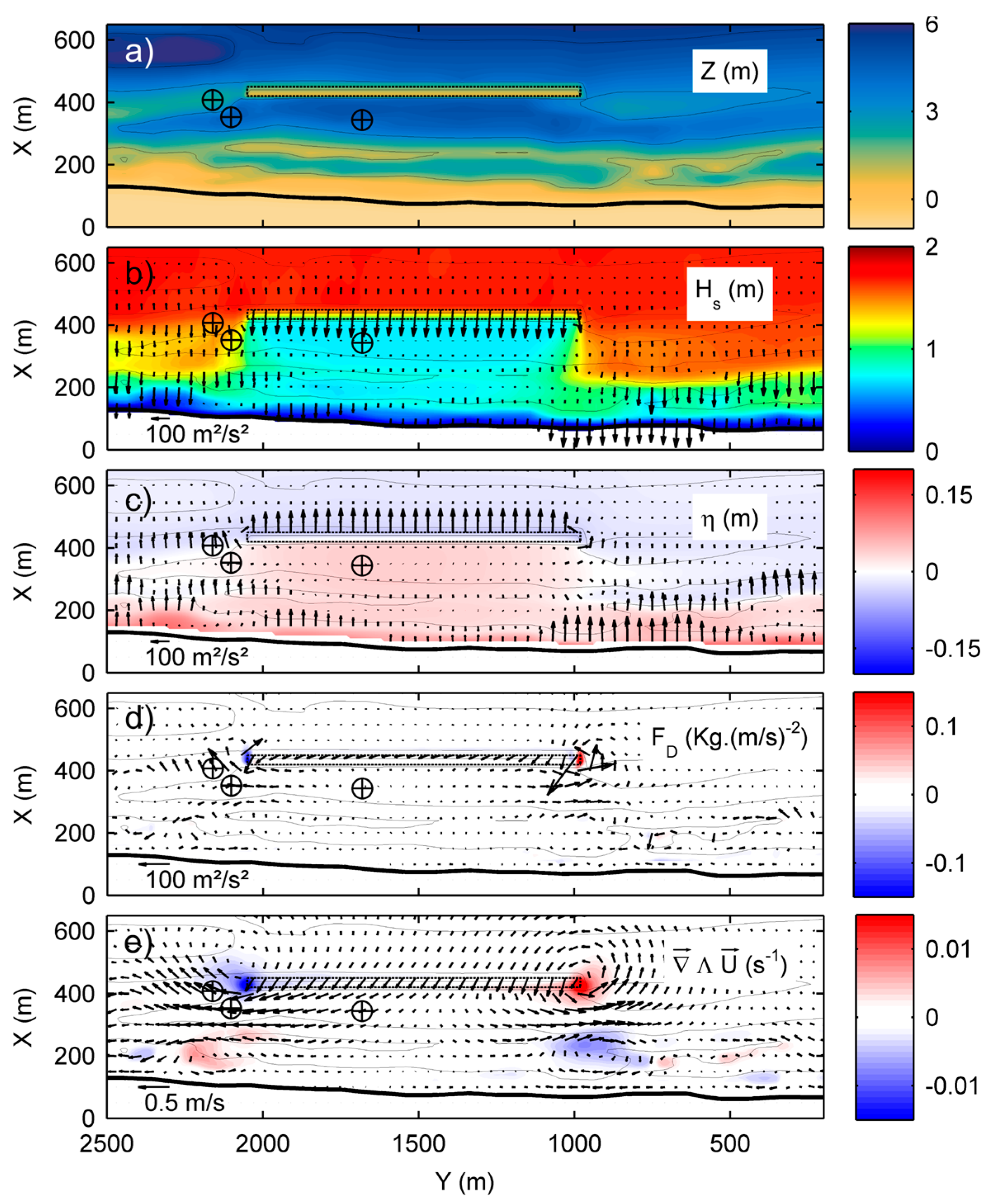
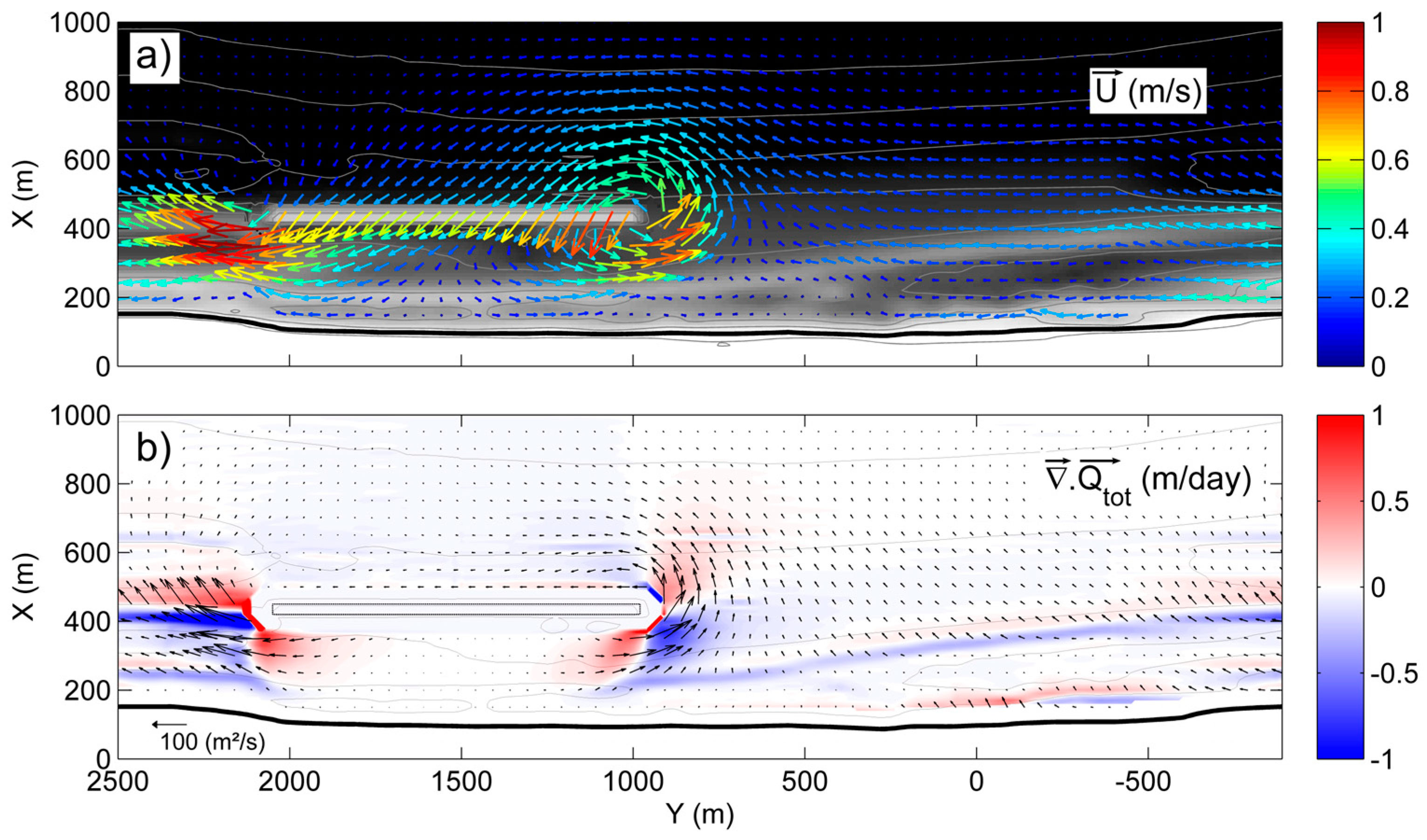
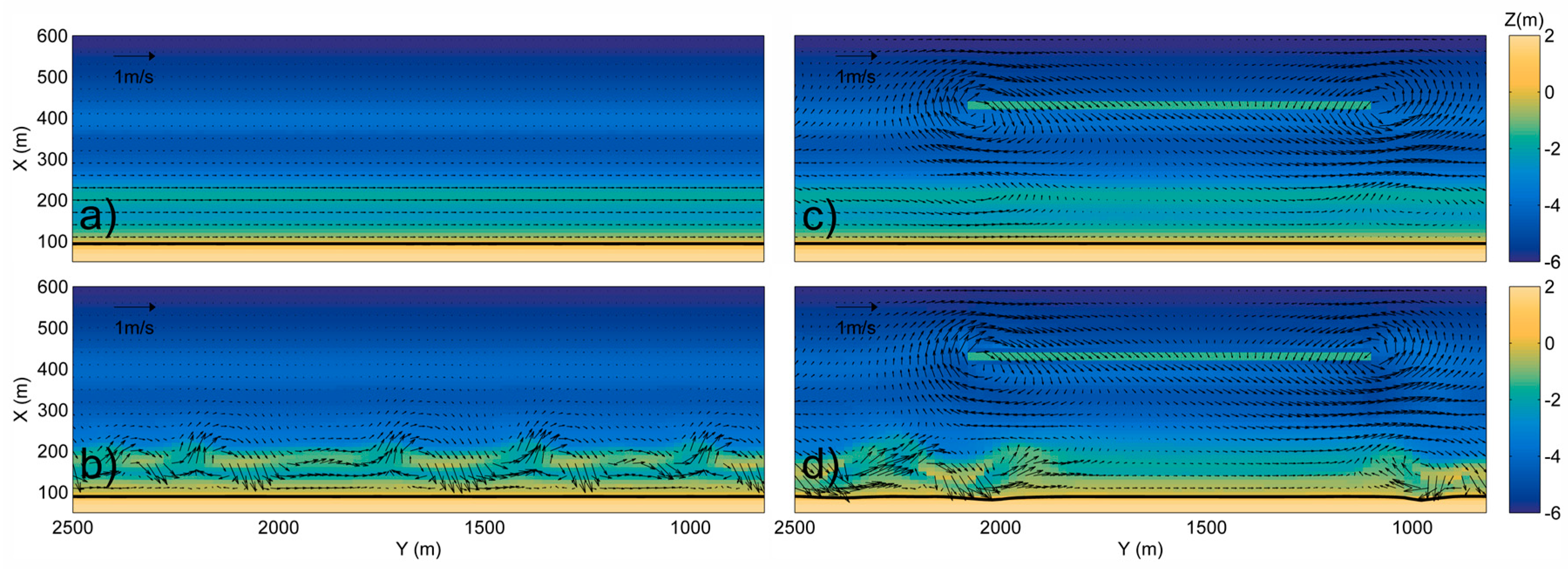
4.3. Driving Mechanisms of Rip-Cell Circulation at the Extremities of the Submerged Breakwater (SBW)
4.4. Hydrodynamics During Representative Severe Storms
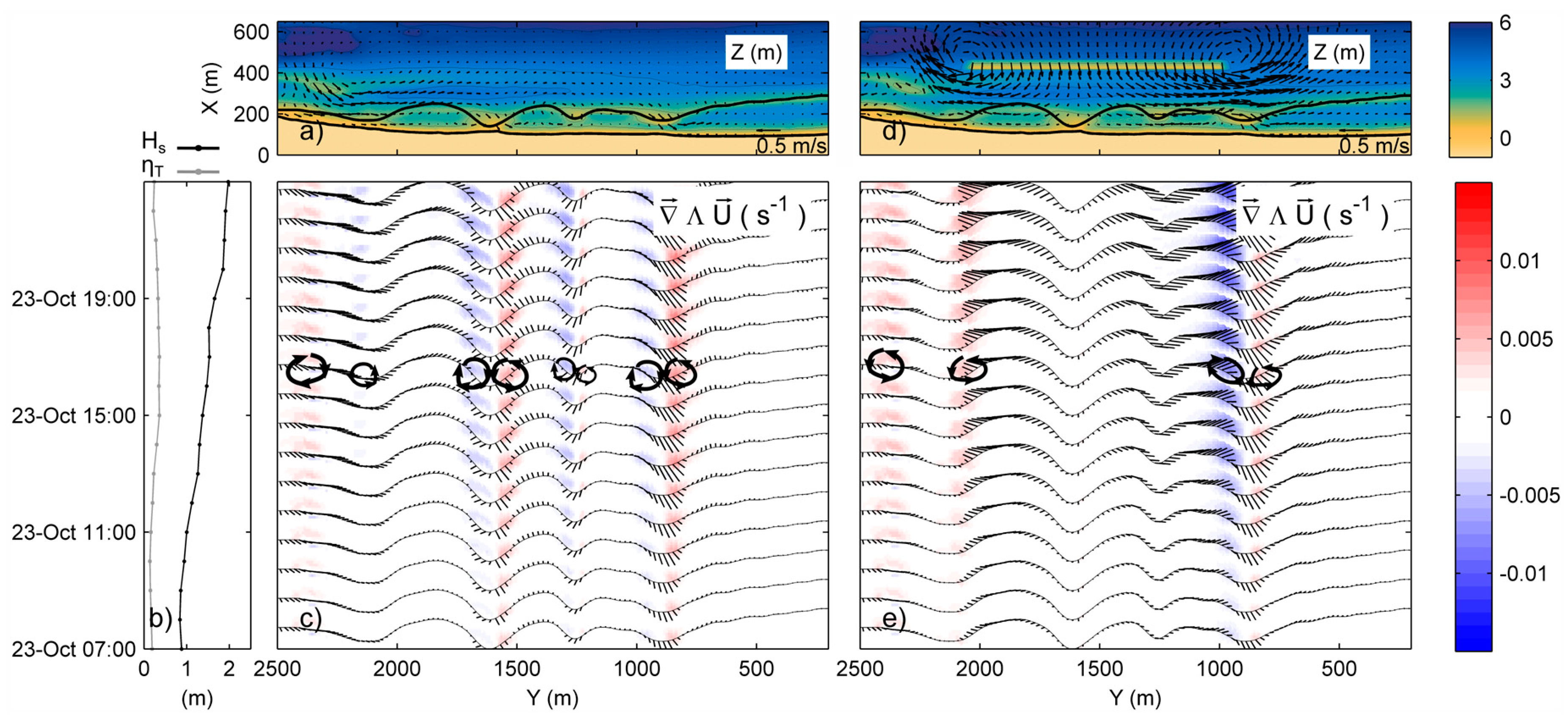
4.4.1. The October 2011 Event
4.4.2. The December 2013 Event
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Charlier, R.H.; De Meyer, C.P. Coastal defense and beach renovation. Ocean Shorel. Manag. 1989, 12, 525–543. [Google Scholar] [CrossRef]
- Nordstrom, K.F. Living with shore protection structures: A review. Estuar. Coast. Shelf Sci. 2014, 150, 11–23. [Google Scholar] [CrossRef]
- Charlier, R.H.; Chaineux, M.C.P.; Morcos, S. Panorama of the History of Coastal Protection. J. Coast. Res. 2005, 21, 79–111. [Google Scholar] [CrossRef]
- van Rijn, L.C. Coastal erosion and control. Ocean Coast. Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Black, K.P.; Andrews, C.J. Sandy Shoreline Response to Offshore Obstacles Part 1: Salient and Tombolo Geometry and Shape. J. Coast. Res. 2001, 82–93. [Google Scholar] [CrossRef]
- Evans, P.; Ranasinghe, R. Artificial Surfing Reefs: A New Paradigm in Coastal Protection? In Proceedings of the 15th Australasian Coastal and Ocean Engineering Conference, the 8th Australasian Port and Harbour Conference, Gold Coast, QLD, Australia, 25–28 September 2001; pp. 128–133. [Google Scholar]
- Wamsley, T.; Hanson, H.; Kraus, N. Wave Transmission at Detached Breakwaters for Shoreline Response Modeling; ERDC/CHL CHETN-II45; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2002. [Google Scholar]
- Isebe, D.; Azerad, P.; Bouchette, F.; Ivorra, B.; Mohammadi, B. Shape optimization of geotextile tubes for sandy beach protection. Int. J. Numer. Methods Eng. 2008, 74, 1262–1277. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Briganti, R.; Zanuttigh, B.; Wang, B. Wave transmission and reflection at low-crested structures: Design formulae, oblique wave attack and spectral change. Coast. Eng. 2005, 52, 915–929. [Google Scholar] [CrossRef]
- Calabrese, M.; Vicinanza, D.; Buccino, M. 2D Wave setup behind submerged breakwaters. Ocean Eng. 2008, 35, 1015–1028. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J.; Lamberti, A.; Zanuttigh, B.; Dixen, M.; Gislason, K.; Di Penta, A.F. Local scour at roundhead and along the trunk of low crested structures. Coast. Eng. 2005, 52, 995–1025. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Turner, I.L. Shoreline response to submerged structures: A review. Coast. Eng. 2006, 53, 65–79. [Google Scholar] [CrossRef]
- Tomasicchio, U. Submerged Breakwaters for the Defence of the Shoreline at Ostia Field Experiences, Comparison. In Proceedings of the 25th Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: New York, NY, USA, 1996; pp. 2404–2417. [Google Scholar]
- Lamberti, A.; Mancinelli, A. Italian Experience on Submerged Barriers as Beach Defence Structures. In Proceedings of the 25th Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: New York, NY, USA, 1996; pp. 2352–2365. [Google Scholar]
- Dean, R.; Chen, R.; Browder, A. Full scale monitoring study of a submerged breakwater, Palm Beach, Florida, USA. Coast. Eng. 1997, 29, 291–315. [Google Scholar] [CrossRef]
- Johnson, H.K.; Karambas, T.V.; Avgeris, I.; Zanuttigh, B.; Gonzalez-Marco, D.; Caceres, I. Modelling of waves and currents around submerged breakwaters. Coast. Eng. 2005, 52, 949–969. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Turner, I.L.; Symonds, G. Shoreline response to multi-functional artificial surfing reefs: A numerical and physical modelling study. Coast. Eng. 2006, 53, 589–611. [Google Scholar] [CrossRef]
- Bruneau, N.; Bonneton, P.; Castelle, B.; Pedreros, R. Modeling rip current circulations and vorticity in a high-energy mesotidal-macrotidal environment. J. Geophys. Res. Ocean. 2011, 116, C07026. [Google Scholar] [CrossRef]
- Castelle, B.; Scott, T.; Brander, R.W.; McCarroll, R.J. Rip current types, circulation and hazard. Earth-Sci. Rev. 2016, 163, 1–21. [Google Scholar] [CrossRef]
- Utizi, K.; Corbau, C.; Rodella, I.; Nannini, S.; Simeoni, U. A mixed solution for a highly protected coast (Punta Marina, Northern Adriatic Sea, Italy). Mar. Geol. 2016, 381, 114–127. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Larson, M.; Savioli, J. Shoreline response to a single shore-parallel submerged breakwater. Coast. Eng. 2010, 57, 1006–1017. [Google Scholar] [CrossRef]
- Zanuttigh, B. Numerical modelling of the morphological response induced by low-crested structures in Lido di Dante, Italy. Cost. Eng. 2007, 54, 31–47. [Google Scholar] [CrossRef]
- Thornton, E.B.; MacMahan, J.; Sallenger, A.H. Rip currents, mega-cusps, and eroding dunes. Mar. Geol. 2007, 240, 151–167. [Google Scholar] [CrossRef]
- van de Lageweg, W.I.; Bryan, K.R.; Coco, G.; Ruessink, B.G. Observations of shoreline–sandbar coupling on an embayed beach. Mar. Geol. 2013, 344, 101–114. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujan, S.; Splinter, K.D.; Robinet, A.; Sénéchal, N.; Ferreira, S. Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments. Geomorphology 2015, 238, 135–148. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. Quantification of sand bar morphology: A video technique based on wave dissipation. J. Geophys. Res. 1989, 94, 995. [Google Scholar] [CrossRef]
- Alexander, P.S.; Holman, R.A. Quantification of nearshore morphology based on video imaging. Mar. Geol. 2004, 208, 101–111. [Google Scholar] [CrossRef]
- Holman, R.A.; Symonds, G.; Thornton, E.B.; Ranasinghe, R. Rip spacing and persistence on an embayed beach. J. Geophys. Res. 2006, 111, C01006. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Pape, L.; Turner, I.L. Daily to interannual cross-shore sandbar migration: Observations from a multiple sandbar system. Cont. Shelf Res. 2009, 29, 1663–1677. [Google Scholar] [CrossRef]
- Almar, R.; Castelle, B.; Ruessink, B.G.; Sénéchal, N.; Bonneton, P.; Marieu, V. Two- and three-dimensional double-sandbar system behaviour under intense wave forcing and a meso-macro tidal range. Cont. Shelf Res. 2010, 30, 781–792. [Google Scholar] [CrossRef]
- Gallop, S.L.; Bryan, K.R.; Coco, G.; Stephens, S.A. Storm-driven changes in rip channel patterns on an embayed beach. Geomorphology 2011, 127, 179–188. [Google Scholar] [CrossRef]
- Bouvier, C.; Balouin, Y.; Castelle, B. Video monitoring of sandbar-shoreline response to an offshore submerged structure at a microtidal beach. Geomorphology 2017, 295, 297–305. [Google Scholar] [CrossRef]
- Balouin, Y.; Tesson, J.; Gervais, M. Cuspate shoreline relationship with nearshore bar dynamics during storm events—Field observations at Sete beach, France. J. Coast. Res. 2013, 65 (Suppl. 1), 440–446. [Google Scholar] [CrossRef]
- Gervais, M.; Balouin, Y.; Belon, R. Morphological response and coastal dynamics associated with major storm events along the Gulf of Lions Coastline, France. Geomorphology 2012, 143, 69–80. [Google Scholar] [CrossRef]
- Certain, R.; Barusseau, J.P. Conceptual modelling of sand bars morphodynamics for a microtidal beach (Sète, France). Bull. Soc. Geol. Fr. 2005, 176, 343–354. [Google Scholar] [CrossRef]
- Balouin, Y.; Rey-Valette, H.; Picand, P.A. Automatic assessment and analysis of beach attendance using video images at the Lido of Sète beach, France. Ocean Coast. Manag. 2014, 102, 114–122. [Google Scholar] [CrossRef]
- BCEOM. Etude générale pour la protection et l’aménagement durable du lido de Sète à Marseillan, Synthèse générale; Artelia: Marseille, France, 2001. [Google Scholar]
- Bouvier, C.; Balouin, Y.; Castelle, B. Nearshore bars and shoreline dynamics associated with the implementation of a submerged breakwater: Topo-bathymetric analysis and video assessment at the Lido of Sète beach. In Proceedings of the Coastal Dynamics, Helsingør Denmark, 12–16 June 2017; pp. 534–543. [Google Scholar]
- Castelle, B.; Marieu, V.; Coco, G.; Bonneton, P.; Bruneau, N.; Ruessink, B.G. On the impact of an offshore bathymetric anomaly on surf zone rip channels. J. Geophys. Res. Earth Surf. 2012, 117, f1. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Castelle, B.; Bonneton, P.; Sénéchal, N.; Dupuis, H.; Butel, R.; Michel, D. Dynamics of wave-induced currents over an alongshore non-uniform multiple-barred sandy beach on the Aquitanian Coast, France. Cont. Shelf Res. 2006, 26, 113–131. [Google Scholar] [CrossRef]
- Mei, C.; Stiassnie, M.; Yue, D. Theory and Applications of Ocean Surface Waves: Part 1: Linear Aspects Part 2: Nonlinear Aspects; World Scientific: Singapore, 1989; Volume 23, p. 506. [Google Scholar]
- Phillips, O.M. The Dynamics of the Upper Ocean, 2nd ed.; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Battjes, J. Modeling of turbulence in the surf zone. In Proceedings of the Symposium on Modeling Techniques, ASCE, San Francisco, CA, USA, 3–5 September 1975; pp. 1050–1061. [Google Scholar]
- Hsu, T.-J.; Elgar, S.; Guza, R.T. Wave-induced sediment transport and onshore sandbar migration. Coast. Eng. 2006, 53, 817–824. [Google Scholar] [CrossRef]
- Dubarbier, B.; Castelle, B.; Marieu, V.; Ruessink, G. Process-based modeling of cross-shore sandbar behavior. Coast. Eng. 2015, 95, 35–50. [Google Scholar] [CrossRef]
- Dubarbier, B.; Castelle, B.; Ruessink, G.; Marieu, V. Mechanisms controlling the complete accretionary beach state sequence. Geophys. Res. Lett. 2017, 44, 5645–5654. [Google Scholar] [CrossRef]
- Cavaleri, L.; Rizzoli, P.M. Wind wave prediction in shallow water: Theory and applications. J. Geophys. Res. 1981, 86, 10961. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, K.; Hasselmann, K.; Komen, G.J.; Hasselmann, K.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Madsen, O.S.; Poon, Y.-K.; Graber, H.C. Spectral Wave Attenuation by Bottom Friction: Theory. In Proceedings of the 21st Conference on Coastal Engineering, Costa del Sol-Malaga, Spain, 20–25 June 1988; American Society of Civil Engineers: New York, NY, USA, 1989; pp. 492–504. [Google Scholar]
- Valentini, N.; Saponieri, A.; Damiani, L. A new video monitoring system in support of Coastal Zone Management at Apulia Region, Italy. Ocean Coast. Manag. 2017, 142, 122–135. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due to Breaking of Random Waves. In Proceedings of the 16th Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; American Society of Civil Engineers: New York, NY, USA, 1978; pp. 569–587. [Google Scholar]
- Battjes, J.A.; Stive, M.J.F. Calibration and verification of a dissipation model for random breaking waves. J. Geophys. Res. 1985, 90, 9159. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Zijlema, M.; Allier, P.-E.; Holthuijsen, L.H.; Booij, N.; Meixner, J.D.; Proft, J.K.; Dawson, C.N.; Bender, C.J.; Naimaster, A.; et al. Limiters for spectral propagation velocities in SWAN. Ocean Model. 2013, 70, 85–102. [Google Scholar] [CrossRef]
- Davidson, M.A.; Splinter, K.D.; Turner, I.L. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Bouvier, C.; Balouin, Y.; Castelle, B.; Holman, R. Modelling camera viewing angle deviation to improve nearshore video monitoring. Coast. Eng. 2019, 174, 99–106. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical Use of Video Imagery in Nearshore Oceanographic Field Studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Duarte Nemes, D.; Fabián Criado-Sudau, F.; Nicolás Gallo, M.; Duarte Nemes, D.; Fabián Criado-Sudau, F.; Nicolás Gallo, M. Beach Morphodynamic Response to a Submerged Reef. Water 2019, 11, 340. [Google Scholar] [CrossRef]
- Calvete, D.; Dodd, N.; Falqués, A.; van Leeuwen, S.M. Morphological development of rip channel systems: Normal and near-normal wave incidence. J. Geophys. Res. Ocean. 2005, 110, C10. [Google Scholar] [CrossRef]
- Garnier, R.; Falqués, A.; Calvete, D.; Thiébot, J.; Ribas, F. A mechanism for sandbar straightening by oblique wave incidence. Geophys. Res. Lett. 2013, 40, 2726–2730. [Google Scholar] [CrossRef]
- Castelle, B.; Ruessink, B.G. Modeling formation and subsequent nonlinear evolution of rip channels: Time-varying versus time-invariant wave forcing. J. Geophys. Res. Earth Surf. 2011, 116, f4. [Google Scholar] [CrossRef]
| Station | BSS | RMSE | R2 | |
|---|---|---|---|---|
| 0.52 | 0.06 | 0.26 | 0.07 | |
| 0.83 | 0.08 | 0.63 | 0.13 | |
| 0.45 | 0.08 | 0.33 | 0.11 | |
| 0.13 | 0.05 | 0 | 0.04 | |
| 0.33 | 0.07 | 0 | 0.07 | |
| 0.77 | 0.10 | 0.42 | 0.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouvier, C.; Castelle, B.; Balouin, Y. Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics. J. Mar. Sci. Eng. 2019, 7, 117. https://doi.org/10.3390/jmse7040117
Bouvier C, Castelle B, Balouin Y. Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics. Journal of Marine Science and Engineering. 2019; 7(4):117. https://doi.org/10.3390/jmse7040117
Chicago/Turabian StyleBouvier, Clément, Bruno Castelle, and Yann Balouin. 2019. "Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics" Journal of Marine Science and Engineering 7, no. 4: 117. https://doi.org/10.3390/jmse7040117
APA StyleBouvier, C., Castelle, B., & Balouin, Y. (2019). Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics. Journal of Marine Science and Engineering, 7(4), 117. https://doi.org/10.3390/jmse7040117






