A Numerical Assessment of Artificial Reef Pass Wave-Induced Currents as a Renewable Energy Source
Abstract
1. Introduction
2. Methods
2.1. Numerical Model
2.1.1. Cross-Shore Benchmark Case
2.1.2. Artificial Breakwater Configurations
- W is the width of the reef pass
- is the distance from the shore to the reef pass
- is the length of each wing
- is the breakwater angle
- D is the breakwater width
- H is the breakwater top depth, which is constant for a given case.
2.2. Strategy
2.3. Power Estimation
3. Results
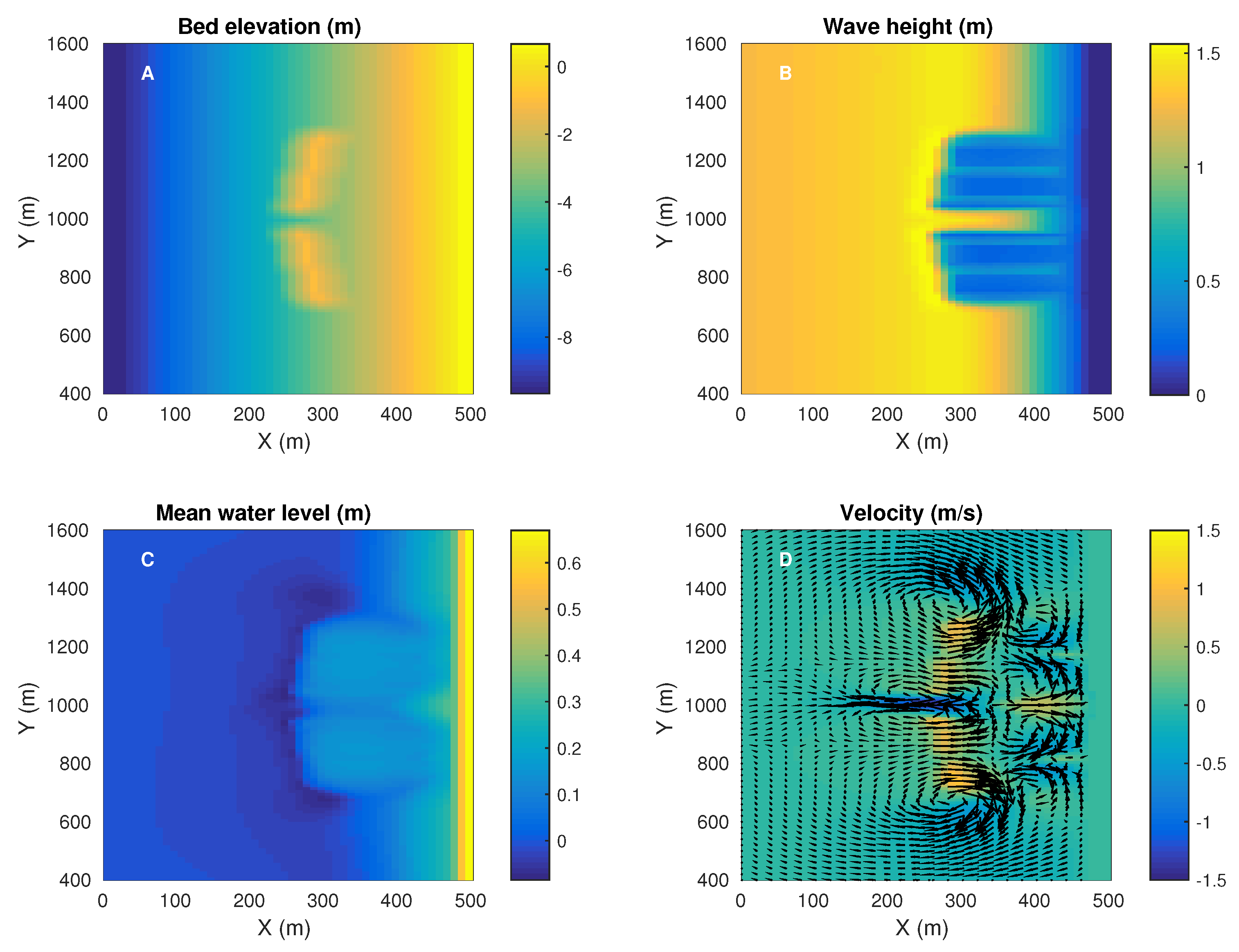
3.1. Reference Case
3.1.1. Basic Reef Hydrodynamics
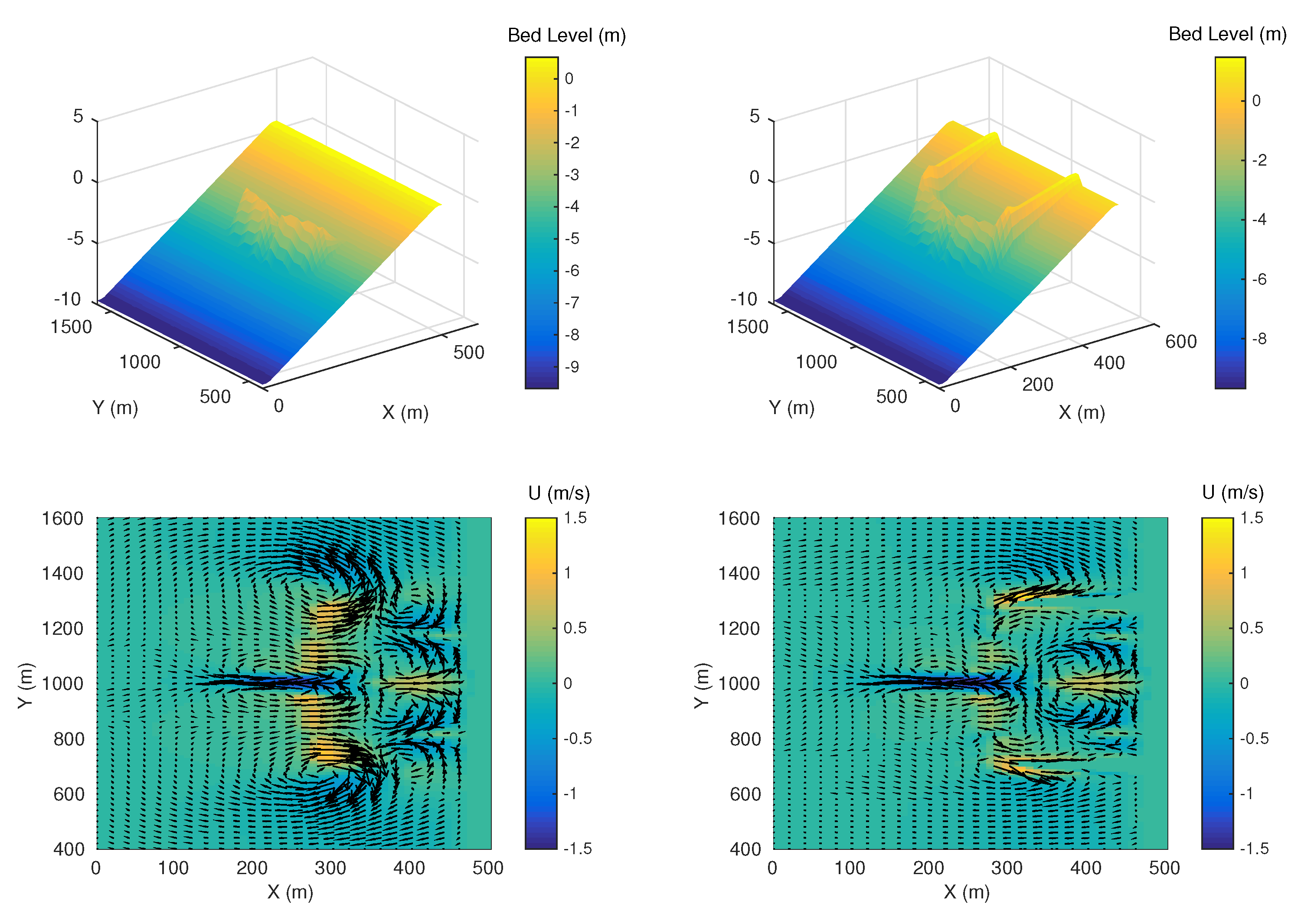
3.1.2. Side Wall Effect
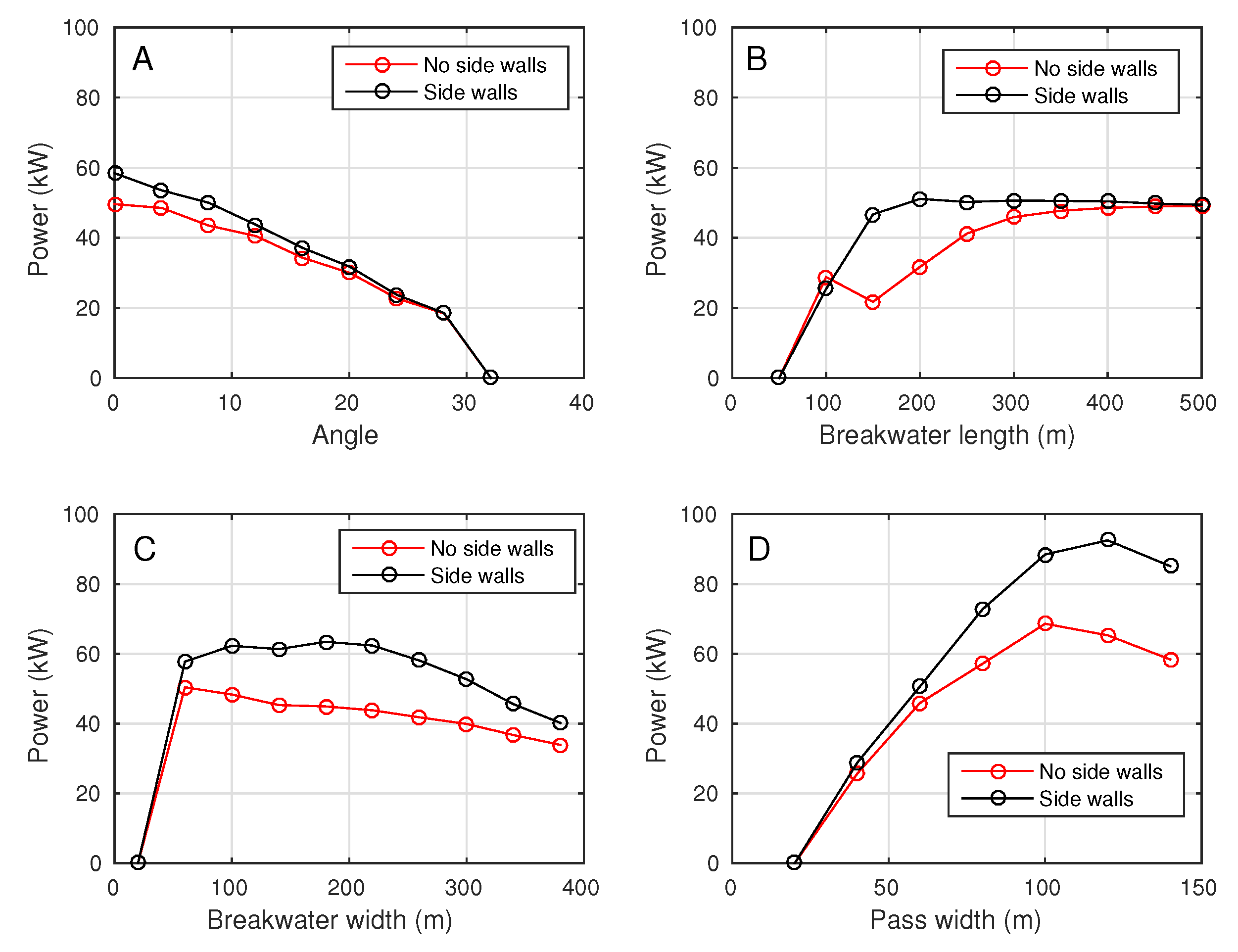
3.1.3. Parameters Optimization
3.2. Dependency on External Forcings
3.2.1. Wave and Tide Effect
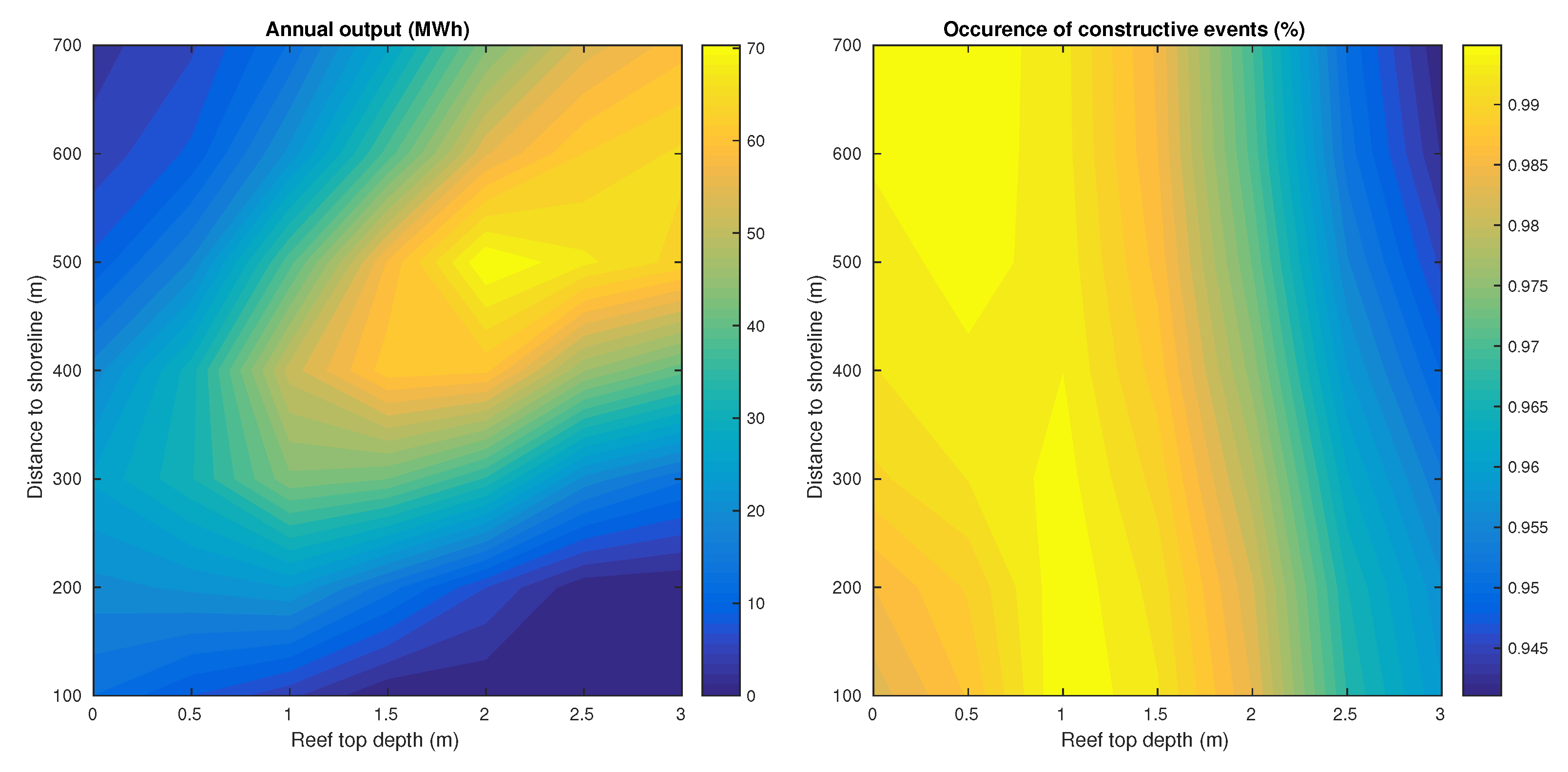
3.2.2. Optimization for an Annual Synthetic Climate
3.2.3. Beach Protection
4. Discussions
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Sato, M.; Hearty, P.; Ruedy, R.; Kelley, M.; Masson-Delmotte, V.; Russell, G.; Tselioudis, G.; Cao, J.; Rignot, E.; et al. Ice melt, sea level rise and superstorms: Evidence from paleoclimate data, climate modeling, and modern observations that 2 C global warming could be dangerous. Atmos. Chem. Phys. 2016, 16, 3761–3812. [Google Scholar] [CrossRef]
- Brown, A.; McLachlan, A. Sandy shore ecosystems and the threats facing them: Some predictions for the year 2025. Environ. Conserv. 2002, 29, 62–77. [Google Scholar] [CrossRef]
- Defeo, O.; McLachlan, A.; Schoeman, D.S.; Schlacher, T.A.; Dugan, J.; Jones, A.; Lastra, M.; Scapini, F. Threats to sandy beach ecosystems: A review. Estuar. Coast. Shelf Sci. 2009, 81, 1–12. [Google Scholar] [CrossRef]
- Schlacher, T.A.; Schoeman, D.S.; Dugan, J.; Lastra, M.; Jones, A.; Scapini, F.; McLachlan, A. Sandy beach ecosystems: Key features, sampling issues, management challenges and climate change impacts. Mar. Ecol. 2008, 29, 70–90. [Google Scholar] [CrossRef]
- Semeoshenkova, V.; Newton, A. Overview of erosion and beach quality issues in three Southern European countries: Portugal, Spain and Italy. Ocean Coastal Manag. 2015, 118, 12–21. [Google Scholar] [CrossRef]
- Phillips, M.R.; Jones, A.L. Erosion and tourism infrastructure in the coastal zone: Problems, consequences and management. Tour. Manag. 2006, 27, 517–524. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Introduction to Coastal Engineering and Management; World Scientific: Singapore, 2010; Volume 30. [Google Scholar]
- Mueller, M.; Wallace, R. Enabling science and technology for marine renewable energy. Energy Policy 2008, 36, 4376–4382. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Combourieu, A.; Lawson, M.; Babarit, A.; Ruehl, K.; Roy, A.; Costello, R.; Laporte Weywada, P.; Bailey, H. WEC3: Wave Energy Converter Code Comparison Project: Preprint; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2017.
- Ozkop, E.; Altas, I.H. Control, power and electrical components in wave energy conversion systems: A review of the technologies. Renew. Sustain. Energy Rev. 2017, 67, 106–115. [Google Scholar] [CrossRef]
- Mustapa, M.; Yaakob, O.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Henry, A.; Folley, M.; Whittaker, T. A conceptual model of the hydrodynamics of an oscillating wave surge converter. Renew. Energy 2018, 118, 965–972. [Google Scholar] [CrossRef]
- Franzitta, V.; Catrini, P.; Curto, D. Wave energy assessment along Sicilian coastline, based on DEIM point absorber. Energies 2017, 10, 376. [Google Scholar] [CrossRef]
- Rezanejad, K.; Soares, C.G.; López, I.; Carballo, R. Experimental and numerical investigation of the hydrodynamic performance of an oscillating water column wave energy converter. Renew. Energy 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Contestabile, P.; Iuppa, C.; Di Lauro, E.; Cavallaro, L.; Andersen, T.L.; Vicinanza, D. Wave loadings acting on innovative rubble mound breakwater for overtopping wave energy conversion. Coast. Eng. 2017, 122, 60–74. [Google Scholar] [CrossRef]
- Algie, C.; Ryan, S.; Fleming, A. Predicted power performance of a submerged membrane pressure-differential wave energy converter. Int. J. Mar. Energy 2017, 20, 125–134. [Google Scholar] [CrossRef]
- Vicinanza, D.; Stagonas, D.; Müller, G.; Nørgaard, J.H.; Andersen, T.L. Innovative breakwaters design for wave energy conversion. Coast. Eng. Proc. 2012, 1, 1. [Google Scholar] [CrossRef]
- Vicinanza, D.; Contestabile, P.; Di Lauro, E. Overtopping Breakwater for Wave Energy Conversion: Status and Perspective. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; Volume 27, pp. 1194-1–1194-9. [Google Scholar]
- Zhang, X.; Zeng, Q.; Liu, Z. Hydrodynamic Performance of Rectangular Heaving Buoys for an Integrated Floating Breakwater. J. Mar. Sci. Eng. 2019, 7, 239. [Google Scholar] [CrossRef]
- Rosa-Santos, P.; Taveira-Pinto, F.; Clemente, D.; Cabral, T.; Fiorentin, F.; Belga, F.; Morais, T. Experimental Study of a Hybrid Wave Energy Converter Integrated in a Harbor Breakwater. J. Mar. Sci. Eng. 2019, 7, 33. [Google Scholar] [CrossRef]
- Lowe, R.J.; Falter, J.L.; Bandet, M.D.; Pawlak, G.; Atkinson, M.J.; Monismith, S.G.; Koseff, J.R. Spectral wave dissipation over a barrier reef. J. Geophys. Res. Oceans 2005, 110, 1–16. [Google Scholar] [CrossRef]
- Monismith, S.G. Hydrodynamics of coral reefs. Annu. Rev. Fluid Mech. 2007, 39, 37–55. [Google Scholar] [CrossRef]
- Lugo-Fernández, A.; Roberts, H.; Wiseman, W., Jr.; Carter, B. Water level and currents of tidal and infragravity periods at Tague Reef, St. Croix (USVI). Coral Reefs 1998, 17, 343–349. [Google Scholar] [CrossRef]
- Hearn, C.J. wave breaking hydrodynamics within coral reef systems and the effect of changing relative sea level. J. Geophys. Res. Oceans 1999, 104, 30007–30019. [Google Scholar] [CrossRef]
- Gourlay, M.R.; Colleter, G. Wave-generated flow on coral reefs—An analysis for two-dimensional horizontal reef-tops with steep faces. Coast. Eng. 2005, 52, 353–387. [Google Scholar] [CrossRef]
- Bonneton, P.; Lefebvre, J.P.; Bretel, P.; Ouillon, S.; Douillet, P. Tidal modulation of wave-setup and wave-induced currents on the Aboré coral reef, New Caledonia. J. Coast. Res. 2007, 50, 762–766. [Google Scholar]
- Sous, D.; Tissier, M.; Rey, V.; Touboul, J.; Bouchette, F.; Devenon, J.L.; Chevalier, C.; Aucan, J. Wave transformation over barrier reefs. Cont. Shelf Res. 2019. [Google Scholar] [CrossRef]
- Chevalier, C.; Sous, D.; Devenon, J.L.; Pagano, M.; Rougier, G.; Blanchot, J. Impact of cross-reef water fluxes on lagoon dynamics: A simple parameterization for coral lagoon circulation model, with application to the Ouano Lagoon, New Caledonia. Ocean. Dyn. 2015, 1509–1534. [Google Scholar] [CrossRef]
- Symonds, G.; Black, K.P.; Young, I.R. Wave-driven flow over shallow reefs. J. Geophys. Res. Oceans 1995, 100, 2639–2648. [Google Scholar] [CrossRef]
- Lowe, R.J.; Falter, J.L.; Monismith, S.G.; Atkinson, M.J. Wave-driven circulation of a coastal reef–lagoon system. J. Phys. Oceanogr. 2009, 39, 873–893. [Google Scholar] [CrossRef]
- Pomeroy, A.; Lowe, R.; Symonds, G.; Van Dongeren, A.; Moore, C. The dynamics of infragravity wave transformation over a fringing reef. J. Geophys. Res. Oceans 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Lowe, R.; Pomeroy, A.; Trang, D.M.; Roelvink, D.; Symonds, G.; Ranasinghe, R. Numerical modeling of low-frequency wave dynamics over a fringing coral reef. Coast. Eng. 2013, 73, 178–190. [Google Scholar] [CrossRef]
- Buckley, M.; Lowe, R.; Hansen, J. Evaluation of nearshore wave models in steep reef environments. Ocean Dyn. 2014, 64, 847–862. [Google Scholar] [CrossRef]
- Zijlema, M. Modelling wave transformation across a fringing reef using SWASH. Coast. Eng. Proc. 2012, 1, 26. [Google Scholar] [CrossRef]
- Lashley, C.H.; Roelvink, D.; van Dongeren, A.; Buckley, M.L.; Lowe, R.J. Nonhydrostatic and surfbeat model predictions of extreme wave run-up in fringing reef environments. Coast. Eng. 2018, 137, 11–27. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Su, S.F.; Ma, G. Modeling two-dimensional infragravity motions on a fringing reef. Ocean Eng. 2018, 153, 256–267. [Google Scholar] [CrossRef]
- Liu, W.; Shao, K.; Ning, Y. A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model. J. Mar. Sci. Eng. 2019, 7, 109. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; de Vries, J.v.T.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Walstra, D.; Roelvink, J.; Groeneweg, J. 3D calculation of wave-driven cross-shore currents. In Proceedings of the 27th International Conference on Coastal Engineering, Sydney, Australia, 16–21 July 2000; pp. 16–21. [Google Scholar]
- Holthuijsen, L.; Booij, N.; Herbers, T. A prediction model for stationary, short-crested waves in shallow water with ambient currents. Coast. Eng. 1989, 13, 23–54. [Google Scholar] [CrossRef]
- Janssen, T.; Battjes, J. A note on wave energy dissipation over steep beaches. Coast. Eng. 2007, 54, 711–716. [Google Scholar] [CrossRef]
- Sous, D.; Chevalier, C.; Devenon, J.L.; Blanchot, J.; Pagano, M. Circulation patterns in a channel reef–lagoon system, Ouano lagoon, New Caledonia. Estuar. Coast. Shelf Sci. 2017, 196, 315–330. [Google Scholar] [CrossRef]
- Péquignet, A.C.; Becker, J.; Merrifield, M.; Boc, S. The dissipation of wind wave energy across a fringing reef at Ipan, Guam. Coral Reefs 2011, 30, 71–82. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Q.; Chen, S.; Tang, Z. Effects of reef morphology variations on wave processes over fringing reefs. Appl. Ocean Res. 2019, 82, 52–62. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Taborda, R. Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Model. 2010, 31, 120–131. [Google Scholar] [CrossRef]
- Charles, E.; Idier, D.; Thiébot, J.; Le Cozannet, G.; Pedreros, R.; Ardhuin, F.; Planton, S. Present wave climate in the Bay of Biscay: Spatiotemporal variability and trends from 1958 to 2001. J. Clim. 2012, 25, 2020–2039. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R. Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Isebe, D.; Azerad, P.; Bouchette, F.; Ivorra, B.; Mohammadi, B. Shape optimization of geotextile tubes for sandy beach protection. Int. J. Numer. Methods Eng. 2008, 74, 1262–1277. [Google Scholar] [CrossRef]
- Vermaak, H.J.; Kusakana, K.; Koko, S.P. Status of micro-hydrokinetic river technology in rural applications: A review of literature. Renew. Sustain. Energy Rev. 2014, 29, 625–633. [Google Scholar] [CrossRef]
- Khan, M.; Iqbal, M.; Quaicoe, J. River current energy conversion systems: Progress, prospects and challenges. Renew. Sustain. Energy Rev. 2008, 12, 2177–2193. [Google Scholar] [CrossRef]
- Ibarra-Berastegi, G.; Sáenz, J.; Ulazia, A.; Serras, P.; Esnaola, G.; Garcia-Soto, C. Electricity production, capacity factor, and plant efficiency index at the Mutriku wave farm (2014–2016). Ocean Eng. 2018, 147, 20–29. [Google Scholar] [CrossRef]
- Lehmann, M.; Karimpour, F.; Goudey, C.A.; Jacobson, P.T.; Alam, M.R. Ocean wave energy in the United States: Current status and future perspectives. Renew. Sustain. Energy Rev. 2017, 74, 1300–1313. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.; Charpentier, J.F.; Scuiller, F.; Tang, T. Developments in large marine current turbine technologies—A review. Renew. Sustain. Energy Rev. 2017, 71, 852–858. [Google Scholar] [CrossRef]
- Bouvier, C.; Castelle, B.; Balouin, Y. Modeling the Impact of the Implementation of a Submerged Structure on Surf Zone Sandbar Dynamics. J. Mar. Sci. Eng. 2019, 7, 117. [Google Scholar] [CrossRef]
- Duarte Nemes, D.; Fabián Criado-Sudau, F.; Nicolás Gallo, M. Beach Morphodynamic Response to a Submerged Reef. Water 2019, 11, 340. [Google Scholar] [CrossRef]
- Isebe, D.; Azerad, P.; Mohammadi, B.; Bouchette, F. Optimal shape design of defense structures for minimizing short wave impact. Coast. Eng. 2008, 55, 35–46. [Google Scholar] [CrossRef]



© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sous, D. A Numerical Assessment of Artificial Reef Pass Wave-Induced Currents as a Renewable Energy Source. J. Mar. Sci. Eng. 2019, 7, 284. https://doi.org/10.3390/jmse7090284
Sous D. A Numerical Assessment of Artificial Reef Pass Wave-Induced Currents as a Renewable Energy Source. Journal of Marine Science and Engineering. 2019; 7(9):284. https://doi.org/10.3390/jmse7090284
Chicago/Turabian StyleSous, Damien. 2019. "A Numerical Assessment of Artificial Reef Pass Wave-Induced Currents as a Renewable Energy Source" Journal of Marine Science and Engineering 7, no. 9: 284. https://doi.org/10.3390/jmse7090284
APA StyleSous, D. (2019). A Numerical Assessment of Artificial Reef Pass Wave-Induced Currents as a Renewable Energy Source. Journal of Marine Science and Engineering, 7(9), 284. https://doi.org/10.3390/jmse7090284




