A Quality Control Method for Broad-Beam HF Radar Current Velocity Measurements
Abstract
:1. Introduction
2. Radar Spectral Theory
3. Analysis for Radial Current Velocities
4. Application of Quality Control for Derived Radial Velocities
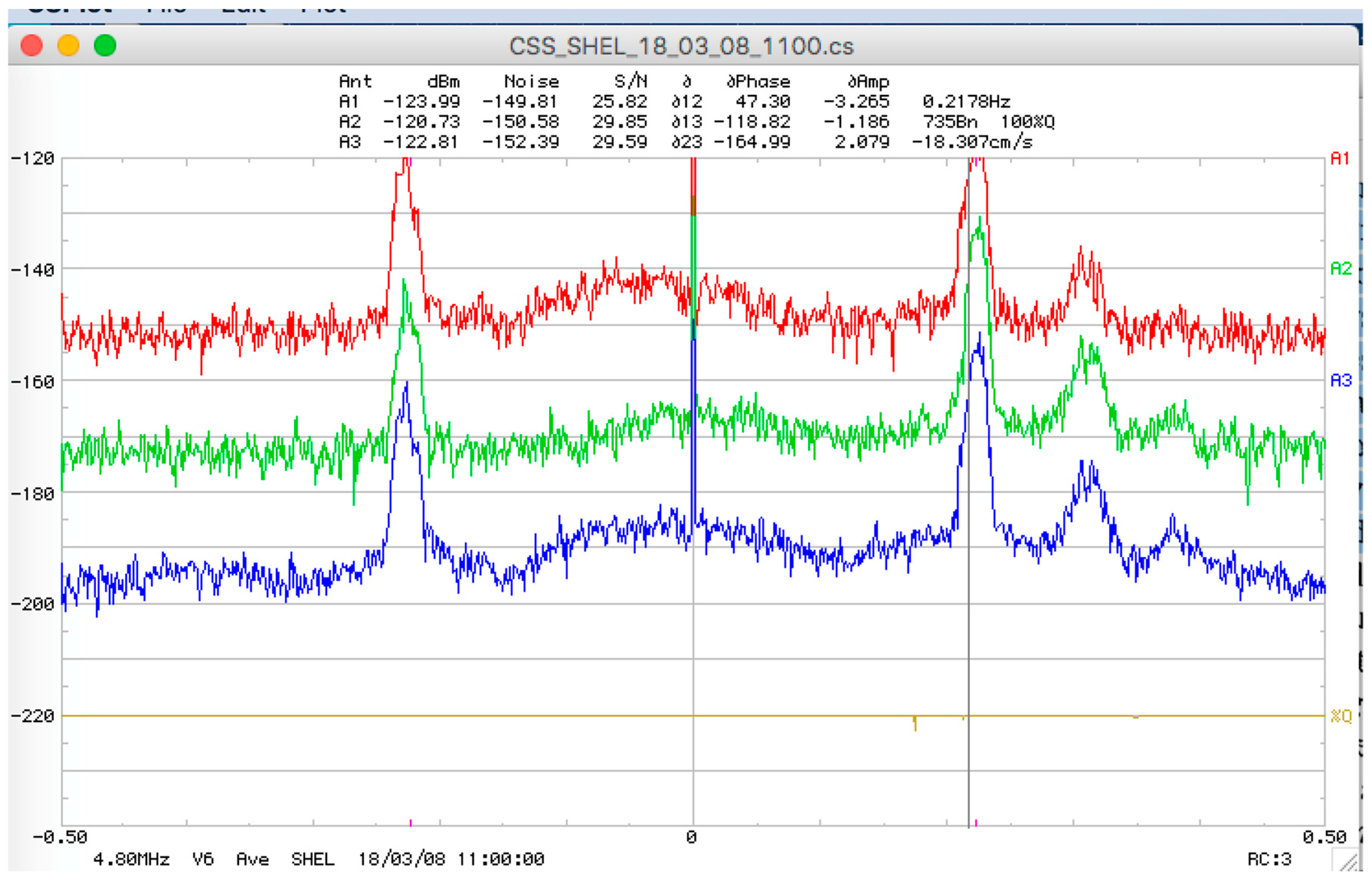
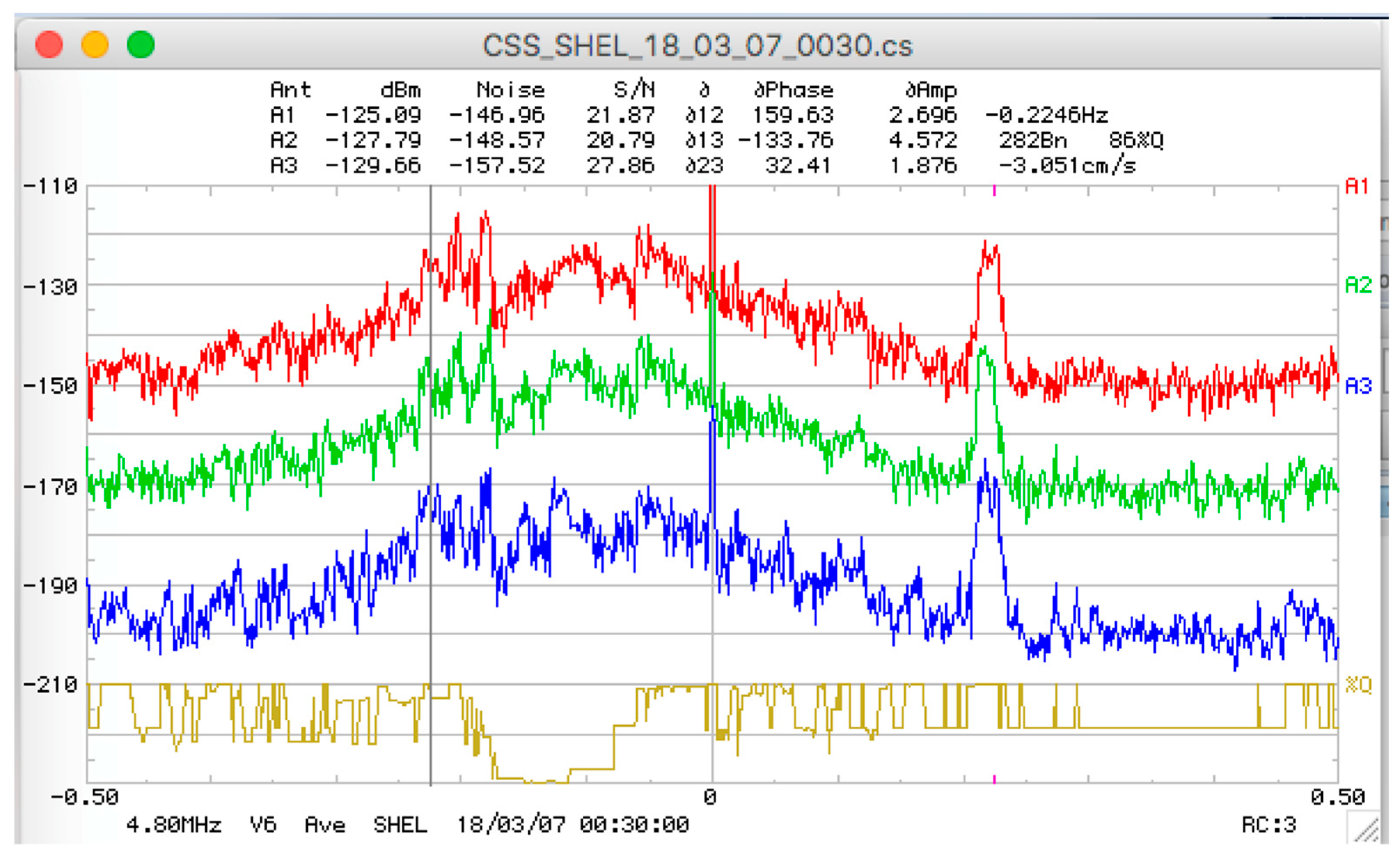
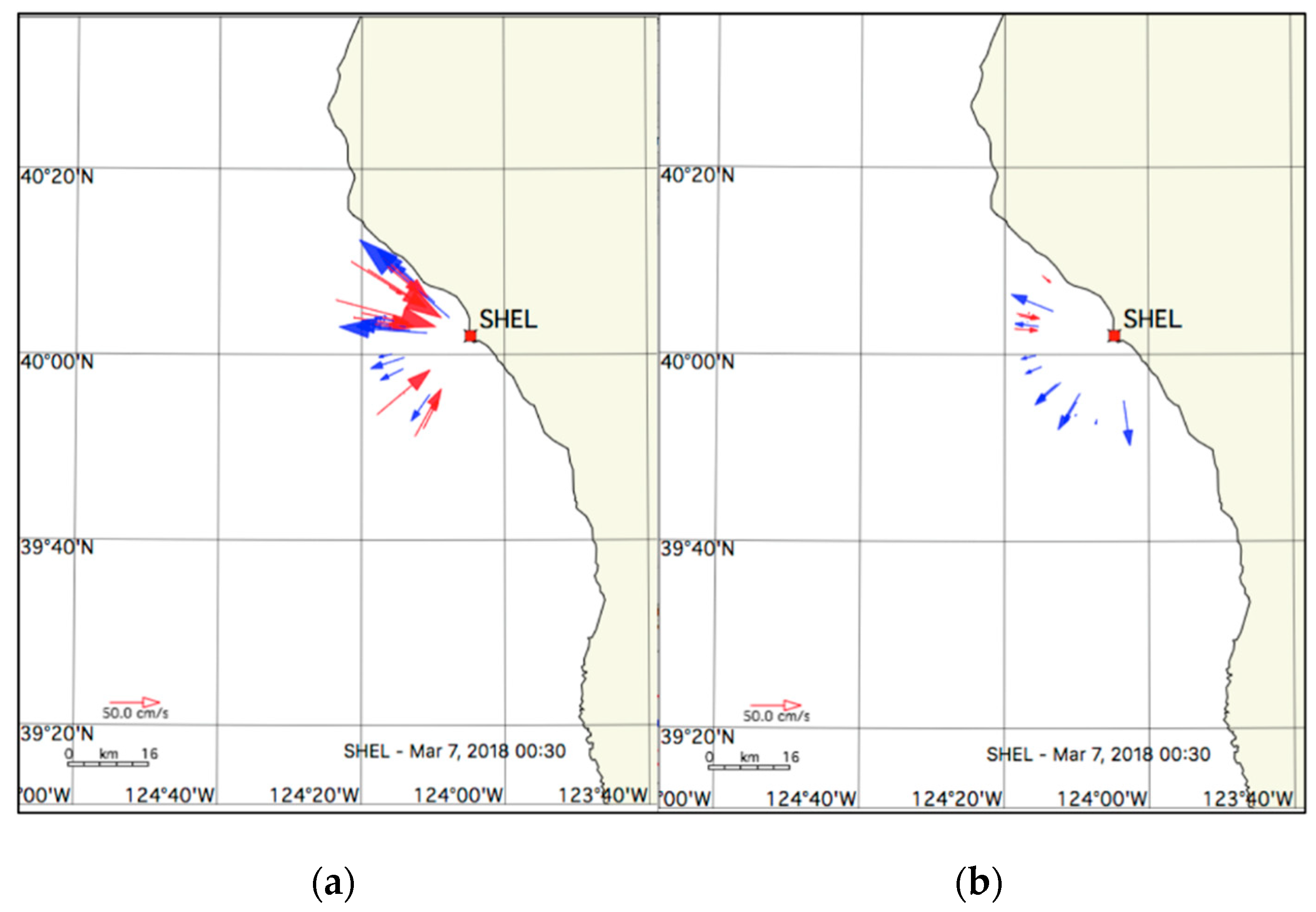
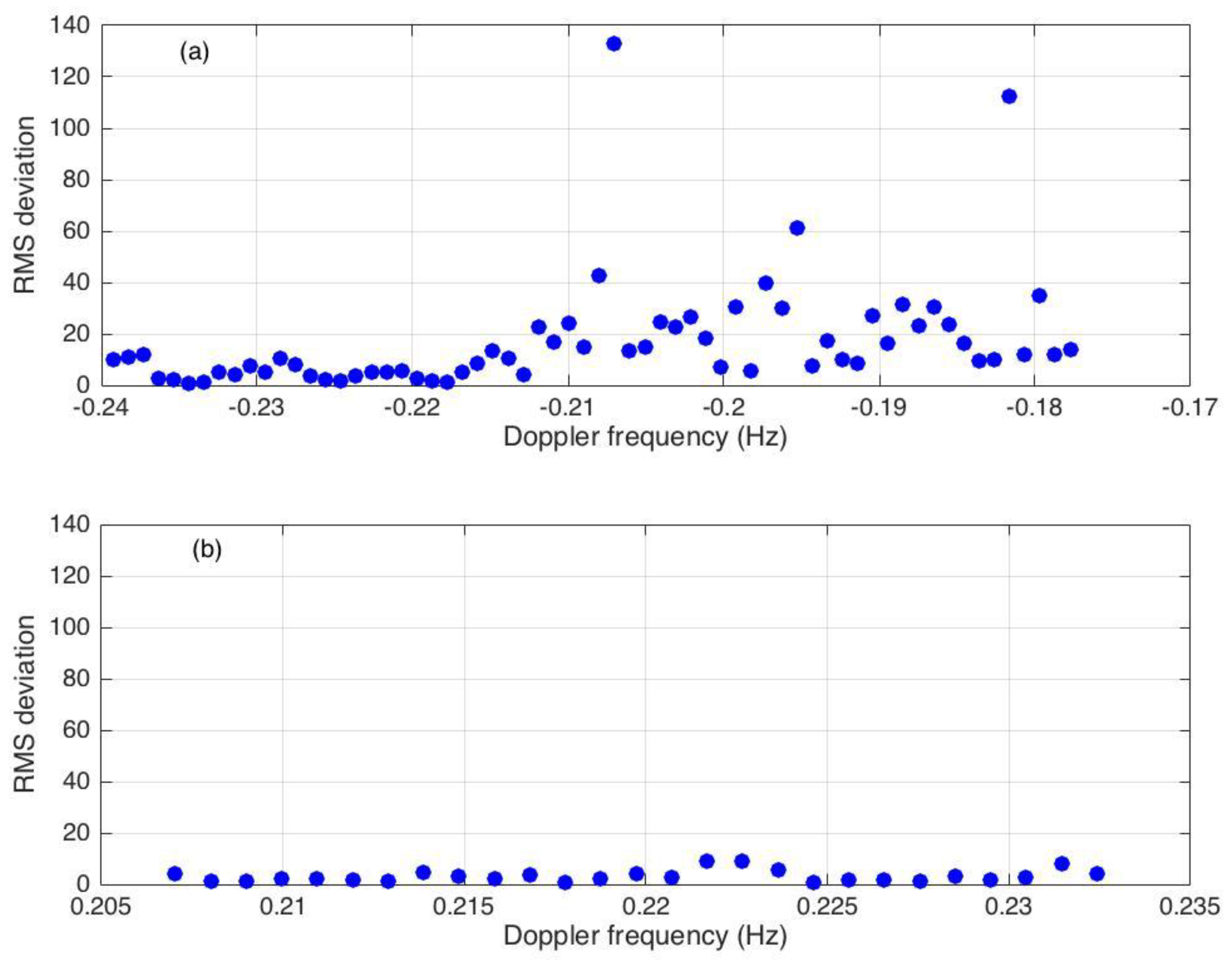
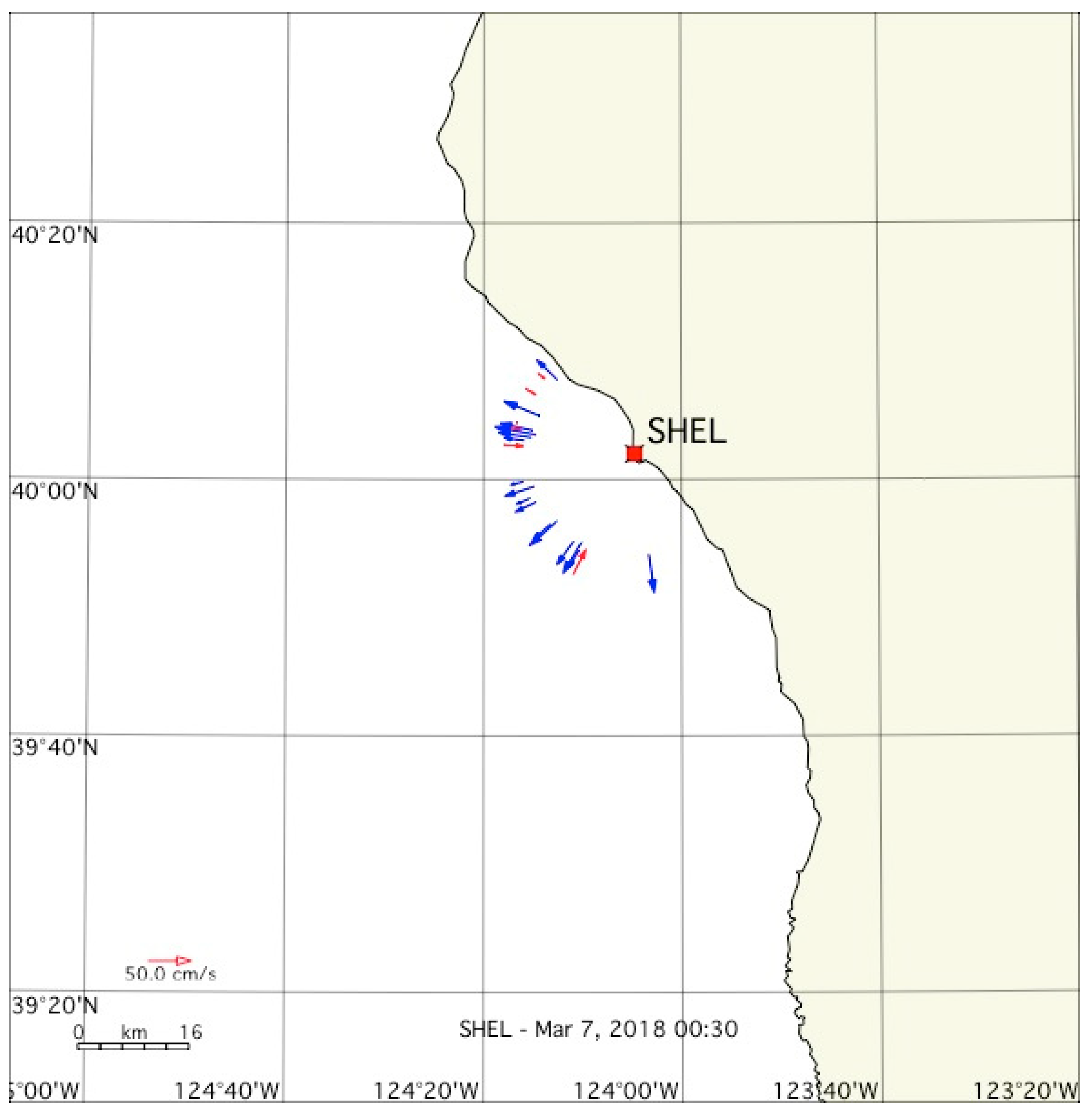
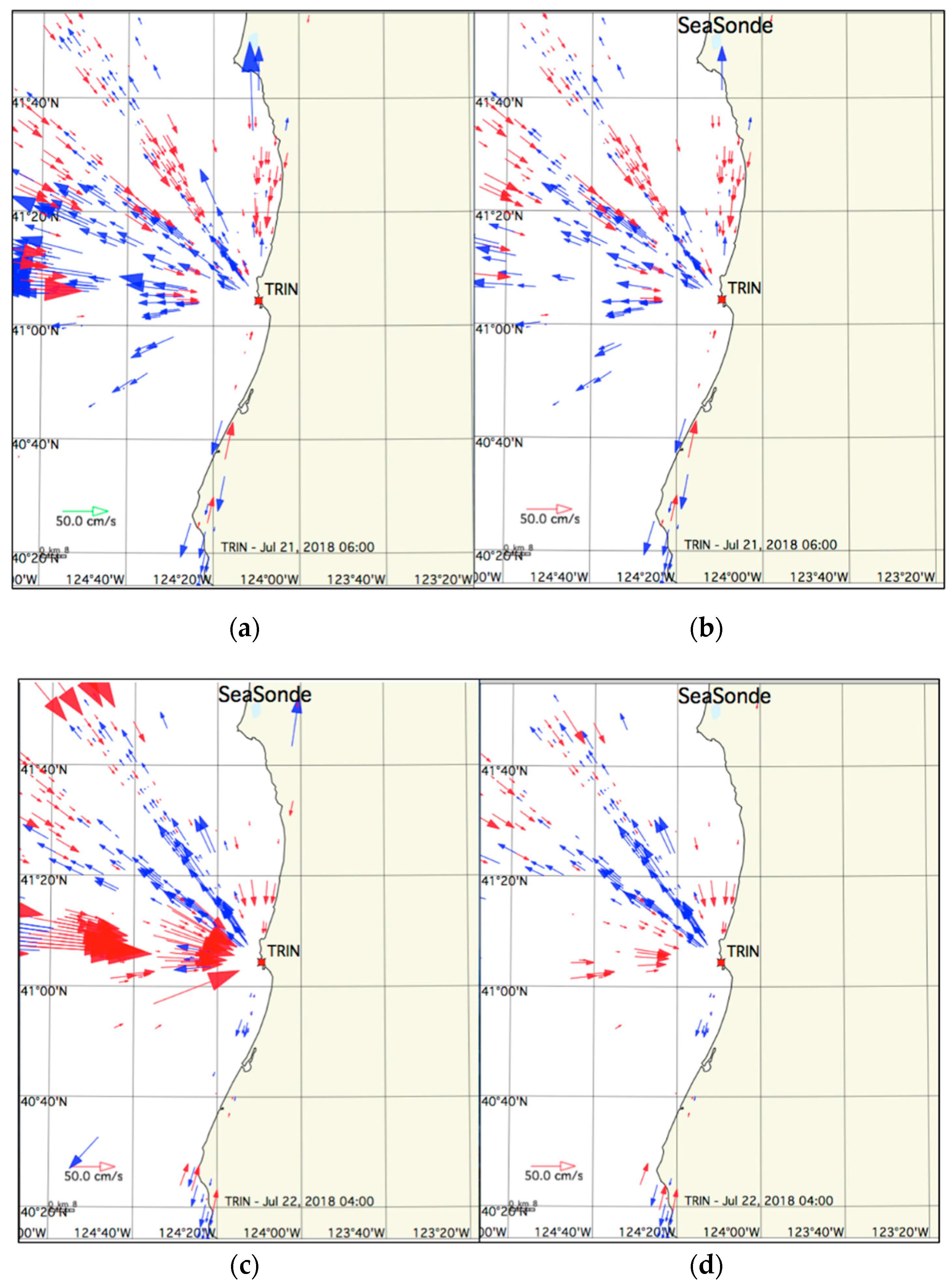
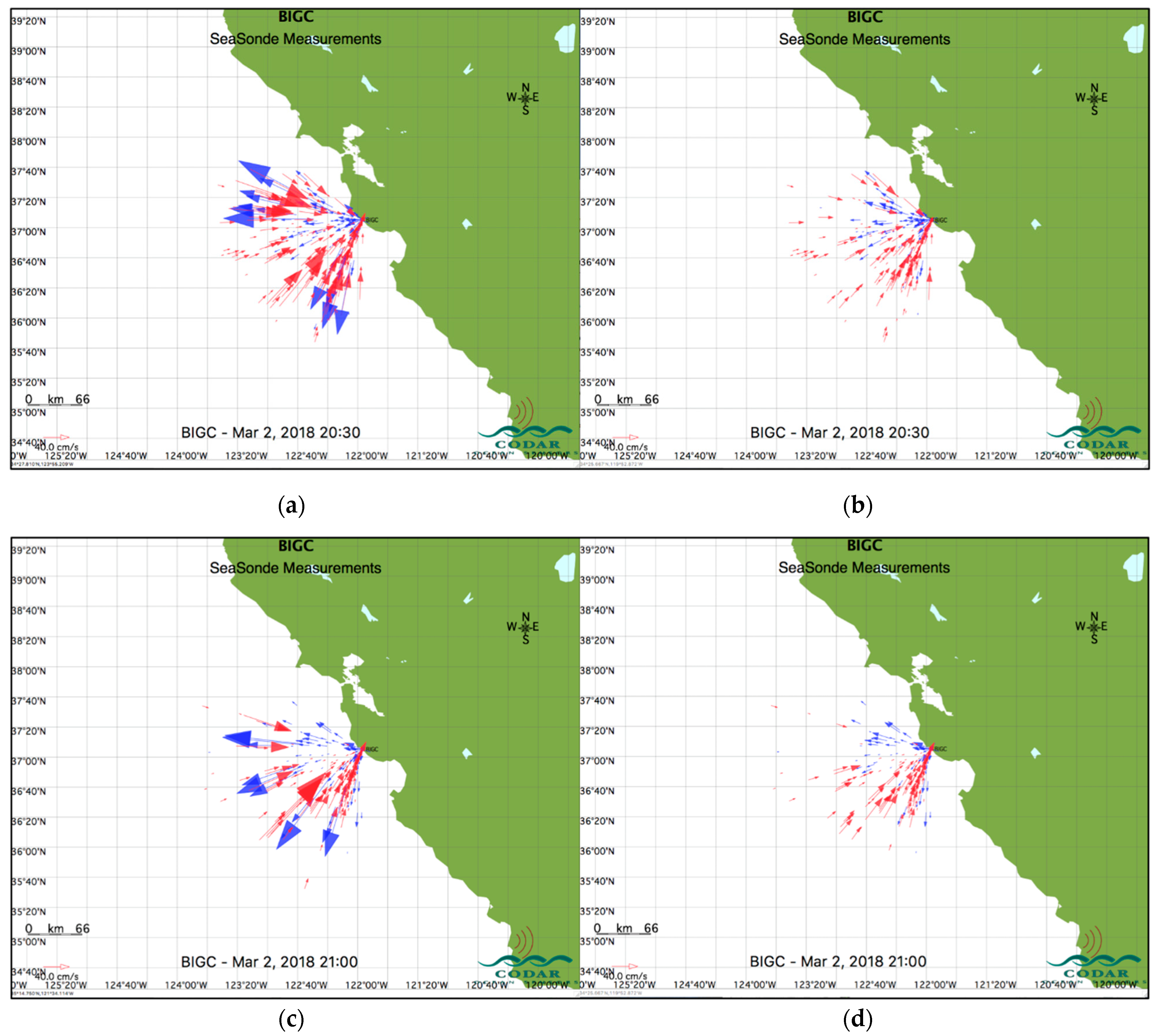
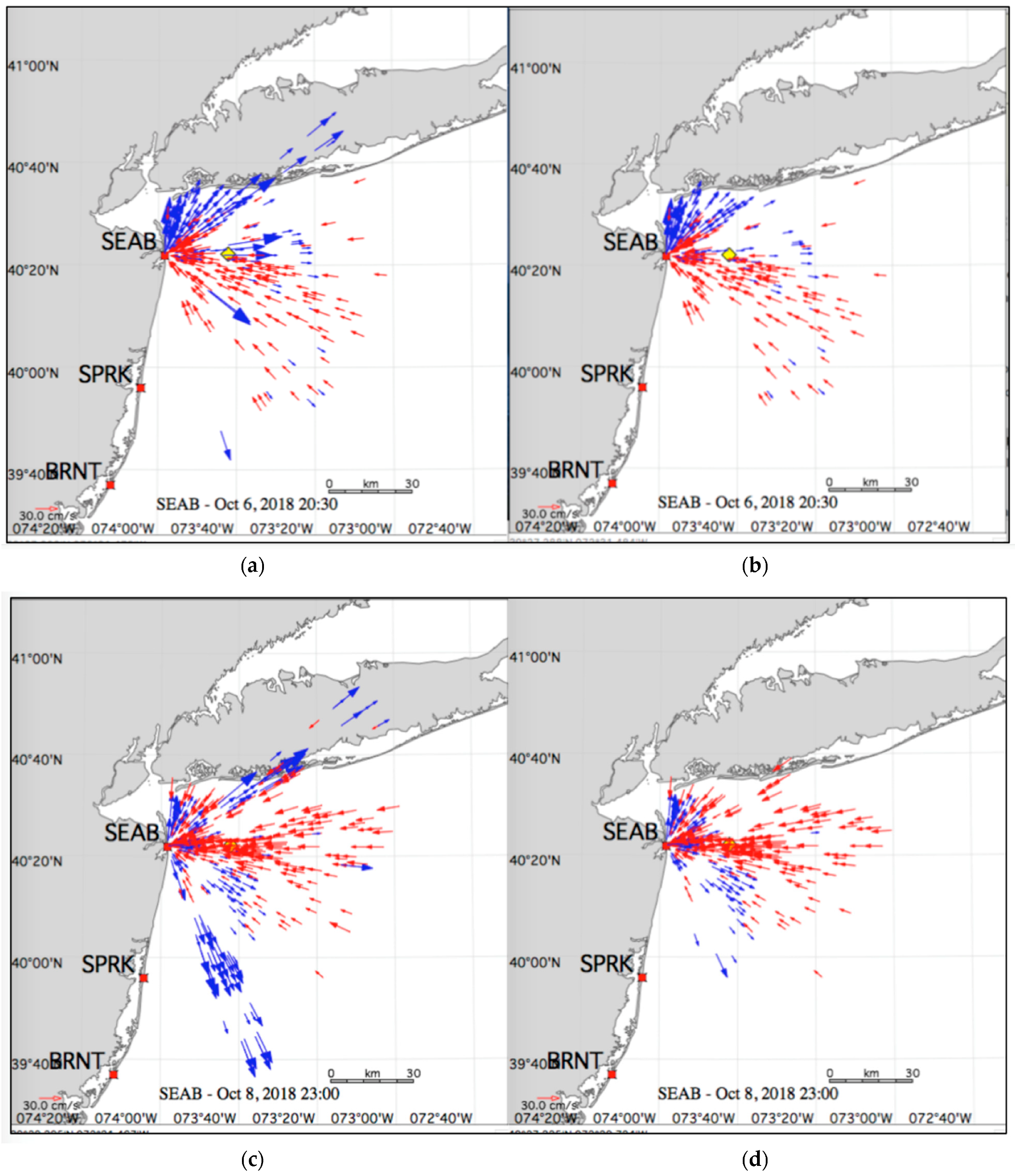
5. Examples of Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc/s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.E. First-order theory and analysis of MF/HF/VHF scatter from the Sea. IEEE Trans. Antennas Propag. 1972, AP-20, 2–10. [Google Scholar] [CrossRef]
- Barrick, D.E. Remote sensing of sea-state by radar. In Remote Sensing of the Troposphere; Derr, V.E., Ed.; U.S. National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1972; pp. 12-1–12-46. [Google Scholar]
- Lipa, B.J.; Barrick, D.E. Least-squares methods for the extraction of surface currents from CODAR crossed-loop data: Application at ARSLOE. IEEE J. Ocean. Eng. 1983, 8, 226–253. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B.; Ullman, D.; Terrill, E. SeaSonde Radial Velocities: Derivation and Internal Consistency. IEEE J. Ocean. Eng. 2006, 31, 850–861. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D. Analysis Methods for Narrow-Beam High-Frequency Radar Sea Echo; Technical Report 420-WP; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, Environmental Research Laboratories: Washington, DC, USA, 1982; Volume 56.
- Lipa, B.; Barrick, D. Extraction of sea state from HF radar sea echo: Mathematical theory and modeling. Radio Sci. 1986, 21, 81–100. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B. Directional wave information from the seasoned. IEEE J. Ocean. Eng. 2005, 30, 221–231. [Google Scholar] [CrossRef]
- Stewart, R.; Joy, J. HF radio measurements of surface currents. Deep Sea Res. 1974, 21, 1039–1049. [Google Scholar] [CrossRef]
- Barrick, D.; Headrick, J.; Bogle, R.; Crombie, D. Sea backscatter at HF: Interpretation and utilization of the echo. Proc. IEEE 1974, 62, 673–680. [Google Scholar] [CrossRef]
- Barrick, D.; Evans, M.; Weber, B. Ocean surface currents mapped by radar. Science 1977, 198, 138–144. [Google Scholar] [CrossRef]
- Barrick, D.; Lipa, B. A compact transportable HF radar system fordirectional coastal wave field measurements. In Ocean Wave Climate; Earle, M.D., Malahoff, A., Eds.; Plenum: New York, NY, USA, 1979; pp. 153–201. [Google Scholar]
- The SeaSonde. Available online: http://www.codar.com/SeaSonde.shtml (accessed on 10 April 2019).
- Harlan, J.; Terrill, E.; Hazard, L.; Keen, C.; Barrick, D.; Whelan, C.; Howden, S.; Kohut, J. The Integrated Ocean Observing System High-Frequency Radar Network: Status and Local, Regional, and National Applications. Mar. Technol. Soc. J. 2010, 44, 122–132. [Google Scholar] [CrossRef]
- Fujii, S.; Heron, M.; Kim, K.; Lai, J.-W.; Lee, S.-H.; Wu, X.; Wu, X.; Wyatt, L.; Yang, W.-C. An Overview of Developments and Applications of Oceanographic Radar Networks in Asia and Oceania Countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Rubio, A.; Mader, J.; Corgnati, L.; Mantovani, C.; Griffa, A.; Novellino, A.; Quentin, C.; Wyatt, L.; Schulz-Stellenfleth, J.; Horstmann, J.; et al. HF Radar Activity in European Coastal Seas: Next Steps toward a Pan-European HF Radar Network. Front. Mar. Sci. 2017, 4–8. [Google Scholar] [CrossRef]
- Jena, B.; Arunraj, K.; Suseentharan, V.; Tushar, K.; Karthikeyan, T. Indian coastal ocean radar network. Curr. Sci. 2019, 116, 372–378. [Google Scholar]
- Saviano, S.; Kalampokis, A.; Zambianchi, E.; Uttieri, M. A Year-Long Assessment of Wave Measurements Retrieved from an HF Radar Network in the Gulf of Naples (Tyrrhenian Sea, Western Mediterranean Sea). J. Oper. Oceanogr. 2019, 1–15. [Google Scholar] [CrossRef]
- Daugharty, M.; Lipa, B.; Barrick, D.; Roarty, H.; Dicopoulos, J. Mapping Wave Variation in MARACOOS with SeaSonde Compact HF Radar. In Proceedings of the ORCA Conference, Okinawa, Japan, 2–4 June 2018. [Google Scholar]
- Abascal, A.; Castanedo, S.; Fernandez, V.; Medina, R. Backtracking Drifting Objects using Surface Currents from High-Frequency (HF) Radar. Ocean Dyn. 2012, 58, 1–18. [Google Scholar] [CrossRef]
- Bellomo, A.; Griffa, S.; Cosoli, P.; Falco, R.; Gerin, I.; Iermano, A.; Kalampokis, Z.; Kokkini, A.; Lana, M.; Magaldi, I.; et al. Toward an integrated HF radar network in the Mediterranean Sea to improve search and rescue and oil spill response: The TOSCA project experience. J. Oper. Oceanogr. 2015, 8, 95–107. [Google Scholar] [CrossRef]
- Abascal, A.; Sanchez, J.; Chiri, H.; Ferrer, M.; Cárdenas, M.; Gallego, A.; Castanedo, S.; Medina, R.; Alonso-Martirena, A.; Berx, B.; et al. Operational Oil Spill Trajectory Modelling Using HF Radar Currents: A Northwest European Continental Shelf Case Study. Mar. Pollut. Bull. 2017, 119, 336–350. [Google Scholar] [CrossRef]
- Cardenas, M.; Abascal, A.; Castanedo, S.; Chiri, S.; Ferrer, M.; Sanchez, J.; Medina, R.; Turrell, W.; Hughes, S.; Gallego, A.; Berx, B. Spill Trajectory Modeling Based on HF Radar Currents in the North Sea: Validation with Drifter Buoys. In Proceedings of the Thirty Eighth AMOP Technical Seminar, Vancouver, BC, Canada, 2–5 June 2015; pp. 123–142. [Google Scholar]
- Whelan, C.; Barrick, D.; Lilleboe, P.; Breivik, Ø.; Kjelaas, A.; Fernandez, V.; Alonso-Martirena, A. Rapid Deployable HF RADAR for Norwegian emergency spill operations. In Proceedings of the Oceans 2010 IEE, Sydney, Australia, 24–27 May 2010; pp. 1–3. [Google Scholar]
- Roarty, H.; Smith, M.; Glenn, S.; Barrick, D.; Page, E.; Statscewich, H.; Weingartner, T. Expanding Maritime Domain Awareness Capabilities in the Arctic: High Frequency Radar Vessel-tracking. In Proceedings of the IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–5. [Google Scholar]
- Sciascia, R.; Berta, M.; Carlson, D.; Griffa, A.; Panfili, M.; La Mesa, M.; Corgnati, L.; Mantovani, C.; Domenella, E.; Fredj, E.; et al. Linking Sardine Recruitment in Coastal Areas to Ocean Currents Using Surface Drifters and HF Radar: A Case Study in the Gulf of Manfredonia, Adriatic Sea. Ocean Sci. 2018, 14, 1461–1482. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Isaacson, J. Coastal Tsunami Warning with Deployed HF Radar Systems; Mokhtari, M., Ed.; InTechOpen: Rijeka, Croatia, 2016; Available online: http://www.intechopen.com/books/tsunami/coastal-tsunami-warning-with-deployed-hf-radar-systems (accessed on 10 April 2019). [CrossRef]
- Cook, T.; Hazard, L.; Otero, M.; Zelenke, B. (Eds.) Deployment and Maintenance of a High-Frequency Radar (HFR) for Ocean Surface Current Mapping: Best Practices; University of California San Diego, Scripps Institution of Oceanography for SCCOOS: La Jolla, CA, USA, 2008; 19p, Available online: https://www.oceanbestpractices.net/handle/11329/368 (accessed on 10 April 2019).
- Kohut, J.; Glenn, S. Improving HF Radar Surface Current Measurements with Measured Antenna Beam Patterns. J. Atmos. Ocean. Technol. 2003, 20, 1303–1316. [Google Scholar] [CrossRef]
- Emery, B.; Washburn, L.; Whelan, C.; Barrick, D.; Harlan, J. Measuring Antenna Patterns for Ocean Surface Current HF Radars with Ships of Opportunity. J. Atmos. Ocean. Technol. 2014, 31, 1564–1582. [Google Scholar] [CrossRef]
- Washburn, L.; Romero, E.; Johnson, C.; Emery, B.; Gotschalk, C. Measurement of Antenna Patterns for Oceanographic Radars Using Aerial Drones. J. Atmos. Ocean. Technol. 2017, 34, 971–981. [Google Scholar] [CrossRef]
- Whelan, C.; Hubbard, M.; Trockel, D.; Parikh, H. Benefits of Multiple Antenna Pattern Measurement Methods for Maintaining a Regional HF Radar Network. In Proceedings of the ORCA Conference, Okinawa, Japan, 2–4 June 2018. [Google Scholar]
- U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Ocean Service, Integrated Ocean Observing System. Manual for Real-Time Quality Control of High Frequency Radar Surface Currents Data: A Guide to Quality Control and Quality Assurance of High Frequency Radar Surface Currents Data Observations. Volume 54, 2016. Available online: https://cdn.ioos.noaa.gov/media/2017/12/HFR_QARTOD_Manual_05_26_16.pdf (accessed on 10 April 2019).
- Kirincich, A.; de Paolo, T.; Terrill, E. Improving HF Radar Estimates of Surface Currents Using Signal Quality Metrics, with Application to the MVCO High-Resolution Radar System. J. Atmos. Ocean. Technol. 2012, 29, 1377–1390. [Google Scholar] [CrossRef]
- De Paolo, T.; Terrill, E.; Kirincich, A. Improving SeaSonde radial velocity accuracy and variance using radial metrics. In Proceedings of the OCEANS MTS/IEEE Conference, Genoa, Italy, 18–21 May 2015; pp. 1–9. [Google Scholar]
- Cosoli, S.; Grcic, B.; de Vos, S.; Hetzel, Y. Improving Data Quality for the Australian High Frequency Ocean Radar Network through Real-Time and Delayed-Mode Quality-Control Procedures. Remote Sens. 2018, 10, 1476. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipa, B.; Barrick, D.; Whelan, C. A Quality Control Method for Broad-Beam HF Radar Current Velocity Measurements. J. Mar. Sci. Eng. 2019, 7, 112. https://doi.org/10.3390/jmse7040112
Lipa B, Barrick D, Whelan C. A Quality Control Method for Broad-Beam HF Radar Current Velocity Measurements. Journal of Marine Science and Engineering. 2019; 7(4):112. https://doi.org/10.3390/jmse7040112
Chicago/Turabian StyleLipa, Belinda, Donald Barrick, and Chad Whelan. 2019. "A Quality Control Method for Broad-Beam HF Radar Current Velocity Measurements" Journal of Marine Science and Engineering 7, no. 4: 112. https://doi.org/10.3390/jmse7040112
APA StyleLipa, B., Barrick, D., & Whelan, C. (2019). A Quality Control Method for Broad-Beam HF Radar Current Velocity Measurements. Journal of Marine Science and Engineering, 7(4), 112. https://doi.org/10.3390/jmse7040112



