A Fast Simulation Method for Damaged Ship Dynamics
Abstract
:1. Introduction
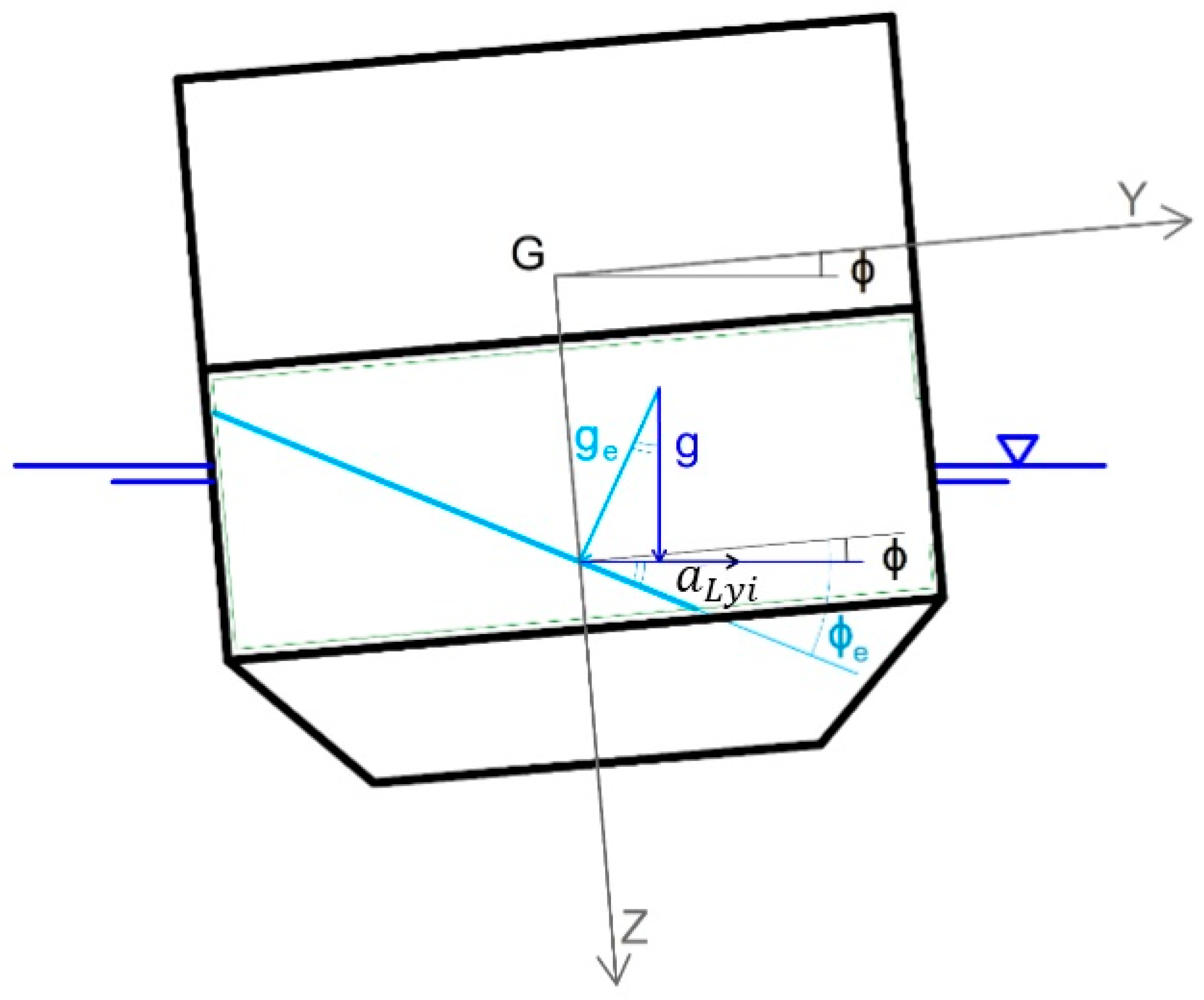
2. Numerical Model
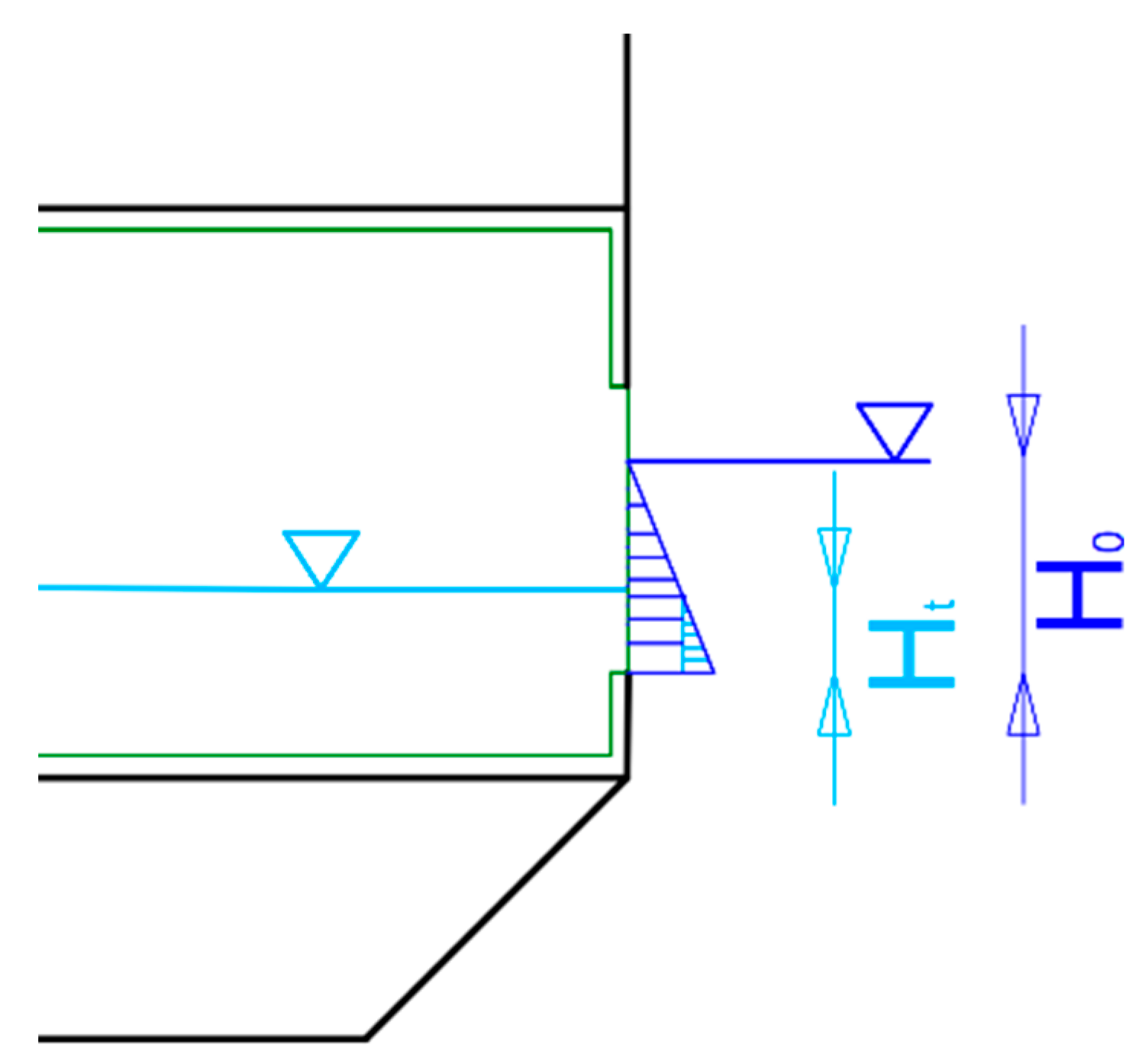
3. Flooding Law Modelling
4. Case Studies
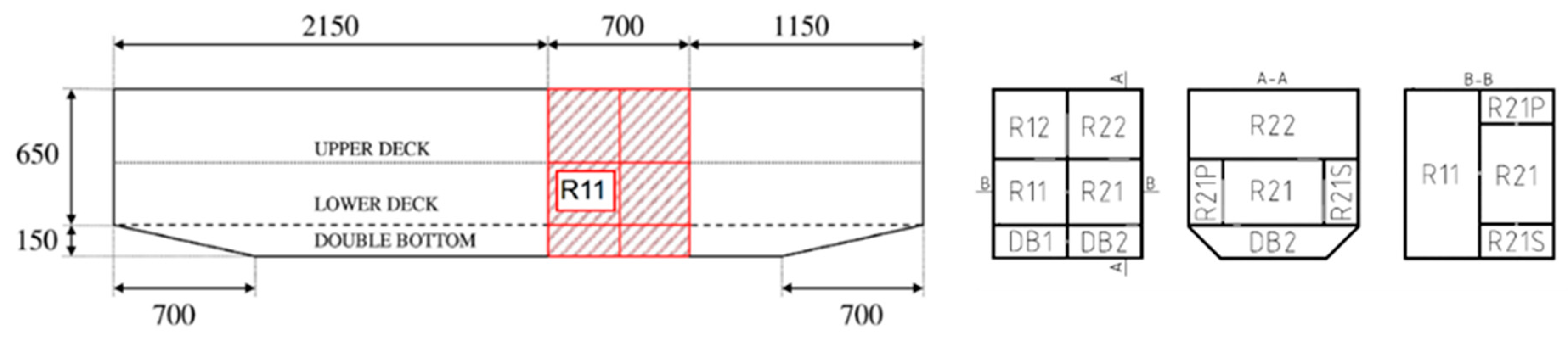
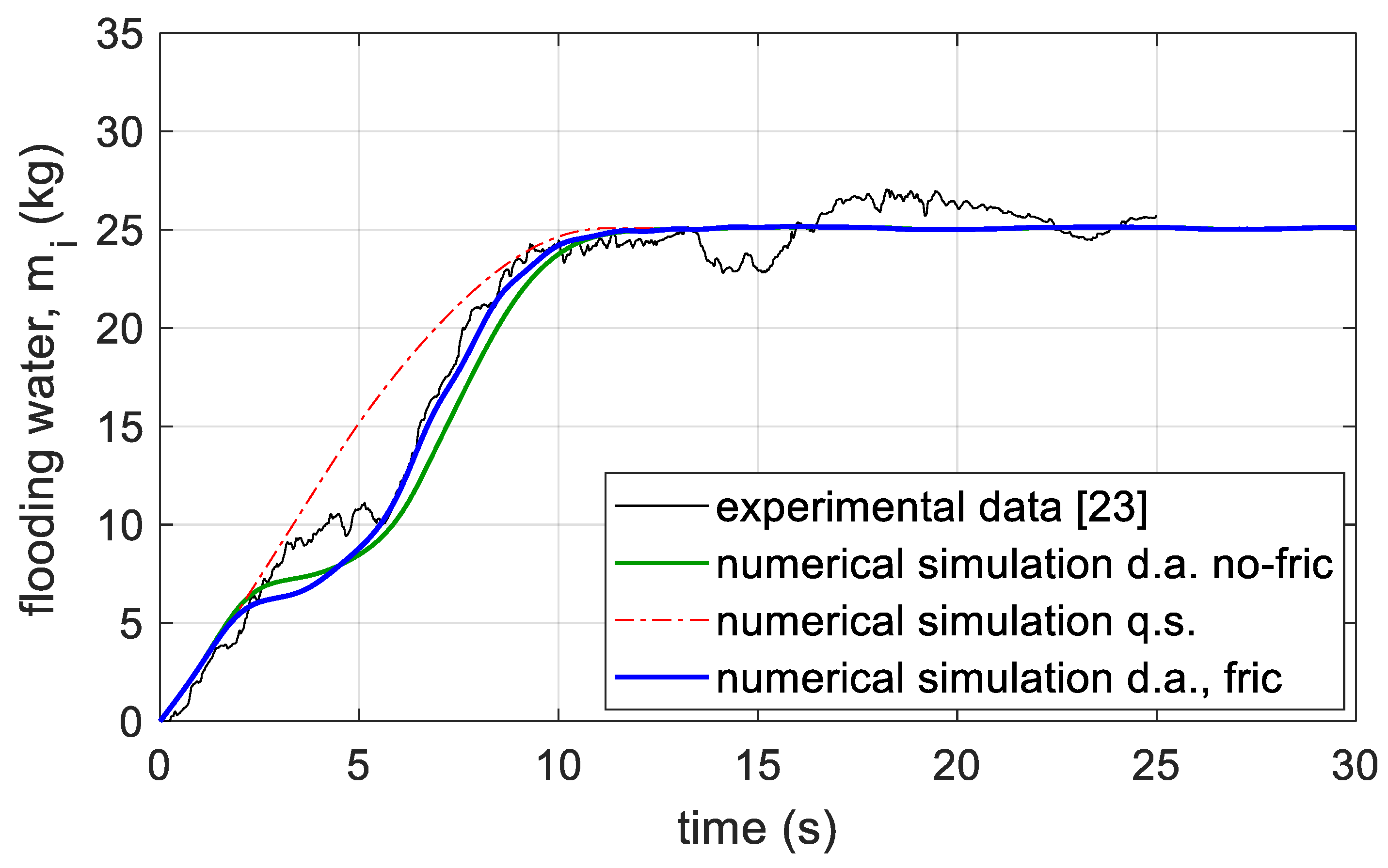
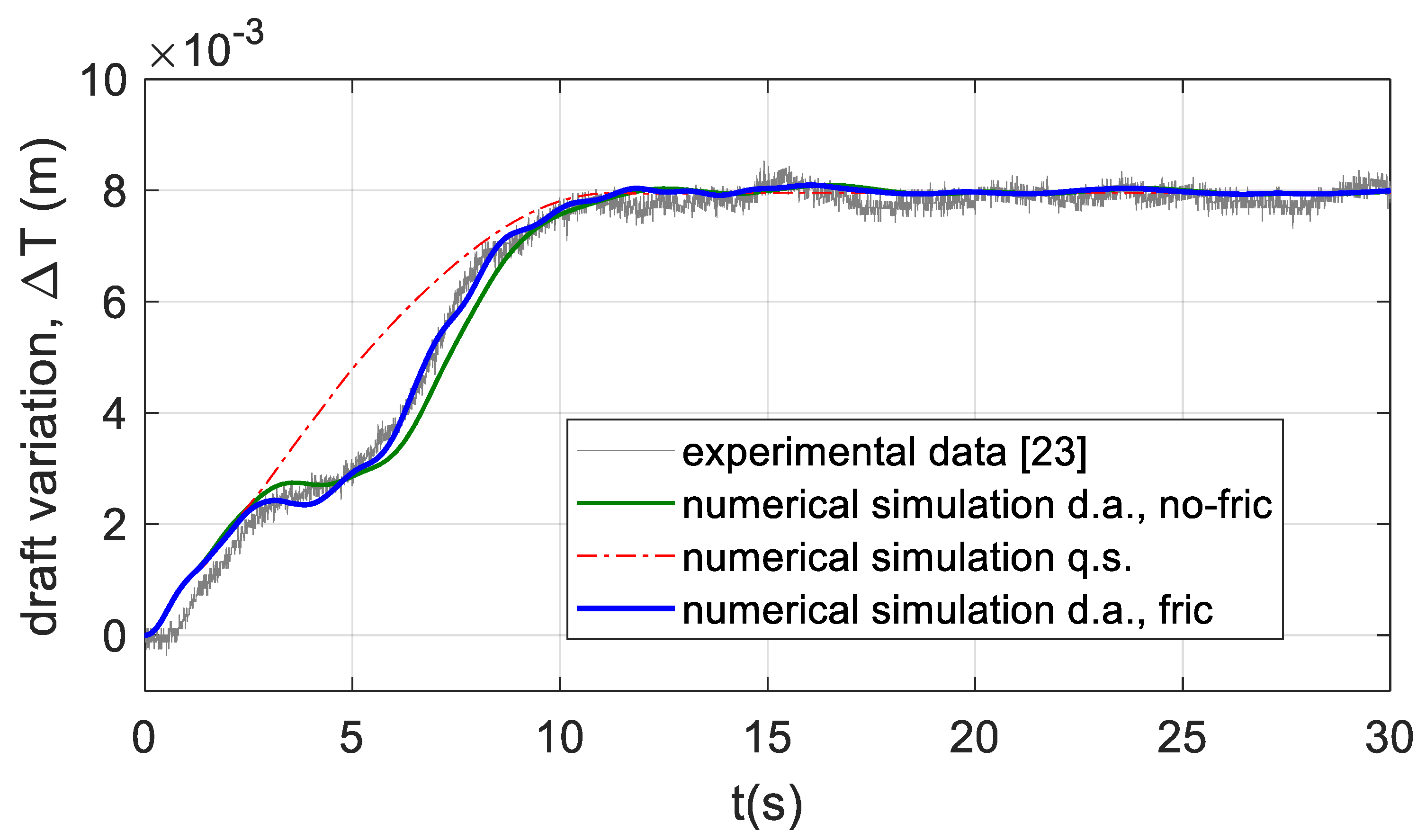
4.1. Flooding Simulations on the Barge Model
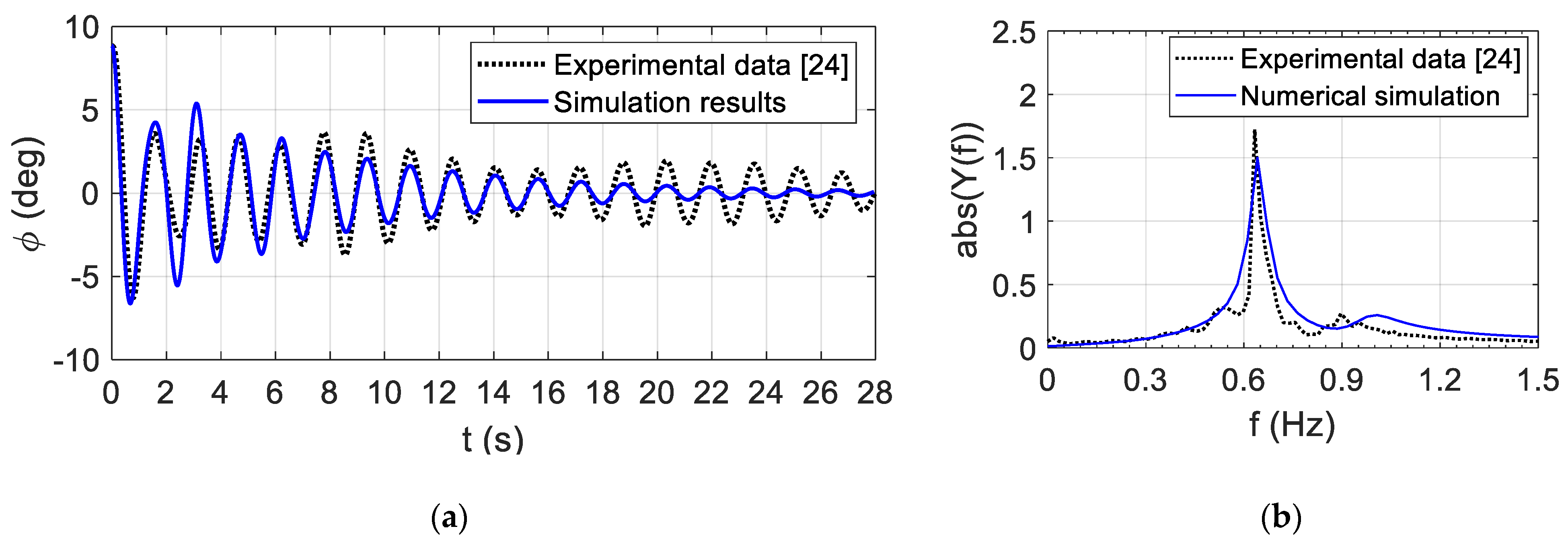
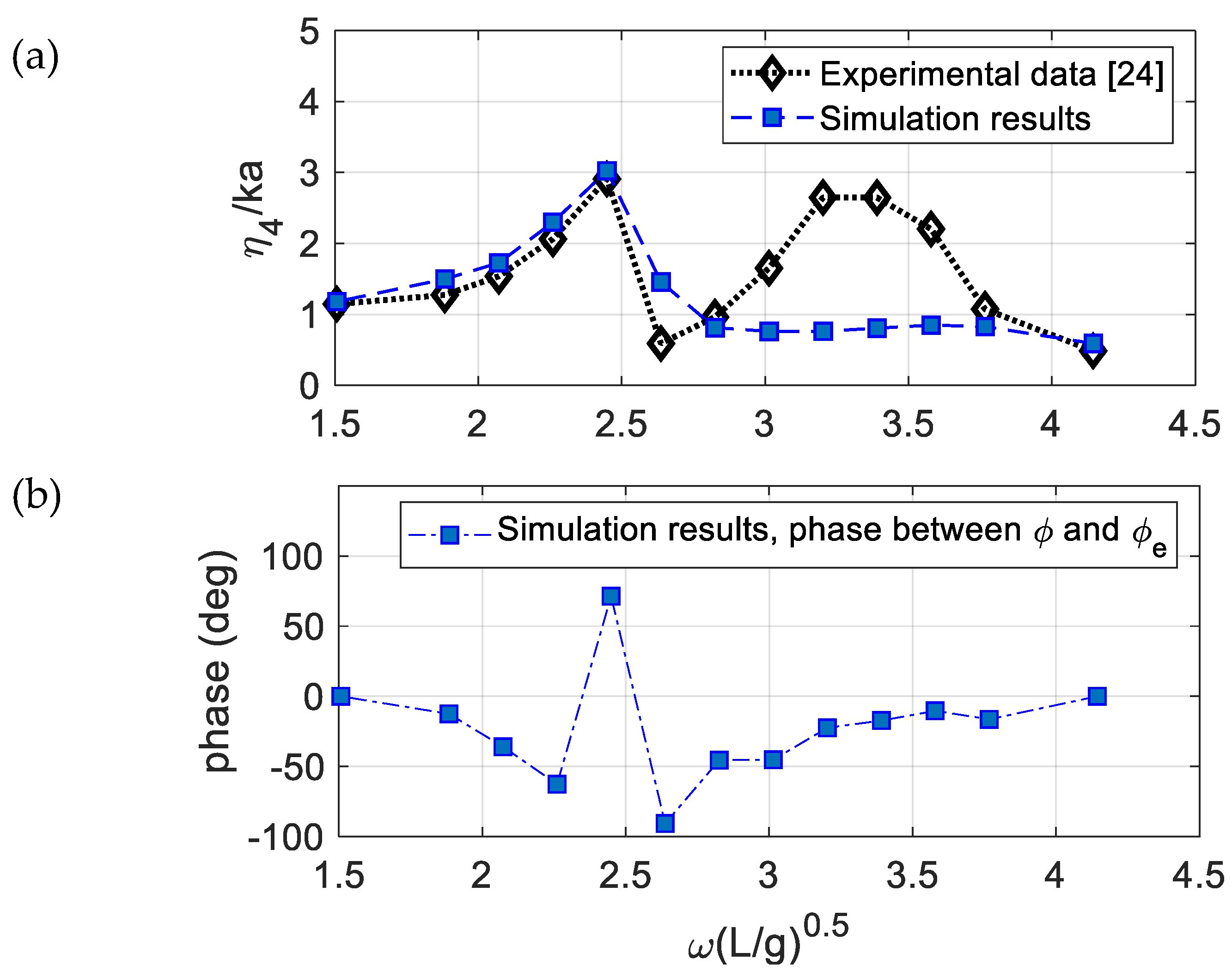
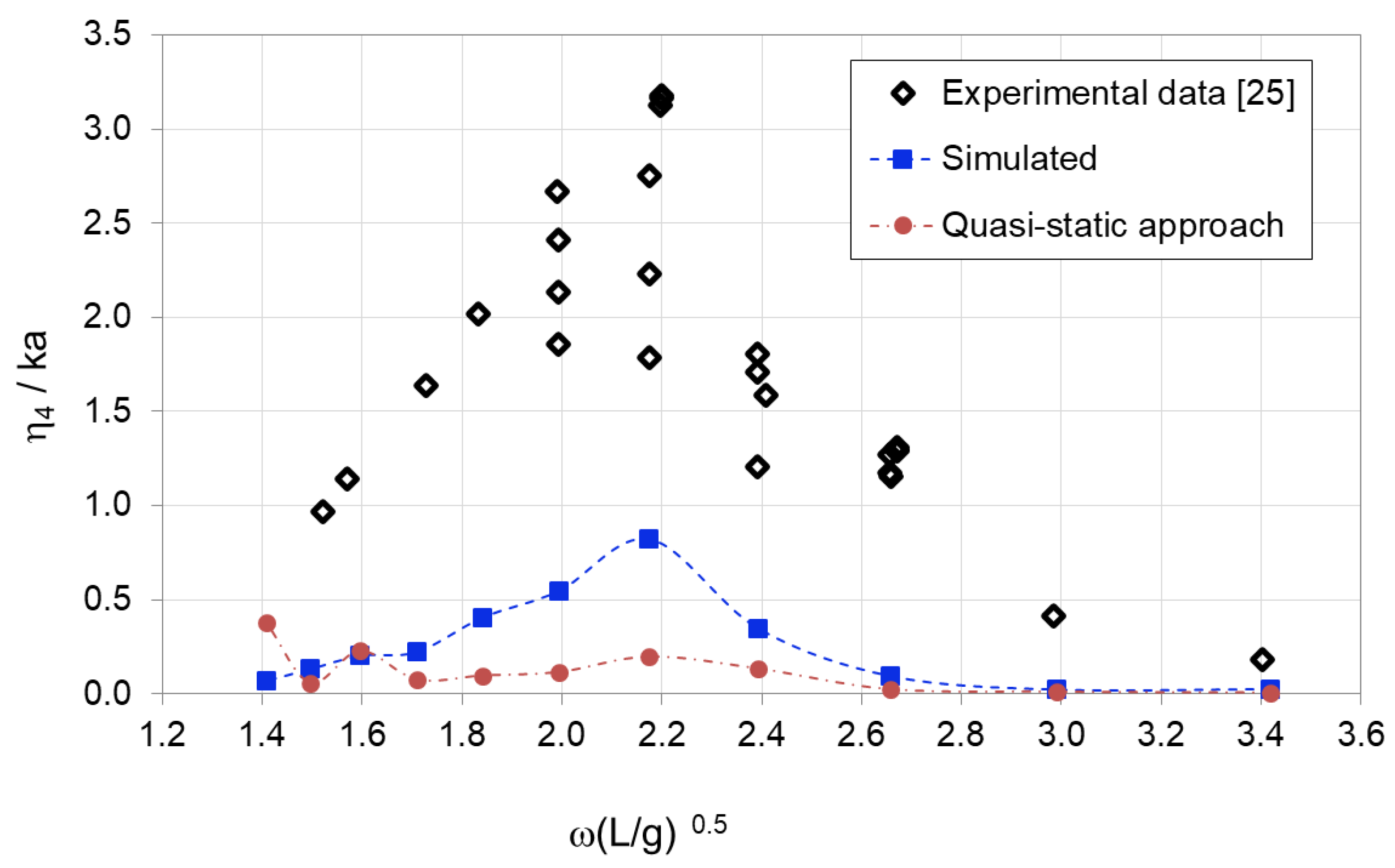
4.2. Roll Decay Simulations and Roll Response in Beam Waves on the Ferry Model
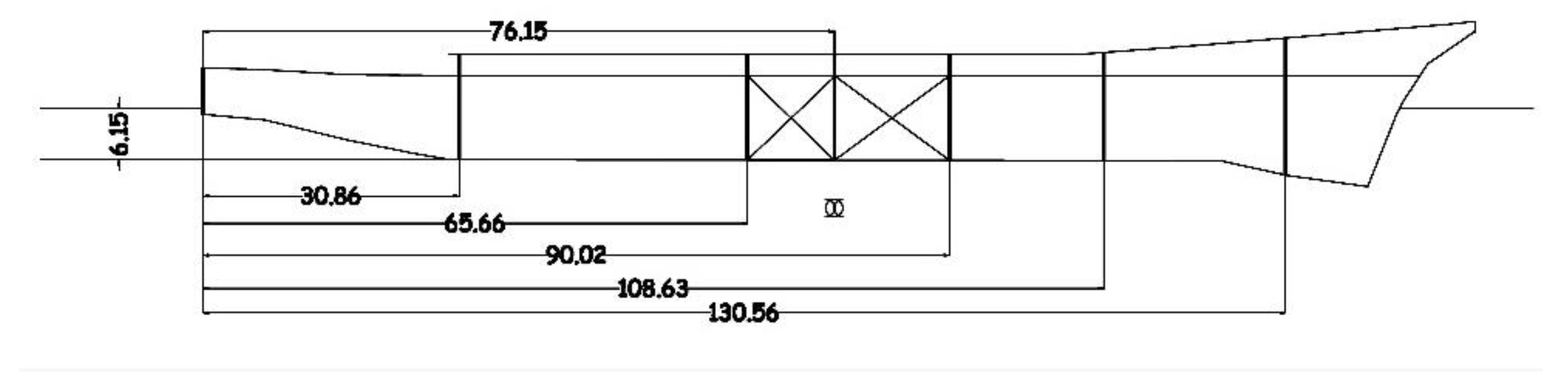
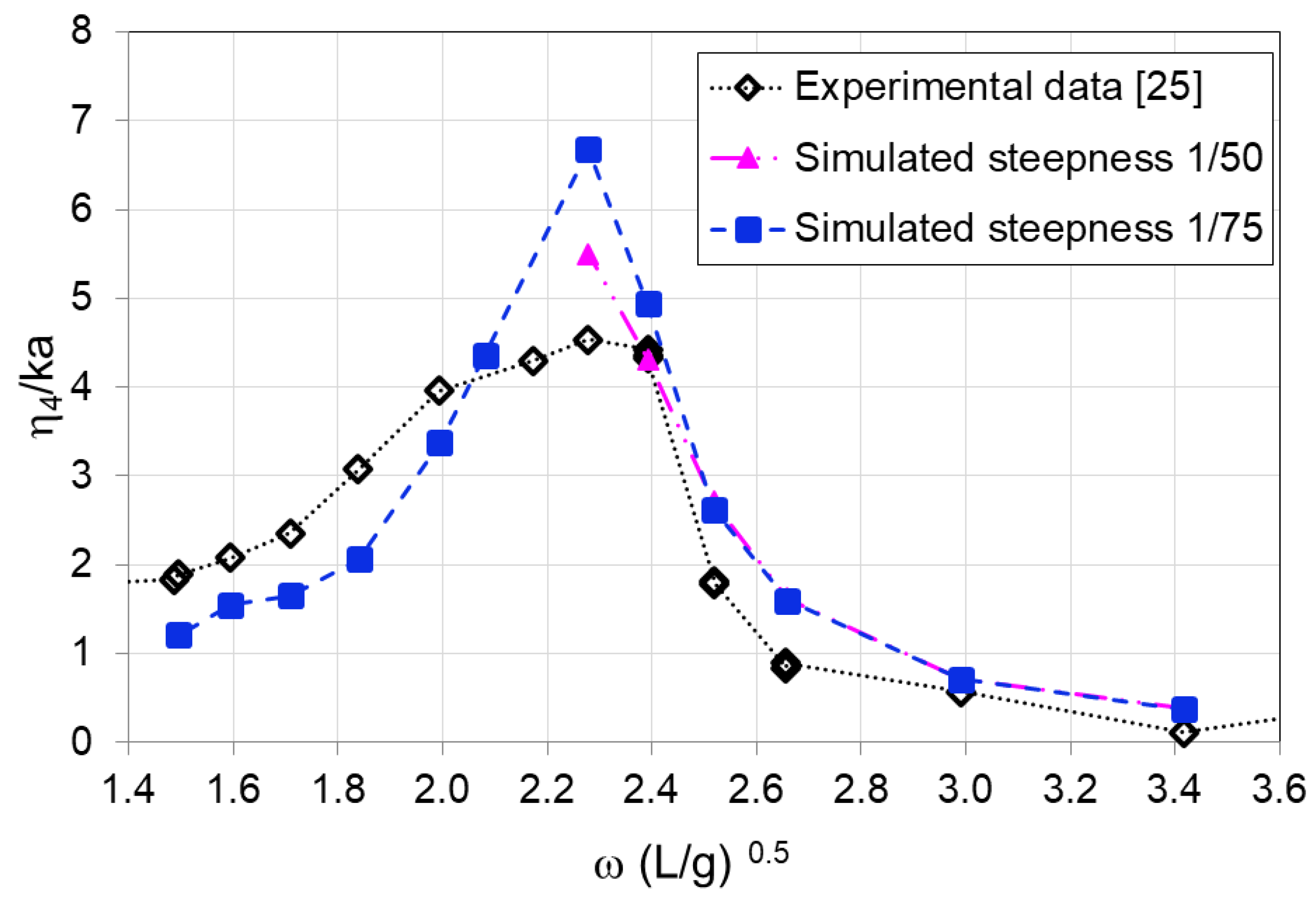
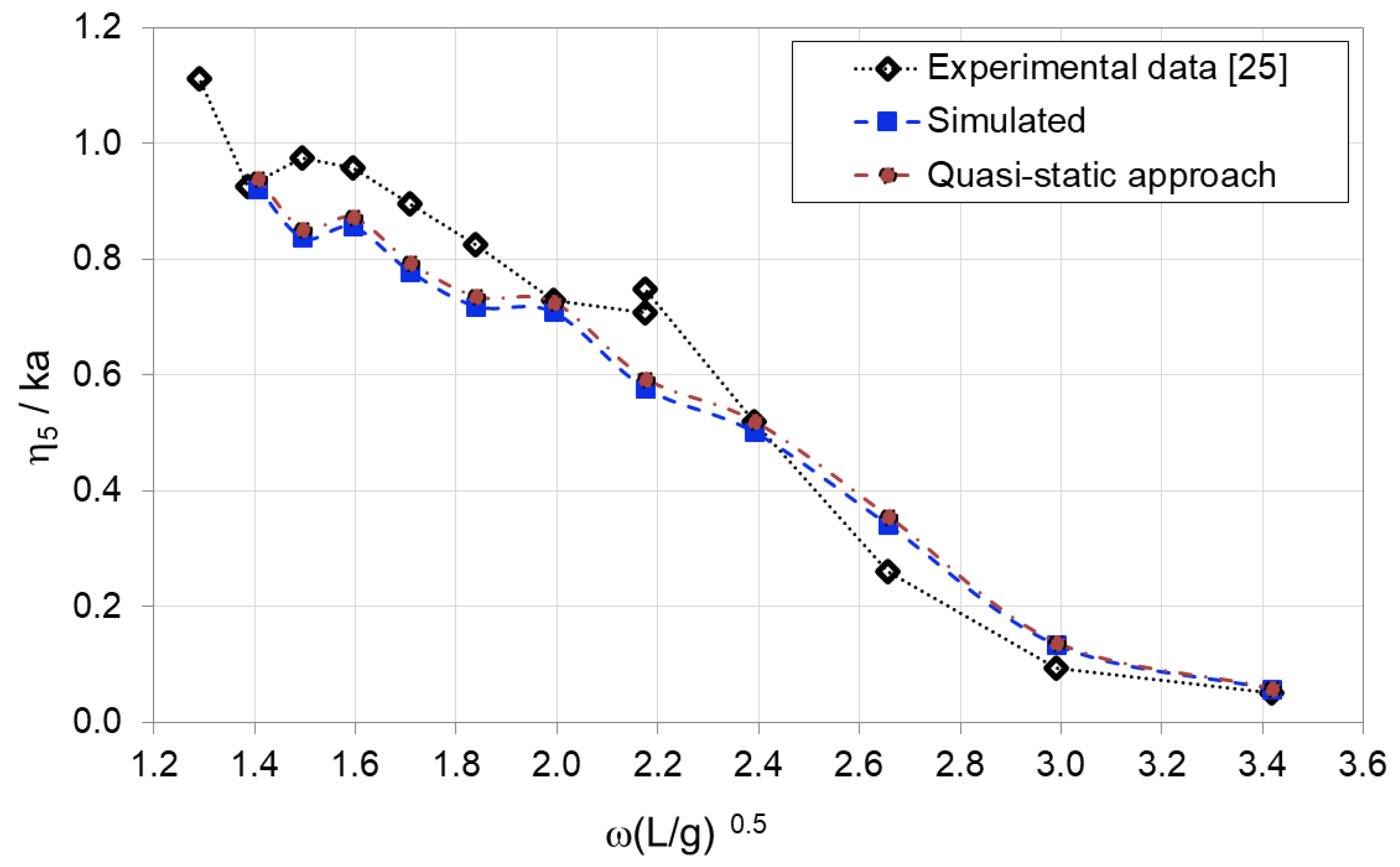
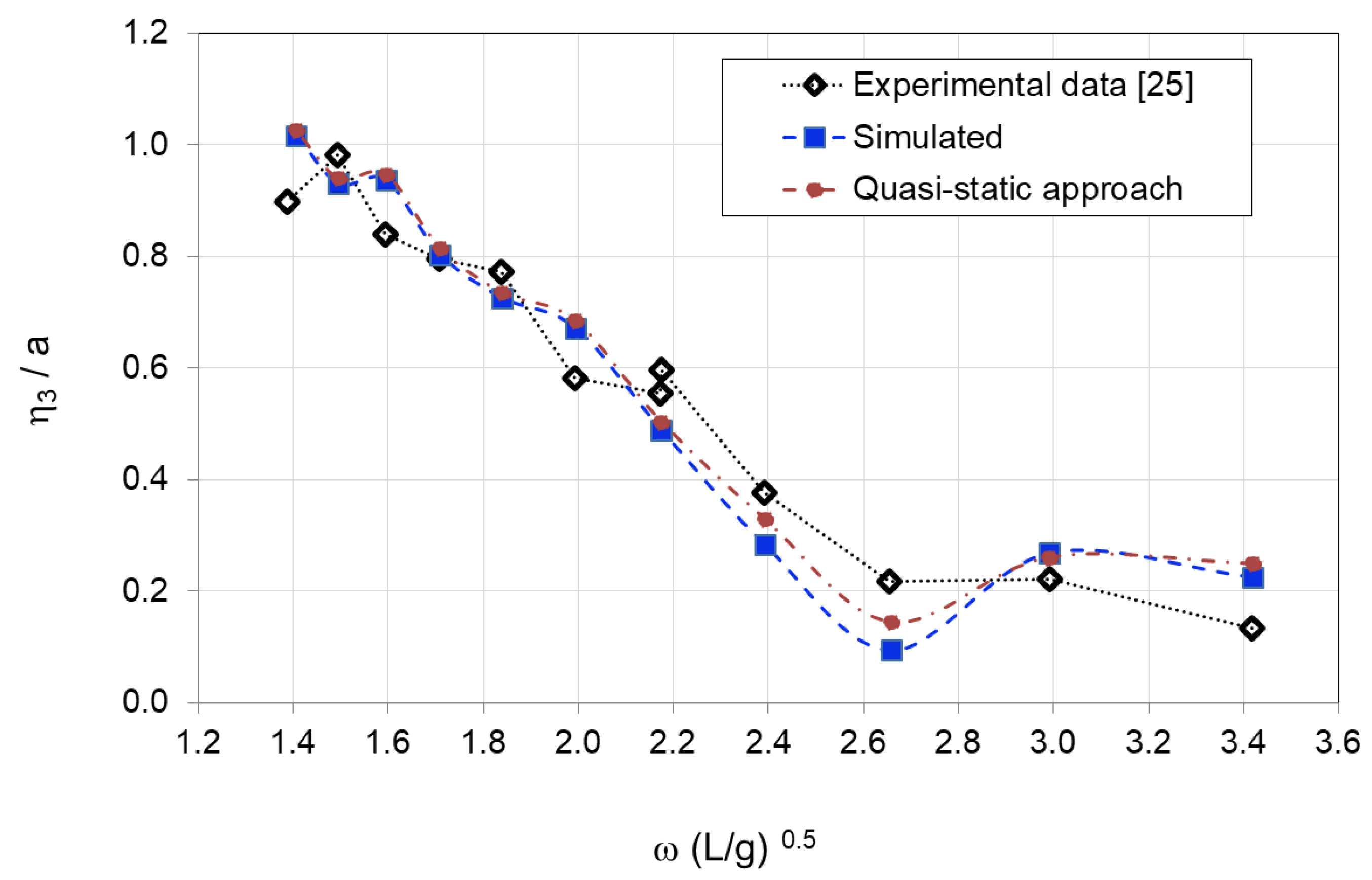
4.3. Motion Responses in Beam and Head Waves on the DTMB5415 Model
- Non-linear damping.
- Internal viscous effects.
- Longitudinal dynamic effects on the free surface.
- Water exchange through the opening.
- Wave actions.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Description |
| aL | acceleration of the lumped mass (m/s2) |
| aLx | acceleration of the lumped mass horizontal component (m/s2) |
| aLy | acceleration of the lumped mass transversal component (m/s2) |
| aLz | acceleration of the lumped mass vertical component (m/s2) |
| fext | external forces (N) |
| ge | apparent gravity (m/s2) |
| H0 | height of the undisturbed sea water (m) |
| I | matrix of inertia (kg m2) |
| m | body mass (kg) |
| mext | external moments (Nm) |
| Q(t) | flow rate (m3/s) |
| ri | position vector of the lamped mass (m) |
| u | velocity vector (m/s) |
| ω | angular velocity vector (rad/s) |
| Symbol | GREEK ALPHABET |
| ϕ | instantaneous roll angle (rad) |
| θ | instantaneous pitch angle (rad) |
| dissipation of the energy of standing waves in rectangular tanks (-) | |
| λw | wave length (m) |
| Symbol | TANK PROPERTIES |
| l | length of a rectangular tank (m) |
| b | breadth of a rectangular tank (m) |
| h | water height in the tanks (m) |
| k | k = π/b tank wave number (1/m) |
| natural frequency of sloshing (rad/s) | |
| Ht | the height of the flooded water in the compartment (m) |
| CD | discharge coefficient (-) |
References
- Vassalos, D.; Jasionowski, A. Emergency Response in Ship Flooding Casualties. In Proceedings of the 13th International Ship Stability Workshop, Brest, Brittany, France, 23–26 September 2013; pp. 259–263. [Google Scholar]
- Varela, J.M.; Rodrigues, J.M.; Soares, C.G. On-board decision support system for ship flooding emergency response. Procedia Comput. Sci. 2014, 29, 1688–1700. [Google Scholar] [CrossRef]
- Le Touzé, D.; Marsh, A.; Oger, G.; Guilcher, P.M.; Khaddaj-Mallat, C.; Alessandrini, B.; Ferrant, P. SPH simulation of green water and ship flooding scenarios. J. Hydrodyn. 2010, 22, 231–236. [Google Scholar] [CrossRef]
- Touzé, L.; Hashimoto, H.; Grenier, N.; Sueyoshi, M. Comparisons of MPS and SPH methods: Forced Roll Test of a Two-dimensional Damaged Car Deck. In Proceedings of the 29th International Workshop on Water Waves and Floating Bodies, Osaka, Japan, 30 March–2 April 2014; pp. 1–4. [Google Scholar]
- Ogawa, Y.; Ohashi, K. Studies on an Assessment of Safety with regard to the Damage Stability of Passenger Ships. In Proceedings of the 12th International Ship Stability Workshop, Washington, DC, USA, 12–15 June 2011; pp. 271–275. [Google Scholar]
- Strasser, C.; Jasionowski, A.; Vassalos, D. Calculation of the time-to-flood of a box-shaped barge by using CFD. In Proceedings of the 10th International Conference on Stability of Ships and Ocean Vehicles, Sankt Petersburg, Russia, 22–26 June 2009; pp. 733–740. [Google Scholar]
- Hosseini, S.H. CFD and EFD study of damaged ship stability in calm water and regular waves. In Proceedings of the 11th International Conference on Stability of Ships and Ocean Vehicles, Athens, Greece, 23–28 September 2012. [Google Scholar]
- Li, X.; Zhang, T.; Zhang, Y.O.; Wang, Y.X. Numerical analysis of ship motion coupled with tank sloshing. In Oceans 2014; IEEE: Taipei, Taiwan, 2014. [Google Scholar]
- Krata, P. The Impact of Sloshing Liquids on Ship Stability for Various Dimensions of Partly Filled Tanks. Trans. Nav. Int. J. Mar. Navig. Saf. Sea Transp. 2013, 7, 481–489. [Google Scholar] [CrossRef]
- Manderbacka, T.L.; Mikkola, T.; Jacob, V.; Carriot, T. Sloshing Forces on a Tank with Two Compartments, Application of the Pendulum Model and CFD. In Proceedings of the Omae 2014 Conference, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Gao, Z.; Gao, Q.; Vassalos, D. Numerical study of damaged ship flooding in beam seas. Ocean Eng. 2013, 61, 77–87. [Google Scholar] [CrossRef]
- Wang, X.; Arai, M. A numerical study on coupled sloshing and ship motions of a liquefied natural gas carrier in regular and irregular waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2013, 229, 3–13. [Google Scholar] [CrossRef]
- Fonfach, J.M.; Manderbacka, T.; Neves, M.A.S. Numerical sloshing simulations: Comparison between lagrangian and lumped mass models applied to two compartments with mass transfer. Ocean Eng. 2016, 114, 168–184. [Google Scholar] [CrossRef]
- Manderbacka, T.; Mikkola, T.; Ruponen, P.; Matusiak, J. Transient response of a ship to an abrupt flooding accounting for the momentum flux. J. Fluids Struct. 2015, 57, 108–126. [Google Scholar] [CrossRef]
- Santos, T.A.; Soares, C.G. Study of damaged ship motions taking into account floodwater dynamics. J. Mar. Sci. Technol. 2008, 13, 291–307. [Google Scholar] [CrossRef]
- Lorkowski, O.; Dankowski, H.; Kluwe, F. An Experimental Study on Progressive and Dynamic Damage Stability Scenarios. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; pp. 1–10, Paper No. OMAE2014-23388. [Google Scholar]
- De Kat, J. Dynamics of a Ship with Partially Flooded Compartment. In Contemporary Ideas on Ship Stability; Elsevier Science Ltd.: Okford, UK, 2000; pp. 249–263. [Google Scholar]
- Letizia, L. Damage Survivability of Passenger Ships in a Seaway; University of Strathclyde: Glasgow, UK, 1996. [Google Scholar]
- Lee, D.; Hong, S.Y.; Lee, G.J. Theoretical and experimental study on dynamic behavior of a damaged ship in waves. Ocean Eng. 2007, 34, 21–31. [Google Scholar] [CrossRef]
- Acanfora, M.; Cirillo, A. A simulation model for ship response in flooding scenario. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 231, 153–164. [Google Scholar] [CrossRef]
- Acanfora, M.; Cirillo, A. On the development of a fast modeling of floodwater effects on ship motions in waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 877–887. [Google Scholar] [CrossRef]
- Ruponen, P. Adaptive time step in simulation of progressive flooding. Ocean Eng. 2014, 78, 35–44. [Google Scholar] [CrossRef]
- Manderbacka, T.; Ruponen, P.; Kulovesi, J.; Matusiak, J. Model experiments of the transient response to flooding of the box shaped barge. J. Fluids Struct. 2015, 57, 127–143. [Google Scholar] [CrossRef]
- Acanfora, M.; de Luca, F. An experimental investigation into the influence of the damage openings on ship response. Appl. Ocean Res. 2016, 58, 62–70. [Google Scholar] [CrossRef]
- Begovic, E.; Mortola, G.; Incecik, A.; Day, A.H. Experimental assessment of intact and damaged ship motions in head, beam and quartering seas. Ocean Eng. 2013, 72, 209–226. [Google Scholar] [CrossRef]
- Matusiak, J. Dynamics of a Rigid Ship, SCIENZE +; Aalto University Publication: Helsinki, Finland, 2013. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990; Volume 1. [Google Scholar]
- ITTC. Numerical Estimation of Roll Damping; ITTC: Rio De Janeiro, Brazil, 2011; pp. 1–33. [Google Scholar]
- White, F.M. Pressure Distribution in a Fluid. In Fluid Mechanics, 4th ed.; McGraw-Hill: Boston, MA, USA, 2010; Volume 6. [Google Scholar]
- Keulegan, G.H. Energy dissipation in standing waves in rectangular basins. J. Fluid Mech. 1959, 6, 33–50. [Google Scholar] [CrossRef]
- Magnus, F.O.; Alexander, T. Sloshing; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Lloyd, A.R.J.M. Seakeeping: Ship Behaviour in Rough Weather; Ellis Horwood Limited: Chichester, UK, 1998. [Google Scholar]
- Lee, S.; You, J.M.; Lee, H.H.; Lim, T.; Park, S.T.; Seo, J.; Rhee, S.H.; Rhee, K.P. Experimental Study on the Six Degree-of-Freedom Motions of a Damaged Ship Floating in Regular Waves. IEEE J. Ocean. Eng. 2016, 41, 40–49. [Google Scholar]
- Mancini, S.; Begovic, E.; Day, A.H.; Incecik, A. Verification and validation of numerical modelling of DTMB 5415 roll decay. Ocean Eng. 2018, 162, 209–223. [Google Scholar] [CrossRef]
- Begovic, E.; Day, A.H.; Incecik, A. An experimental study of hull girder loads on an intact and damaged naval ship. Ocean Eng. 2017, 133, 47–65. [Google Scholar] [CrossRef]

| Symbol | Description | Model Scale |
|---|---|---|
| LOA | Length over all | 4.000 m |
| BOA | Breadth over all | 0.800 m |
| D | Depth | 0.800 m |
| m | Total mass | 657 kg |
| T | Draft | 0.253 m |
| GM02 | Initial metacentric height of the intact ship | 0.0274 m |
| hb | Damage opening height from the compartment bottom | 50 mm |
| l0 | Dimension of the square damage opening | 200 mm |
| Symbol | Description | Ship Scale | Model Scale |
|---|---|---|---|
| LBP | Length between perpendicular | 77.55 m | 3.525 m |
| B | Breadth | 17.930 m | 0.815 m |
| T | Draft | 3.960 m | 0.180 m |
| Δ | Displacement | 1810 t | 0.170 t |
| KG | Vertical centre of gravity | 6.886 m | 0.313 m |
| GM0 | Transversal metacentric height of the intact ship | 5.808 m | 0.264 m |
| ω0 | Natural roll frequency | 1.173 rad/s | 5.507 rad/s |
| kxx | Roll radius of inertia in air | 5.450 m | 0.247 m |
| kyy | Pitch radius of inertia in air | 24.384 m | 1.108 m |
| kzz | Yaw radius of inertia in air | 24.499 m | 1.113 m |
| Lt | Length of the compartment | 16.940 m | 0.767 m |
| Bt | Width of the compartment | 17.930 m | 0.815 m |
| df | Flooded water depth | 3.674 m | 0.167 m |
| df/Bt | Aspect ratio | 0.205 | 0.205 |
| Wt | Flooded water weight | 688.9 t | 64.7 kg |
| Symbol | Description | Ship Scale | Model Scale |
|---|---|---|---|
| LBP | Length between perpendicular | 142.200 m | 2.788 m |
| B | Breadth on waterline | 19.082 m | 0.374 m |
| T | Draft | 6.150 m | 0.120 m |
| D | Depth | 12.470 m | 0.244 m |
| Δ | Displacement | 8635 t | 63.5 kg |
| KG | Vertical centre of gravity | 7.555 m | 1.375 m |
| GM0 | Transversal metacentric height of the intact ship | 1.938 m | 0.038 m |
| kxx | Roll radius of inertia in water | 6.932 m | 0.136 m |
| kyy | Pitch radius of inertia in air | 36.802 m | 0.696 m |
| kzz | Yaw radius of inertia in air | 36.802 m | 0.696 m |
| Lt | Length of the compartment | 24.360 m | 0.478 m |
| Bt | Width of the compartment | 19.458 m | 0.382 m |
| Wt | Flooded water weight | 2638.9 t | 19.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acanfora, M.; Begovic, E.; De Luca, F. A Fast Simulation Method for Damaged Ship Dynamics. J. Mar. Sci. Eng. 2019, 7, 111. https://doi.org/10.3390/jmse7040111
Acanfora M, Begovic E, De Luca F. A Fast Simulation Method for Damaged Ship Dynamics. Journal of Marine Science and Engineering. 2019; 7(4):111. https://doi.org/10.3390/jmse7040111
Chicago/Turabian StyleAcanfora, Maria, Ermina Begovic, and Fabio De Luca. 2019. "A Fast Simulation Method for Damaged Ship Dynamics" Journal of Marine Science and Engineering 7, no. 4: 111. https://doi.org/10.3390/jmse7040111
APA StyleAcanfora, M., Begovic, E., & De Luca, F. (2019). A Fast Simulation Method for Damaged Ship Dynamics. Journal of Marine Science and Engineering, 7(4), 111. https://doi.org/10.3390/jmse7040111







