A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model
Abstract
:1. Introduction
2. Brief Description of the Numerical Model
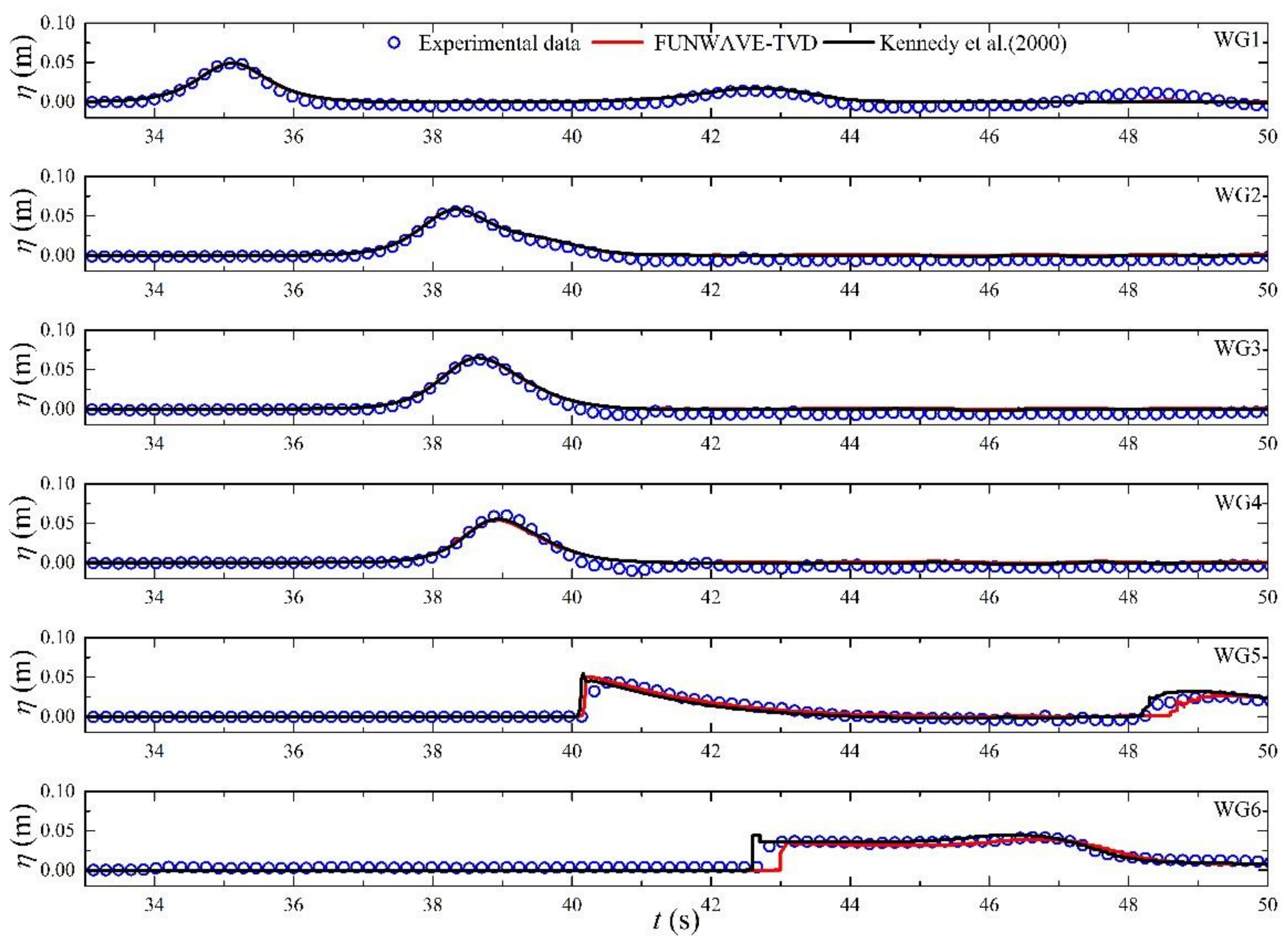
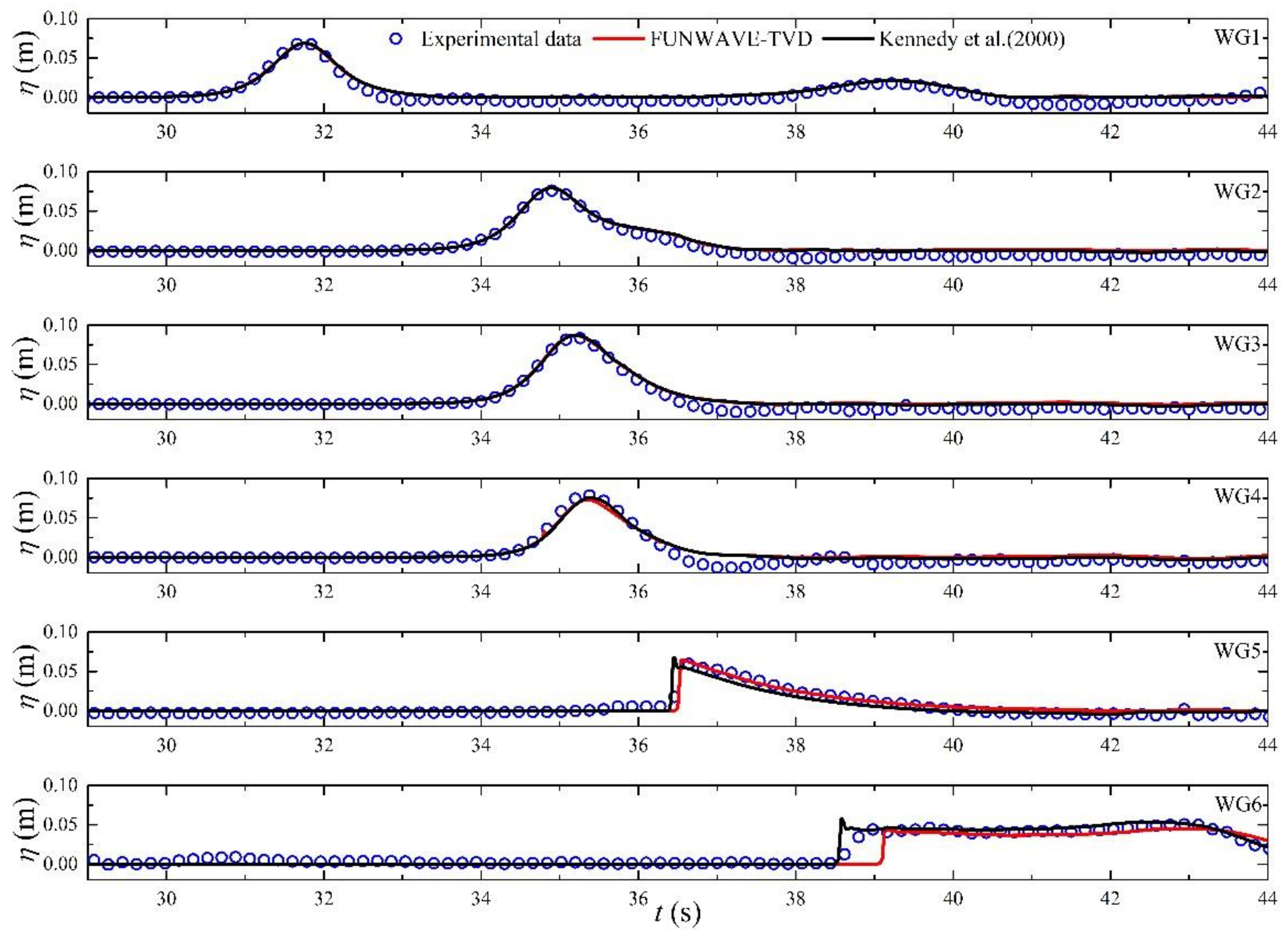
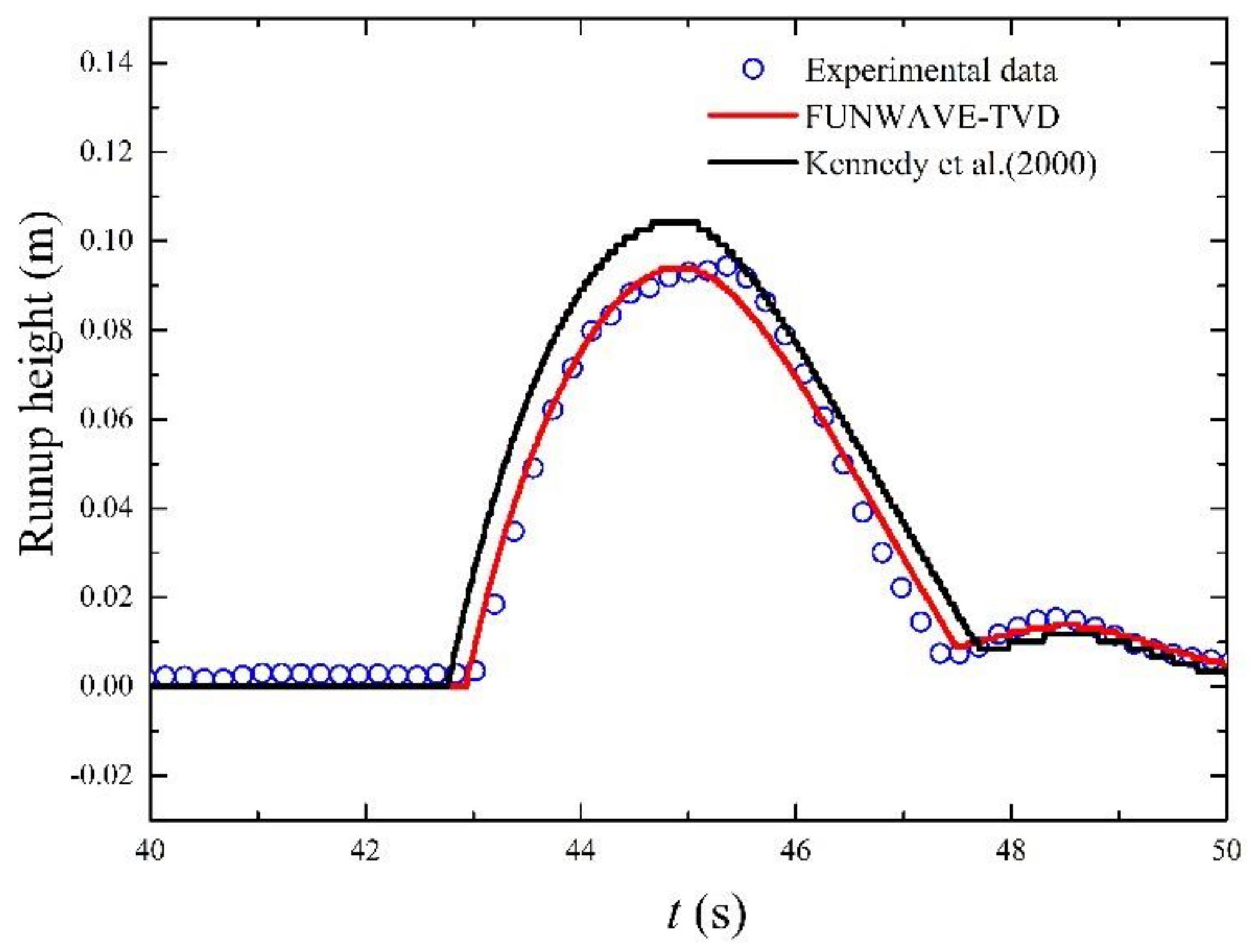
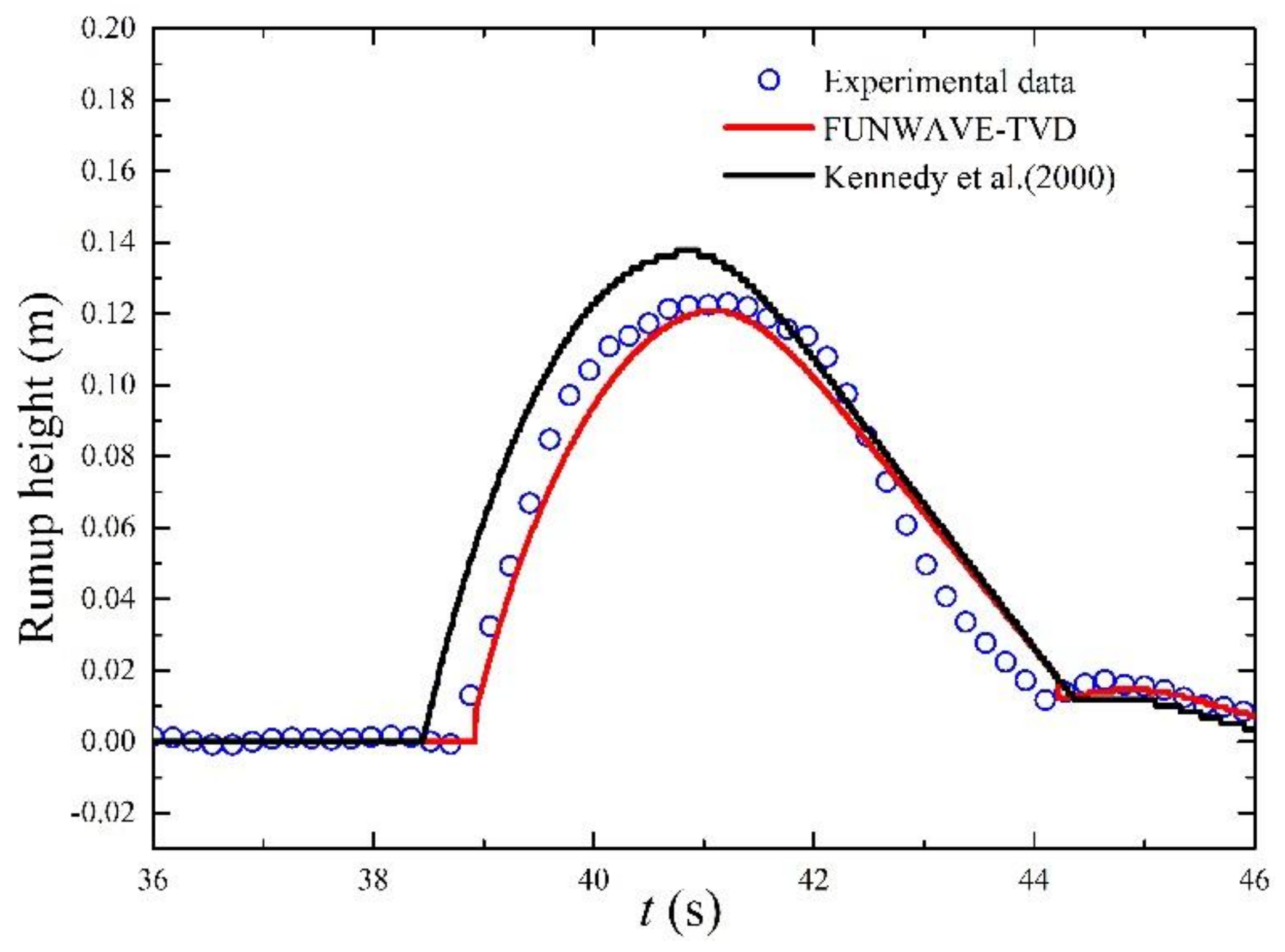
3. Model Validation
4. Numerical Results and Discussions
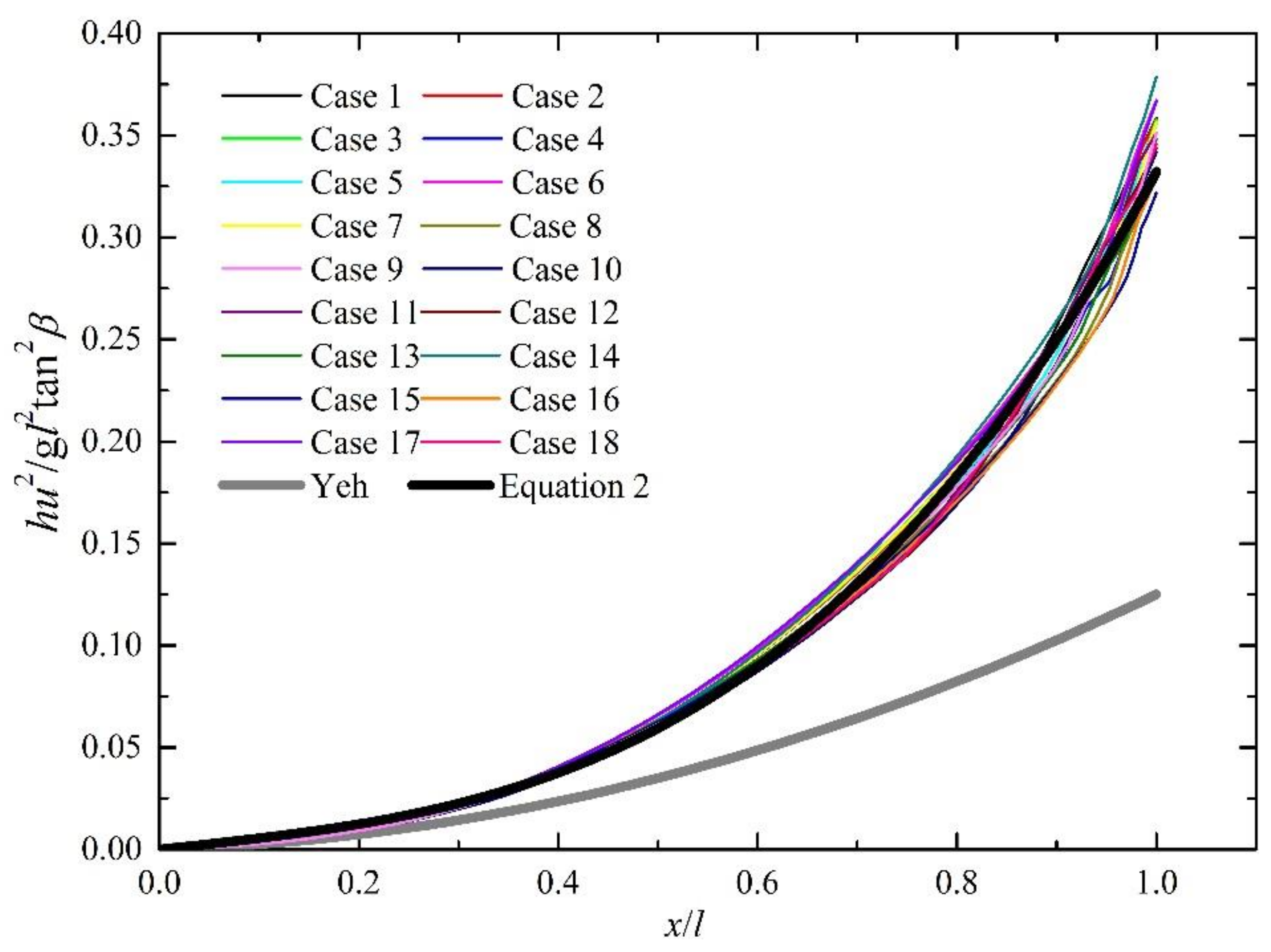
4.1. Maximum Momentum Flux Distribution in the Run-Up Zone
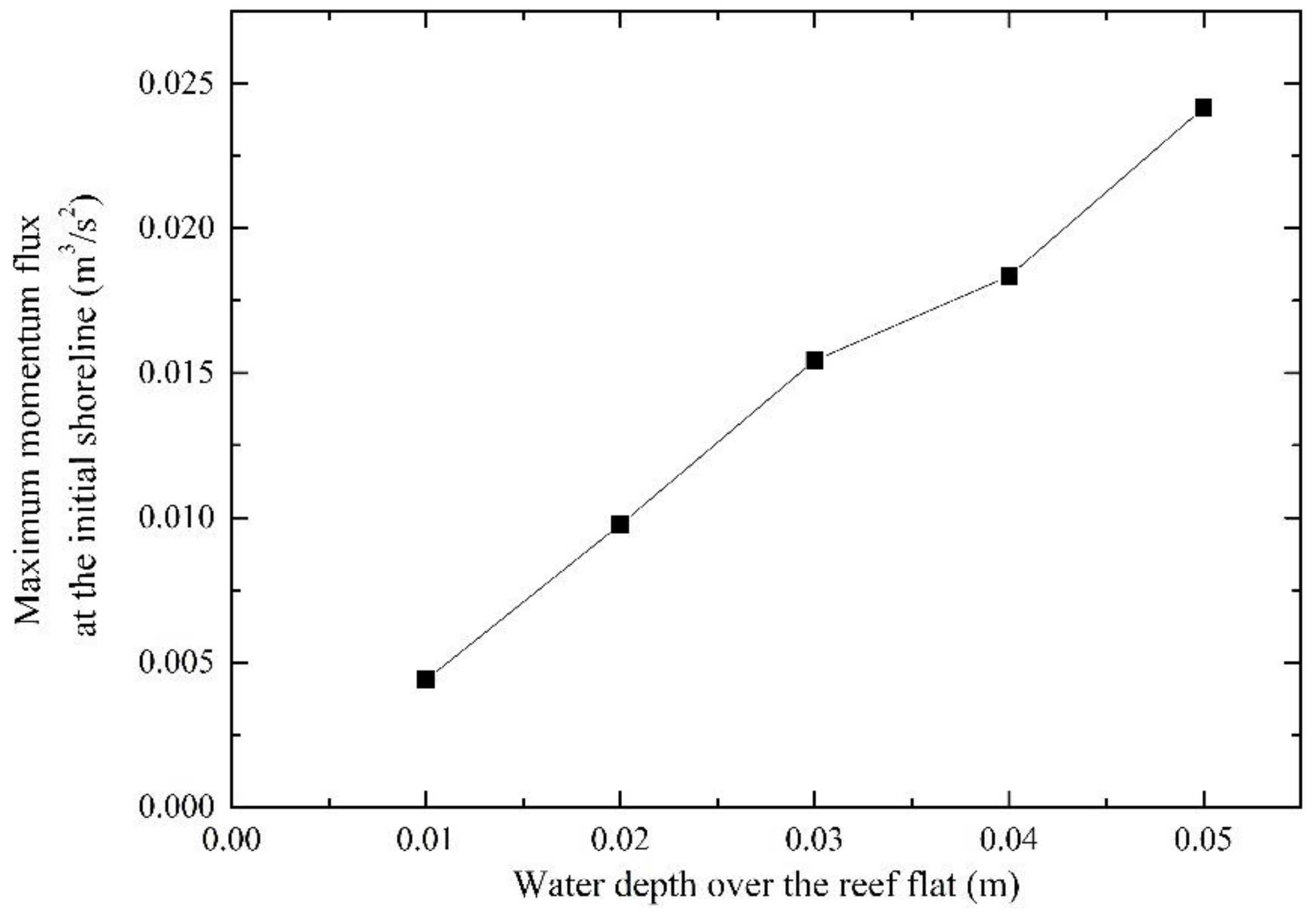
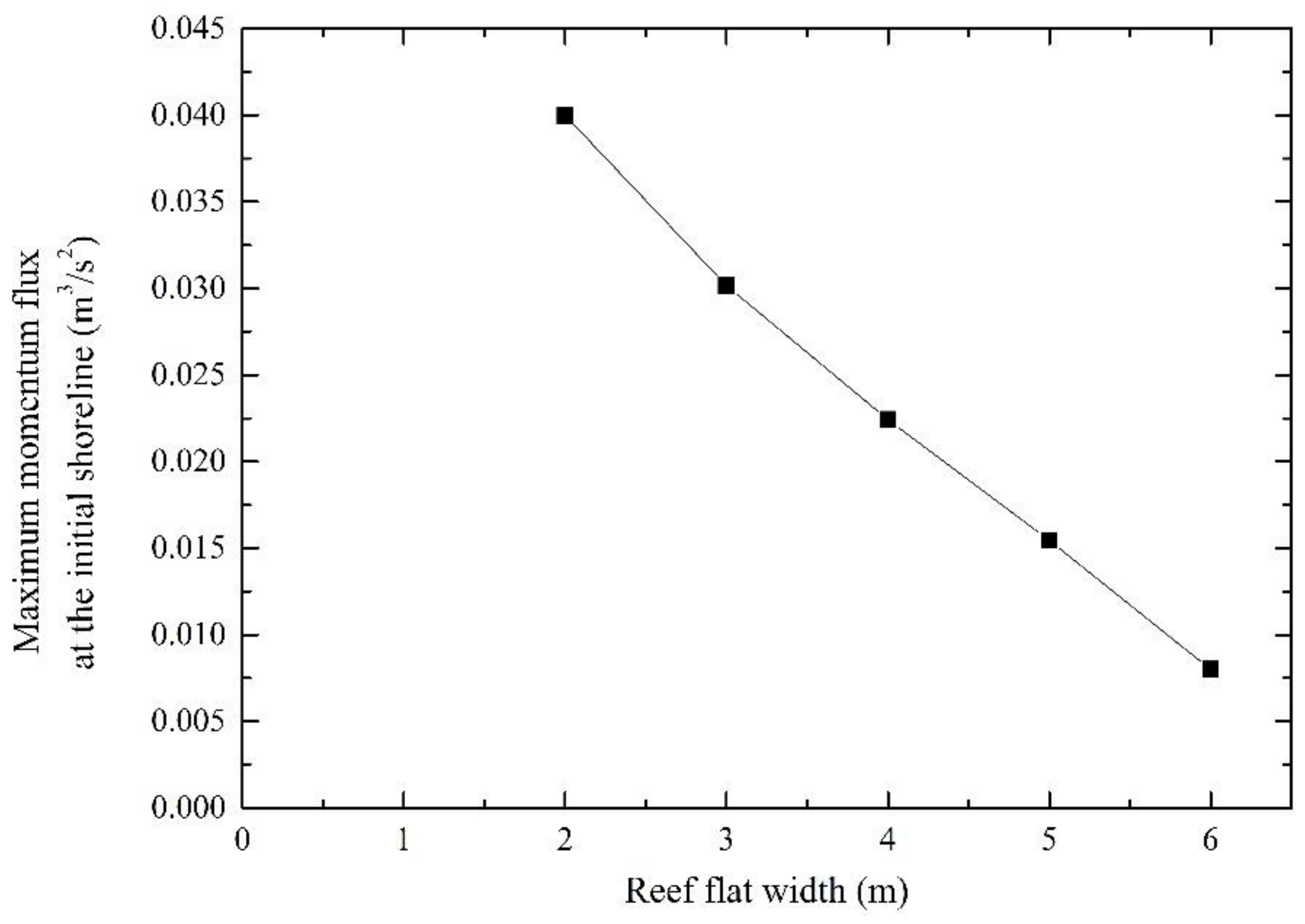
4.2. Effects of Reef Parameters
5. Conclusions
- Validation results of solitary wave transformation and run-up over a typical reef-beach profile clearly showed that with a proper grid size, FUNWAVE-TVD can reasonably reproduce solitary wave breaking and propagation over the sharply varying reef bathymetry and predict the run-up height over the back-reef slope better than the previous version of FUNWAVE using the eddy viscosity breaking model.
- A new equation can be obtained with a curve fit of the numerical experiment results for the envelope of the spatial distribution of the maximum momentum flux within the solitary wave run-up zone over the back-reef beach. The new equation obtained for reef-lined coasts in this study, which is a cubic function, is different from the one obtained in previous studies for uniformly-sloping beds, which is a quadratic function.
- The effects of the water depth over the reef flat and reef flat width on the maximum momentum flux at the initial shoreline were similar to the ones on the run-up height. The maximum momentum flux at the initial shoreline increased significantly with the increase of the water depth over the reef flat and decreased significantly with the increase of the reef flat width. However, the effect of the fore-reef slope angle on the maximum momentum flux at the initial shoreline is different from the one on the run-up height. A steeper fore-reef slope may induce larger momentum flux at the initial shoreline. The results indicated that despite the run-up height, investigating tsunami forces within the solitary wave run-up zone is also necessary for a better understanding of the role of fringing reefs in the mitigation of tsunami hazard.
Author Contributions
Funding
Conflicts of Interest
References
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Maiti, S.; Sen, D. Computation of solitary waves during propagation and runup on a slope. Ocean Eng. 1999, 26, 1063–1083. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Hwang, K.-S.; Hwung, H.-H. Large-scale laboratory measurements of solitary wave inundation on a 1:20 slope. Coast. Eng. 2009, 56, 1022–1034. [Google Scholar] [CrossRef]
- Quiroga, P.D.; Cheung, K.F. Laboratory study of solitary-wave transformation over bed-form roughness on fringing reefs. Coast. Eng. 2013, 80, 35–48. [Google Scholar] [CrossRef]
- Lin, P. A numerical study of solitary wave interaction with rectangular obstacles. Coast. Eng. 2004, 51, 35–51. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R.; Schäffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Aniel-Quiroga, Í.; Quetzalcóatl, O.; González, M.; Guillou, L. Tsunami run-up estimation based on a hybrid numerical flume and a parameterization of real topobathymetric profiles. Nat. Hazards Earth Syst. Sci. 2018, 18, 1469–1491. [Google Scholar] [CrossRef]
- Madsen, P.A.; SchÄFfer, H.A. Analytical solutions for tsunami runup on a plane beach: Single waves, N-waves and transient waves. J. Fluid Mech. 2010, 645, 27–57. [Google Scholar] [CrossRef]
- Aniel-Quiroga, Í.; Vidal, C.; Lara, J.L.; González, M.; Sainz, Á. Stability of rubble-mound breakwaters under tsunami first impact and overflow based on laboratory experiments. Coast. Eng. 2018, 135, 39–54. [Google Scholar] [CrossRef]
- Esteban, M.; Jayaratne, R.; Mikami, T.; Morikubo, I.; Shibayama, T.; Thao Nguyen, D.; Ohira, K.; Ohtani, A.; Mizuno, Y.; Kinoshita, M.; et al. Stability of Breakwater Armor Units against Tsunami Attacks. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 188–198. [Google Scholar] [CrossRef]
- Guler, H.G.; Arikawa, T.; Oei, T.; Yalciner, A.C. Performance of rubble mound breakwaters under tsunami attack, a case study: Haydarpasa Port, Istanbul, Turkey. Coast. Eng. 2015, 104, 43–53. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; McCulley, J.L.; Mendis, S.G.; Perera, K. Coral poaching worsens tsunami destruction in Sri Lanka. Eos Trans. Am. Geophys. Union 2005, 86, 301–304. [Google Scholar] [CrossRef]
- Goff, J.; Liu, P.L.F.; Higman, B.; Morton, R.; Jaffe, B.E.; Fernando, H.; Lynett, P.; Fritz, H.; Synolakis, C.; Fernando, S. Sri Lanka Field Survey after the December 2004 Indian Ocean Tsunami. Earthq. Spectra 2006, 22, 155–172. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Samarawickrama, S.P.; Balasubramanian, S.; Hettiarachchi, S.S.L.; Voropayev, S. Effects of porous barriers such as coral reefs on coastal wave propagation. J. Hydro Environ. Res. 2008, 1, 187–194. [Google Scholar] [CrossRef]
- Adger, W.N.; Hughes, T.P.; Folke, C.; Carpenter, S.R.; Rockström, J. Social-Ecological Resilience to Coastal Disasters. Science 2005, 309, 1036. [Google Scholar] [CrossRef]
- Baird, A.H.; Campbell, S.J.; Anggoro, A.W.; Ardiwijaya, R.L.; Fadli, N.; Herdiana, Y.; Kartawijaya, T.; Mahyiddin, D.; Mukminin, A.; Pardede, S.T.; et al. Acehnese Reefs in the Wake of the Asian Tsunami. Curr. Biol. 2005, 15, 1926–1930. [Google Scholar] [CrossRef]
- Fujima, K.; Shigihara, Y.; Tomita, T.; Honda, K.; Nobuoka, H.; Hanzawa, M.; Fujii, H.; Ohtani, H.; Orishimo, S.; Tatsumi, M.; et al. Survey results of the indian ocean tsunami in the maldives. Coast. Eng. J. 2006, 48, 81–97. [Google Scholar] [CrossRef]
- Seelig, W.N. Laboratory Study of Reef-Lagoon System Hydraulics. J. Waterw. Port Coast. Ocean Eng. 1983, 109, 380–391. [Google Scholar] [CrossRef]
- Gourlay, M.R. Wave set-up on coral reefs. 1. Set-up and wave-generated flow on an idealised two dimensional horizontal reef. Coast. Eng. 1996, 27, 161–193. [Google Scholar] [CrossRef]
- Nwogu, O.; Demirbilek, Z. Infragravity Wave Motions and Runup over Shallow Fringing Reefs. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 295–305. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Z.; Monismith, S.G.; Lo, E.Y.M. Characteristics of Monochromatic Waves Breaking over Fringing Reefs. J. Coast. Res. 2013, 29, 94–104. [Google Scholar] [CrossRef]
- Yao, Y.; He, W.; Du, R.; Jiang, C. Study on wave-induced setup over fringing reefs in the presence of a reef crest. Appl. Ocean Res. 2017, 66, 164–177. [Google Scholar] [CrossRef]
- Yao, Y.; He, F.; Tang, Z.; Liu, Z. A study of tsunami-like solitary wave transformation and run-up over fringing reefs. Ocean Eng. 2018, 149, 142–155. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Fang, K.; Liu, Z.; Zou, Z. Fully nonlinear modeling wave transformation over fringing reefs using shock-capturing Boussinesq model. J. Coast. Res. 2016, 32, 164–171. [Google Scholar] [CrossRef]
- Kobayashi, N.; DeSilva, G.S.; Watson, K.D. Wave transformation and swash oscillation on gentle and steep slopes. J. Geophys. Res. 1989, 94, 951–966. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Q.; Kesserwani, G.; Hall, J.W. A 2D shallow flow model for practical dam-break simulations. J. Hydraul. Res. 2011, 49, 307–316. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R.; Schäffer, H.A. Surf zone dynamics simulated by a Boussinesq type model. Part I. Model description and cross-shore motion of regular waves. Coast. Eng. 1997, 32, 255–287. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Z.; Monismith, S.G.; Lo, E.Y.M. 1DH Boussinesq modeling of wave transformation over fringing reefs. Ocean Eng. 2012, 47, 30–42. [Google Scholar] [CrossRef]
- Skotner, C.; Apelt, C.J. Application of a Boussinesq model for the computation of breaking waves: Part 1: Development and verification. Ocean Eng. 1999, 26, 905–925. [Google Scholar] [CrossRef]
- Yao, Y.; Becker, J.M.; Ford, M.R.; Merrifield, M.A. Modeling wave processes over fringing reefs with an excavation pit. Coast. Eng. 2016, 109, 9–19. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid finite volume—Finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43-44, 36–51. [Google Scholar] [CrossRef]
- Fang, K.; Zou, Z.; Dong, P.; Liu, Z.; Gui, Q.; Yin, J. An efficient shock capturing algorithm to the extended Boussinesq wave equations. Appl. Ocean Res. 2013, 43, 11–20. [Google Scholar] [CrossRef]
- Kazolea, M.; Delis, A.I.; Synolakis, C.E. Numerical treatment of wave breaking on unstructured finite volume approximations for extended Boussinesq-type equations. J. Comput. Phys. 2014, 271, 281–305. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhan, J.-M.; Li, Y.S. Parametric Investigation of Breaking Solitary Wave Over Fringing Reef Based on Shock-Capturing Boussinesq Model. Coastal Eng. J. 2016, 58, 1650007. [Google Scholar] [CrossRef]
- Ning, Y.; Liu, W.; Sun, Z.; Zhao, X.; Zhang, Y. Parametric study of solitary wave propagation and runup over fringing reefs based on a Boussinesq wave model. J. Mar. Sci. Technol. 2018, 1–14. [Google Scholar] [CrossRef]
- Yeh, H. Tsunami Forces in The Runup Zone. In Caribbean Tsunami Hazard; World Scientific: Singapore, 2006. [Google Scholar]
- Yeh, H. Maximum Fluid Forces in the Tsunami Runup Zone. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 496–500. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Synolakis, C.E.; Yeh, H.H. Report on the International Workshop on Long-Wave Run-up. J. Fluid Mech. 1991, 229, 675–688. [Google Scholar] [CrossRef]
- Carrier, G.F.; Wu, T.T.; Yeh, H. Tsunami run-up and draw-down on a plane beach. J. Fluid Mech. 2003, 475, 79–99. [Google Scholar] [CrossRef]
- Kirby, J.T.; Wei, G.; Chen, Q.; Kennedy, A.B.; Dalrymple, R.A. Fully Nonlinear Boussinesq Wave Model. Documentation and User’s Manual; Center for Applied Coastal Research, Department of Civil and Environmental Engineering, University of Delaware: Delaware, DE, USA, 1998. [Google Scholar]
- Chen, Q. Fully nonlinear Boussinesq-type equations for waves and currents over porous beds. J. Eng. Mech. 2006, 132, 220–230. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Kirby, J.T.; Chen, Q.; Dalrymple, R.A. Boussinesq-type equations with improved nonlinear performance. Wave Motion 2001, 33, 225–243. [Google Scholar] [CrossRef]
- Quataert, E.; Storlazzi, C.; Rooijen, A.; Cheriton, O.; Van Dongeren, A. The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines. Geophys. Res. Lett. 2015, 42, 6407–6415. [Google Scholar] [CrossRef]
- Guizien, K.; Barthélemy, E. Accuracy of solitary wave generation by a piston wave maker. J. Hydraul. Res. 2002, 40, 321–331. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T. Time-Dependent Numerical Code for Extended Boussinesq Equations. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 251–261. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Shimozono, T.; Tajima, Y.; Kennedy, A.B.; Nobuoka, H.; Sasaki, J.; Sato, S. Combined infragravity wave and sea-swell runup over fringing reefs by super typhoon Haiyan. J. Geophys. Res. 2015, 120, 4463–4486. [Google Scholar] [CrossRef]
- Arnason, H. Interactions between an incident bore and a free-standing coastal structure. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2005. [Google Scholar]
- Kunkel, C.M.; Hallberg, R.W.; Oppenheimer, M. Coral reefs reduce tsunami impact in model simulations. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Gelfenbaum, G.; Apotsos, A.; Stevens, A.W.; Jaffe, B. Effects of fringing reefs on tsunami inundation: American Samoa. Earth Sci. Rev. 2011, 107, 12–22. [Google Scholar] [CrossRef]
- Lynett Patrick, J. Effect of a Shallow Water Obstruction on Long Wave Runup and Overland Flow Velocity. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 455–462. [Google Scholar] [CrossRef]
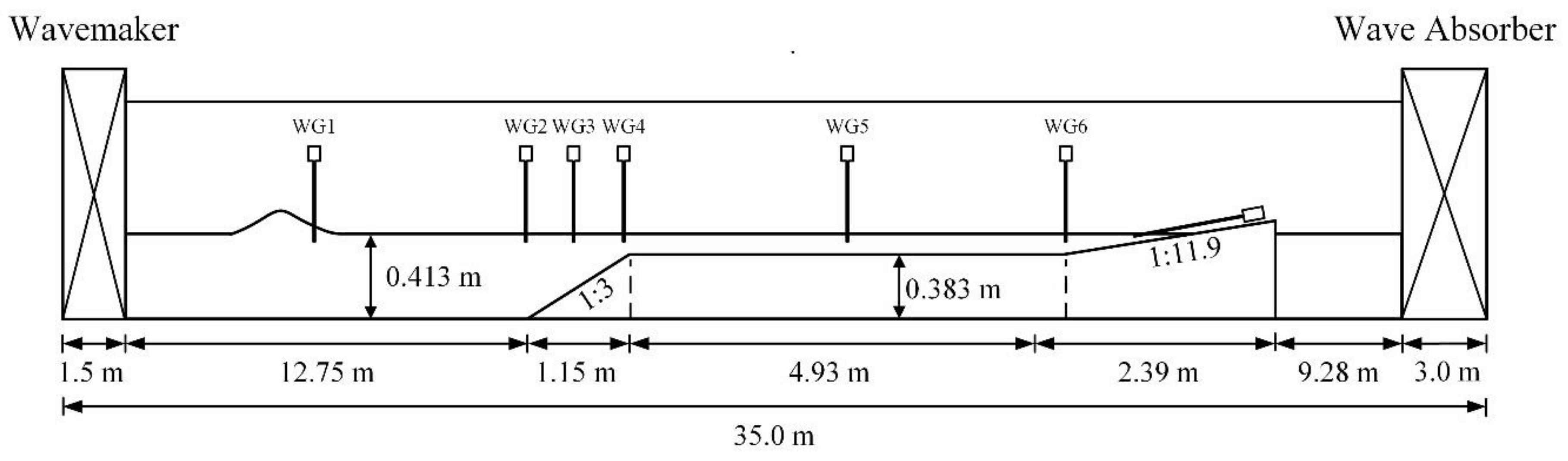



| Case No. | Hi (m) | hr (m) | w (m) | tanθ | tanβ |
|---|---|---|---|---|---|
| 1 | 0.03 | 0.03 | 5 | 1:3 | 1:11.9 |
| 2 | 0.04 | 0.03 | 5 | 1:3 | 1:11.9 |
| 3 | 0.05 | 0.03 | 5 | 1:3 | 1:11.9 |
| 4 | 0.05 | 0.01 | 5 | 1:3 | 1:11.9 |
| 5 | 0.05 | 0.02 | 5 | 1:3 | 1:11.9 |
| 6 | 0.05 | 0.04 | 5 | 1:3 | 1:11.9 |
| 7 | 0.05 | 0.05 | 5 | 1:3 | 1:11.9 |
| 8 | 0.05 | 0.03 | 5 | 1:2 | 1:11.9 |
| 9 | 0.05 | 0.03 | 5 | 1:5 | 1:11.9 |
| 10 | 0.05 | 0.03 | 5 | 1:7 | 1:11.9 |
| 11 | 0.05 | 0.03 | 5 | 1:9 | 1:11.9 |
| 12 | 0.05 | 0.03 | 5 | 1:12 | 1:11.9 |
| 13 | 0.05 | 0.03 | 5 | 1:3 | 1:10 |
| 14 | 0.05 | 0.03 | 5 | 1:3 | 1:14 |
| 15 | 0.05 | 0.03 | 2 | 1:3 | 1:11.9 |
| 16 | 0.05 | 0.03 | 3 | 1:3 | 1:11.9 |
| 17 | 0.05 | 0.03 | 4 | 1:3 | 1:11.9 |
| 18 | 0.05 | 0.03 | 6 | 1:3 | 1:11.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Shao, K.; Ning, Y. A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model. J. Mar. Sci. Eng. 2019, 7, 109. https://doi.org/10.3390/jmse7040109
Liu W, Shao K, Ning Y. A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model. Journal of Marine Science and Engineering. 2019; 7(4):109. https://doi.org/10.3390/jmse7040109
Chicago/Turabian StyleLiu, Weijie, Keqi Shao, and Yue Ning. 2019. "A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model" Journal of Marine Science and Engineering 7, no. 4: 109. https://doi.org/10.3390/jmse7040109
APA StyleLiu, W., Shao, K., & Ning, Y. (2019). A Study of the Maximum Momentum Flux in the Solitary Wave Run-Up Zone over Back-Reef Slopes Based on a Boussinesq Model. Journal of Marine Science and Engineering, 7(4), 109. https://doi.org/10.3390/jmse7040109






