Second Path Planning for Unmanned Surface Vehicle Considering the Constraint of Motion Performance
Abstract
:1. Introduction
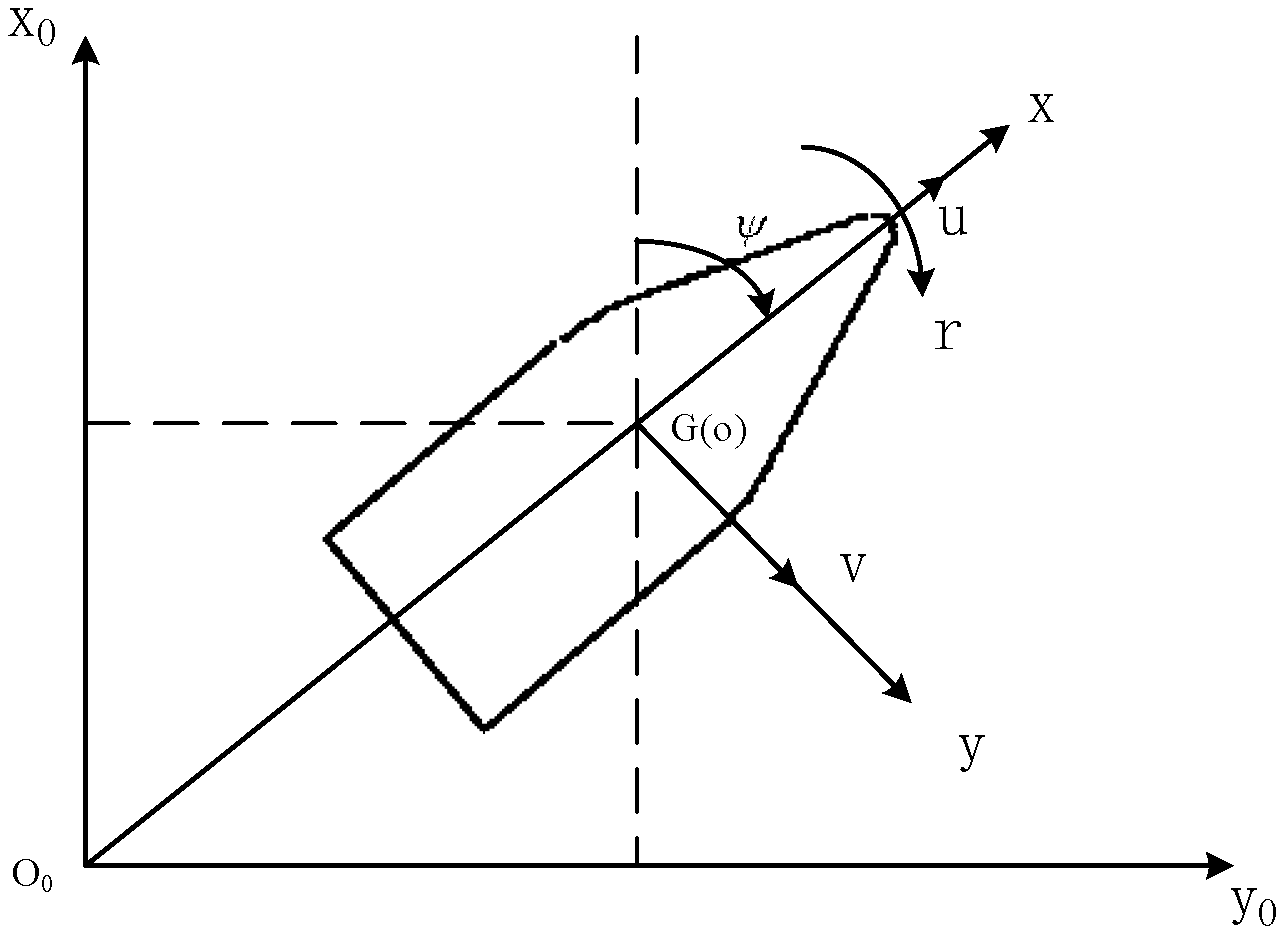
2. Analyzing the Motion Performance of USV
2.1. Modeling the USV Maneuverability
2.2. Integral Nonlinear Least Squares Method
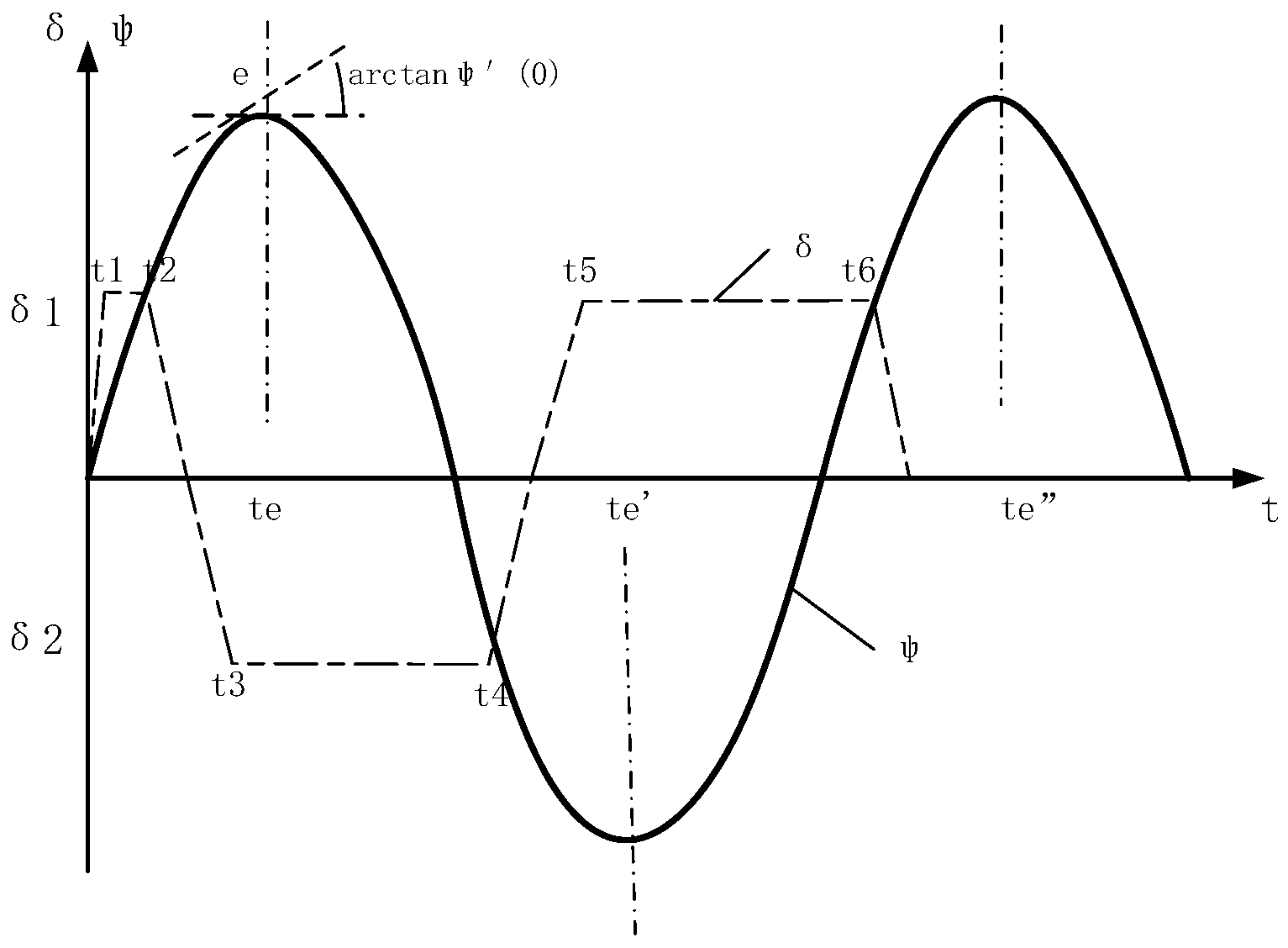
2.3. Identification of Maneuverability and Analysis of Motion Ability
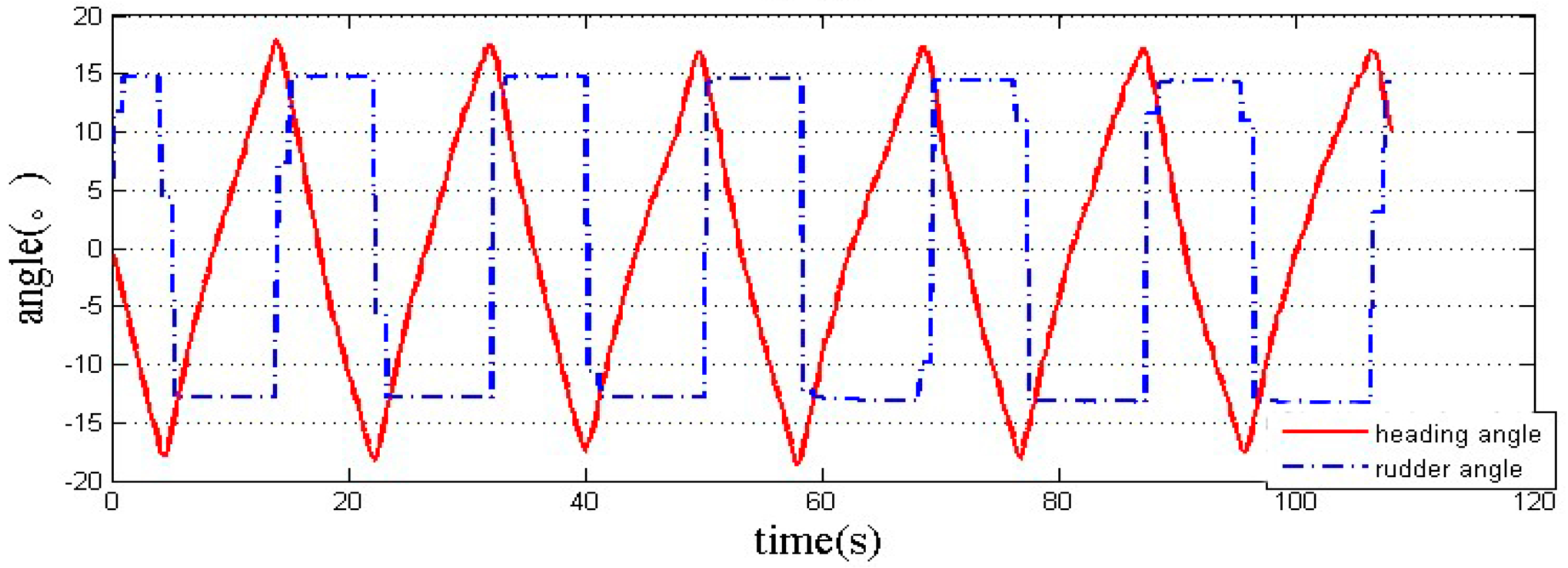
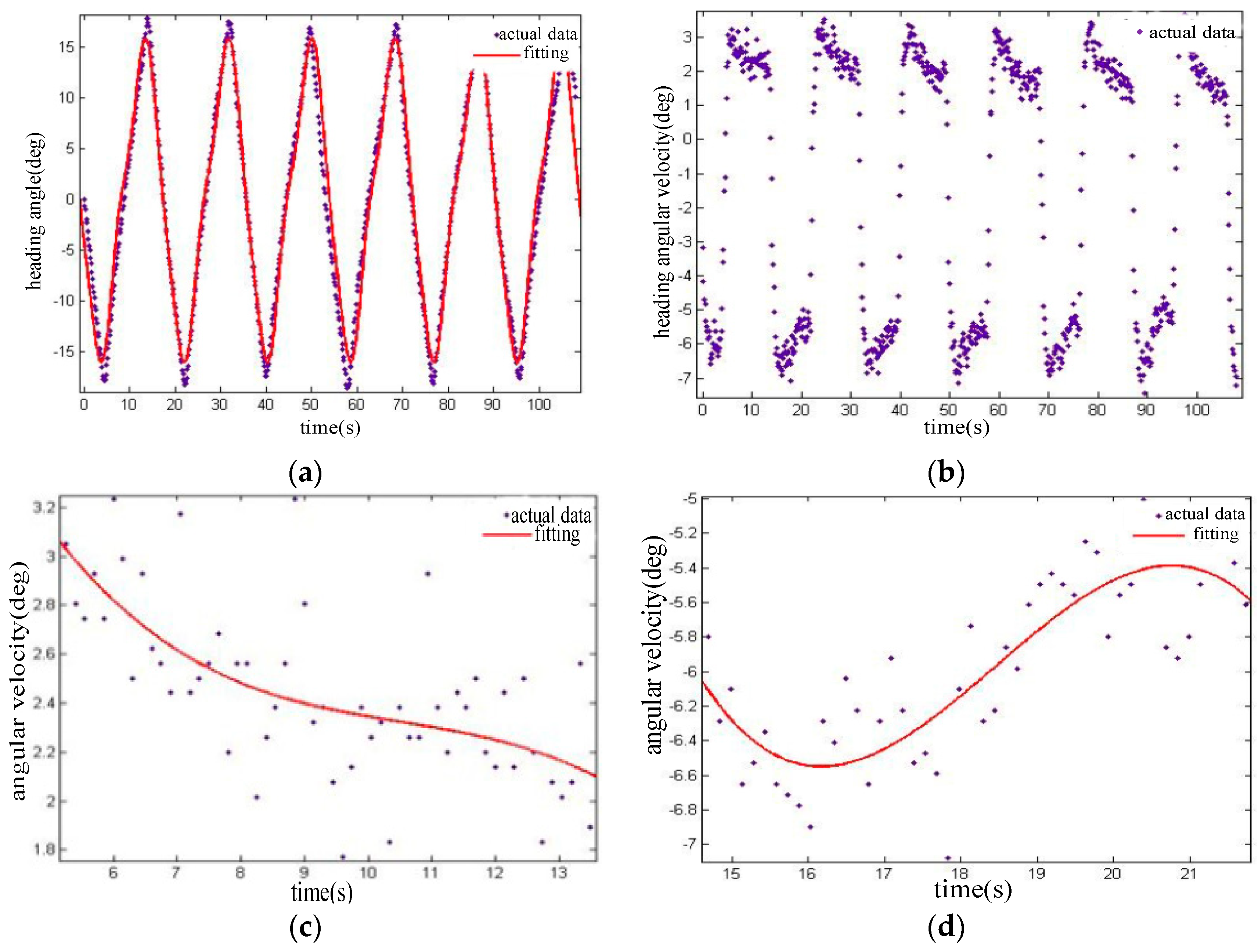
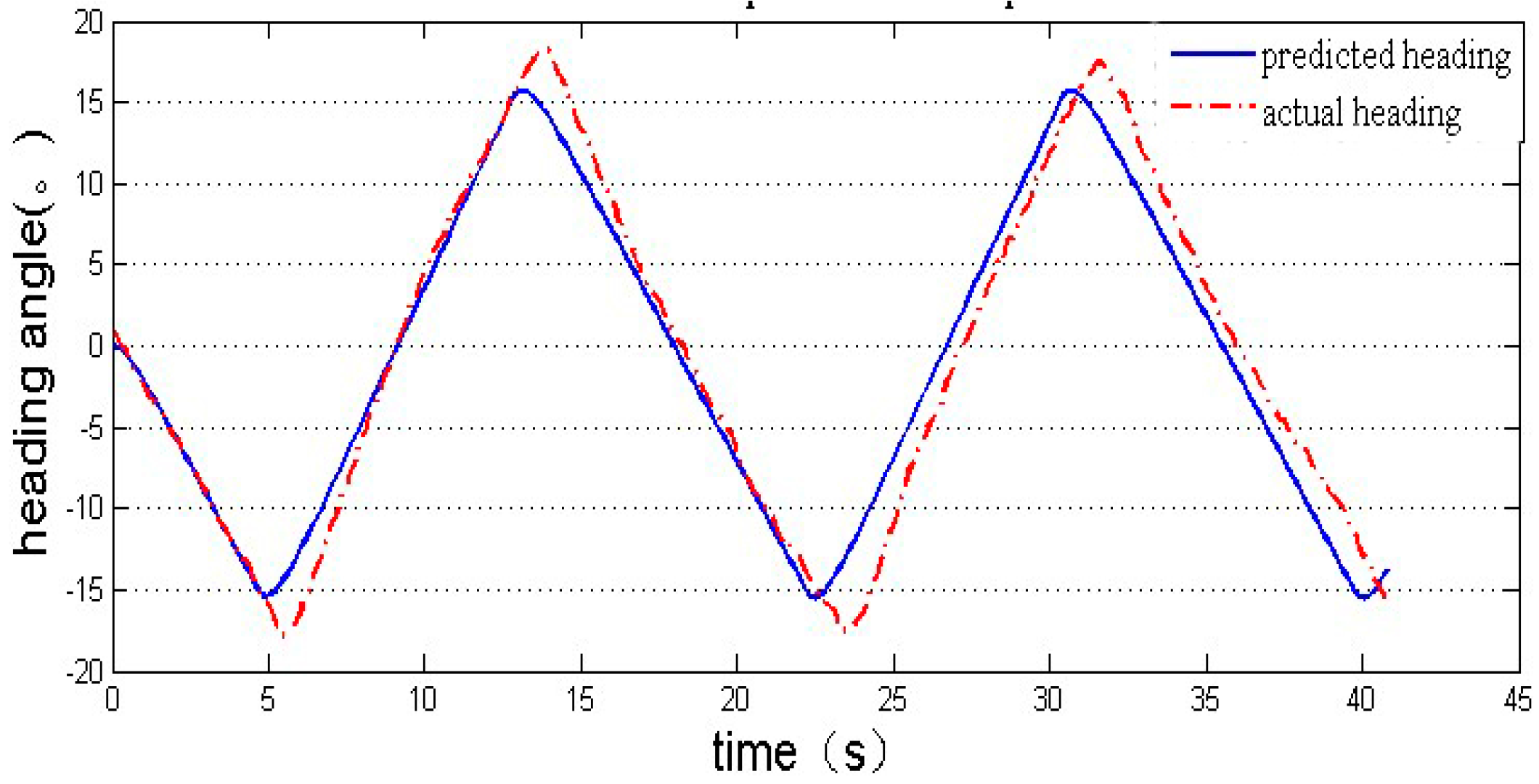
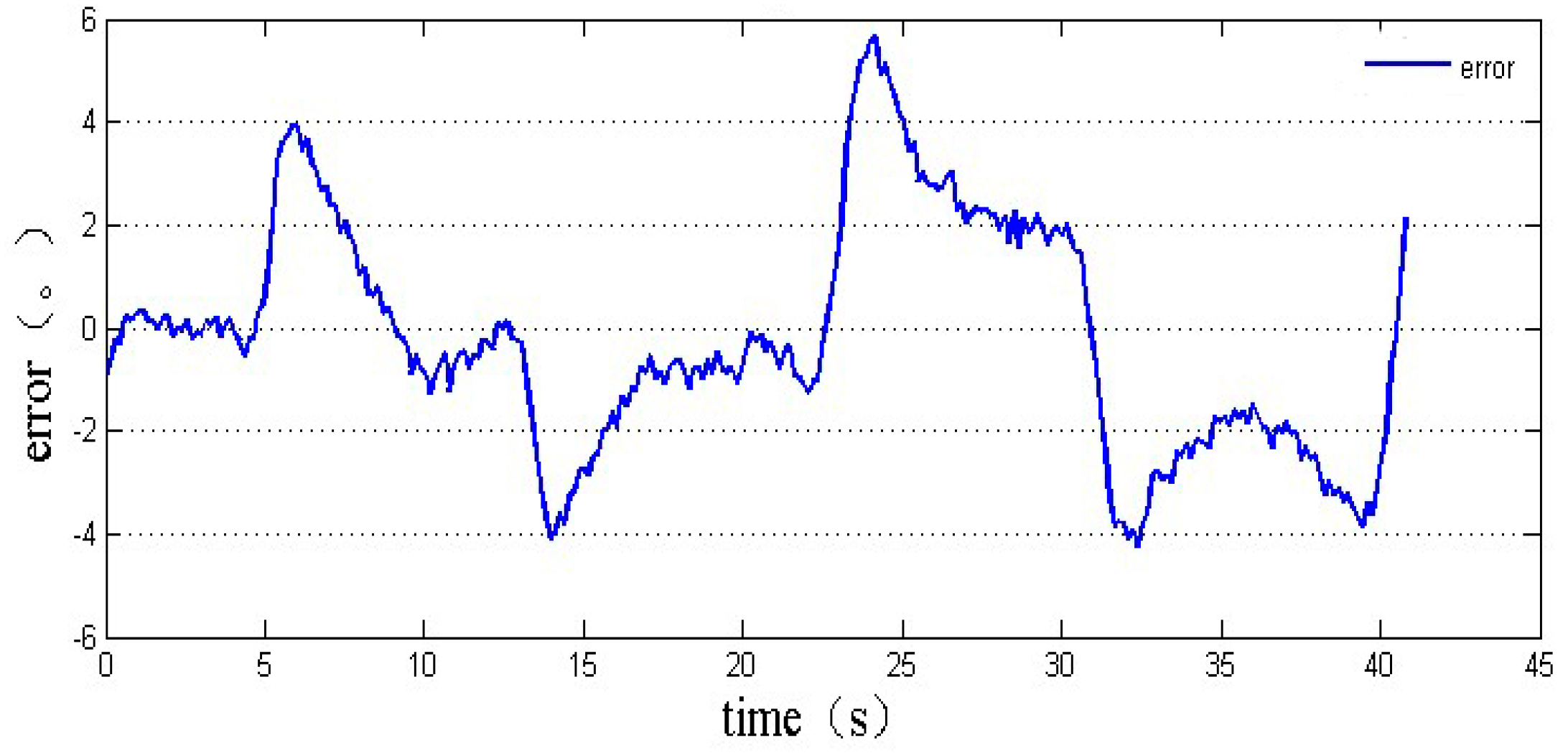
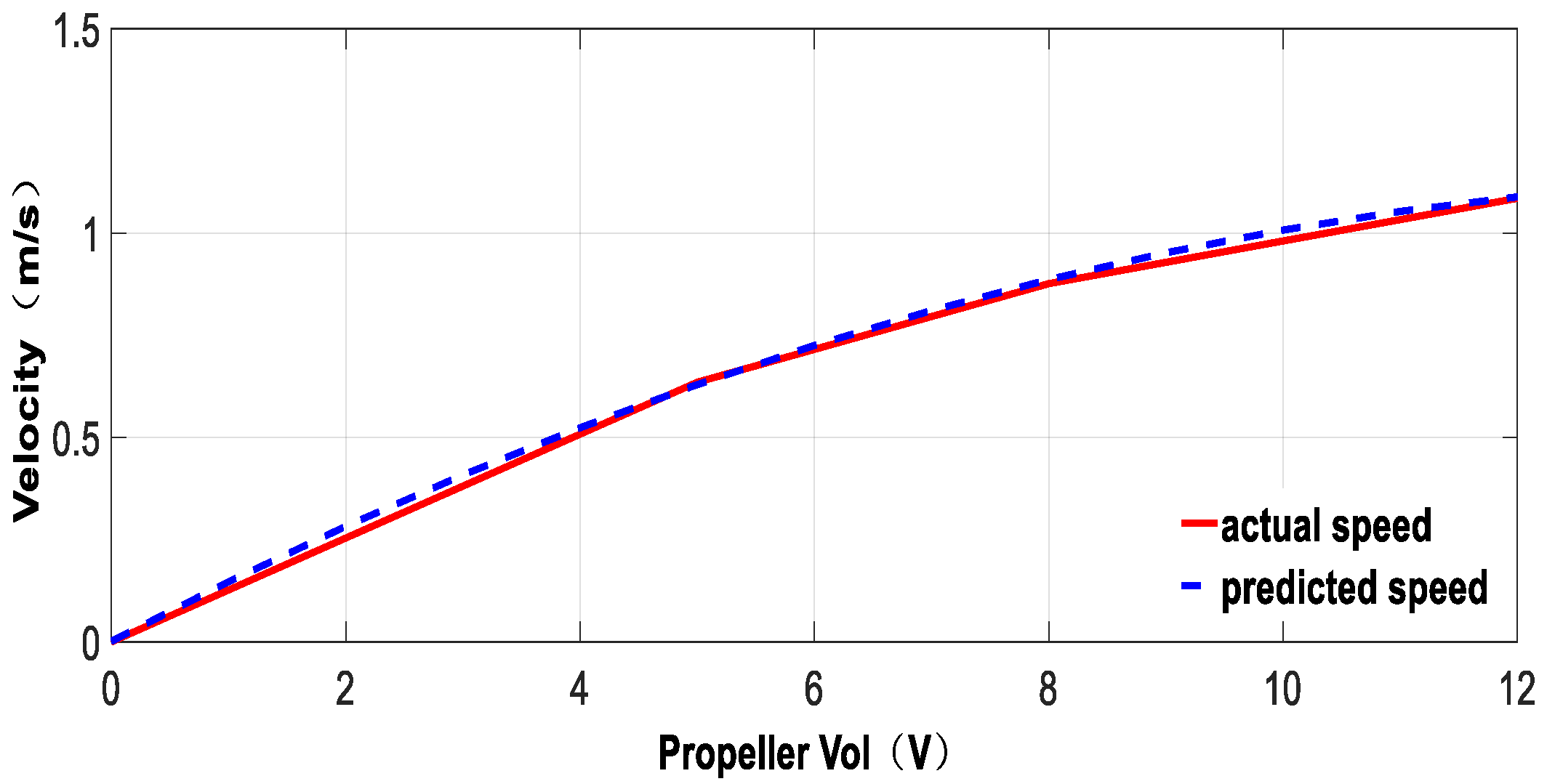
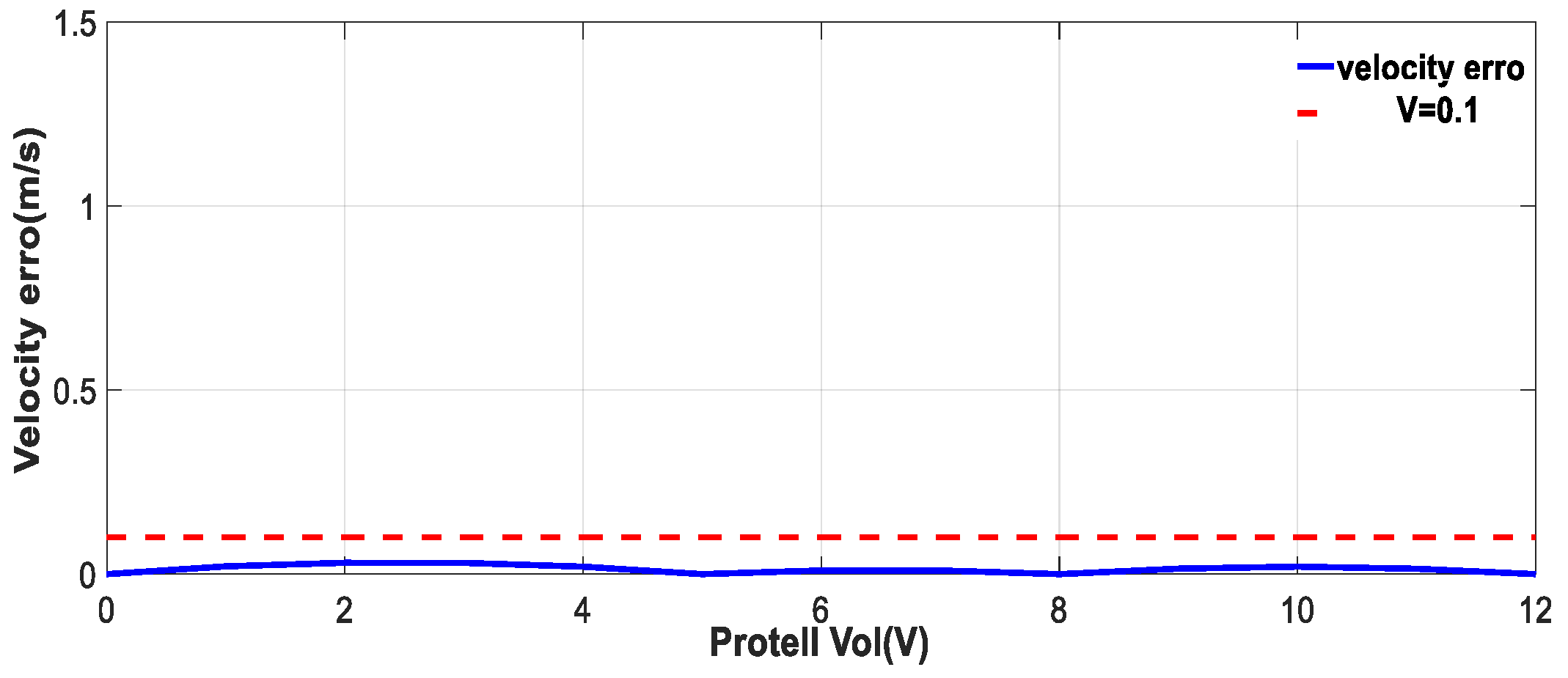
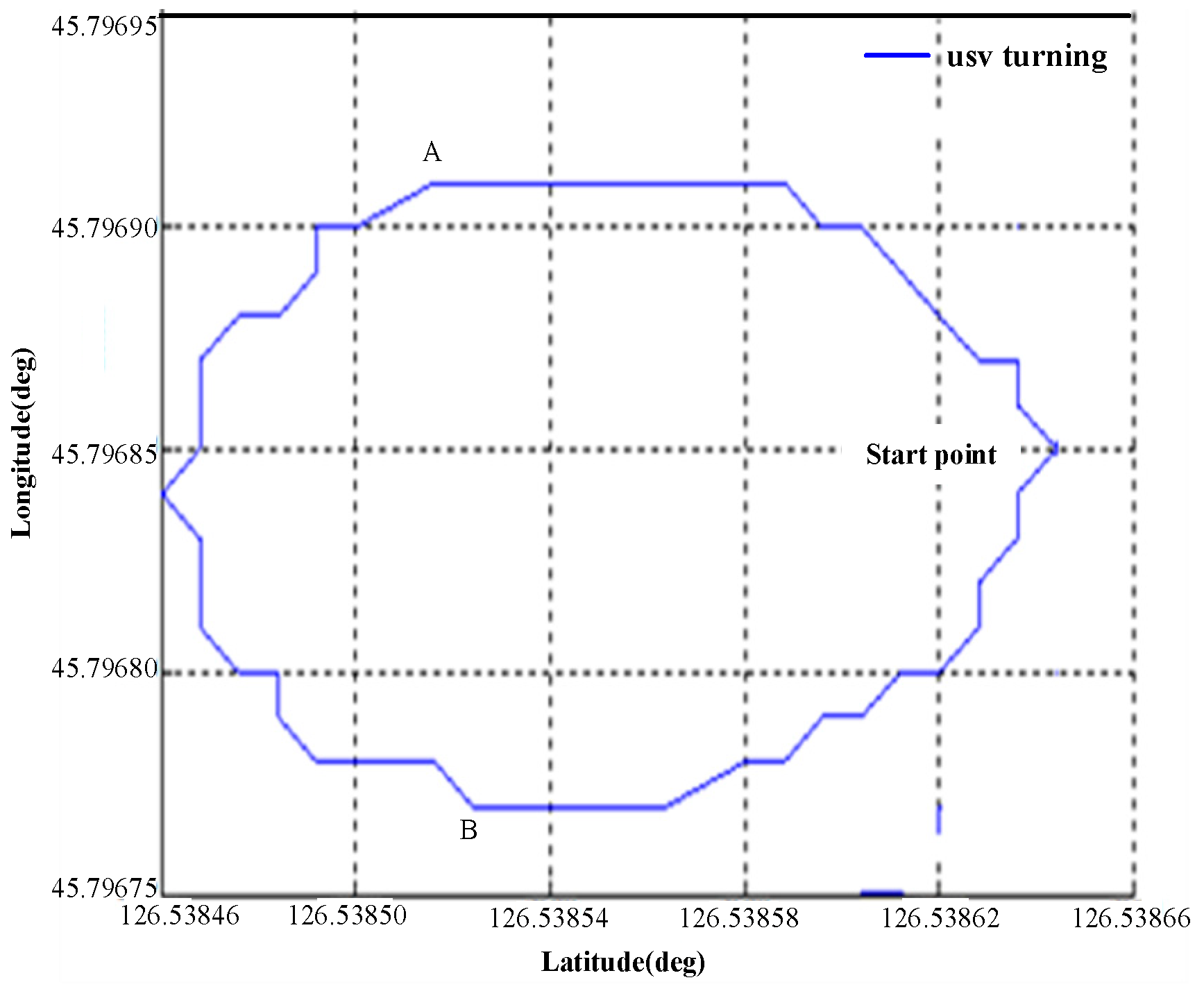
2.3.1. Identification of USV Maneuverability by Field Test Data
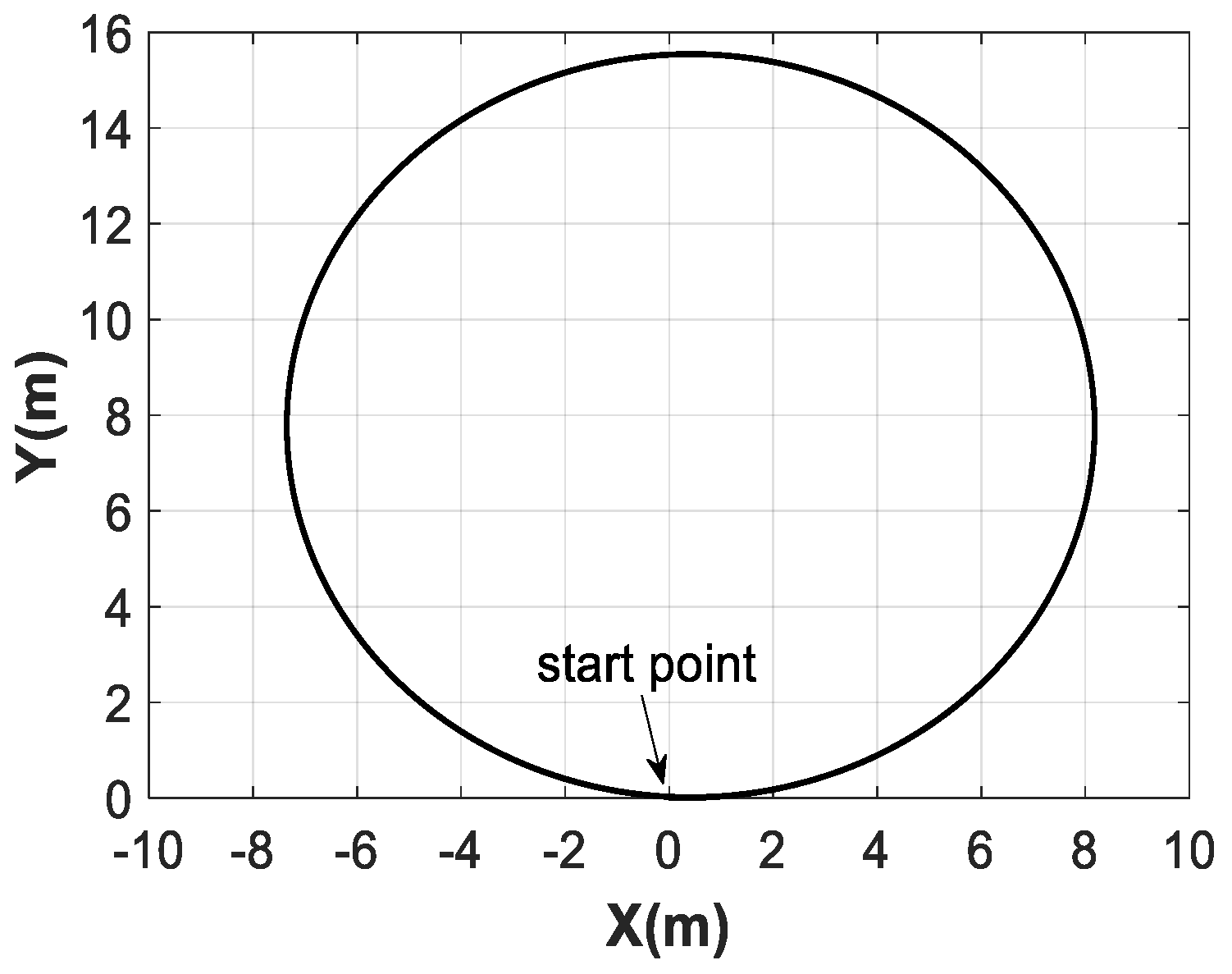
2.3.2. Simulation and Analysis of USV Motion
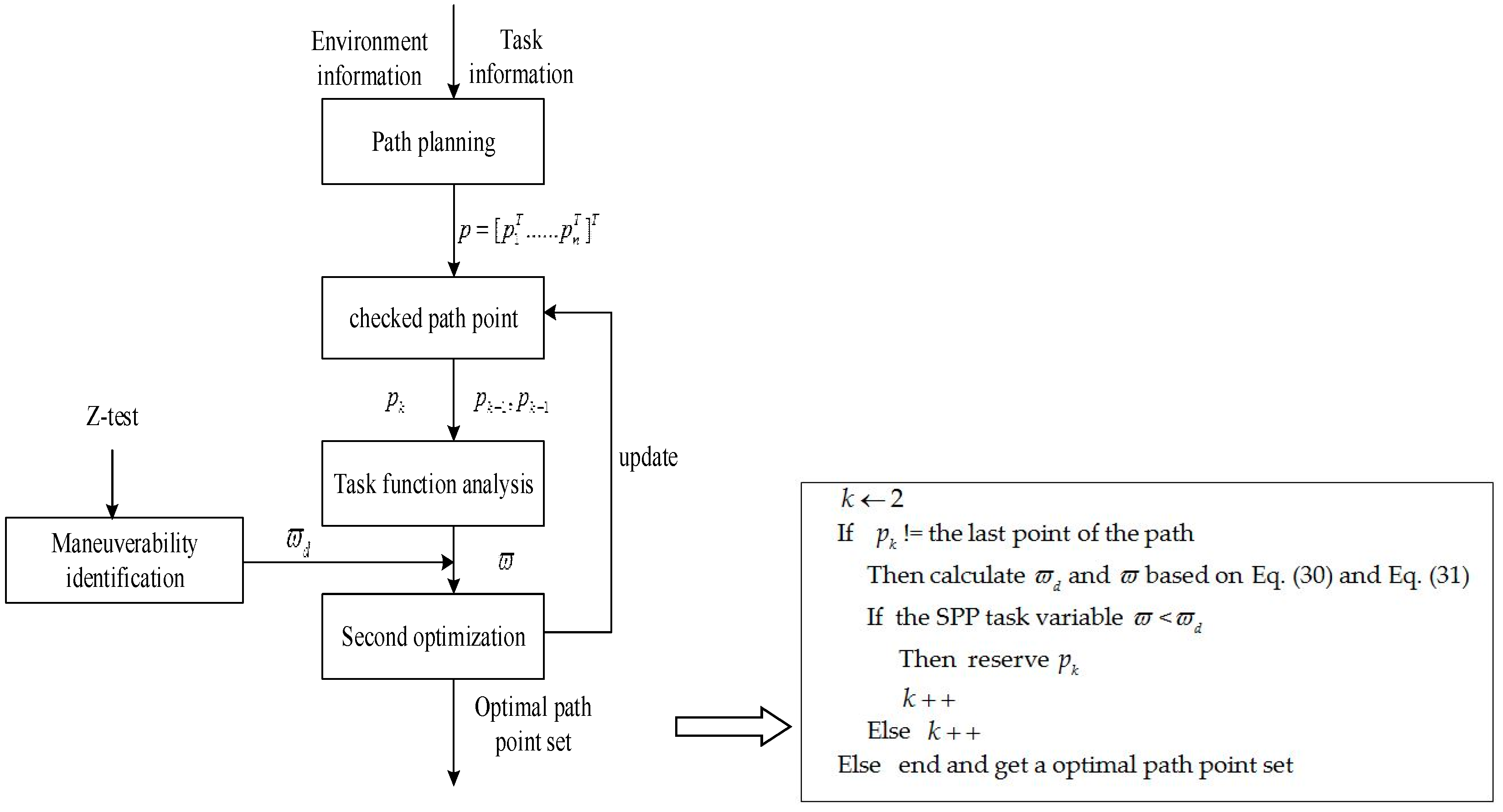
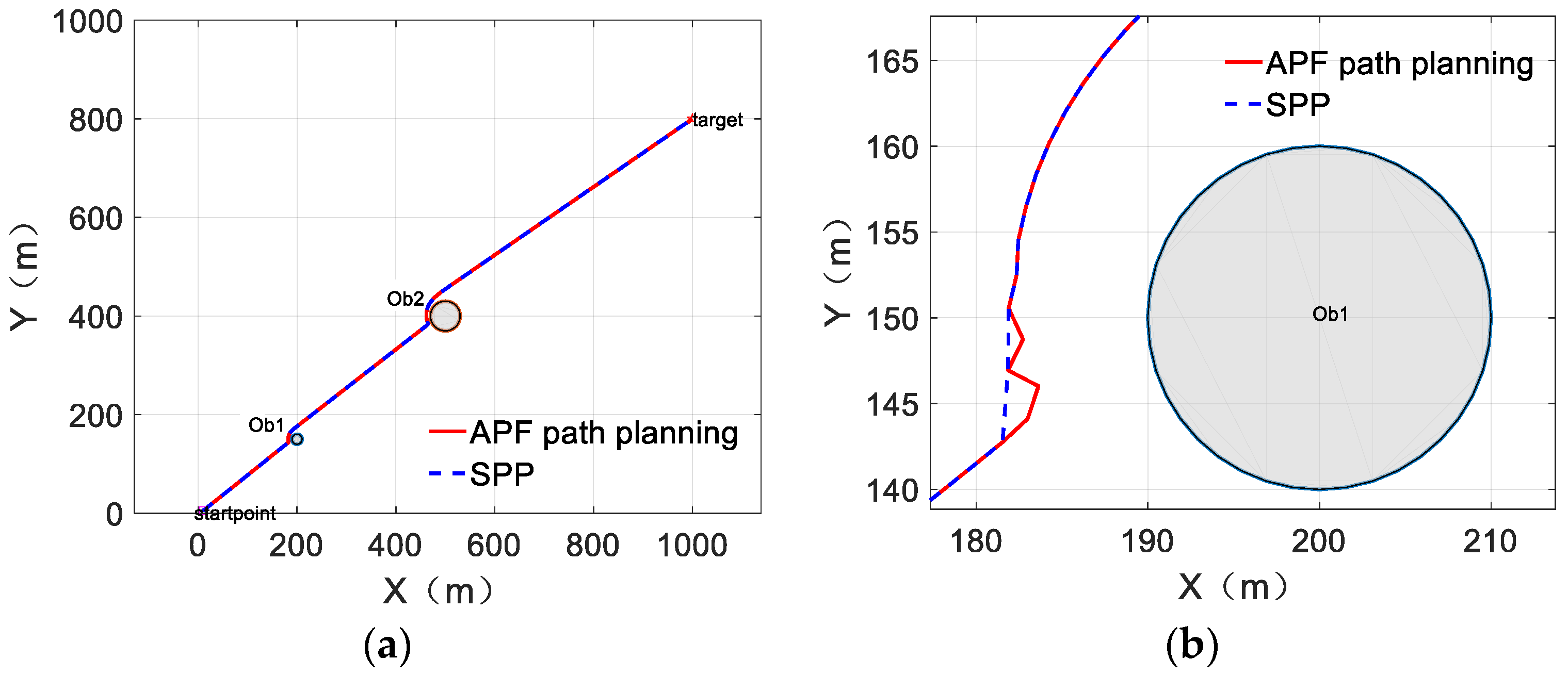
3. SPP of USV
3.1. SPP Model
3.2. An Improved Path Planning for the Artificial Potential Field Method
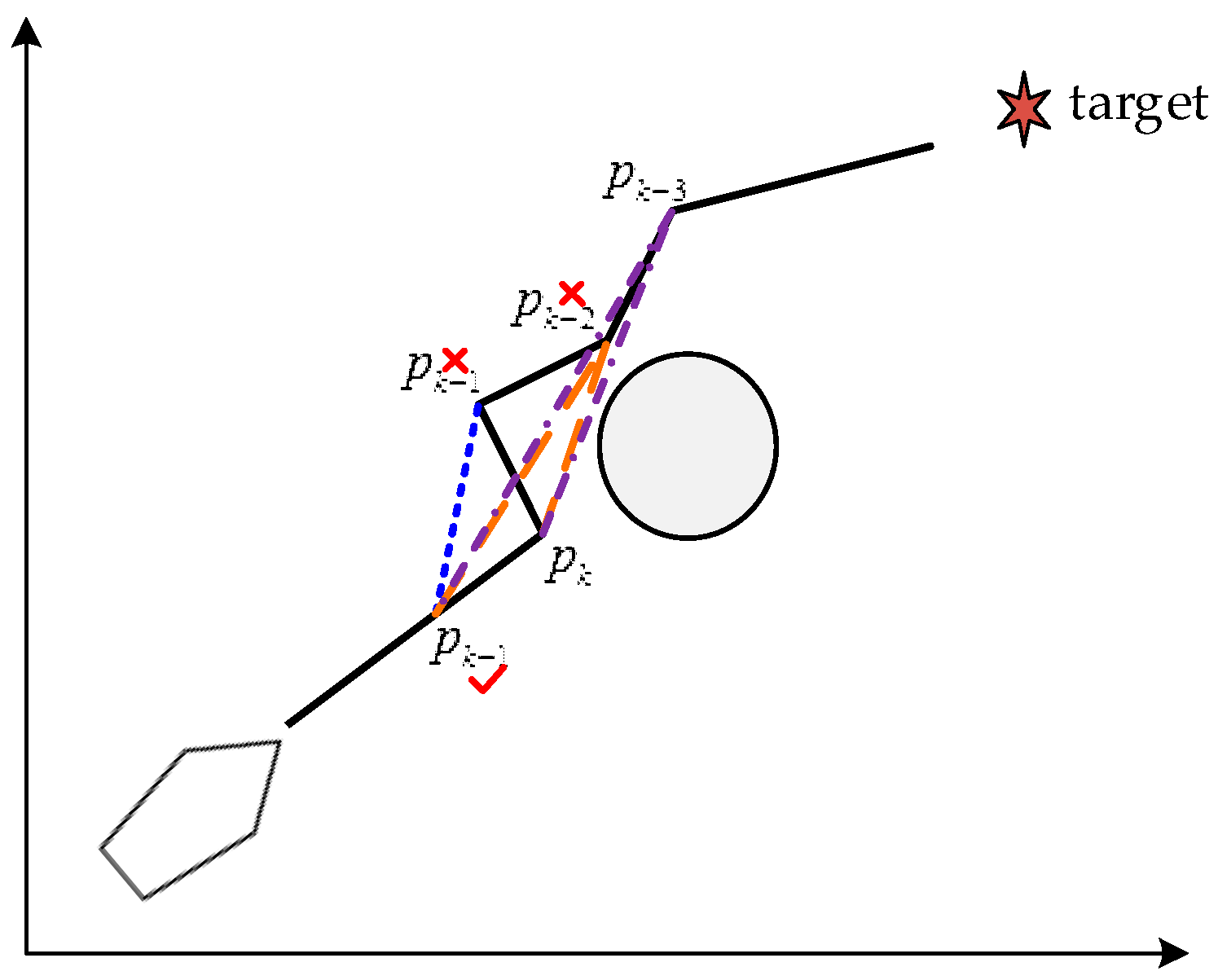
3.3. SPP of the Improved Artificial Potential Field Method
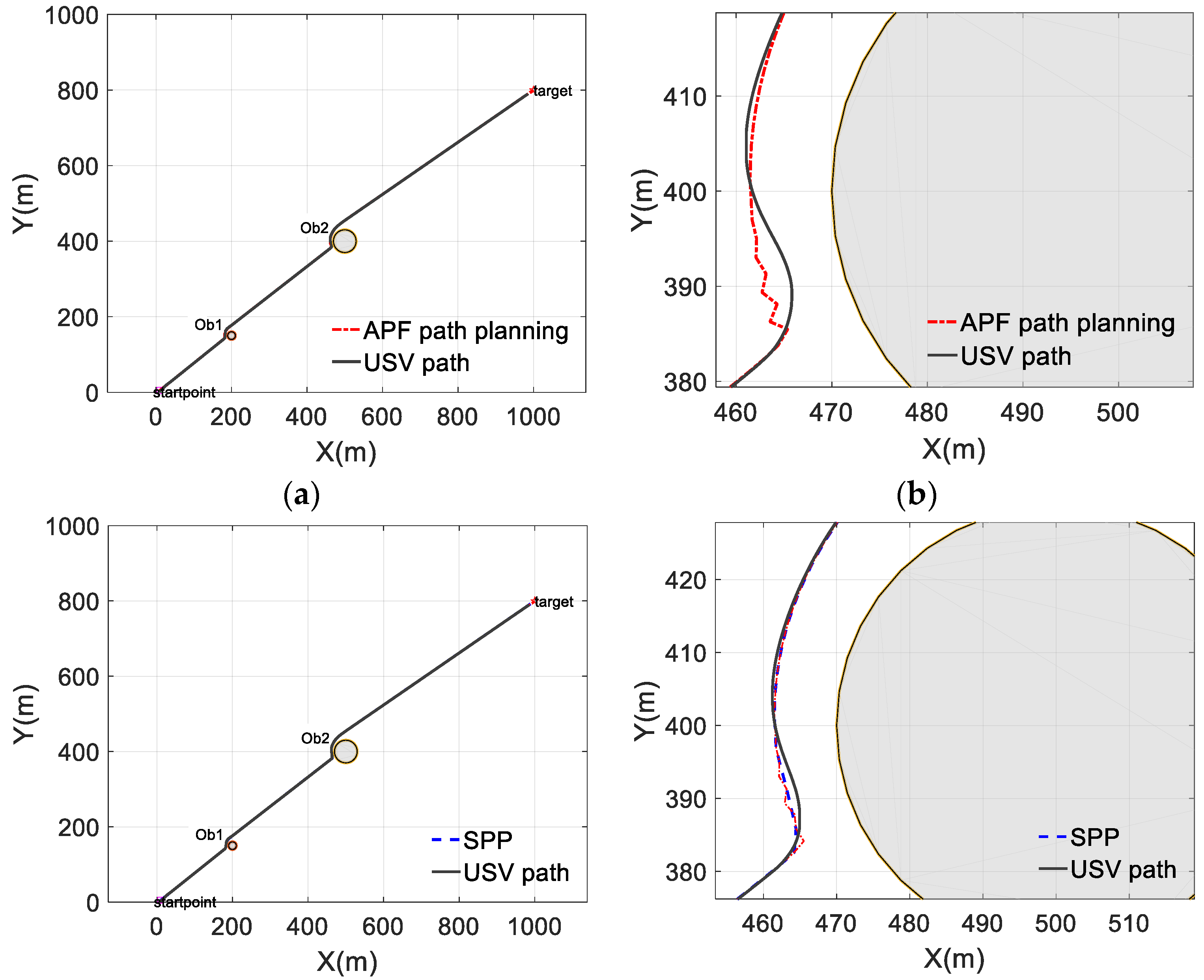
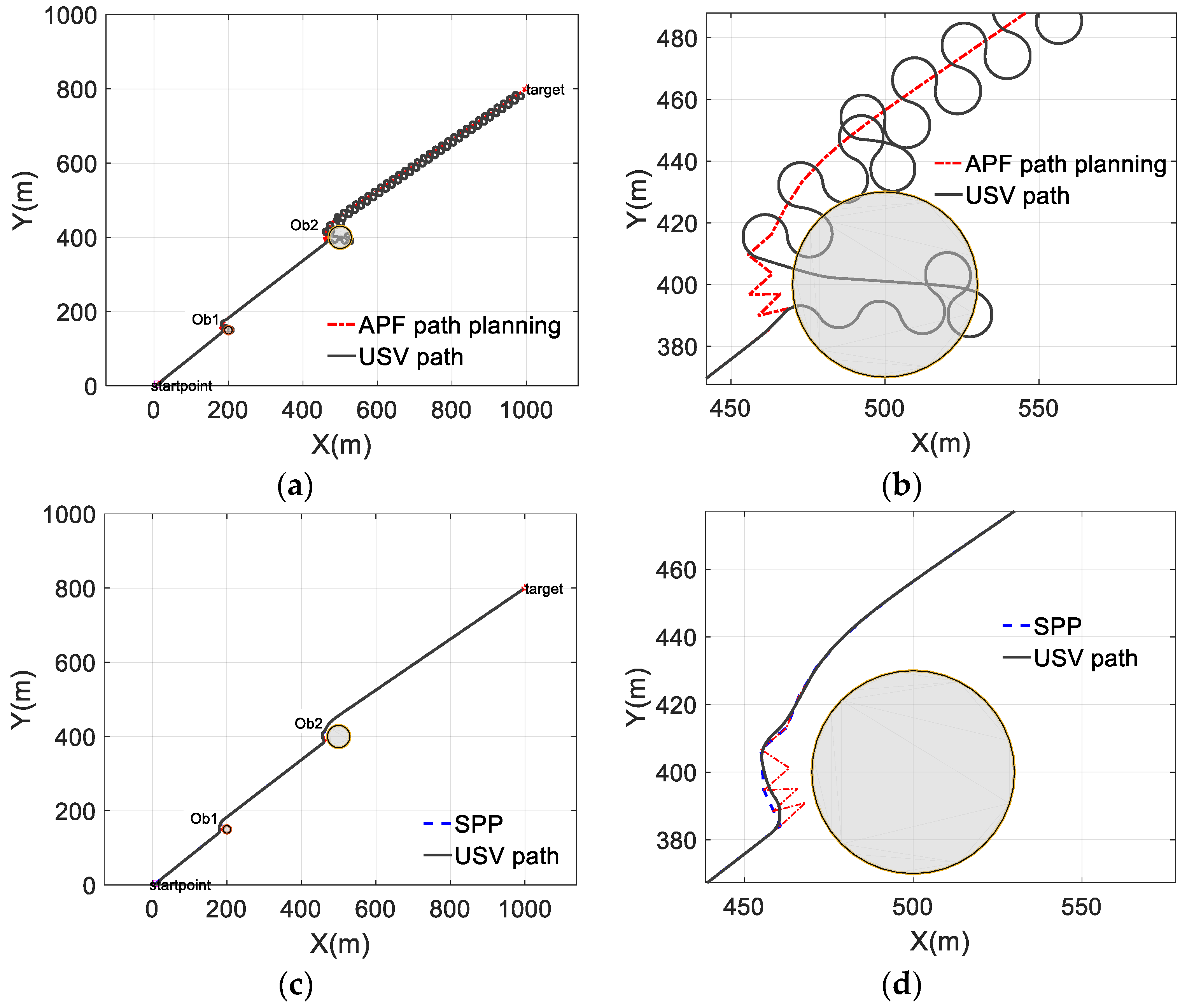
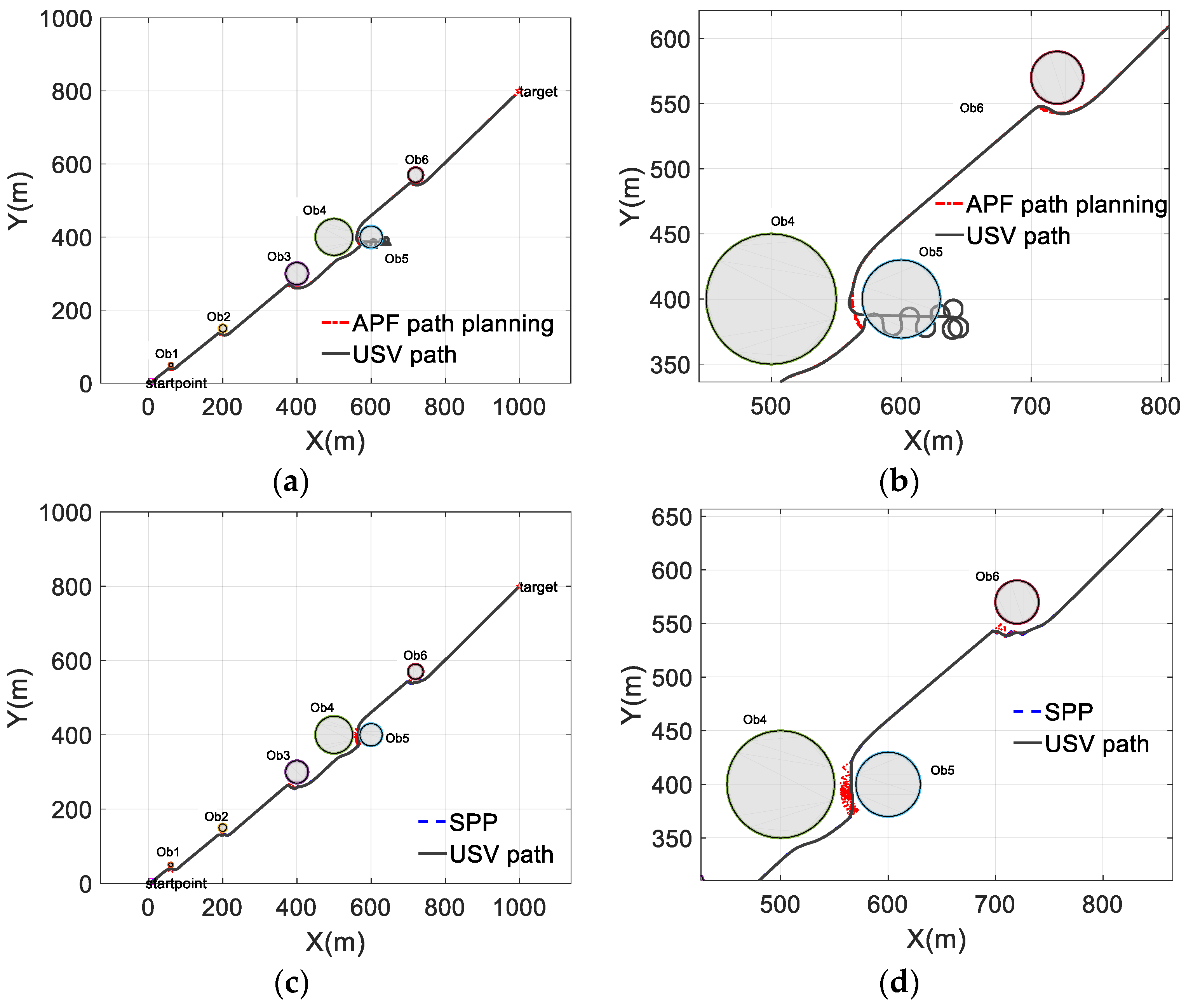
4. Simulation Test of Trajectory Tracking of USV by SPP Method
4.1. Comparative Experiment of Small Planning Step
4.2. Comparative Experiment of Large Planning Step
4.3. Comparative Experiment of Multi-Obstacle Path Planning
5. Discussion
- (1)
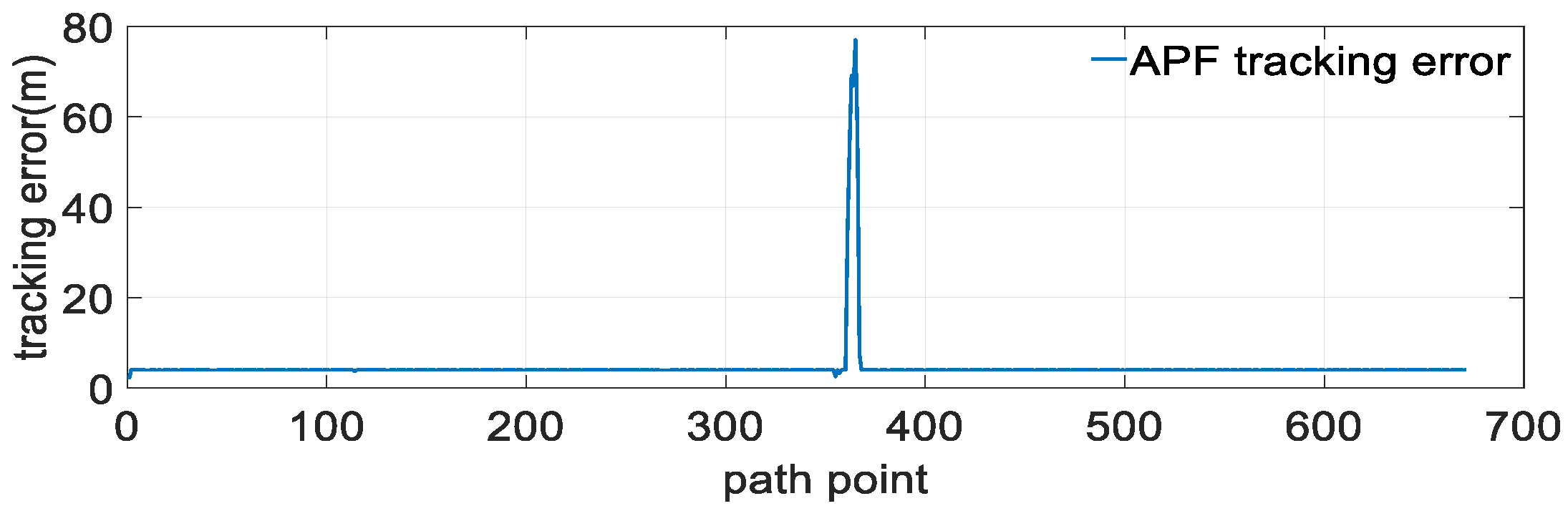
- By the analysis of the path planning theory and the USV control model, the traditional path planning method was found to lead to the ‘planning failure’ phenomenon when applied to the trajectory tracking field of the USV path planning.
- (2)
- In this study, an integral nonlinear least squares method was developed. In the case of limited test data, a nonlinear motion model of USV was rapidly identified by merely conducting a type of maneuvering experiment, which can effectively predict the motion performance indexes, such as the rotatory curvature of the vehicle.
- (3)
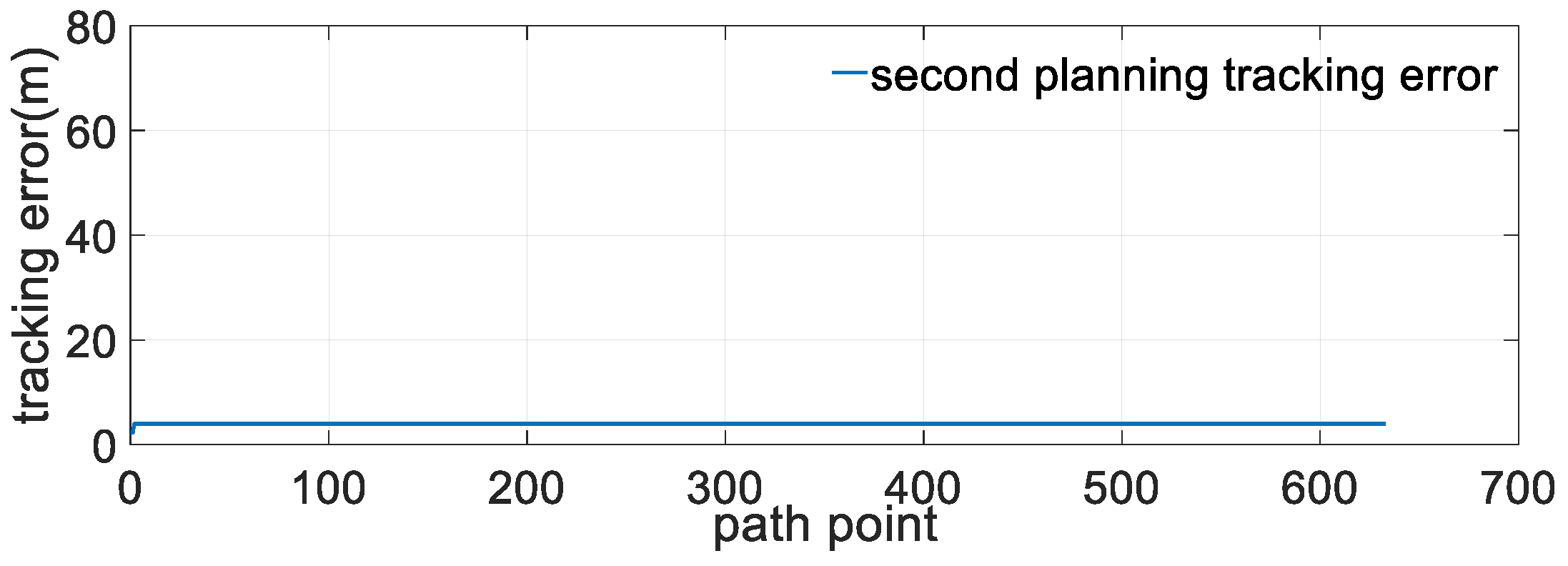
- The SPP method was presented under the consideration of the USV motion performance, which reduces the influence of the motion performance of the vehicle during the trajectory tracking and helps lower the risk of failing to complete the obstacle avoidance task using the traditional path planning method. The proposed SPP method can effectively prevent the issue of an untraceable USV and improve the USV tracking accuracy.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liao, Y.L.; Zhang, M.J.; Wan, L.; Li, Y. Trajectory tracking control for underactuated unmanned surface vehicles with dynamic uncertainties. J. Cent. South Univ. Technol. 2016, 23, 370–378. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.F.; Liao, Y.L.; Jiang, Q.Q.; Pan, K.W. Heading MFA control for unmanned surface vehicle with angular velocity guidance. Appl. Ocean Res. 2018, 80, 57–65. [Google Scholar] [CrossRef]
- Liu, Y.; Bucknall, R. A survey of formation control and motion planning of multiple unmanned vehicles. Robotica 2018, 36, 1019–1047. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D. Path planning of an autonomous surface vehicle based on artificial potential fields in a real-time marine environment. In Proceedings of the 16th International Conference on Computer and IT Applications in the Maritime Industries, Cardiff, UK, 15–17 May 2017. [Google Scholar]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. Feasibility study of a constrained Dijkstra approach for optimal path planning of an unmanned surface vehicle in a dynamic maritime environment. In Proceedings of the 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Torres Vedras, Portugal, 25–27 April 2018; pp. 117–122. [Google Scholar]
- Fu, B.; Chen, L.; Zhou, Y.T.; Zheng, D. An improved A algorithm for the industrial robot path planning with high success rate and short length. Robot. Auton. Syst. 2018, 106, 26–37. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, J.Z.; Zhao, J.; Wu, X.G.; Liu, G. Global path planning and local obstacle avoidance of searching robot in mine disasters based on grid method. J. Cent. South Univ. 2011, 11, 3421–3428. [Google Scholar]
- Qu, Y.H.; Zhang, Y.T.; Zhang, Y.M. A global path planning algorithm for fixed-wing UAVs. J. Intell. Robot. Syst. 2018, 91, 691–707. [Google Scholar] [CrossRef]
- Sfeir, J.; Saad, M.; Saliah, H. An improved artificial potential field approach to real –time mobile robot path planning in an unknown environment. In Proceedings of the IEEE International Symposium on Robotic and Sensors Environments, Montreal, QC, Canada, 17–18 September 2011; pp. 208–213. [Google Scholar]
- Pei, Z.B.; Chen, X.B. Improved ant colony algorithm and its application in obstacle avoidance for robot. CAAI Trans. Intell. Syst. 2015, 1, 90–96. [Google Scholar]
- Wang, J.; Wu, X.X.; Guo, B.L. Robot path planning using improved particle swarm optimization. Comput. Eng. Appl. 2012, 48, 240–244. [Google Scholar]
- Yan, Z.P.; Li, J.Y.; Wu, Y.; Zhang, G.S. A real-time path planning algorithm for AUV in unknown underwater environment based on combining PSO and waypoint guidance. Sensors 2019, 19, 20. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.W.; Ma, Y.; Xie, Y.; Guo, M. Mobile robot optimal path planning based on smoothing A* algorithm. J. Tongji Univ. (Nat. Sci.) 2010, 38, 1647–1650. [Google Scholar]
- Conte, G.; Capua, G.P.; Scaradozzi, D. Designing the NGC system of a small ASV for tracking underwater targets. Robot. Auton. Syst. 2016, 76, 46–57. [Google Scholar] [CrossRef]
- Doostie, S.; Hoshiar, A.K.; Nazarahari, M. Optimal path planning of multiple nanoparticles in continuous environment using a novel Adaptive Genetic Algorithm. Precis. Eng. 2018, 53, 65–78. [Google Scholar] [CrossRef]
- Wu, C.; Wu, Q.; Ma, F.; Wang, S.W. A situation awareness approach for USV based on Artificial Potential Fields. In Proceedings of the International Conference on Transportation Information and Safety 2017, Banff, AB, Canada, 8–10 August 2017; pp. 232–235. [Google Scholar]
- Yang, J.M.; Tseng, C.M.; Tseng, P.S. Path planning on satellite images for unmanned surface vehicles. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 87–99. [Google Scholar] [CrossRef]
- Abbas, S.; Abbas, K.; Troy, R.; Saeid, N. Smooth path planning using biclothoid fillets for high speed CNC machines. Int. J. Mach. Tools Manuf. 2018, 132, 36–49. [Google Scholar]
- Brezak, M.; Petrovic, I. Path smooth using clothoids for differential drive mobile robots. IFAC Proc. Vol. 2011, 44, 1133–1138. [Google Scholar] [CrossRef]
- Shi, W.F.; Huang, X.H.; Zhou, W. Planning of mobile robot based on improved artificial potential. J. Comput. Appl. 2010, 30, 2021–2023. [Google Scholar]
- Liao, Y.L.; Zhang, M.J.; Wan, L. Serret-Frenet frame based on path following control for underactuated unmanned surface vehicles with dynamic uncertainties. J. Cent. South Univ. Technol. 2015, 22, 214–223. [Google Scholar] [CrossRef]
- Nomoto, K.; Taguchi, K.; Honda, K.; Hirano, S. On the steering qualities of ships. Int. Shipbuild. Prog. 1957, 4, 354–370. [Google Scholar] [CrossRef]
- Christian, R.S.; Craig, A.W. Modeling, identification, and control of an unmanned surface vehicle. J. Field Robot. 2013, 30, 371–398. [Google Scholar]
- Nikola, M.; Zoran, V. Fast in-field identification of unmanned marine vehicles. J. Field Robot. 2011, 28, 101–120. [Google Scholar]
- Podisuk, M.; Chundang, U.; Sanprasert, W. Single step formulas and multi-step formulas of the integration method for solving the initial value problem of ordinary differential equation. Appl. Math. Comput. 2007, 190, 1438–1444. [Google Scholar] [CrossRef]
- Li, H.L.; Zhang, A.W.; Meng, X.G.; Hu, S.X. A remote sensing image sub-pixel registration method based on curve fitting and improved Fourier-Mellin transform. J. Chin. Comput. Syst. 2015, 36, 2763–2768. [Google Scholar]
- Liao, Y.L.; Li, Y.M.; Wang, L.F.; Li, Y.; Jiang, Q.Q. The heading control method and experiments for an unmanned wave glider. J. Cent. South Univ. Technol. 2017, 24, 1–9. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Parhi, D.H.; Panda, A.K. Potential field method to navigate several mobile robots. Appl. Intell. 2006, 25, 321–333. [Google Scholar] [CrossRef]
- Liu, Z.X.; Yang, L.X.; Wang, J.G. Soccer robot path planning based on evolutionary artificial field. Adv. Mater. Res. 2012, 562, 955–958. [Google Scholar] [CrossRef]
- Koren, Y.; Borenstein, J. Potential field methods and their inherent limitations for mobile robot navigation. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 2, pp. 1398–1404. [Google Scholar]
- Liang, K.; Li, Z.Y.; Chen, D.Y. Improved artificial potential field for unknown narrow environments. In Proceedings of the IEEE International Conference on ROBIO, Shenyang, China, 22–26 August 2004; pp. 688–692. [Google Scholar]
- Geva, Y.; Shapiro, A. A combined potential function and graph search approach for free gait generation of quadruped robots. In Proceedings of the IEEE International Conference on Robotics and Automation River Centre, Saint Paul, MN, USA, 14–18 May 2012; pp. 5371–5376. [Google Scholar]
- Qi, N.N.; Ma, B.J.; Liu, X.E.; Zhang, Z.X.; Ren, D.C. A modified Artificial Potential Field Algorithm for Mobile Robot Path Planning. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; Volume 7, pp. 2603–2607. [Google Scholar]
- Liao, Y.L.; Wang, L.F.; Li, Y.M.; Li, Y.; Jiang, Q.Q. The intelligent control system and experiments for an unmanned wave glider. PLoS ONE 2016, 11, 1–24. [Google Scholar] [CrossRef]
- Liao, Y.L.; Jia, Z.H.; Zhang, W.B.; Jia, Q.; Li, Y. Layered berthing method and experiment of unmanned surface vehicle based on multiple constraints analysis. Appl. Ocean Res. 2019, 86, 47–60. [Google Scholar] [CrossRef]
- Liao, Y.L.; Jiang, Q.Q.; Du, T.P.; Jiang, W. Redefined output model-free adaptive control method and unmanned surface vehicle heading control. IEEE J. Ocean. Eng. 2019. [Google Scholar] [CrossRef]



| 1 | / | / | / | ||
| 2 | / | / | |||
| 3 | / | ||||
| 4 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Li, Y.; Liao, Y.; Jiang, W.; Wang, L.; Jia, Q.; Wu, H. Second Path Planning for Unmanned Surface Vehicle Considering the Constraint of Motion Performance. J. Mar. Sci. Eng. 2019, 7, 104. https://doi.org/10.3390/jmse7040104
Fan J, Li Y, Liao Y, Jiang W, Wang L, Jia Q, Wu H. Second Path Planning for Unmanned Surface Vehicle Considering the Constraint of Motion Performance. Journal of Marine Science and Engineering. 2019; 7(4):104. https://doi.org/10.3390/jmse7040104
Chicago/Turabian StyleFan, Jiajia, Ye Li, Yulei Liao, Wen Jiang, Leifeng Wang, Qi Jia, and Haowei Wu. 2019. "Second Path Planning for Unmanned Surface Vehicle Considering the Constraint of Motion Performance" Journal of Marine Science and Engineering 7, no. 4: 104. https://doi.org/10.3390/jmse7040104
APA StyleFan, J., Li, Y., Liao, Y., Jiang, W., Wang, L., Jia, Q., & Wu, H. (2019). Second Path Planning for Unmanned Surface Vehicle Considering the Constraint of Motion Performance. Journal of Marine Science and Engineering, 7(4), 104. https://doi.org/10.3390/jmse7040104





