Modeling Tidal Datums and Spatially Varying Uncertainty in the Texas and Western Louisiana Coastal Waters
Abstract
:1. Introduction
2. Model, Data, and Methods
2.1. Hydrodynamic Model and Its Configuration
2.1.1. Model Configuration
- (1)
- nonlinear quadratic bottom friction with a spatially constant bottom friction coefficient of 0.002;
- (2)
- a spatially constant horizontal eddy viscosity of 5.0 m2/s for the momentum equations;
- (3)
- wetting and drying process enabled with a minimum water depth of 0.05 m as a wet node/element criterion;
- (4)
- a spatially uniform Generalized Wave-Continuity Equation (GWCE) weighting factor of 0.02;
- (5)
- advective terms were included;
- (6)
- no atmospheric forcing and river flow were imposed;
- (7)
- tidal potential body force of eight principal tidal constituents (K1, O1, P1, Q1, M2, S2, N2, and K2) was included;
- (8)
- water elevations from the same eight principal tidal constituents: K1, O1, P1, Q1, M2, S2, N2, and K2 were used at the open ocean boundary. That is, open ocean boundary forcing equals the sum of the elevations of the eight tidal harmonic constituents, which were extracted from the EC2015 tidal database [20,21].
- (9)
- a total of 67 days of the ADCIRC model run. A hyperbolic tangent ramp function was specified, and the beginning six days were used to ramp up ADCIRC forcings from zero. The time step for the ADCIRC model run is 3 s. The output from the ADCIRC model run is the 6-min water level time series at each model grid point from the final 60-day run, which were used for computing tidal datums at each model grid point.
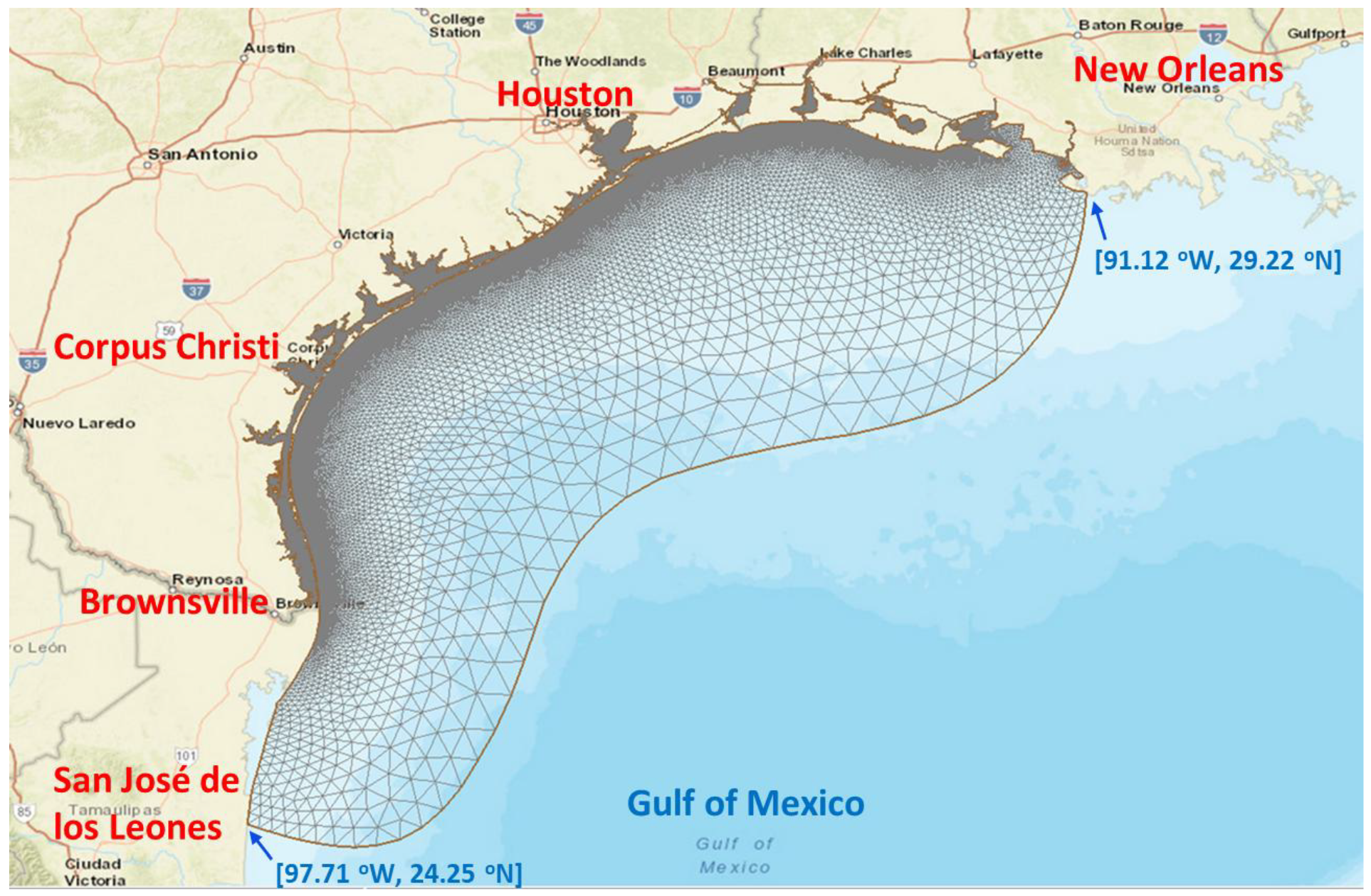
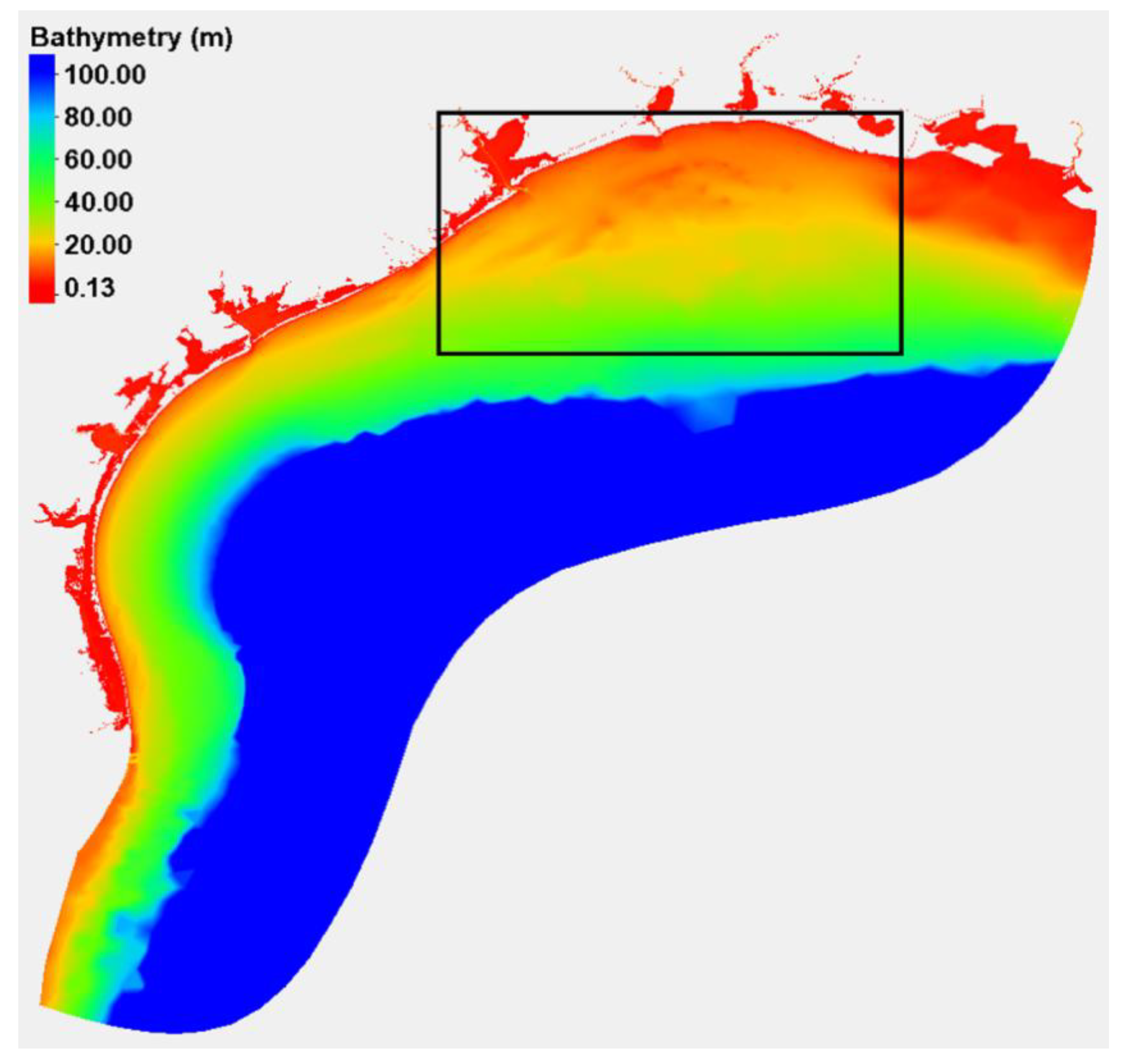
2.1.2. Model Domain
2.2. Data
2.2.1. NOAA’s Continually Updated Shoreline Product (CUSP)
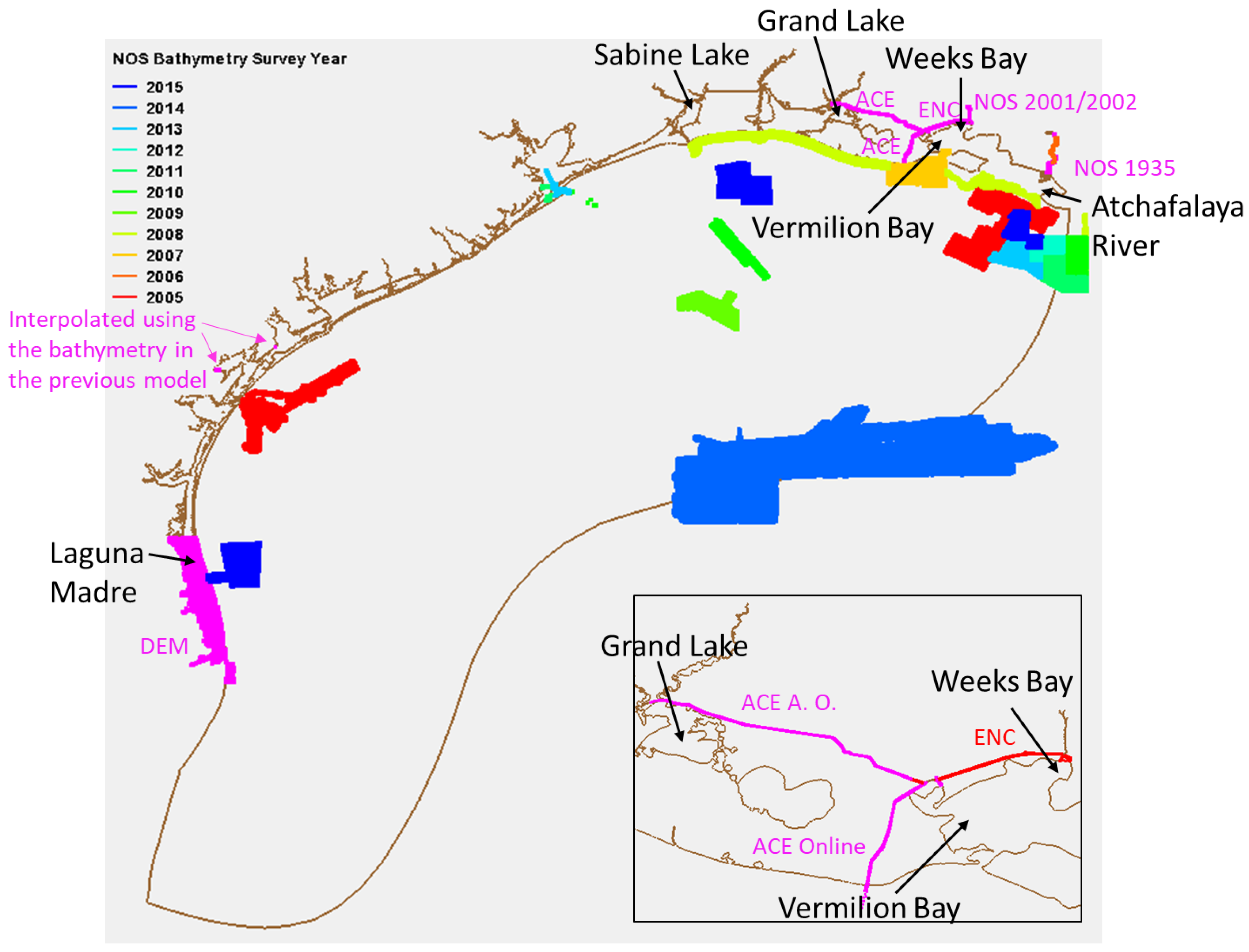
2.2.2. Bathymetry Data
2.2.3. Observed Tidal Datums and Associated Root-Mean-Square (RMS) Errors
2.3. Methods
2.3.1. Calculation of Observed Tidal Datums
2.3.2. Calculation of ADCIRC Tidal Datums
2.3.3. Statistical Interpolation of Tidal Datums and Their Associated Spatially Varying Uncertainties
2.3.4. Estimates of Non-Tidal Zones and VDatum Marine Grid Population
3. Results and Discussion
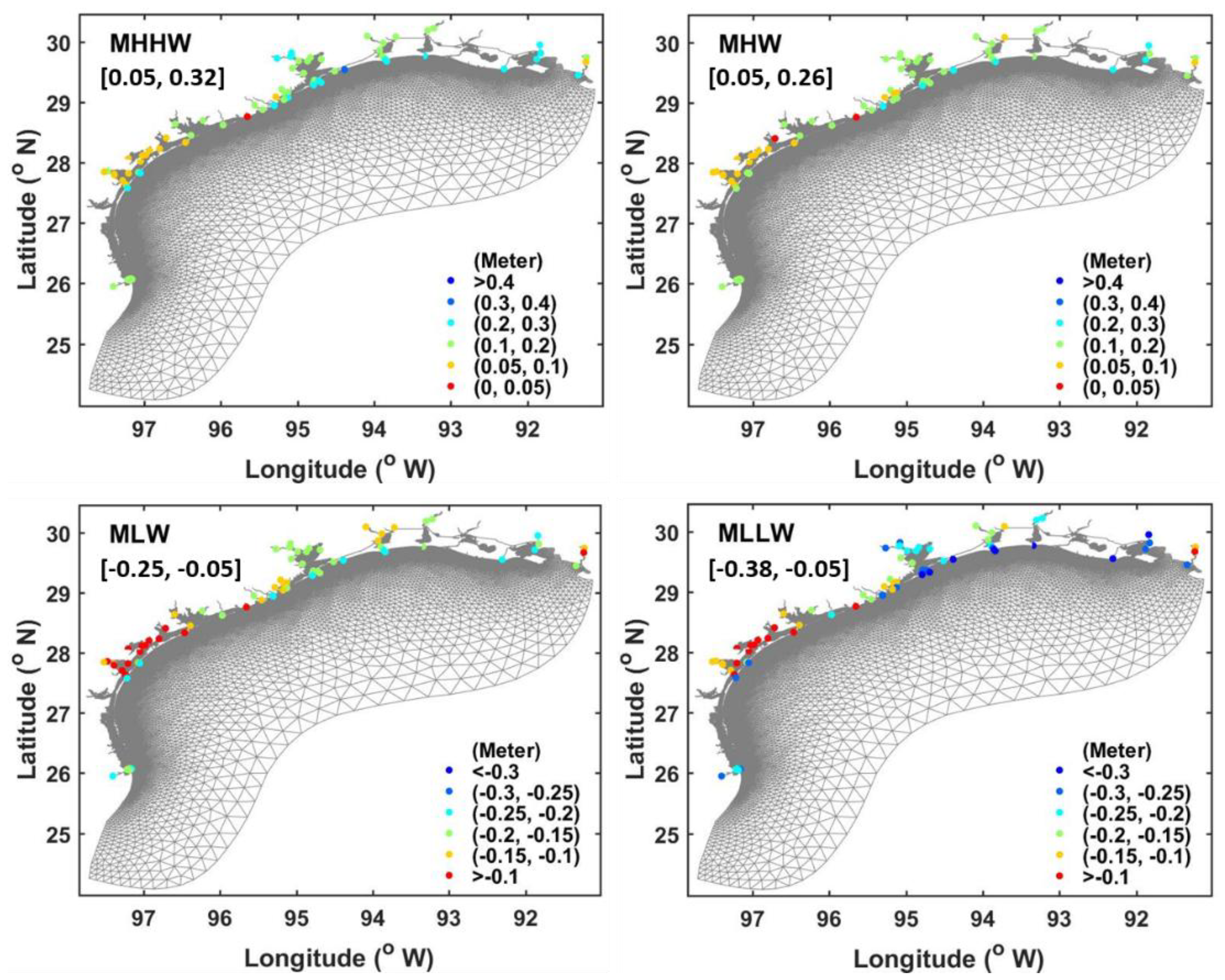
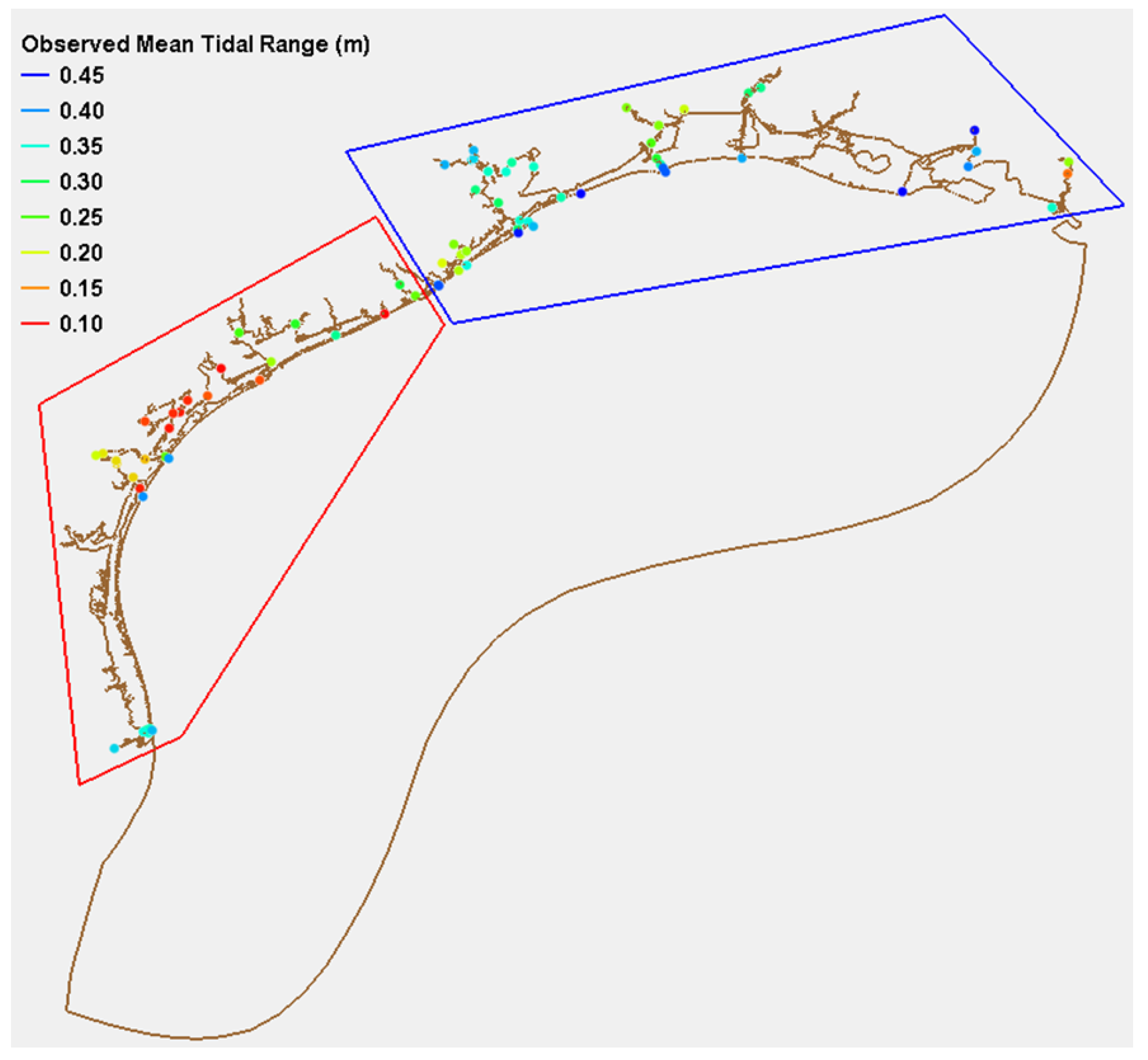
3.1. Observed Tidal Datums
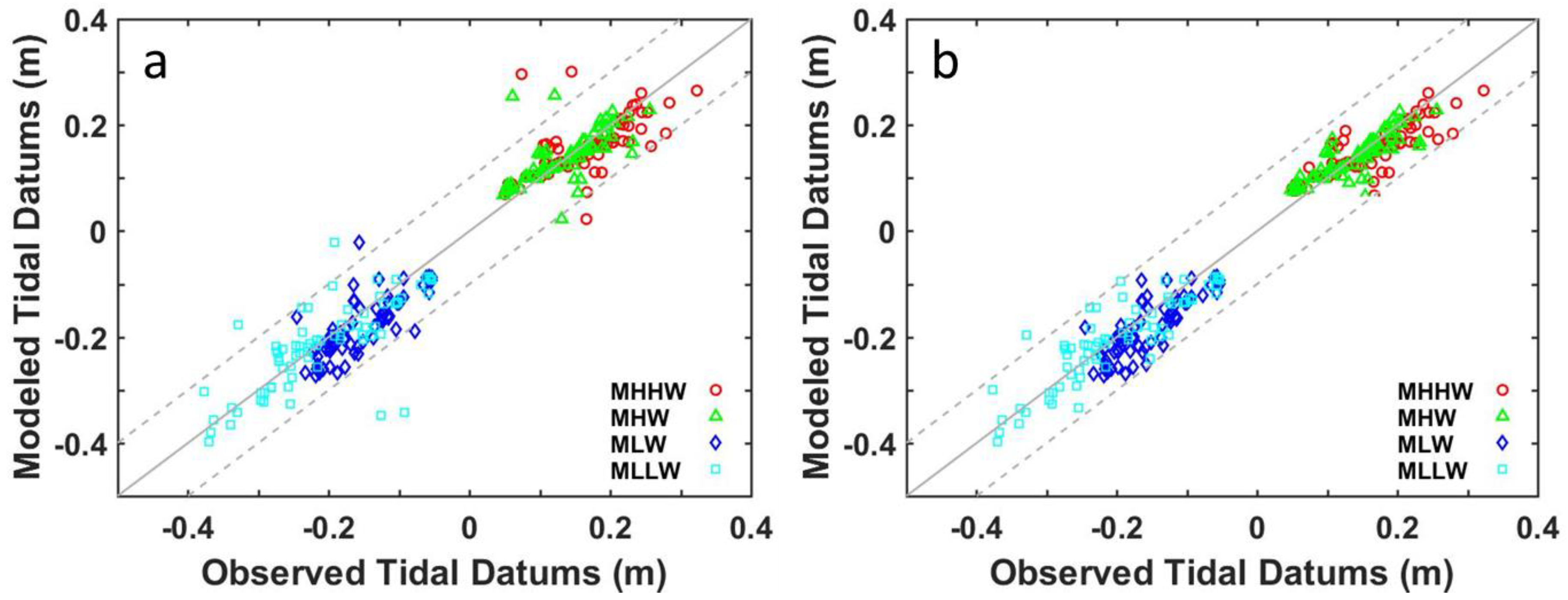
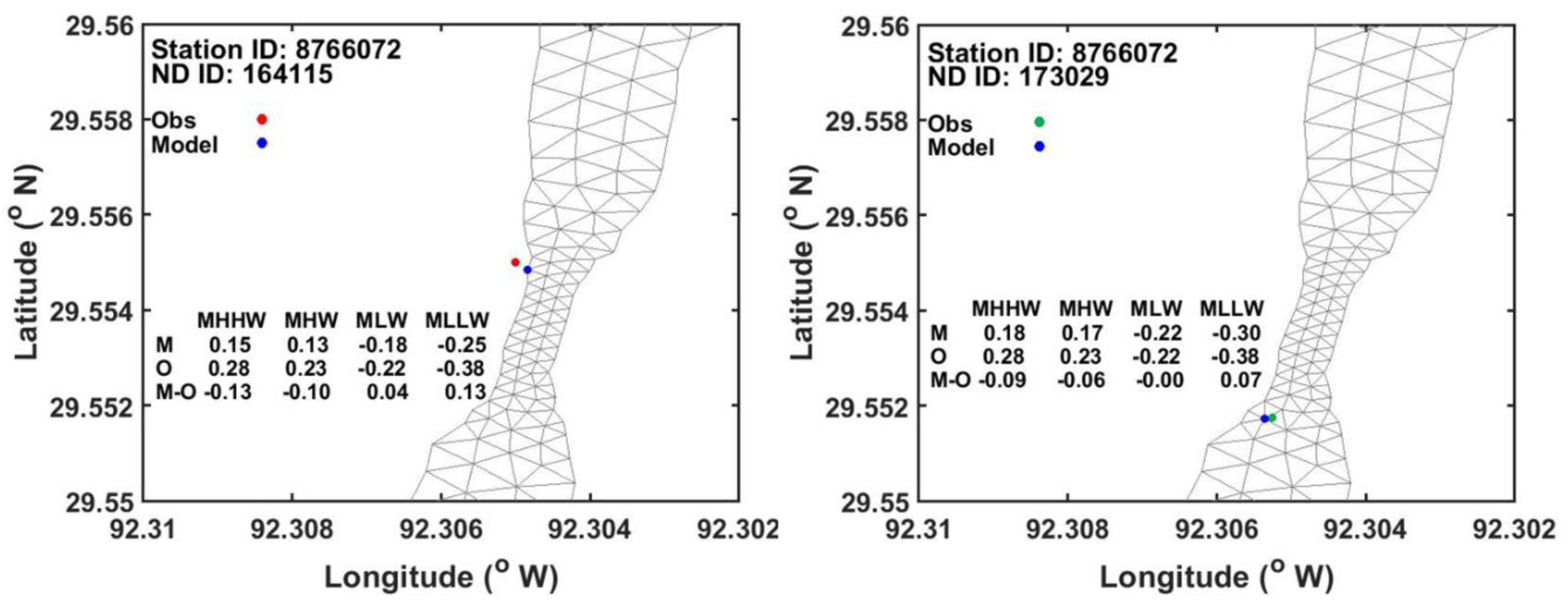
3.2. The Assessment and Improvement of ADCIRC Modeled Tidal Datums
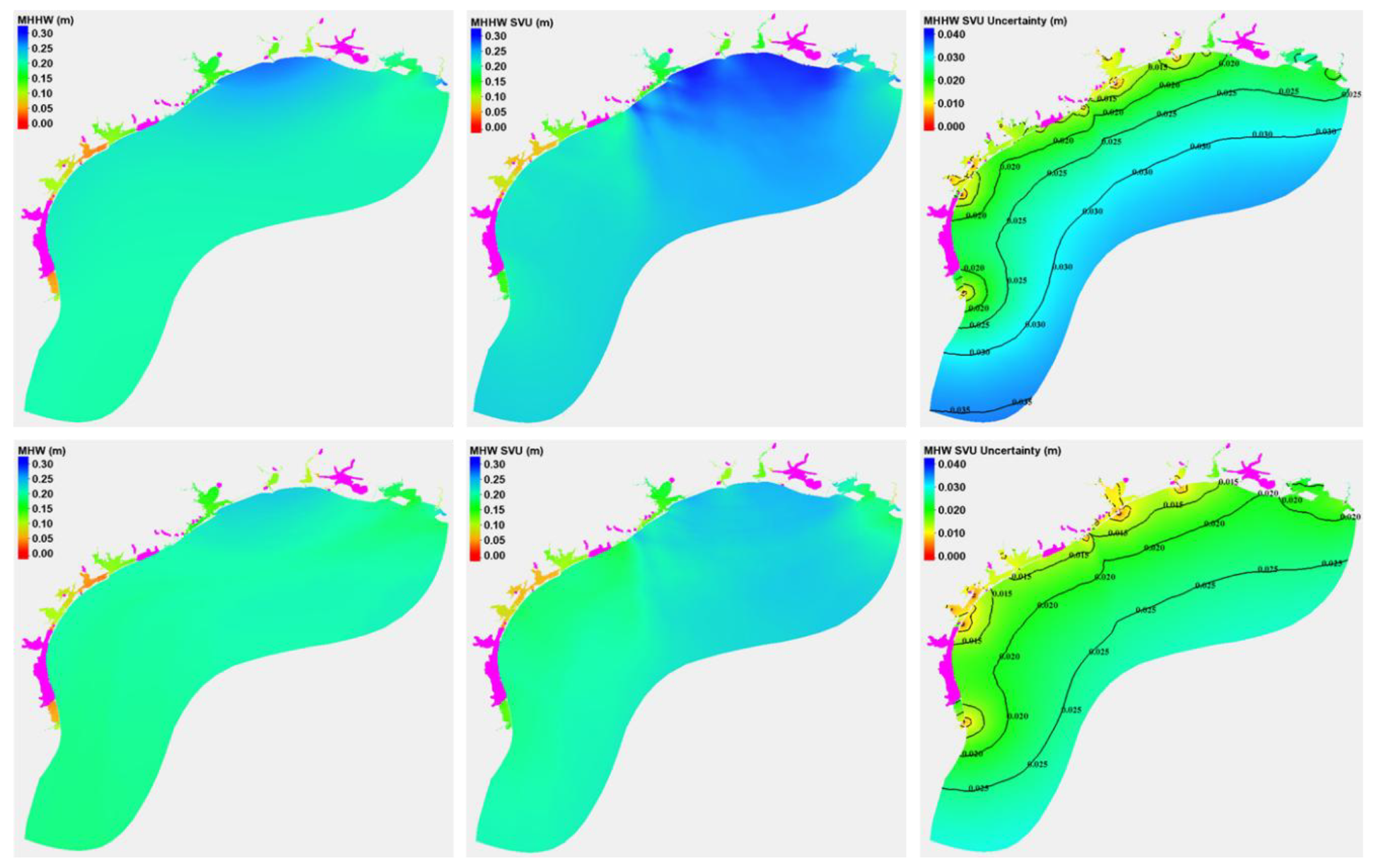
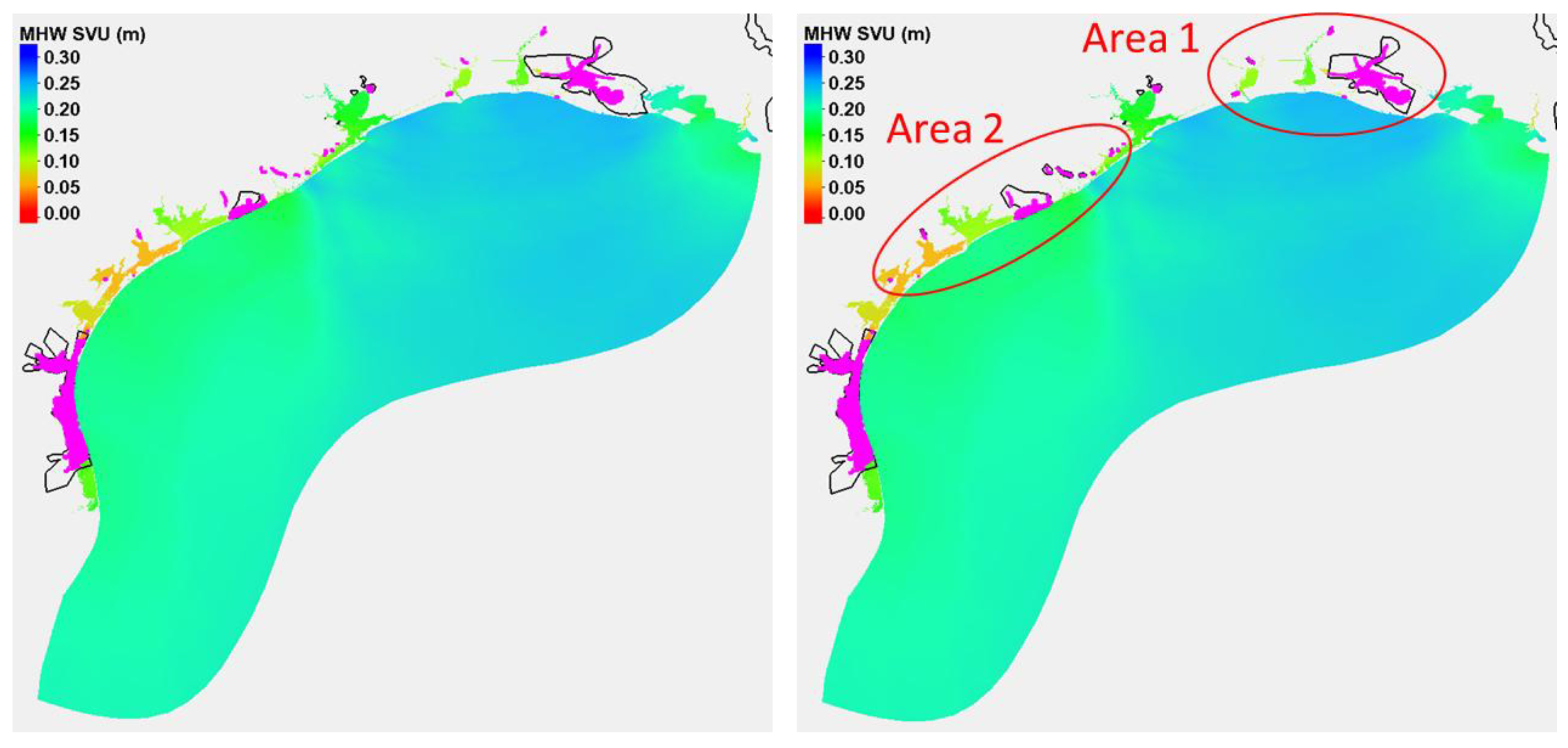
3.3. Statistical Interpolation of Modeled Tidal Datums and Associated Uncertainties
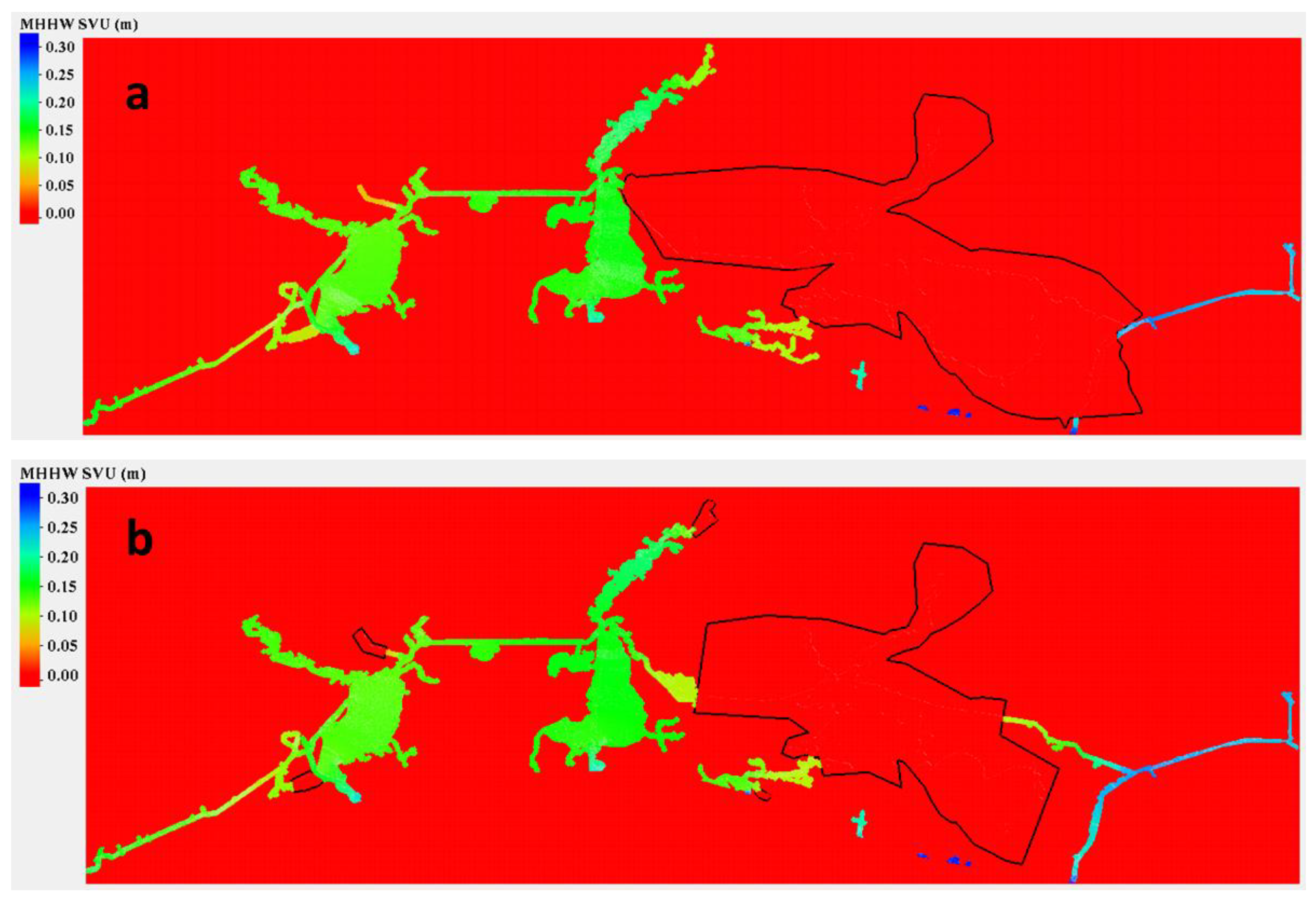
3.4. Non-Tidal Polygon Upgrade and VDatum Marine Grid Population
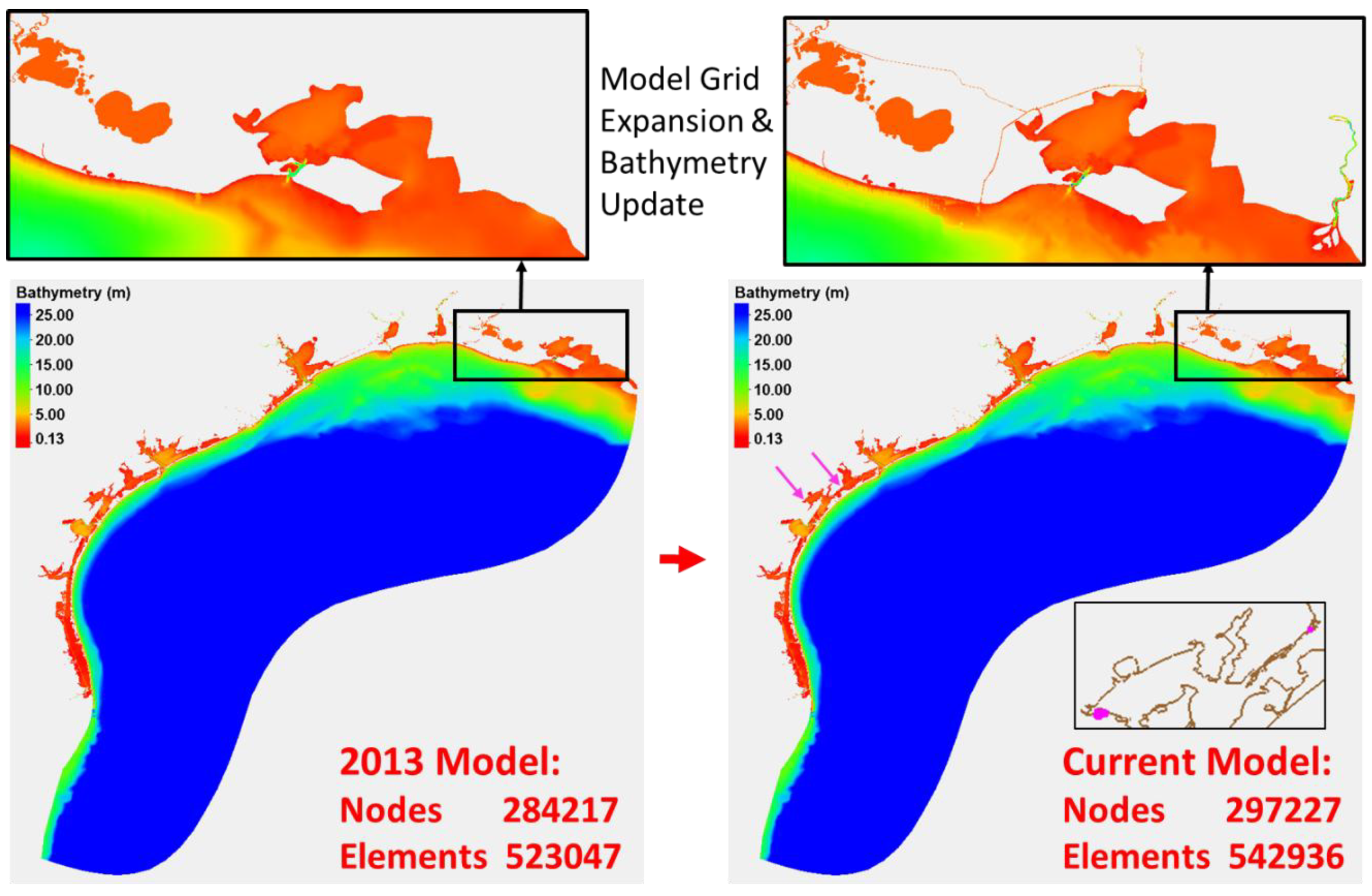
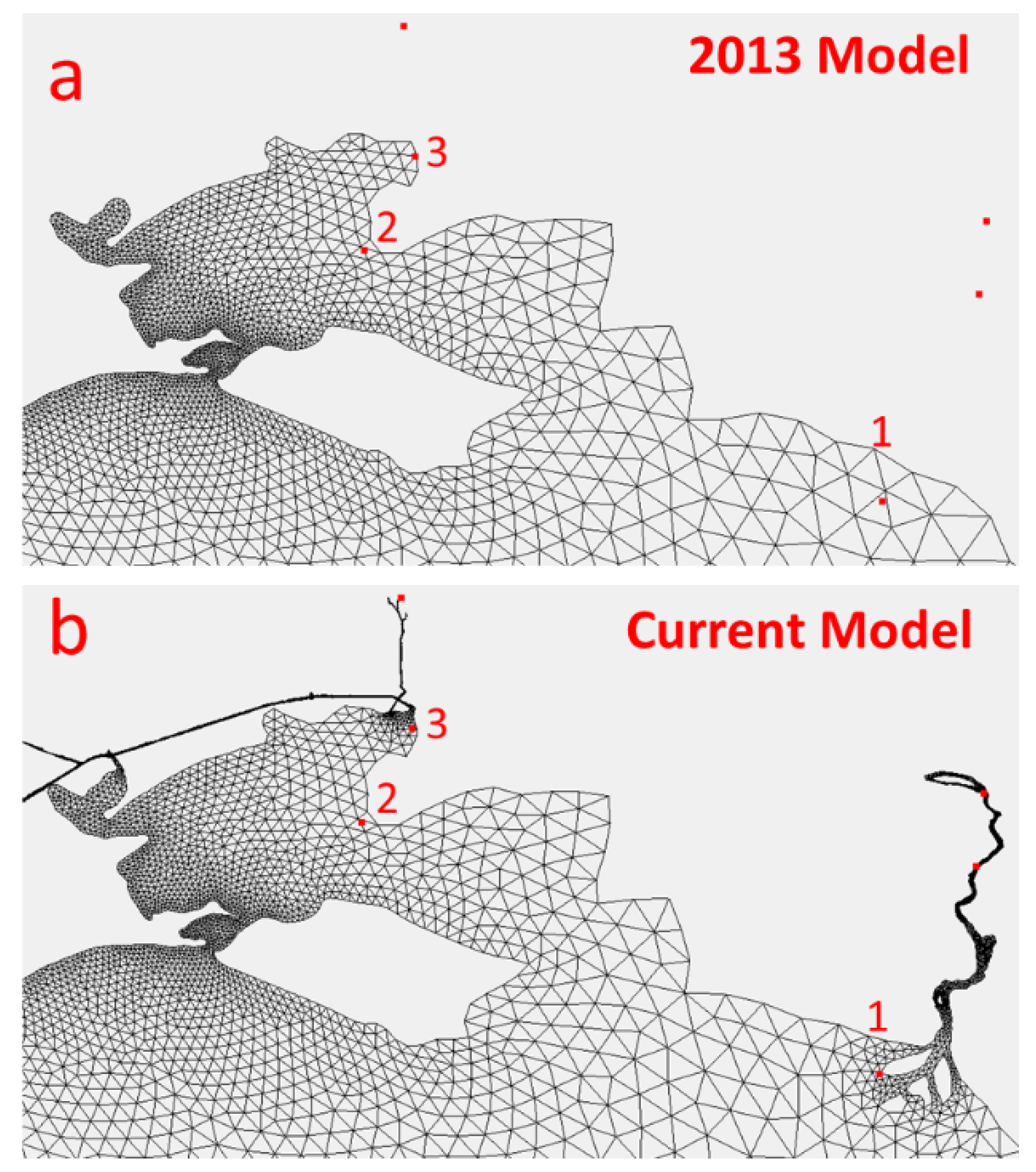
3.5. Comparisons of the Updated Tidal Model with the Previous Tidal Model
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NOAA/NOS VDatum Website. Available online: https://vdatum.noaa.gov/ (accessed on 6 February 2019).
- Gill, S.; Schultz, J. Tidal Datums and Their Applications; NOAA Special Publication NOS CO-OPS 1: Silver Spring, MD, USA, 2000. Available online: http://www.tidesandcurrents.noaa.gov/publications/tidal_datums_and_their_applications.pdf (accessed on 6 February 2019).
- Myers, E.P. Review of progress on VDatum, a vertical datum transformation tool. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; pp. 974–980. [Google Scholar]
- Myers, E.; Hess, K.; Yang, Z.; Xu, J.; Wong, A.; Doyle, D.; Woolard, J.; White, S.; Le, B.; Gill, S.; et al. VDatum and strategies for national coverage. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–8. [Google Scholar]
- Hess, K.; Kenny, K.; Myers, E. Standard Procedures to Develop and Support NOAA’s Vertical Datum Transformation Tool, VDATUM (Version 2010.08.03); NOAA NOS Technical Report; NOAA NOS: Silver Spring, MD, USA, 2012.
- Xu, J.; Myers, E. Modeling tidal dynamics and tidal datums along the coasts of Texas and Western Louisiana. In Proceedings of the 11th International Conference on Estuarine and Coastal Modeling, Seattle, WA, USA, 4–6 November 2009. [Google Scholar]
- Xu, J.; Myers, E.P.; Jeong, I.; White, S.A. VDatum for the Coastal Waters of Texas and Western Louisiana: Tidal DAtums and Topography of the Sea Surface; NOAA: Silver Spring, MD, USA, 2013.
- ADCIRC Users Manuals. Available online: https://adcirc.org/home/documentation/users-manuals-compile-options-faqs-wiki/ (accessed on 6 February 2019).
- Luettich, R.A., Jr.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 1. Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; Coastal Engineering Research Center: Vicksburg, MS, USA, 1992. [Google Scholar]
- Westerink, J.J.; Luettich, R., Jr.; Scheffner, N. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 3. Development of a Tidal Constituent Database for the Western North Atlantic and Gulf of Mexico; Coastal Engineering Research Center: Vicksburg, MS, USA, 1993; Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a268685.pdf (accessed on 6 February 2019).
- Westerink, J.; Luettich, R., Jr.; Blain, C.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 2. User’s Manual for ADCIRC-2DDI; Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1994; Available online: file:///C:/Users/Wei.Wu/Downloads/ADCIRC_An_Advanced_Three-Dimensional_Circulation_M%20(1).pdf (accessed on 6 February 2019).
- National Hurricane Center Tropical Cyclone Report. Available online: https://www.nhc.noaa.gov/data/tcr/ (accessed on 6 February 2019).
- Shi, L.; Myers, E. Statistical Interpolation of Tidal Datums and Computation of Its Associated Spatially Varying Uncertainty. J. Mar. Sci. Eng. 2016, 4, 64. [Google Scholar] [CrossRef]
- Gill, S.; Michalski, M. Classification of a Water Level Station as Non-Tidal; NOAA SOP # 7.3.A.1; NOAA: Silver Spring, MD, USA, 2016.
- Mao, M.; Xia, M. Dynamics of wave–current–surge interactions in Lake Michigan: A model comparison. Ocean Model. 2017, 110, 1–20. [Google Scholar] [CrossRef]
- Akbar, M.K.; Luettich, R.A.; Fleming, J.G.; Aliabadi, S.K. CaMEL and ADCIRC Storm Surge Models—A Comparative Study. J. Mar. Sci. Eng. 2017, 5, 35. [Google Scholar] [CrossRef]
- Vinogradov, S.; Myers, E.; Funakoshi, Y.; Moghimi, S.; Calzada-Morrero, J. Real-Time Storm Surge Forecasting Systems Research, Design, and Development. In Proceedings of the 98th American Meteorological Society Annual Meeting, Austin, TX, USA, 7–11 January 2018; Available online: https://ams.confex.com/ams/98Annual/webprogram/Paper327250.html (accessed on 6 February 2019).
- Funakoshi, Y.; Feyen, J.C.; Aikman, F.; van der Westhuysen, A.J.; Tolman, H.L. The Extratropical Surge and Tide Operational Forecast System (ESTOFS) Atlantic Implementation and Skill Assessment; NOAA Technical Report NOS CS 32; NOAA: Silver Spring, MD, USA, 2013; 147p.
- Xu, J.; Feyen, J.C. The Extra Tropical Surge and Tide Operational Forecast System for the Eastern North Pacific Ocean (ESTOFS-Pacific): Development and Skill Assessment; NOAA Technical Report NOS CS 36; NOAA: Silver Spring, MD, USA, 2016; 153p.
- ADCIRC EC2015 Tidal Database. Available online: http://adcirc.org/products/adcirc-tidal-databases/ (accessed on 9 February 2019).
- Szpilka, C.; Dresback, K.; Kolar, R.; Feyen, J.; Wang, J. Improvements for the Western North Atlantic, Caribbean and Gulf of Mexico ADCIRC Tidal Database (EC2015). J. Mar. Sci. Eng. 2016, 4, 72. Available online: https://doi.org/10.3390/jmse4040072 (accessed on 6 February 2019). [CrossRef]
- Mukai, A.Y.; Westerink, J.J.; Luettich, R.A., Jr.; Mark, D. Eastcoast 2001, a Tidal Constituent Database for Western North Atlantic, Gulf of Mexico, and Caribbean Sea; Engineer Research and Development Center Vicksburg Ms Coastal and Hydraulicslab: Technical Report, ERDC/CHL TR-02-24; US Army Engineer Research and Development Center, Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2002; 201p, Available online: https://coast.nd.edu/reports_papers/2001-Mukai-TR-02-24.pdf (accessed on 6 February 2019).
- Egbert, G.D.; Svetlana, Y.E. The OSU TOPEX/Poseidon Global Inverse Solution TPXO. Available online: http://volkov.oce.orst.edu/tides/global.html (accessed on 6 February 2019).
- Egbert, G.D.; Svetlana, Y.E. OTIS Regional Tidal Solutions. Available online: http://volkov.oce.orst.edu/tides/Mex.html (accessed on 6 February 2019).
- SMS—The Complete Surface-water Solution. Available online: https://www.aquaveo.com/software/sms-surface-water-modeling-system-introduction (accessed on 6 February 2019).
- NOAA Shoreline Website—NOAA Continually Updated Shoreline Product (CUSP). Available online: https://www.ngs.noaa.gov/CUSP/ (accessed on 6 February 2019).
- NOAA’s Continually Updated Shoreline Product (CUSP). Available online: https://www.ngs.noaa.gov/INFO/OnePagers/CUSP_One-Pager.pdf (accessed on 6 February 2019).
- The U.S. Army Corps of Engineers (USACE) Hydrographic Survey Data. Available online: http://www.mvn.usace.army.mil (accessed on 6 February 2019).
- NOAA’s Electronic Navigational Chart (ENC, Chart #11345). Available online: http://www.charts.noaa.gov/OnLineViewer/11345.shtml (accessed on 6 February 2019).
- NOAA’s National Geophysical Data Center (NGDC) High-Resolution Digital Elevation Model (DEM) Data. Available online: https://www.ngdc.noaa.gov/ (accessed on 6 February 2019).
- CO-OPS. Computational Techniques for Tidal Datums Handbook; NOAA Special Publication NOS CO-OPS 2; NOAA: Silver Spring, MD, USA, 2003. Available online: https://www.tidesandcurrents.noaa.gov/publications/Computational_Techniques_for_Tidal_Datums_handbook.pdf (accessed on 6 February 2019).
- Parker, B. Tidal Analysis and Prediction; NOAA Special Publication NOS CO-OPS 3, 2007. Available online: https://tidesandcurrents.noaa.gov/publications/Tidal_Analysis_and_Predictions.pdf (accessed on 6 February 2019).
- Gill, S.; Hovis, G.; Kriner, K.; Michalski, M. Implementation of Procedures for Computation of Tidal Datums in Areas with Anomalous Trends of Relative Mean Sea Level. NOAA Technical Report NOS CO-OPS 068; 2014. Available online: https://tidesandcurrents.noaa.gov/publications/NOAA_Technical_Report_NOS_COOPS_68.pdf (accessed on 6 February 2019).
- Gill, S.; Hubbard, J.; Dingle, G. Tidal Characteristics and Datums of Laguna Madra, Texas. NOAA Technical Memorandum NOS OES 008; 1995. Available online: https://tidesandcurrents.noaa.gov/publications/Noaa_Technical_Memorandum_NOS_OES_008.pdf (accessed on 6 February 2019).
- Hess, K.; Schmalz, R.; Zervas, C.; Collier, W. Tidal Constituent and Residual Interpolation (TCARI): A New Method for the Tidal Correction of Bathymetric Data; NOAA Technical Report NOS CS 4; NOAA: Silver Spring, MD, USA, 1999.
- Hess, K.W. Spatial Interpolation of Tidal Data in Irregularly-shaped Coastal Regions by Numerical Solution of Laplace’s Equation. Estuar. Coast. Shelf Sci. 2002, 54, 175–192. Available online: https://doi.org/10.1006/ecss.2001.0838 (accessed on 6 February 2019). [CrossRef]
- Hess, K. Water level simulation in bays by spatial interpolation of tidal constituents, residual water levels, and datums. Cont. Shelf Res. 2003, 23, 395–414. [Google Scholar] [CrossRef]
- NOAA/NOS Vertical Datums Transformation, Estimation of Vertical Uncertainties in VDatum. 2016. Available online: https://vdatum.noaa.gov/docs/est_uncertainties.html (accessed on 6 February 2018).
- Stewart, R. Introduction to Physical Oceanography (Version 2008). Available online: https://www.colorado.edu/oclab/sites/default/files/attached-files/stewart_textbook.pdf (accessed on 6 February 2019).
- Weston, N. Benefits and Impacts to Nautical Charting by Adopting a New Reference. 2018. Available online: https://www.eiseverywhere.com/ehome/chc-nsc2018/home/ (accessed on 6 February 2019).
- DiMarco, S.F.; Reid, R.O. Characterization of the principal tidal current constituents on the Texas-Louisiana shelf. J. Geophys. Res. Ocean. 1998, 103, 3093–3109. Available online: https://doi.org/10.1029/97JC03289 (accessed on 6 February 2019). [CrossRef]
- Oey, L.-Y.; Ezer, T.; Lee, H.-C. Loop Current, rings and related circulation in the Gulf of Mexico: A review of numerical models and future challenges. In Circulation in the Gulf of Mexico: Observations and Models; Sturges, W., Lugo-Fernandez, A., Eds.; Geophysical Monograph Series; Geophysical Monograph-American Geophysical Union: Washington, DC, USA, 2005; Volume 161, pp. 31–56. Available online: http://www.ccpo.odu.edu/~tezer/PAPERS/2005_AGU_GOM.pdf (accessed on 6 February 2019).




| Data Type | MHHW | MHW | MLW | MLLW |
|---|---|---|---|---|
| Maximum Value | ||||
| Observation | 0.32 | 0.26 | −0.25 | −0.38 |
| ADCIRC | 0.28 (0.063) | 0.24 (0.067) | −0.31 (0.072) | −0.43 (0.132) |
| ADCIRC-SVU | 0.31 (0.010) | 0.25 (0.010) | −0.27 (0.010) | −0.45 (0.010) |
| SVU Uncertainty | 0.036 | 0.033 | 0.034 | 0.046 |
| Minimum Value | ||||
| Observation | 0.05 | 0.05 | −0.05 | −0.05 |
| ADCIRC | 0.03 (−0.010) | 0.03 (−0.088) | −0.03 (−0.093) | −0.03 (−0.089) |
| ADCIRC-SVU | 0.03 (−0.010) | 0.03 (−0.010) | 0.00 (−0.010) | −0.03 (−0.010) |
| SVU Uncertainty | 0 | 0 | 0 | 0 |
| Mean Value | ||||
| Observation | 0.16 | 0.14 | −0.15 | −0.20 |
| ADCIRC | 0.16 (0.028) | 0.15 (0.021) | −0.18 (0.035) | −0.21 (0.032) |
| ADCIRC-SVU | 0.17 (0.005) | 0.15 (0.005) | −0.16 (0.005) | −0.22 (0.005) |
| SVU Uncertainty | 0.015 | 0.013 | 0.015 | 0.018 |
| STD | ||||
| Observation | 0.066 | 0.052 | 0.053 | 0.090 |
| ADCIRC | 0.066 (0.035) | 0.056 (0.028) | 0.074 (0.033) | 0.102 (0.042) |
| ADCIRC-SVU | 0.069 (0.006) | 0.055 (0.006) | 0.057 (0.007) | 0.095 (0.006) |
| SVU Uncertainty | 0.004 | 0.004 | 0.005 | 0.006 |
| Tide Station | MHHW (M-O) | MHW (M-O) | MLW (M-O) | MLLW (M-O) |
|---|---|---|---|---|
| 1 | −0.011 (0.009) | 0.009 (0.032) | −0.093 (−0.022) | −0.078 (−0.090) |
| 2 | −0.057 (−0.063) | −0.029 (−0.046) | −0.001 (0.013) | 0.050 (0.049) |
| 3 | −0.025 (−0.030) | −0.016 (−0.030) | −0.012 (0.005) | 0.037 (0.038) |
| Mean |Error| | 0.031 (0.034) | 0.018 (0.036) | 0.035 (0.013) | 0.055 (0.059) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Myers, E.; Shi, L.; Hess, K.; Michalski, M.; White, S. Modeling Tidal Datums and Spatially Varying Uncertainty in the Texas and Western Louisiana Coastal Waters. J. Mar. Sci. Eng. 2019, 7, 44. https://doi.org/10.3390/jmse7020044
Wu W, Myers E, Shi L, Hess K, Michalski M, White S. Modeling Tidal Datums and Spatially Varying Uncertainty in the Texas and Western Louisiana Coastal Waters. Journal of Marine Science and Engineering. 2019; 7(2):44. https://doi.org/10.3390/jmse7020044
Chicago/Turabian StyleWu, Wei, Edward Myers, Lei Shi, Kurt Hess, Michael Michalski, and Stephen White. 2019. "Modeling Tidal Datums and Spatially Varying Uncertainty in the Texas and Western Louisiana Coastal Waters" Journal of Marine Science and Engineering 7, no. 2: 44. https://doi.org/10.3390/jmse7020044
APA StyleWu, W., Myers, E., Shi, L., Hess, K., Michalski, M., & White, S. (2019). Modeling Tidal Datums and Spatially Varying Uncertainty in the Texas and Western Louisiana Coastal Waters. Journal of Marine Science and Engineering, 7(2), 44. https://doi.org/10.3390/jmse7020044




