An Improved Ship Collision Risk Evaluation Method for Korea Maritime Safety Audit Considering Traffic Flow Characteristics
Abstract
1. Introduction
2. Ulsan Port Characteristics and Data
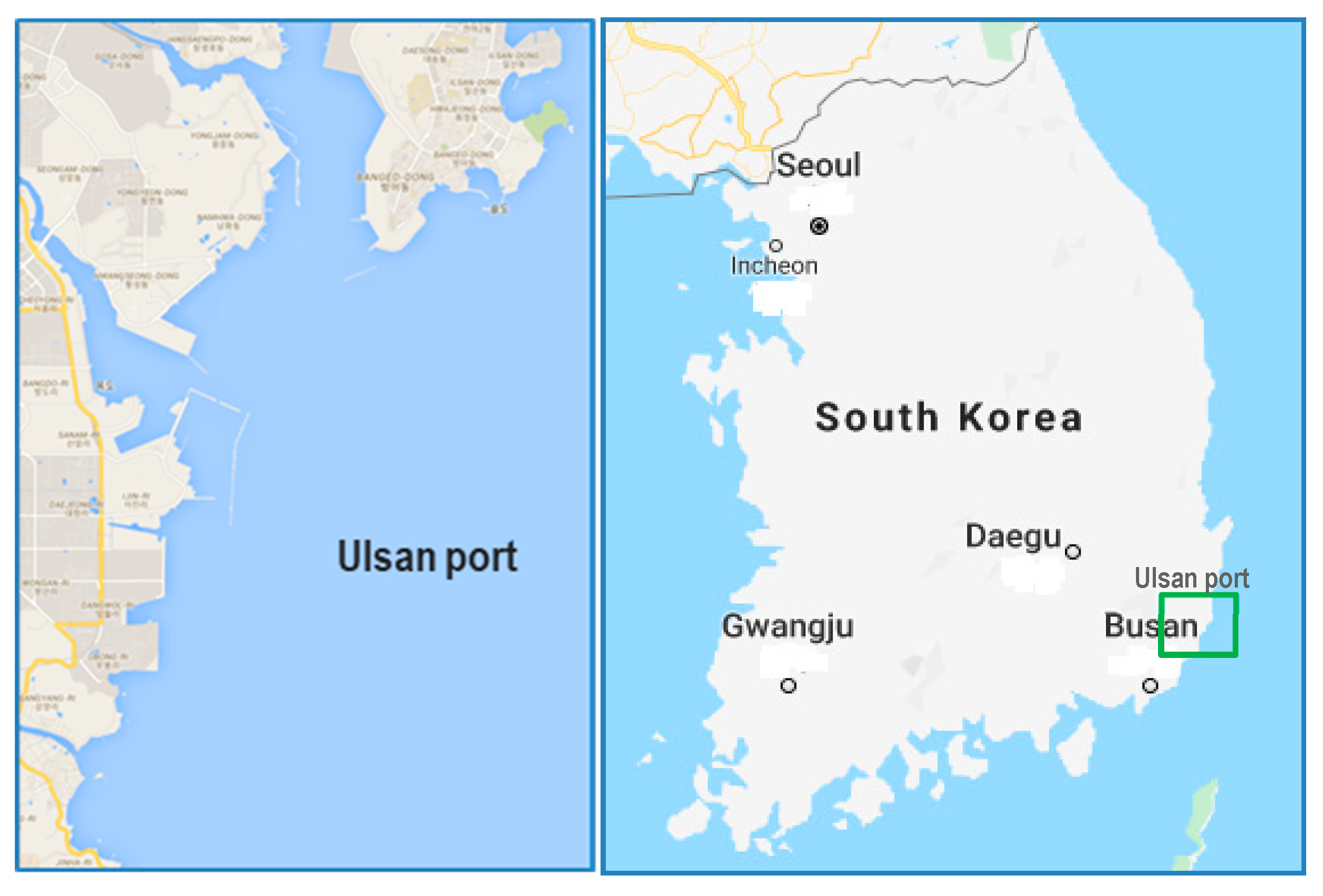
2.1. Target Port
2.2. Automatic Identification System (AIS) Data
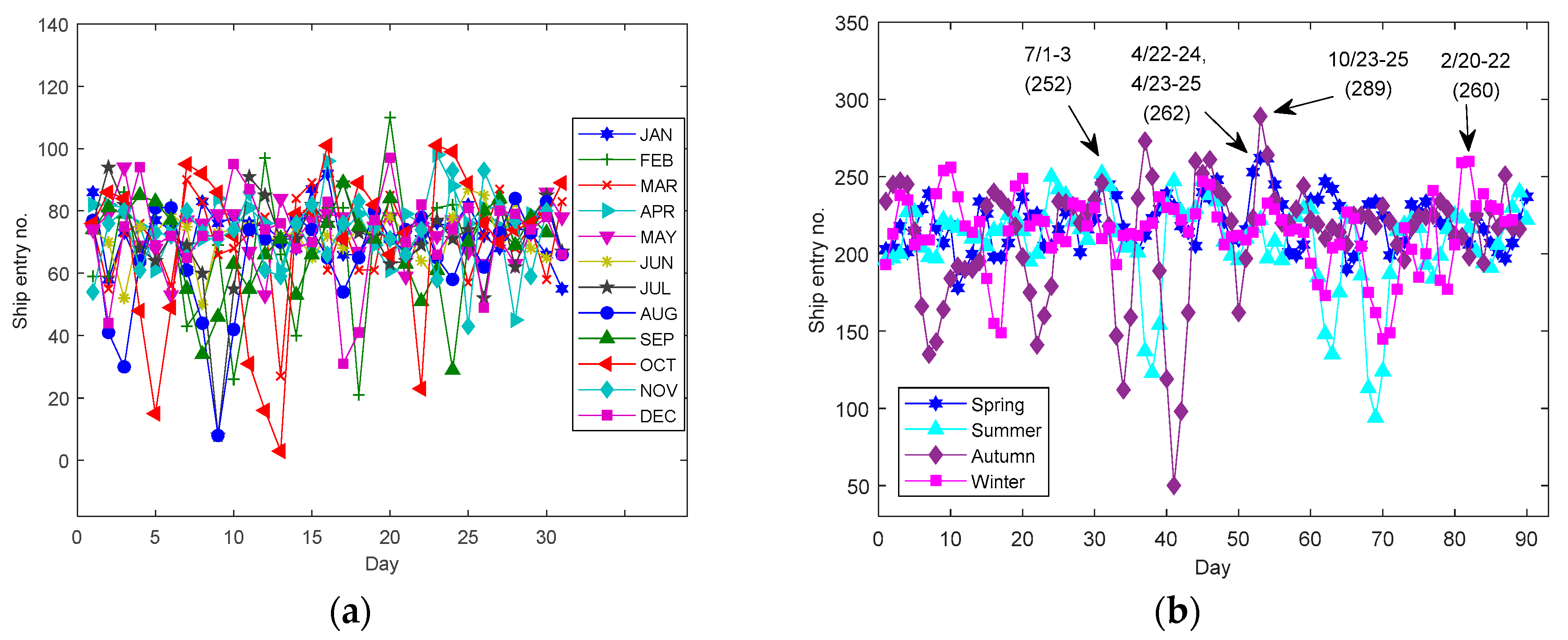
3. Ship Traffic Distribution Characteristics
4. Collision Risk Simulation
4.1. Collision Frequency Model
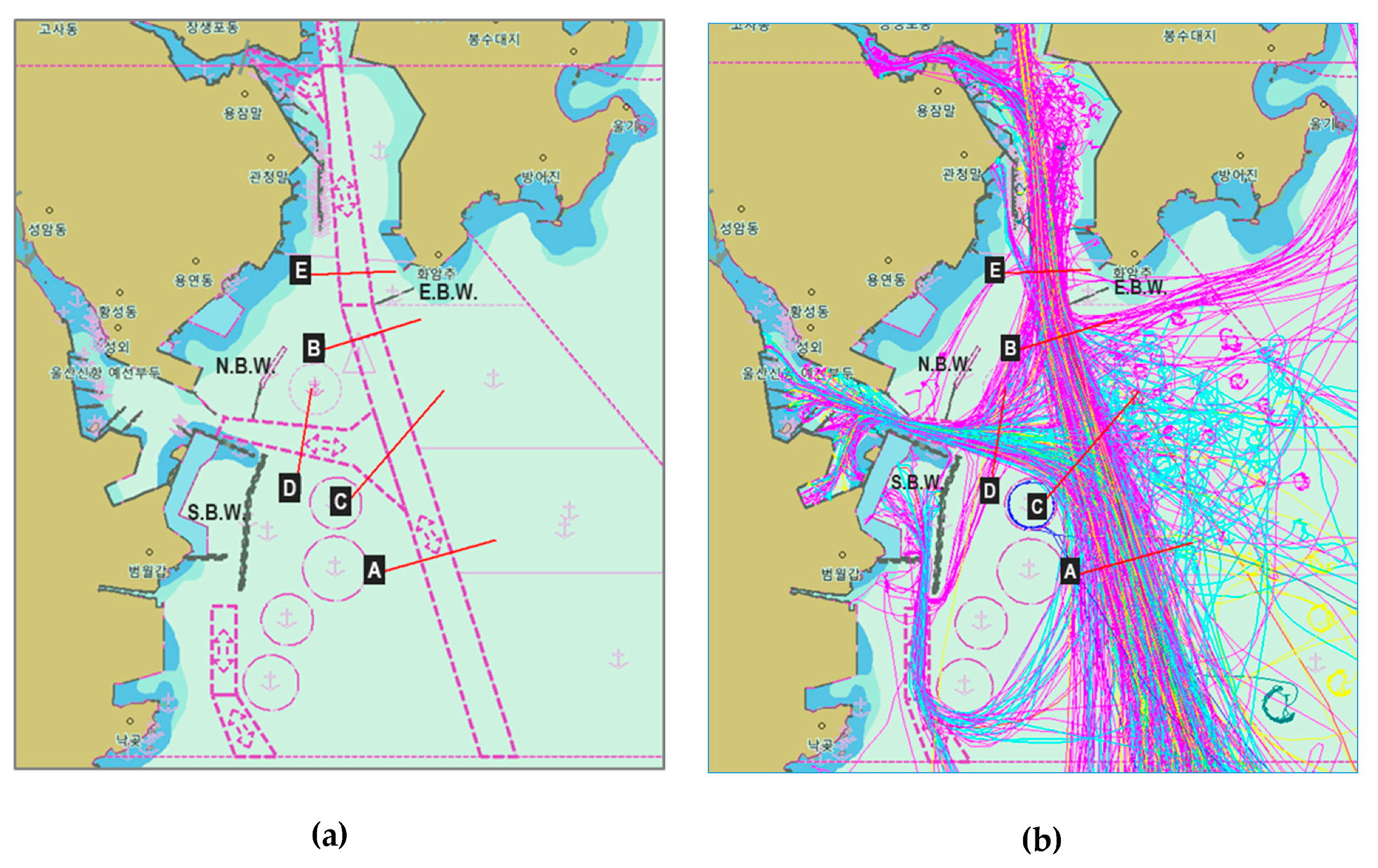
4.2. Simulation Conditions
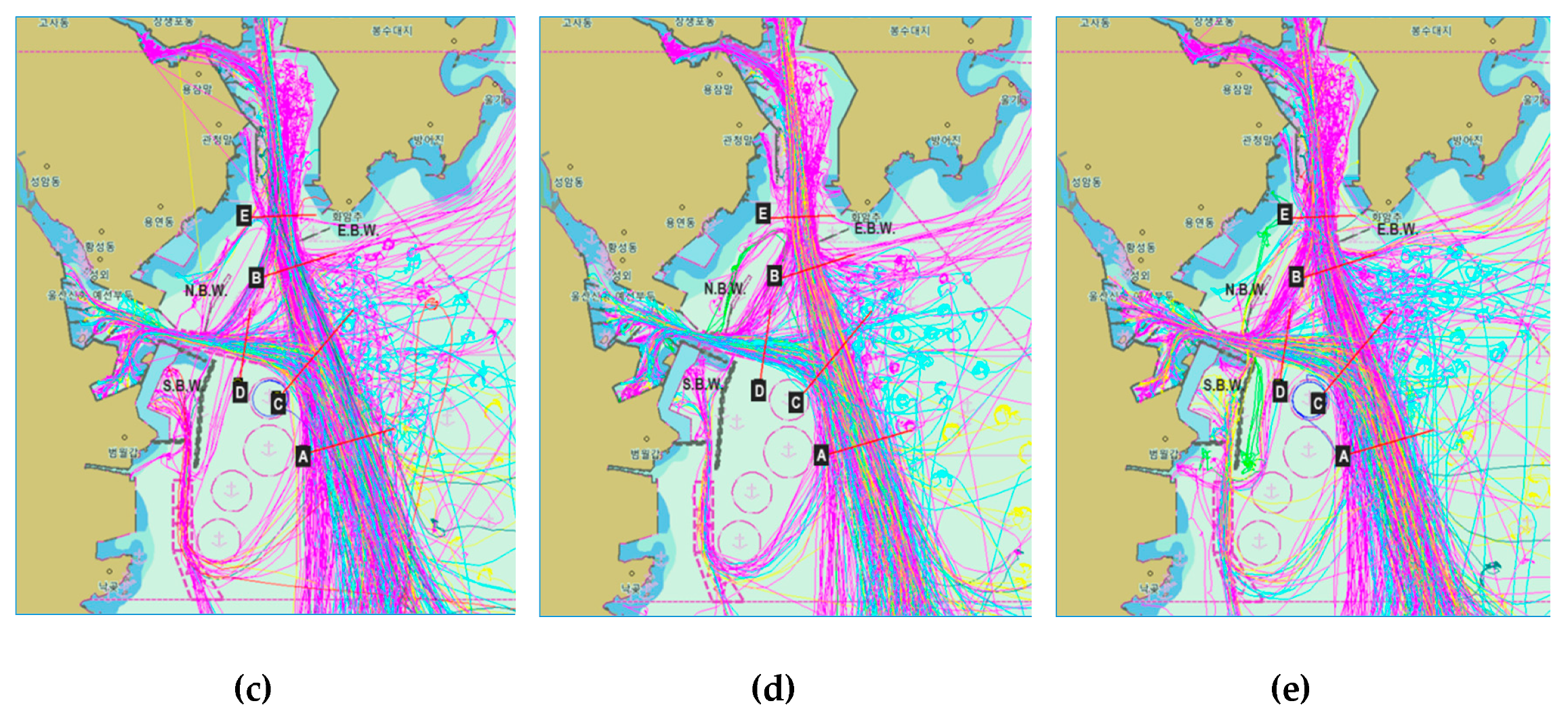
4.3. Simulation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- KMST (Korean Maritime Safety Tribunal). 2018 Annual Report of Marine Accident Statistics. Available online: https://www.kmst.go.kr/ (accessed on 15 August 2019).
- KLTC (Korea Law Translation Center). Maritime Safety Act-Article 15. Available online: https://elaw.klri.re.kr/kor_service/lawView.do?hseq=47116&lang=ENG (accessed on 28 October 2019).
- Cho, I.S.; Kim, I.C.; Lee, Y.S. The introductory concept of maritime safety audit as a tool for identifying potential hazards. J. Navig. Port Res. 2010, 34, 699–704. [Google Scholar] [CrossRef]
- Cho, I.S.; Lee, S.J.; Kim, L.C.; Hwang, E.S.; Lim, K.T. Introduction to maritime safety audit and its guidelines. In Proceedings of the 2009 Korean Society of Marine Environment and Safety Symposium, Busan, Korea, 4–5 June 2009; pp. 699–704. [Google Scholar]
- MLTMA (Ministry of Land, Transport and Maritime Affairs). A Study on Maritime Safety Audit and Its Guideline, Technical Report of Korea Ship Safety Technology Authority; MLTMA: Gwacheon, Korea, 2009.
- AASHTO (American Association of State Highway and Transportation Officials). Guide Specifications and Commentary for Vessel Collision Design of Highway Bridges, 2nd ed.; AASHTO: Washington, DC, USA, 2009. [Google Scholar]
- Manuel, L.; Kallivokas, L.F.; Williamson, E.B.; Bomba, M.; Berlin, K.B.; Cryer, A.; Henderson, W.R. A Probabilistic Analysis of the Frequency of Bridge Collapse Due to Vessel Impact; Technical Report no. FHWA/TX-07/0-4650-1; Center for Transportation Research at the University of Texas at Austin: Austin, TX, USA, 2006. [Google Scholar]
- Yim, J.B. Development of collision risk evaluation model between passing vessel and Mokpo harbor bridge. J. Navig. Port Res. 2010, 34, 405–415. [Google Scholar] [CrossRef][Green Version]
- Yim, J.B.; Kim, D.H. Statistical parameter estimation to calculate collision probability between Mokpo harbour bridge and passing vessels. J. Navig. Port Res. 2010, 34, 609–614. [Google Scholar] [CrossRef]
- Bae, Y.G.; Lee, S.L. Ship collision risk assessment and sensitivity analysis for sea-crossing bridges. J. Korean Soc. Civ. Eng. 2013, 33, 1753–1763. [Google Scholar] [CrossRef]
- Kim, S.C.; Kwon, Y.M. A review of proximity assessment measurements according to fairway patterns and ship size. J. Korean Soc. Mar. Environ. Saf. 2017, 23, 783–790. [Google Scholar] [CrossRef]
- Fujii, J.; Tanaka, K. Traffic capacity. J. Navig. 1971, 24, 543–552. [Google Scholar] [CrossRef]
- Goodwin, E.M. A statistical study of ship domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Coldwell, T.G. Marine traffic behaviour in restricted waters. J. Navig. 1983, 36, 431–444. [Google Scholar] [CrossRef]
- Hansen, M.G.; Jensen, T.K.; Lehn-Schiøler, T.; Melchild, K.; Rasmussen, F.M.; Ennemark, F. Empirical ship domain based on AIS data. J. Navig. 2013, 66, 931–940. [Google Scholar] [CrossRef]
- Wang, Y.; Chin, H.C. An empirically-calibrated ship domain as a safety criterion for navigation in confined waters. J. Navig. 2016, 69, 257–276. [Google Scholar] [CrossRef]
- Dinh, G.H.; Im, N. The combination of analytical and statistical method to define polygonal ship domain and reflect human experiences in estimating dangerous area. Int. J. E-Navig. Mar. Econ. 2016, 4, 97–108. [Google Scholar] [CrossRef]
- Pietrzykowski, Z. Ship’s fuzzy domain—a criterion for navigational safety in narrow fairways. J. Navig. 2008, 61, 499–514. [Google Scholar] [CrossRef]
- Pietrzykowski, Z.; Uriasz, J. The ship domain—A criterion of navigational safety assessment in an open sea area. J. Navig. 2009, 62, 93–108. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, H.; Liu, J. Domain and its model based on neural networks. J. Navig. 2001, 54, 97–103. [Google Scholar] [CrossRef]
- Davis, P.V.; Dove, M.J.; Stockel, C.T. A computer simulation of marine traffic using domains and arenas. J. Navig. 1980, 33, 215–222. [Google Scholar] [CrossRef]
- Davis, P.V.; Dove, M.J.; Stockel, C.T. A computer simulation of multi-ship encounters. J. Navig. 1982, 35, 347–352. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, F.; Li, Z.; Wang, M.; Liu, R.W. Dynamic ship domain models for capacity analysis of restricted water channels. J. Navig. 2016, 69, 481–503. [Google Scholar] [CrossRef]
- Montewka, J.; Krata, P.; Goerlandt, F.; Mazaheri, A.; Kujala, P. Marine traffic risk modelling–An innovative approach and a case study. Proc. Inst. Mech. Eng. J. Risk Reliab. 2011, 225, 307–322. [Google Scholar] [CrossRef]
- Rawson, A.; Rogers, E.; Foster, D.; Phillips, D. Practical application of domain analysis: Port of London case study. J. Navig. 2014, 67, 193–209. [Google Scholar] [CrossRef]
- Wang, N.; Meng, X.; Xu, Q.; Wang, Z. An intelligent spatial collision risk based on the quaternion ship domain. J. Navig. 2010, 63, 733–749. [Google Scholar] [CrossRef]
- Wang, N. A novel analytical framework for dynamic quaternion ship domains. J. Navig. 2013, 66, 265–281. [Google Scholar] [CrossRef]
- Friis-Hansen, P. Basic Modelling Principles for Prediction of Collision and Grounding Frequencies; Working document; Technical University of Denmark: Copenhagen, Denmark, 2008. [Google Scholar]
- Kim, D.W.; Park, J.S.; Park, Y.S. Comparison analysis between the IWRAP and the ES model in Ulsan waterway. J. Navig. Port Res. 2011, 35, 281–287. [Google Scholar] [CrossRef]
- Kim, K.I.; Park, G.K.; Jeong, J.S. Analysis of marine accident probability in Mokpo waterways. J. Navig. Port Res. 2011, 35, 729–733. [Google Scholar] [CrossRef]
- Ylitalo, J. Modelling Marine Accident Frequency. Master’s Thesis, Alto University, Espoo, Finland, 2010. [Google Scholar]
- MOF (Ministry of Oceans and Fisheries). Safety Assessment of Ship Routes, Working Document of Korea Maritime and Ocean University; MOF: Sejong, Korea, 2015.
- UPA (Ulsan Port Authority). 2018 Statistical Yearbook of Ulsan Port in Korea. Available online: https://upa.or.kr/ (accessed on 13 August 2019).
- Fukunaga, K. Introduction to Statistical Pattern Recognition, 2nd ed.; Academic Press: Tokyo, Japan, 1990; pp. 75–84. [Google Scholar]
- Fujii, Y.; Yamanouchi, H.; Mizuki, N. Some factors affecting the frequency of accidents in marine traffic. II-The probability of stranding and III-The effect of darkness on the probability of collision and stranding. J. Navig. 1974, 27, 239–247. [Google Scholar] [CrossRef]
- Macduff, T. The probability of vessel collisions. Ocean Ind. 1974, 9, 144–148. [Google Scholar]
- Pedersen, P.T. Collision and grounding mechanics. The Danish Society of Naval Architects and Marine Engineers, Copenhagen. Proc. WEGEMT 1995, 95, 125–157. [Google Scholar]
- IMO (International Maritime Organization). Automatic Identification Systems (AIS). Available online: http://www.imo.org/en/OurWork/Safety/Navigation/Pages/AIS.aspx (accessed on 28 October 2019).
- Port-MIS (Management Information System). Ship Entry Data of Ulsan Port in Korea. Available online: https://new.portmis.go.kr/ (accessed on 10 December 2015).
- GICOMS (General Information Center on Maritime Safety and Security). 2014 AIS Data of Ulsan Port. Available online: https://www.gicoms.go.kr/ (accessed on 10 December 2015).
- KMGL (Korea Ministry of Government Legislation). Act on the Arrival, Departure, etc. of Ships. 2017. Available online: https://elaw.klri.re.kr/kor_service/lawTotalSearch.do (accessed on 23 August 2017).
- KMGL (Korea Ministry of Government Legislation). Maritime Safety Act. Available online: https://elaw.klri.re.kr/kor_service/lawTotalSearch.do (accessed on 23 August 2017).
- Pedersen, P.T.; Zhang, S. Collision analysis for MS Dextra. In Proceedings of the 1999 SAFER EURORO Spring Meeting, Nantes, France, 28 April 1999; pp. 1–33. [Google Scholar]
- Fowler, T.G.; Sørga, R.E. Modeling ship transportation risk. Risk Anal. 2000, 20, 225–244. [Google Scholar] [CrossRef]
- Karlsson, M.; Rasmussen, F.M.; Frisk, L. Verification of ship collision frequency model. In Ship Collision Analysis, Proceedings of 1998 International Symposium on Advances in Ship Collision Analysis, Copenhagen, Denmark, 10–13 May 1998; A.A. Balkema Publishers: Copenhagen, Denmark, 1998; pp. 117–121. [Google Scholar]
- Otto, S.; Pedersen, P.T.; Samuelides, M.; Sames, P.C. Elements of risk analysis for collision and grounding of a RoRo passenger ferry. Mar. Struct. 2002, 15, 461–474. [Google Scholar] [CrossRef]

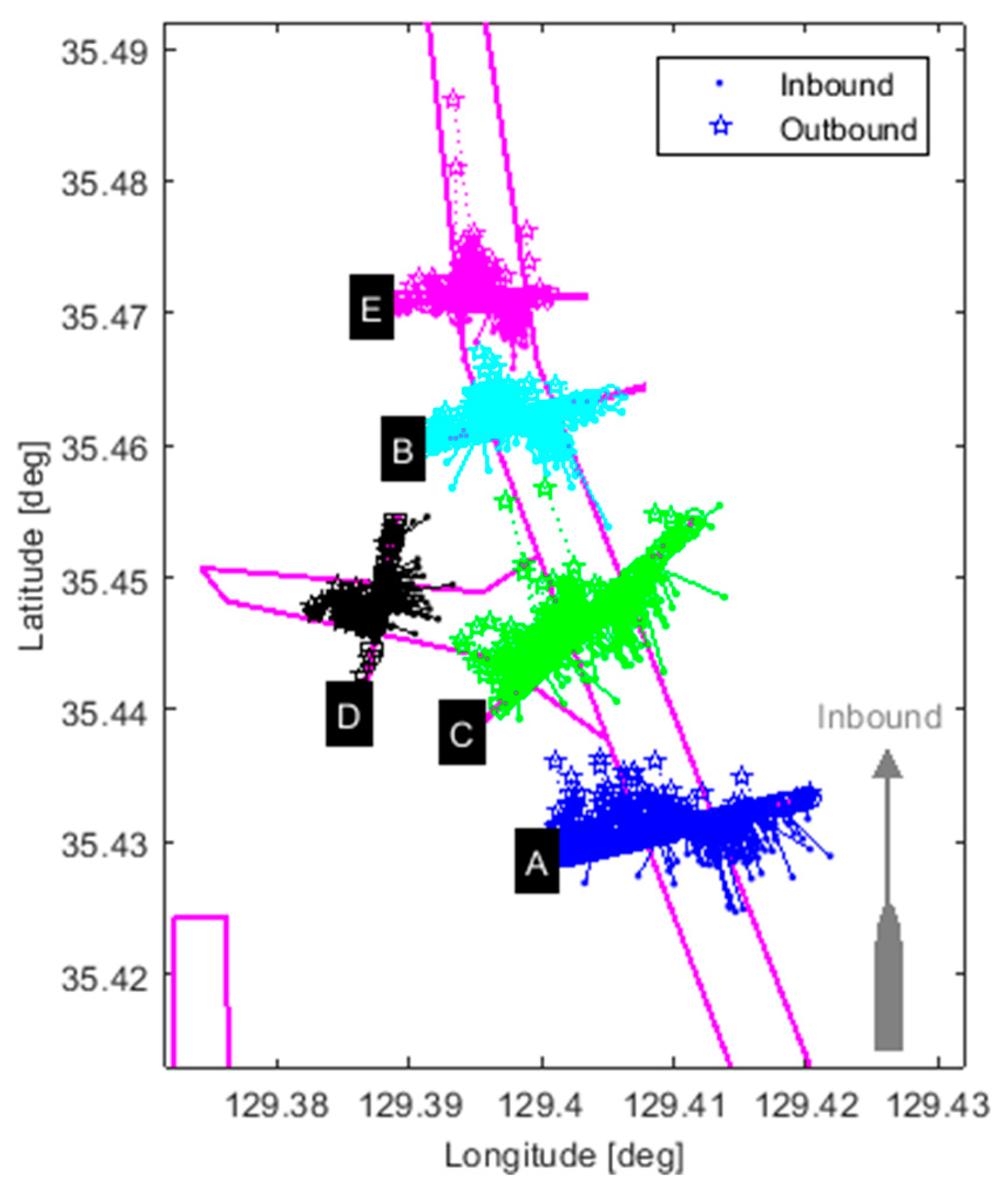
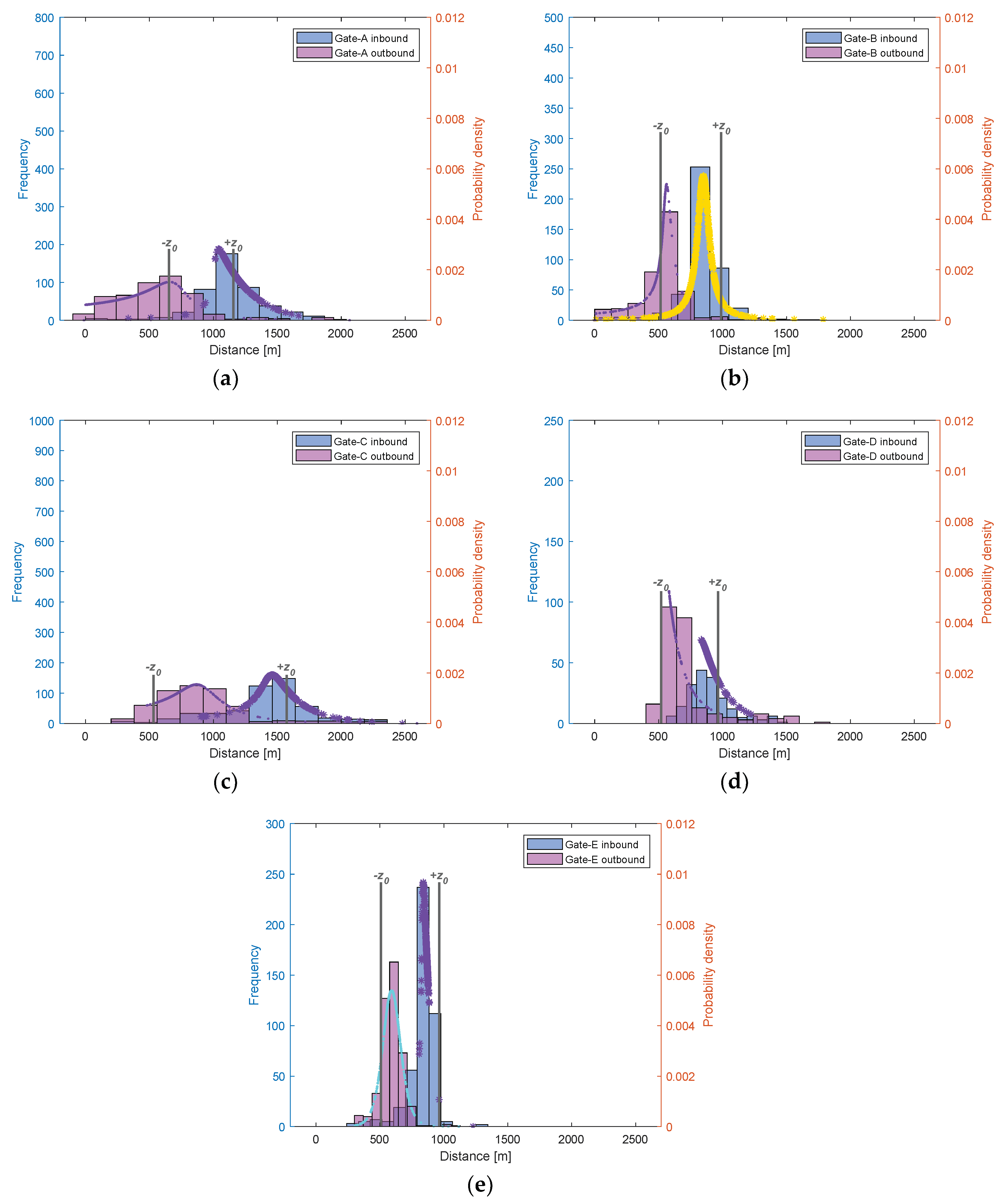
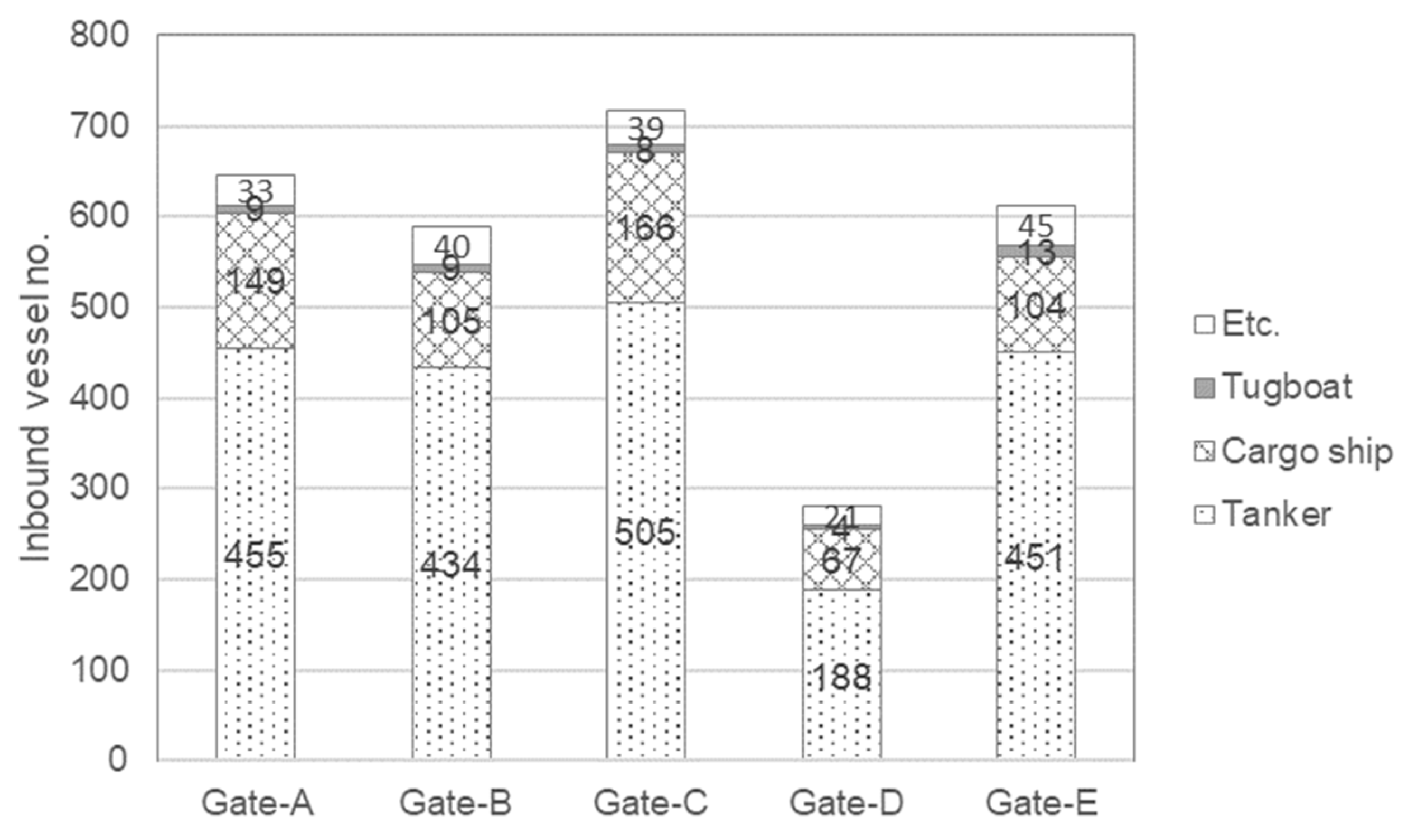
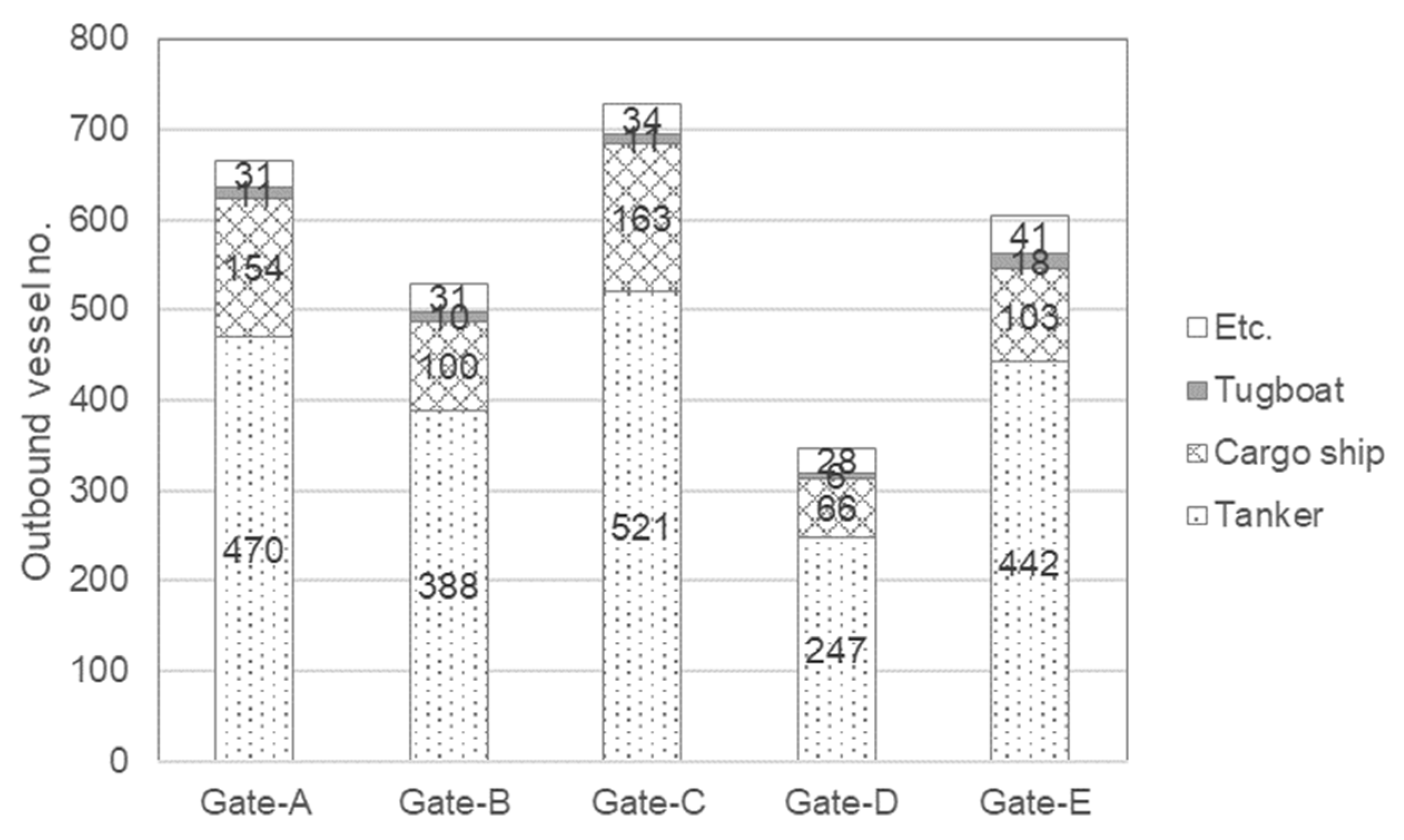
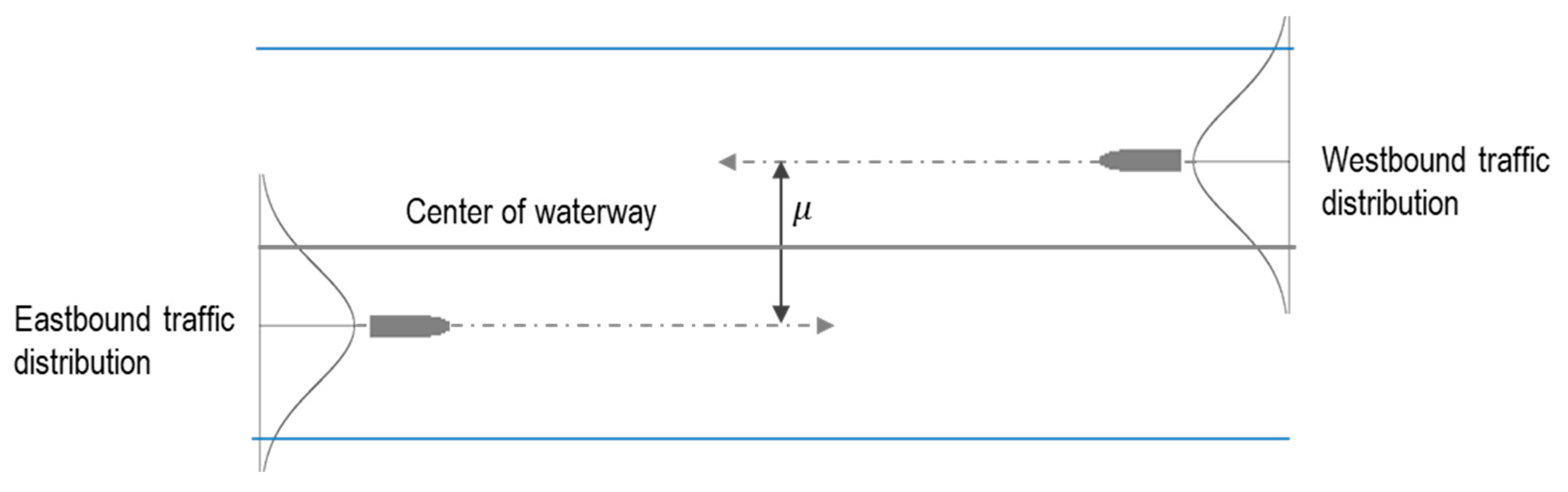
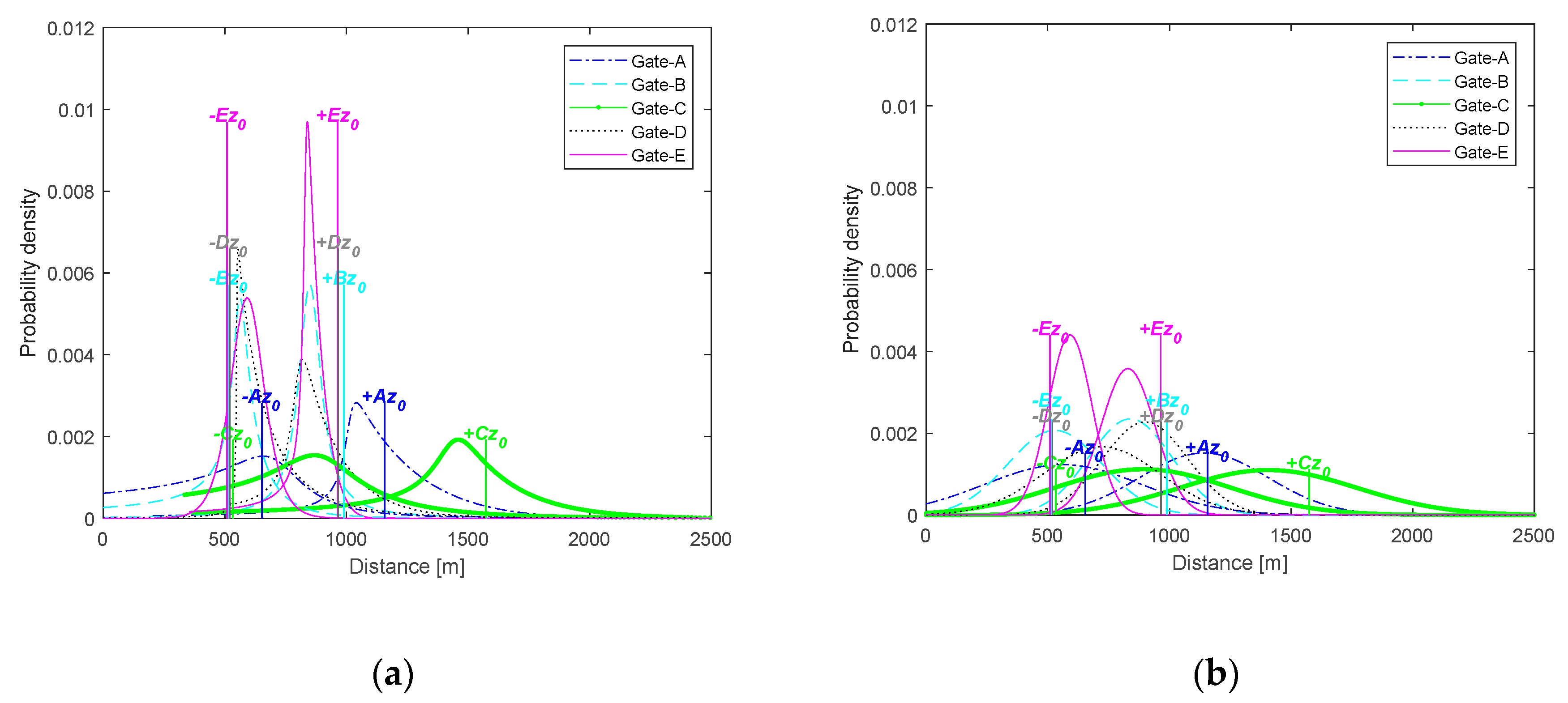
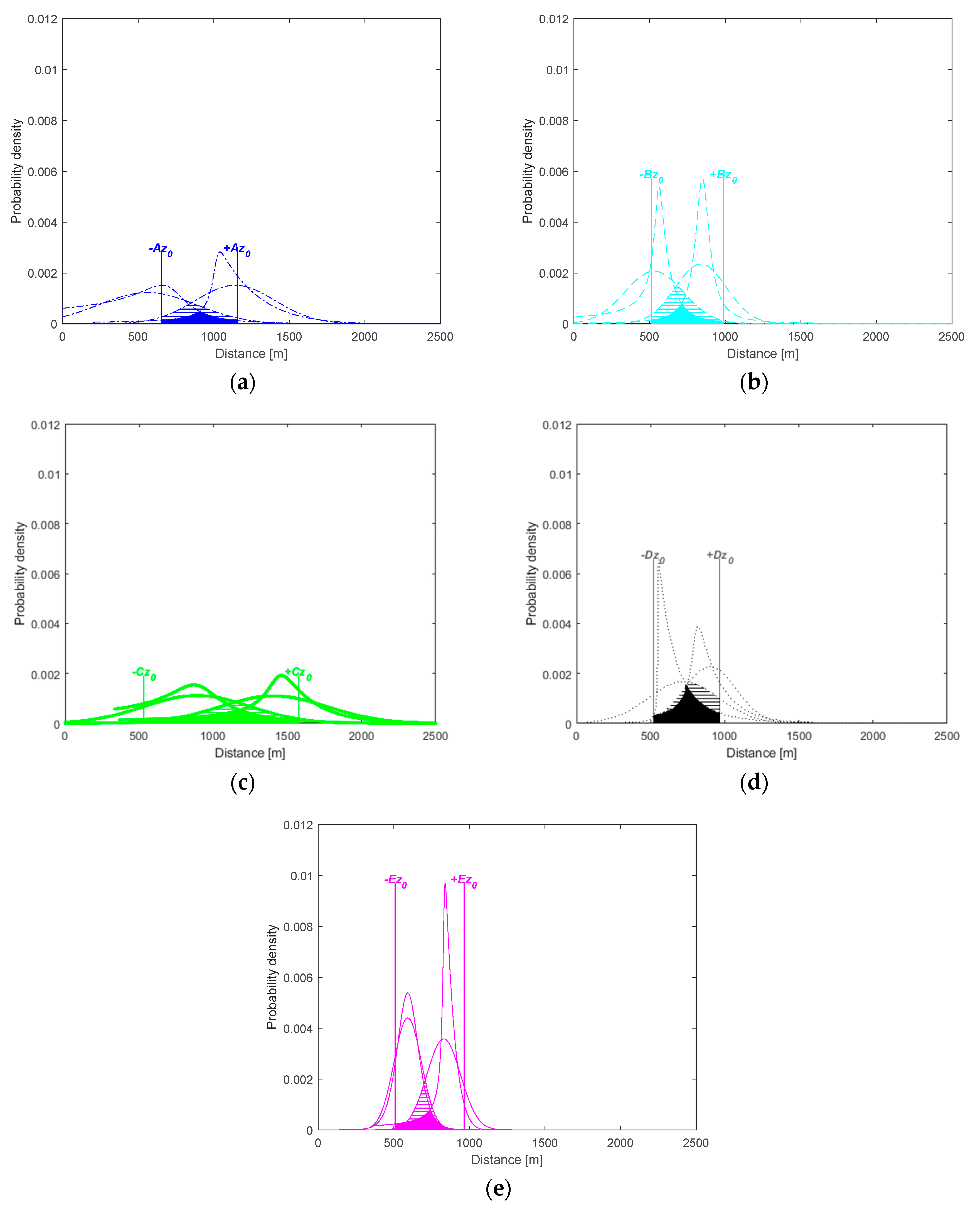
| Unit | Port | Ship Entry Status by Year | ||||
|---|---|---|---|---|---|---|
| 2014 | 2015 | 2016 | 2017 | 2018 | ||
| [No.] | Ulsan | 25,717 | 25,705 | 25,199 | 24,034 | 23,285 |
| Busan | 47,718 | 49,047 | 50,089 | 49,842 | 47,345 | |
| Incheon | 17,700 | 18,766 | 18,708 | 18,118 | 15,676 | |
| Pyeongtaek | 9304 | 9688 | 9968 | 9726 | 9424 | |
| Gwangyang | 23,375 | 24,117 | 26,136 | 25,658 | 24,111 | |
| [GT] | Ulsan | 213,875,396 | 216,051,513 | 219,158,717 | 222,436,611 | 220,646,198 |
| Busan | 557,173,490 | 627,934,559 | 666,044,444 | 669,137,031 | 676,842,443 | |
| Incheon | 175,349,658 | 189,093,493 | 193,280,773 | 196,075,235 | 190,259,801 | |
| Pyeongtaek | 143,900,622 | 144,004,241 | 144,220,879 | 143,198,116 | 144,023,889 | |
| Gwangyang | 332,634,575 | 351,594,407 | 361,755,946 | 339,055,110 | 336,020,127 | |
| Year | Total Annual No. Accidents (Collisions) | Total No. Accidents by Sea Area | ||
|---|---|---|---|---|
| Ulsan | Busan | Incheon | ||
| 2014 | 1330 (180) | 25 | 45 | 14 |
| 2015 | 2101 (235) | 58 | 66 | 22 |
| 2016 | 2307 (209) | 47 | 85 | 37 |
| 2017 | 2582 (258) | 52 | 52 | 22 |
| 2018 | 2671 (250) | 30 | 19 | 43 |
| Season | Date | Number of Ships |
|---|---|---|
| Spring | Apr. 22–24, 23–25 | 262 |
| Summer | Jul. 1–3 | 252 |
| Autumn | Oct. 23–25 | 289 |
| Winter | Feb. 20–22 | 260 |
| Direction | Ship Type | Gate-A | Gate-B | Gate-C | Gate-D | Gate-E |
|---|---|---|---|---|---|---|
| In-bound | Tanker | Wakeby | Cauchy | Wakeby | Wakeby | Wakeby |
| Cargo ship Tug etc. All ships | Wakeby Wakeby Wakeby | Wakeby Gumbel Min Cauchy | Wakeby Wakeby Wakeby | Wakeby Log-Logistic Wakeby | Gen. Logistic Wakeby Wakeby | |
| Out-bound | Tanker | Wakeby | Wakeby | Wakeby | Wakeby | Log-Logistic |
| Cargo ship Tug etc. All ships | Wakeby Gen. Gamma Wakeby | Dagum Wakeby Wakeby | Wakeby Wakeby Wakeby | Wakeby Cauchy Wakeby | Burr Cauchy Log-Logistic |
| Direction | Gate | Parameters | |
|---|---|---|---|
| In-bound | A | Wakeby Normal | = 15068, = 20.068, = 244.41, = −0.09851, = 204.26 = 262.99, = 1141.9 |
| B | Cauchuy Normal | = 55.722, = 849.55 = 169.81, = 839.21 | |
| C | Wakeby Normal | = 6805.6, = 7.2289, = 217.16, = −0.0098, = 364.34 = 363.02, = 1406.4 | |
| D | Wakeby Normal | = 1633, = 9.6576, = 174.17, = −0.04329, = 580.43 = 175.27, = 900.61 | |
| E | Wakeby Normal | = 6123, = 13.479, = 60.486, = −0.14439, = 353.8 = 111.5, = 829.55 | |
| Out-bound | A | Wakeby Normal | = 1538, = 2.6269, = 94.764, = 0.32259, = −1.1807 = 324.53, = 562.77 |
| B | Wakeby Normal | = 3854.2, = 7.1665, = 56.133, = 0.29464, = −22.028 = 192.8, = 529.5 | |
| C | Wakeby Normal | = 1550.4, = 3.7744, = 183.73, = 0.20747, = 334.01 = 356.48, = 890.58 | |
| D | Wakeby Normal | = 66,095, = 121.82, = 134.16, = 0.27034, = 0 = 239.47, = 721.57 | |
| E | Log-Logistic Normal | = 147.91, = 6863.7, = −6271.4 = 90.681, = 591.7 |
| DIR. | Variables | Simulation Value | ||||
|---|---|---|---|---|---|---|
| Gate-A | Gate-B | Gate-C | Gate-D | Gate-E | ||
| Line length [m] | 2500 | |||||
| Causation factor | 0.5 × 10−4 | |||||
| In-bound | Number of ships | 13480 | 13201 | 15360 | 5718 | 13718 |
| Ship length [m] | 101.68 | 94.30 | 104.43 | 111.25 | 93.74 | |
| Ship breadth [m] | 16.39 | 15.37 | 16.92 | 17.90 | 15.27 | |
| Ship speed [kts] | 10.26 | 9.90 | 9.77 | 8.97 | 9.41 | |
| Traffic distribution | Wakeby | Cauchy | Wakeby | Wakeby | Wakeby | |
| Out-bound | Number of ships | 14296 | 11802 | 15847 | 7513 | 13444 |
| Ship length [m] | 102.86 | 96.50 | 101.97 | 102.84 | 93.72 | |
| Ship breadth [m] | 16.66 | 15.70 | 16.47 | 16.53 | 15.21 | |
| Ship speed [kts] | 10.24 | 9.59 | 9.66 | 9.69 | 9.89 | |
| Traffic distribution | Wakeby | Wakeby | Wakeby | Wakeby | Log-Logistic | |
| Gate | Best-Fit PDF | Normal PDF | Difference (Normal–Best-Fit) |
|---|---|---|---|
| Gate-A | 0.13003160 | 0.25656075 | 0.12652915 |
| Gate-B | 0.14628881 | 0.35555483 | 0.20926602 |
| Gate-C | 0.28527105 | 0.43753759 | 0.15226654 |
| Gate-D | 0.32598540 | 0.47764972 | 0.15166432 |
| Gate-E | 0.13524928 | 0.23568791 | 0.10043863 |
| Gate | Best-Fit PDF [×10−4] | Normal PDF [×10−4] | Ratio (Normal/Best-Fit) |
|---|---|---|---|
| Gate-A | 0.29000875 | 0.57225031 | 1.97306464 |
| Gate-B | 0.28982374 | 0.70427709 | 2.43049916 |
| Gate-C | 0.70605710 | 1.08257684 | 1.53376093 |
| Gate-D | 0.34748959 | 0.49912077 | 1.46524883 |
| Gate-E | 0.29152857 | 0.50794805 | 1.74261853 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, Y.; Kim, T.-G. An Improved Ship Collision Risk Evaluation Method for Korea Maritime Safety Audit Considering Traffic Flow Characteristics. J. Mar. Sci. Eng. 2019, 7, 448. https://doi.org/10.3390/jmse7120448
Yoo Y, Kim T-G. An Improved Ship Collision Risk Evaluation Method for Korea Maritime Safety Audit Considering Traffic Flow Characteristics. Journal of Marine Science and Engineering. 2019; 7(12):448. https://doi.org/10.3390/jmse7120448
Chicago/Turabian StyleYoo, Yunja, and Tae-Goun Kim. 2019. "An Improved Ship Collision Risk Evaluation Method for Korea Maritime Safety Audit Considering Traffic Flow Characteristics" Journal of Marine Science and Engineering 7, no. 12: 448. https://doi.org/10.3390/jmse7120448
APA StyleYoo, Y., & Kim, T.-G. (2019). An Improved Ship Collision Risk Evaluation Method for Korea Maritime Safety Audit Considering Traffic Flow Characteristics. Journal of Marine Science and Engineering, 7(12), 448. https://doi.org/10.3390/jmse7120448





