Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties
Abstract
:1. Introduction
2. Underwater Vehicle Model
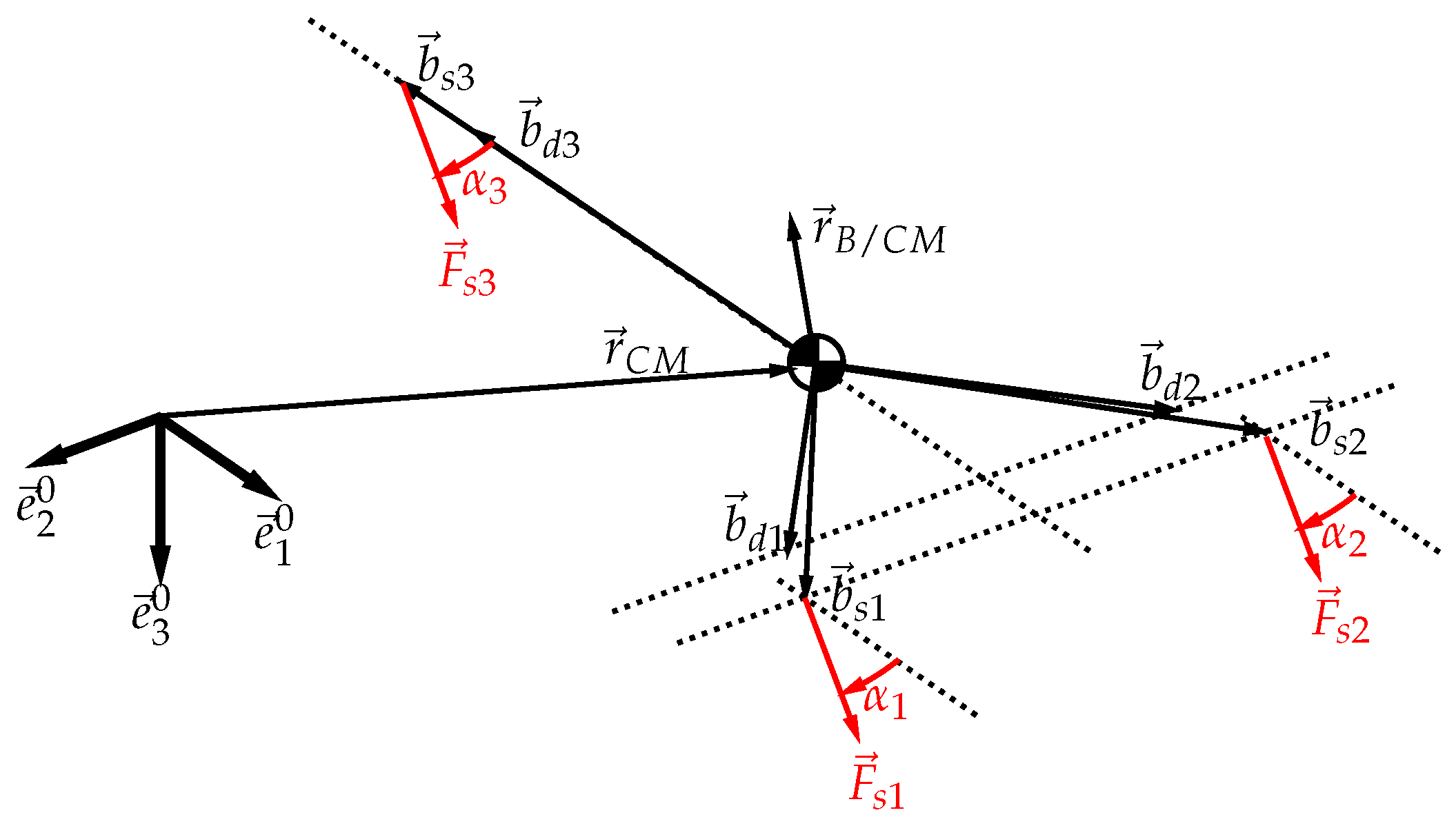
2.1. Model Design
- : world frame attached to earth surface
- : body-fixed frame attached to the AUV
2.2. Lagrange Method
2.3. Water Currents
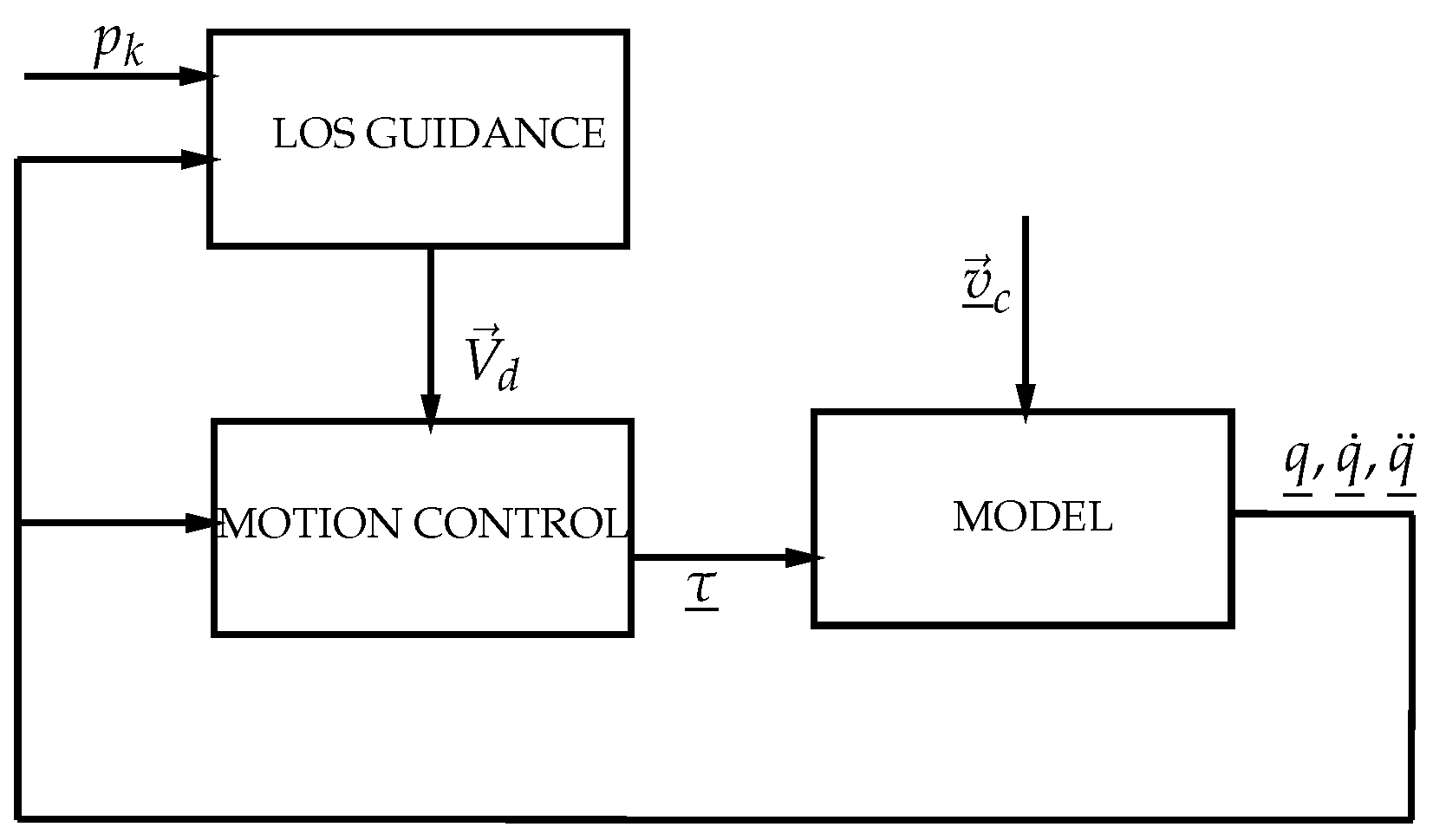
3. Design of The Controller
3.1. General Control Problem Formulation
3.2. Auxiliary Control and Disturbance Cancellation
3.3. Closed-Loop Stability
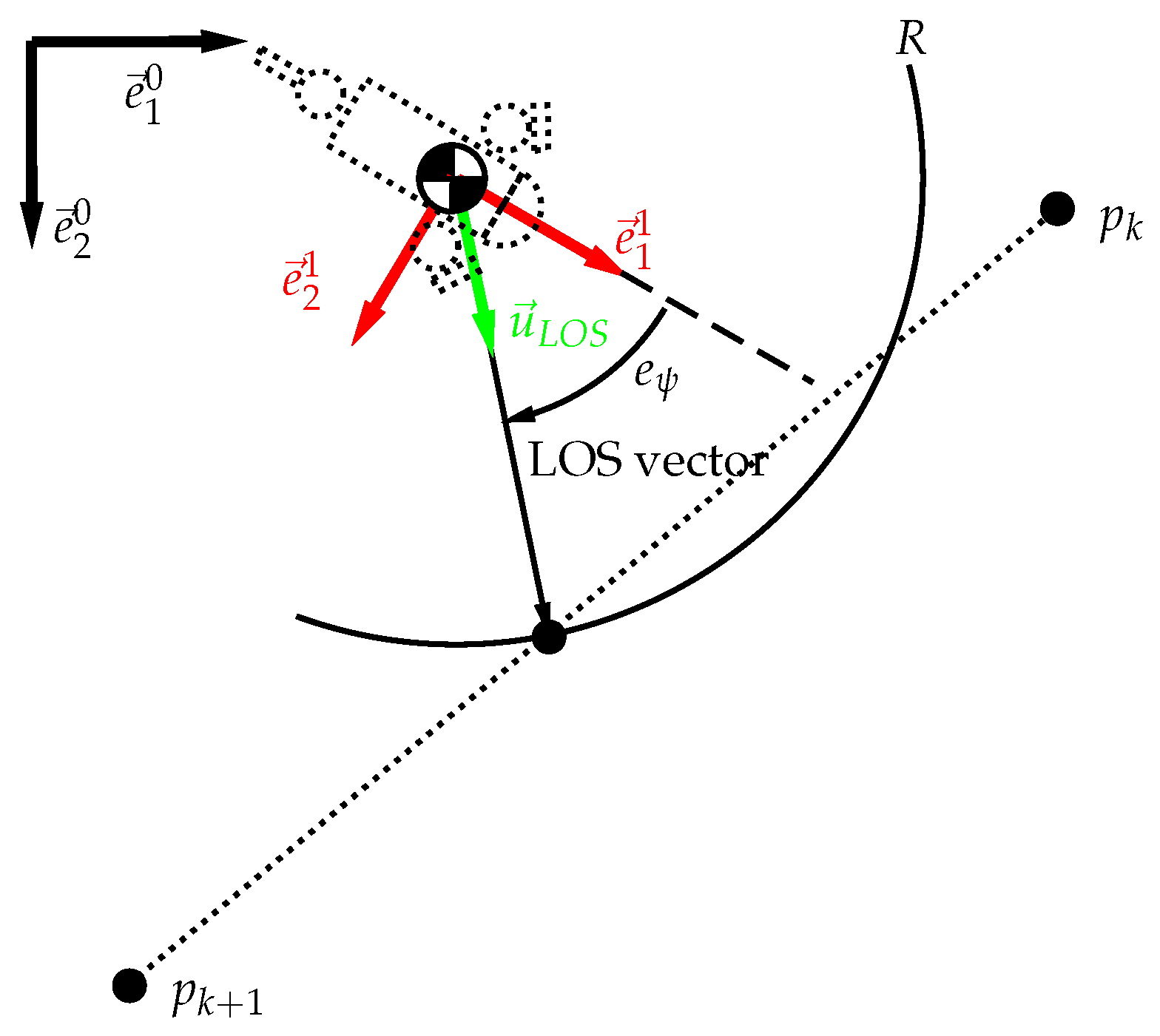
4. Path-Following
- which means no real solution for : there is no intersection between the sphere and the path. The LOS vector shall be defined as the vector from to the AUV position to .
- are both superior to 0: the LOS is ahead . The LOS vector shall also be defined as the vector from to the AUV position to .
- and : is the solution to compute the LOS vector.
- and : is the solution to compute the LOS vector (corresponds to the closest intersection point to ).
5. Numerical Simulations and Results
5.1. Numerical Parameters
5.2. Results
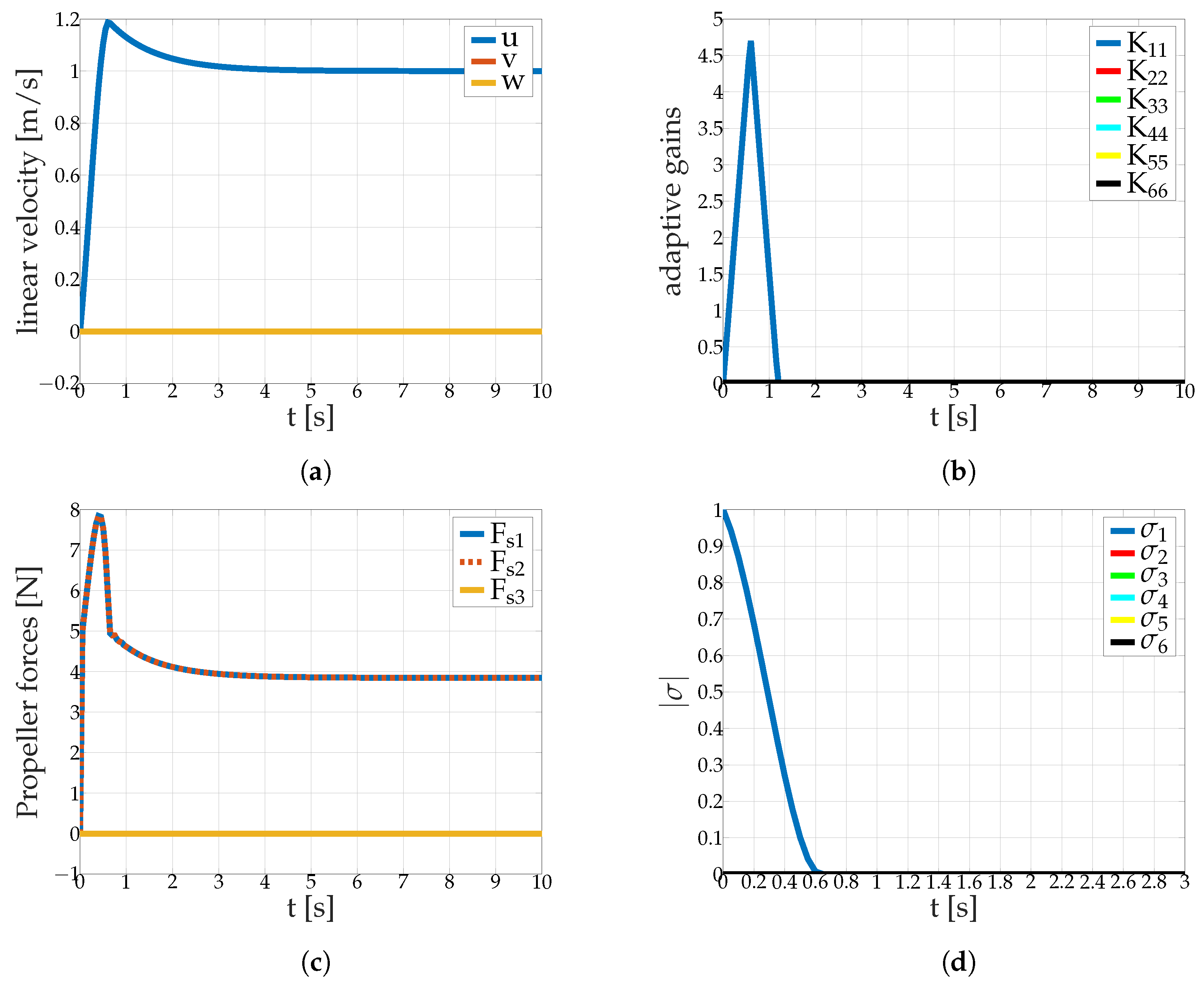
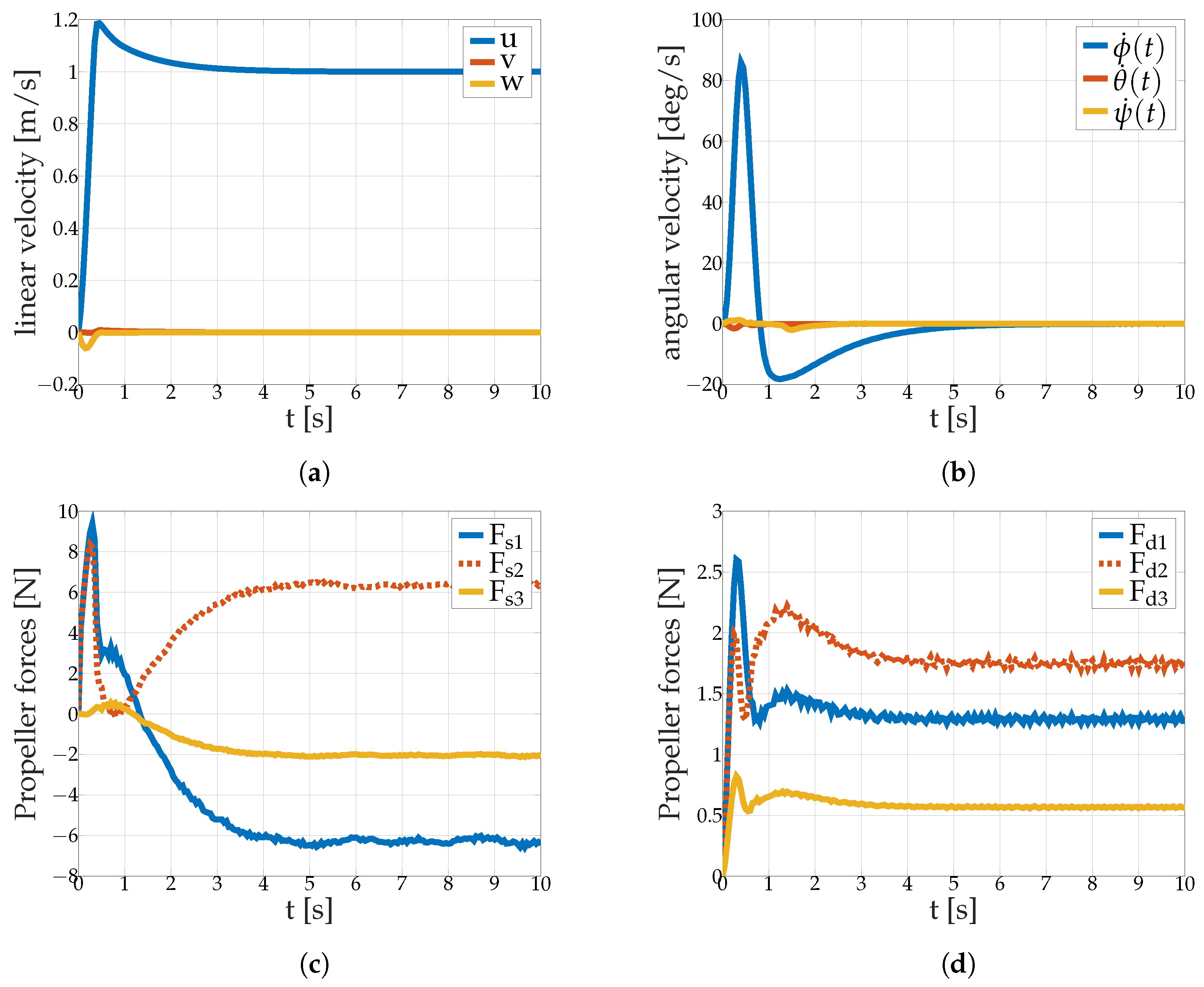
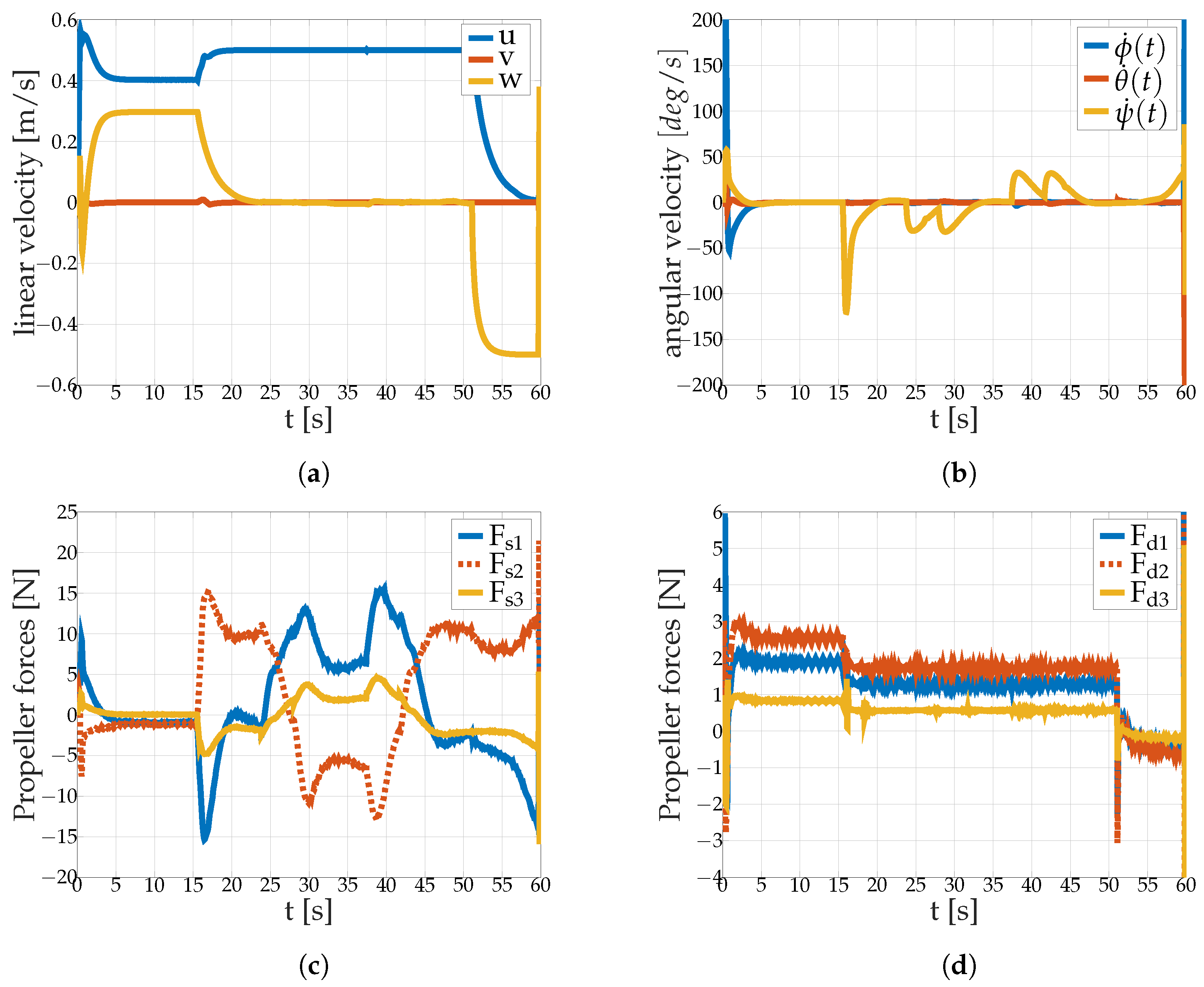
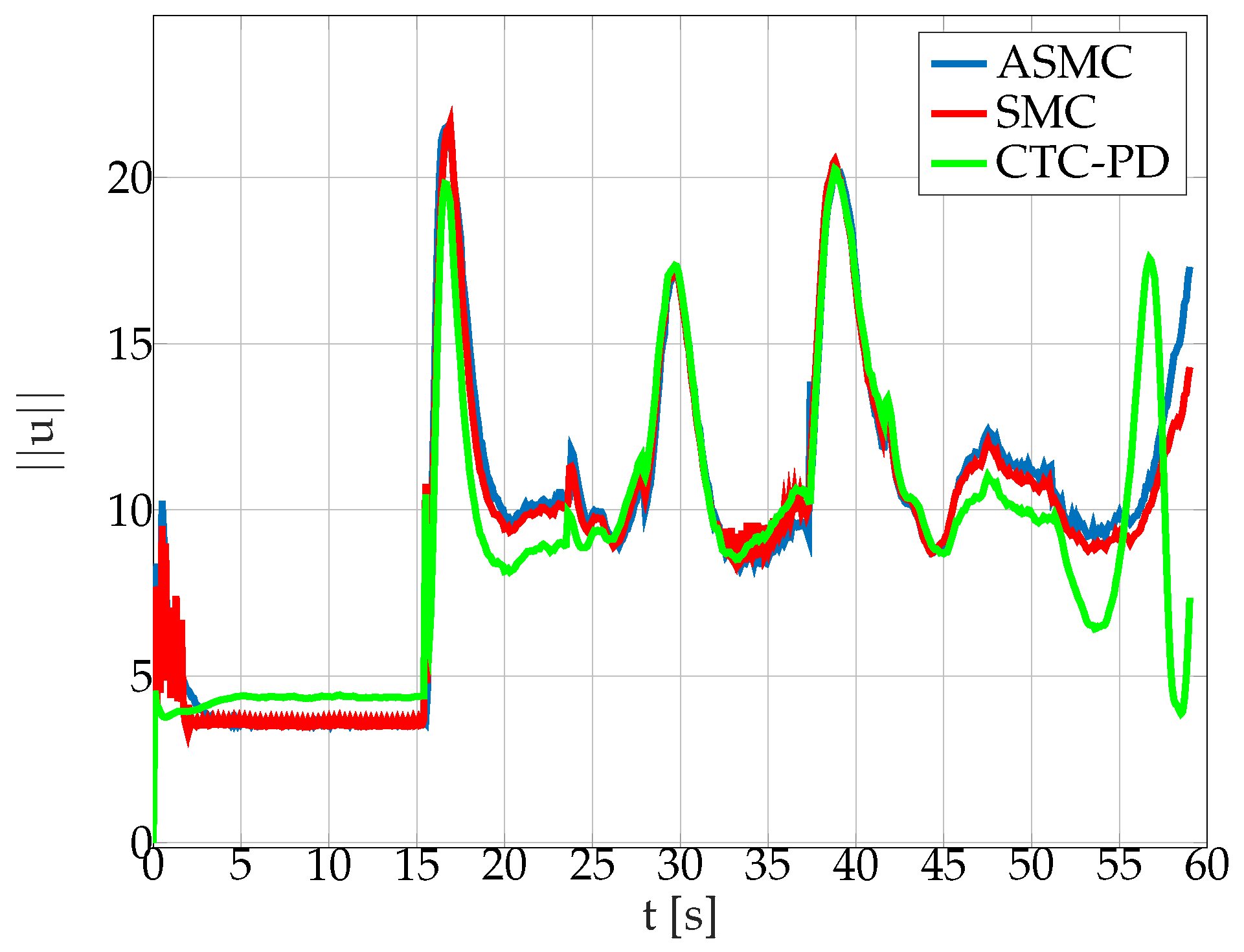
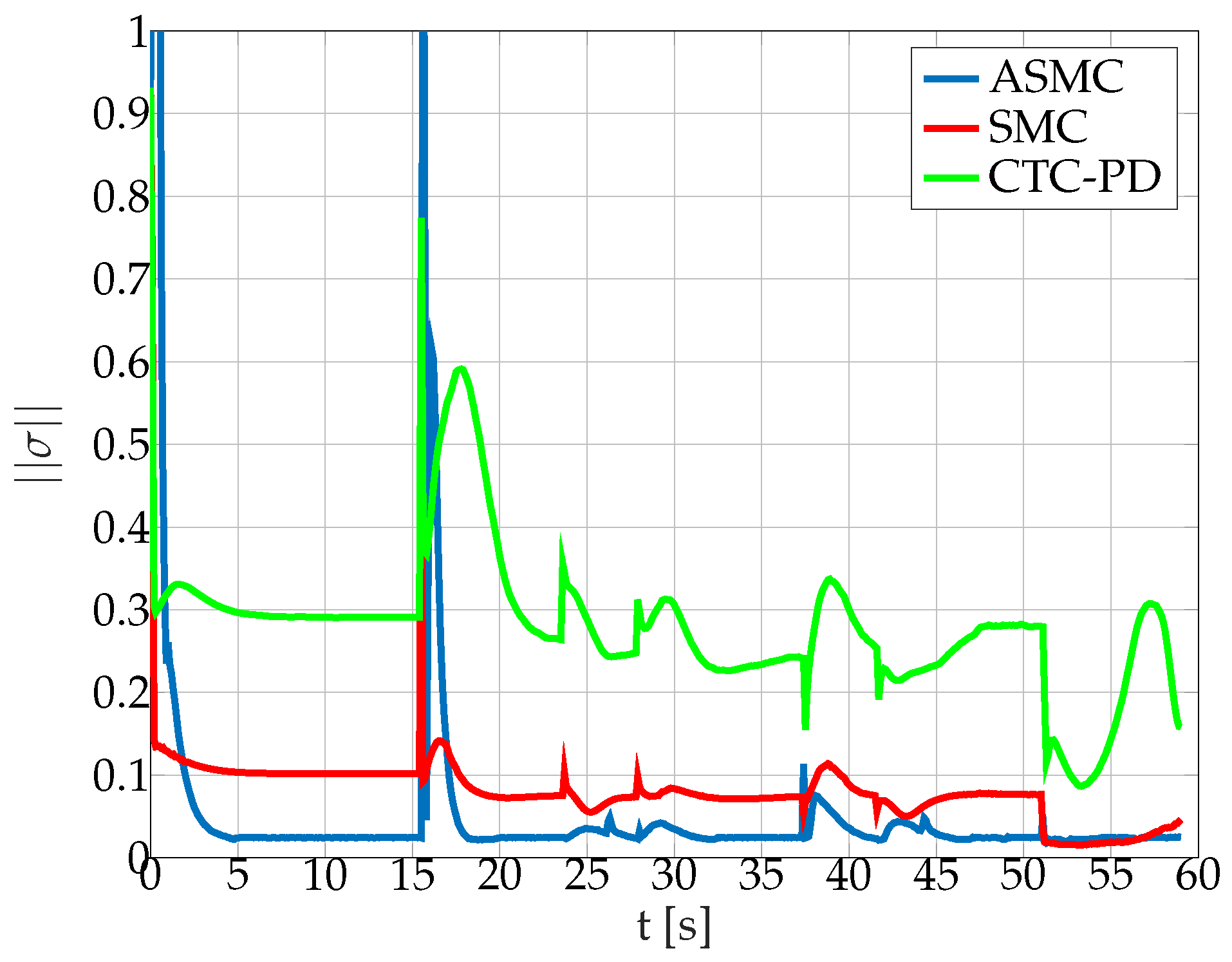
- Step response to a velocity command with and without internal and external perturbations
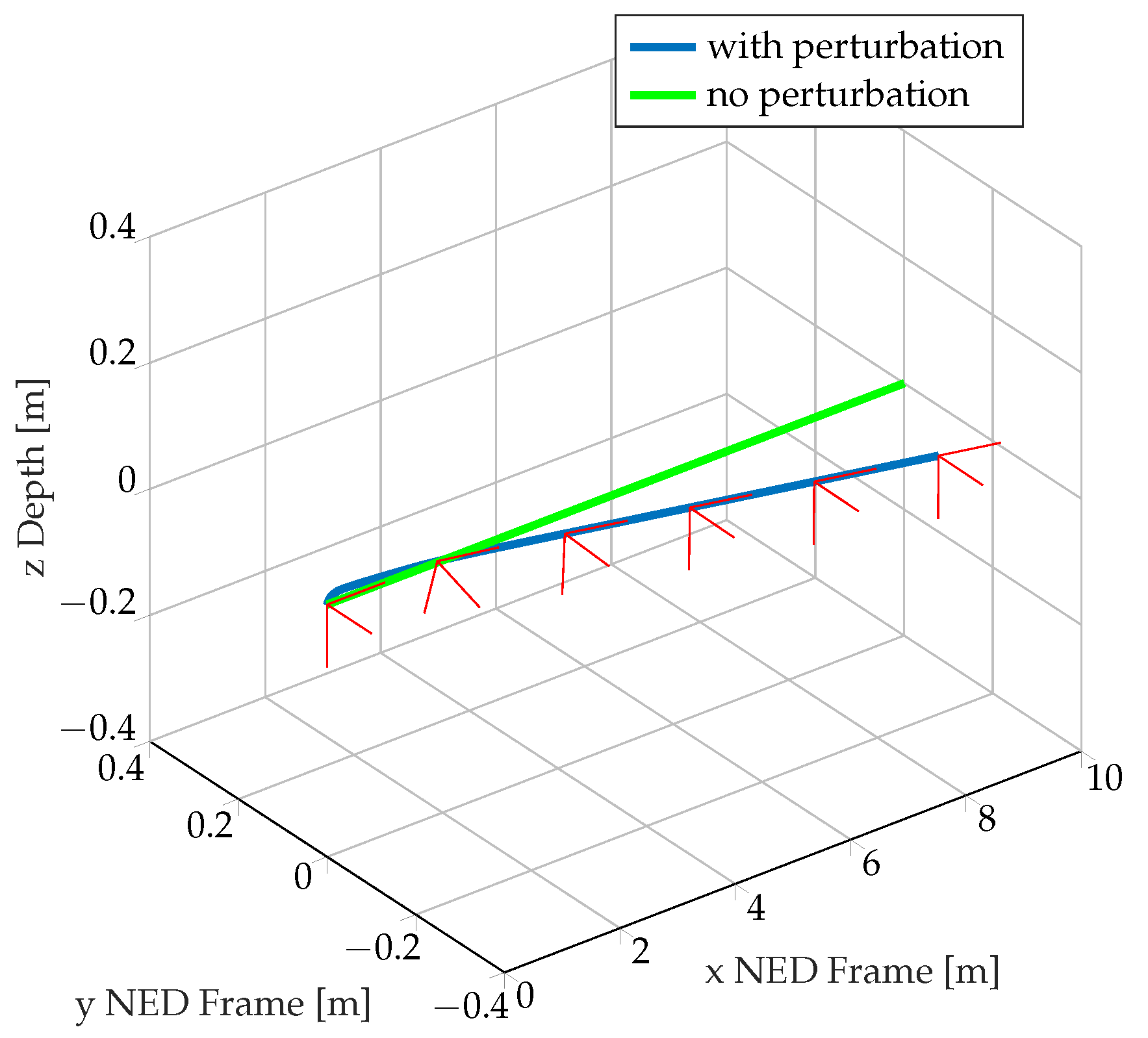
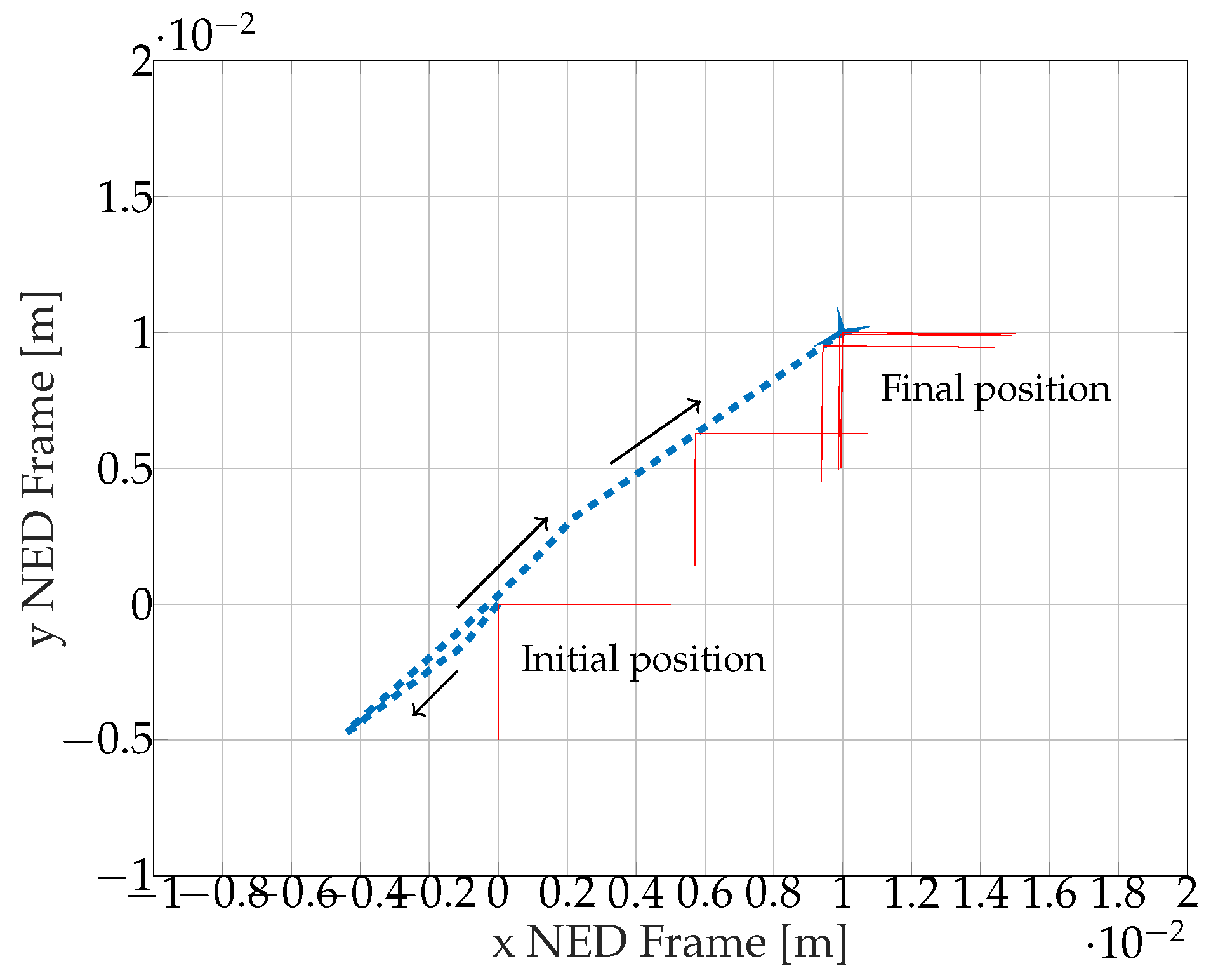
- The AUV remains in steady state under perturbations
- The AUV follows a defined path under perturbations
5.2.1. Surge Velocity Control Avoiding Sideslip
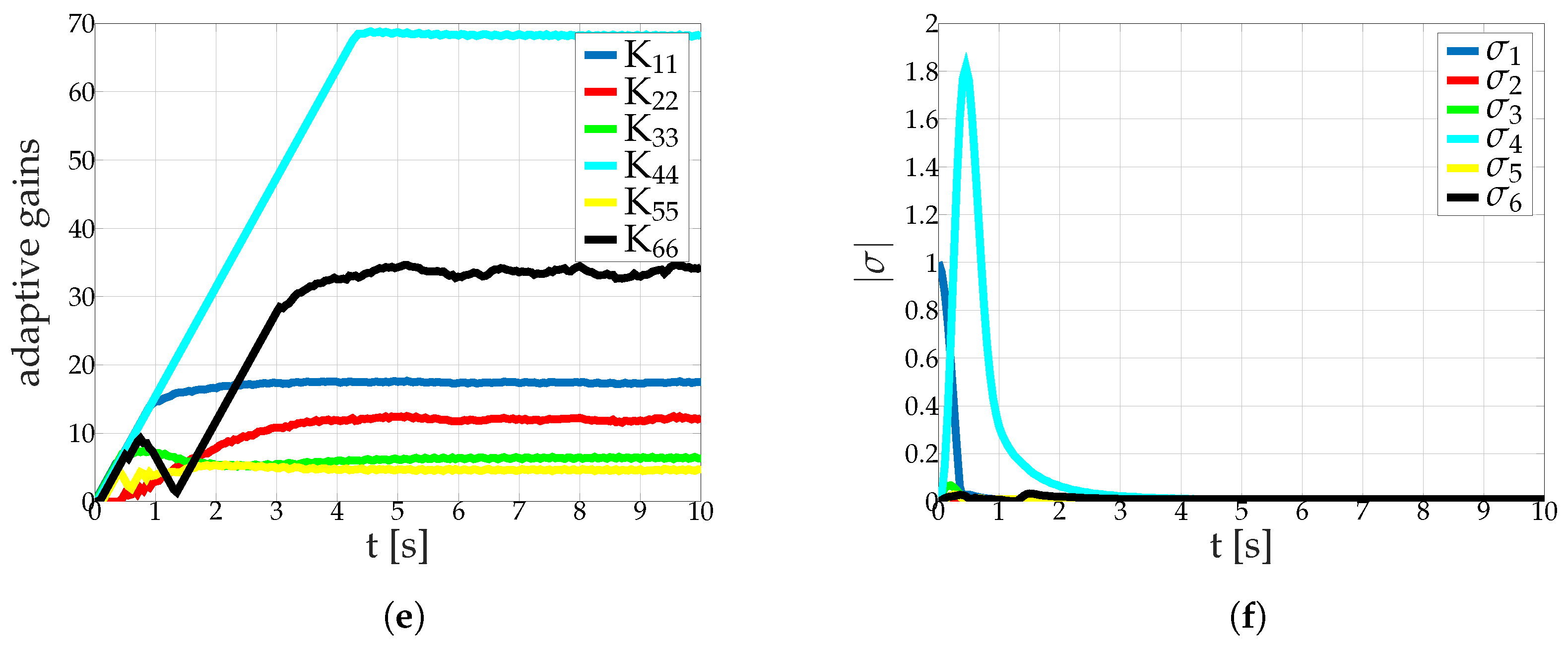
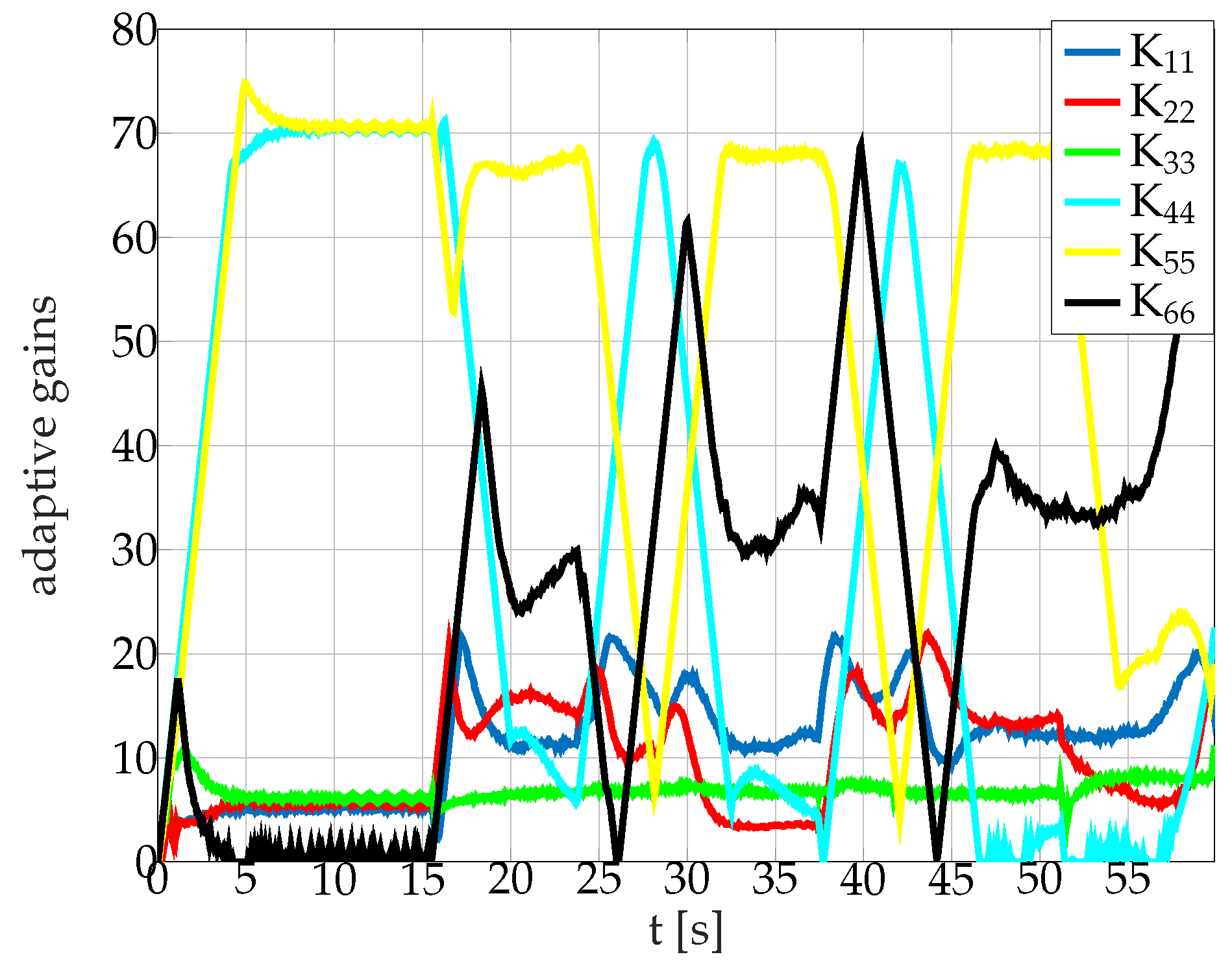
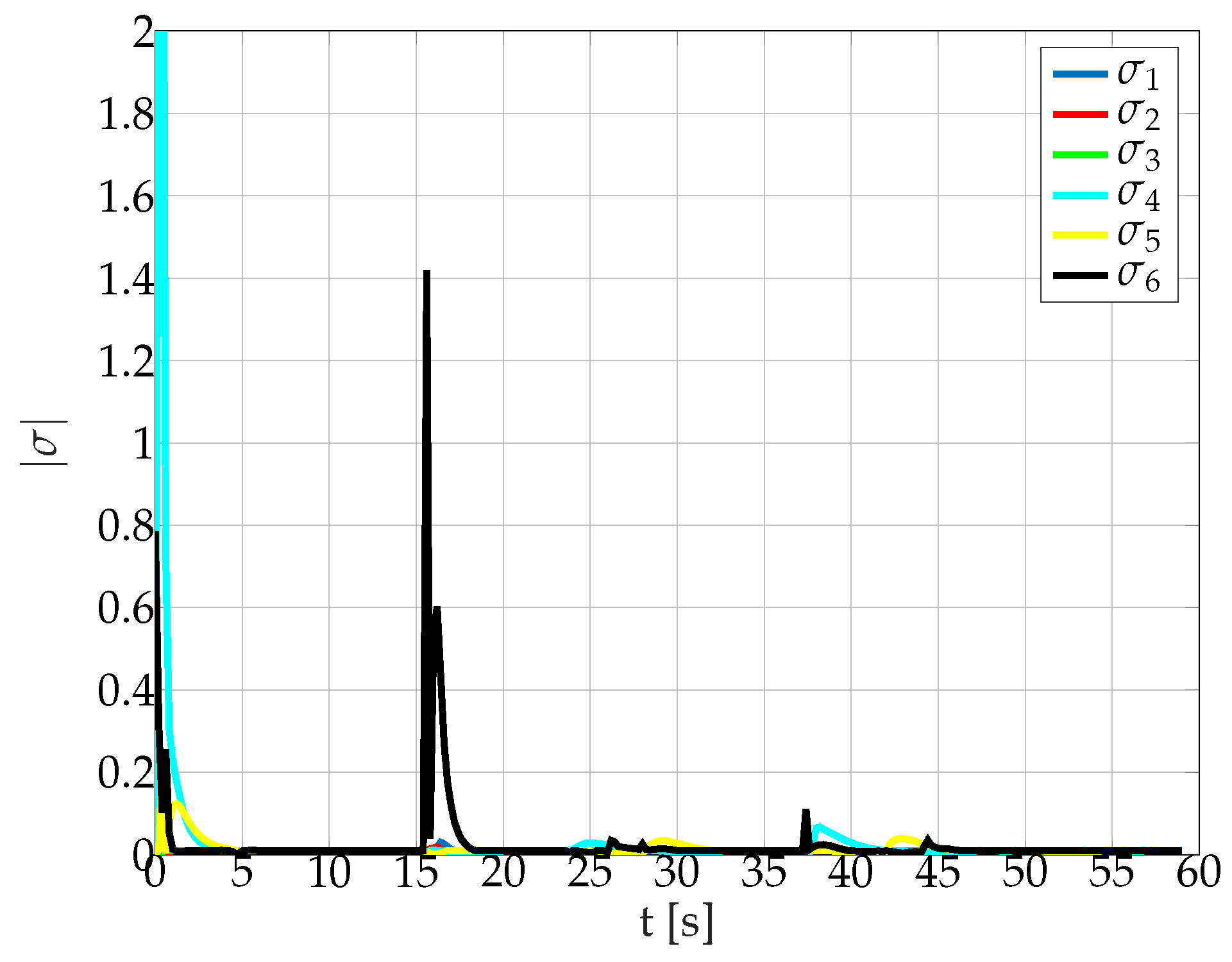
5.2.2. Steady State stabilization
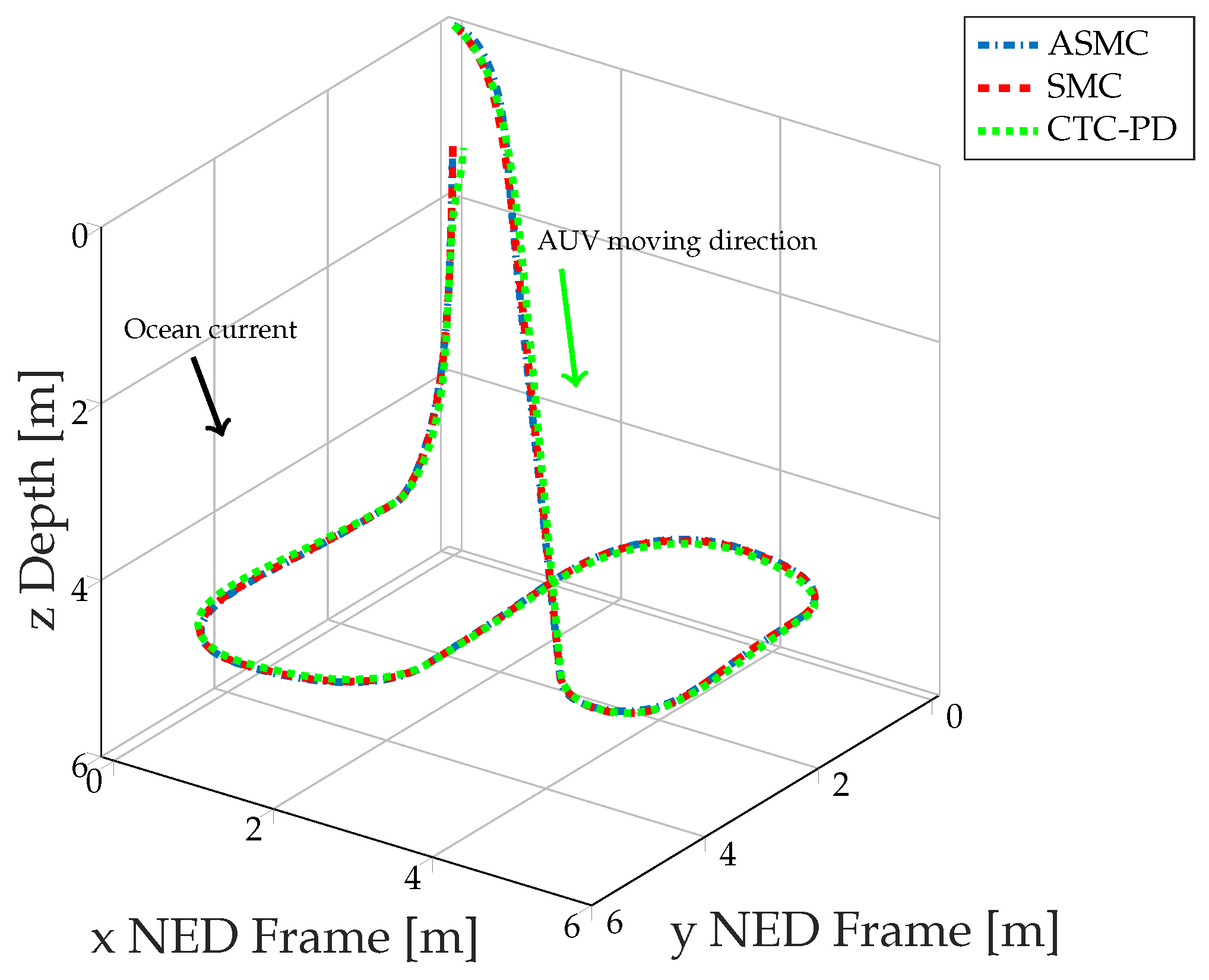
5.2.3. Path-Following Task
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zereik, E.; Bibuli, M.; Mišković, N.; Ridao, P.; Pascoal, A. Challenges and future trends in marine robotics. Annu. Rev. Control 2018, 46, 350–368. [Google Scholar] [CrossRef]
- Roberts, G.N.; Sutton, R. Advances in Unmanned Marine Vehicles; Book IEEE Control Series; IEEE: Piscataway, NJ, USA, 2006; pp. 13–42. [Google Scholar]
- García-Valdovinos, L.G.; Salgado-Jiménez, T.; Bandala-Sánchez, M.; Nava-Balanzar, L.; Hernández-Alvarado, R.; Cruz-Ledesma, J.A. Modelling, Design and Robust Control of a Remotely Operated Underwater Vehicle. Int. J. Adv. Robot. Syst. 2014, 11, 1. [Google Scholar] [CrossRef] [Green Version]
- De Souza, E.C.; Maruyama, N. Intelligent UUVs: Some Issues on ROV Dynamic Positioning. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 214–226. [Google Scholar] [CrossRef]
- Christ, R.D.; Wernli, R.L., Sr. The ROV Manual: A User Guide for Remotely Operated Vehicles, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 14–31. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics And Motion Control, 1st ed.; Wiley: Hoboken, NJ, USA, 2011; Volume 167–186, pp. 241–284. [Google Scholar]
- Fossen, T.I. Marine Control Systems. Guidance, Navigation and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernectics AS: Trondheim, Norway, 2002; pp. 88–103. [Google Scholar]
- Antonelli, G.; Chiaverini, S.; Sarkar, N.; West, M. Adaptive Control of an Autonomous Underwater Vehicle: Experimental Results on ODIN. IEEE Trans. Control Syst. Technol. 2001, 9, 756–765. [Google Scholar] [CrossRef]
- Chen, C.W.; Kouh, J.S.; Tsai, J.F. Modeling and Simulation of an AUV Simulator with Guidance System. IEEE J. Ocean. Eng. 2013, 38, 211–225. [Google Scholar] [CrossRef]
- Ribas, D.; Palomeras, N.; Ridao, P.; Carreras, M.; Mallios, A. Girona 500 AUV: From Survey to Intervention. IEEE/ASME Trans. Mechatron. 2012, 17, 46–53. [Google Scholar] [CrossRef]
- Carreras, M.; Hernández, J.D.; Vidal, E.; Palomeras, N.; Ribas, D.; Ridao, P. Sparus II AUV—A Hovering Vehicle for Seabed Inspection. IEEE J. Ocean. Eng. 2018, 43, 344–355. [Google Scholar] [CrossRef]
- Jalving, B. The NDRE-AUV Flight Control System. IEEE J. Ocean. Eng. 1994, 19, 497–501. [Google Scholar] [CrossRef]
- Naeem, W.; Sutton, R.; Ahmad, S.M. LQG/LTR Control of an Autonomous Underwater Vehicle Using a Hybrid Guidance Law. Int. Fed. Autom. Control J. 2003, 36, 31–36. [Google Scholar] [CrossRef]
- Fjellstad, O.-E.; Fossen, T.I. Position and Attitude Tracking of AUVs: A Quaternion Feedback Approach. IEEE J. Ocean. Eng. 1994, 19, 512–518. [Google Scholar] [CrossRef]
- Cui, R.; Chen, L.; Yang, C.; Chen, M. Extended State Observer-Based Integral Sliding Mode Control for an Underwater Robot With Unknown Disturbances and Uncertain Nonlinearities. IEEE Trans. Ind. Electron. 2017, 64, 6785–6795. [Google Scholar] [CrossRef] [Green Version]
- Chin, C.S.; Lin, W.P. Robust Genetic Algorithm and Fuzzy Inference Mechanism Embedded in a Sliding-Mode Controller for an Uncertain Underwater Robot. IEEE/ASME Trans. Mechatron. 2018, 23, 655–666. [Google Scholar] [CrossRef]
- Fossen, T.I.; Sagatun, S. Adaptive control of nonlinear systems: A Case Study of Underwater Robotics Systems. J. Robot. Syst. 1991, 8, 393–412. [Google Scholar] [CrossRef]
- Refsnes, J.E.; Sørensen, A.J.; Pettersen, K.Y. Model-Based Output Feedback Control of Slender-Body Underactuated AUVs: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2008, 15, 930–946. [Google Scholar] [CrossRef]
- Antonelli, G. On the Use of Adaptive/Integral Actions for Six-Degrees-of-Freedom Control of Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2007, 32, 300–312. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Previdi, F.; Dester, A.; Bittanti, S.; Ruggeri, A. Modeling, Identification, and Analysis of Limit-Cycling Pitch and Heave Dynamics in an ROV. IEEE J. Ocean. Eng. 2004, 29, 407–417. [Google Scholar] [CrossRef]
- Soylu, S.; Proctor, A.A.; Podhorodeski, R.P.; Bradley, C.; Buckham, B.J. Precise Trajectory Control for an Inspection Class ROV. Ocean Eng. 2016, 111, 508–523. [Google Scholar] [CrossRef]
- Lapierre, L.; Jouvencel, B. Robust Nonlinear Path-Following Control of an AUV. IEEE J. Ocean. Eng. 2008, 33, 89–102. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, X.; Cui, D. Adaptive Sliding Mode Attitude Control for Autonomous Underwater Vehicles with Input Nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Guerrero, J.; Torres, J.; Creuze, V.; Chemori, A. Trajectory Tracking for Autonomous Underwater Vehicle: An adaptive Approach. Ocean Eng. 2019, 172, 511–522. [Google Scholar] [CrossRef] [Green Version]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014. [Google Scholar]


| Variable | Description | Value | Unit |
|---|---|---|---|
| AUV mass | [kg] | ||
| x-axis added mass | [kg] | ||
| y-axis added mass | [kg] | ||
| z-axis added mass | [kg] | ||
| roll inertia | [kg·m] | ||
| pitch inertia | [kg·m] | ||
| yaw inertia | [kg·m] | ||
| added roll inertia | [kg·m] | ||
| added pitch inertia | [kg·m] | ||
| added yaw inertia | [kg·m] | ||
| Buoyancy | [0 0 0] | [m] | |
| propeller position | [0.06 0.126 0] | [m] | |
| propeller position | [0.06 −0.126 0] | [m] | |
| propeller position | [−0.28 0 0] | [m] | |
| propeller position | [0.03 0.1 0] | [m] | |
| propeller position | [0.03 −0.1 0] | [m] | |
| propeller position | [−0.19 0 0] | [m] | |
| propeller orientation | −40/180· | [rad] | |
| propeller orientation | 40/180· | [rad] | |
| propeller orientation | [rad] | ||
| water density | 1000 | [kg·m | |
| g | gravity | [m·s | |
| V | dry volume | [m | |
| quadratic damping | 5.85 | [N·m·s] | |
| quadratic damping | 0.048 | [N·m·s] | |
| quadratic damping | 11.98 | [N·m·s] | |
| quadratic damping | 0 | [N·m·s] | |
| quadratic damping | 21.85 | [N·m·s] | |
| quadratic damping | 0.044 | [N·m·s] | |
| quadratic damping | 5.85 | [N·m·s] | |
| quadratic damping | 0 | [N·m·s] | |
| quadratic damping | 11.98 | [N·m·s] | |
| quadratic damping | 0 | [N·m·s] | |
| quadratic damping | 21.85 | [N·m·s] | |
| quadratic damping | 0 | [N·m·s] | |
| R | LOS radius | 1 | [m] |
| current parameter | 1 | ||
| average | 1 | ||
| standard deviation | 0.5 | ||
| current velocity vector | [m·s |
| Variable | Value |
|---|---|
| 1 | |
| 16 | |
| 1 | |
| ASMC | SMC | CTC-PD | |
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, J.; Castañeda, H.; Gordillo, J.L. Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties. J. Mar. Sci. Eng. 2019, 7, 445. https://doi.org/10.3390/jmse7120445
Rodriguez J, Castañeda H, Gordillo JL. Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties. Journal of Marine Science and Engineering. 2019; 7(12):445. https://doi.org/10.3390/jmse7120445
Chicago/Turabian StyleRodriguez, Jonathan, Herman Castañeda, and J. L. Gordillo. 2019. "Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties" Journal of Marine Science and Engineering 7, no. 12: 445. https://doi.org/10.3390/jmse7120445
APA StyleRodriguez, J., Castañeda, H., & Gordillo, J. L. (2019). Design of an Adaptive Sliding Mode Control for a Micro-AUV Subject to Water Currents and Parametric Uncertainties. Journal of Marine Science and Engineering, 7(12), 445. https://doi.org/10.3390/jmse7120445





