A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting
Abstract
:1. Introduction
2. Methods
2.1. Selection of Study Sites
- Availability of high-quality wave data for wave model validation and wind data for evaluation of the quality of the modeled wind products;
- high wave energy resource and proximity to shore; and
- representativeness of regional distribution.
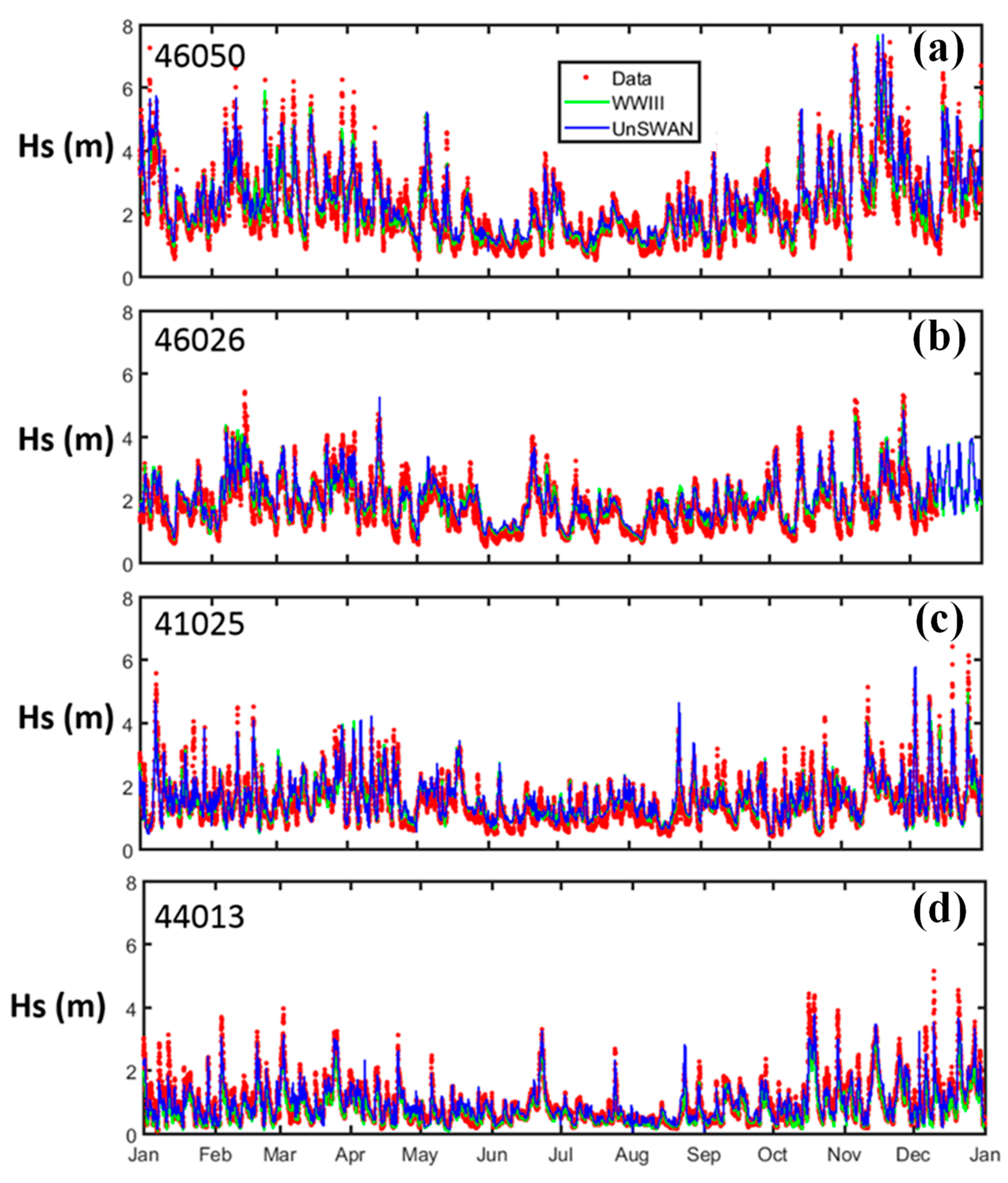
- NDBC 46050, Stonewall Bank, Oregon, USA. This site was selected because of its high wave resource potential and high-quality wave and wind data, as well as its intermediate water depth and proximity to shore (20 nautical miles from Newport, OR, USA). It is also adjacent to the North Energy Test Site, managed by the Pacific Marine Energy Center, and has been studied extensively [6,13,14,15,16].
- NBDC 46026, San Francisco, California, USA. This site was selected to represent the wind and wave characteristics of the California coast. NDBC 46026 is located 18 nautical miles from San Francisco and has long-term wind and wave records dating back to 1982. Unlike the narrow continental shelf off the Oregon and northern California coasts, the continental shelf off San Francisco Bay is relatively broad and NDBC 46026 is at a shallow-water depth of 53 m. This study site will provide insight into the effect of wind forcing on shallow-water wave modeling on the West Coast.
- NDBC 44013, Boston, Massachusetts, USA. Although wave resources on the East Coast are smaller than those on the West Coast, the New England region still has a significant amount of wave energy, according to the Electric Power Research Institute, Inc. (Palo Alto, CA, USA) [17]. Based on a recent analysis by the National Renewable Energy Laboratory (NREL) [18], the Massachusetts coast is among the highest-ranked sites in terms of wave resources and market potential. Therefore, the Boston Harbor and coast were selected for their relatively high wave resource as being representative of the New England region. NDBC 44013 is located 16 nautical miles offshore at a water depth of 64.5 m. It also has good quality, long-term observed wave and wind data dating back to 1984.
- NDBC 41025, Diamond Shoals, NC, USA. North Carolina’s coast is the only region identified as a high-resource and -market potential site south of the New England coast in NREL’s study [18]. NDBC 41025 is located near the edge of the continental shelf break and the Hatteras Canyon. It is located at a water depth of 68.3 m and about 16 nautical miles from Cape Hatteras. The North Carolina coast is also regularly subjected to the threat of tropical cyclones. Therefore, this study site will provide important information regarding the effect of extreme wind events on the accuracy of model simulations for large waves.
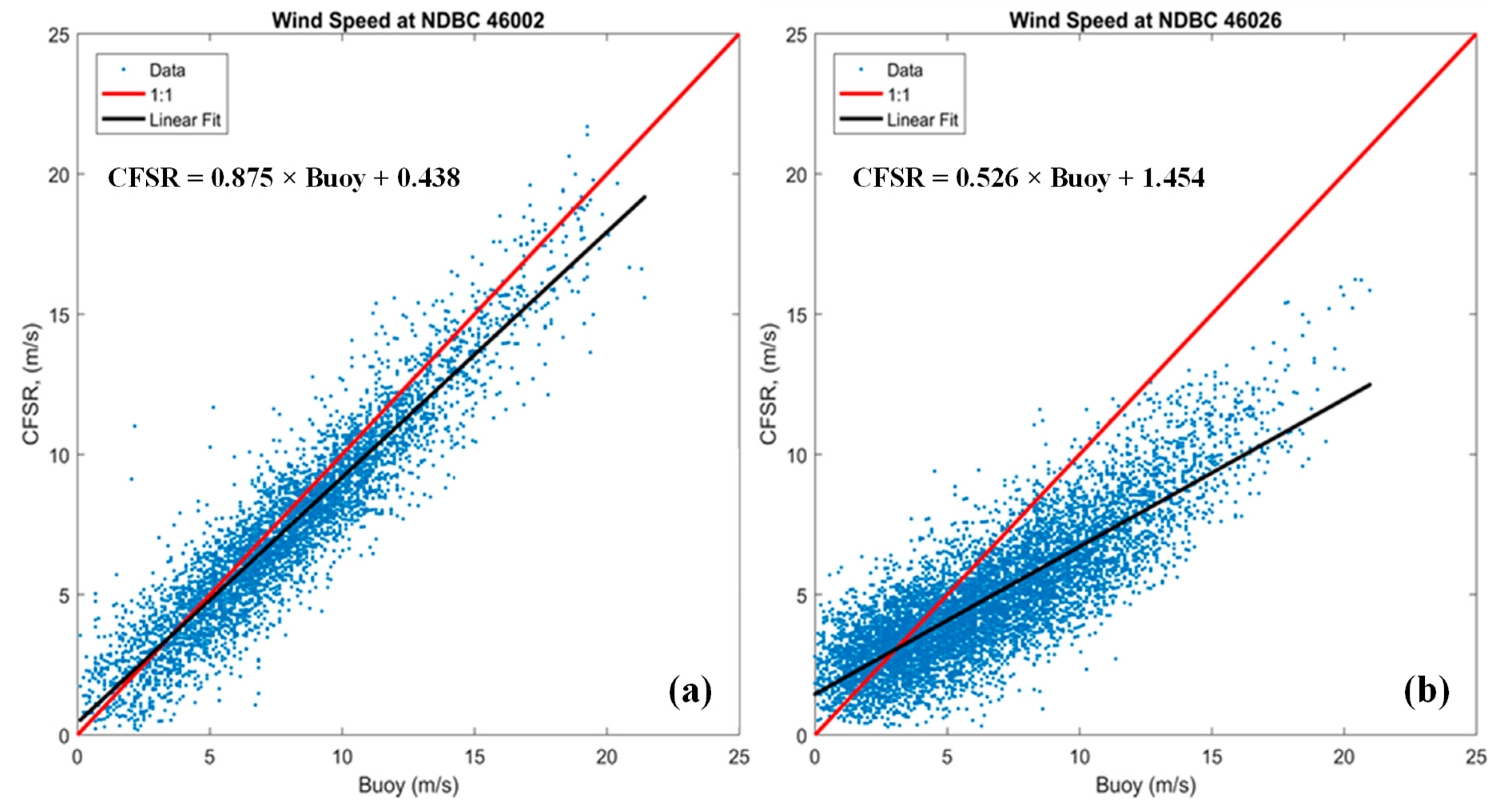
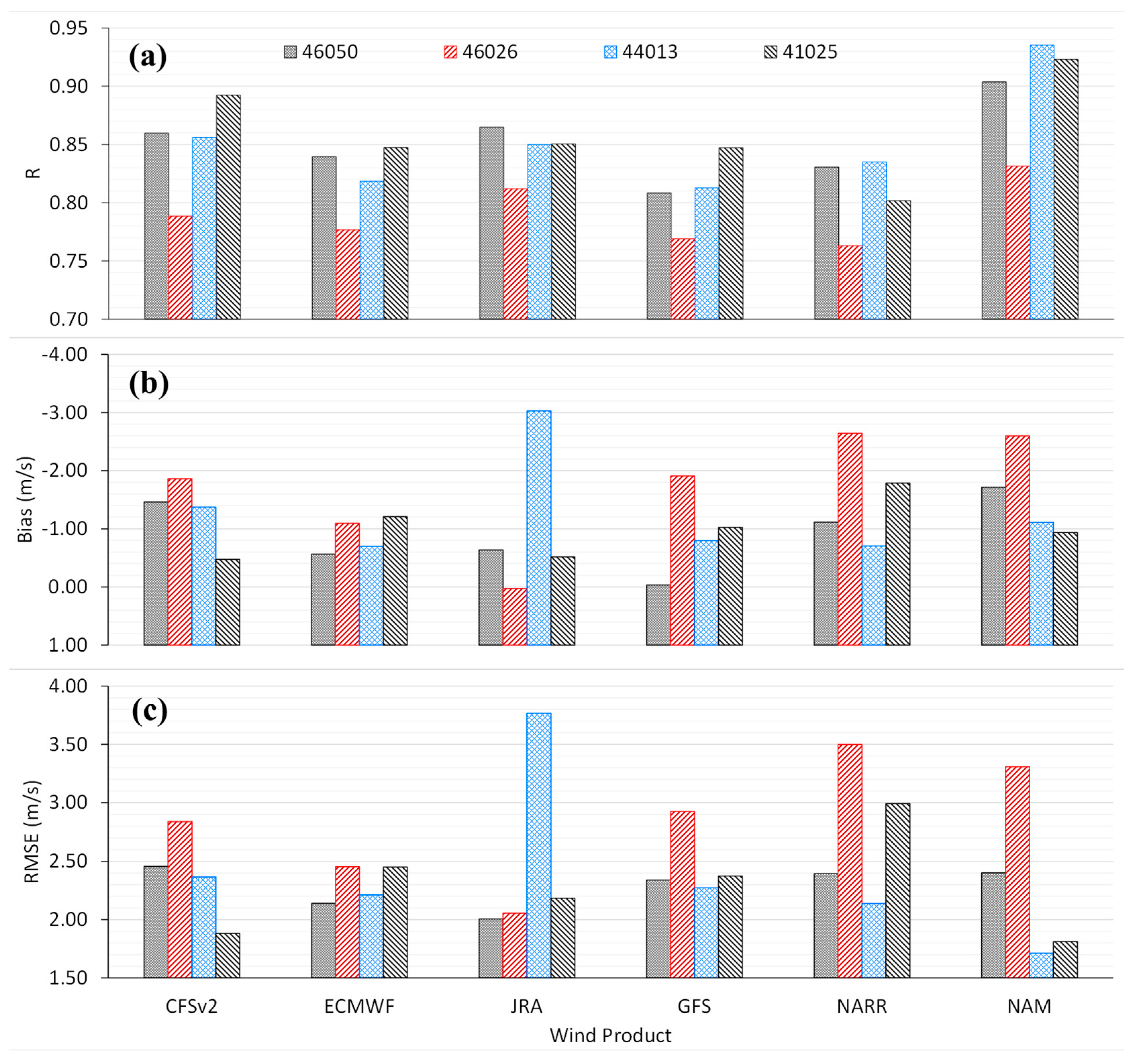
2.2. Review of Wind Products
- NOAA NCEP’s CFSR. Since 2011, the CFSR was upgraded to CFS Version 2 (CFSv2);
- NOAA NCEP’s Global Forecast System (GFS);
- European Centre for Medium-Range Weather Forecasts (ECMWF);
- Japan Meteorological Agency’s Japanese ReAnalysis (JRA);
- NCEP’s North American Regional Reanalysis (NARR); and
- NCEP’s North American Mesoscale Forecast System (NAM).
2.3. Model Configuration
2.4. Model Simulations
3. Results and Discussion
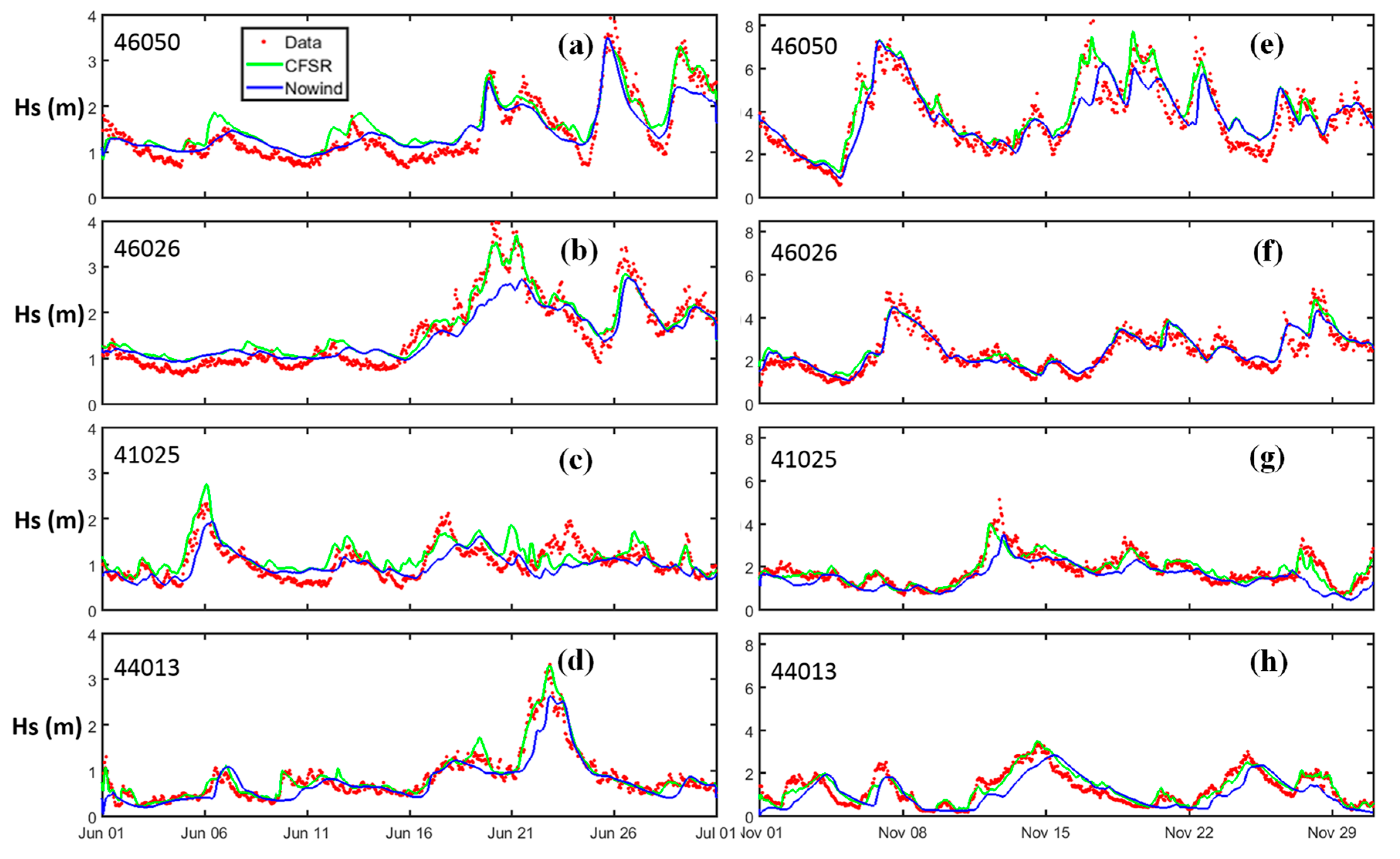
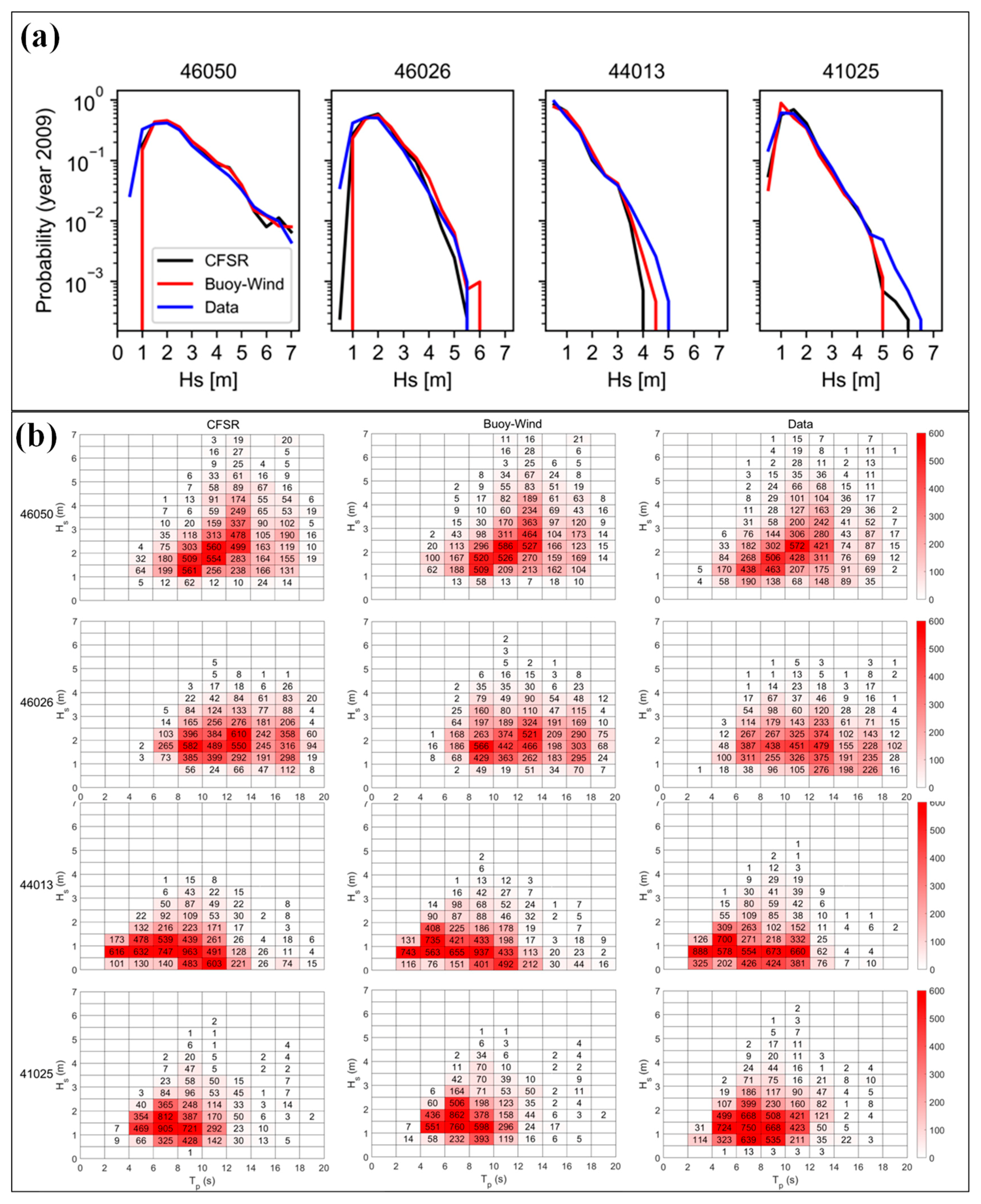
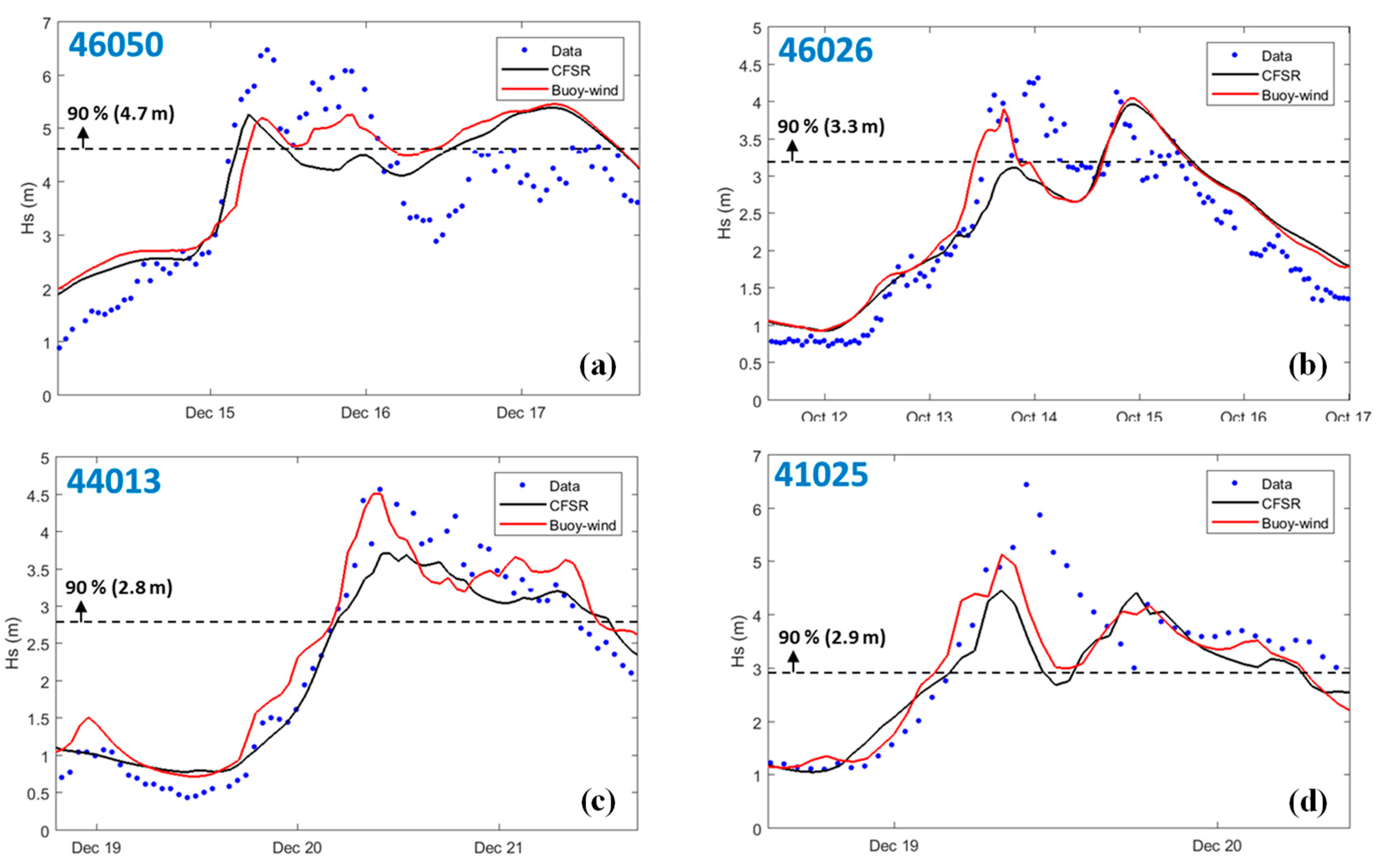
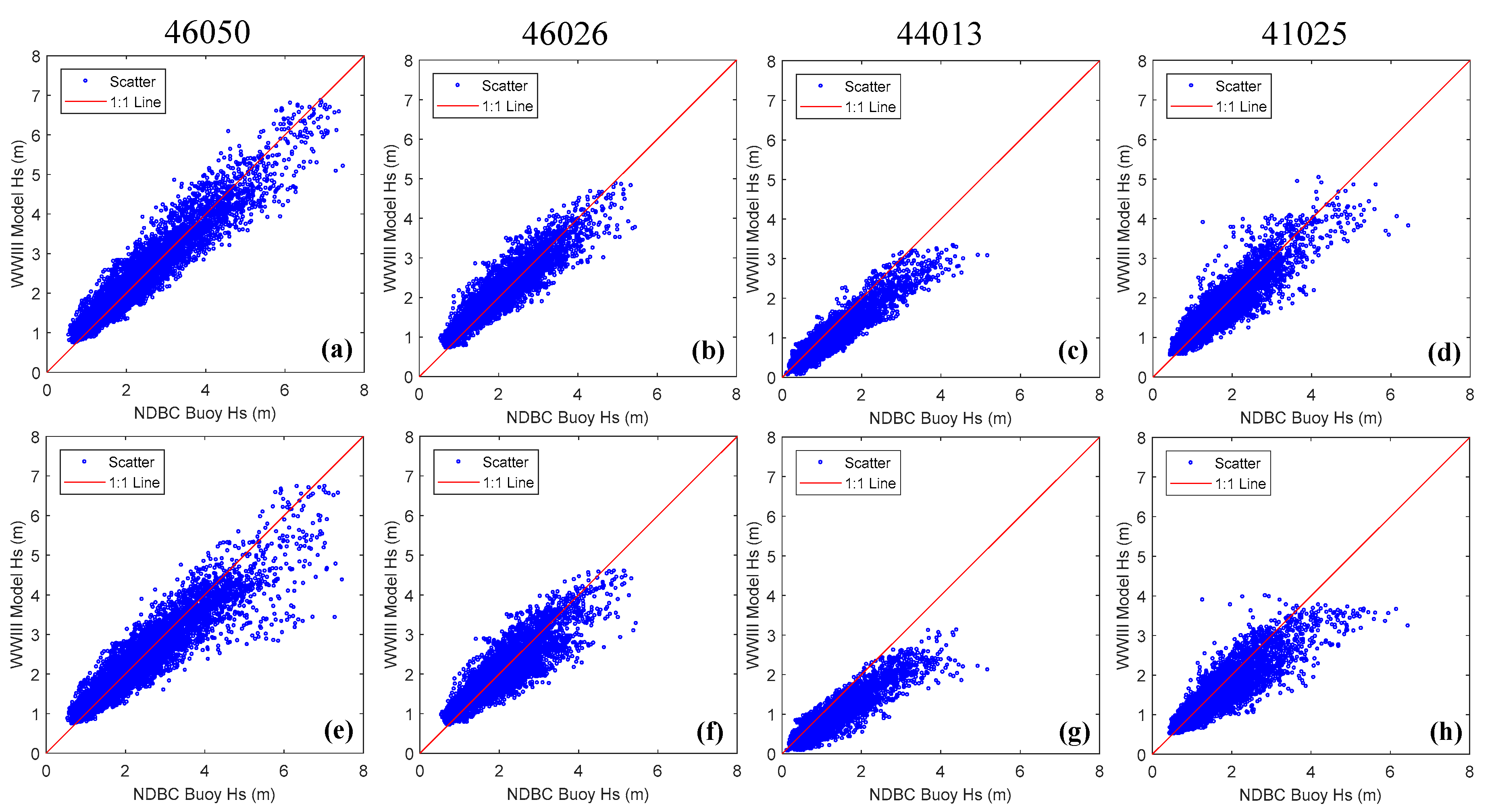
3.1. Baseline Condition with CFSR Wind
3.2. Simulation without Wind Forcing
3.3. Simulation with Observed Wind
3.4. Simulation with NARR Wind
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- International Electrotechnical Commission. Marine Energy—Tidal and Other Water Current Converters—Part. 101: Wave Energy Resource Assessment and Characterization; Report No. IEC TS 62600-101; International Electrotechnical Commission: Geneva, Switzerland, 2015. [Google Scholar]
- Bidlot, J.-R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Intercomparison of the performance of operational ocean wave forecasting systems with buoy data. Weather Forecast. 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Pan, S.-Q.; Fan, Y.-M.; Chen, J.-M.; Kao, C.-C. Optimization of multi-model ensemble forecasting of typhoon waves. Water Sci. Eng. 2016, 9, 52–57. [Google Scholar] [CrossRef]
- Ellenson, A.; Özkan-Haller, H.T. Predicting large ocean wave events characterized by bimodal energy spectra in the presence of a low-level southerly wind feature. Weather Forecast. 2018, 33, 479–499. [Google Scholar] [CrossRef]
- Chawla, A.; Spindler, D.M.; Tolman, H.L. Validation of a thirty year wave hindcast using the climate forecast system reanalysis winds. Ocean Model. 2013, 70, 189–206. [Google Scholar] [CrossRef]
- Yang, Z.; Neary, V.S.; Wang, T.; Gunawan, B.; Dallman, A.R.; Wu, W.-C. A wave model test bed study for wave energy resource characterization. Renew. Energy 2017, 114, 132–144. [Google Scholar] [CrossRef]
- Wu, W.C.; Yang, Z.; Wang, T. Wave Resource Characterization Using an Unstructured Grid Modeling Approach. Energies 2018, 11, 605. [Google Scholar] [CrossRef]
- Chawla, A.; Spindler, D.; Tolman, H. WAVEWATCH III Hindcasts with Re-Analysis Winds. Initial Report on Model Setup; NOAA/NWS/NCEP Technical Note 291; NOAA: Silver Spring, MD, USA, 2011; 100p.
- Tolman, H.; WAVEWATCH III Development Group. User Manual and System Documentation of WAVEWATCH III Version 4.18; NOAA/NWS/NCEP Technical Note 316; NOAA: College Park, MD, USA, 2014; 311p.
- Zijlema, M. Computation of wind-wave spectra in coastal waters with swan on unstructured grids. Coast. Eng. 2010, 57, 267–277. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Cavaleri, L. Wave modeling missing the peaks. J. Phys. Oceanogr. 2009, 39, 2757–2778. [Google Scholar] [CrossRef]
- Lenee-Bluhm, P.; Paasch, R.; Özkan-Haller, H.T. Characterizing the wave energy resource of the US Pacific Northwest. Renew. Energy 2011, 36, 2106–2119. [Google Scholar] [CrossRef]
- Garcá-Medina, G.; Özkan-Haller, H.T.; Ruggiero, P.; Oskamp, J. An inner-shelf wave forecasting system for the US Pacific Northwest. Weather Forecast. 2013, 28, 681–703. [Google Scholar] [CrossRef]
- Garcá-Medina, G.; Özkan-Haller, H.T.; Ruggiero, P. Wave resource assessment in Oregon and southwest Washington, USA. Renew. Energy 2014, 64, 203–214. [Google Scholar] [CrossRef]
- Neary, V.; Yang, Z.; Wang, T.; Gunawan, B.; Dallman, A.R. Model Test Bed for Evaluating Wave Models and Best Practices for Resource Assessment and Characterization; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2016.
- Jacobson, P.; Hagerman, G.; Scott, G. Mapping and Assessment of the United States Ocean Wave Energy Resource; Electric Power Research Institute: Palo Alto, CA, USA, 2011. [Google Scholar]
- Kilcher, L.; Thresher, R. Marine Hydrokinetic Energy Site Identification and Ranking Methodology Part I: Wave Energy; National Renewable Energy Lab (NREL): Golden, CO, USA, 2016.
- Ardhuin, F.; Rogers, E.; Babanin, A.; Filipot, J.-F.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.-M.; Aouf, L. Semiempirical dissipation source functions for ocean waves. Part I: Definition, calibration, and validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Alberello, A.; Chabchoub, A.; Gramstad, O.; Toffoli, A. Non-Gaussian properties of second-order wave orbital velocity. Coast. Eng. 2016. [Google Scholar] [CrossRef]
- Alberello, A.; Chabchoub, A.; Monty, J.P.; Nelli, F.; Lee, J.H.; Elsnab, J.; Toffoli, A. An experimental comparison of velocities underneath focussed breaking waves. Ocean Eng. 2018, 155. [Google Scholar] [CrossRef]
| Product Name | Spatial Coverage | Spatial Resolution | Temporal Range | Temporal Resolution | |
|---|---|---|---|---|---|
| CFSR | CFSR | Global | 0.5 degree | 1979–2010 | Hourly |
| CFSv2 | Global | 0.5 degree | 2011–present | Hourly | |
| ECMWF | ERA-Interim | Global | 0.703 degree | 1979–present | 3-hourly |
| ERA-20C | Global | 1.125 degree | 1900–2010 | 3-hourly | |
| GFS | Global | 0.5 degree | 2007–2014 | 3-hourly | |
| Global | 0.25 degree | 2015–present | 3-hourly | ||
| JRA | Global | 0.562 degree | 1957–2016 | 3-hourly | |
| NARR | North America | 32.463 km | 1979–present | 3-hourly | |
| NAM | North America | 12.19 km | 2004–present | 6-hourly | |
| Run# | Model Runs | Model Grids | Wind Forcing |
|---|---|---|---|
| 1 | Baseline WWIII | WWIII Domains | CFSR |
| 2 | Baseline UnSWAN | UnSWAN Domains | CFSR |
| 3 | UnSWAN without Wind | UnSWAN Domains | Zero |
| 4 | UnSWAN with Observed Wind | UnSWAN Domains | Observed |
| 5 | WWIII with NARR | WWIII Domains | CFSR + NARR |
| Model Run | Station | RMSE | PE (%) | SI | Bias | Bias (%) | R |
|---|---|---|---|---|---|---|---|
| WWIII | 46050 | 0.35 | 5.48 | 0.15 | 0.04 | 1.63 | 0.95 |
| 46026 | 0.30 | 8.57 | 0.16 | 0.09 | 4.63 | 0.93 | |
| 44013 | 0.30 | −13.55 | 0.31 | −0.17 | −17.21 | 0.94 | |
| 41025 | 0.31 | 7.34 | 0.20 | 0.05 | 2.95 | 0.91 | |
| UnSWAN | 46050 | 0.43 | 12.0 | 0.18 | 0.17 | 7.6 | 0.94 |
| 46026 | 0.33 | 12.0 | 0.16 | 0.15 | 8.2 | 0.93 | |
| 44013 | 0.24 | 7.0 | 0.25 | 0.0 | 0.1 | 0.93 | |
| 41025 | 0.35 | 10.0 | 0.22 | 0.08 | 5.3 | 0.87 |
| Station | Wind | RMSE | PE (%) | SI | Bias | Bias (%) | R |
|---|---|---|---|---|---|---|---|
| 46050 | CFSR | 0.81 | −5.1 | 0.15 | −0.29 | −5.1 | 0.67 |
| Observed | 0.77 | −4.7 | 0.14 | −0.27 | −4.8 | 0.68 | |
| 46026 | CFSR | 0.49 | −5.2 | 0.13 | −0.22 | −5.6 | 0.57 |
| Observed | 0.48 | 2.4 | 0.12 | 0.08 | 2.0 | 0.58 | |
| 44013 | CFSR | 0.6 | −12.7 | 0.21 | −0.44 | −13.3 | 0.55 |
| Observed | 0.58 | −9.6 | 0.19 | −0.34 | −10.2 | 0.47 | |
| 41025 | CFSR | 0.83 | −9.9 | 0.25 | −0.41 | −11.0 | 0.47 |
| Observed | 0.69 | −5.2 | 0.2 | −0.23 | −6.4 | 0.55 |
| Station | Wind | RMSE | PE (%) | SI | Bias | Bias (%) | R |
|---|---|---|---|---|---|---|---|
| 46050 | CFSR | 0.35 | 5.48 | 0.15 | 0.04 | 1.63 | 0.95 |
| NARR | 0.43 | 1.50 | 0.19 | −0.06 | −2.87 | 0.93 | |
| 46026 | CFSR | 0.30 | 8.57 | 0.16 | 0.09 | 4.63 | 0.93 |
| NARR | 0.35 | 4.24 | 0.19 | 0.00 | 0.10 | 0.89 | |
| 44013 | CFSR | 0.30 | −13.55 | 0.31 | −0.17 | −17.21 | 0.94 |
| NARR | 0.40 | −21.75 | 0.41 | −0.26 | −26.08 | 0.92 | |
| 41025 | CFSR | 0.31 | 7.34 | 0.20 | 0.05 | 2.95 | 0.91 |
| NARR | 0.37 | −1.29 | 0.23 | −0.10 | −6.13 | 0.88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Yang, Z.; Wu, W.-C.; Grear, M. A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting. J. Mar. Sci. Eng. 2018, 6, 139. https://doi.org/10.3390/jmse6040139
Wang T, Yang Z, Wu W-C, Grear M. A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting. Journal of Marine Science and Engineering. 2018; 6(4):139. https://doi.org/10.3390/jmse6040139
Chicago/Turabian StyleWang, Taiping, Zhaoqing Yang, Wei-Cheng Wu, and Molly Grear. 2018. "A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting" Journal of Marine Science and Engineering 6, no. 4: 139. https://doi.org/10.3390/jmse6040139
APA StyleWang, T., Yang, Z., Wu, W.-C., & Grear, M. (2018). A Sensitivity Analysis of the Wind Forcing Effect on the Accuracy of Large-Wave Hindcasting. Journal of Marine Science and Engineering, 6(4), 139. https://doi.org/10.3390/jmse6040139







