Abstract
The two-dimensional, laterally-averaged mechanistic eutrophication model CE-QUAL-W2 version 3.72 was used to predict chlorophyll-a concentrations across two different time periods in the Neuse River Estuary, North Carolina. Chlorophyll calibration was performed for two time periods simultaneously by performing a full-factorial experiment that tested seven algal kinetic growth parameters over three levels for a single algal group. A cluster of up to six computers each running between two and ten instances of the program was used to complete and manage the data for 2187 runs for each period. Six numeric criteria were used to determine which runs performed acceptably, yielding a group of 27 cases that met all of the criteria. Calibration performance of the set of cases outperformed a previously calibrated model using three algal groups that met only four of the six selection criteria. Calibration performed this way allowed for a more rational specification of model calibration performance and provided uncertainty estimates of model predictions, albeit at the cost of a considerable increase in computational requirements that necessitated the use of a computer cluster.
1. Introduction
Algal blooms have plagued the Neuse River Estuary (NRE) for decades [1,2] and multiple models have been employed to study eutrophication in the estuary [3,4,5]. Despite the development of a water quality model-based total maximum daily load (TMDL) analysis and regulations to reduce total nitrogen (N) loading to the estuary by 30% from the 1995 baseline year, algal blooms still occur throughout the estuary [6]. The fraction of water samples that exceed the chlorophyll-a criteria of 40 µg/L has decreased in some, and increased in other parts of the estuary [7].
The timing, extent, and magnitude of the blooms appears to be affected by hydrologic variability affecting water residence time and nutrient supply, as well as seasonal variations in temperature and light [6,8]. In addition, although inorganic N loading to the estuary has been reduced by 15–25% since the 1990s, this reduction has been offset by an increase in organic N loading of approximately 15% and an increase in N loading from the Trent River tributary of approximately 30% [7].
These changes and the continued presence of blooms and water quality criteria violations point to the need to better understand trends in water quality in the Neuse Estuary that have been observed since the model-based TMDL was performed more than ten years ago. In that previous work, algal species with similar growth characteristics were grouped together to form three functional phytoplankton groups (i.e., diatoms + dinoflagellates, chlorophytes + cryptophytes, and cyanobacteria). Water quality calibration was achieved on a constituent-by-constituent basis, adjusting relevant kinetic parameters by trial and error to provide the best agreement between predicted and observed concentrations [9], as based upon multiple calibration criteria.
This article reexamines the procedure used to calibrate the algal constituents in a process-based multi-dimensional water quality model of the Neuse River Estuary that has been further developed to simulate a second, more recent multi-year period. A mechanistic, two-dimensional, laterally-averaged model (CE-QUAL-W2) was used to simulate water quality dynamics in the estuary. Multi-dimensional mechanistic eutrophication models such as CE-QUAL-W2 typically have more than twenty water quality constituents and upwards of one hundred kinetic parameters that must each be calibrated. The algal constituents pose a particular problem for calibration because of the need to specify how algal growth rate simultaneously depends upon light intensity, temperature, and the concentrations of multiple nutrients. Specifying these growth rate relationships typically requires specification of ten to twenty parameters per algal constituent. Traditionally, calibration of parameters in a water quality model has been done via a trial and error approach that seeks to minimize the difference between observations of a water quality constituent and corresponding model predictions of that constituent in the water body [10,11,12].
Several innovative calibration approaches have recently been developed for mechanistic water quality models. Huang and Liu utilized a hybrid genetic algorithm parameter search method together with a neural network based approximation of the input–output relationships of the mechanistic model to calibrate twenty-nine parameters of a CE-QUAL-W2 based lake water quality model [13]. A particle swarm automatic calibration method was used as part of a multi-objective calibration of a CE-QUAL hydrodynamic and temperature model for a reservoir. Ten parameters were calibrated automatically by optimizing a goodness-of-fit based objective function for temperature and water surface elevation [14,15]. While most researchers have based eutrophication model calibration on algal biomass (i.e., chlorophyll-a concentrations), some have based their calibration on comparisons of model predicted and observed algal productivity and photosynthesis-irradiance (P-I) curves [16]. In this case, researchers found significant differences in model predicted algal productivity using their approach as compared to a corresponding model calibrated using the traditional biomass-based approach. Arhonditsis et al. developed a statistically based Bayesian calibration methodology to determine parameter values and their uncertainty for a six-parameter water quality model [17] of a coastal embayment in Greece. In related work, the Bayesian calibration methodology has been employed for a mesotrophic lake in Washington State, USA [18].
In this study, a rigorous investigation of the algal parameter space was undertaken by a full-factorial design testing seven algal parameters at three different levels for a single algal group, with the objective of finding the optimum combination of parameters to characterize phytoplankton growth in the estuary. Of particular interest was how this automated calibration approach using a single algal constituent would compare with respect to calibration performance to an earlier Neuse River Estuary model that used three algal constituents calibrated using the traditional trial and error approach [9]. A secondary objective of the work was to develop a multi-objective calibration utilizing numeric criteria that reflected the intended use of the model for environmental management purposes. We sought to demonstrate a paradigm shift in how mechanistic models are calibrated. Instead of a single “optimal” parameter set, we systematically searched the parameter space for many parameter sets that meet our criteria for the necessary calibration performance. This work was part of a larger, comprehensive project whose goal was to determine the effect of inorganic versus organic nitrogen loading reduction on phytoplankton growth and biomass, and the fate of anthropogenic nutrient loading to the estuary [19]. The two-dimensional, laterally-averaged mechanistic eutrophication model CE-QUAL-W2 version 3.72 [20] was used to predict chlorophyll-a concentrations across two different periods—a previously modeled period and a more recent one. To make the large number of runs needed to independently vary the parameters, a program was written that would allow multiple computers to work in parallel to perform many model runs and individually report their progress to a cloud-based file that was used so that all model runs were completed by the computer cluster.
2. Materials and Methods
2.1. Model Set-Up
CE-QUAL-W2 (Portland State University, Portland, OR, USA) is a two-dimensional (longitudinal and vertical) hydrodynamic and water quality model. The model assumes lateral (bank to bank) homogeneity, and is therefore best suited for long and narrow bodies. It has been applied to rivers, lakes, reservoirs, estuaries, and combinations of waterbodies [20]. For this study, version 3.72 was obtained from the developers as FORTRAN source code and was compiled to create executables that could be run on Windows, OS-X, and LINUX workstations.
In addition to its hydrodynamics aspects, Version 3.72 allows the user to track 28 water-quality variables, 14 of which were used in this model (Table 1), and 60 derived variables. The W2 computational grid used here consisted of 151 segments divided into 11 branches with five tributaries of branch 1, the main branch (Figure 1). In the z-grid vertical layering scheme, each segment consisted of up to eighteen 0.5–2.0 m thick active vertical layers, depending on the local water depth. Model input and calibration data were based upon a long-term dataset provided by the University of North Carolina Institute of Marine Sciences (IMS) and the North Carolina Department of Environmental Quality (NCDEQ). Eleven mid-river water quality sampling stations (i.e., IMS Neuse River Estuary Modeling and Monitoring Project (MODMON) stations 0‒180) are sampled and analyzed for a broad array of water quality constituents on a bi-weekly basis [21,22]. The two modeling periods (1998–2000 and 2006–2008) were chosen on the basis of data availability, the presence of events that could provide insight into eutrophication dynamics in the estuary (e.g., flow extremes and large algal blooms), and the composition of nitrogen loading. In both cases, initial conditions were handled by starting the model from constant values and allowing at least six months for it to “spin up” to stable conditions. Flows, temperatures, and constituent inflow concentrations were specified for each branch and tributary within the modeled area. The amount, temperature, and nitrogen concentration of precipitation in addition to other meteorological variables (i.e., air temperature, dewpoint temperature, wind speed, wind direction, and cloud cover) were also specified. Elevation head, temperature, and constituent concentrations were provided at the downstream boundary of the branch 1 (i.e., segment 77) near the mouth of the NRE at Pamlico Sound. All components were assumed to vary linearly in time between monitoring events, and vertical profiles of temperature and constituent concentrations were created through interpolation of near-surface and near-bottom data.

Table 1.
Neuse Estuary Eutrophication Model (NEEM) water quality constituents.
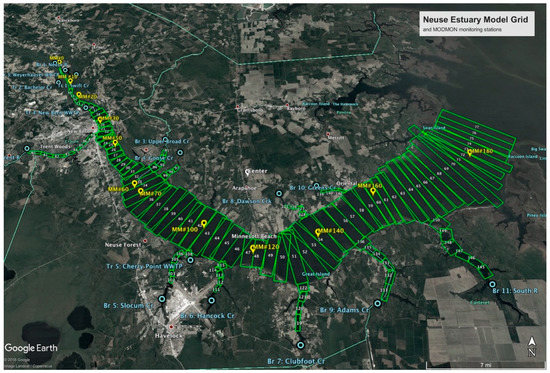
Figure 1.
W2 model grid and IMS ModMon monitoring stations.
Hydrodynamic and conservative transport model calibration were performed by comparing model predictions of water temperature and salinity to observed data. Incident short-wave solar radiation, bottom roughness, bottom elevation, wind-sheltering, vertical mixing, and downstream boundary salinity were varied to produce the best agreement between model predictions and observed values at twelve Neuse River Estuary Modeling and Monitoring Project (ModMon) stations for both the bottom and surface layers.
In previous modeling work on the Neuse, water quality calibration was achieved on a constituent by constituent basis, adjusting relevant kinetic parameters to provide the best agreement between predicted and observed concentrations of orthophosphate, ammonium, nitrate-nitrite, and dissolved oxygen [9]. The initial phase of water quality calibration in this investigation began with a similar approach, varying the parameters governing zero-order sediment oxygen demand (SOD), water-column denitrification rate, light extinction coefficients, and phosphorous partitioning until satisfactory preliminary results were obtained. The results were considered preliminary because concentrations of these constituents can both influence and be influenced by algal growth in the estuary, and the calibration of chlorophyll-a (chl-a) was saved for last.
When a similar trial-and-error approach was attempted for the factors controlling algal growth, the performance of the model in predicting chlorophyll-a concentrations was less than satisfactory. Despite having comparable R2 to earlier work and low mean error, the model’s predicted cumulative distribution function (CDF) showed significant deviation from the observed CDF at higher chlorophyll-a values. As a result, exceedance probabilities (i.e., the frequency of chl-a > 40 ug/L) were underestimated, and response to nitrogen-load reduction was minimal. Since the prediction of algal blooms was integral to the goals of the larger study, it was decided that a full-factorial analysis of algal growth parameters was warranted.
2.2. Algal Growth Parameters
W2v3.72’s algal rate equation (Equation (1)) is a function of six processes, but only five were modeled here (i.e., loss due to feeding by zooplankton was not used, since zooplankton concentration was not modeled).
The rate of each process is the product of a maximum first order rate constant (i.e., maximum algal growth, A; respiration, AR; excretion, AE; mortality rate, AM; and settling rate, AS), a multiplier for the limiting growth factor, and multipliers for the effect of temperature. Nutrient growth-limiting factors are calculated using a Monod formulation dependent upon nutrient concentration and a half-saturation constant (phosphorus, AHSP; nitrogen, AHSN; and silica, AHSSI), while the growth limiting factor for light is a function of the available light and light saturation intensity at maximum photosynthetic rate, ASAT [23].
AG, AHSP, AHSN, and ASAT were varied over three levels (Table 2) independently, while the four parameters affecting algal sink (AR, AE, AM, and AS) were varied over three levels, but not independently of each other. The three levels were chosen so that the parameter varied by a factor of ten over the levels with the middle level representing that used in the previous version of the Neuse Estuary Eutrophication model (NEEM).

Table 2.
Algal growth parameters and levels tested via full-factorial design.
The multipliers for the effect of temperature are determined from the rising and falling limb of a rate multiplier curve [24] modeled by specifying four temperatures (AT1‒AT4) and the fraction of the maximum rate at each temperature (AK1‒AK4). Varying all eight of these parameters would result in a prohibitively large number of permutations, so only two aspects of the temperature relative growth rate function (i.e., the “width” of the curve and the location of its midpoint) were varied over three levels. Values were chosen to give a narrow, medium, and wide range of the function as well as to provide a low, middle, and high midpoint of the function (Figure 2). The fraction of the maximum rate (AK1–AK4) was not varied, so that all cases had the same shape for the relative growth rate vs. temperature function, as shown in Figure 2.
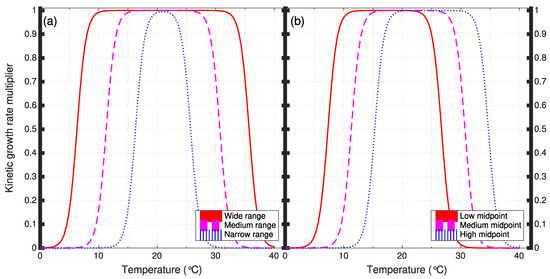
Figure 2.
Example kinetic growth rate multiplier curves for tested algal growth temperature levels. Panel (a) shows the effect of varying the width of the function while maintaining a constant temperature optimum. Panel (b) shows the effect of varying the temperature optimum while maintaining the width of the function.
2.3. Run Management
A MATLAB script was written that would allow multiple computers to work in parallel (Figure 3). When the program is run, the individual computer in the cluster generates a list of runs needed to be performed and compares it to a centrally-stored file containing a log of runs completed. The computer identifies the next run to be made, generates a control file that corresponds to the values of the algal parameters for that run, and then performs the run. Each computer will continue to make runs (at different processing speeds) until all are completed. The cluster of up to six computers each running between two and ten instances of the program took approximately 1300 hours of computational time to complete all 2187 runs for both periods. A statistics script was then used to read the time series output files of the model for each run and report calibration performance and other relevant data to a central file.
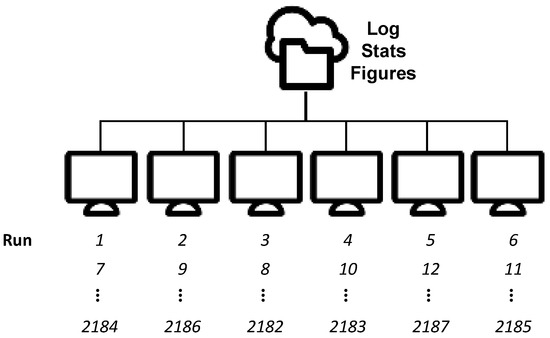
Figure 3.
Conceptual representation of the computer cluster used to perform parallel runs.
3. Results
The results were evaluated by analyzing each run’s combined calibration performance over the 1998–2000 and 2006–2008 periods. Six calibration performance criteria were utilized that captured bottom and surface chlorophyll-a predictions at all ModMon stations (Table 3). Normalized mean error and coefficient of determination were used to assess agreement between model-predicted and observed chlorophyll-a. However, it was found that a run could have comparatively good values on these statistics, yet still fail to match the observed cumulative distribution function (CDF) adequately, especially at higher chlorophyll concentrations. Thus, CDF error, log CDF error, and exceedance probability were added to assess these “fit” characteristics. CDF error was defined as the total area between the predicted and observed cumulative distribution function curves (in units of µg/L chlorophyll-a). Log CDF error was defined the same way but was computed on the log-transformed chlorophyll-a data, and then transformed back into standard chlorophyll units.

Table 3.
Performance criteria for selection of algal growth parameter runs.
Exceedance probability was defined as the probability of the model-predicted chlorophyll-a exceeding 40 µg/L. This statistic was calculated to assess how well the model matched observed frequency of chlorophyll-a concentrations that are above North Carolina’s water quality criteria. Finally, dissolved inorganic nitrogen (DIN) exceedance probability was defined as the probability of the total DIN concentration (i.e., ammonia + nitrate + nitrite) exceeding the half-saturation constant for nitrogen-limited growth (AHSN). This last criterion was added to prioritize runs where algal growth was sensitive to nitrogen concentrations in the estuary.
In this study, it was not our intention to seek an “optimal” parameter set, and in fact, no single model performed significantly better with respect to our six calibration criteria. Instead, it was found that the vast majority of runs fared relatively poorly on one or more of the calibration criteria. Histograms of each calibration criterion were created (Figure 4) to assess the performance distribution for each criterion across the full set of cases. For each criterion, the initial threshold performance was set based upon judgement as to the necessary performance of the model. Minor changes in the threshold performance for individual criterion were also set iteratively so that degree of selectivity was roughly similar between criteria. The performance criteria were also adjusted slightly to give a reasonable number of cases that met all six performance criteria. Only the cases that met all six calibration criteria were considered suitable parameter sets, conditional upon their performance on the other hydrodynamic and water quality criteria. Once specified, these same model calibration criteria were used to test the previously calibrated Neuse River Estuary model that used three algal subgroups and the prior set of algal kinetic and temperature parameters. The model was run for both periods (1998–2000, 2006–2008) and the overall calibration performance assessed. This case met only four of the six calibration criteria, failing to meet the conditions for chlorophyll and DIN exceedance probability.
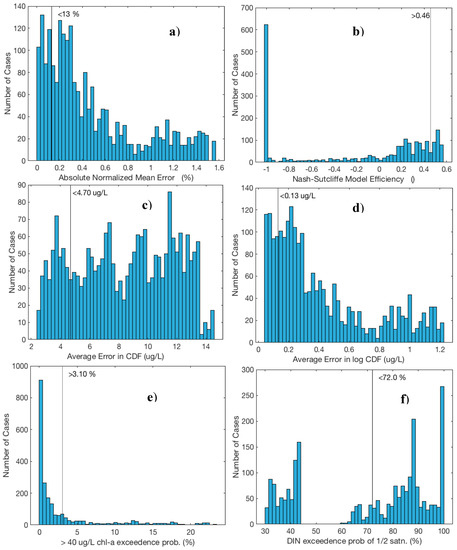
Figure 4.
Histograms of calibration performance for the six criteria used to select model parameter sets (#1-5 used chl-a concentrations, #6 used DIN concentrations). The six criteria were: (a) absolute value of normalized mean model error (%); (b) Nash–Sutcliffe model efficiency; (c) average CDF error; (d) average log-transformed CDF error; (e) percentage of chl-a predictions above 40 ug/L; and (f) percentage of DIN concentrations above N ½ saturation constant for growth.
The mean and standard deviation of the fit statistics (normalized mean error, normalized mean absolute error, normalized root mean squared error, and coefficient of determination) across the 27 cases give an indication of how well the cases performed and how much variation exists between cases (Table 4). No case performed so poorly on these constituents as to justify its removal from the pool of cases.

Table 4.
Mean and standard deviation of calibration performance statistics across 27 runs.
As expected, varying algal growth parameters had no effect on temperature, salinity, or extinction coefficients, resulting in no variation among the 27 selected cases. The other five constituents were sensitive to algal growth parameters, with orthophosphate performance showing the highest degree of variation between runs.
Scatter plots (Figure 5 and Figure 6), cumulative frequency distributions (Figure 7), and time histories (Figure 8, Figure 9, Figure 10 and Figure 11) of model predicted versus observed values were constructed for both periods using the best performing run for each constituent. Time histories are shown here for a representative station in the upper estuary station (ModMon 30) and a station in the middle estuary (ModMon 100) for one of the twenty-seven runs that met all six calibration performance criteria. For the cumulative frequency distributions (CDFs), the data for both periods were combined into one plot, since CDF error was used as a selection criterion.
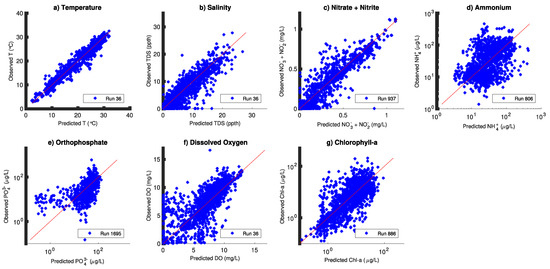
Figure 5.
Predicted versus observed scatter plots for hydrodynamic and water quality parameters for 1998–2000. The predicted = observed line is shown in red. Panels show (a) temperature, (b) salinity, (c) nitrate + nitrite, (d) ammonium, (e) orthophosphate, (f) dissolved oxygen, and (g) chlorophyll-a.
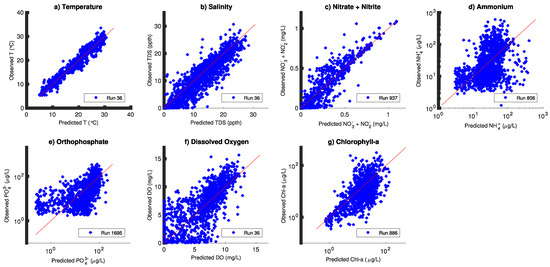
Figure 6.
Predicted versus observed scatter plots for hydrodynamic and water quality parameters for 2006–2008. The predicted = observed line is shown in red. Panels show (a) temperature, (b) salinity, (c) nitrate + nitrite, (d) ammonium, (e) orthophosphate, (f) dissolved oxygen, and (g) chlorophyll-a.
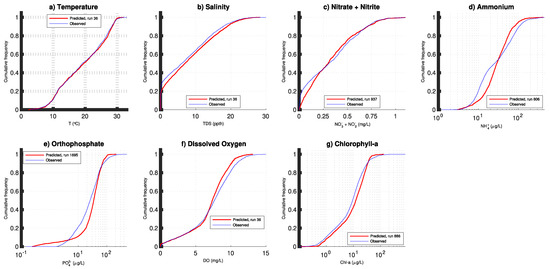
Figure 7.
Cumulative frequency distributions for hydrodynamic and water quality variables for 1998–2000 and 2006–2008 combined. Panels show (a) temperature, (b) salinity, (c) nitrate + nitrite, (d) ammonium, (e) orthophosphate, (f) dissolved oxygen, and (g) chlorophyll-a.
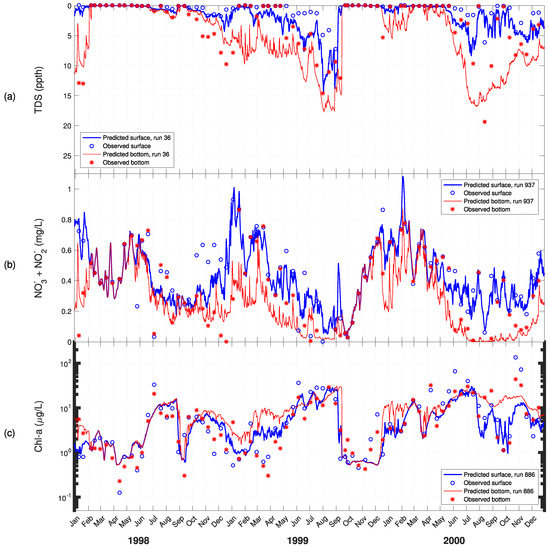
Figure 8.
Time series for predicted versus observed values of: (a) salinity; (b) nitrate + nitrite; and (c) chlorophyll-a at ModMon 30 for 1998–2000.
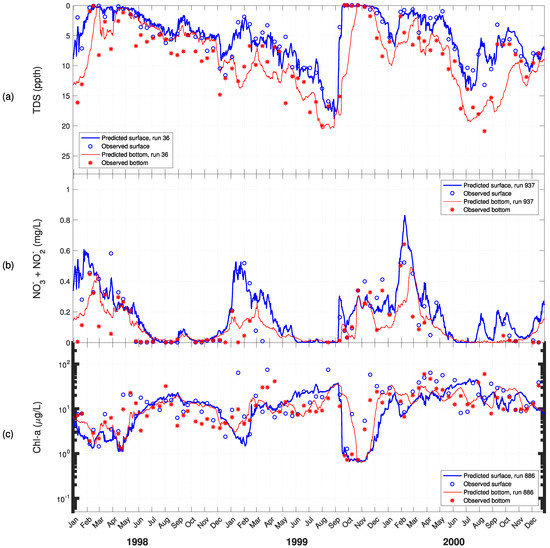
Figure 9.
Time series for predicted versus observed values of: (a) salinity; (b) nitrate + nitrite; and (c) chlorophyll-a at ModMon 100 for 1998–2000.
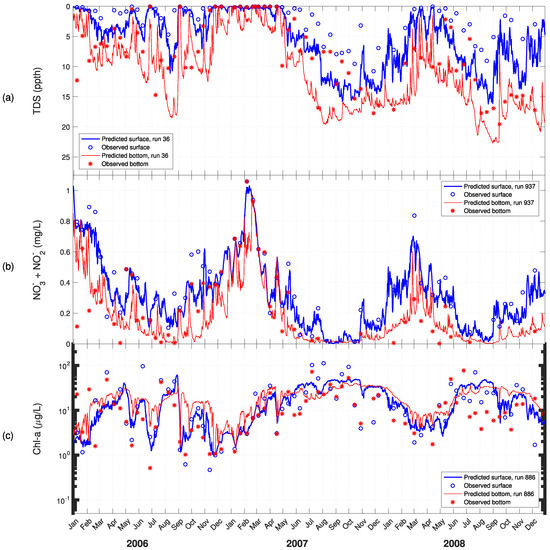
Figure 10.
Time series for predicted versus observed values of: (a) salinity; (b) nitrate + nitrite; and (c) chlorophyll-a at ModMon 30 for 2006–2008.
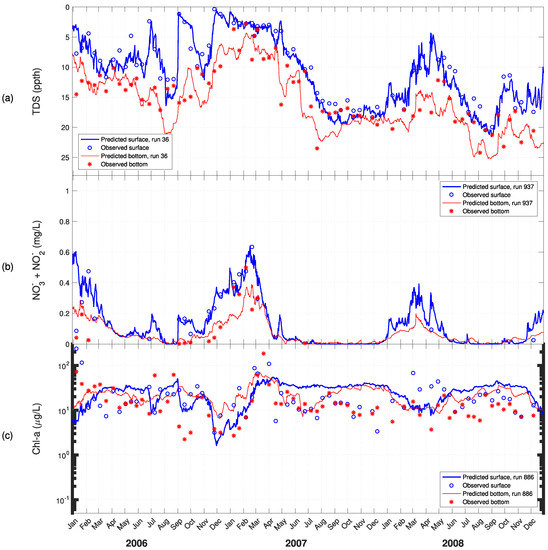
Figure 11.
Time series for predicted versus observed values of: (a) salinity; (b) nitrate + nitrite; and (c) chlorophyll-a at ModMon 100 for 2006–2008.
4. Discussion
The full-factorial analysis calibration method used was found to be practical in this instance only by considering a limited number of kinetic parameters for a single algal group and by utilizing the collective computational power of a computer cluster. Even with the cluster, running all 2187 cases for two separate periods took nearly a week and approximately 1300 hours of total computational time. Only seven adjustable parameters were utilized, yet the previous Neuse Estuary Eutrophication Model used three algal groups with 17 adjustable algal kinetic parameters for each group. A full factorial analysis done in the same fashion with 51 = 3 × 17 algal parameters would have required testing 2.1 × 1024 cases. Even limiting the growth rate specification of each algal group to only seven parameters as was done here would have required 3(3 × 7) = 1.5 × 1010 cases. We found that there are still some significant drawbacks to conducting calibration in the manner done here. There are, however, some advantages that were realized with the method. First, the simultaneous consideration of multiple criteria necessitated an intentional consideration of the necessary performance of the calibrated model. In doing this, we decided that it was reasonable to consider more than the typical set of model “fit” criteria such as the mean error and the Nash–Sutcliffe model efficiency [25,26]. We added criteria that considered how well the model would simulate the observed distribution of chl-a values, and the frequency of chl-a values above the current numeric water quality criteria. These sorts of criteria will likely be important should the model eventually be used as a regulatory tool. Another advantage of this method is that it provides an estimate of model uncertainty. Degree of model fit is given not as a single set of numbers but as a range over the 27 cases (Table 4). Understanding how planned nutrient reduction scenarios might affect algal growth is integral to the management of eutrophication in the Neuse Estuary. Such scenario testing with the model would also include a range of values, and would provide model users an estimate of the reliability of model predictions. Thus, the outputs of the method described here more closely align with the way similar models have been used for nutrient-management in the estuary. Finally, the full-factorial calibration method, using a single algal group outperformed the previous model that used three algal groups. Using the full-factorial approach, we found 27 cases that met all six calibration criteria, yet the previous model, which had but a single set of parameters, met only four of the six calibration criteria.
With regard to calibration performance of our set of 27 acceptable model parameter sets, we found that model predictions of chlorophyll-a correlated moderately well (Table 4) with those observed at ModMon stations (mean Nash–Sutcliffe Model Efficiency = 49.3%) but were slightly higher on average than the corresponding observed data (ME = 11.6%). Variation in mean error between the 27 selected runs was minimal, with no case having lower than a 10% mean error or explaining greater than 52% of the variation in the observed data. There was considerable difference in the performance of the model between the two periods, as 1998–2000 had both a considerably better mean error (6.0% vs. 15.9%) and a higher model efficiency (57% vs. 27%). The previously calibrated Neuse Estuary Eutrophication Model (NEEM) had a lower mean error (∑0.17%) for the 1998–2000 period but accounted for less of the observed variation in the data as compared with the updated NEEM (36.5% vs. >52%).
The chl-a observed data from 1998–2000 and 2006–2008 show a seasonal pattern where maximum values are reached during the summer months (Figure 8c, Figure 9c, Figure 10c, and Figure 11c). This pattern is interrupted by periods where high flow events wash algae out of the upper and middle estuary sections, causing chlorophyll-a to drop sharply (e.g., April 1998, September 1998, January 1999, September–November 1999, July 2006, September 2006, and December 2006). With the exception of April 1998, this pattern is captured reasonably well by the model at ModMon 30 for both periods. As noted previously, the model responds more slowly than the observed data after the major storms of Hurricanes Floyd and Irene during September and November of 1999 (Figure 8c). Observed chlorophyll-a concentrations begin trending upward immediately after the November storm, but the model takes unit mid-December to respond similarly. In addition, the model has some difficulty in capturing the pattern in observed chlorophyll-a concentrations registered during the six summers modeled plus November 2000 and March 2006. This behavior is also evident in the cumulative distribution frequency diagram where the model generally overpredicts chlorophylls lower than 40 µg/L, but underpredicts the ones above (Figure 7g).
As shown in the time history plots of model predicted vs. observed chlorophyll-a concentrations, similar behavior is seen for ModMon 100 with the exception of the last half of the 2006–2008 period (Figure 11c). Aside from the small dip in the spring of 2008 in response to a series of small storms, the model’s predictions of chlorophyll-a are almost totally unresponsive. The observed low in December 2007 succeeded by a high the following March are absent from the model’s predictions.
Another difference of note is the way stratification is predicted by the model. During period of stratification, the observed chlorophylls almost always exceed those of the bottom at that time and place. This is as expected, since the availability of light, and, thus, algal growth should be greatest in the surface layers. However, when the model predicts stratification, it often predicts higher chlorophylls at the bottom. This behavior is more prominent at ModMon 30 (Figure 8c and Figure 10c) than at ModMon 100 (Figure 9c and Figure 11c).
The model in this investigation used a simple linear regression to vary the extinction coefficient with salinity, since salinity is closely associated with the clarity and color of water in the estuary. However, salinity only accounts for 44% of the variation in the extinction coefficient. Since previous research has demonstrated that light availability affects phytoplankton productivity in the NRE [27], it is necessary in future versions of the NEEM to be able to predict extinction coefficients with greater reliability.
Elevation data came from many different locations, times, agencies, and methods. In addition, no elevation data were available for 1 January 2000–31 May 2002 and after 1 January 2009. A more frequent, accurate, and complete source of elevation data is needed to predict tidal flows into and out of the estuary.
All flows in the eleven branches and three non-WWTP tributaries were scaled from the Neuse and Trent Rivers using the ratios of drainage areas. Thus, the assumption was made that the drainage areas have the same runoff coefficients. In the future, it may be possible to capture both the spatially and temporally varying runoff characteristics of the drainage areas with a GIS-based tool. This information can then be used to more accurately predict the flows in the non-gauged branches and tributaries.
The simple treatment of sediment employed in this model uses a combination of a constant zero-order SOD and a temperature-dependent, first-order SOD. Furthermore, denitrification was modeled as solely a water-column process, and as such was not DO-dependent. The model does not calculate sediment to water column nutrient fluxes based on organic matter delivery to the sediments. The previous version of the Neuse River Estuary featured a custom sediment diagenesis subroutine and may explain why it was better able to predict ammonia, orthophosphate, and dissolved oxygen. We are currently working to assess whether the updated sediment model of the latest version of CE-QUAL-W2 (Version 4) can better simulate sediment/water-column fluxes, nutrients and dissolved oxygen in this system.
5. Summary
Chlorophyll calibration was performed for both time periods simultaneously by performing a full-factorial experiment consisting of testing seven algal kinetic growth parameters over three levels. Six criteria were used to determine which runs performed acceptably. As a result, the mean and standard deviation of the 27 cases that met all of the criteria were used in all subsequent analyses. The set of algal kinetic parameters used in the previous W2 study of the Neuse River Estuary [9] did not meet all six criteria.
Although average chlorophyll performance for the new model period (2006–2008) was relatively weak, performance for the earlier time period improved considerably over previous work [4,9,28]. Compared to the most recent W2 effort, the average calibration performance for both periods combined decreased significantly for ammonia, decreased slightly for phosphate and dissolved oxygen and increased for nitrate + nitrite. The results of the work suggest that improvements in the model should focus on improving the downstream boundary specification, specification of non-point source nutrient loads from the most downstream part of the watershed, and improving the sediment diagenesis sub-model.
Author Contributions
Conceptualization, J.B.; Methodology, J.B.; Software, J.B. and N.H.; Validation, J.B. and N.H.; Formal Analysis, N.H.; Investigation, J.B and N.H.; Resources, J.B.; Data Curation, J.B. and N.H.; Writing-Original Draft Preparation, N.H.; Writing-Review & Editing, J.B. and N.H.; Visualization, J.B. and N.H.; Supervision, J.B.; Project Administration, J.B.; Funding Acquisition, J.B.
Funding
This research was funded by the North Carolina Water Resources Research Institute grant number 2016-0454-01, and by the U.S. Geological Survey grant number 2016-1887-01.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Paerl, H.W. Nuisance phytoplankton blooms in coastal, estuarine, and inland waters. Limnol. Oceanogr. 1988, 33, 823–847. [Google Scholar] [CrossRef]
- Pinckney, J.L.; Millie, D.F.; Vinyard, B.T.; Paerl, H. Environmental controls of phytoplankton bloom dynamics in the Neuse River Estuary, North Carolina, USA. Can. J. Fish. Aquat.Sci. 1997, 54, 2491–2501. [Google Scholar] [CrossRef]
- Stow, C.A.; Roessler, C.; Borsuk, M.E.; Bowen, J.D.; Reckhow, K.H. Comparison of estuarine water quality models for total maximum daily load development in Neuse River Estuary. J. Water Resour. Plan. Manag. 2003, 129, 307–314. [Google Scholar] [CrossRef]
- Bowen, J.D.; Hieronymus, J.W. A CE-QUAL-W2 model of Neuse Estuary for total maximum daily load development. J. Water Resour. Plan. Manag. 2003, 129, 283–294. [Google Scholar] [CrossRef]
- Bowen, J.D.; Hieronymus, J. Neuse River Estuary Modeling and Monitoring Project Stage 1: Predictions and Uncertainty Analysis of Response to Nutrient Loading Using a Mechanistic Eutrophication Model; Report No. 325 for Water Resources Research; Institute of the University of North Carolina: Raleigh, NC, USA, October 2000. [Google Scholar]
- Paerl, H.W.; Hall, N.S.; Peierls, B.L.; Rossignol, K.L.; Joyner, A.R. Hydrologic variability and its control of phytoplankton community structure and function in two shallow, coastal, lagoonal ecosystems: the Neuse and New River Estuaries, North Carolina, USA. Estuaries Coasts 2014, 37, 31–45. [Google Scholar] [CrossRef]
- Lebo, M.E.; Paerl, H.W.; Peierls, B.L. Evaluation of progress in achieving TMDL mandated nitrogen reductions in the Neuse River Basin, North Carolina. Environ. Manag. 2012, 49, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Paerl, H.W.; Valdes, L.M.; Piehler, M.F.; Stow, C.A. Assessing the effects of nutrient management in an estuary experiencing climatic change: The Neuse River Estuary, North Carolina. Environ. Manag. 2006, 37, 422–436. [Google Scholar] [CrossRef] [PubMed]
- Hieronymus, J.; Bowen, J.D. Calibration and Verification of a Two-dimensional Laterally Averaged Mechanistic Model of the Neuse River Estuary; Report No. 343c for Water Resources Research; Institute of the University of North Carolina: Raleigh, NC, USA, July 2004. [Google Scholar]
- Liu, W.C.; Chen, W.B.; Kimura, N. Impact of phosphorus load reduction on water quality in a stratified reservoir-eutrophication modeling study. Environ. Monit. Assess. 2009, 159, 393–406. [Google Scholar] [CrossRef] [PubMed]
- Etemad-Shahidi, A.; Afshar, A.; Alikia, H.; Moshfeghi, H. Total dissolved solid modeling; Karkheh reservoir case example. Int. J. Environ. Res. 2009, 3, 671–680. [Google Scholar]
- Gelda, R.K.; Effler, S.W. Testing and application of a two-dimensional hydrothermal model for a water supply reservoir: Implications of sedimentation. J. Environ. Eng. Sci. 2007, 6, 73–84. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L. Multiobjective water quality model calibration using a hybrid genetic algorithm and neural network–based approach. J. Environ. Eng. 2010, 136, 1020–1031. [Google Scholar] [CrossRef]
- Afshar, A.; Kazemi, H.; Saadatpour, M. Particle swarm optimization for automatic calibration of large scale water quality model (CE-QUAL-W2): Application to Karkheh Reservoir, Iran. Water Resour. Manag. 2011, 25, 2613–2632. [Google Scholar] [CrossRef]
- Afshar, A.; Shojaei, N.; Sagharjooghifarahani, M. Multiobjective calibration of reservoir water quality modeling using multiobjective particle swarm optimization (MOPSO). Water Resour. Manag. 2013, 27, 1931–1947. [Google Scholar] [CrossRef]
- Grangere, K.; Lefebvre, S.; Ménesguen, A.; Jouenne, F. On the interest of using field primary production data to calibrate phytoplankton rate processes in ecosystem models. Estuar. Coast. Shelf Sci. 2009, 81, 169–178. [Google Scholar] [CrossRef]
- Arhonditsis, G.B.; Papantou, D.; Zhang, W.T.; Perhar, G.; Massos, E.; Shi, M. Bayesian calibration of mechanistic aquatic biogeochemical models and benefits for environmental management. J. Mar. Syst. 2008, 73, 8–30. [Google Scholar] [CrossRef]
- Arhonditsis, G.B.; Qian, S.S.; Stow, C.A.; Lamon, E.C.; Reckhow, K.H. Eutrophication risk assessment using Bayesian calibration of process-based models: Application to a mesotrophic lake. Ecol. Model. 2007, 208, 215–229. [Google Scholar] [CrossRef]
- Bowen, J.; Harrigan, N.B. Comparing the Impact of Organic Versus Inorganic Nitrogen Loading to the Neuse River Estuary With a Mechanistic Eutrophication Model; Report No. 470 for Water Resources Research; Institute of the University of North Carolina: Raleigh, NC, USA, September 2017. [Google Scholar]
- Cole, T.M.; Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 3.72 User Manual; Technical Report; Department of Civil and Environmental Engineering, Portland State University: Portland, OR, USA, 2015. [Google Scholar]
- Paerl, H.W.; Rossignol, K.L.; Hall, S.N.; Peierls, B.L.; Wetz, M.S. Phytoplankton community indicators of short-and long-term ecological change in the anthropogenically and climatically impacted Neuse River Estuary, North Carolina, USA. Estuaries Coasts 2010, 33, 485–497. [Google Scholar] [CrossRef]
- Paerl, H.W.; Valdes, L.M.; Peierls, B.L.; Adolf, J.E.; Harding, L.J.W. Anthropogenic and climatic influences on the eutrophication of large estuarine ecosystems. Limnol. Oceanogr. 2006, 51, 448–462. [Google Scholar] [CrossRef]
- Steele, J.H. Environmental control of photosynthesis in the sea. Limnol. Oceanogr. 1962, 7, 137–150. [Google Scholar] [CrossRef]
- Thornton, K.W.; Lessem, A.S. A temperature algorithm for modifying biological rates. Trans. Am. Fish. Soc. 1978, 107, 284–287. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Boyer, J.N.; Christian, R.R.; Stanley, D.W. Patterns of phytoplankton primary productivity in the Neuse River estuary, North Carolina, USA. Mar. Ecol. Prog. Ser. 1993, 97, 287–297. [Google Scholar] [CrossRef]
- Wool, T.A.; Davie, S.R.; Rodriguez, H.N. Development of three-dimensional hydrodynamic and water quality models to support total maximum daily load decision process for the Neuse River Estuary, North Carolina. J. Water Resour. Plan. Manag. 2003, 129, 295–306. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).