Simulation of the Arctic—North Atlantic Ocean Circulation with a Two-Equation K-Omega Turbulence Parameterization
Abstract
1. Introduction
- to present a new splitting algorithm for solving turbulence equations that allows to reduce the complete system to the stages of transport-diffusion and generation-dissipation;
- to find an analytical solution of equations at the generation-dissipation splitting stage that is impossible for and closures;
- to demonstrate possibilities of controlling the obtained analytical solution of equations through its coefficients by means of different physical factors. We take into account such physical factors as climatic annual mean buoyancy frequency (AMBF) and Prandtl number as function of the Richardson number to goal this aim;
- to compare results of numerical experiments with the INMOM + to data on the hydrographic structure of the North Atlantic and Arctic Ocean to demonstrate physical effects of the accounting AMBF and variations of the Prandtl number.
2. Model and Methods
2.1. Equations of the Ocean General Circulation Model
2.2. The Two-Equation K-Omega Turbulence Model
2.3. Boundary and Initial Conditions
2.4. Numerical Algorithm
- The symmetrized form gives the form of the adjoint operator, which is close to the original one.
- This form leads to the finite difference approximation retaining the main properties typical of original differential operators (symmetry, skew-symmetry, nonnegativeness).
- From the form naturally follows the splitting of the problem operator into the sum of simple nonnegative operators.
3. Scenarios of Numerical Experiments
- , , and ;
- , , and .
4. Discussion
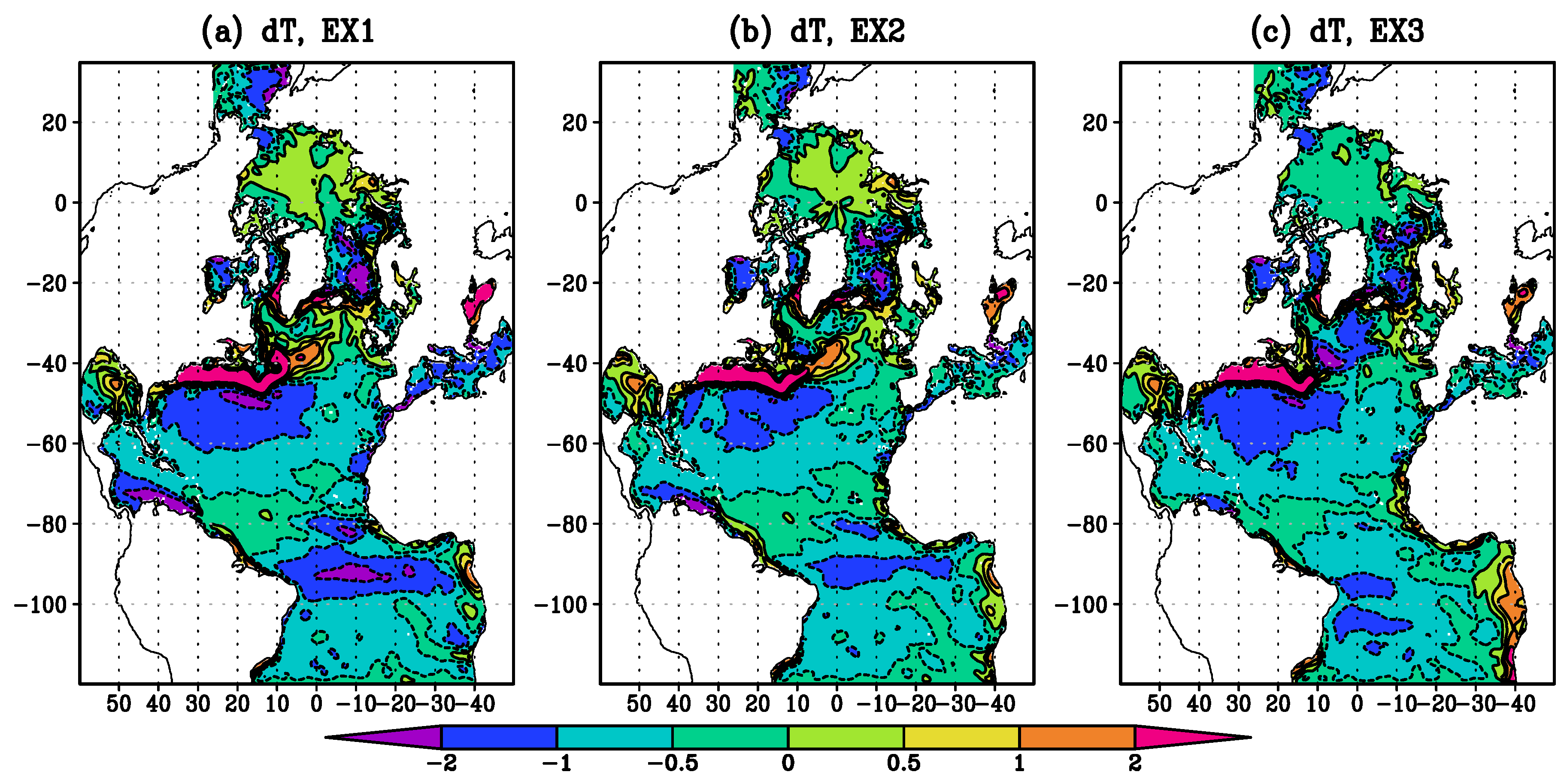
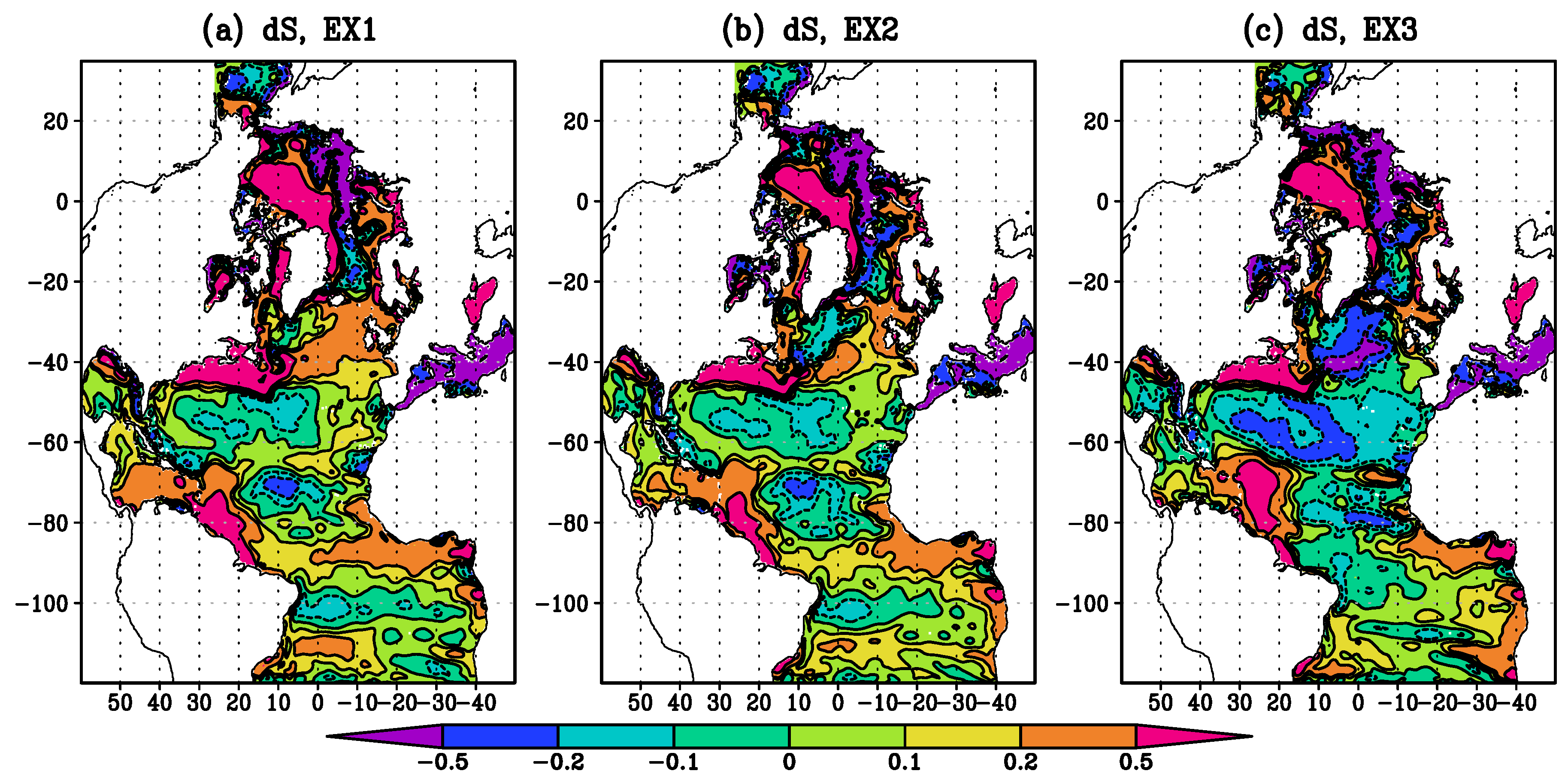
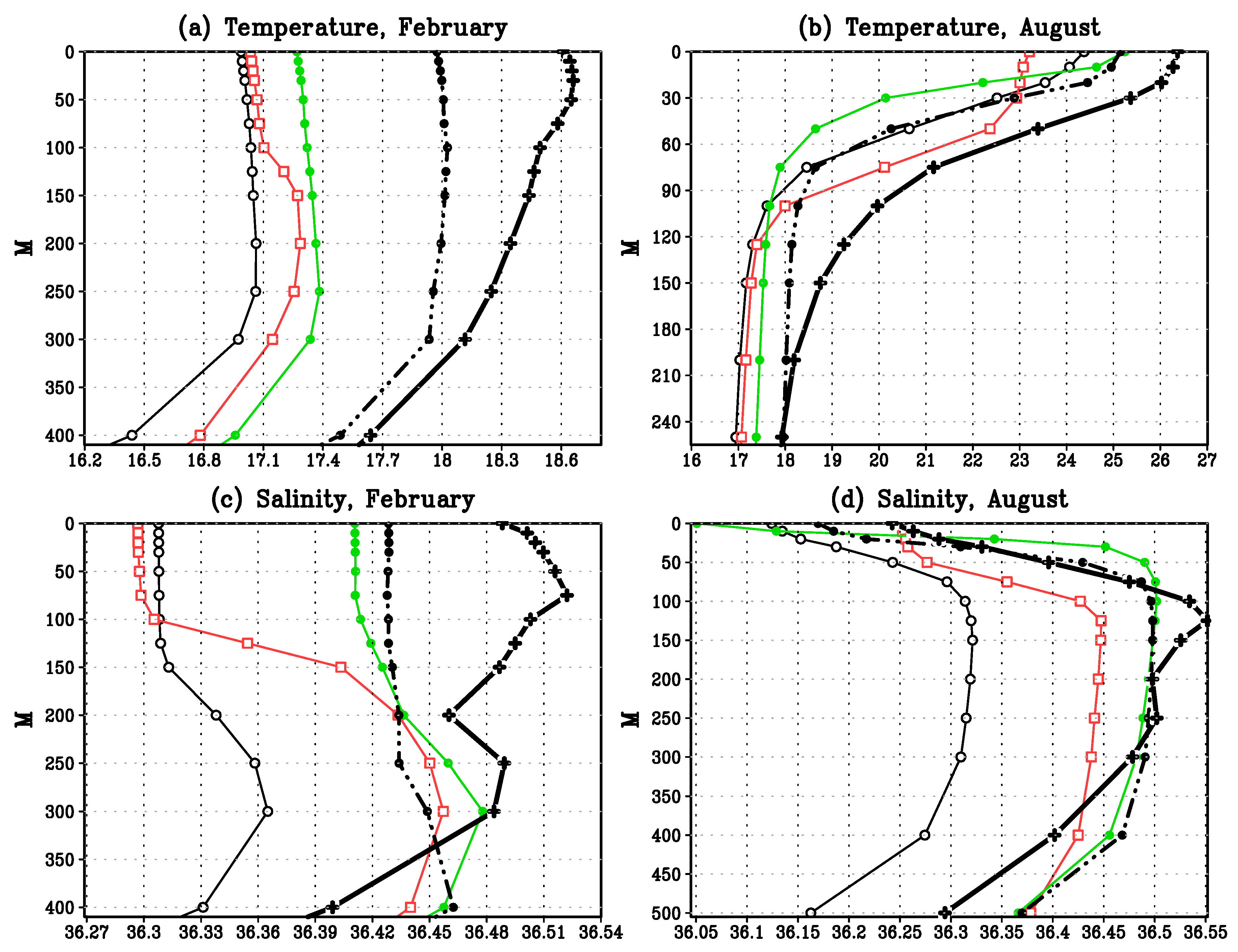
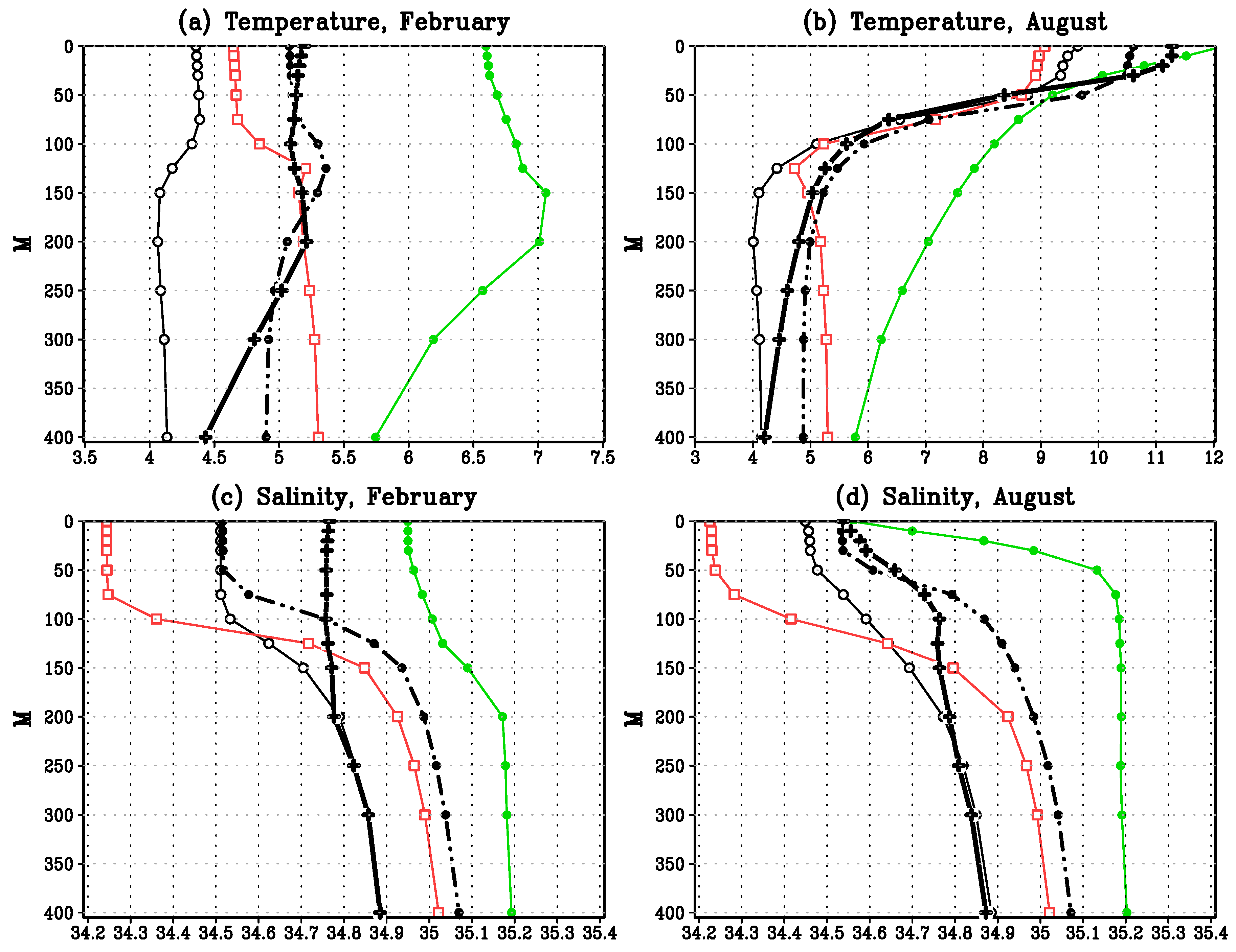
4.1. Comparison to the Generalized Observational Data
4.2. Sensitivity of Ocean Model Characteristics to the Changes in Mixing Parametrization
4.3. Turbulent Energy and Omega
4.4. Numerical Aspects, Data Assimilation
5. Summary
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMBF | Annual Mean Buoyancy Frequency |
| INMOM | Institute of Numerical Mathematics Ocean Model |
| OGCM | Ocean General Circulation Model |
| STA | Splitting Turbulence Algorithm |
References
- Ibrayev, R.; Khabeev, R.; Ushakov, K.V. Eddy-resolving 1/10° model of the World Ocean. Izv. Atmos. Ocean. Phys. 2012, 48, 37–46. [Google Scholar] [CrossRef]
- Maslowski, W.; Kinney, J.; Marble, D.; Jakacki, J. Towards Eddy-Resolving Models of the Arctic Ocean. In Ocean Modeling in an Eddying Regime; American Geophysical Union: Washington, DC, USA, 2013; pp. 241–264. [Google Scholar] [CrossRef]
- Mellor, G. Users guide for a three-dimensional, primitive equation, numerical ocean model. In Program in Atmospheric and Oceanic Sciences; Princeton University: Princeton, NJ, USA, 2004. [Google Scholar]
- Zalesny, V.; Gusev, A. Mathematical model of the World Ocean dynamics with algorithms of variational assimilation of temperature and salinity fields. Russ. J. Numer. Anal. Math. Model. 2009, 24, 171–191. [Google Scholar] [CrossRef]
- Zalesny, V.; Marchuk, G.; Agoshkov, V.; Bagno, A.; Gusev, A.; Diansky, N.; Moshonkin, S.; Tamsalu, R.; Volodin, E. Numerical simulation of large-scale ocean circulation based on the multicomponent splitting method. Russ. J. Numer. Anal. Math. Model. 2010, 25, 581–609. [Google Scholar] [CrossRef]
- Sarkisyan, A.; Sündermann, J. Modelling Ocean Climate Variability; Springer Science+Business Media B.V.: Berlin, Germany, 2009; p. 374. [Google Scholar]
- Moshonkin, S.; Alekseev, G.; Bagno, A.; Gusev, A.; Diansky, N.; Zalesny, V. Numerical simulation of the North Atlantic—Arctic Ocean—Bering Sea circulation in the 20th century. Russ. J. Numer. Anal. Math. Model. 2011, 26, 161–178. [Google Scholar] [CrossRef]
- Pacanowski, R.; Philander, S. Parameterization of Vertical Mixing in Numerical Models of Tropical Oceans. J. Phys. Oceanogr. 1981, 11, 1443–1451. [Google Scholar] [CrossRef]
- Moshonkin, S.; Gusev, A.; Zalesny, V.; Byshev, V. Mixing parameterizations in ocean climate modeling. Izv. Atmos. Ocean. Phys. 2016, 52, 196–206. [Google Scholar] [CrossRef]
- Moshonkin, S.; Tamsalu, R.; Zalesny, V. Modeling sea dynamics and turbulent zones on high spatial resolution nested grids. Oceanology 2007, 47, 747–757. [Google Scholar] [CrossRef]
- Moshonkin, S.; Zalesny, V.; Gusev, A.; Tamsalu, R. Turbulence modeling in ocean circulation problems. Izv. Atmos. Ocean. Phys. 2014, 50, 49–60. [Google Scholar] [CrossRef]
- Noh, Y.; Kang, Y.; Matsuura, T.; Iizuka, S. Effect of the Prandtl number in the parameterization of vertical mixing in an OGCM of the tropical Pacific. Geophys. Res. Lett. 2005, 32, L23609. [Google Scholar] [CrossRef]
- Noh, Y.; Ok, H.; Lee, E.; Toyoda, T.; Hirose, N. Parameterization of Langmuir Circulation in the Ocean Mixed Layer Model Using LES and Its Application to the OGCM. J. Phys. Oceanogr. 2016, 46, 57–78. [Google Scholar] [CrossRef]
- Semenov, E. Numerical modeling of White Sea dynamics and monitoring problem. Izv. Atmos. Ocean. Phys. 2004, 40, 114–126. [Google Scholar]
- Warner, J.; Sherwood, C.; Arango, H.; Signell, R. Performance of four turbulence closure models implemented using a generic length scale method. Ocean Modell. 2005, 8, 81–113. [Google Scholar] [CrossRef]
- Kantha, L.; Clayson, C. An improved mixed layer model for geophysical applications. J. Geophys. Res. Oceans 1994, 99, 25235–25266. [Google Scholar] [CrossRef]
- Kolmogorov, A. Equations of turbulent motion of an incompressible fluid. Izv. Acad. Sci. USSR Phys. Ser. 1942, 6, 56–58. [Google Scholar]
- Mellor, G.; Yamada, T. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. J. Atmos. Sci. 1974, 31, 1791–1806. [Google Scholar] [CrossRef]
- Saffman, P. A model for inhomogeneous turbulent flow. Proc. R. Soc. Lon. A Math. Phys. Eng. Sci. 1970, 317, 417–433. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Mellor, G.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Noh, Y.; Min, H.; Raasch, S. Large Eddy Simulation of the Ocean Mixed Layer: The Effects of Wave Breaking and Langmuir Circulation. J. Phys. Oceanogr. 2004, 34, 720–735. [Google Scholar] [CrossRef]
- Madec, G.; The NEMO Team. NEMO Ocean Engine. TKE Turbulent Closure Scheme; Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL): France, 2016. [Google Scholar]
- Umlauf, L.; Burchard, H.; Hutter, K. Extending the k − ω turbulence model towards oceanic applications. Ocean Modell. 2003, 5, 195–218. [Google Scholar] [CrossRef]
- Canuto, V.; Howard, A.; Cheng, Y.; Muller, C.; Leboissetier, A.; Jayne, S. Ocean turbulence, III: New GISS vertical mixing scheme. Ocean Modell. 2010, 34, 70–91. [Google Scholar] [CrossRef]
- Marchuk, G. Methods of Numerical Mathematics, 2nd ed.; Stochastic Modelling and Applied Probability; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zalesny, V.; Gusev, A.; Ivchenko, V.; Tamsalu, R.; Aps, R. Numerical model of the Baltic Sea circulation. Russ. J. Numer. Anal. Math. Model. 2013, 28, 85–100. [Google Scholar] [CrossRef]
- Brydon, D.; Sun, S.; Bleck, R. A new approximation of the equation of state for seawater, suitable for numerical ocean models. J. Geophys. Res. Oceans 1999, 104, 1537–1540. [Google Scholar] [CrossRef]
- Yakovlev, N. Reproduction of the large-scale state of water and sea ice in the Arctic Ocean in 1948–2002: Part I. Numerical model. Izv. Atmos. Ocean. Phys. 2009, 45, 357–371. [Google Scholar] [CrossRef]
- Burchard, H.; Bolding, K.; Villarreal, M. GOTM, A General Ocean Turbulence Model: Theory, Implementation and Test Cases; EUR/European Commission, Space Applications Institute: Gujarat, India, 1999. [Google Scholar]
- Miropolski, Y.Z. Non-stationary model of the layer of the convective-wind mixing in the ocean. Izv. Atmos. Ocean. Phys. 1970, 6, 1284–1294. [Google Scholar]
- Zaslavskii, M.; Zalesny, V.; Kabatchenko, I.; Tamsalu, R. On the self-adjusted description of the atmospheric boundary layer, wind waves, and sea currents. Oceanology 2006, 46, 159–169. [Google Scholar] [CrossRef]
- Marchuk, G. Splitting and alternative direction methods. In Handbook of Numerical Analysis; Ciarlet, P., Lions, J., Eds.; Springer: Amsterdam, The Netherlands, 1990; pp. 197–462. [Google Scholar]
- Lebedev, V. Difference analogies of orthogonal decompositions of basic differential operators and some boundary value problems. J. Comput. Math. Math. Phys. 1964, 4, 449–465. [Google Scholar]
- Mesinger, F.; Arakawa, A. (Eds.) Global Atmospheric Research Program World Meteorological Organization: Switzerland. In Numerical Methods Used in Atmospheric Models; Wiley: Hoboken, NJ, USA, 1976; Volume 1. [Google Scholar]
- National Geophysical Data Center, NOAA. 2-Minute Gridded Global Relief Data (ETOPO2) V2; National Geophysical Data Center: Boulder, MT, USA, 2006. [CrossRef]
- Large, W.; Yeager, S. The global climatology of an interannually varying air–sea flux data set. Clim. Dyn. 2009, 33, 341–364. [Google Scholar] [CrossRef]
- Steele, M.; Morley, R.; Ermold, W. PHC: A Global Ocean Hydrography with a High-Quality Arctic Ocean. J. Clim. 2001, 14, 2079–2087. [Google Scholar] [CrossRef]
- Blanke, B.; Delecluse, P. Variability of the Tropical Atlantic Ocean Simulated by a General Circulation Model with Two Different Mixed-Layer Physics. J. Phys. Oceanogr. 1993, 23, 1363–1388. [Google Scholar] [CrossRef]
- Unesco. Tenth Report of the Joint Panel on Oceanographic Tables and Standards: Sidney, B.C., Canada 1–5 SEptember 1980 Sponsored by Unesco, ICES, SCOR, IAPSO; Unesco Technical Papers in Marine Science; UNESCO: Paris, France, 1981. [Google Scholar]
- Locarnini, R.; Mishonov, A.; Antonov, J.; Boyer, T.; Garcia, H.; Baranova, O.; Zweng, M.; Johnson, D. World Ocean Atlas 2009, Volume 1: Temperature; Levitus, S., Ed.; NOAA Atlas NESDIS 68; U.S. Government Printing Office: Washington, DC, USA, 2010; p. 184.
- Antonov, J.; Seidov, D.; Boyer, T.; Locarnini, R.; Mishonov, A.; Garcia, H.; Baranova, O.; Zweng, M.; Johnson, D. World Ocean Atlas 2009, Volume 2: Salinity; Levitus, S., Ed.; NOAA Atlas NESDIS 69; U.S. Government Printing Office: Washington, DC, USA, 2010; p. 184.
- Munk, W.; Anderson, E. Notes on a theory of the thermocline. J. Mar. Res. 1948, 7, 276–295. [Google Scholar]
- De Boyer Montégut, C.; Madec, G.; Fischer, A.; Lazar, A.; Iudicone, D. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. J. Geophys. Res. Oceans 2004, 109, C12003. [Google Scholar] [CrossRef]
- Monin, A.; Ozmidov, R. Oceanic Turbulence; Hydrometeoizdat: Leningrad, Russia, 1981; p. 320. [Google Scholar]
- Blum, J.; Le Dimet, F.; Navon, I. Data Assimilation for Geophysical Fluids. In Special Volume: Computational Methods for the Atmosphere and the Oceans; Temam, R., Tribbia, J., Eds.; Handbook of Numerical Analysis; Elsevier: New York, NY, USA, 2009; Volume 14, pp. 385–441. [Google Scholar]
- Marchuk, G.; Paton, B.; Korotaev, G.; Zalesny, V. Data-computing technologies: A new stage in the development of operational oceanography. Izv. Atmos. Ocean. Phys. 2013, 49, 579–591. [Google Scholar] [CrossRef]
- Korotaev, G.; Oguz, T.; Dorofeyev, V.; Demyshev, S.; Kubryakov, A.; Ratner, Y. Development of Black Sea nowcasting and forecasting system. Ocean Sci. 2011, 7, 629–649. [Google Scholar] [CrossRef]
- Korotaev, G.; Saenko, O.; Koblinsky, C. Satellite altimetry observations of the Black Sea level. J. Geophys. Res. Oceans 2001, 106, 917–933. [Google Scholar] [CrossRef]
- Agoshkov, V.; Zalesny, V. Variational Data Assimilation Technique in Mathematical Modeling of Ocean Dynamics. Pure Appl. Geophys. 2012, 169, 555–578. [Google Scholar] [CrossRef]
- Zalesny, V.; Agoshkov, V.; Shutyaev, V.; Le Dimet, F.; Ivchenko, V. Numerical modeling of ocean hydrodynamics with variational assimilation of observational data. Izv. Atmos. Ocean. Phys. 2016, 52, 431–442. [Google Scholar] [CrossRef]

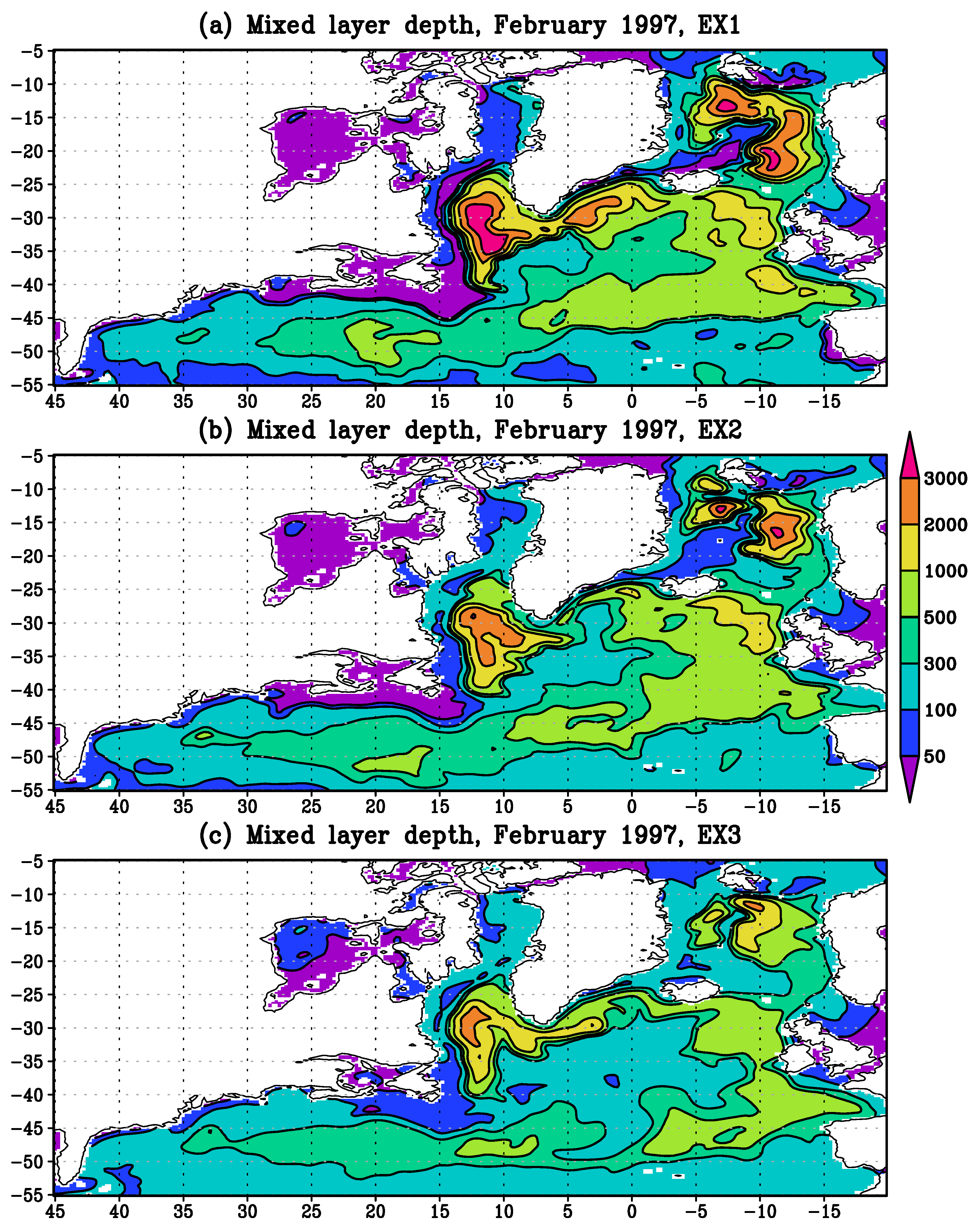

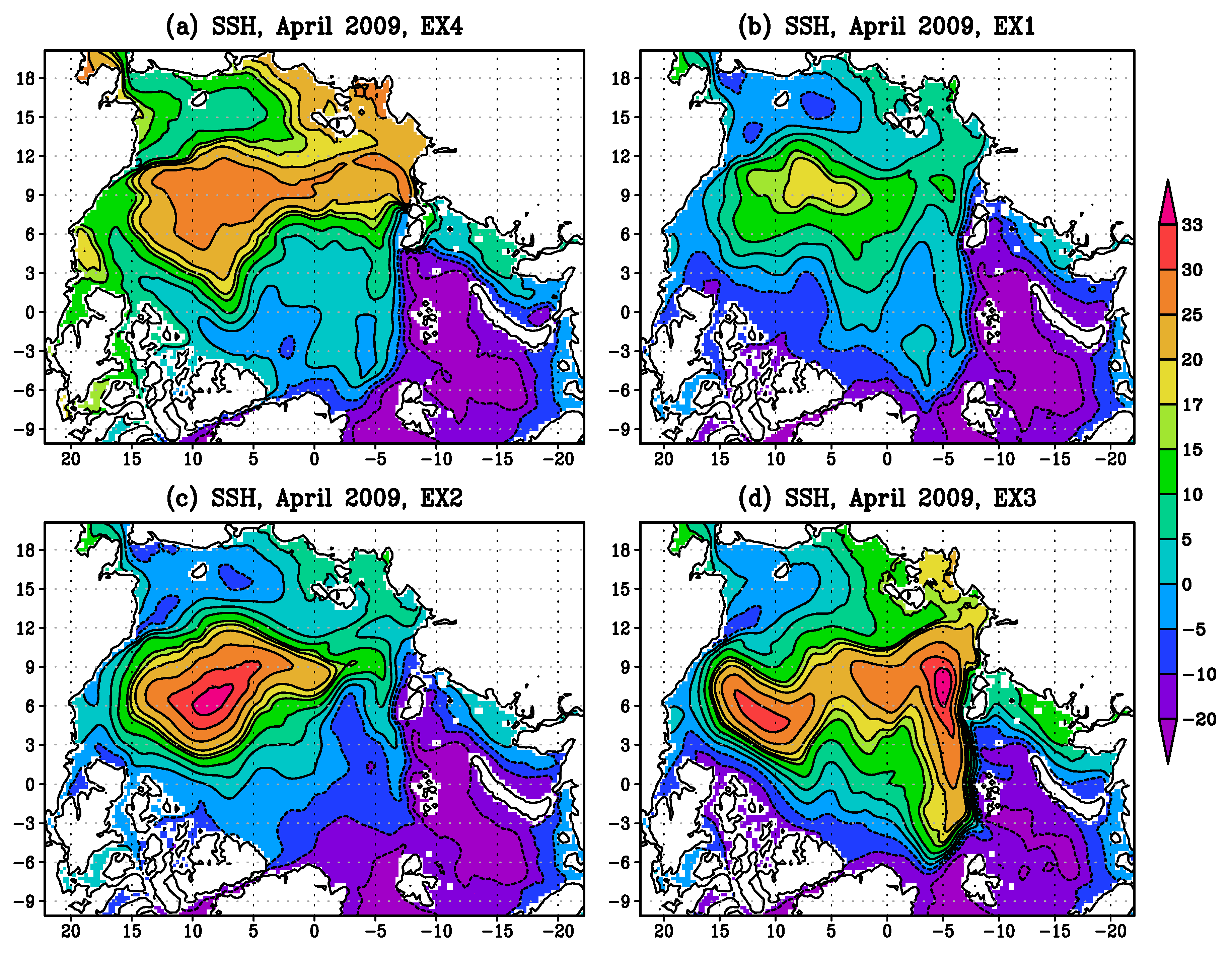
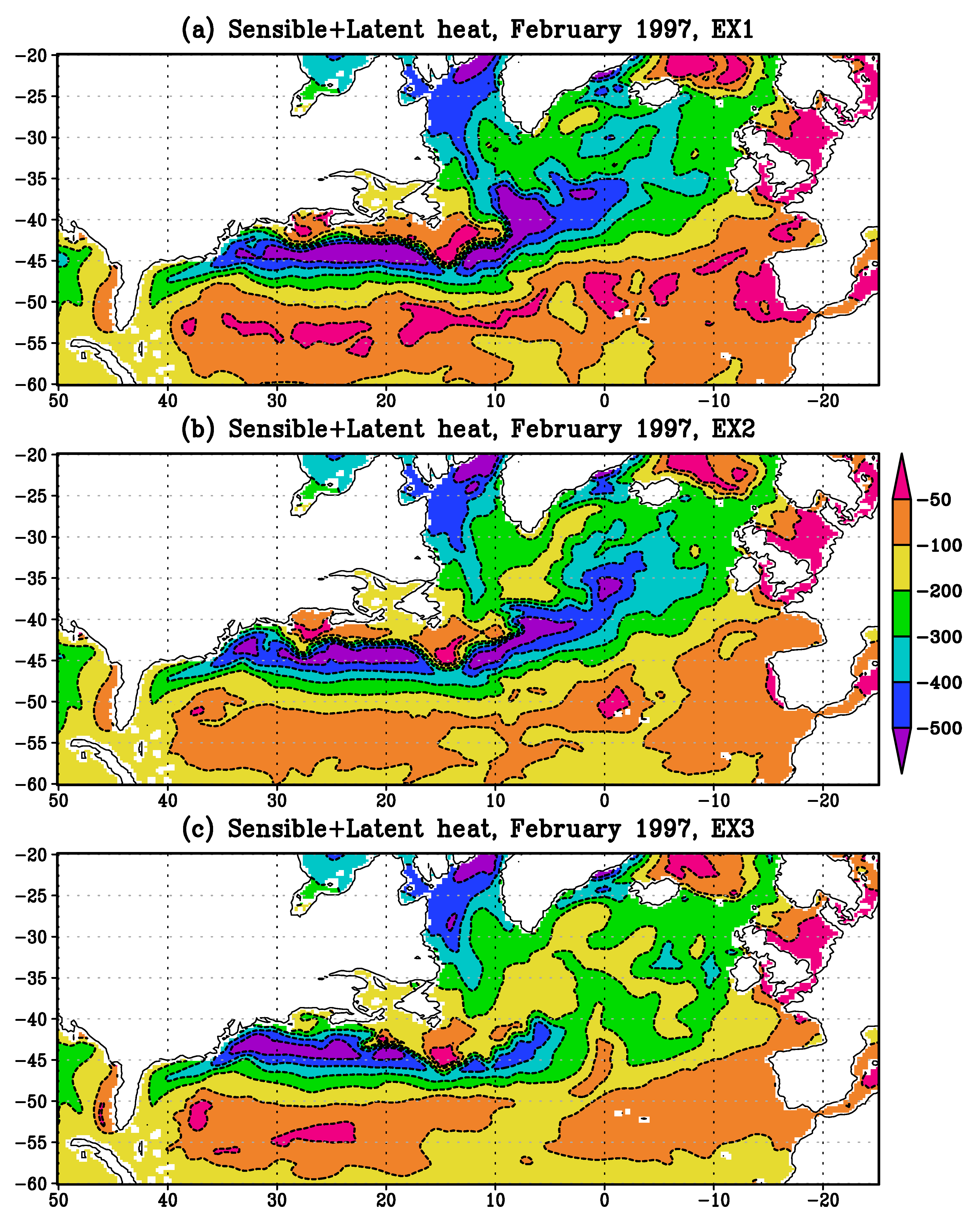

| Experiments | Prandtl Number | Computation of k and | Accounting AMBF | Viscosity and Diffusivity |
|---|---|---|---|---|
| EX1 | ||||
| EX2 | ||||
| EX3 | ||||
| EX4 | No | No | No |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moshonkin, S.; Zalesny, V.; Gusev, A. Simulation of the Arctic—North Atlantic Ocean Circulation with a Two-Equation K-Omega Turbulence Parameterization. J. Mar. Sci. Eng. 2018, 6, 95. https://doi.org/10.3390/jmse6030095
Moshonkin S, Zalesny V, Gusev A. Simulation of the Arctic—North Atlantic Ocean Circulation with a Two-Equation K-Omega Turbulence Parameterization. Journal of Marine Science and Engineering. 2018; 6(3):95. https://doi.org/10.3390/jmse6030095
Chicago/Turabian StyleMoshonkin, Sergey, Vladimir Zalesny, and Anatoly Gusev. 2018. "Simulation of the Arctic—North Atlantic Ocean Circulation with a Two-Equation K-Omega Turbulence Parameterization" Journal of Marine Science and Engineering 6, no. 3: 95. https://doi.org/10.3390/jmse6030095
APA StyleMoshonkin, S., Zalesny, V., & Gusev, A. (2018). Simulation of the Arctic—North Atlantic Ocean Circulation with a Two-Equation K-Omega Turbulence Parameterization. Journal of Marine Science and Engineering, 6(3), 95. https://doi.org/10.3390/jmse6030095







