Abstract
Headland bypassing is the transport of sediment around rocky headlands by wave and tidal action, associated with high-energy conditions and embayment circulation (e.g., mega-rips). Bypassing may be a key component in the sediment budget of many coastal cells, the quantification of which is required to predict the coastal response to extreme events and future coastal change. Waves, currents, and water levels were measured off the headland of a sandy, exposed, and macrotidal beach in 18-m and 26-m depths for 2 months. The observations were used to validate a Delft3D morphodynamic model, which was subsequently run for a wide range of scenarios. Three modes of bypassing were determined: (i) tidally-dominated control during low–moderate wave conditions [flux O (0–102 m3 day−1)]; (ii) combined tidal- and embayment circulation controls during moderate–high waves [O (103 m3 day−1)]; and (iii) multi-embayment circulation control during extreme waves [O (104 m3 day−1)]. A site-specific bypass parameter is introduced, which accurately (R2 = 0.95) matches the modelled bypass rates. A 5-year hindcast predicts bypassing is an order of magnitude less than observed cross-shore fluxes during extreme events, suggesting that bypassing at this site is insignificant at annual timescales. This work serves a starting point to generalise the prediction of headland bypassing.
1. Introduction
A key component in assessing the dynamic behaviour of a coastal cell [1,2] is knowledge of the sediment budget [3,4,5], including sediment fluxes in the cross-shore and alongshore. Cross-shore transport includes sediment movement to and from dunes (e.g., [6]), through the intertidal to sub-tidal beach (e.g., [7]) and out to and beyond the depth of closure (e.g., [8]). In the alongshore, sediment transport on long, straight, sandy beaches is a function of wave energy and direction [9], with sediment flux peaking for large and high-oblique waves. Alongshore transport is complicated by the presence of estuaries that may be sources or sinks of sediment (e.g., [10]) and by headlands or engineered structures that may act as partial or complete barriers to transport. Bypassing is the process of sediment transport around rigid obstructions to longshore transport on beaches, forced by waves and mean currents [11,12]. The occurrence of bypassing may invalidate the assumption of a coastal cell as a closed compartment (e.g., [13]), making the quantification of sediment budgets and longer-term coastal change more complex as inputs and outputs will have to be known.
Substantial research effort has been given to investigate bypassing around human-made structures [14,15]. Engineered scenarios are often amenable to analytical solutions that estimate sand bypassing rates and shoreline change using simplifying assumptions, including one-line models, straight shorelines, and geometrically idealised structures. Similarly, longshore and rip currents in the vicinity of groynes may be estimated with simple parameterisations [16] due to near-idealised geometry. Natural headlands on embayed beaches are more geometrically complex and the estimation of currents and bypassing rates in these instances may not be well predicted by simple analytical models [17]. Sediment transport in the vicinity of headlands likely involves significant wave–current interaction [18,19], with wave oscillations stirring bottom sediment, while mean currents contribute significantly to sediment transport [20]. One solution to address this complexity is the application of two-dimensional (2D)-horizontal or three-dimensional (3D) processed-based numerical models that couple waves, hydrodynamic, and morphodynamic processes.
For relatively larger headlands with deeper water (>10 m) off the toe of the headland, bypassing is often thought to occur only during extreme wave events [21] or not at all. Additionally, field observations in the vicinity of headlands are limited, possibly due to the energetic and hazardous conditions presented by this environment. As a consequence, natural headland bypassing is a poorly-researched area, but one that constitutes a critical component of sediment budgets on a variety of embayed coastlines worldwide. It is therefore necessary to develop a greater understanding of headland bypassing on rocky and embayed coasts to manage such coastlines and predict how they will adapt under varying wave forcing and sea levels in the future.
Headland bypassing has only recently become an area of focussed research, with early descriptions being primarily qualitative [21]. Three mechanisms for bypass were suggested by [22], including the following: (i) headland attached bars that build-up against a headland, then gradually migrate around the headland in moderate- to high-energy waves; (ii) mega-rip bypassing during major storms, with sediment transported by the rip current out beyond the headland; and (iii) across-embayment bypassing, where sediment is transported directly across an embayment in deeper water.
Both the mega-rip and across-embayment mechanisms are examples of embayment-cellular circulation [23], which has been described for idealised scenarios using the embayed beach state model [21,24], where the end-member states include the following: (i) ‘normal’ beach circulation, with rip cells occurring along the beach, and the headlands having minimal impact; and (ii) cellular circulation with two large headland rips or a single large embayment-cellular rip at the centre of the beach. These large-scale, hard-morphology controlled circulations are often simply described as mega-rips [25,26] and can result in extreme morphological changes within embayments [27,28]. Despite the clear importance of embayment cellular circulation in hydrodynamic forcing around headlands, little effort has been made to relate embayment circulation to headland bypassing.
Direct observations of sediment transport around headlands are extremely limited, for example through sediment trapping methods [12] or sediment tracers [29], and are restricted to low–moderate wave conditions. Headland bypassing has in some instances been inferred from changes in beach volume [30], without direct measurement. Morphological characteristics of headlands, such as length, width, and offshore slope, have been examined through multi-variate statistical analysis [31], finding that large headlands with acute apexes are more effective at preventing sediment bypassing than small headlands with rounded apexes. Numerical simulations of the morphodynamics of embayed beaches exist [24,32,33,34,35] but are limited to flow and sediment transport within, but not between, embayments. Similarly, many coastal evolution models (e.g., [36]; COVE, [37]) are designed for open coasts or within embayments and do not account for headlands and other hard morphological features that may impede transport or control circulation, effectively treating headlands as boundaries impermeable to sediment flux.
Other efforts have attempted to use numerical models of idealised headlands to determine the major controls on bypassing [38] and found, as expected, that sediment bypassing increases under larger, more oblique waves. However, such efforts have limited predictive capacity if they become too abstracted from naturally observed headlands. Hydro-morphodynamic modelling, using a validated numerical model, of a group of adjacent natural headlands has been undertaken [12], with quantification of predicted bypassing of individual headlands for a given year. Additionally, an examination of the impact of varying wave, wind, and tidal conditions on bypassing for this same group of headlands [39,40] found that for a micro-tidal climate, waves were the greater driving force by two orders of magnitude; however, the effect of tide in a macrotidal climate has not been examined. While [40] described the broad impact of wave–tide controls across multiple nearby headlands, it did not examine detailed circulatory controls across any individual embayment or provide a means to predict bypassing for the observed headlands. Several recent efforts [12,31,41] have concluded that many coastal embayments previously assumed to be closed cells may in reality experience some degree of headland bypassing, making them open systems.
As yet, no quantitative method is available for predicting headland bypass rates and no conceptual model exists for assessing the influence of embayment circulatory behaviour on bypassing. Our long-term objective is to develop a relatively simple and generalised sediment bypass prediction formulation. An interim step is to investigate case studies of individual headlands and to generate site-specific methods of bypass prediction that may be used to inform later development of a generalised model. The aims of the study are, therefore, the following: (i) to calibrate and validate the wave and hydrodynamic components of a hydro-morphodynamic numerical model for a single observed natural headland in an exposed and macrotidal environment; (ii) to identify the major wave and tidal controls on embayment circulation and rates of headland bypass; (iii) to determine the primary modes of embayment circulation that prevail under varying wave–tide scenarios; and (iv) to generate a site-specific parameterisation of modelled bypass rates in order to predict daily sediment flux, based only on offshore wave parameters and tidal level, then use this to hindcast annual bypassing. A future goal is to generalize this site-specific parameter to be more widely applicable. Section 2 introduces the study site; Section 3 describes the field observations, numerical modelling, and statistical methods; Section 4 outlines the model results; Section 5 introduces a conceptual model for embayment circulation modes and proposes a parameterisation of headland bypass with implications for future research, and conclusions are given in Section 6.
2. Study Site
Perranporth Beach is a 3.5-km long sandy beach located on the north coast of Cornwall, United Kingdom (UK, Figure 1). The site is fully exposed to North Atlantic swells, with an annual average significant wave height (Hs) of 1.6 m and average peak period (Tp) of 10–11 s from the W-WNW (Figure 1b), obtained from a Coastal Channel Observatory (CCO) directional wave buoy located in approximately 20-m water depth near the southern end of the embayment (Figure 1c). The wave climate is seasonal with moderate-energy summers (Hs = 1.2 m, Tp = 9 s), high-energy winters (Hs = 2.2 m, Tp = 12 s), and extreme wave heights exceeding Hs = 8 m and Tp = 19 s [42,43]. The beach is macrotidal, with a spring range of 6.3 m and a neap range of 2.7 m. The mean sediment size (D50) is medium sand (0.33 mm; [44]). The beach morphology is classified as low-tide bar-and-rip [45,46], with a wide, low-gradient intertidal with cross-shore extent of ~500 m, an inner-bar system with well-developed rip channel morphology and an outer subtidal bar [7].
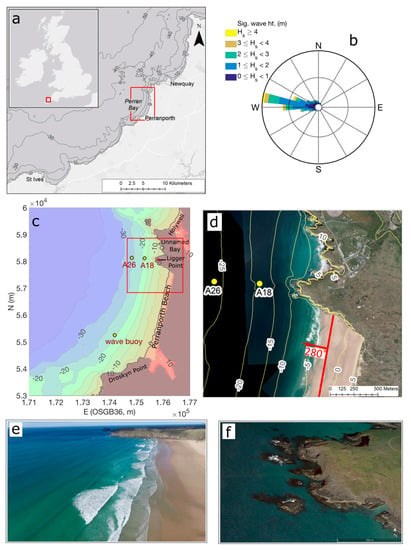
Figure 1.
Study site: (a) regional map of a section of North Cornwall; (b) wave rose for Perranporth using 10 years of wave buoy data; (c) Perranporth embayment, with instrument positions; (d) aerial photo of the headland of interest at spring low tide (United Kingdom Hydrographic Office (UKHO), 2011) with shore-normal orientation indicated (280°); (e) Ligger Point headland at the northern end of Perranporth Beach [photo: P. Ganderton]; and (f) oblique Google Earth image of Ligger Point. The projection and coordinate system are BNG/OSGB36. Contours in (c,d) are in Ordnance Datum Newlyn (ODN) coordinates and are based on 2016 surveys (note the aerial image in (d) is taken in 2011).
The headland of interest (Ligger Point) is at the northern end of the beach (Figure 1), with an alongshore width of 450 m and a cross-shore extent of 500 m from the mean sea level shoreline, ±200 m at spring tides. The internal angle at the apex of the headland is ~30° and is near symmetrical. The headland is comprised of steeply-dipping metamorphic rocks, with cliffs at the apex of the headland dropping near-vertically to −5 to −7 m Ordnance Datum Newlyn (ODN). For the observed coastline, mean sea level is approximately 0.3 m ODN. Isolated rocks are present around the apex of the headland at depths of 5–10 m, with sand visible around these rocks in aerial imagery (Figure 1f). Beyond the 11-m contour, approximately 100 m from the cliff face, the contours are generally smooth and inferred to be sand covered with few exposed rocks. The bed slope ratio offshore of the headland is 0.02. The morphological depth of closure is −15 m ODN, and a transition from sand to gravel occurs between −20 m and −26 m ODN [47], which can be used to infer the base of the active profile.
At the southern end of the embayment is a 1.5 km stretch of cliffs and headlands extending NNE-SSW, collectively referred to here as Droskyn Point (Figure 1c). Immediately north of Ligger Point is a small (~100 m) unnamed embayment (herein ‘Unnamed Bay’). A small island and a sub-aqueous ridge extending WNW-ESE divide Unnamed Bay from Holywell Beach at the northeast corner of the domain (Figure 1b).
3. Materials and Methods
3.1. Field Observations
3.1.1. Wave and Hydrodynamic Observations
Wave, current, and water level observations were obtained from two 600 kHz RDI Workhorse acoustic Doppler current profilers (ADCPs) deployed off the north Perranporth headland (Figure 1) from 28 June 2016 to 31 August 2016; A18 was at −18 m ODN, and A26 was at −26 m ODN. The vertical bin size was 0.5 m with a maximum of 55 bins for A18 and 70 bins for A26. The data from bins above and immediately below the instantaneous water surface were excluded. The currents were ensemble-sampled at 5-min intervals, with each ensemble consisting of 90 samples at 0.33 Hz (over 270 s) and then 30 s with no sampling. The waves and water level were sampled every 2 h, with 20-min bursts of 2400 samples at 2 Hz. For use in model validation, the currents were averaged over the full water column. The currents then had a 30-min moving average applied. The water levels were spline-interpolated (due to the low sampling frequency) to the model output time step, while wave statistics were linearly interpolated. Hourly summary wave statistics including significant wave height (Hs), peak period (Tp), and mean direction (Dir) were obtained from a Channel Coastal Observatory (CCO) wave buoy located in 20-m water depth at the southern end of the embayment (Figure 1).
3.1.2. Survey Data
A digital elevation model (DEM) of the Perranporth embayment was produced from a composite of survey datasets. Single-beam echosounder bathymetry of the lower-intertidal (50-m line spacing) to upper sub-tidal (100-m line spacing) was conducted from an Arancia inflatable vessel during August of 2016. A higher resolution single-beam survey was conducted to provide bathymetry in the area immediately surrounding the headland (October 2017), which used no fixed grid and had average line spacing of ~25–50 m, extending up to 100 m from the headland, surveying as near to the headland as possible while avoiding hazardous areas of exposed rocks and breaking waves. Calculated vertical uncertainty for the single-beam echosounder survey, transformed to ODN, is <0.14 m determined from multiple observations over a control surface (95% confidence level; [47]). A multibeam echosounder survey provided 1-m gridded, full seafloor coverage, high-resolution survey data for the sub-tidal embayment from depths of ~10–40 m (August 2016), with calculated spatially variable uncertainty of (0.06–0.3 m; at 95% confidence level). Topography from the intertidal to the dune foot was obtained through real-time kinematic Global Positioning System (RTK-GPS) surveying from an all-terrain vehicle (August 2016), with line spacing of 20–25 m and uncertainty of <0.03 m. Additional survey data around the periphery of the DEM include drone structure-from-motion photogrammetry gridded to 1-m grid resolution (October 2016), Lidar at 1-m grid resolution (March 2016, CCO), and offshore multibeam bathymetry at 50-m grid resolution surveyed in 2011 by the United Kingdom Hydrographic Office (UKHO). A composite DEM of 10-m grid resolution was generated using the natural neighbour method, which was subsequently used for interpolation of the model domain grids.
3.2. Numerical Modelling
Delft3D [48] is a process-based numerical model that couples hydrodynamics, wave forcing, wind forcing, and sediment transport. The model can be run in 3D or 2D mode and has been demonstrated to accurately reproduce hydrodynamic behaviour and morphologic change, over event to multi-annual timescales, on energetic sandy coastlines when run in 2D mode [49]. For this study, a Delft3D model in 2D mode was setup for a domain encompassing Perranporth Beach (Figure 2). The Delft3D modules for wave transformation, hydrodynamics, and sediment transport were run in online-coupled mode, including wind forcing.
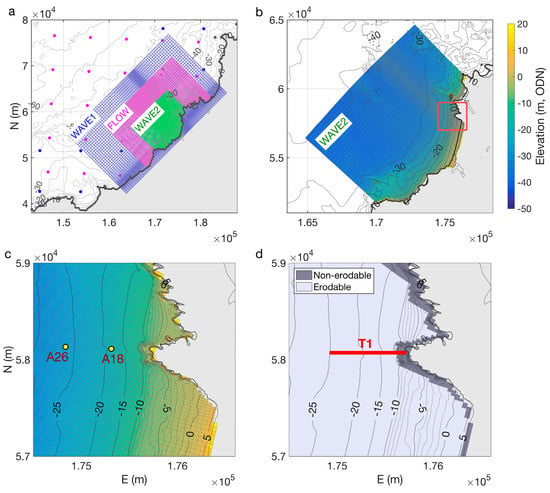
Figure 2.
Delft3D model grids: (a) WAVE and FLOW model grids, blue dots indicate Wave Watch III (WW3) wave model nodes (see Section 3.2.1), pink dots indicate Forecasting Ocean Assimilation Model 7 km Atlantic Margin model (FOAM-AMM7) hydrodynamic model nodes (see Section 3.2.2); (b) WAVE2 grid; (c) FLOW grid in vicinity of Perranporth north headland; and (d) erodibility grid with transect used for analysis (T1) indicated.
3.2.1. Wave Model
Delft3D uses the spectral wave model simulating waves nearshore (SWAN; [50]), packaged within Delft3D as “WAVE”, to transform waves from deep to shallow water. Two curvilinear wave grids were employed (Figure 2a,b), including an outer grid (WAVE1) with an extent of 33 km by 17 km and resolution of 250–500 m, and an inner grid (WAVE2, 13 km by 10 km) with a maximum resolution of 25 m by 25 m around the headland of interest. The wave boundary conditions were linearly interpolated to the WAVE1 grid from a Wave Watch III model (WW3; [51]) produced by the UK Met Office, with 8-km resolution (blue dots, Figure 2a). Parameterised values of wave characteristics (Hs, Tp, Dir, and directional spread) were used as inputs to WAVE, interpolated to the outer wave grid boundaries. WAVE was run in stationary mode.
The Roller model is an optional additional wave model within Delft3D that modifies wave breaking and effectively shifts the position of the alongshore current [52]; it uses the period and wave angles from the SWAN wave model, to solve a wave energy and roller energy balance within the FLOW model, required to compute radiation stress gradients [53]. The Roller model was implemented in this study as it was found to give the best model/data comparison. The breaking dissipation formulation (gamma), which is the wave height-to-depth ratio associated with irregular wave breaking, was set to the default value of 0.55. The Roller model, when implemented in default mode, was the only simulation that effectively simulated observed wave-driven currents off the headland during storm conditions.
3.2.2. Hydrodynamic Model
FLOW is the hydrodynamic component of Delft3D. The FLOW model as implemented in this study solves the 2D (depth-averaged) non-linear shallow water equations [53]. The depth is assumed to be small relative to horizontal scale, which allows for the vertical momentum equation to be reduced to the hydrostatic pressure relationship; thus, vertical accelerations are assumed to be small and are not accounted for. We address the limitations of the 2D model in Section 3.2.8 and Section 5.4. A curvilinear 2D FLOW grid (Figure 2a) was employed with a 23 km by 16 km extent and 25 m × 25 m resolution around the headland (Figure 2c). The sections of the FLOW grid overlapping the inner WAVE grid match identically. No significant instabilities were observed relating to the inner WAVE grid being within the FLOW grid. The water level boundary conditions were obtained from the Forecasting Ocean Assimilation Model 7 km Atlantic Margin model (FOAM-AMM7; [54]). The offshore boundary was driven by water levels interpolated from the FOAM-AMM7 model (pink dots, Figure 2a), and the lateral (shore-normal) boundaries were set as water level gradients (Neumann boundaries). FLOW was run with a 0.2-min time-step for the majority of simulations and at a 0.1-min time-step for synthetic simulations with extreme wave heights (Hs ≥ 6 m), to avoid excessively high Courant number values. The coupling interval between WAVE and FLOW was conducted every 60 min. The FLOW grid was coupled to both the WAVE grids (WAVE1 and WAVE2). The values for water levels, current, and bathymetric changes from the FLOW grid were used by the WAVE grids but not extended beyond the bounds of the FLOW grid. The Chezy formulation for bottom roughness was used, with a value of 55 m1/2 s−1 (default is 65 m1/2 s−1). Other formulations were tested, including variable bottom roughness but resulted in lower model skill. For bottom stress due to waves, the default Delft3D formulation was used (Fredsøe 1984; [55]).
3.2.3. Wind and Pressure Inputs
The local wind and pressure conditions were applied across both the WAVE and FLOW domains. The wind conditions were obtained from the IFREMER CERSAT global surface wind climatology model at 0.25° resolution. The pressure data were from the National Oceanic and Atmospheric Administration (NOAA) Climate Forecast System Version 2 (CFSv2) at 0.5° resolution. The wind and pressure forcing models were linearly interpolated and applied as spatially varying inputs across the WAVE and FLOW domains. We do not examine wind variation in detail, and it is noted that [40] determined that local winds contribute minimally to total bypassing rates.
3.2.4. Non-Erodible Layer
A buffer of non-erodible cells was imposed around the cliffs of the headland (Figure 2d) to prevent unrealistic bed- and cliff-collapse during morphodynamic simulations. Additionally, it was determined that the area of isolated rocks immediately off the apex of the headland (Figure 1f) should also be set as non-erodible. It is clear that some of this area does contain sediment and also that the rocky outcrops in this area would present a significant partial barrier to transport; however, the ~25 m × 25 m FLOW grid cannot resolve these features individually. Therefore, the entire headland-toe zone is set to be non-erodible (Figure 2d) to an elevation of −10 m ODN. Note that sediment can still pass through this zone but applying these settings prevents unrealistically high levels of erosion from the toe of the headland and accounts for the role of the exposed rocks off the headland (Figure 1f) impeding transport.
3.2.5. Model Calibration
The approach was to first calibrate and validate the wave and hydrodynamic components of the model using field observations and then use sediment transport settings that have been validated by previous comparable studies produced by the model developer Deltares (e.g., [49,56]). In line with these contributions, significant alterations to default settings for hydro- and morphodynamic model parameters were employed (Table 1).

Table 1.
Delft3D model settings.
The model was run for a 1-week calibration period from 17 August 2016 to 24 August 2016, which encompasses the largest wave event (Hs = 4.5 m) during the period of ADCP deployment. This short calibration period was selected as it contained an extensive range of wave conditions and encompassed a spring tide period. Model outputs were compared to wave observations (Hs and Tp) at the wave buoy and two ADCPs (Figure 1c) and against flow velocity (magnitude and direction) at the ADCP locations. The model performance was optimised for the calibration period, including the changes to default Delft3D settings indicated in Table 1. The optimised settings were then validated against the full two-month period (July–August 2016) of ADCP observations, with the 1-week calibration period omitted from model skill results.
Sediment transport settings were adopted to match those used by [49], as these were demonstrated to accurately model the morphodynamic behaviour of the sand engine in the Netherlands. These include using the ‘TRANSPOOR2004’ [57] transport formulation and the ‘ThetSD’ factor for erosion of adjacent dry cells that encourages intertidal accretion.
Morphologic change was switched on with no morphodynamic acceleration (MORFAC = 1). For all calibration and validation runs, the first 24-h period was excluded from correlations to allow for model spin-up time including morphodynamic adjustment. We have opted to allow morphological updating to occur to permit this period of initial adjustment; however, the morphological changes observed were minimal and are not a focus of the analysis. Bed changes were generally small (<0.2 m), apart from cells immediately adjacent to the headland, where elevation changes up to 1 m were predicted.
Model skill was evaluated with three statistics, including root-mean-square error (RMSE), co-efficient of determination (R2), and Brier skill score (BSS). The BSS is calculated as per [58] as follows:
where is a measured variable, is the model-predicted variable, is measurement error, and is a benchmark model, here taken as a linear trend fitted to the data. Vertical lines indicate absolute values and angular brackets represent time-averaging over the testing period. The BSS measures the ratio of the improvement of the model prediction over the benchmark. BSS values >0.8 are considered “excellent”, while (0.6 > BSS > 0.8) are considered “good”. Measurement errors used for BSS calculation include the following: Hs (0.1 m); Tp (1 s); wave direction (5°); water level (0.05 m); flow speed (0.02 m s−1); and flow direction (5°). The directional error was determined based upon manual calibration of the compass. Flow velocity and wave statistic measurement errors were informed by previous determinations [59,60].
3.2.6. Additional Synthetic Simulations
The above model settings were used to conduct simulations of the following: (i) a zero-wave condition “Flow-only”; and (ii) a zero-tide condition “Wave-only”. Both simulations types were performed over the 1-week calibration period, without wind forcing. Additionally, a matrix of 90 synthetic wave/tide scenarios were tested (Table 2). The synthetic wave conditions were selected to cover a broad, though non-exhaustive, extent of the observed wave climate (Figure 1d; [43]), including six wave heights, two representative peak periods, and three representative wave directions. For each scenario, a 48-h simulation was run, with only the final 25 h used for analysis, such that it contained two full semidiurnal tidal cycles. An evaluation of the model outputs confirmed that a period of 23 h was sufficient for model stabilisation.

Table 2.
Synthetic wave–tide condition scenarios.
3.2.7. Headland Transect for Bypassing Analysis
A transect (T1, Figure 2d) extending from the headland apex to −25 m ODN was used for analysis of mean currents, shear stress, and integrated sediment flux bypassing the headland. Although there may be potential for sediment transport beyond this depth, an abrupt medium sand to fine gravel transition has been observed to occur between −20 m and −26 m ODN [47], implying a base of the active profile or a break in sediment transport regimes. Additionally, the FLOW model was run with a uniform sediment size of 0.33 mm and is therefore not designed to assess the potential transport of gravel at >25 m depth. Therefore, the seaward extent of the analysis transect was set at −25 m ODN.
3.2.8. Model Design Assumptions and Limitations
Delft3D in 2D-mode has been shown to be effective at reproducing longshore transport, including within the surf zone [49,52]. However, 2D-mode is less effective at simulating cross-shore processes, and sandbar morphodynamics in particular are poorly resolved [49]. Additionally, we note several assumptions and limitations with regard to model design: (i) the high-resolution morphological features and localised surf zone processes off the headland (<10 m scale) are not resolved; (ii) we are unable to validate the sediment transport, opting to use a previously validated formulation (Table 1); and (iii) the area off the toe of the headland is set to be non-erodible to account for the sub-grid size exposed rocks in this area that will act as a partial barrier to transport. Given these limitations, the headland bypassing rates presented in this study should be considered as exploratory in nature, requiring future field validation.
In order to justify these design assumptions and to gain some idea of the related uncertainty in headland bypassing, two additional comparative tests were run over the 1-week calibration period, including the following: (i) use of the default Delft3D sediment transport formulation; and (ii) setting grid cells off the apex of the headland, from approximately −5 m to −10 m ODN, to be erodible to a 1-m depth. The additional comparative tests are presented in Section 4.1.1. The limitations are further discussed in Section 5.4.
4. Results
4.1. Model Calibration and Validation
WAVE output for the calibration period (17–24 August 2016) is shown for A18 (ADCP, −18 m ODN) and A26 (ADCP, −26 m ODN) in Figure 3. A wave event occurred on 20–21 August 2016 with significant wave heights over 4 m and period decreasing from 14 s to 10 s over the course of the event. From visual inspection, the model satisfactorily reproduces wave height, period, and direction.
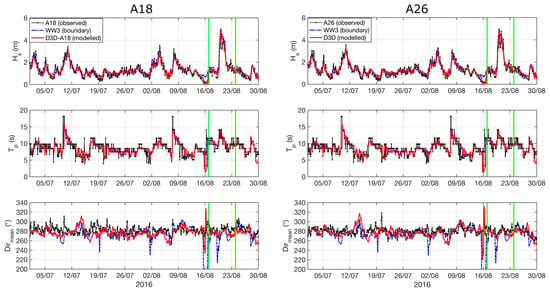
Figure 3.
Wave observations at acoustic Doppler current profilers (ADCPs) A18 (left column) and A26 (right column) with Delft3D model output at each location, for the July–August 2016 validation period. WW3 offshore boundary conditions are also indicated. Observed wave direction has a 5-point moving average filter applied. The green vertical lines indicate the 1-week calibration period, including the peak wave event. The wave height is obtained from the Roller model; period and direction are from the WAVE (simulating waves nearshore (SWAN)) model.
A comparison of observed and modelled current behaviour is provided in Figure 4, showing a limited 16-day neap-to-neap period for clarity. The water levels and flow velocities are visually well reproduced by the model. The flow was primarily alongshore (v, northward current), with minimal cross-shore currents (u, eastward current), and a residual northward current (Figure 4b,e) of 0.05–0.2 m s−1. An increase in residual current velocities (~0.1 m s−1) was apparent during the storm event (20–22 August), coinciding with spring tides. For example, for A18, during the wave event, northward flow over the flood tide exceeded 0.4 m s−1, while a brief southward current (up to 0.4 m s−1) occurred during the first half of the ebb-tide. The sign and magnitude of the residual current was critical to bypassing rates during moderate–high waves, and the varying contribution of waves and tides to the residual flow will be examined in Section 4.3.
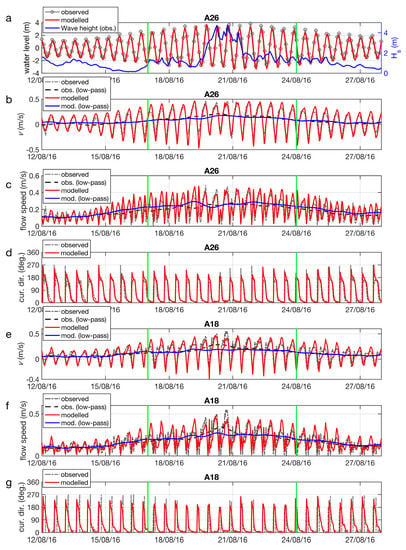
Figure 4.
ADCP (A26, A18) water level and flow velocity observations compared with FLOW model output, including the following: water level comparison for A26, with wave height indicated (a); northward current, flow speed, and direction for A26 (b–d); and northward current, flow speed, and direction for A18 (e–g). The observed water levels (120-min) are spline interpolated to the FLOW time-step (30-min). The observed and modelled current speed and direction are 30-min averages. Low-pass current speed has a Fourier transform filter applied, with a 25-h cut-off. Vertical green lines indicated the 1-week calibration period.
The wave height obtained from the Roller model was well predicted for both the calibration and validation periods (BSS; Table 3). The peak period prediction was good, with poorer correlations during small wave periods when swell and wind waves can have similar peak energy levels. The observed wave direction (Figure 3) had a large amount of high-frequency variation (hours), with relatively little longer-term variation (days–weeks), oscillating around shore-normal (~280°), as defined by the shoreline adjacent to the headland (Figure 1c). For this reason, the R2 and BSS values for the wave direction showed poor or no correlation, in particular during periods of low waves (Hs < 1 m). In this instance, RMSE was a better indicator of model precision, with RMSE <11° when low waves were excluded (Hs < 1 m, Table 3) and RMSE <13° when all waves were included. It was reasonable to exclude low waves in this context, as it will be later demonstrated that wave directions during periods of low waves have near-zero impact on bypassing rates. The skill values for the wave direction found here were comparable to a range of mean absolute error values for the wave direction of 9–36° in a similar study [12]. The observations of the wave buoy direction were not used, as they contained an erroneous tidal oscillation thought to be related to tidal currents affecting the buoy. The water levels were accurately modelled (BSS > 0.96). The water level RMSE absolute values were relatively high (0.3 m over the validation period) compared with [12] but represent a similar ratio of the total tidal range, noting that the spring tidal range in this instance is >6 m. The flow magnitude and direction were found to be important to bypassing rates and were considered to be the key indicators of model suitability for the present study. The flow velocity model outputs were all in the good-to-excellent range for both the calibration period (mean BSS = 0.74; averaging flow speed and direction skill values) and the validation period (mean BSS = 0.70). The flow direction was generally well reproduced; however, the high RMSE values (>30°) were due to time offsets between the model and observations in the switch between northerly and southerly flows (Figure 4c,f), resulting in brief directional errors of ~180°. Critically, residual flow speeds were excellently predicted for the full validation period (BSS ≥ 0.9, RMSE = 0.02 m). Over the short calibration period, the residual flow correlations were lower due to isolated under- or overpredictions over individual tidal cycles (e.g., A26 on 19 August 2016, Figure 4c). Overall, the model performed well at predicting wave and hydrodynamic conditions and is considered suitable for modelling morphodynamic behaviour, based on the settings outlined in Table 1.

Table 3.
Model calibration and validation.
4.1.1. Additional Tests to Assess Sediment Transport Rates
Two additional comparative tests were run over the 1-week calibration period to assess the uncertainties associated with the model assumptions and sediment transport outcomes. The absolute figures for headland bypassing sediment flux are presented in Section 4.3 and Section 4.4; here, we present only comparative ratios.
First, the model was run with default Delft3D sediment transport formulation, with a resultant 22% increase in longshore sediment flux past the headland transect. This gives some indication of the uncertainty surrounding the different sediment transport formulae for this case study. Second, the model was run with the grid cells off the Ligger Point headland (Figure 2d), erodible to a depth of 1 m (as opposed to being non-erodible). This was intended to simulate the observed headland if there were no exposed rocks off the apex of the headland acting as partial barriers to transport (Figure 1f) and is presented as an extreme upper-bound on the flux. The latter test produced a 76% increase in the longshore sediment flux, with the most significant increase occurring during low waves and relatively little difference during storm conditions.
To summarise, given the model assumptions and the range of comparative tests conducted, the results for sediment transport presented herein are constrained to at best within a factor of 2. This is considered reasonable and is typical of the uncertainty between computed and measured sediment transport rates [57]. High-resolution morphology, hydrodynamics, and morphodynamics off the headland cannot be resolved in this study; thus, the results presented on bypassing rates must be considered exploratory in nature. Limitations are further discussed in Section 5.4.
4.2. Synoptic Flow Behaviour
Key spatial and temporal characteristics of flow behaviour across the embayment and in the vicinity of the northern headland, related to tidal and wave forcing, are now described. First, the role of the residual northward current off the headland was examined during moderate wave conditions (Hs ~ 1.5 m), showing a period of two days before the spring tide peak (Figure 5). The residual northward flow seen in timeseries (Figure 4b,e) can be observed spatially as a series of synoptic snapshots (Figure 5) beginning with a brief period (~2 h) of southward flow off the headland during the initial ebb-tide. Over the middle ebb-tide (Figure 5b,d), an eddy forms off ‘Unnamed Bay’, and opposing currents occur, with northward flow near the Ligger Point headland and southward flow further offshore. The northward flow begins as a narrow current immediately off the headland, expanding and propagating further offshore. This can be observed in the timeseries of modelled flow directions at the ADCP locations, with a shorter period of southward flow predicted for the inner ADCP location (A18, Figure 5f) compared with the deeper ADCP location (A26, Figure 5f). The last part of the ebb-tide and the full flood tide (~8 h/tidal cycle) are dominated by northward flow (Figure 5c). These localised effects are important controls on the strength of the residual current off the headland, which will later be shown to be critical to modelled sediment bypassing rates during modal (~1–2 m) wave conditions.
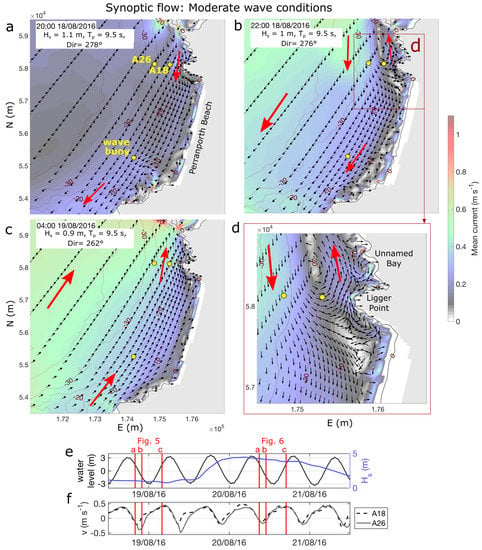
Figure 5.
Synoptic snapshots (30-min averages) of simulated flow during moderate wave conditions. ADCP and wave buoy locations are indicated with yellow dots in (a–d). (d) is a magnified inset of (b), with a higher resolution of current vectors indicated. The black arrows in (a–d) indicate direction, not magnitude; the red arrows are interpretations of primary currents. A timeseries of water level and wave height (e) and alongshore velocity (f) are provided with snapshot times for Figure 5a–c and Figure 6a–c, indicated by red lines.
The snapshots of flow during storm conditions are depicted in Figure 6, with panels (a–c) selected at the same points in the tidal cycle as Figure 5a–c for comparative purposes. A critical region during higher waves was the WSW-ENE aligned coast to the south of the embayment (Droskyn Point, Figure 1b), where a persistent northward current, at times >1 m s−1, was observed across all tidal stages (Figure 6a–c), which was forced by waves breaking at an angle to the coastline in that region. The periods of southward tidal flow (Figure 6a,b) act in opposition to the northward current off the southern headland, converging to form a large-scale (1-km wide), diffuse embayment-cellular rip [23], also described as a mega-rip [25], at the centre of the embayment, which was strongest in the later ebb-tide (Figure 6b). During northerly tidal flow (Figure 6c), which occurred over the majority of the tidal cycle, the wave- and tidal-currents acted in the same direction, with a 0.5-m s−1 current that extended northward across the entire embayment at the −20-m contour. Mega-rips were predicted off the headland during storm conditions (Figure 6d); however, these were of a much smaller scale than the mid-embayment offshore flow described above. The high-resolution view of the headland (Figure 6d) also showed southward flow within the surf zone. In summary, the flow during storm conditions became more complex due to the generation of wave-forced currents and the initiation of embayment circulation, which may act in combination with or against tidal flows.
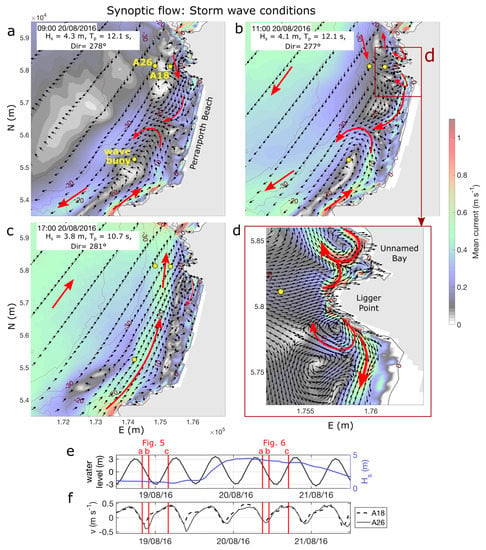
Figure 6.
Synoptic snapshots (30-min averages) of simulated flow during storm conditions. ADCP and wave buoy locations are indicated with yellow dots in (a–d). (d) is a magnified inset of (b), with a higher resolution of current vectors indicated. The black arrows in (a–d) indicate direction, not magnitude; the red arrows are interpretations of primary currents. A timeseries of water level and wave height (e) and alongshore velocity (f) are provided with snapshot times for Figure 5a–c and Figure 6a–c, indicated by red lines.
4.3. Wave and Tidal Controls on Flow and Sediment Transport
In this section, we compare the coupled morphodynamic model outputs (as described in Section 4.1 and Section 4.2), with synthetic model runs that isolate wave and tidal forcing controls on headland currents and bypassing rates. For the analysis, velocity and sediment flux variables were integrated across the transect T1 (Section 3.2, Figure 2d), which extended from the sub-aerial toe of the headland to −25 m ODN.
A time series is presented (Figure 7) for 17 August 2016–24 August 2016, a period which included the highest energy event, occurring concurrently with spring tides. Three model simulations were conducted: (i) ‘Flow-only’; (ii) ‘Wave-only’; and (iii) ‘Coupled’ simulations. The water level, wave height, and direction are provided for reference (Figure 7a,b), with hydro- and morphodynamic variables indicated (Figure 7c–f) to help discern the controls on bypassing rates.
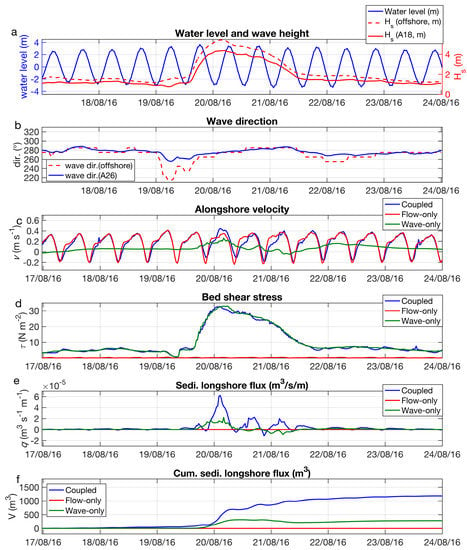
Figure 7.
Timeseries of model outputs for ‘Coupled’, ‘Wave-only’, and ‘Flow-only’ simulations, including the following: (a) water level [left axis] and wave height [right axis]; (b) wave direction; (c) alongshore velocity; (d) bed shear stress; (e) instantaneous sediment volume longshore flux; and (f) cumulative sediment volume longshore flux. The variables are averaged (c,d) or integrated (e,f) over the transect (T1) in Figure 2d.
First, examining the ‘Wave-only’ simulation (green line; Figure 7c–f), the wave-generated alongshore current off the headland (Figure 7c) reached a maximum of 0.2 m s−1 (northward) at the initial peak of the storm (20 August 2016), when the offshore wave direction was 265°, which was south of shore-normal (280°). At the end of the storm (21 August 2016), the offshore wave direction was 285°, slightly northward of shore-normal, and a southward current of −0.1 m s−1 was generated. The bed shear stress is a function of the wave height (Figure 7d), as tidal currents and water level variations were absent, with peak values above 30 N m−2 during the storm event. The slight variations in wave direction resulted in reversals of sediment flux (Figure 7e), with a net northward flux of 300 m3 over the simulation period. Next, the ‘Flow-only’ simulation (red line, Figure 7d–f) displayed very similar alongshore current magnitude to the coupled model. However, due the absence of waves, the shear stress was minimal (Figure 7d), resulting in insignificant (though non-zero) sediment flux past the headland (Figure 7e,f).
Lastly, looking at the coupled simulation (blue line; Figure 7d–f), the wave and tidal alongshore currents did not linearly sum to the coupled model output. Rather, the coupled flow velocities (Figure 7c) closely resembled the ‘flow-only’ simulation, with wave forcing adding up to ±0.2 m s−1, depending on the wave direction. The maximum bed shear stresses were similar to the ‘wave-only’ run, with a small tidal fluctuation (~2 N m−2). The sediment flux rates showed a strong tidal signal during peak wave conditions, with peak northward flux from low tide through the flooding tide, with near-zero flux to weak southward transport from high tide through the initial stages of the ebb-tide. Despite the variations in the wave angle around shore-normal, the sediment flux for the coupled simulation was persistently northward (Figure 7e) due to the residual longshore current (Figure 4b,e). The sediment flux during lower wave conditions, for the spring tide period shown, was northward at ~50–100 m3 day−1. The flux during the Hs = 4.5 m storm was approximately an order of magnitude greater at ~400–600 m3 day−1, with a net flux of 1200 m3 northward over the week. In summary, there must be wave-induced bed shear stress present for significant bypassing to occur around this particular headland, but the presence of a residual tidal current increased total headland bypassing by a factor of 4 for the simulated period.
4.4. Synthetic Wave–Tide Scenarios
The previous results have been limited to the observed 2-month summer period of ADCP deployment. To expand the analysis of headland bypassing forcing controls and sediment transport pathways, a matrix (Table 2) of 25-h (~two tidal cycle) simulations were conducted to explore the full parameter space of possible wave-tide conditions. The results of these synthetic simulations are presented in Figure 8, with the outputs for each run averaged across the headland apex transect (T1; Figure 2). Shore-normal was approximately 280° (Figure 1c), so the three wave angles were 20° south of shore normal, shore normal, and 20° north of shore normal. Wave heights of up to 9 m were included in the simulation, which have been observed to occur on this coastline [43].
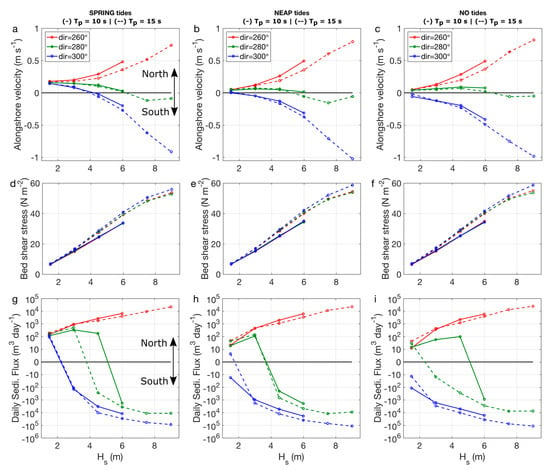
Figure 8.
Summary of 90 synthetic model runs covering a range of wave–tide scenarios, each point represents a separate 25-h simulation. Alongshore velocity (top row) and bed shear stress (middle row) are averaged across transect T1 (Figure 2d); daily sediment flux (bottom row) is integrated across T1. Three tidal stages are simulated including spring tides (left column), neap tides (middle column), and no tides (right column). The y-axis for sediment flux (bottom row) has a log-scale; all other axes are linear. The line colour indicates offshore wave direction, including the following: red (260°); green (280°); and blue (300°). Tp = 10 s is indicated with solid lines; Tp = 15 s is indicated with dashed lines.
During spring tides (Figure 8, left column) and modal wave conditions (Hs = 1.5 m), the mean velocities past the headland were northward (positive), due to the residual tidal current described above (Figure 4, Figure 5 and Figure 6). This resulted in a daily northward flux of ~100 m3 day−1 that was not influenced by the wave direction (Figure 8g, Hs = 1.5 m). By contrast, for neap and no-tide simulations, the wave direction became a factor with southward transport during low–moderate northerly waves (Figure 8h,i; blue line; Hs = 1.5 m). As the wave heights increased, the tide became less of a factor, with similar flux rates across all tidal conditions when Hs ≥ 6 m and flux direction was only controlled by the wave direction.
The increasing wave period resulted in increased bed-shear stress (Figure 8, middle row), as predicted by linear wave theory. However, the impact of the varying wave period on hydrodynamics and sediment transport was non-linear and complex. For example, for southerly waves, shorter periods resulted in slightly greater flow velocities (Figure 8, top row; solid red line), while the opposite was predicted for northerly waves (Figure 8, top row; blue lines). These variations were related to site-specific spatial variations in predicted refraction and the wave generated currents. The changes in the period for moderate–high (3 m < Hs < 5 m), shore-normal waves at times resulted in predictions of opposing directions of transport (Figure 8i; green solid and dashed lines), with the longer period waves more likely to induce low rates of net southward transport and the shorter period waves generating northward transport. This was due to the longer period waves generating greater southward-directed surf zone currents in ‘Unnamed Bay’ north of the Ligger Point headland. Further details on synoptic flow are provided in Section 4.5.
Interestingly, a non-linear response to changes in the wave height was predicted by the model. The alongshore current and sediment flux direction for shore-normal waves switched from northward during small to moderate waves (e.g., Hs = 3 m; green line in Figure 8a,g) to southward for large to extreme waves (e.g., Hs = 6 m; green line in Figure 8a,g). During small–moderate waves, transport was biased towards the north. This was consistent with observations of northward residual currents off the headland for the full 2-month period of observations (Figure 4), during which the offshore significant wave height did not exceed 5 m. However, the model predictions suggested that for Hs > 5 m, transport was biased towards the south. For example, shore-normal waves Hs = 7.5 m and Tp = 15 s were predicted to generate a southward headland bypassing rate on the order of 10,000 m3 day−1.
4.5. Tide-Averaged Embayment-Circulation
The nature of this non-linear response to the wave height (Figure 8) becomes clear with synoptic examination of tide-averaged embayment circulation under modal conditions, high waves, and extreme waves. For modal conditions (Figure 9), the dominant current was the northward residual tidal current in the vicinity of Ligger Point, extending northward where it was constricted around the island off Holywell Beach. For spring tides, the residual current was 0.3 m s−1 off Ligger Point (Figure 9a), dropping to ≤0.1 m s−1 during neaps (Figure 9b).
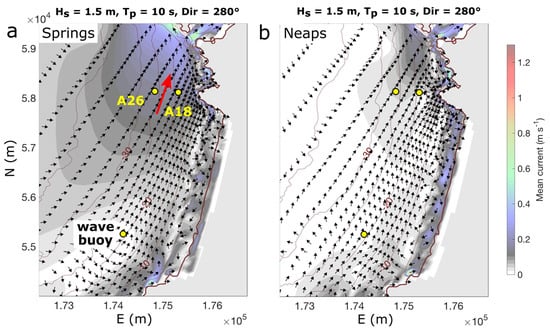
Figure 9.
Time-averaged currents under modal conditions, averaged across two tidal cycles, for (a) spring tides and (b) neap tides. The black arrows indicate current direction, not magnitude.
For moderate–high wave forcing (3–5 m) during neap tides (Figure 10a), oblique wave breaking along the coastline to the south of the domain generated a persistent northward current that was added to by wave breaking along the Droskyn Headland (Figure 10c) with a maximum velocity of 0.5 m s−1 in the immediate vicinity of the headland, which was deflected offshore near the southern end of Perranporth Beach. A weak embayment scale circulation cell was generated with northward flow outside the surf zone of 0.1–0.2 m s−1, consistent with increased northward flow past the ADCPs during the observed storm (Figure 4). At the northern headland (Ligger Point), some of this flow passes the headland northward, the remainder of the flow is deflected onshore and then southward (Figure 10c), resulting in southward flow within the surf zone.
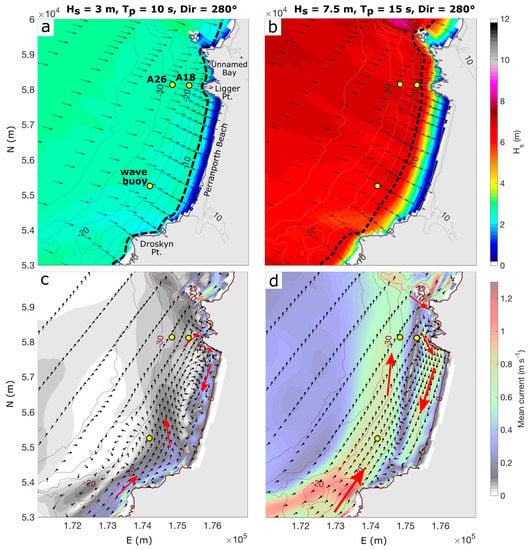
Figure 10.
Circulation under moderate–high waves (left column) and extreme waves (right column) averaged over a 25-h period during neap tides. The synoptic plots include the wave height (top-row) and current velocity (bottom row). In all panels, uniformly sized arrows indicate the direction while colour indicates magnitude. The ADCP and wave buoy locations are indicated by yellow circles. The approximate extent of the surf zone is indicated by black dashed lines in (a,b).
By contrast, for extreme (>5 m) wave forcing (Figure 10b), wave breaking began to occur beyond the headlands. A strong northward current was predicted to occur at the southern Droskyn Headland that was a combination of inertial currents beyond the surf zone generated by wave breaking further southward and by intense oblique wave breaking off the Droskyn Headland (Figure 10d). This current was deflected further offshore by the opposing southward current. High-oblique wave breaking off the island and offshore-ridge north of ‘Unnamed Bay’ generated a southward current that propagated southward toward Ligger Point, combining with breaking offshore of Ligger Point itself. The nature of the circulation shifted from single-embayment (Perranporth only) to multi-embayment circulation, with the small bay to the north becoming part of the greater circulation cell. The flow off the northern Perranporth headland (now within the surf zone) was a strong (~1 m s−1), narrow, southward-directed counter-flow.
5. Discussion
5.1. Modes of Embayment Circulation and Bypassing
The model-predicted rates of headland bypassing for the observation period (Section 4.1, Section 4.2 and Section 4.3) and the synthetic wave-tide conditions (Section 4.4 and Section 4.5) are synthesised into Table 4, and a conceptual interpretation of embayment-scale circulation under varying forcing conditions is presented in Figure 11. Under modal wave forcing, residual tidal currents at the northern headland (Figure 11a) were the primary control on transport direction (uniformly northward) and magnitude, with bypassing of ~101 m3 day−1 during neaps and ~102 m3 day−1 during springs (Table 4).

Table 4.
Headland bypassing rates for the observed headland under various forcing.
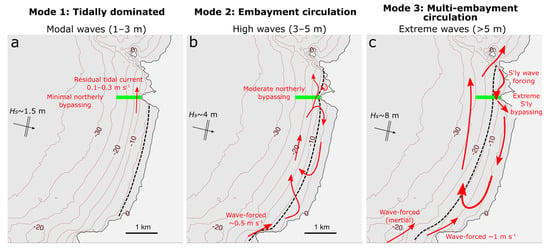
Figure 11.
Idealised modes of embayment circulation. The red lines indicate currents. The sediment flux will generally follow current streamlines, but sediment availability may restrict transport in some regions. The green line is the transect T1, used in the analysis. The black dashed line indicates the seaward edge of the surf zone.
During high wave conditions (Figure 11b), embayment-scale clockwise circulation develops, and wave-forced currents play an increased role in transport direction, in addition to residual tidal flows. For shore-normal waves, moderate northward headland bypassing occurred across the apex of Ligger Point. For extreme wave events (Figure 11c), waves broke beyond the Ligger Point headland, and multi-embayment circulation developed. The wave direction dominated transport direction, and for shore-normal extreme waves, high rates of southward transport occurred off Ligger Point.
Northward transport beyond −30 m ODN may occur if sediment is present; however, the outer embayment may in reality be limited in sediment availability, with [47] inferring limited transport below 26 m due to a transition to coarser sediment. The sediment may also be limited to the far southern (Droskyn Point) and northern (the offshore ridge and island) limits of the domain for the same reason.
Large-scale morphologic features important to multi-embayment circulation (Figure 11c) include the following: (i) the alignment of the coastline to the south of the domain, which is slightly oblique to the offshore wave direction, allowing for strong longshore current development; and (ii) the island, sub-aqueous ridge and headland at the north of the domain, against which high-oblique breaking occurs, combined with deflection of the offshore northward flow back toward the south.
5.2. Daily Headland Bypass Parameter
A simple site-specific parameterisation of headland bypassing is desirable in order to achieve the following: (i) assess the dominant controls on bypassing rates; (ii) quickly predict long-term (multi-year) rates of bypassing without the application of a full process-based numerical model; and (iii) provide a starting-point for a generalised bypassing parameter, to be refined in future efforts. Accordingly, the aim here is to produce a simple, site-specific parameter to estimate rates of daily headland bypassing for the observed headland. The modelled rates of headland bypassing within this section are based on the following outputs: (i) the 2-month simulation of the ADCP observation period (Section 4.1, Section 4.2 and Section 4.3); and (ii) the 90 synthetic wave-tide condition simulations (Table 2; Section 4.4 and Section 4.5), with total daily flux integrated over transect T1 (Figure 2d).
A previous effort [17] had some success in comparing rates of bypassing of idealised groynes on a straight beach, between a process-based numerical simulation (XBeach) and simplified analytical estimates [14,15]. Such analytical models are of limited use for representing realistic embayed settings, as they assume a simplified shoreline and idealised structures. We take a data-driven approach to empirically fit curves to parameterisations of the primary controls of wave- and tidal-forcing (Equation (2)), using only offshore wave conditions and tidal data as inputs, to maximise the simplicity of application. Our approach is to determine a daily sediment flux rate that accounts for the residual tidal currents (~2 tidal cycles), rather than the instantaneous tidal current, while allowing for adequate resolution of changes in wave energy.
Sediment flux is primarily a function of bed shear stress and mean currents [53]; accordingly, we seek to parameterise the combined action of wave-forced currents and shear stress as , while the combination of tidal currents and total (wave and tide) shear stress is incorporated into . The subscripts (wave and tide) indicate the force driving the mean currents being parameterised. Broadly, is intended to quantify tidally dominated transport (Mode 1, Figure 11), while encompasses the embayment and multi-embayment circulation modes (Modes 2–3, Figure 11).
To determine , we begin with a simple parameterisation of alongshore sand transport [9].
where is longshore dry sand transport, is the significant wave height at breaking (m), is the wave angle relative to shore-normal at breaking, and = 40 kg s−1 m−3.
For (Equation (4)), we first adapt Equation (3) to account for net daily volume flux per day past the headland, using an empirically determined wave rate parameter ( = 2.5 × 10−3 day−1) and a daily mean significant wave height (). The rate coefficient () addresses the sensitivity of bypass rates to changes in the wave height, including how efficiently sediment is transported around the headland. The controls on will be further discussed in Section 5.4. Second, it was empirically determined (through curve-fitting and linear correlation) that the wave height raised to the fourth power provided a better fit to the data, and in order to maintain the dimensionality , we include median grainsize () in the formulation of .
Third, we require that accounts for the complex response of embayment circulation to extreme waves, as described in Figure 11. This is incorporated into [4] as a ‘dynamic shore-normal angle’ ():
where is the angle between wave direction and shore-normal (280°; positive clockwise) and the embayment circulation parameter () is a function of wave height. For the Perranporth north headland, an effective linear fit was found to be as follows:
This formulation provides a simple linear solution to the complex transitions between circulation behaviour predicted by the Delft3D model (Mode 2 and 3 in Figure 11), effectively rotating shore-normal northward (positive ) during smaller waves and southward during larger waves. The result is that shore-normal waves will produce low–moderate northward transport under small waves and large southward sediment flux under large waves.
The second component of (Equation (2)) is the combined action of residual tides and wave-stirring (), parameterised as follows:
where the tidal rate parameter () is an empirically determined coefficient ( = 25 m2 day−1), and is a normalised tidal coefficient, linearly interpolated to each day, such that the maximum spring tides during the validation period have a value of 1 and minimum neap tides equal 0. Note that is always positive in this instance, due to the uniformly northward residual tide (Figure 4).
The method for optimising the coefficients (i.e., was through curve-fitting, not physical analysis. After initial tests to determine approximate coefficient values, over 105 Monte Carlo-type simulations were performed to maximise the correlation between the Delft3D-modelled headland bypass rates and the parameterisation.
A comparison of Delft3D-modelled daily sediment flux and parameterised flux () is presented in Figure 12. The coefficients of (i.e., have been optimised to fit the combined observed conditions (red dots, Figure 12c) and synthetic simulations (green dots, Figure 12c). Goodness of fit statistics comparing the parameter to model-predicted rates include the following: RMSE (10 to the power of 0.58 m3 day−1, noting the log transform in Figure 12c); R2 = 0.947; and adjusted R2 = 0.946 (accounting for 5 coefficients: ). The parameter is effective at matching the model-predicted bypass directions and rates, with a few outliers at smaller magnitudes and a positive bias at very low (~101 m3 day−1) transport rates. There is a slight bias to under-prediction, for both north and south transport, for extreme wave heights (i.e., where ). It must be noted that the parameter does not account for predicted transport at depths >25 m in the outer embayment during extreme conditions, as [47] observed a transition to gravel below this depth, indicating a paucity of transportable sediment. Additionally, sediment availability is not well constrained at these depths, and the Delft3D-FLOW model is not optimised for modelling gravel transport.
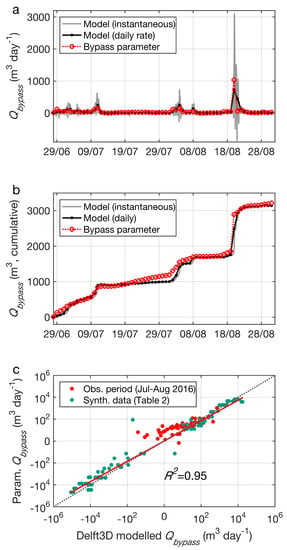
Figure 12.
Performance of the headland bypass parameter (), including the following: (a) timeseries of instantaneous and daily bypass rates for Delft3D model simulation compared against over the 2-month period of the ADCP deployment; (b) a comparison of cumulative rates of bypassing; and (c) a linear correlation of Delft3D predicted bypass against parameterised () rates, for simulation of the 2-month ADCP deployment period (red dots) and synthetic wave-tide simulations (green dots).
The introduction of the parameter is useful in that it allows for the quantification of the dominant controls on bypassing for the studied headland. The wave height and direction are determined to be the primary control on the flux (), with the tide being a secondary control (O [0–100 m3 day−1], Table 4). Additionally, the bypass parameter highlights that a non-linear response in sediment circulation pattern within a complex embayment setting may be amenable to a simple parameterisation based on dynamically adjusting the wave angle relative to shore-normal. The parameter as presented here is highly site-specific, and future efforts should seek to generalise and preferably non-dimensionalise the parameter by applying this approach to multiple headlands.
It is important to stress the limitations and level of uncertainty in these exploratory modelling results (Section 3.2.8) and predictions of bypassing. Given the model design assumptions and the complex dynamics occurring in shallow water off the headland, the predicted rates of bypassing are likely to be at best within a factor of 2 of the actual transport rates (Section 4.1.1).
5.3. Prediction of Annual Headland Bypassing Rates
We now extend the application of the parameter to predict headland bypass at the northern Perranporth headland for a 5-year period (2013–2017; source of wave data: Met Office WW3 model). A comparison is required to test against the parameter; however, the computational requirements for a 5-year Delft3D model run are excessive, so we opted for two alternative approaches: (i) a Delft3D run of a 19-day extreme energy period from 24 January 2014 to 11 February 2014 [43], including four storms with daily-averaged significant wave heights ranging from 6 m to >8 m (Figure 13a); and (ii) an interpolation of the existing Delft3D model runs that can be used to quickly estimate daily rates of bypassing over a multi-year period.
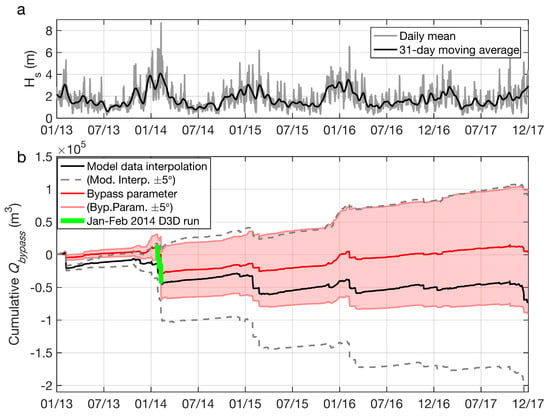
Figure 13.
5-year headland bypass prediction, (a) significant wave height, with daily mean and monthly moving average, and (b) cumulative bypass volumes, positive values are northward. The red line is the parameterised daily flux [, Equation (2)]; the red-shaded region indicates cumulative uncertainty bounds for a ±5° variation in wave direction. The black line in (b) is daily flux interpolated from combined model results (see text), and the grey dashed lines are ±5° variation in wave direction for the model data interpolation. The green line in (b) is obtained from a Delft3D run of the extreme wave period from 24 January 2014 to 11 February 2014, offset to begin at the cumulative value of flux for on 24 January 2014.
The second comparative method, the Delft3D model data interpolation, effectively involves interpolating from all the Delft3D model runs in Figure 12c, including both the July–August 2016 ADCP observations period and the 90 synthetic runs (Table 2, Figure 8). The flux rates for large wave heights are sensitive to the wave direction (); therefore, the Delft3D model interpolation was determined by an initial linear interpolation of log-transformed flux rates at 5° intervals of wave direction between the existing synthetic model runs (i.e., between Dir = 260°, 280°, 300°; Figure 8, bottom row). Then, a scattered linear interpolant was generated across all model runs, with the daily bypass rates interpolated across three input parameters: significant wave height, the wave direction, and the tidal coefficient. The tidal coefficient is normalised such that spring tides have a coefficient of 1, while the coefficient for neap tides is 0. The wave direction for the observed data is capped at ( = 260°; = 300°), to avoid erroneous extrapolation. A limitation of the model data interpolation is that the wave period is not included, in part due to having only two representative modelled periods (10 s and 15 s) and also due to the complex, non-linear response of the period presenting difficulties in interpolation and extrapolation of the model data.
The 5-year estimate of headland bypass is presented for the parameter (red line, Figure 13b), in addition to the two comparative tests, including the 24 January 2014–11 February 2014 Delft3D run (green line, Figure 13b) and the Delft3D model data interpolation (black line, Figure 13b). Both and the model data interpolation offer a convenient means of rapidly estimating long-term bypass rates, and both are derived from the earlier Delft3D model outputs (Figure 12c). As for all the Delft3D results in this study, no observations of currents existed for wave heights above 5 m, and therefore, these results must be treated as exploratory in nature.
First, we compared with the Delft3D run for the extreme wave period at the start of 2014 (green line, Figure 13b). For this period, predicted a southerly flux of ~ while the Delft3D run predicted a southerly flux of ~ (i.e., an underprediction of ~20% relative to the Delft3D). Given the simplicity of the bypass parameter and the extreme values within this period (January–February 2014), this was considered a strong indication of the effectiveness of the parameter for matching Delft3D predictions of bypassing direction and approximate magnitude, well within a factor of 2 in this instance.
Second, we compared with the Delft3D model data interpolation (black line, Figure 13b). The predicted seasonal and annual bypass rates are summarised in Table 5. Both methods predicted a seasonal pattern, with gradual and sustained northward-transport of ~104 m3 over spring–autumn (Table 5), which was consistent with the observed residual currents over summer in this study (Figure 13b). This trend was reversed during winter, with episodic and rapid southward transport due to large storms (as supported by the January–February 2014 Delft3D run) generating the multi-embayment circulation described in Figure 11c, with seasonal flux of up to −4 × 104 m3 (Table 5). The bypass parameter predicted a near-zero net flux over 5 years, while the model data interpolation predicted a cumulative loss of 7 × 104 m3 towards the south, mostly due to higher predictions for individual storm events during winter, which was related to underprediction of the flux by the parameter compared with Delft3D outputs for extreme events (Figure 12c), in particular for more northerly waves. Both methods predicted large southward transport over the extreme winter of 2013–2014 [61]. An uncertainty range of ±5° in the wave direction is shown for the parameter (red shaded area, Figure 13b) and the model data interpolation (grey dashed lines, Figure 13b) to indicate the model and bypass parameter sensitivity to small changes in wave direction. The large range in bypass predictions due to small variations in the wave direction emphasises the need for accurate and precise wave direction in model boundary conditions to predict net transport direction.

Table 5.
Seasonal and annual bypassing rates.
The estimated annual rates of bypass are approximately an order of magnitude less than the observed maximum annual cross-shore transport rates, based on inter-tidal and subtidal surveys [42,43] of >100 m3 m−1, which integrates to >4 × 105 across the embayment. Unknown sediment availability and composition in the outer embayment and at the north–south boundaries of the domain also limit the ability to predict long-term net transport rates. Given the relatively low rates of bypassing, large uncertainty due to unvalidated sediment transport and model design assumptions (Section 3.2.8 and Section 4.1.1) and inability to constrain the long-term trend, the conclusion of this brief assessment of long-term bypassing is that the northern headland of Perranporth is open, but net transport is insignificant at the annual timescale, relative to other sediment fluxes within the embayment.
By comparison, a similar modelling approach [12,40] predicted annual bypassing rates on the order of 104 m3 for multiple headlands in a micro-tidal, moderate–high energy environment, which is comparable to the results of this study. Similarly, the embayment circulation controls across seven headlands seen in [40] are in broad agreement with those described in this study; however, the present effort adds a greater level of detail on the combined effects of wave- and tidal-controls within an individual embayment and, in particular, demonstrates (i) the increased level of control exerted by tidal-forcing in a macrotidal environment and (ii) that bypassing rates can be parameterised.
5.4. Implications, Limitations, and Future Research
Few studies have examined natural headland bypassing, and all are variously affected by limitations in the extent of field observations (e.g., [22]) and/or numerical simulations that extend morphodynamic simulations beyond the observed range of field data (e.g., this study, [12,40]). Examinations of embayment circulation (e.g., [27]), have generally focused within embayments and have not considered beyond the headlands. The control of offshore canyons on large-scale wave-forced currents has been investigated [62] but not in relation to headland bypassing. This study has examined embayment circulation and headland bypassing through a sequence of methods that become increasingly abstracted from direct observation: (i) direct measurement of currents off a headland combined with surveys of topo-bathymetry; (ii) a wave- and hydrodynamic numerical model of the embayment, validated off the apex of the headland for Hs < 5 m; (iii) morphodynamic modelling of sediment transport for the simulated waves and currents based on previously validated methods [49,56] in comparable scenarios; and (iv) unvalidated morphodynamic modelling of a full spectrum of wave–tide conditions that extend beyond the range of observations. With each step away from observation, the results should be treated with increasing caution but are nevertheless informative as being indicative of the processes involved. We first address model limitations, then discuss the contribution of the present study to what is a poorly understood component of coastal sediment budgets.
A limitation of this study is the use of 2D simulations and a grid size, which does not resolve all the morphologic features (exposed rocks) off the headland. This results in limitations in the simulation of complex surf zone dynamics and cross-shore processes [49], including sandbar morphodynamics. A recent effort using a 3D simulation [40] has shown the importance of cross- and alongshore processes in cyclic bar migration near multiple adjacent headlands. For the headland in this study, bathymetric surveying [47] does not indicate major bar migration near the headland; therefore, the attached bar mechanism is not considered to be of primary importance for the observed headland, and the use of a 2D model is considered reasonable for this first-pass assessment. Future efforts may require 3D simulations to determine the importance of cyclic headland-attached bar migration on this coastline.
A second limitation is the lack of direct observations of sediment transport off the headland of interest. Such observations are rare [12] and do not exist for high-energy conditions. We have validated against current velocities and then used a previously validated transport formulation [57]; however, this does not necessarily represent actual bypassing rates. An attempt has been made to constrain this uncertainty with a number of additional tests (Section 3.2.8 and Section 4.1.1); yet, without field validation, all the results must be considered as exploratory.
This study has shown that embayment-scale circulation is an important control on bypassing, and mega-rips that occur adjacent to headlands are one form of embayment circulation; yet, little effort has been made to relate headland mega-rip hydro-morphodynamics to headland bypassing. Quantitative observations of headland mega-rip channel morphologic evolution are sparse [27,28], direct mega-rip current measurements are extremely rare [26], and no study has directly measured headland bypassing via mega-rip. Only a handful of studies have measured flow adjacent to natural headlands (e.g., [63]), and none have simultaneously measured flow adjacent to and beyond the headland or sought to combine long-term (months) flow measurements with regular bathymetric surveys. Future efforts should take this approach to better understand the role of headland rip currents in sediment transport and bypassing. Such an approach may be able to directly observe the cyclic occurrence of ‘headland-attached bars’ migrating around the headland [21,22], similar to the numerical simulations of [40], where varying wave directions were required to generate cross-shore, then alongshore transport.
For the beach observed in this case study, multi-embayment cellular circulation became an important control for simulations with Hs > 5 m when waves began to break beyond the headland of interest. This can be related to the embayed beach state model [21,24] ‘normal’ and ‘cellular’ modes. In particular, [24] related embayed beach circulation modes to the cross-shore extent of the surf zone relative to the alongshore length of the beach. In addition, [16] demonstrated the critical importance of groyne length relative to surf zone width in controlling boundary rip current and groyne embayment circulation characteristics. Our simulations suggest that an additional circulation mode emerges when waves begin to break beyond the extent of a given headland, diminishing the role of the headland as an obstruction to alongshore transport and allowing for complex, multi-embayment circulation behaviours to develop (Figure 11).
The impact on circulation and bypassing of commonly observed coastal features, such as islands, ridges, and canyons, as well as headlands of varying size, shape, and alignment should be investigated. The latter was undertaken by [31,38] but is not yet at a stage where informative predictions can be made for an unseen headland. Our site-specific method of predicting headland bypass offers a convenient means of estimating bypassing rates for a single, site-specific headland. To be of general use for an unseen headland, future efforts will be required to isolate the factors that determine the coefficients (wave rate, Equation (4)), (embayment circulation control, Equation (5)), and (tidal rate, Equation (7)). This may be achieved through the evaluation of a range of headlands (real and idealised), in order to constrain and predict these coefficients. Controls on likely include the following: bed slope, depth of bed at toe of headland, headland cross-shore extent, and asymmetries in headland bathymetry [31]. is likely to be a function residual tidal velocity and headland morphological characteristics. Resolving will likely involve larger scale geomorphic features, such as embayment length [16], barriers (e.g., islands, sub-aqueous ridges), and coastal alignment relative to the wave direction beyond the boundaries of the embayment. A useful next step would be to take a broad scale examination of multiple nearby headlands (as per [40]) and attempt to fit the headland bypass parameter described here to headlands with a variety of morphological characteristic and levels of exposure.
6. Conclusions
This study examined wave and tidal controls on embayment circulation and headland bypassing for a single headland on a high-energy, macrotidal beach. A Delft3D wave and hydrodynamic model was validated against observations taken by two ADCPs situated off the headland for a period of two months in July–August of 2016. The sediment transport was simulated based on previously validated settings for Delft3D, and a matrix of synthetic wave–tide conditions were simulated to explore the full range of forcing controls. Three primary modes of circulation and bypassing were identified for the predominantly shore-normal wave climate:
- During low–moderate wave conditions (Hs = 1–3 m), residual tidal currents are the primary control on bypassing direction and magnitude. However, wave-induced shear stress is required to initiate transport. Bypassing rates at the headland of interest are O (0 to +102 m3 day−1).
- For higher waves (Hs = 3–5 m), embayment scale circulation is initiated. For the studied headland, embayment circulation and residual tidal current predominantly acted in the same direction. Bypassing rates are O (103 m3 day−1).
- For extreme waves (Hs > 5 m), waves begin to break beyond the headland, and multi-embayment circulation occurs. For this site, the result was a reversal of the direction of bypassing, overwhelming the forcing of the residual tidal current. Bypassing rates are up to −104 m3 day−1.
A site-specific daily headland bypass parameter based on offshore wave-conditions and water levels () was shown to accurately (R2 = 0.95) match the Delft3D model outputs, allowing quantification of the key forcing controls and allowing for simple calculation of bypassing rates for the observed headland. A 5-year hindcast of bypassing rates suggested that during spring–autumn, a gradual and sustained northward flux occurred (mode 1–2). During winter, episodic and rapid southward transport occurred due to large wave events (mode 3). Predicted bypassing during an extreme winter is up to 5 × 104 m3, which is an order of magnitude less than the observed embayment-wide cross-shore flux (>4 × 104 m3) over the same period. This embayment was judged to be open, but net headland bypassing is considered insignificant relative to cross-shore transport, at annual timescales.
It is encouraging that waves and tidal controls could be effectively parameterised to predict bypass rates for the observed headland. Further work is required to determine the contribution of localised headland and broader embayment-scale morphologic controls on bypassing. The present effort contributes to our understanding of a poorly quantified area of coastal sediment budgeting and provides a pathway toward a generalised parametric approach that will allow for simple estimates of bypassing rates for headlands on rocky coasts worldwide.
Author Contributions
Conceptualization, R.J.M., G.M., and N.G.V.; Methodology, R.J.M., E.K., G.M., N.G.V., D.C., and T.S.; Software, R.J.M., E.K., and N.G.V.; Validation, R.J.M. and E.K.; Formal Analysis, R.J.M. and N.G.V.; Investigation, R.J.M.; Resources, G.M., N.V., T.S., and D.C.; Data Curation, R.J.M., T.S., and N.V.; Original Draft Preparation, R.J.M.; Review and Editing of Manuscript, R.J.M., G.M., N.V., T.S., E.K., and D.C.; Visualization, R.J.M.; Project Administration, G.M.; and Funding Acquisition, G.M., T.S., and D.C.
Funding
This research was funded by the UK Natural Environment Research Council (NE/M004996/1; BLUE-coast project).
Acknowledgments
Thank you to all those who assisted with the Perranporth surveying and ADCP deployment, in particular Mark Wiggins, Peter Ganderton, and Aaron Barrett. Additional data were provided by the Plymouth Coastal Observatory (PCO), the Channel Coast Observatory (CCO), and United Kingdom Hydrographic Office (UKHO), containing public sector information licensed under the Open Government License v3.0. The authors thank Andy Saulter for providing Met Office Wave Watch III data. We thank the four anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Davies, J.L. The coastal sediment compartment. Aust. Geogr. Stud. 1974, 12, 139–151. [Google Scholar] [CrossRef]
- Bray, M.J.; Carter, D.J.; Hooke, J.M. Littoral Cell Definition and Budgets for Central Southern England. Source J. Coast. Res. J. Coast. Res. 1995, 11, 381–400. [Google Scholar] [CrossRef]
- Cowell, P.J.; Stive, M.J.F.; Niedoroda, A.W.; De Vriend, H.J.; Swift, D.J.P.; Kaminsky, G.M.; Capobianco, M. The Coastal-Tract (Part 1): A Conceptual Approach to Aggregated Modeling of Low-Order Coastal Change. J. Coast. Res. 2003, 19, 812–827. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Coastal erosion and control. Ocean Coast. Manag. 2011, 54, 867–887. [Google Scholar] [CrossRef]
- Kinsela, M.; Morris, B.; Linklater, M.; Hanslow, D. Second-Pass Assessment of Potential Exposure to Shoreline Change in New South Wales, Australia, Using a Sediment Compartments Framework. J. Mar. Sci. Eng. 2017, 5, 61. [Google Scholar] [CrossRef]
- Castelle, B.; Bujan, S.; Ferreira, S.; Dodet, G. Foredune morphological changes and beach recovery from the extreme 2013/2014 winter at a high-energy sandy coast. Mar. Geol. 2017, 385, 41–55. [Google Scholar] [CrossRef]
- Masselink, G.; Austin, M.; Scott, T.; Poate, T.; Russell, P. Role of wave forcing, storms and NAO in outer bar dynamics on a high-energy, macro-tidal beach. Geomorphology 2014, 226, 76–93. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.D. Exploring shoreface dynamics and a mechanistic explanation for a morphodynamic depth of closure. J. Geophys. Res. Earth Surf. 2016, 121, 442–464. [Google Scholar] [CrossRef]
- Van Rijn, L.C. A simple general expression for longshore transport of sand, gravel and shingle. Coast. Eng. 2014, 90, 23–39. [Google Scholar] [CrossRef]
- Dan, S.; Stive, M.J.F.; Walstra, D.J.R.; Panin, N. Wave climate, coastal sediment budget and shoreline changes for the Danube Delta. Mar. Geol. 2009, 262, 39–49. [Google Scholar] [CrossRef]
- Evans, O.F. The relation of the action of waves and currents on headlands to the control of shore erosion by groins. Proc. Okla. Acad. Sci. 1943, 24, 9–13. [Google Scholar]
- Da Silva, G.V.; Toldo, E.E.; Klein, A.H.D.F.; Short, A.D.; Woodroffe, C.D. Headland sand bypassing—Quantification of net sediment transport in embayed beaches, Santa Catarina Island North Shore, Southern Brazil. Mar. Geol. 2016, 379, 13–27. [Google Scholar] [CrossRef]
- Hsu, J.R.C.; Evans, C. Parabolic Bay Shapes and Applications. Proc. Inst. Civ. Eng. 1989, 87, 557–570. [Google Scholar] [CrossRef]
- Pelnard-Considere, R. Essai de theorie de l’evolution des formes de rivage en plages de sable et de galets. In Les Energies la Mer Compte Rendu Des Quatr. Journees L’hydraulique, Paris 13, 14 15 Juin 1956; Quest. III, Rapp. 1, 74–1-10; Société hydrotechnique de France: Paris, France, 1956. [Google Scholar]
- Larson, M.; Hanson, H.; Kraus, N.C. Analytical solutions of one-line model for shoreline change near coastal structures. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 180–191. [Google Scholar] [CrossRef]
- Scott, T.; Austin, M.; Masselink, G.; Russell, P. Dynamics of rip currents associated with groynes—Field measurements, modelling and implications for beach safety. Coast. Eng. 2016, 107, 53–69. [Google Scholar] [CrossRef]
- Ab Razak, M.S.; Dastgheib, A.; Roelvink, D. Sand bypassing and shoreline evolution near coastal structure, comparing analytical solution and XBeach numerical modelling. J. Coast. Res. 2013, 65, 2083–2088. [Google Scholar] [CrossRef]
- Grant, W.D.; Madsen, O.S. Combined wave and current interaction with a rough bottom. J. Geophys. Res. Ocean. 1979, 84, 1797–1808. [Google Scholar] [CrossRef]
- Olabarrieta, M.; Medina, R.; Castanedo, S. Effects of wave-current interaction on the current profile. Coast. Eng. 2010, 57, 643–655. [Google Scholar] [CrossRef]
- Tambroni, N.; da Silva, J.F.; Duck, R.W.; McLelland, S.J.; Venier, C.; Lanzoni, S. Experimental investigation of the impact of macroalgal mats on the wave and current dynamics. Adv. Water Resour. 2016, 93, 326–335. [Google Scholar] [CrossRef]
- Short, A.D.; Masselink, G. Embayed and structurally controlled embayed beaches. In Handbook of Beach and Shoreface Morphodynamics; Wiley: Hoboken, NJ, USA, 1999; pp. 230–250. [Google Scholar]
- Goodwin, I.D.; Freeman, R.; Blackmore, K. An insight into headland sand bypassing and wave climate variability from shoreface bathymetric change at Byron Bay, New South Wales, Australia. Mar. Geol. 2013, 341, 29–45. [Google Scholar] [CrossRef]
- Castelle, B.; Scott, T.; Brander, R.W.; McCarroll, R.J. Rip current types, circulation and hazard. Earth-Sci. Rev. 2016, 163, 1–21. [Google Scholar] [CrossRef]
- Castelle, B.; Coco, G. The morphodynamics of rip channels on embayed beaches. Cont. Shelf Res. 2012, 43, 10–23. [Google Scholar] [CrossRef]
- Short, A.D. Rip-current type, spacing and persistence, Narrabeen Beach, Australia. Mar. Geol. 1985, 65, 47–71. [Google Scholar] [CrossRef]
- Coutts-Smith, A.J. The Significance of Mega-Rips along an Embayed Coast. Ph.D. Thesis, University of Sydney, Sydney, Australia, 2004. [Google Scholar]
- Loureiro, C.; Ferreira, Ó.; Cooper, J.A.G. Extreme erosion on high-energy embayed beaches: Influence of megarips and storm grouping. Geomorphology 2012, 139–140, 155–171. [Google Scholar] [CrossRef]
- McCarroll, R.J.; Brander, R.W.; Turner, I.L.; Leeuwen, B. Van Shoreface storm morphodynamics and mega-rip evolution at an embayed beach: Bondi Beach, NSW, Australia. Cont. Shelf Res. 2016, 116, 74–88. [Google Scholar] [CrossRef]
- Duarte, J.; Taborda, R.; Ribeiro, M.; Cascalho, J.; Silva, A.; Bosnic, I. Evidences of sediment bypassing at Nazaré headland revealed by a large scale sand tracer experiment. In Proceedings of the 3rd as Jornadas de Engenharia Hidrográica, Lisboa, Portugal, 24–26 June 2014; Volume 2014, pp. 289–292. [Google Scholar]
- Klein, A.H.F.; Ferreira, Ó.; Dias, J.M.A.; Tessler, M.G.; Silveira, L.F.; Benedet, L.; de Menezes, J.T.; de Abreu, J.G.N. Morphodynamics of structurally controlled headland-bay beaches in southeastern Brazil: A review. Coast. Eng. 2010, 57, 98–111. [Google Scholar] [CrossRef]
- George, D.A.; Largier, J.L.; Storlazzi, C.D.; Barnard, P.L. Classification of rocky headlands in California with relevance to littoral cell boundary delineation. Mar. Geol. 2015, 369, 137–152. [Google Scholar] [CrossRef]
- Castelle, B.; Coco, G. Surf zone flushing on embayed beaches. Geophys. Res. Lett. 2013, 40, 2206–2210. [Google Scholar] [CrossRef]
- Ab Razak, M.S.; Dastgheib, A.; Suryadi, F.X.; Roelvink, D. Headland structural impacts on surf zone current circulations. J. Coast. Res. 2014, 70, 65–71. [Google Scholar] [CrossRef]
- Daly, C.J.; Bryan, K.R.; Winter, C. Wave energy distribution and morphological development in and around the shadow zone of an embayed beach. Coast. Eng. 2014, 93, 40–54. [Google Scholar] [CrossRef]
- Daly, C.J.; Bryan, K.R.; Gonzalez, M.R.; Klein, A.H.F.; Winter, C. Effect of selection and sequencing of representative wave conditions on process-based predictions of equilibrium embayed beach morphology Topical Collection on the 7th International Conference on Coastal Dynamics in Arcachon, France, 24–28 June 2013. Ocean Dyn. 2014, 64, 863–877. [Google Scholar] [CrossRef]
- Ashton, A.; Murray, A.B.; Arnault, O. Formation of coastline features by large-scale instabilities induced by high-angle waves. Nature 2001, 414, 296–300. [Google Scholar] [CrossRef] [PubMed]
- Hurst, M.D.; Barkwith, A.; Ellis, M.A.; Thomas, C.W.; Murray, A.B. Exploring the sensitivities of crenulate bay shorelines to wave climates using a new vector-based one-line model. J. Geophys. Res. F Earth Surf. 2015, 120, 2586–2608. [Google Scholar] [CrossRef]
- George, D.A.; Largier, J.L.; Pasternack, G.B.; Erikson, L.H.; Storlazzi, C.D.; Barnard, P. Modeling Sediment Bypassing around Rocky Headlands. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2016. [Google Scholar]
- Da Silva, G.V.; Toldo, E.E.; Klein, A.H.F.; Short, A.D.; Tomlinson, R.; Strauss, D. A comparison between natural and artificial headland sand bypassing in Santa Catarina and the Gold Coast. In Proceedings of the Australasian Coasts & Ports 2017: Working with Nature, Cairns Convention Centre, Cairns, Australia, 21–23 June 2017; p. 1111. [Google Scholar]
- Da Silva, G.V.; Toldo, E.E., Jr.; Klein, A.H.D.F.; Short, A.D. The influence of wave-, wind-and tide-forced currents on headland sand bypassing–Study case: Santa Catarina Island north shore, Brazil. Geomorphology 2018, 312, 1–11. [Google Scholar] [CrossRef]
- Valiente, N.G.; Masselink, G.; Scott, T.; Conley, D. Depth of Closure Along an Embayed, Macro-Tidal and Exposed Coast: A Multi-Criteria Approach. Coast. Dyn. 2017, Paper 185. 1211–1222. [Google Scholar]
- Scott, T.; Masselink, G.; O’Hare, T.; Saulter, A.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/2014 winter storms: Beach recovery along the southwest coast of England. Mar. Geol. 2016, 382, 224–241. [Google Scholar] [CrossRef]
- Masselink, G.; Scott, T.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/2014 winter storms: Hydrodynamic forcing and coastal response along the southwest coast of England. Earth Surf. Process. Landf. 2016, 41, 378–391. [Google Scholar] [CrossRef]
- Prodger, S.; Russell, P.; Davidson, M.; Miles, J.; Scott, T. Understanding and predicting the temporal variability of sediment grain size characteristics on high-energy beaches. Mar. Geol. 2016, 376, 109–117. [Google Scholar] [CrossRef]
- Masselink, G.; Short, A.D. The effect of tide range on beach morphodynamics and morphology: A conceptual beach model. J. Coast. Res. 1993, 9, 785–800. [Google Scholar]
- Scott, T.; Masselink, G.; Russell, P. Morphodynamic characteristics and classification of beaches in England and Wales. Mar. Geol. 2011, 286, 1–20. [Google Scholar] [CrossRef]
- Valiente, N.G.; Masselink, G.; Scott, T.; Conley, D.; McCarroll, R.J. Evaluation of the role of waves and tides on depth of closure and potential for headland bypassing. Mar. Geol. 2018. under review. [Google Scholar]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Luijendijk, A.P.; Ranasinghe, R.; de Schipper, M.A.; Huisman, B.A.; Swinkels, C.M.; Walstra, D.J.R.; Stive, M.J.F. The initial morphological response of the Sand Engine: A process-based modelling study. Coast. Eng. 2017, 119, 1–14. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Tolman, H.L. A Third-Generation Model for Wind Waves on Slowly Varying, Unsteady, and Inhomogeneous Depths and Currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Hsu, Y.L.; Dykes, J.D.; Allard, R.A.; Kaihatu, J.M. Evaluation of Delft3D Performance in Nearshore Flows; Naval Research Laboratory: Washington, DC, USA, 2006. [Google Scholar]
- Hydraulics, D. Delft3D-FLOW User Manual; Deltares: Delft, The Netherlands, 2006. [Google Scholar]
- O’Dea, E.J.; Arnold, A.K.; Edwards, K.P.; Furner, R.; Hyder, P.; Martin, M.J.; Siddorn, J.R.; Storkey, D.; While, J.; Holt, J.T.; et al. An operational ocean forecast system incorporating NEMO and SST data assimilation for the tidally driven European North-West shelf. J. Oper. Oceanogr. 2012, 5, 3–17. [Google Scholar] [CrossRef]
- Fredsøe, J. Turbulent boundary layer in wave-current motion. J. Hydraul. Eng. 1984, 110, 1103–1120. [Google Scholar] [CrossRef]
- Grunnet, N.M.; Walstra, D.J.R.; Ruessink, B.G. Process-based modelling of a shoreface nourishment. Coast. Eng. 2004, 51, 581–607. [Google Scholar] [CrossRef]
- Van Rijn, L.C. A unified view of sediment transport by currents and waves. II: Suspended transport. J. Hydr. Eng. 2006, 133, 649–667. [Google Scholar] [CrossRef]
- Davidson, M.A.; Lewis, R.P.; Turner, I.L. Forecasting seasonal to multi-year shoreline change. Coast. Eng. 2010, 57, 620–629. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Wasltra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J.P. The predictability of cross-shore bed evolution of sandy beaches at the time scale of storms and seasons using process-based profile models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Grasmeijer, B.T.; Ruessink, B.G. Measurement Errors of Instruments for Velocity, Wave Height, Sand Concentration and Bed Levels in Field Conditions; Hydraulic Engineering Reports; Deltares: Delft, The Netherlands, 2000. [Google Scholar]
- Masselink, G.; Castelle, B.; Scott, T.; Dodet, G.; Suanez, S.; Jackson, D.; Floc’h, F. Extreme wave activity during 2013/2014 winter and morphological impacts along the Atlantic coast of Europe. Geophys. Res. Lett. 2016, 43, 2135–2143. [Google Scholar] [CrossRef]
- Long, J.W.; Özkan-Haller, H.T. Offshore controls on nearshore rip currents. J. Geophys. Res. Ocean. 2005, 110, 1–21. [Google Scholar] [CrossRef]
- McCarroll, R.J.; Brander, R.W.; Turner, I.L.; Power, H.E.; Mortlock, T.R. Lagrangian observations of circulation on an embayed beach with headland rip currents. Mar. Geol. 2014, 355, 173–188. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).