Abstract
Hurricanes pose major threats to coastal communities and sensitive infrastructure, including nuclear power plants, located in the vicinity of hurricane-prone coastal regions. This study focuses on evaluating the storm surge and wave impact of low-probability hurricanes on the lower Delaware Bay using the Delft3D dynamically coupled wave and flow model. The model comprised Overall and Nested domains. The Overall model domain encompassed portions of the Atlantic Ocean, Delaware Bay, and Chesapeake Bay. The two-level Nested model domains encompassed the Delaware Estuary, its floodplain, and a portion of the continental shelf. Low-probability hurricanes are critical considerations in designing and licensing of new nuclear power plants as well as in establishing mitigating strategies for existing power facilities and other infrastructure types. The philosophy behind low-probability hurricane modeling is to establish reasonable water surface elevation and wave characteristics that have very low to no probability of being exceeded in the region. The area of interest (AOI) is located on the west bank of Delaware Bay, almost 16 miles upstream of its mouth. The model was first calibrated for Hurricane Isabel (2003) and then applied to synthetic hurricanes with very low probability of occurrence to establish the storm surge envelope at the AOI. The model calibration results agreed reasonably well with field observations of water surface elevation, wind velocity, wave height, and wave period. A range of meteorological, storm track direction, and storm bearing parameters that produce the highest sustained wind speeds were estimated using the National Weather Service (NWS) methodology and applied to the model. Simulations resulted in a maximum stillwater elevation and wave height of 7.5 m NAVD88 and 2.5 m, respectively, at the AOI. Comparison of results with the U.S. Army Corps of Engineers, North Atlantic Coastal Comprehensive Study (USACE-NACCS) storm surge values at the AOI demonstrates that the estimated elevation has an annual exceedance probability of less than .
1. Introduction
Tropical cyclones, hurricanes, and typhoons can be categorized among the most dramatic and fatal natural phenomena. Hurricanes have been the costliest and deadliest natural hazards in U.S. history [1]. The damages to the Washington D.C. area during Hurricane Isabel (2003) were estimated to cost 3.3 billion dollars [2,3]. Similarly, the National Hurricane Center (NHC) of the National Oceanic & Atmospheric Administration (NOAA), reported an economic cost of 27 billion dollars to New York City and New Jersey as a result of Hurricane Sandy (2012). More than 650,000 homes were destroyed and 8 million people lost power in these two densely populated metropolitan areas. The combination of those events and of the 11 March 2011 accident at the Fukushima Daiichi nuclear power plant resulting from the Great Tohoku Earthquake and subsequent tsunami necessitated the reevaluation of risk to sensitive infrastructure from various types of hazards, including storm surge, river flooding, dam failure, local intense precipitation, tsunami, and ice-induced flooding. The focus of this study is on storm surges and waves generated by hurricanes.
Several researchers stated that the rising trend of sea surface temperature (SST) caused by global warming has the tendency to increase both severity and recurrence of events such as hurricanes [4,5,6]. This has also been predicted by other research, such as Webster et al. [7]. Therefore, considering the highly hazardous risk to specific infrastructure, including nuclear power plants, vulnerabilities should be checked against probable maximum storm surge (PMSS), and not limited to highly probable events. The PMSS is a hypothetical surge that has virtually no probability of being exceeded in a region resulting from a rare hurricane producing the highest sustained wind speed recorded at a specified coastal location [8].
The NHC defines a tropical cyclone as a warm-core non-frontal synoptic-scale (i.e., large scale) storm, originating over tropical or subtropical waters, with organized deep convection and a closed-surface wind circulation about a well-defined center. Tropical cyclones with maximum sustained wind speed of 119 km/h (74 mph) and more are categorized as a hurricane or a typhoon. The terms hurricane and typhoon refer only to the geographical location of the storm. The main characteristics of hurricane/typhoon include central pressure, maximum wind radius, forward speed, and maximum wind speed. Storm surge and wave modeling are required to evaluate the coastal flooding impact/risk of past (hindcasting), current, and future (forecasting) hurricanes.
Numerical modeling plays a critical role in planning for, responding to, and mitigating coastal flood hazards. Storm surge is the rise of water generated by a storm, over and above the predicted astronomical tides.
Hurricane modeling research has been done based on various techniques, goals, approaches, and methodologies. Wang et al. [9] focused on predicting high-resolution street-level-scale inundation modeling of the Washington D.C. area during various flooding events, including Hurricane Isabel and the Great Potomac Flood of 1936. They used a finite volume with semi-implicit Eulerian–Lagrangian scheme on an overall and nested grid with 200-m and 10-m resolution, respectively. Three main breakthrough aspects of their study were implementing high-resolution LiDAR data in the sub-grid, combining river and coastal flooding, and increasing the computational efficiency of the model.
Garzon and Ferreira [3] investigated uncertainties associated with the selection of physical parameters or processes involved in storm surge modeling in large estuaries, such as Chesapeake Bay. They specially explored the coupled ADvanced CIRCulation (ADCIRC) + Simulating WAves Nearshore (SWAN) modeling package. Two historical storms [Irene (2011) and Sandy (2012)] and two synthetic storms, derived from Isabel (2003), were used for testing the model sensitivity. Their original (i.e., high-resolution) mesh was the Federal Emergency Management Agency (FEMA) Region III mesh [10]. They reported that the mesh resolution impacted storm surge more on the upper part of the bay, where the surges were lower. They further observed a 0.15-m decrease in storm surge magnitude within the Middle Bay when the mesh resolution was increased almost 25 times. This indicates that their low-resolution mesh with approximate grid size of 500 m is still capable of generating storm surge with reasonable accuracy in the lower part of the bay. Manning’s “n” coefficient influence on estimating peak maximum elevation, currents, flood duration, and extension in overland areas was found to be significant.
Cho et al. [11] studied the response of Chesapeake Bay to Hurricanes Floyd (1999) and Isabel (2003). They found two distinct stages, the initial by remote winds and the primary with local winds, for the interaction of hurricanes and salinity intrusion. Lin et al. [2] examined multiple hazards posed to the Chesapeake Bay by Hurricane Isabel (2003). Weather Research and Forecasting (WRF) and ADCIRC models are coupled to simulate storm surge. They stated that the simulation underestimated the wind speeds in the right quadrant of the storm. This is due to the simulated wind maxima being centered along the track. They reported good representation of the storm surge at the lower Chesapeake Bay compared with that at the upper portion.
A qualitative review of the available historical hurricanes and their impact might imply that hurricane storm surge and wave with very low probability is of no concern; however, recent research, such as Dailey et al. and Donnelly et al. [12,13,14], suggests that analysis using only historical hurricane records is, at best, inconclusive. Delaware Bay and its floodplain received less attention than their surrounding estuaries and coastal regions, especially with the impact of low-probability hurricanes. In this study, care is taken to filling this gap and addressing the practical aspects of storm surge and wave modeling as it relates to vulnerable sensitive infrastructures, low-probability events, optimized parameter selection, wind-field generation, calibration, and computational needs. The goal was to develop a numerical model with the least computational requirement and capable of being used for facilities located near coastal regions.
Deterministic vs. Probabilistic
Two broad approaches in performing studies associated with flood hazards are deterministic and probabilistic. In the deterministic approach, the probable maximum storm surge is determined by modeling the synthetic hurricane tracks generated using the National Weather Service (NWS) Report 23 [15] guideline. NWS Report 23 provided the criteria for determining wind field for the most severe hurricane with highest sustained wind speed at a specified coastal location, yet reasonably probable. The wind field is then run in a hydrodynamic model, such as ADvanced CIRCulation (ADCIRC), Delft3D, TELEMAC, etc., to determine the probable maximum water surface elevation (i.e., low probability storm surge). Meteorological parameters evaluated in NWS Report 23 are central pressure (P), peripheral pressure (P), radius of maximum winds (R), forward speed (V), track direction (), and inflow angle ().
Probabilistic flood hazards are used to estimate the frequency of external flooding scenarios. For sensitive infrastructures, including nuclear power plants, the extrapolation of the hazard to extremely low frequency (less than 10) is required. There are various frequency estimation methods, such as gage analysis, Monte Carlo, Empirical Simulation Technique (EST), Joint Probability Method (JPM), and JPM-OS (Optimal Sampling) [16,17]. EST is a bootstrapping, resampling-based method that assumes similar magnitude and frequency between past and future events. The JPM and JPM-OS approaches are used more commonly today. JPM utilizes a parametric representation of tropical cyclones characterizing intensity, size, track, and speed [18]. It then assigns a joint probability to each combination of storm parameters. JPM relies on a numerical method to calculate coastal flood elevations that would be generated by those storms. One advantage of the probabilistic versus deterministic approach is the ability to assign a frequency to the event. In this study, the deterministic approach is followed to establish the parameters required for developing a very low-probability wind field. The probability of estimated surge values is found indirectly by comparing them to the probability of other studies.
2. Methodology
2.1. Study Area
The area of interest (AOI) is located on the west bank of Delaware Bay (Bay) at approximately 32 km north of its confluence with the Atlantic Ocean and 12 km northeast of Milford, Delaware.
The Bay has a length of 210 km starting from its riverine portion at Trenton, New Jersey to its connection with the Atlantic Ocean at the bay side [19]. The Bay width gradually increases from upstream to downstream. The mouth of the Bay extends between Cape May and Cape Henlopen with a width of 18 km. The estuary reaches its maximum width of 45 km (see Figure 1) approximately 11 km northwest of the mouth. The Bay has an average bathymetry of 7 m [20] with a channel (deeper than 28 m) passing in the middle of the Bay. The channel acts as a conduit for connecting the Atlantic Ocean to the ports and facilities upstream. The estuary has an axis that is tilted 35 degrees counterclockwise west of due north.
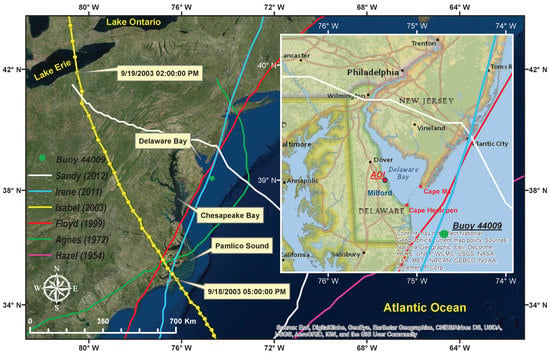
Figure 1.
Location map for the area of interest. Six colored lines indicate major historical hurricane tracks within the region.
The AOI is within a wetlands area with a saline fringe geographic setting. Reed et al. [21] concluded that with approximately 2 mm/year of sea level rise, the wetlands around the AOI would be marginal and transformed into open water. This is very important as the wetlands tend to act as a buffer in attenuating the storm surge [22,23,24]. Shorelines of the AOI are undisturbed sand beaches.
Since 1749, 108 tropical cyclones, including some that became extratropical, have affected the area [25]. Most have occurred in September, which coincides with the peak of the Atlantic hurricane season. The majority of the tropical cyclones that have occurred in Delaware have brought only rainfall or strong waves (higher than 1.5 m), though a few have caused deaths in the state. Six of the most deadly hurricanes with their general track are graphed in Figure 1. Hurricane Isabel was selected for calibration purposes as is described in Section 2.4.5. For Hurricane Isabel, the hourly position of the eye is shown in yellow circles.
2.2. Computational Models
Delft3D (Version 4, Deltares, Delft, The Netherlands) is a highly developed computational model with several modules and utilities that are fully integrated for solving multi-disciplinary problems in coastal, river, and estuarine environments [26]. Three Delft3D components, FLOW, WAVE and WES, are dynamically coupled in this study for the automatic transfer and exchange of relevant data. Major features of each module relevant to the hurricane modeling are described in following subsections.
2.2.1. Delft3D-FLOW Module
The FLOW module is the heart of Delft3D and a multidimensional hydrodynamic and transport simulation program that calculates non-steady flow and transport phenomena resulting from riverine, tidal, and meteorological (i.e., atmospheric, winds, and waves) forcing [27].
The Delft3D-Flow module in two-dimensional (2D), depth-averaged, hydrostatic, and unsteady form is used for characterizing the hydrodynamics of the historical and synthetic hurricanes. In this format, the continuity [Equation (1)] and Reynolds-averaged Navier–Stokes [Equations (2) and (3)] equations for an incompressible fluid are solved over an orthogonal curvilinear grid in spherical coordinates:
where u and v are depth-averaged velocities along the x and y directions, is the water surface elevation above the still water level, f is the Coriolis parameter, g is the gravitational acceleration, is the water density, d is the water depth above the bottom of and below the still water level, is the horizontal viscosity coefficient, and are wind velocities at 10-m height above the still water level along the x and y directions, n is the Manning coefficient, and is the wind-drag coefficient dependent on and .
Manning’s “n” and wind-drag values () are two important calibration coefficients in all coastal flood modeling efforts. Manning’s “n” is a factor of land cover and changes from 0.02 in open water to 0.15 in high-density and developed areas [28]. Manning’s roughness has been used in similar hurricane storm surge studies. Garzon and Ferreira [3] study results suggested that the Manning’s “n” coefficient can significantly impact the model accuracy in estimating peak of maximum elevation, currents, flood duration, and extension in overland areas.
Wind-drag translates the wind speed into wind setup along the coastline [27] and growth of surface waves [29]. Wind-drag coefficient increases with increasing wind speed and then is capped at a higher breakpoint wind speed (e.g., 30 m/s based on Vatvani et al. [30]). This reflects the dependence of surface roughness on wind speed. Wind-drag functionality has been studied and modified by various research, including [31,32,33,34,35]. They showed that ranges from 0.0015 to 0.005. Delft3D-FLOW module introduces the three breakpoint piece-wise formulation [27] of the wind speed and drag relation. Such functionality provides flexibility in defining several relations.
2.2.2. Delft3D-WAVE Module
The Delft3D-WAVE module is the Simulating WAves Nearshore (SWAN) model. SWAN is a fully spectral third-generation wave model that can realistically simulate generation, propagation, transformation, breaking, and associated hydrodynamic forcing of random, short-crested, wind-generated waves [36]. The SWAN model is properly formulated to consider most important physical aspects of wave propagation, generation, and dissipation [37]. Coupling FLOW and WAVE modules is essential in storm-surge modeling as water levels, currents, and waves are interconnected and affect each other through radiation stress gradients.
SWAN has traditionally been used for nearshore and shallow waters. Dietrich et al. [38] provided a comprehensive examination of applying SWAN to deep waters with hurricane modeling applications. The SWAN model has been used extensively to simulate waves in both shallow and deep waters [3,30,36,39,40].
SWAN calculates the evolution, in 2D geographical -space and time t, of the wave action density N using the action balance equation:
The left side of Equation (4) is the kinematic part, which represents, respectively, the temporal variation of the action density, the propagation of action in geographical space (with representing group velocity and the ambient current), shifting of the relative frequency due to variation in depth and current (with as propagation velocity in -space), depth-induced and current-induced refraction (with as propagation velocity in -space). The term on the right-hand side is the source term in terms of energy density representing the effects of generation, dissipation, and nonlinear wave–wave interactions [36].
2.2.3. Delft3D-WES Module
Generation of spatially-varying wind and atmospheric pressure fields from hurricane characteristics is a critical and significant step in storm surge and wave modeling [17,41,42,43,44]. Several schemes and models have been developed by researchers and scientists. Few of these schemes/models include Holland [45], NWS Report 23, Rankine, TC96, WeatherFlow Regional Atmospheric Modelling System (WRAMS), Mesoscale Meteorological Model (MM5) model [46], and Wind Enhanced Scheme (WES).
Holland [45] introduced a scaled hyperbolic pressure profile used in gradient wind equations. The main hurricane-related parameters required in this model are radius of maximum wind (), maximum wind speed , central pressure (), peripheral pressure (), and track angle (). The Holland model has been used in numerous studies, including [47] and [48].
The NWS Report 23 vortex model [15] analytically recreates the spatially distributed hurricane wind and pressure fields. The Rankine model [49] assumes solid body rotation inside the with decaying wind speed beyond the . TC96 is a highly-refined mesoscale-moving vortex formulation based on the equation of horizontal motion, vertically averaged through the depth of the planetary boundary layer. It was first developed by Chow [50] and then modified by Cardone et al. [51]. The WRAMS model is an implementation of the Regional Atmospheric Modeling System (RAMS) by WeatherFlow. RAMS [52,53] is a mesoscale, nonhydrostatic, 3D modeling system. It has recently been used to evaluate the impact of the areas affected by Hurricane Sandy [9]. MM5 [46] is a nonhydrostatic scheme that simulates the atmospheric circulation.
WES is a modification of the Holland scheme to introduce asymmetry features of a real hurricane. This asymmetry is brought about by applying the translation speed of the cyclone center displacement as steering current and by introducing rotation of wind speed due to friction. Delft3D uses the WES technique in generating the wind field, which is the applied model in this study. In Delft3D, wind fields are generated on a moving spider web grid using Equation (5). Spider web is a grid in polar coordinate that is centered on the center of the tropical cyclone. At the center, this circular grid system has a high-grid resolution, which enables capturing strong variation of wind and pressure gradients in the center area of the typhoon. The grid resolution decreases proportionally with increase of the distance from the center of the grid:
where r is the distance from the center of the cyclone, f is Coriolis parameter, is density of air (i.e., 1.10 kg m), is difference between peripheral and central pressure, is the maximum sustained wind speed, is the radius of maximum wind, and e is the base of natural logarithm (i.e., ). Laknath et al. [54] compared the wind field generated by the MM5 model and by the WES techniques. They reported that the WES technique underestimates wind for areas located far from the center of the storm. However, in general, a hurricane contribution would be minimal to those remote areas and, therefore, is not considered a flaw of the WES scheme.
2.3. Model Configurations
2.3.1. Model Domain
The physics-based numerical models, such as Delft3D, are valuable for accurately predicting the physical processes involved in hurricane surge response over large regions; however, they are computationally intensive when used at the spatial resolution required for accurate surge estimation [55].
Spectral, temporal, and spatial resolution are major decision points in each modeling mechanisms as they impose limitation on circulation and wave analysis. Nesting of structured meshes is a well-known technique in improving the negative impact of resolution. In this technique, the size of the model mesh decreases in a progressive fashion around the AOI. It is established that the storm surge models are sensitive to the open-boundary conditions, spatial resolution, and the size of model domain [38]. However, any model should also be economically justifiable and efficient with limiting the model error within an acceptable range or in making conservative assumptions.
Li et al. [56] investigated the impact of the model domain size on storm surge. They identified a threshold where increasing domain size, both cross-shore and alongshore, has no further impact on simulation results. They also showed that the domain size is not impacted by hurricane intensity, but has linear relation with the hurricane radius of maximum wind (). This finding enables a modeler to establish a model domain that is calibrated for a significant hurricane and then apply it for a lower-probability event.
Another consideration in defining a cost-effective and efficient model domain is the location of the offshore boundary. A study by Garzon and Ferreira [3] suggested that the location of the open boundary might not impact the simulation results as long as the model resolution is sufficient to properly model the movement of water. However, Blain et al. [57] showed that locating the offshore boundary of the model in an area with significant surge, causes the near-shore surge to be underestimated. This indirectly indicates that the offshore boundary should be located beyond the continental shelf. Li et al. [56] reported that the slope of the Atlantic continental shelf ranges from 0.0003 to 0.01. Their study, combined with Irish et al. [58], showed that the storm surge increases with decrease of the slope of the continental shelf. They concluded that, for a shallow bathymetry, the domain size should be increased to avoid artificial impact of the slope. The width of the shelf near our study area is approximately 154 km. Based on Li et al. [56], storm surge is not sensitive to the change in shelf width for width higher than 100 km. According to their analysis, the appropriate domain size for this study, considering the width of the shelf, is 100 km (cross-shore) by 150 km (along-shore). In addition, considering the hurricane categories (higher than 5), the minimum domain size is 200 km (cross-shore) by 250 km (along-shore).
The above findings and preliminary sensitivity analysis resulted in one Overall and two Nested domains (see Figure 2) in this study. All domains are set up in a 2D fashion. RGFGRID tool of Delft3D is used to generate the curvilinear grid. Primary grid properties including curvature, smoothness, length of edge, and orthogonality are used to increase grid quality. Figure 3 and Figure 4, respectively, show the bathymetry of the Overall and Nested domains. Coastline and bathymetry are from the ADvanced CIRCulation (ADCIRC) Federal Emergency Management Agency (FEMA) Region III model [59]. The bathymetry is developed by the Coastal Process Branch of the Flood and Storm Protection Division, U.S. Army Engineering Research and Development Center (ERDC) using best available data. The QUICKIN tool of Delft3D combined with ArcGIS from Esri are used to assign bathymetry data to model grids. In addition, high-resolution Light Detection and Ranging (LiDAR) data were used to complement the topography near the study area.
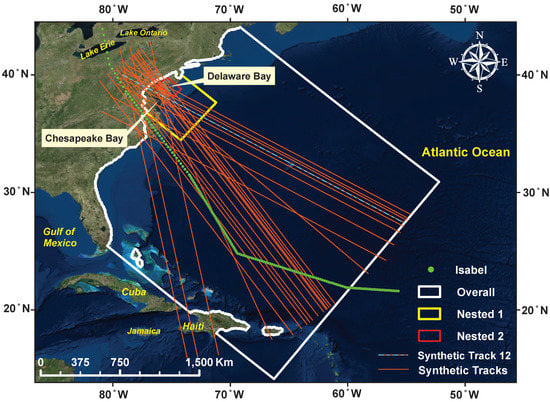
Figure 2.
Location map for the extent of three model domains. Hourly location of hurricane Isabel shown in green solid circles. Orange lines present synthetic hurricane tracks.
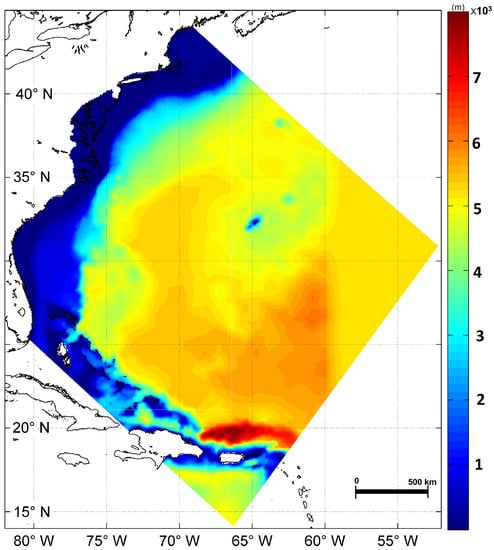
Figure 3.
Map showing elevation of topography and bathymetry incorporated into the Overall model domain.
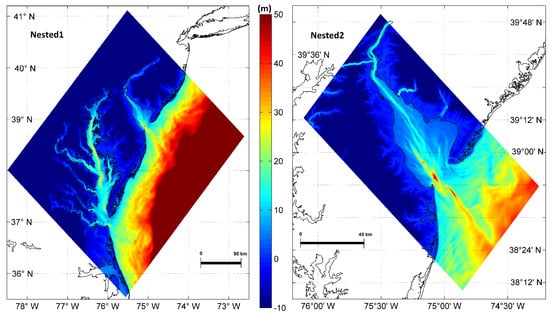
Figure 4.
Map showing elevation of topography and bathymetry incorporated into the Nested1 and Nested2 model domains.
All model domains are oriented along the axis of the Delaware Bay, which is southeast towards northwest. Considering their size, all model domains are in a spherical coordinate system. Other major properties associated with each model domain are presented in following subsections.
2.3.2. Overall Domain
The Overall domain includes the Delaware Bay extending from the mouth to the Commodore Barry Bridge on the Delaware River (Figure 2). The offshore portion of the domain extends approximately 2100 km toward the Atlantic Ocean and beyond the continental shelf. The model domain has a total length of 2700 km and width of 2400 km. The grid contains 87,963 cells, covering an area of 5.1 million km. The Overall model domain has grids with an averaged constant resolution of 7.5 km (i.e., 0.06). The Overall domain is considered large enough to ensure that the wind field gradient and offshore winds are properly captured. This resolution was determined to be optimal in resolving offshore surge and wave characteristics. Sensitivity analysis was performed with coarser and finer resolution models, but resulted in similar results. For example, increasing the number of grid points from 87,963 to 160,000, almost twice, improved the model results by only 3 cm. However, the model run time was increased by a factor of 5.
2.3.3. Nested Domains
Two domains with progressively finer mesh are nested inside the Overall domain. They are identified as Nested1 and Nested2 in Figure 2. Longitudinally, the Nested1 domain starts 180 km southeast of the Delaware Bay mouth and extends another 188 km northwest along the axis of the Delaware Bay. Laterally, the Nested1 domain starts 143 km northeast of the Delaware Bay mouth and extends another 289 km southwest along the axis of the Delaware Bay. The Nested1 model domain contains 44,700 cells, with a constant size of 1.9 km (i.e., 0.017), covering an area of 0.16 million km. The Nested2 domain extends longitudinally from 41 km southeast of the Delaware Bay mouth to 100 km northwest of the mouth. Nested2 domain extends laterally from 57 km northeast of the Delaware Bay mouth to 21 km southwest of the mouth. The Nested2 model domain covers an area of 11,000 km, with 196,000 cells having a constant size of 245 m (i.e., 0.002). These resolutions were determined to be optimal in resolving surge and wave characteristics. The variation in water level of less than 50 cm was considered as the criteria. Sensitivity analysis was performed with coarser and finer resolution domains, but resulted in similar results.
2.3.4. Standard Setting
Delft3D-Flow uses the standard Alternating Direction Implicit (ADI) for solving the shallow water equations described above. Sensitivity tests are carried out in order to determine the largest time step for which the ADI-method still yields accurate results. Temporal differencing for the simulation is set at three minutes for the Overall grid and one minute for the Nested grids to avoid numerical instabilities. Delft3D-Wave (i.e., SWAN) is based on implicit numerical schemes, and, therefore, it is not limited by the Courant stability criterion as a balance between time and space. In this sense, the time step in SWAN is not restricted. However, the accuracy of the SWAN results is obviously affected by the time step. The Sheng et al. [60] study showed that, for slow-moving hurricanes, the stationary mode of SWAN yields reasonable wave conditions as compared to the non-stationary mode. In simulating storm surge, coupling between flow and wave models as well as coupling between Overall and Nested grids is common. The flow and wave simulations are performed in one-way coupling mode for the Overall domain, meaning that only currents and water levels from the flow model are fed into the wave model. After establishing the open-boundary conditions for the Nested1 domain, surge and wave are coupled in two-way fashion, where results calculated by one (i.e., water levels and current by Delft3D-FLOW and radiation stresses gradient by Delft3D-Wave) are fed back and forced to the other within a specified time steps. All domains always use the same wind field and drag relations.
Flow and wave models are run on the same grids to produce a seamless coupling. SWAN is a slow-running model and is typically run only once for a few flow model time steps. Sensitivity analysis and literature review showed that a 20-min coupling provides satisfactory results. This means that, after twenty 60-s Delft3D-Flow time steps, flow and wave models mutually exchange information. In this fashion, Delft3D-Flow receives radiation stresses; in return, Delft3D-Wave updates water level and current.
The main flow model parameters include initial water level of 0.0 m, fluid density of 1025 kg m, and constant horizontal eddy viscosity of 10 m s. Drying and flooding are included in all models with the criterion set to 10 cm.
The spectral resolution in SWAN was configured with 36 frequency bins over a range of 0.04–0.6 Hz and directional space bins of 10. The frequency range is found through extensive literature review and sensitivity analysis. Results showed that the lowest frequency must be somewhat smaller than 0.7 times the value of the lowest expected frequency. The highest frequency must be at least 2.5 to 3 times the highest expected frequency. For example, hurricane Isabel frequency varied from 0.06 to 0.2 Hz.
The 2nd generation of SWAN, with bottom friction of 0.067 m s parameterized in the JONSWAP formulation, is used. Sensitivity analysis on using both 3rd and 2nd generation schemes were performed. The 2nd generation resulted in improvement in the wave results and reduced the model run time. Findings are compatible with other researchers such as [61]. In order to set the bottom friction in JONSWAP model, a range of frictions from 0.038 m s to 0.067 m s, as suggested by Vledder et al. [62], were tested. The depth-induced process of wave breaking is not entirely understood yet in spectral mode. In contrast, the dissipation is simulated using the bore model that conserves the spectral shape [63]. In this study, a disputation coefficient of = 1.00 and a breaking parameter of = 0.73 is applied. Whitecapping, nonlinear triad, refraction, and frequency shift were not considered. Sensitivity analysis showed inclusion of these formulations has minimal impact on the ultimate result, which is the maximum probable storm surge at the AOI.
The default drag coefficient () of 0.0012 underestimated the generated wave heights at the buoy locations. Therefore, after sensitivity analysis, the drag coefficient was set to vary linearly from 0.0012 at 0 m/s wind speed to 0.004 at 30 m/s wind speed. Such modification has been reported in other recent studies, such as [48,64].
2.4. Model Forcing
Tides and winds are the primary forces considered in this study as described in following subsections.
2.4.1. River Discharges
Kerr et al. and Resio et al. [44,65] studies showed that river discharge can significantly impact storm surge along confined rivers; however, they also stated that the river discharge can be neglected. In this study, the AOI is located in the bay side of the Delaware Estuary, which is significantly wider than the upstream portion (i.e., beyond the confluence of Chesapeake and Delaware Bay Canal and Delaware Bay). Simulating storm surges using a range of river flows applied to Trenton, New Jersey resulted in negligible difference in water levels in the study area. Therefore, no river discharge is considered in this analysis.
2.4.2. Tides
As shown in Figure 2, the Overall, Nested1, and Nested2 domains each contain three open boundaries: the south, west, and east. All open boundaries are far from the study area and calibration locations to cancel out negative impact of open boundaries. Tidal heights are imposed along all open boundaries of the Overall domain by specifying amplitude and phases. The Nested domains take their boundaries from their associated nested grid. In this region, the lunar semi-diurnal (M2) is the dominant tidal constituent [66]. Other constituents considered in the tidal boundary are K1, K2, Q1, S2, O1, M6, N2 and M4. Delaware Bay is classified as semi-diurnal, mesotidal, with tides ranging between 2 m and 4 m. The following is used in Delft3D to combine all of the constituents and develop the variable water level:
In the equation above, represents temporal variation of water level, k the number of constituents, i the constituent index, the local amplitude of tide, the constituent phase, the nodal amplitude factor, the period, and the astronomical argument. The and are input variables for each selected constituent. Delft3D calculates , , and for each constituent.
In Delft3D, the phase and amplitude are required on both sides of each open boundary. ADCIRC is used to create these parameters from the western North Atlantic, Caribbean Ocean and Gulf of Mexico tidal databases [67]. Tides were applied only to the calibration portion of the study and not the performance runs. In order to estimate the probable maximum storm surge, 10% exceedance high tide (EHT) is used as initial condition in all performance runs. Based on ANSI standard [68], this has a value of 1.7 m above Mean Low Water (MLW) near the study area at the Breakwater Harbor, Delaware. Converting the MLW to NAVD88 (same as bathymetry data) makes the 10% EHT equal to 0.95 m NAVD88.
2.4.3. Meteorological Forcing—Wind Field
Precise prediction of the maximum water level requires the accurate computation of the storm surge, which, again, depends on the accuracy of the wind forcing it receives. Wind fields were developed for both historical and synthetic storms for input to the Delft3D-Flow and Wave modules using the methodology described in Section 2.2.3, with the following inputs.
2.4.4. Delft3D-WES Setting
As mentioned above, the Delft3D-WES module computes the hurricane wind and pressure fields on a so-called spiderweb, which provides a moving snapshot of the hurricane wind field. Several parameters, including radius of the tropical cyclone (2000 km), number of rows (60), and number of columns (1200), define the size of the spiderweb grid. These parameters were carefully selected through a series of sensitivity analyses and calibration. The resolution in the radial direction then becomes equal to 1666 m. A resolution between 1000 and 2000 m is required especially when analyzing compact cyclones with high wind gradients [69]. Sensitivity analysis of Hurricane Isabel showed that increasing cyclone radius results in increased generated winds until a threshold, where its increase has no more impact. Increasing the number of rows and columns in the spiderweb did not have a significant impact on the results.
Considering the available input parameters, seven methods are implemented inside the WES module. Method 3, requiring location of cyclone eye (i.e., latitude and longitude), maximum sustained wind speed (), pressures drop (, i.e., difference between peripheral pressure and the minimum central pressure), and the radius of maximum winds () was used. A peripheral pressure of 1013 mb was applied.
2.4.5. Historical Storm
Based on U.S. Nuclear Regulatory Commission (NRC) guidelines, models being used for forecasting low-probability events should be validated using the most significant and recent event relevant to the region. In addition, considering the counterclockwise rotation of hurricanes, only those with a track line located west of the study area have the capability of producing sustained wind speed along the estuary. The major historical hurricanes that impacted the region were extracted from NOAA database [70]. They are Sandy (October, 2012), Irene (August, 2011), Isabel (September, 2003), Floyd (September, 1999), Agnes (June, 1972), and Hazel (October, 1954). The tracks of these hurricanes are shown in Figure 1. Among the six hurricanes, Isabel was selected for validation purposes because of the high quality of its re-analysis report and the overall body of its documentation.
Hurricane Isabel formed on 1 September 2003, from a tropical wave off the coast of Africa [2,71]. It intensified to a Category 5 hurricane on 11 September 2003, with a maximum sustained wind speed of 314.8 km/h (170 knots). Hurricane Isabel’s forward speed was approximately 11–15 km/h [6–8 knots] [60] during landfall near Drum Inlet on the outer banks of North Carolina (Figure 1) at 5:00 p.m. UTC 18 September 2003. It can be categorized as a very slow-moving system. Upon landfall, it continued the same northwesterly track over North Carolina and Virginia to the northeast of West Virginia.
The combination of National Hurricane Center (NHC), also known as HURDAT [72], and extended best-track datasets [73] were used for establishing the model inputs. Data analysis showed that Hurricane Isabel can be divided into seven segments with similar characteristics (see Table 1). The hourly position of the hurricane, along with their characteristics, was then interpolated from these seven segments. The Hurricane Isabel track with hourly position of the eye is presented in Figure 1. Velocities shown in Table 1 are the 1-min maximum sustained surface winds.

Table 1.
Hurricane Isabel characteristics at a time 161 h before until 31 h after the landfall.
2.4.6. Synthetic Storms
Probabilistic storm surge studies require large sets of storm tracks, on the order of thousands, to adequately cover the parameter and probability spaces. For example, more than 17,000 storm tracks were used in Hanson et al. [10], more than 8000 tracks in Lin et al. [2], and more than 1050 synthetic tropical cyclones in Nadal et al. [74]. Lack of sufficient historical records makes the development of synthetic hurricane tracks a critical step in estimating hazards from coastal flooding [17]. Such tracks should follow similar statistical properties as recorded historical hurricanes within the study area [6,75,76].
Numerical surge and wave models are then used to translate stochastically generated hurricane tracks into coastal hazard estimates. However, a majority of these studies rely on fast-running models, such as Sea, Lake, and Overland Surges (SLOSH) developed by NOAA [77], in order to perform screening and, thereby, reducing the number of tracks required on the order of hundreds. However, SLOSH simulation may not be able to capture some unusual water responses to storms at locations with complex geophysical features. Other computationally intensive hydrodynamic models, such as ADCIRC, Delft3D, or TELEMAC3D, may be used to evaluate tracks selected by SLOSH. The probability of each storm is then combined with the modeling surge values to create a cumulative distribution function (CDF) to estimate the flood risk.
Researchers have shown that only hurricanes passing through a narrow band of landfall locations that generate maximum wind speed near the study site area will result in the largest surges at that specific location [44,55]. Furthermore, in the Northern Hemisphere, the Coriolis effect causes the peak of the storm surge to fall to the right of the storm track at landfall [78,79]
In this study, the range of meteorological hurricane parameters is estimated combining the evaluation of site-specific features and the NWS Report 23 [15]. This guideline provides criteria for determining wind fields along the Gulf of Mexico and East Coast of the U.S., for the most severe hurricane reasonably possible at the study area known as Probable Maximum Hurricane (PMH). NWS Report 23 provides a single value for the peripheral and central pressure, along with upper and lower limits for other hurricane parameters, such as radius of maximum winds, forward speed, track direction, and maximum sustained wind speed. The procedure starts with calculating the distance between the study area and the U.S.–Mexico border in nautical miles (nm). The AOI has a NWS mile post of 4074.4 km (2200 nm). Other parameters are found based on this location index. The parameters estimated using NWS Report 23 are adjusted after evaluating the major historical hurricanes within the study area, ensuring that the most severe hurricane range is enveloped. Historical hurricane parameters are accessible from [80,81]. The range of the hurricane parameters extracted from major hurricanes within the region is presented in Table 2.

Table 2.
Major historical hurricane characteristics impacting area of interest.
After performing sensitivity analysis on numerous hurricane tracks, 41 categorized in 25 common landfalls and angles were used for the analysis (see Figure 2). Table 3 presents the range of parameters used to construct the synthetic hurricanes. Another important parameter in estimating the maximum sustained wind speed is the Holland B. Ref. [82] shows that the Holland B parameter is a factor of sea surface temperature (SST) and varies from 0.75 to 2. For the Delaware Bay, the SST during the hurricane season (August–October), varies from 20 to 25 degrees Celsius. Referring to [82], the average Holland parameter becomes one for the region. Sensitivity analysis on forward speed showed that it only changes the timing of the peak and not its magnitude; therefore, forward speed is used only to control the hurricane approach toward the AOI.

Table 3.
Range of PMH Parameters.
2.5. Model Calibration and Sensitivity
Several studies have been performed to understand the impact of various model parameters on storm surge estimation [56,57,83].
Bastidas et al. [17] performed a comprehensive sensitivity analysis for storm surge and wave modeling using Delft3D within the hurricane hazard framework. Findings of such studies are appropriate; however, it is noted that parameter sensitivity suited for one hurricane or one region may not be appropriate for others. Therefore, in addition to considering the findings of previous research, further sensitivity analyses were performed as part of this modeling effort. In calibrating the models, it should be emphasized that the sole goal was to determine the maximum values and not the timing, as the intent would be for power plant designs. Therefore, only the peak values were used for calibrating and not the timing aspects. Further calibration would be required if used for flood timing assessment.
2.5.1. Observations
Hourly measurements of wind speed from buoy 44009 [84] were used to evaluate Delft3D-WES reproduction of the wind speed time series. Peak significant wave height and period during Hurricane Isabel were extracted from buoy 44009. This station is located 48 km southeast of Cape May, New Jersey, at a water depth of 43 m, which is the closest to the study area. They were used to evaluate Delft3D-Wave reproduction of significant wave height and period.
Hourly water level records from several NOAA tidal stations [85], including Atlantic City, Ocean City, Cape May, Lewes, and Brandywine Shoal Light, were evaluated as part of the calibration and are presented in Figure 5. The figure shows that the Brandywine Shoal Light tide gauge has the highest range of water level and is the one closest to the study area. Therefore, it was used to evaluate the Delft3D-Flow ability to reproduce water level elevations during Hurricane Isabel.
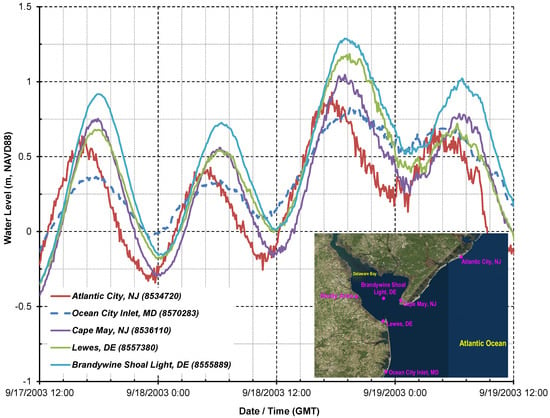
Figure 5.
Observed water surface elevations during the passage of hurricane Isabel. For Hurricane Isabel track refer to Figure 2.
2.5.2. Calibration Model Comparison
Delft3D-FLOW and WAVE models are both calibrated. The calibration procedure is further discussed in detail in this section. A 15-day ramping period, including only tidal forcing, was completed prior to the validation run to ensure that water levels were correctly represented at the start of the simulations. The model was then run for eight days, from 12 September 2003, to 20 September 2003, with forcing as discussed above. In this period, Hurricane Isabel propagated from the southern boundary of the Overall model domain, followed a northwest track, made landfall on 18 September 2003, and dissipated over land. Wind field, water level, significant wave height, and wave period were all compared with the observed data at their associated stations. Model performance was tested by calculating root-mean-squared error (RMSE), bias, and scatter index (SI) using the following:
where are observations, are model predictions and N is the total number of points. Comparison of simulated and observed wind at NDBC station 44009 is presented in Figure 6. Model results show that the simulated peak wind speed and trend are matching the observed values. The wind field is over-predicted with RMSE of 1.1 m/s, particularly when the peak of the storm reaches the targeted buoy, near the mouth of the Delaware Bay. Figure 7 shows the wind field at 5:42 a.m. EST and 8:42 p.m. EST on 18 September 2003, approximately 12 h prior to and 5 h after the storm’s first landfall near Drum Inlet on the outer banks of North Carolina. Maximum wind speeds in the mouth of the Delaware Bay area grow from 15 to 25 m/s, and change direction from east to south. Figure 8 shows the storm surge and wind direction approximately 12 h before and after Hurricane Isabel’s first landfall. Storm surge regionally built up to levels of 2–2.5 m in and around the study area over time. Computed storm surge movement was rather uniform along the axis of the Delaware Bay, as Hurricane Isabel followed its northwesterly direction. Current vectors show water being driven into the region from the southeast by wind. This southeast-to-northwest movement of water was the predominant pattern after the landfall. The time series of water levels, both sampled and simulated, are illustrated in Figure 9 at the location of the Brandywine Shoal Light NOAA station. Peak storm surge occurs on 18 September 2003, at 7:00 p.m. Simulated and observed values are agreed well, with an RMSE of only 0.16 m.
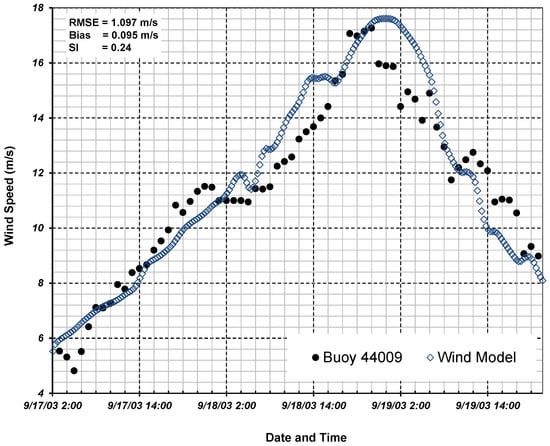
Figure 6.
Comparison of calculated and observed wind speed at NOAA Buoy 44009. Location of the buoy is shown in Figure 1 with green filled circle.
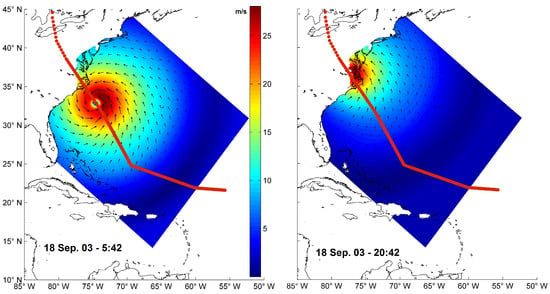
Figure 7.
Wind speed (m/s) and direction snapshot from Overall Delft3D model domain at 5:42 a.m. EST (left) and 8:42 p.m. EST (right) on 18 September 2003.
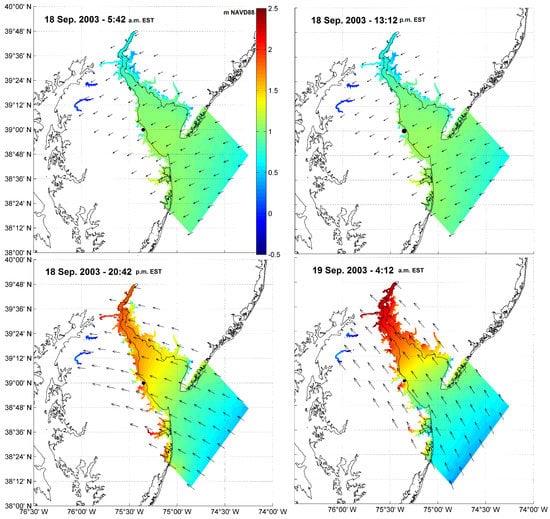
Figure 8.
Wind direction and storm surge elevation (m NAVD88) from Nested2 Delft3D model domain at four different snapshots in time. The AOI is shown in black filled circle.
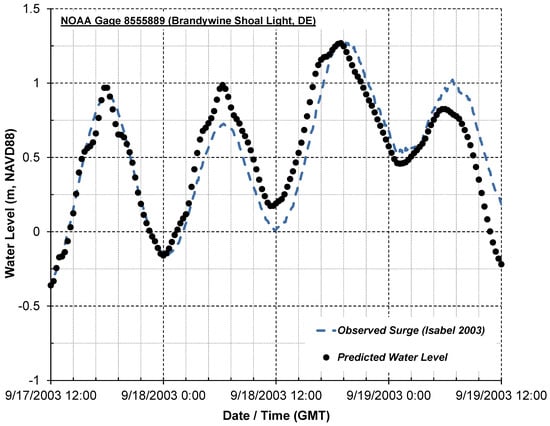
Figure 9.
Comparison of calculated and observed water level at Brandywine Shoal Light, DE.
Several model simulations were undertaken to calibrate the Delft3D-WAVE model, with each run varying specific parameter or friction factor. Calibration was conducted against measured significant wave height and peak wave period at NDBC Buoy 44009 described earlier. The final parameters set after this process were described in Section 2.3.4. Wave calibration results are presented in Table 4. Results are provided for all three levels of the model domain to show the improvement brought about with implementation of the nesting technique. In general, the wave model tends to overestimate the larger wave heights (i.e., waves beyond the Continental shelf) during the peak of the hurricane. Results best matched for the Nested2 grid, with an RMSE of 0.27 m and 1.0 s for significant wave height and peak period, respectively. Similar to previous studies, such as Dietrich et al. [38], the significant wave height timing deviation between simulated and recorded values was observed. The model captures well the peak significant wave height and storm surge, with only slight overestimation of 0.04 m and 0.3 m, respectively. Overall, given the magnitude of errors, the model performance was accepted, especially around the study area.

Table 4.
Wave calibration results and statistics. Hs is the significant wave height, T is the peak wave period.
As described earlier, observed waves are not available inside the bay. Therefore, in order to ensure proper calibration of the Delft3D-WAVE model inside the bay and close to the site, results are compared with their associated values generated using FEMA Region III [10]. Comparison is made for Hurricane Isabel at a location near the NOAA tidal gage at Brandywine Shoal Light, DE. The peak significant wave height by FEMA Region III and Delft3D-WAVE models are 2.3 m and 2.37 m, respectively. The difference is only 7 cm, which is an indication of great model performance.
Some models use a cluster of hundreds of computers to handle high-resolution computations over a large domain. The usage of cluster is avoided in this study; however, high-resolution computations are provided near the area of interest (AOI). The simulations for this modeling effort were performed on a Dell OptiPlex 7010 PC Workstation with Windows 7 Enterprise (64-bit edition) and an Intel Xeon E5-2690 Processor (2.99 GHz) with 16 GB RAM. Combined storm surge and wave model run for 1 h on this computer to simulate each three days of real time.
3. Results and Discussion
Upon satisfactory calibration of the model for wind, wave, and water level, the model is used to further simulate synthetic hurricane tracks (Section 2.4.6) and estimate the probable maximum hurricane. Of all the synthetic hurricane tracks, the one with a central pressure of 920 mb, radius of maximum wind of 45 nm, and a maximum sustained wind speed of 108 knots resulted in the highest water level of 7.54 m NAVD88 at AOI. The track, as highlighted in Figure 2, is oriented 60 counterclockwise due north. It makes landfall approximately 45 nm west of the Delaware Bay mouth near Thurf Marsh Islands. The left panel of Figure 10 shows the colored pattern of water surface elevation, in meters NAVD88; vectors show depth-averaged current velocities in m/s (length of the vector is proportional to current speed). The right panel shows a colored pattern of wind speed in m/s; wind vectors are also shown.
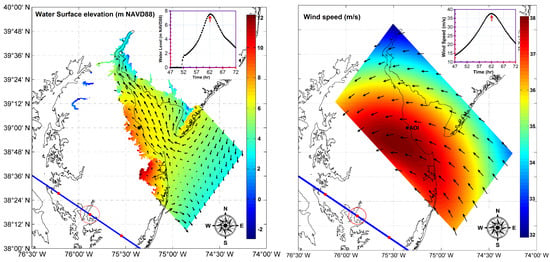
Figure 10.
Wind speed (m/s) and direction snap-shot (right) and storm surge elevation (m NAVD88) snap-shot (left) from Nested2 model at the time of the peak surge. Time history of water level (top left) and wind speed (top right). Synthetic hurricane track is shown in blue color with the hourly location of the storm center in red filled circles.
The primary force of generating surge and surface waves is the wind [86]. In this hurricane track, a constant wind blows from the southeast, east, and south, across the Continental Shelf for several days. These prevailing directions are due to counter-clockwise rotation of the storm around the center as it moves northwest through the Atlantic Ocean. Wind speeds increased exponentially from 10 m/s 16 h before the storm’s first landfall to 37.6 m/s 2 h after landfall, where the maximum wind speed and surge occurs, and then subsides after landfall, with approximate image mirror of the upward slope.
The water surface elevation at the AOI rapidly increases to 2 m NAVD88 8 h before the storm’s first landfall, when the center of the hurricane is 300 km offshore. It then grows exponentially to the maximum of 7.54 m NAVD88 2 h after landfall. Site grade elevation is 1.5 m NAVD88, and, therefore, there will be approximately 6 m of water at the site during the peak of storm. The AOI stays inundated for 20 h. The peaks of the storm surge and wind speed are synchronized; however, there is a 9-h lag between the growth of wind speed and water level. A comparison between storm surges generated by Hurricane Isabel and Synthetic Track 12 shows that the synthetic hurricane resulted in approximately six times higher surge than the historical event of Isabel.
Storm surge regionally built up to levels of 7–10 m NAVD88 in and around the AOI (see Figure 10). Computed storm surge was rather uniform along the axis of the lower Delaware Bay. Current vectors show water being driven into the region from the southeast by wind. This southeast-to-northwest path was the predominant pattern prior to landfall. Storm surge that had built up near the AOI propagated 18 km beyond the shoreline. As the storm continued to move northwest, surge surrounding the AOI continued to decrease along its entire periphery.
The pattern of the significant wave height (Hs) for the Nested2 model at the time of maximum wave along with associated time series is presented in Figure 11. The synthetic hurricane that resulted in maximum storm surge is used. Hs started to grow at the AOI 10 h before landfall and increased exponentially up to a maximum of 2.54 m 2 h after landfall. The associated maximum peak wave period was 7.4 s. Hs varied from 2 m to 4 m around the site with larger waves in the range of 10 m at about 48 km offshore. The peak of Hs, storm surge, and wind speed are synchronized; however, there is an 8-h lag between the growth of wind speed and significant wave height.
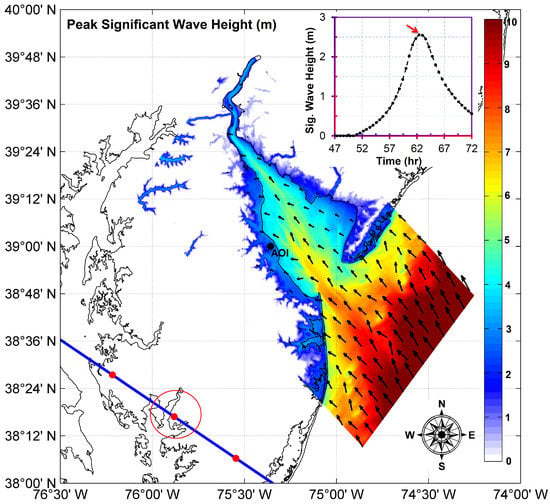
Figure 11.
Significant wave height (m) and direction snap-shot from Nested2 model at the time of the maximum wave. Time history of significant wave height (top right). Synthetic hurricane track is shown in blue color line with the hourly location of the storm center in red filled circles (bottom left). The location of hurricane center at the time of this plot is identified with a red circle.
The combined Overall, Nested1, and Nested2 Delft3D models’ application provided accurate calculations of, and extremely valuable insights into, the development and propagation of hurricane-induced storm surge into the region.
Comparing the impact of various synthetic hurricanes on the water surface elevation (WSEL) at the AOI (see Table 5), the following results are yielded:

Table 5.
Maximum Water Surface Elevation (WSEL) and wave height results for selected synthetic hurricane tracks. Landfall location is a multiplication of the R, nm stands for nautical miles, and mb stands for milibar. Each knot is 1.15 mile per hour.
- Of the tracks with the same landfall location, central pressure (), radius of maximum winds (), and maximum wind speed () those that rotated counterclockwise from the axis of the Delaware Bay resulted in the highest WSEL (see Figure 12a). Tracks passing from the axis of the Delaware Bay (i.e., landfall equal to zero) were the only exceptions. Such orientation pushes the water in a more straightforward path toward the site.
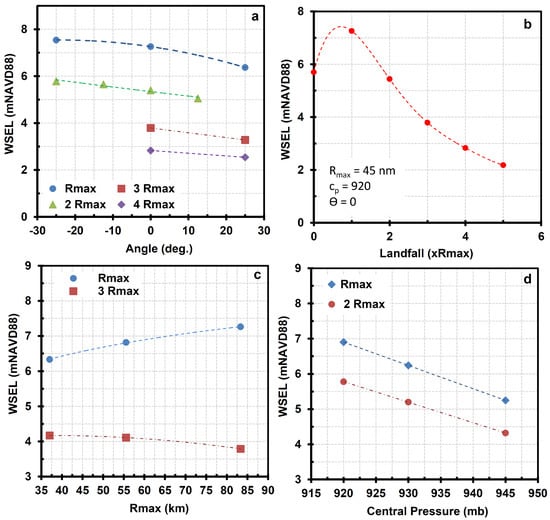 Figure 12. Relationship between major hurricane parameters including central pressure, radius of maximum wind, landfall location, and orientation with water surface elevation (WSEL) at the area of interest (AOI). The legend of (a,c,d) shows the closest distance between the AOI and synthetic hurricane track normalized with Rmax. Same applies to horizontal axis of (b).
Figure 12. Relationship between major hurricane parameters including central pressure, radius of maximum wind, landfall location, and orientation with water surface elevation (WSEL) at the area of interest (AOI). The legend of (a,c,d) shows the closest distance between the AOI and synthetic hurricane track normalized with Rmax. Same applies to horizontal axis of (b). - For tracks with the same angle or orientation, , , and ; those with a landfall location spaced 1 west of the study area resulted in highest WSEL (see Figure 12b). Increasing the distance beyond that reduces the water levels. This could be attributed to locating the maximum winds closest to the AOI and is similar to findings from others, such as Irish et al. [58].
- Keeping all the parameters constant except , if the hurricane makes landfall on the west side of the site at a distance 1 away, the WSEL increases with increasing the (see Figure 12c). However, this would not be the case for tracks located farther from the AOI. The same explanation as given in the above article again applies.
- Results show a linear relation between the central pressure and storm surge (see Figure 12d). Decreasing the central pressure increases the pressure drop, which eventually enhances maximum wind speeds and results in higher impacts during its passage. Each 1 millibar drop in the central pressure results in approximately 0.6 m increase in storm surge.
Assigning a specific probability to the modeled water surface elevation was out of the scope of this study. However, the North Atlantic Coastal Comprehensive Study (NACCS, [87]) is used to approximately find the probability of the storm surge values presented here. NACCS is comprised of several models, including ADCIRC, WAve Model (WAM), and STeady state spectral WAVE (STWAVE). A total of 1050 synthetic tropical storms and 100 extratropical historical storms are simulated as part of the NACCS. The resolution of the unstructured grid varies from 30 to 50 m near the coast and 100 km offshore. Statistical analyses of past storms are employed in developing the synthetic storms. NACCS reports storm responses at 19,000 locations along the Atlantic Coast from frequent storms (e.g., 1-year AEP) to extremely rare (10 AEP). NACCS reports a mean surge of 5.62 m NAVD88 at AOI with a 10 AEP, which is approximately 35% lower than the surge estimated in this study. Therefore, using the same trend as those reported in NACCS, a surge of 7.52 m NAVD88 has, with high confidence, an AEP between 10 and 10.
4. Conclusions
In this study, high-resolution numerical simulations of coupled storm surge, tides, and waves, forced by historical and synthetic tropical cyclones (TC) were used to examine the overall impact of low-probability hurricanes on a specific location within the lower Delaware Bay and estimate the probable maximum storm surge (PMSS). First, the combination of Overall, Nested1, and Nested2 Delft3D models were calibrated and validated with data from Hurricane Isabel (2003). WES, FLOW, and WAVE modules of the Delft3D software were calibrated by comparing the simulated values against observed ones. Then, they were used to simulate synthetic TCs that led to estimating a PMSS that has a very low probability of between 10 and 10.
The greatest surge levels were experienced along the western boundary of the lower Delaware Bay during the passage of a synthetic hurricane that makes landfall west of that area. Model results showed that the combination of placing maximum winds over the area and pushing the water towards the area results in highest impact. It should be clarified that the percentage impact of waves on storm surge are considered out of the scope of this study.
For storms making landfall west of the AOI at a distance equal to , a positive logarithmic relation was found between increasing the distance and the maximum surge at the site. Li et al. and Irish et al. [56,88] also reported that the maximum storm surge increases with increasing hurricane .
Acknowledgments
The author greatly appreciates Deltares (Delft, The Netherlands) for providing technical support throughout this study. The author acknowledges the FEMA, NOAA, USACE, U.S. Geological Survey (USGS), and National Ocean Service (NOS) public-domain internet sites from which various inputs were accessed and used in this study. Three anonymous reviewers as well as journal editors are gratefully acknowledged for comments which improved the manuscript. Lastly, the author also thanks Messrs. James Kirby and Nikhil Patel of Sargent & Lundy for general editorial assistance with this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Emanuel, K. Climate and Tropical Cyclone Activity: A New Model Downscaling Approach. J. Clim. 2006, 19, 4797–4802. [Google Scholar] [CrossRef]
- Lin, N.; Smith, J.A.; Villarini, G.; Marchok, T.P.; Baeck, M.L. Modeling Extreme Rainfall, Winds, and Surge from Hurricane Isabel (2003). Weather Forecast. 2010, 25, 1342–1361. [Google Scholar] [CrossRef]
- Garzon, J.L.; Ferreira, C.M. Storm Surge Modeling in Large Estuaries: Sensitivity Analyses to Parameters and Physical Processes in the Chesapeake Bay. J. Mar. Sci. Eng. 2016, 4, 45. [Google Scholar] [CrossRef]
- Emanuel, K.; Sobel, A. Response of Tropical Sea Surface Temperature, Precipitation, and Tropical Cyclone—Related Variables to Changes in Global and Local Forcing. J. Adv. Model. Earth Syst. 2013, 5, 447–458. [Google Scholar] [CrossRef]
- Wu, L.; Tao, L.; Ding, Q. Influence of Sea Surface Warming on Environmental Factors Affecting Long-Term Changes of Atlantic Tropical Cyclone Formation. J. Clim. 2010, 23, 5978–5989. [Google Scholar] [CrossRef]
- Emanuel, K.; Ravela, S.; Vivant, E.; Risi, C. A Statistical Deterministic Approach to Hurricane Risk Assessment. Bull. Am. Meteorol. Soc. 2006, 87, 299–314. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.R. Changes in Tropical Cyclone Number, Duration, and Intensity in a Warming Environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed]
- NUREG-800. Standard Review Plan for the Review of Safety Analysis Reports for Nuclear Power Plants; U.S. Nuclear Regulatory Commission—Office of Nuclear Regulation: Washington, DC, USA, 2014; Volume 2000.
- Wang, H.V.; Loftis, J.D.; Liu, Z.; Forrest, D.; Zhang, J. The Storm Surge and Sub-Grid Inundation Modeling in New York City during Hurricane Sandy. J. Mar. Sci. Eng. 2014, 2, 226–246. [Google Scholar] [CrossRef]
- Hanson, J.; Wadman, H.; Blanton, B.; Roberts, H. Coastal Storm Surge Analysis: Modeling System Validation, Report 4: Intermediate Submission No. 2.0. In Technical Report TR-11-1; The US Army Engineer Research and Development Center (ERDC): Vicksburg, MS, USA, 2013. [Google Scholar]
- Cho, K.H.; Wang, H.V.; Shen, J.; Valle-Levinson, A.; cheng Teng, Y. A Modeling Study on the Response of Chesapeake Bay to Hurricane Events of Floyd and Isabel. Ocean Model. 2012, 49, 22–46. [Google Scholar] [CrossRef]
- Dailey, P.S.; Zuba, G.; Ljung, G.; Dima, I.M.; Guin, J. On the Relationship between North Atlantic Sea Surface Temperatures and U.S. Hurricane Landfall Risk. J. Appl. Meteorol. Climatol. 2009, 48, 111–129. [Google Scholar] [CrossRef]
- Donnelly, J.P.; Bryant, S.S.; Butler, J.; Dowling, J.; Fan, L.; Hausmann, N.; Newby, P.; Shuman, B.; Stern, J.; Westover, K.; et al. A 700 Year Sedimentary Record of Intense Hurricane Landfalls in Southern New England. GSA Bull. 2001, 113, 714–727. [Google Scholar] [CrossRef]
- Donnelly, J.P.; Butler, J.; Roll, S.; Wengren, M.; Webb, T. A Backbarrier Overwash Record of Intense Storms from Brigantine, New Jersey. Mar. Geol. 2004, 210, 107–121. [Google Scholar] [CrossRef]
- Schwerdt, R.; Ho, F.; Watkins, R. Meteorological Criteria for Standard Project Hurricane and Probable Maximum Hurricane Wind Fields, Gulf and East Coasts of the United States; United States National Oceanic National Weather Service and National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1979.
- Toro, G.R.; Resio, D.T.; Divoky, D.; Niedoroda, A.W.; Reed, C. Efficient Joint-probability Methods for Hurricane Surge Frequency Analysis. Ocean Eng. 2010, 37, 125–134. [Google Scholar] [CrossRef]
- Bastidas, L.A.; Knighton, J.; Kline, S.W. Parameter Sensitivity and Uncertainty Analysis for a Storm Surge and Wave Model. Nat. Hazards Earth Syst. Sci. 2016, 16, 2195–2210. [Google Scholar] [CrossRef]
- Resio, D.; Wamsley, T.; Cialone, M.; Massey, T. The Estimation of Very-low Probability Hurricane Storm Surges for Design and Licensing of Nuclear Power Plants in Coastal Areas; NUREG/CR-7134; Nuclear Regulatory Commission: Washington, DC, USA, 2012. [Google Scholar]
- Whitney, M.M.; Garvine, R.W. Simulating the Delaware Bay Buoyant Outflow: Comparison with Observations. J. Phys. Oceanogr. 2006, 36, 3–21. [Google Scholar] [CrossRef]
- Eagleson, P.; Ippen, A. Estuary and Coastline Hydrodynamics; McGraw-Hill Book Co.: New York, NY, USA, 1966. [Google Scholar]
- Reed, D.J.; Bishara, A.D.; Cahoon, D.; Donnelly, J.; Kearney, M.; Kolker, A.; Orson, A.R.; Stevenson, J. Site-specific Scenarios for Wetlands Accretion as Sea Level Rises in the Mid-Atlantic Region, Section 2.1. In Background Documents Supporting Climate Change Science Program Synthesis and Assessment Product 4.1; Titus, J.G., Strange, E.M., Eds.; EPA 430R07004; U.S. EPA: Washington, DC, USA, 2008. [Google Scholar]
- Barbier, E.B.; Koch, E.W.; Silliman, B.R.; Hacker, S.D.; Wolanski, E.; Primavera, J.; Granek, E.F.; Polasky, S.; Aswani, S.; Cramer, L.A.; et al. Coastal Ecosystem-Based Management with Nonlinear Ecological Functions and Values. Science 2008, 319, 321–323. [Google Scholar] [CrossRef] [PubMed]
- Cochard, R.; Ranamukhaarachchi, S.L.; Shivakoti, G.P.; Shipin, O.V.; Edwards, P.J.; Seeland, K.T. The 2004 Tsunami in Aceh and Southern Thailand: A Review on Coastal Ecosystems, Wave Hazards and Vulnerability. Perspect. Plant Ecol. Evol. Syst. 2008, 10, 3–40. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, H.; Li, Y.; Xu, H.; Shen, J.; Rhome, J.; Smith, T.J. The Role of Mangroves in Attenuating Storm Surges. Estuar. Coast. Shelf Sci. 2012, 102, 11–23. [Google Scholar] [CrossRef]
- Wikipedia, S. Hurricanes in Delaware: List of Delaware Hurricanes, Hurricane Floyd, Effects of Hurricane Jeanne in the Mid-Atlantic Region. In General Books; NOAA: Silver Spring, MD, USA, 2011. [Google Scholar]
- Lesser, G.; Roelvink, J.; van Kester, J.; Stelling, G. Development and Validation of a Three-dimensional Morphological Model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Deltares. User Manual of Delft3D-FLOW Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments; Deltares: Delft, The Netherlands, 2003. [Google Scholar]
- Brater, E.; King, H. Handbook of Hydraulics: For the Solution of Hydraulic Engineering Problems; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Deltares. Delft-3D-WAVE, Simulation of Short-Crested Waves with SWAN, 3.05 ed.; Deltares: Delft, The Netherlands, 2014. [Google Scholar]
- Vatvani, D.; Zweers, N.C.; van Ormondt, M.; Smale, A.J.; de Vries, H.; Makin, V.K. Storm Surge and Wave Simulations in the Gulf of Mexico using a Consistent Drag Relation for Atmospheric and Storm Surge Models. Nat. Hazards Earth Syst. Sci. 2012, 12, 2399–2410. [Google Scholar] [CrossRef]
- Powell, M.; Vickery, P.; Reinhold, T.A. Reduced Drag Coefficient for High Wind Speeds in Tropical Cyclones. Int. J. Sci. 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.B.; Saltzman, E.S. On the Limiting Aerodynamic Roughness of the Ocean in Very Strong Winds. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Makin, V.K. A Note on the Drag of the Sea Surface at Hurricane Winds. Bound.-Layer Meteorol. 2005, 115, 169–176. [Google Scholar] [CrossRef]
- Vickery, P.J.; Masters, F.J.; Powell, M.D.; Wadhera, D. Hurricane Hazard Modeling: The Past, Present, and Future. J. Wind Eng. Ind. Aerodyn. 2009, 97, 392–405. [Google Scholar] [CrossRef]
- Andreas, E.L.; Mahrt, L.; Vickers, D. A New Drag Relation for Aerodynamically Rough Flow over the Ocean. J. Atmos. Sci. 2012, 69, 2520–2537. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-generation Wave Model for Coastal Regions: 1. Model Description and Validation. J. Geophys. Res. Oceans 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Delft University of Technology. SWAN Cycle III, Scientific and Technical Documentation, 41.10 ed.; Delft University of Technology: Delft, The Netherlands, 2014. [Google Scholar]
- Dietrich, J.; Zijlema, M.; Westerink, J.; Holthuijsen, L.; Dawson, C.; Luettich, R.; Jensen, R.; Smith, J.; Stelling, G.; Stone, G. Modeling Hurricane Waves and Storm Surge using Integrally-coupled, Scalable Computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A Third-generation Wave Model for Coastal Regions: 2. Verification. J. Geophys. Res. Oceans 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Gorman, R.M.; Neilson, C.G. Modelling Shallow Water Wave Generation and Transformation in an Intertidal Estuary. Coast. Eng. 1999, 36, 197–217. [Google Scholar] [CrossRef]
- Zhong, L.; Li, M.; Zhang, D.L. How do Uncertainties in Hurricane Model Forecasts Affect Storm Surge Predictions in a Semi-enclosed Bay? Estuar. Coast. Shelf Sci. 2010, 90, 61–72. [Google Scholar] [CrossRef]
- Taflanidis, A.A.; Kennedy, A.B.; Westerink, J.J.; Smith, J.; Cheung, K.F.; Hope, M.; Tanaka, S. Probabilistic Hurricane Surge Risk Estimation through High-fidelity Numerical Simulation and Response Surface Approximations. In Vulnerability, Uncertainty, and Risk; ASCE: Reston, VA, USA, 2011. [Google Scholar]
- Lin, N.; Chavas, D. On Hurricane Parametric Wind and Applications in Storm Surge Modeling. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Resio, D.T.; Irish, J.L.; Westerink, J.J.; Powell, N.J. The effect of uncertainty on estimates of hurricane surge hazards. Nat. Hazards 2013, 66, 1443–1459. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Grell, G.; Dudhia, J.; Stauffer, D. A Description of the Fifth-generation Penn State/NCAR Mesoscale Model (MM5); National Center for Atmospheric Research: Boulder, CO, USA, 1994. [Google Scholar]
- Mulligan, R.; Walsh, J.; Wadman, H.M. Storm Surge and Surface Waves in a Shallow Lagoonal Estuary during the Crossing of a Hurricane. J. Waterw. Port Coast. Ocean Eng. 2015, 141, A5014001. [Google Scholar] [CrossRef]
- Bennett, V.C.; Mulligan, R.P. Evaluation of Surface Wind Fields for Prediction of Directional Ocean Wave Spectra during Hurricane Sandy. Coast. Eng. 2017, 125, 1–15. [Google Scholar] [CrossRef]
- Depperman, C.E. Notes on the Origin and Structure of Philippine Typhoons. Bull. Am. Meteorol. Soc. 1947, 28, 399–404. [Google Scholar]
- Chow, S.H. A Study of the Wind Field in the Planetary Boundary Layer of a Moving Tropical Cyclone. Master’s Thesis, New York University, New York, NY, USA, 1971. [Google Scholar]
- Cardone, V.J.; Greenwood, C.V.; Greenwood, J.A. Unified Program for the Specification of Hurricane Boundary Layer Winds Over Surfaces of Specified Roughness; US Army Corps of Engineers: Washington, DC, USA, 1992; Volume 2000.
- Pielke, R.A.; Cotton, W.R.; Walko, R.L.; Tremback, C.J.; Lyons, W.A.; Grasso, L.D.; Nicholls, M.E.; Moran, M.D.; Wesley, D.A.; Lee, T.J.; et al. A Comprehensive Meteorological Modeling System—RAMS. Meteorol. Atmos. Phys. 1992, 49, 69–91. [Google Scholar] [CrossRef]
- Cotton, W.R.; Pielke, R.A., Sr.; Walko, R.L.; Liston, G.E.; Tremback, C.J.; Jiang, H.; McAnelly, R.L.; Harrington, J.Y.; Nicholls, M.E.; Carrio, G.G.; et al. RAMS 2001: Current Status and Future Directions. Meteorol. Atmos. Phys. 2003, 82, 5–29. [Google Scholar] [CrossRef]
- Laknath, D.; Ito, K.; Honda, T.; Takabatake, T. Storm Surge Simulation in Nagasaki during the Passage of 2012 Typhoon Sanba. Coast. Eng. Proc. 2013, 1, 4. [Google Scholar] [CrossRef]
- Irish, J.L.; Resio, D.T. A Hydrodynamics-based Surge Scale for Hurricanes. Ocean Eng. 2010, 37, 69–81. [Google Scholar] [CrossRef]
- Li, R.; Xie, L.; Liu, B.; Guan, C. On the Sensitivity of Hurricane Storm Surge Simulation to Domain Size. Ocean Model. 2013, 67, 1–12. [Google Scholar] [CrossRef]
- Blain, C.A.; Westerink, J.J.; Luettich, R.A. The Influence of Domain Size on the Response Characteristics of a Hurricane Storm Surge Model. J. Geophys. Res. Oceans 1994, 99, 18467–18479. [Google Scholar] [CrossRef]
- Irish, J.L.; Resio, D.T.; Cialone, M.A. A Surge Response Function Approach to Coastal Hazard Assessment. Part 2: Quantification of Spatial Attributes of Response Functions. Nat. Hazards 2009, 51, 183–205. [Google Scholar] [CrossRef]
- Forte, M.F.; Hanson, J.L.; Stillwell, L.; Blanchard-Montgomery, M.; Blanton, B.; Luettich, R.; Roberts, H.; Atkinson, J.; Miller, J. FEMA Region III Storm Surge Study, Coastal Storm Surge Analysis System Digital Elevation Model, Report 1: Intermediate Submission No. 1.1.; U.S. Army Corps of Engineers: Washington, DC, USA, 2011.
- Sheng, Y.P.; Alymov, V.; Paramygin, V.A. Simulation of Storm Surge, Wave, Currents, and Inundation in the Outer Banks and Chesapeake Bay during Hurricane Isabel in 2003: The Importance of Waves. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Holthuijsen, L.; Booij, N.; Haagsma, I. Comparing 1st-, 2nd- and 3rd-Generation Coastal Wave Modelling. Coast. Eng. Proc. 2001. [Google Scholar] [CrossRef]
- Vledder, G.; Zijlema, M.; Holthuijsen, L. Revisiting the JONSWAP Bottom Friction Formulation. Coast. Eng. Proc. 2011, 1, 41. [Google Scholar] [CrossRef]
- Battjes, J.A.; Janssen, J.P.F.M. Energy Loss and Set-Up Due to Breaking of Random Waves. Coast. Eng. 1978, 1978, 569–587. [Google Scholar]
- Fan, Y.; Rogers, W.E. Drag Coefficient Comparisons between Observed and Model Simulated Directional Wave Spectra under Hurricane Conditions. Ocean Model. 2016, 102, 1–13. [Google Scholar] [CrossRef]
- Kerr, P.C.; Westerink, J.J.; Dietrich, J.C.; Martyr, R.C.; Tanaka, S.; Resio, D.T.; Smith, J.M.; Westerink, H.J.; Westerink, L.G.; Wamsley, T.; et al. Surge Generation Mechanisms in the Lower Mississippi River and Discharge Dependency. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 326–335. [Google Scholar] [CrossRef]
- Walters, R.A. A Model Study of Tidal and Residual Flow in Delaware Bay and River. J. Geophys. Res. Oceans 1997, 102, 12689–12704. [Google Scholar] [CrossRef]
- Mukai, A.; Westerink, J.; Luettich, R. Guidelines for Using the Eastcoast 2001 Database of Tidal Constituents within the Western North Atlantic Ocean, Gulf of Mexico and Caribbean. In Technical Report IV-XX; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2001. [Google Scholar]
- American National Standard for Determining Design Basis Flooding at Power Reactor Sites; ANSI/ANS-2.8; American National Standard—American Nuclear Society: La Grange Park, IL, USA, 1992; Volume 2000.
- Deltares. Delft-3D-WES Wind Enhance Scheme for Cyclone Modelling, 3.01 ed.; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- NOAA-AOML. Hurricane Research Division: Re-Analysis Project. National Oceanic and Atmospheric Administration, Atlantic Oceanographic and Meteorological Laboratory (NOAA AOML). Available online: http://www.aoml.noaa.gov/hrd/hurdat/DataByYearandStorm.html (accessed on 20 January 2017).
- Lawrence, M.B.; Avila, L.A.; Beven, J.L.; Franklin, J.L.; Pasch, R.J.; Stewart, S.R. Atlantic Hurricane Season of 2003. Mon. Weather Rev. 2005, 133, 1744–1773. [Google Scholar] [CrossRef]
- Landsea, C.; Franklin, J.; Beven, J. The Revised Atlantic Hurricane Database (HURDAT2). Available online: http://www.nhc.noaa.gov/data/hurdat/hurdat2-format-atlantic.pdf (accessed on 24 January 2017).
- Demuth, J.; DeMaria, M.; Knaff, J. Extended Best Track Data—Atlantic Basin Dataset 1988 to 2015 (Corrected Version); NOAA, Center for Satellite Applications and Research (STAR): College Park, MD, USA, 2006.
- Nadal-Caraballo, N.C.; Melby, J.A.; Gonzalez, V.M.; Cox, A.T. Coastal Storm Hazards from Virginia to Maine, North Atlantic Coast Comprehensive Study (NACCS). In Technical Report TR-15-5; US Army Corps of Engineers, Engineering Research and Development Center (ERDC): Vicksburg, MS, USA, 2015. [Google Scholar]
- Resio, D.T.; Irish, J.; Cialone, M. A Surge Response Function Approach to Coastal Hazard Assessment—Part 1: Basic Concepts. Nat. Hazards 2009, 51, 163–182. [Google Scholar] [CrossRef]
- Vickery, P.J.; Skerlj, P.F.; Twisdale, L.A. Simulation of Hurricane Risk in the U.S. Using Empirical Track Model. J. Struct. Eng. 2000, 126, 1222–1237. [Google Scholar] [CrossRef]
- SLOSH. Sea, Lake, and Overland Surges from Hurricanes (SLOSH) Model; National Oceanic and Atmospheric Administration—Evaluation Branch—Meteorological Development Lab—National Weather Service: Silver Spring, MD, USA, 2017.
- Bertin, X.; Bruneau, N.; Breilh, J.F.; Fortunato, A.B.; Karpytchev, M. Importance of Wave age and Resonance in Storm Surges: The case Xynthia, Bay of Biscay. Ocean Model. 2012, 42, 16–30. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Gravois, U.; Zachry, B.C.; Westerink, J.J.; Hope, M.E.; Dietrich, J.C.; Powell, M.D.; Cox, A.T.; Luettich, R.A.; Dean, R.G. Origin of the Hurricane Ike forerunner surge. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Bell, G.; Goldenberg, S.; Landsea, C.; Blake, E.; Kimberlain, T.; Schemm, J.; Pasch, R. Tropical Cyclones—Atlantic Basin, State of the Climate in 2012. In Technical Report 94; Bulletin of the American Meteorological Society: Boston, MA, USA, 2013. [Google Scholar]
- Landsea, C.W.; Hagen, A.; Bredemeyer, W.; Carrasco, C.; Glenn, D.A.; Santiago, A.; Strahan-Sakoskie, D.; Dickinson, M. A Reanalysis of the 1931-43 Atlantic Hurricane Database. J. Clim. 2014, 27, 6093–6118. [Google Scholar] [CrossRef]
- Vickery, P.J.; Wadhera, D. Statistical Models of Holland Pressure Profile Parameter and Radius to Maximum Winds of Hurricanes from Flight-Level Pressure and H*Wind Data. J. Appl. Meteorol. Climatol. 2008, 47, 2497–2517. [Google Scholar] [CrossRef]
- Edwards, K.L.; Veeramony, J.; Wang, D.; Holland, K.T.; Hsu, Y.L. Sensitivity of Delft3D to Input Conditions. In OCEANS 2009; IEEE: Piscataway Township, NJ, USA, 2009; pp. 1–8. [Google Scholar]
- NOAA-NBDC. National Oceanic and Atmospheric Organization (NOAA), National Buoy Data Center (NBDC). Available online: https://www.ndbc.noaa.gov/ (accessed on 4 October 2017).
- NOAA-TIDE. NOAA Tides and Currents Website. Center for Operational Oceanographic Products and Services. Available online: https: //tidesandcurrents.noaa.gov/ (accessed on 10 September 2017).
- Barnard, P.L.; van Ormondt, M.; Erikson, L.H.; Eshleman, J.; Hapke, C.; Ruggiero, P.; Adams, P.N.; Foxgrover, A.C. Development of the Coastal Storm Modeling System (CoSMoS) for Predicting the Impact of Storms on High-energy, Active-margin Coasts. Nat. Hazards 2014, 74, 1095–1125. [Google Scholar] [CrossRef]
- Nadal-Caraballo, N.C.; Melby, J.A.; Gonzalez, V.M.; Cox, A.T. North Atlantic Coast Comprehensive Study (NACCS), Coastal Storm Hazards from Virginia to Maine. In Technical Report TR-15-5; US Army Corps of Engineers: Washington, DC, USA, 2015. [Google Scholar]
- Irish, J.L.; Resio, D.T.; Ratcliff, J.J. The Influence of Storm Size on Hurricane Surge. J. Phys. Oceanogr. 2008, 38, 2003–2013. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).