1. Introduction
Propeller-induced noise and vibration is one of the major issues that threatens onboard comfort, causes mechanical failures, and potentially impacts marine animals. To resolve these issues during the design stage, it is important to have a reliable prediction of the propeller-induced hull pressures. Research has been done on predicting the hull pressure both experimentally and numerically. Most of the experimental studies are performed in the model-scale with multiple pressure transducers mounted on the hull surface above the propeller to monitor the hull pressure [
1,
2]. According to the level of simplification that can be made, the numerical approaches for underwater noise simulations can be divided into compressible Navier–Stokes equation-based approaches, Lighthill equation-based approaches, Ffowcs–Williams–Hawkings equation-based approaches [
3,
4], Helmholtz equation-based approaches [
5], and hybrids of any two. These equations are usually implemented by either a finite volume method in which the propeller is modelled by a rotating boundary [
4,
6] or by the boundary element method (BEM) [
3,
7] in which the propeller is represented by sources and dipoles on the boundary surface.
To numerically predict the propeller-induced hull pressure, the BEM method is often used because the propeller induced pressure field is a small-amplitude high-frequency field which can be decoupled from the background flow. Most of these BEM applications focus on the effect of cavitation because it is the main contributor of high-level noise and vibrations [
7,
8]. For a cavitating propeller, the cavitation source is the major excitation in the acoustic BEM model so that the influence of the propeller lifting force, the blade thickness, and the blade trailing wake can all be neglected. However, the continuous low-level noise and vibration induced by non-cavitating propellers or marginally-cavitating propellers can also be a problem. In this case, the lifting surface, the blade thickness, and the wake all have a comparable influence on the induced pressure.
This paper focuses on a streamlined procedure of predicting the ship hull pressures. A BEM/RANS
1 interactive scheme is first used to predict the effective wake and the propeller-induced pressure field under this effective wake [
9,
10]. Then, a pressure-BEM solver is used to predict the diffraction pressure which leads to the solid boundary factor. The method considers the lifting surface effect, the blade thickness effect, cavitation source effect, and trailing wake effect so that it can predict the hull pressure induced by either a wetted propeller or a cavitating propeller.
2. Methodology
2.1. Boundary Element Method
The BEM can be used to solve various types of partial differential equations. In this application, the control Equation (1) can be obtained by inserting the Laplace equation into the Green’s third identity. G is Green’s function; represents all the boundary surfaces in the fluid domain; is the normal vector at the point pointing into the flow field.
Equation (1) states that the value of the at any point on the boundary surface depends only on the values of and at any point on the boundary of the body . Moreover, the value of can be expressed as the superposition of the potentials due to distribution of sources and normal dipoles on the boundary of the body of strengths and repectively.
Special care should be given to the branch wake surface
behind the hydrofoil of propeller. By considering the wake surface, Equation (1) renders:
After enforcing the kinematic boundary condition on the strength of the source potential
and the Morino’s condition on the wake strength
, Green’s foumula finally becomes:
where
is the inflow velocity. Equation (3) is a Fredholm integral equation of the second kind for the unknown
. This analytic formulation will be solved for the unknown quantity,
by using numerical implementation.
To predict the propeller performance, the total flow can be docomposed to the known inflow (or background flow) and the unknown propeller induced flow , which can be treated as a potential flow. Therefore, the propeller perturbation potential is governed by the Laplace equation and can be solved via the boundary element method. In the current boundary element solver, constant strength panels are placed on the surface of the propeller and on the propeller trailing wake surfaces. Equation (3) can then be discretized into a linear matrix system which can be solved by either a direct method or an iterative method.
2.2. Wake Alignment Model
Assuming a propeller blade is a lifting body and the blade trailing wake is a material surface on which the potential field is not continuous, the trailing wake surfaces can be treated as a boundary in the BEM model. The strength of the trailing wake is calculated by the Kutta condition and the location of the wake sheet in the downstream is determined by the wake alignment model, which ensures both sides of the wake surface have the same pressure (force free condition).
The basic philosophy behind the wake alignment model is that the wake sheet is a material surface that needs to convect with the local stream. Two types of wake alignment models are available in the current BEM solver depending the time dependency: the steady wake alignment model and the unsteady wake alignment model. Whether the time variation of the incoming flow is considered (unsteady) or not (steady) is the major difference when implementing the alignment procedure. Brief description of each alignment scheme is as follows:
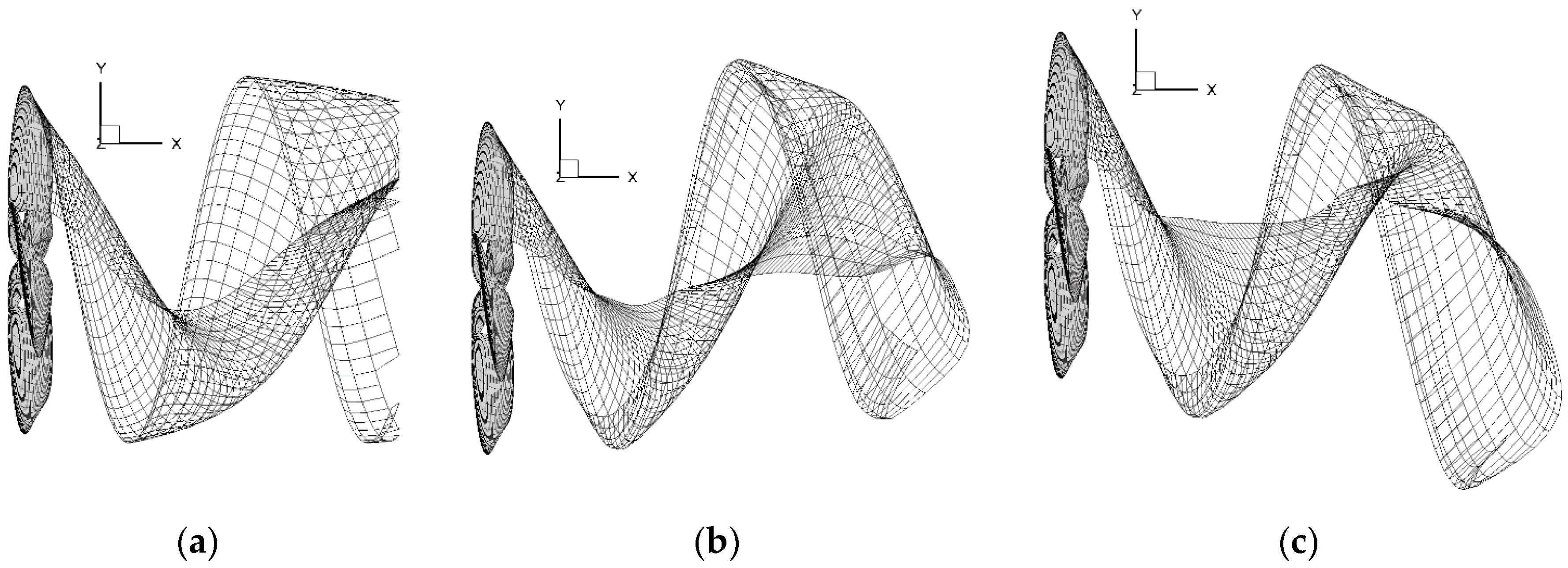
(a) Steady wake alignment: the full wake alignment (FWA) scheme [
11,
12] considers only the zeroth harmonic of the inflow velocity, therefore the higher harmonic components are neglected in the alignment process. Axisymmetric variation of the incoming flow in radial direction is the most general case, and consequently the propeller performance becomes invariant to the angular position of the blade. The shape of the blade wake is the same for all blades.
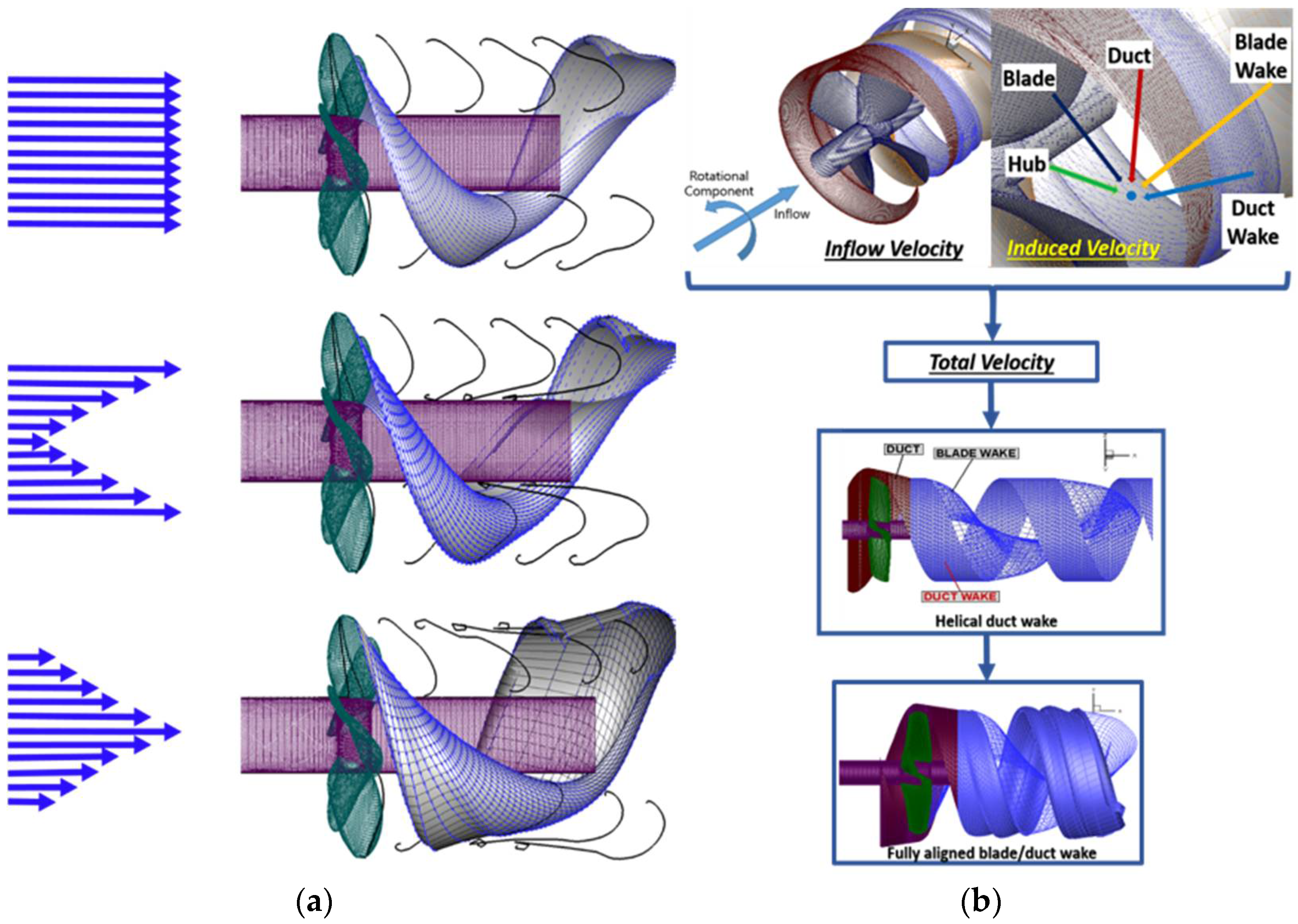
Figure 1a shows propellers under three different axisymmetric inflows. The induced velocity (or, perturbation velocity)
in
Figure 1b is evaluated based on the effects from the blade, hub, duct (in case duct geometry is included), and the wake itself. Along with the axisymmetric inflow, the induced velocity constitutes the total velocity prior to implementing the alignment procedure in the FWA.
(b) Unsteady wake alignment: it is similar to the steady case, but the consideration of time variation of the incoming flow is included. Full harmonics in the inflow are considered to evaluate the velocity components on the wake panels depending on their locations. The alignmen starts with the FWA in steady state ( and procedes into the unsteady alignment model ( using the Euler-explicit sceheme with revolutions in a progressive manner.
In the above equations, i and denote the ith node point at the nth time step, is the total velocity, and Δt is the time step size. X, Y, and Z are the coordinates of the nodal points on the wake surfaces. Due to the time consideration of the total flow, each blade has a different wake geometry for different blade angles. At each time step, only the key wake is aligned, updated, and then saved before proceeding to the next time step. After that, the saved key wake can be used for other blades when they reach the same blade angle in the future time steps. This procedure will be repeated for several revolutions until the converged unsteady force performances are obtained.
In the current panel model, some elements of the steady wake alignment scheme introduced by Tian & Kinnas [
11] are coupled with the unsteady wake alignment model by Lee [
13] to improve the convergence of the alignment procedure. Different from the Lee’s unsteady scheme, which evaluates the total velocity at the panel center and then interpolates it into the panel corners, the coupled scheme calculates the total velocity directly at the four corners on each wake panel, as shown in
Figure 2. This improves the numerical accuracy and stability. The convergence study on the wake panel numbers showed that the predicted propeller performance was irrelevant to the panel number after 100 panels are used. Detailed description of the unsteady wake alignment model coupled with the FWA can be found in [
12].
2.3. Boundary Element/Reynolds-Averaged Navier-Stokes Interactive Scheme
In
Section 2.1, the BEM solver is used to evaluate the perturbation potential when the inflow
is given. However, this inflow information is not always available. Some researchers monitor the flow (nominal wake) on the propeller disk plane without the existence of the propeller and then perform an adjustment to the nominal wake to predict the effective wake
. The effective wake considers the propeller’s influence on the flow and can be defined by Equation (5).
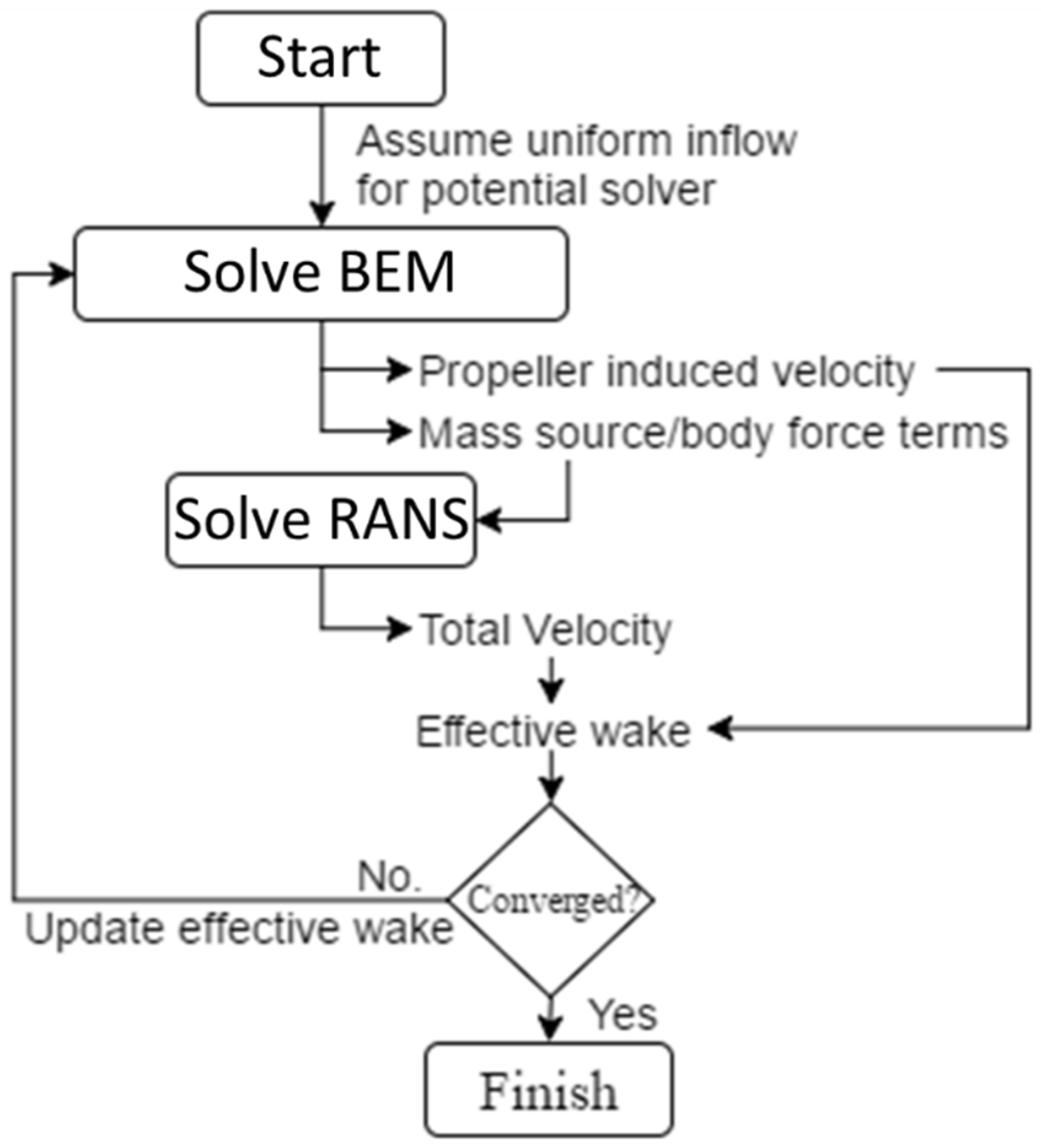
To predict the effective wake, BEM solver is coupled with a RANS solver, as shown in
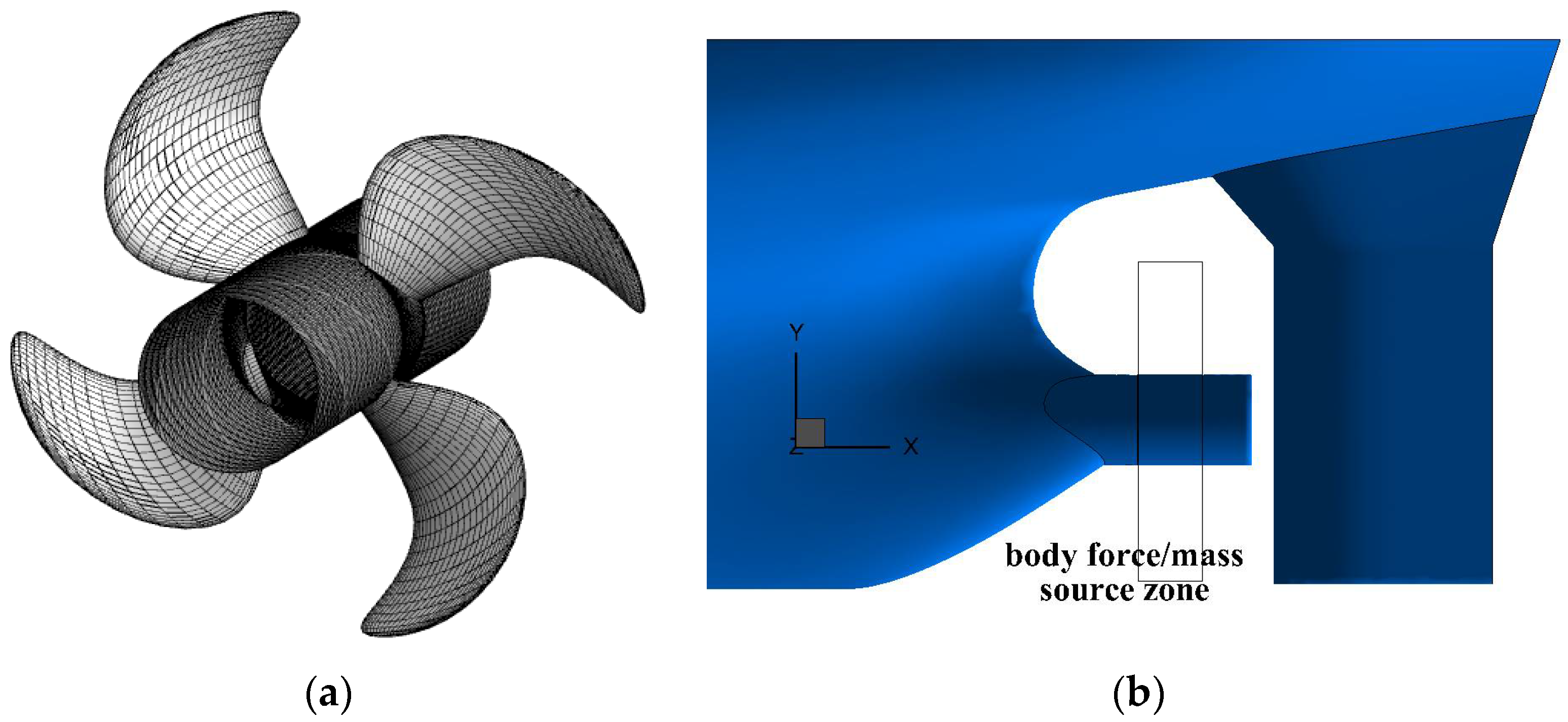
Figure 3. In the RANS solver, the propeller is represented by a local mass source term which is added to the continuity equation and a local body force term which is added to the momentum equation. The strength of the mass source term and the body force term is determined by the BEM solver. The total flow
is evaluated out of the RANS solver and can be used to calculate the effective wake by Equation (5). The details of this scheme can also be found in the work of Su & Kinnas [
10]. Unlike some other similar implementations, the mass source term is included in the RANS model. It is found that a consistent representation of the blockage effect in both the total flow and the propeller-induced flow is important for the accurate prediction of the effective wake field [
10].
2.4. Boundary Element—Solver for the Oscillating Hull Pressure
According to the Bernoulli equation, the small amplitude pressure oscillation can be represented by the steady velocity potential , as shown in Equation (6). In this equation, is the angular velocity of the propeller, is the number of blades, and the velocity potential magnitude at a certain frequency.
Instead of solving the oscillating pressure field, the velocity potential field is solved at different frequencies. The potential field is governed by the Helmholtz equation. For the near-field small-amplitude pressure fluctuation caused by marine propellers, an infinite sound speed can be assumed so that the Helmholtz equation is reduced to a Laplace equation, as shown in Equation (7).
Similar to the hydrodynamic BEM, the nth total velocity potential field can be decomposed to a radiated potential field (taken equal to the potential due to the propeller flow in the absence of the hull) and a diffraction potential field . The radiated potential fields is the Fourier series of the unsteady perturbation potential field in the hydrodynamic BEM model which represents the propeller. The lowest frequency for the Fourier decomposition is the blade-passing frequency .
Based on the boundary element method, the total potential field can be solved by Equation (8) where is the hull surface and is the image of the hull.
Different from the hydrodynamic BEM model, the total potential, instead of the diffraction potential, is solved. This eliminates the source-induced potentials term in the boundary integral equation which saves computational time. However, the method cannot be used for the hydrodynamic BEM model because the total velocity field can be vortical and not governed by the Laplace equation. Equation (8) can be solved the same way as in
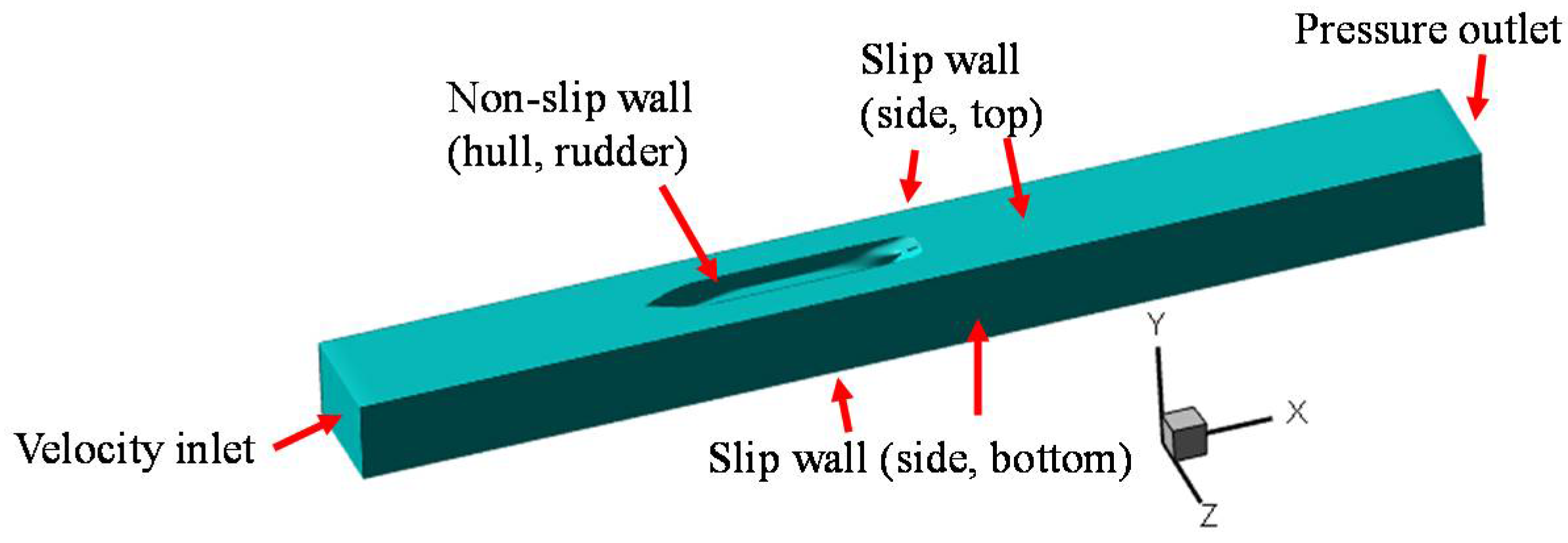
Section 2.1. Constant strength dipole panels are placed on the ship hull and the rudder. The effect from the top tunnel wall is included by an image model. Finally, the unsteady pressure field on the ship hull can be calculated by Equation (8).
4. Results and Comparison with Experiment
In this paper, all the dimensionless numbers are defined based on the propeller diameter , ship speed , and the propeller rps n. The advance ratio , the thrust coefficient , the torque coefficient , the cavitation number , and the pressure coefficient are defined by the following equations.
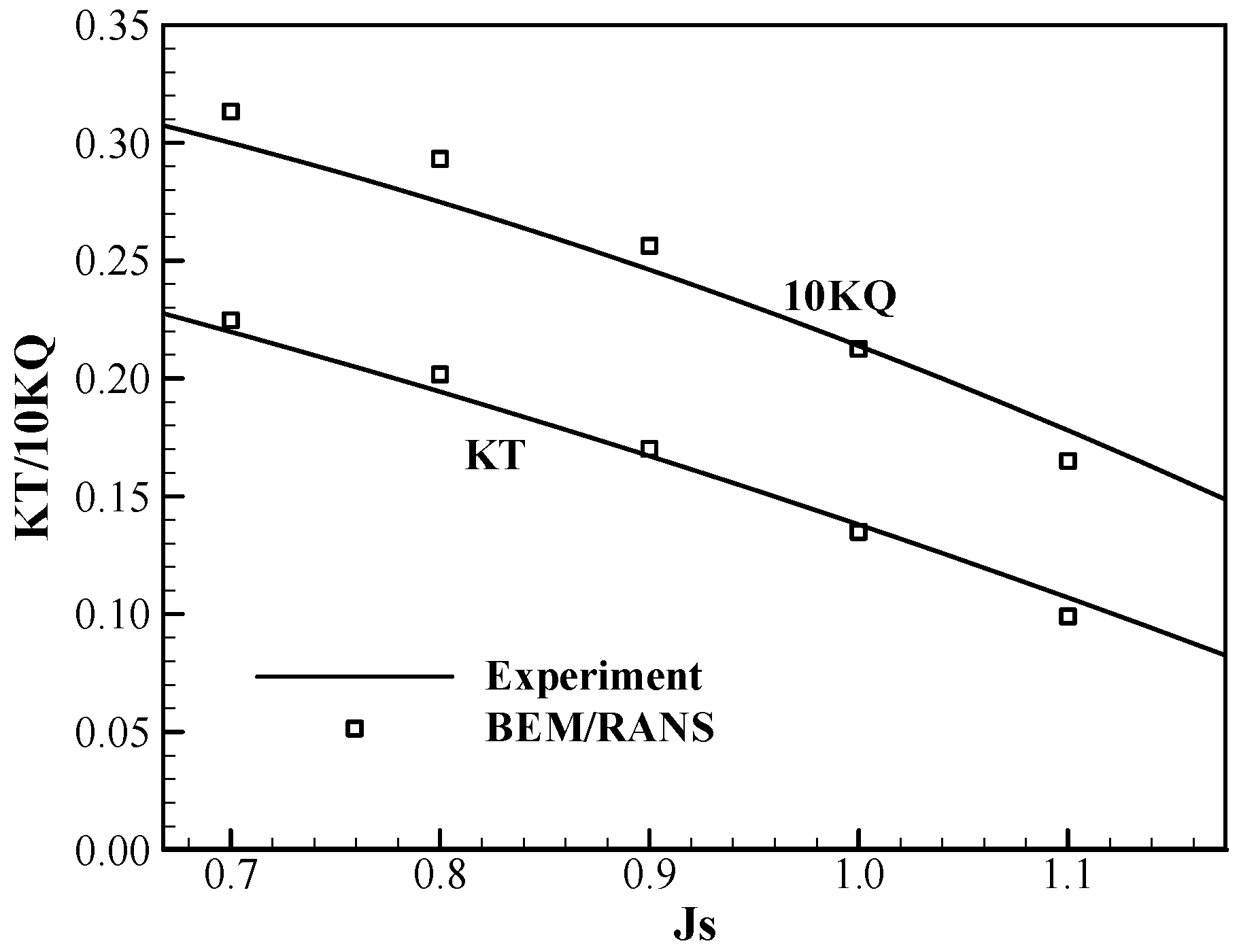
First, the BEM/RANS interactive scheme is applied to different load conditions by changing advance ratios. The predicted propeller forces are compared to the experimental data, as shown in
Figure 8. In the experiment and the BEM/RANS model, the propeller is working behind the ship hull at different advance ratios. A good agreement is obtained between the two.
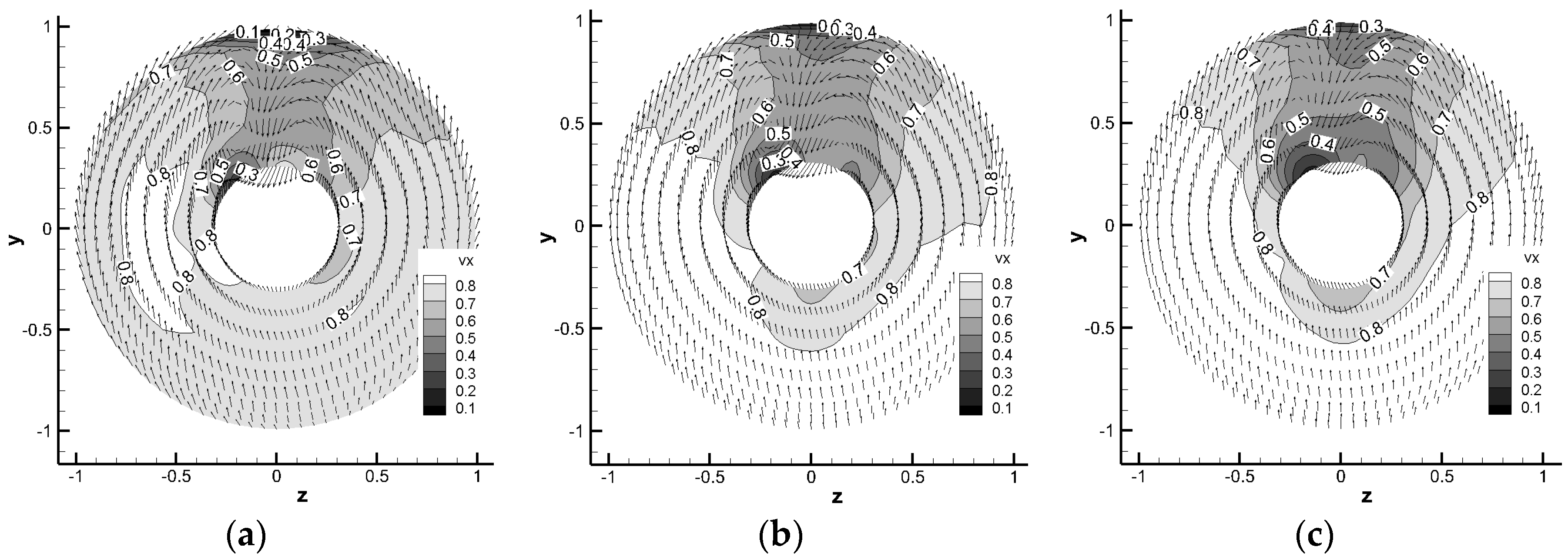
Figure 9 shows the predicted effective wake field for different advance ratios. In
Figure 9, the axial effective wake velocity is represented by the gray scale and the in-plane effective wake velocity is plotted by vectors. Since the effective wake is defined at the center of the blade panels, only the mid-chord disk of the 3-dimensional wake field is plotted.
Then, the same scheme is applied to another load condition in which the advance ratio Js is 0.808 and the cavitation number σ is 7.34. The solution of the BEM/RANS scheme is imported to the pressure-BEM model to evaluate the hull pressure fluctuation on the eight different locations where the pressure transducers are placed. For this load condition, several comparisons are made.
The first comparison study is on the different wake alignment models. Both the steady wake alignment model and the unsteady wake alignment model are tested. In the steady wake alignment scheme, all the non-axisymmetric components of the effective wake are neglected so that the wake geometry, as shown in
Figure 10a, does not change with time. More importantly, the positive velocity in the vertical direction of the effective wake, as shown in
Figure 9, is neglected. Therefore, the steady wake goes along the axial direction without any inclination. On the other hand, the unsteady wake alignment scheme considers the non-axisymmetric part of the effective wake so that the wake geometry is a function of time (or blade angle), as shown in
Figure 10b,c. All the geometries in
Figure 10 are plotted in a rotating coordinate which is fixed to the propeller shaft. When the BEM solver is used to predict the propeller mean performance, the difference between the steady and unsteady wake alignment model are not significant. However, if the results of the BEM solver are used to evaluate the hull pressure fluctuations, the accurate prediction of the wake geometry becomes more vital.
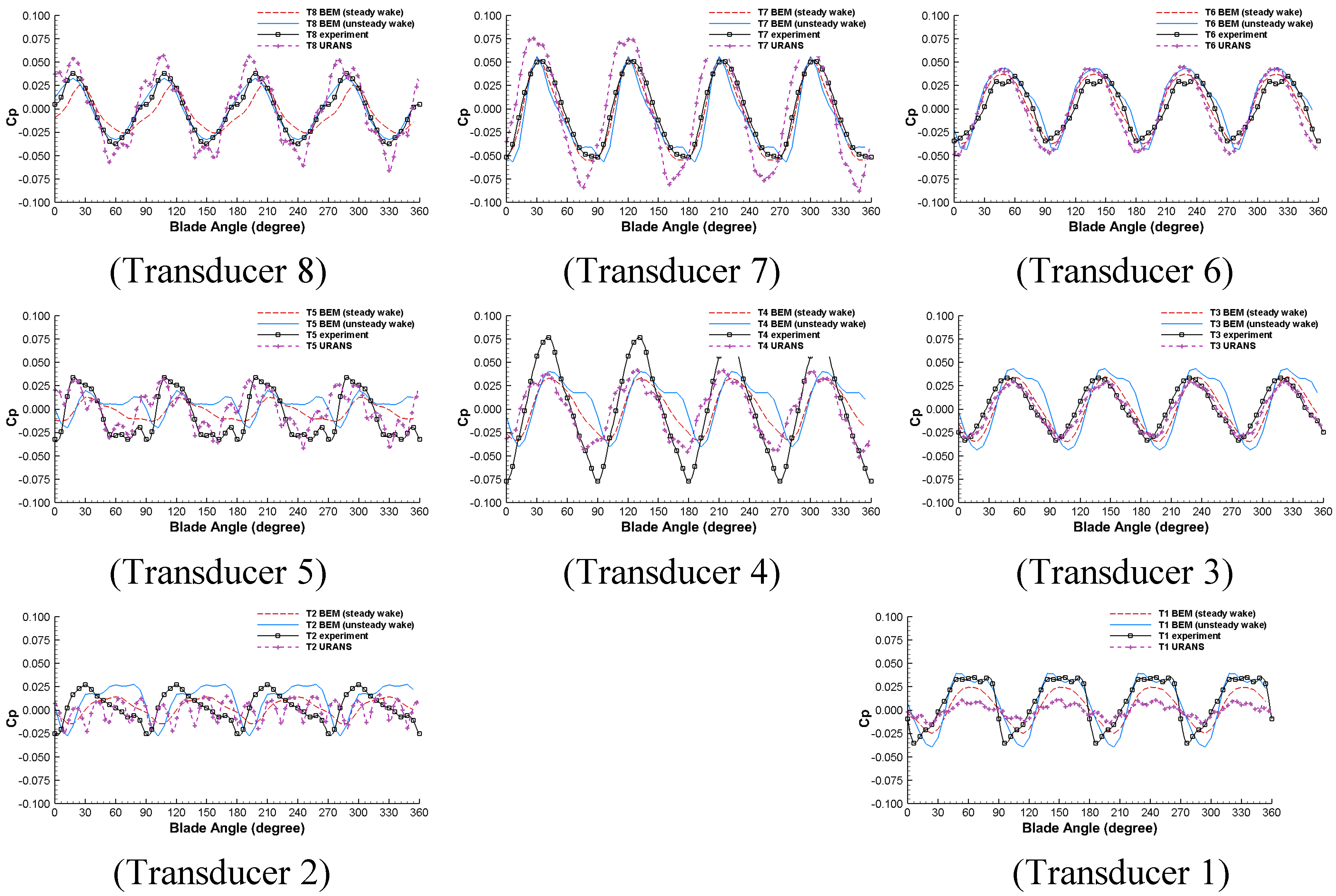
To study the influence of different wake alignment models, the pressure history monitored by the pressure transducers and by the URANS model are compared with the pressure fluctuation predicted by our scheme with either a steady wake or an unsteady wake. Results are plotted in
Figure 11. The unsteady RANS results have a good agreement with the experimental data on transducer T3, T5, T6, and T8. It also correctly predicted the peak pressure pulse amplitude while the location of the peak pressure is shifted towards upstream (see pressure on location T4 and T7). URANS severely under-predicted the pressure pulse at downstream locations (T1 and T2). This can be explained by the numerical diffusion caused by the unstructured mesh. Because the pressure pulses at T1 and T2 highly rely on the behavior of the blade trailing wakes, too much downstream diffusion can smooth out the vortices and diminish the hull pressure pulse.
In terms of the pressure pulses predicted by the pressure-BEM method, the influence of different wake alignment models is not significant for upstream transducer locations (T3–T8), due to their relative long distance to the trailing wake. For downstream points (T1 and T2), however, the difference becomes bigger and unsteady wake alignment improves the results. This is because the non-axisymmetric component of the effective wake pushes the wake towards the hull so that the wake has a stronger influence on the hull pressure.
On transducers T1, T3, T6, T7, and T8, a good agreement is obtained between the BEM-predicted pressure pulses and the experimental data. On transducer T2, the fluctuation amplitude is correctly predicted but the phase angle of the pressure peak is not accurate. This might be attributable to the ignored rudder effect in the unsteady wake alignment model. In other words, although the tip vortex of a blade is close enough to the hull to induce a correct pressure fluctuation amplitude, the time when the tip vortex reaches the closest point to the hull might not be well predicted due to the ignored rudder effect. The complete description of the developed tip vortex cavity in BEM is provided in Lee & Kinnas [
16]. On transducer T4 and T5, current numerical scheme under-predicts the pressure fluctuation amplitudes. Unlike the pressure pulses from the URANS model and from the experimental data, the pressure fluctuation amplitude predicted by the pressure-BEM method is not symmetric about the ship center; the scheme tends to under-predict the pressure pulses on the port side. This phenomenon can be traced back to the non-symmetric pattern of the effective wake, as can be seen in
Figure 9. As a result, the loading on the blade tip is relatively smaller on the port side and larger on the starboard side.
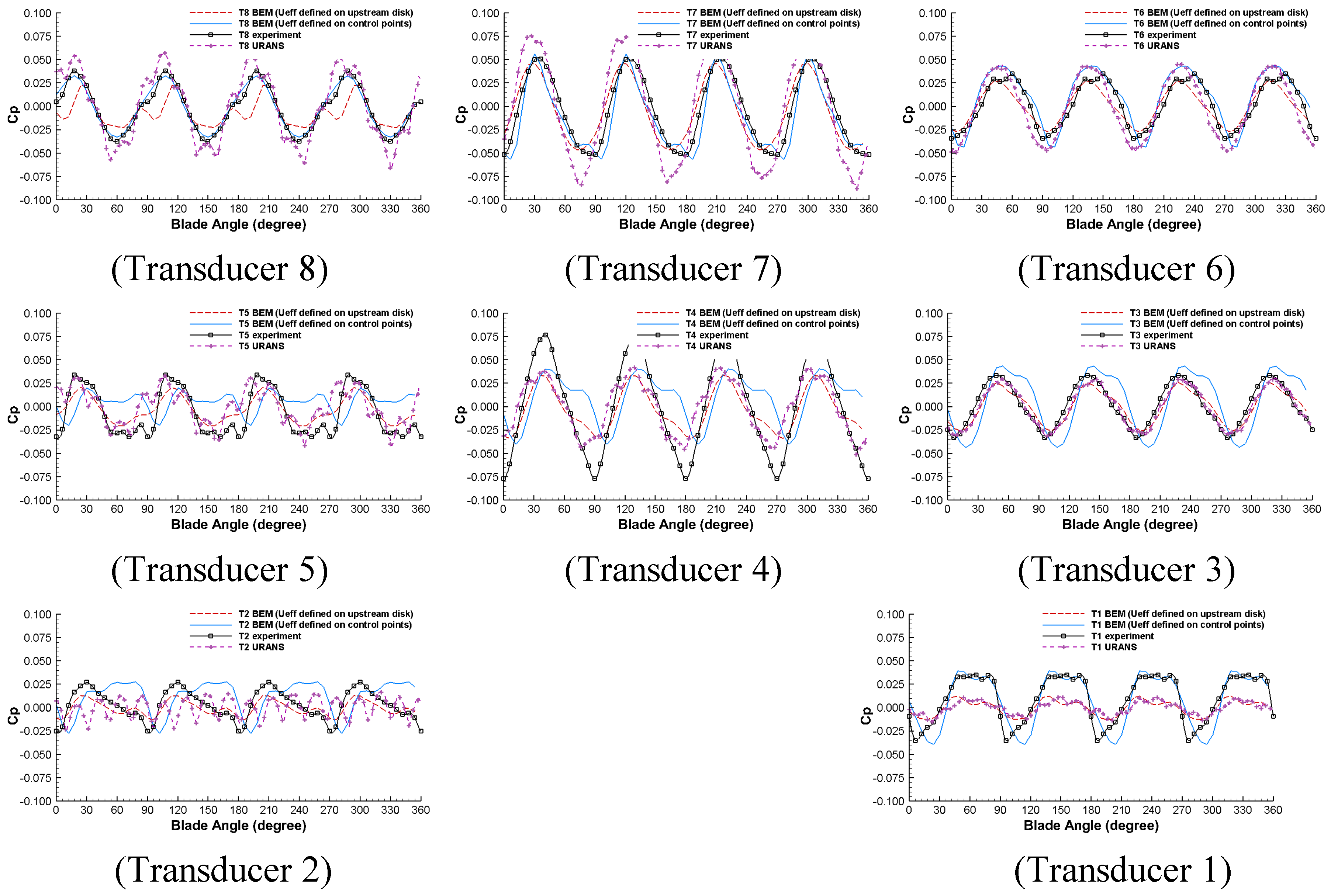
To understand how the hull pressure is affected by the different ways of evaluating the effective wake, another study was made. Two cases were tested in this study and the results are compared with URANS/experiments, as shown in
Figure 12. In the first case, the effective wake is evaluated at the center of every BEM panel on the blade. In the second case, the axial-varying effective wake field from the first case is extrapolated to a disk near the leading edge. The disk conforms to the leading edge and has a constant distance (2% of max radius) to the leading edge. The details of both schemes can be found in Tian et al. [
9].
Based on
Figure 12, the change of locations for evaluating the effective wake can significantly change the predicted hull pressures, especially for downstream monitors. For monitors T1, T2, and T8, defining the effective wake at the center of every blade panel shows a clear advantage over the other method which defines the effective wake at a leading-edge disk. At other monitors (T3 to T7), there is no clear advantage for either of methods. In summary, the hull pressure pulses are shown to be very sensitive to the effective wake field. Although our current axial-varying effective wake shows some advantages, it still needs to be improved due to the inconsistency in the pressure of several monitors between the BEM results and the experimental data.
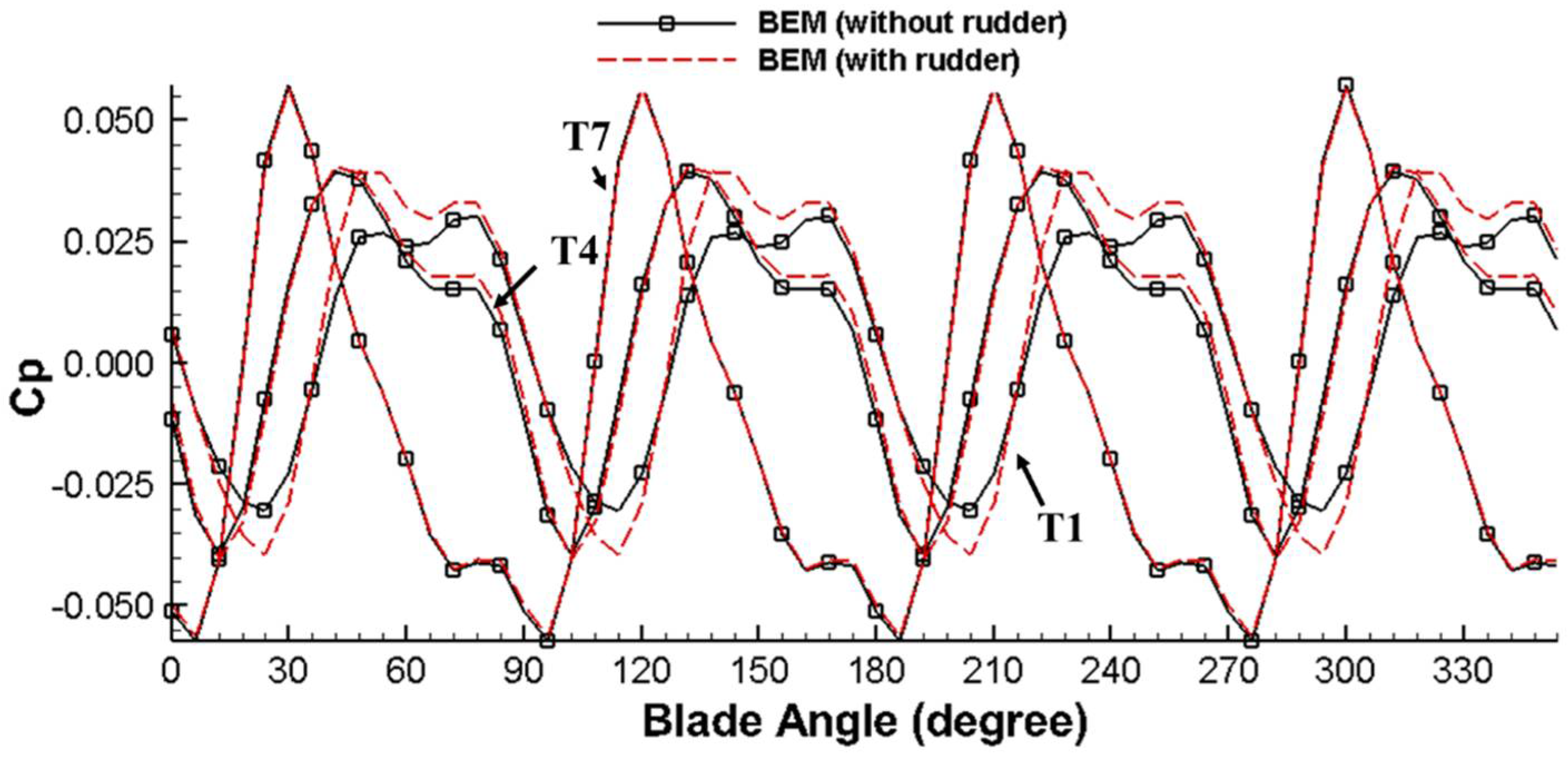
The last comparison study focuses on the effect of the rudder. According to
Section 3.3, in order to maintain numerical stability, only the upper part of the rudder is used in the pressure-BEM model, as can be seen in
Figure 7a. The underlying assumption is that the lower part of the rudder is far from the pressure transducer locations and therefore, has a negligible influence towards the hull pressure fluctuation. To study whether this is a good approximation, we tried two different rudder geometries in the pressure-BEM model: one is the original geometry which is shown in
Figure 7a; the other geometry totally neglects the rudder part, as can be seen in
Figure 7b. The predicted hull pressures from both cases are compared in
Figure 13. According to the figure, the difference is negligible on T4 and T7 while the pressure on T1 is affective by the rudder geometry. This is because T1 is at a downstream location which is close to the leading edge of the rudder. We can also further claim that by including the upper part of the rudder, only the local pressure field is noticeably affected. This supports our original assumption that the lower part of the rudder would have an even smaller influence on the predicted hull pressures, given its relatively longer distance from the hull.
It is worth noting that a more complete way for solving the numerical stability issue is to include the wake-rudder interaction in both the unsteady wake alignment model and the pressure-BEM model. This can be a future topic of this research.
Another neglected effect is from the blade boundary layer. The boundary layer effect, similar to the blade thickness, can be represented by source panels in the BEM model. The BEM solver can be used together with a boundary integral solver to determine the displacement thickness [
17,
18]. Then, the thickness can be converted into source strength and applied to the BEM solver. The displacement thickness can be as large as 15% of the blade thickness. Also, the source induced pressure decays slower (
) with distance compared to the dipole induced pressure (
). Therefore, it is possible that the boundary layer effect contributes to the downstream hull pressure fluctuation. The effect of boundary layer is another future topic of this research.