1. Introduction
In recent years, Building with Nature solutions (soft solutions, such as sand nourishments) are increasingly considered as an alternative in flood protection, see e.g., Van Slobbe et al. [
1]. These soft solutions are considered as a supplement to the usual hard measures (dikes, coastal structures). Three types of soft defences can be distinguished [
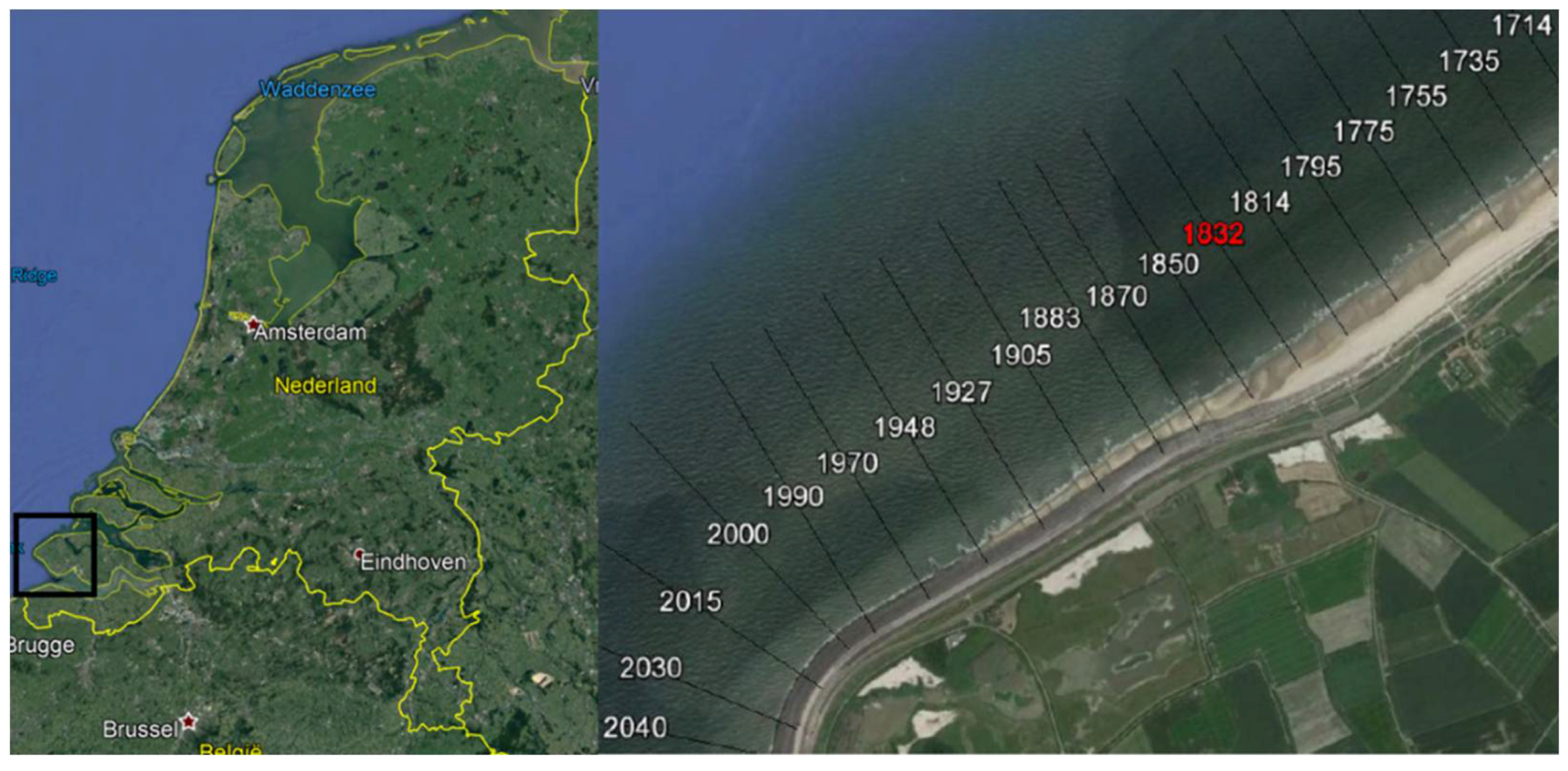
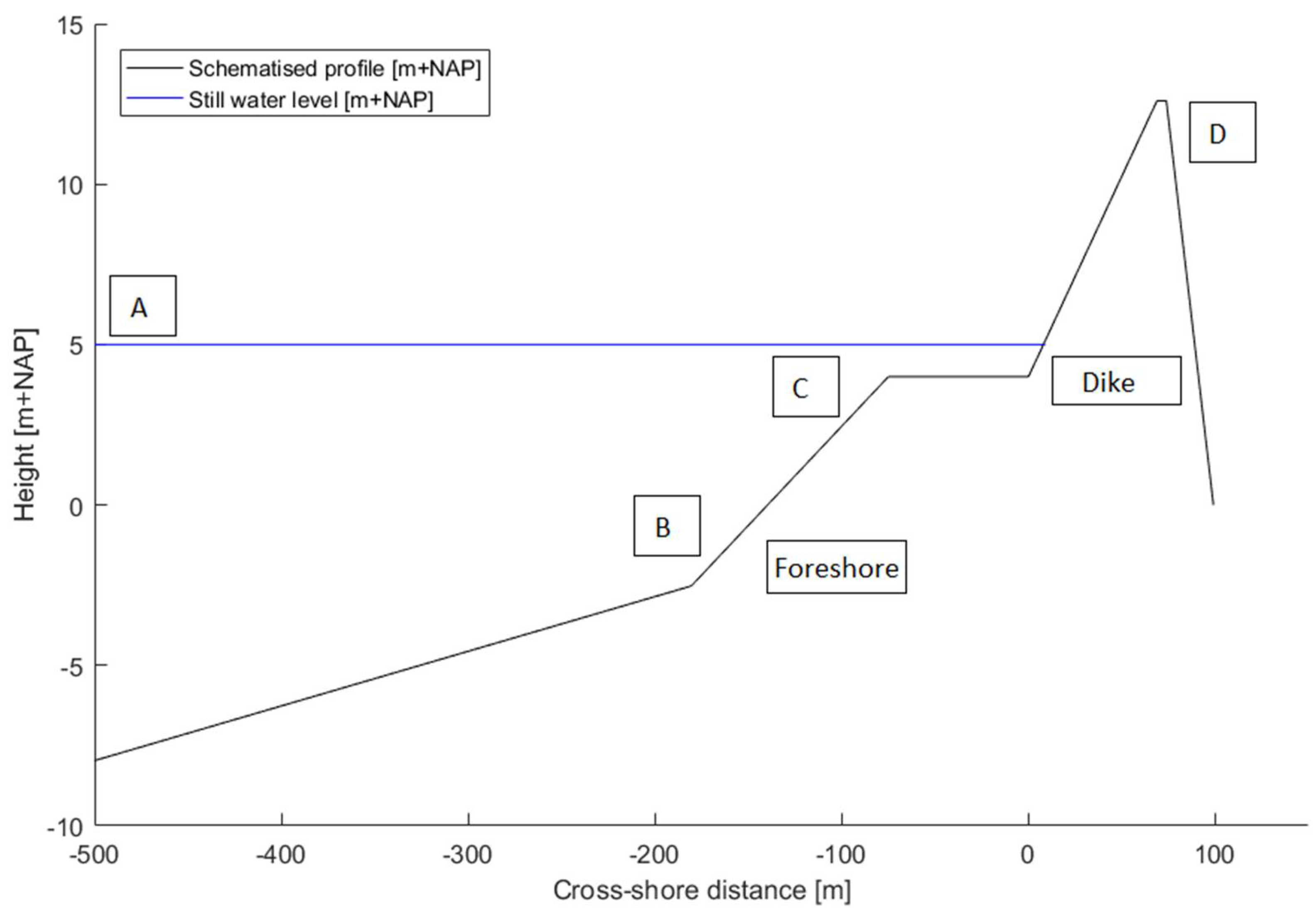
2]. Here, one of these types is considered: a hybrid defence, more specifically a dike with a shallow sandy foreshore. This dike-foreshore system is a combination of a traditional dike and a nourished foreshore, consisting of a body of sand, possibly covered with vegetation. The foreshore reduces the loads on the dike. The dike remains part of the defence. A hybrid defence really is a combination in which both parts are of importance in the flood protection. Constructing a sandy foreshore in front of a dike can be a method to decrease the failure probability. However, the uncertainty in the morphological development of these foreshores leads to uncertainty with respect to their contribution in protection against flooding. The morphological stability of a foreshore during extreme conditions is not well-known. Furthermore, the influence of infragravity waves generated on the foreshore on the wave overtopping and failure probability is largely unknown. Increasing interest in soft solutions of dike managers, as well as local inhabitants (getting a nice beach), makes it interesting to investigate the contribution of foreshores to flood protection further.
The risk management and optimization of coastal structures have gained much attention the last years. In order to optimize a design, the uncertainties need to be taken into account as detailed as possible, by using probabilistic approaches. However, currently these approaches are often deterministic or semi-probabilistic. For example, the currently used methods in the Netherlands to determine the probability of dike failure due to wave overtopping only include a few stochastic variables and use a model to determine the wave hydrodynamics that does not include infragravity waves or morphological changes. By using a full-probabilistic approach, the risks could potentially be further reduced and the designs further optimized, see e.g., Wainwright et al. [
3].
During a storm, several processes occur at a dike-foreshore system. Wave energy is dissipated on the foreshore by wave breaking, which causes a shift in the wave spectrum from the peak frequency to the lower frequencies due to the generation of infragravity waves, see e.g., Symonds et al.; Longuet-Higgins & Stewart [
4,
5]. The breaking waves also lead to erosion of the foreshore. Finally, if water levels and wave heights are large enough, wave overtopping may occur over the dike. Hence, the generation of infragravity waves, morphological changes of the foreshore and wave overtopping are important aspects in the design of dike-foreshore systems.
Infragravity waves are generated by groups of wind induced waves, and are sometimes called long waves or surfbeat in the surf zone. Infragravity waves are known to be important on dissipative beaches and for run-up [
5]. Typical infragravity wave periods range from 25–30 s to 250–300 s [
6]. As previous studies on dike-foreshore systems [
4,
7] indicated that wave energy dissipation causes a shift in the wave spectrum from the peak frequency to the lower frequencies (due to generation of infragravity waves), instead of the wave peak period, the
Tm−1,0 wave period was recommended as a measure in these situations to calculate the wave run-up or wave overtopping [
8,
9,
10]. This period is defined as
Tm−1,0 =
m−1/m0, with
mk being the
kth moment of the wave spectrum. The period is commonly used in coastal structure design [
11], and the use of the
Tm−1,0 wave period is incorporated in manuals like the EurOtop manual [
12]. Furthermore, it was found, that on high foreshores where intense breaking occurs, the wave set-up becomes important for the wave run-up and overtopping as well [
13].
Roeber & Bricker [
14] showed that during Typhoon Haiyan, at the town of Hernani, the Philippines, an infragravity wave steepened into a tsunami-like wave that caused excessive damage and casualties. The fringing reef present near the town protected the community from moderate storms, but increased flooding during this extreme event. Typical for these reef environments is a very short wave-breaking zone over a steep reef face, which releases the bound infragravity waves with little energy loss. This indicates that it can be important to include the infragravity waves in the design of dike-foreshore systems.
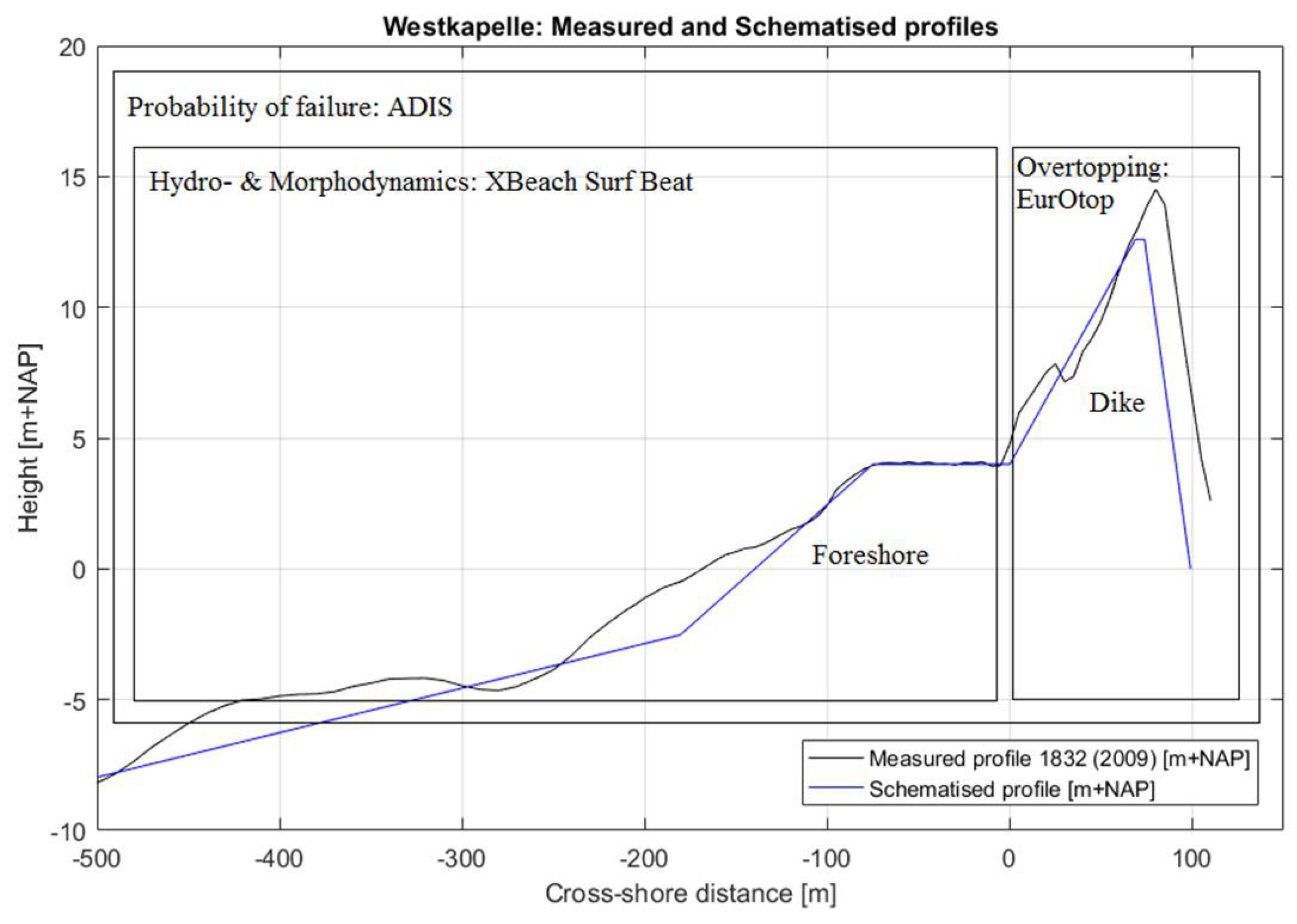
For this paper, the failure mechanism wave overtopping was chosen, because it is one of the most important failure modes of dike-foreshore systems. The overtopping discharge depends on the wave conditions at the toe, slope geometry, and the existing freeboard. The most commonly used equations to describe wave overtopping are the ones from EurOtop [
12].
Suzuki et al. [
7] concluded that beach nourishments do not always reduce the wave overtopping discharge, due to set-up and generation of bores and infragravity waves. Van Gent & Giarrusso [
15] found that for foreshores characterized by a bar, trough and terrace in front of a dike, the contribution of low frequency energy to the total wave energy could reach 30%. It has to be noted that most of the previous studies did not include the wave directional spreading, because they were based on physical flume model tests. However, the wave directional spreading can have a large influence on the generation of infragravity waves and the wave period [
11].
Bakker & Vrijling; Madsen et al. [
16,
17] give extensive descriptions of many of the different available probabilistic calculation methods. The Joint Committee on Structural Safety [
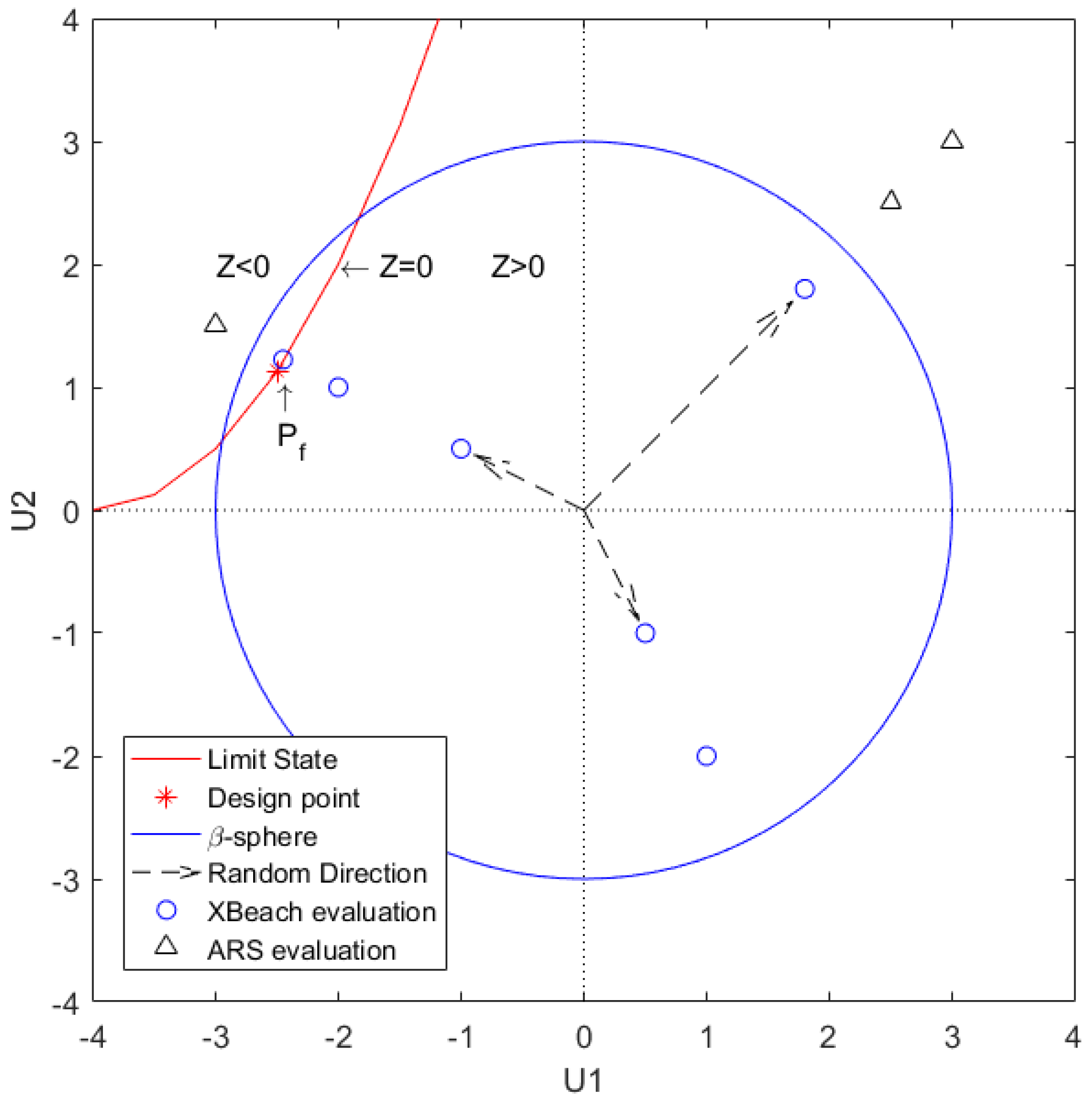
18] proposed a level-classification of probabilistic calculation methods for the reliability of an element (now ISO 2394:2015). Here, level I methods do not calculate failure probabilities, but use partial safety factors. Level II methods linearize the limit state function in the design point and approximate the probability distribution of each variable by a standard normal distribution. Level III methods or fully probabilistic methods calculate the probability of failure by considering the probability density functions of all variables.
Previous research considering probabilistic methods was often focused on different processes and failure mechanisms than wave overtopping (e.g., [
19,
20,
21,
22]). Furthermore, the previous research mostly considered only a few stochastic variables, with simple 1D empirical or numerical models and probabilistic methods like Monte Carlo Simulation, which require a large number of simulations (e.g., [
19,
20,
21,
22,
23]).
Overall, probabilistic methods have been applied to coastal dikes and dunes, but not yet to the issues studied in this paper. Hence, a method which includes the influence of complex hydrodynamics such as infragravity waves, and morphological changes of a sandy foreshore on the probability of dike failure due to wave overtopping does not yet exist. Therefore, the main goal of this paper is to develop a framework to calculate the probability of sea dike failure due to wave overtopping, taking into account the morphological changes of the foreshore and complex hydrodynamics like infragravity waves. Furthermore, the goal is to determine the influence of using a process-based model with complex hydrodynamics versus using a calculation rule, and to determine the influence of morphological changes of the foreshore on the probability of failure due to wave overtopping for the here considered case.
First, the case study location is described (
Section 2.1), then the choice and validation of the model framework are discussed (
Section 2.2). Next, the input of the probabilistic calculations is briefly described (
Section 2.3). After that, the results are given (
Section 3), followed by a discussion (
Section 4). The paper ends with several conclusions (
Section 5).
3. Results
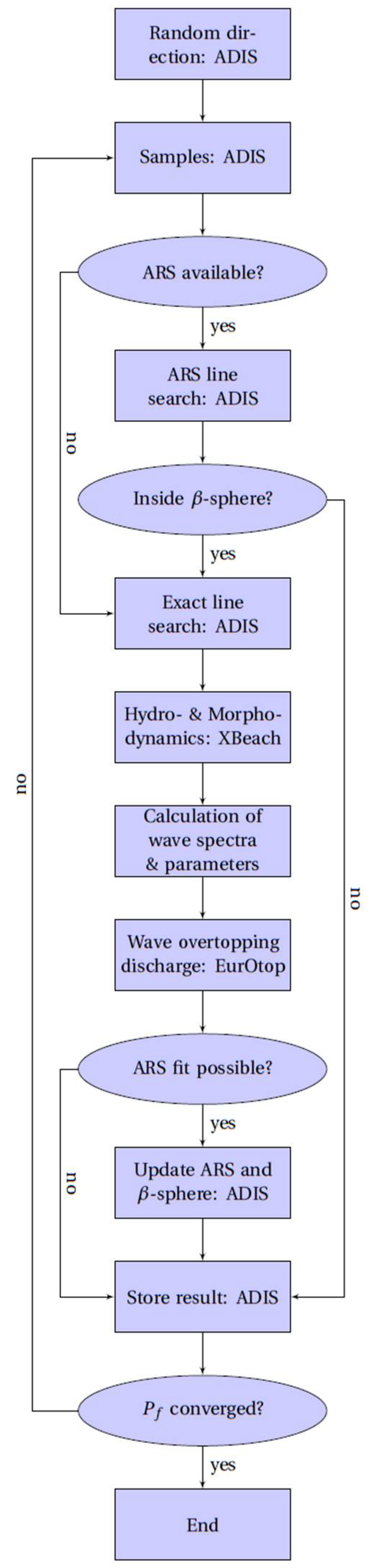
This section gives a description of the probabilistic (ADIS) calculations that were performed with the framework and their results. The influence of the complex hydrodynamics, model and wave parameters, time of the peak of the storm, morphological changes and probabilistic method are described in the sub-sections below.
Table 3 shows an overview of the different probabilistic (ADIS) calculations that were performed with the framework and their results. The table gives the type of hydrodynamic (and morphological) model that was used (column 2), which physical processes were included (columns 4–8), and the resulting number of stochastic variables that were applied (column 3,5–8). Moreover, the resulting probability of failure
Pf and the reliability index
β are given (columns 9,10), as well as the number of simulations necessary and the calculation duration in days (columns 11,12).
To determine the influence of using a process-based model with complex hydrodynamics compared to a calculation rule, calculations 1 and 2 were performed and will be compared. To determine the influence of including the model and wave parameters as stochastic variables, calculations 2 and 3 will be compared. To determine the influence of including the storm duration and time of the peak of the storm, calculations 3 and 4 will be compared. The influence of morphological changes of the foreshore on the probability of failure due to wave overtopping is determined by comparing calculation 4 and 5.
To determine the influence of the wave directional spreading (short-crested waves), an extra calculation was performed with XBeach 2D and the three offshore conditions as stochastic variables (calculation 6), which is compared to calculation 2.
To determine the added value of using the advanced and fully probabilistic method ADIS as well, the calculated probabilities of failure by the framework were compared to an approach where the same probability exceedance value for each of the stochastic parameters is used (not in table), see
Section 3.6.
3.1. Influence of the Complex Hydrodynamics
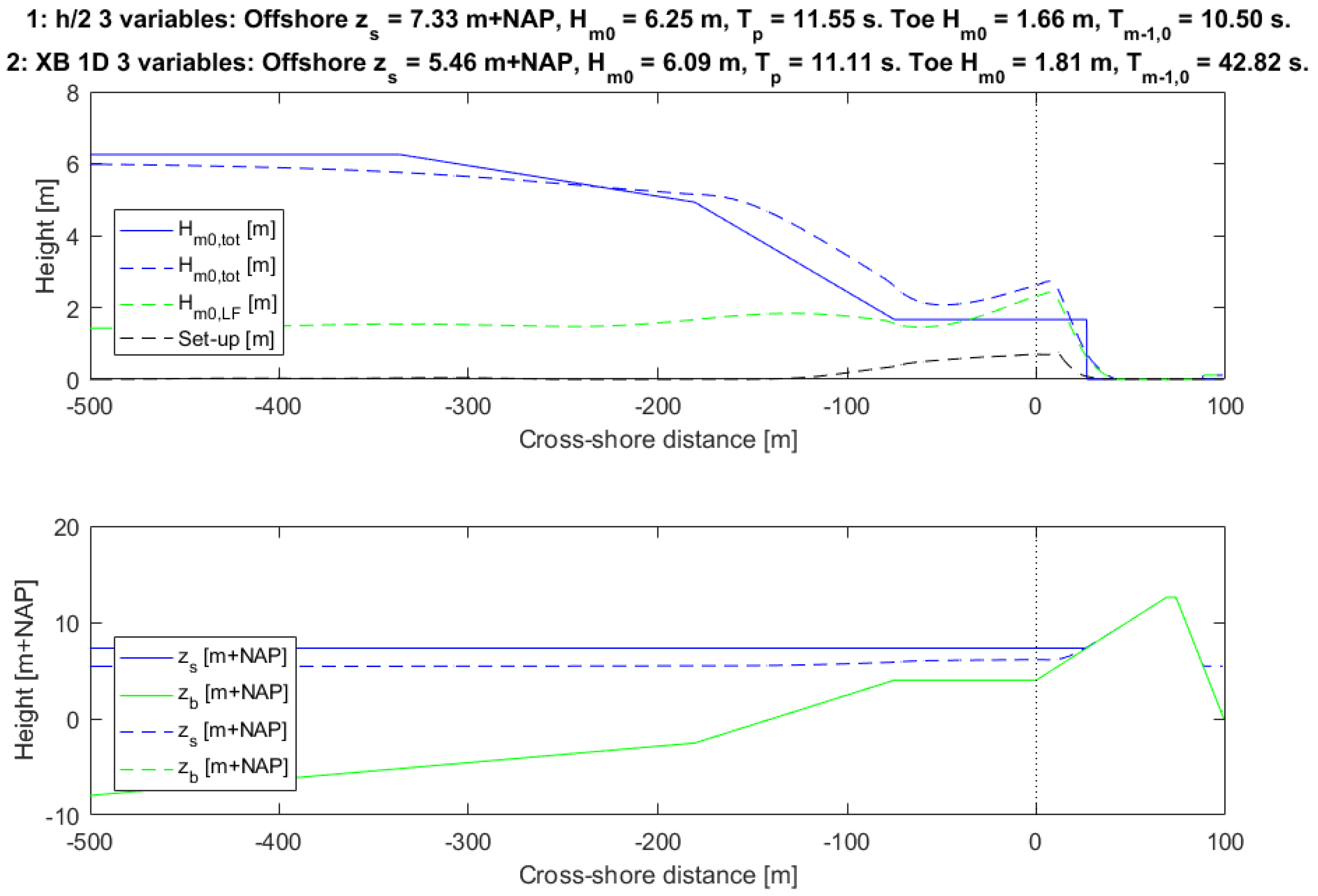
The results of calculations 1 and 2 are shown in
Figure 7, comparing the calculation rule
h/2-assumption (solid lines) with the process-based model XBeach (dashed lines). The figure shows the results of calculations at the (closest to the) design point. The top plot shows the development of the significant wave height for both situations (blue lines), as well as the low-frequency part of the wave height (green) and wave set-up (black) for XBeach. The bottom plot shows the water levels (blue) and the cross-shore profile (green). The title of the figure gives the conditions offshore and at the toe of the dike for both situations. Note that not the whole profile is visible, but rather the part from −500 m to 100 m relative to the toe of the dike. Using XBeach leads to a much larger failure probability than when the
h/2-assumption is used (factor 10
3, see
Table 3). The dominant parameter in the calculation with the
h/2-assumption was the water level, which was very large (7.33 m+NAP), see
Figure 7. As can be seen from
Figure 7, approximately the same amount of wave overtopping occurs for much less extreme hydraulic conditions (a water level that almost 2 m lower), when including the complex hydrodynamics. The difference in offshore wave height was not as large as for the water level (6.25 m versus 6.09 m). However, the wave set-up in XBeach leads to a somewhat larger wave height at the toe. The main difference lies in the wave period. Offshore, the difference is almost negligible, but due to the inclusion of the wave period transformation and generation of infragravity wave energy, the wave period at the toe is much larger with XBeach. The severe wave breaking on the foreshore leads to a transfer of wave energy to the lower frequencies, which increases the
Tm−1,0 wave period strongly (10.50 s versus 42.82 s, see
Figure 7). Hence, compared to a calculation rule, using a process-based model that includes complex hydrodynamics like wave set-up, infragravity waves and wave period transformation leads to larger wave heights and much larger wave periods at the toe of the dike. The ratio between the high frequency and low frequency wave heights at the toe (
Hm0,HF/
Hm0,LF) as calculated by XBeach 1D is only 0.5 in this case. The infragravity waves have a significant contribution to the total wave energy in this 1D case with foreshore. Thus, it can be concluded that it is of importance to include these hydrodynamic processes for these kinds of situations with severe wave breaking on a shallow foreshore. This means that a complex hydrodynamic model is necessary, which further necessitates an efficient probabilistic model.
3.2. Influence of the Model and Wave Parameters
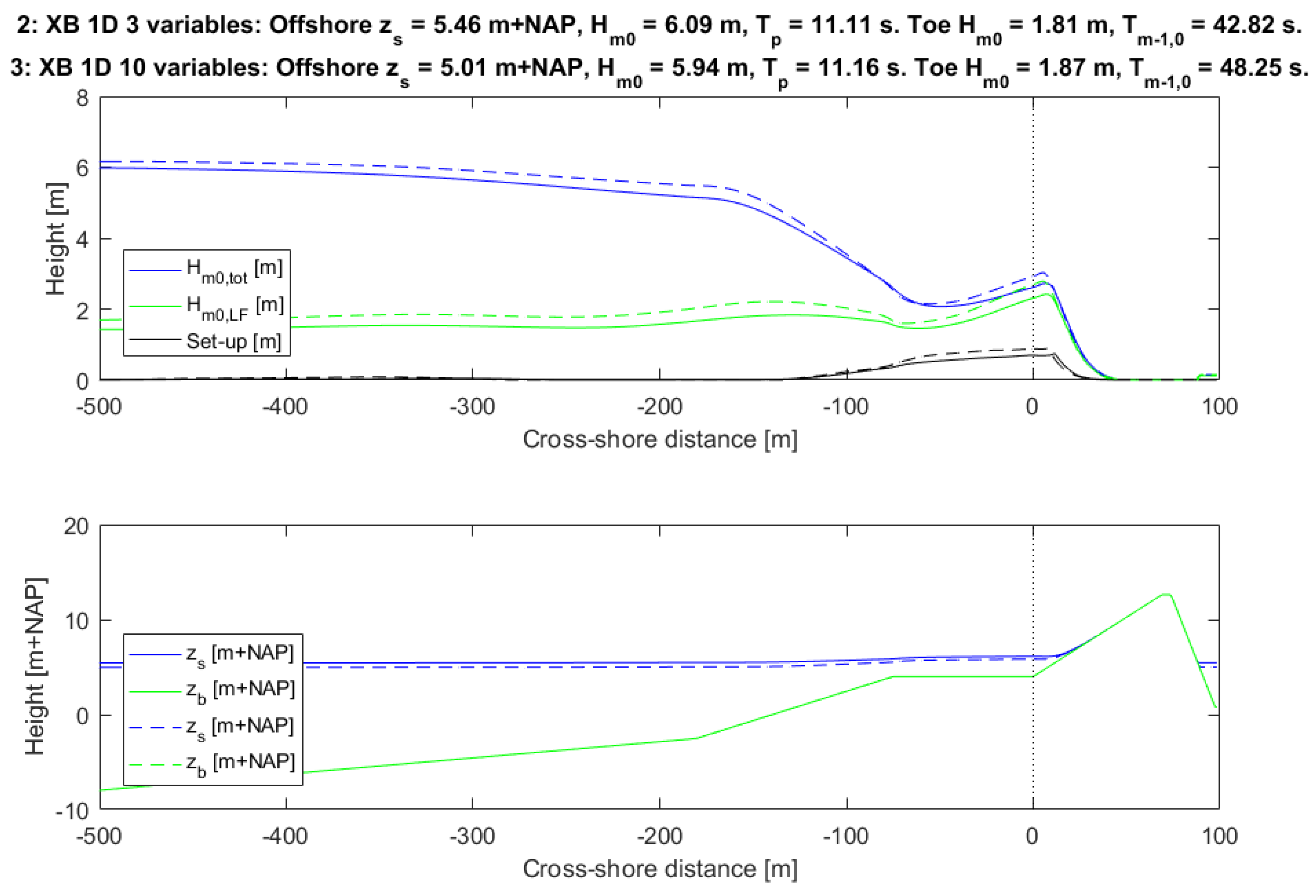
The inclusion of the model and wave parameters as stochastic (10 stochastic variables, calc. 3) leads to a probability of failure that is approximately 20 times larger than the calculation with only stochastic offshore conditions (calc. 2), see
Table 3. Hence, the influence is much smaller than the influence of including the complex hydrodynamics such as infragravity waves. The results of calculations 2 and 3 are shown in
Figure 8, again showing the calculations in the design point. As can be seen in the figure, a lower water level with approximately the same offshore wave conditions leads to the same amount of wave overtopping in the calculation with 10 stochastic variables, compared to the situation with 3 stochastic variables. The main difference lies in the breaker index
γ which is now a stochastic variable. In the design point, the value for this parameter was higher (0.63 versus 0.54 for the deterministic value). This larger breaker index leads to less wave breaking (larger maximum wave height
Hmax at incipient breaking) and thus larger wave heights at the toe of the dike and more wave overtopping. The difference in probability of failure shows that it can be important to include more stochastic variables than just the offshore conditions. Again, a large wave set-up and strong generation of infragravity wave energy is visible. As a result of this, the
Tm−1,0 wave periods at the toe are again quite large. The ratio between the high frequency and low frequency wave heights at the toe (
Hm0,HF/Hm0,LF) as calculated by XBeach 1D is only 0.4 in this case. This again shows that it is of importance to include hydrodynamic processes like infragravity waves and wave set-up in the calculations.
3.3. Influence of the Storm Duration and Time of the Peak of the Storm
The next step was to include the storm duration
tstorm and time of the peak of the storm
ϕ as stochastic variables, leading to a calculation with 12 stochastic variables (calc. 4). Including these parameters as stochastic led to a probability of failure that was approximately 2 times smaller than the calculation with 10 stochastic parameters (calc. 3), see
Table 3. Hence, the influence of including these parameters is rather small. The reduction in probability of failure can be explained by the time of the peak of the storm relative to the tide. When this parameter is considered as deterministic, it is assumed that the maximum surge occurs at the same moment as tidal high water. When this parameter is considered stochastic, the moment of maximum surge does not necessarily correspond to the moment of the maximum tidal water level, which reduces the probability of failure. The rest of the stochastic parameter values in the design point of the calculations with 10 and 12 stochastic parameters corresponded almost exactly, which explains the small difference in probability of failure. The small difference in probability of failure shows that for this case, the storm duration and time of the peak of the storm can be neglected as stochastic variables.
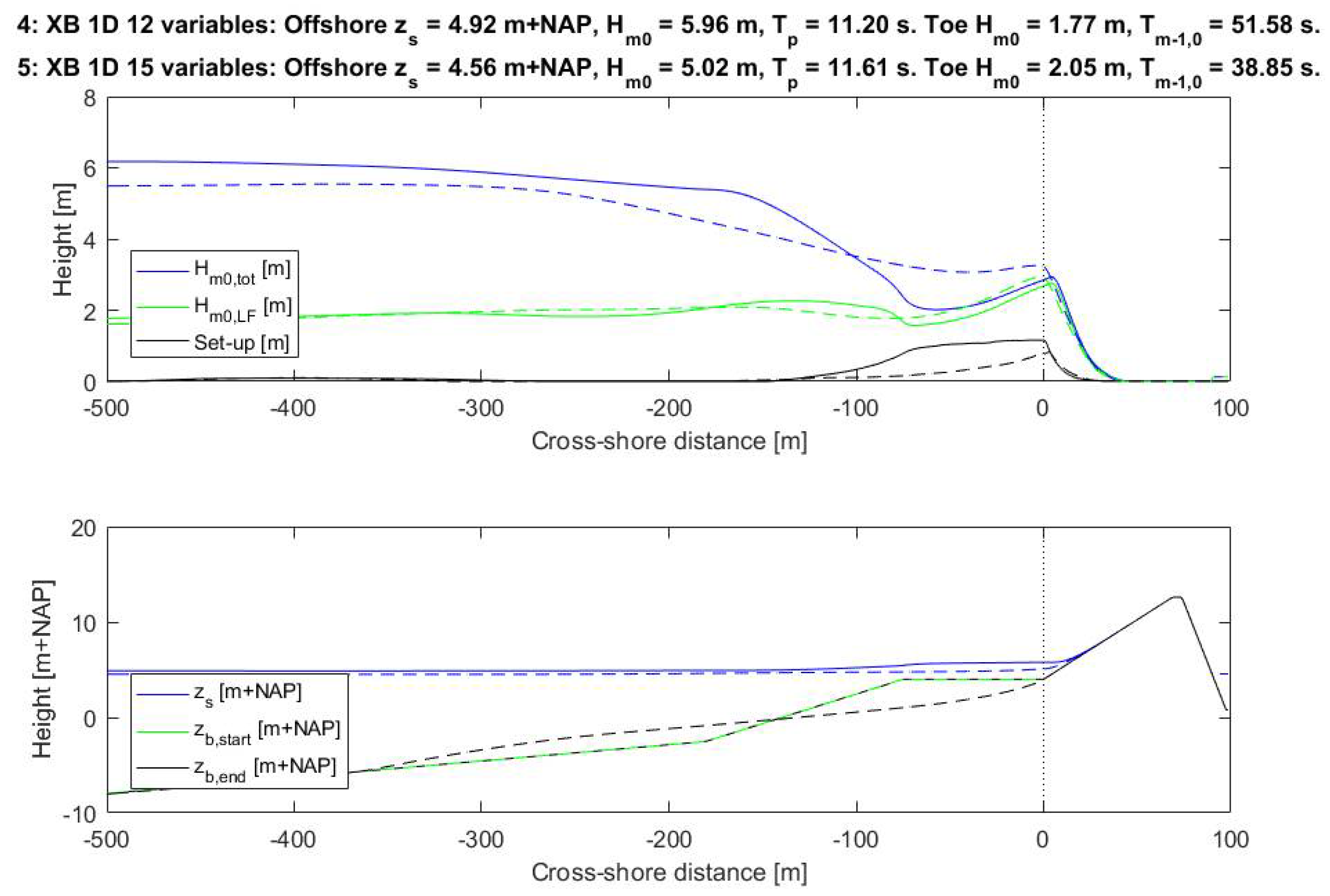
3.4. Influence of Morphological Changes
The inclusion of morphological changes of the foreshore during a storm and the corresponding three extra stochastic variables led to a failure probability that was somewhat larger (factor four higher with morphological changes included, see
Table 3). The extra stochastic variables, compared to the calculations described in the previous subsections, increased the number of calculations necessary to reach a converged probability of failure. This is a direct result of the inclusion of more parameters, which enlarges the search space (more dimensions).
Figure 9 presents the results of the simulations without morphological changes with 12 stochastic variables (calc. 4) and with morphological changes with 15 variables (calc. 5) at the design point. The top plot shows the development of the total significant wave height (blue), the low frequency part of the wave height (green) and set-up (black). The bottom plot shows the water level (blue) and the cross-shore profile at the beginning of the storm (green) and end of the storm (black). The inclusion of morphological changes leads to a somewhat larger probability of failure of about a factor four, as can be seen in
Table 3. This change is not very large when compared to the influence of the complex hydrodynamics as infragravity waves and wave set-up for the case considered here. Due to the erosion of the foreshore, the wave dissipation becomes less, which gives larger wave heights at the toe of the dike (2.05 m versus 1.77 m). However, the transfer from high frequency wave energy to the lower frequencies becomes less as well, which gives a smaller
Tm−1,0 wave period (38.85 s versus 51.58 s). In this case, the effects of the difference in wave height and wave period almost cancel one another out. This leads to the small difference in probability of failure, despite the quite large differences in the bathymetry due to erosion of the foreshore. Concluding, for this case, the inclusion of the morphological development of the foreshore and related stochastic variables only led to small differences in the probability of failure.
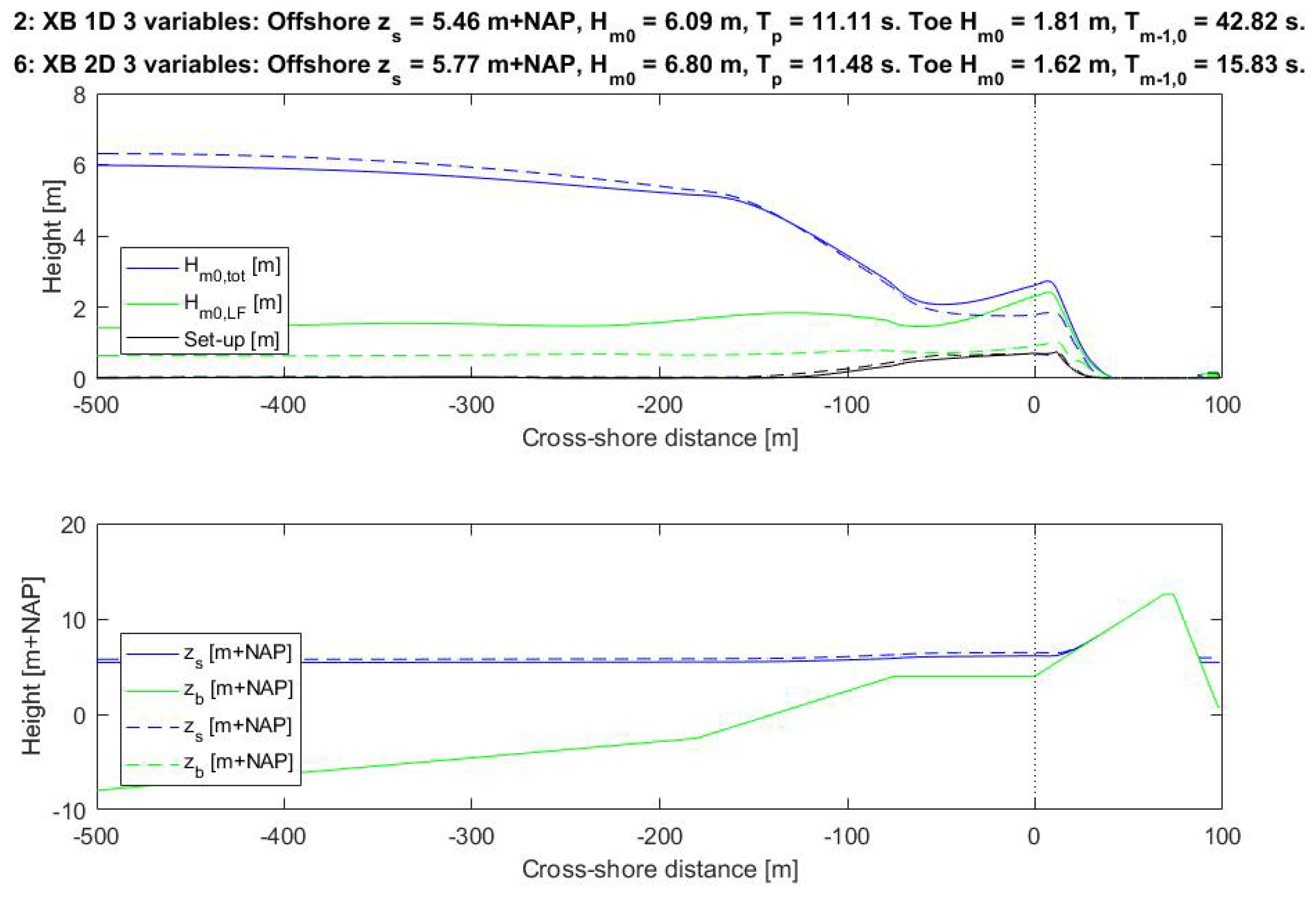
3.5. Influence of Wave Directional Spreading
To determine the influence of the wave directional spreading (short-crested waves), an extra calculation was performed with XBeach 2D and the three offshore conditions as stochastic variables (calc. 6), which is compared to XBeach 1D (calc. 2).
As shown in the previous subsection, rather large amounts of low-frequency energy and
Tm−1,0 wave periods are found at the toe of the dike when using a 1D simulation. The 1D XBeach calculations can be considered as a wave flume, with long-crested waves without directional spreading. This causes a stronger forcing of the infragravity waves compared to a situation with directional spreading. In reality, wind waves in extreme storms are short-crested. Therefore, an extra calculation was performed with XBeach 2DH with the same three stochastic parameters. With a 2D simulation, the wave directional spreading is included. Thus, the main differences between a 1D and 2D simulation lie within the fact that the 1D simulation does not include the wave directional spreading (hence, long-crested waves), which the 2D simulation does (hence, short-crested waves). For the 2D model, in the alongshore direction, a section of 1 km was modelled with grid cell sizes of 50 m. The wave directional information was solved in 10 degree bins, spanning 110 degrees (55 degrees to both sides of shore normal). Note that the mean wave angle in all simulations was shore-normal and that we use the methodology of Roelvink et al. [
34] to resolve the propagation of wave groups in the model domain. The results are shown in
Figure 10.
The calculated probabilities of failure are 1.6 × 10
−5 for the 1D case and 1.6 × 10
−6 for the 2D case, a difference of a factor 10. The lower probability of failure as found for the 2D case can be explained by the forcing of the infragravity waves, which is less than in the 1D case, because the 2D XBeach calculations include the wave directional spreading. This leads to less low-frequency energy and therefore a smaller wave period at the toe (15.83 s versus 42.82 s), which results in less wave overtopping. For instance Hofland et al. [
11] show as well that the generation of low-frequency wave energy is decreased by the directional spreading. With the inclusion of the wave directional spreading, the results of a 2D simulation are more realistic compared to a 1D simulation, since wind waves in extreme storms are short-crested (see also e.g., Van Dongeren et al. [
50]). The ratio between the high frequency and low frequency wave heights at the toe (
Hm0,HF/
Hm0,LF) is 1.6 for the 2D case (compared to 0.5 for the 1D case). Thus, even in 2D the infragravity waves have a significant contribution to the total wave energy.
3.6. Influence of the Probabilistic Method
The influence of using the level III probabilistic method ADIS on the number of simulations necessary was determined before in
Section 2.2.3., as well as in Den Bieman et al.; Grooteman [
21,
36]. An indication of the added value of using this level III method can be gained by comparing the ADIS results with probabilistic calculations that use the same probability exceedance value for each of the stochastic parameters. This means that the stochastic parameters are considered as fully correlated. This was done for XBeach 1D with the three offshore condition parameters (water level, wave height and wave period) as stochastic variables. The results are given in
Table 4. It can be seen that a difference of a factor 12.5 in the probability of failure is found between ADIS and the fully dependent estimate. Hence, when using a level III fully probabilistic approach, a lower probability of failure and a lower required crest height of the dike are found. It can be imagined, that if more stochastic variables would be included in this comparison, the difference between the estimate and the advanced probabilistic approach would be even larger. Thus, using ADIS in the design of dike-foreshore systems can lead to lower required crest levels.
4. Discussion
The calculation duration of some of the probabilistic calculations was rather large, in the order of a day without morphological changes (either 1D or 2D), in the order of a week (1D) with morphological changes, on 8 nodes with 16 GB of RAM. For this paper, the calculations with large numbers of stochastic variables and morphological changes were only performed with XBeach 1D. With the current computational capacities, using XBeach 2D and including the morphological changes in the probabilistic framework is not feasible in an engineering context yet, but it is for an academic context. As shown before, for the present case the morphological response has a relatively small influence on the failure probability. As the morphological response is expected to become lower when using a 2D calculation with short-crested waves, this will further decrease the influence of morphology on the failure probability, a consequence of the decreased infragravity wave height. With increasing computational power, the feasibility of XBeach 2D will likely increase in the future. As well, a possible measure could be to use a morphological acceleration factor in XBeach. Also, recently, a prediction formula for the
Tm−1,0 on mildly sloping shallow foreshores was determined [
11]. This equation can be used for simple cross-shore profiles and could be implemented in the model framework to save calculation time for such cases. For more complex cross-shore profiles, XBeach will remain necessary.
In the calculations with morphological changes, XBeach created a characteristic storm profile with an offshore bar, the foreshore itself was largely eroded. As mentioned before, XBeach has been extensively calibrated and validated [
26,
27]. However, even if the calculated offshore bar height would not be completely correct, this would hardly affect the wave conditions at the toe and related overtopping discharge. Van Gent & Giarrusso [
15] found that the wave conditions at the toe of the structure are hardly affected by the level of the offshore bar (and/or trough), but are strongly affected by the level of the foreshore.
As mentioned before, the focus of this paper is on the dominant short term storm morphological changes, not on the long term changes by the daily climate. The bathymetrical profile after the storm with conditions corresponding to the parameter values in the design point was compared to the bathymetrical profiles at Westkapelle 1 year after construction of the foreshore and 5 years after construction of the foreshore. The morphological changes of the ‘design point storm’ were much larger than the changes by the daily climate after five years. This does not mean that the after-storm erosion profile of a pre-storm situation with a foreshore without much sand in it is the same as the erosion profile for a pre-storm situation with much sand in the foreshore. For maintenance, this means that the design foreshore profile should be maintained as much as possible. Furthermore, it is expected that the role of short term (storm) changes of the foreshore become more important when the foreshore is designed smaller (less sand in the profile). Finally, these findings are case-specific. At other locations, there may be more or less dynamic behavior, and also the ratio between the erosion by daily and storm conditions can vary.
Much of the validation for wave overtopping was performed in wave flumes (1D, no directional spreading), which inherently includes the stronger forcing of the infragravity waves, like in XBeach 1D. As was shown, a large part of the difference in the results between 1D and 2D XBeach was caused by differences in the
Tm−1,0 wave period at the toe and uncertainties in the sensitivity of the EurOtop equations with respect to this wave period. Since the
Tm−1,0 wave period is very sensitive to the low frequencies, it is unclear if this wave period is still applicable for situations with large amounts of low frequency energy, such as the ones considered in this paper. Treating the complex combination of infragravity wave energy and wind wave energy with a single parameter as the
Tm−1,0 wave period might be an oversimplification, however the
Tm−1,0 wave period is the wave period that is currently used in all the most commonly used wave run-up and wave overtopping equations. A new equivalent slope concept was determined for wave overtopping at shallow foreshores in Altomare et al. [
51] and could be considered a first step. However, still more research is required to be able to validate the influence of the infragravity waves on wave overtopping, for this case, as well as for other cases.
5. Conclusions
This paper presented a probabilistic model framework which is capable of including complex hydrodynamics like infragravity waves and morphodynamics of a sandy foreshore in the calculation of the probability of sea dike failure due to wave overtopping. The method was applied to a test case loosely based on the Westkapelle sea defence, a hybrid defence consisting of a dike with a sandy foreshore. Moreover, the influence of the physical processes like infragravity waves and morphological changes on the probability of dike failure due to wave overtopping were determined. By using the fully probabilistic level III method ADIS, the number of simulations necessary is greatly reduced, which allows for the use of more advanced and detailed hydro- and morphodynamic models. The framework is able to compute the probability of failure with up to 15 stochastic variables and to describe feasible physical processes. Furthermore, the framework is completely modular, which means that any model or equation can be plugged into the framework, whenever updated models with improved representation of the physics or increases in computational power become available.
The model framework as described in this paper, includes more stochastic variables in the determination of the probability of dike failure due to wave overtopping compared to the currently used methods in the Netherlands, where also infragravity waves or morphological changes are not included.
Including a process-based hydrodynamic model led to much larger failure probabilities for the hybrid defence considered in this paper (factor 103). This difference was mainly caused by the difference in wave period at the toe of the dike, which is not accounted for by the simple calculation. Hence, this indicates that it can be important to include the complex hydrodynamics such as infragravity waves and wave set-up for these kinds of situations.
The inclusion of 7 extra stochastic model and wave parameters led to a probability of failure that was approximately 20 times larger than the calculation with 3 offshore condition stochastic parameters. The influence is much smaller than the influence of including the complex hydrodynamics such as infragravity waves, but the difference in probability of failure shows that it can still be important to include more stochastic variables than just the offshore conditions in the calculations. Furthermore, for this case the storm duration and time of the peak of the storm have a negligible influence as stochastic variables.
The inclusion of the morphological changes led to a failure probability that was only somewhat larger (factor 4) for the case considered here (relative to e.g., the much larger influence of the complex hydrodynamics that was found). Hence, for this case, the influence of the morphological changes of the foreshore on the failure probability was not that large. In this case, the effects of the difference in wave height and wave period at the toe almost cancelled one another out.
More research is required to be able to validate the influence of the infragravity waves on wave overtopping, for this case, as well as for other cases, especially in connection to short-crested waves. The results of a 2D simulation are more realistic compared to a 1D simulation, see also e.g., Van Dongeren et al. [
50], as wind waves in extreme storms are short-crested. The long-crested waves in XBeach 1D create a stronger forcing of the infragravity waves. With the current computational capacities, a 2D calculation and including the morphological changes in the level III probabilistic framework is not feasible in an engineering context yet, but it is for an academic context. With increasing computational power, the feasibility will likely increase in the future.
Using the framework offers more insight into the physics, and can be used to determine the contribution of foreshores to flood protection. It is recommended to apply the framework to other cases as well, to determine if the effects of complex hydrodynamics as infragravity waves and morphological changes on the probability of sea dike failure due to wave overtopping as found in this paper hold for other cases as well. Furthermore, it is recommended to investigate broader use of the method, e.g., for safety assessment, reliability analysis and design.