How Well Do AR5 Sea Surface-Height Model Projections Match Observational Rates of Sea-Level Rise at the Regional Scale?
Abstract
1. Introduction
- 5 ice components (Greenland dynamic ice and surface-mass balance, Antarctic dynamic ice and surface-mass balance, and glaciers);
- 3 ocean-related components, all of which are derived from CMIP5 models (dynamic SSH, global thermosteric SSH anomaly, and the inverse barometer effect from the atmosphere);
- land water storage (also called terrestrial water); and
- glacial isostatic adjustment (GIA, as a change in sea level “relative” to land).
2. Data and Methods
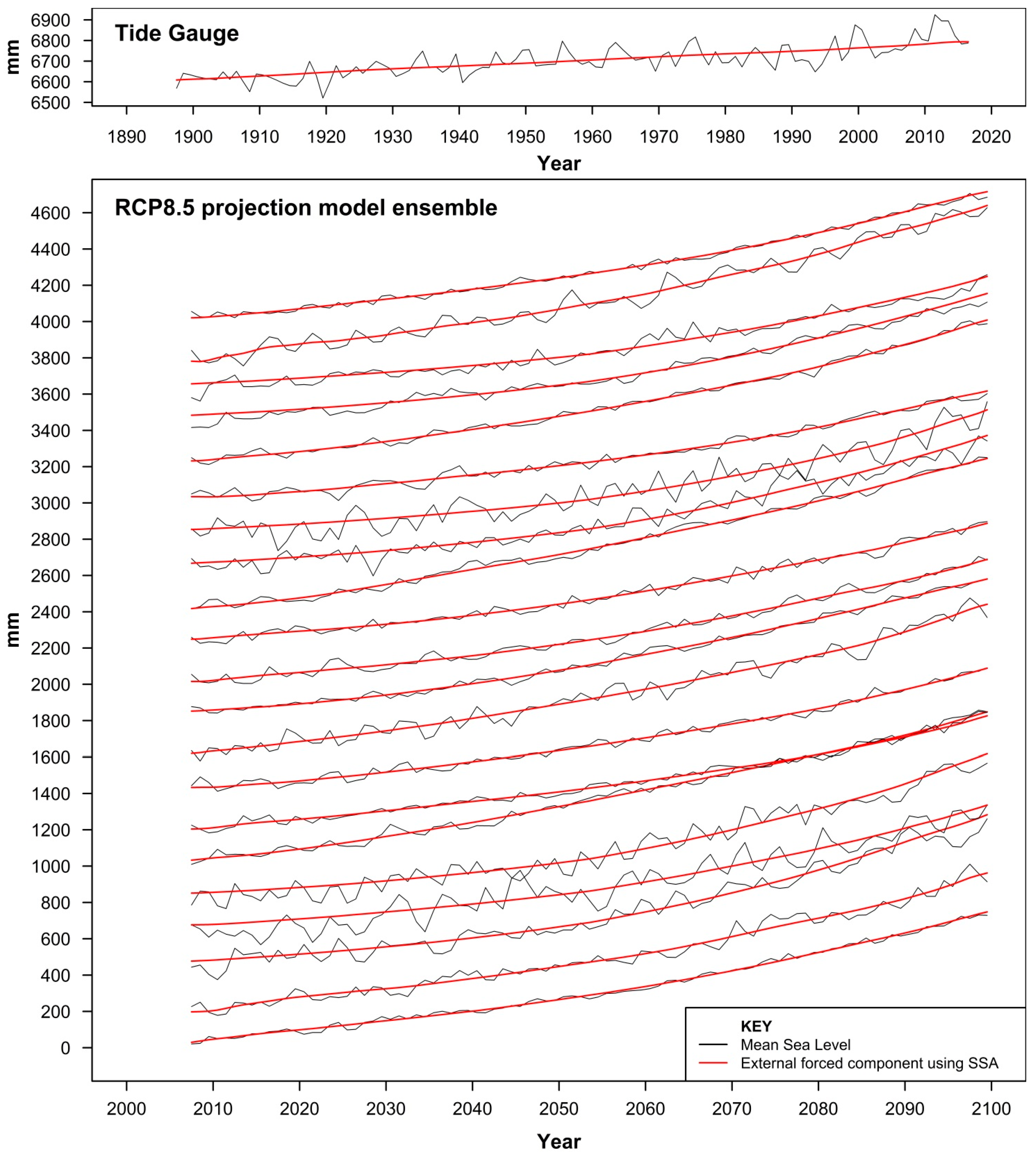
2.1. Historical Tide-Gauge Analysis
2.2. AR5 Sea Surface-Height (SSH) Projection-Model Output Analysis
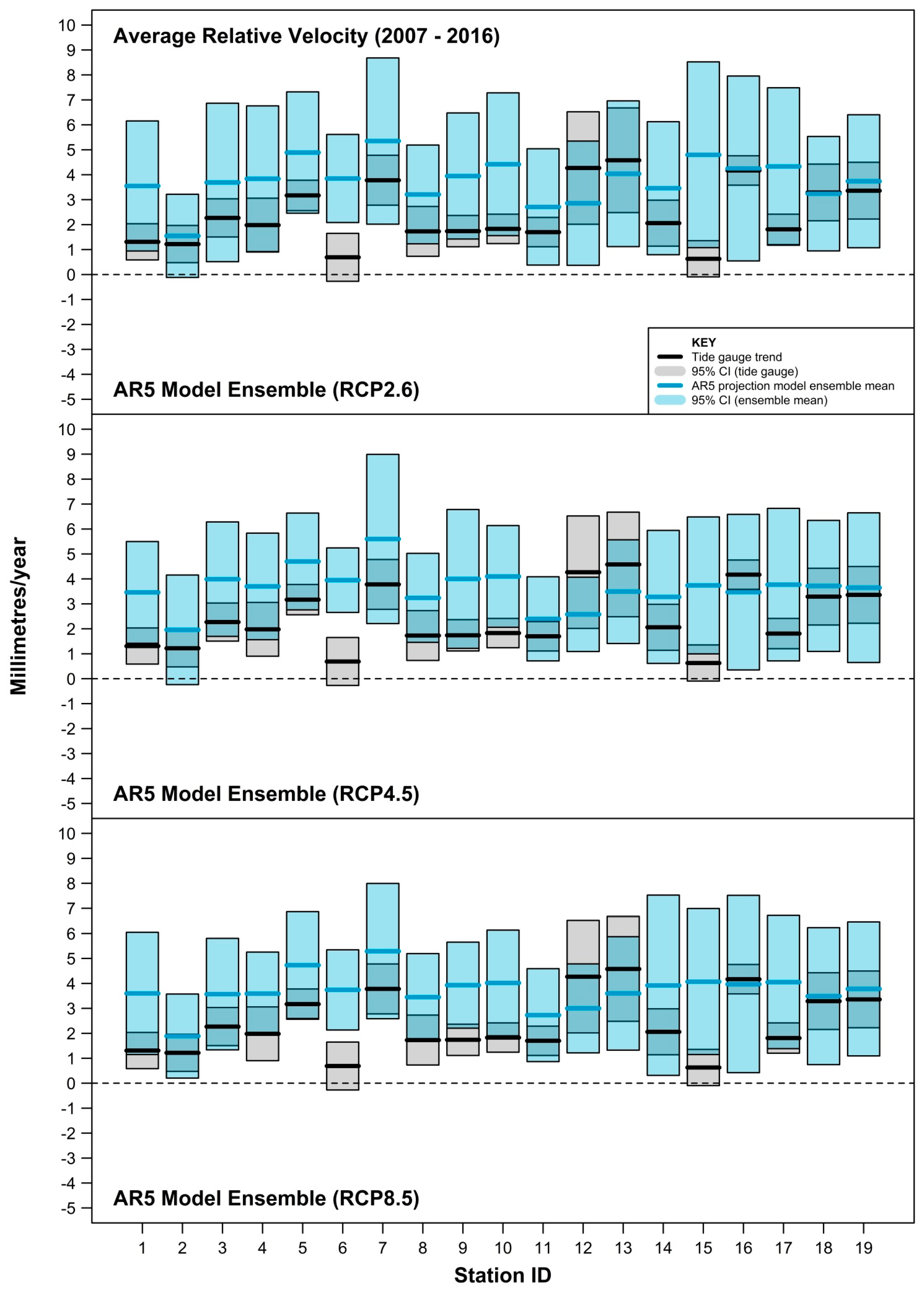
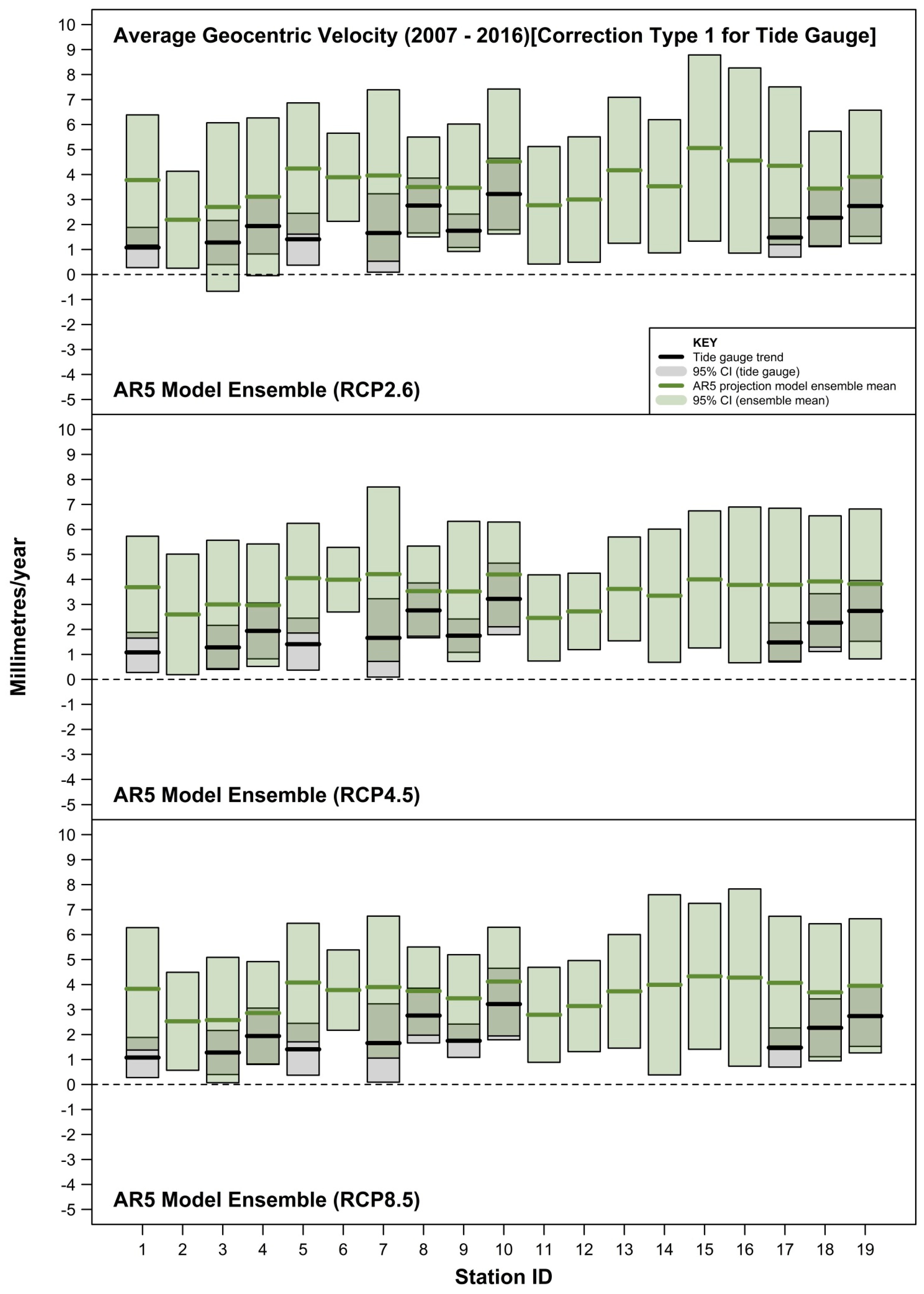
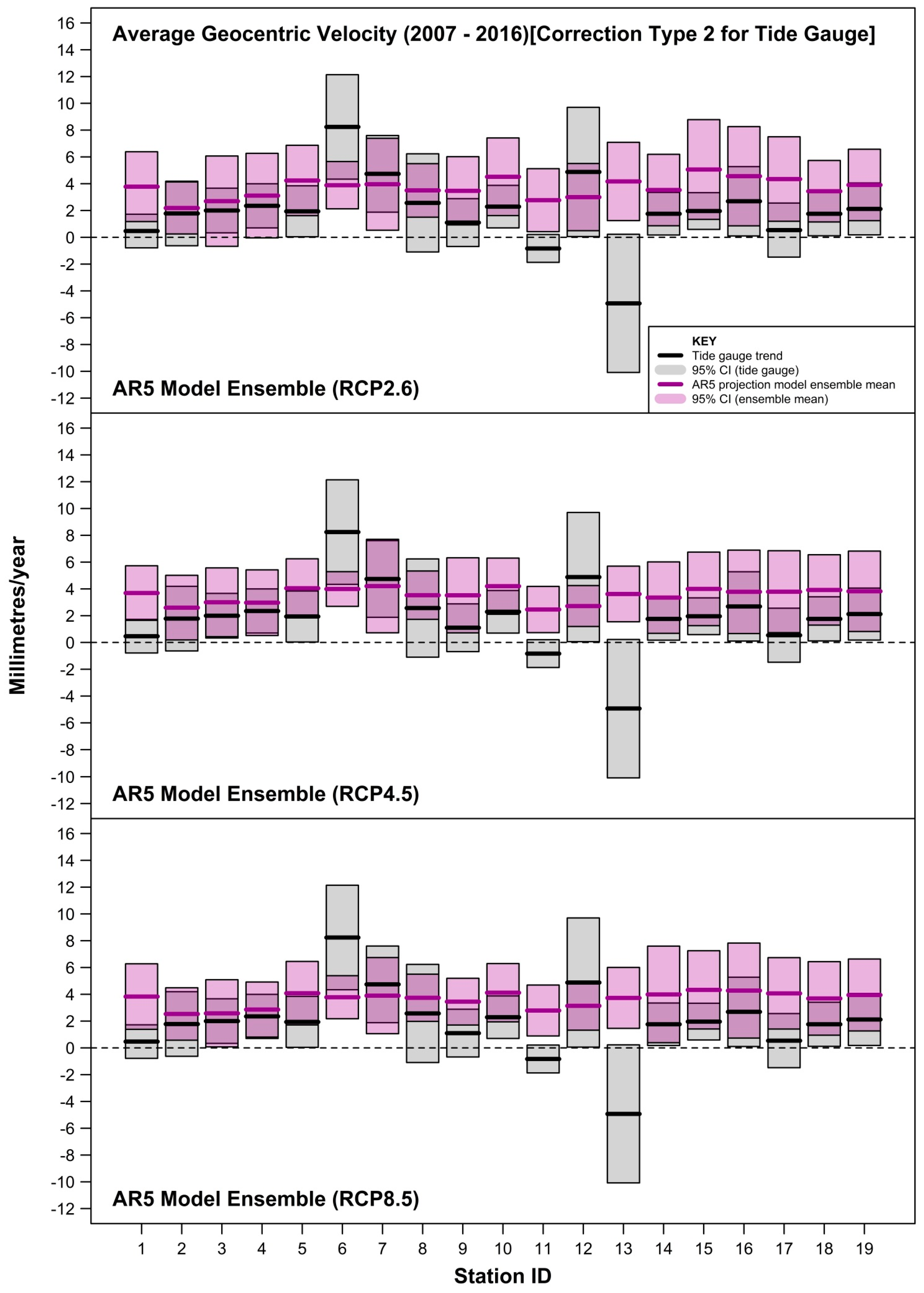
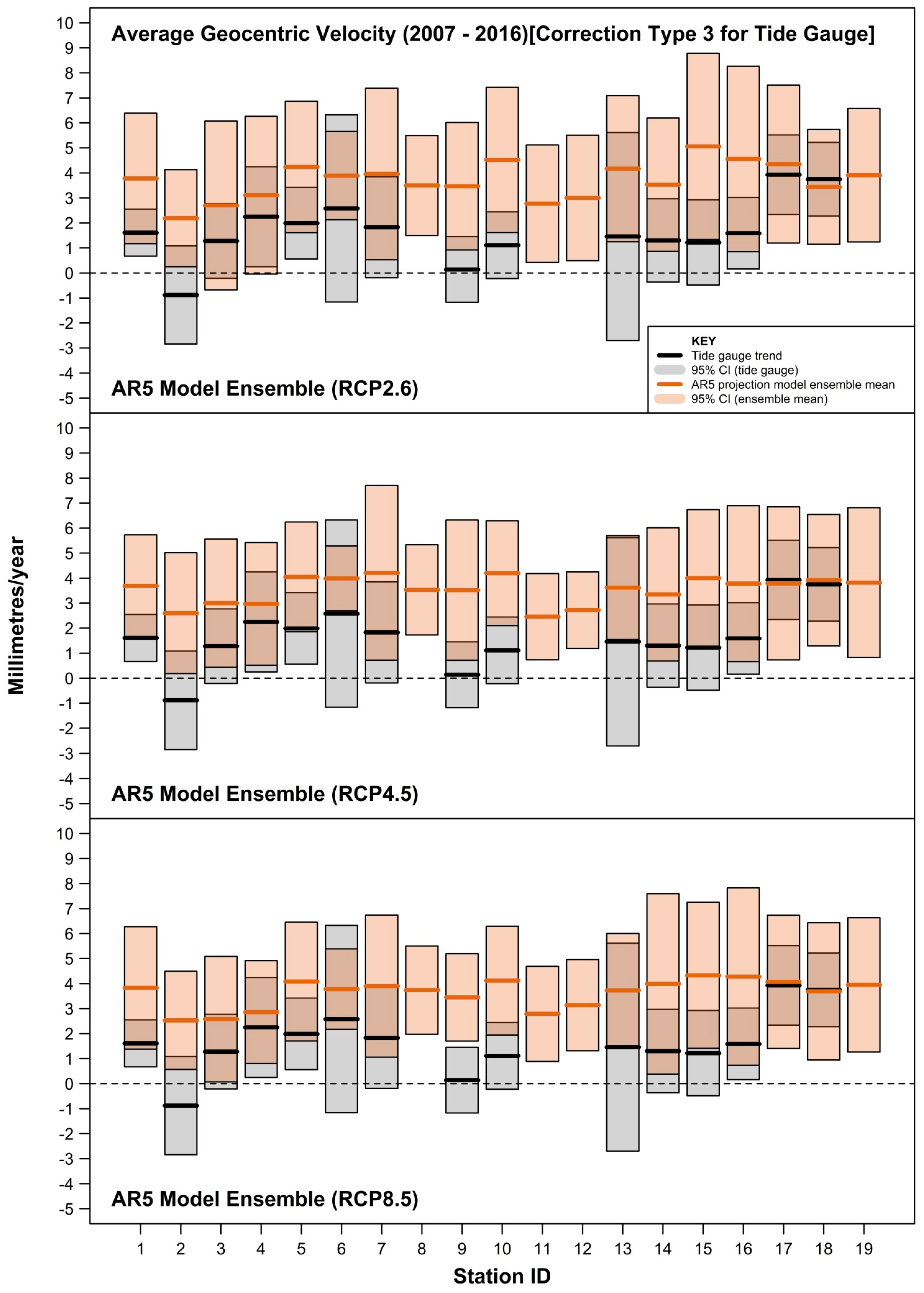
3. Results
4. Discussion
- AR5 projection-model outputs were not designed to be necessarily rigorous at the decadal time scale;
- an overlapping decade is a relatively small window over which to compare the characteristics of long-term phenomena such as mean sea-level rise. Furthermore, time-series analysis techniques are ubiquitously affected by end effects and the analysis herein is attempting to investigate and compare the characteristics of the end of one time series (tide-gauge data to present) with the start of another (AR5 projections from 2007);
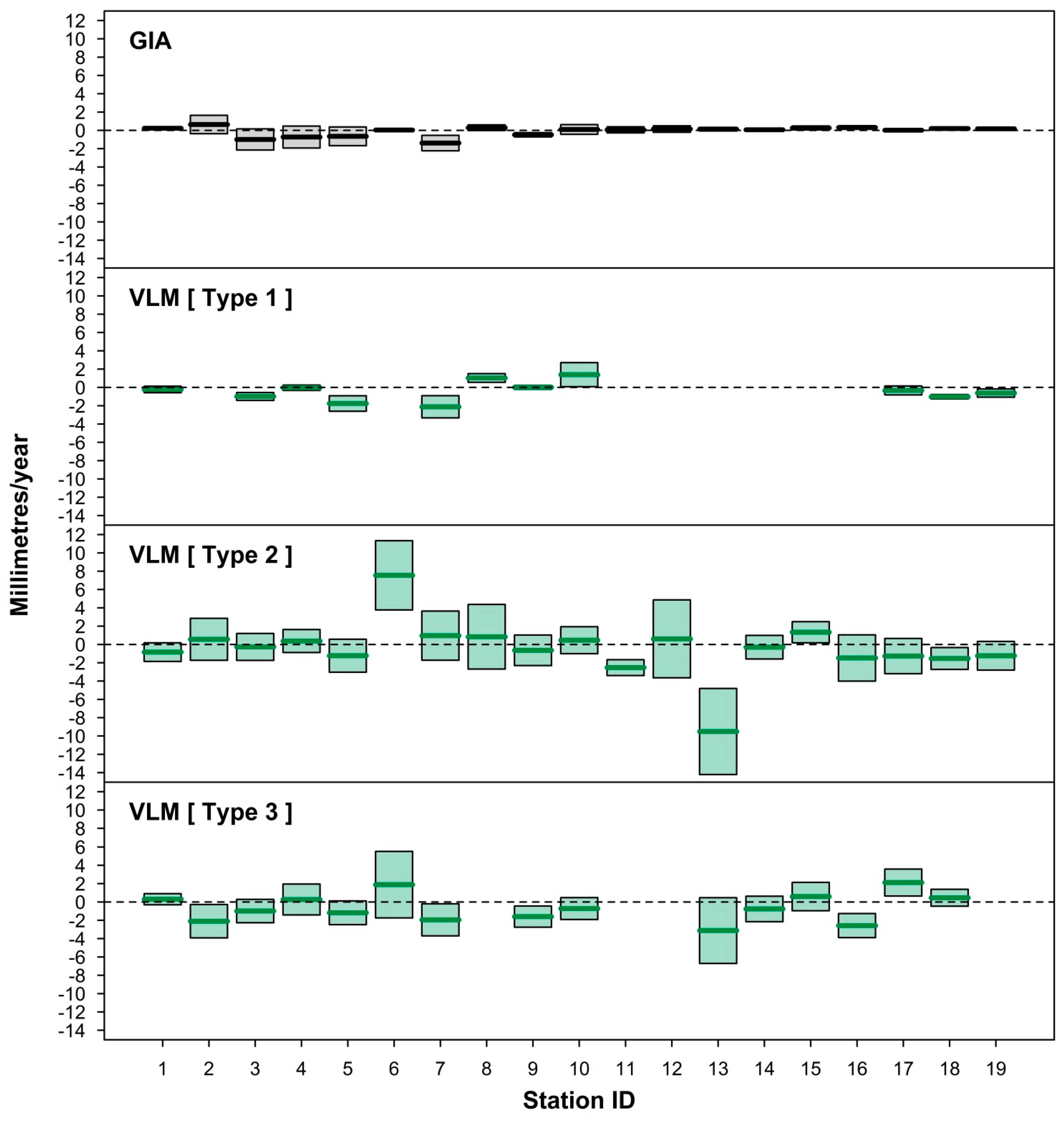
- estimating and accommodating the ubiquity of VLM resulting from multiple origins (including tectonics, subsidence, etc., as well as GIA) embedded within tide-gauge records. As evident in this study, co-located GPS measurements are not available for many tide-gauge sites or are at best quite short records (often <10 years) [29,30]. The more complete and longer VLM estimates based on the method of Ostanciaux et al. 2012 [31] are reliant on satellite altimetry data [14] on a spatial resolution grid of 0.25° × 0.25° and could be a maximum of ≈20 km from the tide-gauge site. Similarly, the AR5 approach of correcting projection outputs for GIA to better approximate mean sea-level rise “relative” to the land ignores the many other VLM origins present at tide-gauge sites. This is highlighted clearly in Figure 7, where the GIA estimates at Balboa [ID = 6] and Ko Taphao Noi [ID = 13] differ markedly from the actual VLM observed via differing techniques. At both sites, the estimated GIA is <0.2 mm/year, whereas the VLM associated with the tectonic uplift of the Panama Arc at Balboa [35] and subsidence due to groundwater and aquifer mining at Ko Taphao Noi [36] are of the order of several mm/year;
- the highest density of long tide-gauge records are predominantly clustered around Europe and North America in the northern hemisphere [25]. There is only a relatively small pool of records available outside these domains with sufficient length and apparent robustness (i.e., absence of warning flags in the PSMSL database) to consider for meaningful global coverage; and
- the postulated theory that the Mt Pinatubo eruption in the Philippines in 1991 has had the effect of masking (or delaying) the rate of global sea-level rise [37] which would also be reflected in the tide-gauge records.
5. Conclusions
- searching for additional tide-gauge data records of sufficient length (at least 75–80 years) to improve the global spatial coverage of the station records used in this paper, in particular around important margins including the southern coasts of the African continent and along the coastlines of China;
- investigating methods to fill long records in other key areas such as Aden, Yemen (dating back to 1879) and Takoradi, Ghana (dating back to 1930), supplementing the critical work already undertaken to extend PSMSL records (e.g., [13]); and
- contributing data custodians ensuring up-to-date data is supplied in a timely manner.
Supplementary Materials
Acknowledgments
- David Bate and Port of Auckland Limited (Auckland, New Zealand) for permitting access to recent data for Auckland;
- Mark Carson (Institute of Oceanography, University of Hamburg, Germany) who provided advice on specifics of the SSH projection-model outputs used in AR5, made available via the Integrated Climate Data Center, University of Hamburg;
- James Chittleborough (Tidal Unit, Bureau of Meteorology, Australia) for providing recent data at Fremantle and Sydney;
- Stefan Kern (Institute of Oceanography, University of Hamburg, Germany) who provided access to the Ssalto/Duacs satellite altimetry products. The altimeter products were produced by Ssalto/Duacs in collaboration with LOcean and CTOH and distributed by Aviso, with support from Cnes (http://www.aviso.altimetry.fr/);
- Glen Rowe, LINZ (Land Information, New Zealand) for providing recent data at Dunedin and Auckland;
- Thiago Dos Santos (Land and Atmospheric Science, University of Minnesota, MN, USA) who provided advice on R scripting code to facilitate extraction of data from netCDF format files;
- Aimée Slangen (Royal Netherlands Institute for Sea Research, The Netherlands) for wide-ranging advice and discussions on climate-modelling products that improved the study; and
- PSMSL, ICDC and SONEL for their publicly accessible data repositories.
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. (Eds.) Climate Change 2007: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 333. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Evaluation of Climate Models. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 741–866. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1137–1216. [Google Scholar] [CrossRef]
- Integrated Climate Data Center (ICDC) Website for AR5 Sea Level Data. Available online: http://icdc.cen.uni-hamburg.de/1/daten/ocean/ar5-slr.html (accessed on 8 April 2017).
- IPCC. Press Release—IPCC Agrees Special Reports. AR6 workplan, 2016/03/PR, 14 April 2016. Available online: http://www.ipcc.ch/news_and_events/pdf/press/160414_pr_p43.pdf (accessed on 15 April 2017).
- Slangen, A.B.A.; Carson, M.; Katsman, C.A.; van de Wal, R.S.W.; Köhl, A.; Vermeersen, L.L.A.; Stammer, D. Projecting twenty-first century regional sea-level changes. Clim. Chang. 2014, 124, 317–332. [Google Scholar] [CrossRef]
- Slangen, A.A.; Meyssignac, B.; Agosta, C.; Champollion, N.; Church, J.A.; Fettweis, X.; Ligtenberg, S.R.M.; Marzeion, B.; Melet, A.; Palmer, M.D.; et al. Evaluating Model Simulations of Twentieth-Century Sea-Level Rise. Part I: Global Mean Sea-Level Change. J. Clim. 2017, 30, 8539–8563. [Google Scholar] [CrossRef]
- Meyssignac, B.; Slangen, A.A.; Melet, A.; Church, J.A.; Fettweis, X.; Marzeion, B.; Agosta, C.; Ligtenberg, S.R.M.; Spada, G.; Richter, K.; et al. Evaluating Model Simulations of Twentieth-Century Sea-Level Rise. Part II: Regional Sea-Level Changes. J. Clim. 2017, 30, 8565–8593. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New data systems and products at the permanent service for mean sea level. J. Coast. Res. 2012, 29, 493–504. [Google Scholar] [CrossRef]
- Permanent Service for Mean Sea Level (PSMSL) Website. Available online: http://www.psmsl.org (accessed on 8 April 2017).
- Hogarth, P. Preliminary analysis of acceleration of sea level rise through the twentieth century using extended tide gauge data sets (August 2014). J. Geophys. Res. Oceans 2014, 119, 7645–7659. [Google Scholar] [CrossRef]
- AVISO Website. Available online: http://www.aviso.altimetry.fr/duacs/ (accessed on 10 June 2017).
- Integrated Climate Data Center (ICDC) Website for AVISO SSH Data. Available online: http://icdc.cen.uni-hamburg.de/1/daten/ocean/ssh-aviso.html (accessed on 10 June 2017).
- Watson, P.J. Identifying the best performing time series analytics for sea-level research. In Time Series Analysis and Forecasting: Contributions to Statistics; Rojas, I., Pomares, H., Eds.; Springer International Publishing: Berlin, Switzerland, 2016; pp. 261–278. [Google Scholar] [CrossRef]
- Alexandrov, T.; Bianconcini, S.; Dagum, E.B.; Maass, P.; McElroy, T.S. A review of some modern approaches to the problem of trend extraction. Econ. Rev. 2012, 31, 593–624. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman and Hall/CRC Press: London, UK, 2001. [Google Scholar]
- Alexandrov, T.; Golyandina, N. Automatic extraction and forecast of time series cyclic components within the framework of SSA. In Proceedings of the 5th St. Petersburg Workshop on Simulation, St. Petersburg, Russia, 26 June–2 July 2005; pp. 45–50. [Google Scholar]
- Project for Statistical Computing Website. Available online: https://www.r-project.org/ (accessed on 8 April 2017).
- Watson, P.J. Development of a unique synthetic data set to improve sea-level research and understanding. J. Coast. Res. 2015, 31, 758–770. [Google Scholar] [CrossRef]
- Watson, P.J. How to improve estimates of real-time acceleration in the mean sea level signal. J. Coast. Res. 2016, 75, 780–784. [Google Scholar] [CrossRef]
- Watson, P.J. Acceleration in US Mean Sea Level? A New Insight using Improved Tools. J. Coast. Res. 2016, 32, 1247–1261. [Google Scholar] [CrossRef]
- Watson, P.J. Acceleration in European Mean Sea Level? A New Insight Using Improved Tools. J. Coast. Res. 2017, 33, 23–38. [Google Scholar] [CrossRef]
- Watson, P.J. Improved Techniques to Estimate Mean Sea Level, Velocity and Acceleration from Long Ocean Water Level Time Series to Augment Sea Level (and Climate Change) Research. Ph.D. Thesis, University of New South Wales, Sydney, Australia. under review, submitted for examination October 2017.
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef]
- Stineman, R.W. A consistently well-behaved method of interpolation. Creat. Comput. 1980, 6, 54–57. [Google Scholar]
- SONEL Website. Available online: http://www.sonel.org/spip.php?page=gps&idStation=2722 (accessed on 8 April 2017).
- Santamaría-Gómez, A.; Gravelle, M.; Collilieux, X.; Guichard, M.; Míguez, B.M.; Tiphaneau, P.; Wöppelmann, G. Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob. Planet. Chang. 2012, 98, 6–17. [Google Scholar] [CrossRef]
- Ostanciaux, É.; Husson, L.; Choblet, G.; Robin, C.; Pedoja, K. Present-day trends of vertical ground motion along the coast lines. Earth-Sci. Rev. 2012, 110, 74–92. [Google Scholar] [CrossRef]
- Pfeffer, J.; Allemand, P. The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet. Sci. Lett. 2016, 439, 39–47. [Google Scholar] [CrossRef]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Lambeck, K.; Smither, C.; Johnston, P. Sea-level change, glacial rebound and mantle viscosity for northern Europe. Geophys. J. Int. 1998, 134, 102–144. [Google Scholar] [CrossRef]
- O’Dea, A.; Lessios, H.A.; Coates, A.G.; Eytan, R.I.; Restrepo-Moreno, S.A.; Cione, A.L.; Collins, L.S.; de Queiroz, A.; Farris, D.W.; Norris, R.D.; et al. Formation of the Isthmus of Panama. Sci. Adv. 2016, 2, e1600883. [Google Scholar] [CrossRef] [PubMed]
- Phien-Wej, N.; Giao, P.H.; Nutalaya, P. Land subsidence in Bangkok, Thailand. Eng. Geol. 2006, 82, 187–201. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Nerem, R.S.; Hamlington, B. Is the detection of accelerated sea level rise imminent? Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Minobe, S. Resonance in bidecadal and pentadecadal climate oscillations over the North Pacific: Role in climatic regime shifts. Geophys. Res. Lett. 1999, 26, 855–858. [Google Scholar] [CrossRef]
- Sturges, W.; Douglas, B.C. Wind effects on estimates of sea level rise. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Multidecadal sea level and gyre circulation variability in the northwestern tropical Pacific Ocean. J. Phys. Oceanogr. 2012, 42, 193–206. [Google Scholar] [CrossRef]
- Chambers, D.P.; Merrifield, M.A.; Nerem, R.S. Is there a 60-year oscillation in global mean sea level? Geophys. Res. Oceans 2012, 39, 39. [Google Scholar] [CrossRef]
- Calafat, F.; Chambers, D. Quantifying recent acceleration in sea level unrelated to internal climate variability. Geophys. Res. Lett. 2013, 40, 3661–3666. [Google Scholar] [CrossRef]
- Houston, J.R.; Dean, R.G. Effects of sea-level decadal variability on acceleration and trend difference. J. Coast. Res. 2013, 29, 1062–1072. [Google Scholar] [CrossRef]
- Richter-Menge, J.; Overland, J.E.; Mathis, J.T. (Eds.) Arctic Report Card. 2016. Available online: http://www.arctic.noaa.gov/Report-Card (accessed on 25 May 2017).
- Provisional World Meteorological Organization Statement on the Status of the Global Climate in 2016. Press Release No. 15, Published 14 November 2016. Available online: https://public.wmo.int/en/media/press-release/provisional-wmo-statement-status-of-global-climate-2016 (accessed on 6 May 2017).
- IOC-UNESCO and UNEP. Open Ocean: Status and Trends, Summary for Policy Makers; United Nations Environment Programme (UNEP): Nairobi, Kenya, 2016.
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Wuebbles, D.J.; Fahey, D.W.; Hibbard, K.A.; Dokken, D.J.; Stewart, B.C.; Maycock, T.K. (Eds.) Climate Science Special Report: Fourth National Climate Assessment; U.S. Global Change Research Program: Washington, DC, USA, 2017. [Google Scholar]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future coastal population growth and exposure to sea-level rise and coastal flooding-a global assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [PubMed]
- Watkiss, P. The ClimateCost Project. Final Report, Volume 1: Europe; Stockholm Environmental Institute: Stockholm, Sweden, 2011; ISBN 978-91-86125-35-6. [Google Scholar]
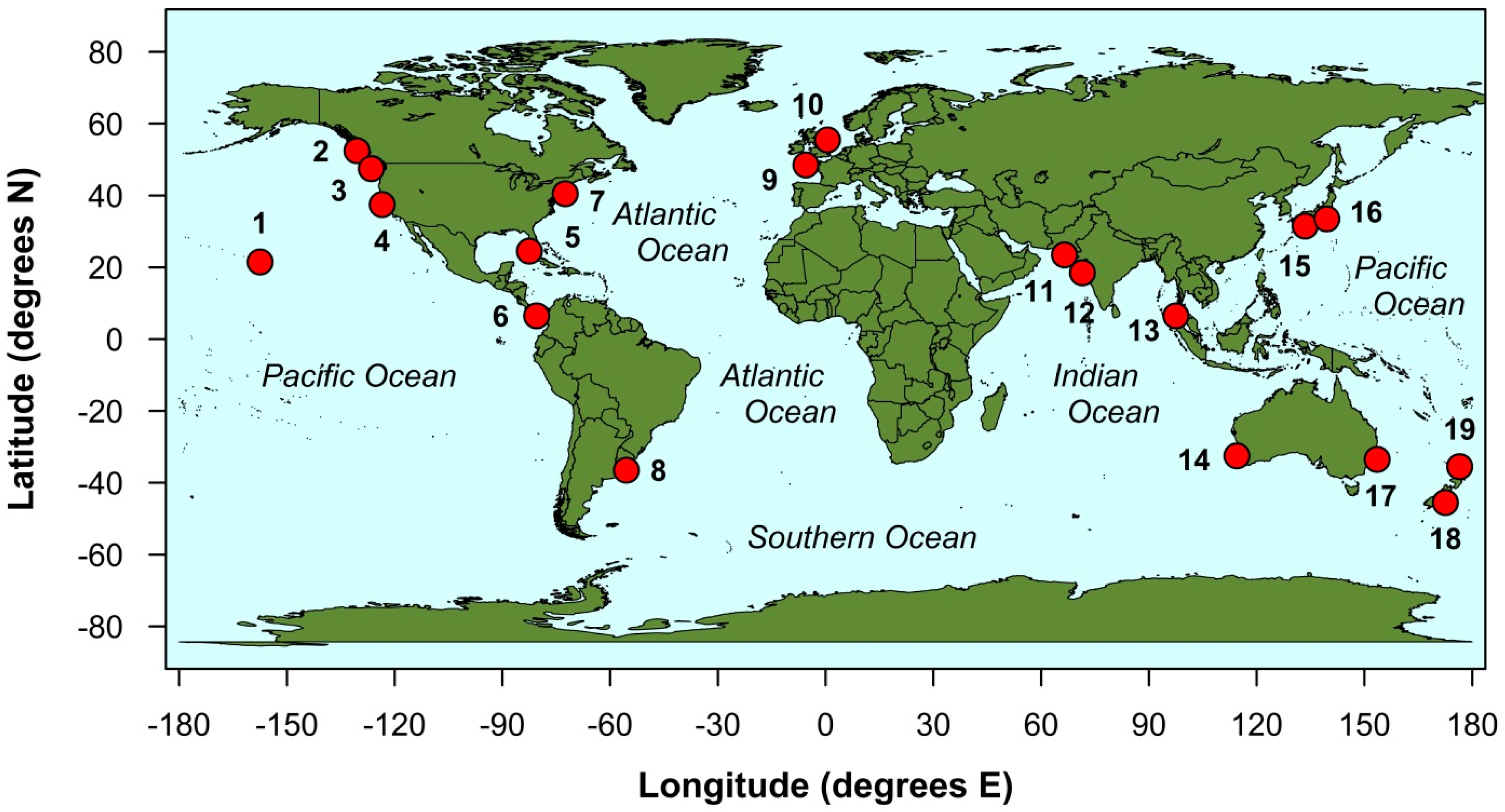
| Station ID 1 | Tide Gauge Record 2 | Start (year) 2 | End (year) 2 | AR5 Lat (° N) 5 | AR5 Long (° E) 5 | Altimetry Lat (° N) 6 | Altimetry Lat (° E) 6 |
|---|---|---|---|---|---|---|---|
| 1 | Honolulu 3 | 1891 | 2016 | 21.5 | 202.5 | 21.125 | 202.125 |
| 2 | Prince Rupert 3 | 1903 | 2016 | 52.5 | 229.5 | 54.125 | 228.875 |
| 3 | Seattle | 1899 | 2016 | 47.5 | 233.5 | 47.375 | 235.125 |
| 4 | San Francisco 3 | 1855 | 2016 | 37.5 | 236.5 | 37.625 | 237.375 |
| 5 | Key West | 1913 | 2016 | 24.5 | 277.5 | 24.375 | 278.125 |
| 6 | Balboa | 1908 | 2016 | 6.5 | 279.5 | 8.875 | 280.625 |
| 7 | New York 3 | 1853 | 2016 | 39.5 | 287.5 | 40.375 | 286.125 |
| 8 | Buenos Aires 3,4 | 1905 | 2016 | −36.5 | 304.5 | −34.625 | 301.625 |
| 9 | Brest | 1807 | 2016 | 48.5 | 354.5 | 48.125 | 355.375 |
| 10 | North Shields 3 | 1895 | 2016 | 55.5 | 0.5 | 54.875 | 358.875 |
| 11 | Karachi | 1868 | 2014 | 23.5 | 66.5 | 24.625 | 66.875 |
| 12 | Mumbai | 1878 | 2012 | 18.5 | 71.5 | 18.875 | 72.675 |
| 13 | Ko Taphao Noi | 1940 | 2016 | 7.5 | 96.5 | 7.625 | 98.375 |
| 14 | Fremantle | 1897 | 2016 | −32.5 | 114.5 | −32.125 | 115.625 |
| 15 | Hosojima | 1930 | 2016 | 31.5 | 133.5 | 32.375 | 131.875 |
| 16 | Aburatsubo | 1930 | 2016 | 33.5 | 139.5 | 31.625 | 131.625 |
| 17 | Sydney | 1886 | 2016 | −33.5 | 153.5 | −33.875 | 151.375 |
| 18 | Dunedin 3 | 1900 | 2016 | −45.5 | 172.5 | −46.125 | 170.375 |
| 19 | Auckland | 1899 | 2016 | −35.5 | 176.5 | −36.675 | 174.875 |
| Station ID 1 | Site | Peltier GIA 3 (mm/Year) | AR5 GIA 2,4 (mm/Year) | Type 1 VLM 2,5 (mm/Year) | Type 2 VLM 2,6 (mm/Year) | Type 3 VLM 2,7 (mm/Year) |
|---|---|---|---|---|---|---|
| 1 | Honolulu | −0.17 | 0.23 ± 0.07 | −0.23 ± 0.18 | −0.84 ± 0.52 | 0.30 ± 0.31 |
| 2 | Prince Rupert | 0.33 | 0.64 ± 0.51 | NA | 0.56 ± 1.17 | −2.10 ± 0.93 |
| 3 | Seattle | −1.10 | −0.99 ± 0.59 | −0.99 ± 0.22 | −0.27 ± 0.75 | −0.99 ± 0.65 |
| 4 | San Francisco | −1.00 | −0.73 ± 0.61 | −0.04 ± 0.15 | 0.37 ± 0.64 | 0.27 ± 0.86 |
| 5 | Key West | −0.75 | −0.65 ± 0.52 | −1.76 ± 0.43 | −1.23 ± 0.92 | −1.18 ± 0.66 |
| 6 | Balboa | −0.26 | 0.04 ± 0.08 | NA | 7.55 ± 1.93 | 1.89 ± 1.85 |
| 7 | New York | −1.80 | −1.39 ± 0.43 | −2.12 ± 0.62 | 0.96 ± 1.37 | −1.95 ± 0.89 |
| 8 | Buenos Aires | 0.70 | 0.29 ± 0.16 | 1.03 ± 0.24 | 0.84 ± 1.80 | NA |
| 9 | Brest | −0.60 | −0.48 ± 0.12 | 0.01 ± 0.11 | −0.64 ± 0.85 | −1.60 ± 0.59 |
| 10 | North Shields | 0.11 | 0.10 ± 0.27 | 1.39 ± 0.67 | 0.46 ± 0.75 | −0.72 ± 0.61 |
| 11 | Karachi | 0.33 | 0.06 ± 0.17 | NA | −2.53 ± 0.44 | NA |
| 12 | Mumbai | 0.31 | 0.14 ± 0.18 | NA | 0.61 ± 2.17 | NA |
| 13 | Ko Taphao Noi | 0.16 | 0.13 ± 0.10 | NA | −9.51 ± 2.40 | −3.12 ± 1.83 |
| 14 | Fremantle | −0.33 | 0.07 ± 0.01 | NA | −0.30 ± 0.66 | −0.76 ± 0.71 |
| 15 | Hosojima | 0.43 | 0.26 ± 0.11 | NA | 1.33 ± 0.59 | 0.59 ± 0.79 |
| 16 | Aburatsubo | 0.47 | 0.31 ± 0.10 | NA | −1.48 ± 1.29 | −2.58 ± 0.67 |
| 17 | Sydney | −0.23 | 0.02 ± 0.06 | −0.33 ± 0.25 | −1.27 ± 0.98 | 2.12 ± 0.75 |
| 18 | Dunedin | −0.02 | 0.20 ± 0.04 | −1.02 ± 0.12 | −1.53 ± 0.61 | 0.46 ± 0.47 |
| 19 | Auckland | 0.03 | 0.17 ± 0.01 | −0.62 ± 0.23 | −1.24 ± 0.80 | NA |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watson, P.J. How Well Do AR5 Sea Surface-Height Model Projections Match Observational Rates of Sea-Level Rise at the Regional Scale? J. Mar. Sci. Eng. 2018, 6, 11. https://doi.org/10.3390/jmse6010011
Watson PJ. How Well Do AR5 Sea Surface-Height Model Projections Match Observational Rates of Sea-Level Rise at the Regional Scale? Journal of Marine Science and Engineering. 2018; 6(1):11. https://doi.org/10.3390/jmse6010011
Chicago/Turabian StyleWatson, Phil J. 2018. "How Well Do AR5 Sea Surface-Height Model Projections Match Observational Rates of Sea-Level Rise at the Regional Scale?" Journal of Marine Science and Engineering 6, no. 1: 11. https://doi.org/10.3390/jmse6010011
APA StyleWatson, P. J. (2018). How Well Do AR5 Sea Surface-Height Model Projections Match Observational Rates of Sea-Level Rise at the Regional Scale? Journal of Marine Science and Engineering, 6(1), 11. https://doi.org/10.3390/jmse6010011





