1. Introduction
Experiments show that propeller-driven wakes evolve from a complicated near wake with discernible propeller-blade features, to a far wake, in which these features have mixed together to form a nearly-axisymmetric field [
1,
2]. Sirviente and Patel [
3] show that the near-wake region transitions to the far wake in roughly twelve initial wake diameters, but the development of the far wake can be delayed by appendages on the body [
4]. This transition is influenced by the Reynolds number, body geometry, and operation of the propulsor [
5], which itself has a large impact on the ingested stern boundary layer and downstream turbulence [
6,
7]. The swirling propeller induces helical vortices that are shed from the roots and tips of the individual blades. In the near wake, these vortices break down, which is a topic of extensive study [
8]. Although experiments show the contribution of swirl [
9], its role in the evolution from near to far wake is not well-characterized.
In a stratified wake, a mixed patch is formed by swirl from the propeller, turbulent mixing, and potential effects from the upstream body [
10]. This mixed patch can further modify the far wake in the event of a mixed-patch collapse when buoyancy forces are large [
11,
12,
13,
14]. Numerous experiments have explored the interaction between stratification and wake evolution with close observation to the generation of internal gravity waves and coherent structures [
15,
16]. Direct Numerical Simulation (DNS) provides further insight into the physics of the flow, particularly with its turbulence properties [
17,
18]. Background turbulence increases the turbulent kinetic energy and energy transfer in the wake, which in turn lowers the mean velocity and increases horizontal spreading [
19]. Excess momentum leads to changes in increased turbulent kinetic energy and qualitative changes in the wake dynamics, particularly in downstream vortical structures [
20]. High levels of stratification in the wake create a non-equilibrium region in which the mean velocity decay is reduced [
21,
22]. By reducing the level of potential energy in the near wake thermal-haline distribution, the effects of buoyancy in the far wake can be reduced.
Originally studied as a disc-with-center-jet [
23] and later with self-propelled axisymmetric bodies [
24,
25], the net-zero-momentum wake functions as a theoretical model of a self-propelled marine vehicle. Beyond experiment, the study of self-propelled wakes includes several numerical methods. Ordered by increasing fidelity and computational expense, these methods include [
26]: panel/lattice methods, actuator models, and fully resolved rotating geometry. Generalized actuator models include the Actuator Disk (AD), Actuator Line (AL), and Actuator Surface (AS) models. Each of these models imposes a body force over a volume in a Computational Fluid Dynamics (CFD) simulation to simulate the effects of a propeller on the surrounding fluid. Although a fully resolved propeller may offer more fidelity, its computational requirements are often large, so an actuator model provides a cost-effective alternative [
27].
In a self-propelled near wake, the mixed-patch structure and overall potential energy depend largely on the propulsor. A single propeller will mix fluid unopposed within the swirling region of the wake. Contra-rotating propellers of equivalent thrust will modify the initial swirl profile thereby changing the shape of the downstream mixed patch and reducing its potential energy. Contra-rotating propeller blades add additional complexity to the interaction between root and tip vortices and reduce the swirling kinetic energy of the wake. These influences on the near wake may be compared to the simplified case of a zero-swirl, jet-propelled configuration with uniform-velocity, which results in the smallest generation of the potential energy in the wake.
The present study is an extension of Jones and Paterson [
28]. The unsteady Reynolds-Averaged Navier–Stokes (URANS) equations are solved to examine the near-wake evolution of the stratified, turbulent, net-zero-momentum propeller wake of the axisymmetric Iowa Body using three different propulsion schemes: single propeller, dual contra-rotating propellers (CRP), and a zero-swirl, uniform-velocity jet. The propellers are simulated using the AL model. The Iowa Body hull geometry is chosen for comparison to the non-stratified experiment by Hyun and Patel [
2], which is the only known experiment to have phase-averaged propeller data for a self-propelled axisymmetric body. The authors have previously shown good agreement to this experiment for towed and self-propelled configurations [
27]. Flow visualization reveals the interaction between propeller-root and tip vortices and the additional complexity introduced by CRP. Comparison between instantaneous and time-averaged cross-plane profiles demonstrates the transition from near- to far-wake regions. Circumferentially-averaged profiles of velocity reveal the evolution of momentum, with observations drawn in comparison to the theoretical disc-with-center-jet that is often used in far-wake simulations [
11]. Mixed-patch velocity and temperature-deviation cross-plane profiles show the structure of kinetic and potential energy in the developed wake. Finally, the relative growth, decay, or persistence of integrated kinetic and potential energy of each propulsion scheme is considered. Compared to the single-propeller configuration, the CRP configuration is more effective at reducing potential and swirling kinetic energy in the wake, with potential energy reductions similar to that of the zero-swirl jet.
2. Approach
2.1. Governing Equations
This fluid-flow problem is defined by the unsteady Reynolds-averaged Navier–Stokes (RANS) equations in Boussinesq form with an additional body force term
to account for the propeller model.
The equations are written in terms of the non-inertial velocity . In the equations, t is time, is the kinematic viscosity, and is density. The density is expressed as , where is a reference value and is the deviation from that value. The gravitational vector points downward in the negative z direction, where z is the upward-positive, vertical position. This formulation includes the piezometric pressure, where g is the magnitude of the gravitational vector.
The governing equations are solved using a custom solver written with the CFD framework OpenFOAM. This custom solver takes into account salinity and temperature transport and the corresponding turbulent fluctuations. The transport of temperature
T and salinity
S in the stratified environment are determined through the following equations with the diffusion coefficients
and
.
The Reynolds stresses
and turbulent fluxes
and
are determined using a linear eddy-viscosity closure model.
In these equations,
is the eddy viscosity,
is the mean rate of strain, and
k is the turbulent kinetic energy. For this study, the
turbulence model is chosen to compute
due to its ease of implementation and relative advantage in computing the attached flow over a body [
29]. Production terms in the
equations are modified to include buoyancy effects, but in the near wake they are small in comparison to the production due to shear. Wall functions are used in the computation of
k and specific turbulence dissipation
at wall boundaries to relax mesh requirements near the hull in the high Reynolds-number flow.
Density is computed by solving the UNESCO seawater equation of state [
30]. For the given problem, it is appropriate to approximate the secant bulk modulus as constant at sea-level conditions, even though it is a function of salinity, temperature, and pressure. Thus, the secant bulk modulus is
where
is atmospheric pressure. Additionally, substituting the hydrostatic pressure for the total pressure, the equation of state becomes,
where
,
,
and
terms are empirical coefficients given in
Table 1. Because the environment in the present study is isohaline, only changes in temperature from the thermally-stratified background affect changes in density.
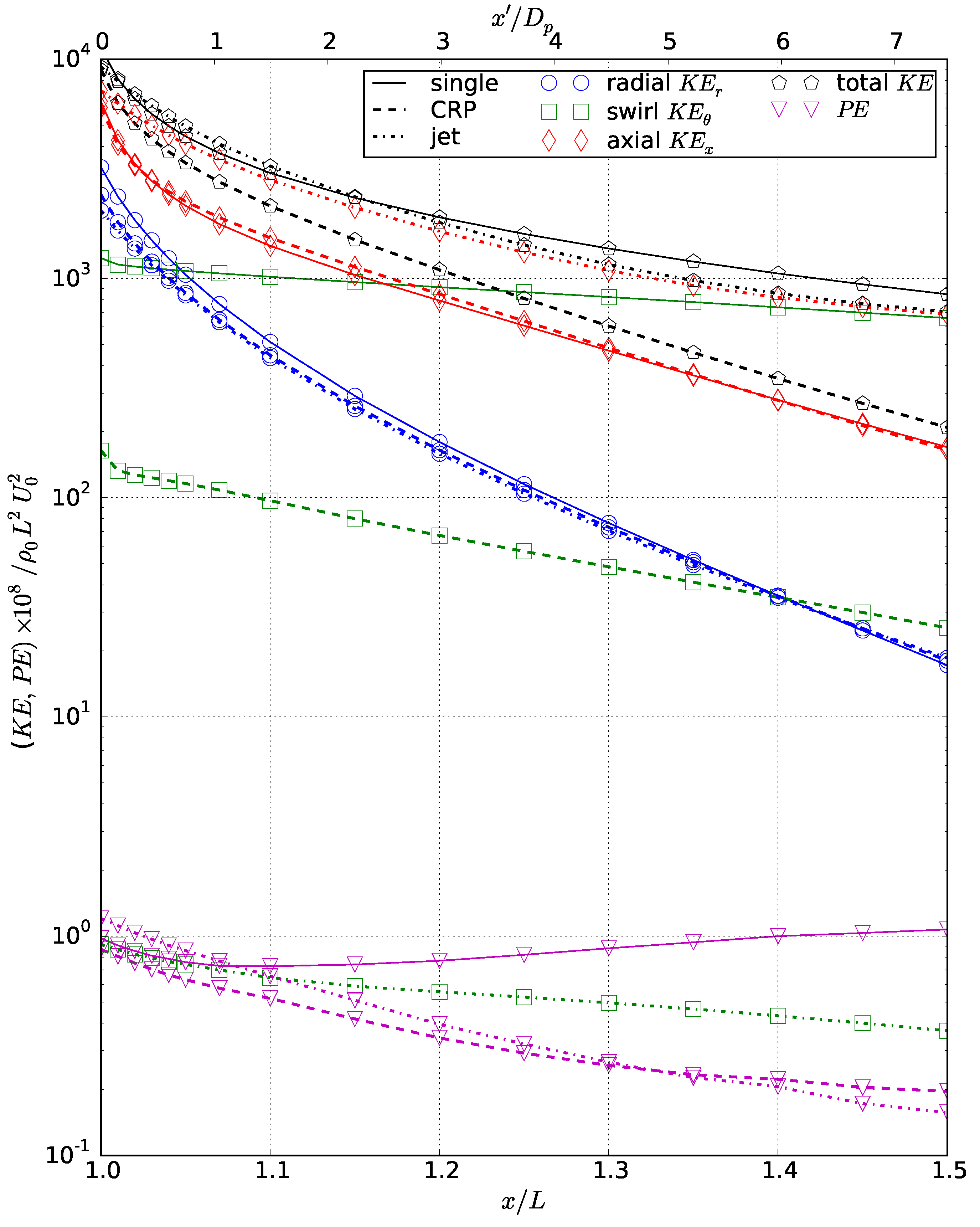
2.2. Kinetic and Potential Energy
The evolution and transfer of energy in the wake is examined in the form of kinetic and potential energy defined as,
The per-unit-volume energy
, and
may be integrated over an axial slice of area
A in the wake to find energy per-unit-length,
and
, as functions of downstream distance. Kinetic energy is computed for the magnitude of velocity and also individually for each component of velocity in cylindrical coordinates. The potential energy per-unit-volume pe follows the formulation of Holliday and McIntyre [
31].
2.3. Actuator-Line Model
The unsteady propeller for each non-BOR hull form is simulated using an AL model from the Simulator fOr Wind Farm Applications (SOWFA) library [
32]. The AL model projects a distributed line of force
in the place of each propeller blade,
where
is the actuator element force composed of contributions from lift
and drag
. The distance between CFD cell center and actuator point is
r, and
controls the Gaussian width. This function decays to 1% of its maximum value when
. If
is too small, numerical oscillations arise, and if
is too large, the applied body forces will be smoothed considerably. Troldborg [
33] recommends
where
is the grid spacing at the actuator position. Martınez et al. [
34] developed best practices for AL modeling and suggested
. For the present study,
was selected because it eliminated the numerical instabilities that arose when
was assigned. The Cartesian-mesh region of the propeller was refined to a resolution such that,
, where
is the width of each hydrofoil section. Martınez et al. [
34] suggests a value smaller than 0.75. Lift and drag at each section are computed from a lookup table of lift and drag coefficients
and
as functions of
,
where
is the density,
is the local flow speed,
c is the chord and
w is the width of the actuator section. The relationship between
and
with
must be predetermined from experiment, simulation, or theory for each hydrofoil section.
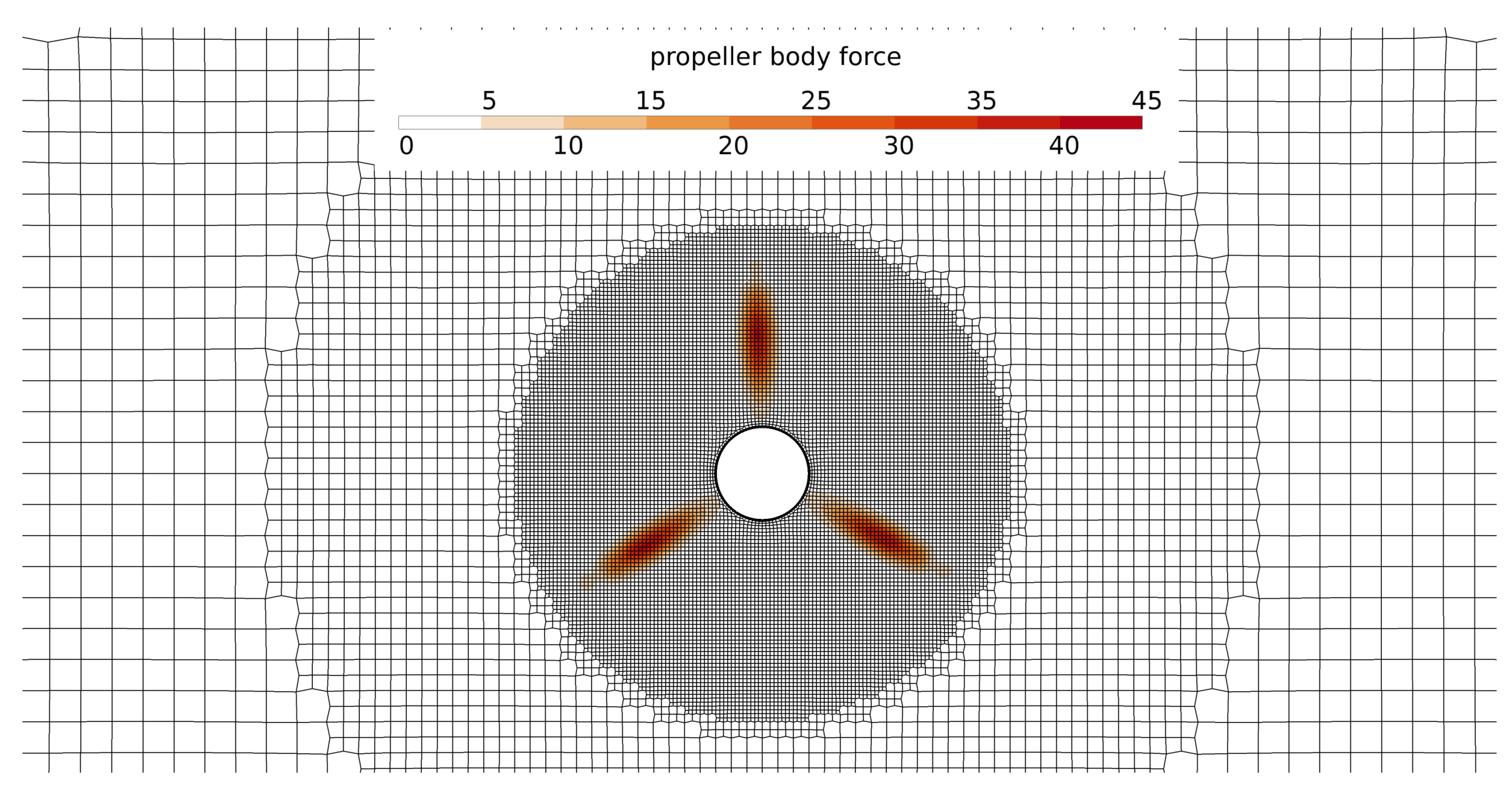
Figure 1 shows the magnitude of the projected propeller body force
on the AL propeller plane of the single-propeller case, where
is the propeller radius and rps is the propeller rotations per second.
2.4. Iowa Body
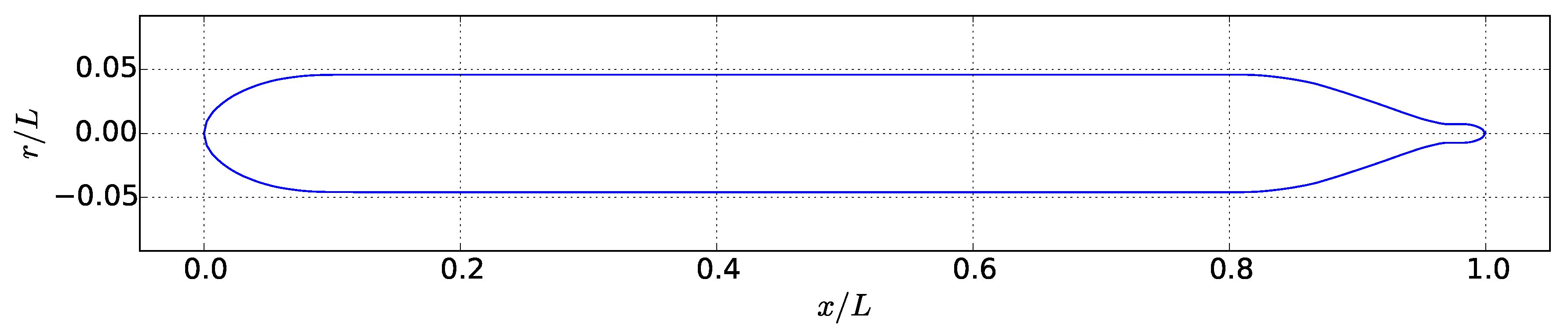
The axisymmetric Iowa Body, described in the experiment by Hyun and Patel [
2], is shown in
Figure 2 for the standard, single-propeller case. This geometry is representative of a typical marine vehicle without appendages. Features of this geometry are listed in
Table 2 where
L is the body length,
D is the body diameter,
is the propeller diameter, and
is the hub diameter.
Minor modifications are made to the Iowa Body hull for the CRP and jet configurations. For the CRP configuration, the hub is extended by the length of the rotating portion so that a second propeller may be placed directly downstream of the first. For the jet configuration, the hub is truncated at the propeller plane to function as an exhaust port. In effect, the zero-swirl, uniform-velocity jet exhausts with an initial diameter of .
2.5. Iowa Body Propeller
The Iowa Body propeller is defined by 36 discrete sections to account for variations in radial propeller-blade geometry. Sectional lift
is computed using the analytic expression of Brockett [
35] for the NACA 66-Modified foil,
where
is the local flow angle of attack,
is the maximum thickness ratio, and
f is the maximum camber ratio. Sectional drag
is imposed by combining viscous and induced drag at each section,
where
is the viscous drag,
e is the efficiency factor, and
is the aspect ratio.
For the present unsteady simulations,
at each section of the propeller blades remains below
at every instant in time. Because
remains small, these analytic expressions do not require additional conditions for stall. Pitch, chord, thickness, and camber distributions for the Iowa Body propeller blade are tabulated in Hyun [
1]. The Iowa Body propeller has zero rake and zero skew.
2.6. Computational Mesh
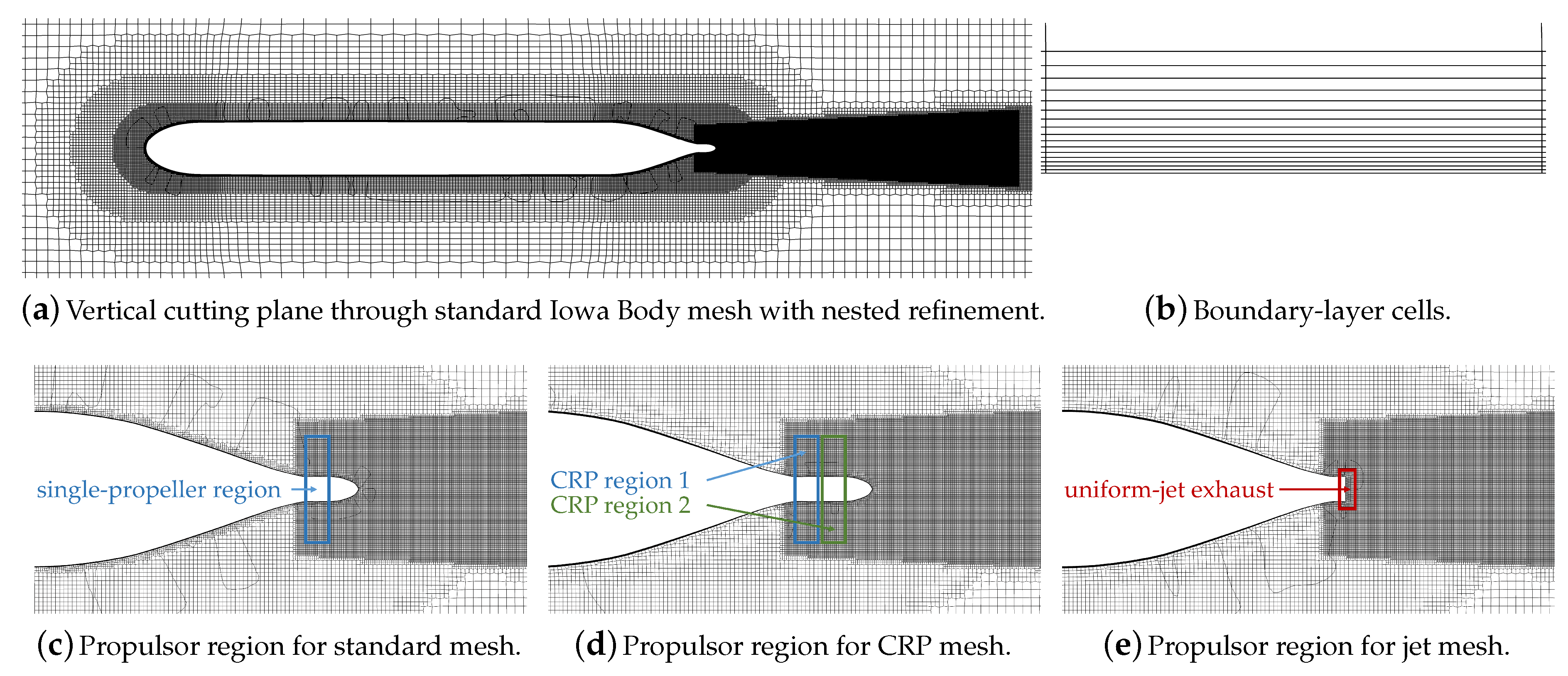
The three computational meshes were generated using the software
cfMesh [
36]. Cells are focused near the body, the propulsor region, and in the wake. The hull is located at a depth of one body length. The inlet, outlet, and far-field boundaries are located two body lengths away from the hull. Comparison to simulations from spatially-larger meshes showed that the boundaries of the computational domain did not affect the solution. Mesh design and quality features are listed in
Table 3. Because wall functions are used in the computation of turbulence variables, the dimensionless wall distance requirement of
can capture the boundary layer effects and the viscous drag of the hull even for boundary cells where
. A grid-refinement study of the propeller- and wake-region cells showed that 100 cells/
adequately resolved the AL model and downstream wake cross-plane profiles. These meshes are also visualized in
Figure 3. Cutting planes reveal the distribution of cells surrounding the hull and in the wake region. Views of the propulsor region show how the mesh is modified for each configuration. A single AL-modeled propeller is implemented within the highlighted region for the single-propeller case. For the CRP configuration, the hub is extended with one AL-modeled propeller placed behind the first. There is no AL model for the jet configuration since there is no propeller. Instead, fluid is exhausted from the truncated hub.
2.7. Numerical Methods
The Navier–Stokes unsteady mass and momentum equations are solved using the Pressure-Implicit with Splitting of Operators (PISO) method [
37]. This segregated approach decouples operations on pressure and velocity variables. At each time step, the following procedure is followed in the customized OpenFOAM solver. First, the momentum equations are solved to provide velocity by using pressure from the previous time step. Next, the pressure-Poisson equation is solved iteratively with corrections to velocity to conserve mass. Three inner iterations are are used in the present study, each with an additional mesh non-orthogonality correction step. After completion of these inner iterations, turbulence quantities are solved for, followed by salinity and temperature. The time step is then advanced.
Implicit, second-order, backward differencing is used in temporal discretization, while the cell-centered finite volume method is used in spatial discretization. A second-order, linear-upwind scheme is applied to the advective term of the momentum equations. A first-order, upwind scheme is applied to turbulence quantities, and a second-order, linear scheme is applied to all other divergence terms. Laplacian terms are discretized using a second-order, linear scheme that is partially-limited to correct for mesh non-orthogonality.
Two iterative methods are employed to solve the resulting systems of algebraic equations. The pressure equation is solved using the Preconditioned Conjugate Gradient (PCG) method with a residual tolerance of . The momentum, scalar transport, and turbulence equations are solved using the Pre-Conditioned Bi-Conjugate Gradient (PBiCG) scheme with a residual tolerance of .
2.8. Initial and Boundary Conditions
Several boundary conditions are employed. Velocity at the inlet is set to the freestream velocity through a Dirichlet boundary condition. The no-slip condition is set on the hull boundary, and the slip condition is set in the far field. Zero-gradient conditions are specified for velocity and pressure in the outlet. Background turbulence values of k and are computed assuming a turbulence intensity of 1% and eddy viscosity ratio of 100. Turbulence variables on the hull boundary are computed with wall functions. Other variables satisfy the zero-gradient Neumann boundary condition.
Initial conditions for pressure and velocity are computed by solving the potential flow equations. The PISO algorithm is then used in the transient simulation. Distributed body forces from the propeller-blades rotate at each time step at the propeller’s rotation rate. The simulation is then run until initial-transient flow features advect far downstream and a periodic wake flow field is found.
2.9. Flow Field Analysis
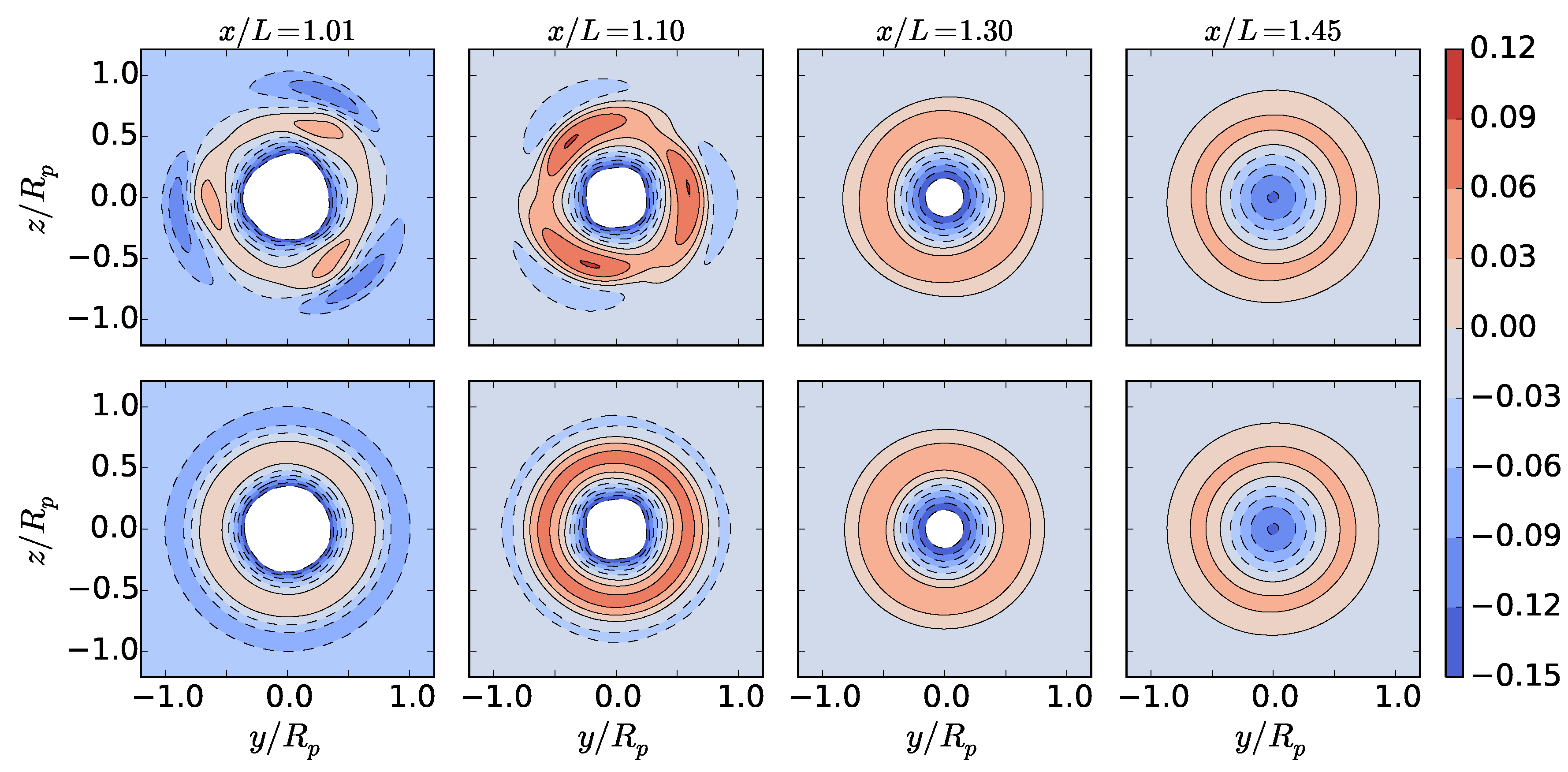
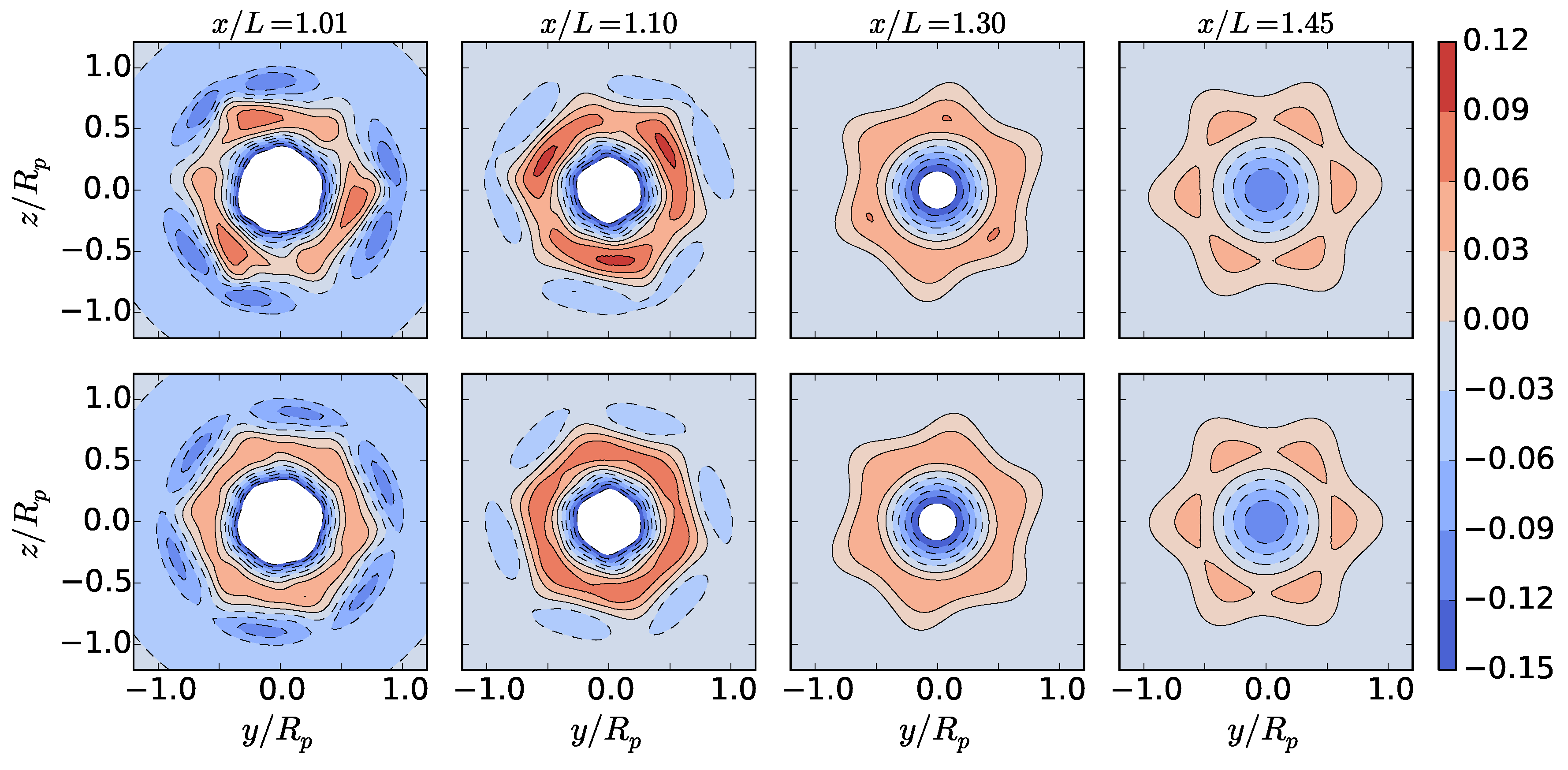
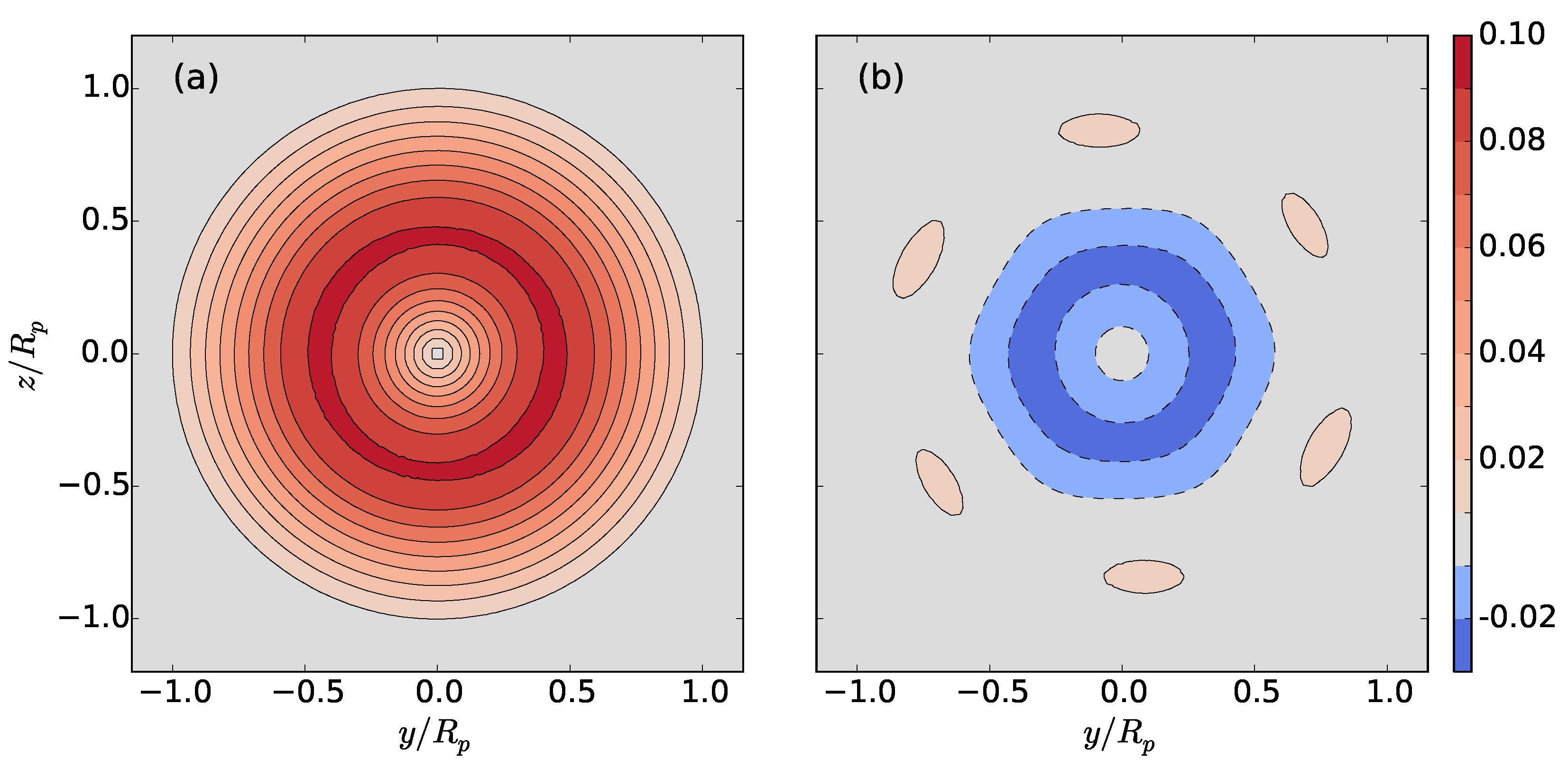
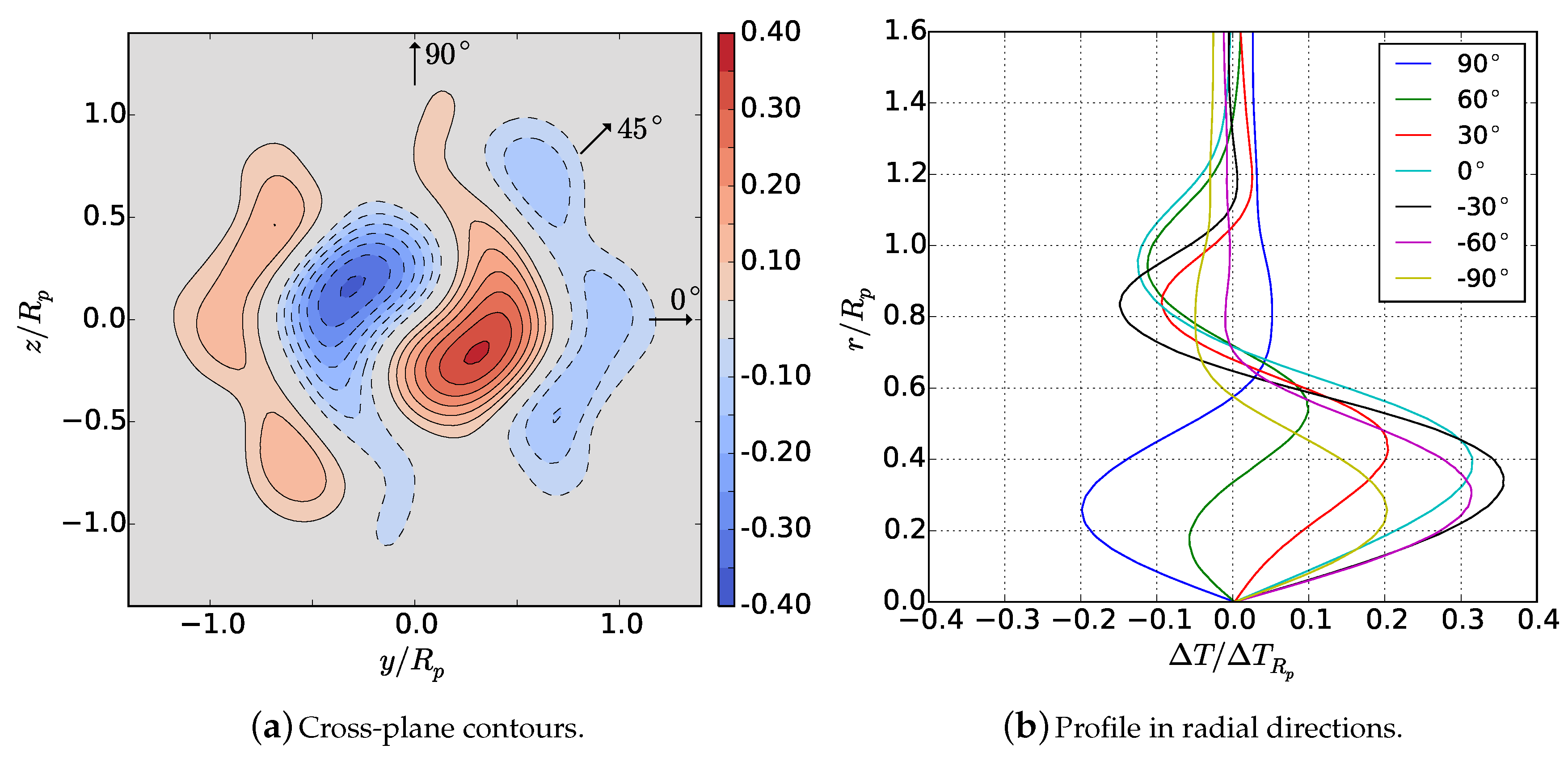
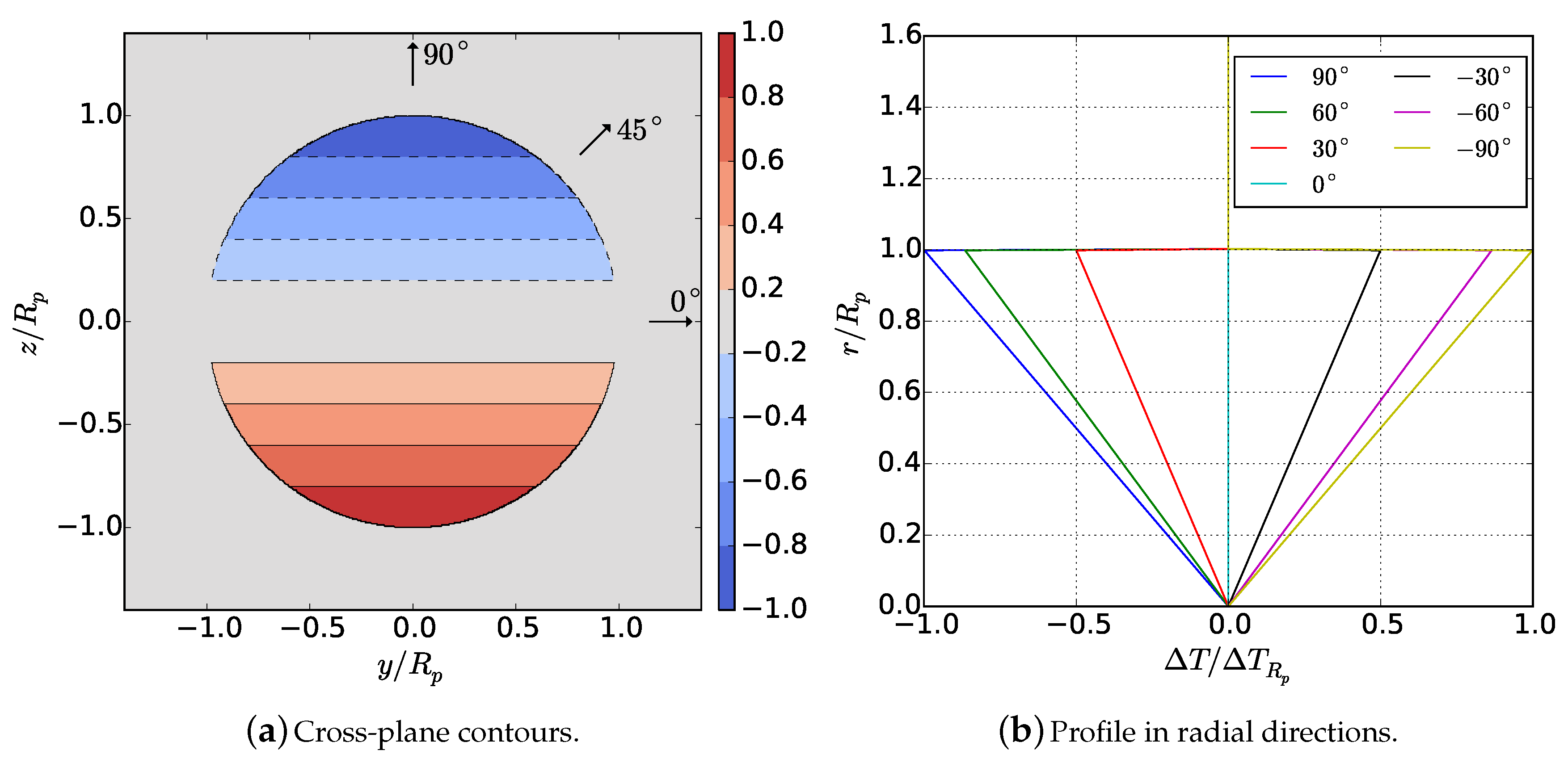
This study examines primary flow variables including: deviation of temperature from the background and the axial, radial, and azimuthal velocities , , and , respectively. The second invariant of the velocity gradient tensor Q is computed to visualize vortical structures. The cross-plane-integrated kinetic and potential energies are examined, where the kinetic energy is considered exclusively for each of the three components of velocity , , and . Data are extracted in axial planes within where x is the downstream distance from the bow of the body and L is the body length.
2.10. Flow Coefficients and Case Studies
Several of the important flow coefficients for this propeller-driven flow are the Reynolds number
, advance ratio
J, thrust coefficient
, and torque coefficient
. An alternate expression for the thrust coefficient
is computed for comparison to the jet configuration.
For these expressions,
is the freestream velocity,
is kinematic viscosity,
is the diameter of the propeller,
R is the radius of the Iowa Body,
n is the propeller speed in revolutions per second,
is the thrust, and
is the torque. The thrust-to-drag ratio is
. The Reynolds number for this study is
, a typical operating condition in the ocean. Other coefficients are listed in
Table 4. The fore and aft propellers are listed individually for the CRP case, and total thrust is equivalent for all cases.
The Froude number
provides a measure of the density stratification, where an infinite
means zero stratification, and a small
means high levels of stratification. The present study considers a linearly varying temperature stratification, typical of an ocean environment, with a Froude number of
, where,
In these expressions
N is the Brunt Väisälä frequency,
g is acceleration due to gravity, and
z is the vertical coordinate. The influence of buoyancy on the near-wake fluid dynamics is often small and can be quantified by the Richardson number
, which is the ratio of buoyancy to flow gradient terms [
15].
where
is a reference temperature,
is the mean temperature, and
is the mean velocity. For the single-propeller case,
which indicates that the near-wake inertial forces of the propeller dominate the buoyancy forces. As the local velocity
decays,
increases and buoyancy forces become important further downstream in the far wake, beyond the geometric bounds of these simulations.
4. Conclusions
The influence of swirl on the evolution of self-propelled, stratified near wakes and the development of the mixed patch has not previously been well-characterized. In this study, the linearly stratified near wake of the Iowa body was investigated with three separate propulsor configurations: single propeller, contra-rotating propellers, and a zero-swirl, uniform-velocity jet. Unsteady, rotating propeller blades were simulated using an AL model in a URANS computation. Comparison between the configurations revealed unique differences in the evolution of the near wake.
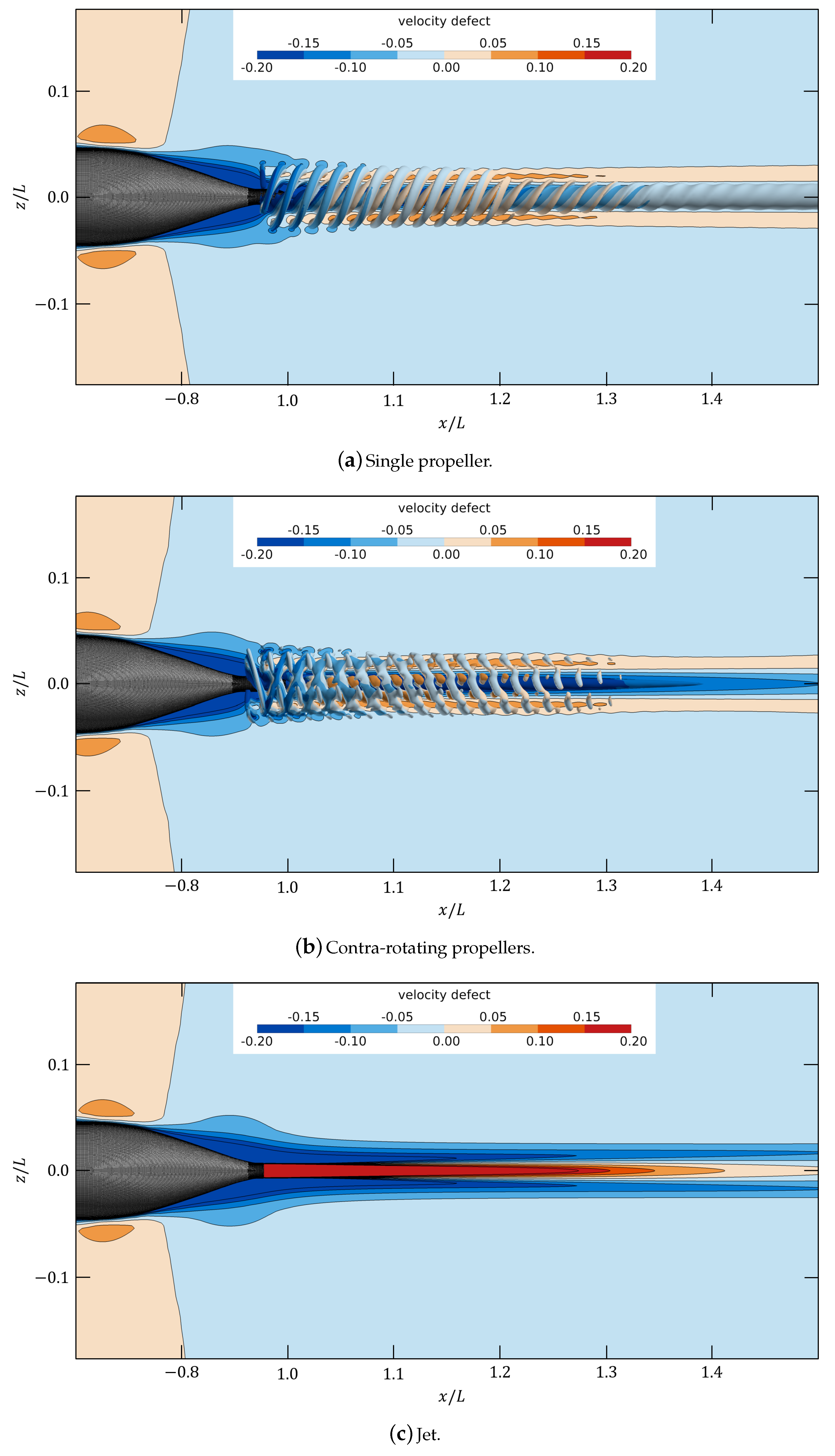
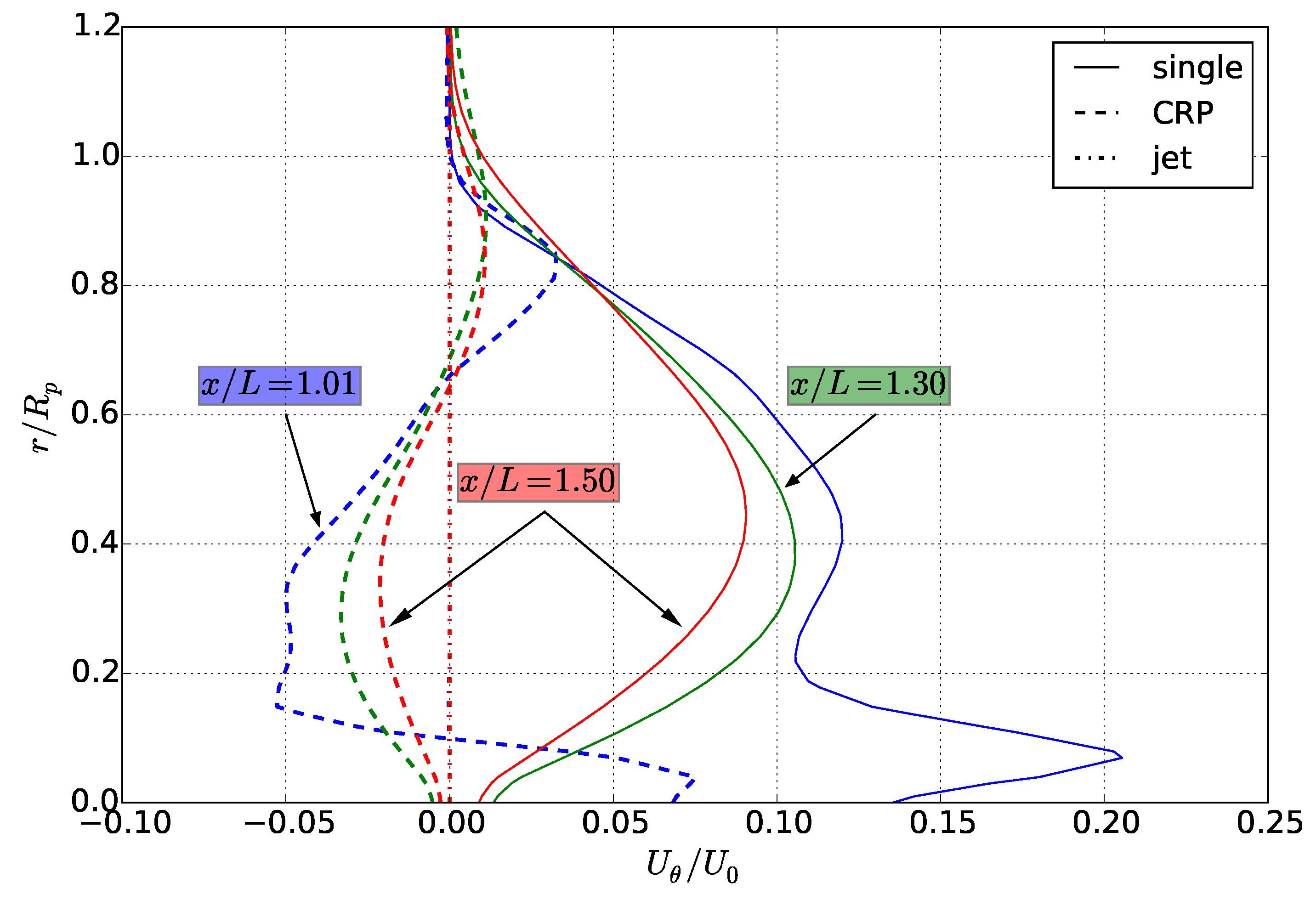
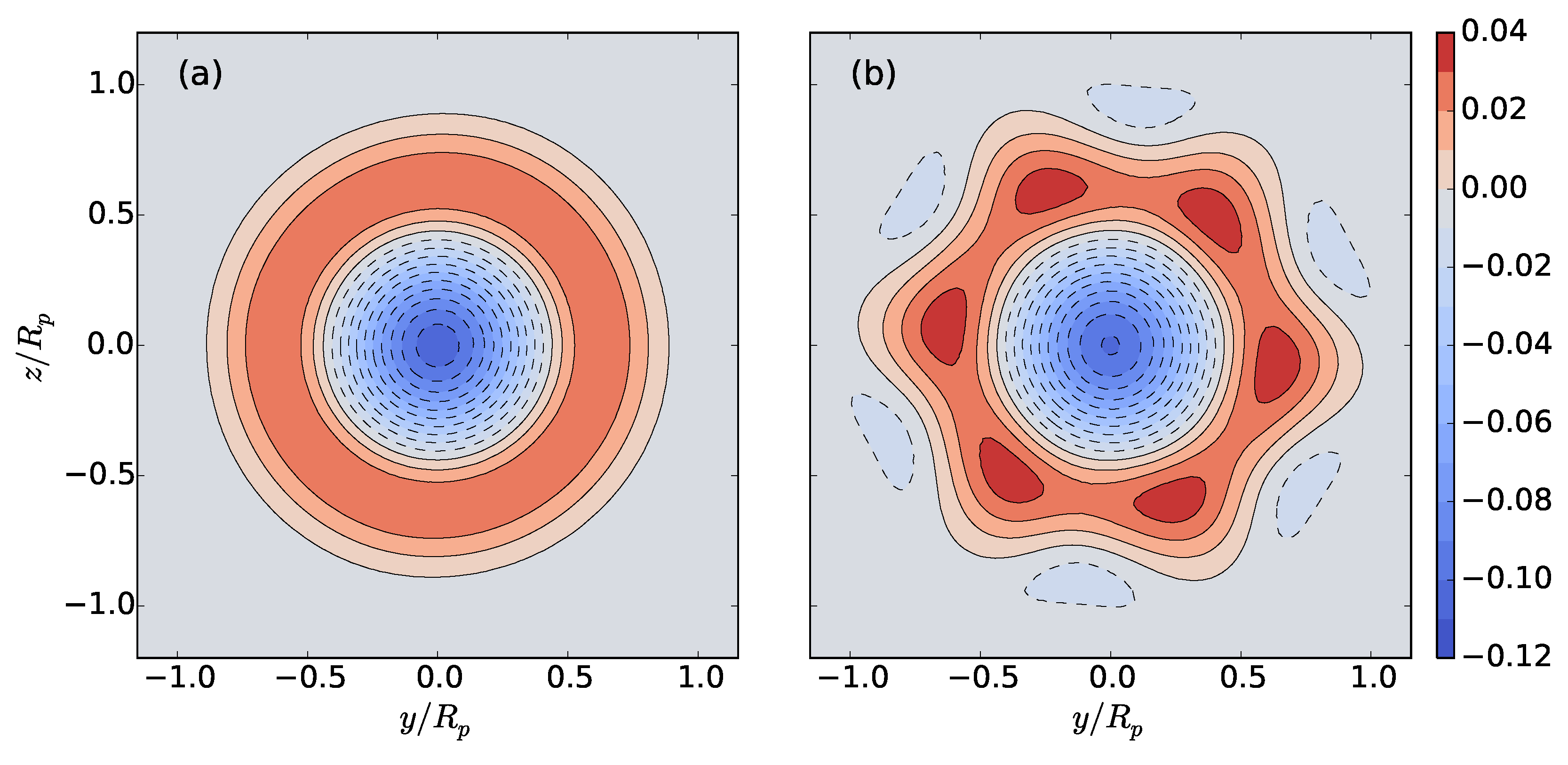
While clear root and tip vortices were visible in the single-propeller case, the CRP disrupted these structures, introducing additional complexity in the wake evolution. Nevertheless, by half of a body length downstream, the wake flow fields were steady in time. The single-propeller and CRP cases shared similar circumferentially-averaged axial velocity defect profiles due to similar spanwise loading in the propulsor. Swirl velocity, however, varied between the two propeller-driven cases, with the CRP introducing both positive and negative swirl regions exhibiting half of the magnitude of the single-propeller case. Furthermore, by half of a body length downstream, the magnitude of the temperature deviation for the CRP was less than half of that of the single propeller. The jet magnitude was the smallest, due to the absence of swirl. Contour maps of velocity revealed that the single propeller has an axisymmetric profile, whereas the CRP exhibits a unique hexagonal structure as a result of its two three-bladed propellers. The evolution of kinetic and potential energy varied as a direct result of the swirl imparted by each propulsor. Because of the interaction of positive and negative swirl, the CRP configuration showed an order of magnitude lower swirling kinetic energy compared to the single propeller configuration. Additionally, its potential energy was similar in decay and magnitude to that of the swirl-free jet, and the total kinetic energy decayed most rapidly out of the three propulsion schemes. These results indicate that the CRP can effectively reduce potential energy that would otherwise develop from a single-propeller configuration. By removing potential energy, buoyancy effects in the far wake will be weakened.