1. Introduction
The performance of marine propellers during realistic and off-design conditions nowadays represents a topic worth of investigation for the perspective of both scientific research and marine technology development. Traditionally, the propeller performance was analyzed considering the wake of the ship advancing at the desired speed in calm water. However, a seagoing ship is often subjected to environmental perturbations or desired control maneuvering actions that depart it from the ideal straight ahead motion. In these circumstances, the inflow to the propeller is altered with respect to the one adopted for the blade shape optimization and, consequently, the developed loads may change considerably. During motion in waves or maneuvering, the cross flow induced by the motion and the consequent modification of the viscous wake of the hull alter the blade hydrodynamics and, consequently, the resultant propeller loads. In particular, in addition to the modification of thrust and torque, undesired in-plane forces and moments that further stress the propulsion system (shaftline and bearings) and hull structure are generated.
An extensive investigation carried out by different Classification Societies (i.e., DNV, ABS, Germanisher Lloyd) stressed that the failure of the tail shaft bearing resulted one of the most frequent accident of the propulsion system for on–going vessels. In fact, due to the the higher power installed to achieve higher speed in modern designs, very large radial loads are developed by the propeller during maneuvers [
1,
2]. Moreover, this aspect is central for the safe mechanical sizing of orientable propulsive devices; these novel propulsive devices replace the rudder to control and maneuver the ship and, hence, might operate at relatively high drift angles. Moreover, free running CFD maneuvering simulations highlighted that the in-plane forces acting on the propeller are not negligible during large amplitude motions and, therefore, their quantification is fundamental to correctly predict the response of the vessel during maneuvering [
3,
4,
5] or in motion in waves.
Recently, propeller design procedures oriented to account for realistic ship operative scenario were explored by the NATO STO Task Group AVT-204, “Assess the Ability to Optimize Hull Forms of Sea Vehicles for the Best Performance in a Sea Environment” [
6]. A marine propeller design optimization procedure was proposed accounting for hull wakes calculated by CFD at different relative position of the hull with respect to the wave profile. A systematic analysis on the effect of waves on propeller performance, cavitation and pressure pulses was addressed in [
7,
8,
9]. In these works, it became apparent that changes of the wake distribution on the propeller disk play a crucial role in the performance of the propulsion device and the related problems of fluid structure interactions with the hull.
Although an increased level of attention is paid to the understanding and quantification of the propeller performance in off-design condition, studies (both numerical and experimental) are limited and mainly focused on idealized conditions for the isolated propeller [
10,
11,
12,
13,
14,
15,
16,
17,
18]. In fact typical size of ship models makes it challenging the installation of dedicated devices to measure all propeller loads in behind hull conditions; from the computational perspective, although CFD techniques were successfully applied to many topics of naval architecture, including off-design scenario such as ship maneuvering, the direct simulation of rotating propeller in behind hull is beyond the computational availability of day-by-day design applications.
Numerical simulations employing the discretization of the rotating propeller for self–propulsion or ship maneuvering studies are limited in the open literature [
19,
20,
21,
22,
23]. Moreover, even if at disposal, the detailed description of the propeller behavior is not provided and the results on hub and blade loads are not validated with experiments. In turn, the availability of experimental data or validated, high accurate data can be useful to improve low order propeller models usually coupled with CFD solvers for ship motion predictions, this being an established approach to speed-up the simulations.
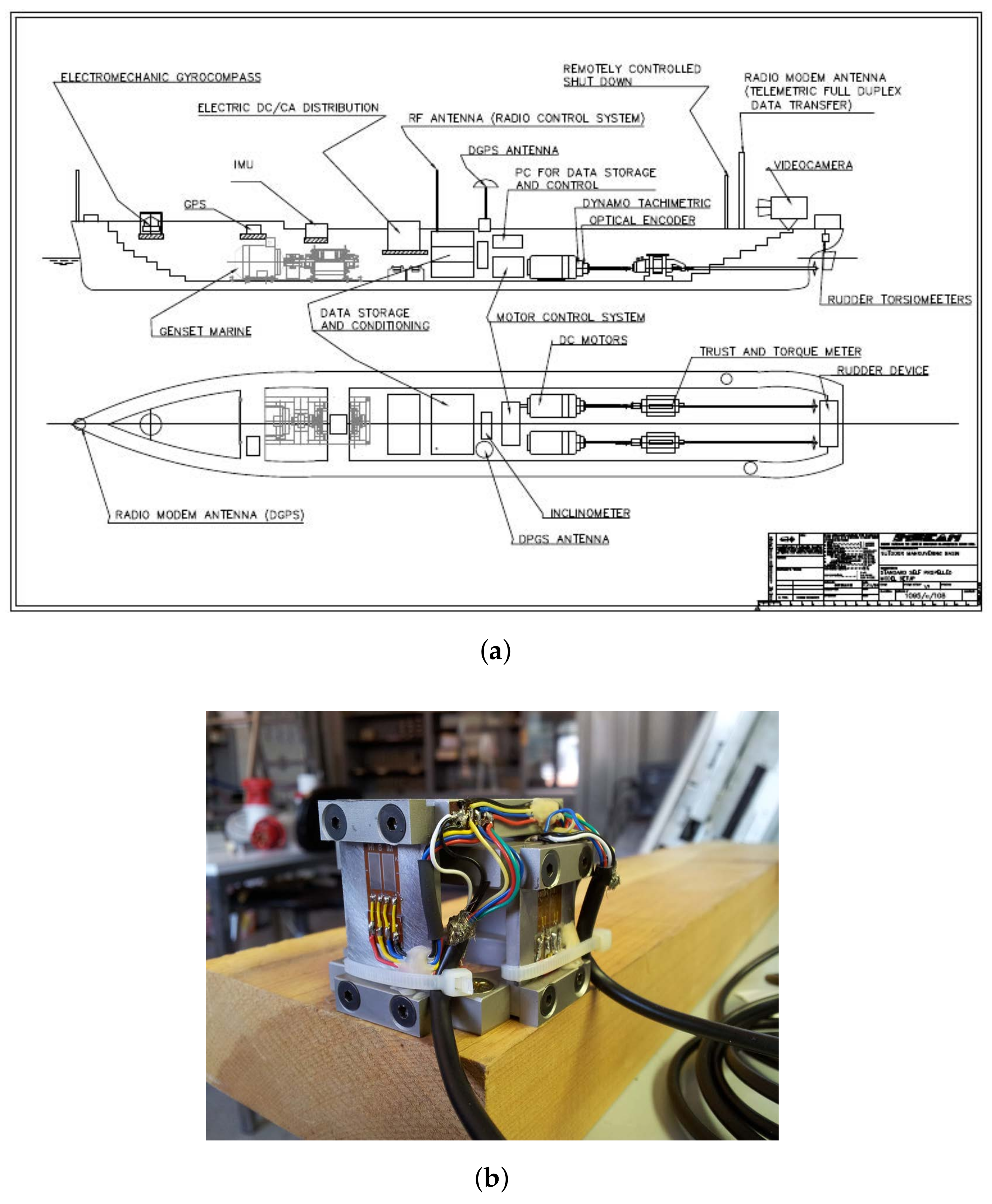
A series of free running model tests were carried out at CNR–INSEAN to investigate systematically these issues. In particular, twin screw configuration was the subject of the investigation, because the inflow conditions for the propellers cause their off-design operation more critical with respect to single screw ships. In fact, in twin screw propulsive configurations, the propellers are located at larger distance from wall of the hull and, during maneuvering, the “shadow” effect of hull is weaker; for this reason, the external propeller experiences an inflow inclined by an equivalent angle given by the kinematic of the model (during tight maneuver this angle might be of the order of 30
). On the contrary, the internal propeller has the higher probability to be impinged by coherent structures detached from the fore portion of the hull or appendages that are convected toward the leeward side. Moreover, the quantification of the asymmetric behavior of the propellers is of utmost importance in case of cross-connect configurations, because the reduction gear can experience very large fatigue loads. In particular, in [
24] the analysis was entirely focused to monitor the overloading and unbalancing phenomena of propeller thrust and torque during maneuvering conditions for a modern twin screw ship. The same experimental set-up and the model was also considered for a campaign dedicated to the quantification of the in-plane loads developed by the propeller during steady and unsteady maneuvers [
25,
26]; for this purpose, a novel 2–component transducer was developed. The relation between the motion and propeller loads were preliminary assessed by simple momentum theory. The analysis was then broadened by CFD computation and the use of simplified propeller modeling in order to clarify the effects of the wake evolution on propeller loads [
27,
28,
29]. In the present work, a synthesis of the experimental and numerical activity of these works is proposed to recap the key aspects that drive the propeller performance in off-design functioning. In particular, the asymmetric behavior of the propellers of the twin screw configuration is related to the wake morphology obtained by CFD computations analyzed by blade element propeller solver. Since the problem of damages of the bearing loads is a critical aspect for the reduction of maintenance costs of a vessel, the problem to full scale extrapolation of model test data was tackled. For this purpose, the blade element theory was modified in order to analyze the effects of Reynolds number and cavitation number on blade loads, with particular emphasis on the in-plane forces and moments. Finally, the future research activities inspired by the present work on the off–design propeller performance are briefly introduced.
3. Models and Methodologies
The CFD code solves the Navier-Stokes Equations for unsteady high Reynolds number (turbulent) free surface–flows around complex geometries. The interested reader is referred to [
17,
19,
30,
31,
32,
33,
34] for detailed description of the features of the solver.
The basic concepts of the propeller model are briefly described, because are useful to follow the discussion of the results and the correlation of the propeller loads with the wake features. The propeller solver is based on the blade element method. In the present work, the basic solver described in [
27,
35] was modified to account for scale effects; in this paragraph the basic algorithm is briefly reviewed (the interested reader can refer to [
27,
35]) and the modified one is discussed in
Section 6.
The blade element method synthesizes the blade performance by the contribution provided by its cross sections, each one formally treated independent from the others by the
airfoil representation. Formally, the propeller loads are obtained by summation of the contribution provided by each blade section once the “polar” characteristics, i.e., the coefficients of lift (
) and drag (
), and the inflow (velocity magnitude and incidence angle
) are known. Referring to a representative section of the propeller blade (see
Figure 5a), the inflow and the elemental forces are described in
Figure 5b. According to the
representation, we neglect the radial components. Without loss of generality, the representation neglects the effects of the self–induced velocity. In particular:
where
is the geometric pitch of the blade and
is the inflow angle of the section, given by the velocity system in the plane of the section (
is the tangential velocity given by the combination of the components of the wake in the plane of the propeller in the azimuthal direction, see
Figure 5a). In addition, therefore, the loads are given by:
where
is the lift and drag coefficients. Once lift and drag forces generated by the foil are determined, the elemental contribution to thrust
and tangential force
can be derived:
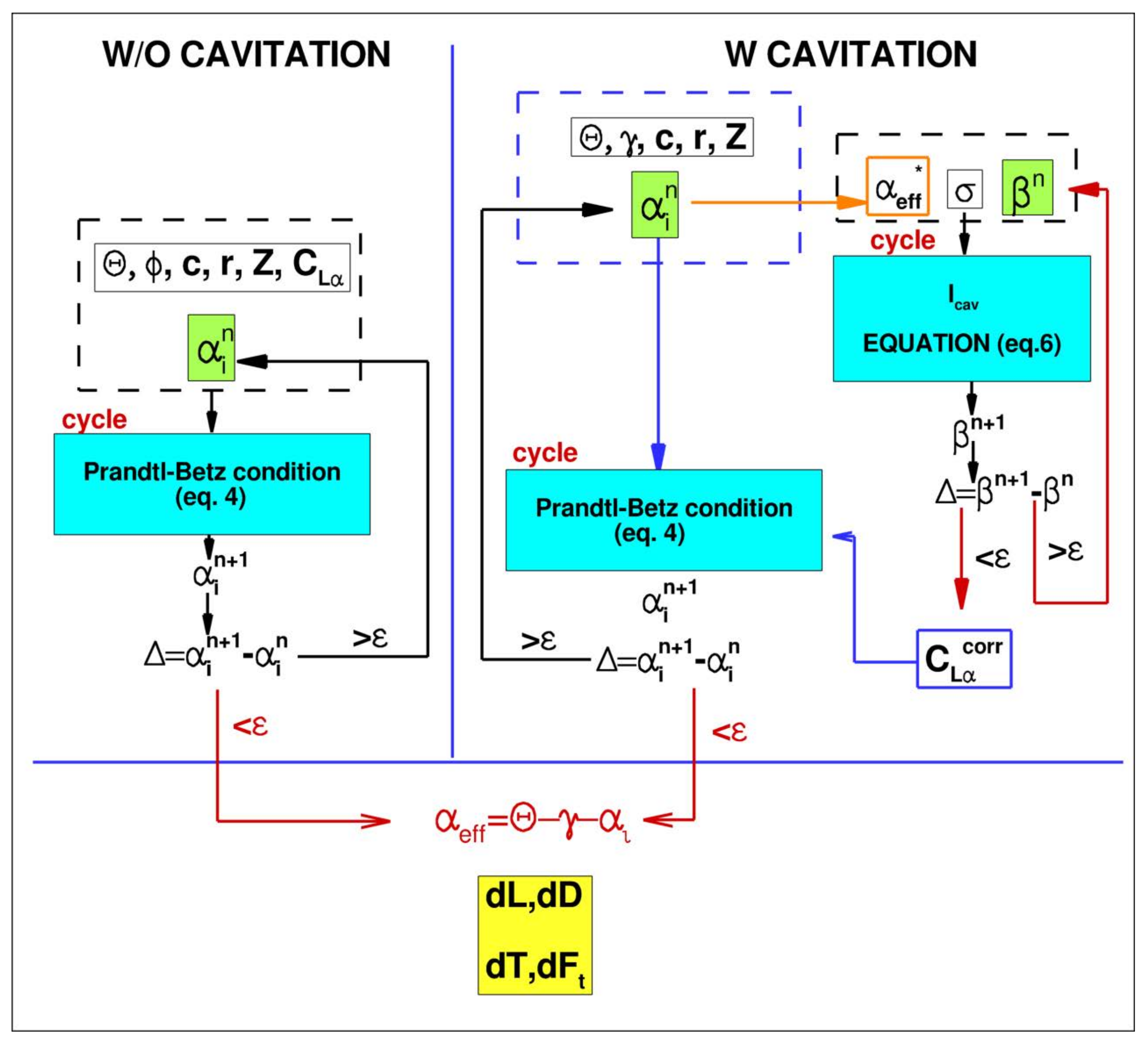
The step from a pure 2D representation to a three dimensional one that tries to model the key physic of the blade (self–induced velocity due to trailing vortices and blade–to–blade interaction) can be achieved by solving the non linear Prandtl–Betz relation for every section:
where
Z is the number of blades,
r and
c are the spanwinse position and chord of the foil, respectively,
is the picth angle of the section and
is inflow angle of the nominal flow (see
Figure 5b); the equation is non-linear and it is solved iteratively in terms of the self induction angle
. The flow chart reported on the left half of
Figure 6, explains the pseudo-code of the non-cavitating propeller solver: given the nominal incidence and the geometric details of the section, the Prandtl-Betz equation is solved to determine the self-induced velocity field. The strict coupling between the lift (circulation) generated by the section and the induced velocity field give rise to the non linear nature of the Prandtl-Betz equation.
It has to be stressed that the
model is inherently quasi steady, because the Prandtl–Betz condition implicitly assumes the balance of the load developed by the blade strip and the vorticity (constant) carried by trailing vortex. However, as long as the inflow is time–varying, this equilibrium condition is not suddenly met and its lag depends on the time rate of circulation detached at the trailing edge of the airfoil, because it is responsible of an additional perturbation to the blade section [
36].
4. Results
In this section, the experimental results are synthesized with the complementary
results and wake analysis by the BEMT solver. The discussion is carried out qualitatively to focus on the key mechanisms that govern the off-design performance of the propeller and a comparison of the numerical and experimental work is not reported. BEMT is reliable to capture the trends and the order of magnitude of the loads, although absolute errors were rather high. These discrepancies were ascribed, aside from the approximation of the propeller solver, to the off-line analysis of the nominal wake. By this approach, the modification of the wake due to the self–induction effect of the propeller is obviously neglected and, consequently, the prediction of the loads might be affected. In particular, on the internal side, this interaction can modify the strength and distribution of the swirling flow and, on the external shaft, the flow around the appendages and the shaft. For this reasons, weakly-coupled
simulations in transverse plane should be carried out to achieve a more accurate prediction of these loads; moreover, the real attitude in the transverse plane (roll angle) should be considered in the simulation, because the in-plane loads are sensitive to the wake and load distribution over the propeller disk as described in the following analysis. The interested reader is referred to [
27,
28] for a deeper discussion on these aspects.
The velocity profiles are referred to the hub reference system, the propeller disk is viewed from the stern, and the circumferential coordinate
is positive signed when oriented in the same sense of propeller rotation (that is, increases clockwise and anticlockwise for the port and starboard propellers, respectively). In the discussion, the propeller disk is divided into four sectors, the first one being defined by
, and so on. Finally, consistently with [
25,
26], results for propeller loads are summarized in unified graphs, where positive and negative rudder angles correspond respectively to internal and external propellers.
In the following, all the quantities are made non dimensional using as reference quantities the length between perpendiculars (), the approach speed at model scale (), and the density of water ( kg/m). The propeller loads are expressed in terms of coefficients defined, as usual, by dividing the thrust and torque by the factors and respectively, where D is the propeller diameter and N is the propeller rate of revolution (RPS). Without loss of generality, kinematic values, forces and moments are always presented in terms of ratio with respect to values in the approach phase (identified with the subscript “0”).
Experimental Results
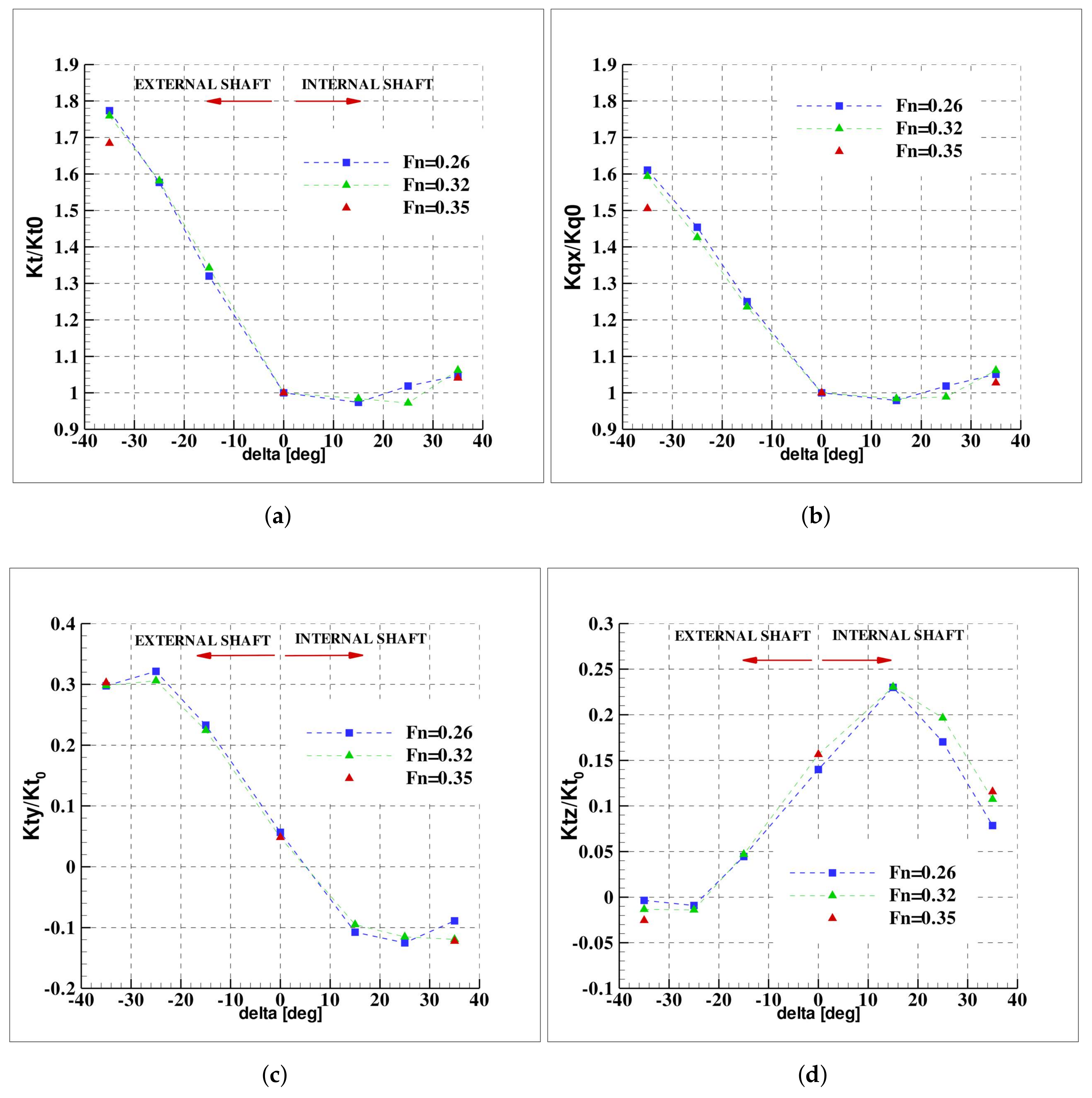
The experimental results are reported in
Figure 7 in terms of thrust, torque and radial force components ratio for the three different
. The results refer to the starboard propeller.
In general, a marked asymmetry of the loads generated by the external and internal propeller is experienced. Moreover, the effect of speed is negligible: this fact is indicative of the limited effect of the
on the maneuvering response, as was also reported in terms of kinematic response and macroscopic parameter of the maneuver in [
25]. In other words, the propeller inflow (and therefore, the propeller performance) would be morphologically similar for maneuvers carried out at the same rudder angle.
The thrust and torque show a similar behavior; on the external propeller () a remarkable increase of almost 80% and 60% of the value in the approach phase, can be evidenced for thrust and torque, respectively. The increase is almost linear with . On the internal side, the overloading is considerably weaker (less than 10% for both thrust and torque) and the trend non-linear, the slope being negative for and then positive.
The side force,
Figure 7c, is always oriented to stabilize the vessel, i.e., it is oriented toward the centre of curvature of the trajectory. During straight ahead motion, this force is oriented toward the plane of simmetry of the model. On the internal side, the force shows a non-linear trend, it slightly increases up to
and then diminishes in case of the tighter maneuver. The average value over the range of rudder angles corresponds to about about 15% of
. On the external side, this force increases almost linearly up to
(where it reaches a value doubled with respect to the internal shaft) and at
slightly diminishes. The external propeller develops a side force that is more than doubled with respect to internal propeller.
The vertical component, reported in
Figure 7d, resembles the same character of
. At
the force is upwards oriented due to the inclination of the shafts and the mean direction of the flow in the stern region; on the internal side, the trend is markedly non linear,
experiencing first a maximum at
and thereby a linear decrease til
(50% lower than the value observed during the approach phase). On the external shaft, this component gradually weakens and achieves a negligible value with respect to the side force at the maximum rudder angle. In general, it is interesting to observe that, although the absolute magnitude of the radial force (given by the combination of
and
) is similar for the internal and external shaft, it is developed at completely different maneuvering conditions that lead to completely different inflow conditions to the propeller, as described in the next section.
5. Discussion
The different behavior of the propeller loads during the maneuvers, synthesized by a marked asymmetry between the internal and external propeller and a linear variation of the loads on the external side by contrast to a non-linear trend on the internal side, has to be ascribed to the different evolution of the inflow to the propellers. The nominal wake experienced by the propellers in straight ahead motion and during maneuvering conditions at small and high turning rates (
and
) is described in terms of axial velocity contours and tangential velocity and field in
Figure 8 and
Figure 9a,
Figure 10a. In order to relate the flow field with the system of vortices detached from the hull and appendages,
Figure 9b and
Figure 10b visualize the coherent structures obtained by the vortex identification method based on the
–criterion [
37].
In rectilinear motion (see
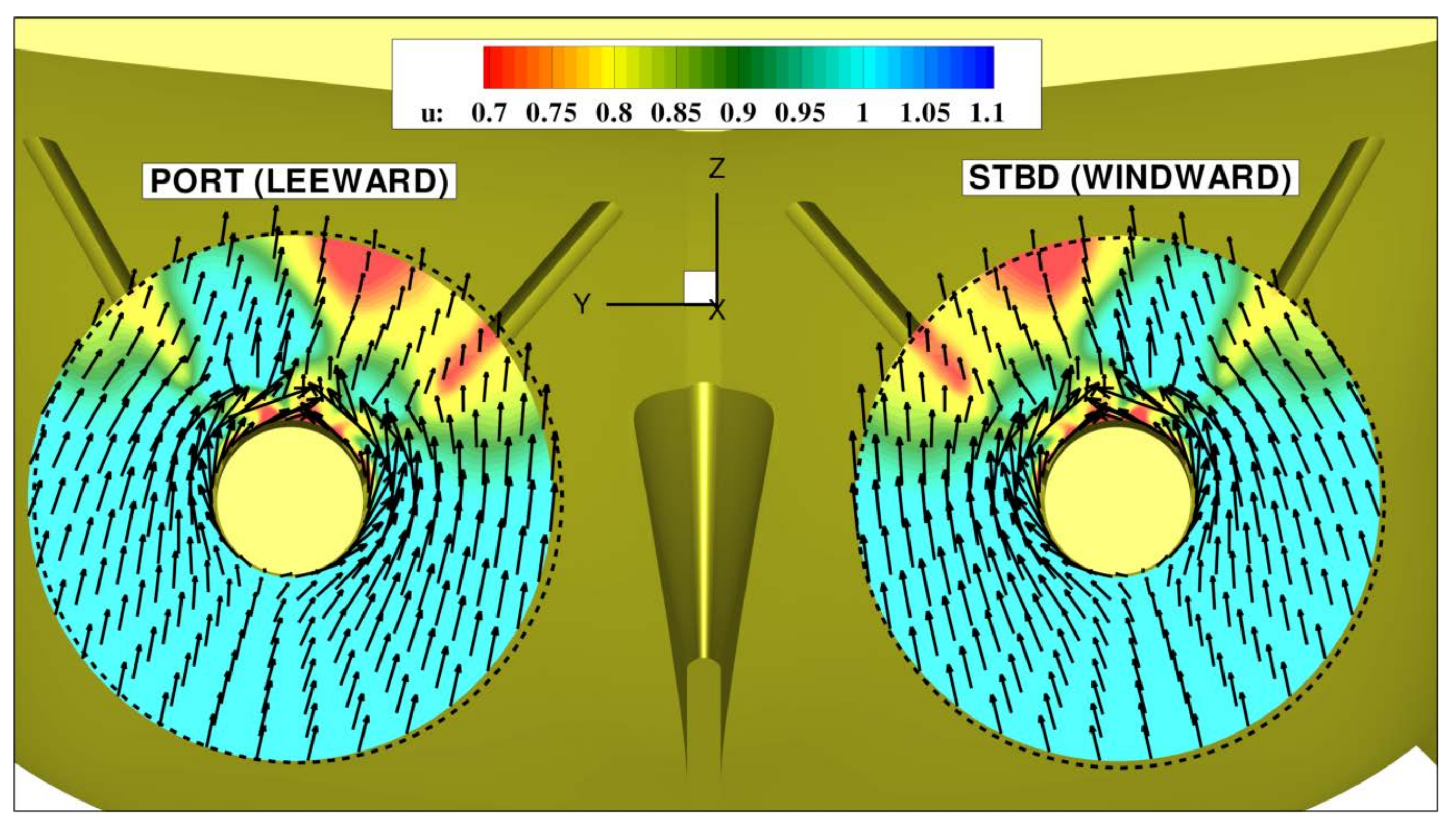
Figure 8) the inflow to the propeller is perturbed only on the upper half of the disk, the velocity defect being associated to the wake past the brackets and the boundary layer of the hull; moreover, the tangential flow on the propeller disk (represented with vectors) is directed upwards due to the inclination of the shaft and the mean orientation of the flow along the stern cut-off of the hull [
25,
27].
During maneuvering conditions, the wake is gradually modified and the asymmetry between the internal and external propeller are evident also for the weaker maneuver at
. In fact, on the external shaft, the flow always resembles a pure oblique flow, the axial flow being almost homogeneous and the tangential flow oriented horizontally; it can be noticed that at
, the propeller is moderately affected by the disturbance of a vortex detached from the bilge keel in the 1st quadrant, whereas at
the disk is weakly affected by smaller structures detached from the propeller shaft (see
Figure 9b and
Figure 10b). On the contrary, the inflow to the internal propeller develops in relation to the evolution and interaction of the vortical structures detached from the hull and appendages. In fact, at
, the strong recirculation region in the 1st quadrant of the port propeller (see
Figure 9a) is associated to the passage of the vortex detached at the skeg and deflected toward the propeller disk (see
Figure 9b). At
, the propeller is completely immersed in a large vortical structure formed by the combination of skeg and bilge keel vortices; this large structure interacts also with the shaft and brackets and causes the separation of smaller structures, whose trace is for example evidenced by the recirculation region in the upper half of the disk (see
Figure 10a).
The relation of the wake with the propeller loads can be effectively established focusing on the single blade performance. Moreover, in the framework of blade element description (see
Section 3), a very effective and simple method can be introduced to explain the onset of the in-plane loads and moments and to better synthesize the blade loads during the period of revolution [
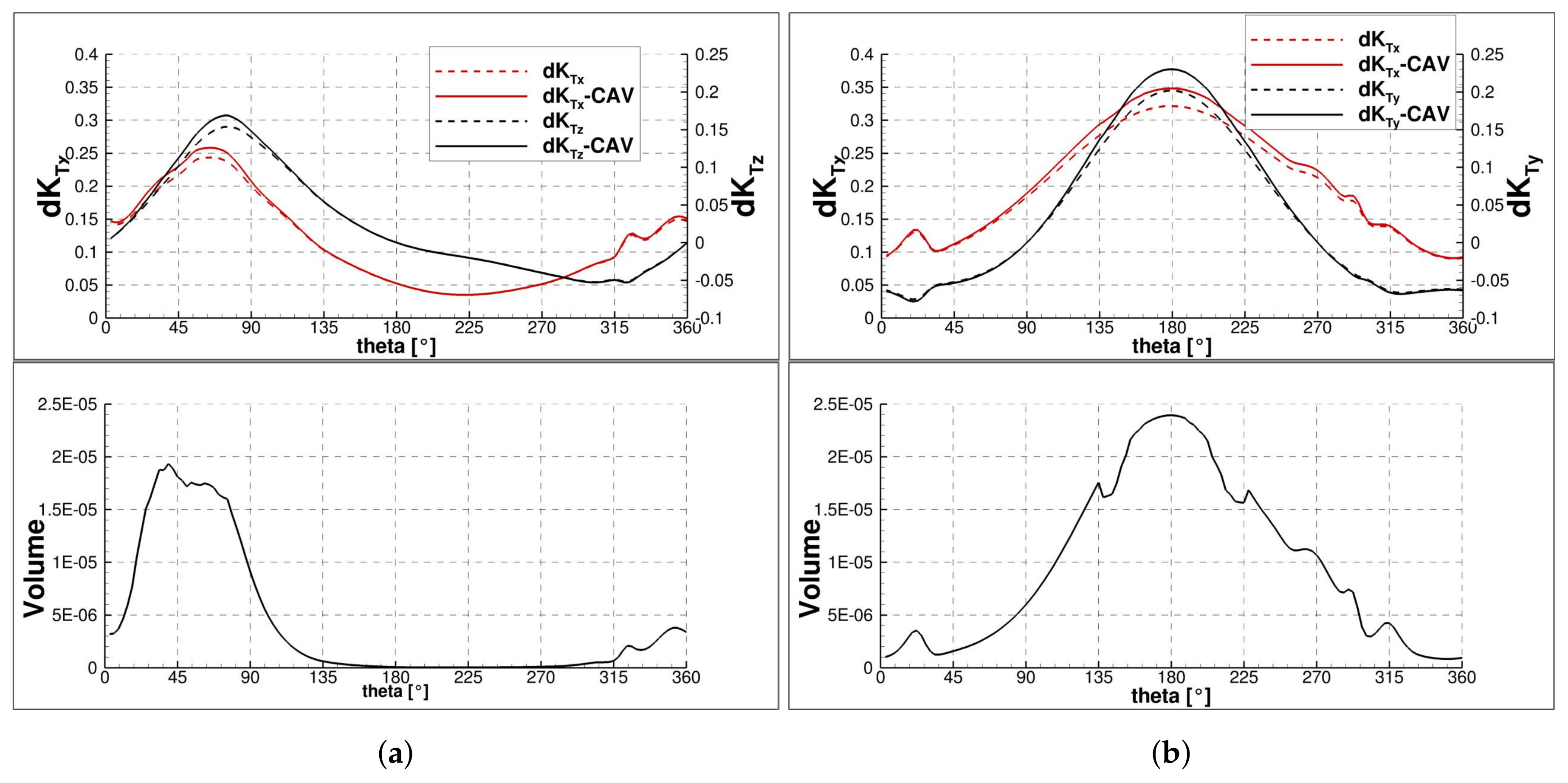
27]. For example, the in-plane force, i.e., the lateral force, is due to the imbalance of the force developed by the blade in the upper and lower half of the disk. Similarly, considering the thrust force, this asymmetric variation of the blade loads generates the pitching moment. Similar conclusion can be easily derived for the components relative to the vertical axis.
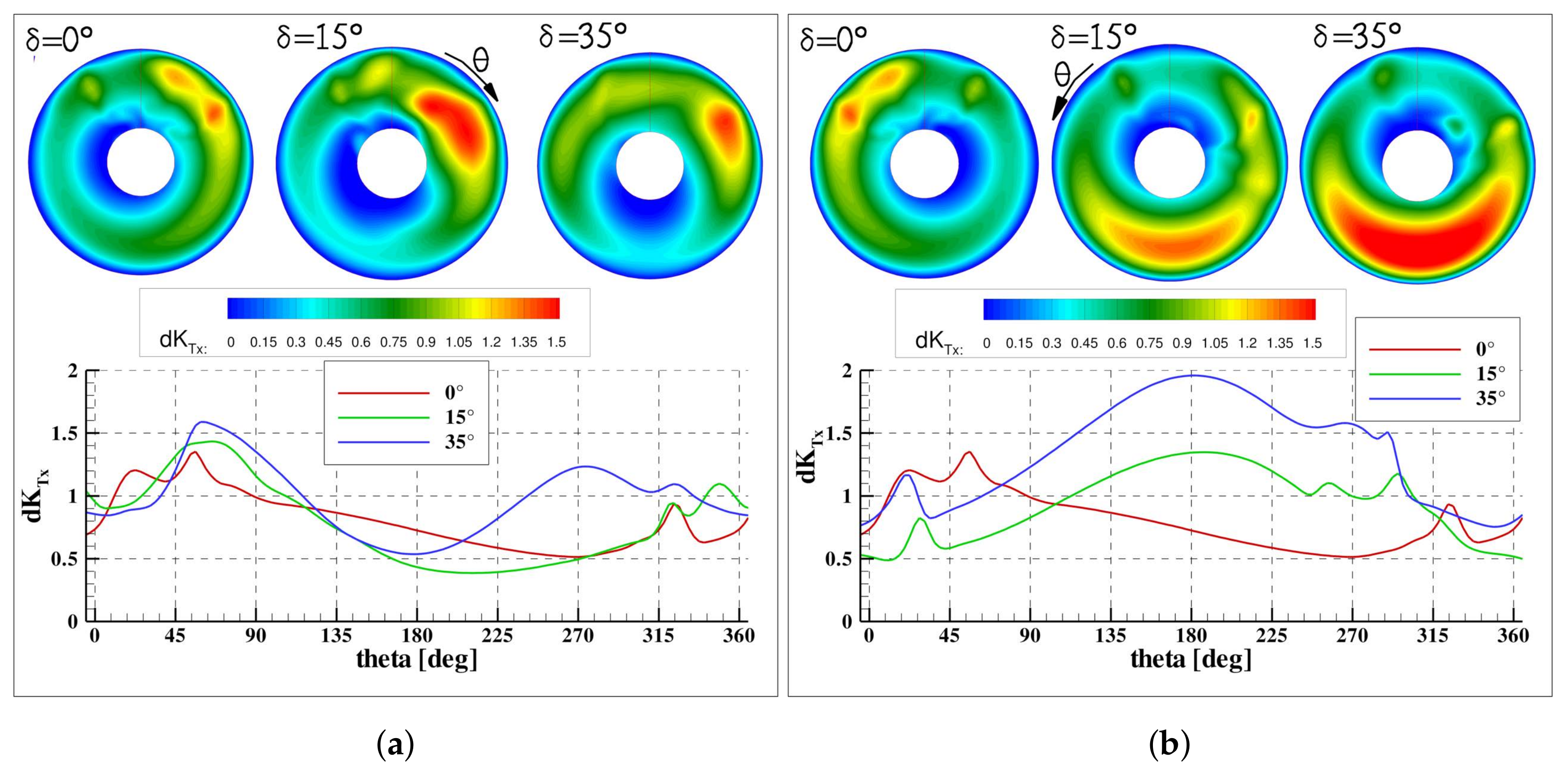
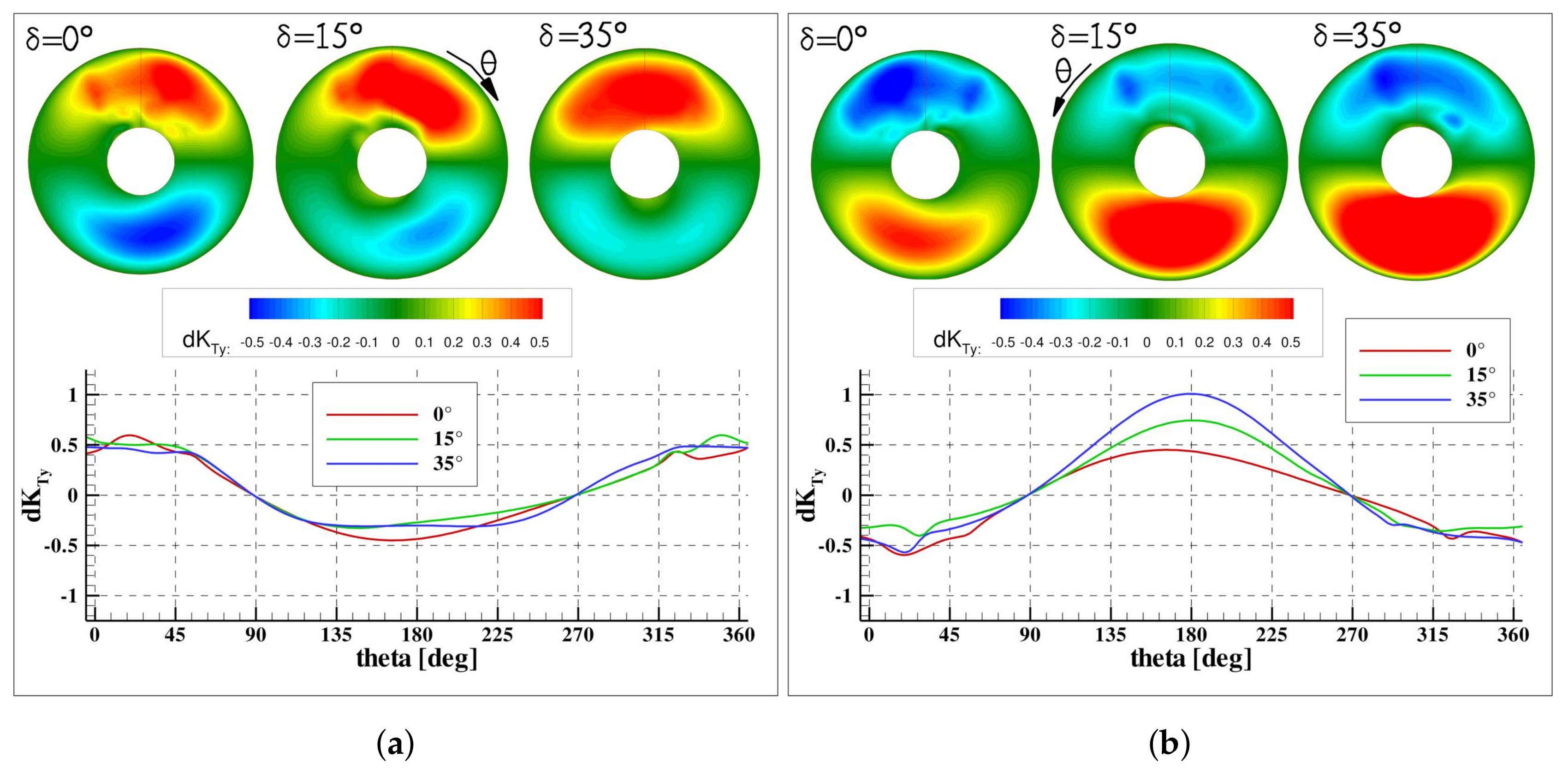
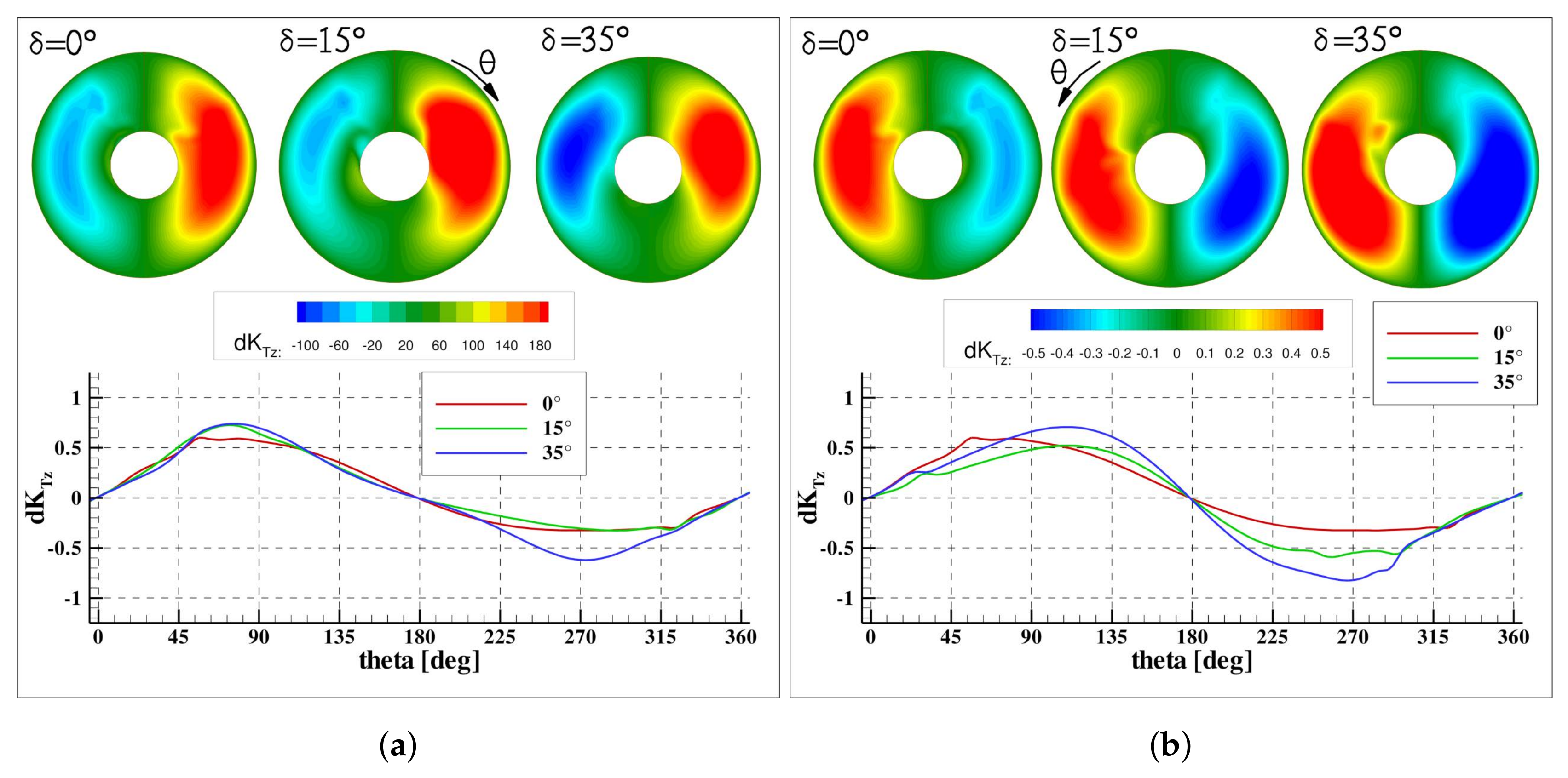
The thrust, side and vertical forces developed by the single blade and their distribution over the disk are reported in
Figure 11,
Figure 12 and
Figure 13; the integral on single halves that support the simplified description of the generation of the in-plane loads are reported in
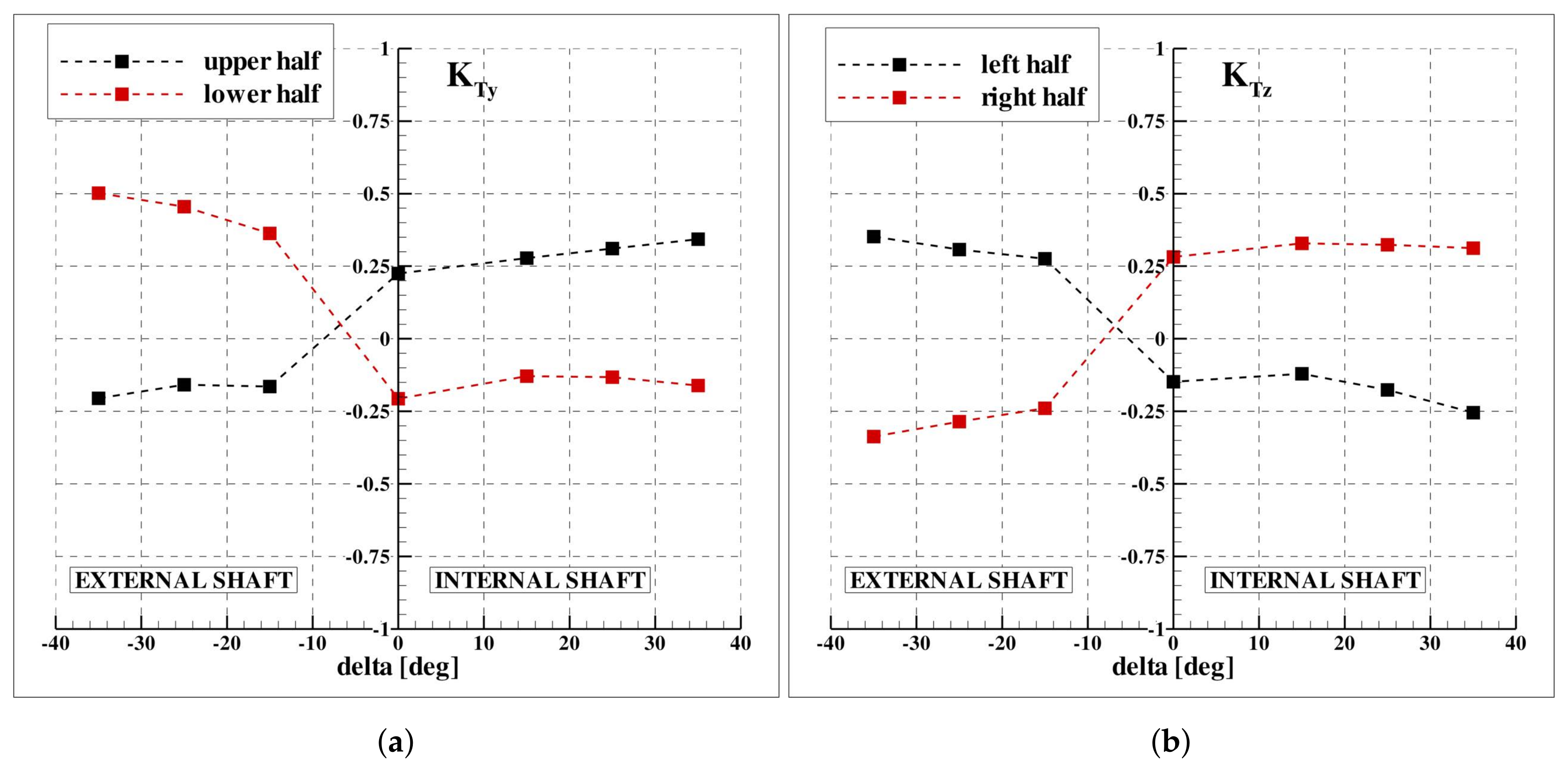
Figure 14 and
Figure 15.
At
, the blade experiences higher local incidence angle in the 1st and 2nd quadrants (downstroke cycle),
(red line in
Figure 11a,b) due to the velocity defect and the upwards tangential velocity that acts to increase the local angle of incidence of the blade sections (according to a blade element representation). Consistently, the blade develops higher thrust in this sector, as clearly described by its distribution over the disk at the top half of
Figure 11, causing the generation of in-plane moments (see
Figure 14); considering the starboard propeller (and the hub frame of reference in
Figure 5a), these consist of a positive pitching moment and a negative yaw moment. Moreover, the vertical force is dominant with respect to the side force, because the asymmetry of the load distribution is stronger between the left–right halves of the disk. This aspect is quantitatively supported by the imbalance of
and
in the bottom/upper and left/right halves of the disk in
Figure 15a,b and by the trend of the single blade loads at the correspondent sectors (red line in
Figure 12b and
Figure 13b).
In maneuvering conditions, the performance of the external propeller is markedly affected by the cross flow, its behavior being similar to the functioning of a propeller in pure oblique flow. In general, the load distribution over the disk is very different with respect to the rectilinear motion and shows an imbalance between the lower half (2nd and 3rd quadrants) and upper half (1nd and 2rd quadrants) of the disk. The blade develops higher load in the lower half of the disk with respect to the opposite half. In fact, the cross flow induced by the motion, being opposite to the blade rotation, acts to increase the tangential flow experienced by the blade and consequently the developed loads; differently, this mechanism is inverted in the upper half. This behavior is similar for the maneuvers considered and it gradually amplifies with the increase of rudder angle
, as it can be clearly evidenced by the distribution of the loads over the disk and the trend of the single blade loads (thrust and in-plane forces) visualized in the figures. Specifically, the imbalance of the thrust causes a negative pitching moment that is prevalent with respect to the yaw moment (see
Figure 14); the side force, oriented in the positive direction, is originated in the lower half of the disk, its partial contribution increasing faster with respect to the upper half (where it is almost constant) (see
Figure 15a). Obviously, the vertical force is negligible, the counteracting contributions from the left and right halves of the disk being almost coincident. It has to be stressed that the effects of the cross flow is the primary element that determines the behavior of the external propeller synthesized in
Figure 7a–d [
27]. In fact, the self-similar character of the blade hydrodynamics determines the linear increase of thrust, torque and side force and, conversely, the smooth drop of the vertical force; moreover, the marked overload with respect to the internal propeller has to be also ascribed to the increase of the sectional incidence angle by the cross flow, since the mean velocity defect is stronger on the internal propeller (see
Figure 9a and
Figure 10a).
On the contrary, on the internal side the blade hydrodynamics is more complicated, because the disturbance due to the wake of the hull and appendages is superposed to the cross flow. As a matter of fact, the blade hydrodynamics is affected by the wake and interaction with vortical structures in the upper half of the disk, while by cross-flow in the lower half. At
, interaction of the blade with the skeg vortex (it acts to increase the tangential speed relative to the section, and consequently, the loads) causes the localized increase of thrust at about
, and amplifies its fluctuation during the cycle (see
Figure 11a). This interaction also provokes the increase of the magnitude of in-plane moments and the relevant peak of the vertical force reported in
Figure 7d. In particular, the increase of the vertical force has to be ascribed to this localized phenomenon, because the trend of this load developed by the single blade is similar to the one experienced in rectilinear motion with the exception of the passage about
. Moreover, because of the reduction of blade load in the lower half of the disk due to cross flow, the side force increases (see
Figure 15a). At the maximum rudder angle,
, the localized effect of the skeg vortex is weakened, since the vortex moved further to the lee side. The further buildup of thrust is originated in the left half of the disk, as it is proved by the increase of the single blade load for
(see
Figure 7a); this is associated to the combination of velocity defect and speed drop (experienced by the model during the maneuver), since the tangential flow, upwards oriented (see
Figure 10a), acts to reduce the incidence angle of the blade sections. The increase of the pitch moment and the yaw moment is weakened, as demonstrated by the inversion of the trend of the load in the lower and left halves of the disk (see
Figure 14). Consistently, the in-plane loads are also reduced: the drop of
has to be ascribed to the weakening of left/right imbalance of the load associated to the increase of the magnitude of vertical force in the left half of the disk (see
Figure 7d and
Figure 15b); similarly, the increase of the side force in the lower half of the disk counteracts the force on the upper half and, hence, the asymmetry with respect to the horizontal axis is reduced.
7. Conclusions
Present work is a contribution to the understanding of the mechanisms that rule the performance of a propeller operating in off-design conditions (maneuvering). In particular, the work consisted of a synthesis of the results of free running model tests and their phenomenological assessment with numerical computations performed with a maneuvering simulations and simplified propeller model based on Blade Element Momentum Theory. The test case for the study was a twin screw model; the propulsive configuration is particularly suitable for this study, since the regime of the propellers on the leeward and windward sides is markedly different.
In fact, the propeller on the external side operates in a pure oblique flow condition and the increase of the loads is almost linear with the rudder angle. This propeller experiences the most critical condition with respect to the internal one at maximum rudder angle. In fact, the thrust and torque increases up to 80% and 60% of the value in straight ahead sailing; moreover, since the inflow is directed almost in the horizontal direction, the propeller develops only a side force that acts to stabilize the vessel and amounts to about 30% of the thrust generated in the approach phase of the maneuver. On the other hand, on the internal side, the propeller hydrodynamics is markedly affected by the evolution of the wake detached from the hull, the interaction with vortical structures convected through the propeller disk and the cross-flow induced by the motion. The dominance of one effect with respect to the other at different maneuvering conditions is the reason of the non-linear variation of the loads with rudder angle. Although the thrust and torque did not experience a large overload (10% with respect to the value during the approach phase), the behavior of the in-plane loads resulted sensitive to these flow conditions; indeed, the asymmetries and localized gradients of the inflow to the propeller was responsible to a marked imbalance of the periodic blade loads, with the consequence that the maximum magnitude of the radial force was comparable to the one developed on the external shaft. Moreover, the peak of the radial force was experienced during a weaker maneuver () and was ascribed to the interaction of propeller blades with a coherent structure developed past the appendages. These results stressed that also mild variations from the straight ahead conditions can be critical for the propulsive system, even to the same extent of heavy off-design conditions, and can possibly generate undesired noise emission, vibrations and fatigue loads on the shafting system.
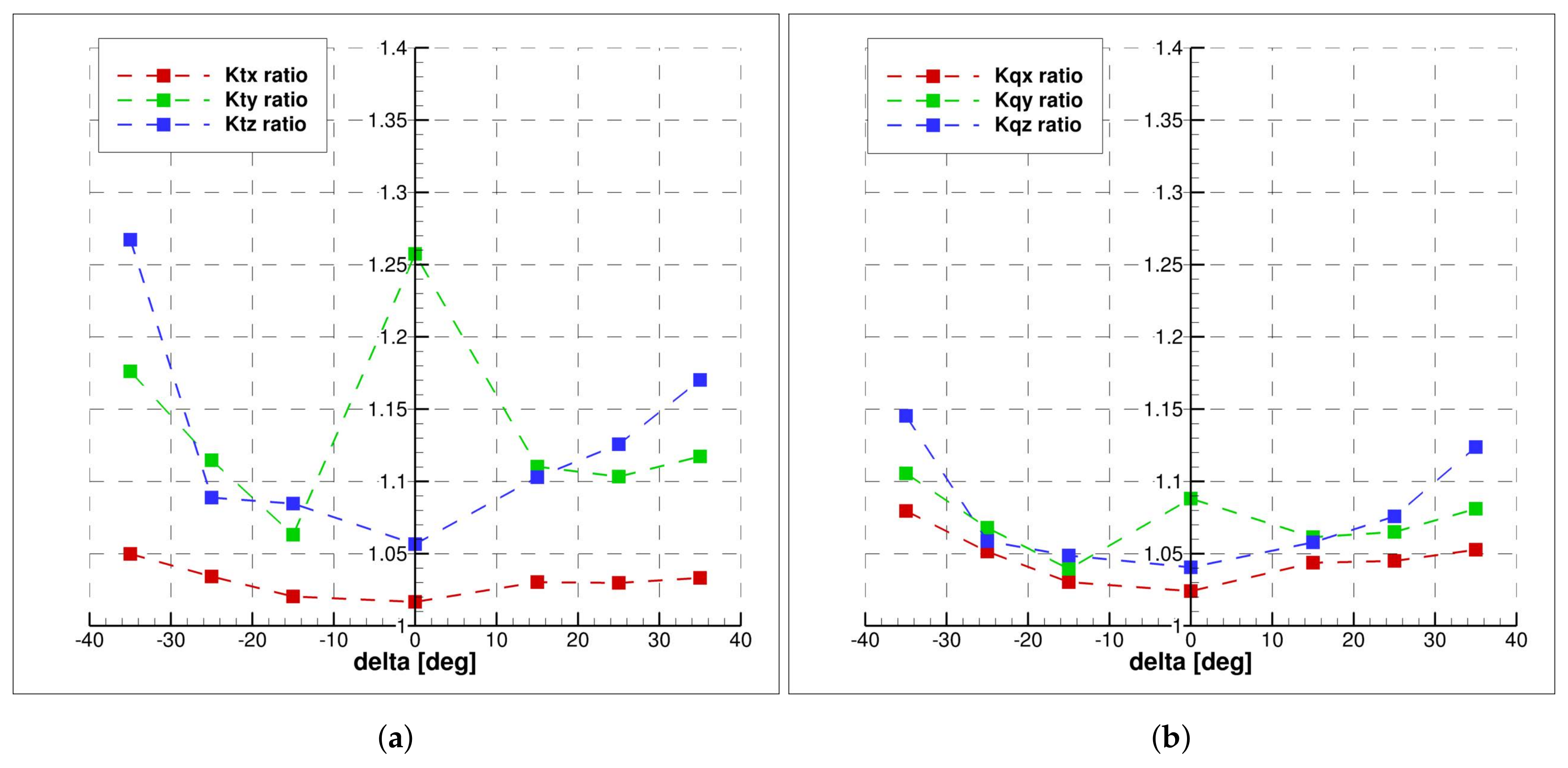
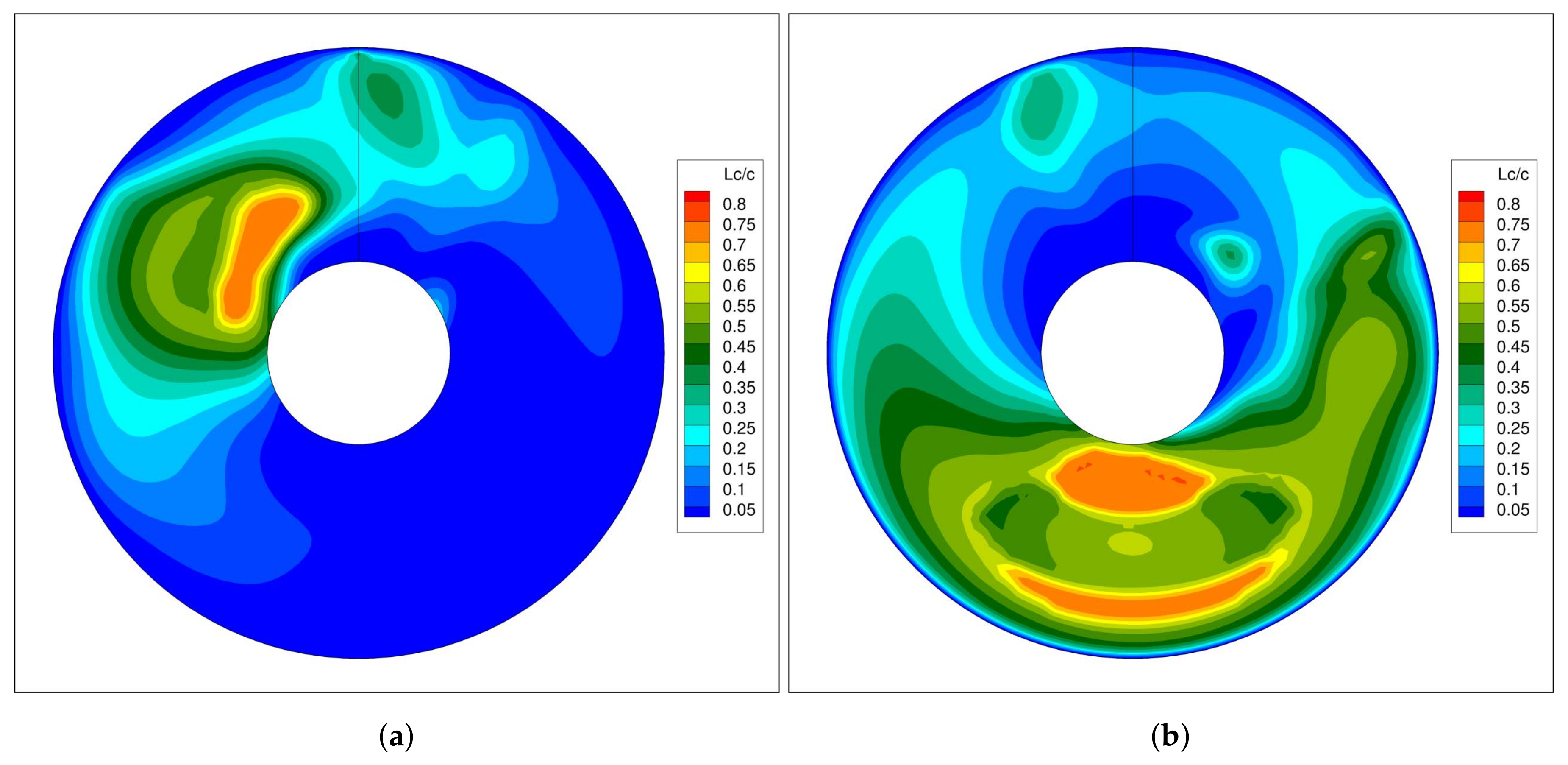
Finally, a preliminary analysis on the scale effects on the propeller loads was carried out. In particular, the study considered only the scale effects for the propeller, i.e., the Reynolds number and cavitation number on propeller loads. To this aim, the propeller solver was modified to calculate the loads corrections by the ITTC method for the former problem; for the second issue, the propeller solver was enhanced with a linear, partially cavitating, hydrofoil theory, accounted in a consistent way with the solution for the self–induced velocity field. The study highlighted that viscous effects on the propeller loads are negligible with respect to cavitation; moreover, the in-plane loads are more sensitive to cavitation with respect to thrust and torque because it increases the asymmetry of blade loads during the cycle. The amplification of the loads due to cavitation is experienced on the external shaft at the maximum angle for the present propulsive configuration (propellers inward rotating from the top); therefore, a viable scaling procedure during the design phase could be to complement free running maneuvering tests with measurements or computation for the isolated propeller at the critical incidence and equivalent loading condition in cavitating and non-cavitating conditions for achieving the scaling factor. A complete analysis of the propeller performance at full scale cannot be performed without considering cavitation and its related effect; simulations with weak coupling with propeller models are feasible. More accurate analysis could be possible by a multi–phase solver (with discretized propeller); the computational burden is prohibitive for design purposes and thus far this kind of simulation has not yet been carried out.
Reynolds number effects on the modification of the nominal wake to the propeller is a very challenging issue, since scale effects the maneuvering response and, therefore, the evolution of the wake. These effects are also important to correctly predict the cavitation volume and, in particular, it dynamics in order to predict accurately propeller hull induced vibrations and acoustic emission. In this regard, can provide a valuable insight on the modification of the wake and, moreover, contribute to understand whether the development of scaling techniques similar to those applied in straight ahead motion are a plausible way to a safer extrapolation of the loads to full-scale. Obviously, measurements at full scale, despite difficult to set up, could provide useful hints to tune the extrapolation procedure; unfortunately, at present the availability of data is extremely poor or restricted by industry.
To better understand the complex phenomenology of the propeller behavior in off-design conditions, in particular to relate the loads to physic experienced at blade rate frequency, the set-up of the free running model has been recently improved for the characterization of the single blade loads. On the basis of these measurements, all the system of loads acting on the propeller can be determined and these measurements represent a basis for deeper investigation also on propeller side effects related to propeller vibration, pressure pulses and noise emission. In
Figure 19a,b a partial overview of the ad–hoc design propeller to house the measurement system of the single blade and in the behind hull configurations are showed. The test case is a twin screw ships with a different stern geometry with respect the one considered in this study and the model size is smaller. The experiments will be carried out at the same experimental conditions on a free running, self propelled maneuvering model.