4.1. Ocean Temperature
The displacement of water masses in the water column caused by the deployment of OTEC systems introduces perturbations in temperature, salinity and other characteristics. It is important to understand in what way the ocean responds to such perturbations. In particular, how ocean temperature changes, and how this change influences OTEC power production.
For reference (control), we use the steady state solution that does not include OTEC perturbations, which we label as experiment CTL. For discussion below, we take the solution obtained with wcw = 15 m year−1 and the modified ocean-atmosphere boundary condition R-W × 40, which we label as experiment W15. This choice for the volume flow rate of OTEC deep seawater per unit (latitude-longitude) area corresponds to overall OTEC peak power among R-W × 40 simulation scenarios. The computed temperature difference δT between W15 and CTL is referred to as temperature anomaly.
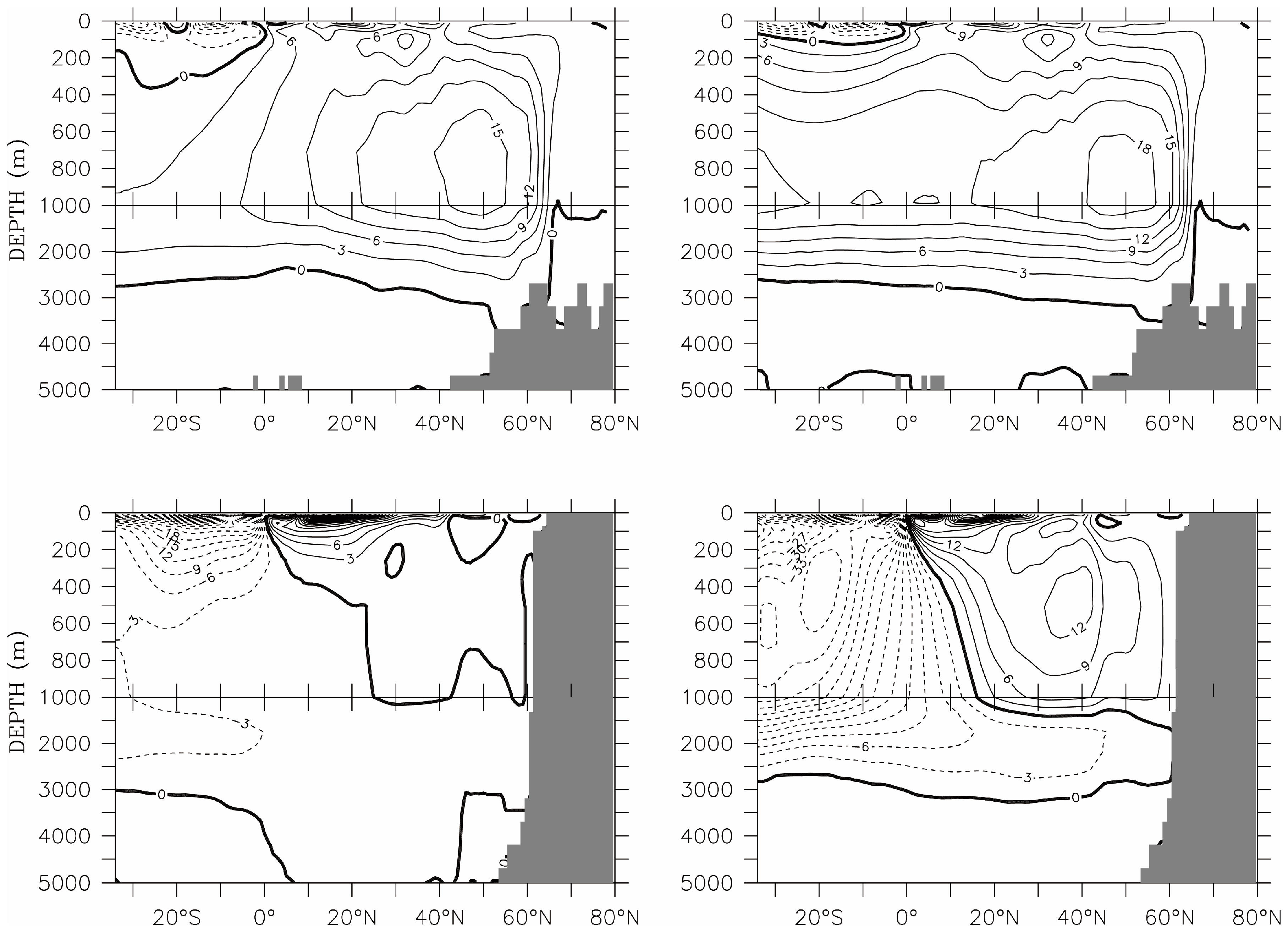
Figure 4 shows the
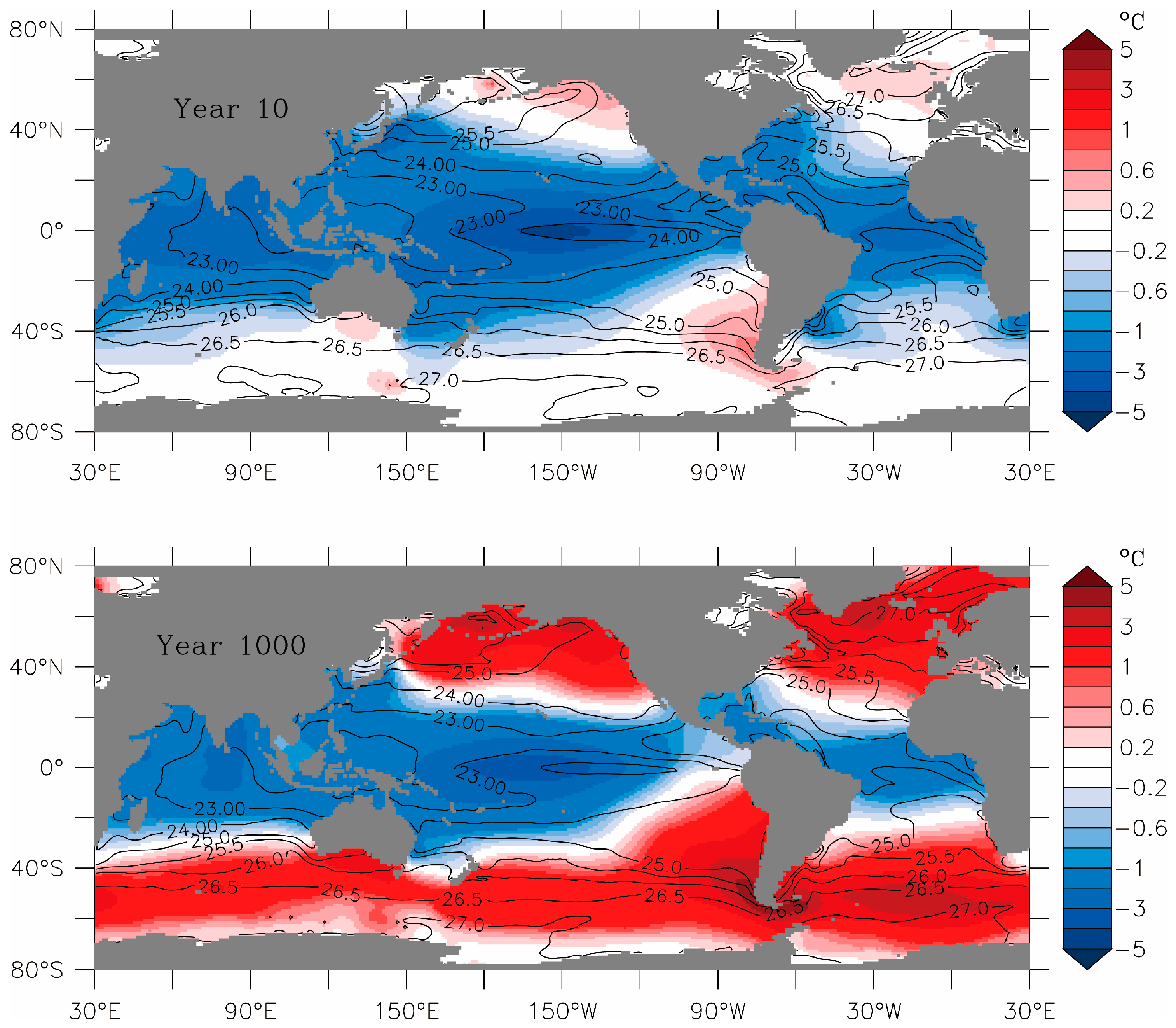
δT distribution (color) at the model’s uppermost layer (mid-depth of 5 m) 10 years (upper panel) and 1000 years (equilibrium solution, lower panel) after the activation of OTEC, overlaid with
σθ from
CTL (contours).
σθ is defined as the seawater potential density (referenced to sea surface pressure) minus 1000 in units of kg m
−3. Striking features in
Figure 4 are the cooling within the equatorial region and warming in the high latitudes. It turns out that the equatorial cooling begins within one year of OTEC activity. The high latitude warming emerges as a weak signal south of Australia and against the eastern and northern land boundaries of the Pacific and Atlantic basins within 10 years, and enhances with time.
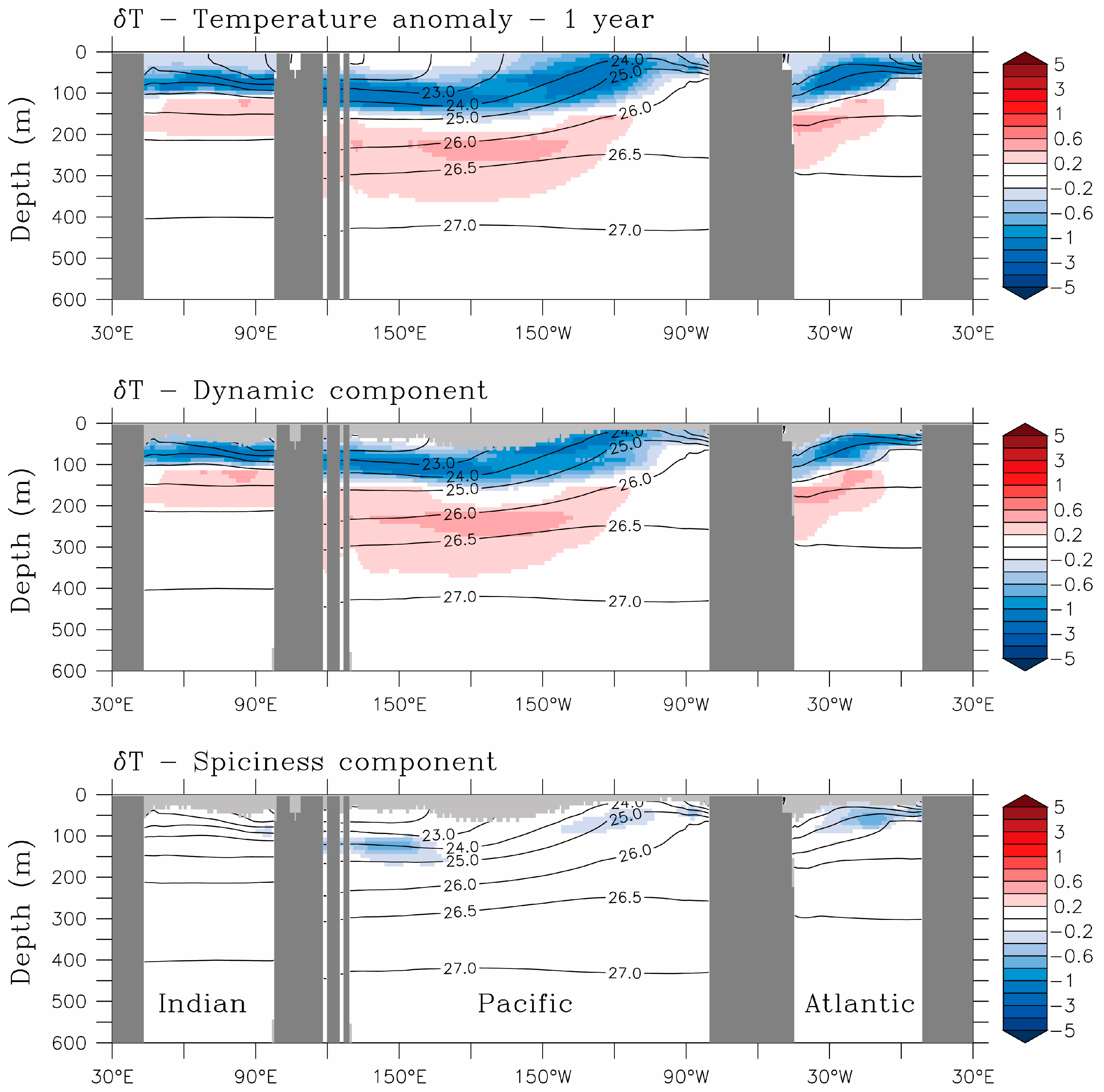
Figure 5 and
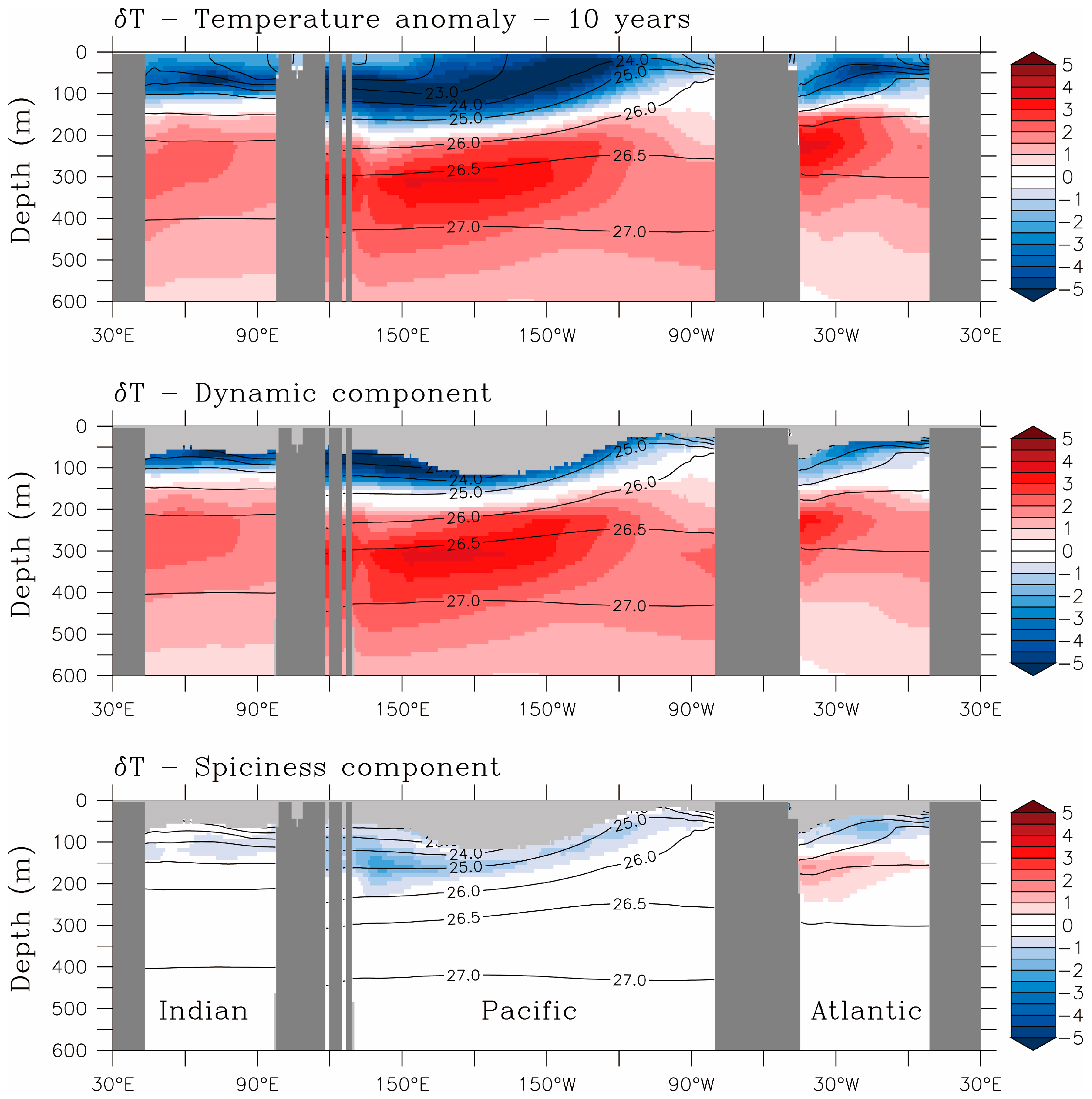
Figure 6 show a zonal section of
δT near the Equator (0.5° N) in the first and tenth year of OTEC activity, respectively (color). Focusing on the upper panels for now, we see cool and warm anomalies separated around the depth where OTEC effluents are discharged. The slight spatial variation of this depth reflects a choice in the simulation protocol that OTEC effluents are locally returned where they would be neutrally buoyant at the start of OTEC activity. Notice that the cool and warm anomalies are approximately aligned with the sloping density surfaces in
Figure 6 (contours of
σθ from
CTL). This can be understood as follows: the volume of OTEC effluent of a certain density, discharged at a depth of neutral buoyancy, would expand water of that density relative to the reference state (
CTL), thus displacing potential density surfaces and resulting in positive (denser) and negative (lighter) potential density anomalies above and below the discharge depth, respectively. Since potential density is a function of temperature and salinity, this would also mean that anomalies of opposite signs across the discharge depth would also emerge in the temperature and salinity fields.
Based on the fundamentals of ocean dynamics, a localized potential density perturbation in the ocean would lead to an unbalanced pressure field, thus an unbalanced ocean state. The adjustment process towards a new balance involves the generation and propagation of particular types of ocean waves, such as Rossby waves, and equatorial and coastal Kelvin waves. These waves spread the density disturbance, and along with it, are able to modify the temperature and salinity fields of remote regions far away from the region of initial perturbation. Temperature and salinity anomalies can also be advected by the flow field in the same way as passive tracers; this occurs when the two properties happen to vary in a compensating manner, for example from warm and salty to cold and fresh, such that they do not result in a change in potential density. Furue et al. give details on how to separate
δT into a wave component (dynamical anomaly) and an advective component (spiciness anomaly) [
33], and provide examples on how they propagate in the tropical Pacific. These components are displayed in the middle and lower panels of
Figure 5 and
Figure 6. We see that the dynamical anomaly plays a dominant role, as expected given the dynamical nature of OTEC perturbations.
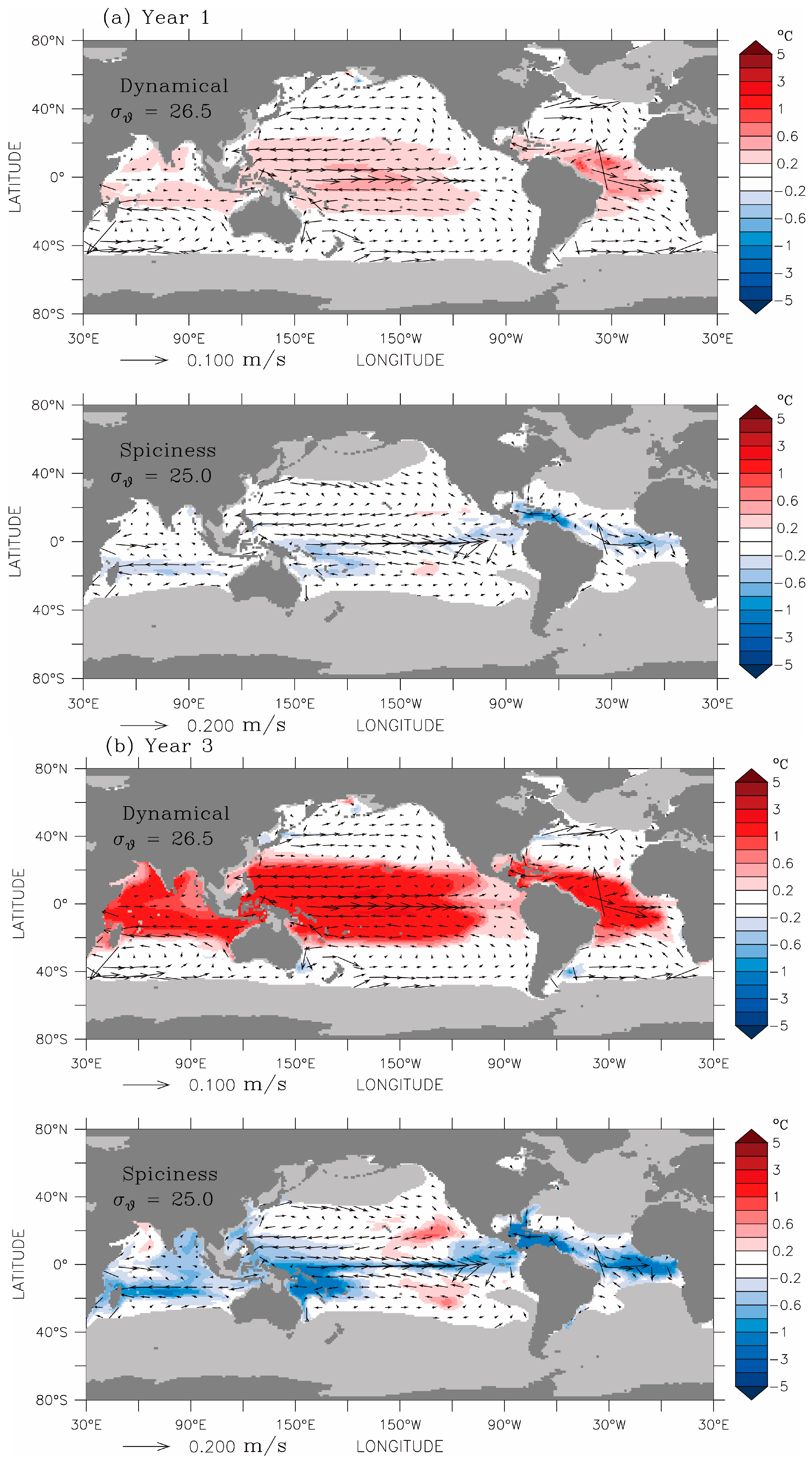
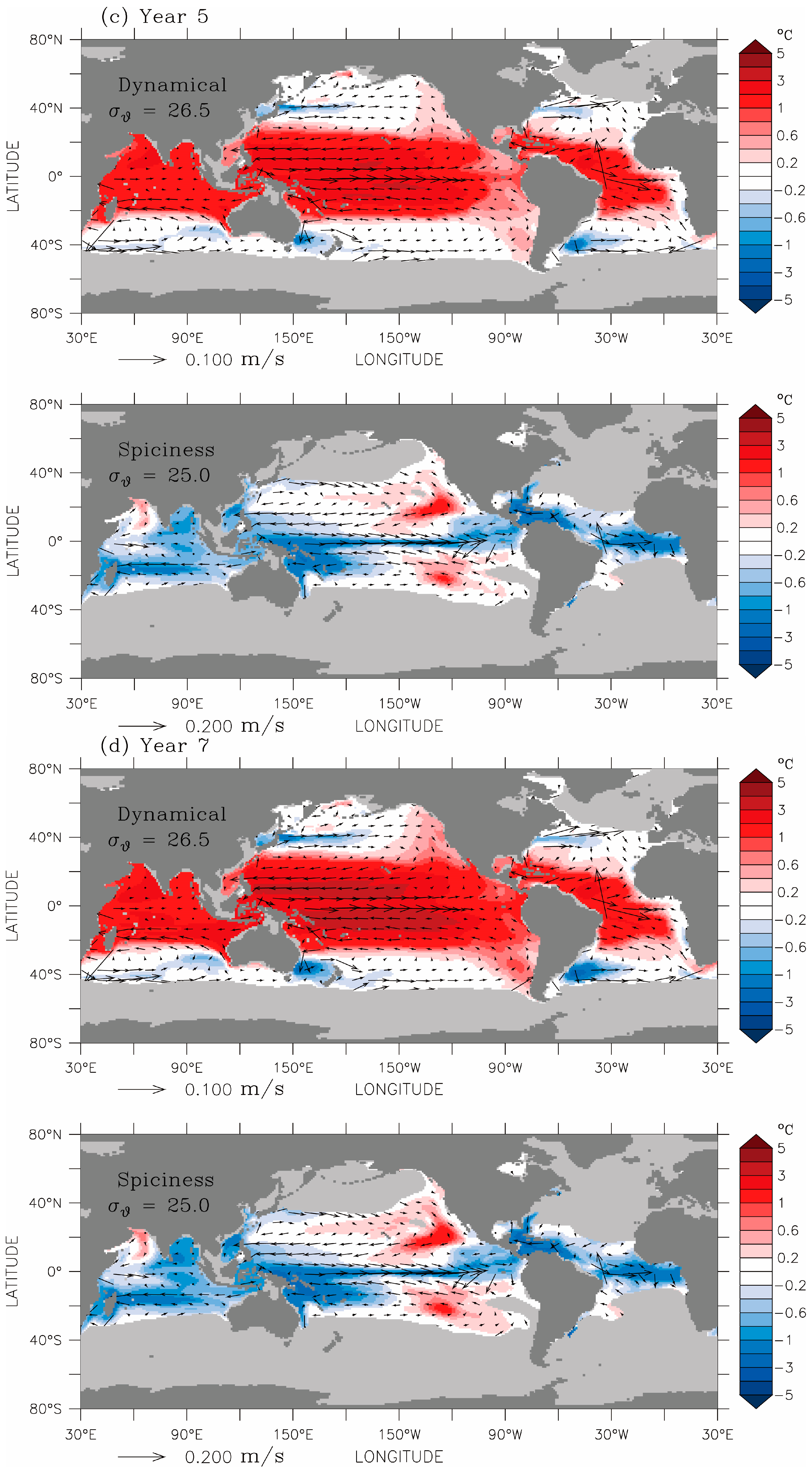
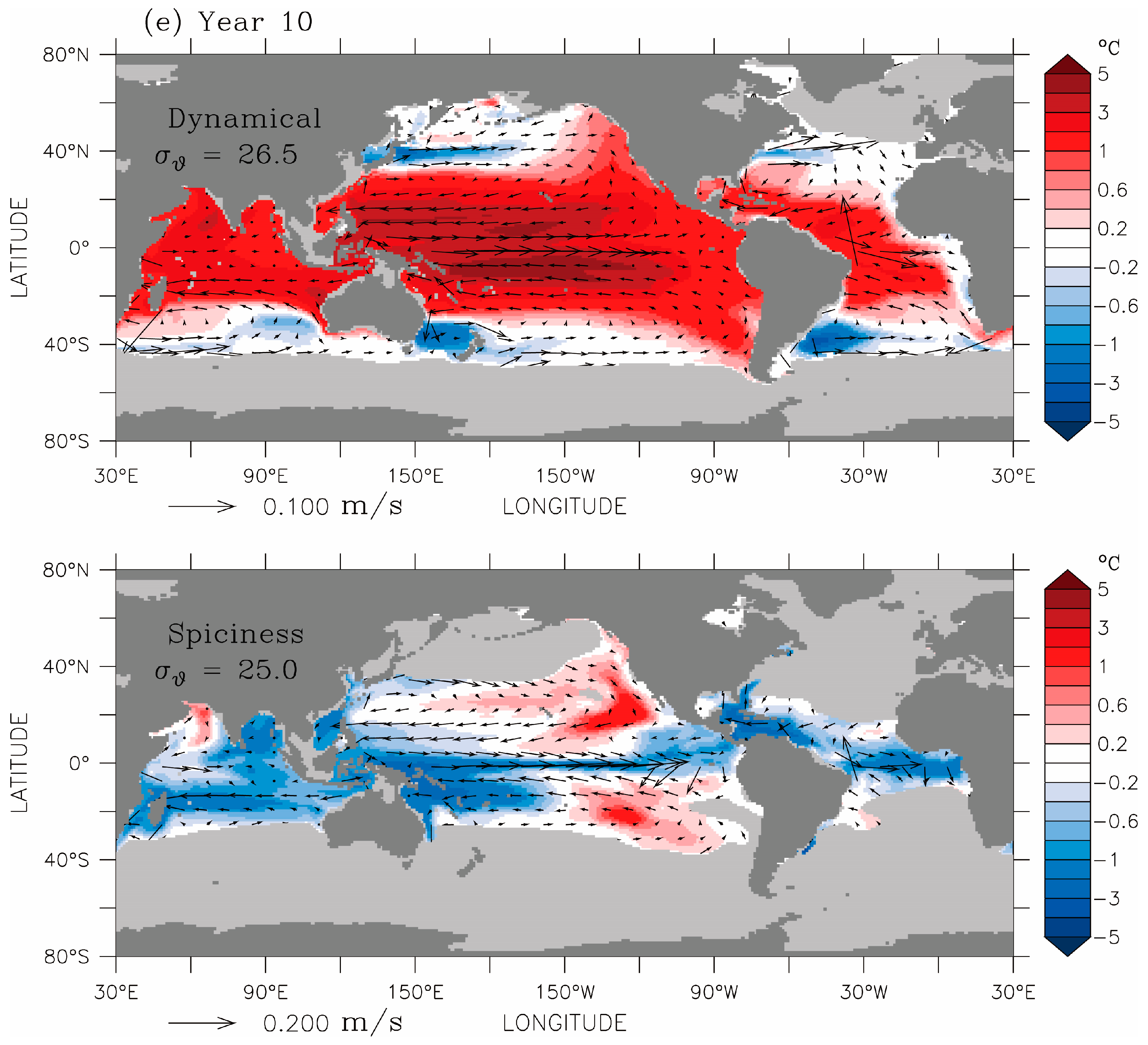
Figure 7a,e contrasts the ways in which the dynamical and spiciness components of the temperature anomaly spread in time throughout the domain, on density surfaces
σθ = 26.5 for the dynamical component (upper panel) and
σθ = 25.0 for the spiciness component (lower panel). These are the surfaces where the components have their respective maxima along the Equator in the Pacific sector, positive for the dynamical anomaly and negative for the spiciness anomaly (middle and lower panels in
Figure 6). The snapshots in the sequence correspond to simulation times representing 1, 3, 5, 7 and 10 years after the onset of OTEC deployment, respectively. Arrows represent the ocean circulation in
CTL. In
Figure 7a, merely one year after the start of OTEC operations, the warm dynamical anomaly is confined within the OTEC zone. By Year 10 (
Figure 7e, upper panel), its magnitude has gradually increased and the region of anomaly greatly expanded. In particular, there is clear indication of its poleward extension along the eastern boundary in each basin, opposite to the direction of flow. This represents the action of Kelvin waves. Within the equatorial wave guide (in a latitude range approximately 4° wide across the Equator), equatorial Kelvin waves propagate eastward, spreading the dynamical component to the eastern boundary, where they split into poleward-travelling coastal Kelvin waves to reach the coast of Alaska and the tip of South America in the Pacific Ocean, the southern coast of Australia in the Indian Ocean, and South Africa in the Atlantic. In the high latitudes of the North Atlantic where the surface mixed layer water is heavier than this density surface (light grey, see also the contours in
Figure 4), the warm dynamical anomaly reaches the high latitudes along denser surfaces (e.g.,
σθ = 27.5, not shown). The signatures of Rossby waves can also be seen in this figure. Rossby waves are reflected from the coastal Kelvin waves to propagate due west. Since the phase speeds of Rossby waves are fastest in the tropical latitudes and decrease sharply towards the high latitudes, the westward extension of the warm anomaly narrows sharply poleward, which is seen most clearly in the Pacific Ocean. Within the OTEC zone and outside the equatorial wave guide, OTEC activity can also generate Rossby waves that carry temperature anomalies to the western boundary, where they turn equatorward as coastal Kelvin waves, and then eastward as equatorial Kelvin waves which then split into poleward coastal Kelvin waves at the eastern boundary. Rossby and Kelvin waves would propagate cool dynamical anomalies on lighter potential density surfaces in the same manner as for the warm anomalies on denser potential density surfaces. The main difference is that lighter
σθ surfaces rise to intersect the ocean surface at lower latitudes, bringing a cool anomaly to the tropical region, while the denser
σθ surfaces affect the ocean surface temperature at higher latitudes. This explains the temperature anomaly distribution shown in
Figure 4 at the ocean surface.
The spiciness anomaly, transported by the flow field, is very weak initially but its magnitude and distribution evolve with time. In
Figure 7e (lower panel), there are two striking features in the Pacific Ocean: a cold anomaly being transported along the Equator from west to east by the equatorial undercurrent, and two patches of warm anomaly spread by the equatorward and westward branches of the subtropical gyres. The cold anomaly has its origin in the western part of the basin inside the OTEC zone. The warm patches appear near the edges of the OTEC zone in the eastern part of the basin initially, and are later joined by additional warm anomalies advected into the OTEC zone from the outcrops of this surface in the northeast and southeast. Here outcrops refer to the locations where this potential density surface intersects the base of the surface mixed layer. The intrusion of warm anomalies is by the action of subduction, a process that transfers surface mixed layer water into the pycnocline (a highly stratified layer below the surface mixed layer). The warm anomaly of the surface layer in the high latitudes comes from the dynamical anomaly as discussed earlier.
4.2. Ocean Circulation
One important aspect of the ocean circulation is the meridional overturning circulation, evaluated by a streamfunction [
30],
where
v is the meridional component of velocity in the ocean (positive northward), including contributions from both the large-scale flow field and the eddy-induced transport from the Gent and McWilliams scheme [
25]. The zonal integral in
x, following a parallel at latitude
y, can be around the whole globe or across an ocean sector bounded by land. The vertical integral starts from the ocean bottom −
H(
x,
y), where
ϕ = 0 by definition, to a depth
z. As implied, the streamfunction diagnoses the zonally integrated volume transport in the meridional direction.
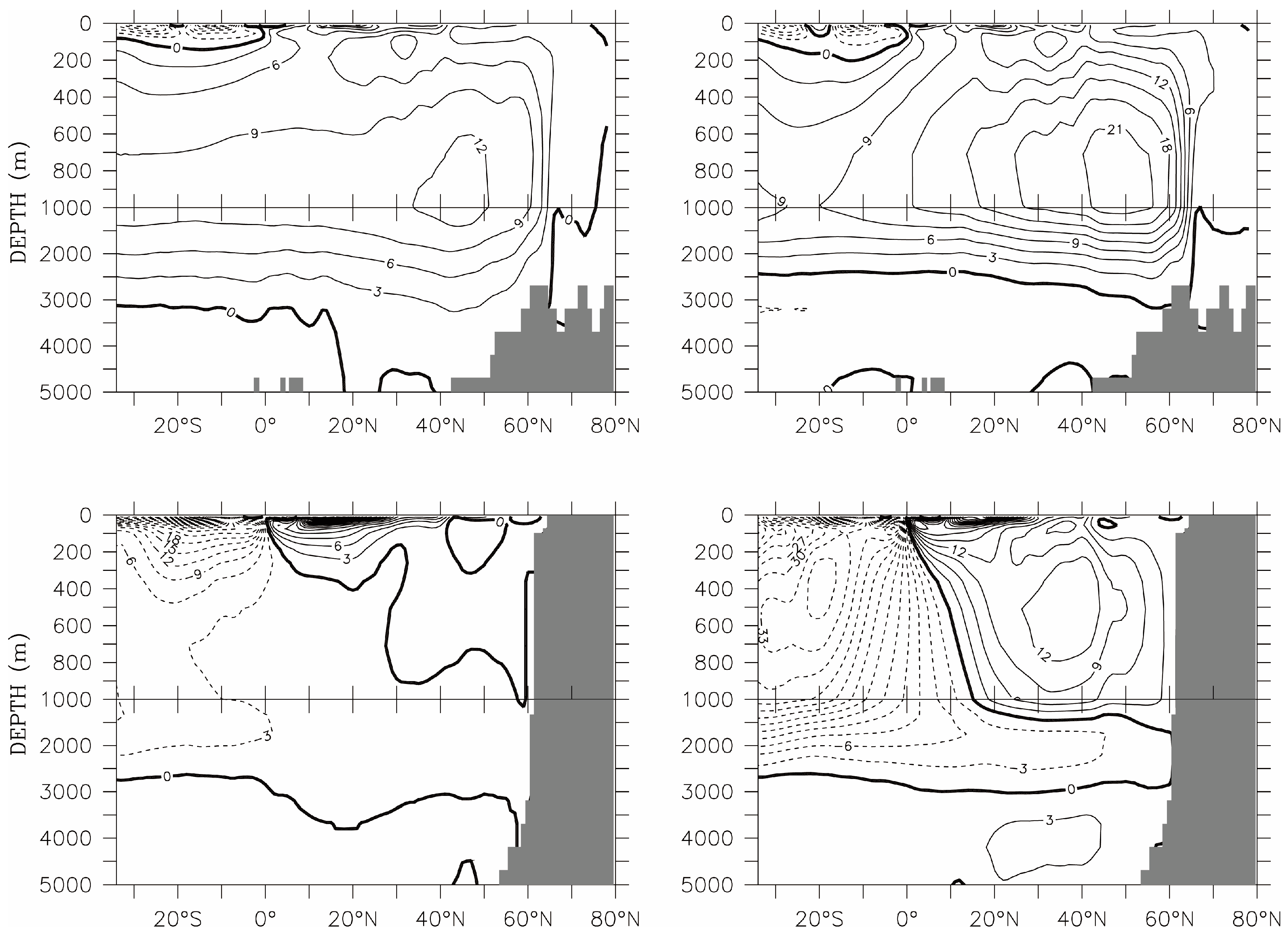
Figure 8 displays the annual mean of
ϕ(
y,
z) for the sectors of Atlantic (upper panels) and Indo-Pacific (lower panels), and experiments
CTL (left panels) and
W15 (right panels).
The Atlantic Meridional Overturning Circulation (AMOC) is dominated by a deep clockwise cell in
ϕ(
y,
z) (
Figure 8, upper-left), resulting from the northward flow of near-surface warm water, the sinking at high northern latitudes (~60° N) due to surface cooling, and the southward flow of the cold North Atlantic Deep Water (NADW) at depth. This circulation cell transports much of the heat gain in the tropics to the high northern latitudes, and thus plays an important role in regulating the climate system. One estimate of the annual mean transport strength is 18.7 ± 5.6 Sv [
34], based on field data collected along 26.5° N during a one-year period (March 2004–March 2005). In experiment
CTL, we obtain a lower value of around 12 Sv, but well within the range of 8–28 Sv produced by simulations from a collection of ocean-ice models [
35].
The Indian and Pacific basins, connected in the Indonesian Archipelago, are combined to form one closed sector, Indo-Pacific, in the evaluation of
ϕ(
y,
z). The characteristics of the meridional circulation in this sector are the two shallow wind-driven cells on either side of the Equator known as the subtropical cells (STCs) [
36]. They consist of (1) subduction of surface mixed layer water into the pycnocline in the subtropical region, (2) equatorward advection of cool subsurface water into the tropics, (3) upwelling at the Equator, and (4) poleward flow of warm surface water back to the subtropics (
Figure 8, lower-left). These shallow cells also exist in the Atlantic, except that the dominant northward flow of AMOC weakens their signatures in
ϕ(
y,
z).
In the real ocean, cooling from heat loss at surface and salinification from brine rejection during ice formation also result in convective mixing around Antarctica, leading to the formation of the Antarctic Bottom Water (AABW), primarily in the Ross and Weddell Seas. AABW sinks, spreads northward across all ocean basins, gains buoyancy through abyssal mixing with overlying less-dense water and returns to the Southern Ocean, forming an anti-clockwise meridional circulation beneath the AMOC cell. Observationally-based estimates of the strength of this bottom cell range from 13 to 27 Sv [
37,
38]. Models tend to produce lower values from 0 to 15 Sv [
39]. This cell is absent from our model simulations (reflected by the lack of contours below 4000 m depth in
Figure 8, left), as a result of the crude representation of processes associated with ice formation.
In model simulations, large-scale OTEC activity significantly modifies the circulation patterns described above. This can be appreciated in the right-hand side panels of
Figure 8, representing the stream function for
W15. The most striking feature is an apparent intense upwelling within the OTEC zone, seen as near-vertical contours that originate near 1000 m depth to reach the sea surface in the Indo-Pacific basin, and to a lesser extent, in the Atlantic basin. We use the word “apparent” because vertical contours of
ϕ(
y,
z) cannot be interpreted as straightforward signatures of actual streamlines wherever the flow field is divergent in the mathematical sense, i.e., when the divergence operator applied to the velocity vector does not vanish. In physical terms, from mass conservation, this rare situation only occurs in the immediate neighborhood of fluid sources and sinks. While there is no issue without OTEC (
CTL), the activation of OTEC in the model consists of introducing two sinks and one source within the water column of a selected region. Therefore, the inference of fluid velocity from
ϕ(
y,
z) would be incorrect at or near depths where the OTEC flow singularities are active. The deep cold seawater intake centered at 1160 m, for example, draws a convergent flow throughout the OTEC zone to replenish a loss of water (deep sink). Similarly, the mixed effluent discharge above generates a divergent flow (source). While the streamlines connecting deep intake and discharge may be expected to be quasi vertical, as shown by the vertical contours in the right-hand side panels of
Figure 8, the flow itself would not behave like an upwelling through the water column. Instead, the direction of flow would change depending on depth, i.e., vertical location relative to those of the OTEC deep sink and source. This is illustrated, for example, in
Figure 9, where the computed vertical velocity averaged between 2°S and 2°N across the Equator, exhibits additional sign changes through the water column when OTEC is activated (lower panel).
Figure 9 also shows that in the upper ocean, equatorial upwelling is unambiguously intensified by OTEC activity (compare the upper and lower panels). This stems from the action of the OTEC effluent discharge (source). Although the discharge is distributed across the tropical region, upwelling occurs only within the equatorial belt (approximately within 2° of the Equator). Off the Equator, flow at subsurface is directed equatorward towards the upwelling region (e.g.,
Figure 7a–e). The upwelled water is transported poleward in both hemispheres in the Indo-Pacific, and primarily northward in the Atlantic (dense horizontal contours near the surface on either side of the Equator in
Figure 8, right panels). Since the OTEC warm seawater intake (shallow sink), at 27.5 m depth, is within the poleward flowing surface layer, there is immediate replenishment by upwelled water transported from the Equator.
We now get back to a more comprehensive interpretation of the streamline contours in the right-hand-side of
Figure 8. In the Atlantic, the effects of OTEC activity are relatively weak in the southern hemisphere, and the exchange with the Southern Ocean is practically unchanged at approximately 9 Sv (the
ϕ(
y,
z) value at 35°S near 1000 m depth in
Figure 8, upper), with inflow of upper layer water and outflow of the NADW. In the northern hemisphere, AMOC is greatly enhanced by OTEC-induced flows: the convergent flow towards the equator at the deep OTEC sink depth and the northward flow in the upper ocean from the increased equatorial upwelling. In the Indo-Pacific sector (
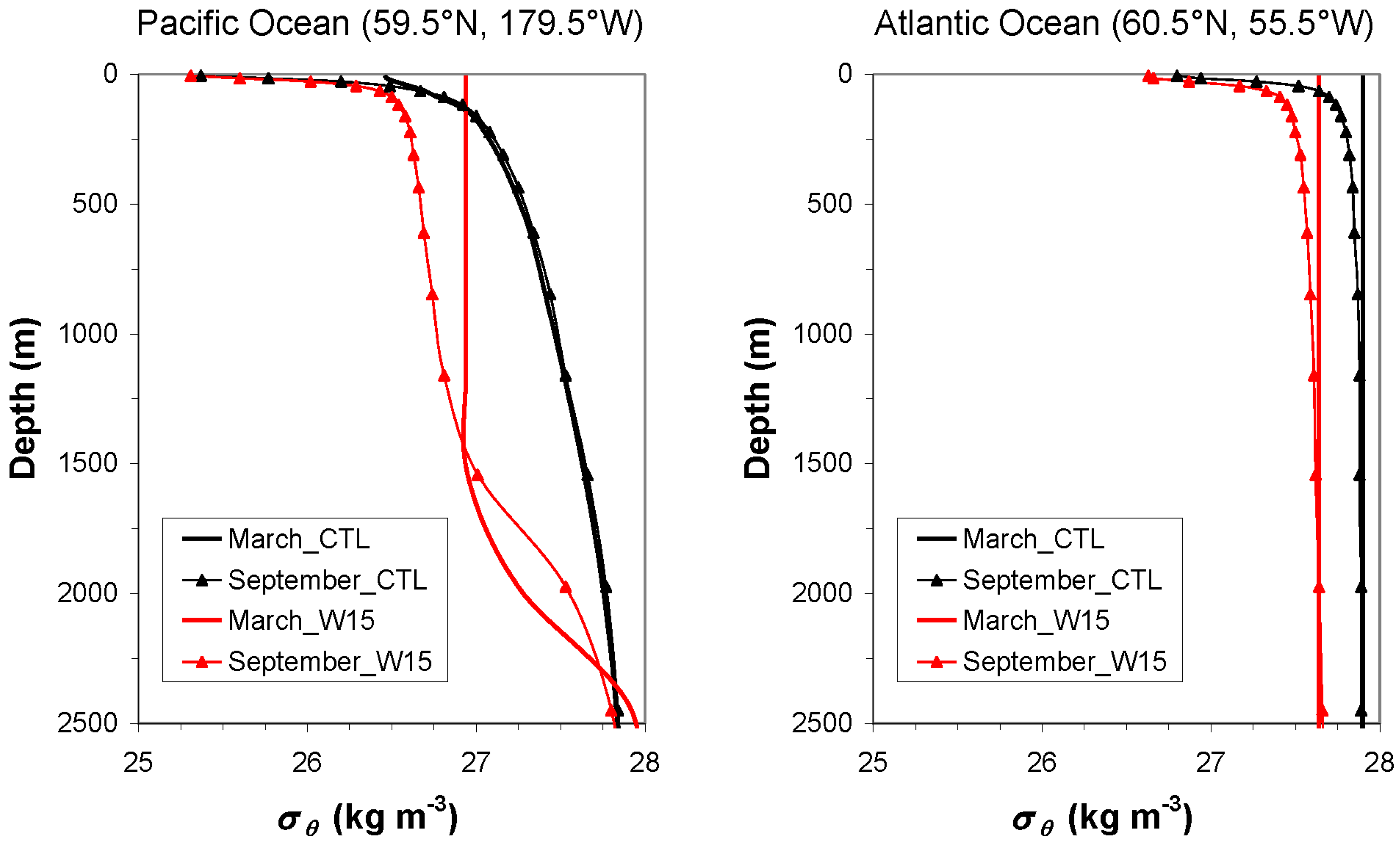
Figure 8, lower-right), exchange with the Southern Ocean increases dramatically when OTEC is active. Superimposed over the original shallow wind-driven cell is the strong southward flow into the Southern Ocean in the upper 500 m, and the deep northward flow at depth extending into the northern hemisphere. In addition, OTEC activity induces a deep overturning cell in the northern hemisphere that very much resembles AMOC. The sinking near 60° N suggests that there are deep mixing events in the North Pacific. Indeed, mixed layer depth at several locations reaches 1600 m around the dateline in winter. The density profiles at one such location are shown in
Figure 10 (left). Without OTEC, stratification changes very little from summer to winter below the seasonally affected surface layer. With OTEC, stratification at this location is much weakened with deep convective mixing events in winter, inducing an AMOC-like circulation. As a comparison, also shown in
Figure 10 (right), are the density profiles at a location within the Labrador Sea in the North Atlantic, where winter convective mixing reaches below 2000 m with or without OTEC. With OTEC, the Labrador Sea Water, a contributor to the deep southward flowing branch of AMOC, is produced at a lighter density.
The modeled effects of large scale OTEC implementation on ocean circulation, as discussed in the previous paragraphs, seem to be substantially different depending on which basin is considered, the Atlantic or the Indo-Pacific. Such differences, however, may largely reflect the very different ocean circulation patterns that prevail in each basin even without OTEC (e.g., left-hand-side panels of
Figure 8). The modeling scenario selected to illustrate potential large scale environmental effects from OTEC corresponds to
W15 (i.e., R-W × 40 with
wcw = 15 m year
−1 at maximum OTEC power production), and covers the entire so-called OTEC region (GLOBAL). Therefore, specific effects directly resulting from OTEC activity would be superimposed on the existing circulation.
The equatorward convergent flow at depth and poleward divergent flow at the ocean surface associated with OTEC activities introduce a clockwise meridional circulation in the northern hemisphere and a counterclockwise meridional circulation in the southern hemisphere. Their signatures are clearly visible in Indo-Pacific through deep overturning cells in both hemispheres, and in the North Atlantic through the enhancement of AMOC (
Figure 8, right). In the South Atlantic where the OTEC-induced flows are expected to counteract the existing AMOC, it is puzzling that the exchange with the Southern Ocean seems little affected.
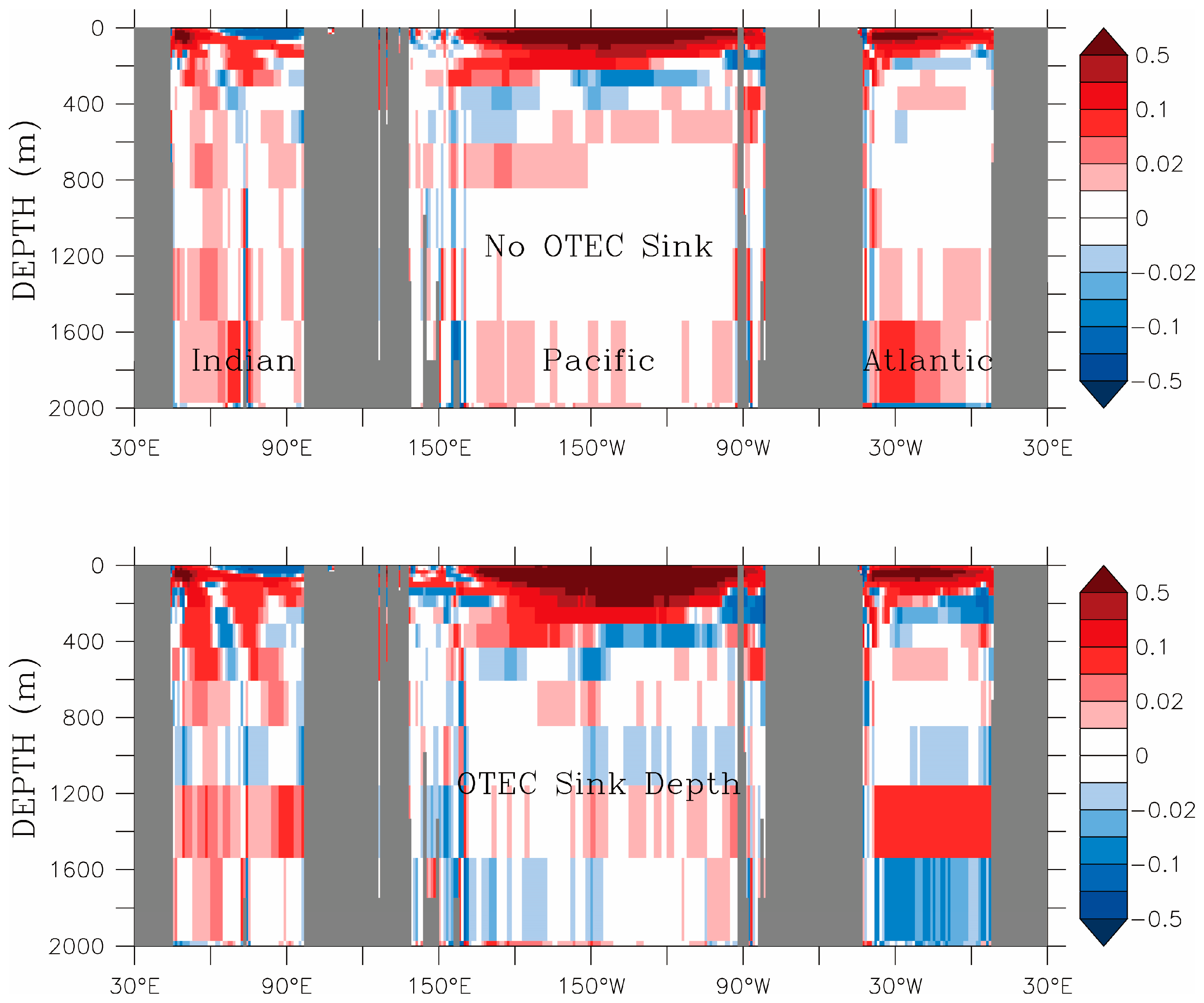
To further elucidate OTEC specific effects, we ran two numerical experiments similar to
W15, but with implementation areas limited to either the Atlantic, or to the Indo-Pacific, as defined in Rajagopalan and Nihous [
18]. The areas covered by these separate OTEC regions are quite different in size, i.e., 21 × 10
6 km
2 for the Atlantic versus 95 × 10
6 km
2 for the Indo-Pacific; therefore, the single value of the OTEC cold seawater flow rate per horizontal area used here,
wcw = 15 m year
−1, corresponds to relatively much larger overall OTEC flow rates in the Indo-Pacific. This might skew or complicate
a priori a comparison between basins, and simulations with two different values of
wcw might be considered in the future. When separate OTEC power production maxima were determined for the two regions [
18], however, with a value of
wcw twice as large in the Atlantic as in the Indo-Pacific, reported environmental effects did not qualitatively contradict the foregoing results [
18] (
Figure 5 and
Figure 6).
In the experiment with OTEC activated in the Atlantic only, there is a modest increase (~3 Sv) in AMOC in the North Atlantic and now there is also a reduction (~6 Sv) in the exchange with the Southern Ocean at 35° S, as anticipated, while circulation in the Indo-Pacific sector is little affected (compare
Figure 8 and
Figure 11, left panels). When OTEC is activated in the Indo-Pacific only, the strong deep circulation cells generated in the Indo-Pacific sector very much resemble those from the GLOBAL scenario (
Figure 8 and
Figure 11, lower-right panels). In contrast to the Atlantic-only experiment, however, changes in circulation in the Indo-Pacific basins have significant effects on the Atlantic, with an increase in AMOC strength by approximately 6 Sv (compare
Figure 8, upper-left panel with
Figure 11, upper-right panel). It appears that combined OTEC activities in the Atlantic and Indo-Pacific basins result in a net enhancement of AMOC in the North Atlantic, while their effects essentially cancel each other in the South Atlantic.
The sensitivity of Atlantic circulation to OTEC activities in Indo-Pacific stems from the global nature of AMOC. The formation of NADW through surface cooling in the polar regions of the North Atlantic has long been recognized as a major driving force of the global overturning circulation, forming the downwelling branch of AMOC. In recent years, upwelling in the Southern Ocean, driven by winds and eddies, has been identified to play a vital role in bringing NADW back to the surface for the closure of AMOC [
40].
Upon exiting the South Atlantic, NADW is drawn into the Antarctic Circumpolar Current (ACC) system. After some circuitous routes including excursions to the Indo-Pacific basins (weak signatures of NADW can be seen in the lower-left panels of
Figure 8 and
Figure 11 around 1000 m depth), it eventually upwells to the surface in the Southern Ocean where it participates in the formation of Antarctic water masses that spread into all ocean basins. The northward flowing upper branch of AMOC is a convergence of near surface waters from all the ocean basins facilitated by ACC, specifically from the Pacific Ocean via the Drake Passage and from the Indian Ocean through the leakage of Agulhas Current Retroflection at the southern tip of Africa. The OTEC-induced flows in the southern Indo-Pacific basins effectively introduce an additional component to the Southern Ocean upwelling through the transformation of deep water to surface water, leading to the strengthening of AMOC.