Abstract
The impacts of coastal erosion are expected to increase through the present century, and beyond, as accelerating global mean sea-level rise begins to enhance or dominate local shoreline dynamics. In many cases, beach (and shoreline) response to sea-level rise will not be limited to passive inundation, but may be amplified or moderated by sediment redistribution between the beach and the broader coastal sedimentary system. We describe a simple and scalable approach for estimating the potential for beach erosion and shoreline change on wave-dominated sandy beaches, using a coastal sediment compartments framework to parameterise the geomorphology and connectivity of sediment-sharing coastal systems. We apply the approach at regional and local scales in order to demonstrate the sensitivity of forecasts to the available data. The regional-scale application estimates potential present and future asset exposure to coastal erosion in New South Wales, Australia. The assessment suggests that shoreline recession due to sea-level rise could drive a steep increase in the number and distribution of asset exposure in the present century. The local-scale example demonstrates the potential sensitivity of erosion impacts to the distinctive coastal geomorphology of individual compartments. Our findings highlight that the benefits of applying a coastal sediment compartments framework increase with the coverage and detail of geomorphic data that is available to parameterise sediment-sharing systems and sediment budget principles. Such data is crucial to reducing uncertainty in forecasts by understanding the potential response of key sediment sources and sinks (e.g., the shoreface, estuaries) to sea-level rise in different settings.
1. Introduction
Beach erosion is a natural process often caused by high waves (and temporarily raised coastal sea levels) during storms that drive the rapid (hours to days) transfer of large volumes of sand from the sub-aerial beach and dunes to the adjacent surf zone and shoreface. Using aerial LiDAR surveys, Harley et al. [1] found that 11.5 million m3 of sand was temporarily lost to the sea from 177 km of shores in southeast Australia during a single storm in June 2016, with an average of 65 m3 (and maximum of 228 m3) being lost from each metre of beach alongshore. While the loss of sand offshore is usually temporary, full beach recovery to the pre-storm state may take several months to several years, depending on the post-storm wave climate and frequency of storms [2,3,4]. Future change in modal and storm wave climates, due to climate change, may drive changes in shoreline orientation and the range of shoreline variability, as the distinctive morphology of different beaches adjusts to new hydrodynamic conditions [5,6,7].
Severe beach erosion can generate significant socio-economic and environmental impacts for coastal communities, relating to the damage or loss of: assets (properties, infrastructure, utilities, and public facilities), recreational and commercial beach amenity (including tourism), coastal habitats, and ecosystem services [8,9,10,11]. The increasing cost of these impacts has prompted a growing research focus on coupled physical-economic modelling of coastal systems, to examine the value and equity of potential solutions [12,13,14,15]. Areas that are subject to beach erosion impacts at present may require careful management and coastal engineering solutions, while future impacts can be minimised by locating new development beyond the future reach of erosion, and by maintaining naturally resilient beaches with sufficient sand supplies to accommodate erosion and recovery cycles.
Global sea-level rise through the present century, and beyond, is expected to drive mean-trend shoreline recession, where the underlying sediment supply to beaches is insufficient to oppose the passive and morphodynamic influences of sea-level rise on shoreline migration [16,17]. In many settings, the rate of shoreline recession will not be simply the rate of passive inundation, but may be enhanced by the cumulative loss of sediment from the beach and dunes, as the beach morphology responds to new boundary conditions [18]. In that case, sand may be progressively lost from the beach and dunes to other depositional environments of the coastal system (e.g., tidal inlets, estuaries, the shoreface), or alongshore. Shoreline recession exposes land (and assets) that has been historically protected from coastal hazards by natural dune buffers to the impacts of beach erosion.
While process-based modelling suggests that global mean sea level may rise by around 0.44 m (RCP2.6 median value) to 0.74 m (RCP8.5 median value) by the end of this century [19], other evidence suggests the potential for global sea-level rise up to 2.5 m by 2100 [20], due to accelerated ice loss from glaciers and ice sheets that is not captured in process-based models. Uncertainty regarding the impact of sea-level rise on global shorelines during the present century and beyond, due to the wide range of sea-level projections, and local controls on sediment redistribution (and thus shoreline response), compels the development of methods for shoreline forecasting that capture the complexity of coastal depositional systems, and communicate the spectrum of potential impacts.
One approach to understanding (and predicting) shoreline change that is caused by a sediment budget imbalance at the beach (whether positive or negative), as may be imposed by sea-level rise, is to model the redistribution of sediments within the coastal depositional system. The approach is founded on the premise that beaches are elements of broader sediment-sharing coastal systems (or coastal tracts), which include the key depositional environments of coastal barrier systems (i.e., rivers, estuaries, tidal inlets, dunes, beach, shoreface, continental shelf) [21]. Assuming the perspective of the beach, these depositional environments meet at the littoral sediment transport system, which also connects the coastal tract to adjacent depositional systems (and their beaches) alongshore. Sediment budget principles [22,23] can be applied to map and model sediment exchanges between the various depositional environments, and the resulting shoreline change [24,25].
Coastal sediment compartments (and littoral sediment cells) are spatial tools for understanding (and quantifying) sediment connectivity within and between sediment-sharing coastal systems. Sediment compartments identify more or less contained systems, and are usually based on the broad-scale structure of the coastline and prominent features that impede alongshore transport [26]. Littoral cells are usually finer in scale and identify sectors of uniform alongshore sediment transport, which are separated by convergence and divergence points. Sediment compartments and littoral cells have been mapped in many jurisdictions, including the United States (US) [27], United Kingdom (UK) [28,29], and Australia [30,31,32], to ensure coastal management and planning initiatives reflect that local beach dynamics are influenced by sediment exchanges with other depositional environments of the sediment-sharing system. They have been applied as qualitative templates simply to identify beaches that are connected by sediment transport, or quantitatively, to parameterise and model sediment budgets and shoreline change. Sediment compartment mapping was recently completed for the entire Australian coastline to inform the national assessment of coastal hazard impacts and risks [33,34]. The benefits of a sediment compartments approach are most fully realised where the framework can be applied to parameterise and model sediment budgets and shoreline change within a sediment-sharing system.
We describe a scalable method for using sediment compartments to assess potential exposure to shoreline change on embayed wave-dominated beaches in New South Wales (NSW), Australia. The sediment compartments framework is used to parameterise coastal morphology and quantify sediment exchanges between sources and sinks. A simple volumetric shoreline encroachment model is applied within the framework to estimate the impact of modelled sediment redistribution on shoreline change. We use a Monte Carlo sampling regime to estimate and communicate uncertainty in shoreline change forecasts statistically, which is necessitated by the intrinsic uncertainty around: environmental change (e.g., sea-level rise), sediment transport processes, and the shoreline model. We demonstrate the approach at a regional scale to develop a second-pass assessment of exposure to shoreline change along the NSW coast this century, and at a local scale to demonstrate the flexibility of the method in capturing the sensitivity of shoreline response to fine-scale geomorphic variability.
The method that we demonstrate is intended to provide a second-pass assessment of potential exposure to coastal erosion and shoreline change. While the approach accounts for the distinctive geomorphology of individual sediment compartments and beaches, we adopt several simplifying assumptions to account for poorly understood or documented processes, with the goal to apply a consistent shoreline response model to all of the NSW beaches. The suitability of those assumptions for individual beaches should be evaluated in any local-scale assessment of shoreline change.
2. Regional Setting
We consider present and future exposure to beach erosion and shoreline change along the coastline of New South Wales (NSW) in southeast Australia. The oceanic coast is roughly 2065 km in length, including 1038 km of sandy shorelines, which are divided into 721 beaches that are primarily influenced by open-coast processes [35,36]. Most beaches are backed by readily erodible Quaternary (Holocene or late Pleistocene) beach and dune deposits [37]. In some locations, emergent bedrock or engineered structures (e.g., sea walls) may restrict the potential extent of beach erosion, or weakly cemented sediments (e.g., indurated sand) may impede the rate of shoreline change. About 45% of all sandy shorelines occur within or are immediately backed by National Park reserves, where infrastructure and development are restricted to minimal recreational amenities, and beach systems generally occur in natural states. Around 15% (150 km) of sandy shorelines along the NSW coast are located within 110 m of existing property lot boundaries.
2.1. Coastal Geomorphology and Processes
The NSW coast is situated on the tectonically passive southeast Australian continental margin (Figure 1A). The geometry of the continental shelf is relatively deep and narrow (30–50 km wide) when compared with classic passive margins (e.g., US Atlantic), meaning that wave energy from the moderate- to high-energy wave climate experiences minimal attenuation before arriving at the coast [38]. Swell and storm wave directions are typically south to south-east [39], driving a northward littoral sediment transport system, which is most effective along the northern third of the coast where the coastal morphology supports relatively continuous alongshore transport [40,41]. The coast is periodically impacted by extratropical cyclones that intensify in the Tasman Sea [42], generating high waves and temporarily raised sea levels (storm surges) that can cause severe beach erosion [1].
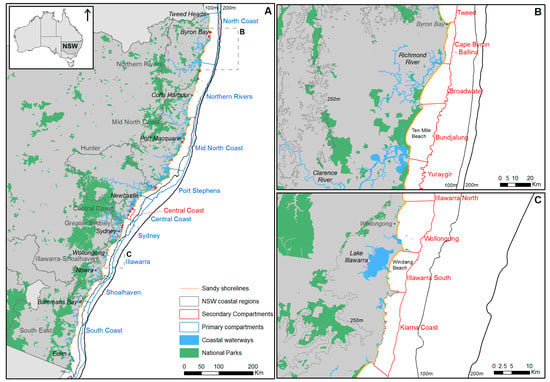
Figure 1.
(A) Location and orientation of the New South Wales (NSW) coastline, showing: the distribution of sandy shorelines; the variable geometry of the continental shelf (indicated by 100 and 200 m isobaths); the nine primary coastal sediment compartments (including names) [33,34]; and, the seven NSW coastal regions considered in the exposure assessment. The small red dots indicate identified erosion hot spots [44]. Representative secondary sediment compartments [33,34] from the (B) North Coast and (C) Illawarra primary compartments are also shown. The 250-m elevation contour shown in (B) and (C) compares coastal relief between the North Coast and Illawarra regions. The location of the Central Coast secondary sediment compartment (Figure 3A) is shown in (A).
The coast features embayed sandy beaches of varying lengths, which are separated alongshore by rocky headlands and cliff coasts that trace the ancient geological framework of the coastline [43]. The northern third of the coast features broader and shallower embayments, low hinterland and broad coastal plains, large rivers, and a more gently sloping inner-continental shelf (Figure 1B). In contrast, the central and southern coasts feature smaller embayments, rugged hinterland and narrow coastal plains, coastal lakes and lagoons with small rivers or streams, and a steeper and narrower inner shelf (Figure 1C). At a finer scale, compartment dimensions and geology, sediment type and availability, and exposure to regional wave climates, all control beach morphodynamics in this wave-dominated and microtidal (approximately 2 m spring tidal range) setting [35,36].
Sediment cover across the inner shelf is relatively thin, except where relict coastal barriers and shelf sand bodies accumulated during lower sea levels, prior to erosional reworking during the late Holocene post-glacial marine transgression and subsequent sea-level highstand [45,46]. A marine abrasion surface extends along 300 km of the central to southern coast, frequently outcropping across the submerged inner-shelf seabed [46]. The abrasion surface is related to the prominent coastal escarpment that is evident on steeper sectors of the coast, and is thought to have formed by cyclic erosion and planation of the Palaeozoic to Mesozoic bedrock by coastal processes, as the shoreline migrated in and out across the margin during late Quaternary sea level fluctuations [46]. The extent of the marine abrasion surface captured in detailed seabed mapping off the Sydney coastline [47] suggests that many central and southern compartments may be sediment deficient offshore.
Most NSW beaches are elements of coastal sand barriers, which are composite sand bodies that comprise shoreface, beach, dune, and estuarine deposits [48]. The sand barriers are late Pleistocene to Holocene in age, and separate the ocean beaches from back-barrier water bodies (rivers, coastal lakes, and lagoons) and the coastal hinterland [43]. The sub-aerial surfaces of the sand barriers include relatively low-lying coastal plains of varying extents, depending on the compartment dimensions and barrier type [49]. Development is often concentrated on the coastal plains due to their flat and regular morphology. Unlike low-gradient passive margins (e.g., US Atlantic and Gulf coasts), which feature narrow, low-lying barrier islands that are dominated by barrier-bypassing processes (e.g., washover and tidal inlet migration), the bay barriers of NSW are typically higher, wider, and more stable in comparison, and mostly feature well-developed dune morphology formed over hundreds to thousands of years by south easterly wave and wind climates [48,49]. As such, dunes are most developed in the northern ends of embayments, and sediment exchanges between beaches and back-barrier environments are usually via stable tidal inlets (not washover).
2.2. Exposure to Coastal Erosion
Properties and infrastructure along several NSW beaches have been damaged or destroyed by erosion in the past [50,51,52]. Beach erosion is usually caused by extratropical cyclones (ETCs)—locally termed East Coast Cyclone (ECC) or East Coast Low (ECL) storms. The storms originate from various locations on or adjacent to the Australian continent, depending on the synoptic pattern, and intensify over the NSW coast or in the Tasman Sea, generating high waves (usually with ESE to SE directions) and elevated coastal sea levels [7,42]. An unusual storm featuring a coupled ETC and anticyclonic intensification impacted the entire southeast Australian coast in June 2016, generating high waves with ENE to E directions, and causing severe beach erosion along the NSW coast. The storm coincided with a spring high tide, and the unusual easterly storm-wave direction resulted in minimal wave transformation prior to entering coastal embayments and impacting beaches [1,53]. Considerable damage to properties and infrastructure occurred at several NSW beaches (e.g., Figure 2).

Figure 2.
Wamberal Beach, in the Central Coast secondary compartment (Figure 1A), before (A), and after (B,C,D), severe erosion caused by a storm during June 2016 that featured an anomalous easterly storm-wave direction. The beach is underlain by a cemented siltstone unit (D) that outcrops on the beach face and in the frontal dune along the central part of the beach during severe erosion events.
Because many beaches along the northern NSW coast are connected via a northward-directed littoral sand transport system [40], temporary or persisting divergences in transport rates can also drive periodic beach erosion or ongoing shoreline recession. Periodic erosion may occur where wave climate variability supports only intermittent sediment bypassing of prominent headlands [41,54]. On the other hand, persistent and ongoing shoreline recession may result from a long-term sediment budget imbalance within a coastal sediment compartment. For example, Ten Mile Beach (Figure 1B) is part of a receding sand barrier, where long-term shoreline recession associated with net northward sand transport has exposed indurated sand (coffee rock) along the beach face [55].
Fifteen coastal erosion hot spots [44] have been identified along the NSW coast, where multiple properties are presently threatened by erosion (Figure 1A). However, the total present and future exposure to coastal erosion along the NSW coast is relatively poorly known. A first-pass national assessment of climate change risks to Australia’s coasts [56] estimated that 3600 residential buildings in NSW might be at risk from coastal erosion within the present century (i.e., are located within 110 m of erodible shorelines), including 700 buildings that may be presently at risk (i.e., are located within 55 m of erodible shorelines). However, the generalised proximity analysis method that is used, in which all of the properties within fixed distances of erodible sandy shorelines were considered as being potentially exposed, implies that the estimated exposure is only a first approximation.
Coastal erosion hazard zones are defined by local governments in NSW for management and planning purposes, and provide another estimate of potential exposure to coastal erosion impacts at present and in the future. Present-day (immediate) and future (e.g., 2050, 2100) hazard zones are usually defined, accounting for the impacts of storms, as well as historical shoreline trends and projected sea-level rise. However, the existing coverage of erosion hazard zones is incomplete, and the erosion components considered and analysis and modelling methods that are used vary between the 26 local government areas along the open coast of NSW [57,58].
3. Materials and Methods
3.1. Coastal Sediment Compartments Framework
Our approach uses a coastal sediment compartments framework (a hierarchy of compartments and sub-compartments), to parameterise the depositional environments of coastal tract systems [21]. The hierarchy is used to conceptualise and map the cross-shore and alongshore extents of sediment sharing between sources and sinks, for timescales relevant to coastal management and planning (years to centuries) [34]. The framework reflects the natural hierarchy of coastal depositional systems [21], and allows for the model parameterisation to reflect the spatial and temporal scales of the forecast, and the resolution of available geomorphology and process data. The compartments framework is the basis for developing aggregated morphological data models that capture the surface dimensions and relief of depositional landforms within the sediment-sharing systems [24].
The Australian coastline was recently divided into 100 primary sediment compartments that capture the limits of sediment sharing at long timescales (centuries to millennia), as defined by the geological framework of the coast and large coastal landforms [33]. Within the primary sediment compartments, 359 secondary compartments have been identified, representing sediment sharing at intermediate (decadal to centennial) timescales [33,34]. The NSW coast includes 9 primary and 47 secondary sediment compartments (Figure 1A).
As the broad scale of the secondary compartments often includes several embayed beaches (Figure 3A), tertiary compartments, and sub-compartments are often mapped to represent coastal landforms at finer spatial scales, commensurate with sediment sharing at short to intermediate timescales (years to decades). For example, sub-compartment mapping has been carried out in West Australia using high-resolution marine LiDAR data [59], and for the Illawarra-Shoalhaven region of NSW (Figure 1A) using nearshore seabed data and sediment transport modelling [60].
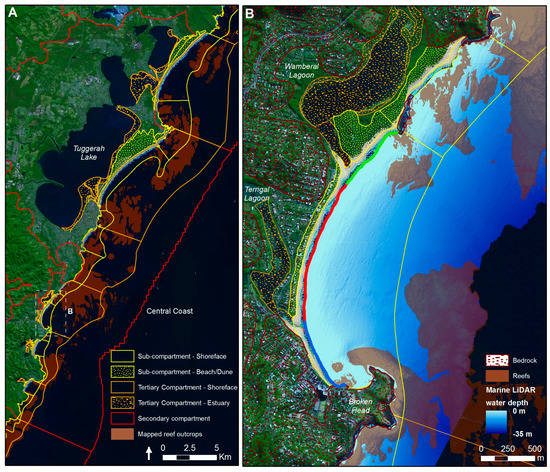
Figure 3.
(A) Example of sub-compartment mapping for the Central Coast secondary compartment (Figure 1A). Secondary compartments extend to 50 m water depth and capture the Quaternary depositional systems onshore. Tertiary compartments extend to 40 m water depth and include coastal barrier and estuarine flood-tide delta deposits onshore. Sub-compartments extend to 20 m water depth and include beach and dune deposits onshore. (B) The Terrigal-Wamberal sub-compartment includes Terrigal (blue), Wamberal (red) and Wamberal North (green) beaches. Marine LiDAR data reveals the distribution of sediments and reef outcrops (shaded brown) across the shoreface seabed.
Within the NSW secondary sediment compartments, we identified 137 tertiary compartments (inter-annual to decadal timescales), most of which contain multiple sub-compartments (annual to inter-annual timescales), to facilitate the application of our shoreline change model to all NSW beaches. In the absence of high-resolution bathymetry and seabed substrate data for the whole NSW coast, our delineation of tertiary compartments and sub-compartments was based on the:
- (1)
- dimensions and average orientation of coastal sectors and embayments;
- (2)
- prominence and alongshore extent of coastal headlands, cliffs and visible nearshore reefs;
- (3)
- extent of tidal inlets and training walls (where present); and,
- (4)
- shoreface geometry depicted in regional-scale bathymetry data.
3.2. Simple Shoreline Encroachment Model
We use a simple shoreline encroachment model that scales in complexity with the detail of data available to inform the modelling approach [61]. Encroachment refers to cumulative erosion into a pre-existing beach-dune system, in which sediment is progressively lost from the beach to the littoral zone, where it may be transferred offshore, alongshore, or into tidal inlets [62]. This is different from shoreline migration by barrier rollover, in which barrier-bypassing processes (washover and tidal-inlet sequestration) dominate, transferring sand from the beach face and frontal dune to back-barrier depositional environments [63]. Our model does not support continuous (rollover) or discontinuous (drowning, overstepping) dynamic barrier behaviours [64,65], and is therefore only applicable to simulating shoreline recession on relatively steep, moderate to high energy wave-dominated coasts, where the existing beach and dune morphology is well-developed. The model is not suitable for simulating shoreline change on low-lying barrier island coasts, where dynamic barrier behaviour controls shoreline change [64,65,66].
The encroachment response is likely to characterise the initial (i.e., present century) response of most NSW beaches to sea-level rise, as dune morphology is typically well developed and continuous alongshore, relative to the predominant wave energy conditions. However, the assumption may be violated where barrier-bypassing processes become dominant as sea level rises—i.e., where existing dune morphology is overwhelmed by combined raised sea level and elevated wave run-up heights. The assumptions and limitations of the simple shoreline encroachment model are considered by the authors to be suitable for the purposes of a second-pass shoreline change exposure assessment, but should be evaluated on a case by case basis for any finer-scale applications.
3.2.1. Volumetric Beach Response
Beach response to changing boundary conditions (e.g., storm wave conditions, sediment supply, sea-level rise) is quantified as the time-averaged sediment-flux change in the littoral transport system, which connects the beach with sources and sinks, both proximal (e.g., surf zone, tidal inlet) and distal (e.g., shoreface, flood-tide delta, up-drift river, down-drift beach). A change in the sediment balance of the littoral transport system is reflected at the beach (in erosion or accretion), and is estimated by solving the sum of the sediment volume redistribution, relative to the initial (present-day) beach volume. For example, a deficit in response to the generation of new sediment accommodation across sediment sinks may contribute to shoreline instability and encroachment, but may be offset or moderated by sediment supply from sources. We use the coastal sediment compartments framework (Section 3.1) to identify and (as far as is possible) quantify the sources and sinks, and sediment exchanges between the depositional environments of sediment-sharing coastal systems.
We parameterise sediment redistribution within each compartment and beach response (and thus shoreline change) volumetrically. This means that the predicted shoreline change can closely reflect between-site and alongshore variability in beach and dune morphology, which is now captured in high resolution, and at large spatial scales using remote sensing techniques (e.g., LiDAR).
The method differs from the simple Bruun model [67,68,69], which is based on idealised beach-dune morphology that is maintained as sea level rises. That is, because the Bruun profile is measured from the dune crest, as the shoreline recedes into the dune system by means of cumulative erosion, the dunes are presumed to aggrade at the same pace as sea level rises. This implies that rates of sand supply and dune aggradation are sufficient to maintain vertical dune growth at the same pace as sea-level rise. Otherwise, the relative dune crest height would decrease and the Bruun profile would flatten as sea level rises. However, we observe that the beach response to sediment deficit conditions on contemporary receding beaches in NSW reflects encroachment, in which cyclic dune scarping and destabilisation manifests as progressive erosion into the relict dune system, with minimal or no dune growth. The prospect of a rapid acceleration in sea-level rise in the present century adds further uncertainty to an assumption of instantaneous dune aggradation during encroachment in this setting. Adopting a risk-averse approach, our model assumes that the dunes on NSW beaches will not aggrade at the same pace as projected sea-level rise within this century.
The encroachment model calculates the sediment volume (V) lost from the initial beach and dunes at the end of the forecast period, in cubic metres per metre of beach shoreline (m3/m), due to fluctuating (F) and cumulative (C) erosion processes:
The functions describing F and C may vary in complexity depending on available data and knowledge. We define F using a gamma probability function that approximates the potential range and relative likelihoods of fluctuating erosion on fully exposed open-coast NSW beaches:
The form of F may include multiple components of fluctuating erosion (e.g., erosion due to storms, periodic shoreline rotation) if sufficient data is available. The rationale for the form (i.e., shape, range, and tail) of the gamma distribution in Equation (2) is described in Section 3.4.1. The coefficient cf (Equation (1)) is used to scale F between beaches, or along a beach (Figure 4). It is used in the regional-scale application (Section 3.4.1) in order to account for variation in exposure to the wave climate between beaches or beach sectors, and in the local-scale application (Section 3.4.2) to account for alongshore variation the resistance of the beach-dune substrate to erosion. Variable substrate resistance may occur, for example, where bedrock or cemented sediments outcrop intermittently along the beach-dune system. Both influences may limit the fluctuating erosion volume along parts of a beach.
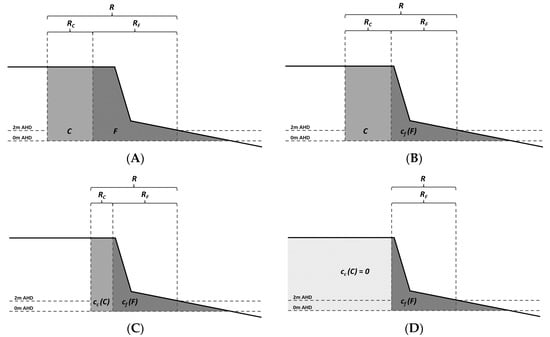
Figure 4.
Illustration of the influence of the cf and cc scaling coefficients (Equation (1)) on modelled fluctuating (F) and cumulative (C) beach erosion, and the corresponding influence on the shoreline recession distance (R). The parameterisations are (A) cf = 1, cc = 1, (B) cf < 1, cc = 1, (C) cf < 1, cc < 1, and (D) cf < 1, cc = 0. Note that erosion is calculated above mean sea level (0 m AHD) and landward from the beach berm position, which is estimated here by the 2-m AHD elevation contour.
Cumulative erosion (C) reflects a long-term imbalance in the littoral sediment budget at the beach, which is driven by persisting sediment redistribution between sources and sinks, in response to ongoing or past change in boundary conditions (e.g., sea-level rise, altered wave climate). We define C as the net sum of interactions between the potential sources and sinks for NSW beaches:
where t is the forecast period (in years) and l is the total length (m) of sandy shorelines within the tertiary compartment containing the beach system to which the model is applied (Section 3.1).
Where data exists describing mean-trend change in the beach volume due to cross-shore (x) or alongshore (y) sediment transport processes (e.g., photogrammetry analysis, beach survey record, geohistorical data), the qx and qy parameters ((m3/m)/year) may be used to describe underlying change in the littoral sediment budget. The VS (Equation (5)) and VE (Equation (6)) variables (m3/m) capture the response of the shoreface and estuarine flood-tide delta sinks to sea-level rise, respectively, over the forecast period (t). The VA, VO, VM, VB, and VR variables (m3/year) represent annual sediment losses (or gains) within the relevant tertiary compartment, due to: aeolian processes, barrier washover, mega-rips, biogenic sediment production, and river supply, respectively. While such processes may not occur uniformly along the length of sandy shorelines (l), their impacts on shoreline change are distributed alongshore throughout the tertiary compartments by the littoral transport system.
The coefficient cc (Equation (1)) scales C between or along beaches, which may be desired where complete or partial substrate resistance is anticipated to stop or slow the rate of shoreline recession. For example, well-cemented and alongshore-continuous indurated sands throughout the dune system may slow the overall rate of shoreline recession. Figure 4 illustrates the influence of different parameterisations of cf and cc on modelled fluctuating (F) and cumulative (C) beach volume change, and the corresponding effect on the respective components of shoreline change (R).
The beach response to sea-level rise considers the influence of two potential sediment sinks on the beach system: (1) the shoreface adjacent to sandy shorelines; and, (2) the flood-tide (marine origin) deltas of estuaries within each tertiary compartment. Redistribution of sand from the beach to these sinks, to maintain surface morphology in balance with the prevailing geomorphic and hydrodynamic controls under rising sea level, may become a long-term driver of shoreline recession. As sea-level rise exposes dunes to increased erosion during storms, some of the sand that was previously only temporarily lost to the littoral transport system, may be permanently lost to new sediment accommodation that is generated by sea-level rise, rather than returning to the beach during the recovery phase following an erosion event. Successive instances of beach erosion, followed by only partial recovery may contribute to cumulative shoreline recession.
The shoreface component of the response to sea-level rise (VS) includes the potential sediment accommodation generated across the shoreface by rising sea level. In the modelled response, we assume that sea-level rise drives an upward and landward translation of the shoreface. The potential shoreface sediment accommodation space is estimated using a volumetric implementation of the standard concept of erosion that is caused by sea-level rise, as proposed by Bruun [67,68,69]. The significance of the modelled shoreface response to sea-level rise depends on the dimensions and geometry of the shoreface, the sampled sea-level rise (S), and the sampled closure depth (hc), which determines the offshore extent of sediment accommodation and morphologic response across the shoreface.
The geometry of the shoreface is approximated by fitting the following power function through the available shoreface hydrographic data,
where A and m are tuning parameters that are freely determined using linear regression fitting. The sediment accommodation volume generated between the baseline shoreline (x0), and the offshore position of the sampled shoreface closure depth (xc), is calculated as the difference between the initial shoreface geometry and the response shoreface geometry, following sea-level rise:
The potential shoreface sediment accommodation volume is halved to reflect the concept of upward and landward profile translation in response to sea-level rise, as in Bruun’s standard model of erosion caused by sea-level rise [67,68,69]. That is, the shoreface surface does not simply aggrade, the shoreface profile also translates landward with the retreating shoreline.
The scaling coefficient cs (Equation (3)) allows for the modelled shoreface response to be limited to only the sedimentary portion of a mixed sediment-reef shoreface. Exposed reef outcrops that protrude above an otherwise sedimentary shoreface surface suggest that sediment cannot accumulate there under the prevailing energy conditions. To account for the negative accommodation profile of reef outcrops, we assume that they do not represent potential sediment accommodation. This assumption is not suitable for application in sediment-deficit compartments, where extensive low-profile reef may be exposed, simply due to a lack of sediment in the shoreface environment.
The third term in Equation (3) (VE) represents the estuarine flood-tide delta component of the response to sea-level rise. This considers the influence of potential sediment accommodation that is generated within tidal inlets and estuaries by rising sea level, which may support the vertical growth (aggradation) of delta deposits with sand sequestered from the adjacent beach and shoreface. The sediment loss from the beach is the product of the sea-level rise (S), and the surface area of submerged active flood-tide delta deposits (AD). The total response over the forecast period may be moderated using the ce coefficient (Equation (3)), to simulate a slower (not instantaneous) rate of delta response:
We assume the existence of a morphodynamic balance between the hydrodynamic conditions of tidal inlets and delta morphology [70,71,72,73], which is supposed to have developed during prolonged sea-level stability that has been experienced in NSW during the late Holocene [45]. The likely rates of flood-tide delta response to sea-level rise are uncertain and may be site specific [72,73]. The potential sand loss to estuaries is distributed along the length (l) of sandy shorelines within the compartment.
3.2.2. Calculating Shoreline Change
We use the Australian beach database [35,36] as a framework for parameterising morphology and response variables for individual NSW beaches, or beach sectors as defined along some longer beaches. Airborne LiDAR topography data is used to calculate shoreline encroachment distances based on the modelled beach volume change. For example, airborne LiDAR covering the entire NSW coast captured between 2009–2014 [74] was used in the region-scale application. Depending on the resolution of the application, the beach face and dune morphology may be characterised by an alongshore-averaged (aggregated) beach-dune terrain profile [21,24] for each beach or beach sector (Section 3.4.1), or by a series of beach-dune profiles that are regularly spaced along the shoreline (Section 3.4.2). In either case, the encroachment distance is calculated by applying the modelled beach change volume (above 0 m AHD) across the beach-dune profile, moving landward from the baseline shoreline (Figure 5). To achieve consistency in defining the present-day baseline at different beaches, we use the 2 m AHD elevation contour as derived from LiDAR topography, which approximates the modal run-up or berm position on NSW beaches.
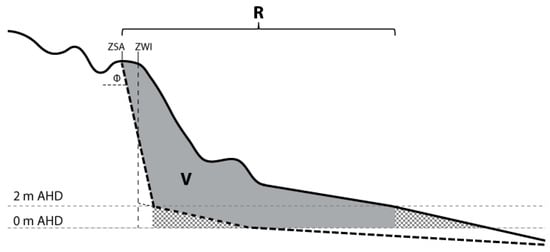
Figure 5.
The modelled net sediment volume change (V, Equation (1)) is applied to high-resolution beach-dune terrain profiles to calculate the shoreline change distance (R). The sediment volume is applied above 0 m AHD (present mean sea level), and landward of the 2-m AHD elevation contour baseline (beach berm height on NSW beaches), with an allowance included for dune slumping [75].
To account for dune slumping following encroachment into pre-existing dune morphology, we apply a commonly used allowance that is proportionate to the crest level of the dune erosion escarpment and the angle of repose of the substrate material [75]. Once the net encroachment distance, or the zone of wave impact (ZWI) has been determined using the cumulative volume of the beach-dune profile, the slumping allowance, or zone of slope adjustment (ZSA), is calculated based on the sampled dune height at that location, and the allowance is then added to determine the total encroachment distance (Figure 5). The angle of repose may be a discrete value, or a range of values (using a probability function), depending on confidence in the composition and behaviour of the substrate material. We assume a conservative angle of repose (Φ) for unconsolidated sand of 30°.
3.3. Uncertainty Management
Uncertainty is unavoidable in shoreline change forecasts due to: the potential range of future forcing conditions, the incomplete knowledge-base about beach and shoreline dynamics, and the intrinsic limitations of beach and shoreline response models. Forecasts should be communicated in the context of the uncertainty space to support informed and transparent decision making.
In reference to Earth-surface models, Murray et al. [76] argue that, uncertainty quantification techniques are most suited to simulation models, rather than exploratory models, although most models fall somewhere between clearly defined end members of the two. For process-based simulation models that are used to predict short-term beach response to storms, model boundary conditions (e.g., waves and water levels) are relatively well known to high spatial and temporal resolutions, and so statistical techniques to manage the not insignificant uncertainty that is introduced by the selected parameterisation of complex models are of particular importance [77]. For behaviour-based models that are typically used to predict long-term shoreline change, similar techniques have been demonstrated to manage uncertainty in boundary conditions and model parameterisation [78,79,80,81]. Awareness and demand for uncertainty management in beach erosion and shoreline change predictions is growing within the coastal management community [58,81].
While our modelling approach is intended to provide quantitatively reasonable estimates of the potential for shoreline change using simple sediment budget principles, it nonetheless includes many basic assumptions about poorly understood phenomena, such as the nature of the shoreface as a sediment source or sink during sea-level change. When considering the spatial extent and required resolution of forecasts in our regional-scale application, our approach to uncertainty management is designed to support rapid simulation, generating a probability distribution of shoreline change predictions based on 106 model iterations, for present-day and future forecasts (2050 and 2100) for all relevant NSW beaches (395 beaches in total).
Based on the general description of uncertainty in modelling provided by Roy and Oberkampf [82], uncertainty in shoreline change forecasts emerges from: (1) the stochastic nature of environmental forcing and coastal processes, such as storms and sea-level rise (aleatory uncertainty); (2) a limited understanding of the sediment transport processes that drive beach and shoreline response to changing environmental conditions (epistemic uncertainty); and, (3) the simplified representation of complex three-dimensional coastal morphodynamics by aggregated morphology and parameters that describe morphologic response (model form uncertainty).
Aleatory uncertainty is typically expressed using a probability distribution that describes the likelihood of occurrence across the feasible range of magnitudes. For example, we use a gamma probability function (Equation (2)) to describe the likelihood of experiencing fluctuating beach erosion, within a feasible range, in the final year of the simulation forecast period. In each model run, the value of F is randomly sampled from Equation (2), and it is combined with the cumulative beach change (C) to calculate the total beach change volume V (Equation (1)). The width and shape of the function is based on available data and knowledge of episodic beach erosion in NSW (Section 3.4.1). Fluctuating beach erosion (F) is described using an asymmetric gamma distribution to reflect the significantly reduced likelihood of experiencing the most severe erosion events in any given year.
We use a Monte Carlo sampling regime to manage epistemic uncertainty in cumulative beach change (C) due to sediment redistribution within and between compartments [78]. The feasible range and most likely values for all of the parameters and variables in Equations (3), (5) and (6) (except t, l, x0), are defined by triangular probability functions, which require the definition of lower (a) and upper (c) bounds, and a modal or most likely (b) value only. This simplistic representation of the uncertainty space is commensurate with the state of knowledge, in that sufficient data or scientific understanding may exist to define the feasible range and best estimate value of a model parameter or variable, although the exact shape of the probability distribution remains largely unknown [78]. The triangular functions capture the estimated uncertainty space around the best estimate value, which might represent an average of measurements or simply the most likely value based on expert knowledge.
The simplicity of the shoreline encroachment model implies that model form uncertainty is unavoidable in our findings. However, given the exploratory nature of the long-term forecasts, in particular, few datasets exist with which to calibrate or test model predictions. Furthermore, the volumetric design of the model expresses a direct relationship between the sediment budget principles that control the redistribution of sand from the beach to other depositional features, and the simulated beach-volume and shoreline change. While our assumptions underlying sediment redistribution in response to sea-level rise are founded on geological evidence, and historical observations from naturally evolving or modified systems, the applicability of these assumptions to all NSW beaches requires further scrutiny. In particular, the significance of shoreface and estuarine response in long-term forecasts suggests that a detailed appraisal of the scope for these responses to sea-level rise in different settings would greatly improve our approach. Without such information, we adopt a risk-averse position in developing a second-pass coastal erosion exposure assessment.
3.4. Model Applications
We present regional- and local-scale applications of the modelling approach to demonstrate the utility of the coastal sediment compartments framework for parameterising coastal geomorphology and applying sediment budget principles, and the flexibility of the simple shoreline encroachment model in scaling to suit the available data and required resolution of shoreline change forecasts. The objective of the regional-scale application is to develop a second-pass estimate of potential exposure to coastal erosion and shoreline change in NSW. The local-scale application provides an example of how the approach may be applied to develop more refined shoreline forecasts where more detailed sediment budget data is available. We stress, however, that the local-scale example also applies speculative values for some sediment budget components, due to limited available data. Thus, the example should not be interpreted as a reliable forecast, but serves to highlight key sediment budget components that would benefit from more detailed observations and knowledge.
3.4.1. Regional Scale (NSW Coast)
First, we consider the property and infrastructure exposure to coastal erosion along 395 NSW beaches, comprising 70% of the total length of open-coast sandy shorelines along the NSW coast, and covering the full extent of potential property and infrastructure exposure to coastal erosion. The remaining open-coast beaches, where the modelling approach was not applied, are characterised by non-erodible backshore substrates and thus have limited or no exposure to coastal erosion.
The fluctuating component of shoreline change is described by a gamma probability function (Equation (2)), which is intended to approximate the feasible range and likelihood of fluctuating erosion on fully exposed open-coast NSW beaches. The dominant component of fluctuating change is the so-called “storm demand”, which refers to the volume of sand removed from the beach by raised water levels and high waves experienced during an individual or closely grouped series of coastal storms. Gordon [83] presented a relationship for the probability of storm demand on NSW beaches from measured and estimated (i.e., based on beach surveys and photogrammetry analysis) beach erosion volumes (Figure 6A). That relationship, along with more recent storm demand observations in NSW [84], and simulation experiments based on the long-term beach measurement dataset at Collaroy-Narrabeen Beach [85,86], form the basis for our parameterisation of the gamma distribution that is used to describe F (Equation (2)) for fully exposed open-coast NSW beaches (Figure 6B).
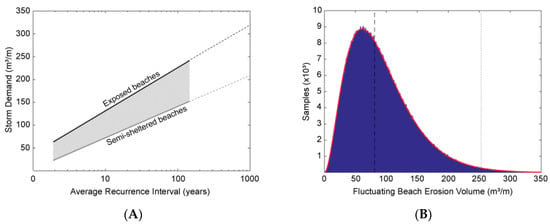
Figure 6.
(A) Estimated Average Recurrence Interval (ARI) of storm demand on exposed (black line) to semi-sheltered (grey line) NSW beaches [83]. The functions have been extrapolated here (dashed lines) to consider their relationship to more severe erosion events. (B) Gamma function (red line) used to describe the probability of fluctuating beach erosion (Equation (2)), with 106 random samples (blue columns). The 50th (dashed line) and 99th (dotted line) percentile values are shown.
Consideration was also given to geo-historical evidence including the depositional records from prograded coastal barriers, which store wave climate and shoreline response records for previous centuries. Those records suggest that the recent historical period (including all of the observation data) has been characterised by lower intensity storm conditions relative to previous centuries [87]. As such, it may be imprudent to assume that historical measurements have captured the maximum potential storm demand on NSW beaches. When considering that the upper tail of our F distribution (Figure 6B) also accommodates the possibility of enhanced erosion due to: historically unprecedented storm clustering and wave climate extremes, rips, and other beach processes that are known to enhance the average erosion response, or the coincidence of a severe storm demand with the cyclic differential shoreline oscillation phenomena known as beach rotation [6,88,89].
As a modest beach erosion event is likely to occur in any given year, the mode of the F distribution is 65 m3/m (Figure 6B), which approximates a two-year average recurrence interval storm demand based on the relationship in Figure 6A. The 50th percentile F value is 82 m3/m, and the 99th percentile (1% exceedance level) F value is 250 m3/m (Figure 6B), which is about equivalent to the estimated 100-year average recurrence interval storm demand for exposed beaches (Figure 6A). For sheltered beaches, F values sampled from the gamma probability function (Figure 6B) were scaled (using cf, Equation (1)) based on the average shoreline orientation for each beach or sector [36], to account for the effects of enhanced refraction on incident wave energy at the shoreline. The cf scaling values based on average shoreline orientation are provided in Appendix A.
To evaluate the suitability of Equation (2) (Figure 6B) for describing the range and likelihood of fluctuating erosion on NSW beaches, comparisons were made between modelled erosion on exposed open-coast beaches, and the locations of historical maximum erosion escarpments where available (i.e., mapped dune scarps associated with the most severe historical erosion event at each beach). The comparisons demonstrate that low-probability (e.g., 99th percentiles) modelled beach erosion based on Equation (2) is consistent with mapped historical maximum erosion escarpments (Appendix B).
We applied a limited sediment budget parameterisation to model cumulative erosion (C) for the regional-scale application, using only the first three terms in Equation (3). Photogrammetry analysis of historical shoreline change, recorded in aerial photographs captured intermittently since the 1960s, has been carried out for more than 150 NSW beaches. Where a consistent and ongoing long-term shoreline recession trend has been identified in photogrammetry records, the annual average rate of sand volume loss at the beach was applied using the qy parameter (Equation (3)).
There is the potential for sand supply from the shoreface to NSW beaches. The occurrence of prograded Holocene sand barriers along parts of the central and southern NSW coast, where fluvial sources and the alongshore sand transport system is limited, suggests that shoreface sand supply to beaches was an important process during recent geological time, and may persist today at significant rates along some parts of the coast [24,90,91]. That potential was considered using the regional rates of sand supply to NSW beaches,, which was derived from the analysis of geohistorical records spanning the last several centuries [87], which was applied as annual average rates of sand supply using the qx parameter (Equation (3)). The shoreface may act as a source or sink, depending on the relationship between the geomorphic setting of the beach, the local wave climate, and the sea-level rise scenario.
When considering Equations (5) and (6), the modelled beach response to sea-level rise is a function of the sampled values of: (1) sea-level rise, (2) compartment-averaged shoreface geometry (Equation (4)), (3) the shoreface closure depth, and (4) the “active” surface area of estuarine flood-tide deltas.
Figure 7A shows the range of sea-level rise projections that were applied in the model to calculate shoreline response, which reflect the Intergovernmental Panel on Climate Change (IPCC) global mean sea-level rise (GMSL) projections from the Fifth Assessment Report [19]. The IPCC projections for southeast Australia suggest a sea-level rise of around 0–10% above the global average [92,93]. As GMSL projections presented in the Fifth Assessment Report (AR5) were restricted to the “likely” range (17th to 83rd percentiles), we used linear extrapolation to extend the distribution tails to cover the 0–100th percentile range. The triangular distributions shown in Figure 7A reflect the combined range of GMSL projections for the three emissions pathways (RCP2.6, RCP4.5, and RCP8.5) considered in AR5. The bounds of the triangular distributions for 2050 (blue) and 2100 (red) reflect the 0th and 100th percentiles of the combined range, while the modes reflect the 50th percentiles of the combined ranges of the three emissions pathways (Figure 7A).
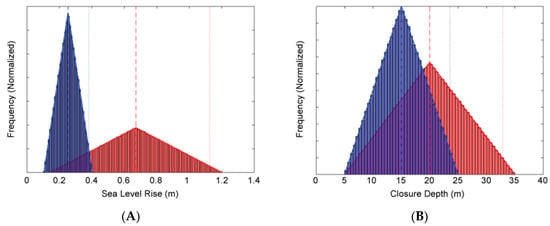
Figure 7.
Input triangular probability distributions applied in the modelling for (A) sea-level rise, and (B) shoreface closure depth, for the 2050 (blue) and 2100 (red) forecast periods, with 106 random samples (columns) also shown. The 50th (dashed line) and 99th (dotted line) percentile values for each forecast period are indicated.
We acknowledge that the range of GMSL projections that were applied in the modelling do not reflect the full uncertainty space for the present century. The AR5 GMSL projections were limited to the consideration of climate process model forecasts only and omitted the potential influence of rapid ice melt this century. Sweet et al. [20] recently reviewed and revised the AR5 GMSL projections in the context of the latest research on upper-end GMSL projections that reflect rapid ice melt processes, and recommended that scenarios covering the range 0.3–2.5 m be considered in assessing the potential impacts of sea-level rise at 2100. However, we limit our consideration of GMSL this century to the AR5 findings, in order to enable comparison between our findings and existing coastal erosion hazard studies that have been developed by local governments in NSW for coastal management and planning.
We approximated the shoreface geometry of each beach to calculate the potential shoreface sediment accommodation volume generated by sea-level rise (Figure 8A). The shoreface geometry was generated by fitting Equation (4) to regional-scale bathymetry, averaged alongshore within each sediment compartment. For each beach, the average distance from all of the sandy shorelines within the relevant sub-compartment to the 10 and 20 m isobaths was calculated, while the 30 and 40 m depth coordinates represent the average distance from all of the sandy shorelines within the relevant tertiary compartment to the corresponding isobaths (e.g., Figure 3). The method reflects greater alongshore variability in upper-shoreface (0–20 m water depth) geometry between NSW beaches, relative to lower-shoreface (20–40 m) geometry, which is relatively consistent at the tertiary compartment scale.
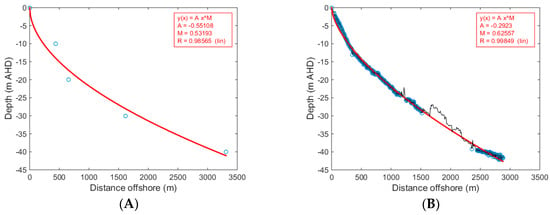
Figure 8.
(A) Example of estimated shoreface geometry (red line) fitted to alongshore-averaged regional-scale bathymetric data (blue circles) at Wamberal Beach (Figure 3B). (B) Local-scale shoreface geometry (red line) at Wamberal Beach fitted to high-resolution hydrographic data (blue circles) with protruding reef outcrops (black line) omitted. Curve fitting was carried out using the ezyfit.m tool.
The triangular function for shoreface closure depth (hc) widens from 2050 to 2100 (Figure 7B) to reflect the increasing potential for sediment-accommodation generation and surface response across the lower shoreface at longer timescales [94,95,96]. The upper limits of shoreface closure depth in Figure 7B reflect representative values of Hallermeier’s [97] outer shoal zone limit [98,99], and the only long-term observation dataset [100] for this region. When combined with the widening uncertainty space for accelerating sea-level rise (Figure 7A), and when considering the typical cross-shore extent of shorefaces in this region (Figure 8A), the modelled shoreface sediment-accommodation potential may represent a significant driver of the simulated shoreline recession, particularly for the 2100 forecast period.
The surface area of active submerged flood-tide delta deposits (AD) was mapped for each NSW estuary using the NSW Coastal Quaternary Geology Data Package [101,102] and recent aerial imagery. The surface area AD is applied in Equation (6) to calculate the potential sediment accommodation volume generated in estuaries by sea-level rise. Depending on the location of each estuary and connectivity with adjacent beaches, summed values of AD were applied at the sub-compartment or tertiary compartment resolution, with the influence of estuarine sediment sinks distributed along the total sandy shoreline length (l) corresponding to the relevant compartment. Summary statistics describing the total area of the shoreface and estuarine (flood-tide delta) sediment sinks in each primary sediment compartment (Figure 1A), and the relative difference (i.e., total sink areas divided by the length of sandy shoreline in each compartment), are provided in Appendix C.
3.4.2. Local Scale (Wamberal Beach)
We apply the simple shoreline encroachment model in higher resolution to Wamberal Beach (Figure 3) to investigate sensitivity to local-scale geomorphic complexities. Wamberal Beach is the central sector of the Terrigal-Wamberal sub-compartment, and spans from Terrigal Lagoon inlet in the south to Wamberal Lagoon inlet in the north (Figure 3B). Wamberal Beach fronts a narrow stationary-receded beach barrier comprising a frontal dune only, which is anchored to the bedrock framework in the north, and which separates Terrigal Lagoon from the ocean in the south. Both the frontal dune and back-barrier flat feature moderate density residential development. Historically, Wamberal Beach has been impacted by erosion that is caused by coastal storms, resulting in significant damage and loss of properties [52]. Many beachfront properties were damaged by severe erosion (Figure 2) that was caused by a storm that impacted the entire NSW coast in June 2016 [1]. However, the barrier morphostratigraphy (stationary-receded) suggests that from a geohistorical perspective, Wamberal beach has been relatively stable or very slowly receding during the mid-late Holocene.
In the local-scale example, we use the same alongshore-averaged beach-dune terrain profile to model cumulative shoreline erosion (C) as was used in the regional-scale example (i.e., the red profile in Figure 9). However, we use beach-dune terrain profiles extracted from LiDAR data along regular alongshore-spaced (25 m) transects (Figure 10) to model fluctuating erosion (F). This allows for the modelled RC (Figure 4) to reflect the distributed influence (i.e., along the length of the beach) of cumulative sand loss from the sub-compartment, while the modelled RF (Figure 4) reflects alongshore variability in beach-dune geomorphology along Wamberal Beach. Our approach assumes that as the shoreline recedes by encroachment in a time-averaged sense, due to cumulative sand loss from the sub-compartment, nearshore wave processes that are operating at a higher frequency maintain a dynamic or ephemeral beach face with time-averaged sand volume consistent with the present-day setting.
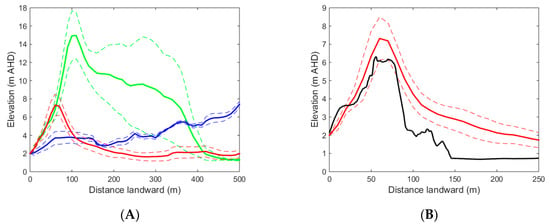
Figure 9.
(A) Alongshore-averaged beach-dune terrain profiles, within envelopes of ± one standard deviation (dashed), for Terrigal (blue), Wamberal (red) and Wamberal North (green) beach sectors (Figure 3B). (B) Comparison between the alongshore-averaged terrain profile for Wamberal Beach (red), and a profile from the narrow point (black) of the Wamberal Beach sand barrier (Figure 10).

Figure 10.
Wamberal Beach, which is the central sector of the Terrigal-Wamberal sub-compartment (Figure 3B), showing the distribution of 25-m alongshore-spaced beach-dune profiles that were used to calculate fluctuating shoreline change. The black profile spans the narrow point of the barrier. Beach berm positions (2 m AHD elevation contour) based on airborne LiDAR surveys carried out in 2011 and 2016 (April) are shown with the hybrid (orange) baseline representing a fully accreted beach. Bore holes sampled by Hudson [104] are also shown, indicating where a buried siltstone deposit approaches the beach face (red). The base of the erosion escarpment (yellow) and the limit of wave run-up (blue) from the June 2016 storm were mapped using RTK-GNSS immediately after the storm.
Figure 9A shows the alongshore-averaged beach-dune terrain profiles for the three sectors of the Terrigal-Wamberal sub-compartment (Figure 3B). The three averaged terrain profiles capture the gross alongshore gradient in beach-dune morphology. This emerges from the influence of the prominent Broken Head on transformation of the predominant south to southeast wave climate to the nearshore, which results in greatly reduced exposure along Terrigal Beach relative to Wamberal and Wamberal North beaches (Figure 3B). In the local-scale example, cumulative shoreline change (RC) is calculated by applying the cumulative beach change volume (C) to the alongshore-averaged profile above 0 m AHD and landward of the 4 m AHD elevation contour (not the 2 m AHD contour), which reflects the position of the frontal dune face. This ensures that RC reflects sediment loss from the dune, not the beach face, which is a transient feature affected by fluctuating processes.
The modelled fluctuating beach change volume (F) is applied to each 25-m alongshore-spaced profile, above 0 m AHD and landward of the 2 m AHD elevation contour, which reflects the beach berm position. Figure 9B compares the alongshore-averaged terrain profile for Wamberal Beach, with a profile from the narrow point of the sand barrier (Figure 10), as an example of terrain variability relative to the alongshore-averaged profile. As the greatest beach erosion volumes are typically achieved when the pre-storm beach state is fully accreted [75], we derive the 25-m alongshore-spaced beach-dune profiles from two LiDAR surveys, which together capture a fully accreted beach state along the northern and southern parts of Wamberal Beach. The 2011 LiDAR survey, from which the alongshore-averaged profile was derived (Figure 9), captured an accreted state along the southern two-thirds of the beach, while a 2016 LiDAR survey [1] captured an accreted state along the northern third of the beach. Similarly, the baseline (2 m AHD elevation contour) from which we measure modelled fluctuating shoreline change (RF), is a hybrid beach berm position based on both LiDAR surveys, representing a fully accreted beach state along the length of Wamberal Beach (Figure 10).
The local-scale model configuration included the gamma probability function for fluctuating erosion (F) for fully exposed open-coast beaches (Equation (2)), as we applied in the regional-scale example (Figure 6B). Measurements of historical beach erosion within the Terrigal-Wamberal sub-compartment suggest that the Wamberal Beach sector is fully exposed to the impacts of storms. For example, Worley Parsons [103] reported that storm-induced beach erosion volumes that were determined using photogrammetry analysis of historical aerial photographs reached 250 m3/m along parts of the beach following a series of severe storms in 1974, and since then, beach erosion volumes on the order of 200 m3/m have been measured in response to several other historical storm events.
However, the scaling coefficient for fluctuating erosion (cf) was used to account for potential alongshore variation in substrate resistance. An investigation of the subsurface geology of Wamberal Beach [104] found that an underlying siltstone deposit approaches the beach face along a 200-m sector of the northern half of the beach. This is indicated in Figure 10 by the bore holes that are marked in red. Severe erosion in June 2016 exposed the siltstone deposit along that sector of beach (Figure 2D). Additional geotechnical studies that were carried out for private development applications have found that the siltstone deposit rises to 6–8 m AHD within the frontal dune along parts of that same sector.
Given that the siltstone unit is preserved within the dune and beneath the beach, but that it is not exposed on the beach face under modal conditions, and the shoreline curvature appears undisturbed, we consider the material to provide no significant resistance to shoreline recession. This is supported by inspection of the siltstone in June 2016, when the exposed material was found to be easily disturbed. However, an exposure within the dune at 6–8 m AHD elevation may restrict the extent of beach erosion during an individual erosion event. As such, cf was applied as a triangular probability function (a = 0.7, b = 0.85, c = 1), thereby allowing a maximum 30% reduction in the fluctuating beach erosion volume, due to the presence of the siltstone material in the frontal dune. That is consistent with the reduced response to storms observed at Lake Cathie Beach on the Mid-North Coast (Figure 1A), where indurated sand (coffee rock) lenses within the frontal dune contribute to about a 30% reduction in beach erosion relative to similarly exposed beaches in the region [61].
Photogrammetry analysis for Wamberal Beach does not indicate any steady and persistent trend in shoreline change through the period of historical aerial photographs. Rather, the data suggests variable accretion and erosion along different parts of the beach between aerial photograph captures [103]. This is supported by the variable alignment of beach berm positions (i.e., 2 m AHD elevation contour), which were derived from airborne LiDAR surveys that were carried out in 2011 and 2016 (Figure 10). Thus the photogrammetry data likely reflects short- to medium-term beach oscillation associated with wave climate variability [6,88,89], and the impacts of individual storm events, rather than any underlying shoreline recession or accretion that would be anticipated to persist indefinitely along the sub-compartment. There is limited prospect for alongshore sand transport around Broken Head into the sub-compartment, which is indicated by the prominence and orientation of Broken Head relative to the modal wave direction, and the continuous offshore reefs (Figure 3B). Therefore, no underlying rate of beach volume change was applied using the qy parameter (Equation (3)).
The shoreface of the Terrigal-Wamberal sub-compartment has been mapped using side-scan sonar [47], single-beam echosounder, and marine LiDAR (Figure 3B), and the substrate has been investigated using seismic reflection and seabed grab samples [105]. The upper- to mid-shoreface is mostly sandy to around 20 m water depth, beyond which extensive reef outcrops protrude through the sandy shoreface (Figure 3B and Figure 8B). Sediment thickness is generally less than 5 m, except where it approaches or slightly exceeds 10 m around a buried palaeo-drainage channel in the northern sector of the sub-compartment [105], which is represented by the only continuous sediment pathway to the lower shoreface (Figure 3B). The stationary-receded barrier morphostratigraphy, and character of the shoreface substrate, both suggest the limited potential for sand supply from the shoreface, and thus no persisting rate of sand supply to the beach was applied using the qx parameter (Equation (3)).
Rather than using the regional-scale shoreface geometry (Figure 8A) in order to calculate the potential shoreface sediment accommodation volume, more accurate shoreface geometry was determined by fitting Equation (4) to detailed hydrographic survey data (Figure 8B), omitting the reef outcrops to estimate the shoreface geometry if the seabed were entirely composed of unconsolidated sediments. The same triangular probability functions for sea-level rise and shoreface closure depth, as applied in the regional-scale example, were also used in the local-scale application (Figure 7). The shoreface response scaling coefficient (cS) was applied to account for the mixed sediment-reef substrate within the Terrigal-Wamberal sub-compartment (Figure 3B). That is, the intermittent protruding reefs with relief of several metres represent potential sediment accommodation space that is already filled by reef outcrops, and thus is not available to be filled by sand lost from the beach. The scaling coefficient was defined using a triangular function (a = 0.65, b = 0.7, c = 0.75), reflecting that about 30% of the total shoreface area, extending to the shoreface toe (35 m water depth) within the alongshore extent of sub-compartment, is reef (Figure 3B). That parameterisation of cS means that only 65–75% of the shoreface represents potential sediment-accommodation space during sea-level rise.
To demonstrate our approach, we also include allowances for other potential influences on the sub-compartment sediment budget, including mega-rips and change in the biogenic (carbonate) sediment component. A previous modelling investigation of future shoreline change at Avoca Beach, immediately south of Broken Head, identified both of the influences as relevant considerations for future sediment budgets within this region [79]. Based on that study, which surveyed a panel of experts to determine appropriate values for sediment budget parameters, we apply VM as a triangular function (a = 0, b = 815, c = 1630) to consider cumulative sediment loss via mega-rips, which equates to a maximum 0.5 m3/m sediment volume loss from the beach per year. Application of VM recognises the potential for sand loss offshore from this sub-compartment during severe storms, with limited potential for sand to return due to the character of the shoreface substrate. Similarly, we apply VB as a triangular function (a = −1630, b = 815, c = 3260) to consider carbonate sediment dissolution at rates up to 1 (m3/m)/year, or enhanced carbonate production up to a maximum rate of 0.5 (m3/m)/year.
3.5. Exposure Assessment
We applied standard spatial-overlay analysis techniques using ArcGIS to identify potentially exposed properties and infrastructure, which are defined as those that are intersected by the modelled coastal erosion hazard zones for each forecast period and exceedance level. We use both the NSW Cadastre dataset and the Geo-coded Urban and Rural Address System (GURAS) to identify addresses that are potentially exposed to coastal erosion. Whereas, the Cadastre describes the location and character of property lots, the GURAS database stores the details of each address within a property lot. While some lots contain multiple addresses, some addresses occupy multiple lots. By jointly querying both databases, all of the valid addresses that were potentially exposed to coastal erosion were identified, including both primary (houses and multi-dwelling buildings) and secondary (individual apartments within multi-dwelling buildings) address types.
Simply counting the number of potentially exposed addresses only partially communicates the relative exposure between beaches or regions. To assess the relative impacts of modelled beach erosion and shoreline change on potentially exposed properties, we also calculate for each potentially exposed property lot, the proportion of land area that is affected by the modelled coastal erosion hazard zones. This is achieved by dividing the land area of the lot that is affected by the modelled coastal erosion hazard zone by the total lot area. Based on that analysis, all of the potentially exposed addresses (including primary and secondary address types) were categorised into five groups, based on the proportion of each property lot that is potentially affected by coastal erosion: <10%, 10–25%, 25–50%, 50–90%, and >90% lot-area identified as exposed.
We also applied spatial-overlay analysis to identify lengths of roadways that are potentially exposed to coastal erosion for each forecast period and exceedance level scenario. Roadways exposure is categorised into five road types: vehicular track, local road, arterial road, primary road, and motorway (by increasing significance, associated infrastructure, and replacement costs). For simplicity, we restrict our assessment of infrastructure exposure to roadways, as many other infrastructure and utilities assets scale in a relatively linear relationship with roadways.
4. Results
4.1. Regional Scale (NSW Coast)
Figure 11 shows examples of the regional-scale coastal erosion hazard modelling for Ten Mile Beach in the Northern Rivers region (Figure 1B), and Windang Beach in the Illawarra-Shoal haven region (Figure 1C). Shaded hazard zones for the present (red) and 2050 (orange) forecast periods represent areas that were exceeded by only 1% of model predictions for each forecast period. Three hazard zones (50%, 10%, 1% exceedance) are shown for the 2100 forecast period (yellow), indicating areas that were exceeded by 50%, 10%, and 1% of model predictions. The forecast extent of coastal erosion increases for longer forecast periods and lower exceedance levels, reflecting increased sand loss from the beach due to simulated sediment redistribution to estuarine and shoreface sinks.

Figure 11.
Regional-scale coastal erosion hazard mapping for (A) Ten Mile Beach in the Bundjalung compartment (Figure 1B), and (B) Windang Beach in the Illawarra South compartment (Figure 1C). The 1% exceedance level is shown for the present and 2050 forecast periods, while 50%, 10% and 1% exceedance levels are shown for the 2100 forecast period. At Shark Bay (A), for the 2100-10% and 1% exceedance level scenarios, the encroachment model exceeds the low-volume dune system and erodes into very low-lying back-barrier terrain. In reality, barrier rollover would ensue, and the associated back-barrier deposition suggests that the actual shoreline change would be less than depicted here. In that case, the basic assumptions of the simple shoreline encroachment model are violated.
The influence of low back-barrier morphology on modelled shoreline change, once the frontal dune has been breached, is evident in the 2100-10% exceedance and 2100-1% exceedance forecast shoreline positions along the southern end of Ten Mile Beach, at Shark Bay (Figure 11A). The extent of the 2100-10% exceedance and 2100-1% exceedance hazard areas from the baseline shoreline is much greater along that sector, compared with the beach to the north, because of the lower dune and back-barrier morphology along the Shark Bay sector. Along the Shark Bay sector, the encroachment response assumption is violated, and the shoreline change forecast is likely over-estimated. In that location, barrier-rollover processes (washover) would result in back-barrier deposition upon breaching of the frontal dune.
A similar effect is not apparent at Windang Beach, where even the southern end of the beach features relatively well-developed dune morphology that is not breached by the 2100-1% exceedance scenario (Figure 11B). There, most of the coastal development is set back more than 200 m from the shoreline, well behind the frontal dunes, and thus the forecast hazard zones suggest that most development is not likely to be exposed to coastal erosion within the present century, even for low-probability scenarios.
Figure 12 shows model forecast sample distributions of V for Windang Beach, for the present (i.e., F only) and 2050 (combined F and C) forecast periods. The V distribution for the present scenario (Figure 12A) reflects the input gamma probability function for F (Figure 6B), and the fitted cumulative distribution is a gamma function (Figure 12B). The 50%, 10%, and 1% exceedance beach change (F) volumes were 83, 167, and 255 m3/m, respectively. The V distribution for the 2050 scenario (Figure 12C) reflects the combined distributions of the gamma probability function for F, and the symmetrical input triangular functions for the various C components (e.g., Figure 7). The fitted cumulative distribution is a generalised extreme value (GEV) function (Figure 12D). The 50%, 10%, and 1% exceedance beach change volumes were 234, 342, and 447 m3/m, respectively.
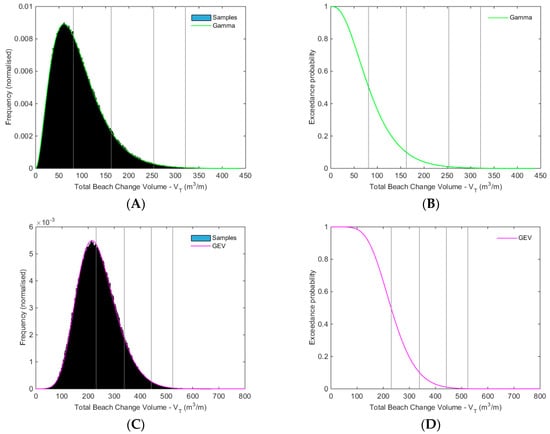
Figure 12.
Model forecasts of beach volume change for Windang Beach (Figure 11B) for the present (A,B) and 2050 (C,D) forecast periods. Frequency distributions of the modelled beach volume change (A,C), and the corresponding cumulative probability functions (B,D) are shown for the present and 2050 forecast periods, with (left to right) 50th, 90th, 99th and 99.9th sample population percentiles (50%, 10%, 1%, and 0.1% exceedance levels, respectively) indicated on each plot as grey vertical lines.
Figure 13 summarises the forecast shoreline change distances for all 395 modelled beaches, grouped by the nine primary sediment compartments of the NSW coast (Figure 1A). The blue boxes cover the 25th to 75th percentile range of forecast shoreline change (landward from the 2 m AHD beach-berm baselines) for modelled beaches within each primary compartment, with the red lines indicating the median values. The black dashed lines cover approximately ±2.7σ for each sample set, while the red markers indicate values beyond that range that are interpreted as outliers.
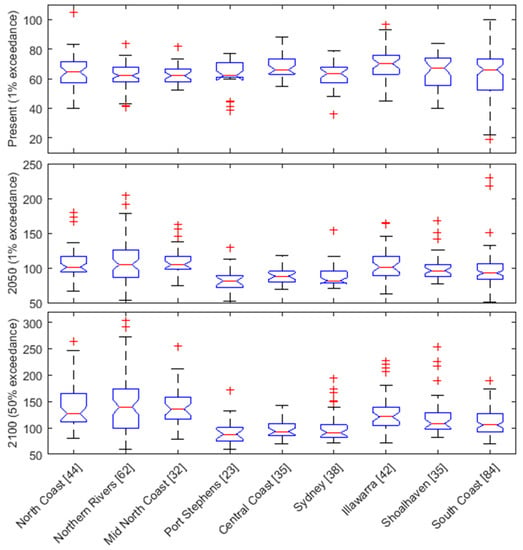
Figure 13.
Box plots summarising the modelled shoreline recession distances (m) from the regional-scale application, for each NSW primary compartment (Figure 1A), as measured from the beach berm baseline (2-m AHD elevation contour). The number of beaches modelled in each compartment is indicated in square brackets. Modelled shoreline change distances are shown for the present-1% exceedance (top), 2050-1% exceedance (middle), and 2100-50% exceedance (bottom) scenarios.
The median forecast shoreline change distances are relatively similar along the coast for the present (F only) scenario, in the 60–70 m range in all of the primary compartments (Figure 13). The Illawarra compartment features the highest forecast erosion due to fluctuating processes. Variation within compartments is greater for the northern and southern NSW compartments relative to the central NSW coast, due to both larger sample sizes and greater variability in beach-dune morphology. For example, the South Coast compartment includes several very protected beaches within Batemans Bay (a deeply indented open-ocean embayment featuring prominent islands at the bay mouth), which contribute to very high variability in shoreline change forecasts within that compartment.
As expected, given the design of the simple shoreline encroachment model, forecast shoreline change increases in all of the compartments for the 2050 and 2100 (combined F and C) scenarios (Figure 13). The north coast and south coast compartments are characterised by above average forecast shoreline recession, due to the increasing sediment demand from broader shoreface and estuarine sediment sinks, relative to average beach-dune morphology. Variation between compartments also increases, which is evident in higher deviation about the 25th–75th percentile ranges and increased outlier values for those compartments. For example, the north coast compartments feature large potential shoreface sediment sinks and relatively low dune morphology, particularly in less exposed southern corners of compartments (e.g., Figure 11A), resulting in above average forecast shoreline recession and high variability between individual beaches.
The exposure assessment based on the regional-scale modelling identified approximately 1200 property lots (2300 total addresses) in NSW that are potentially affected by coastal erosion at present (1% exceedance level). Property exposure rises to around 3100 lots (5200 total addresses) at 2050 (1% exceedance level), and 4800 lots (8200 total addresses) at 2100 (50% exceedance level). However, many potentially affected lots may be only partially exposed to coastal erosion, in which case assets on the property may not be affected. When considering only properties for which more than half of the lot area was intersected by the modelled coastal erosion hazard zones (and consequently for which assets are likely to be affected), the property exposure numbers above decrease to 247 property lots (455 total addresses) that may be affected at present, rising to around 1862 lots (2718 total addresses) at 2050, and 3300 lots (5076 total addresses) at 2100.
Figure 14 shows the distribution of property exposure to coastal erosion between the seven NSW regions (Figure 1A), based on the regional-scale modelling. The exposure assessment findings are organised by the NSW planning regions, rather than the primary sediment compartments, reflecting the intended application of our investigation. All of the regions except for Hunter and South East feature significant property exposure to coastal erosion at present (based on the 1% exceedance scenario). Property exposure at 2050 (1% exceedance) and 2100 (50% exceedance) increases most significantly in the Northern Rivers, Mid North Coast, and Illawarra-Shoalhaven regions. Large increases in addresses for which more than half of the property lot is affected by modelled coastal erosion (orange and red shading) highlights regions that may experience a very significant increase in exposure to coastal erosion during the present century.
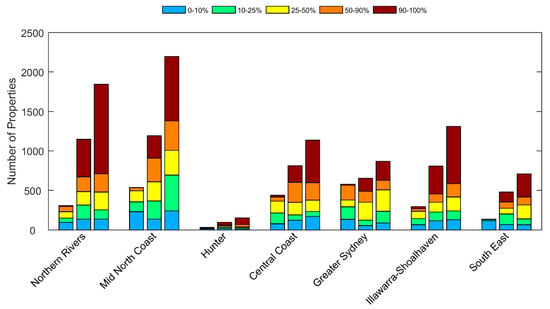
Figure 14.
Total address exposure by NSW regions (Figure 1A) for the present-1% exceedance (left column in each group), 2050-1% exceedance (middle columns) and 2100-50% exceedance (right columns) scenarios. The colouring categorises exposed addresses by the proportion of each associated property lot that was intersected by the modelled erosion hazard zones for each region and scenario.
Based on the regional-scale modelling, about 70 km of NSW roadways may be exposed to coastal erosion at present (1% exceedance), increasing to 196 km at 2050 (1% exceedance), and 311 km at 2100 (50% exceedance). However, Figure 15 shows that, at present, vehicular tracks account for most of the roadway exposure behind NSW beaches. The analysis shows that increasing lengths of local and arterial roads may be exposed to coastal erosion by 2050 and 2100. No primary roads or motorways were affected by the three forecast period/exceedance level scenarios that were considered in the regional-scale exposure assessment. Roadway exposure was found to be relatively low in the Hunter, Central Coast, and Greater Sydney regions, moderate in the Illawarra-Shoalhaven and South East regions, and highest in the Northern Rivers and Mid North Coast regions (Figure 15).
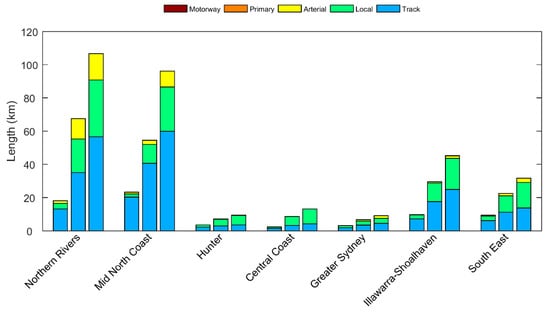
Figure 15.
Roadway exposure by NSW regions (Figure 1A) for present-1% exceedance (left columns), 2050-1% exceedance (middle columns) and 2100-50% exceedance (right columns) scenarios. The colouring indicates the types of roadways that were identified as potentially exposed to coastal erosion based on each scenario.
4.2. Local Scale (Wamberal Beach)
In the local-scale application, we consider the sensitivity of fluctuating erosion to variation in geomorphology along the beach, using 25-m alongshore-spaced profiles to calculate RF. (Figure 10). Figure 16A shows the 50%, 10%, and 1% exceedance level present-day (F only) erosion hazard zones for Wamberal Beach. The impact of the 50% exceedance erosion event (82 m3/m) is limited to the beach face, while the 10% (160 m3/m) and 1% (250 m3/m) exceedance erosion events also impact the frontal dune. The effect of applying cf along the 200 m stretch of the beach where the buried siltstone unit rises to the surface (indicated by the red drill hole markers) is evident in the closer spacing between the forecast shoreline positions for the three exceedance levels, and the relative proximity of the forecast shoreline positions to the model baseline in that location. Nonetheless, the modelling suggests that almost all of the properties immediately fronting Wamberal beach may be exposed to severe beach erosion caused by extreme coastal storms (e.g., a 1% exceedance level erosion event).

Figure 16.
Local-scale coastal erosion hazard zones for Wamberal Beach, the central sector of the Terrigal-Wamberal sub-compartment (Figure 3B). (A) 50%, 10% and 1% exceedance level forecasts for fluctuating erosion only (at present). (B) 2050-50% exceedance, 2050-10% exceedance, and 2050-1% exceedance forecasts (combined fluctuating and cumulative erosion). Bore holes sampled by Hudson [104] are shown, with red markers indicating where a buried siltstone deposit approaches the beach face, and rises up to between 6–8 m AHD elevation within some parts of the adjacent frontal dune.
Figure 16B adds cumulative erosion (C) by 2050, based on the alongshore-averaged beach-dune profile, to the fluctuating erosion (F), as shown in Figure 16A, for the corresponding exceedance levels. At 2050, the modelling suggests that the combined impacts of F and C at the 50% exceedance level for each component would be limited to the beach and the face of the frontal dune. For the combined 10% and 1% exceedance levels, the impacts of coastal erosion extend across the frontal dune. The results suggest that the combined 1% scenario (i.e., a 1% exceedance level fluctuating beach erosion event with a 1% exceedance shoreline recession) may lead to breaching of the dune at the narrow point of the barrier. While the effect of scaling fluctuating erosion (using cf) along the 200-m stretch of the beach where the buried siltstone unit rises to the surface is preserved in the combined model forecast, as seen in closer spacing of hazard zones along that section of the beach (Figure 16B), the influence becomes less prominent as the relative magnitude of cumulative erosion increases.
5. Discussion
5.1. Modelling Approach and Limitations
Application of the simple shoreline encroachment model at a regional-scale demonstrates the potential variation in the sensitivity of NSW beaches to projected sea-level rise, primarily relating to the influence of differences in the dimensions of estuarine and shoreface sediment sinks between sediment compartments along the coast. The volumetric design of the model allows for the consideration of the impacts of sediment redistribution between all of the potential sources and sinks on shoreline change. Because the modelling approach does not assume that existing dune morphology will aggrade at the same pace as sea-level rise (e.g., in contrast to Bruun’s model), the impacts of sediment redistribution at the shoreline reflect erosion into the contemporary morphology of each NSW beach, as measured by airborne LiDAR surveys. In that way, the modelled shoreline recession reflects the behaviour of presently receding beaches on this coastline, in which the beach and shoreline encroach into the dune system. This is a risk-averse position, consistent with other assumptions in our approach, as dune deposition during sea-level rise may slow the rate of shoreline recession. Our modelling approach and applications are subject to many limitations arising from the model design, and the datasets available to inform the model parameterisation.
Regarding the model design, a key limitation is the assumption of an encroachment response [62], and the lack of support for shoreline recession by barrier roll-over [63]. This may lead to an inaccurate estimation of the rate of shoreline retreat where the frontal dune is breached by fluctuating and/or cumulative erosion, and the remaining dune or back-barrier morphology is low enough to support washover processes. In that case, the assumption of an encroachment response is no longer valid, and the model will likely over-estimate potential shoreline recession. When considering the well-developed dune morphology of most NSW beaches, relative to low-relief barrier island coasts e.g., [64], and following manual review of the regional-scale model predictions, we are confident that this limitation does not affect the model scenarios that are considered in our exposure assessment (i.e., present-1% exceedance, 2050-1% exceedance, and 2100-50% exceedance forecasts). In some settings, however, low-exceedance (e.g., 1%) and long-term (e.g., 2100) forecasts may over-estimate potential shoreline change (Figure 11A). Around estuary entrances, and for very narrow coastal barriers or typically sheltered NSW beaches, low dune and back-barrier morphology means that the assumption of an encroachment response may be invalid for model predictions that include high sampled sea-level rise and broad sediment sinks. Because we use alongshore-averaged beach-dune profiles to model cumulative erosion in both examples, low and/or narrow barrier morphology must be consistent along the length of the beach for it to influence shoreline change forecasts.
Another important limitation of the model design is the absence of dune growth during sea-level rise. Although we suggest that dune aggradation at the same pace as projected accelerating sea-level rise seems unlikely in this setting, aeolian deposition and dune growth is likely to play some role in shoreline response. While the washover parameter (VO) could be used to simulate the effect of washover deposition or dune growth in slowing the rate of shoreline recession, we neglect its use due to lack of data or previous examples. Nonetheless, a more rigorous dynamic barrier model [64,65,78] could be implemented within the framework to address these processes in more detail. We emphasise again that the model as applied here is intended to provide a risk-averse mid-resolution forecast of potential shoreline change. Future applications should consider more refined methods to describe the sediment transport processes that drive sediment redistribution and shoreline change.
Regarding our model parameterisation, the most significant limitation is the assumption that the shoreface will act as a sediment sink during sea-level rise in all settings along the NSW coast. Where this is not the case, the model is likely to over-predict shoreline recession (e.g., Figure 11A). While a sampled closure depth at the low end of the uncertainty space, such as 5–10 m (Figure 7B), assumes that only the nearshore surf zone acts as a sediment sink during sea-level rise, which is reasonable in any setting to maintain surf zone morphodynamics, a deeper closure depth imposes a more extensive sediment sink across the mid to lower shoreface. In reality, whether the shoreface represents a source or sink at each NSW beach will depend on the relationship between present shoreface geomorphology and the prevailing depositional controls (e.g., sediment distribution, type, and availability, and the energy regime). The presence of Holocene prograded barriers along parts of the central and southern NSW coasts is evidence that some of the shorefaces have acted as a source of sediments for adjacent beaches during the mid to late Holocene [24,90,91]. Whether or not the shoreface remains a significant source of sand supply for these NSW beaches, particularly under conditions of accelerating sea-level rise, remains an area of ongoing research [91]. Along the lower gradient northern NSW coast and shelf (Figure 1), the complete filling of many embayments with Pleistocene barrier deposits (and consequent absence of Holocene barrier deposits) [43], and the strong northward alongshore transport system, together make it more difficult to determine the current depositional relationship between beaches and the shoreface. Even where the shoreface does act as a sediment sink, the extent and timescale of shoreface response will likely depend on the rate and ultimate magnitude of future sea-level rise [96]. Similarly, the timescales and extent of estuarine response to sea-level rise [70,71,72,73] also remains largely unstudied and unknown on this coast, and for the larger north coast systems (Figure 1A) in particular, the volume and rate of river sediment supply is crucial to understanding the relative contribution from fluvial and littoral sources.
Comparison between the model parameterisations of shoreface geometry and composition, between the regional- and local-scale applications (Figure 8), demonstrates the importance of high-resolution coastal seabed mapping and sampling for understanding and quantifying coastal sediment budgets, and forecasting the potential for sediment redistribution and future shoreline change. Beyond the relationship between shoreface geometry and the prevailing depositional controls, the structure and composition of the seabed (Figure 3B) provides a direct insight to the potential for sediment accommodation across the shoreface—or the potential for ongoing shoreface sediment supply. For example, the presence of extensive low-relief reefs may be evidence of a sediment-deficient compartment, or the occurrence of protruding reef outcrops on an otherwise sedimentary shoreface suggests that sediment cannot accumulate in such areas under the prevailing energy conditions, thereby reducing the potential shoreface accommodation space. Understanding the balance of supply and accommodation in each sediment compartment is critical for interpreting if shoreface reefs represent negative sediment accommodation, an insufficient sediment supply, or both, in the context of sediment redistribution in response to sea-level rise.
Our approach provides a simple and scalable method to model potential shoreline change that considers distinctive beach morphology and compartment-based sediment budget principles, which we demonstrate through regional- and local-scale applications. However, we acknowledge that the approach remains a framework that would benefit from site-specific investigations and observation data to determine the applicability of our assumptions, and more rigorous methods of simulating shoreline response to sediment redistribution. While such data and methods already exist for some settings, and could be applied within our framework, our assumptions and the limitations of our approach highlight focus areas for future research. As a first step, an improved understanding of the probability distributions that describe key model variables (including sea-level rise) would help.
5.2. Exposure to Beach Erosion and Shoreline Change
Despite the limitations described above, regional-scale application of our modelling approach has enabled a second-pass assessment of property and infrastructure exposure to coastal erosion in NSW, which accounts for variation in the response of different beaches to both fluctuating and cumulative erosion—the first analysis and dataset of its kind. This is a considerable improvement on an earlier national-scale first-pass exposure assessment, which identified exposed assets simply by applying a uniform buffer distance (110 m) around all of the sandy and potentially erodible shorelines [56]. In comparison, our approach considers the distinctive morphology of individual NSW beaches (using LiDAR topography), in the context of the distinctive characteristics of the 47 secondary sediment compartments of the NSW coast. The regional-scale coastal erosion hazard mapping and exposure data that we present is designed for state-wide applications, such as to guide strategic planning along the NSW coast, and does not negate the need for more detailed investigations to inform local-scale coastal management and planning initiatives [106].
In NSW, assets that fall within the immediate (present-day) erosion hazard management zones, as defined by local governments, are considered to be potentially exposed to fluctuating beach erosion at present. Erosion hazard management zones are also defined for land and asset planning periods (often to 2050 and 2100), which consider the impacts of fluctuating beach erosion, the persistence of historical trends in shoreline change, and the potential response to sea-level rise. While the existing erosion hazard management zones may provide some indication of state-wide exposure, the coverage of NSW beaches is incomplete, and often focusses on locations that have been historically impacted by coastal erosion [57,58]. Therefore, while an analysis of the existing erosion hazard management zones may provide some indication of present exposure, it is anticipated that the potential future exposure is currently under-estimated.
To investigate this, we compiled the existing coastal erosion hazard mapping that is used by local governments to compare the identified exposure with our regional-scale modelling. We apply the same exposure assessment method (Section 3.5) to the incomplete coverage of local government erosion hazard management zones to determine the current definition of exposure. The results suggest that more than 2000 addresses are identified as being potentially exposed to coastal erosion at present, while that number increases to over 3700 and 6800 addresses by 2050 and 2100, respectively (Figure 17). When considering only properties for which more than half of the lot area may be affected, the exposure numbers reduce to 210 property lots (321 total addresses) potentially affected at present, rising to around 731 lots (1134 total addresses) at 2050, and 2040 lots (3315 total addresses) at 2100. The exposure figures that are based on existing coastal erosion hazard mapping compare with 247 property lots (455 total addresses) at present, 1862 lots (2718 total addresses) at 2050, and 3300 lots (5076 total addresses) at 2100, based on our regional-scale modelling (Figure 14).
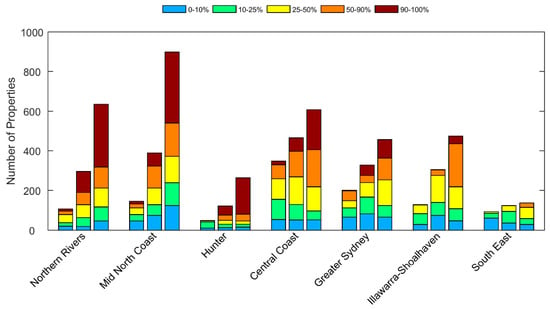
Figure 17.
Address exposure by NSW regions (Figure 1A) for present (left column), at 2050 (middle column) and at 2100 (right column), based on existing coastal erosion hazard management zones prepared for local governments. Colouring categorises the exposed addresses by the proportion of each associated property lot that was intersected by local government erosion hazard zones.
As anticipated, the comparison suggests that the existing mapping likely captures most of the present-day exposure, but may under-estimate future exposure, due to the coverage bias toward locations at present risk from erosion. Comparison between Figure 14 and Figure 17 shows that the distribution of exposure between the NSW regions is similar based on our regional-scale modelling and the existing erosion hazard management zones, respectively. Present exposure is highest in the relatively small area of central NSW (Central Coast and Greater Sydney regions), relative to northern NSW (Northern Rivers, Mid North Coast, and Hunter regions), and southern NSW (Illawarra-Shoalhaven and South East regions). This is reflected by the distribution of identified coastal erosion hot spots (Figure 1A). Exposure to coastal erosion increases in all of the regions by 2050 and 2100, with the majority of the increase representing addresses for which more than 25% of the property lot could be affected by erosion. The relative increase in exposure within and between regions is consistent with the patterns seen in Figure 14.
Differences in the rate and degree (as quantified by the affected land-area of exposed properties) of increasing exposure between regions reflects both regional coastal geomorphology, and the distribution of coastal development within each region. In central NSW, and southern NSW in particular, steeper and more rugged coastal geomorphology, coupled with higher exposure to the predominantly S-SE wave climate, contribute to well-developed dune morphology and relatively reduced dimensions of potential sediment sinks, such as the shoreface and estuaries (Appendix C). Combined with the restricted dimensions of low-lying coastal plains (for exposed developments to occur), and historically low development in southern NSW, these factors contribute to a lower potential increase in future exposure to coastal erosion relative to northern NSW. In contrast, the broad dimensions of potential sediment sinks in northern NSW suggests the potential for a greater increase in future exposure, based on our approach (Figure 14) and current practice (Figure 17).
The comparison between exposure figures based on our regional-scale modelling (Figure 14), and existing erosion hazard management zones that are used by local governments (Figure 17), suggests that: (1) the distribution and coverage of existing erosion hazard management zones along the NSW coast may be biased towards present exposure; and, (2) allowances for cumulative erosion through the present century in existing erosion hazard management zones may not reflect the full potential for sediment redistribution within coastal systems. This is evident in comparable present exposure being identified using both datasets, but considerably different exposure numbers for the 2050 and 2100 forecast periods. Kinsela and Hanslow [57] reviewed the various methods used to define erosion hazard management zones in NSW, and found that consideration of the potential response to sea-level rise, in particular, was often limited in scope by the application of a profile closure depth restricted to the upper shoreface (10–12 m water depth) only (c.f., Figure 7B), and the lack of consideration for the influence of sea-level rise on other sediment sinks, such as flood-tide delta environments within estuaries and tidal inlets. In contrast, our second-pass assessment and regional-scale mapping may over-estimate exposure where the shoreface and estuaries do not represent sediment sinks during sea-level rise (Section 5.1), again highlighting the need for improved data and methods to understand and model coastal sediment budgets.
5.3. Improving the Sediment Compartments Approach
Our approach demonstrates the utility of the sediment compartments framework, coupled with a statistical (Monte Carlo) model input sampling regime, for investigating the sensitivity of beach erosion and future shoreline change to depositional controls and coastal geomorphology, as defined at regional or local scales. Although we use the simple shoreline encroachment model to demonstrate the potential sensitivity of future shoreline change to the distribution, dimensions, and responses of sources and sinks within sediment-sharing coastal systems, more complex beach response and shoreline change models could be applied within our modelling approach. In any application, the model design and parameterisation should reflect the coverage and detail of available input data, and the intended purpose and required resolution of the model forecasts.
Our regional-scale application (Section 3.4.1) was limited by the availability of data for all NSW beaches to inform the parameterisation of various sediment budget components that may influence shoreline response on NSW beaches (Equation (3)). However, the resolution of the morphological data models captured the distinctive beach and dune topography of individual beaches, and was commensurate with the scale and intended application of the model predictions. The local-scale application (Section 3.4.2) demonstrates the scope for improvement in application of the approach where high-resolution data describing the coastal geomorphology (and processes) is available. For example, the use of regularly spaced (25-m alongshore) beach-dune profiles to capture the impact of fluctuating beach erosion, and alongshore-averaged beach-dune profiles to capture the distributed impact of cumulative sediment loss on shoreline change, is an important consideration where alongshore variability in the substrate and beach-barrier morphology presents the prospect of complex shoreline responses (Figure 10).
Beyond the simple assumption that the shoreface and estuaries act as sediment sinks during sea-level rise, uncertainty in both the second and third terms in Equation (3) also stems from limited knowledge regarding the response timescales of the shoreface [95,96] and estuarine depositional environments [72,73]. The fourth term in Equation (3) contains several volumetric sediment budget components that are potentially relevant to the future shoreline change on NSW beaches. However, those components remain difficult to quantify due to a limited understanding of the associated sediment transport processes, and were omitted from the regional-scale application. In our local-scale example (Section 3.4.2), we relied on expert opinion from a nearby beach to estimate the potential contribution of VM and VB to apply in our approach. As such, the second, third, and fourth terms of Equation (3) highlight focus areas for future research to better understand sediment dynamics on the NSW coast (and elsewhere), particularly considering the projected effects of global climate change within the present century.
A rigorous sub-compartment classification, and the mapping and quantification of sediment sources, sinks, and pathways, relies on an adequate understanding of the depositional environments of coastal sediment-sharing systems. Undoubtedly, the potential for the sediment compartments framework to improve the reliability of shoreline change forecasts depends on the coverage and detail of geomorphic data describing the distribution, dimensions, and connectivity of sources and sinks within coastal systems. Our understanding of sediment transport processes then determines uncertainty in the rate and volume of sediment redistribution in response to environmental change (e.g., sea-level rise). Confidence in our tertiary- and sub-compartment classification (Section 3.1) was limited by the coverage and resolution of bathymetry and seabed substrate data that is available along the NSW coastline. However, our examples suggest that increased effort in geomorphic data collection should lead to more reliable forecasts of future shoreline change, by enabling much refined sediment budget parameterisations, and providing new insights to the likely response of key sources and sinks to sea-level rise. While detailed geomorphic mapping has been completed for the coastal plains and valleys of the NSW coast [74,101,102], equivalent mapping describing the geomorphology of the inner-continental shelf, in particular, is essential to developing more refined shoreline change forecasts using the sediment compartments framework and sediment budget principles.
6. Conclusions
- Coastal sediment compartments provide a hierarchical framework to conceptualise and quantify potential sediment redistribution between the various depositional environments (sources and sinks) of sediment-sharing coastal systems. Sub-compartment classifications allow for sediment transport processes, which accumulate into meaningful sediment exchanges between sources and sinks across varying time scales, to be connected with the spatial scales of their impact on beach fluctuation and cumulative shoreline change.
- Volumetric approaches to modelling fluctuating and cumulative erosion provide a means to forecast the impacts of compartment-based sediment redistribution on beach and shoreline response, which reflects both compartment sediment budgets and transport pathways, and the distinctive beach-face and dune morphology of individual beaches.
- Based on our simplistic modelling approach and assumptions, exposure to coastal erosion is expected to increase into the future on open-coast NSW beaches, primarily due to the influence of sea-level rise on shoreline recession, driven by the redistribution of beach and dune sand to adjacent depositional environments (sediment sinks). The increase in exposure will vary between NSW beaches, reflecting regional- and local-scale variation in coastal geomorphology, and the present (and future) distribution of coastal development within each region.
- Assumptions regarding the response of key depositional environments (e.g., the shoreface and estuaries) to sea-level rise remains the most significant limitation to the reliability of long-term shoreline change forecasts, because of the overwhelming potential sediment demand that is imposed on littoral sediment budgets. Site-specific data and investigation is necessary to determine the likely roles and morphological response rates of these depositional environments, as sources or sinks within sediment-sharing systems.
- Opportunities to improve shoreline change forecasting based on the sediment compartments framework increase with the coverage and resolution of geomorphic data that is available to describe the distribution, dimensions, and depositional histories of sediment sources and sinks. For example, detailed seabed mapping and sampling covering the inner-continental shelf and estuary inlets is critical to reducing uncertainty in the future responses of shoreface and flood-tide delta depositional environments to sea-level rise.
Acknowledgments
This study was funded by research grants from the New South Wales (NSW) Environment Trust, Climate Change Fund, and Office of Emergency Management (Natural Disasters Resilience Program). The authors thank the School of Aviation and the Water Research Laboratory at UNSW Sydney for the use of airborne LiDAR data collected at Wamberal Beach in 2016, funded by the Australian Research Council (DP150101339) with assistance from the NSW Office of Environment and Heritage Coastal Processes and Responses Node. The authors thank Bruce Thom, Andrew Short, Angus Gordon and Marc Daley for helpful comments on the design of the modelling approach. The authors also thank two anonymous journal reviewers for detailed, insightful and constructive comments that greatly improved the manuscript.
Author Contributions
M.A.K. and D.J.H. conceived the overall approach. M.A.K. lead the design and development of the erosion modelling and exposure assessment methods, and carried out the modelling and analyses. B.D.M. contributed to the design of the erosion modelling and exposure assessment methods and lead the development of the modelling and analysis tools. M.L. contributed to the sediment sub-compartment classification methods and lead the development of the sediment compartment datasets. M.A.K. prepared the manuscript with input from all co-authors. D.J.H. provided input and review on all aspects of the study.
Conflicts of Interest
The authors declare no conflict of interest. The funding bodies had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A
The shoreline orientation of each beach, as recorded in the Australian beach database, was used as a pragmatic means to scale fluctuating erosion (F) for sheltered NSW beaches. The scaling coefficient for fluctuating beach erosion (cf in Equation (1)) was adjusted based on the average shoreline orientation of each beach or beach sector, as described in Table A1. The a, b and c parameters describe the lower bound, mode, and upper bound of triangular probability functions respectively. A beach with shoreline orientation of 90° faces due east on average, while a beach with shoreline orientation of 180° faces due south. The relatively higher exposure of north coast beaches to easterly storm wave conditions, which are more common in northern NSW, was accounted for by scaling fluctuating erosion for beaches with shoreline orientation <80°. In contrast, for central and southern NSW beaches, scaling was applied for shoreline orientations <90°. Considering the south to southeast wave climate, fluctuating erosion was also scaled for all beaches with shoreline orientation >180°.

Table A1.
Scaling values for fluctuating erosion (F) applied in the regional-scale example, to account for shoreline exposure to wave climate. Exposure varies between beaches based on the average shoreline orientation for each beach or sector. The a, b and c and values correspond to the lower bound, mode and upper bound, respectively, of the triangular probability functions used to represent cf.
Table A1.
Scaling values for fluctuating erosion (F) applied in the regional-scale example, to account for shoreline exposure to wave climate. Exposure varies between beaches based on the average shoreline orientation for each beach or sector. The a, b and c and values correspond to the lower bound, mode and upper bound, respectively, of the triangular probability functions used to represent cf.
| Shoreline | South/Central | North | ||||
|---|---|---|---|---|---|---|
| (°) | a | b | c | a | b | c |
| 0–29 | 0.5 | 0.55 | 0.6 | 0.5 | 0.55 | 0.6 |
| 30–59 | 0.6 | 0.65 | 0.7 | 0.6 | 0.65 | 0.7 |
| 60–70 | 0.7 | 0.75 | 0.8 | 0.7 | 0.75 | 0.8 |
| 70–74 | 0.7 | 0.75 | 0.8 | 0.8 | 0.85 | 0.9 |
| 75–79 | 0.7 | 0.75 | 0.8 | 0.9 | 0.95 | 1 |
| 80–84 | 0.8 | 0.85 | 0.9 | 1 | 1 | 1 |
| 85–89 | 0.9 | 0.95 | 1 | 1 | 1 | 1 |
| 90–179 | 1 | 1 | 1 | 1 | 1 | 1 |
| 180–189 | 0.9 | 0.95 | 1 | 0.9 | 0.95 | 1 |
| 190–199 | 0.8 | 0.85 | 0.9 | 0.8 | 0.85 | 0.9 |
| 200–219 | 0.7 | 0.75 | 0.8 | 0.7 | 0.75 | 0.8 |
| 220–239 | 0.6 | 0.65 | 0.7 | 0.6 | 0.65 | 0.7 |
| 240–299 | 0.5 | 0.55 | 0.6 | 0.5 | 0.55 | 0.6 |
| 300–360 | 0.4 | 0.45 | 0.5 | 0.4 | 0.45 | 0.5 |
Appendix B
To evaluate the suitability of the gamma function (Figure 6B) for describing the probability of fluctuating erosion (F) on fully exposed NSW beaches, we compared model predictions from our present-1% exceedance level scenario, with historical maximum erosion escarpments where they have been mapped on NSW beaches. A recent investigation of the geohistorical record of beach response to severe storms on this coastline compiled historical maximum erosion escarpments from 10 NSW beaches, which were identified using photogrammetry analysis of aerial photographs [87]. Figure A1 shows the result of the comparison for three representative fully exposed NSW beaches from that dataset. The comparison indicates that the 1% exceedance level fluctuating erosion volume in our approach is consistent with the impacts of some of the most severe coastal storms that have occurred during the recent historical period.

Figure A1.
Comparison between mapped historical maximum erosion escarpments and the present-1% exceedance erosion scenario from our regional-scale modelling. Examples are provided for the following exposed NSW beaches where historical maximum erosion escarpments have been mapped (year of maximum erosion event is indicated): (A) Nine Mile Beach at Tuncurry, Mid North Coast compartment (1963); (B) Bennetts Beach, Port Stephens compartment (1974); and (C) Redhead Beach, Central Coast compartment (1974). See Figure 1A for compartment locations.
Appendix C
The shoreface (VS) and estuarine flood-tide delta (VE) depositional environments represent prominent sediment sinks in the cumulative erosion function of the simple shoreline encroachment model (Equation (3)). The degree of influence that they have on forecast shoreline change varies within each model simulation, depending on the input values randomly sampled from the relevant probability functions (e.g., Figure 7). However, low-exceedance forecasts (e.g., 1% exceedance level) are representative of input values sampled from the upper tails of the input probability distributions.
To interpret the relative influence of the shoreface and estuary sediment sinks on variability in forecast shoreline change along the NSW coast, we provide their total summed surface areas for each primary compartment in Table A2. The surface areas are also normalised by dividing by the length of sandy shorelines within each compartment, to account for the varying alongshore extents of the primary compartments (Figure 1A). Generally speaking, the simple shoreline encroachment model assumes that beaches within compartments with higher normalised shoreface and estuary delta surface areas will experience greater sediment loss to these sinks during sea-level rise.

Table A2.
Summary statistics by primary sediment compartment (Figure 1A) describing the total length of sandy shorelines, total shoreface surface area (0–40 m water depth) and total surface area of estuarine flood-tide deltas. The shoreface and estuary delta areas are also expressed as area per metre of sandy shoreline to account for the varying alongshore extents of the compartments.
Table A2.
Summary statistics by primary sediment compartment (Figure 1A) describing the total length of sandy shorelines, total shoreface surface area (0–40 m water depth) and total surface area of estuarine flood-tide deltas. The shoreface and estuary delta areas are also expressed as area per metre of sandy shoreline to account for the varying alongshore extents of the compartments.
| Primary Compartment | Shoreline Length 1 (km) | Total Shoreface Area (km2) | Normalised Shoreface Area 2 (m2/m) | Total Estuary Delta Area (km2) | Normalised Estuary Delta Area 3 (m2/m) |
|---|---|---|---|---|---|
| North Coast | 152.1 | 841.7 | 5534.5 | 15.0 | 98.6 |
| Northern Rivers | 164.0 | 1080.6 | 6587.7 | 23.8 | 144.9 |
| Mid North Coast | 157.4 | 875.3 | 5562.4 | 7.3 | 46.5 |
| Port Stephens | 118.4 | 502.7 | 4246.0 | 3.2 | 27.2 |
| Central Coast | 66.0 | 355.3 | 5383.7 | 4.8 | 73.0 |
| Sydney | 66.0 | 174.8 | 2647.5 | 0.76 | 11.5 |
| Illawarra | 79.7 | 474.1 | 5946.7 | 3.5 | 44.3 |
| Shoalhaven | 93.3 | 369.3 | 3956.3 | 2.2 | 23.7 |
| South Coast | 167.3 | 635.4 | 3797.2 | 8.8 | 52.5 |
1 Sandy shorelines primarily influenced by open-coast processes as defined by Smartline [37]. 2 Total shoreface (0–40 m water depth) surface area divided by sandy shoreline length. 3 Total estuarine flood-tide delta surface area divided by sandy shoreline length.
References
- Harley, M.D.; Turner, I.L.; Kinsela, M.A.; Middleton, J.H.; Mumford, P.J.; Splinter, K.D.; Phillips, M.S.; Simmons, J.A.; Hanslow, D.J.; Short, A.D. Extreme coastal erosion enhanced by anomalous extratropical storm wave direction. Sci. Rep. 2017, 7, 6033. [Google Scholar] [CrossRef] [PubMed]
- Thom, B.G.; Hall, W. Behavior of beach profiles during accretion and erosion dominated periods. Earth Surf. Process. Landf. 1991, 16, 113–127. [Google Scholar] [CrossRef]
- Phillips, M.S.; Harley, M.D.; Turner, I.L.; Splinter, K.D.; Cox, R.J. Shoreline recovery on wave-dominated sandy coastlines: The role of sandbar morphodynamics and nearshore wave parameters. Mar. Geol. 2017, 385, 146–159. [Google Scholar] [CrossRef]
- Harley, M.D.; Turner, I.L.; Middleton, J.H.; Kinsela, M.A.; Hanslow, D.J.; Splinter, K.D.; Mumford, P.J. Observations of beach recovery in SE Australia following the June 2016 east coast low. In Proceedings of the Coasts & Ports 2017, Cairns, Australia, 21–23 June 2017. [Google Scholar]
- Barnard, P.L.; Short, A.D.; Harley, M.D.; Splinter, K.D.; Vitousek, S.; Turner, I.L.; Allan, J.; Banno, M.; Bryan, K.R.; Doria, A.; et al. Coastal vulnerability across the Pacific dominated by El Niño/Southern Oscillation. Nat. Geosci. 2015, 8, 801–807. [Google Scholar] [CrossRef]
- Mortlock, T.R.; Goodwin, I.D. Impacts of enhanced central Pacific ENSO on wave climate and headland-bay beach morphology. Cont. Shelf Res. 2016, 120, 14–25. [Google Scholar] [CrossRef]
- Goodwin, I.D.; Mortlock, T.R.; Browning, S. Tropical and extratropical-origin storm wave types and their influence on the East Australian longshore sand transport system under a changing climate. J. Geophys. Res. Oceans 2016, 121, 4833–4853. [Google Scholar] [CrossRef]
- Leatherman, S.P. Social and economic costs of sea level rise. Int. Geophys. 2001, 75, 181–223. [Google Scholar]
- Phillips, M.R.; Jones, A.L. Erosion and tourism infrastructure in the coastal zone: Problems, consequences and management. Tour. Manag. 2006, 27, 517–524. [Google Scholar] [CrossRef]
- Barbier, E.B.; Hacker, S.D.; Kennedy, C.; Kock, E.W.; Stier, A.C. The value of estuarine and coastal ecosystem services. Ecol. Monogr. 2011, 81, 169–193. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Smith, M.D.; Slott, J.M.; Murray, A.B. The value of disappearing beaches: A hedonic pricing model with endogenous beach width. J. Environ. Econ. Manag. 2011, 61, 297–310. [Google Scholar] [CrossRef]
- Murray, A.B.; Gopalakrishnan, S.; McNamara, D.E.; Smith, M.D. Progress in coupling models of human and coastal landscape change. Comput. Geosci. 2013, 53, 30–38. [Google Scholar] [CrossRef]
- Williams, Z.C.; McNamara, D.E.; Smith, M.D.; Murray, A.B.; Gopalakrishnan, S. Coupled economic-coastline modeling with suckers and free riders. J. Geophys. Res. Earth Surf. 2013, 118, 887–899. [Google Scholar] [CrossRef]
- Lazarus, E.D.; Ellis, M.A.; Murray, A.B.; Hall, D.M. An evolving research agenda for human-coastal systems. Geomorphology 2016, 256, 81–90. [Google Scholar] [CrossRef]
- Jongejan, R.; Ranasinghe, R.; Wainwright, D.; Callaghan, D.P.; Reyns, J. Drawing the line on coastline recession risk. Ocean Coast. Manag. 2016, 122, 87–94. [Google Scholar] [CrossRef]
- FitzGerald, D.M.; Fenster, M.S.; Argow, B.A.; Buynevich, I.V. Coastal impacts due to sea-level rise. In Annual Review of Earth and Planetary Sciences; Annual Reviews: Palo Alto, CA, USA, 2008; pp. 601–647. [Google Scholar]
- Stive, M.J.F.; Cowell, P.J.; Nicholls, R.J. Impacts of Global Environmental Change on Beaches, Cliffs and Deltas. In Geomorphology and Global Environmental Change; Slaymaker, O., Spencer, T., Embleton-Hamann, C., Eds.; International Association of Geomorphologists, Cambridge University Press: Cambridge, UK, 2009; pp. 158–179. [Google Scholar]
- Zhang, K.; Douglas, B.C.; Leatherman, S.P. Global warming and coastal erosion. Clim. Chang. 2004, 64, 41–58. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. 2013: Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Sweet, W.V.; Kopp, R.E.; Weaver, C.P.; Obeysekera, J.; Horton, R.M.; Thieler, E.R.; Zervas, C. Global and Regional Sea Level Rise Scenarios for the United States; National Oceanic and Atmospheric Administration (NOAA): Silver Spring, MD, USA, 2017.
- Cowell, P.J.; Stive, M.J.F.; Niedoroda, A.W.; de Vriend, H.J.; Swift, D.J.P.; Kaminsky, G.M.; Capobianco, M. The coastal-tract (part 1): A conceptual approach to aggregated modeling of low-order coastal change. J. Coast. Res. 2003, 19, 812–827. [Google Scholar]
- Komar, P.D. The budget of littoral sediments: Concepts and applications. Shore Beach 1996, 64, 18–26. [Google Scholar]
- Rosati, J.D. Concepts in sediment budgets. J. Coast. Res. 2005, 21, 307–322. [Google Scholar] [CrossRef]
- Cowell, P.J.; Stive, M.J.F.; Niedoroda, A.W.; Swift, D.J.P.; de Vriend, H.J.; Buijsman, M.C.; Nicholls, R.J.; Roy, P.S.; Kaminsky, G.M.; Cleveringa, J.; et al. The coastal-tract (part 2): Applications of aggregated modeling of lower-order coastal change. J. Coast. Res. 2003, 19, 828–848. [Google Scholar]
- French, J.; Burningham, H.; Thornhill, G.; Whitehouse, R.; Nicholls, R.J. Conceptualising and mapping coupled estuary, coast and inner shelf sediment systems. Geomorphology 2016, 256, 17–35. [Google Scholar] [CrossRef]
- Davies, J.L. The coastal sediment compartment. Aust. Geogr. Stud. 1974, 12, 139–151. [Google Scholar] [CrossRef]
- Patsh, K.; Griggs, G. Development of Sand Budgets for California’s Major Littoral Cells: Eureka, Santa Cruz, Southern Monterey Bay, Santa Barbara, Santa Monica (Including Zuma), San Pedro, Laguna, Oceanside, Mission Bay, and Silver Strand Littoral Cells; Institute of Marine Sciences, University of California: Santa Cruz, CA, USA, 2007. [Google Scholar]
- Bray, M.J.; Carter, D.J.; Hooke, J.M. Littoral cell definition and budgets for central southern England. J. Coast. Res. 1995, 11, 381–400. [Google Scholar]
- Cooper, N.J.; Pontee, N.I. Appraisal and evolution of the littoral “sediment cell” concept in applied coastal management: Experiences from England and Wales. Ocean Coast. Manag. Coast. Manag. 2006, 49, 498–510. [Google Scholar] [CrossRef]
- Sanderson, P.G.; Eliot, I. Compartmentalisation of beachface sediments along the southwestern coast of Australia. Mar. Geol. 1999, 162, 145–164. [Google Scholar] [CrossRef]
- Eliot, I.; Gozzard, B.; Nutt, C. Geologic frameworks for coastal planning and management. In Proceedings of the Australasian Coasts & Ports Conference 2011, Perth, Australia, 28–30 September 2011. [Google Scholar]
- Eliot, I.; Nutt, C.; Gozzard, J.; Higgins, M.; Buckley, E.; Bowyer, J. Coastal Compartments of Western Australia: A Physical Framework for Marine and Coastal Planning; Damara WA Pty. Ltd.: Perth, Australia, 2011. [Google Scholar]
- McPherson, A.; Hazelwood, M.; Moore, D.; Owen, K.; Nichol, S.; Howard, F.J.F. The Australian Coastal Sediment Compartments Project: Methodology and Product Development; Record 2015/25; Geoscience Australia: Canberra, Australia, 2015.
- Thom, B.G.; Eliot, I.; Eliot, M.; Harvey, N.; Rissik, D.; Sharples, C.; Short, A.D.; Woodroffe, C.D. National sediment compartment framework for Australian coastal management. Ocean Coast. Manag. 2017, in press. [Google Scholar]
- Short, A.D. Australian beach systems—Nature and distribution. J. Coast. Res. 2006, 22, 11–27. [Google Scholar] [CrossRef]
- Short, A.D. Beaches of the New South Wales Coast, 2nd ed.; Sydney University Press: Sydney, Australia, 2007. [Google Scholar]
- Sharples, C.; Mount, R.; Pedersen, T.; Lacey, M.; Newton, J.; Jaskierniak, D.; Wallace, L. The Australian Coastal Smartilne Geomorphic and Stability Map Version 1: Project Report; School of Geography and Environmental Studies (Spatial Sciences), University of Tasmania: Hobart, Tasmania, 2009. [Google Scholar]
- Wright, L.D. Nearshore wave-power dissipation and coastal energy regime of Sydney-Jervis Bay region, New-South-Wales—Comparison. Aust. J. Mar. Freshw. Res. 1976, 27, 633–640. [Google Scholar] [CrossRef]
- Short, A.D.; Trenaman, N.L. Wave climate of the Sydney region, an energetic and highly variable ocean wave regime. Aust. J. Mar. Freshw. Res. 1992, 43, 765–791. [Google Scholar] [CrossRef]
- Boyd, R.; Ruming, K.; Goodwin, I.; Sandstrom, M.; Schroder-Adams, C. Highstand transport of coastal sand to the deep ocean: A case study from Fraser Island, southeast Australia. Geology 2008, 36, 15–18. [Google Scholar] [CrossRef]
- Goodwin, I.D.; Freeman, R.; Blackmore, K. An insight into headland sand bypassing and wave climate variability from shoreface bathymetric change at Byron Bay, New South Wales, Australia. Mar. Geol. 2013, 341, 29–45. [Google Scholar] [CrossRef]
- Browning, S.A.; Goodwin, I.D. Large-scale influences on the evolution of winter subtropical maritime cyclones affecting Australia’s east coast. Mon. Weather Rev. 2013, 141, 2416–2431. [Google Scholar] [CrossRef]
- Roy, P.S.; Thom, B.G. Late Quaternary marine deposition in New South Wales and southern Queensland—An evolutionary model. J. Geol. Soc. Aust. 1981, 28, 471–489. [Google Scholar] [CrossRef]
- NSW Coastal Erosion Hot Spots. Office of Environment and Heritage (OEH). Available online: http://www.environment.nsw.gov.au/coasts/coasthotspots.htm (accessed on 8 August 2017).
- Thom, B.G.; Roy, P.S. Relative sea levels and coastal sedimentation in southeast Australia in the Holocene. J. Sediment. Petrol. 1985, 55, 257–264. [Google Scholar]
- Thom, B.G.; Keene, J.B.; Cowell, P.J.; Daley, M. East Australian marine abrasion surface. In Australian Landscapes; Bishop, P., Pillans, B., Eds.; Geological Society: London, UK, 2010; pp. 57–59. [Google Scholar]
- Gordon, A.D.; Hoffman, J.G. Sediment features and processes of the Sydney continental shelf. In Recent Sediments in Eastern Australia—Marine Through Terrestrial; Frankel, E., Keene, J.B., Waltho, A.E., Eds.; Geological Society of Australia Special Publication: Sydney, Australia, 1986; pp. 29–51. [Google Scholar]
- Roy, P.S.; Cowell, P.J.; Ferland, M.A.; Thom, B.G. Wave dominated coasts. In Coastal Evolution: Late Quaternary Shoreline Morphodynamics; Carter, R.W.G., Woodroffe, C.D., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 121–186. [Google Scholar]
- Thom, B.G. Transgressive and regressive stratigraphies of coastal sand barriers in southeast Australia. Mar. Geol. 1984, 56, 137–158. [Google Scholar] [CrossRef]
- Thom, B.G. Coastal erosion in eastern Australia. Search 1974, 5, 198–209. [Google Scholar] [CrossRef]
- Chapman, D.M.; Geary, M.; Roy, P.S.; Thom, B.G. Coastal Evolution and Coastal Erosion in New South Wales; Coastal Council of New South Wales: Sydney, Austrilia, 1982.
- Hanslow, D.J.; Howard, M. Emergency Management of Coastal Erosion in NSW. In Planning for Natural Hazards—How Can We Mitigate the Impacts? Morrison, R.J., Quin, S., Bryant, E.A., Eds.; Proceedings of the Symposium on Natural Hazards: Wollongong, Austrilia, 2005; pp. 103–116. [Google Scholar]
- Mortlock, T.; Goodwin, I.; McAneney, J.; Roche, K. The June 2016 Australian East Coast Low: Importance of Wave Direction for Coastal Erosion Assessment. Water 2017, 9, 121. [Google Scholar] [CrossRef]
- Proudfoot, M.; Petersen, L.S. Positive SOI, negative PDO and spring tides as simple indicators of the potential for extreme coastal erosion in northern NSW. Aust. J. Environ. Manag. 2011, 18, 170–181. [Google Scholar] [CrossRef]
- Chapman, D.M. Coastal erosion and the sediment budget, with special reference to the Gold Coast, Australia. Coast. Eng. 1981, 4, 207–227. [Google Scholar] [CrossRef]
- Climate Change Risks to Australia’s Coasts: A First Pass National Assessment; Australian Government Department of Climate Change: Canberra, Australia, 2009.
- Kinsela, M.A.; Hanslow, D.J. Coastal erosion risk assessment in New South Wales: Limitations and future directions. In Proceedings of the 22nd NSW Coastal Conference, Port Macquarie, Australia, 12–15 November 2013. [Google Scholar]
- Wainwright, D.J.; Ranasinghe, R.; Callaghan, D.P.; Woodroffe, C.D.; Cowell, P.J.; Rogers, K. An argument for probabilistic coastal hazard assessment: Retrospective examination of practice in New South Wales, Australia. Ocean Coast. Manag. 2014, 95, 147–155. [Google Scholar] [CrossRef]
- Stul, T.; Gozzard, J.R.; Eliot, I.G.; Eliot, M.J. Coastal Sediment Cells between Cape Naturaliste and the Moore River, Western Australia; Geological Survey of Western Australia for the Western Australian Department of Transpo: Perth, Australia, 2012.
- Carvalho, R.C.; Woodroffe, C.D. From catchment to inner shelf: Insights into NSW coastal compartments. In Proceedings of the 24th NSW Coastal Conference, Forster, Australia, 11–13 November 2015. [Google Scholar]
- Kinsela, M.A.; Morris, B.D.; Daley, M.J.A.; Hanslow, D.J. A flexible approach to forecasting coastline change on wave-dominated beaches. J. Coast. Res. 2016, SI75, 952–956. [Google Scholar] [CrossRef]
- Cowell, P.J.; Roy, P.S.; Jones, R.A. Simulation of large-scale coastal change using a morphological behavior model. Mar. Geol. 1995, 126, 45–61. [Google Scholar] [CrossRef]
- Leatherman, S.P. Barrier dynamics and landward migration with Holocene sea-level rise. Nature 1983, 301, 415–417. [Google Scholar] [CrossRef]
- Moore, L.J.; List, J.H.; Williams, S.J.; Stolper, D. Complexities in barrier island response to sea level rise: Insights from numerical model experiments, North Carolina Outer Banks. J. Geophys. Res. 2010, 115, F03004. [Google Scholar] [CrossRef]
- Lorenzo-Trueba, J.; Ashton, A.D. Rollover, drowning, and discontinuous retreat: Distinct modes of barrier response to sea-level rise arising from a simple morphodynamic model. J. Geophys. Res. Earth Surf. 2014, 119, 779–801. [Google Scholar] [CrossRef]
- Walters, D.; Moore, L.J.; Vinent, O.D.; Fagherazzi, S.; Mariotti, G. Interactions between barrier islands and backbarrier marshes affect island system response to sea level rise: Insights form a coupled model. J. Geophys. Res. Earth Sci. 2014, 119, 2013–2031. [Google Scholar] [CrossRef]
- Bruun, P. Sea level rise as a cause of shore erosion. J. Waterw. Harb. Div. ASCE 1962, 88, 117–130. [Google Scholar]
- Bruun, P. Review of conditions for uses of the Bruun Rule of erosion. Coast. Eng. 1983, 7, 77–89. [Google Scholar] [CrossRef]
- Bruun, P. The Bruun Rule of erosion by sea-level rise—A discussion on large-scale two- and three-dimensional usages. J. Coast. Res. 1988, 4, 627–648. [Google Scholar]
- Eysink, W.D. Morphologic response of tidal basins to changes. In 22nd International Conference on Coastal Engineering; American Society of Civil Engineers: Reston, VA, USA, 1990; pp. 1948–1961. [Google Scholar]
- Stive, M.J.F.; Capobianco, M.; Wang, Z.B.; Ruol, P.; Buijsman, M.C. Morphodynamics of a tidal lagoon and the adjacent coasts. In 8th International Biennial Conference on Pysics of Estuaries and Coastal Seas; Dronkers, J., Scheffers, M., Eds.; Elsevier: Roterdam, The Netherland, 1998; pp. 397–407. [Google Scholar]
- Van Goor, M.A.; Zitman, T.J.; Wang, Z.B.; Stive, M.J.F. Impact of sea-level rise on the morphological equilibrium state of tidal inlets. Mar. Geol. 2003, 202, 211–227. [Google Scholar] [CrossRef]
- Kragtwijk, N.G.; Zitman, T.J.; Stive, M.J.F.; Wang, Z.B. Morphological response of tidal basins to human interventions. Coast. Eng. 2004, 51, 207–221. [Google Scholar] [CrossRef]
- Spatial Services Imagery and Elevation Programs: NSW Digital Elevation Data Set. Available online: http://spatialservices.finance.nsw.gov.au/mapping_and_imagery/imagery_programs (accessed on 5 August 2017).
- Nielsen, A.F.; Lord, D.B.; Poulos, H.G. Dune stability considerations for building foundations. Civil Eng. Trans. Inst. Eng. Aust. 1992, CE34, 167–174. [Google Scholar]
- Murray, A.B.; Gasparini, N.M.; Goldstein, E.B.; van der Wegen, M. Uncertainty quantification in modeling earth surface processes: More applicable for some types of models than for others. Comput. Geosci. 2016, 90, 6–16. [Google Scholar] [CrossRef]
- Simmons, J.A.; Harley, M.D.; Marshall, L.A.; Turner, I.L.; Splinter, K.D.; Cox, R.J. Calibrating and assessing uncertainty in coastal numerical models. Coast. Eng. 2017, 125, 28–41. [Google Scholar] [CrossRef]
- Cowell, P.J.; Thom, B.G.; Jones, R.A.; Everts, C.H.; Simanovic, D. Management of uncertainty in predicting climate-change impacts on beaches. J. Coast. Res. 2006, 22, 232–245. [Google Scholar] [CrossRef]
- Mariani, A.; Flocard, F.; Carley, J.T.; Drummond, C.D.; Guerry, N.; Gordon, A.D.; Cox, R.J.; Turner, I.L. East Coast Study Project—National Geomorphoc Framework for the Management and Prediction of Coastal Erosion; Water Research Laboratory, University of New South Wales: Sydney, Australia, 2013. [Google Scholar]
- Anderson, T.R.; Fletcher, C.H.; Barbee, M.M.; Frazer, N.; Romine, B. Doubling of coastal erosion under rising sea level by mid-century in Hawaii. Nat. Hazards 2015, 78, 75–103. [Google Scholar] [CrossRef]
- Wainwright, D.J.; Ranasinghe, R.; Callaghan, D.P.; Woodroffe, C.D.; Jongejan, R.; Dougherty, A.J.; Rogers, K.; Cowell, P.J. Moving from deterministic towards probabilistic coastal hazard and risk assessment: Development of a modelling framework and application to Narrabeen Beach, New South Wales, Australia. Coast. Eng. 2015, 96, 92–99. [Google Scholar] [CrossRef]
- Roy, C.J.; Oberkampf, W.L. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput. Methods Appl. Mech. Eng. 2011, 200, 2131–2144. [Google Scholar] [CrossRef]
- Gordon, A.D. Beach fluctuations and shoreline change—NSW. In Proceedings of the 8th Australasian Conference on Coastal and Ocean Engineering, Launceston, Australia, 1987. [Google Scholar]
- Rollason, V.; Gordon, A. Back to the future of beach fluctuations and shoreline change. In Proceedings of the 24th NSW Coastal Conference, Forster, Australia, 11–13 November 2015. [Google Scholar]
- Callaghan, D.P.; Nielsen, P.; Short, A.; Ranasinghe, R. Statistical simulation of wave climate and extreme beach erosion. Coast. Eng. 2008, 55, 375–390. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Ranasinghe, R.; Roelvink, D. Probabilistic estimation of storm erosion using analytical, semi-empirical, and process based storm erosion models. Coast. Eng. 2013, 82, 64–75. [Google Scholar] [CrossRef]
- Goodwin, I.D.; Burke, A.; Mortlock, T.; Freeman, R.; Browning, S.A. Technical Report of the Eastern Seaboard Climate Change Initiative on East Coast Lows (ESCCI-ECLs) Project 4: Coastal System Response to Extreme East Coast Low Clusters in the Geohistorical Archive; Marine Climate Risk Group, Climate Futures, Macquarie University: Sydney, Australia, 2015. [Google Scholar]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. A reevaluation of coastal embayment rotation: The dominance of cross-shore versus alongshore sediment transport processes, Collaroy-Narrabeen Beach, southeast Australia. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Davies, G.; Callaghan, D.P.; Gravios, U.; Jiang, W.; Hanslow, D.; Nichol, S.; Baldock, T. Improved treatment of non-stationary conditions and uncertainties in probabilistic models of storm wave climate. Coast. Eng. 2017, 127, 1–19. [Google Scholar] [CrossRef]
- Cowell, P.J.; Stive, M.J.F.; Roy, P.S.; Kaminsky, G.M.; Buijsman, M.C.; Thom, B.G.; Wright, L.D. Shoreface sand supply to beaches. In Proceedings of the 27th International Coastal Engineering Conference, Sydney, Australia, 16–21 July 2001; pp. 2495–2508. [Google Scholar]
- Kinsela, M.A.; Daley, M.J.A.; Cowell, P.J. Origins of Holocene coastal strandplains in Southeast Australia: Shoreface sand supply driven by disequilibrium morphology. Mar. Geol. 2016, 374, 14–30. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Domingues, C.M.; Monselesan, D.P.; Miles, E.R. Sea-Level and Ocean Heat-Content Change, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013; p. 103. [Google Scholar]
- Church, J.A.; McInnes, K.L.; Monselesan, D.; O’Grady, J. Sea-Level Rise and Allowances for Coastal Councils around Australia—Guidance Material; Commonwealth Scientific and Industrial Research Organisation (CSIRO): Canberra, Australia, 2016.
- Niedoroda, A.W.; Swift, D.J.P.; Hopkins, T.S.; Ma, C.M. Shoreface morphodynamics on wave-dominated coasts. Mar. Geol. 1984, 60, 331–354. [Google Scholar] [CrossRef]
- Stive, M.J.F.; de Vriend, H.J. Modeling shoreface profile evolution. Mar. Geol. 1995, 126, 235–248. [Google Scholar] [CrossRef]
- Kinsela, M.A.; Cowell, P.J. Controls on shoreface response to sea level change. In Proceedings of the Coastal Sediments ’15, San Diego, CA, USA, 11–15 May 2015. [Google Scholar]
- Hallermeier, R.J. A profile zonation for seasonal sand beaches from wave climate. Coast. Eng. 1981, 4, 253–277. [Google Scholar] [CrossRef]
- Meleo, J.F. Shoreface Variability in Southeastern Australia; The University of Sydney: Sydney, Australia, 1994. [Google Scholar]
- Cowell, P.J.; Hanslow, D.J.; Meleo, J.F. The shoreface. In Handbook of Beach and Shoreface Morphodynamics; Short, A.D., Ed.; John Wiley: Hoboken, NJ, USA, 1999; p. 392. [Google Scholar]
- Patterson, D.C. Shoreward sand transport outside the surf zone, northern Gold Coast, Australia. In Proceedings of the 33rd International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar]
- Troedson, A.L.; Hashimoto, T.R. Coastal Quaternary Geology—North and South Coast of NSW; Geological Survey of New South Wales: Sydney, Australia, 2008.
- NSW Coastal Quaternary Geology Data Package (Version 3)—Geological Survey of New South Wales. Available online: https://search.geoscience.nsw.gov.au/product/40 (accessed on 5 August 2017).
- Worley Parsons Open Coast and Broken Bay Beaches Coastal Processes and Hazard Definition Study; Worley Parsons for Gosford City Council: Sydney, Australia, 2014.
- Hudson, J.P. Gosford City Council Open Ocean Beaches Geotechnical Investigations; Coastal & Marine Geosciences: Sydney, Australia, 1997.
- Hudson, J.P. Gosford City Beach Nourishment Feasibility Study—Stage 2—Investigation of Marine Sand Resources; Coastal & Marine Geosciences: Sydney, Australia, 1999.
- Hanslow, D.J.; Dela-Cruz, J.; Morris, B.D.; Kinsela, M.A.; Foulsham, E.; Linklater, M.; Pritchard, T.R. Regional scale coastal mapping to underpin strategic land use planning in south east Australia. J. Coast. Res. 2016, 75, 987–991. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).