Information Theoretic Source Seeking Strategies for Multiagent Plume Tracking in Turbulent Fields

Abstract

We present information theoretic search strategies for single and multi-robot teams to localize the source of biochemical contaminants in turbulent flows. The robots synthesize the information provided by sporadic and intermittent sensor readings to optimize their exploration strategy. By leveraging the spatio-temporal sensing capabilities of a mobile sensing network, our strategies result in control actions that maximize the information gained by the team while minimizing the time spent localizing the biochemical source. By leveraging the team’s ability to obtain simultaneous measurements at different locations, we show how a multi-robot team is able to speed up the search process resulting in a collaborative information theoretic search strategy. We validate our proposed strategies in both simulations and experiments.

1. Introduction

We are interested in enabling autonomous mobile robot teams to collaboratively search and localize the source of a biochemical contaminant dispersed in turbulent media. Specifically, we are interested in applications where autonomous robots can be deployed to effectively and efficiently localize the source of a biochemical or radiological contaminant leakage, such as an oil spill or a radioactive dispersal, and track the contaminant dispersion in turbulent flows. In general, variations in material concentrations from a source in a flow field is heavily dependent on the Reynolds numbers. While gradient-based strategies work well in lower Reynolds regimes where variations in material concentrations tend to be smooth [1], material transport becomes dominated by turbulent mixing in high Reynolds number media, e.g., in the atmosphere or in the ocean [1,2]. The result is a highly anisotropic and unsteady sensory landscape where sensor measurements become the sporadic and intermittent, rendering many gradient-based strategies ineffective [3,4].

Existing work in source seeking seeking and plume tracking can be grouped into three categories. Works in the first category focus on measuring the local concentration gradient of the plume along the robot’s trajectory to steer the robot towards the source with or without inferring the dynamics of the surrounding medium [5,6,7,8]. Since these strategies rely solely on the local gradient, they become unreliable when material concentrations do not vary in a smooth and continuous fashion. Existing works in the second category leverage the spatial distribution of observations that can be obtained using a team of mobile sensors to build a local flow model. The model is then used to predict changes in the material concentrations by integrating locally estimated flow functions [9,10] or building a map of the contamination distribution [11,12]. The third category consists of search strategies primarily concerned with the accuracy and robustness of the measurements when employing a gradient-based search strategy in a turbulent medium. Since material transport is dominated by turbulence in high Reynolds regimes, information about the source location must be inferred from intermittent sensor detections. As such, these works focus on developing search strategies that can infer the source location from these intermittent observations [2,13,14].

In this work, we build upon [2] and our existing results in [15] to formulate the source seeking/plume localization problem as an information theoretic search problem. The proposed search strategy consists of determining actions that maximize the change in entropy of the source location belief distribution. Similar to [16] and [17], we employ a particle filter representation of the posterior belief distribution to make the strategy computationally tractable for large complex spaces and distributable for mobile sensing teams. Our preliminary results demonstrate the viability of the strategy for single and multiple robots in simulation [15] where the plume is a three dimensional (3D) time-varying computational fluid model of the 2010 Deep Water Horizon oil spill [18,19]. Similar to works in the second category, we leverage the spatial distribution of a team of coordinated mobile sensors to more efficiently locate the source. When coordinating a group of mobile robots, a significant challenge is determining what information should be exchanged between the various team members. As a robot searches for the source of the dispersed contaminants, it would randomly obtain both positive and negative sensor readings in regards to the presence of the contaminant in the medium. While it may seem that positive detections should be shared among the robots, negative detections also play a vital role in shaping the source belief distribution.1

In [15] we extend the gradient-free information based search strategy first describe in [2] to a team of mobile sensing agents. The work in [18] builds upon this result to develop a computationally tractable search strategy suitable for large complex spaces and distributable for mobile sensing teams through the use of particle filters. Additionally, the extensions described in [18] were validated using a realistic 3D time-varying computational fluid model of the 2010 Deep Water Horizon oil spill [19]. In this work, we consolidate and build upon [15,18] to develop coordinated search strategies for mobile sensing teams to effectively find and localize the source of a dispersed contaminant in turbulent media. Specifically, we extend our existing strategy to account for the uncertainty in each robot’s estimated pose which is important in underwater environments where pose estimates can be very noisy. In addition, we employ Gaussian functions to provide an estimate of the source position and present an improved information sharing framework for the team to more efficiently perform the search. We validate our strategies in simulation and in experiments using a mixed-reality experimental framework.

The paper is organized as follows: Section 2 provides a summary of our modeling framework and assumptions. Section 3 describes our methodologies for accounting for the robot pose uncertainty, the use of Gaussian functions to describe the estimates of the source position, and the coordination framework. Simulation and experimental results are presented in Section 4 where the proposed methods are validated and compared to the performance of random methods. Finally, the comprehensive strategy is validated using the simulation of the 2010 Deep Water Horizon Oil Spill. A summary of the contributions is provided in Section 5.

2. Preliminaries

In this paper we address the problem of finding the source of a contaminant, such as a hazardous waste plume, in a turbulent medium. We restrict our search to a two dimensional (2D), obstacle-free environment in which every robot has the ability to localize itself within the workspace and, if necessary, measure the magnitude and direction of the local flow field. In this work, we assume robots can reliably communicate with one another even though the objective will be to minimizing inter-robot communications. Finally, sensor measurements are binary – the material is either present or not at the robot’s current position in the workspace.

The expected rate of a positive plume detection in the environment depends on the material properties of both the medium and contaminant, the distance of the sensor to the source, the dynamics of the surrounding flow field, the geometry of the environment. For a robot searching for the position of the source, the observation model is a Binomial distribution with the chance of positive sensor readings far smaller than negative ones. The law of rare events states that at its limit we can approximate the probability of such an observation with a Poisson distribution [20]. The mean rate of odor detection events at the position with coordinate r dispersed by a source located at $r_0$ is given by the following equation:

$$\begin{array}{c}\hfill \mathcal{R}(r|r_0)=\frac{R}{ln(\frac{\lambda }{a})}{e}^{\frac{V}{2D}|r-r_0|}{K}_0\left(\frac{\mid r-r_0\mid }{\lambda }\right),\mathrm{with}\lambda =\sqrt{\frac{D\tau }{1+\left(\frac{V^2\tau }{4D}\right)}}\end{array}$$

where R is the emission rate of the source, τ is the expected lifetime of the chemical patch before its concentration falls outside the detectable range, D is the isotropic effective diffusivity of the medium, V is the average velocity of the medium, or wind, and $K_0(·)$ is the modified Bessel function of the second kind [2].

In the search for the source, the set of chemical detections along the search trajectory carries information about the relative location of the source with respect to the robot. Thus, a robot can construct the probability distribution function over the position of the source using Bayes’ rule:

$$\begin{array}{c}\hfill P(r_0|{\mathcal{T}}_t)=\frac{P({\mathcal{T}}_t|r_0)P(r_0)}{\int P({\mathcal{T}}_t|r)P(r)dr}\end{array}$$

(1)

As such, ${\mathcal{T}}_t$ encapsulates the history of the uncorrelated plume observations it receives along its trajectory, and $P({\mathcal{T}}_t|r_0)$ denotes the probability of experiencing such a history if the source of the dispersion is at $r_0$. Assuming that the probability of detecting a plume at each point is independent, Poisson’s law can be used to estimate the probability of ${\mathcal{T}}_t$ as:

$$\begin{array}{c}\hfill P({\mathcal{T}}_t|r_0)=exp\left(-{\int }_0^t\mathcal{R}(r(\overline{t})|r_0)d\overline{t}\right)\prod _i\mathcal{R}(r(t_i)|r_0)\end{array}$$

(2)

where $r(t)$ is the search trajectory, and $r(t_i)$ is the position of each detection along the trajectory, and $\mathcal{R}(r(t)|r_0)$ is the expected rate of encounters at $r(t)$ for a source at $r_0$ [2]. It is important to mention that the assumption of independence of detection events holds since the location of the source of dispersion is unknown.

Estimating the position of the source follows the traditional procedure of the Bayesian filter: estimate, observe, and update. The procedure starts with estimating the probability over the position of the source. This estimate is used to calculate the expected rate of plume detection at the current position using the observation model given by Equation (1). After an observation is made, the estimated probability distribution is then updated accordingly [15].

The current estimate of the belief distribution over the location of the source is used to predict the expected rate of positive sensor measurements at the next robot position and is given by:

$$h(r(t^{\prime }))=\int P({\mathcal{T}}_t|r_0)\mathcal{R}(r|r_0)d{r}_0$$

(3)

The probability of detecting a chemical cue at the next way point follows Poisson’s law:

$$\rho (r(t^{\prime }))=h(r(t^{\prime }))e^{(-h(r(t^{\prime })))}$$

(4)

Observations gathered at each time step are used to update the probability distribution function the robot constructs to estimate the source location, denoted by $P_t(r)$, which is used for motion planning. A successful search strategy should drive the robot(s) toward unexplored regions in the workspace and maximize information gained about the source location. One way to accomplish this goal is to drive the robot(s) in directions that result in the steepest decrease in the entropy of $P_t(r)$. In general, such a control strategy does not directly lead the robots to the source but rather directs them to collect meaningful observations that enables the fast convergence of the source belief distribution to its true value. Nevertheless, the control strategy will lead the robots to the source location since observations with predicted high information gain will inevitably be positioned near the source over time.

The estimated rate of information gathered at each time step of the proposed search strategy can be computed as the expected change in entropy of the estimated field:

$$\begin{array}{c}\mathbf{E}[\Delta S(r\mapsto r^{\prime })]=P(r^{\prime }|{\mathcal{T}}_t)[-S_t]\hfill \\ +[1-P(r^{\prime }|{\mathcal{T}}_t)][(1-\rho (r(t^{\prime })))\Delta S_0+\rho (r(t^{\prime }))\Delta S_1]\hfill \end{array}$$

(5)

where, $S_t=-\int P_t(r_0|{\mathcal{T}}_t)log(P_t(r_0|{\mathcal{T}}_t))dr$ is the Shannon entropy of the estimated probability field and $\Delta S_0$ and $\Delta S_1$ are the calculated change in the entropy of the estimation if at the next waypoint the robot does or does not register a positive sensor reading, respectively. The first part of the Equation (5) corresponds to expected change in entropy upon finding the source at the very next step, and the second term of Equation (5) accounts for the case when the source is not at $r(t^{\prime })$.

The belief distribution for the source location, $P_t(r)$, is maintained over all possible source positions during the search. Storing and representing the belief distribution becomes computationally challenging especially when the search space spans large physical scales and/or contains complex geometry and relies on a fine grid map to calculate the log-likelihood of the belief distribution. Thus, we employ a particle filter to represent the belief distribution with limited and tractable amount of randomly drawn particles. The use of a particle filter allows us to bound the computational burden on each robot by shifting focus towards more probable hypotheses while disregarding the rest.

3. Methodology

In this work, we assume each robot stores the estimated belief distribution of the source location, $P_t(r)$, using a manageable number of weighted particles, $\left\{{\widehat{r}}_i,{\omega }_i\right\}$, with ${\widehat{r}}_i$ representing the hypothesis of the state (position) and ${\omega }_i$ representing the corresponding weight (probability) of hypothesis i [21,22]. The probability mass function represented by these set of particles is mathematically equivalent to the sum of the weighted spatial impulse functions given by [23]:

$$\begin{array}{c}\hfill {\widehat{P}}_t(r)\approx {\displaystyle \sum _i}{\omega }_i\delta ({\widehat{r}}_i-r)\end{array}$$

(6)

where ${\widehat{r}}_i$ is a hypothesis that survived the re-sampling procedure of the previous step. The weights of the particles, ${\omega }_i$, are modified as follows:

$$\begin{array}{c}\hfill {\omega }_i(t)={\omega }_i(t-1)e^{-\left(\mathcal{R}(r(t)|r_0)\right)}{\left(\mathcal{R}(r(t)|r_0)\right)}^{\mathit{hit}}\end{array}$$

(7)

where hit is one if the sensor readings indicate the contaminant’s presence and zero otherwise. These weights have to be normalized to sum to one. To calculate the entropy of the particle representation of the belief distribution we use the approach presented in [16] given by:

$$\begin{array}{c}\hfill S\approx -{\displaystyle \sum _{k=1}^N}{w}_{(t-1),k}^{(i)}log(w_{(t-1),k}^{(i)})\end{array}$$

(8)

This information greedy control strategy directs the robot such that it achieves the largest decrease in entropy of its estimate of the source position. The maximum distance the robot can reach in a time step is considered to be equal to M grid cells in each direction. At each time step, the expected information gain from an observation at the next potential robot position, constrained to a maximum of M moves on the grid, is calculated. If no particles are within the robot’s set of reachable points on the grid then any point that is M moves away from the robot’s current position is chosen as the next step. The single robot search strategy is summarized in Algorithm 1.

Algorithm 1: Single robot search strategy.

Input: Current estimate of the belief distribution over the possible position of the source.

Output 1: Next waypoint on the search trajectory.

Output 2: Updated estimate of the belief distribution over the possible position of the source.

Remark 1.

We note that the weight update given by Equation (7) is different from most particle filter implementations [16,17]. The weights of the particle before the re-sampling represents the predicted distribution while after re-sampling the samples themselves represent the target probability distribution. For general target localization applications, robots often have access to large amounts of high frequency measurement data which allows for continuous and fast updates to their estimates. However, when localizing the source of a plume, the algorithm relies heavily on the spatial distribution of the sporadic sensory detections along a robot’s search trajectory. As such, the re-sampling serves the role of integrating past information into the current estimate of the source position. Therefore, one must take the probability of the detection history, Equation (2), into account during the update and eliminate the less probable hypotheses when re-sampling.

Remark 2.

In general, when robots are limited to using only the chemical sensor to determine the presence of a material plume, it is often hard to verify a hypothesis without directly checking by going to the predicted source location. Thus, once our confidence measure reaches a certain level, a robot must be tasked to verify the estimated source position by direct observation. In this work, the entropy of the estimated probability distribution or the consistency of the sensor detections the robot receives over some period of time can be used as the confidence measure.

3.1. Motion Model Uncertainty

Uncertainty is inherent to any mobile robot. When the robot moves the motion model adds to the uncertainty around the position of the robot and even after all the measurements and observations are made there will be residual error associated with any estimations made. This uncertainty around the position of the robot is reflected in the positions of the particles. If we use the Gaussian model to represent the motion of the robot, then after each step the particle positions can be replaced with a Gaussian probability distribution function for which the mean is the previous position of the particle and the variance is the output of the position estimation algorithm used to estimate the state of the robot. After the robot makes an observation, it must update the estimate it has over the position of the source. The overall probability distribution represented in Equation (6) can be replaced with the Gaussian Mixture model given by

$$\begin{array}{c}\hfill {\widehat{P}}_t(r)\approx {\displaystyle \sum _i}{\omega }_i\mathcal{N}(r;{\widehat{r}}_i,\Sigma )\end{array}$$

(9)

where ${\widehat{r}}_i$s are the previous position of the particles, and Σ is the motion uncertainty of the robot. This introduces two sources of complexity to the calculations. First, use of the traditional low-variance re-sampling method is no longer possible since only the state of a particle plays a role in the chance of it surviving re-sampling. This is the same as ignoring the uncertainty around the state of the particle which does not account for the uncertainty associated with the motion model. Second, to determine the information captured within the Gaussian mixture probability distribution requires more calculations.

To re-sample the Gaussian mixture model probability distribution representing the position of the source of the dispersion we use a simplified version of the Gibbs sampling method [24]. The procedure has two steps:

• Randomly select one of the Gaussian models. Probability of selecting each model is to be proportional to the weight of Gaussian in the mixture model.
• Generate a sample from the selected Gaussian probability distribution.

Comparing to the low-variance re-sampling of the particle filter, re-sampling the Gaussian mixture model requires at least two times more computational time. On the other hand, the number of particles needed to initialize the particle filter in this case is substantially less than the previous cases.

Even though we re-sample the Gaussian mixture model and store the particles after each step, it is important that we assume some uncertainty around the position of the particles in the prediction step. Thus, when calculating the control input, we need to predict the expected change in the information encapsulated in the Gaussian mixture model for each waypoint. As such, we employ the steps described in [16] to calculate the information utility function as follows:

$$\begin{array}{c}\hfill S\approx -{\int }_{\theta }\left\{\left({\displaystyle \sum _{i=1}^N}{w}_{(t-1)}^{(i)}p({\theta }_t|{\theta }_{t-1}={\widehat{\theta }}_{(t-1)}^{(i)})\right)·log\left({\displaystyle \sum _{i=1}^N}{w}_{(t-1)}^{(i)}p({\theta }_t|{\theta }_{t-1}={\widehat{\theta }}_{(t-1)}^{(i)})\right)\right\}d\theta \end{array}$$

(10)

where $p({\theta }_t|{\theta }_{t-1}={\widehat{\theta }}_{(t-1),k}^{(i)})$ is the robot’s motion model and is given by a Gaussian probability distribution centered on the position of the $i^{th}$ particle. The vector ${\theta }_t$ is the joint vector of position and the orientation of the robot. Unfortunately there is no closed form representation for this integral and numerical computation of this integral is expensive. To reduce the computational burden, we employ the approximation strategy described in [17,25] that has been shown to yield good results.

The foundation of the approximation used to calculate this integral is a Taylor expansion of the second part of the expression inside the integral. This approach yields a good approximation since the error of the Taylor expansion around the mean of each Gaussian function is multiplied by another Gaussian function that has a maximum at the mean value point and decreases quickly as we move away from the mean. In the simulations for this paper, we use three terms of the approximation in given by:

$$\begin{array}{cc}\hfill \log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left(X;{\mu }_j,{\mathrm{C}}_j\right)\right){|}_{{\mu }_i}& \approx \log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)\right)\hfill \\ & +{\left(X-{\mu }_i\right)}^T\frac{\partial }{\partial X}{\left[\log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left(X;{\mu }_j,{\mathrm{C}}_j\right)\right)\right]}_{{\mu }_i}\hfill \\ & +\frac{1}{2}{\left(X-{\mu }_i\right)}^T\frac{{\partial }^2}{\partial X^T\partial X}{\left[\log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left(X;{\mu }_j,{\mathrm{C}}_j\right)\right)\right]}_{{\mu }_i}\left(X-{\mu }_i\right)+\cdots \hfill \end{array}$$

By substituting the fist three terms of this Taylor expansion into the equation of the Shannon entropy we can find a linear equation free from the logarithmic terms. This will simplify the integral a great deal:

$$\begin{array}{cc}\hfill H\left[p\left(X\right)\right]& =-\int {\displaystyle \sum _{i=1}^m}{\omega }_i\mathcal{N}\left(X;{\mu }_i,{\mathrm{C}}_i\right)\log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left(X;{\mu }_j,{\mathrm{C}}_j\right)\right)dX\hfill \\ & \approx -\int {\displaystyle \sum _{i=1}^m}{\omega }_i\mathcal{N}\left(X;{\mu }_i,{\mathrm{C}}_i\right)\left\{Estimationofthe\left[\log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left(X;{\mu }_j,{\mathrm{C}}_j\right)\right)\right]arround{\mu }_i\right\}dX\hfill \\ & =-\int {\displaystyle \sum _{i=1}^m}{\omega }_i\mathcal{N}\left(X;{\mu }_i,{\mathrm{C}}_i\right)\left[{\Gamma }_0({\mu }_i)-{\left(X-{\mu }_i\right)}^T{\Gamma }_1({\mu }_i)-\frac{1}{2}{\left(X-{\mu }_i\right)}^T{\Gamma }_2({\mu }_i)\left(X-{\mu }_i\right)\right]dX\hfill \end{array}$$

(11)

in which

$$\begin{array}{cc}\hfill {\Gamma }_0\left({\mu }_i\right)& \stackrel{\mathrm{def}}{=}\log \left({\displaystyle \sum _{j=1}^m}{\omega }_j\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)\right)\hfill \\ \hfill {\Gamma }_1\left({\mu }_i\right)& \stackrel{\mathrm{def}}{=}\frac{{\sum }_{j=1}^m{\omega }_j{\mathrm{C}}_j^{-1}\left({\mu }_i-{\mu }_j\right)\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)}{\left[{\sum }_{j=1}^m{\omega }_j\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)\right]}\hfill \end{array}$$

and

$${\Gamma }_2\left({\mu }_i\right)\stackrel{\mathrm{def}}{=}\frac{{\sum }_{j=1}^m{\sum }_{k=1}^m{\omega }_j{\omega }_k\left({\mathrm{C}}_j^{-T}-{\mathrm{C}}_j^{-1}\left(X-{\mu }_j\right){\left({\mathrm{C}}_j^{-1}\left(X-{\mu }_j\right)+{\mathrm{C}}_k^{-1}\left(X-{\mu }_k\right)\right)}^T\right)\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)\mathcal{N}\left({\mu }_i;{\mu }_k,{\mathrm{C}}_k\right)}{{\left[{\sum }_{j=1}^m{\omega }_j\mathcal{N}\left({\mu }_i;{\mu }_j,{\mathrm{C}}_j\right)\right]}^2}$$

3.2. Gaussian Radial Basis Functions to Estimate the Probability Field

Although the number of the particles needed to estimate the position of the source in the proposed method is much lower than previous cases, the computational complexity of calculating the entropy of the estimation remains intractable. While a sufficient set of particles is necessary to cover the possible positions where the source of the dispersion might be found, particles tend to quickly disappear during re-sampling. By replacing the particles with continuous Gaussian functions we are can more adequately cover the search field. Furthermore, with proper coverage, it is possible to decrease the number of Gaussian functions used to cover the candidate source positions.

To mitigate the loss of particles during the re-sampling process and to ensure proper coverage of the remaining Gaussian functions, we propose a new method for estimating the position of the source using radial basis function (RBF) networks [26]. RBF neural networks have applications in function approximation, time series prediction, classification, and system control. They produce a linear combination of radial basis functions similar to Gaussian functions. In the training stage, the parameters of these functions, like the mean and covariance, are adjusted to present the best estimate of the underlying model of the datasets.

We initialize the estimate with a number of particles randomly scattered on the search arena. Then, we replace each particle with a Gaussian function, reflecting the uncertainty in the position of the robot. Since the re-sampling process is no longer in the estimation and control loop, the number of particles needed to initialize the estimate is as low as 100 particles, comparing to the 3000 particles used to initialize the previous method.

3.3. Multi-Robot Collaborative Search Strategies

To speed up the search we extend the proposed single robot strategy to a team of robots. This effectively increases the chance of positive encounters decreasing the time needed to localize the source. In this work, we assume a reliable and fully connected communication graph for the team and reasonable localization uncertainty for each robot. This enables each robot to access all the information gathered by the other members of the group at the current timestep. In general, reliable inter-robot communication and accurate localization are significant challenges in the underwater environment. In our simulations, we briefly address the impact of robot localization uncertainty on the performance of our strategies, but leave a more comprehensive treatment of these challenges as directions for future work.

Instead, we focus on determining which sensor readings from the team should be factored into a robot’s estimation process: all sensor readings including positive and negative ones, just the positive detections, or all positive with some of the negative detection. Since positive sensor detections are rare, it makes sense to consider every team member’s positive sensor detections. However, this is not enough since localizing the source requires the identification of a Poisson process which cannot be done by relying on positive detections alone. As such, it is important to consider both positive and negative sensor detections.

3.3.1. Simple Collaborative Search

Since a negative sensor reading, i.e., not detecting a plume, also carries information about the relative position of the source, robots should incorporate both positive and negative observations from the rest of the team. In fact, the pertinent information is contained within the ratio between the number of positive and negative observations. As such, our first update strategy assumes robots share all their detection events to construct a common belief distribution for the source location. While individual robots can initialize their own belief distributions, we expect these individual belief distributions to eventually converge to the same final distribution since the information contributed to each robot’s estimate is the same.

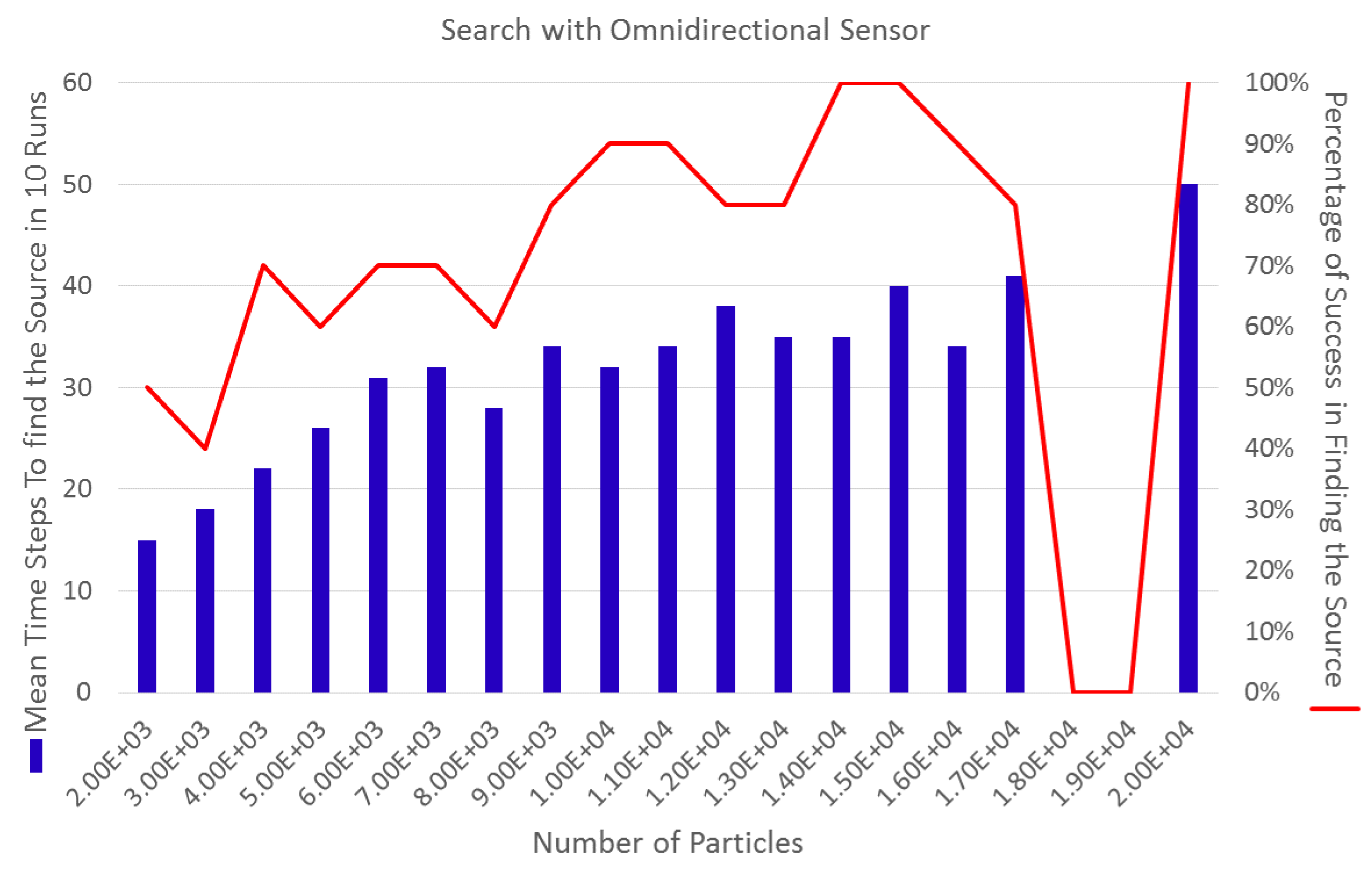
The bar chart in Figure 1 shows the average number of timesteps per 10 runs/trials for a team of three robots to localize the plume source in a 200 × 200 unit workspace using distributions represented by different number of particles. The initial positions of the robots were randomly chosen but held constant through each of the 10 trials. The probability distribution was randomly initialized for each of the 10 trials. The mean distance of the particles to the actual source location was used to determine success for the team to localize the source.

These simulations show that increasing the number of the particles increases the chance of finding the source of dispersion. However, compared to the typical search with a single robot these results indicate that deploying a group of robots does not decrease the time of search nor increase the chance of finding the source of dispersion. This is because the huge number of particles needed to describe the belief distribution significantly increases the computational burden. The large number of particles needed is due to frequency in which the weights of the particles are updated and re-sampling is performed. The overall rate of success is also not satisfactory. Considering the number of particles and the search time, one would expect the robots to perform better. And yet, the success rate is low despite the large number of particles employed and the long duration of the simulation. The large number of the particles needed to describe the belief distribution also presents additional challenges in practice. As we increase the number of particles, the resolution of the grid map that covers the search area must also be increased to accommodate them. However, the grid resolution is dominated by the robot’s localization and control accuracy.

3.3.2. Value of Information

As more robots participate in the search for the source location, the chances of registering the presence of a chemical patch should be higher. However, Figure 1 shows that merely increasing the number of the explorers do not yield better performance. The reason for this is because of how the additional information from the sensors are incorporated the estimation of the belief distribution. Since the detection of the plume is a stochastic event, the simple act of updating the source position estimate with all the detection events results in skewing the estimate. To illustrate this, consider the scenario where one of the robots detects a fair number of sensory cues in the absence of any sensor errors. Eventually, the robot can estimate the source position for the dispersion. At the same time, consider another robot does not detect any plume presence and incorporates the null events into the overall estimate. The result ends up “diluting” the information provided by the first robot. As such, the sharing of all positive and negative plume detections results in an incorrect estimate.

In this work, we introduce the notion of the Value of Information (VoI) which provides us with a way to discriminate informative and useful data that should be used to update a robot’s estimate and data that should be ignored. We define the VoI that any event conveys as the effect of the event in the estimate of the probability distribution and can be quantified by two factors:

• how probable that event is, considering the robot’s current estimate; and,
• how informative the event is as measured by the change it makes in the estimated probability field.

The probability of experiencing the reported event by a robot within the group can be calculated using Equations (3) and (4). If the current probability field over the position of the source estimated with the Robot A is $P_A(r)$, then we can calculate the expected rate of positive sensor measurements and consequently the probability of such an event at the position of the robot B as:

$$h_B=\int P_A(r)\mathcal{R}(r_B\mid r)dr\to {\rho }_B=h_B{e}^{-h_B}$$

(12)

Furthermore, we can calculate how the probability field estimated by Robot A will change if it is certain that a positive sensor reading has happened at the position of robot B. This is similar to the strategy followed by a single robot in Algorithm 1 using Equation (5).

In this proposed strategy, a robot does not always contribute its own positive sensor detection into the estimate of the source location. This is because positive detections are only incorporated if they change the probability landscape considerably despite them being rare. Lastly, we note that this work assumes perfect sensor readings and do not address the challenges of faulty and/or noisy sensor readings. We leave the analysis of these effects as a direction for future work.

4. Simulations

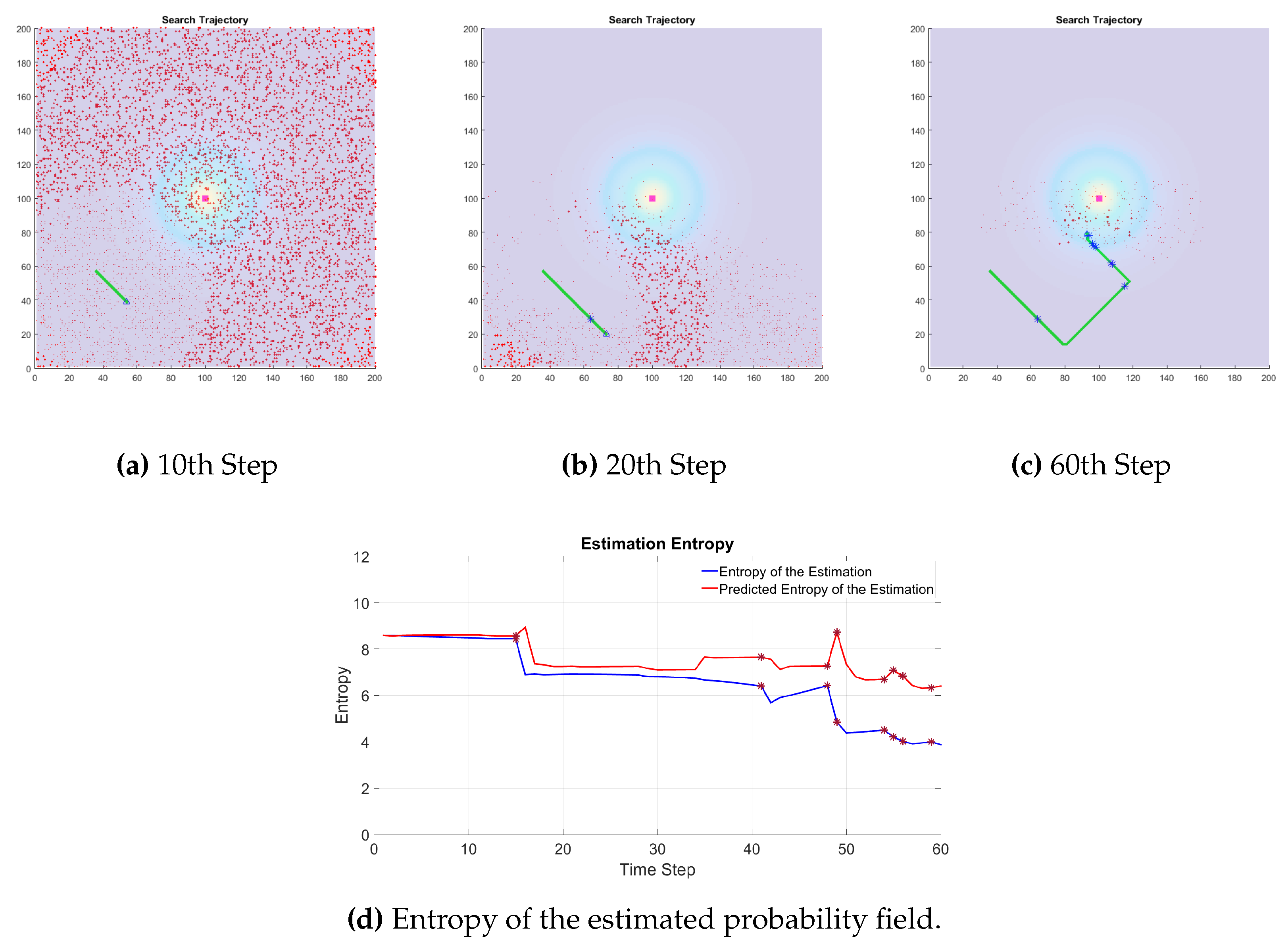
Figure 2 shows the trajectory of the robot searching for the source of dispersion located at the middle of the arena. The dimension of the workspace is 200 × 200 units and the maximum number of moves for the robot at each timestep is set at 2 units. The observation model, $\mathcal{R}(r|r_0)$, is only a function of the distance of the robot from the hypothetical source location. As the robot moves through the environment the algorithm gradually eliminates particles. The number of the particles decreased dramatically after the first detection. After a few more detections the particles tend to concentrate around the estimated position of the source.

In the simulation results shown in Figure 2, it is assumed that the chemical dispersed from the source is propagated symmetrically by means of diffusion. Thus, we assume the robot is able to sample the medium and detect the presence of the plume regardless of its orientation. In a realistic scenario, a robot may be looking for the leakage point in the presence of a background flow using a directional sensor. To simulate these scenarios, we set the probability of registering a material plume by a sensor to depend on both the distance of the sensor from the source and the angle between $(r-r_0)$ and the orientation of robot the immediately before it makes the observation, $\mathbf{v}$:

$$\begin{array}{c}\hfill \mathcal{R}(r|r_0)=\frac{R}{ln(\frac{\lambda }{a})}{e}^{\frac{V}{2D}(r-r_0)·\mathbf{v}}{K}_0\left(\frac{\mid r-r_0\mid }{\lambda }\right)\end{array}$$

(13)

Taking this directionality into account, a robot with a sensor facing towards the source of the dispersion has a greater chance of detecting a plume than when it is facing away. This also affects the prediction step of the estimation. When no plume is detected, the hypotheses in front of the robot are eliminated more decisively than those behind it. Conversely, when the robot does detect a contaminant, the hypotheses in front of the robot are more likely to be retained as the position of the source compared to those behind it.

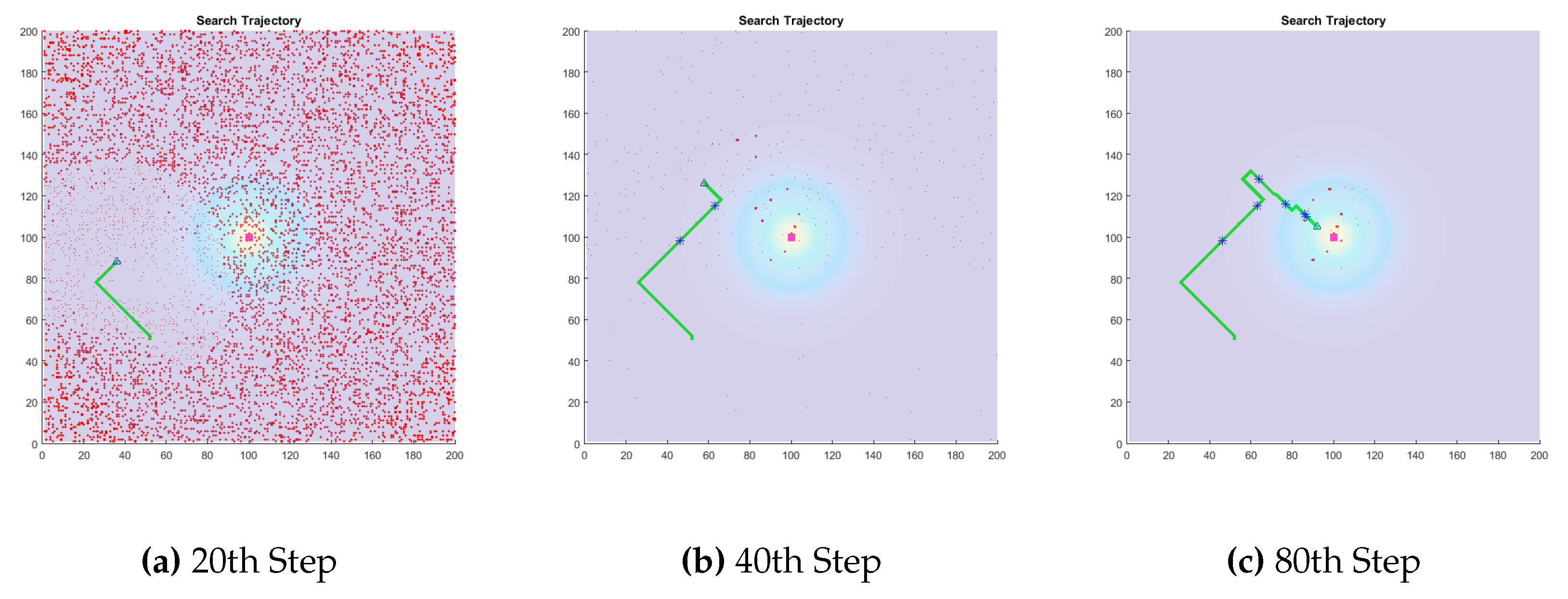
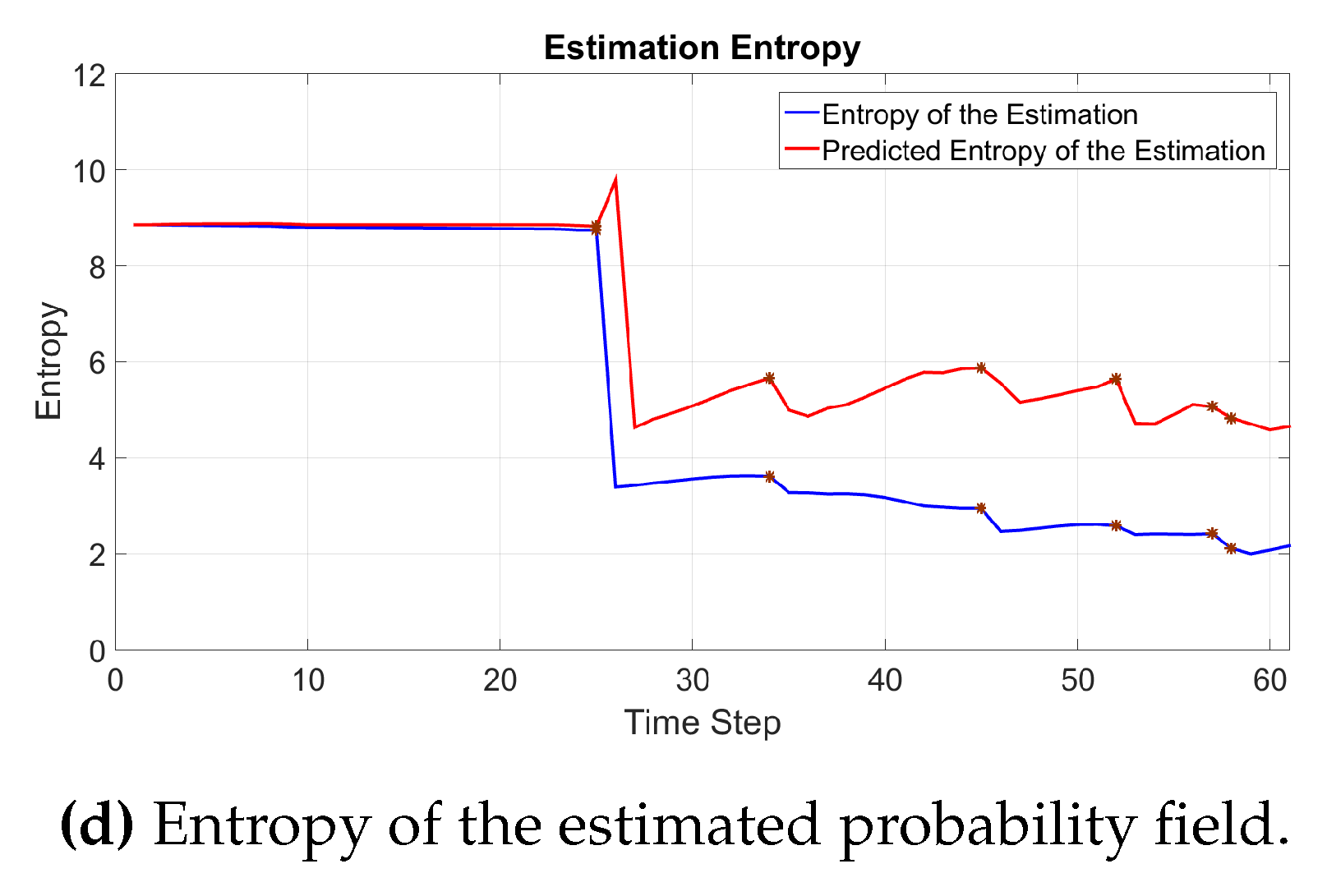
When the direction is involved in the estimate, as seen in Figure 3, the observations do not carry the same amount of information as in the non-directional case. For one, the addition of directionality in the detection conveys a lot of information on the possible locations for the source since it can eliminate all the hypotheses behind the robot. However, an immediate next detection of the plume would not be as informative as the first one since the robot is already confident that the plume source is not behind it.

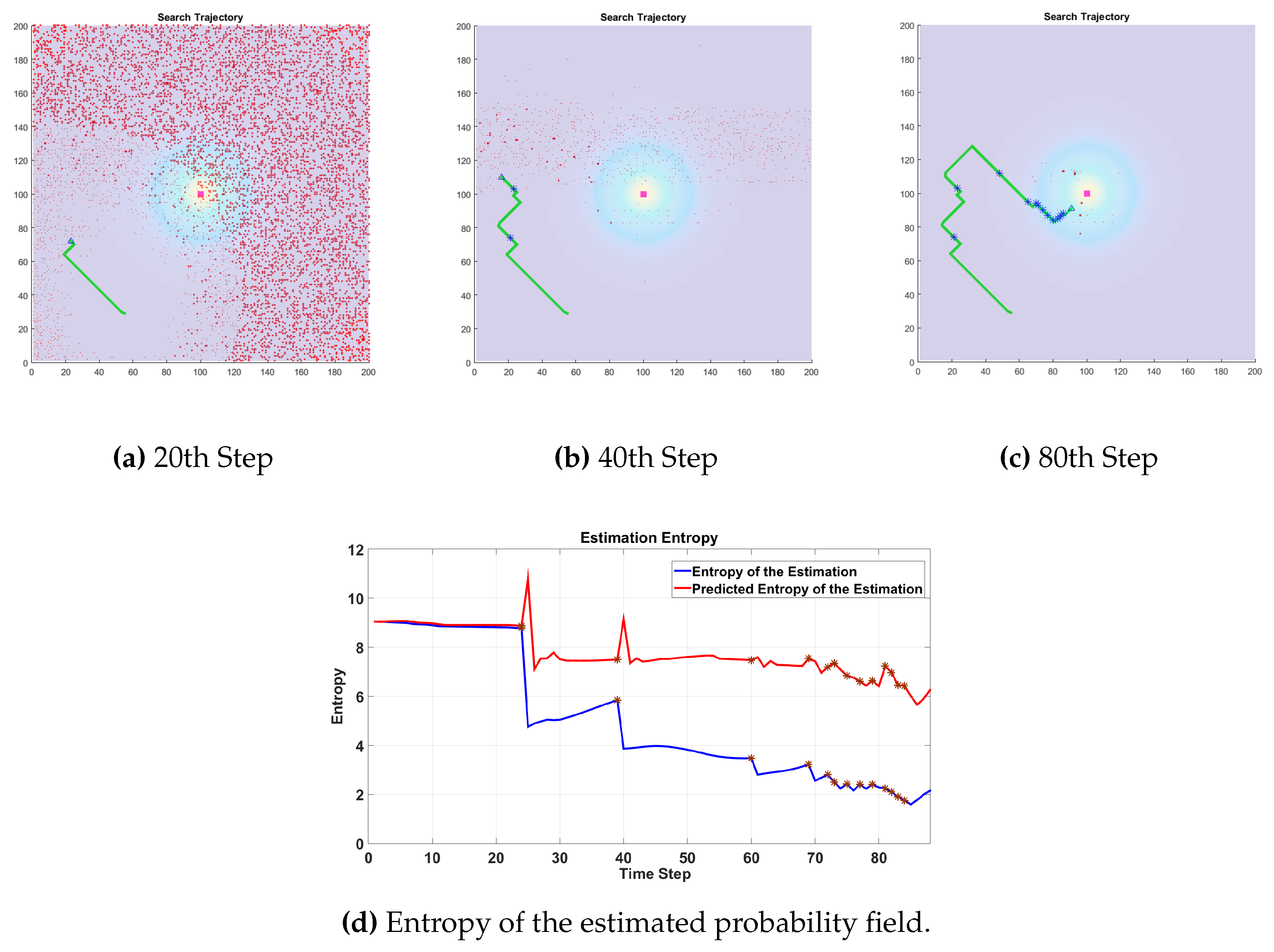
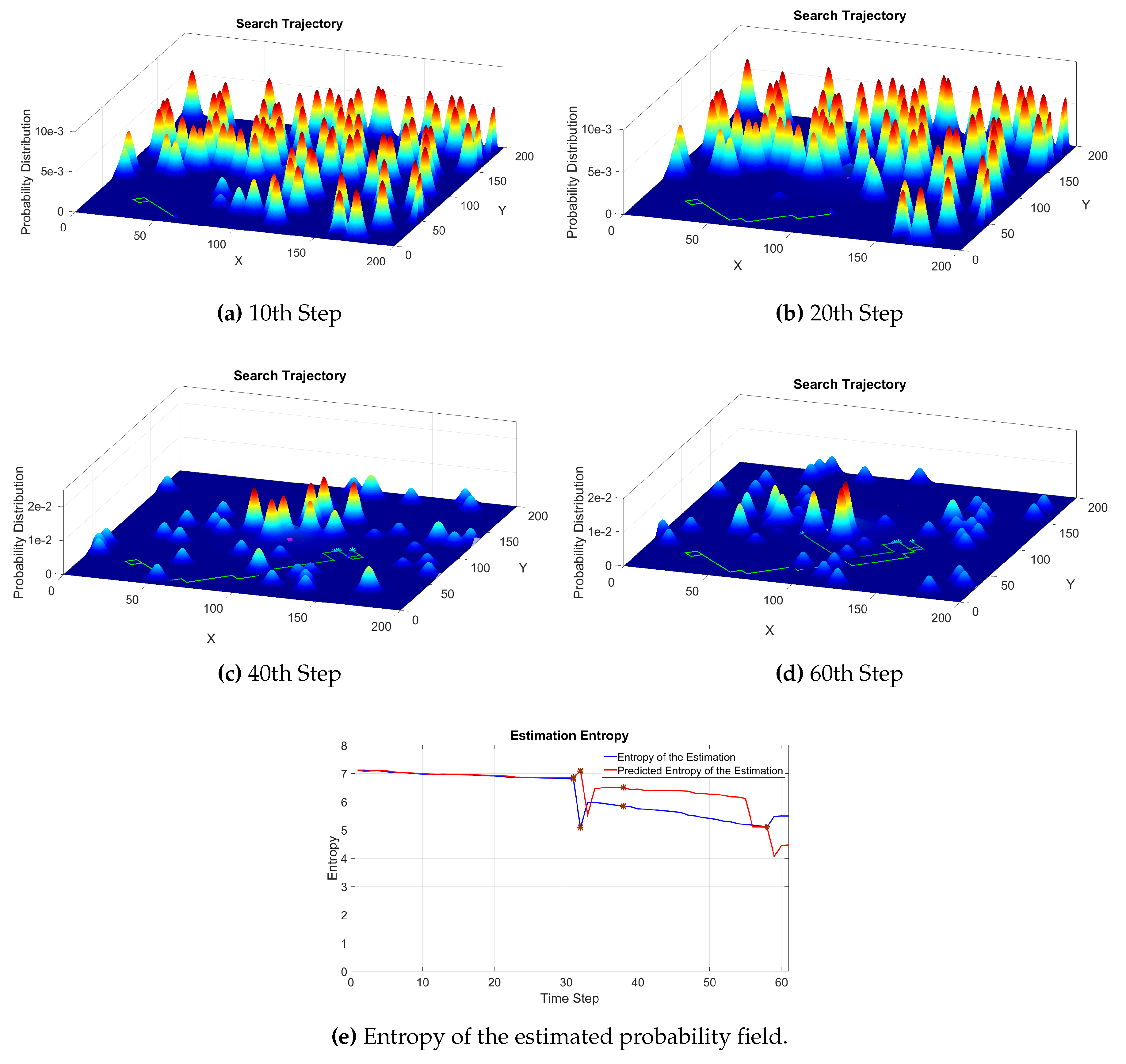
Figure 4 shows the trajectory of the robot in the absence of a strong background flow with an omnidirectional sensor. The initial number of the particles used in the estimation process in this simulation is significantly less than the previous simulations shown in Figure 2 and Figure 3. The dimension of the search space is again 200 × 200. The number of the particles used was about 10, 000 as in previous simulations, which is about a third of the number of the grid cells in the search arena. However, the number of the particles used in the latest method using the Gaussian function to estimate the probability field described in Section 3.2 is about 3000, which is less than a tenth of the number of grid cells. We assume that the covariance of the uncertainty around the estimated position of the robot is 2 units. As such, the covariance matrix in Equation (9) is set to $\Sigma =2\mathbb{I}$ where $\mathbb{I}$ is the identity matrix. In this work, we give an approximate number for the particles used rather than an exact one because particles placed within the same grid cells are counted as one.

Figure 5 shows the trajectory of a robot searching for the source and its belief distribution for the sourced position. The results indicate that a manageable number of Gaussian like basis functions with well-tuned parameters can effectively cover the search area; the estimate efficiently converges to the actual position of the source as new information is incorporated using the proposed method. The estimate update using given by Equations (3),(4),(7) is applied to the weight of each Gaussian function. To determine the search position for the robot, the probability of finding the source at the very next step denoted by $\rho (r(t^{\prime }))$ in Equation (5) is calculated using the Gaussian mixture model used to describe the source belief distribution. The predicted change, $\Delta S$, is also calculated using the same mixture model. The union of these functions directs the robot to the next best search location for the source position in the workspace.

4.1. Multi-Robot Collaborative Search

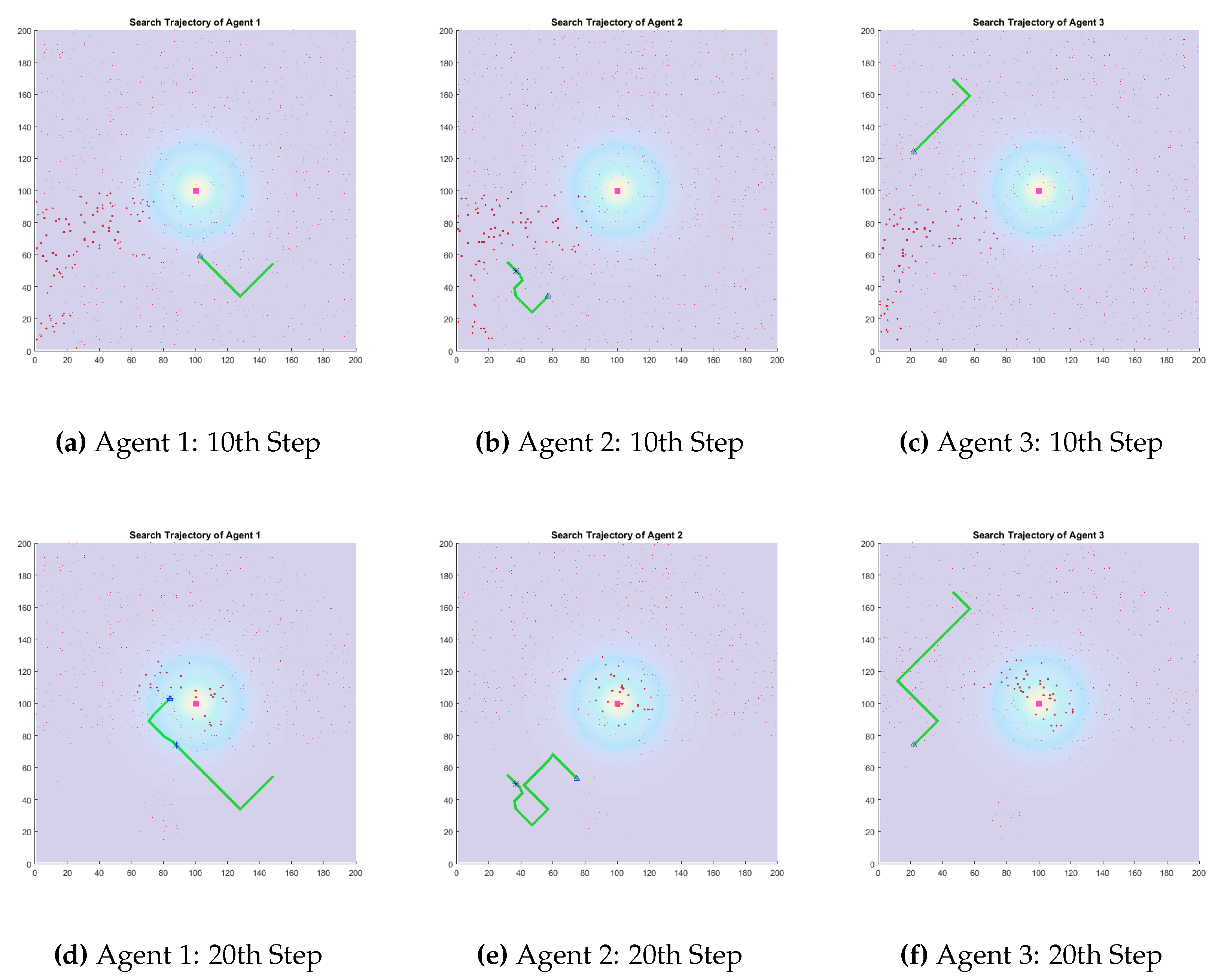
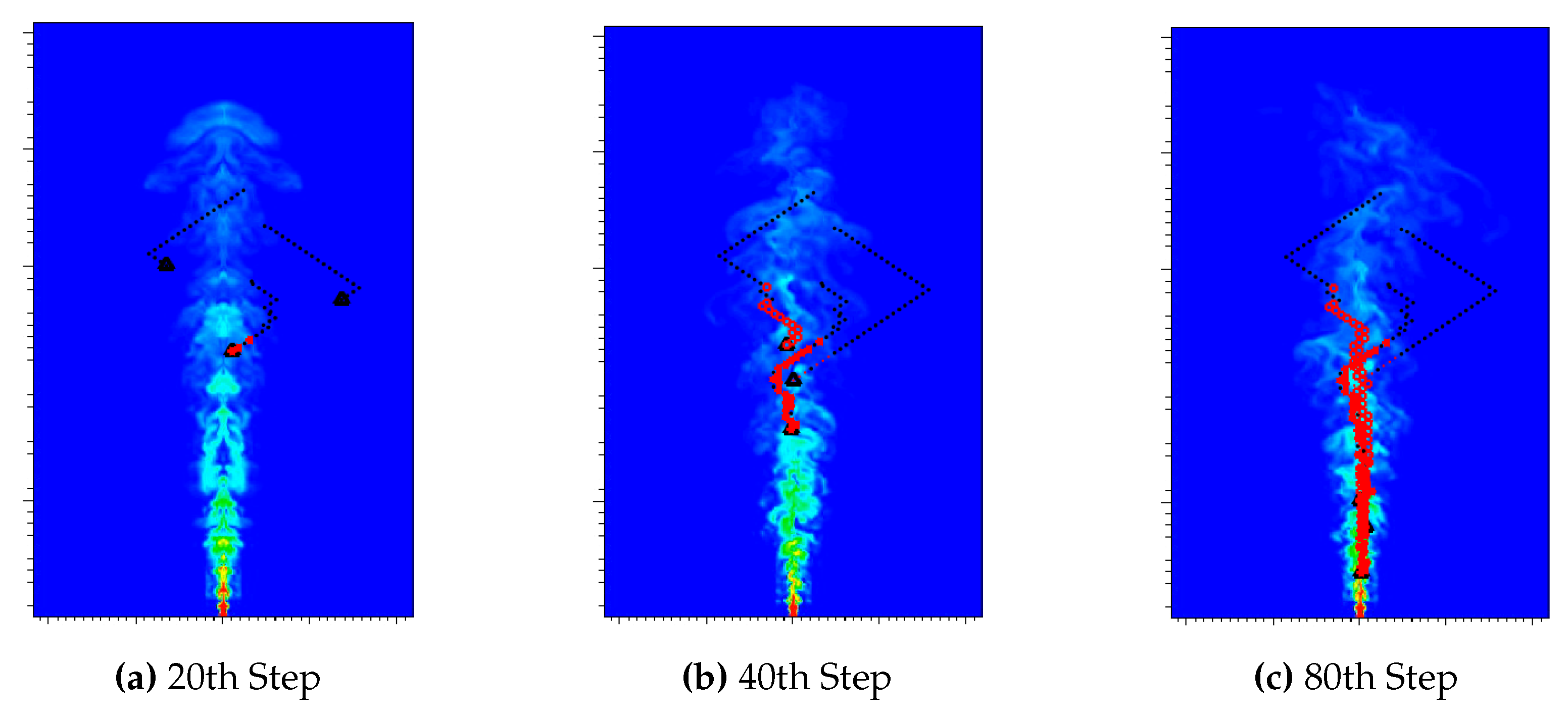
Figure 6 shows the simulation results for a group of three robots. In these simulations, robots synchronized their communications and communicated their sensor detection events at a constant rate. Every message included the robot’s state and corresponding sensor reading. During the exploration, every negative sensor reading results in attenuating the weights of a large number of particles in the estimated probability distribution of the source location. This led to an extensive exploration phase before. Furthermore, the first positive detection by one of the robots resulted in a large number of the particles being lost in the re-sampling. To better understand this, consider a robot moving in some direction for a period of time without obtaining any positive sensor readings. When the robot receives an update from another robot that has detected the presence of a plume while moving in different direction, it loses confidence on its own estimates of the probable position of the source which in turn leads to the elimination of a large number of low probable hypotheses. This phenomena can be seen in the 20th timestep of the simulation shown in Figure 6.

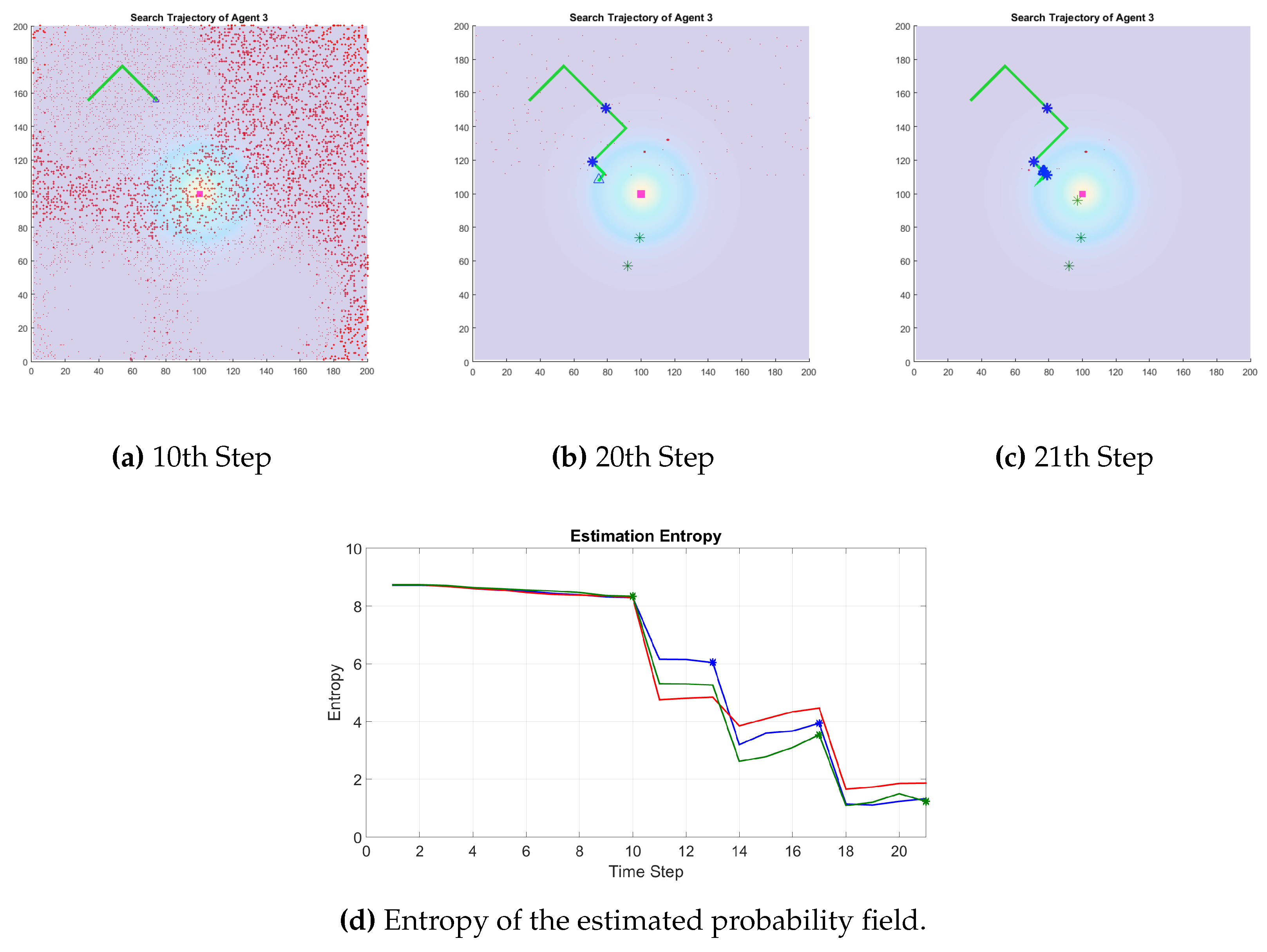
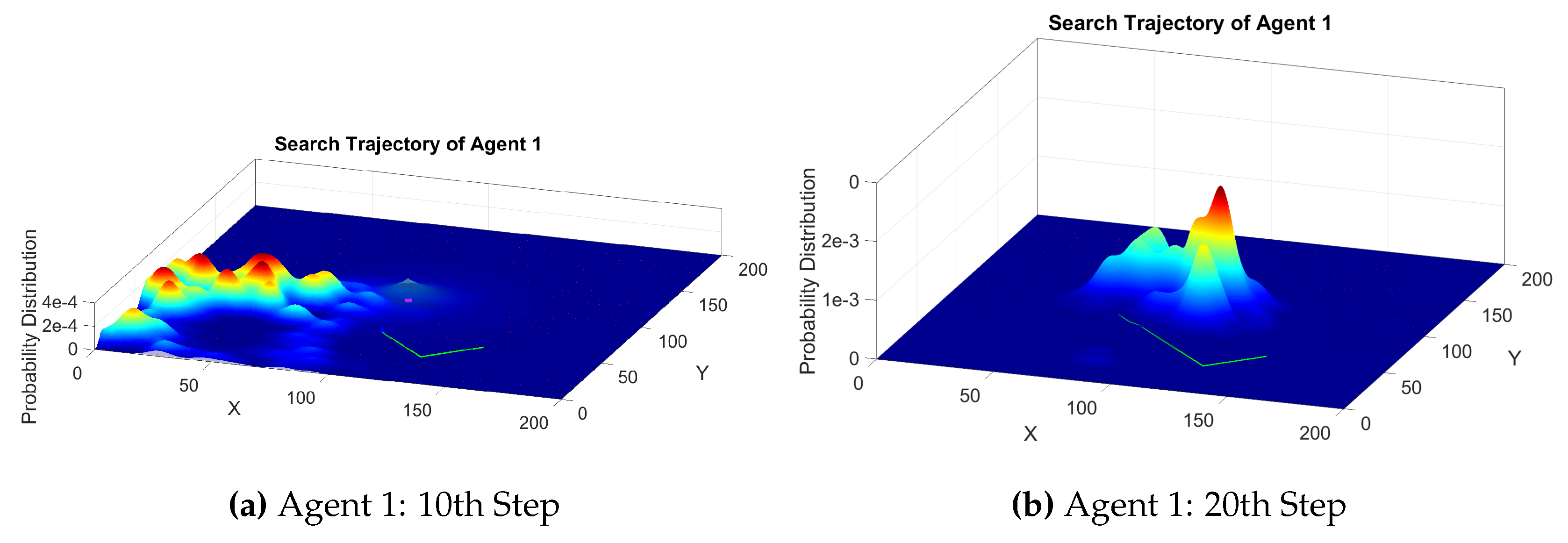
Figure 7 shows the trajectory of every robot in a three robot team and the estimated probability distribution of each robot for the position of the source obtained using 300 Gaussian functions shown as particles in the figure. The particles are placed at the mean of each Gaussian and the size of the particles represent their weight. At each timestep, every robot communicates their sensor reading, positive or negative, and their corresponding state. Each robot then computes the VoI of the information received from the rest of the team to decide whether or not the sensor event should be used to update its belief distribution for the source location. The 3D probability distribution for Robot 1 is shown in Figure 8.

The probability distribution estimated by each robot is different from other robots in the team since each robot have a different initial estimate and individually decides the information it will use to update its belief distribution. However, the simulations show that the strategy results in similar estimates for all the team members. Analytically proving this convergence is a direction for future work.

4.2. Experimental Results

In this section we present the experimental validation of the proposed strategy. First, we present simulation results for a multi-robot team executing the described information theoretic search strategy in a realistic 2D turbulent field. Specifically, the team is tasked to localize the source of a leak using a computational fluid model of the 2010 Deep Water Horizon Oil Spill whose details are presented in [19]. The plume is generated by an inlet buoyancy flux $B_i=g{w}_i{A}_i{\alpha }_{b,i}$ = 5 × 10⁻⁶ m⁴·s⁻³ where g = 9.8 m·s⁻² is the gravity acceleration magnitude, $w_i$ = 4 cm·s⁻¹ is the inlet liquid velocity, $A_i=\pi r_i^2$ = 0.005 m² is the source cross-section area of radius $r_i$ and ${\alpha }_{b,i}=0.026$ is the inlet gas volume fraction. The initially unperturbed ambient fluid is thermally stratified with a constant slope $\zeta$ = 5.1 K·m⁻¹ and the system Coriolis parameter is set to f = 0.01 s⁻¹. The cylindrical computational domain has a height H and diameter D of $H/r_i=D/r_i\approx 67$ with Dirichlet boundary condition at the bottom, no shear and no flux at the top for the momentum and scalars respectively and open lateral boundary conditions with numerical sponges to ensure numerical stability. The domain has been spatially discretized using spectral element methods into $K=7540$ conforming elements in which the solution is approximated with a 14th order polynomial expansion resulting in $\sim 21$ million nodes. The transport equations have been integrated using the nek5000 solver [27] that has demonstrated an excellent scalability on parallel machines [28]. The results used in this work correspond to the statistically stationary solution obtained after approximately 150, 000 core-hours on a Cray XE6 using 960 2.2 GHz AMD Magny-Cours cores.

Figure 9 shows the search trajectories for the three robot team. The dimensions of the simulation arena is 748 × 322 units, and the maximum reach of the robot at each time step is 5 units at each direction. The probability field is spanned by 100 Gaussian functions. At each step of time, every robot propagates the event it experiences. The other robots calculate the VoI of the event and decide whether or not to use it to update its estimation (see Section 3.3.2). The weights of the Gaussian functions are adjusted according to the procedure described in Section 3.2. In this simulation, we assume robots have a directional sensor and the robots can move in any directions.

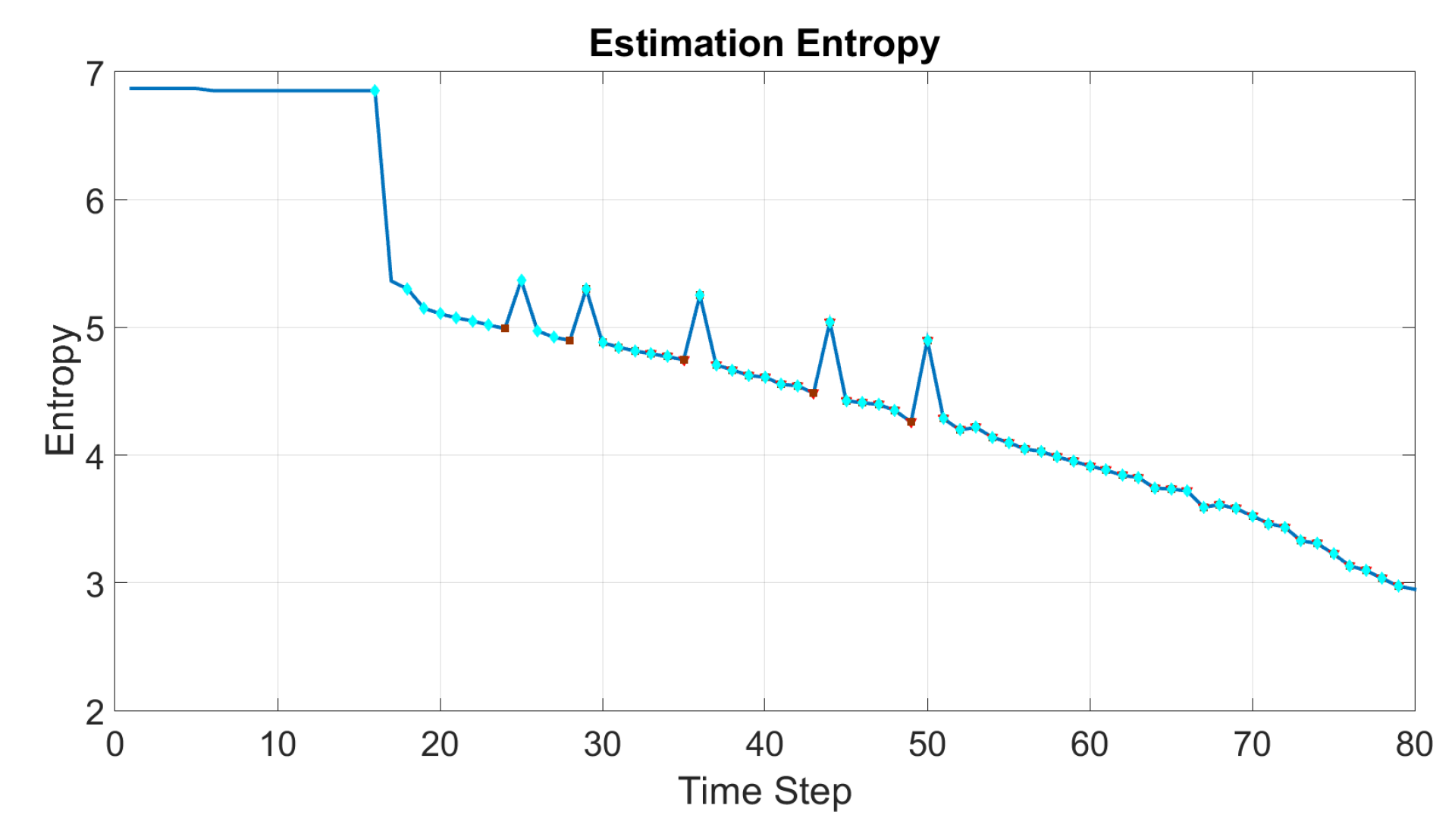
The Gaussian functions used to estimate the probability distribution function span three dimensions, X and Y directions for the robot positions and θ for the robot headings. Figure 10 shows the entropy of the belief distribution estimated by one of the robots over time and shows how the distribution changes over time. Every positive sensor reading adds to the information obtained by the robot and decreases the entropy of its estimate. Also, the information coming from the robot’s teammates are selectively used to update its belief. The small ripples in Figure 10 show how the initial information obtained by the other members of the team are inconsistent with the robot’s own detections. However, over time, the robots reach a consensus on the source position where the shared detection information contribute to the robot’s estimation process.

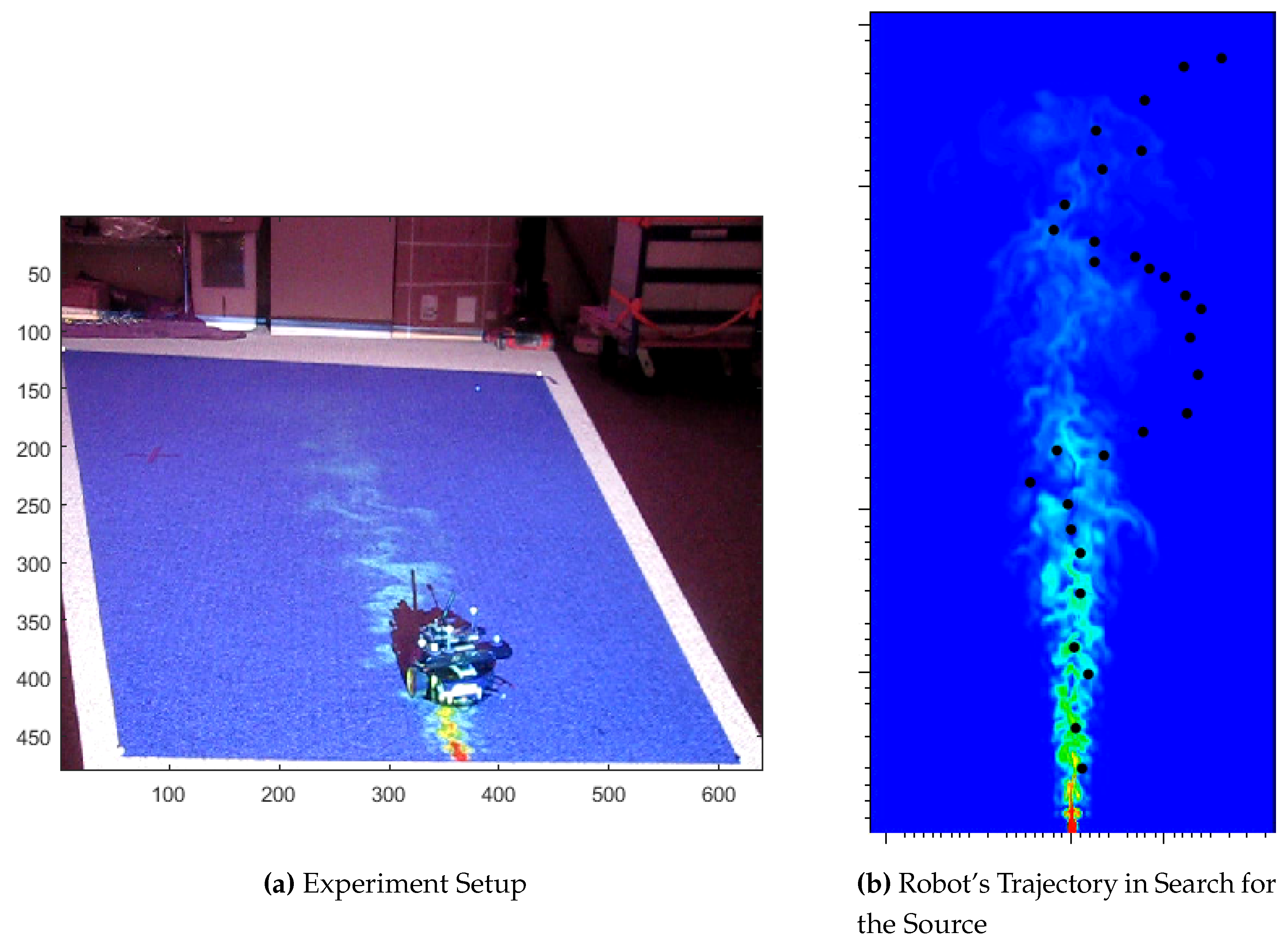
We examine the performance of the algorithm in an actual experiment using a single mobile robot operating in a simulated plume field. Figure 11a shows the experimental setup where the 2D Deep Water Horizon Oil Spill simulation is projected onto the actual workspace to simulate a dispersion event. The SAS Lab’s TIM robot then searches for the source of the oil spill. The TIM robots are differential drive ground vehicles, approximately 20 cm in diameter, equipped with an Odroid-U3+, running the Robot Operating System (ROS), an Asus Xtion Pro Live, and WiFi communication. Localization is provided using a combination of the onboard odometry and an external motion capture system.

Figure 11a shows the robot in the workspace where the simulated is projected onto a workspace of approximately 3.86 m long and 2.64 m wide. The observer error is negligible, however, the robot’s process error is modeled by a zero-mean Gaussian with a standard deviation of 5 cm. The probability distribution is computed using 100 Gaussian functions each with a variance of 5 cm. Given the limited workspace, the experimental validation was limited to one robot. Figure 11b shows the resulting robot trajectory as it localizes the plume source. A movie of the experiment along with the other simulations described in this paper can be found at [29].

5. Conclusions

We have presented information theoretic search strategies to localize the source of a biochemical dispersion based on sporadic and intermittent detections of material plumes in a 2D turbulent field. Specifically, we presented a strategy that leverages particle filters to ease the computational burden while accounting for the impact of robot position uncertainty on the performance of the search. We proposed a new method to estimate the source position using Gaussian functions to describe each particle which requires less number of particles to cover the search area. This further lessened the computational burden and lowered communication bandwidth needed for a team to execute the search. We addressed the concept of the value of information and its role in evaluating what information to use to update the team’s estimate of the belief distribution describing the source location. The proposed method helped robots decide what information from other team members to consider when updating their estimates for the source position. We concluded with with simulation and experimental results for a multi-robot search strategy using a 2D computational model of the 2010 Deep Water Horizon Oil Spill. In our simulations we considered the impact when the observation model for the robot is directional versus not, when the probability density function is described by a manageable number of Gaussian functions, and when the robots consider the value of the information provided by other members in the team. Our results show the effectiveness of the proposed methods.