An Experimental and Numerical Study of Long Wave Run-Up on a Plane Beach

Abstract

This research is to facilitate the current understanding of long wave dynamics at coasts and during on-land propagation; experimental and numerical approaches are compared against existing analytical expressions for the long wave run-up. Leading depression sinusoidal waves are chosen to model these dynamics. The experimental study was conducted using a new pump-driven wave generator and the numerical experiments were carried out with a one-dimensional discontinuous Galerkin non-linear shallow water model. The numerical model is able to accurately reproduce the run-up elevation and velocities predicted by the theoretical expressions. Depending on the surf similarity of the generated waves and due to imperfections of the experimental wave generation, riding waves are observed in the experimental results. These artifacts can also be confirmed in the numerical study when the data from the physical experiments is assimilated. Qualitatively, scale effects associated with the experimental setting are discussed. Finally, shoreline velocities, run-up and run-down are determined and shown to largely agree with analytical predictions.

1. Introduction

On 26 December 2004 at 01:01:09 UTC a submarine earthquake of magnitude $M=9.0$ hit the west coast of Northern Sumatra, Indonesia [1]. The main shock had its epicenter at 3.09° N and 94.26° E, and the fault line extended for 1200 km to 1300 km from Indonesia northward to the Andaman Islands. The generated tsunami waves caused disastrous destruction around the Indian Ocean, with approx. 220,000 casualties, and severe material losses [2]. Run-up heights around the Indian Ocean reached maximal values of about 30 $\text{m}$ [3], where the maximum run-up of waves is commonly defined as the shoreline elevation at maximum inundation above mean sea level (the subsequent or preceding retreat of water is called run-down).

In the light of this and other disastrous flooding events, major efforts have been established to improve the understanding of generation, propagation and run-up of what can be approximated as shallow water waves [4]. These efforts can be roughly classified into three methodological categories: (a) experimental [5,6,7]; (b) numerical/computational [8,9,10,11,12]; and (c) theoretical [13,14].

In physical modeling the ability to generate a wave of a certain type determines quality and reliability of the experimental data. Even in the age of super computers, experiments are still valuable in research, as the data they produce does not result from any model simplifications and is vital for validation and calibration of numerical models. For over 40 years, the solitary wave paradigm has been assumed to yield a good model to study tsunami waves (see, e.g., [4,15,16,17]). However, the findings in [18] demonstrated the shortcomings of this model to represent tsunami waves since temporal and spatial scales of solitary waves are significantly shorter than those of the prototype. Instead, the current state-of-the-art model (see [14]) is the N-wave in its general form, e.g., elevation and depression are of different size.

Analogous to the improvement of the knowledge about wave types, the techniques to generate waves have evolved over the past decades. Very early experiments were carried out in 1844 by Scott Russell who used a sinking box to generate a solitary wave (see an investigation in [19]). In the 1980s, Synolakis conducted experiments in a rectangular wave flume using a piston type wave generator [20,21]. Using this technique, a vertical rectangular wall (a piston) is hydraulically driven forward and backward to transfer momentum into the water column which imitates the depth-averaged particle velocity of a passing wave and finally to generate the wave. In this way one or more solitary waves are generated. By experimental means, and by employing linear and non-linear shallow water wave theory, Synolakis [21] was able to predict the run-up of non-breaking solitary waves. A similar comparison between analytical, numerical and experimental data was conducted by Titov and Synolakis [22] to show that the non-linear shallow water wave equations successfully reproduce experimental results or geophysical tsunamis with complicated small scale bathymetric features.

Another hydraulic approach is the wave generation with a vertically moveable bottom as used by Hammack [23]. In that way it was intended to model a submarine earthquake. According to [24] this technique is not suitable for modeling waves in the vicinity of a coast since a distinction between a generation section and a downstream section has to be made. A third approach to transfer momentum into a water body is to release an amount of water from above the water surface [25]. Although a wave is generated, this dam break like mechanism has the disadvantage that significant turbulence is induced into the water. Furthermore, it is difficult to control the wave characteristics such as amplitude and period [24]. Recently, a new technique to generate long waves has been developed at the Franzius-Institute for Hydraulic, Estuarine and Coastal Engineering in Hannover, Germany. Utilizing a pump-driven wave generator, precise control over the wave characteristics (wave length, amplitude and shape) can be maintained to high accuracy [26]. In particular, different kinds of waves can be generated including single cycle sinusoidal waves, solitary waves and N-waves.

Flood research and forecasting are mainly carried out with the help of computer models that employ robust and accurate numerical techniques to solve equations suitable to describe geophysical fluid flow. Various state-of-the-art discretization techniques can be and are used for this purpose, such as finite difference, finite element and finite volume models (see, e.g., [8,9,12,22,27]). Among these models, discontinuous Galerkin models (as described in, e.g., [28,29]) have recently become popular, because they combine numerical conservation properties with geometric flexibility, high-order accuracy and robustness on structured and unstructured grids. Furthermore, the communication between elements is local making them especially suitable for parallel and high performance computing (see Kelly and Giraldo [30] for a study with a 3D model). Therefore, numerical modeling became a most valuable tool in tsunami science; particularly powerful once employed in combination with analytical and experimental methods.

While a number of analytical solutions are available [31], the present study focuses on the important theoretical results in [14], who applied the methodology originally developed by Synolakis [21] for different wave shapes. Model calibration and validation calls for further realistic experimental data, in order to link numerical modeling with realistic fore- and hindcasting results.

In order to increase confidence in our physical and numerical models, and to test the applicability of the theoretical derivations, the authors investigate the agreement of experimental and numerical modeling results. The present study therefore provides measurements of shoreline motion using an innovative pump-driven wave generator (see [24]), and may serve as a novel benchmark for leading depression sinusoidal waves. The produced data set is used to validate a numerical discontinuous Galerkin non-linear shallow water model concerning shoreline dynamics. With both, experiment and simulation, the authors reproduce the theoretical results for long periodic waves that were presented in [14].

Our main research questions ask, whether run-up, calculated with the shallow water model, is capable of representing shoreline motion adequately in terms of theoretical understanding according to [14,21], and in terms of physical experiments as well as numerical methods, for a single cycle sinusoidal wave as a very basic representation of a tsunami. Once convinced that the numerical method adequately reproduces the theoretical expression, the authors investigate deviations of the experimental results from theory by running numerical simulations with perfect and imperfect initial conditions (as taken from “imperfect” experiments), assuming that impurities in the initial wave setup lead to contaminated run-up results. The overall aim is to showcase how comparative, intermethodological work contributes to the understanding of shoreline motion of long waves.

After summarizing the theoretical results of Madsen and Schäffer [14] at the beginning of Section 2, the experimental and numerical setup of this study is introduced and the novel design of the wave flume is described. Furthermore, the authors provide background of the one-dimensional discontinuous Galerkin non-linear shallow water model. Once convinced that the experimental data are useful and sufficiently accurate (Section 3.1), the authors perform numerical simulations with analytically prescribed wave shapes to validate the numerical model in Section 3.2 in terms of the theoretical expressions. The experimental data is then compared with analytical as well as numerical results in Section 3.3. For further validation and in order to assess useful information on wave impact, maximum as well as minimum run-up and shoreline velocities are addressed in Section 3.4. Finally, an evaluation of all results, conclusions and an outlook is given in Section 4.

2. Methodology

The current study is based on the theoretical findings of Madsen and Schäffer [14], who derived explicit formulae for long wave run-up on a plane beach generated by waves of different shapes. The goal of this study was to reproduce these functional relationships for sinusoidal waves (a) experimentally using a wave flume facility at the Leibniz Universität Hannover; and (b) by numerical simulations with a one-dimensional shallow water model. After summarizing the results of Madsen and Schäffer [14] for periodic sinusoidal waves, the experimental setup and the numerical model used for this study are introduced in this section. At the end the boundary conditions (BC) are detailed, which the authors used to generate the waves in the experimental and the numerical model.

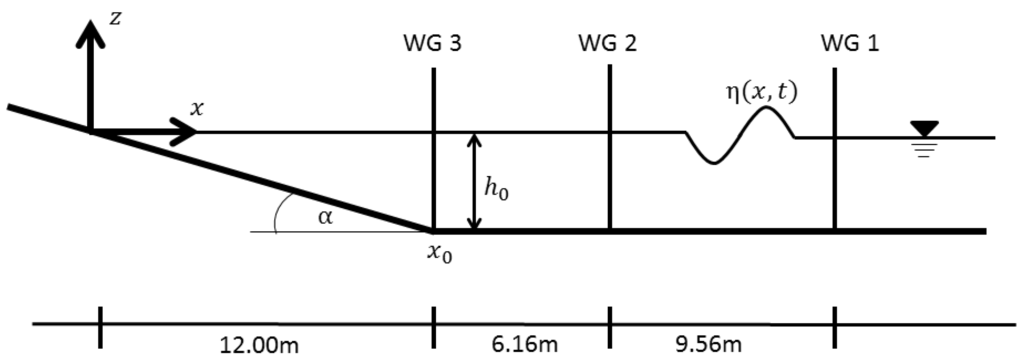
Figure 1. Schematic cross section of the considered setup: A constant depth region is attached to a linearly sloping beach with angle $\gamma =tan\alpha$, where γ is the beach slope. Also indicated are the wave gauges (WG) from the experimental setup.

Figure 1. Schematic cross section of the considered setup: A constant depth region is attached to a linearly sloping beach with angle $\gamma =tan\alpha$, where γ is the beach slope. Also indicated are the wave gauges (WG) from the experimental setup.

2.1. Theoretical Background

The explicit formulae for the run-up/run-down of incoming waves with fixed shape from Madsen and Schäffer [14] are given for a one-dimensional bathymetry which consists of a constant depth offshore region of depth $h_0$ attached to a linearly sloping beach with γ being the constant beach slope (cf. Figure 1). In the offshore region the waves are assumed to be solutions of the linearized shallow water equations while they obey the non-linear shallow water equations on the sloping beach. Effects of wave breaking and bottom dissipation are neglected in this theory.

Analytical solutions for the non-linear shallow water equation on a plane beach are already derived by Carrier and Greenspan [13] by using a so-called hodograph transformation in which a new set of independent variables $(\rho ,\lambda )$ and a velocity potential $\psi (\rho ,\lambda )$ are introduced. This leads to a linear differential equation in ψ, for which one can derive exact solutions. In [14] the independent variables are chosen in such a way, that ρ becomes 0 at the shoreline and λ is a modulated time. By letting $\rho \to 0$, the expressions for surface elevation η and velocity v in terms of ρ, λ and ψ lead to explicit formulae for the evolution of run-up elevation R and the associated run-up velocity V. Furthermore, the theory of Carrier and Greenspan [13] yields a theoretical breaking criterion, in which case the time derivative of V and the space derivative of η go to infinity. This corresponds to a discontinuity in these profiles.

Using some further approximations, Madsen and Schäffer [14] finally arrive at the run-up expression for periodic sinusoidal waves. Let the coordinate system have its origin at the still water shoreline with the x-axis being positive in the offshore direction (see Figure 1). The z-axis points upwards. The time series of the incoming wave at the beach toe $x_0=h_0/\gamma$ is prescribed by

$${\eta }_i(x_0,t)=A_{0}cos(\Omega \left[t-t_1\right])$$

(1)

where ${\eta }_i$ is its surface elevation, Ω is the angular frequency, $A_0$ is the offshore wave amplitude, and $t_1$ is aphase shift. The run-up velocity and elevation are then

$$\tilde{V}\left(\lambda \right)=\frac{\Omega R_0}{\gamma }sin(\theta +\pi /4)\text{and}\tilde{R}\left(\lambda \right)=R_{0}cos(\theta +\pi /4)-\frac{\tilde{V}{\left(\lambda \right)}^2}{2g}$$

(2)

with

$$R_0=2A_0\sqrt{\pi \Omega t_0}\text{and}\theta =\Omega (\lambda -t_1-2t_0)$$

(3)

and g being the gravitational constant. Further, $t_0=x_0/\sqrt{g{h}_0}$, and the time is parameterized through λ, i.e.,

$$t\left(\lambda \right)=\lambda +\frac{\tilde{V}{\lambda }^2}{2g}$$

(4)

This describes the temporal variation of $R\left(t\right)=\tilde{R}\left(\lambda \left(t\right)\right)$ and $V\left(t\right)=\tilde{V}\left(\lambda \left(t\right)\right)$. One can also derive the maximum run-up, which occurs for $\theta =-\pi /4$. At this time $R\to R_0$ and $V\to 0$. Similar considerations can be made for the run-down and the extreme values of the velocity.

The maximum values of run-up/run-down elevation and velocity and the theoretical breaking criterion for periodic sinusoidal waves are conveniently given by introducing the non-linearity of a wave $ϵ=A_0/h_0$ and the surf similarity parameter. The latter was originally introduced by Battjes [32] and is defined by $\xi =\gamma /\sqrt{H/L_{\infty }}$, where $H=2A_0$ is the incident wave height and $L_{\infty }=g{T}^2/\left(2\pi \right)$ the deep water wavelength of small amplitude sinusoidal waves with period $T=2\pi /\Omega$. Thus,

$$\xi =\sqrt{\pi }{\left(\frac{A_0}{h}\right)}^{-1/2}{\left(\frac{{\Omega }^{2}h}{g{\gamma }^2}\right)}^{-1/2}$$

(5)

relates the beach slope to the wave steepness. With these definitions one obtains for a given non-linearity the extreme values

$$\frac{R_{\mathrm{up}/\mathrm{down}}(\xi ;ϵ)}{A_0}=\pm \frac{2{\pi }^{3/4}}{{ϵ}^{1/4}{\xi }^{1/2}}\text{and}\frac{V_{\mathrm{up}/\mathrm{down}}(\xi ;ϵ)}{\sqrt{g{A}_0}}=\pm \frac{2{\pi }^{5/4}}{{ϵ}^{1/4}{\xi }^{3/2}}$$

(6)

only depending on the surf similarity parameter. The theoretical breaking criterion is met for

$$\frac{R_{\mathrm{up}/\mathrm{down}}^{\mathrm{limit}}\left(\xi \right)}{A_0}=\pm \frac{1}{\pi }{\xi }^2\text{or}\frac{V_{\mathrm{up}/\mathrm{down}}^{\mathrm{limit}}\left(\xi \right)}{\sqrt{g{A}_0}}=\pm \frac{1}{\sqrt{\pi }}\xi$$

(7)

In this study it will be shown how these results were reproduced in the laboratory experiment, i.e., in a wave flume. Furthermore, they will be used later on to validate the numerical model regarding its treatment of inundation.

2.2. Physical Model

The dynamics of long sinusoidal waves approaching the sloping beach and their subsequent interaction during the run-up and run-down process was studied experimentally in a wave flume at the University of Hannover. The closed-circuit wave flume that was used to generate the sinusoidal waves including the experimental setup is already described in [24,26,33,34,35]. In summary, the wave generation relies on electronically controlled high-capacity pipe pumps which allow for the acceleration and deceleration of a water volume. A control loop feedback system allows the generation of arbitrary wave shapes such as sinusoidal, solitary or N-waves over a large range of wave periods and lengths.

A major advantage of this wave generation method with active control loop is that wave lengths much longer than the available propagation distance of the wave flume can be generated. This feature is accomplished by intrinsic treatment of the seaward propagating re-reflections. These re-reflections would normally limit the effective wave length to be generated to one wave flume length or less. Through inverse pump response, it is possible to compensate for the re-reflected wave components and in principle, a “clean” wave generation is provided over the entire duration of the target surface elevation time series, similar to the active wave absorption technique used in laboratory wind wave generation.

However, a disadvantage of the wave generation is the development of spurious high frequency ripples (or “riding waves”) overlaid with the long wave. These are caused by the active control loop overshooting set reference values (or sometimes called target values) during the generation process, and emanate from excess discharge into the wave flume at short times. In the sequence, this unintentional generation of shorter waves alongside of the long waves gave rise to additional effects occurring where the run-up and run-down took place. Most prominent, these riding waves arrived somewhat delayed with respect to the long wave, broke on the shallow beach and interfered with the targeted long wave run-up process. As will be shown later, some of the presented results are attributed to this fact; a wave generation improvement useful in future studies was yet recently reported by Goseberg et al. [36] or Bremm et al. [37] to circumvent such behavior.

Figure 2 shows a sketch of the facility used for the experiments. Pump station (a), propagation section (b), reservoir section (c), sloping beach (d), and the water storage basin (e) are depicted, respectively. Walls and horizontal bottom sections are made of plasterworks and floating screed and the width of the flume is 1.0 m. A 1 in 40 sloping beach (i.e., beach angle of $\alpha =1.43°$) made of aluminum boards with small surface roughness was used to model the run-up. The effective length of the constant depth propagation section from pump station to the beach toe was 19.92 m. The undisturbed offshore water depth for this study was set to $h_0$ = 0.3 m.

Figure 2. Schematic drawing of the wave flume and its components with position indication of instrumentation. Adapted from [38], with permission from © 2012 World Scientific Publishing Company Incorporated.

Figure 2. Schematic drawing of the wave flume and its components with position indication of instrumentation. Adapted from [38], with permission from © 2012 World Scientific Publishing Company Incorporated.

To control the generation of the waves, a pressure sensor was installed at the water inlet of the pump station. In the deep water region offshore of the beach, wave gauges (Delft Hydraulics) and velocity meters (Delft Hydraulics) completed the instrumentation during the experiments as shown in Figure 2. The surface piercing wave gauges comprised two parallel electrodes. The immersion depth (surface elevation) was determined by measuring the electric resistance between both electrodes. The measurement accuracy was $\pm 0.5\%$. Wave gauges (WG) were located close to the pump (WG1, at $x=27.72$ m), halfway of the flume bend (WG2, at $x=18.16$ m) and at the beach toe (WG3, at $x=12.0$ m). All instruments were carefully tested and calibrated prior to the experiments, and were subsequently set to zero before single experimental runs.

In addition, two high definition cameras (Basler, Pilot pi-1900-32-gc) captured the wave interaction process with a sampling frequency of 32 $\mathrm{Hz}$. Image processing techniques in the form of color space conversion, lens distortion correction, image rectification and projection shore-parallel, and image stitching were used in post processing on the two sets of images. The resulting processed images from the two cameras (whose field of view is indicated in Figure 2) covered a length of 9.80 m with an original overlap of 0.5 m. The time span of image recording was adapted based on the wave period of the experimental run.

Stages of the image processing process are depicted in Figure 3 which includes scene snapshots of each of the cameras and a final result after image processing routines. A manual processing was used as the amount of experimental runs was reasonable to work through. Adhesive tape spaced by 0.1 m was placed on the beach slope and from this, vectors of time and shoreline location along the center line of the flume were determined based on the derived images as shown in Figure 3c. This approach minimized the influence of fluid boundary layers formed on the flume walls. Based on the outlined procedure, an accuracy for the manually processed shoreline location of $\pm 5$ mm was estimated. For 50% of the experimental repetitions, PVC tracers with a diameter of 2 mm were used to increase the traceability of the wave front. The tracers’ density is very close to the density of water which results in small settling velocities and similarly small inertial forces were required to accelerate the tracer particles close to the wave front. It was assured through preliminary tests that the shoreline dynamics were not affected by the presence of the tracers. In particular, this method proved useful for the run-up motion whereas inaccuracies might have occurred due to the fuzzyness of the withdrawing shoreline during the run-down process, which has to be looked into in future studies.

Figure 3. Stages of the image processing with raw data images and final result after image processing routines. (a) First camera scene; (b) Second camera scene; (c) Final stitched image for analysis.

Figure 3. Stages of the image processing with raw data images and final result after image processing routines. (a) First camera scene; (b) Second camera scene; (c) Final stitched image for analysis.

Subsequently, the shoreline velocity was derived from the basic positional information along the center line of the flume based on

$$V_{i+1/2}=\pm \frac{a}{t_{i+1}-t_i}$$

(8)

Here, $V_{i+1/2}$ is conveniently assigned to time $t_{i+1/2}=(t_{i+1}+t_i)/2$ and positively defined in the offshore direction, $a=0.1$ m denotes the distance between adjacent marker tapes, and $t_i$ and $t_{i+1}$ are the times where the shoreline crossed these tapes.

Due to irregular image acquisition measurement gaps occurred in the time series of shoreline location and shoreline velocity. These gaps were not considered in the analysis of the experimental data.

2.3. Scale Effects

The chosen length scale of the Froude-scaled physical model may cause scale effects at times when or at locations where the Reynolds and Weber numbers fall short of commonly accepted thresholds. For example, low Reynolds ($\mathsf{Re}$) numbers in the physical model result in laminar boundary layers which in turn reduce the effective roughness of the down-scaled model as shown in the context of landslide generated waves [39]. In the following, the possible influence of such scale effects in the present experimental setup is briefly discussed. A more general treatise on scale effects can be found in Heller [40].

The Reynolds number during the wave propagation over horizontal bottom, conveniently defined by wave celerity $c=\sqrt{gh}$, initial water depth h, and kinematic viscosity ν, yields

$$\mathsf{Re}=\frac{\sqrt{gh}h}{\nu }=\frac{1.72\times 0.3}{{10}^{-6}}\approx 5.1\times {10}^5$$

(9)

This value is non-critical with boundary layer turbulence fully developed and turbulence effects similar between prototype and scaled model. However, in the sequence of the wave propagation characteristic velocities and water depth decrease significantly during the wave run-up and run-down phase. Local water depth and run-up velocities are then characteristic quantities to define the Reynolds number on the sloping beach. These values eventually approach zero, and so does the corresponding Reynolds number. Schüttrumpf [41] defined a critical threshold of ${\mathsf{Re}}_{\text{crit}}={10}^3$ for overtopping experiments and this might be good guidance in the present case as well. As a direct result, viscous forces are likely to play a more dominant role compared with prototype conditions in the very shallow, phasing-out wave tongue region; Reynolds numbers fall short of the threshold for example for water depth smaller than 1 cm in combination with flow velocities smaller than 0.1 m$·$s${}^{-1}$. This finding aligns well with the analogue requirement for scaled coastal models proposed by Le Méhauté [42] who considered a minimal flow depth smaller than 2 cm and wave periods smaller than 0.35 s as critical. As a matter of fact, the scale effects related to very long wave run-up on gently sloped beaches have not been sufficiently addressed in the literature; experiments with varying model families at different length scales have not been compared until now. An occasional example of scale effect discussion in the context of impulsive wave run-up is a study by Fuchs and Hager [43].

In addition to viscous forces, surface tension has theoretically the potential to bias the experimental results. While in the prototype scale waves are rarely transformed under the forces carried to the water surface by surface tension, the effect might gain significant influence in small scale models. Short waves, which regularly have to be investigated in laboratory studies, can reach the region of capillary waves when the model length scale of a hydraulic scale model is designed too small. Dingemann [44] expressed the effectiveness of the surface tension in an increase of gravitational acceleration, but outlined that the influence of surface tension to wave action is dominant when, for example, capillary waves are investigated. The effect of surface tension is interpreted to be small for large Weber ($\mathsf{We}$) numbers, indicating that driving forces dominate. The Weber number is defined as

$$\mathsf{We}=\frac{\rho v^{2}l}{\sigma }$$

(10)

where ρ is the fluid density, v and l are the characteristic velocity and length scales, and $\sigma =0.073$ N$·$m${}^{-1}$ is the surface tension for 20 ${}^{\circ }\text{C}$ water. Using the equation above, the Weber number in the experiments reported herein was approximately $1.2\times {10}^4$ in the horizontal propagation section (applying the wave celerity c as characteristic velocity and the fluid depth h as length scale). This value, which is well above critical thresholds, also reflects the fact that the length of the long waves and capillary waves differ by orders of magnitude. In the wave tongue region earlier discussed in regard to the viscous effects, where fluid depth and velocity decrease to $l=1$ cm and $v=0.1$ m$·$s${}^{-1}$, Weber numbers were however significantly reduced and yielded values as small as $1.4$. A comprehensive review of small scale models and the influence of the Weber number has been presented in Peakall and Warburton [45]. They summarized various recommendations on the critical flow depth in small scale models reporting critical Weber numbers in the range of $\mathsf{We}=2.5-160$. It is thus likely, that surface tension has a major influence on the wave tip formation during the run-up process, as the Weber number found for the experiments fell below this given threshold. Surface tension does not properly scale in physical models governed by Froude similitude. Therefore, the wave run-up of long waves measured is likely be underestimated to a certain extent since tensile forces along the wave front with small surface radii counteract the inertia forces from the run-up flow.

Summarized, in the constant depth region the flow should be realistically modeled in the wave flume. In the run-up process, however, certainly some inaccuracies arise compared to realistic tsunami conditions. However, these are probably negligible compared to inaccuracies in modeling the topography and other parametrization.

2.4. Numerical Model

The numerical simulations presented in this study were executed using a one-dimensional shallow water model. In this model the equations are solved in conservation form with fluid depth h and discharge (momentum) $hu$ being the primary variables. They are discretized using the explicit Runge-Kutta discontinuous Galerkin (RKDG) finite element method [46] with second-order accuracy. This scheme was chosen as a state-of-the-art discretization for hyperbolic conservation laws with source terms. The method is mass-conservative and preserves the steady state at rest (i.e., it is well-balanced). A comprehensive presentation of the scheme including its validation with respect to the shallow water equations is given in Vater et al. [47].

An important part in the numerical scheme is the treatment of wetting and drying events. Here, the authors pursued a fixed grid approach where initially dry cells can be flooded and wet cells can dry out during the simulation. A cell can be either wet or dry, thus the wet/dry interface is only accurate up to one cell size. The wetting and drying treatment involves only one additional parameter, which is a wet/dry tolerance. Whenever the fluid depth h is below this tolerance, the velocity is set to zero. In [47] it was shown that the specific value of this parameter does not affect the stability of the scheme. It rather influences the accuracy of the wetting and drying computation. In the presented results, this tolerance was always set to ${10}^{-8}$ m.

The fixed grid approach implies that one does not get a continuous representation of the shoreline evolution. Instead, the scheme results in a discrete time series in which the shoreline jumps from one cell interface to the next, whenever one cell gets fully flooded and water penetrates into the next cell, or draining leads to the opposite process. Therefore, similarly to the data processing in the experiments these jumps were identified in the time series as points where the shoreline crossed a cell interface, and the space between the points was linearly interpolated. As the discrete solution led to some oscillations in the shoreline computation where the latter jumped back and forth in some situations only within a few time steps, all oscillations within a window of five time steps were removed in this time series. The shoreline velocity was then computed by a formula equivalent to Equation (8). In this time series, also some oscillations were filtered out, which occurred within a window of two time steps.

For the discretization in time, Heun’s method was used, which is the second-order representative of a standard explicit Runge-Kutta total-variation diminishing (TVD) scheme [48,49]. Its stability is governed by a Courant–Friedrichs–Lewy (CFL) time step restriction [50] with $\Delta t\le \mathrm{cfl}\Delta x/c_{\max }$, where $\Delta t$ and $\Delta x$ are the time step and grid cell size, respectively, $\mathrm{cfl}$ is the CFL number and $c_{\max }=max\left\{\right|u|+\sqrt{gh}\}$ is the maximum speed at which information propagates. To obtain linear stability and positivity of the water depth in the RKDG method, the validity of $\mathrm{cfl}\le 1/3$ has to be ensured [47,51].

The gravitational constant was set to $g=9.81\text{\hspace{0.17em}m\hspace{0.17em}}{\text{s}}^{-2}$ throughout the computations. No parametrization of bottom friction was included in the model, since the theoretical results of Madsen and Schäffer [14] also do not consider friction. However, some deviations compared to the experimental runs might be attributed to this fact. To obtain results, which are comparable to the experiments, the simulated domain was 33 $\text{m}$ long and spanned from the dry area of the sloping beach at $x=-5.28$ m to the first wave gauge (WG1) at $x=27.72$ m. For the discretization the domain was devided into 330 uniform cells with a cell size of $\Delta x=0.1\text{m}$. The time step size was fixed to $\Delta t=0.01\text{s}$, which results in a CFL number of $\mathrm{cfl}=0.18$. The (one-dimensional) bottom topography was given by $b\left(x\right)=max\{0,h_0-x/40\}$. The initial conditions for the numerical simulations were a fluid at rest, with

$$h(x,0)=max\{0,h_0-b\left(x\right)\},\left(hu\right)(x,0)\equiv 0$$

(11)

2.5. Boundary Conditions

In this study, long wave conditions in the vicinity of the shore in shallow water were approximated by sinusoidal waves with leading depression. The chosen boundary conditions (BC) were used throughout this study for the experimental and the numerical method equally. Experimentally, those waves were generated by the pump-driven wave generator, as outlined in Goseberg et al. [26] and in Section 2.2 on the basis of ideal, analytical surface elevation time series of

$${\eta }_{\text{b}}\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{H}{2}cos\left(2\pi \frac{t-t_s}{T}+\frac{\pi }{2}\right)}\hfill & \text{for}{t}_s\le t\le t_e\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\right.$$

(12)

where $H=2A_0$ is the wave height, and T is the wave period. In the experiments only one period of a sinusoidal wave was modeled, which started after 10 $\text{s}$. The initial delay was necessary, because the pipe pumps needed some initialization time. This means that the starting time was set to $t_s=10\text{s}$ and the stopping time to $t_e=T+t_s$. It is to be noted that the experimentally generated waves exhibit imperfections (cf. Section 3.1) which are attributed to the tuning of the control loop as outlined in Section 2.2.

In the numerical simulations, the incident wave was modeled through the right boundary condition. For validation against analytical expressions the fluid depth was prescribed by Equation (12) with $h_{\text{b}}\left(t\right)={\eta }_{\text{b}}\left(t\right)+h_0$. The velocity was then chosen such that the boundary data resulted in a single (simple) wave propagating to the left. In particular, it was set to

$$v_{\text{b}}\left(t\right)=2\left(\sqrt{g{h}_0}-\sqrt{gh}\right)$$

(13)

The starting time in Equation (12) was set to $t_s=0\text{s}$, since no initialization phase is needed for the numerical model. For the stopping time two different simulations were conducted for each wave shape. In one simulation the stopping time was after one period as in the experimental setup, i.e., $t_e=T$. In the other simulation the stopping time was set to infinity, which means that the incoming sinusoidal wave lasted until the end of the simulation. As will be shown in the results, the comparison between the respective two simulations revealed several deviations between the theory of periodic sinusoidal waves and the practical setup of a single period sinusoidal wave.

For comparison with the experiments the right boundary condition of fluid depth and velocity were set using the data from the time series at wave gauge WG1 of the experimentally measured data. The left boundary did not affect the numerical solution as it was in the dry part of the domain.

Table 1 summarizes the boundary conditions used in the current study. The wave characteristics were chosen to cover the significant range of surf similarity parameters ξ. To investigate the run-up of long waves on a plane beach six leading depression, non-breaking, single period sinusoidal waves were selected. The wave period varied from 20 s to 100 s which correspond to laboratory wave lengths from 34.311 m to 71.55 m. The wave height varied from 2 cm to 4 cm. For brevity, wave identifiers (Wave-ID) were used throughout the paper to label the waves used; waves are labeled with a naming scheme “Tx_Hy” where T denotes the wave period in seconds, H denotes the wave height in centimeter and x and y contain the actual quantity values. The long waves covered a range of surf similarity ξ between $4.42\le \xi \le 15.62$. In total 36 experimental runs were conducted, since each wave was reproduced six times. This procedure allowed quantification of the repeatability of the experiments. The data acquisition time for each experiment was 120 s.

Table 1. Characteristics of sinusoidal waves used, surf similarity according to Equation (5), naming scheme indicates period and wave height, respectively.

Wave-ID	Height	Period	Length	Non-linearity	Rel. Amplitude	Surf Similarity
$(-)$	$H\left(m\right)$	$T\left(s\right)$	$L\left(m\right)$	$ϵ=\frac{A_0}{h}(-)$	$\frac{A_0}{L}(-)$	$\xi (-)$
T20_H2	0.02	20.00	34.31	0.033	2.91 × 10${}^{-4}$	4.42
T30_H2	0.02	30.00	51.47	0.033	1.94 × 10${}^{-4}$	6.63
T44_H3	0.03	44.00	75.48	0.050	1.99 × 10${}^{-4}$	7.94
T58_H3	0.03	58.00	99.50	0.050	1.51 × 10${}^{-4}$	10.46
T77_H4	0.04	77.00	132.09	0.067	1.51 × 10${}^{-4}$	12.03
T100_H4	0.04	100.00	171.55	0.067	1.17 × 10${}^{-4}$	15.62

Table 1. Characteristics of sinusoidal waves used, surf similarity according to Equation (5), naming scheme indicates period and wave height, respectively.

Wave-ID	Height	Period	Length	Non-linearity	Rel. Amplitude	Surf Similarity
$(-)$	$H\left(m\right)$	$T\left(s\right)$	$L\left(m\right)$	$ϵ=\frac{A_0}{h}(-)$	$\frac{A_0}{L}(-)$	$\xi (-)$
T20_H2	0.02	20.00	34.31	0.033	2.91 × 10${}^{-4}$	4.42
T30_H2	0.02	30.00	51.47	0.033	1.94 × 10${}^{-4}$	6.63
T44_H3	0.03	44.00	75.48	0.050	1.99 × 10${}^{-4}$	7.94
T58_H3	0.03	58.00	99.50	0.050	1.51 × 10${}^{-4}$	10.46
T77_H4	0.04	77.00	132.09	0.067	1.51 × 10${}^{-4}$	12.03
T100_H4	0.04	100.00	171.55	0.067	1.17 × 10${}^{-4}$	15.62

From now on the term “experimental BC” will be used to indicate that the numerical model was initialized with surface elevation and velocity of a single cycle sinusoidal wave as measured at WG1 in the experiments. Similarly, “analytical BC” indicates numerical runs using a perfect periodic sinusoidal wave.

3. Results

In this section the numerical and experimental results are described and compared with the analytical expressions of Madsen and Schäffer [14]. First, the quality of the experimentally generated waves is discussed, and the numerical model is validated in terms of the explicit expressions of run-up height and velocity as given in [14]. Having confidence in the numerical model, the experimental and numerical results are compared and, where appropriate, matched against the analytical expressions. Finally, the maximum determined run-up/run-down shoreline position as well as velocity are investigated and compared with the analytical expressions from Section 2.1.

3.1. Quality of Experimentally Generated Waves

As the quality of the measured run-up heavily depends on the generated wave signal, the experimentally generated waves are first discussed prior to the presentation of the shoreline evolution in the subsequent sections. Therefore, the wave signal, which was measured by the pressure sensor at the water inlet, and the time series of the surface elevation at the three wave gauges will be investigated.

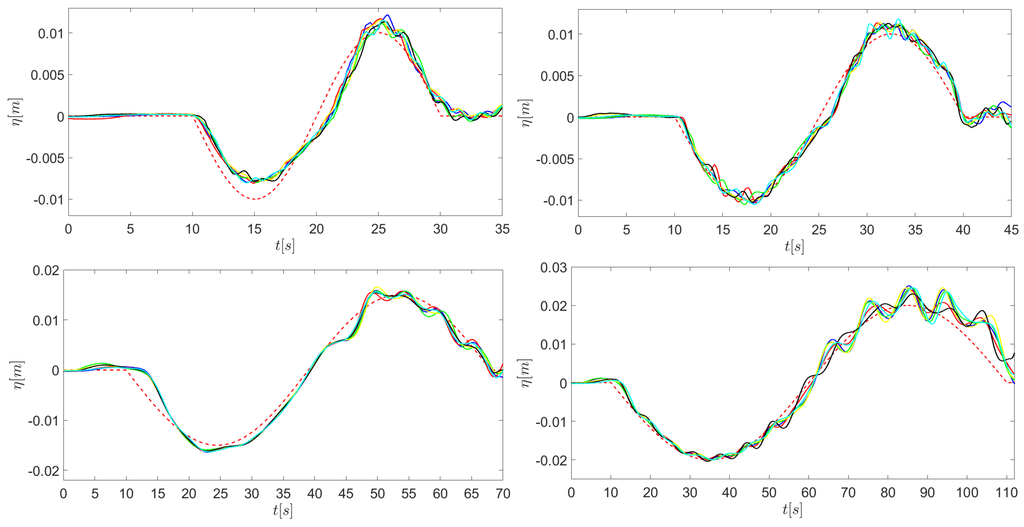
Figure 4. Time series of surface elevation for the reference curve (red dashed) and measured values (solid lines) for all six runs of T20_H2 (top left); T30_H2 (top right); T58_H3 (bottom left) and T100_H4 (bottom right) as measured by the pressure sensor at the water inlet.

Figure 4. Time series of surface elevation for the reference curve (red dashed) and measured values (solid lines) for all six runs of T20_H2 (top left); T30_H2 (top right); T58_H3 (bottom left) and T100_H4 (bottom right) as measured by the pressure sensor at the water inlet.

Figure 4 shows the measured time series of the experimental surface elevation at the water inlet of the pump station for all six reproductions of the waves T20_H2, T30_H2, T58_H3 and T100_H4 compared to the corresponding set point, i.e., reference values. In general, the sinusoidal long waves are generated sufficiently well. Deviations from the reference curve can mostly be attributed to the choice of tuning parameters for the wave generator (e.g., the smaller amplitude of T20_H2, top left); better tuning is principally feasible, but could not be achieved with acceptable effort at the time of the experimental data acquiring. The tuning parameters electronically steer the rate of rotation of the pumps and determine the behavior of the wave generator, therefore they strongly influence the quality of the generated waves. Especially in the second half of the wave period one can observe some spurious, parasitic waves riding on top of the main, long wave, which become more significant for wave shapes with longer wave length. As already discussed in Section 2.2, these riding waves are a result of the applied wave generation strategy.

The authors used the Brier score which is also known as the mean squared error as defined in [52] to further evaluate the quality of the generated experimental waves. Thereto, the Brier score and standard deviation were determined for each experimental run of each wave. Table 2 shows the minimum and maximum Brier score as well as the minimum and maximum standard deviation of the actual curve from the reference curve for all six sinusoidal waves from Table 1. Therewith, the values in Table 2 take into account the individual experimental runs. A Brier score of 0 would be a perfectly reproduced curve. The table shows that the waves T30_H2 and T58_H3 exhibit the best fits, although the latter already contains a significant amount of riding waves as can be seen in Figure 4. The wave T20_H2 has bad Brier scores which is probably due to a too small amplitude during the initial run-down, as opposed to the wave T100_H4 which has bad scores due to the high amount of riding waves present in the signal.

Table 2. Variation of Brier score [52] and standard deviation (STD) of all generated waves.

Wave-ID	Brier Score	STD (cm)
T20_H2	0.65–0.71	0.15–0.19
T30_H2	0.30–0.38	0.10–0.11
T44_H3	0.30–0.40	0.18–0.20
T58_H3	0.22–0.28	0.15–0.17
T77_H4	0.35–0.45	0.24–0.29
T100_H4	0.29–0.48	0.24–0.34

Table 2. Variation of Brier score [52] and standard deviation (STD) of all generated waves.

Wave-ID	Brier Score	STD (cm)
T20_H2	0.65–0.71	0.15–0.19
T30_H2	0.30–0.38	0.10–0.11
T44_H3	0.30–0.40	0.18–0.20
T58_H3	0.22–0.28	0.15–0.17
T77_H4	0.35–0.45	0.24–0.29
T100_H4	0.29–0.48	0.24–0.34

Figure 5 shows the temporal evolution of the surface elevation observed in the experiments and the numerical simulations at the three wave gauges for the same four wave shapes as in Figure 4. In addition to the data from the numerical simulation using experimental BC, also the time series using analytical BC is shown, but shifted by $t_{\mathrm{shift}}=(4.2/\sqrt{g{h}_0}+10)\text{s}$ to account for the additional propagation section between the water inlet and WG1 in the experiments (which was not present in the numerical simulations) and the 10 $\text{s}$ delay in the experimental wave generation (cf. Section 2.5). For all waves, the surface elevation obtained by the experiments and the numerical simulations using experimental BC agree well. Only at larger distances from the wave generation (e.g., at WG2 and WG3) the experimental time series show larger amplitudes, which are probably due to a small inconsistency in the velocity signal at WG1, where the numerical model obtains its boundary data from the experiments. Furthermore, the riding waves on top of the waves with larger period (here T58_H3 and T100_H4) evolve with the main wave towards the sloping beach.

In comparison to the surface elevation obtained from the numerical simulations using analytical BC, it can be seen that the deviation for the initial single cycle sinusoidal wave is mostly the same as in the signal at the wave inlet from Figure 4 at the different wave gauges. Furthermore, for the waves T20_H2 and T30_H2 there is a small hump visible after the sinusoidal wave has passed, which is not present in the “analytical” data. This hump is due to the shut down of the wave generation.

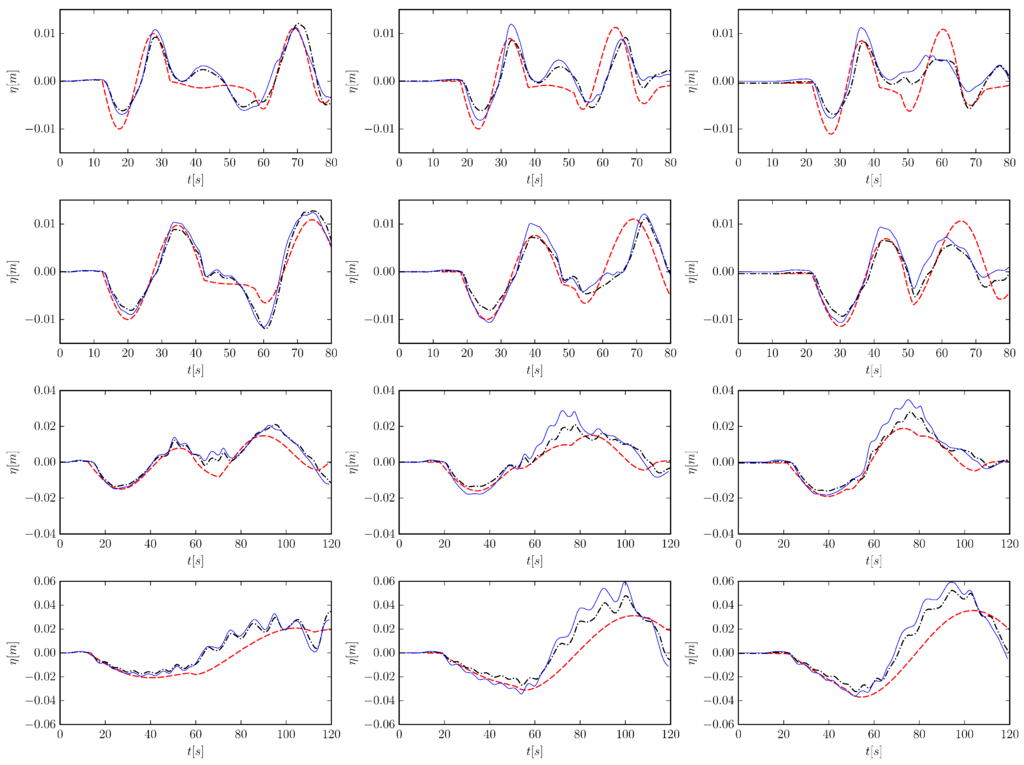
Figure 5. Time series of surface elevation η at wave gauges WG1 (left), WG2 (middle) and WG3 (right) for four different wave shapes. From top to bottom: T20_H2, T30_H2, T58_H3, T100_H4. Experimental data (blue), numerical results with experimental boundary data (black dash-dotted), numerical results with analytical boundary data shifted by $t_{\mathrm{shift}}=(4.2/\sqrt{g{h}_0}+10)\text{s}$ to fit the experimental data (red dashed).

Figure 5. Time series of surface elevation η at wave gauges WG1 (left), WG2 (middle) and WG3 (right) for four different wave shapes. From top to bottom: T20_H2, T30_H2, T58_H3, T100_H4. Experimental data (blue), numerical results with experimental boundary data (black dash-dotted), numerical results with analytical boundary data shifted by $t_{\mathrm{shift}}=(4.2/\sqrt{g{h}_0}+10)\text{s}$ to fit the experimental data (red dashed).

3.2. Validation of the Numerical Model

To have sufficient confidence in the numerical model, it was validated using the analytical BC as defined in Section 2.5. Similar to the experiments, the numerical model was always initialized with a steady state at rest, and the sinusoidal wave was only imprinted by the boundary condition. Note, that this is a deviation from the theory of periodic sinusoidal waves as presented by Madsen and Schäffer [14], whose expressions are derived for permanently incoming waves without any initialization. However, it was not possible to find the correct initial conditions for this setup. Furthermore, the two simulations with a single cycle and a periodic sinusoidal wave as described in Section 2.5 revealed the deviations to be expected between theory and the conducted experiments, which will be shown in the following. This shows the value of concurrent experimental and numerical studies, when it is not possible to design the experimental setup completely according to the theory.

Figure 6 shows a comparison of analytical (red dashed) and numerical shoreline position and shoreline velocity for the waves T20_H2, T44_H3 and T100_H4. For the numerical simulations the results are shown for both, the periodic sinusoidal (blue solid) and the single cycle sinusoidal wave (black dash-dotted). These waves were chosen as representatives for the validation, but the findings are also valid for the other wave shapes. Comparing the simulations using a periodic sinusoidal wave with the analytical expressions, one can see that the numerical model captures the theory well. Only in the beginning, when the still water solution passes on to the periodic one, a fast transition in the shoreline position with a high velocity peak is visible. Note that a positive shoreline velocity corresponds to an actual run-down. This is due to the choice of the coordinate system where the x-axis points positively offshore. One can further notice that the amplitude in the numerical simulations is often a bit too small, and there is a small phase shift, especially for the low frequency waves. These deviations can probably be attributed to the fact that the numerical solution does not oscillate everywhere from the beginning, but needs a spin-up.

Figure 6. Time series of run-up elevation R (top) and velocity V (bottom) using analytical boundary data for three different wave shapes (left: T20_H2; middle: T44_H3; right: T100_H4. Depicted are the theoretical evolution for periodic sinusoidal waves (red dashed), the numerical simulation with a single cycle sinusoidal wave (black dash-dotted) and the simulation with periodic sinusoidal waves (blue solid). Also shown are the positions of the theoretical maximum/minimum run-up elevations (red circles) and velocities (red diamonds) in the first period. The shaded regions depict the intervals where the extreme values for the diagrams in Figure 9 and Figure 10 were computed.

Figure 6. Time series of run-up elevation R (top) and velocity V (bottom) using analytical boundary data for three different wave shapes (left: T20_H2; middle: T44_H3; right: T100_H4. Depicted are the theoretical evolution for periodic sinusoidal waves (red dashed), the numerical simulation with a single cycle sinusoidal wave (black dash-dotted) and the simulation with periodic sinusoidal waves (blue solid). Also shown are the positions of the theoretical maximum/minimum run-up elevations (red circles) and velocities (red diamonds) in the first period. The shaded regions depict the intervals where the extreme values for the diagrams in Figure 9 and Figure 10 were computed.

The numerical results of the single cycle sinusoidal wave follow the one with the periodic sinusoidal wave for about a period. After this time the oscillating solution passes back on to the still water solution, which again comes along with a sharp transition in the shoreline position and an associated velocity peak. This behavior has also implications for the comparison of the experimental results with the analytical expressions of Madsen and Schäffer [14], especially concerning the extreme values in run-up elevation and velocity. In Figure 6, the occurrence of these extreme values in the first period is also indicated by red circles and diamonds, respectively. From this, one can conclude that the maximum run-down cannot be reliably determined in the experiments, since it is always biased by the transition between the still water and the oscillating state—during the initial run-down and after the maximum run-up was reached. This is also true for the maximum run-down velocity for long periods. Therefore, these values will be omitted when the extreme values are compared to theory. On the other hand, the maximum run-up elevation and velocity should be well captured by a single cycle sinusoidal wave, provided there are no other disturbances in the experimental data.

3.3. Shoreline Motion

After having discussed the quality of the experimental wave signal and the reliability of the numerical model concerning shoreline dynamics, the experimentally obtained shoreline motion data is finally presented. Shoreline location and shoreline velocity of a leading depression sinusoidal wave is compared to the numerical results using experimental BC and, where appropriate, to the analytical expressions of Madsen and Schäffer [14].

Figure 7. Time series of run-up elevation R from the experiments and the numerical simulation using experimental boundary data for all six wave shapes (left to right: T20_H2, T30_H2, T44_H3 (top row); T58_H3 (bottom left); T77_H4, T100_H4 (bottom row)). Depicted are the theoretical evolution for periodic sinusoidal waves (red dashed), the numerical simulation (black dash-dotted) and the results from the six experimental measurements (solid lines). The shaded regions depict the intervals where the extreme values for the diagrams in Figure 9 were computed.

Figure 7. Time series of run-up elevation R from the experiments and the numerical simulation using experimental boundary data for all six wave shapes (left to right: T20_H2, T30_H2, T44_H3 (top row); T58_H3 (bottom left); T77_H4, T100_H4 (bottom row)). Depicted are the theoretical evolution for periodic sinusoidal waves (red dashed), the numerical simulation (black dash-dotted) and the results from the six experimental measurements (solid lines). The shaded regions depict the intervals where the extreme values for the diagrams in Figure 9 were computed.

3.3.1. Run-up and Run-down of Long Waves

Figure 7 shows the numerical, experimental and analytical shoreline location for all waves used in this study. The analytical expression (red dashed) represents the run-up of periodic sinusoidal waves while the numerical model was initialized with the surface elevation profiles of a single cycle sinusoidal wave as measured in the experiments. In case of the experimental data (solid lines) the results of all six measurements are shown for each wave as far as data was available. The gaps in the experimental data are consequences of a poor traceability of the shoreline. In particular, the run-down is a transient process, so that there was hardly a distinct evidence to trace the shoreline. In contrast, the shoreline could be traced well during run-up.

Good reproducibility is observed in the experiments. In general, the numerical, experimental and, where the wave has adjusted to the sinusoidal expression, also the analytical shoreline locations agree well for the waves T20_H2, T30_H2 and T44_H3 (top row). For the three longest waves T58_H3, T77_H4 and T100_H4 (bottom row) significant deviations of the experimental shoreline location from the analytical expressions are observed. These oscillations are caused by the over-riding waves, which are already present in the wave signal. One can clearly see that the riding waves overtake the main wave before the maximum run-up height is achieved and lead to false maxima in the measurements. In these intervals there are also some deviations between the experimental and the numerical measurements (e.g., around $t=80\text{\hspace{0.17em}s}$ for the wave T77_H4). They could be due either to the breakdown of the shallow water theory in the vicinity of the shoreline, or to some incorrect measurements in the experimental data. Another deviation is present in the initial run-down, which is often underestimated by the numerical model. This is best visible in the waves T20_H2 and T30_H2, while in the other waves the maximum run-down could often not be determined since its location was located outside the field of observation covered by the cameras. This deviation is attributed to the smaller amplitude in the wave signal, already present in the time series at the wave gauges.

Disregarding the corrupting influence of the riding waves, the analytical shoreline location for periodic waves can be reproduced by laboratory single cycle sinusoidal waves with sufficient accuracy; accuracy will further increase in cases where a sufficient amount of time is spent to tune the wave generator to avoid spurious short waves during the wave generation or by following the improvements outlined in Bremm et al. [37].

Figure 8. Same as Figure 7, but for run-up velocity V. The shaded regions depict the intervals where the extreme values for the diagrams in Figure 10 were computed.

Figure 8. Same as Figure 7, but for run-up velocity V. The shaded regions depict the intervals where the extreme values for the diagrams in Figure 10 were computed.

3.3.2. Shoreline Velocity during Run-up and Run-down

Figure 8 shows the numerical, experimental and analytical shoreline velocity, again for all waves used in this study. As described in Section 2 the experimental shoreline velocity, and similarly the shoreline velocity for the numerical simulations, was derived from the shoreline location using Equation (8). Since the x-axis of the wave flume coordinate system points positively offshore, positive velocity values in Figure 8 indicate the wave run-down.

Similar to the shoreline motion the experimentally determined velocities agree well with the ones from the numerical simulation. In particular, this is true for the initial run-down and the first run-up phase (first maximum and minimum, respectively). As in the numerical runs with analytical BC the first run-down is not in accordance with the analytical shoreline velocity, but the run-up process essentially agrees well. An exception is the wave T20_H2 (top left in Figure 8), where the evolution of the analytical shoreline velocity exhibits a remarkable steep gradient that can neither be reproduced by the numerical model, driven by experimental initial conditions, nor by the physical experiments. The authors attribute this observation to the imperfect wave signal, which exhibits a too small amplitude in surface elevation during the initial depression and results in a shallower slope in the first edge of the sinusoidal cycle (cf. Figure 4). Note that this deviation is not present when computing the wave with (perfect) analytical BC as shown in Figure 6. Due to the the lack of experimental data in the second run-down, a comparison for the velocity during this phase is only possible for the wave T44_H3, which agrees well with the analytical velocities. This is also true for the numerically determined values in these regions for the waves T20_H2, T30_H2 and T44_H3.

Similar to the shoreline location the riding waves also corrupt the experimental shoreline velocity. This becomes evident in high peaks in the time series, as seen around $t=55\text{\hspace{0.17em}s}$ for the wave T44_H3 or around $t=70\text{\hspace{0.17em}s}$ for the wave T58_H3. This effect is also evident for the two longest waves T77_H4 (bottom middle) and T100_H4 (bottom right). However, the numerical model simulates the riding waves well, since an overall good agreement between the numerical and experimental shoreline velocities is observed.

Table 3. Time intervals (in seconds) which were used for the computation of the extreme values in Figure 9 and Figure 10.

Wave-ID	Analyt. BC, Periodic Wave	Experiments/exp. BC, Single Cycle Wave
	All Extreme Values	$R_{\mathrm{up}}$	$R_{\mathrm{down}}$	$V_{\mathrm{up}}$	$V_{\mathrm{down}}$
	(s)	(s)	(s)	(s)	(s)
T20_H2	30–80	40–52	–	40–52	–
T30_H2	30–80	40–57	–	40–57	–
T44_H3	35–120	43–70	–	43–54	60–80
T58_H3	40–150	45–80	–	45–67	–
T77_H4	40–200	50–100	–	50–74	–
T100_H4	50–250	60–110	–	–	–

Table 3. Time intervals (in seconds) which were used for the computation of the extreme values in Figure 9 and Figure 10.

Wave-ID	Analyt. BC, Periodic Wave	Experiments/exp. BC, Single Cycle Wave
	All Extreme Values	$R_{\mathrm{up}}$	$R_{\mathrm{down}}$	$V_{\mathrm{up}}$	$V_{\mathrm{down}}$
	(s)	(s)	(s)	(s)	(s)
T20_H2	30–80	40–52	–	40–52	–
T30_H2	30–80	40–57	–	40–57	–
T44_H3	35–120	43–70	–	43–54	60–80
T58_H3	40–150	45–80	–	45–67	–
T77_H4	40–200	50–100	–	50–74	–
T100_H4	50–250	60–110	–	–	–

3.4. Extremal Shoreline Dynamics

In this section the maximum run-up and run-down as well as the maximum shoreline velocity during run-up and run-down are addressed. If not stated otherwise, these extremal characteristics are investigated for the experimentally generated and the numerically simulated waves, with experimental as well as analytical boundary conditions, and compared with the theoretical results of Madsen and Schäffer [14]. Note, that the normalized maximum run-up shown in the following is defined as the maximum run-up normalized by the respective offshore amplitude of the long waves. Where experimental data was used, the values for maximum run-up and run-down and the corresponding maximum shoreline velocities were obtained through an average of all six runs of the waves. Note, that the extreme values were not taken from the entire time period, but rather from carefully chosen intervals. The respective intervals are given in Table 3 and marked gray in Figure 6, Figure 7 and Figure 8. The reason for this procedure was to detect the intervals in which the actual run-up took place and to disregard time spans where experiments and simulations deviated from the theory by design, or the data was corrupted by riding waves.

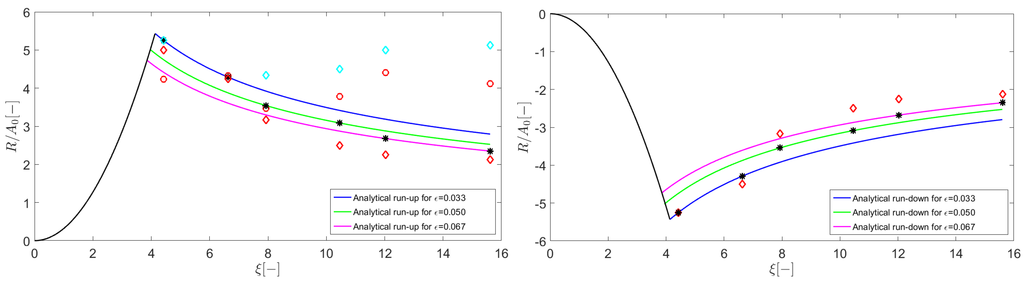
Figure 9. Maximum run-up (left) and maximum run-down (right) of long sinusoidal waves. Analytical (black stars), experimental (red circles) and numerical (diamonds)—with experimental (cyan) and analytical (red) boundary condition. Solid black line according to Equation (7). Colored solid lines are computed according to Equation (6).

Figure 9. Maximum run-up (left) and maximum run-down (right) of long sinusoidal waves. Analytical (black stars), experimental (red circles) and numerical (diamonds)—with experimental (cyan) and analytical (red) boundary condition. Solid black line according to Equation (7). Colored solid lines are computed according to Equation (6).

Figure 10. Maximum shoreline velocities during run-up (left) and run-down (right). Analytical (black stars), experimental (red circles) and numerical (diamonds)—with experimental (cyan) and analytical (red) boundary condition. Solid black line according to Equation (7). Colored solid lines are computed according to Equation (6).

Figure 10. Maximum shoreline velocities during run-up (left) and run-down (right). Analytical (black stars), experimental (red circles) and numerical (diamonds)—with experimental (cyan) and analytical (red) boundary condition. Solid black line according to Equation (7). Colored solid lines are computed according to Equation (6).

3.4.1. Shoreline Location

Figure 9 (left) shows the experimental, numerical and analytical normalized maximum run-up for all long waves used in this study as a function of the surf similarity parameter ξ. The parameter ϵ defines the non-linearity of the wave, which is the ratio between the wave amplitude and the undisturbed water depth as defined in Section 2.1. As already stated in [53] the highest run-up occurs for surf similarity parameters $3\lesssim \xi \lesssim 6$. This is the interval where the theoretical transition from breaking to non-breaking waves occurs. For increasing ξ the analytical expression from Madsen and Schäffer [14] predicts a decrease in the normalized run-up.

Using the analytical boundary conditions (red diamonds), the monotone dependence on ξ can be reproduced with the numerical model. However, the model under-predicts the maximum run-up for larger ξ (i.e., longer wave lengths), which was already noted in Section 3.2 and is attributed to an inconsistency of the velocity signal at WG1. Note that for $\xi =6.63$ (wave T30_H2) only one marker is visible for the numerical run-up. This is because the run-up is identical for both simulations (experimental and analytical BC).

The experimental normalized maximum run-up (circles) agrees well with the analytical expression (stars) for $\xi =6.63$ and $\xi =7.94$ (waves T30_H2 and T44_H3). However for $\xi =4.42$ (wave T20_H2), it is lower than the analytical value, which the authors attribute to friction. For $\xi >10$ the experimentally determined maximum run-up is significantly higher than the analytical run-up due to the riding waves that corrupt the shoreline evolution. Initializing the numerical model with the imperfect surface elevation profiles, i.e., experimental BC, results in even higher run-up heights, which the authors also attribute to the neglected friction in the numerical model. However, the model is generally in good accordance with the experiments.

Figure 9 (right) shows a comparison between the analytical (stars) and numerical (analytical BC, red diamonds) normalized maximum run-down. Maximum run-down values for the experimental and numerical results using experimental BC were not computed, since they both result from a single cycle sinusoidal wave. As stated in Section 3.2, the maximum run-down is always biased by the transition between the still water and the oscillating state in this case and would have been misleading. Similar to the run-up case the maximum run-down is well reproduced by the numerical model using analytical BC, but it results in too small absolute values for large ξ.

3.4.2. Shoreline Velocity

Figure 10 (left) shows a comparison between analytical, experimental and numerical normalized maximum shoreline velocities during wave run-up. As stated in [53] and confirmed in this study, the highest maximum shoreline velocities occur for waves in the transition region with $3\lesssim \xi \lesssim 6$, where the wave T20_H2 exhibiting the lowest surf similarity parameter of 4.42 has the highest shoreline velocity. Using analytical BC, the numerical maximum shoreline velocity agrees well with the analytical values. The maximum shoreline velocity could also be reproduced with the physical and numerical experiments, when the time intervals where riding waves corrupted the signal were excluded in the maximum computation. Deviations only occur for the wave T20_H2 ($\xi =4.42$). This can be probably explained by the imperfect wave signal (cf. Section 3.1). The wave T100_H4 ($\xi =15.62$) was completely corrupted by riding waves when it hit the beach, which made it impossible to determine an interval for a proper calculation of the maximum run-up velocity.

In analogy to the maximum shoreline velocity during run-up now the maximum shoreline velocity during run-down is addressed. The run-down velocity during the first run-down was not considered, since it was biased by the transition to the sinusoidal behavior of the wave. Furthermore, due to the lack of data from the experiments during the second run-down, no maximum values were computed from the experimental time series. One exception is the wave T44_H3, where data from several runs was available. Figure 10 (right) shows the comparison of maximum velocities during run-down.

Regarding the analytical expressions, the correlations between surf similarity ξ, magnitude of the shoreline velocity and wave non-linearity ϵ are the same as for the maximum run-up velocities. Initializing the numerical model with analytical BC yields again an overall good agreement of the numerical normalized maximum run-down velocities with the analytical expressions of Madsen and Schäffer [14]. Running the numerical model with experimental BC results in good agreement with the experimental data. However, since experimental data is available for one wave only, the results have to be interpreted with care.

4. Discussion and Conclusions

This study contributed to the answer of the basic research question, whether shallow water theory can explain and accurately model the run-up behavior of long waves on a plane beach. By conducting physical and numerical experiments and comparing them with analytical expressions derived from the underlying equations, the authors demonstrated the usefulness of such simultaneous experimentation.

A novel wave generator, based on hydraulic pumps that are capable of generating arbitrarily long waves (even exceeding the wave flume length) was used to generate wave periods of 20 to 100 s Combined with appropriate wave heights, surf similarity parameters between $4.4\lesssim \xi \lesssim 15.6$ were realized. Sinusoidal wave shapes were adopted from [14], in order to obtain waves with corresponding analytical reference solutions. Due to the complex control problem for this type of wave generator in the current set-up, spurious over-riding small-scale waves were unavoidable. Scaling effects were also discussed and it could be concluded that the experimental scale imposes at most minor inaccuracies in the run-up area on the experimental results.

A Runge-Kutta discontinuous Galerkin method with a high fidelity wetting and drying scheme was applied to numerically solve the one-dimensional non-linear shallow water equations. Analytical (from [14]) and experimentally generated wave shapes were used as inflow boundary conditions for the numerical experiments.

In order to compare analytical, numerical and experimental data, the wave similarity measured by the Brier score, maximum run-up and run-down height, as well as run-up/run-down velocities were utilized as quantitative metrics. In a first analysis, periodic and non-periodic clean sinusoidal waves were compared to rule out differences due to the single sinusoidal wave generation in the wave flume. On further analysis, significant differences in experimental and analytically expected values are observed. However, with the combination of analytical, numerical, and experimental data it could be demonstrated that spurious over-riding small-scale waves lead to the observed deviations between analytical expression and experimental values. The numerical model serves as a linking element between theoretical and measured results, and can therefore explain rigorously the influence of small-scale spurious pollution.

Future investigations could be directed to solve the following problems: Better feedback control systems could minimize the spurious over-riding waves and allow for a better resemblance of experimental and analytical wave shapes. More appropriate wave shapes, like N-waves or wave shapes, reconstructed from tide gauges, could be generated in order to obtain a better representation of tsunami wave characteristics. Finally, a true two-dimensional simulation could investigate geometrical features of the experiment, taking into consideration small-scale reflections and inhomogeneous meridional velocity and wave height distributions.