Coupling Effect of the Bottom Type-Depth Configuration on the Sonar Detection Range in Seamount Environments

Abstract

Seabed topography exerts a profound influence on underwater acoustic propagation, and the coupling effect between bottom acoustic properties and the source–receiver geometric configuration remains insufficiently quantified, particularly in seamount shielding scenarios. To address this gap, in this study, the BELLHOP ray model was integrated with Earth topography 1 (ETOPO1) topographic data and Hybrid Coordinate Ocean Model (HYCOM) hydrological data for seamounts east of Taiwan. Transmission loss (TL) of 300 Hz sound waves was simulated across four typical bottom types (rock, coarse sand, silt, and clay) under varying source depths (50–1000 m) and receiver depths (50–500 m). The maximum sonar detection range was delineated using an 80 dB TL threshold as the criterion for effective detection. The key findings reveal that the bottom properties are the primary factors that reduce the detection range: the maximum detection range over rock bottom exceeds that over clay by more than 8-fold. Notably, a shallow source–shallow receiver configuration mitigates the acoustic shadow effect induced by seamounts, whereas deep receiver deployment (≥500 m) diminishes the discriminative impact of bottom types on the propagation behavior. Furthermore, a segmented empirical prediction formula was established, which reconciles both the physical mechanisms (e.g., bottom reflection-absorption and seamount shielding) and engineering applicability. This formula provides a robust theoretical basis for evaluating sonar performance in complex seabed topography settings, thereby facilitating optimized underwater detection strategies in seamount-dominated marine environments.

1. Introduction

The influence of the seabed topography on underwater acoustic propagation is an important topic in marine acoustics research. In particular, the acoustic propagation characteristics in seamount environments have attracted widespread attention due to the special physical mechanisms in such environments. With the growth of marine resource development and underwater security needs, accurately predicting acoustic transmission loss and the sonar detection range under seamount topography has become a key issue that urgently needs to be solved [1,2]. When sound waves propagate in the deep sea, they frequently collide with seamounts, causing physical phenomena such as acoustic shielding, focusing, and acoustic shadow zone formation, which significantly affect the detection performance of sonar systems [3]. Previous studies have mostly focused on sound speed profiles and geometric shielding effects and have often simplified the seabed as an ideal rigid or uniform semi-infinite medium, failing to systematically quantify the coupling effect between real bottom types and source–receiver depth configurations.

In recent years, scholars in China and abroad have conducted research on acoustic propagation in complex seabed topography through experiments and simulations. As early as the 1960s, Northrop et al. [4] discovered the slope enhancement effect. In experiments in the Western Pacific, Qin Jixing et al. [5,6,7,8] observed that signals emitted by sound sources can propagate stably over long distances near the sound channel axis depth after propagating through slopes. Through deep-sea experiments in the South China Sea, Li Shenghao et al. [9] found that the three-dimensional horizontal refraction effect caused by seamounts leads to a transmission loss that is more than 10 dB higher than the results calculated using the two-dimensional model. However, existing studies have obvious deficiencies in the quantitative characterization of bottom acoustic properties. In particular, there is a lack of systematic analysis of the coupling effect between different bottom types and depth configurations.

Based on the BELLHOP ray model [10], combined with hybrid coordinate ocean model (HYCOM) hydrological and Earth topography 1 (ETOPO1) topographic data, in this study, we systematically investigated the influence of four types of bottom (rock, coarse sand, silt, and clay) on the propagation of 300 Hz sound waves in the seamount profile east of Taiwan. Innovatively, the dimensionless parameter R/A was introduced to comprehensively characterize the reflection-absorption properties of the bottom [11], quantifying the coupling effect of the bottom types and source–receiver depth configurations on acoustic transmission loss and the maximum sonar detection range. An empirical prediction formula suitable for navigation planning was established, providing theoretical support for sonar performance optimization under seamount topography.

This study selects 300 Hz as the central frequency for simulation analysis, based on the following considerations. First, 300 Hz lies within a typical low-frequency band that exhibits low attenuation and strong long-range propagation capability, making it a key frequency for deep-sea remote sensing applications. Second, the wavelength at this frequency (approximately 5 m) is much smaller than the characteristic scale of the seamounts under investigation (horizontal extent ~30 km, vertical relief ~3000 m), thereby satisfying the geometric acoustics approximation and enabling ray-based models to effectively capture the geometric shadowing effects caused by terrain obstruction. Furthermore, acoustic interactions between 300 Hz sound waves and the seabed are highly sensitive to bottom properties—including density, sound speed, and attenuation coefficient—rendering this frequency ideal for investigating the “bottom type–depth” coupling effect.

The physical mechanism underlying the “bottom type–depth” coupling relationship and the associated empirical prediction model demonstrates broad applicability across low-frequency bands (e.g., 100 Hz–1 kHz). The findings of this study can thus qualitatively inform performance predictions for similar low-frequency sonar systems operating in complex bathymetric environments. For quantitative applications, however, the attenuation term and diffraction gain in the model must be adjusted according to the target frequency’s absorption coefficient and the ratio of acoustic wavelength to terrain characteristic scale.

2. Data and Methods

2.1. Description of Topographic and Hydrological Data

The seamount topography east of Taiwan (as illustrated in Figure 1 below) starts at coordinates 22.33° N, 123.30° E and ends at 22.33° N, 122.63° E. The center of the seamount profile is located near 35 km. At this point, the peak water depth is approximately 2000 m, the basement water depth is about 5000 m, the relative height is 3000 m, and the horizontal span is around 20 km. It is a typical large seamount and is sufficient to produce a significant shielding effect for 300 Hz sound waves.

Hydrological data with a resolution of 1/12° were obtained from HYCOM reanalysis data, and seabed topographic data with a resolution of 1′ were obtained from ETOPO1 [12]. The empirical formula for calculating the speed of sound is $C=1450+4.21\ast T-0.037\ast T^2+1.14\ast \left(S-35\right)+0.0175\ast D$, where C is the speed of sound, T is the temperature, $S \mathrm{i}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{y},\mathrm{a}\mathrm{n}\mathrm{d} D$ is the depth. The specific sound speed profile is shown in Figure 2 below.

Regarding the bottom acoustic parameters, R is the reflection coefficient. The seabed reflection coefficient is determined from the acoustic impedance, $R = {\left[{\displaystyle \frac{z_2- z_1}{z_2+ z_1}}\right]}^2$, where the impedance is $Z = \rho C,\mathrm{a}\mathrm{n}\mathrm{d} \rho$ is the density, The seawater impedance is $Z_w = 1025 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3\times 1500 \mathrm{m}/\mathrm{s}= 1.5375 \times {\displaystyle \frac{{10}^6 \mathrm{k}\mathrm{g}}{{\mathrm{m}}^2·\mathrm{s}}}$. The sound energy absorption capacity of bottom is characterized by the longitudinal wave attenuation coefficient A (dB/λ), which is higher, indicating faster energy loss when penetrating into the bottom layer [13]. The details of the bottom parameters are shown in

Table 1. Bottom acoustic parameters.

Bottom	Density (g/cm3)	Longitudinal Wave Velocity (m/s)	Shear Wave Velocity (m/s)	Longitudinal Wave Velocity (dB/λ)	Shear Wave Attenuation (dB/λ)	Roughness RMS (m)	$\mathbf{R}/\mathbf{A}$	R Reflection Coefficient	Impedance Z (106 Pa·s/m)
Rock	2.65	3000	1200	0.125	0.3	0.5	5.41	0.676	7.95
Coarse sand	1.95	1775	250	0.25	0.5	0.1	1.54	0.385	3.46
Silt	1.6	1600	170	0.35	0.6	0.05	0.71	0.25	2.56
Clay	1.4	1475	150	0.5	0.8	0.015	0.25	0.148	2.07

.

To comprehensively characterize the reflection-absorption properties of the bottom, the dimensionless parameter R/A is introduced, where R is the reflection coefficient and A is the normalized absorption intensity. In this study, the longitudinal wave attenuation coefficient (dB/λ) is used as a proxy variable for A, so a larger R/A value indicates that the bottom is more reflective [14]. For rock, R/A = 5.41, resulting in a strongly reflective seabed. The energy of the sound wave is mainly reflected, making it suitable for long-distance propagation with small seabed loss. For coarse sand boundaries, reflection and absorption are balanced, with partial reflection and partial absorption, making it suitable for medium propagation distances. For clay, R/A = 0.25, making it a strongly absorptive seabed. The energy of the sound wave is mainly absorbed by the seabed, resulting in a limited propagation distance and large seabed loss.

2.2. BELLHOP Model Simulation

The RAM model and BELLHOP model were, respectively, adopted to simulate the influence of different substrates on transmission loss (TL) in the seamount environment, and the results are shown in the figure below. It can be seen from the figure that the calculation results (trends) of the BELLHOP model are close to those of the more accurate RAM model, while its calculation efficiency is much higher than that of the RAM model. Therefore, the BELLHOP ray model will be used for sound field simulation in subsequent research.

The RAM and BELLHOP models were utilized to simulate the impact of different seabed types on transmission loss (TL) in a seamount environment, with the results presented in Figure 3. As shown in the figure, the overall trends of the computational results from both models are largely consistent, with a Mean Absolute Difference of 6.52 dB and a Root Mean Square Difference (RMSD) of 8.19 dB. These discrepancies are mainly due to the systematic bias caused by the ray method’s “neglect of wave effects.” Considering that the horizontal extent of the seamount examined in this study is relatively large and that the BELLHOP model boasts significantly higher computational efficiency compared to the RAM model, it was decided, after comprehensive evaluation, to adopt the BELLHOP model for subsequent acoustic field simulations.

Based on ray acoustics theory, BELLHOP computes sound ray trajectories and their intensities to model propagation in inhomogeneous ocean environments, and is particularly well-suited for mid-to-low frequency problems involving seamount boundaries [8]. Model inputs include: (1) a two-dimensional sound speed profile derived from HYCOM data; (2) ETOPO1 bathymetric data; and (3) elastic parameters for four representative bottom types listed in Table 1 (i.e., density, compressional and shear wave velocities, attenuation coefficient, and roughness). The sea surface is modeled as a pressure-release boundary (i.e., acoustically soft, with zero pressure condition), while the seabed is represented using an elastic half-space model to more realistically capture wave–sediment interactions.

In the simulations, the source is configured as an omnidirectional, single-frequency point source at 300 Hz, with a source level (SL) of 120 dB—consistent with typical specifications for deep-sea long-range sonar systems. The omnidirectional radiation pattern is adopted to eliminate directional bias and isolate the “bottom type–depth” coupling effect. Source depths are set at 50 m, 150 m, 500 m, and 1000 m, spanning the shallow surface duct, mid-water transition zone, and regions near the deep sound channel axis. The receiver is an omnidirectional hydrophone placed at depths of 50 m, 100 m, 200 m, and 500 m, corresponding to depth ranges sensitive to different acoustic propagation paths. Transmission loss (TL) is computed by integrating the intensity contributions along all ray paths. An effective detection threshold of 80 dB is adopted to subsequently estimate the maximum operational range of the sonar system. Simulations are conducted for four bottom types—rock, coarse sand, silt, and clay—to evaluate transmission loss across various source–receiver depth configurations. The results are presented in the Figure 4, Figure 5, Figure 6 and Figure 7 below.

It can be seen from the 300 Hz transmission loss distributions in Figure 4, Figure 5, Figure 6 and Figure 7 that the bottom type has a systematic impact on the range of the acoustic shadow zone behind the seamount, the energy difference inside and outside the shadow zone, and the received signal intensity. This impact maintains a consistent trend with changes in the source depth. The hard, high-impedance, low-absorption rock bottom provides an efficient reflector for sound waves, reducing the shadow zone and retaining more of the arriving energy. In contrast, the soft, high-absorption, low-reflection clay bottom acts as an energy trap, resulting in the largest shadow zone and the weakest signal.

The simulation results of acoustic propagation loss under different seabed sediment environments with the same sound source depth and receiver depth are presented in Figure 8, Figure 9, Figure 10 and Figure 11 below.

Under the condition of a 50 m source depth and shallow receiver (≤100 m), the variation trends of the transmission loss for the four bottom are basically consistent, and the trends for a 50 m receiver depth exhibit the least obvious difference. For the same source depth (except for 50 m), the bottom type has a very sensitive impact on the transmission loss under shallow receiver (≤200 m) conditions, especially on the leeward side of the seamount. With increasing source depth, when the receiver depth is ≥500 m, the transmission loss curves of the different bottom tend to be parallel, indicating that multipath propagation weakens the relative impact of the differences in the bottom.

Analysis of Figure 8, Figure 9, Figure 10 and Figure 11 reveals that the clay resulted in the greatest acoustic transmission loss. This is mainly because the clay had the lowest impedance, leading to a large amount of sound wave transmission into the seabed. The energy was repeatedly absorbed and scattered by the bottom layer, resulting in additional losses. In contrast, the rock had the highest impedance, and the energy was quickly specularly reflected. In the ray model, the proportion of the energy retained in the water column was the highest, exhibiting the lowest loss. Therefore, the order of the transmission losses caused by the different types of bottom from largest to smallest is as follows: clay > silt > coarse sand > rock. The clay resulted in the greatest transmission loss, and the rock resulted in the least transmission loss.

3. Analysis of Results

The extent to which passive sonar detection range is determined can be expressed as: SL − TL − NL + DI − DT ≳ 0 [15]. Taking a source level (SL) of 120 dB, a noise spectral level (NL) of 50 dB, an array gain (DI) of 20 dB, and a detection threshold (DT) of 10 dB, the empirical threshold for effective detection using the transmission loss (TL) for a passive sonar is 80 dB. The results of the maximum sonar detection range are shown in Figure 12 and Figure 13.

In Figure 12 and Figure 13, the blue line represents the TL, and the red dashed line represents the detection threshold (figure of merit, FOM). When TL ≤ FOM, the sonar can detect the target. All of the intersection points of the two lines were extracted, and the abscissa corresponding to the farthest intersection point was taken as the maximum sonar detection range. The maximum range under each working condition is shown in

Table 2. Maximum detection range $R_{max}$ (km, TL ≤ 80 dB).

Source Depth (m)	Receiver Depth (m)	$\mathbf{Rock} {\mathit{R}}_{\mathit{m}\mathit{a}\mathit{x}}$	$\mathbf{Coarse} \mathbf{Sand} {\mathit{R}}_{\mathit{m}\mathit{a}\mathit{x}}$	$\mathbf{Silt} {\mathit{R}}_{\mathit{m}\mathit{a}\mathit{x}}$	$\mathbf{Clay} {\mathit{R}}_{\mathit{m}\mathit{a}\mathit{x}}$	Remarks
50 m	50 m	68.6743	68.6092	68.5073	68.5030	Same depth
50 m	100 m	67.6611	42.8094	33.6605	6.6498
50 m	200 m	66.6190	41.5821	33.3814	5.7474
50 m	500 m	65.9530	40.4283	32.0015	6.2248
150 m	50 m	66.7286	41.9744	33.7407	5.6150
150 m	100 m	66.9931	41.9649	33.6325	6.1476
150 m	200 m	67.2994	42.1976	33.9115	5.4158
150 m	500 m	42.6504	40.8083	34.6093	5.8115
500 m	50 m	41.5098	34.3578	6.2410	6.0953
500 m	100 m	41.4648	34.5435	6.3083	6.1122
500 m	200 m	41.2447	34.2077	6.1615	6.1290
500 m	500 m	46.9816	46.1930	45.7020	45.5134	Same depth
1000 m	50 m	40.3844	25.0032	7.5567	7.4273
1000 m	100 m	38.8536	24.9279	7.5044	7.3206
1000 m	200 m	58.3374	7.9756	7.8523	7.8153
1000 m	500 m	48.6346	48.5820	48.5319	48.5201

.

In the extremely shallow same-depth configuration (source depth of 50 m, receiver depth of 50 m), even an absorptive bottom (silt and clay) can achieve long-distance detection due to the surface sound channel. For the same source–receiver depth configuration (source depth of 500 m, receiver depth of 500 m), the direct ray and reflected ray arrive at similar times, and constructive interference can enhance the signal. In the deep receiver configuration near the axis of the sound channel (source depth of 1000 m, receiver depth of 500 m), the detection ranges of the various bottom types are almost the same, which is mainly determined by the combined effect of the multipath averaging effect of deep-sea acoustic propagation and the dominant mechanism of seamount shielding.

Based on the data in Table 2, to balance the accuracy, robustness of the prediction results, and the rationality of the physical reality, we propose a dual-segment model of “by bottom type + with/without shielding” specifically for the maximum sonar detection range $R_{max}$ (km) behind seamounts. Thresholds are set to capture the modulation of the depth on the bottom effect and to reflect the dominant effect of the bottom.

3.1. Free Field (Not Significantly Affected by Seamount Shielding and Bottom Absorption)

If bottom = rock, $z_{src}\le 150$ m, and $z_{rec}\le 100$ m, then $R_{max}=68.6\mathrm{k}\mathrm{m}$.

If $z_{src}=z_{rec}=50 \mathrm{m}$, regardless of the type of bottom, then $R_{max}=68.6 \mathrm{k}\mathrm{m}.$

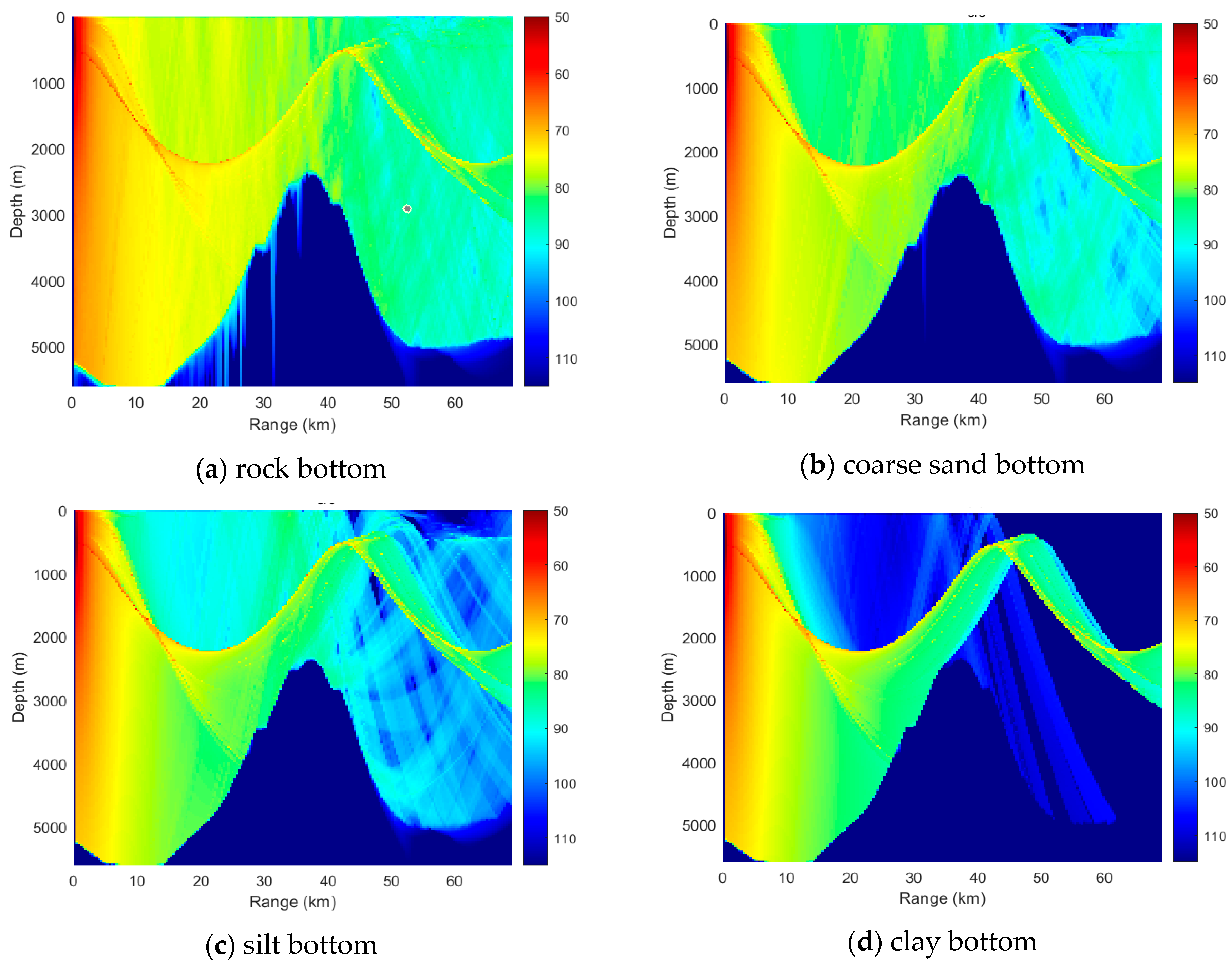
3.2. Shielded Field (Segmented by Bottom)

The maximum sonar detection range $R_{max}$ in the shielded field is empirically parameterized as a function of source depth ($z_{src})$ and receiver depth ($z_{rec}$), with distinct formulations for four typical seafloor bottom types:

(1)

Strongly reflective type (rock):

$$R_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left(68.9-0.0012z_{src}-0.011z_{rec},65.0\right).$$

(2)

Transitional type (coarse sand):

$$R_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left(69.2-0.028z_{src}-0.045z_{rec},40.4\right).$$

(3)

Absorptive type (silt):

$$R_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left(12.8-0.0041z_{src}-0.021z_{rec},5.42\right).$$

(4)

Strongly absorptive type (clay):

$$R_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left(9.9-0.0020z_{src}-0.0085z_{rec},5.42\right).$$

In the empirical formulas for the shielded field, the coefficients of $z_{src} \mathrm{a}\mathrm{n}\mathrm{d} z_{rec}$ are both negative, indicating that the detection range decreases with increasing depth, which is consistent with the law of enhanced seamount shielding. The intercept reflects the bottom reflection capacity, and rock (68.9) > coarse sand (69.2) > silt (12.8) > clay (9.90), which is consistent with the R/A ranking. The model integrates the surface sound channel free field effect (extremely shallow, same depth), reflects the bottom reflection-absorption characteristics through the intercept and slope, reflects the shielding trend through negative coefficients, and provides physical lower limit protection through the 5% quantile stage. The specific error indicators are presented in

Table 3. Model error analysis table (Unit: km).

Bottom	Number of Configurations	Mean Absolute Error (MAE)	Root Mean Square Error (RMSE)	Maximum Deviation	Coefficient of Determination ${\mathit{C}\mathit{V}-\mathit{R}}^2$
rock	16	0.61	0.78	+1.23 (50/100)	0.996
coarse sand	16	2.87	3.42	+5.83 (150/50)	0.942
silt	16	1.22	1.63	+0.98 (1000/50)	0.981
clay	16	1.22	1.65	+1.05 (1000/50)	0.983
Total	64	1.38	1.92	+5.83	0.981

Note: Positive deviation = predicted > measured (overestimating detection capability); Negative deviation = predicted < measured (underestimating, conservative). The value range of $R^2$ is usually (−$\infty$, 1], with an ideal value of 1 (perfect fit).

.

The model achieved an $R^2$ value of 0.981, indicating that the model successfully captures the influences of the major physical factors, including the seamount shielding, bottom type, and depth configuration, on $R_{max}$. The model also achieved a mean absolute error (MAE) of 1.38 km, indicating an average prediction distance deviation of 1.38 km per case, which meets the accuracy requirements for blind zone judgment (usually ±5 km is acceptable). For a low 300 Hz frequency, hard seabeds with high reflection and low absorption trap energy in the water layer, while soft seabeds with strong absorption consume a lot of the energy. The bottom type has a significant regulatory effect on the detection range.

4. Conclusions

This study aimed to quantify how bottom acoustic properties and source–receiver depth configurations jointly influence sonar detection range in seamount environments, addressing a key gap in prior studies that typically modeled the seabed as an idealized medium. By integrating the BELLHOP ray model with ETOPO1 bathymetric data and HYCOM hydrographic data, we systematically demonstrated the dominant influence of both bottom type and depth configuration, and developed a two-regime empirical prediction model (free-field vs. seamount-shielded) with a high coefficient of determination (R² = 0.981) and low mean absolute error (MAE = 1.38 km). The model effectively bridges fundamental physical mechanisms—such as bottom reflection–absorption characteristics and seamount-induced shadowing—with practical engineering needs, offering a robust basis for sonar performance assessment and optimal deployment in complex seamount environments. Detailed conclusions are presented as follows:

(1)

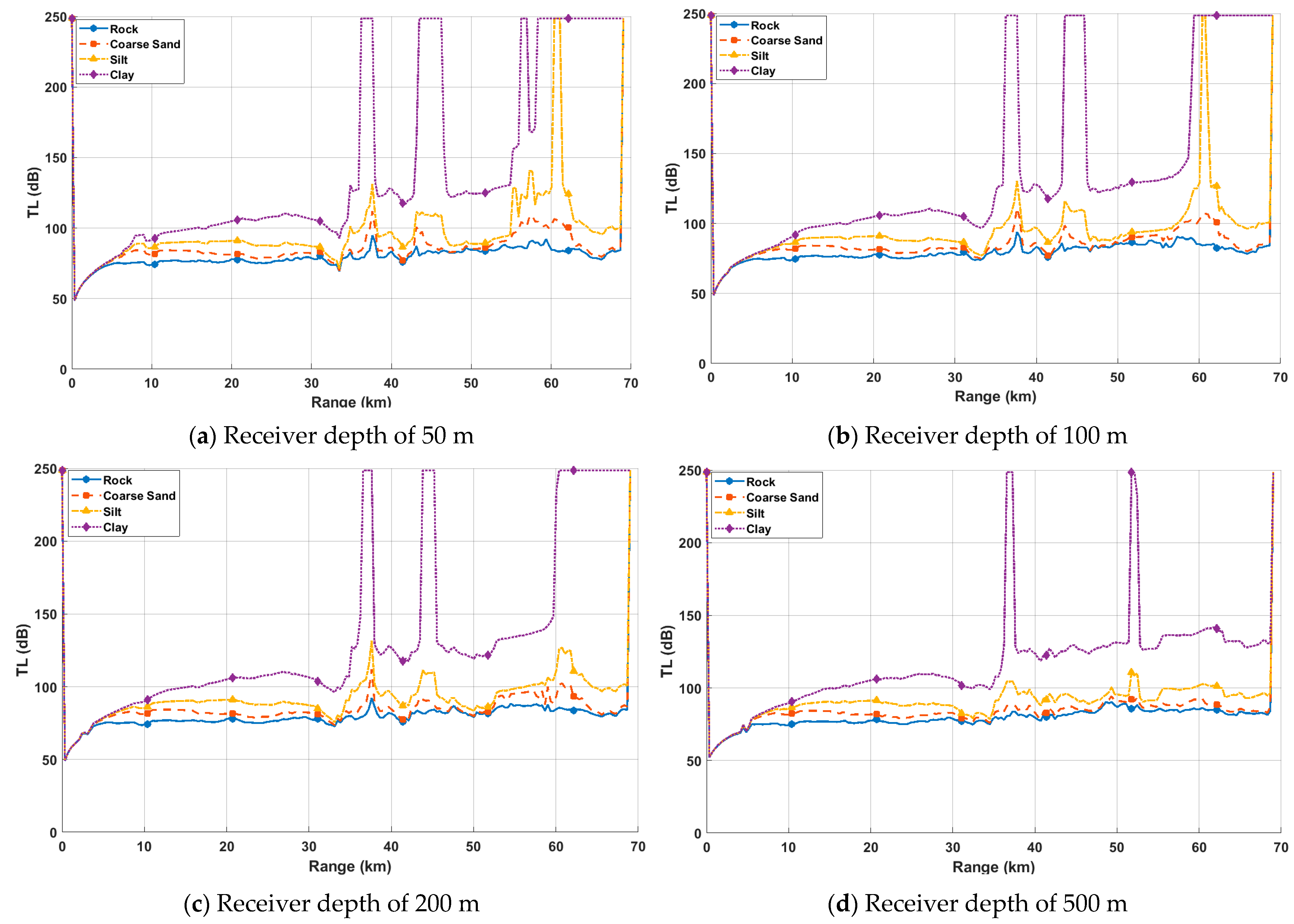
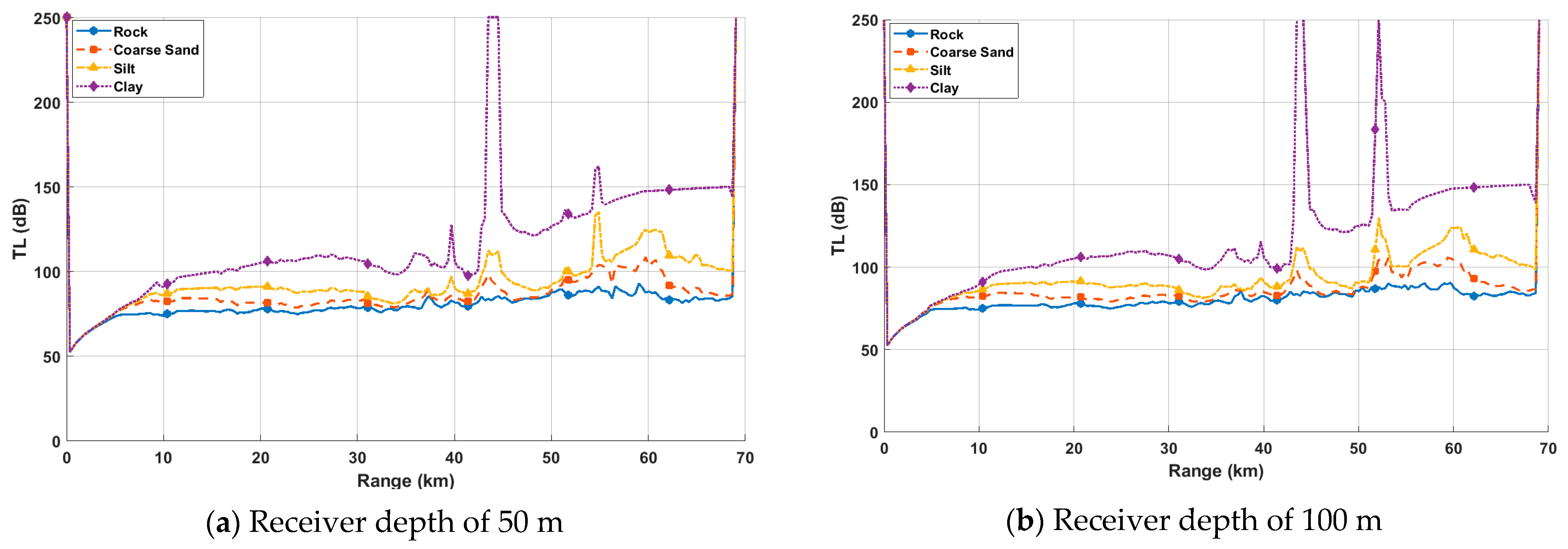
Bottom is the primary factor controlling the maximum sonar detection range in shallow layers (especially < 200 m) in seamount environments. The maximum detection range for rock bottom is almost eight times that of clay, indicating that a highly reflective bottom can effectively buffer the energy attenuation in the seamount acoustic shadow zone.

(2)

After seamount shielding, an absorptive bottom cannot provide effective reflected energy supplementation, and the sound intensity in the shadow zone mainly depends on diffraction. In contrast, deep sources (1000 m) have a large grazing angle for sound rays, making it difficult to diffract the top of the seamount effectively, resulting in a low diffraction gain. As a result, the absorptive bottom + deep source combination significantly amplifies the acoustic shadow effect. In contrast, the rock + shallow source combination effectively enhances the received signal in the shadow zone through the synergistic effect of strong bottom reflection and a surface sound channel waveguide.

(3)

The shallow source–shallow receiver configuration can significantly weaken the seamount shadow effect: 300 Hz sound waves are confined in the surface sound channel, effectively bypassing seamount obstacles through diffraction, forward scattering, and multiple surface reflections.

(4)

The advantage provided by the bottom decreases with increasing receiver depth. When the receiver depth is ≥500 m, multipath propagation causes the transmission loss curves of the different bottom layers to be approximately parallel. The marginal impact of a single interface reflection is averaged, and the path loss is dominated by geometric spreading and multiple interface interactions.

5. Discussion on the Limitations of the BELLHOP Model

Although the BELLHOP ray model successfully reveals the coupling influence of bottom type and depth configuration on acoustic propagation in seamount environments, several limitations should be acknowledged when interpreting the results or extrapolating them to practical scenarios:

(1)

High-frequency limitation and diffraction effects: Ray-based models have limited capability in accurately representing diffraction and scattering when the acoustic wavelength is comparable to or larger than the scale of obstacles. While the 300 Hz frequency and large-scale seamounts in this study fall within the valid regime of ray theory, higher frequencies or fine-scale seabed roughness would require complementary approaches such as normal mode or parabolic equation methods.

(2)

Simplification of three-dimensional effects: The simulations are performed using two-dimensional vertical slices, thereby neglecting horizontal variations in seamount morphology that could induce three-dimensional refraction, focusing, or defocusing. In realistic 3D environments, such lateral effects may lead to more complex spatial patterns of transmission loss.

(3)

Uncertainty in environmental inputs: Model accuracy critically depends on the fidelity of input parameters—particularly the sound speed profile and seabed acoustic properties. The climatological HYCOM data and representative bottom parameters used herein cannot fully capture the spatiotemporal variability of real ocean conditions, potentially introducing prediction errors.

(4)

Treatment of signal coherence: The standard BELLHOP implementation computes incoherent transmission loss (i.e., energy summation), whereas actual sonar signal processing often exploits coherent interference among multipath arrivals. In shallow water or specific depth configurations where strong multipath interference occurs, the incoherent approach may smooth out fine-scale interference structures, leading to localized biases in TL estimation.

Despite these limitations, the BELLHOP model offers significant advantages in computational efficiency, physical interpretability, and its ability to capture dominant propagation mechanisms—such as seamount-induced shadowing. The conclusions of this study regarding the “bottom type–depth” coupling mechanism are therefore robust and provide a valuable semi-empirical framework for evaluating sonar performance in complex underwater terrains.