Research on Ship Hull Hybrid Surface Mesh Generation Algorithm Based on Ship Surface Curvature Features

Abstract

Mesh generation is a critical preprocessing step in Computational Fluid Dynamics. In ship hydrodynamics, existing mesh generation methods lack adaptability to complex hull surface geometries, necessitating repeated optimization. To address these issues, a new hybrid mesh generation strategy was proposed, integrating Non-Uniform Rational B-Spline surface interpolation, advancing front technique, hull surface curvature features, and mesh quality evaluation parameters. Firstly, the ship hull surface was partitioned into multiple regions, and each region was assigned a specific mesh type. Subsequently, the adaptively sized mesh was generated based on local curvature variations. Finally, the angle skewness was employed as an objective function to improve the mesh quality. In addition, considering the actual ship model as an example, the mesh generated by our method and conventional Laplacian smoothing method were used to perform first-order potential flow simulations, and the results were compared against the convergence values. The results indicated that our method has lower root mean square errors in computing the total non-viscous force, steady drift force and ship hull free floating Response Amplitude Operator. This method is applicable to numerical simulations of the ship potential flow, providing high-quality hull meshes for hydrodynamic analysis.

1. Introduction

Mesh generation is a critical preprocessing step in Computational Fluid Dynamics (CFD) analysis. High-quality hull surface mesh is the key to accurately solving ship hydrodynamic problems because it can better characterize the ship’s geometric shape.

Based on the topology of mesh elements, ship hull surface mesh generation methods can be classified into three categories: structured meshing, unstructured meshing, and hybrid meshing. Each method has its own advantages and limitations.

The common structured surface mesh generation method is the mapping method [1]. In essence, it involves the projection of a three-dimensional (3D) surface to a two-dimensional (2D) parameter domain, mesh generation in the parameter domain, and back-projection to obtain the 3D surface mesh results [2]. For the processing of complex surfaces, such as high curvature surfaces with inflection points, or containing degenerate boundaries, mapping methods are classified into mapping element method [3,4,5] and conformal mapping method [6,7]. The mapping element method decomposes a complex surface into simpler subdomains that are easier to parameterize; however, this decomposition typically depends on the researchers’ manual expertise. In contrast, the conformal mapping method does not require explicit geometric decomposition; however, it is difficult to control the mesh shape and density, which restricts its practical applicability. Given the pervasive use of Non-Uniform Rational B-Spline (NURBS) for surface modeling, the mapping method based on NURBS interpolation is a focal research area in structured mesh generation [8,9,10] and has also been extensively adopted in the ship engineering field [11,12,13]. In general, the topological relationship of the structured surface mesh is relatively simple, all mesh nodes are regularly arranged, showing a strict topological structure and orthogonality. Thus, structured surface mesh generation methods are highly efficient. However, the connection method between structured surface mesh elements is not sufficiently flexible, which limits the adaptability of the structured mesh to complex surfaces, such as the bow and stern of a ship.

Common unstructured surface mesh generation methods include the Delaunay triangulation method [14,15,16] and the advancing front method [17,18,19,20,21]. The Delaunay triangulation method distributes points across the geometric domain and constructs triangle elements by enforcing the empty circumcircle criterion and the maximum and max-min angle criterion. However, this method cannot generate high-quality mesh elements when the geometry is a non-convex 3D surface [22,23]. The advancing front method begins by discretizing the domain boundary, then sequentially inserting mesh nodes into the interior, generating new mesh elements, and advancing the front until the entire domain is covered. The advancing front method exhibits strong adaptability to complex geometric boundaries and is capable of generating high-quality mesh elements, making it widely used in various engineering applications. However, owing to the extensive logical decisions and computational overhead involved, its efficiency declines significantly when processing large-scale mesh elements [24].

Among them, the structured surface mesh has high generation efficiency. However, it lacks adaptability to complex surfaces. The unstructured surface mesh can accurately represent the hull surface. However, its mesh generation efficiency is relatively low. If it wants to achieve the same calculation accuracy as the structured surface mesh, it requires many more mesh elements than the structured surface mesh generation method. In the practical application of the ship engineering field, the hybrid mesh is a mesh configuration that combines structured mesh and unstructured mesh, and it has the advantages of the two types of mesh mentioned above [25]. It has high calculation accuracy and generation efficiency. The unstructured mesh can conveniently adjust the size and shape of mesh elements. It can better express surface details. By improving the fitting accuracy of positions that have significant influences on potential flow calculation, such as the ship bow position on the wave-facing side, the unstructured mesh can improve the accuracy of potential flow calculation. On the other hand, most areas of the ship, such as the midship, have simple curvature changes. The approximation degree of the structured mesh and the unstructured mesh to the ship surface is similar. The difference between the normal vectors of the two types of mesh and the surface normal vector is also small. Therefore, in terms of calculation accuracy, compared with the calculation accuracy of generating the unstructured mesh for the entire ship, there is no significant difference in the calculation accuracy of the hybrid mesh. This hybrid mesh is composed of the unstructured mesh generated at the ship bow and ship stern and the structured mesh generated at the midship. In terms of mesh generation efficiency, the structural mesh is significantly more efficient than the unstructured mesh. Placing a large number of structured mesh elements at the midship can effectively improve the mesh generation efficiency.

In practical applications, the initial mesh generated by mesh algorithms often fails to satisfy the quality requirements for engineering analyses. Therefore, mesh optimization is necessary. The common mesh optimization method is the mesh averaging method based on Laplacian smoothing [26]. This method improves the mesh quality by enhancing the uniformity of local elements and iteratively adjusting mesh nodes until all mesh elements meet the predefined quality thresholds. However, conventional Laplacian smoothing does not guarantee optimal mesh quality. It may even lead to element inversion, particularly when applied to regions containing concave polygons [27,28]. To address these issues, many improvement methods have been proposed [29,30,31,32].

In summary, single-type meshes cannot satisfy the requirements of ship hydrodynamic analysis, existing mesh generation algorithms lack adaptability to hull surface features, and manual iterative mesh optimization is time-consuming and laborious. To address these issues, this paper extends the traditional NURBS surface interpolation and advancing front algorithm by integrating a ship hull partitioning scheme, a corner segmentation method for the advancing front, and a surface curvature-driven size correction algorithm. Furthermore, mesh quality evaluation parameters tailored to potential flow calculations are established, forming a hybrid mesh generation and optimization method suitable for ship hydrodynamic evaluation.

The main structure of this paper is as follows: Section 2 introduces the principle of improved ship hull surface hybrid mesh generation and optimization method. Section 3 takes the actual ship type as an example to verify the feasibility and effectiveness of the proposed method. Finally, Section 4 summarizes the full paper and provides conclusions.

2. Structured–Unstructured Hybrid Mesh Generation Method Based on Ship Surface Curvature Features

2.1. The Ship Hull Surface Partition Criterion Based on Surface Curvature Features

The hull surface consists of multiple regions with regular and irregular geometries [33]. To tackle the difficulty in meshing due to irregular regions, instead of generating high-quality mesh elements directly, the surface is first partitioned into subregions, each meshed independently, and then combined to form a complete hybrid mesh of the hull surface. In line with this idea, the structured mesh strategy is adopted in the midship and the ship bilge position, where the curvature change is relatively small. At the same time, in the ship stern and ship bow, the unstructured meshing is more suitable because of its geometric and topological flexibility. According to the specific ship surface features, the ship bow surface and the ship stern surface are further divided. These surfaces are partitioned by judging the inflection points and edges, ensuring that each partition only contains up to four smooth and non-bending boundary curves.

As shown in Figure 1, the ship hull surface can be first divided into three regions: the ship bow, the midship, and the ship stern. According to the judgment criterion of inflection points and edges, the ship stern can be further divided into region 3 and region 4. Among them, the partition boundaries of the ship bow, the midship, and the ship stern need to be segmented based on the surface curvature features of the actual ship type. The judgment method of partition boundaries can be described as follows.

The numbers 1, 2, 3 and 4 marked in Figure 1 are the regions $1\sim 4$ described in the above method, while the numbers 5 and 6 are new regions divided based on the inflection points and edges of the hull surface, namely the stern plate region and stern shaft region.

Firstly, the ship hull surface model is discretized into a 3D point cloud form. Any point on the surface has an infinite number of normal curvatures, where exists a curve whose curvature is maximized, this curvature is the maximum normal curvature $k_1$, and the curvature perpendicular to the maximum curvature surface is the minimum normal curvature $k_2$. These two curvatures are called the principal curvatures; they represent the two extreme values of the normal curvatures.

For the surface $r=r(u,v)$, the principal curvatures can be satisfied as follows:

$$\left\{\begin{array}{c}{k}_1·k_2={\displaystyle \frac{LN-M^2}{EG-F^2}}\\ k_1+k_2={\displaystyle \frac{LG-2MF+NE}{EG-F^2}}\end{array}\right.$$

(1)

where E, F, and G represent the coefficients of the first fundamental form; L, M, and N represent the coefficients of the second fundamental form. They can be represented as follows:

$$\left\{\begin{array}{c}E=r_u·r_u\hfill \\ F=r_u·r_v\hfill \\ G=r_v·r_v\hfill \\ L=-r_u·n_u\hfill \\ M=-r_u·n_v\hfill \\ N=-r_v·n_v\hfill \end{array}\right.$$

(2)

where n represents the unit normal vector of r. It can be represented as follows:

$$n={\displaystyle \frac{r_u\wedge r_v}{\left|r_u\wedge r_v\right|}}$$

(3)

Based on these two principal curvatures, the Gauss curvature and mean curvature of this point can be calculated.

The Gauss curvature can be calculated as follows:

$$K=k_1·k_2$$

(4)

The mean curvature can be calculated as follows:

$$H=\left(\begin{array}{c}{k}_1+k_2\end{array}\right)/2$$

(5)

Comparing the changes of Gauss curvature and mean curvature at various positions on the entire ship, the section with gentle curvature changes is divided into the midship partition, the sections with significant curvature changes are divided into the ship bow and ship stern partitions.

2.2. The Structured Surface Mesh Generation Method and Improvement Based on NURBS Surface Interpolation Mapping

The mapping method [34] is the main method for structured surface mesh generation in CFD analysis. The existing mapping method is difficult to handle NURBS surfaces with trimming and parameterization problems. It also cannot reflect the impact of surface curvature changes on mesh quality.

Therefore, this paper proposes an improvement method. Firstly, the geometric preprocessing is performed on each partition surface of the ship hull to obtain a high-quality ship hull model. For any partition surface, by constructing multiple implicit planes (assuming the number of implicit planes is m) and calculating the intersection points between each implicit plane and the partition surface, m transverse section lines can be generated. Based on the NURBS curve interpolation algorithm, an equal number of discrete points (assuming the number of discrete points is n) can be obtained on each transverse section line, thereby forming a regular topological point cloud with m rows and n columns. Subsequently, based on the NURBS surface interpolation algorithm, this partition surface can be reconstructed. The detailed steps of the intersection algorithm can be referred to in reference [35], and the detailed steps of the NURBS interpolation algorithm can be referred to in reference [36]. This preprocessing can eliminate the trimmed surfaces and problem surfaces in the original ship hull model and construct high-quality NURBS partition surfaces.

Next, the structured mesh generation is performed on the partition surface of the midship that has completed geometric preprocessing. The main process of mesh generation can be described as follows.

(1) Constructing the mapping parameter domain based on the NURBS surface.

By constructing the mapping parameter domain and mapping relationship of the NURBS surface, the space surface can be mapped to the parameter plane. The NURBS surface is a standard expression of current surface modeling technology. Its surface information can be provided through its surface control points, weight factors, and degrees. The coordinates of different positions on the surface can be obtained based on the node vectors in parameter direction u and parameter direction v. The expression of the NURBS surface with degree $p\times q$ is as follows:

$$p(u,v)={\displaystyle \frac{{\displaystyle {\sum }_{i=0}^m}{\displaystyle {\sum }_{j=0}^n}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right){\omega }_{ij}{P}_{ij}}{{\displaystyle {\sum }_{i=0}^m}{\displaystyle {\sum }_{j=0}^n}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right){\omega }_{ij}}}$$

(6)

where $P_{ij}\left(i=0,1,\dots ,m;j=0,1,\dots ,n\right)$ represent the surface control points, which are used to form a rectangular topology array called the control grid; ${\omega }_{\ddot{\eta }}\left(i=0,1,\dots ,m;j=0,1,\dots ,n\right)$ represent the weight factors, which correspond to surface control points separately; $N_{i,p}\left(u\right)$ and $N_{i,q}\left(\nu \right)$ are the B-spline basis functions with degree p, q, which can be defined by the recursive formula, as follows:

$$\left\{\begin{array}{cc}& N_{i,0}\left(u\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{u}_i\le u\le u_{i+1}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \\ & N_{i,k}\left(u\right)={\displaystyle \frac{u-u_i}{u_{i+k}-u_i}}{N}_{i,k-1}\left(u\right)+{\displaystyle \frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}}{N}_{i,k-1}\left(u\right),k\ge 1\hfill \\ & 0/0=0\hfill \end{array}\right.$$

(7)

where k is the degree; $u_i\left(\begin{array}{c}i=0,1,\dots ,m\end{array}\right)$ are the knots, which form the knot vector $U=\left\{\begin{array}{c}{u}_0,u_1,u_2,u_3,u_4,\cdots ,u_{n+k+1}\end{array}\right\}$. Clamped knot vector whose beginning and ending knot values are repeated with multiplicity equal to $k+1$ is usually used, which can make the generated NURBS surface pass through the control polygon and tangents to both ends of the control polygon.

In the standard NURBS surface, the value range of the node vectors U and V is $[0,1]$. And any mesh node on the space surface can correspond to a unique node vector. Therefore, the node vectors U and V can be used as parameter domain coordinates, and a unit-length parameter plane can be constructed as the mapping parameter domain. Based on the NURBS surface expression method, the coordinate conversion between the space surface and the mapping parameter domain can be achieved.

(2) Generating the structured surface mesh based on the mapping parameter domain.

Based on the required number of structured mesh in two dimensions, the node vectors in direction u and direction v of mapping parameter domain are uniformly divided. The positions and topological information of mesh nodes on the mapping plane are obtained. The node coordinate values in row i and column j of the mapping plane mesh topology can be represented as follows:

$$p_{i,j}=\left({\displaystyle \frac{{\displaystyle {\sum }_{k=1}^{i-1}}{\omega }_{k,j}}{{\displaystyle {\sum }_{k=1}^{m-1}}{\omega }_{k,j}}},{\displaystyle \frac{{\displaystyle {\sum }_{l=1}^{j-1}}{\omega }_{i,l}}{{\displaystyle {\sum }_{l=1}^{n-1}}{\omega }_{i,l}}}\right),i=1,2,\dots ,m;j=1,2,\dots ,n$$

(8)

where $\omega$ represents the weight factor of the control point closest to the surface target point, its value range is $[0,1]$; m and n, respectively, represent the number of rows and columns that generate mesh nodes along the direction u and direction v.

In the ship engineering field, the weight factors of all control points on the NURBS surface are usually set to 1, and Equation (8) can be simplified as follows:

$$p_{i,j}=\left({\displaystyle \frac{i-1}{m-1}},{\displaystyle \frac{j-1}{n-1}}\right),i=1,2,\dots ,m;j=1,2,\dots ,n$$

(9)

However, the mesh generated based on the above method cannot accurately represent the hull shape of the location where surface curvature changes significantly. Therefore, our method incorporates a mesh node position optimization algorithm based on surface curvature features, in order to further enhance the mesh quality.

Without changing the topology and number of mesh elements, our method adjusts the parameter domain coordinates of each mesh node on the partition surface boundary based on its curvature and then obtains the parameter domain coordinates of each mesh node inside the partition surface based on the linear interpolation algorithm.

According to Equation (9), the coordinate values of the four boundaries ($u=0$; $u=1$; $v=0$; $v=1$) in the mapping parameter domain can be obtained. Taking the boundary $v=0$ as an example, j is set to 1 at this time. When the weight factors of all control points on the NURBS surface are equal and uniformly discrete, the parameter domain coordinate values of discrete point i on this boundary can be represented as follows:

$$p_{i,1}=\left({\displaystyle \frac{i-1}{m-1}},0\right),i=1,2,\dots ,m$$

(10)

The distance between two adjacent points on this boundary can be represented as follows:

$$\Delta u_{initial}={\displaystyle \frac{1}{m-1}}$$

(11)

Since the boundary NURBS curve expression of the partition surface is known, the coordinate value and curvature of any point on the curve can be obtained. Assuming there is a point i on the boundary with a corresponding curvature $k_i$, the distance between point i and point $i-1$ can be adjusted using the following method.

The distance calculation function that includes curvature features needs to satisfy the following conditions:

(1)

The relationship between curvature and distance should be represented using the non-piecewise function, ensuring the smooth transition for distance adjustment;

(2)

The curve formed by the function should be smooth at both ends and nearly linear in the middle;

(3)

The function should have upper and lower limits to avoid generating excessively large or small mesh elements;

(4)

Since the minimum curvature value is 0, and the maximum curvature value can approach infinity. When using the average curvature to measure the curvature feature, it should be ensured that the curvature transition is smoother when the curvature increases than when it decreases.

To satisfy the above conditions, a combination of exponential function and inverse trigonometric function is used to obtain the objective curve. The distance between two adjacent points in the parameter domain based on curvature features can be represented as follows:

$$\Delta u_i=\Delta u_{initial}\times 2^{{\displaystyle \frac{1}{\pi }}\arctan \left({\displaystyle \frac{\overline{k}-k_i}{\overline{k}}}\right)}$$

(12)

where $\overline{k}$ represents the average curvature of this boundary NURBS curve; $k_i$ represents the curvature of the point i; $\Delta u_{initial}$ represents the initial distance between point i and point $i-1$, which has been given by Equation (11); $\Delta u_i$ represents the adjusted distance between point i and point $i-1$.

According to Equation (12), when $k_i$ is equal to the average curvature $\overline{k}$, $\Delta u_i$ is equal to $\Delta u_{initial}$, indicating that the mesh size remains unchanged. When $k_i$ is less than $\overline{k}$, $\Delta u_i$ increases gradually with the decrease in $k_i$, which means that the curvature decreases, the geometric complexity reduces, and the mesh size increases accordingly. When $k_i$ is greater than $\overline{k}$, $\Delta u_i$ decreases gradually with the increase in $k_i$, which means that the curvature increases, the geometric complexity rises, and the mesh is refined progressively to satisfy the requirement of geometric adaptability.

The minimum value of curvature $k_i$ is 0, and its maximum value can approach infinity. Even in the extreme case, the value range of $\Delta u_i/\Delta u_{initial}$ is approximately between 0.707 and 1.189, which means that through mesh size adjustment, there will not be a huge multiple difference between the maximum mesh size and minimum mesh size, thereby affecting the mesh quality.

Based on the above method, the parameter domain coordinates of all discrete points on this boundary can be calculated iteratively. However, due to the adjustment of the distance between adjacent points (the distance is no longer $\Delta u_{initial}$ but adjusted to $\Delta u_i$), the number of newly generated points on this boundary may be inconsistent with the number of initial points.

If the number of newly generated points is greater than the number of initial points, which means that $\Delta u_i$ is too small, $\Delta u_{initial}$ should be adjusted as follows:

$$\Delta u_{initial}=1.5\times \Delta u_{initial}$$

(13)

If the number of newly generated points is less than the number of initial points, which means that $\Delta u_i$ is too large, $\Delta u_{initial}$ should be adjusted as follows:

$$\Delta u_{initial}=0.75\times \Delta u_{initial}$$

(14)

According to the above strategy, the iterative calculation is performed, $\Delta u_{initial}$ is adjusted and $\Delta u_i$ is recalculated until the number of newly generated points is consistent with the number of initial points.

Based on the above method, the parameter domain coordinates of all discrete points on the four boundaries of the partition surface can be calculated. Then, based on the interpolation algorithm, the parameter domain coordinates of each mesh node inside the partition surface can be calculated.

Assuming two boundaries in direction u ($u=0$; $u=1$), the parameter domain node coordinates of the discrete points in row i are $(0,v_1)$ and $(1,v_2)$, and the line obtained by connecting these two points is $A_1$; there are two boundaries in direction v ($v=0$; $v=1$), and the parameter domain node coordinates of the discrete points in column j are $(u_1,0)$ and $(u_2,1)$. The line obtained by connecting these two points is $A_2$. The node in row i and column j of the mapping plane mesh topology are the intersection point of lines $A_1$ and $A_2$.

Based on the above method, the structured mesh on the mapping parameter plane can be generated, and corresponding node coordinates and mesh topology information can be obtained.

(3) The reverse mapping of mesh nodes in the parameter domain.

The mesh nodes generated in the parameter domain are reverse mapped to 3D space, and the structured mesh of the actual 3D space surface can be generated. Since the point coordinates in the mapping parameter domain represent the knot vectors along U and V dimensions of the NURBS surface, these point coordinates can be input into Equation (7) to calculate the mesh node basis functions $N_{i,p}\left(u\right)$ and $N_{j,q}\left(v\right)$ at these positions. Then, the basis functions can be input into Equation (6), and the coordinate values of the mesh node on the space surface can be obtained.

Since the structured surface mesh generation is based on the ship hull NURBS surface, its mesh nodes strictly adhere to being located on the ship hull surface, the error between the mesh and the actual ship type is equal to the modeling error. Based on the above method, high-quality structured mesh node coordinates can be obtained. By arranging these nodes according to the quadrilateral mesh topology, the ship hull structured surface mesh can be obtained.

2.3. The Unstructured Surface Mesh Generation Method and Improvement Based on Advancing Front Technique

The advancing front method is the common method for unstructured surface mesh generation in CFD analysis. By combining the mapping relationship between the parameter domain and the space surface in the mapping method, the parameter surface is used to calculate the mesh node coordinates, which improves the mesh generation efficiency, and generates high-quality mesh elements [37]. However, due to the non-uniformity of metric mapping between the surface and the parameter plane, it is nearly impossible to accurately describe the distortion of element metric mapping. As a result, the quality of meshes mapped onto the 3D surface cannot be fully guaranteed. Meanwhile, the mesh quality on the parameter plane may deteriorate severely, making it impossible to apply conventional 2D advancing front mesh generation method.

Therefore, this paper proposes the advancing front corner segmentation strategy, according to the size of the angle formed by adjacent fronts, the angle is divided and an unequal number of mesh units is generated, which enhances the controllability and stability of the algorithm. Additionally, this paper optimizes the method based on surface curvature features to ensure that the mesh can accurately reflect the geometric shape of the hull. The influence of surface curvature features is mainly reflected in the following two aspects: the generation of the initial advancing front and the determination of the advancing step length. Its mesh generation process can be described as follows.

(1) Constructing the parameter surface.

Before generating the unstructured mesh of the surface, it is necessary to construct its corresponding parameter surface. In this paper, the parameter surface is the 2D parameter domain, which is composed of node vectors in direction u and direction v of the NURBS surface parameter domain. Therefore, the method of constructing the parameter surface in the unstructured mesh generation is exactly the same as the method of constructing NURBS surface mapping parameter domain in the structured mesh generation. The detail steps can be referred to in Section 2.2, which will not be repeated here.

(2) Constructing the initial advancing front based on the surface curvature feature.

The initial advancing front is the foundation for generating mesh using the advancing front method. It represents discrete points connected in a certain order on the surface boundary. Therefore, from the geometric perspective, this step is also referred to as the discretization of surface boundary points. During construction of the initial front, in order to ensure that the generated mesh element approximates the shape of the equilateral triangle as much as possible, the traditional advancing front method needs to satisfy the approximate equal distance between any two adjacent nodes. Since the parameter surface constructed based on the NURBS surface parameter domain is a unit-length square, the length of each edge along the parameter surface boundary is equal. However, the length of each side along the actual space surface is unequal. To ensure equal distance between adjacent discrete points after the discretization of boundary points, the values of adjacent nodes on each side in the parameter domain can be represented as follows:

$$\Delta u_m={\displaystyle \frac{{\displaystyle {\sum }_{m=1}^4}{L}_m}{N{L}_m-{\displaystyle {\sum }_{m=1}^4}{L}_i}},m=1,2,3,4$$

(15)

where $\Delta u_m$ represents the distance between any two adjacent discrete points on edge m of the surface in the parameter domain, $L_m$ represents the length of edge m on the surface, N represents the total number of discrete points on the surface boundary.

Then, the distance between two adjacent nodes at the initial advancing front can be adjusted based on its curvature. The distance adjustment method is the same as the adjustment method for boundary discrete points in the structured mesh generation method. The distance between point i and point $i-1$ on edge m of the surface in the parameter domain can be represented as follows:

$$\Delta u_i=\Delta u_m\times 2^{{\displaystyle \frac{1}{\pi }}\arctan \left({\displaystyle \frac{\overline{k}-k_i}{\overline{k}}}\right)}$$

(16)

The detailed calculation and iteration steps can be referred to in Section 2.2, which will not be repeated here.

(3) Determining the advancing direction based on the advancing front corner segmentation strategy.

The conventional advancing front method does not always yield ideal results in surface triangulation. The cause lies in the fact that corner points on the surface cannot always be divided into two triangles. In an ideal scenario, when the included angle between two 3D curves at a corner point is ${120}^{\circ }$, the conventional method can achieve good results. 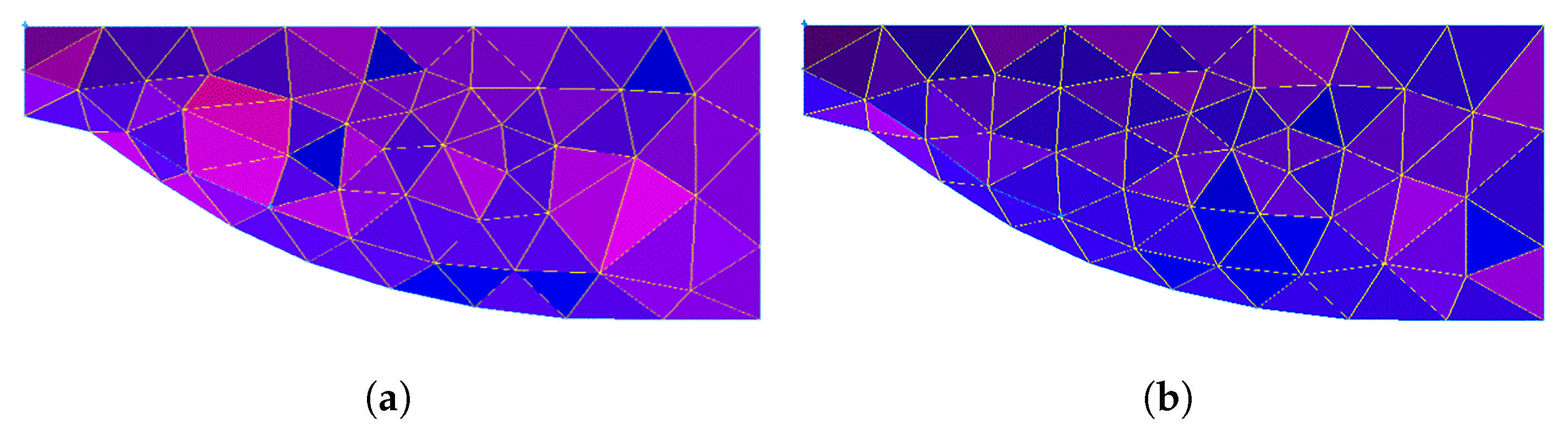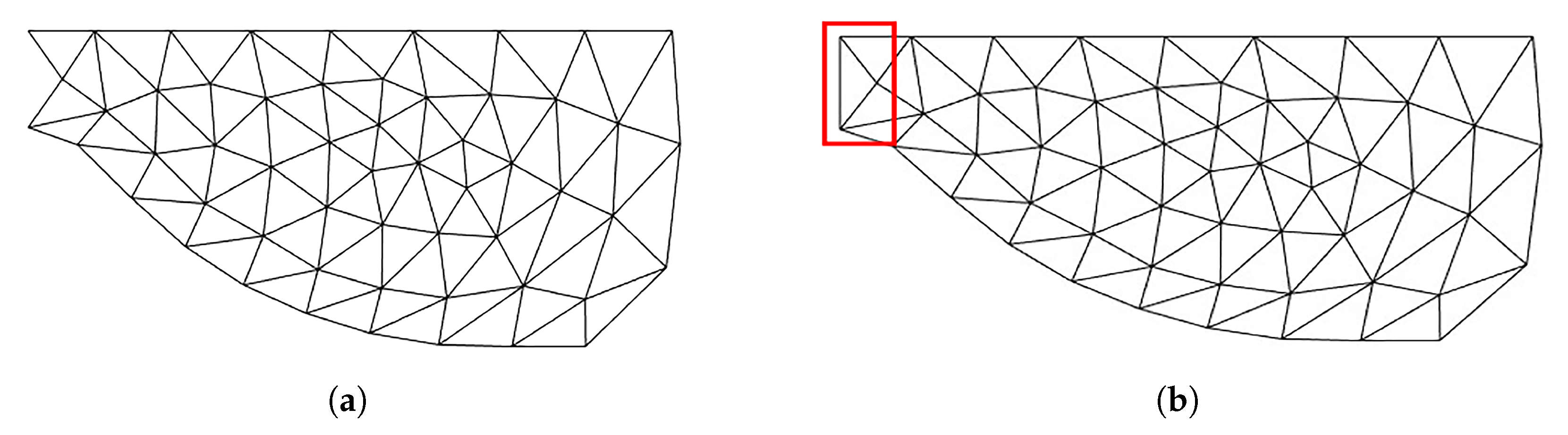However, when the included angle $\alpha$ between the two curves at the corner point deviates significantly from ${120}^{\circ }$, this method is bound to cause intersections of the two triangles at the corner point in the parametric plane (when $\alpha <{120}^{\circ }$) or generate cracks (when $\alpha >{120}^{\circ }$), as shown in Figure 2. To ensure the continuation of the triangulation process, it is necessary to perform compromise processing on the meshes at the intersecting or cracked areas. This compromise will reduce the mesh quality at these locations, deteriorate the advancement results of the next front, and accumulate errors gradually during the progressive advancement.

In many commercial software, such as Pointwise, Gambit, and ANSYS Fluent, there are already solutions for these problems. These software have designed their own mesh element detection methods, which can check the mesh element validity, determine whether the mesh nodes of the newly generated mesh element fall in a reasonable area. If an incorrect mesh element is generated, it will be deleted and a new element will be generated to avoid mesh intersection or crack.

However, the specific principles for solving these problems in these commercial software cannot be found in their public materials. In order to reduce the losses caused by such problems, this paper proposes the advancing front corner segmentation strategy, according to the size of the angle formed by adjacent fronts, the angle is divided and an unequal number of mesh units is generated.

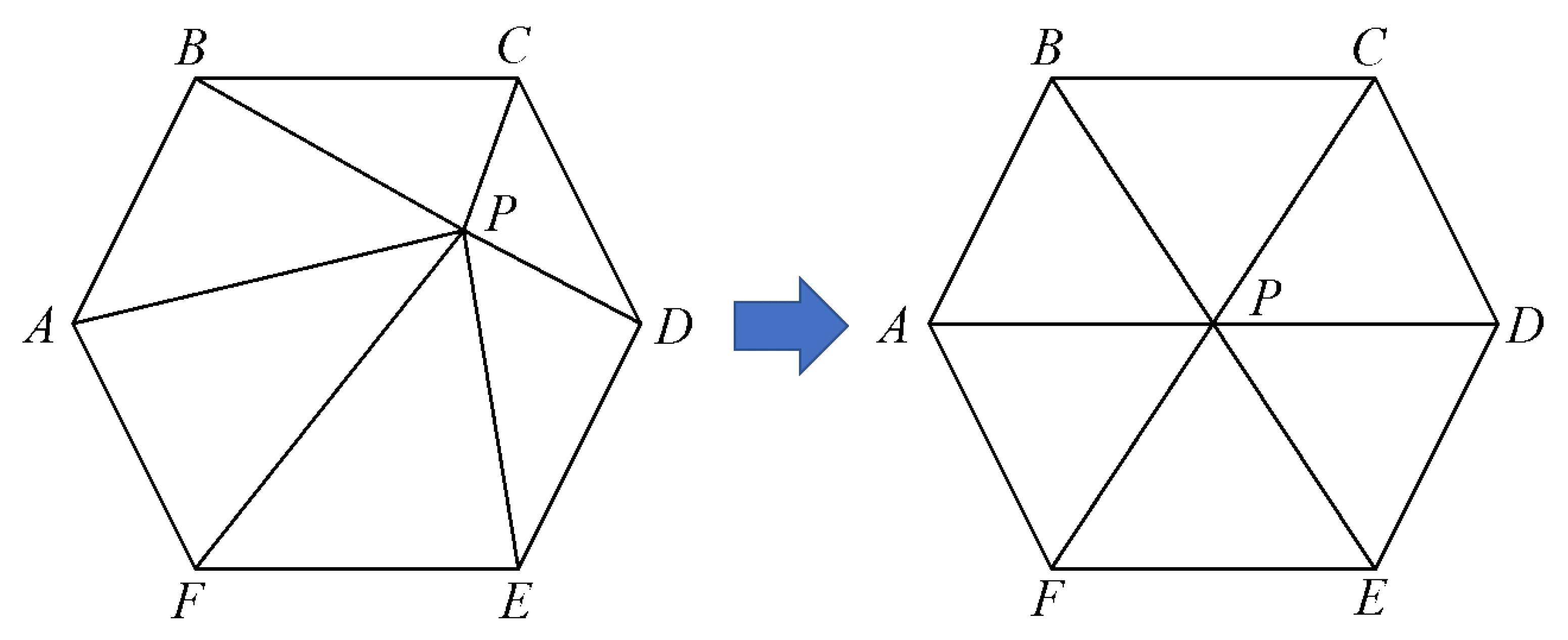
Firstly, the front to be advanced should be determined. Among all front nodes, an angle $\alpha$ is formed by three adjacent front nodes. Each iteration selects the smallest angle in the front for judgment. If $\alpha ⩽{80}^{\circ }$, only one triangle is formed at this corner point; if ${80}^{\circ }<\alpha ⩽{140}^{\circ }$, two triangular elements are formed; if ${140}^{\circ }<\alpha ⩽{180}^{\circ }$, three triangular elements are formed.

As shown in Figure 3, if the angle ${\theta }_{ABC}⩽{80}^{\circ }$, point A and point C are directly connected to form a triangular mesh element. Otherwise, the angle needs to be divided into two or three equal angles, and the shorter edge can be selected to form a new triangular mesh element by generating a new mesh node D.

The red dash line in Figure 3 represents the new topological connection line of the mesh nodes, and the triangle identified by this line is the newly generated triangular mesh element.

(4) Determining the advancing step length based on the surface curvature feature.

As shown in Figure 3, to ensure the quality of the triangular mesh element generated after advancement, the advancing step length $d_{BD}$ is set to be equal to the length $d_{AB}$ of the front edge to be advanced.

Then, the curvature correction parameter can be introduced to adjust the advancing step length $d_{BD}$. Assuming the mapping point of point D on the curve segment $\stackrel{⏜}{AB}$ is M, the mean curvature of the point M is $k_M$, the mean curvature of the point D is $k_D$, the ratio of advancing step lengths of these two positions can be represented as the curvature correction parameter K. By substituting them into Equation (16), it can be represented as follows:

$$K={\displaystyle \frac{\Delta u_D}{\Delta u_M}}={\displaystyle \frac{2^{\frac{1}{\pi }\arctan \left(\frac{\overline{k}-k_D}{\overline{k}}\right)}}{2^{\frac{1}{\pi }\arctan \left(\frac{\overline{k}-k_M}{\overline{k}}\right)}}}$$

(17)

where $\overline{k}$ represents the mean curvature of this partition surface.

By replacing the initial advancing step length $d_{BD}$ with $K{d}_{BD}$, the corrected advancing step length based on curvature features can be obtained. According to Equation (17), compared with the advancing front, when the curvature of node D increases, $\Delta U_D$ decreases, the curvature correction parameter K is less than 1, indicating that the geometric complexity rises and a smaller mesh element is required, resulting in a decrease in the advancing step length; on the contrary, when the curvature of node D decreases, $\Delta U_D$ increases, the curvature correction parameter K is greater than 1, indicating the geometric shape is relatively flat, the advancing step length can be correspondingly increased.

(5) Calculating the mesh nodes based on the parameter surface.

Assuming that two adjacent points on the front are A and B, respectively, the corresponding coordinates of these two points on the parameter surface are a and b, the distance between the target mesh node D and the existing node B is $d_{BD}$, the angle with B as the vertex angle is ${\theta }_{ABD}$. Based on the method described above, the size of angle ${\theta }_{ABD}$ can be determined through the advancing front corner segmentation strategy; the length of distance $d_{BD}$ can be determined through the corrected advancing step length. When ${\theta }_{ABD}$ and $d_{BD}$ are known, the node on the surface has a unique solution.

Firstly, the actual coordinate of the mapping point M of D on the curve segment $\stackrel{⏜}{AB}$ can be calculated. Since $d_{BD}$ and ${\theta }_{ABD}$ are known, the actual coordinate of M can be directly calculated based on the sine theorem. The corresponding point of M on the parameter surface is m, the parameter domain coordinate of m can be calculated based on the linear interpolation algorithm.

Subsequently, the parameter domain coordinate of D can be calculated. Assuming that $X_L$ represents the direction vector of the curve segment $\stackrel{⏜}{AB}$, $Y_L$ represents the unit normal vector at point M; then, the unit advancing vector of the surface at point M, also known as the direction vector of the curve segment $\stackrel{⏜}{MD}$, can be represented as follows:

$$Z_L=X_L\times Y_L$$

(18)

Since the non-overlapping of the two dimensions in the parameter surface, along the parameter direction u and parameter direction v, the partial derivatives of any surface point can be obtained, and the vector product of these two derivatives is not 0. Therefore, for point D and point M, the following equation can be satisfied:

$$\left\{\begin{array}{c}\Delta u({\displaystyle \frac{\partial M}{\partial u}}·X_L)+\Delta v({\displaystyle \frac{\partial M}{\partial v}}·X_L)=0\hfill \\ \\ \Delta u({\displaystyle \frac{\partial M}{\partial u}}·Z_L)+\Delta v({\displaystyle \frac{\partial M}{\partial v}}·Z_L)=d_{MD}\hfill \end{array}\right.$$

(19)

where $\Delta u$ and $\Delta v$, respectively, represent the increments of the coordinate d relative to the coordinate m in the parameter direction u and parameter direction v, d is the corresponding point of D on the parameter surface; $d_{MD}$ represents the distance between the actual coordinates of point M and point D.

The corresponding parameter increments $\Delta u$ and $\Delta v$ can be obtained by solving Equation (19). The position of d on the parameter surface can be represented as follows:

$$\left\{\begin{array}{c}{u}_d=u_m+\Delta u\hfill \\ v_d=v_m+\Delta v\hfill \end{array}\right.$$

(20)

The principle of calculating a new mesh node based on the parameter surface mentioned above can be shown in Figure 4.

After calculating the coordinate of the target node in the parameter domain, it is reverse mapped to 3D space, the corresponding coordinate of the target node on the space surface can be calculated.

(6) Detecting and adjusting the intersecting mesh nodes.

Since the advancing front method only generates one new mesh element at a time, when using this method to advance the mesh, the following situations will always occur: the generated new mesh element overlaps with other existing mesh elements, or the remaining space after advancing the mesh front is difficult to continue generating high-quality mesh elements. The above situations will seriously affect the mesh quality, and even prevent the completion of the mesh generation process.

Based on the method of constructing the detection point, the intersecting mesh detection can be completed. The coordinate of detection point e in the parameter domain can be calculated by using 1.5 times the length of $\Delta u$ and $\Delta v$ as increments. Then the line between a and e, and the line between b and e in the parameter domain can be constructed. By detecting whether these two lines intersect with the lines between other adjacent points on the front, it can be determined whether the intersecting mesh node needs to be adjusted.

For the mesh node that needs to be adjusted, the distance between all nodes on the advancing front and the target mesh node D should be calculated, and D will be moved to the position of the node closest to it, which can avoid the mesh overlapping.

(7) Determining the termination criterion of advancing front method.

In theory, the advancing front method can continuously generate mesh elements until the advancing front does not include any mesh node. However, if the number of mesh nodes on the front is small, continuing to advance may result in low-quality grids due to algorithmic reasons, continuing to advance the mesh front may result in low-quality mesh elements. It is necessary to handle certain specific situations, which can ensure the mesh elements near the center of the surface advancing front have high quality.

When the number of mesh nodes in the convex polygon formed by the advancing front is less than 7, it enters the termination stage of the advancing front algorithm. For the regular hexagon, generating a new node at its centroid position can ensure that all generated mesh elements are equilateral triangles, which means that the mesh elements achieve the theoretically optimal quality. Based on the above description, it is apparent that when the number of mesh nodes is less than 7, only an additional new mesh node needs to be generated, which can meet the requirements of high-quality mesh elements.

Based on the above method, the unstructured mesh can be generated.

2.4. The Surface Mesh Optimization Strategy Based on Mesh Quality Evaluation Parameters

The mesh quality evaluation parameters are the quantitative criteria for measuring mesh quality. The averaging optimization method based on Laplacian smoothing [38] cannot directly improve mesh quality, it requires multiple algorithm iterations to satisfy mesh quality. The mesh node optimization method based on the optimization principle [30] can use mesh quality evaluation parameters as the objective functions to optimize the mesh, which makes the mesh optimization objectives clearer. The specific steps can be described as follows.

(1) Constructing the mesh optimization objective function.

The mesh quality is the criterion for measuring whether the geometric shape and smoothness of the mesh can satisfy the calculation requirements. There are numerous types of mesh quality evaluation parameters, and different software and research often verify mesh quality based on multiple mesh quality evaluation parameters, all of them have different verification criteria. In response to this situation, it is necessary to impose certain limitations on the selection of the objective function during the mesh optimization process.

During the mesh optimization process, the selection of the objective function has the following requirements:

(1)

In the parameter domain, the objective function is a continuous unimodal function, and for any position within the solution domain, there is a unique function value corresponding to this position.

(2)

The objective function that needs to calculate the average value should theoretically have upper and lower limits on the function value, which can avoid individual results with excessively large or small function values affecting the average value; the objective function that needs to calculate the ratio should avoid the range of function values that include 0, or special processing should be applied to results containing 0.

(3)

Since the mesh optimization algorithm can only optimize a single mesh node during each processing, the objective function should ensure that it can reflect the geometric quality of the grid element. The global mesh quality evaluation parameters, such as mesh regularity, cannot be used as the objective functions in the optimization process.

(4)

To ensure the efficiency of mesh optimization, the selected objective function should be as convenient as possible for calculation.

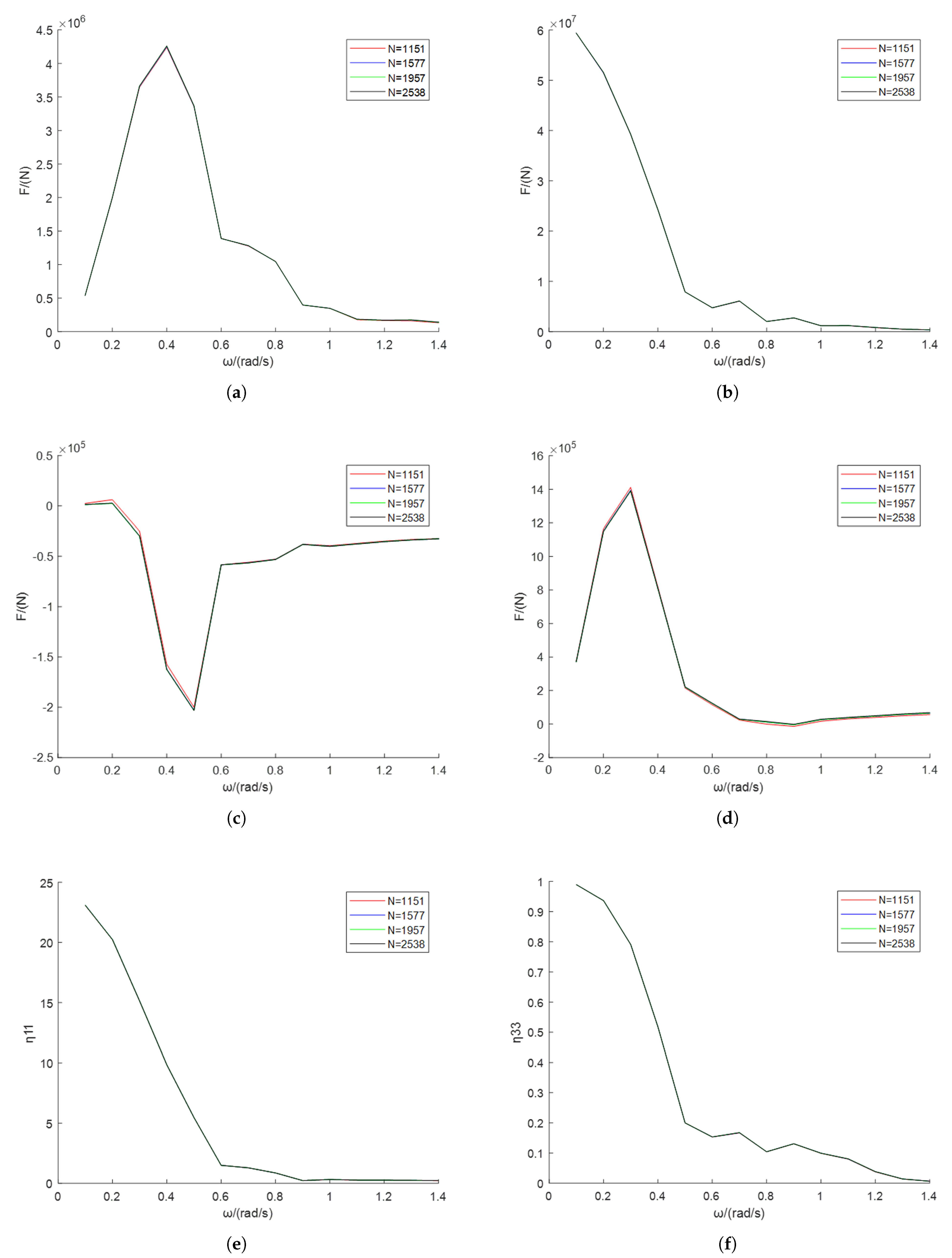
To satisfy the above requirements, some mesh quality evaluation parameters that are common and easy to calculate can be selected, such as angle skewness, aspect ratio, size change. Then these parameters should be normalized. The normalized processing converts these parameter values to values between the interval of $[0,1]$. This paper selects the angle skewness as the objective function for mesh optimization. As the mesh quality improves, the mesh angle skewness will gradually decrease.

(2) Determining the low-quality mesh elements and calculating the optimized mesh node coordinates based on the threshold of the objective function.

When using a certain normalized mesh quality evaluation parameter, we assume that its mesh optimization threshold is $Q_a$. Based on this mesh quality evaluation parameter, all mesh elements on the ship hull can be calculated to verify the mesh quality, and the mesh elements with mesh quality evaluation parameters below threshold $Q_a$ can be selected.

Then, by moving the mesh node to be optimized, the quality of the mesh composed of this node and its surrounding nodes is optimized.

Taking Figure 5 as an example, the angle skewness is selected as the objective function. By moving the node P, the angle skewness values of all triangle meshes connected to node P are optimized.

Since the target mesh node P is located on the surface formed by its surrounding nodes $A\sim F$, the parameter domain coordinate $p(u,v)$ of P must be within the polygon enclosed by the corresponding parameter domain coordinates of $A\sim F$. In the corresponding parameter domain coordinates of $A\sim F$, by extracting the maximum value and minimum value in direction u and direction v, a quadrilateral region can be determined.

Based on the quadtree subdivision algorithm, the quadrilateral region mentioned above can be divided into four subregions. The actual mesh node coordinates corresponding to the center points of these four subregions are calculated separately, and the triangular meshes be constructed by connecting these nodes with nodes $A\sim F$. The angle skewness results of these meshes are compared. The subregion with the best result is selected for the next quadtree subdivision iteration.

This process is repeated until the objective function value at a certain calculation point meets the threshold requirement of the objective function. Then, this calculation point is selected as the parameter domain coordinate values of the optimized mesh node, the actual coordinate values of this node can be calculated to achieve the mesh node optimization.

(3) Determining the termination criterion of the quadtree iteration.

In the practical calculation, since the limit of the mesh element geometric shape, it is possible that the surface mesh cannot reach the mesh optimization threshold, which will lead to an infinite loop in the mesh optimization process. To prevent this situation, it is necessary to set the threshold for the number of iterations. When the required number of iterations is not reached, the optimized node coordinates are obtained, the mesh element must satisfy that the objective function value is larger than the objective function threshold, and the optimized mesh node coordinates can be directly determined. When the required number of iterations is reached, it is necessary to judge the objective function value of the mesh element at this time. If the objective function value is larger than that before optimization, it proves that the objective function has reached the optimization value, the node coordinates can be directly used as the optimized mesh element coordinates. However, if the objective function value is smaller than that before optimization, it means that the quadtree method may have fallen into the local optimum. The original mesh node coordinates should be kept unchanged, and the mesh optimization should not be carried out.

By substituting the normalized mesh quality evaluation parameters into the method described in this section, the optimization of specific mesh quality evaluation parameters can be achieved directly. Since different mesh quality evaluation parameters are measures of the mesh geometric shape, it is impossible to adjust a single mesh quality evaluation parameter while keeping other parameters unchanged. Compared with the Laplacian smoothing algorithm, the mesh node optimization algorithm based on mesh quality evaluation parameters combines the operation of mesh quality evaluation with the operation of mesh quality optimization, the single determined mesh node position is the local optimal position of mesh quality, the repeated iteration optimization for all mesh nodes is not necessary. It can save mesh optimization time, simplify the operation of mesh optimization and evaluation, and make it more efficient overall.

On the other hand, using different objective function thresholds can have two effects. Firstly, it can change the number of low-quality mesh elements to be calculated. Secondly, it can change the iteration number of the mesh node optimization algorithm based on the quadtree method. These adjustments not only affect the mesh optimization time, but also affect the optimized mesh quality. Therefore, by setting different thresholds for the objective function, the mesh generation of different mesh quality can be achieved.

3. Results Discussion and Analysis

3.1. The Ship Hull Surface Hybrid Mesh Generation Based on Surface Features

In the practical engineering field, the ship hull surface is formed by the combination of multiple trimmed surfaces. These trimmed surfaces have different shapes and irregular boundaries and cannot be directly used for mesh generation. It is necessary to preprocess the ship hull surface according to the surface shape. By merging and partitioning these trimmed surfaces, a series of partition surfaces with regular boundaries can be obtained. The mesh can be generated on each partition surface separately, and then all mesh elements can be concatenated to obtain the mesh elements of the entire ship.

The 3600TEU container ship designed by Korea Research Institute of Ships and Ocean Engineering (KRISO) is a standard model recommended by International Towing Tank Conference (ITTC), this model is also called KRISO Contain Ship (KCS) model. KCS model has strong representativeness, and the data available for reference are also abundant. Therefore, we decided to take this ship model as an example to complete the ship hull hybrid surface mesh generation.

The standard KCS surface model can be shown in Figure 6.

Considering that the ship potential flow calculation generally only divides the mesh elements in the underwater region of the hull, we cut the standard KCS model and obtained the underwater part of the ship hull model. The designed draft of the standard KCS model is 10.8 m, taking this value as an example, we obtained the standard KCS surface model under the designed draft, as shown in Figure 7.

Based on the ship hull surface partition criterion, the midship was divided into a single partition, and the ship bow and ship stern were further partitioned according to the ship hull surface features, each partition should ensure that it only contains up to four smooth and non-bending boundary curves. The partition criterion for the standard KCS model under the designed draft can be shown in Figure 8.

As shown in Figure 8, the areas marked by numbers 1, 2, 3 and 4 represent different regions divided according to the ship hull surface partition criterion.

Based on the partition of the KCS hull, preprocessing and reconstruction are carried out for the curved surfaces of each partition to obtain the reconstructed KCS surface model. The reconstructed standard KCS surface model under the designed draft can be shown in Figure 9.

By observing Figure 9, it can be seen that the reconstructed hull surface is significantly simpler than the original hull surface.

Finally, the ship hull surface was divided into four partitions, the areas marked by different numbers represent different partitions, as shown in Figure 10.

To further verify whether the partition is rational, we counted the Gauss curvature values and mean curvature values of each discrete point on the partition surfaces. The corresponding statistics of each partition surface were shown in Figure 11 and Figure 12.

By analyzing the Gauss curvature statistics frequency histogram and mean curvature statistics statistical frequency histogram of each partition, it can be found that the partition 2 has the smallest range of curvature change. The Gauss curvature values of most points are between $-2.5\times {10}^{-3}\sim 1.5\times {10}^{-3}$, and the mean curvature ranges are between $-0.2\sim 0.2$. The curvature change ranges of other partitions are relatively large. In terms of Gauss curvature, the change ranges of partitions 1, 3, and 4 are more than one order of magnitude larger than the change range of partition 2. In terms of mean curvature, although the minimum mean curvature value of partition 3 is larger than that of partition 2, its maximum mean curvature value is much larger. Similarly, the maximum mean curvature value of partition 4 is smaller than that of partition 2, but its maximum average curvature value is much smaller. In other words, the maximum absolute curvature values of these two partitions are large. Based on the above analysis, the rationality of partition can be verified.

After the ship hull surface partition was completed, we considered the mesh continuity between partitions. The mesh generation process for each partition is independent. If we do not consider the mesh continuity between partitions and directly generate the surface mesh, it may lead to mesh misalignment, overlap, and other problems between different partitions, as shown in Figure 13.

The problems of mesh misalignment and overlap between different partitions can affect the continuity of mesh topology, resulting in the inability to form continuous mesh topology between partitions, which can affect the potential flow calculation. Therefore, before generating mesh elements for each partition, it is necessary to pre-fix the mesh nodes on the boundaries of each partition, thereby ensuring the mesh continuity between different partitions.

Firstly, the boundaries of each partition can be determined, and the number of mesh nodes on the boundaries can be also determined. Based on the above curvature method, the mesh node coordinates of the boundary positions can be determined. Then, the mesh elements of each partition can be generated based on these boundary mesh nodes. Since two adjacent partitions have a common boundary, this method must ensure the mesh continuity of the boundary position, and avoid boundary continuity problems such as mesh misalignment and overlap.

As shown in Figure 13, the area marked in the red box is the boundary between partitions 3 and 4, and it can be observed that there is the significant mesh misalignment between these two partitions.

Based on the above method, by constructing two entire ship mesh size adjustment parameters, the macro control of mesh elements between all partitions was carried out. These two parameters respectively represent the number of mesh nodes at the boundary between the ship bow and midship and the number of mesh nodes at the shortest boundary of the ship hull surface; this shortest boundary is generally located at the ship stern shaft position.

The number of mesh nodes at the boundary between the ship bow and midship was set to 10, the number of mesh nodes at the ship stern shaft position was set to 3, and the number of mesh nodes at other boundaries was calculated based on curvature features. The final generated initial advancing front can be shown in Figure 14.

By observing Figure 14, we can find that the mesh nodes at the boundaries of each partition have been fixed, and there is no problem of misalignment or overlap. There are ten mesh nodes at the boundary between the ship bow and midship, and three mesh nodes at the ship stern shaft position.

Subsequently, for partition 2, we used the mapping method based on NURBS surface interpolation, combined with surface curvature features, constructed the quadrilateral topology elements, and generated the structured mesh; for partitions 1, 3, and 4, we used the advancing front method, combined with the curvature features of the positions to be advanced, determined the direction and step length of the front, generated the new triangular topological elements, updated the front until the partition surface was filled with the mesh elements.

The generated mesh of each partition can be shown in Figure 15 and Figure 16. The entire ship mesh can be shown in Figure 17.

After the initial mesh was generated, we carried out the mesh optimization processing. The midship has a simpler structure, the structured mesh generated based on the NURBS interpolation mapping method can satisfy the requirement of potential flow calculation. Therefore, mesh optimization mainly focuses on the unstructured mesh to ensure the accuracy of the subsequent hydrodynamic calculation. We selected the angle skewness as the objective function to complete the mesh optimization, as well as the angle skewness as the measurement standard. The value range of mesh angle skewness is between 0 and 1. The normalized value interval gives it the advantage in image comparison before and after optimization. The closer the image color is to deep blue, the closer the mesh angle skewness is to 0, which means the higher mesh quality. The closer the image color is to bright red, the closer the mesh angle skewness is to 1, which means the lower mesh quality.

The mesh generation results before and after optimization can be shown in Figure 18, Figure 19 and Figure 20.

It can be seen that the bright red regions of the optimized mesh are significantly reduced; the overall mesh color of these partitions is deeper. These situations can prove that the overall mesh quality has been improved.

Furthermore, based on specific mesh quality evaluation parameters, we completed the quality verification for the mesh before and after optimization. The mesh angle skewness, size skewness, aspect ratio, edge ratio, and size change were selected as parameters for evaluating mesh quality. Referring to the Gambit user’s guide [39], the value ranges and ideal values of these parameters can be shown in

Table 1. The primary mesh quality evaluation parameters, their value ranges, and ideal values.

The Mesh Quality Evaluation Parameter	The Value Range	The Ideal Value
The angle skewness	$[0,1]$	0
The size skewness	$[0,1]$	0
The aspect ratio	$[1,+\infty )$	1
The edge ratio	$[1,+\infty )$	1
The size change	$(0,+\infty )$	1

.

Based on the above parameters, we compared the quality of two meshes before and after optimization. The values can be shown in

Table 2. The mesh quality of partition 1 before and after mesh optimization.

The Mesh Quality Evaluation Parameter	The Parameter Value Before Mesh Optimization	The Parameter Value After Mesh Optimization
The average angle skewness	0.260	0.245
The maximum angle skewness	0.846	0.609
The average size skewness	0.140	0.135
The maximum size skewness	0.966	0.462
The average aspect ratio	1.262	1.125
The maximum aspect ratio	10.366	1.578
The average edge ratio	1.394	1.358
The maximum edge ratio	3.324	2.509
The average size change	1.313	1.260
The maximum size change	3.829	3.233

,

Table 3. The mesh quality of partition 3 before and after mesh optimization.

The Mesh Quality Evaluation Parameter	The Parameter Value Before Mesh Optimization	The Parameter Value After Mesh Optimization
The average angle skewness	0.302	0.185
The maximum angle skewness	0.738	0.738
The average size skewness	0.116	0.085
The maximum size skewness	0.892	0.892
The average aspect ratio	1.137	1.092
The maximum aspect ratio	5.221	5.220
The average edge ratio	1.329	1.283
The maximum edge ratio	4.205	4.202
The average size change	1.306	1.188
The maximum size change	7.686	3.106

and

Table 4. The mesh quality of partition 4 before and after mesh optimization.

The Mesh Quality Evaluation Parameter	The Parameter Value Before Mesh Optimization	The Parameter Value After Mesh Optimization
The average angle skewness	0.229	0.201
The maximum angle skewness	0.626	0.377
The average size skewness	0.110	0.088
The maximum size skewness	0.588	0.243
The average aspect ratio	1.172	1.066
The maximum aspect ratio	1.932	1.221
The average edge ratio	1.355	1.295
The maximum edge ratio	2.462	1.633
The average size change	1.270	1.165
The maximum size change	2.012	1.595

.

By observing Table 2, it can be found that through grid optimization, all mesh quality evaluation parameter values of partition 1 have significantly decreased. It is particularly noteworthy that before mesh optimization, the maximum angle skewness of partition 1 was 0.846, which is already the low-quality mesh with severe distortion in the conventional sense. After mesh optimization, the mesh quality has been significantly improved, and its maximum angle skewness has been reduced to 0.609. Meanwhile, the maximum aspect ratio has decreased from 10.366 to 1.578, which is also a significant improvement.

By observing Table 3, it can be found that the average values of all mesh quality evaluation parameters of partition 3 have significantly decreased, which means the mesh quality has been significantly improved. However, before and after mesh optimization, the values of maximum angle skewness, the maximum size skewness, the maximum aspect ratio and the maximum edge ratio remained largely unchanged; this is because the position where the mesh element with these maximum values appears has the rapid curvature change feature. The mesh size at this position has already reached the minimum value, and it is no longer possible to improve the mesh quality at this position through mesh optimization. The solution of this problem is to further divide the partition surface into multiple partitions at that position or generate the finer mesh by modifying the initial setting mesh size parameters.

By observing Table 4, the maximum angle skewness values of partition 4 before and after mesh optimization differ by 1.7 times, which means that the mesh quality has been significantly improved. The maximum values of the remaining mesh quality evaluation parameters have also increased by 1.3–2.4 times, indicating that the optimization algorithm has the significant effect.

Furthermore, for all three partitions, after mesh optimization, the average values of all mesh quality evaluation parameters which can represent the overall mesh quality significantly decreased. This situation proves that the overall mesh quality has been significantly improved.

In order to satisfy the requirement of subsequent hydrodynamic calculation, it is necessary to ensure the water tightness of the ship hull. The stern shaft of the standard KCS model needs to be equipped with the propeller, it is not enclosed during the modeling process. For this region, we repaired the water tightness of the stern shaft and added a new mesh element, as shown in Figure 21.

As shown in Figure 21, the mesh element marked in the red box in (b) is a newly generated mesh element located at the stern shaft, ensuring that the ship hull surface mesh meets the requirement of water tightness.

Finally, the mesh elements of all partitions were concatenated. The entire ship hull hybrid mesh can be shown in Figure 22.

By importing the ship hull hybrid mesh into the corresponding CFD simulation software, the hydrodynamic analysis can be performed.

3.2. The Ship Hull Surface Hybrid Mesh Hydrodynamic Analysis Based on Surface Features

Taking the above standard KCS model as an example, we respectively used the conventional hybrid mesh generation method (the mesh generation method based on NURBS surface interpolation and advancing front technique) and our improved method to generate the ship hull surface mesh, and we imported the mesh into the ship potential flow analysis software. By comparing the hydrodynamic calculation results, we can verify the advantage of our method in hydrodynamic calculation.

Firstly, we set the calculation condition for the example. We assumed that the standard KCS model under the designed draft is located in infinitely deep water. Then, we analyzed the various potential flow calculation results at different frequencies.

The KCS potential flow calculation model can be shown in Figure 23.

The principal dimension parameters of the standard KCS model can be shown in

Table 5. The principal dimension parameters of the standard KCS model.

The Principal Dimension Parameter	The Value
Length between perpendiculars ($L_{pp}$)	230 m
Ship breadth (B)	32.2 m
Draft depth (D)	10.8 m
The height of the gravity center from the baseline ($KG$)	14.32 m
The roll inertia radius ($k_{xx}$)	12.88 m
The pitch inertia radius ($k_{yy}$)	57.96 m

.

The environmental variables were set as follows: we set the wave as the regular wave with a wave direction of ${180}^{\circ }$, and ignored the influence of ocean current speed and wind speed.

In the potential flow calculation, the surface mesh has high sensitivity to the calculation of first-order hydrodynamics. Therefore, we can choose first-order forces to compare and analyze our mesh and conventional mesh and verify the advantage of our mesh.

We set the ship speed to 0 knots per hour, then calculated and analyzed the total non-viscous forces, steady drift forces and ship hull free floating Response Amplitude Operator (RAO) values corresponding to the frequencies in the range of $0.1\sim 0.4$. Among them, the total non-viscous force is the superposition of the Froude–Krylov (F-K) force and diffraction force acting on a floating body in the regular wave.

Firstly, we conducted the mesh independence verification. Based on the principle of finite element analysis, we can know that the finer the mesh elements divided, the higher the accuracy of the solution result. However, in practical engineering design and application, a sharp increase in the number of mesh elements will lead to a significant increase in calculation time, and when the number of mesh elements reaches a certain level, the improvement of calculation accuracy is not significant.

Based on the hybrid mesh generation algorithm mentioned above, we generated the ship hull surface mesh. By setting different entire ship mesh size adjustment parameters, we obtained the half ship meshes of the KCS underwater section with 1151, 1577, 1957, and 2538 mesh elements. Then we calculated their total non-viscous forces, steady drift forces, and ship hull free floating RAO values. The mesh results can be shown in Figure 24.

By importing the ship hull hybrid mesh into the potential flow simulation software, the calculation time can be shown in

Table 6. The relationship between the calculation time and the number of mesh elements.

The Number of Mesh Elements	The Calculation Time (s)
1151	36.92
1577	66.10
1957	88.17
2538	128.95

.

By observing Table 6, we can find the relationship between the calculation time and the number of mesh elements. With the increase in the number of mesh elements, the calculation time increases. Therefore, in order to ensure the calculation efficiency, we need to minimize the number of mesh elements as much as possible while ensuring the calculation accuracy.

The calculation results of total non-viscous forces, steady drift forces and ship hull free floating RAO values with different numbers of mesh elements can be shown in Figure 25.

Then we used the near field method and far field method and calculated the surge steady drift forces of the standard KCS model with different numbers of mesh elements. The results can be shown in Figure 26.

The root mean squared error $RMSE$ of the results obtained by near field method and far field method with different numbers of mesh elements can be calculated. The calculation formula can be represented as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{(Y_i-{\widehat{Y}}_i)}^2}$$

(21)

where $Y_i$ and ${\widehat{Y}}_i$, respectively, represent the surge steady drift force results of the target mesh model with a specific frequency; these two values can be calculated based on the near field method and far field method. n represents the number of frequencies calculated.

The root mean squared error $RMSE$ of the surge steady drift force result with different numbers of mesh elements can be shown in

Table 7. The root mean squared error statistics of surge steady drift force calculation.

The Number of Mesh Elements	The RMSE of Surge Steady Drift Force Calculation
1151	6087.933
1577	3989.511
1957	3722.506
2538	3706.913

.

By analyzing Table 7, it can be found that with the increase in the number of mesh elements, the root mean squared error decreases gradually. After testing, when the number of mesh elements reaches 2538, increasing the number of mesh elements cannot cause the significant change in the root mean squared error. Combined with the calculation results with different numbers of mesh elements in Figure 26, it can be considered that the calculation result has converged when the number of mesh elements is 2538.

In order to the convenience of result analysis, we used the potential flow calculation results when the number of half ship mesh elements is 2538 as the convergence values, calculated the average relative error of potential flow calculation results with different numbers of mesh elements. The average relative error can reflect the deviation degree of the calculation results from the convergence value, it can be represented as follows:

$$\delta ={\displaystyle \frac{2\times RMSE}{\max \left(\widehat{Y}\right)-\min \left(\widehat{Y}\right)}}$$

(22)

where $\max \left(\widehat{Y}\right)$ and $\min \left(\widehat{Y}\right)$, respectively, represent the maximum value and minimum value of the convergence results, $RMSE$ represents the root mean squared error, and its calculation formula is shown in Equation (13). $Y_i$ represents the potential flow calculation result of the target mesh model with a specific frequency, ${\widehat{Y}}_i$ represents the convergence value of the potential flow calculation with that specific frequency. It should be noted that although the formula for $RMSE$ here is the same as the above formula, the meanings of the parameters are different. Here, it represents the potential flow calculation results at a certain frequency and the convergence values. In this paper, the convergence value was the potential flow calculation result when the number of mesh elements is 2538.

The average relative errors of potential flow calculation results with different numbers of mesh elements can be shown in

Table 8. The average relative errors between calculation values and convergence values in potential flow calculation (/%).

The Number of Mesh Elements	The Total Non-Viscous Force (Surge)	The Total Non-Viscous Force (Heave)	The Steady Drift Force (Surge)	The Steady Drift Force (Heave)	Free Floating RAO Value (Surge)	Free Floating RAO Value (Heave)
1151	0.584	0.119	2.234	1.717	0.056	0.143
1577	0.301	0.097	0.216	0.441	0.074	0.074
1957	0.135	0.017	0.183	0.328	0.045	0.036
2538	0	0	0	0	0	0

.

By observing Table 8, it can be found that when the number of mesh elements reaches 1577 or more, all average relative errors between potential flow calculation values and convergence values are less than $0.5\%$. It can be considered that the potential flow calculation results tend to converge, the influence of the number of mesh elements on the accuracy of potential flow calculation is small. We can choose the ship hull hybrid mesh with more than 1577 mesh elements to further compare the impact of different mesh generation methods on the accuracy of ship potential flow calculation.

Additionally, we further compared the conventional mesh generation method and the mesh generation method based on ship surface features, determined the impact of these two methods on the accuracy of ship potential flow calculation. By setting the same number of mesh elements to 1577, we used two different methods to generate the ship hull surface mesh, and used the potential flow calculation results with 2538 mesh elements as the convergence value, calculated the ratio between root mean squared errors of various potential flow calculation results. The smaller the ratio, the more accurate the calculation results of ship potential flow analysis. The corresponding root mean square error comparison of potential flow calculation can be shown in

Table 9. The root mean squared error comparison of ship potential flow calculation based on different mesh generation methods.

The Ship Potential Flow Calculation	The RMSE of New Mesh Generation Method	The RMSE of Conventional Mesh Generation Method	The Ratio of RMSE
The total non-viscous force (surge)	6189.768	9052.015	0.684
The total non-viscous force (heave)	28,686.157	39,294.803	0.730
The steady drift force (surge)	222.321	236.280	0.941
The steady drift force (heave)	3070.236	4190.747	0.733
Free floating RAO value (surge)	0.00850	0.00953	0.892
Free floating RAO value (heave)	0.000366	0.000473	0.774

.

By observing Table 9, it can be seen that all ratios between $RMSE$ of our method and $RMSE$ of conventional method are less than 1, which means that for the same number of mesh elements, the mesh generated based on our method has higher calculation accuracy.

Meanwhile, we compared the calculation time of these two meshes in the potential flow solver. In the case of the same number of mesh elements, our method has a calculation time of 88.17 s, while the conventional method takes 111.72 s, which means that the mesh generated based on our method has higher calculation efficiency.

4. Conclusions

This paper proposed a hybrid mesh generation strategy suitable for ship hydrodynamic evaluation by combining the actual ship surface curvature feature information with the mesh quality evaluation parameters. Firstly, the principle of the improved hybrid mesh generation method was introduced. Considering the targeted optimization of ship hull surface shape on mesh generation strategy, the adaptive mesh generation method based on the ship hull surface curvature features and mesh quality evaluation parameters was presented. Then, the ship hull surface mesh generation of the KCS model was taken as an example to verify the feasibility of our method. Meanwhile, combined with the potential flow calculation results, the mesh generated in this paper and the mesh generated based on conventional method were compared, and the hydrodynamic performance of the mesh was analyzed and verified.

The ship hull hybrid surface mesh generated by our method can combine the advantages of both structured mesh and unstructured mesh; it has high calculation accuracy. By comparing the mesh qualities before and after optimization, the reliability of the mesh optimization algorithm can be verified. By analyzing the calculation results of ship potential flow hydrodynamic analysis, we can obtain the following conclusions. Firstly, by optimizing specific mesh quality evaluation parameters, various mesh quality evaluation parameter values are significantly reduced, and the mesh quality is significantly improved, which can provide high-quality mesh for potential flow calculation. Secondly, in the potential flow calculation, compared with the mesh generated based on conventional method, the mesh generated based on our method has lower root mean squared errors and less calculation time in total non-viscous force calculation, steady drift force calculation, and ship hull free floating RAO calculation, which proves that the mesh generation method proposed in this paper is more reliable in the potential flow calculation and can improve the accuracy and efficiency of calculation results.