Wind-Induced Seismic Noise and Stable Resonances Reveal Ice Shelf Thickness at Pine Island Glacier

Abstract

Antarctic ice shelves regulate ice-sheet discharge and global sea-level rise, yet their rapid retreat underscores the need for new, low-cost monitoring tools. We analyze ambient seismic noise recorded by seismometers on the Pine Island Glacier ice shelf to characterize wind-induced signals and detect persistent structural resonances. Power spectral analysis shows that wind sensitivity is strongly damped compared with bedrock sites: noise increases only 5–7 dB from 0 to 25 m s⁻¹ winds, versus a 42 dB increase at an inland bedrock station, reflecting the contrasted coupling environments of floating and grounded substrates. The horizontal-to-vertical spectral ratio (HVSR) spectrograms reveal two temporally stable peaks at ~2.2 Hz and ~4.3 Hz that persist across stations and remain independent of environmental forcing. Forward modeling indicates that these peaks correspond to S-wave resonances within the ice shelf. The inferred ice-water interface depth (~440 m) agrees with the Bedmap2 thickness estimate (466 m). This work demonstrates that HVSR provides an effective passive, single-station method for measuring ice shelf thickness.

1. Introduction

Antarctic ice shelves act as buffers that regulate the flow of inland ice to the ocean [1]. Their stability is a key control on future global sea-level change, and many, such as Pine Island, Thwaites, Smith, and Kohler glaciers, are undergoing rapid retreat [2]. This rapid change makes floating ice shelves critical environments for observations. One of the important parameters for understanding ice-shelf stability and change is thickness, which influences flexural rigidity, fracture behavior, and basal melting. Direct measurements of ice thickness from airborne or ground-based surveys provide accurate estimates but remain costly and spatially and temporally limited [3,4]. Satellite altimetry provides broad coverage but requires the hydrostatic equilibrium assumption [5]. These limitations motivate continuous ice-shelf thickness monitoring using robust, low-cost, and non-invasive geophysical methods [6,7].

Passive seismology using earthquake signals and ambient seismic noise has become a powerful tool in cryospheric studies because it can operate year-round and does not require active sources [8,9]. Because Antarctica is relatively aseismic compared with tectonically active regions, ambient noise provides important continuous signals for inferring ice properties and structure [10,11].

The Antarctic ambient noise field is multi-source and frequency-dependent [12]. Noise sources include oceanic processes such as infragravity waves and swell [13,14], but also atmospheric wind forcing [15,16]. Because these sources vary in time, the noise field can change substantially with environmental conditions. Understanding these sources is essential for interpreting ice-shelf properties with seismic noise.

Ambient noise also carries subsurface information, allowing structural properties to be inferred using techniques such as the horizontal-to-vertical spectral ratio (HVSR) method and ambient noise cross-correlation. The HVSR method uses three-component ambient noise recorded at a single station to identify resonance peaks associated with subsurface structures [17,18]. HVSR has been used to estimate the thickness of grounded glaciers and ice sheets [19,20,21]. Additionally, ambient noise cross-correlation between station pairs can retrieve wave propagation that enables inference of velocity structure [22]. In cryoseismology, cross-correlation studies have focused on shallower structures, such as firn properties [23,24,25] or subglacial water cavities [26]. However, the use of stable HVSR peaks to determine the full thickness of a floating ice shelf has not yet been demonstrated.

In this study, we analyze ambient seismic data collected on the Pine Island Glacier (PIG) ice shelf. First, we characterize the high-frequency noise field and quantify its relationship with atmospheric wind forcing, comparing it with an inland bedrock site. Environmental forcing signals may obscure ice-shelf structural signals; therefore, we quantify wind-noise behavior before interpreting structural resonances. Second, we identify stable, low-frequency HVSR peaks and show that they are independent of environmental forcing and represent the structural resonance associated with the full ice shelf thickness above the underlying ocean.

2. Study Site and Data

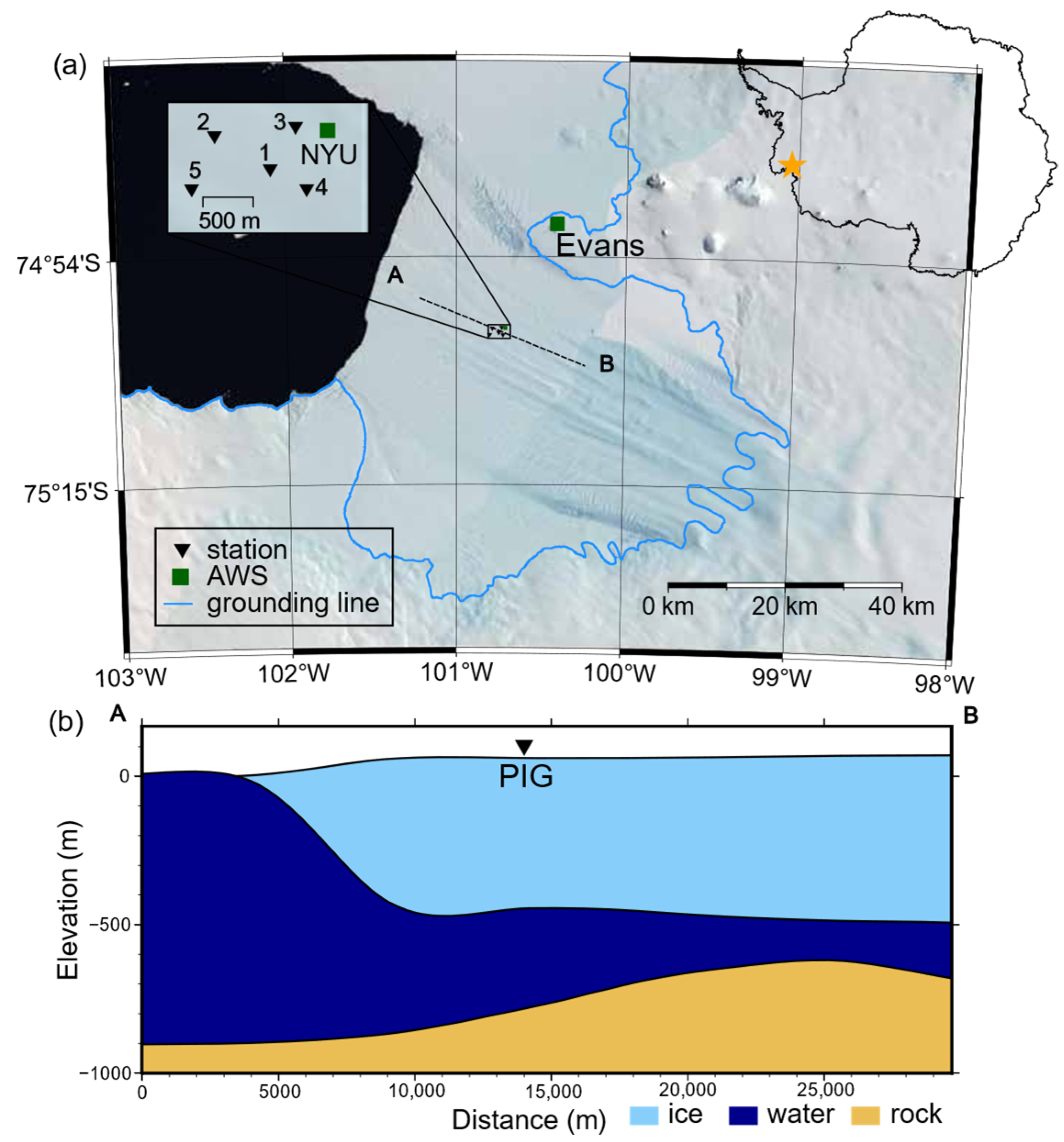
Our study site is located on the PIG ice shelf, a major outlet of the West Antarctic Ice Sheet (WAIS) flowing into the Amundsen Sea (Figure 1a). A seismic array of five broadband seismometers (Nanometrics Trillium 120 Sec Response, 100 Hz sampling rate; Nanometrics Inc., Kanata, ON, Canada) was deployed near the ice shelf centerline from 2012 to 2013 [27]. The array (inset, Figure 1a) consists of stations spaced 0.82–2.10 km apart. All stations are positioned on the floating ice shelf, which features a surface marked by longitudinal ridges and troughs [28]. A Bedmap2 cross-section (Figure 1b) shows that at the array location, the ice thickness is ~466 m (surface elevation ~65 m, bed elevation −810 m) [29]. Bedmap2 thickness values are derived primarily from airborne and ground-based radio-echo sounding surveys, complemented by satellite remote sensing (surface elevation, surface velocity) and mass-conservation modeling in data-sparse areas [29]. At Pine Island Glacier, the Bedmap2 ice-shelf thickness uncertainty is ±150 m [29].

In this study, we analyzed continuous seismic records from 1 February 2012 to 30 November 2013. Data from stations PIG1, PIG2, PIG3, and PIG4 were used. PIG5 was excluded due to poor data quality (Figure S1). Meteorological data, including wind speed and air temperature, were obtained from two nearby automatic weather stations (AWS) shown in Figure 1a: Evans AWS [32], located ~22 km from the array, and the NYU AWS [33], collocated with the seismic array. Because the Evans dataset is more complete and the air temperatures recorded by both stations show no difference during overlapping periods (Figure S2), we adopted the Evans record for all analyses.

3. Methods

To quantify the relationship between wind velocity and the seismic noise field, we adapted the methodology of Frankinet et al. [16]. We first computed hourly Power Spectral Densities (PSDs), which describe how the power of a seismic signal is distributed across different frequencies, for the PIG2 station using the ObsPy package (Python v3.10.18; Obspy v1.4.2) [34,35]. The data were segmented into non-overlapping 1 h windows. PSDs were computed over a frequency range from 0.02 to 50 Hz, and the resulting spectral power values were accumulated into a probabilistic distribution using 0.25 dB bins spanning −200 to −80 dB. In this context, probabilistic PSD was calculated to account for the statistical distribution of PSDs across many 1 h time windows, from which percentile values are extracted (e.g., 5th percentile or median value) [36]. For visualization, PSDs were smoothed in logarithmic frequency bins with a width of 1/40 octaves, using an octave step of 1/80, which means each bin edge is spaced by a constant multiplicative ratio: 2^1/80.

Following Frankinet et al. [16], we linked each hourly PSD to the corresponding average hourly wind speed and grouped the PSD values into wind-speed bins spanning from 0 to 25 m s⁻¹ with 0.25 m s⁻¹ wide bins. For each wind speed bin, we defined the base noise level as the 5th percentile of noise power from the probabilistic PSD result. This statistic is preferred over the mean because it is less sensitive to transient outlier events (e.g., icequakes) and better reflects the background noise floor. Glaciers generate frequent transient signals detectable on ocean-bottom and surface seismometers, which have been linked to glacier slip and crevasse propagation [35,37].

We then measured the change in noise power as a function of wind speed for each discrete frequency using the vertical-component seismic record. For each frequency, we fit the noise power to wind speed. This was performed using a weighted linear regression. For each wind-speed bin and each frequency, we computed the within-bin standard deviation from the distribution of hourly PSD values. Regression weights were defined as the inverse of the standard deviation of this distribution. Only wind speed bins with 10 or more observations were considered. We found that a single linear relationship provided a robust fit to the PSD values across the 0 to 25 m s⁻¹ wind speeds. This relationship is described by the function $\mathrm{y}=\mathrm{a}\mathrm{x}+\mathrm{b}$, where $\mathrm{y}$ is the 5th percentile noise power (dB) at a given frequency, $\mathrm{x}$ is the wind speed (m s⁻¹), and $\mathrm{a}$ (slope) and $\mathrm{b}$ (intercept) are the regression parameters for this specific frequency. We therefore repeat the wind-speed binning independently for each frequency, producing a two-dimensional relationship between wind speed and PSD value as a function of frequency.

To investigate structural signals, daily HVSR curves (0.1–40 Hz) were computed from three-component seismic data recorded at the PIG stations using hvsrpy [38], with 60 s non-overlapping windows, Konno–Ohmachi smoothing method (b = 40) [39], and geometric averaging of the horizontal components [40].

HVSR spectrograms were then generated by stacking the daily HVSR curves in chronological order to track changes in resonant properties over time. To test the hypothesis that the observed low-frequency HVSR peaks correspond to structural resonances, we computed synthetic HVSR curves using OASES, a seismo-acoustic modeling package [41] that solves wave propagation in layered fluid-solid media.

A simplified 1D structural model of the PIG ice shelf, underlying water cavity, and bedrock was constructed with parameters listed in

Table 1. Model parameters. The depth of the water layer (the ice-water interface) is the varied parameter. The depth to bedrock was kept fixed.

Layer	Depth to Top of Layer (m)	${\mathbf{V}}_{\mathbf{p}}$ (m s−1)	${\mathbf{V}}_{\mathbf{s}}$ (m s−1)	$\mathsf{\rho }$ (kg m−3)
Ice	0	3800	1900	920
Water	300 to 640 (in 10 m steps)	1500	0	1025
Bedrock (Half-space)	870	3700	2400	2400

and based on Diez et al. [42]. To examine the sensitivity of the HVSR response to ice-water interface depth, we performed a suite of forward models in which ice thickness was varied while total depth to bedrock was held constant.

Synthetic seismograms were generated by computing frequency-domain solutions across the bandwidth of interest and applying an inverse Fourier transform to obtain time-domain signals. HVSR curves were then calculated from the synthetic horizontal and vertical component seismograms.

4. Results

4.1. Wind-Induced Seismic Noise

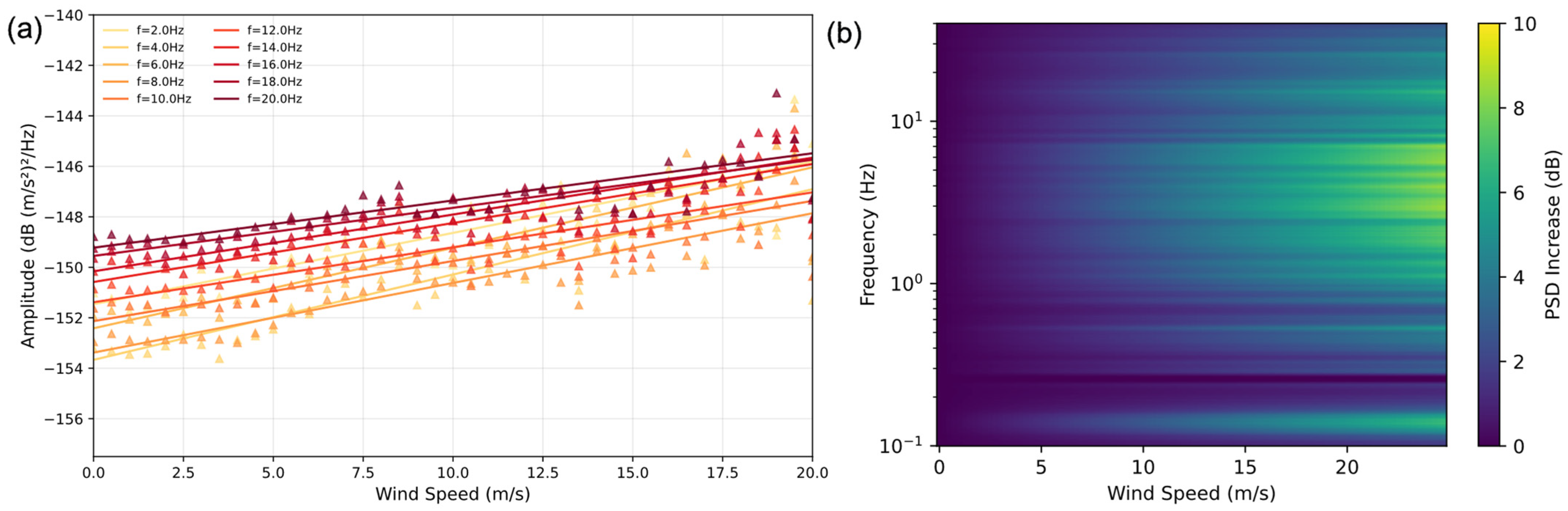
Figure 2a shows the PSDs for all three components at station PIG2, binned by wind speed from 0 to 25 m s⁻¹ and averaged within each bin. The results clearly demonstrate a frequency-dependent relationship in which noise power increases with wind speed across the full frequency range, with a stronger effect at higher frequencies (mostly above 1 Hz). This correlation is consistent with observations by Frankinet et al. [16] at the Belgian Princess Elisabeth Antarctica Station (PEAS). However, a direct comparison with the PEAS reference noise models (dashed and dotted lines in Figure 2a, representing 0 and 25 m s⁻¹ wind, respectively) reveals differences in both overall noise levels and wind speed sensitivity.

First, the dynamic range of wind-induced noise at PIG is much smaller. Frankinet et al. [16] reported a 42 dB noise increase at 10 Hz between 0 and 25 $\mathrm{m} {\mathrm{s}}^{-1}$ wind at PEAS, whereas our PIG data (Figure 2a) shows only a 5–7 dB increase over the same range. Second, the noise power limits differ substantially between the two sites. PEAS located on bedrock is significantly quieter during calm conditions: its lower noise limit (0 m s⁻¹, dashed line) is more than 20 dB lower (e.g., at 10 Hz) than the quietest noise observed at PIG. Under high winds, however, PEAS becomes much louder, with its upper noise limit (25 m s⁻¹, dotted line) is ~15 dB higher than the loudest conditions at PIG.

To quantify wind-driven noise variations at PIG, we developed a synthetic noise model based on linear regression of noise power on wind speed at each frequency. Figure 2b shows the regression parameters a and b. Figure 2c illustrates the fit at 5 Hz (dashed red line in Figure 2b), where wind-induced noise increases by ~6 dB from 0 to 20 m s⁻¹. Figure 3a further shows that noise power across multiple discrete frequencies (2–20 Hz) can be well described by individual linear regressions.

With all linear parameters, we produced a synthetic PSD spectrum. Figure 3b shows the modeled PSD increase (in dB) across frequency and wind speed. We also computed the RMS (root mean square) ground velocity in the 1–40 Hz band, where cryoseismicity is expected, from these synthetic PSDs. Even at a high wind speed of 25 m s⁻¹, the resulting ground velocity is only 0.07 μm s⁻¹. This level is far below typical icequake signals (0.3 μm s⁻¹) [43], suggesting that wind-induced noise is not a primary limiting factor for icequake detection on the PIG ice shelf.

4.2. HVSR Temporal Variations and Stable Peaks

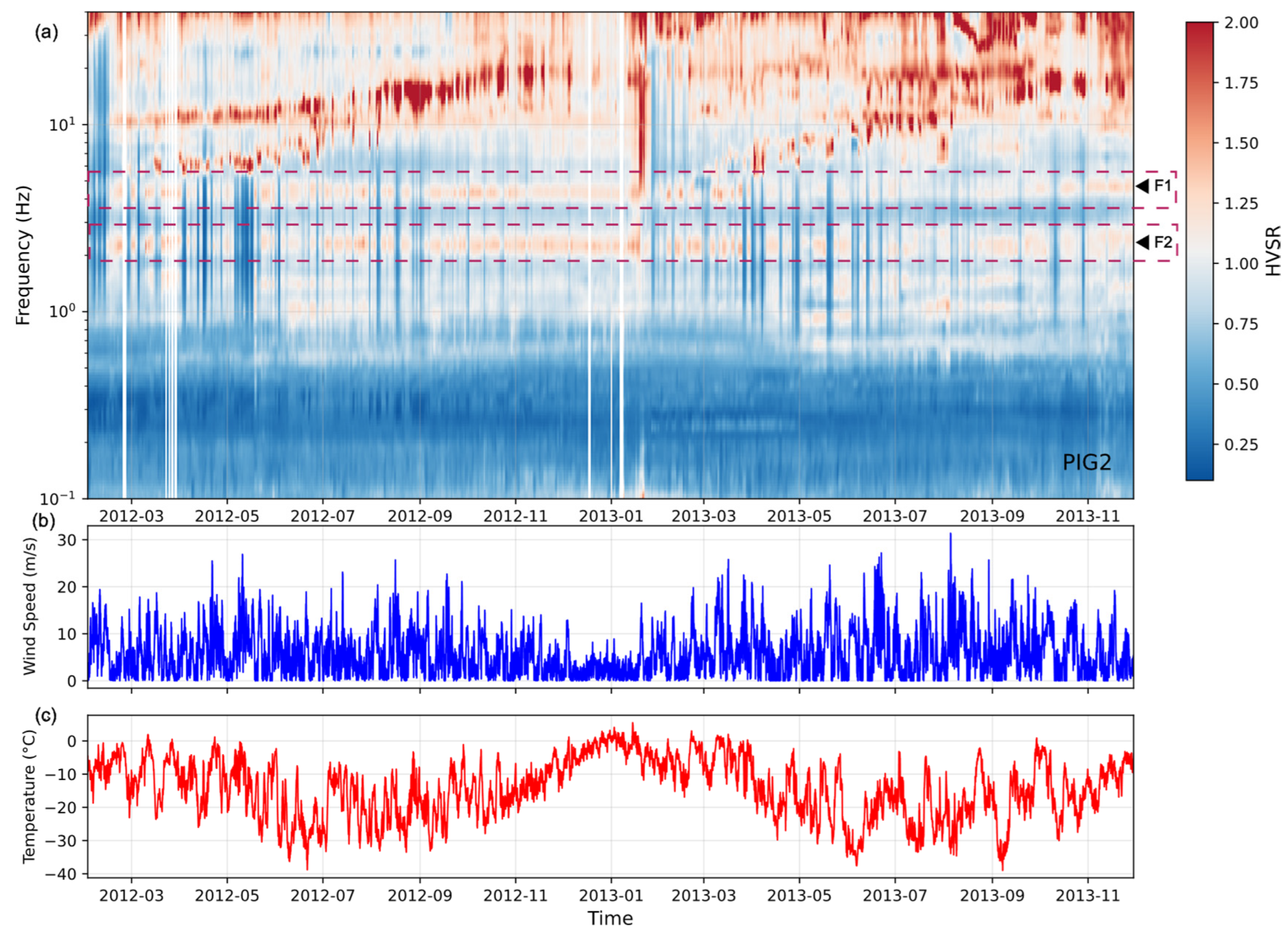
Having characterized the high-frequency, wind-driven noise, we now analyze the temporal characteristics of the HVSR. The HVSR spectrograms, which stack HVSR curves over time (shown for station PIG2 in Figure 4), exhibit three distinct phenomena.

First, the high-frequency HVSR band (e.g., >7 Hz) is highly variable (Figure 4a), with shifting peaks. Although the relationship between HVSR variability and meteorological conditions (Figure 4b,c) is complicated, the variability in this band suggests dominance by environmental forcing and sensitivity to near-surface (firn) conditions. 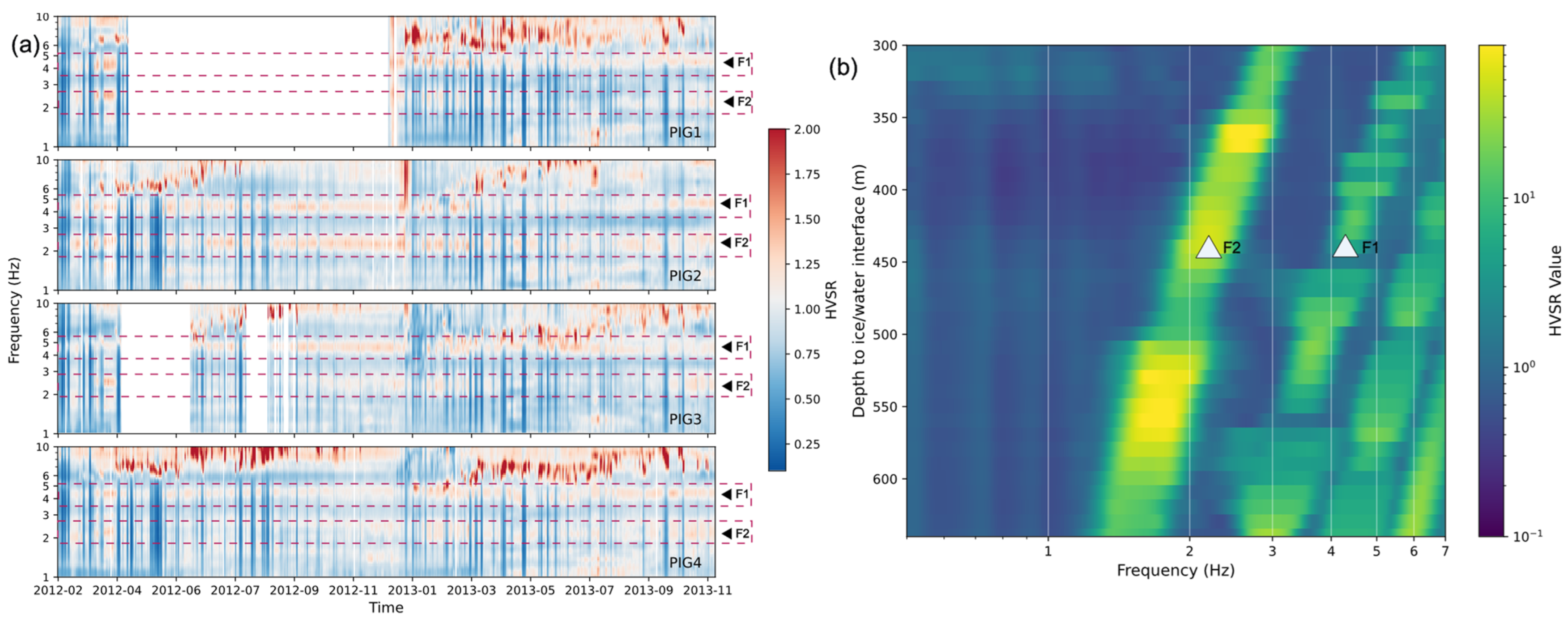Second, the low-frequency band (<7 Hz) is dominated by blue shading (Figure 4a), indicating HVSR values consistently below 1 (HVSR troughs). This baseline pattern indicates that vertical (V) motion exceeds the horizontal (H) motion across the entire band. Third, and most importantly, two distinct features, F1 (~4.3 Hz) and F2 (~2.2 Hz), appear as clear HVSR peaks at all four seismic stations (Figure 5a). Although their peak amplitudes vary over time, their frequencies remain remarkably stable. These peaks show no correlation with fluctuations in wind speed or air temperature.

This contrast between the highly variable high-frequency HVSR band and the stable low-frequency peaks strongly suggests that F1 and F2 are not atmospheric or firn-related signals. We hypothesize that their stability reflects a deeper structural origin, resonances of the ice-water-bedrock system.

4.3. Forward Modeling

To test whether the stable F1 and F2 peaks represent structural resonances, we modeled the HVSR response of the ice-water-bedrock system using OASES. The results (Figure 5b) strongly support this hypothesis.

The modeled HVSR curves reproduce resonance peaks at frequencies closely matching F1 and F2. The modeling shows that these peaks are sensitive to the ice-water interface depth: as the ice layer thins, the resonance frequencies shift higher.

The observed frequencies for F1 (~4.3 Hz) and F2 (~2.2 Hz) (indicated by the white triangles in Figure 5b) align with a modeled ice-water interface depth of ~440 m (Figure 5b).

5. Discussion

Our investigation of the 0.1–40 Hz ambient noise field on the PIG ice shelf shows two types of signals: wind-driven noise amplification and stable HVSR peaks that persist independently of environmental forcing, reflecting the underlying ice-shelf structure.

5.1. Damped Signature of Wind on a Floating Ice Shelf

Wind-noise analysis reveals a complicated, two-part contrast between PIG and bedrock stations, such as PEAS [16]. First, during calm wind conditions, baseline noise at PIG is much higher (e.g., >20 dB higher at 10 Hz) than at PEAS. Second, PIG is far less sensitive to wind: whereas PEAS exhibits a ~42 dB noise increase between low and high wind speeds, PIG shows only a ~5–7 dB increase, meaning that even under strong winds, absolute noise levels at PIG remain lower than those at PEAS. Frankinet et al. [16] used two linear models at PEAS because they observed a change in noise-wind behavior at 6 m s⁻¹. In contrast, we find no such breakpoint at PIG; a single linear regression fits the data very well, consistent with Lott et al. [44] and Johnson et al. [45]. Explaining the behavior difference at PEAS is beyond the scope of this study.

The higher ambient noise baseline at PIG is consistent with expectations for floating ice shelves. As Baker et al. [14] showed for the Ross Ice Shelf, floating ice is strongly coupled to oceanic processes, such as swell and infragravity waves, producing a noisy seismic wavefield. Inland bedrock sites, such as PEAS, which lack this direct oceanic coupling, naturally exhibit a much lower noise floor.

The stark contrast in wind sensitivity likely arises from differences in near-surface coupling. At PEAS, sensors are directly coupled to bedrock [16], enabling efficient transfer of wind energy into seismic motion. At PIG, sensors are installed within the firn layer, which acts as a mechanical insulator and reduces wind. Our synthetic noise modeling further shows that, even under strong winds, RMS ground velocities in the cryoseismic band (1–40 Hz) remain well below typical icequake signal amplitudes. The opposite is true for PEAS, where wind noise can obscure events. Thus, site-specific coupling conditions (bedrock vs. firn) can influence the completeness of ice-quake catalogs and should be considered when comparing cryoseismicity across locations.

5.2. The Structural Resonance

The HVSR spectrograms (Figure 4a and Figure 5a) show that in the low-frequency band (<7 Hz), baseline HVSR values are consistently below 1, indicating that vertical (V) motion exceeds horizontal (H) motion. This behavior is consistent with observations from the Amery Ice Shelf by Zhan et al. [46], who showed that the sub-ice-shelf water layer acts as a strong low-velocity waveguide. The water column traps P-wave energy, causing near-vertical resonance and amplifying the vertical component of ambient noise.

Superimposed on this vertically dominated baseline are two stable HVSR peaks, F1 (~4.3 Hz) and F2 (~2.2 Hz). Unlike the highly variable high-frequency HVSR features, these peaks show no correlation with environmental forcings (Figure 4) and appear consistently across all stations (Figure 5a). We interpret them as S-wave resonances within the solid ice layer.

OASES forward modeling strongly supports this interpretation (Figure 5b). The modeled resonance peaks match F1 and F2 closely and demonstrate that their frequencies are sensitive to the ice-water interface depth. The observed peaks correspond to a modeled ice thickness of ~440 m, in close agreement with the Bedmap2 estimate of 466 m at the station location.

The physical origin of these peaks follows from the boundary conditions of the ice shelf and its S-wave transfer function [47]. The system forms an extreme “stiff-over-soft” structure, with an elastic ice layer overlying seawater. Carcione et al. [47] showed that, in such a configuration, the classic quarter-wavelength (${{\mathrm{f}}_0=\mathrm{V}}_{\mathrm{s}}/4\mathrm{h}$), typical of soft-over-rigid media, is suppressed. Instead, the fundamental S-wave resonance corresponds to half-wavelength (${\mathrm{f}}_1={\mathrm{f}}_0/2={\mathrm{V}}_{\mathrm{s}}/2\mathrm{h}$), with frequencies given by:

$${\mathrm{f}}_{\mathrm{n}}={\displaystyle \frac{\mathrm{n}{\mathrm{V}}_{\mathrm{S}}}{2\mathrm{h}}},\mathrm{n}=\mathrm{1,2},3,\dots ,$$

(1)

where ${\mathrm{V}}_{\mathrm{s}}$ is the S-wave velocity of the ice, $\mathrm{h}$ is the ice thickness, and n is the nth frequency peak or higher modes.

Using parameters from our 1D model (Table 1; ${\mathrm{V}}_{\mathrm{s}}=1900$ m s⁻¹) and the modeled ice thickness ($\mathrm{h}\approx 440$ m), this formula predicts the following:

• First resonance peak (n = 1): ${\mathrm{f}}_1\approx 2.16 \mathrm{Hz}$;
• Second resonance peak (n = 2): ${\mathrm{f}}_2\approx 4.32 \mathrm{Hz}$;

These frequencies are double those predicted by the standard ${\mathrm{f}=\mathrm{V}}_{\mathrm{s}}/4\mathrm{h}$ formula used for grounded ice [19,20], align well with the observed peaks: F2 (~2.2 Hz) and F1 (~4.3 Hz). This confirms that F2 represents the fundamental S-wave resonance peak of the ice shelf, and F1 is its first overtone.

The uncertainty in the estimated thickness arises from the uncertainty in the resonance frequency $\mathrm{f}$ (typically $∆\mathrm{f}/\mathrm{f}\approx$ 2–4% for HVSR peaks), and the S-wave velocity of ice ${\mathrm{V}}_{\mathrm{s}}$ which varies with fabric, temperatures, and porosity (${\mathrm{V}}_{\mathrm{s}}=$ 1800–1950 m s⁻¹; ${∆\mathrm{V}}_{\mathrm{s}}/{\mathrm{V}}_{\mathrm{s}}\approx$ 3–5%). Propagating these errors through Equation (1) yields $\Delta \mathrm{h}/\mathrm{h}={({\left(\Delta \mathrm{f}/\mathrm{f}\right)}^2+{\left(\Delta {\mathrm{V}}_{\mathrm{s}}/{\mathrm{V}}_{\mathrm{s}}\right)}^2)}^{1/2}\approx$ 4–6%, thus $\Delta \mathrm{h}\approx$ 18–26 m with h = 440 m. The ~26 m difference (<6%) between modeled ice-thickness and Bedmap 2 estimates lies within the uncertainties of both the 1D model and Bedmap2 uncertainty (±150 m).

It is worth noting that the HVSR method has several limitations when applied to ice shelves. The method assumes a laterally homogeneous and horizontally layered ice-water-bedrock system, such that the estimated thickness represents an average value over a certain radius surrounding the station, with an effective radius empirically approximated as one quarter of the dominant frequency [19]. Consequently, HVSR cannot resolve small-scale structural features such as basal channels and crevasses. In addition, strong localized noise sources that generate energy at or near the resonance frequencies may obscure HVSR peaks, reducing the reliability of peak identification.

6. Conclusions

This study characterizes the ambient seismic noise field on the PIG ice shelf, revealing a wind-induced noise response that differs markedly from that at an inland bedrock site and identifying persistent structural signals using the HVSR method. Unlike the bedrock station, the ice shelf site exhibits higher noise levels during calm conditions and much lower sensitivity to strong winds. This behavior most likely reflects the sensor coupling to firn rather than rigid bedrock, underscoring the importance of understanding site-specific noise environments when interpreting cryoseismicity across different glacier settings.

Across all stations, we identify two stable HVSR peaks at ~2.2 Hz (F2) and ~4.3 Hz (F1), independent of meteorological variability. Our analysis confirms that these two peaks correspond to S-wave resonances within the ice shelf. Forward modeling gives an ice-water interface depth of ~440 m, in close agreement with the Bedmap2 thickness estimate (466 m), supporting the robustness of this resonance-based interpretation.

This work demonstrates a new application of the HVSR technique for estimating the thickness of a floating ice shelf. With further validation, continuous tracking of these stable HVSR peaks may enable real-time monitoring of ice-shelf thickness changes. This passive, low-cost approach offers a valuable complement to remote sensing and radar surveys and provides important insights into ice-shelf stability in a changing climate.