Typhoon-Induced Wave–Current Coupling Dynamics in Intertidal Zones: Impacts on Protective Device of Ancient Forest Relics

Abstract

Extreme weather events, such as typhoons, induce strong wave–current interactions that significantly alter nearshore hydrodynamic conditions, particularly in shallow intertidal zones. This study investigates the influence of wind speed and water depth on wave–current coupling under typhoon conditions in Shenhu Bay, southeastern China—a semi-enclosed bay that hosts multiple ancient forest relics within its intertidal zone. A two-tier numerical modeling framework was developed, comprising a regional-scale hydrodynamic model and a localized high-resolution model centered on a protective structure. Validation data were obtained from in situ field observations. Three structural scenarios were tested: fully intact, bottom-blocked, and damaged. Results indicate that wave-induced radiation stress plays a dominant role in enhancing flow velocities when wind speeds exceed 6 m/s, with wave contributions approaching 100% across all water depths. However, the linear relationship between water depth and wave contribution observed under non-typhoon conditions breaks down under typhoon forcing. A critical depth range was identified, within which wave contribution peaked before declining with further increases in depth—highlighting its potential sensitivity to storm energy. Moreover, structural simulations revealed that bottom-blocked devices, although seemingly more enclosed, may be vulnerable to vertical pressure loading due to insufficient water exchange. In contrast, perforated designs facilitate an internal–external hydrodynamic balance, thereby enhancing protective effect. This study provides both theoretical and practical insights into intertidal structure design and paleo-heritage conservation under extreme hydrodynamic stress.

1. Introduction

The intertidal zone represents a dynamic interface between terrestrial and marine environments [1]. Characterized by periodic submergence and exposure, it plays a vital role in coastal sediment transport, nutrient cycling, and ecosystem stability [2]. As a transitional coastal environment, it exhibits complex, nonlinear morphodynamics governed by coupled allogenic and autogenic drivers—including wave climate, sediment supply, and relative sea-level change [3]. Due to its shallow depth and frequent exposure to hydrodynamic forcing, the intertidal zone is highly susceptible to environmental disturbances, particularly from wave–current interactions. Such interactions can be intensified during extreme weather events, especially typhoons, which generate strong winds, high waves, and storm surges capable of reshaping coastal morphology, damaging ancient forest relics, and undermining protective structures. These vulnerabilities highlight the need for a better understanding of wave–current interaction processes in intertidal zones.

Wave–current interactions were first observed in tidal regimes by Rayleigh. The foundational theory was formalized in the 1960s when Longuet-Higgins and Stewart (1960) derived the shallow-water radiation stress tensor [4]. This work was advanced by Bretherton and Garret (1968), whose collective contributions established the theoretical basis for modern numerical simulations of wave–current coupling [5]. Wave–current coupling has received increasing attention in recent coastal hydrodynamic studies [6,7,8]. It has been demonstrated that wave-induced radiation stress significantly alters current velocity, sediment resuspension, and nearshore flow patterns [9,10]. A previous study indicated that oceanic parameters and flow-field characteristics are significantly altered during typhoon conditions [11]. However, most existing research has focused on open coasts or estuarine systems, while the interaction between waves and tidal currents in intertidal zones, especially under typhoon conditions, remains insufficiently explored [12,13]. In addition, studies rarely address the influence of structural integrity on hydrodynamic performance during extreme events, despite the application of protective devices for coastal heritage preservation.

Located along the southeastern coast of China, Shenhu Bay is a semi-enclosed bay frequently exposed to typhoons and high-energy wave environments. The bay features a wide intertidal zone and hosts ancient forest relics that date back thousands of years [14]. These submerged forest remains, composed primarily of in situ tree stumps, are highly vulnerable to erosion and hydrodynamic damage [15]. Given their cultural and geological significance, effective strategies are required to assess and mitigate the impacts of extreme hydrodynamic events on these fragile coastal relics.

This study aims to investigate wave–current interactions in the intertidal zone of Shenhu Bay under typhoon conditions and to evaluate the protective performance of structural device surrounding ancient forest relics. A two-tier numerical modeling framework is established, consisting of a regional-scale model covering the entire bay and a localized high-resolution model centered on the protective structure. Three structural scenarios—intact, bottom-blocked, and damaged—are simulated to assess their effectiveness in dissipating flow energy. The results provide new insights into the mechanisms of wave–current coupling in shallow intertidal zone and offer practical guidance for the design, maintenance, and optimization of protective measures for intertidal heritage conservation under extreme climate conditions.

2. Materials and Methods

2.1. Study Area

Shenhu Bay is located in Jinjiang City, Fujian Province, China, with its bay head oriented to the east [14]. The water depth within the bay is shallow, averaging 10 m, and extends toward the bay mouth along a south-to-north axis, roughly parallel to the shoreline. The average slope inside the bay is approximately 0.23% [16]. Shenhu Bay experiences a regular semi-diurnal tidal current with an average tidal range of 3.61 m. The tidal current is primarily influenced by coastal currents [17]. The region has a subtropical marine climate characterized by a significant monsoon effect, with prevailing northerly winds in winter and southerly winds in summer, wind waves within the bay are substantial [17,18]. Located along China’s southeastern coast, Shenhu Bay is frequently affected by typhoons [19] (Figure 1).

2.2. Typhoon “Doksuri”

The fifth typhoon of 2023, “Doksuri” formed over the northwest Pacific Ocean on 21 July 2023. It moved in a west–northwest direction, bypassed northern Luzon Island in the Philippines, and entered the South China Sea. On the morning of July 28, it made landfall on the coast of Jinjiang, Fujian Province, and thereafter passed south of Shenhu Bay (Figure 1) [20]. At landfall, Doksuri was classified as a strong typhoon, with maximum wind speeds near its center reaching 50 m/s, a wind force of 15 on the Beaufort scale, and a minimum central pressure of 945 hPa [21]. It was the second most powerful typhoon to make landfall in Fujian since the founding of the People’s Republic of China. Typhoon Doksuri caused significant damage to infrastructure, and the intense hydrodynamic forces accompanying its landfall posed substantial challenges to the construction of protective devices for the ancient forest relics (Figure 1).

2.3. Data

Wind and wave data were derived from the publicly available ERA5 reanalysis dataset grid data provided by CCMP (https://cds.climate.copernicus.eu/ (accessed on 1 May 2025)). This dataset combined cross-calibrated satellite remote sensing sea surface wind field data and instrumental observation data through a variational assimilation analysis method to generate high-resolution grid data with a 1 h time interval and a spatial resolution of 0.25°. The dataset provided parameters such as wind speed, wind direction, wave height, wave direction, and wave period for the study area, which were used as boundary conditions for the model. During the typhoon, the maximum wind speed in the area was approximately 14 m/s, with southwest and north (N) as the dominant wind directions. The maximum wave height reached 3 m, with the dominant wave directions being south (S) and southwest (SW) (Figure 2).

A fixed hydrological monitoring station deployed in the intertidal zone of Shenhu Bay collected high-quality, long-term observations from February to October 2023 at 10 min intervals. It acquired key hydrological data during the landfall of Typhoon “Doksuri” on the Fujian coast in July (Figure 3). Intertidal elevation data were also obtained with a Phantom 4 RTK unmanned aerial vehicle (SZ DJI Technology Co., Ltd., Shenzhen, Guangdong, China) at 0.01 m spatial resolution. During typhoons, the flow velocity in the intertidal zone can reach up to 1.2 m/s, with predominant flow directions toward north-east-east (NEE) and south-west-west (SWW) (Figure 2).

2.4. Basic Principle

The MIKE numerical model utilized in this study is a professional water flow simulation system developed by the Danish Hydraulic Institute. It is widely employed in complex marine hydrodynamics, including wave–current coupling and sediment erosion and deposition processes. The MIKE numerical model performs calculations using an unstructured grid, offering several advantages such as a reliable algorithm, stable computations, a user-friendly interface, and robust pre- and post-processing capabilities. It has been applied in many countries, with hundreds of documented successful applications and reliable results, earning widespread recognition within the industry [22,23,24,25,26].

This study established a two-dimensional positive pressure tidal current mathematical model and a new-generation wave spectrum mathematical model. These models accurately described the entire process of wind wave generation, growth, and attenuation following strong winds while accounting for the effects of wind stress and wave radiation stress on the tidal current field [27]. Additionally, to determine the extreme conditions caused by typhoons, a three-dimensional hydrodynamic model was developed.

Basic governing equations of three-dimensional hydrodynamic forces are as shown in Equations (1)–(5).

$${\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}+{\displaystyle \frac{\partial w}{\partial z}}=S$$

(1)

$${\displaystyle \frac{\partial u}{\partial t}}+{\displaystyle \frac{\partial u^2}{\partial x}}+{\displaystyle \frac{\partial vu}{\partial y}}+{\displaystyle \frac{\partial wu}{\partial z}}=fv-g{\displaystyle \frac{\partial \zeta }{\partial x}}-{\displaystyle \frac{1}{{\rho }_0}}{\displaystyle \frac{\partial P_a}{\partial x}}-{\displaystyle \frac{g}{{\rho }_0}}{\int }_z^{\zeta }{\displaystyle \frac{\partial \rho }{\partial x}}dz-{\displaystyle \frac{1}{{\rho }_{0}h}}\left({\displaystyle \frac{\partial S_{xx}}{\partial x}}+{\displaystyle \frac{\partial S_{xy}}{\partial y}}\right)+F_u+{\displaystyle \frac{\partial }{\partial z}}\left(v_t{\displaystyle \frac{\partial u}{\partial z}}\right)+u_{s}S$$

(2)

$${\displaystyle \frac{\partial v}{\partial t}}+{\displaystyle \frac{\partial v^2}{\partial y}}+{\displaystyle \frac{\partial vu}{\partial x}}+{\displaystyle \frac{\partial wv}{\partial z}}=fu-g{\displaystyle \frac{\partial \zeta }{\partial y}}-{\displaystyle \frac{1}{{\rho }_0}}{\displaystyle \frac{\partial P_a}{\partial y}}-{\displaystyle \frac{g}{{\rho }_0}}{\int }_z^{\zeta }{\displaystyle \frac{\partial \rho }{\partial y}}dz-{\displaystyle \frac{1}{{\rho }_{0}h}}\left({\displaystyle \frac{\partial S_{xy}}{\partial x}}+{\displaystyle \frac{\partial S_{yy}}{\partial y}}\right)+F_v+{\displaystyle \frac{\partial }{\partial z}}\left(v_t{\displaystyle \frac{\partial v}{\partial z}}\right)+v_{s}S$$

(3)

$$F_u={\displaystyle \frac{\partial }{\partial x}}\left(2A{\displaystyle \frac{\partial u}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left(A\left({\displaystyle \frac{\partial u}{\partial y}}+{\displaystyle \frac{\partial v}{\partial x}}\right)\right)$$

(4)

$$F_v={\displaystyle \frac{\partial }{\partial y}}\left(2A{\displaystyle \frac{\partial v}{\partial y}}\right)+{\displaystyle \frac{\partial }{\partial x}}\left(A\left({\displaystyle \frac{\partial u}{\partial y}}+{\displaystyle \frac{\partial v}{\partial x}}\right)\right)$$

(5)

where t represents time. x, y and z are Cartesian coordinates. u, v and w are the velocity components in the x, y and z directions, respectively. f denotes the Coriolis force parameter, defined as f = 2Ωsinφ, where Ω is the Earth’s rotational angular speed, and φ is the geographical latitude. ζ represents the tide level. h = ζ + d represents the total water depth, where d is the distance from the bottom to the stationary sea surface. g is gravitational acceleration. ρ₀ is the reference water density, and ρ is the actual water density. S is the source and sink term. v_t is the vertical eddy viscosity coefficient. P_a is atmospheric pressure. S_xx, S_xy, S_yx, and S_yy are the components of radiation stress. u_s and v_s. are the flow rates of the source and sink terms, respectively. F_u and F_v are the horizontal stress forces. A is the horizontal eddy viscosity coefficient [26].

The conservation equation of wave action used in the wave field is Equation (6).

$${\displaystyle \frac{\partial A}{\partial t}}+{\nabla }_x\left(c_{g}A\right)+{\nabla }_{\theta }\left(c_{\theta }A\right)+{\nabla }_{\sigma }\left(c_{\sigma }A\right)=S$$

(6)

A represents the wave energy density spectrum. σ is the relative frequency, defined as σ = 2πf; c_g denotes the group velocity. c_σ represents the variation in relative frequency due to changes in water depth and current. c_θ accounts for wave refraction caused by water depth and current. θ indicates the wave direction [26,28,29].

S is a source term function expressed as spectral density, which is expressed as Equation (7).

$$S=S_{in}+S_{nl}+S_{ds}+S_{bot}+S_{surf}$$

(7)

S_in represents wind input energy. S_nl denotes energy dissipation caused by nonlinear wave interactions. S_ds represents energy dissipation caused by whitecaps. S_bot accounts for energy dissipation caused by bottom friction. S_surf represents energy dissipation caused by wave breaking induced by changes in water depth [30,31].

2.5. Model Setup

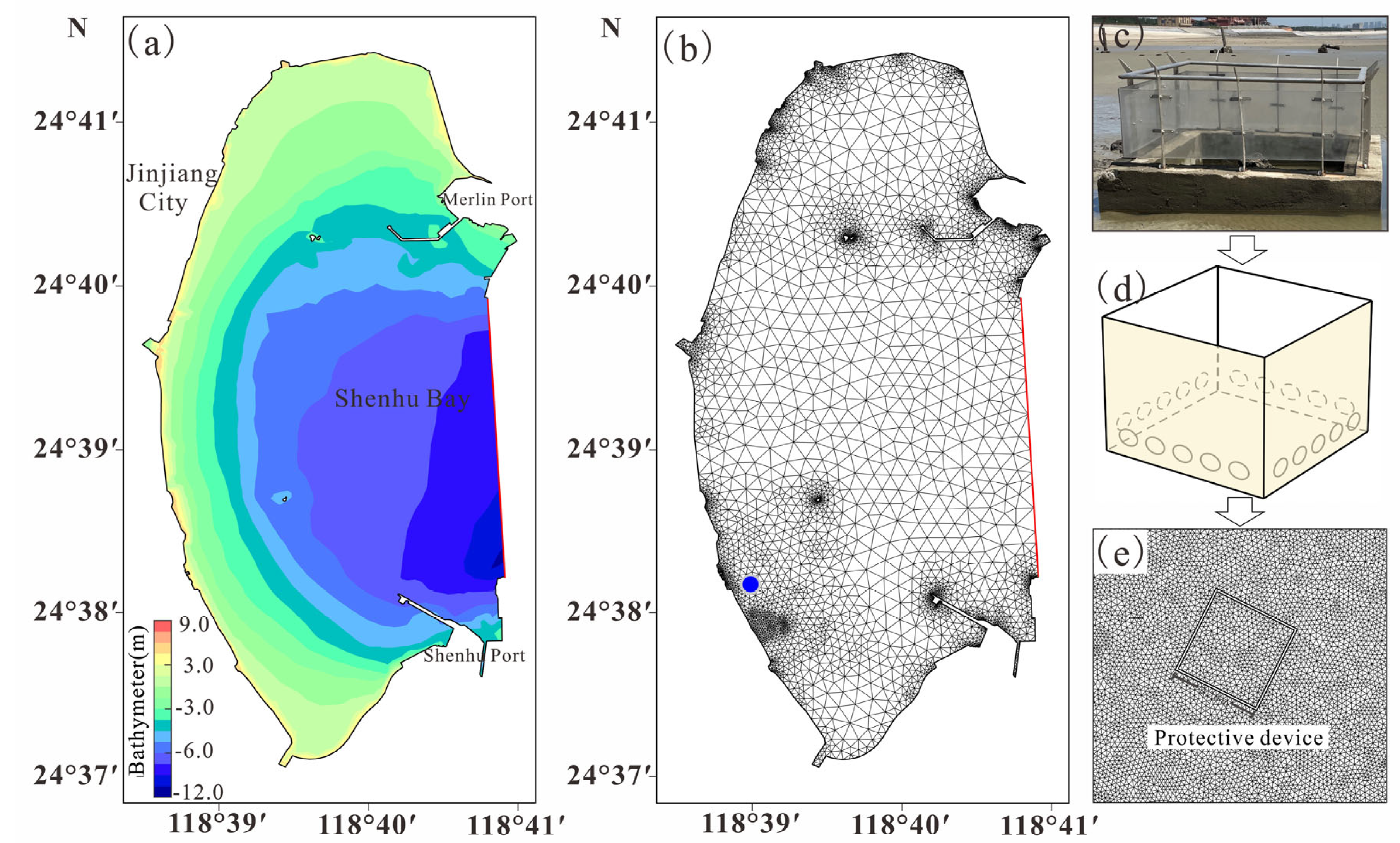
Based on the analysis of hydrology, sediment, topography, shoreline, and other relevant data in the study area, and with the aim of minimizing the influence of boundary effects on the flow field around the protective devices for ancient forest relics, this study defined the calculation domain’s scope. The large-area model was used to model validation and analyze wave–current interactions in the intertidal zone and covered the entire Shenhu Bay, while the small-scale model focused on evaluating the protective performance of the ancient forest relic protection structure within the bay (Figure 4b,e). This study employs Typhoon “Doksuri” as a case to conduct comparative simulations: current-only condition versus wave–current coupled scenario. Current-only condition refer to simulations of tidal currents without wind or wave forcing, whereas wave–current coupled scenario include the effects of both wind and waves.

The small-area model centers on a protective device modeled as a semi-enclosed cubic structure with an open top and vertical side panels, within which the ancient forest relic is positioned at the center (Figure 4d). A detailed three-dimensional hydrodynamic model was developed to simulate flow-structure interactions around this device (Figure 4e). The protective device’s minimum mesh resolution was approximately 0.06 m. Given that the diameter of ancient tree stumps typically ranges from tens of centimeters to 1 m, this resolution was sufficient for studying ancient forest relics (Figure 4e).

Due to the complex hydrodynamic environment of intertidal zone and the dynamic evolution of the protective structure, the device may become gradually buried under sediment or suffer damage from flow erosion. To evaluate protection effectiveness under different conditions, this study designed three device states: fully functional (the device with holes), orifice-obstructed by siltation (the device without holes), and structurally damaged. To assess the protective performance of the three device configurations under typhoon conditions, three experiments were conducted using identical environmental and hydrodynamic parameters.

3. Results

3.1. Model Validation

By comparing the model results with the measured data from fixed hydrological observation station in the study area’s intertidal zone, the simulated water depth and velocity generally matched the observed trends in the flow field. However, the simulated flow velocity showed some degree of variability. Typhoons had a significant impact on water reduction in Shenhu Bay, with the average velocity increasing during these events (Figure 5). These findings indicated that extreme typhoon conditions enhanced water dynamics in the intertidal zone, posing substantial challenges to the protection of ancient forest relics.

Specifically, the observed discrepancies between simulated and measured currents can be attributed to (i) inherent limitations in the turbulence closure scheme, which may not adequately represent the complex, non-equilibrium turbulent processes characteristic of shallow intertidal environments, and (ii) insufficient resolution of the wind forcing data, particularly in capturing the localized, high-intensity wind fields associated with typhoon events over Shenhu Bay. Despite these discrepancies, the model reproduces the observed current trends well and is therefore suitable for subsequent analyses.

3.2. Flow Field in the Intertidal Zone Under Wave–Current Coupling

We evaluated wind and wave impacts on intertidal hydrodynamic processes at three characteristic tidal phases (high tide, flood tide, ebb tide), with focused analysis on wave-induced contributions to flow fields at 7 characteristic points in the intertidal zone (Figure 6). Results indicate under wind–wave effects, maximum flow velocities exceeded 0.80 m/s at all phases, representing increases >0.75 m/s (>1500% enhancement) compared to current-only conditions. Under current-only condition, flow directions were predominantly S and SE, with velocities approximating 0.03 m/s. Under the condition of considering wind and wave, SE-directed alongshore currents dominated, primarily occurring in depths < 0.24 m. Velocities decreased in zones > 2.4 m depth. This demonstrates depth-dependent modulation of wind–wave effects.

3.3. Impact of Wind Speed on Wave–Current Interactions

Waves are generated by wind-induced surface friction and atmospheric pressure fluctuations over the sea. Wind intensity directly governs wave–current interactions. Consequently, wind field characteristics constitute a critical factor in studying wave–current coupling mechanisms. Owing to spatial and temporal variations in these wind characteristics, the influence of waves on current velocity exhibits significant heterogeneity across both time and location within the intertidal zone. During the typhoon event, prevailing winds were predominantly NNE, with speeds ranging from 5 to 14 m/s. While storm surge effects within the region were negligible, pronounced alterations in current velocity were observed. Overall, at wind speeds below 6 m/s, the wave contribution to current velocity varied substantially by location, ranging from 4% to 96%. In contrast, at wind speeds exceeding 6 m/s, the wave contribution approached 100% uniformly across all observed positions (Figure 7).

Analysis of current velocity–wind speed relationships across seven representative stations reveals pronounced divergence in wave contribution to flow dynamics at wind speeds below 6 m/s, ranging from 4% to 96%. Once wind speeds exceed 6 m/s, the wave contribution asymptotically approaches 100% with increasing wind intensity (Figure 8).

3.4. Impact of Water Depth on Wave–Current Interactions

Significant topographic variability characterizes the intertidal zone. At this study sites (elevation: +0.85 to −1.92 m), water depths are shallower than the wave base, inducing pervasive wave breaking.

Water depth critically modulates wave impacts on currents. Under non-typhoon condition, background currents in the intertidal zone typically remain <0.04 m/s. However, wave–current interactions enhance velocities differentially, with wave contribution increasing seaward. The offshore station P7 exhibited maximum velocity amplification (up to +0.07 m/s at high tide). Thus, in shallow intertidal environments, waves exert disproportionately strong influences on flow fields, exhibiting positive correlations with depth: deeper waters experience greater wave-driven velocity contributions (43–80%) and absolute increases (0.01–0.07 m/s) during routine conditions (Figure 9a).

Under typhoon “Doksuri”, all locations showed strong velocity responses (>95% wave contribution), though depth-dependent sensitivities emerged. Velocity increments ranged from 0.30 to 0.64 m/s, with anomalously high gains (~0.75 m/s) at shallower sites (Figure 9b).

3.5. Impact of Wave–Current Interactions on Protective Device

The engineering of protective device for intertidal targets necessitates hydrodynamic extremes under extreme events. This study therefore positions the protective structure at Station P3—the locus of maximum wave impact during typhoon conditions—subjecting it to peak flow velocities induced by 14 m/s winds to simulate critical hydrodynamic forcing. Moreover, this study simulates holes of protective structures through culvert configuration in hydraulic engineering systems. Two experimental scenarios—current-only and wave–current coupled condition—were designed for comparative analysis. Velocity distributions during critical flow phases across the structure were quantified to determine wave contribution magnitudes.

Comparative experiments reveal analogous flow fields during extreme events. Structural obstruction reduces flow cross-section, accelerating lateral velocities (Figure 10). Most of flow circumvents the structure with lateral dispersion, while minimal discharge penetrates holes. Concurrently, downstream flow reverses upstream to fill the wake void, generating reversed flow vectors and vortex formation behind the structure. Under current-only forcing, ambient velocities remain below 1.8 m/s, whereas wave–current coupling elevates peripheral velocities to ~2.2 m/s. Maximum wave-induced velocity increments reach 1.8 m/s along the flanks. Crucially, the structure effectively shields internal targets from wave energy, limiting interior velocity increases to 0.3 m/s (Figure 11).

3.6. The Protective Effects of Different Forms of Protective Devices Under Typhoon Conditions

In the protective device model with holes, analysis of the typical water flow at a representative moment indicated that the device exhibited a significant buffering effect on water flow, with its effect on flow rate reaching approximately 40%. Water entered the device without noticeable disturbances, and the flow rate in the first half of the device was slightly greater than that in the second half (Figure 10).

The section shown in Figure 12 was selected to cut through the entire model, effectively capturing the water flow process through the culvert inlet device. Prior to the water flow impacting the device, the water level was partially elevated in the upstream region, with the elevation height depending on the flow velocity. Higher flow velocities led to greater elevations; however, the water level did not exceed the top of the device or cause downward impacts on the ancient forest relics. Once the water entered the device, the diversion speed was higher in the front portion of the device, and the water depth was relatively shallow. As water exited from the latter half of the device, the flow rate slowed because of the holes, resulting in increased water depth, though the elevation remained lower than that observed prior to inflow (Figure 13).

When water flowed through the device, the flow rate on both sides of the device was greater than 2 m/s, with the maximum flow rate inside the device measuring 1.12 m/s, which is 56% of the flow rate on the external sides. These results indicate that the protective device effectively functioned as a buffer, reducing the hydrodynamic force’s impact on the ancient forest relics to a certain extent. Variations in flow rate and water depth were observed at different positions within the device. The flow diversion speed was greater in the first half of the device compared to the second half, with the maximum flow rate of 1.12 m/s occurring in the first half. In contrast, the flow rate in the second half ranged from 0.2 to 0.5 m/s, and the water depth in this region was approximately 0.2 m greater than in the first half.

In the model without holes, water flowed through the unit from both sides. The inflow of currents into the interior is effectively blocked, thereby shielding the central ancient forest relic from direct hydrodynamic impact. When the damaged device was subjected to the same flow rate, the water level inside the device rose significantly, with the degree of risk being greater than in the previous two cases. The device demonstrated a buffering effect; however, the flow rate in the middle part of the device was high, with the maximum flow rate reaching 0.32 m/s, which was 45% of the flow rate prior to entering the device (Figure 14).

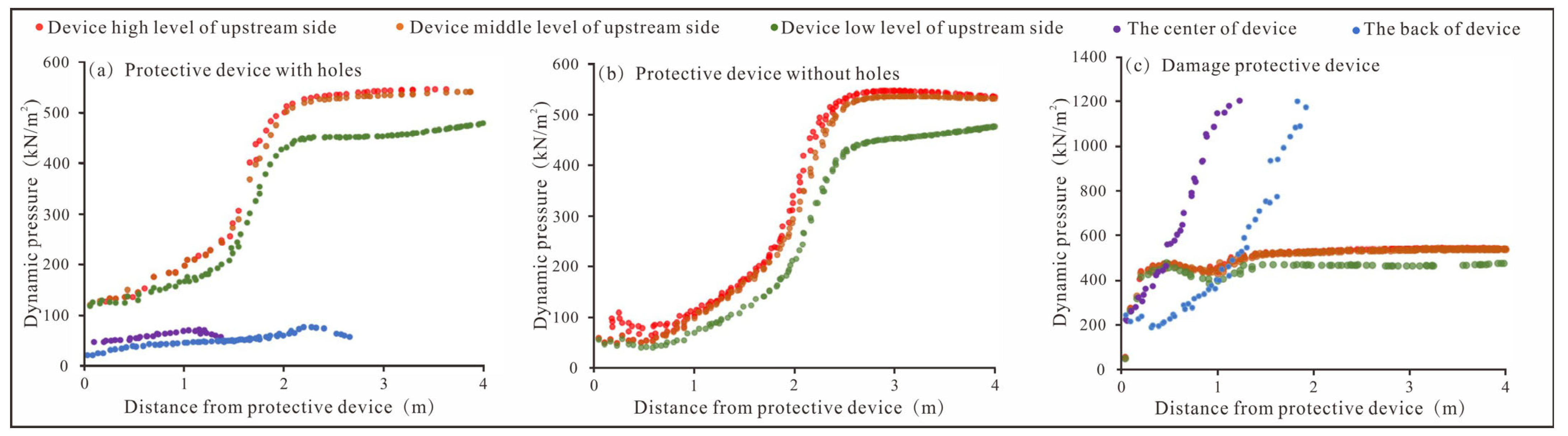
During tidal fluctuations, water continuously impacted the protective device, causing the flow rate at the oncoming surface to rapidly decrease to 0 m/s. This resulted in localized high pressure, which was a significant factor influencing the stability of the protective device. The impact load of water flow on the protective device was calculated using the Bernoulli equation and converted into dynamic pressure.

$$P={\displaystyle \frac{\rho V^2}{2}}$$

(8)

In Equation (8), P represents the dynamic pressure (kN/m²), ρ is the water density (kg/m³), and V is the flow rate (m/s). The three-dimensional model established in this study divided the water flow into 10 layers from bottom to top. Since the dynamic pressure changes among water layers with similar distances were minimal, the inlet pressure of the 9th, 5th, and 2nd layers was calculated and analyzed separately to determine the overall water flow pressure behavior of the protective device. Taking the device with a culvert as an example, the dynamic pressure of the water layer was higher at greater depths, while it decreased slightly toward the bottom. At the higher water level, the dynamic pressure can reach 550 kN/m². Although the dynamic pressure at the bottom layer had decreased, it still reached 480 kN/m². Calculations and analysis of the dynamic pressure in the inner central area of the protective device demonstrated that the device exhibited a significant buffering effect, greatly reducing the impact of water flow on the protected object, with the buffering effect reaching 88.9%. However, in the case of damage, the protective device was unable to perform its protective function; instead, it accelerated water flow, increasing damage to the protected object, with dynamic pressure reaching up to 1200 kN/m² (Figure 15).

4. Discussion

This paper takes Typhoon “Doksuri” as a case study and conducts numerical simulation experiments based on field observation data from Shenhu Bay. It demonstrates that wind speed and water depth play important roles in wave–current interaction in the intertidal zone. Without the wave, the influence of tidal currents is limited, and flow velocities at different depths are generally low. Under wave–current coupling, radiation stress induced by waves produces additional forces that enhance flow velocity, resulting in significant differences under varying conditions. As wind speed increases, the contribution of waves to current velocity generally increases, except in deeper water areas. This is because the intertidal zone is generally shallower than the local wave base, causing waves to break and dissipate energy during shoreward propagation, which reduces their ability to drive the flow. Thus, wave contributions to velocity are limited in shallow areas (P1–P3), while in deeper locations (P4–P7), waves contribute more even under low wind speeds. As shown in Figure 8, when wind speed is low, wave energy is almost fully dissipated in shallow areas, leading to low contribution, while in deeper regions, wave energy is not fully consumed, resulting in higher contributions. When wind speed is below 6 m/s, the wave contribution varies greatly across depths. However, when wind speed reaches 6 m/s, wave energy becomes dominant, and wave contribution to flow velocity approaches 100% at all depths.

Under non-typhoon condition, wave contribution to current velocity exhibits a generally linear increase with water depth. However, under typhoon scenarios—where wind speeds commonly exceed 6 m/s—this linearity is disrupted as wave energy becomes dominant. Under non-typhoon conditions, wave energy is modulated by smooth shoaling and depth-limited breaking, while wave–current feedbacks remain weak; the wave-induced contribution to currents therefore scales almost linearly with water depth. this linearity is disrupted by several interacting nonlinear mechanisms: (i) wave–current interaction modifies effective propagation speeds and breaking thresholds, with opposing flows causing wave blocking and enhanced breaking; (ii) radiation–stress gradients intensify with wave energy and, through coupling with depth-limited breaking and wind-driven surge, render momentum input depth-independent; and (iii) directional misalignment of wind, waves, and tides induces refraction and redistributes momentum along- and offshore, imparting a strong directional dependence to the current response.

Notably, at point P3, which represents an intermediate water depth, wave contribution reaches its maximum. Beyond this point, further increases in water depth result in a decline in wave-induced momentum input. This observation suggests the existence of a critical depth range that is particularly sensitive to typhoon-induced wave forcing. In shallower waters, wave energy is largely dissipated under both calm and stormy conditions, while in deeper areas, wave contributions remain consistently high during fair weather. Determining the precise depth threshold that defines this sensitivity zone requires further targeted investigation in future studies.

This study established three protection device models, which provide a reference for evaluating the protective effectiveness of devices in different structural states. The complete structure exhibited good buffering performance and effectively protected the internal ancient forest remains. When the bottom openings were buried, the device lost its perforated structure, and water was unable to flow into the interior. Although the device without openings seemed to offer better protection, it introduced the risk of direct top-down impact when water levels reached the height of the structure. In contrast, the perforated design allowed water to enter from below, enabling the internal water level to remain consistent with the exterior during tidal fluctuations, thereby avoiding such risks. For future conservation, regular inspection of the protective devices is recommended to assess their effectiveness and promptly repair or replace damaged components to prevent further damage to the heritage.

The ancient forest relics in Shenhu Bay are distributed in the intertidal zone. This study investigated the protection performance for a single relic and offered a multi-perspective reference for future design. Subsequent studies should incorporate field validation data and account for sediment dynamics and long-term morphological evolution to refine the model and enhance its predictive capacity.

5. Conclusions

This study established a two-tier hydrodynamic modeling framework to investigate wave–current interactions in the intertidal zone of Shenhu Bay under typhoon conditions, with a particular focus on evaluating the performance of protective structures surrounding paleo-forest relics. By simulating multiple wind speeds and water depths across three tidal phases, the results revealed several key findings:

(1)

Wave-induced contributions to current velocity increased markedly under typhoon conditions, often exceeding 95%, particularly when wind speeds surpassed 6 m/s.

(2)

The linear relationship between water depth and wave influence observed under normal weather condition was disrupted during storm events, with a critical depth range identified around P3, where wave contribution peaked.

(3)

Structural simulations demonstrated that intact and perforated protection devices provided better hydrodynamic buffering by enabling water exchange, whereas blocked or damaged structures increased vertical flow pressure risk.

These findings not only improve our understanding of wave–current coupling in shallow tidal flats but also provide practical insights for the design, maintenance, and emergency response planning of coastal heritage protection structures under extreme weather conditions. These findings are not site-specific; the framework and key inferences are readily transferable to tropical-subtropical, micro- to mesotidal, wave-dominated semi-enclosed bays with intertidal zone. Future research should incorporate sediment dynamics, long-term morphological evolution, and in situ field validation to enhance model accuracy and applicability. In addition, expanding the modeling framework to include multiple relic sites across the bay would offer a more comprehensive foundation for regional-scale conservation strategies.