Design of an Observing System Simulation Experiment for the Operational Model of the Southwestern Coast of Iberia (SOMA)
Abstract
1. Introduction
2. Algarve General Circulation
3. Observation System Simulation Experiment
4. Data-Assimilation Scheme
5. Methodology
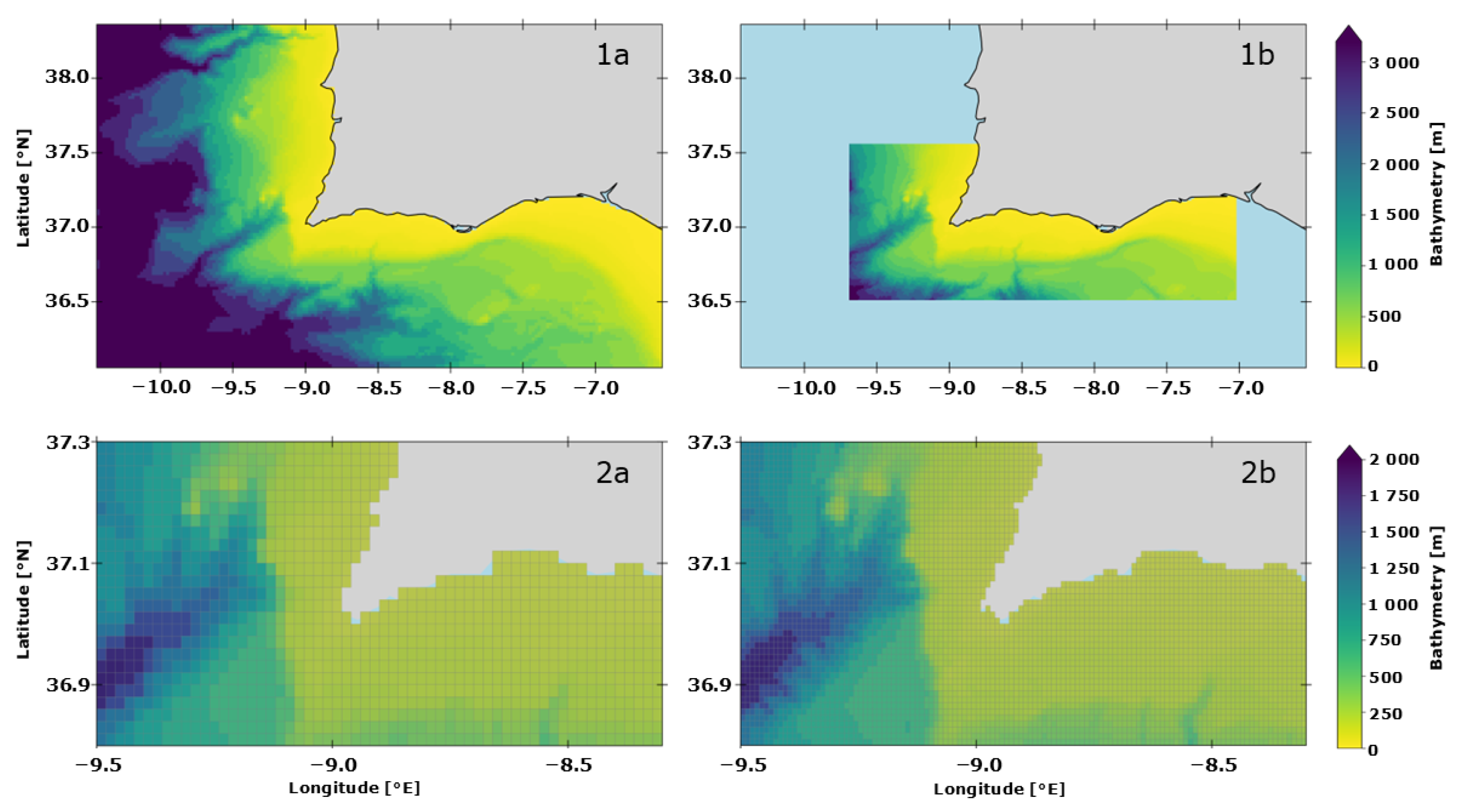
5.1. The Operational Forecasting System of the Algarve
5.2. SOMA OSSE System Design
5.2.1. Nature-Run and Free-Run Configurations
5.2.2. Data-Assimilation System
5.2.3. Synthetic Observations and the Reference OSE
- CMEMS SST NRT ODYSSEA L4 Product [67]: an operational monitoring product providing near-real-time (NRT) SST fields. Updated daily, it is optimized for operational forecasting and rapid environmental monitoring. This product has a finer spatial resolution of and is designed to capture short-term variability.
- CMEMS SST Reprocessed L4 Product [68]: a historical, consistently reprocessed climate product that has been available since 1 January 1982. It offers high-quality SST fields produced with rigorous reanalysis methods and quality-control protocols. The product is intended for climate studies and long-term analyses, with a horizontal resolution of .
6. Results and Discussion
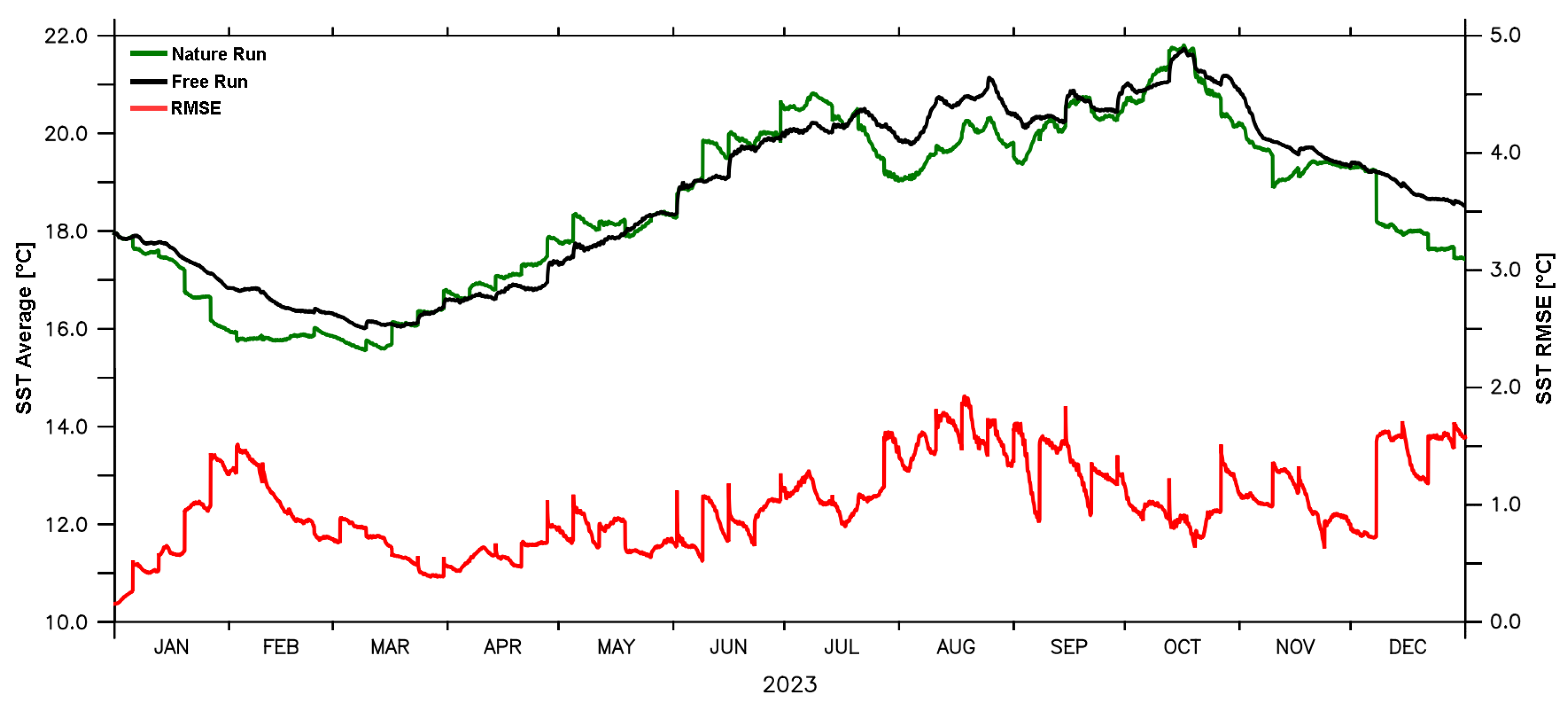
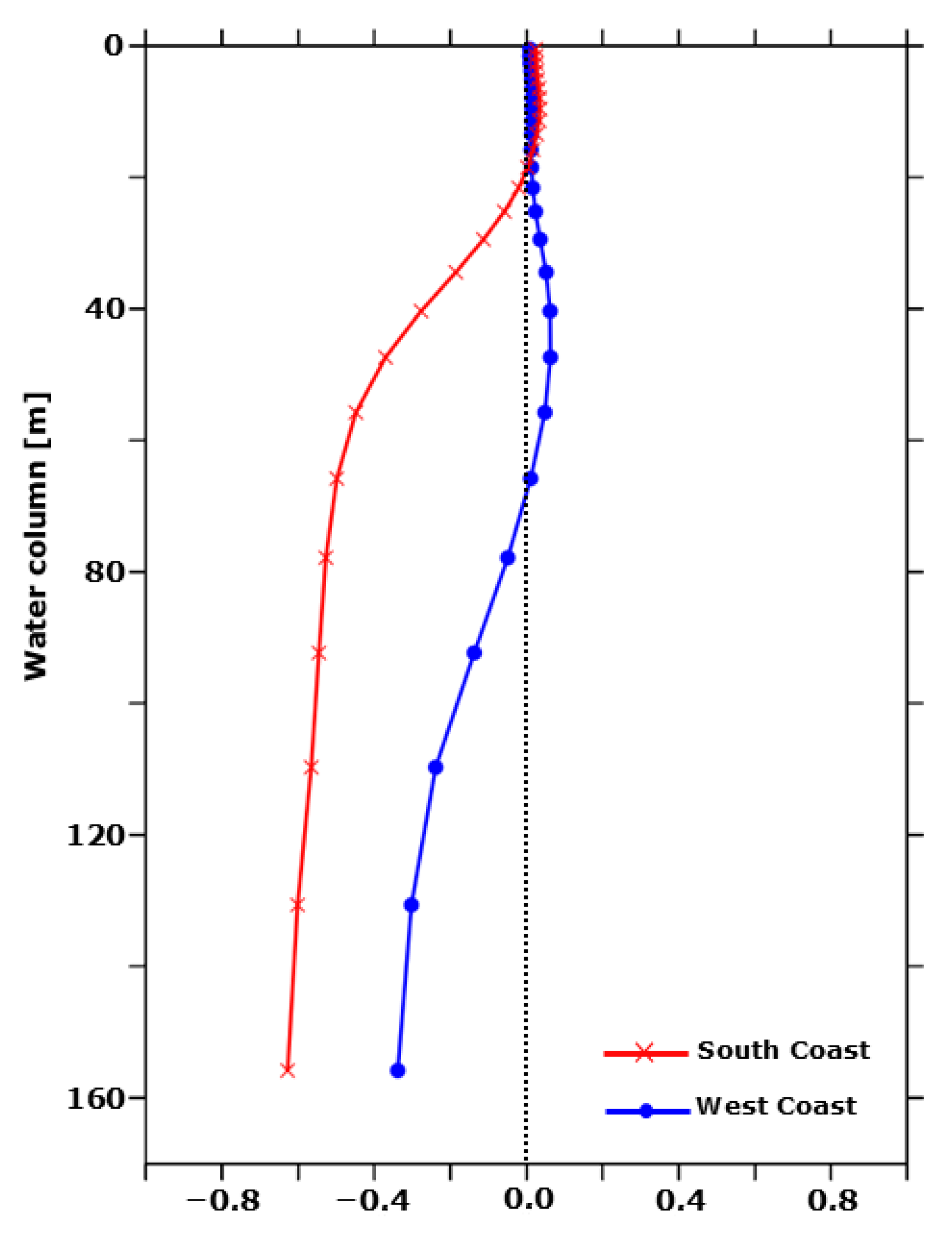
6.1. SOMA Free Run Integration
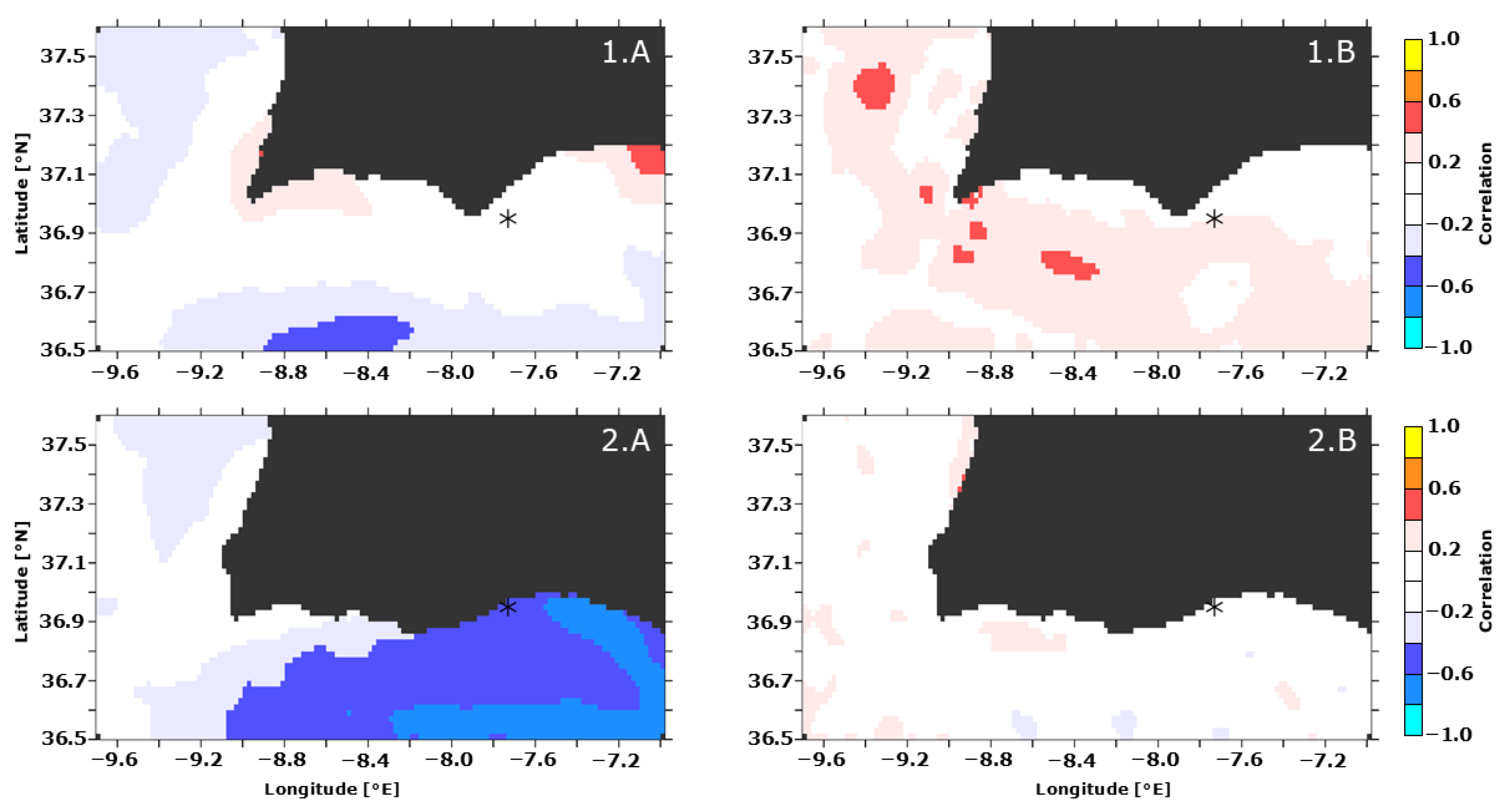
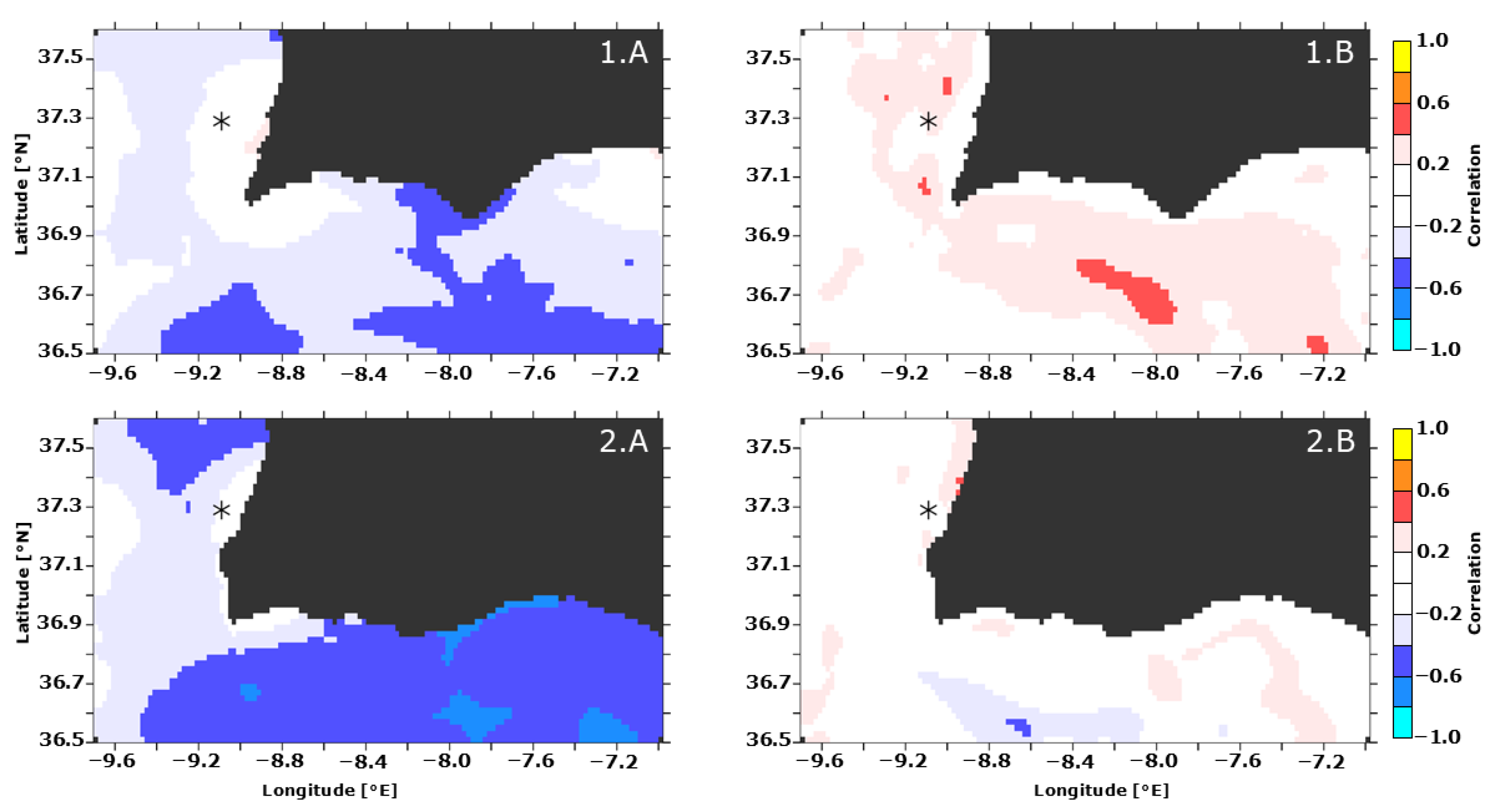
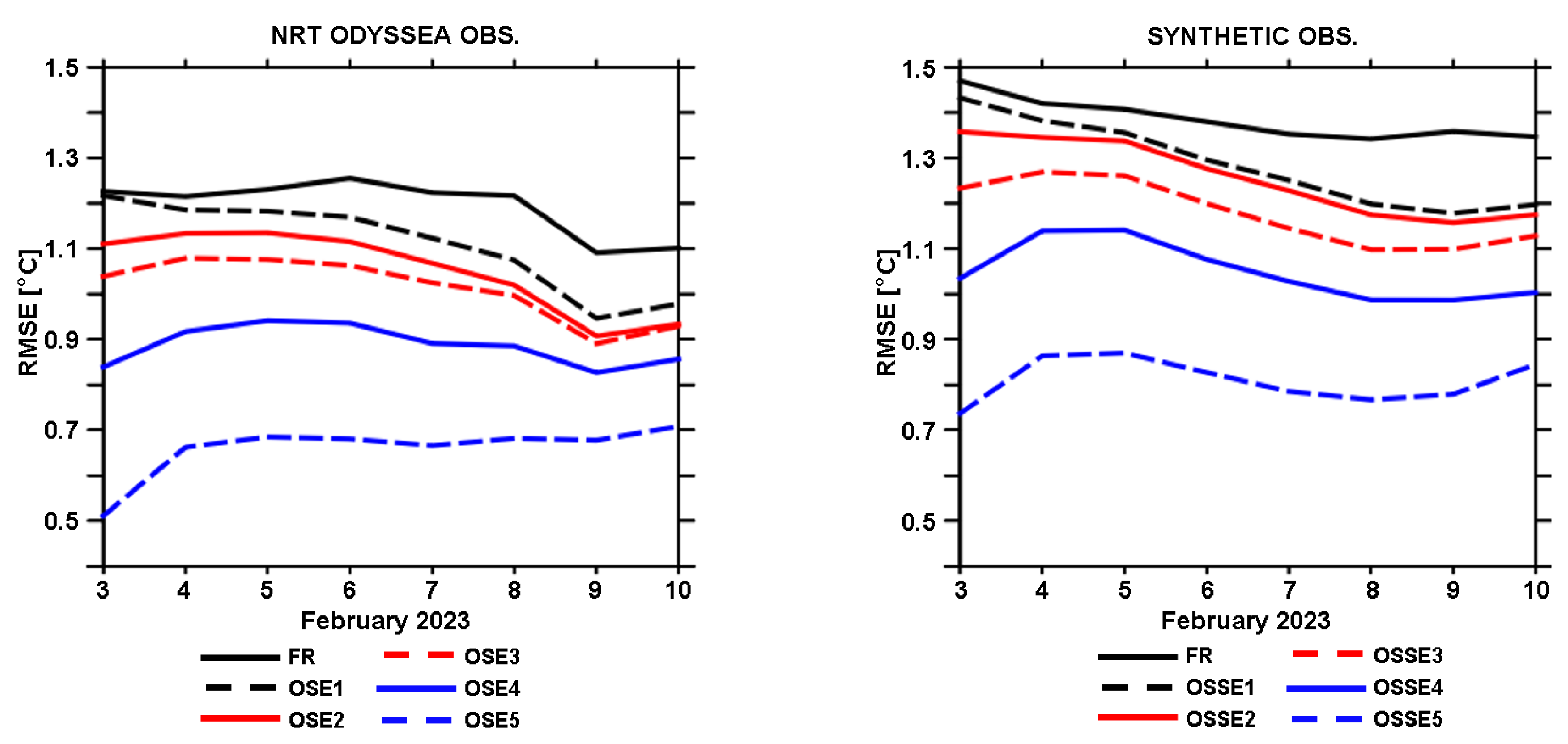
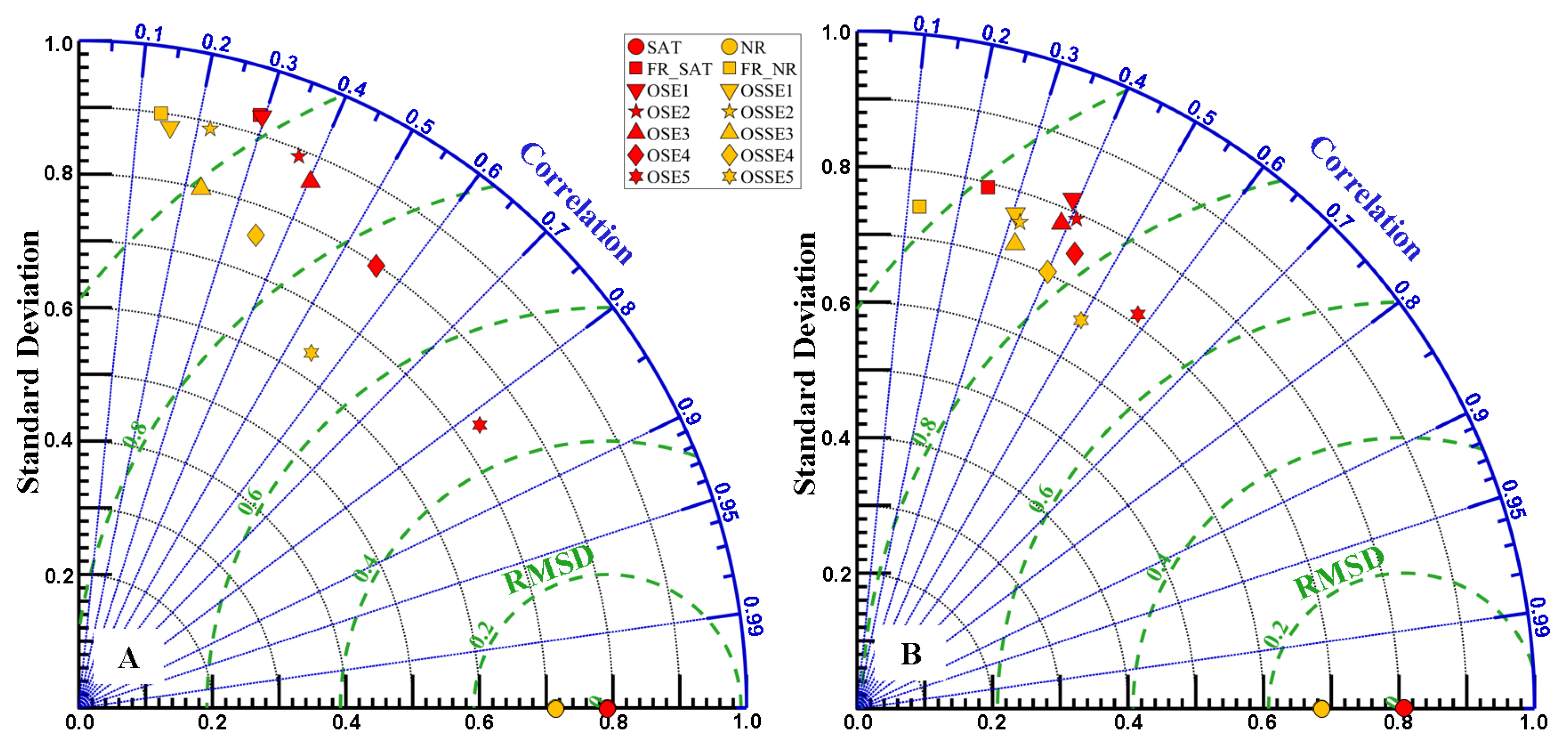
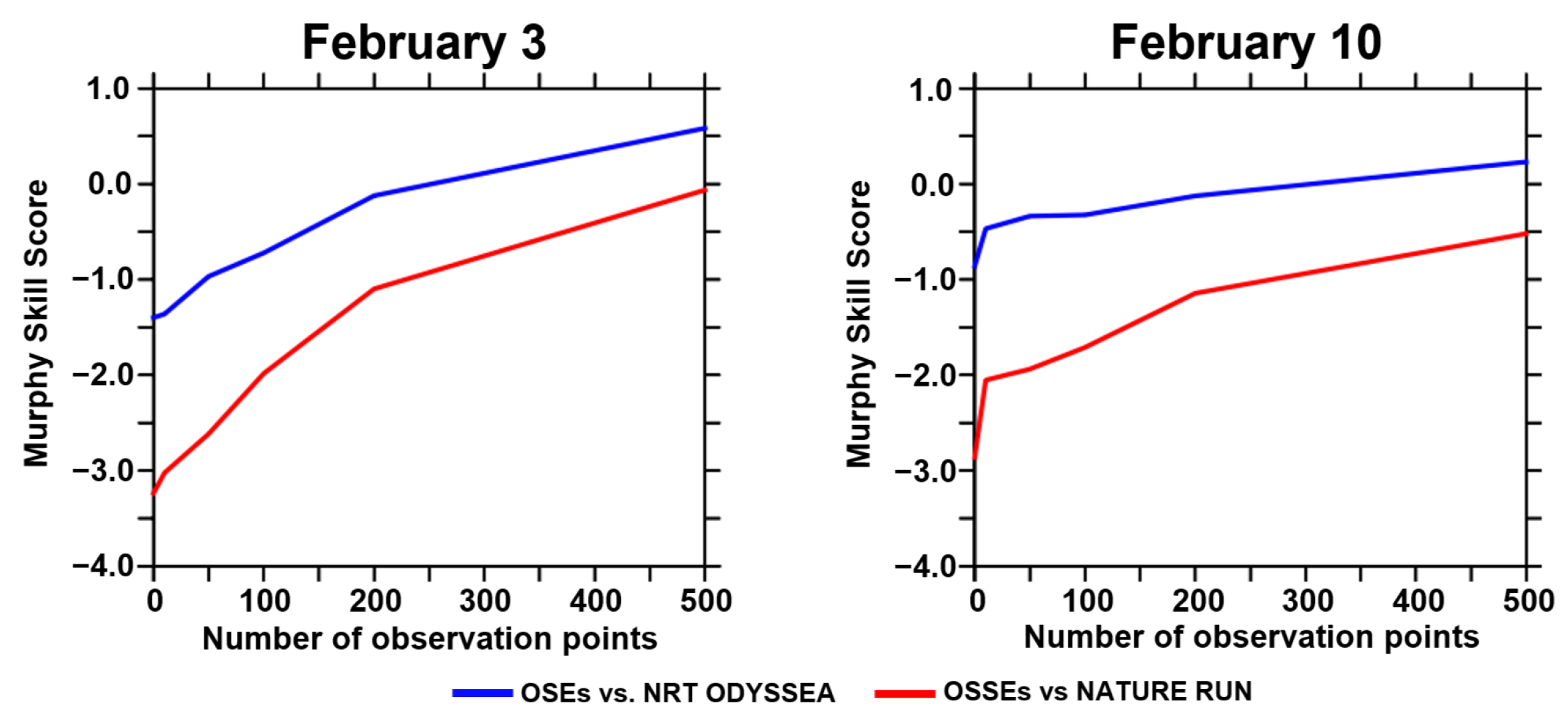
6.2. SOMA OSSE System Assessment
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Statistical Metrics
Appendix A.1. Spatially Integrated Averages and Standard Deviations
Appendix A.2. Spatially Integrated RMSE
Appendix A.3. Temporally Integrated Averages and Standard Deviations
Appendix A.4. Temporally Integrated RMSE
Appendix A.5. Murphy Skill Score
Appendix A.6. Taylor Diagrams
Appendix B. EnOI General Formulation
References
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, 2nd ed.; Prentice Hall: Philadelphia, PA, USA, 2007. [Google Scholar]
- Griffies, S.M. Some Ocean Model Fundamentals. In Ocean Weather Forecasting: An Integrated View of Oceanography; Springer: Dordrecht, The Netherlands, 2006; pp. 19–73. [Google Scholar] [CrossRef]
- Le Traon, P.Y. Satellites and Operational Oceanography. In Operational Oceanography in the 21st Century; Springer: Dordrecht, The Netherlands, 2011; pp. 29–54. [Google Scholar] [CrossRef]
- Frederikse, T.; Landerer, F.; Caron, L.; Adhikari, S.; Parkes, D.; Humphrey, V.W.; Dangendorf, S.; Hogarth, P.; Zanna, L.; Cheng, L.; et al. The causes of sea-level rise since 1900. Nature 2020, 584, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Enri, J.; Aldarias, A.; Mulero-Martínez, R.; Vignudelli, S.; Bruno, M.; Mañanes, R.; Izquierdo, A.; Fernández-Barba, M. Satellite Radar Altimetry Supporting Coastal Hydrology: Case Studies of Guadalquivir River Estuary and Ebro River Delta (Spain). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3587–3599. [Google Scholar] [CrossRef]
- Mills, L.; Janeiro, J.; Martins, F. Baseline climatology of the Canary Current Upwelling System and evolution of sea surface temperature. Remote Sens. 2024, 16, 504. [Google Scholar] [CrossRef]
- Liu, Z.; Xing, X.; Chen, Z.; Lu, S.; Wu, X.; Li, H.; Zhang, C.; Cheng, L.; Li, Z.; Sun, C.; et al. Twenty years of ocean observations with China Argo. Acta Oceanol. Sin. 2023, 42, 1–16. [Google Scholar] [CrossRef]
- Legler, D.; Freeland, H.; Lumpkin, R.; Ball, G.; McPhaden, M.; North, S.; Crowley, R.; Goni, G.; Send, U.; Merrifield, M. The current status of the real-time in situ Global Ocean Observing System for operational oceanography. J. Oper. Oceanogr. 2015, 8, s189–s200. [Google Scholar] [CrossRef]
- Le Traon, P.; Antoine, D.; Bentamy, A.; Bonekamp, H.; Breivik, L.; Chapron, B.; Corlett, G.; Dibarboure, G.; DiGiacomo, P.; Donlon, C.; et al. Use of satellite observations for operational oceanography: Recent achievements and future prospects. J. Oper. Oceanogr. 2015, 8, s12–s27. [Google Scholar] [CrossRef]
- Privé, N.C.; McGrath-Spangler, E.L.; Carvalho, D.; Karpowicz, B.M.; Moradi, I. Robustness of Observing System Simulation Experiments. Tellus A Dyn. Meteorol. Oceanogr. 2023, 75, 309–333. [Google Scholar] [CrossRef]
- Halliwell, G., Jr.; Srinivasan, A.; Kourafalou, V.; Yang, H.; Willey, D.; Le Hénaff, M.; Atlas, R. Rigorous evaluation of a fraternal twin ocean OSSE system for the open Gulf of Mexico. J. Atmos. Ocean. Technol. 2014, 31, 105–130. [Google Scholar] [CrossRef]
- Novellino, A.; Martins, F.A.; Pieri, G.; Misurale, F. New approach to underwater technologies for innovative, low-cost ocean observation (NAUTILOS): Operational field primary capture system. In Proceedings of the 2022 IEEE International Workshop on Metrology for the Sea; Learning to Measure Sea Health Parameters (MetroSea), Milazzo, Italy, 3–5 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 203–208. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Leitão, F.; Relvas, P.; Cánovas, F.; Baptista, V.; Teodósio, A. Northerly wind trends along the Portuguese marine coast since 1950. Theor. Appl. Climatol. 2019, 137, 1–19. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Deser, C. North Atlantic climate variability: The role of the North Atlantic Oscillation. J. Mar. Syst. 2010, 79, 231–244. [Google Scholar] [CrossRef]
- Dias, L.F.; Aparício, B.A.; Nunes, J.P.; Morais, I.; Fonseca, A.L.; Pastor, A.V.; Santos, F.D. Integrating a hydrological model into regional water policies: Co-creation of climate change dynamic adaptive policy pathways for water resources in southern Portugal. Environ. Sci. Policy 2020, 114, 519–532. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of droughts in Portugal. Water Resour. Res. 2010, 46, W03503. [Google Scholar] [CrossRef]
- Fiúza, A.F.; Demacedo, M.; Guerreiro, M. Climatological space and time-variation of the Portuguese coastal upwelling. Oceanol. Acta 1982, 5, 31–40. [Google Scholar]
- Relvas, P.; Barton, E.D. Mesoscale patterns in the Cape Sao Vicente (Iberian peninsula) upwelling region. J. Geophys. Res. Ocean. 2002, 107, 28-1–28-23. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D.; Dubert, J.; Oliveira, P.B.; Peliz, A.; da Silva, J.C.; Santos, A.M.P. Physical oceanography of the western Iberia ecosystem: Latest views and challenges. Prog. Oceanogr. 2007, 74, 149–173. [Google Scholar] [CrossRef]
- Fiúza, A.F. Upwelling patterns off Portugal. In Coastal Upwelling Its Sediment Record: Part A: Responses of the Sedimentary Regime to Present Coastal Upwelling; Springer: Berlin/Heidelberg, Germany, 1983; pp. 85–98. [Google Scholar] [CrossRef]
- Teles-Machado, A.; Peliz, A.; Dubert, J.; Sánchez, R.F. On the onset of the Gulf of Cadiz Coastal Countercurrent. Geophys. Res. Lett. 2007, 34, L12601. [Google Scholar] [CrossRef]
- Garel, E.; Laiz, I.; Drago, T.; Relvas, P. Characterisation of coastal counter-currents on the inner shelf of the Gulf of Cadiz. J. Mar. Syst. 2016, 155, 19–34. [Google Scholar] [CrossRef]
- Haynes, R.; Barton, E.D. A poleward flow along the Atlantic coast of the Iberian Peninsula. J. Geophys. Res. Ocean. 1990, 95, 11425–11441. [Google Scholar] [CrossRef]
- Frouin, R.; Fiúza, A.F.; Ambar, I.; Boyd, T.J. Observations of a poleward surface current off the coasts of Portugal and Spain during winter. J. Geophys. Res. Ocean. 1990, 95, 679–691. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D. A separated jet and coastal counterflow during upwelling relaxation off Cape São Vicente (Iberian Peninsula). Cont. Shelf Res. 2005, 25, 29–49. [Google Scholar] [CrossRef]
- Atlas, R.; Kalnay, E.; Halem, M. Impact of satellite temperature sounding and wind data on numerical weather prediction. Opt. Eng. 1985, 24, 341–346. [Google Scholar] [CrossRef]
- Atlas, R. Atmospheric observations and experiments to assess their usefulness in data assimilation (gtSpecial IssueltData assimilation in Meteology and oceanography: Theory and practice). J. Meteorol. Soc. Jpn. Ser. II 1997, 75, 111–130. [Google Scholar] [CrossRef]
- Mourre, B.; De Mey, P.; Ménard, Y.; Lyard, F.; Le Provost, C. Relative performance of future altimeter systems and tide gauges in constraining a model of North Sea high-frequency barotropic dynamics. Ocean Dyn. 2006, 56, 473–486. [Google Scholar] [CrossRef]
- Oke, P.R.; Schiller, A. Impact of Argo, SST, and altimeter data on an eddy-resolving ocean reanalysis. Geophys. Res. Lett. 2007, 34, L19601. [Google Scholar] [CrossRef]
- Halliwell, G.R., Jr.; Kourafalou, V.; Le Hénaff, M.; Shay, L.K.; Atlas, R. OSSE impact analysis of airborne ocean surveys for improving upper-ocean dynamical and thermodynamical forecasts in the Gulf of Mexico. Prog. Oceanogr. 2015, 130, 32–46. [Google Scholar] [CrossRef]
- Ford, D. Assimilating synthetic Biogeochemical-Argo and ocean colour observations into a global ocean model to inform observing system design. Biogeosciences 2021, 18, 509–534. [Google Scholar] [CrossRef]
- Fennel, K.; Mattern, J.P.; Doney, S.C.; Bopp, L.; Moore, A.M.; Wang, B.; Yu, L. Ocean biogeochemical modelling. Nat. Rev. Methods Prim. 2022, 2, 76. [Google Scholar] [CrossRef]
- Yu, L.; Fennel, K.; Wang, B.; Laurent, A.; Thompson, K.R.; Shay, L.K. Evaluation of nonidentical versus identical twin approaches for observation impact assessments: An ensemble-Kalman-filter-based ocean assimilation application for the Gulf of Mexico. Ocean Sci. 2019, 15, 1801–1814. [Google Scholar] [CrossRef]
- Martin, M.J.; Hoteit, I.; Bertino, L.; Moore, A.M. Data assimilation schemes for ocean forecasting: State of the art. State Planet 2025, 5-opsr, 9. [Google Scholar] [CrossRef]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data assimilation in the geosciences: An overview of methods, issues, and perspectives. Wiley Interdiscip. Rev. Clim. Change 2018, 9, e535. [Google Scholar] [CrossRef]
- Evensen, G.; Vossepoel, F.C.; Van Leeuwen, P.J. Data Assimilation Fundamentals: A Unified Formulation of the State and Parameter Estimation Problem; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Oke, P.; Brassington, G.; Griffin, D.; Schiller, A. Ocean data assimilation: A case for ensemble optimal interpolation. Aust. Meteorol. Oceanogr. J. 2010, 59, 67–76. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Oke, P.R.; Allen, J.S.; Miller, R.N.; Egbert, G.D.; Kosro, P.M. Assimilation of surface velocity data into a primitive equation coastal ocean model. J. Geophys. Res. Ocean. 2002, 107, 3122. [Google Scholar] [CrossRef]
- Counillon, F.; Bertino, L. Ensemble Optimal Interpolation: Multivariate properties in the Gulf of Mexico. Tellus A Dyn. Meteorol. Oceanogr. 2009, 61, 296–308. [Google Scholar] [CrossRef]
- Tanajura, C.; Costa, F.; Silva, R.; Ruggiero, G.; Daher, V. Assimilation of Sea Surface Height Anomalies into Hycom with an Optimal Interpolation Scheme over the Atlantic Ocean Metarea V. BRazilian J. Geophys. 2013, 31, 257–270. [Google Scholar] [CrossRef]
- Hernandez-Lasheras, J.; Mourre, B. Dense CTD survey versus glider fleet sampling: Comparing data assimilation performance in a regional ocean model west of Sardinia. Ocean Sci. 2018, 14, 1069–1084. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, J.; Liu, Z.; Gan, J.; Zhu, J. The Assimilation of Temperature and Salinity Profile Observations for Forecasting the River–Estuary–Shelf Waters. J. Geophys. Res. Ocean. 2021, 126, e2020JC017043. [Google Scholar] [CrossRef]
- Janeiro, J.; Neves, A.; Martins, F.; Relvas, P. Integrating technologies for oil spill response in the SW Iberian coast. J. Mar. Syst. 2017, 173, 31–42. [Google Scholar] [CrossRef]
- Sobrinho, J.; de Pablo, H.; Pinto, L.; Neves, R. Improving 3D-MOHID water model with an upscaling algorithm. Environ. Model. Softw. 2021, 135, 104920. [Google Scholar] [CrossRef]
- Braunschweig, F.; Leitao, P.; Fernandes, L.; Pina, P.; Neves, R. The object-oriented design of the integrated water modelling system MOHID. In Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004; Volume 55, pp. 1079–1090. [Google Scholar] [CrossRef]
- Mayeli, P.; Sheard, G.J. Buoyancy-driven flows beyond the Boussinesq approximation: A brief review. Int. Commun. Heat Mass Transf. 2021, 125, 105316. [Google Scholar] [CrossRef]
- Martins, F.; Leitão, P.; Silva, A.; Neves, R. 3D modelling in the Sado estuary using a new generic vertical discretization approach. Oceanol. Acta 2001, 24, 51–62. [Google Scholar] [CrossRef]
- Martins, F.A.B.d.C.; Neves, R.; Leitão, P.C. A three-dimensional hydrodynamic model with generic vertical coordinate. In Proceedings of the 3rd International Conference on Hydroinformatics, Copenhagen, Denmark, 24–26 August 1998; pp. 1403–1410. [Google Scholar]
- Martins, F. Modelação Matemática Tridimensional de Escoamentos Costeiros e Estuarinos Usando Uma Abordagem de Coordenada Vertical Genérica. Ph.D. Thesis, Universidade Técnica de Lisboa (Portugal), Lisbon, Portugal, 1999. [Google Scholar]
- Janeiro, J.; Zacharioudaki, A.; Sarhadi, E.; Neves, A.; Martins, F. Enhancing the management response to oil spills in the Tuscany Archipelago through operational modelling. Mar. Pollut. Bull. 2014, 85, 574–589. [Google Scholar] [CrossRef] [PubMed]
- Moreira, D.; Janeiro, J.; Tosic, M.; Martins, F. A Generic Operational Tool for Early Warning Oil Spills – Application to Cartagena Bay and the Algarve Coast. In Proceedings of the INCREaSE 2023, Faro, Portugal, 5–7 July 2023; Semião, J.F.L.C., Sousa, N.M.S., da Cruz, R.M.S., Prates, G.N.D., Eds.; Springer: Cham, Switzerland, 2023; pp. 109–120. [Google Scholar] [CrossRef]
- Janeiro, J.; Martins, F.; Relvas, P. Towards the development of an operational tool for oil spills management in the Algarve coast. J. Coast. Conserv. 2012, 16, 449–460. [Google Scholar] [CrossRef]
- CIMA. Operational Modelling and Monitoring System of the Algarve—SOMA; CIMA: London, UK, 2024. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Kantha, L.H. Open boundary condition for circulation models. J. Hydraul. Eng. 1985, 111, 237–255. [Google Scholar] [CrossRef]
- Martinsen, E.A.; Engedahl, H. Implementation and testing of a lateral boundary scheme as an open boundary condition in a barotropic ocean model. Coast. Eng. 1987, 11, 603–627. [Google Scholar] [CrossRef]
- EU Copernicus Marine Service. Global Ocean 1/12° Physics Analysis and Forecast Updated Daily; EU Copernicus Marine Service: Toulouse, France, 2016. [Google Scholar] [CrossRef]
- Carrere, L.; Lyard, F.; Cancet, M.; Guillot, A.; Roblou, L. FES 2012: A New Global Tidal Model Taking Advantage of Nearly 20 Years of Altimetry. In 20 Years of Progress in Radar Altimatry; Ouwehand, L., Ed.; ESA Special Publication; ESA: Paris, France, 2013; Volume 710, p. 13. [Google Scholar]
- Kallos, G.; Nickovic, S.; Papadopoulos, A.; Jovic, D.; Kakaliagou, O.; Misirlis, N.; Boukas, L.; Mimikou, N.; Sakellaridis, G.; Papageorgiou, J.; et al. The regional weather forecasting system SKIRON: An overview. In Symposium on Regional Weather Prediction on Parallel Computer Environments; University of Athens: Athens, Greece, 1997; Volume 15, p. 17. [Google Scholar]
- Papadopoulos, A.; Katsafados, P.; Kallos, G.; Nickovic, S. The Weather Forecasting System for Poseidon—An Overview. J. Atmos. Ocean. Sci. 2002, 8, 219–237. [Google Scholar] [CrossRef]
- Mendonça, F.; Martins, F.; Janeiro, J. SMS-Coastal, a New Python Tool to Manage MOHID-Based Coastal Operational Models. J. Mar. Sci. Eng. 2023, 11, 1606. [Google Scholar] [CrossRef]
- Counillon, F.; Keenlyside, N.; Wang, S.; Devilliers, M.; Gupta, A.; Koseki, S.; Shen, M.L. Framework for an Ocean-Connected Supermodel of the Earth System. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003310. [Google Scholar] [CrossRef]
- Counillon, F.; Bertino, L. High-resolution ensemble forecasting for the Gulf of Mexico eddies and fronts. Ocean Dyn. 2009, 59, 83–95. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- EU-CMEMS. European North West Shelf/Iberia Biscay Irish Seas—High Resolution ODYSSEA L4 Sea Surface Temperature Analysis; EU-CMEMS: Luxembourg, 2019. [Google Scholar] [CrossRef]
- EU-CMEMS. European North West Shelf/Iberia Biscay Irish Seas—High Resolution L4 Sea Surface Temperature Reprocessed; EU-CMEMS: Luxembourg, 2019. [Google Scholar] [CrossRef]
- Turner, M.R.J.; Walker, J.P.; Oke, P.R.; Grayson, R.B. Assimilation of Sea-Surface Temperature into a Hydrodynamic Model of Port Phillip Bay, Australia. In Proceedings of the Coasts and Ports 2005: Coastal Living—Living Coast, Adelaide, Australia, 20–23 September 2005; pp. 511–516. [Google Scholar]
- Murphy, A.H. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather. Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
| Experiment | Number of Points | Data Source | Observation Error | |
|---|---|---|---|---|
| OSE1 | 10 | CMEMS NRT ODYSSEA | from data source | |
| OSE2 | 50 | |||
| OSE3 | 100 | |||
| OSE4 | 200 | |||
| OSE5 | 500 | |||
| OSE6 | 10 | CMEMS Reprocessed | from data source | |
| OSE7 | 50 | |||
| OSE8 | 100 | |||
| OSE9 | 200 | |||
| OSE10 | 500 | |||
| OSSE1 | 10 | SOMA Nature Run | NRT_ODYSSEA × | random_field1 |
| OSSE2 | 50 | random_field2 | ||
| OSSE3 | 100 | random_field3 | ||
| OSSE4 | 200 | random_field4 | ||
| OSSE5 | 500 | random_field5 | ||
| OSSE6 | 10 | SOMA Nature Run | Reprocessed × | random_field6 |
| OSSE7 | 50 | random_field7 | ||
| OSSE8 | 100 | random_field8 | ||
| OSSE9 | 200 | random_field9 | ||
| OSSE10 | 500 | random_field10 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendonça, F.; Martins, F.; Bertino, L. Design of an Observing System Simulation Experiment for the Operational Model of the Southwestern Coast of Iberia (SOMA). J. Mar. Sci. Eng. 2025, 13, 1830. https://doi.org/10.3390/jmse13091830
Mendonça F, Martins F, Bertino L. Design of an Observing System Simulation Experiment for the Operational Model of the Southwestern Coast of Iberia (SOMA). Journal of Marine Science and Engineering. 2025; 13(9):1830. https://doi.org/10.3390/jmse13091830
Chicago/Turabian StyleMendonça, Fernando, Flávio Martins, and Laurent Bertino. 2025. "Design of an Observing System Simulation Experiment for the Operational Model of the Southwestern Coast of Iberia (SOMA)" Journal of Marine Science and Engineering 13, no. 9: 1830. https://doi.org/10.3390/jmse13091830
APA StyleMendonça, F., Martins, F., & Bertino, L. (2025). Design of an Observing System Simulation Experiment for the Operational Model of the Southwestern Coast of Iberia (SOMA). Journal of Marine Science and Engineering, 13(9), 1830. https://doi.org/10.3390/jmse13091830








