A Time-Domain Substructure Method for Simulating Water–Cylinder Interaction Under Dynamic Loadings Considering Boundary Condition of Free Surface Waves
Abstract
1. Introduction
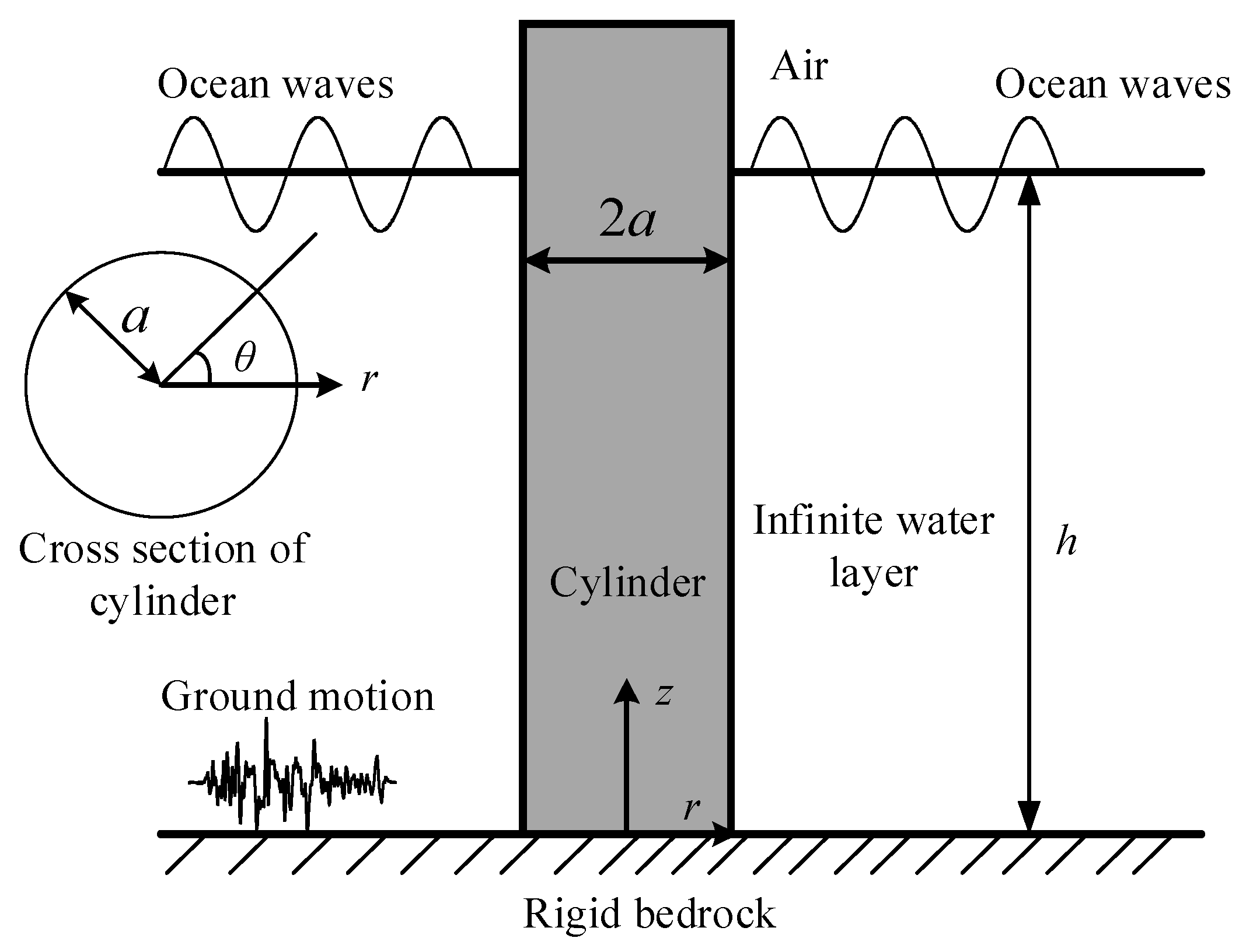
2. Theoretical Formulation and Solution
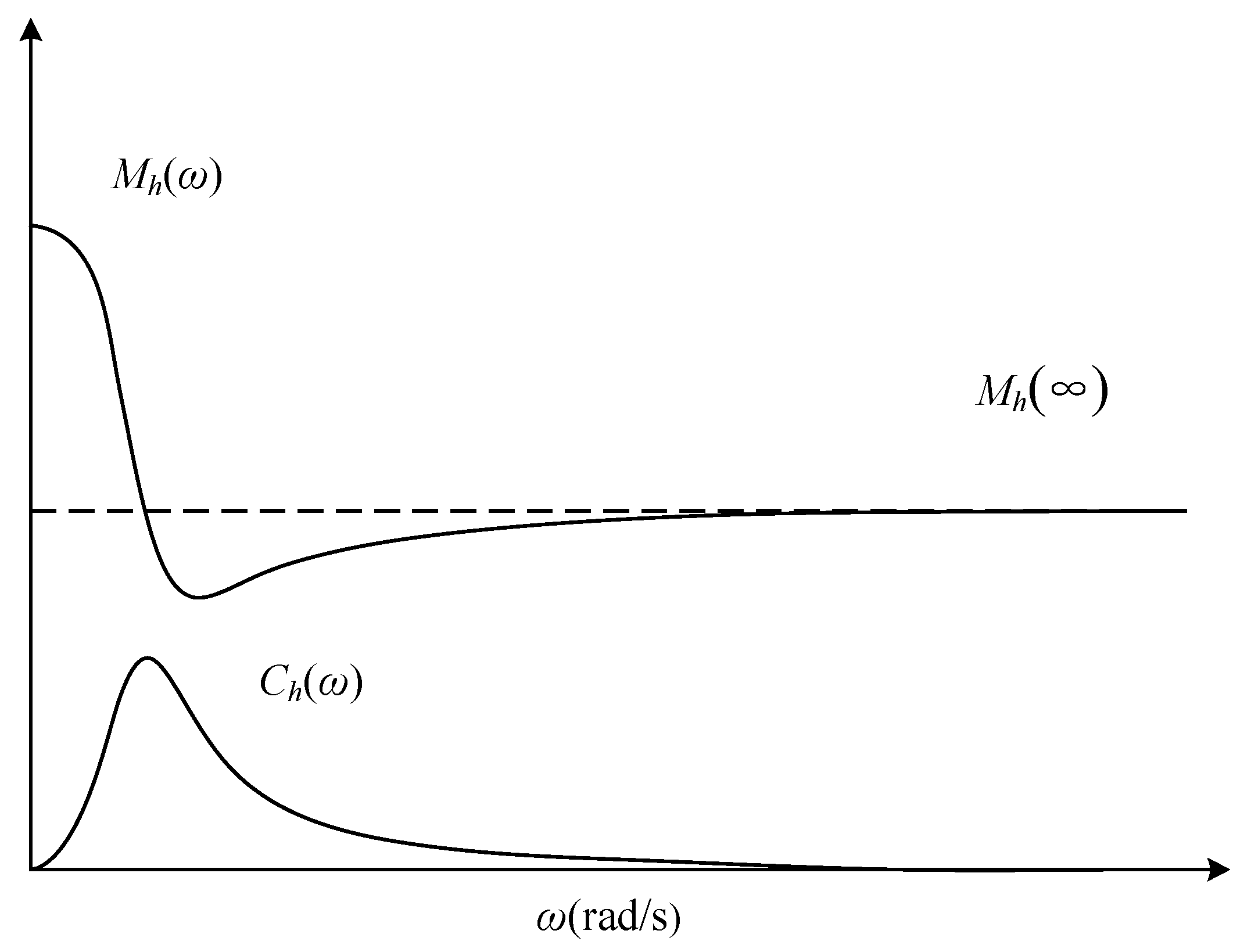
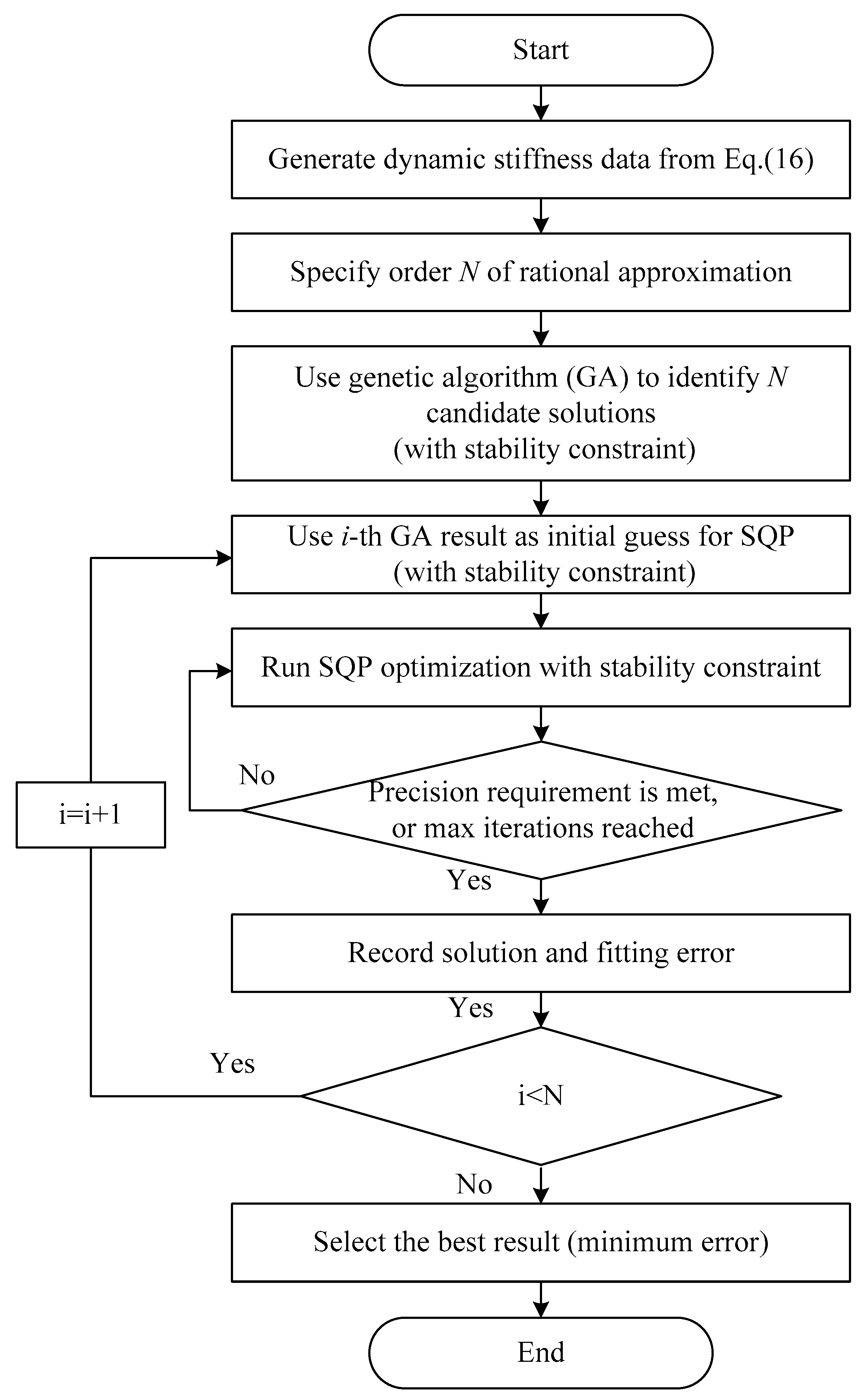
3. Method of Rational Function Approximation
4. Method of Auxiliary Variable Realization
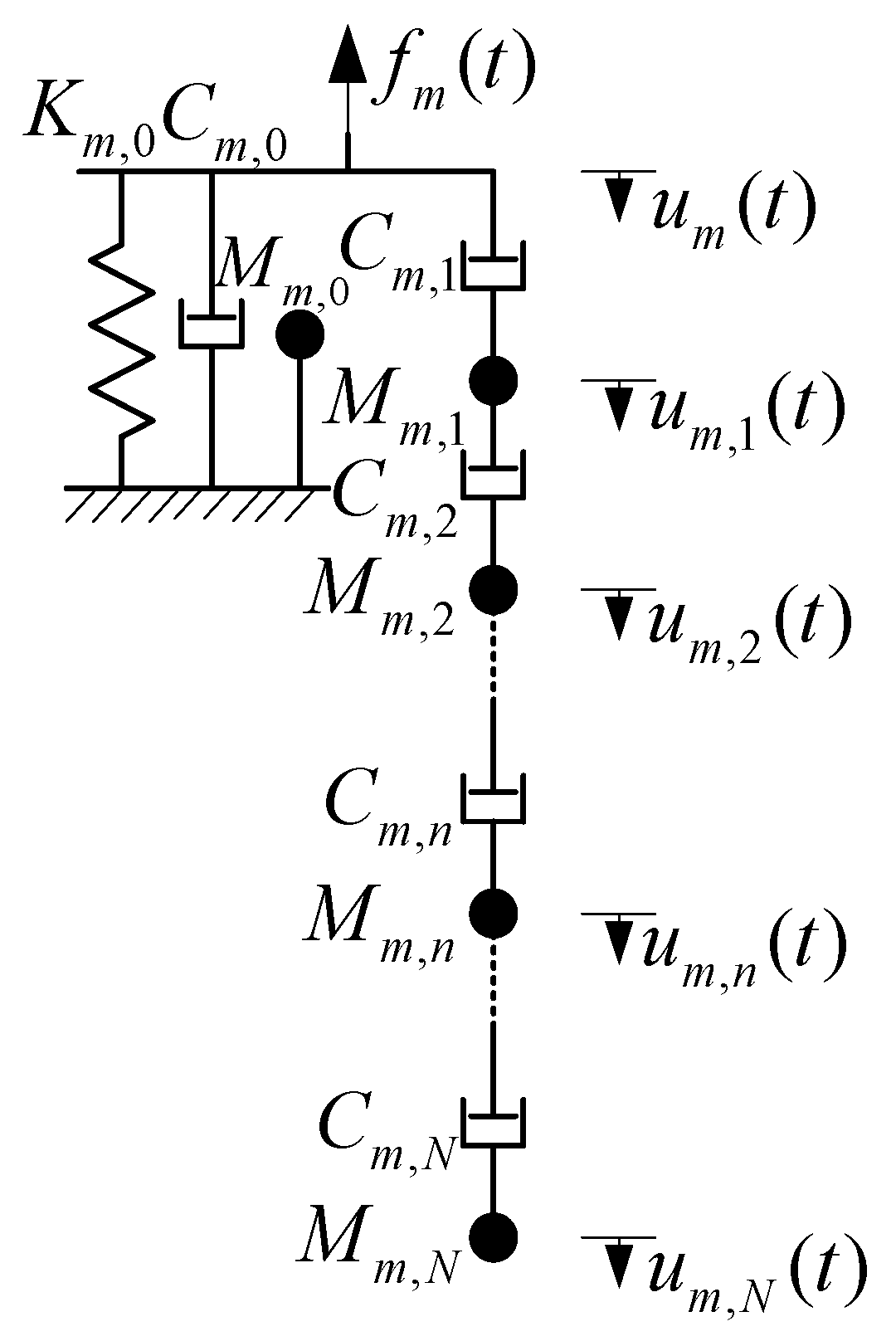
Time-Domain Mechanical Model
5. Results and Discussions
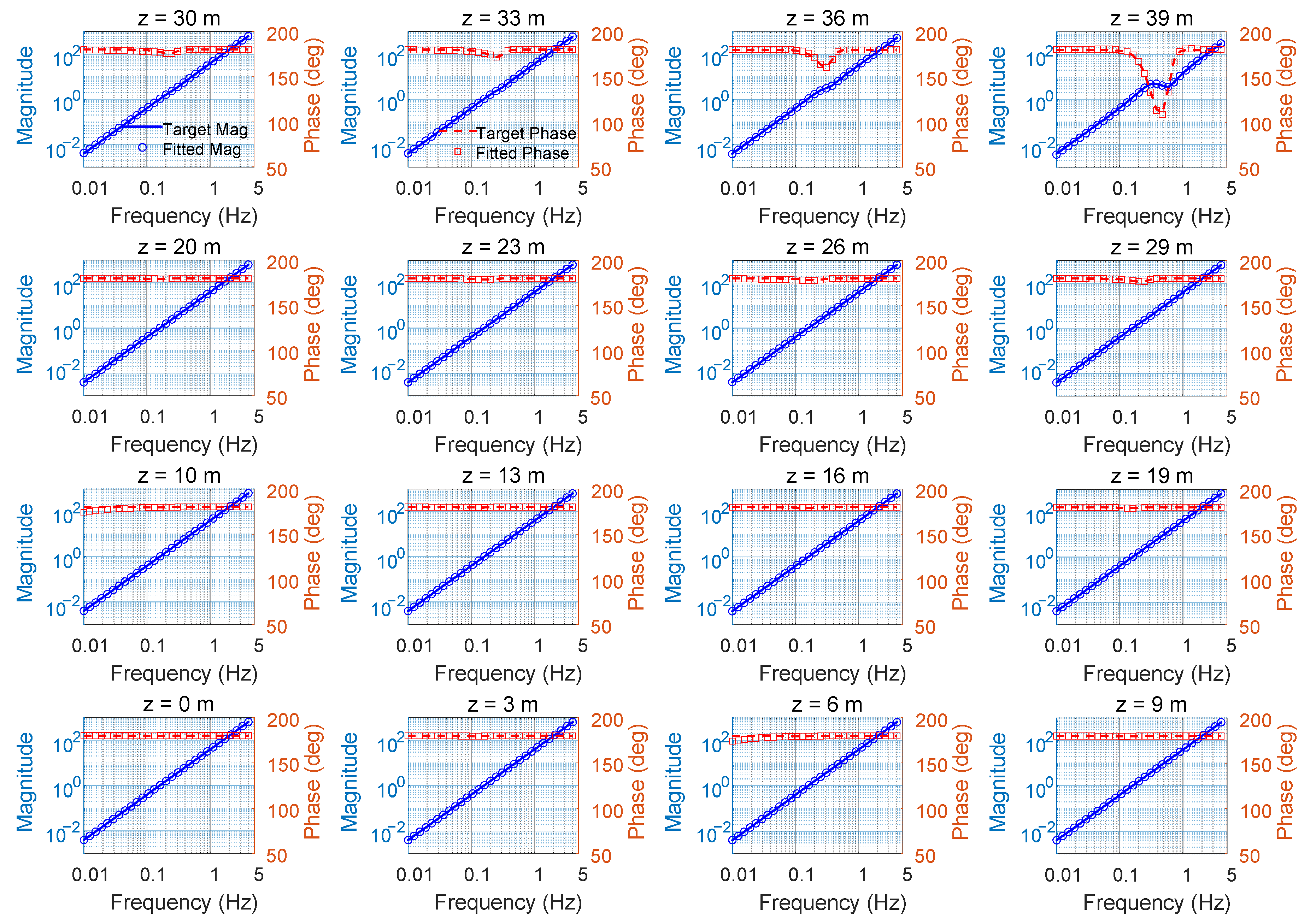
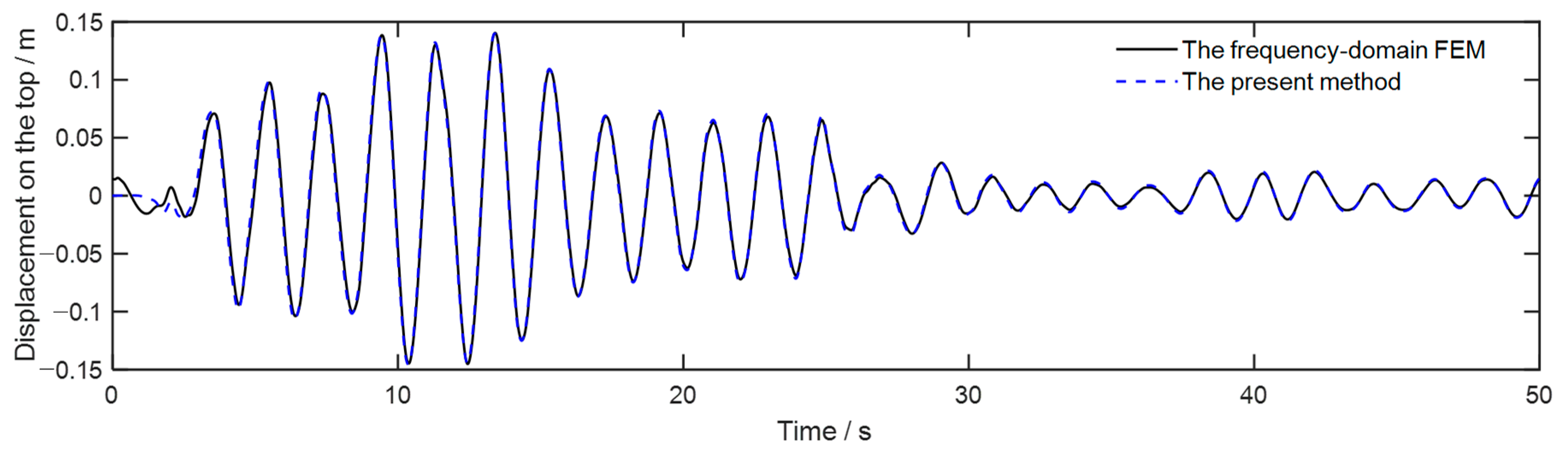
5.1. Verification
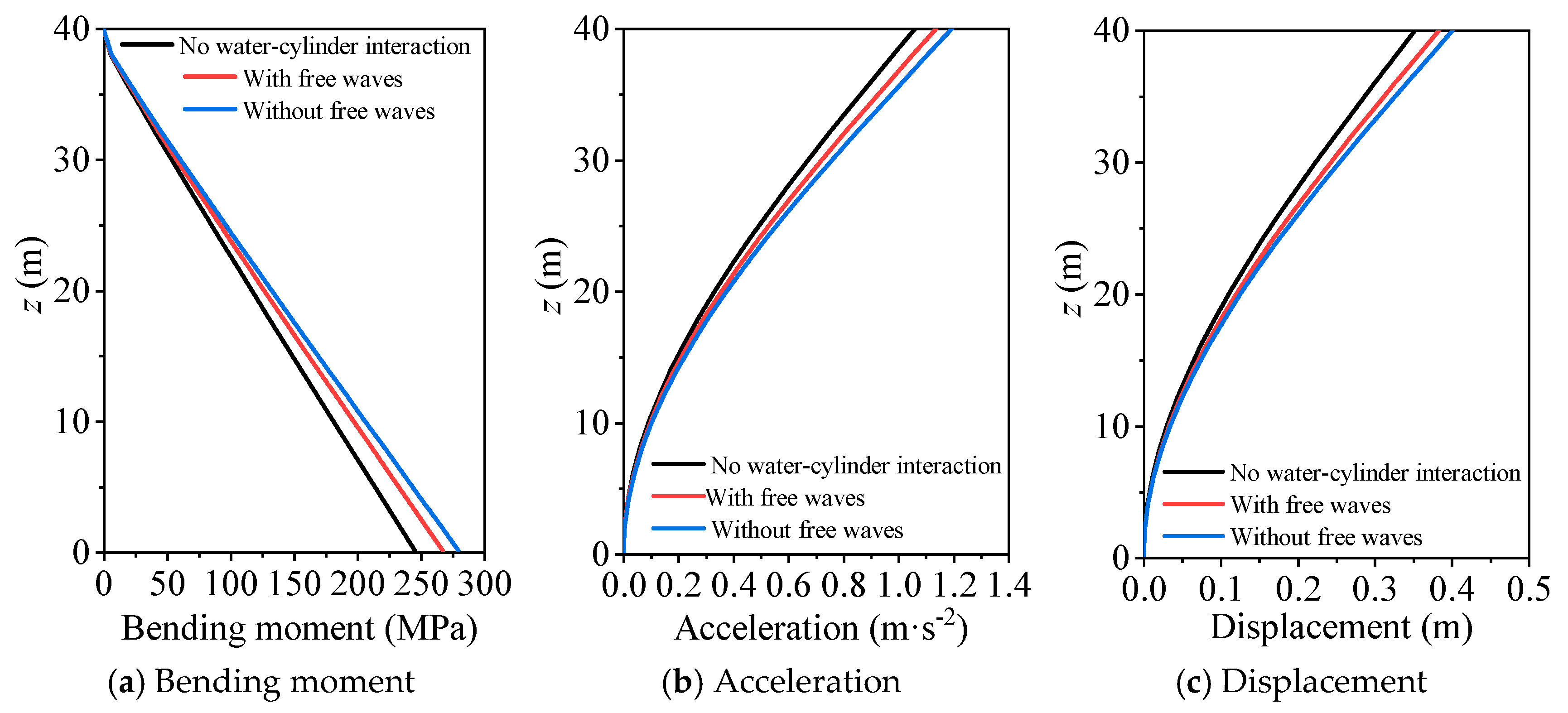
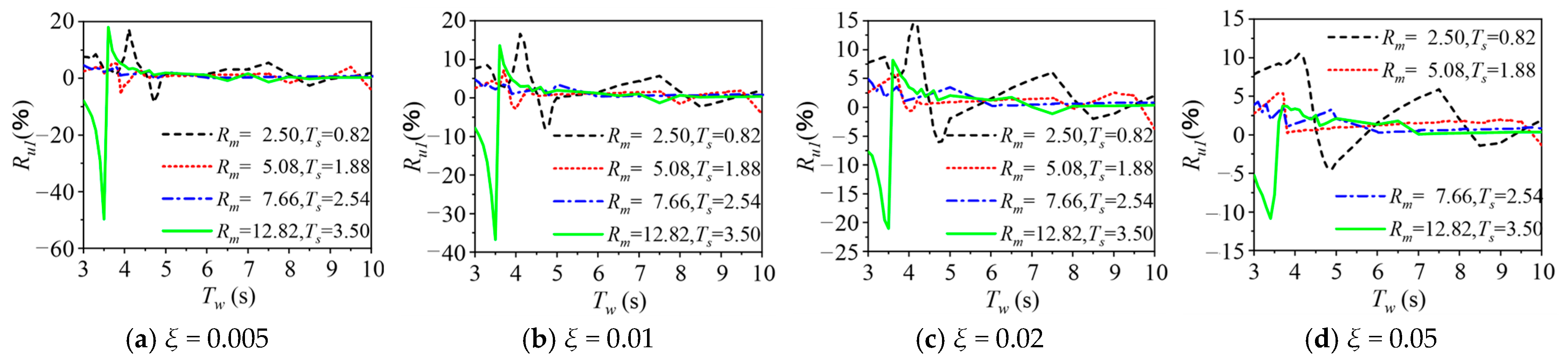
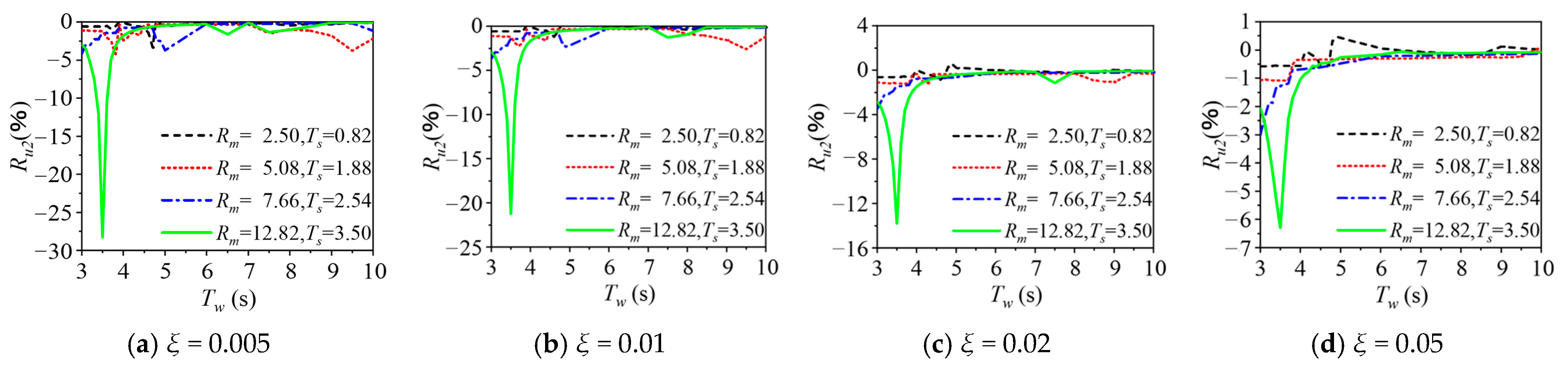
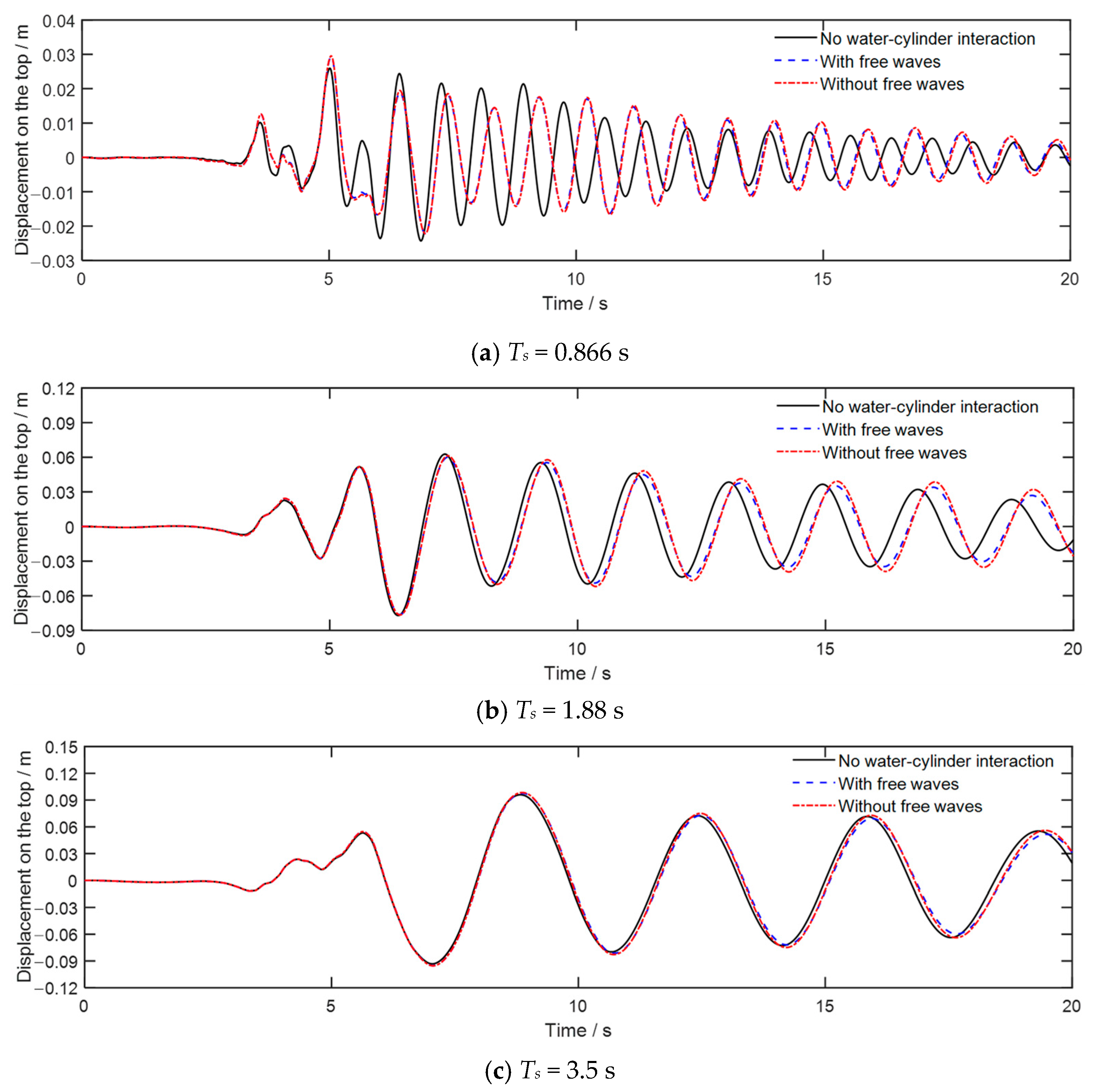
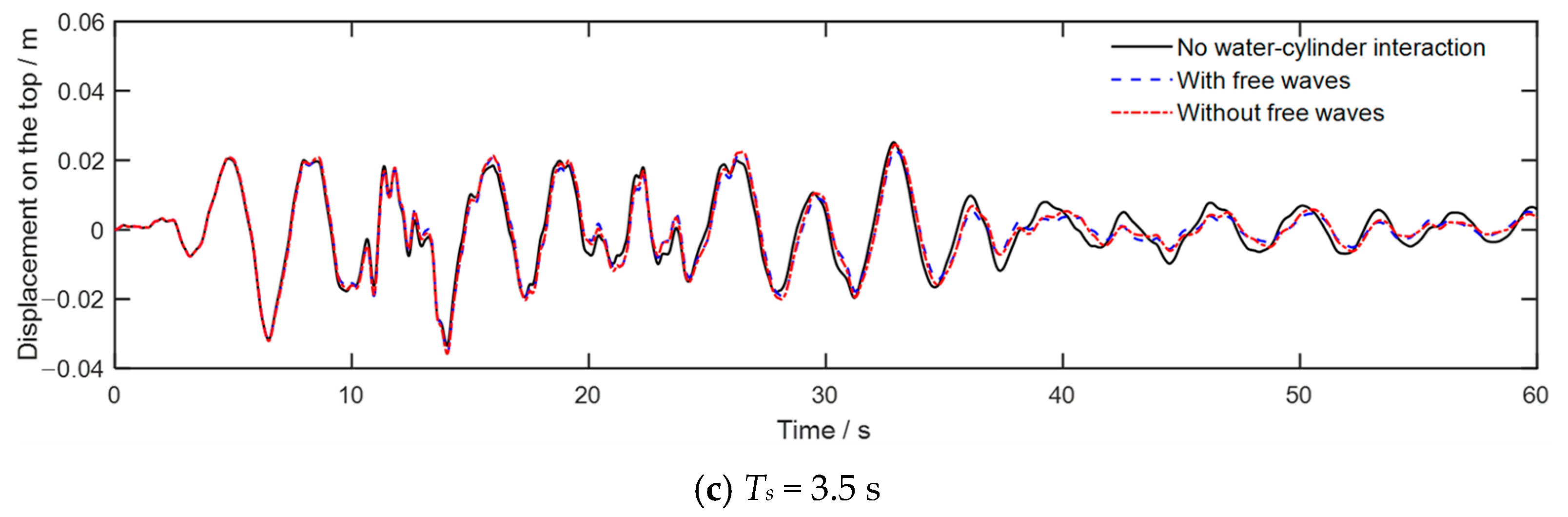
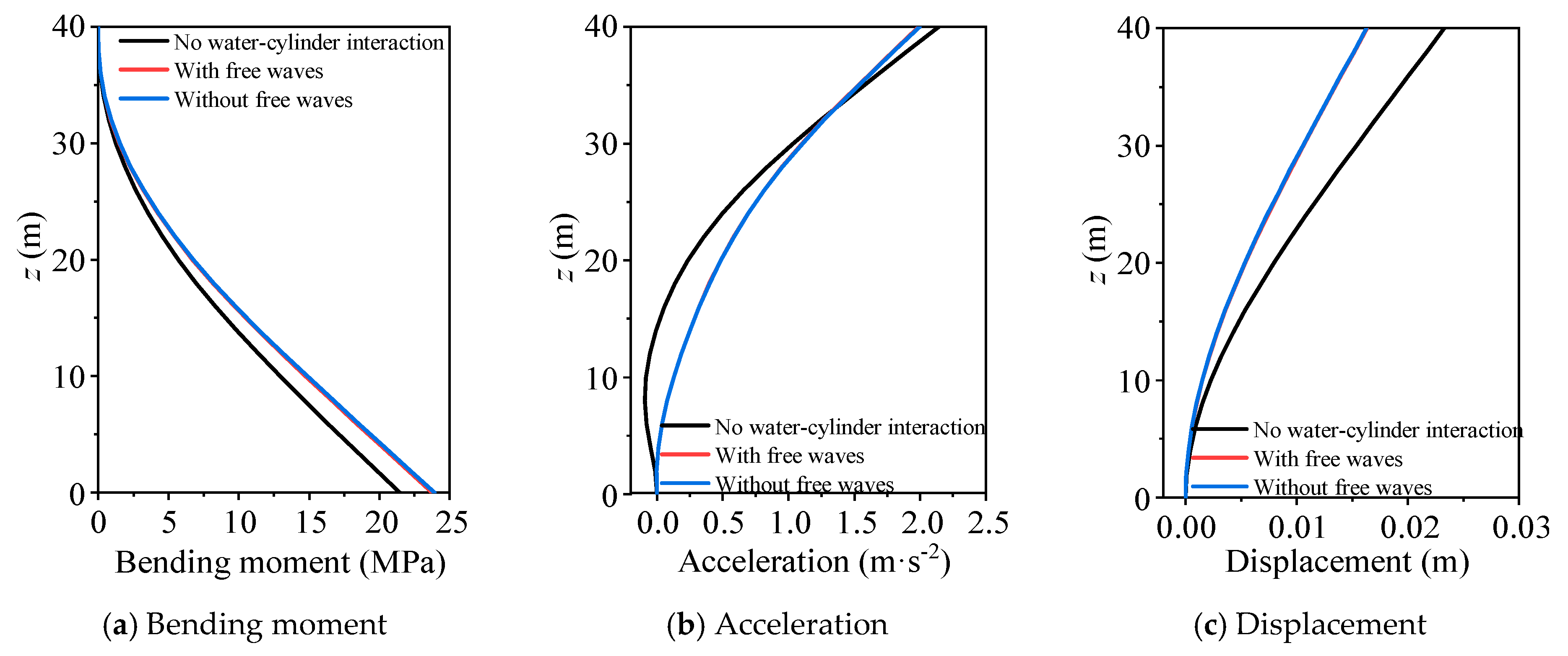
5.2. Wave Loading
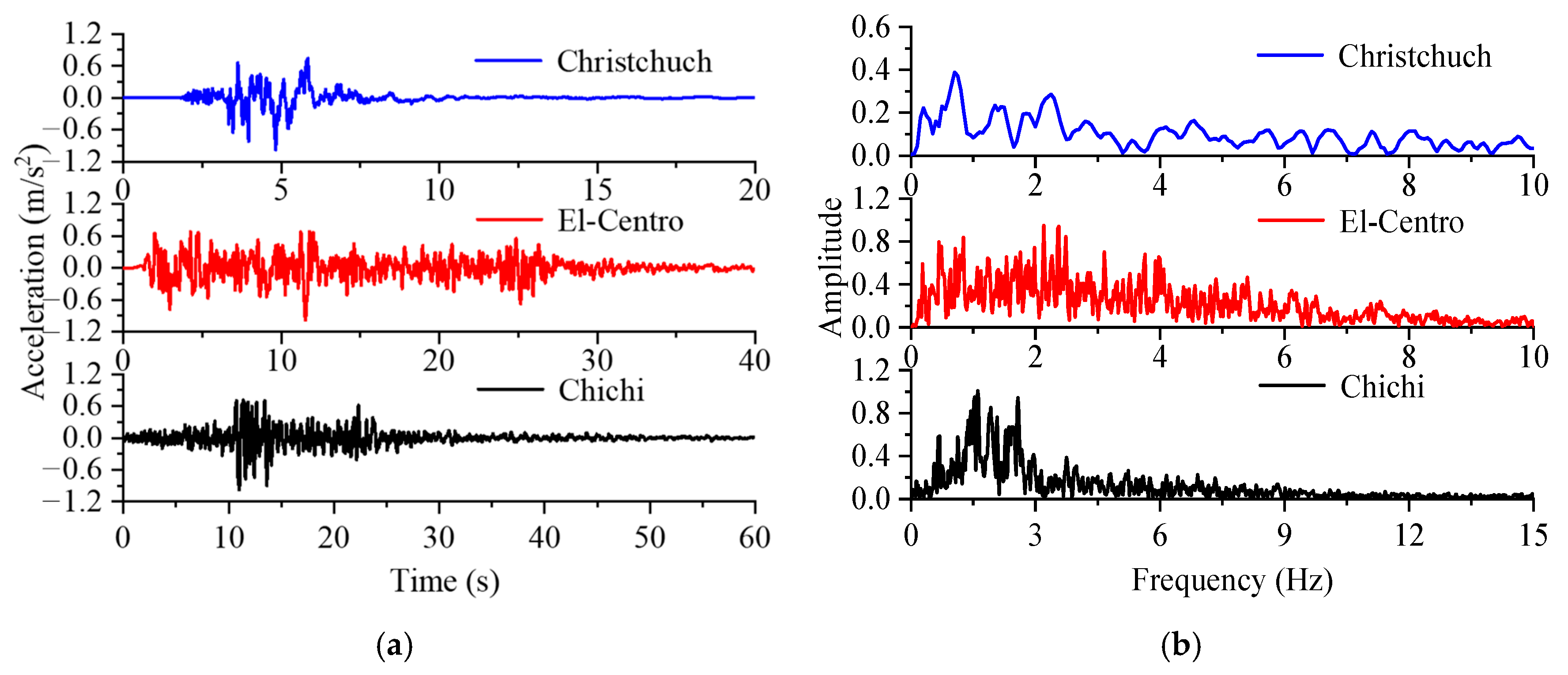
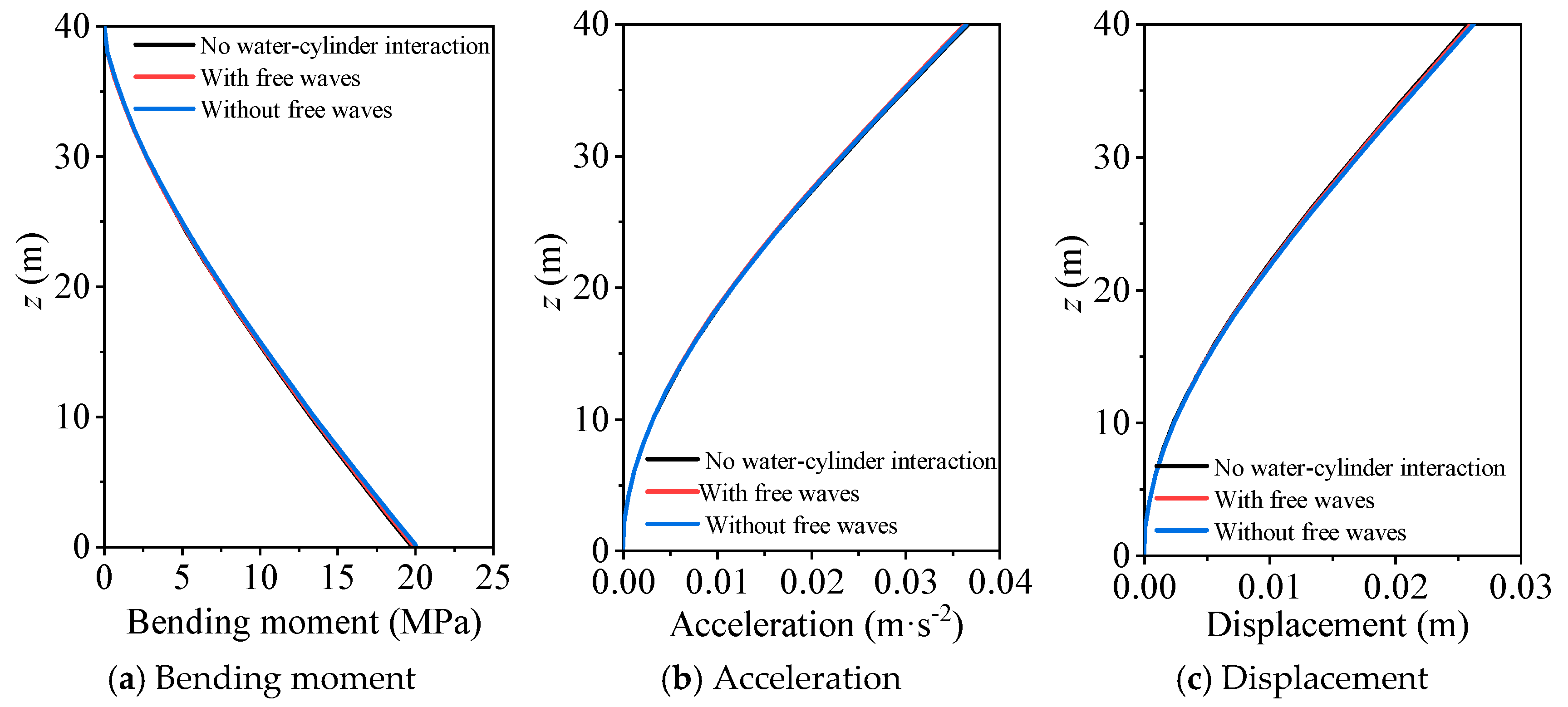
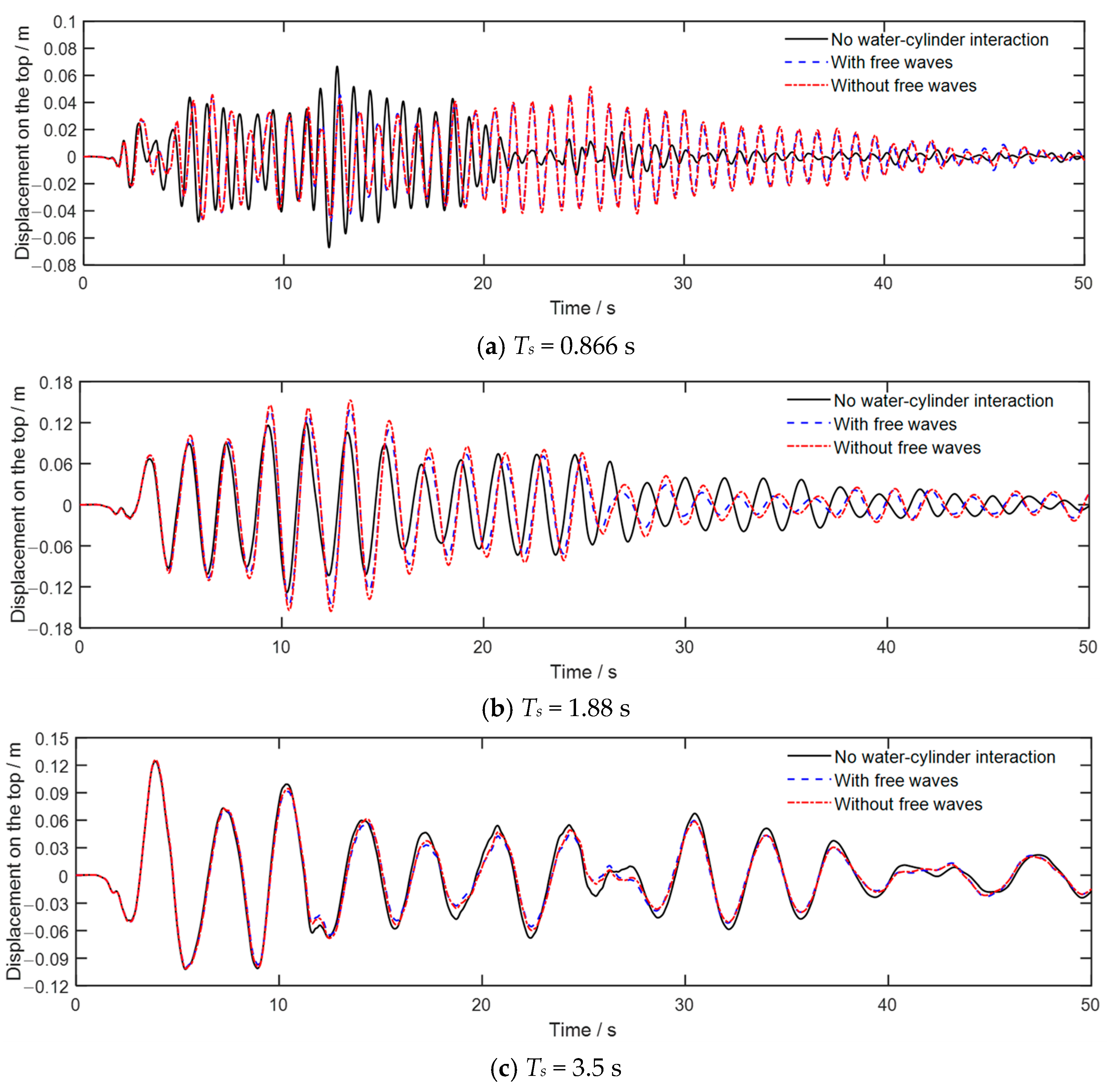
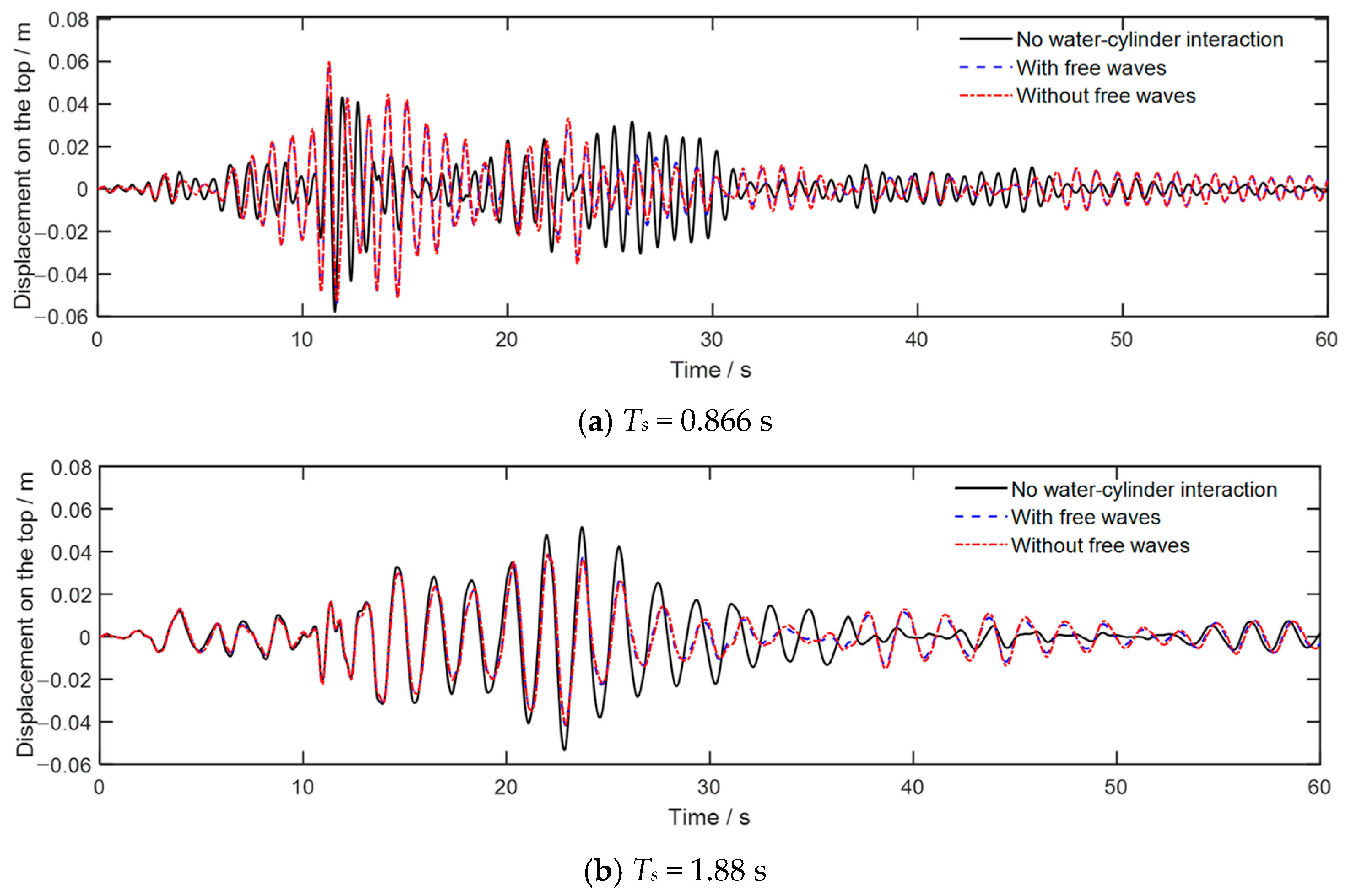
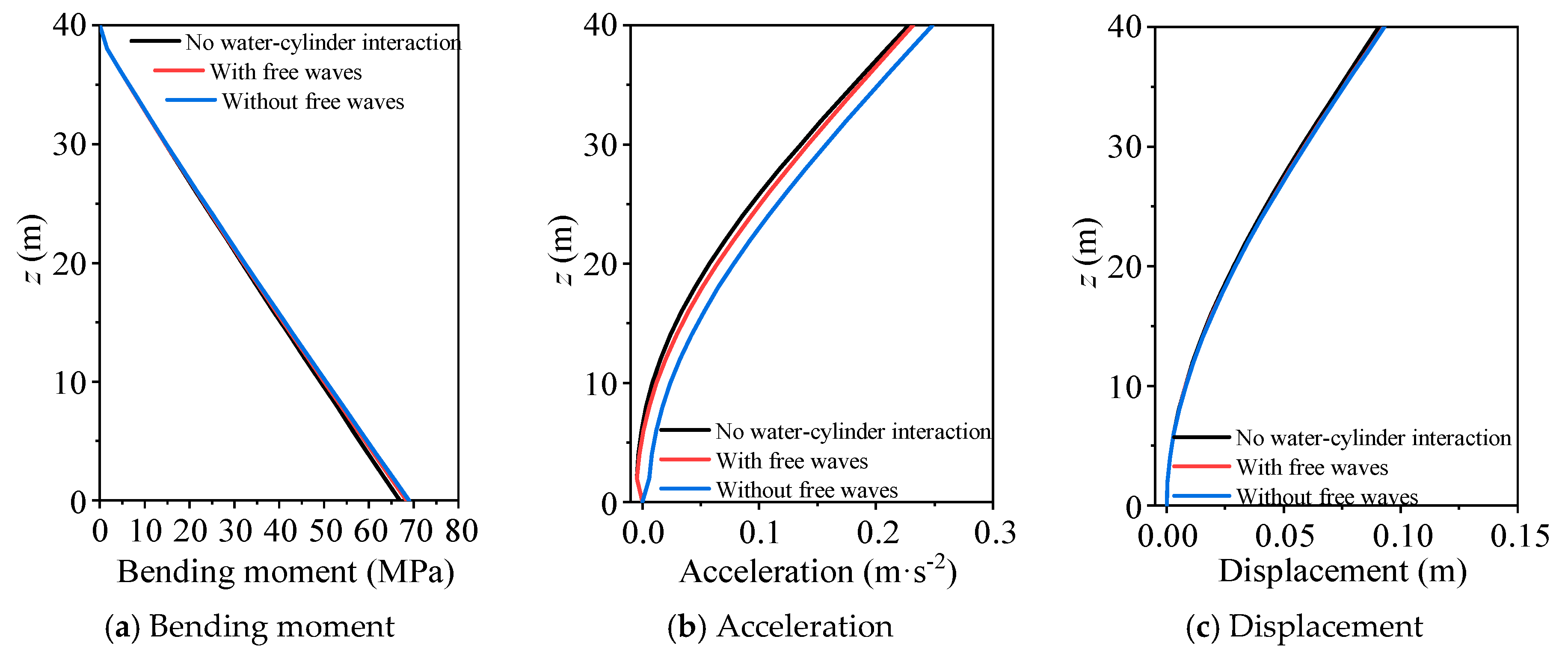
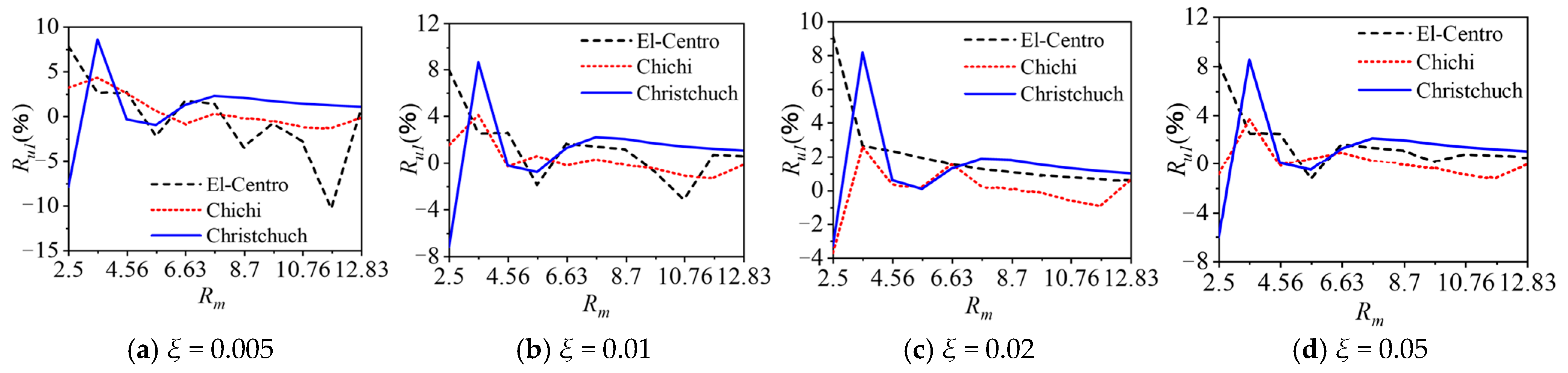
5.3. Earthquake Loading
6. Conclusions
- The proposed time-domain substructure method agrees well with the frequency-domain FEM, while the calculation efficiency is improved by approximately two orders of magnitude.
- Water–cylinder interaction generally increases the displacement and bending moment of the cylinder under wave loads, while it can markedly decrease the dynamic responses when the wave period is close to the natural vibration period. The effects of water–cylinder interaction can be neglected for wave periods greater than 5 s.
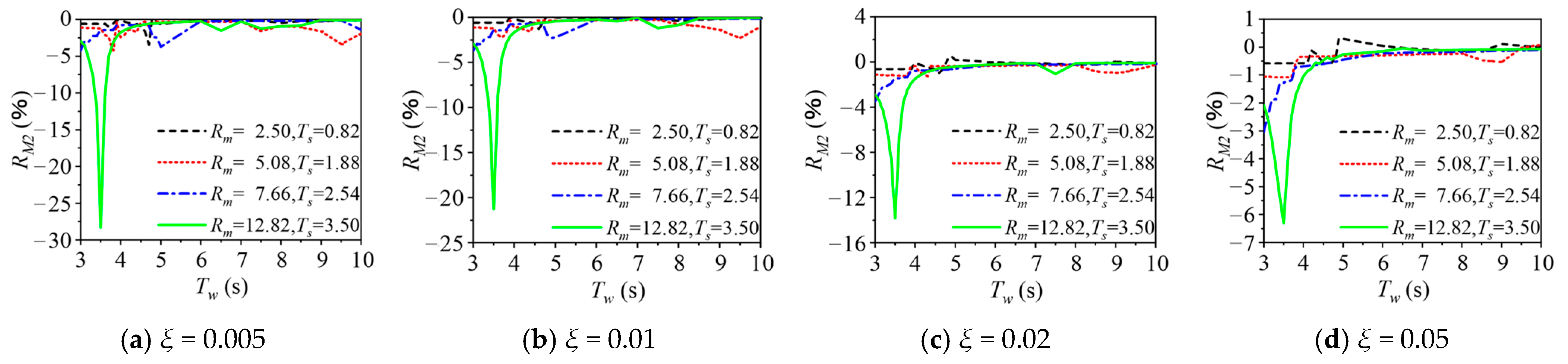
- The boundary condition of free surface waves has a negligible effect (<5%) on wave responses of the cylinder in most cases, while its added damping effect can significantly decrease the dynamic responses of the cylinder when the wave period is near the natural vibration period of the cylinder.
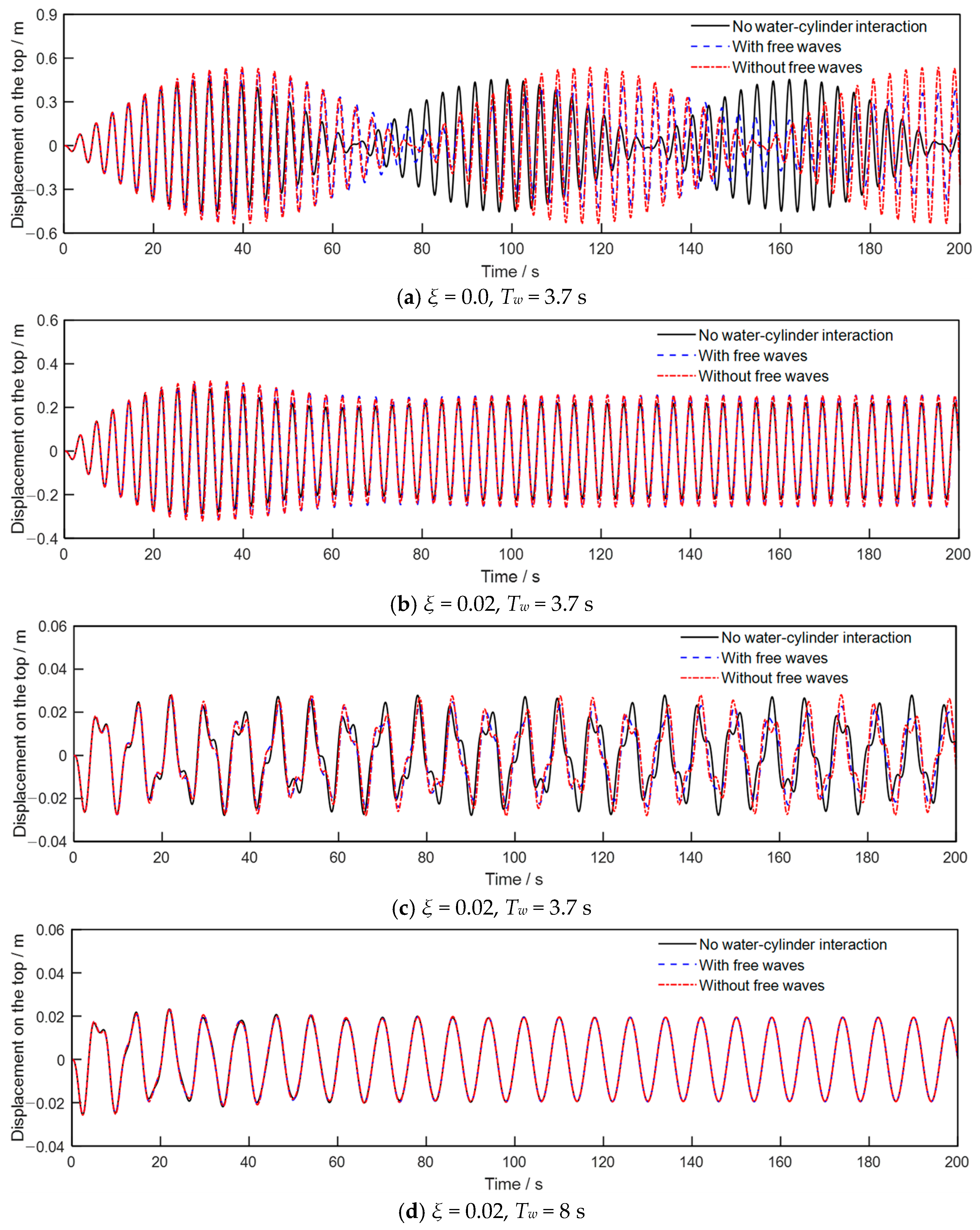
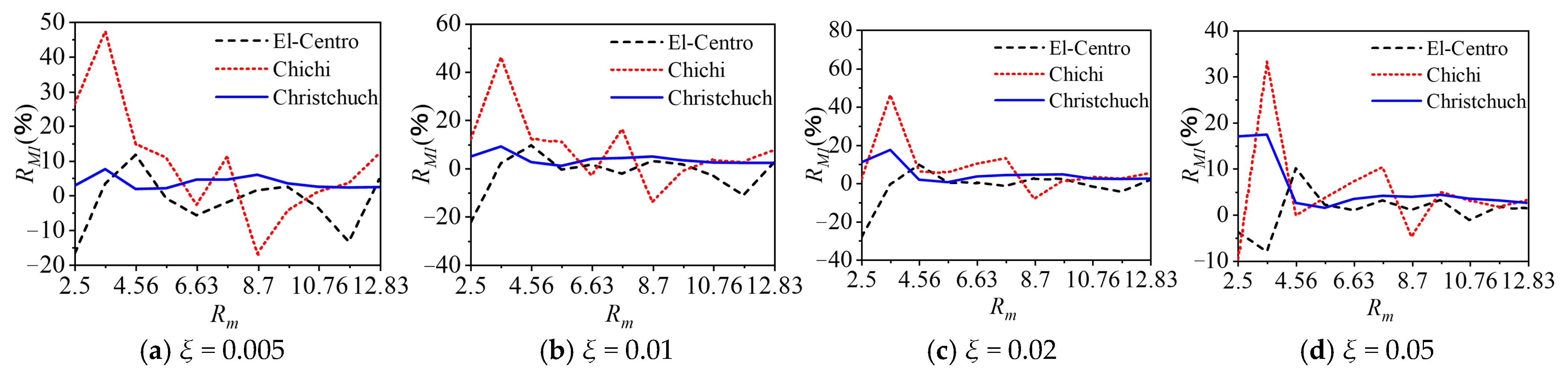
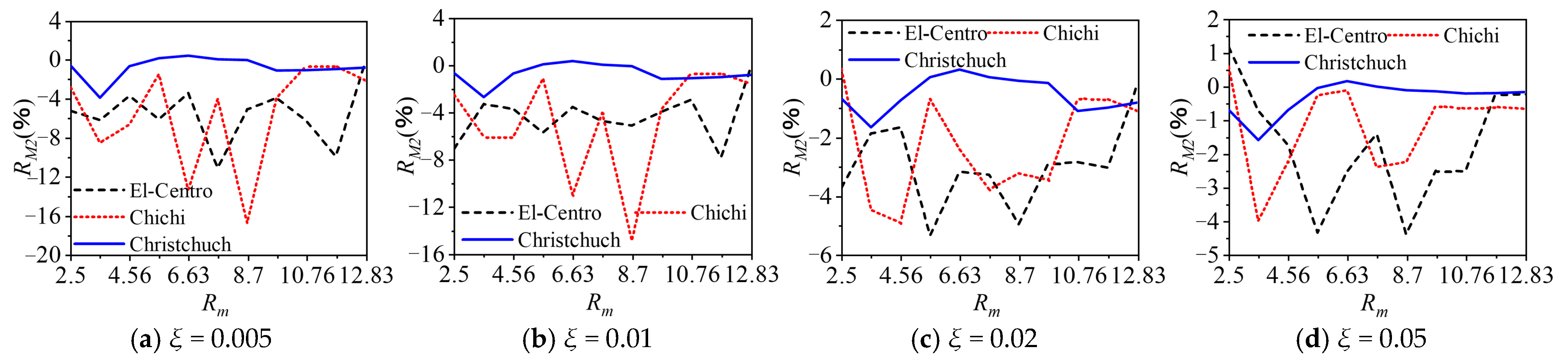
- The water–cylinder interaction can significantly influence the seismic responses of the cylinder, especially when the mass ratio is small. Generally, the effects of water–cylinder interaction decrease as the damping ratio increases.
- The boundary condition of free surface waves can decrease the seismic responses of the cylinder, and this influence significantly decreases as the damping ratio increases. In general, this effect can be neglected when the damping ratio of the cylinder is larger than 0.02.
- Water–cylinder interaction tends to increase the natural vibration period of the cylinder, while the free surface waves have little influence on it.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chaudhari, V.; Somala, S.N. Fragility of offshore wind turbines variation with pulse-period and amplitude: Directivity and Fling step. Structures 2022, 41, 66–76. [Google Scholar] [CrossRef]
- Bai, X.Y.; Jiang, H.; Song, G.S.; Li, X. Extreme responses of sea-crossing bridges subjected to offshore ground motion and correlated extreme wind and wave. Ocean Eng. 2022, 247, 110710. [Google Scholar] [CrossRef]
- Ur Rehman, S.S.; Cui, Y.; Wang, Z.X.; Ang, Y. Performance assessment of pile supported wharves with seismic isolation system considering pile-soil interaction. Ocean Eng. 2024, 312, 119219. [Google Scholar] [CrossRef]
- Han, R.P.S.; Xu, H. A simple and accurate added mass model for hydrodynamic fluid-structure interaction analysis. J. Frankl. Inst. 1996, 333, 929–945. [Google Scholar] [CrossRef]
- Liaw, C.Y.; Chopra, A.K. Dynamics of towers surrounded by water. Earthq. Eng. Struct. Dyn. 1974, 3, 33–49. [Google Scholar] [CrossRef]
- Wei, K.; Yuan, W.C.; Bouaanani, N. Experimental and numerical assessment of the three dimensional modal dynamic response of bridge pile foundations submerged in water. J. Bridge Eng. 2013, 18, 1032–1041. [Google Scholar] [CrossRef]
- Du, X.; Wang, P.; Zhao, M. Simplified formula of hydrodynamic pressure on circular bridge piers in the time domain. Ocean Eng. 2014, 85, 44–53. [Google Scholar] [CrossRef]
- Li, Q.; Yang, W.L. An improved method of hydrodynamic pressure calculation for circular hollow piers in deep water under earthquake. Ocean Eng. 2013, 72, 241–256. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, B.; Bai, X.; Zeng, C.; Zhang, H. Simplified expression of hydrodynamic pressure on deep water cylindrical bridge piers during earthquakes. Bridge Eng. 2017, 22, 04017014. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X. Analytical solution and simplified formula for earthquake induced hydrodynamic pressure on elliptical hollow cylinders in water. Ocean Eng. 2018, 148, 149–160. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X. Simplified formula for earthquake-induced hydrodynamic pressure on round-ended and rectangular cylinders surrounded by water. J. Eng. Mech. ASCE 2019, 145, 04018137. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X.; Liu, J.; Chen, J. Simplified evaluation of earthquake-induced hydrodynamic pressure on circular tapered cylinders surrounded by water. Ocean Eng. 2018, 164, 105–113. [Google Scholar] [CrossRef]
- Wang, P.G.; Wang, X.J.; Zhao, M.; Cheng, X.L.; Du, X.L. A numerical model for earthquake-induced hydrodynamic forces and wave forces on inclined circular cylinder. Ocean Eng. 2020, 207, 107382. [Google Scholar] [CrossRef]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaff, S.A. The force exerted by surface waves on piles. AIME Pet. Trans. 1950, 189, 149–154. [Google Scholar] [CrossRef]
- MacCamy, R.C.; Fuchs, R.A. Wave Forces on Piles: A Diffraction Theory; Report No.TM-69; U.S. Army Corps of Engineers, Beach Erosion Board: Washington, DC, USA, 1954. [Google Scholar]
- Fish, P.R.; Dean, R.B.; Heaf, N.J. Fluid-structure interaction in Morison's equation for the design of offshore structures. Eng. Struct. 1980, 2, 15–26. [Google Scholar] [CrossRef]
- Penzien, J.; Kaul, M.K. Response of offshore towers to strong motion earthquakes. Earthq. Eng. Struct. Dyn. 1972, 1, 55–68. [Google Scholar] [CrossRef]
- Song, B.; Zheng, F.; Li, Y. Study on a simplified calculation method for hydrodynamic pressure to slender structures under earthquakes. J. Earthq. Eng. 2013, 17, 720–735. [Google Scholar] [CrossRef]
- Jian, Y.; Zhan, J.; Zhu, Q. Short crested wave-current forces around a large vertical circular cylinder. Eur. J. Mech. B-Fluids 2008, 27, 346–360. [Google Scholar] [CrossRef]
- Wang, P.G.; Zhao, M.; Du, X.L.; Liu, J.B. Dynamic response of bridge pier under combined earthquake and wave-current action. J. Bridge Eng. 2019, 24, 04019095. [Google Scholar] [CrossRef]
- Wang, P.G.; Zhao, M.; Du, X.L.; Liu, J.B. Analytical solution for the short-crested wave diffraction by an elliptical cylinder. Eur. J. Mech. B-Fluids 2019, 74, 399–409. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Molin, B. Offshore Structure Hydrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Rahman, M.; Bhatta, D.D. Evaluation of added mass and damping coefficients of an osciallating circular cylinder. Appl. Math. Model. 1993, 17, 70–79. [Google Scholar] [CrossRef]
- Wolf, J.P. Consistent lumped-parameter models for unbounded soil: Physical representation. Earthq. Eng. Struct. Dyn. 1991, 20, 11–32. [Google Scholar] [CrossRef]
- Bubnicki, Z. Modern Control Theory; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Tang, Z.Y.; Li, X.; Wang, Z.Y. Stable parameters identification for rational approximation of single-degree-of-freedom frequency response function of semi-infinite medium. Int. J. Numer. Methods Eng. 2023, 124, 5596–5615. [Google Scholar] [CrossRef]
- Wang, P.G.; Zhang, W.Q.; Xu, H.B.; Zhao, M.; Du, X.L. A high-accuracy substructure method in the time domain for simulating pile-soil dynamic interaction in horizontal vibration. Comput. Geotech. 2021, 140, 104479. [Google Scholar] [CrossRef]
- Wang, P.G.; Zhao, M.; Li, H.F.; Du, X.L. An accurate and efficient time-domain model for simulating water-cylinder dynamic interaction during earthquakes. Eng. Struct. 2018, 166, 263–273. [Google Scholar] [CrossRef]
- Zhao, M.; Du, X.; Liu, J.; Li, H. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide. Int. J. Numer. Methods Eng. 2011, 87, 1074–1104. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Water density | 1000 kg/m3 |
| Water depth | 40 m |
| Radius of the cylinder | 2 m |
| Elastic modulus of the cylinder | 30 GPa |
| Density of the cylinder | 2500 kg/m3 |
| Peak acceleration of seismic waves | 0.1 g |
| Wave height | 4 m |
| Case | Mass Ratio | Damping Ratio |
|---|---|---|
| Wave load: wave period set as 3 s to 10 s | 2.5, 5.08, 7.66, 12.82 | 0.0, 0.005, 0.01, 0.02, 0.05 |
| Seismic waves: Chichi, El-Centro, Christchurch | 2.5 to 12.82 | 0.0, 0.005, 0.01, 0.02, 0.05 |
| Time Step (s) | Displacement (m) | Acceleration (m·s−2) |
|---|---|---|
| 0.05 | 0.01743 | −0.01802 |
| 0.02 | 0.01738 | −0.01743 |
| 0.01 | 0.01737 | −0.01733 |
| Mesh Size (m) | Displacement (m) | Acceleration (m·s−2) |
|---|---|---|
| 4 | 0.01742 | −0.01597 |
| 2 | 0.01737 | −0.01734 |
| 1 | 0.01732 | −0.01735 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Fu, H.; Liu, H.; Tang, Z.; Du, X. A Time-Domain Substructure Method for Simulating Water–Cylinder Interaction Under Dynamic Loadings Considering Boundary Condition of Free Surface Waves. J. Mar. Sci. Eng. 2025, 13, 1814. https://doi.org/10.3390/jmse13091814
Wang P, Fu H, Liu H, Tang Z, Du X. A Time-Domain Substructure Method for Simulating Water–Cylinder Interaction Under Dynamic Loadings Considering Boundary Condition of Free Surface Waves. Journal of Marine Science and Engineering. 2025; 13(9):1814. https://doi.org/10.3390/jmse13091814
Chicago/Turabian StyleWang, Piguang, Hao Fu, Hao Liu, Zhenyun Tang, and Xiuli Du. 2025. "A Time-Domain Substructure Method for Simulating Water–Cylinder Interaction Under Dynamic Loadings Considering Boundary Condition of Free Surface Waves" Journal of Marine Science and Engineering 13, no. 9: 1814. https://doi.org/10.3390/jmse13091814
APA StyleWang, P., Fu, H., Liu, H., Tang, Z., & Du, X. (2025). A Time-Domain Substructure Method for Simulating Water–Cylinder Interaction Under Dynamic Loadings Considering Boundary Condition of Free Surface Waves. Journal of Marine Science and Engineering, 13(9), 1814. https://doi.org/10.3390/jmse13091814






