Factors Controlling the Formation and Evolution of the Beach Zone in a Semi-Enclosed Tideless Embayment: The Case of the North Coast of the Messiniakos Gulf (Eastern Mediterranean)
Abstract
1. Introduction
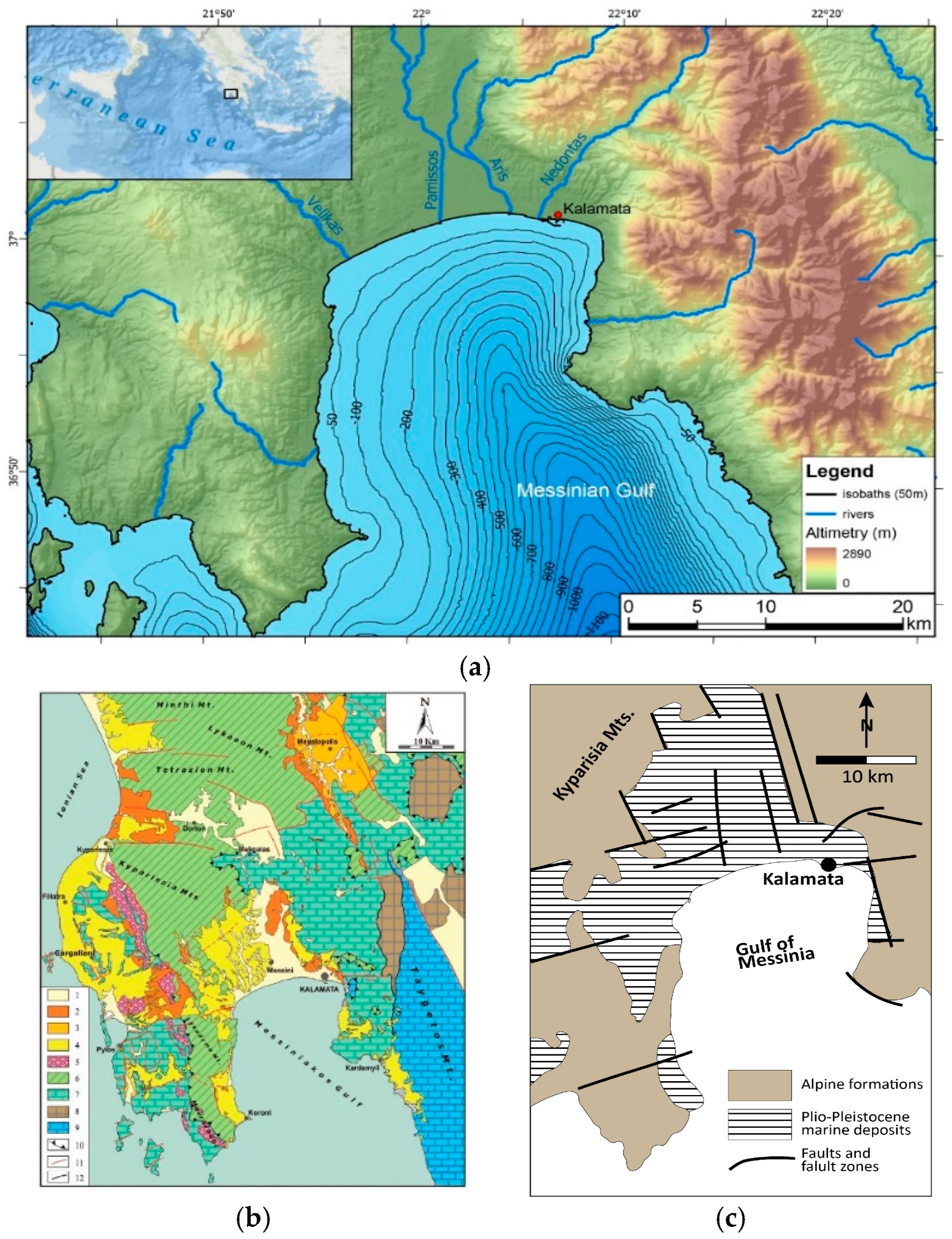
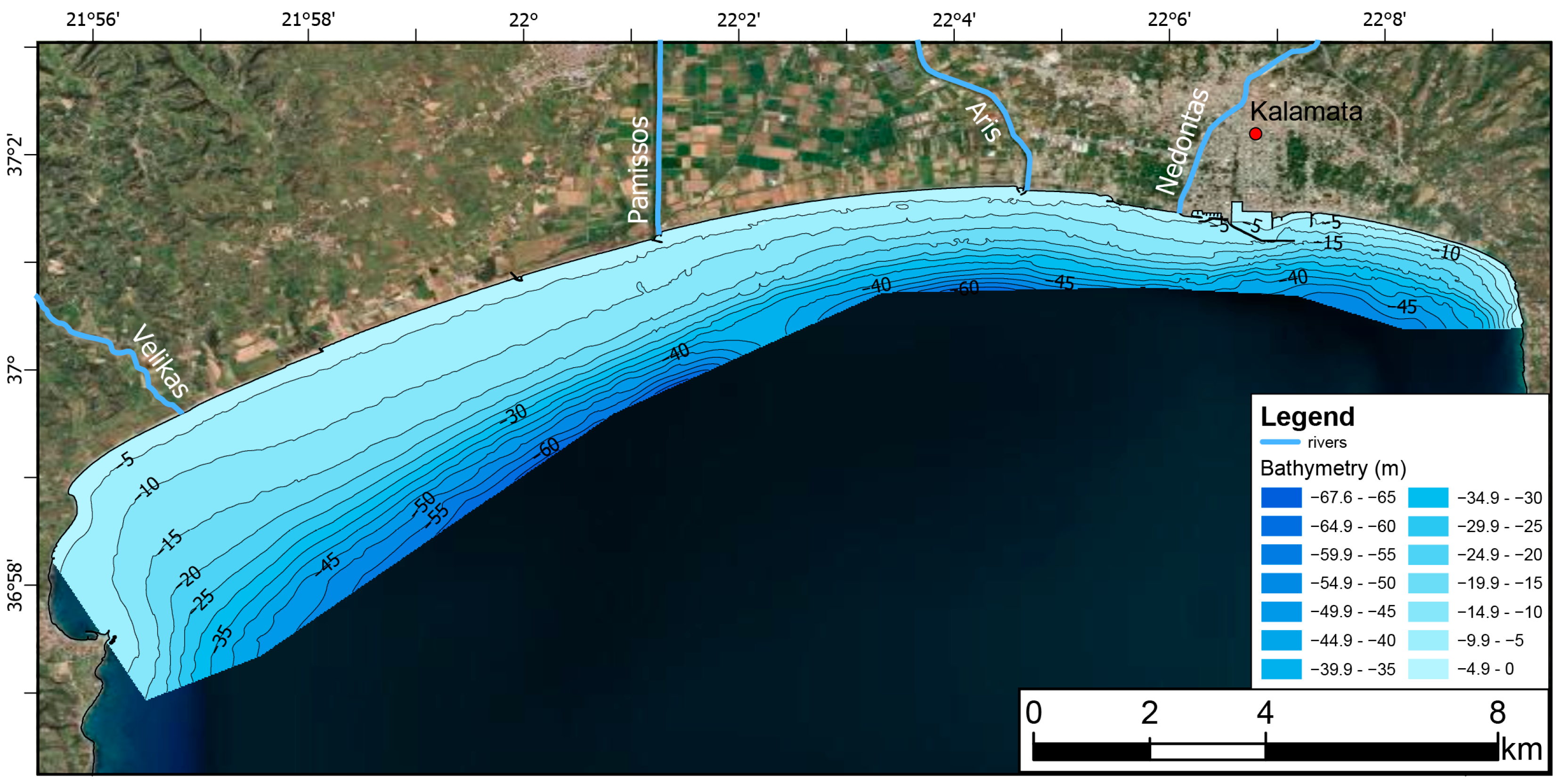
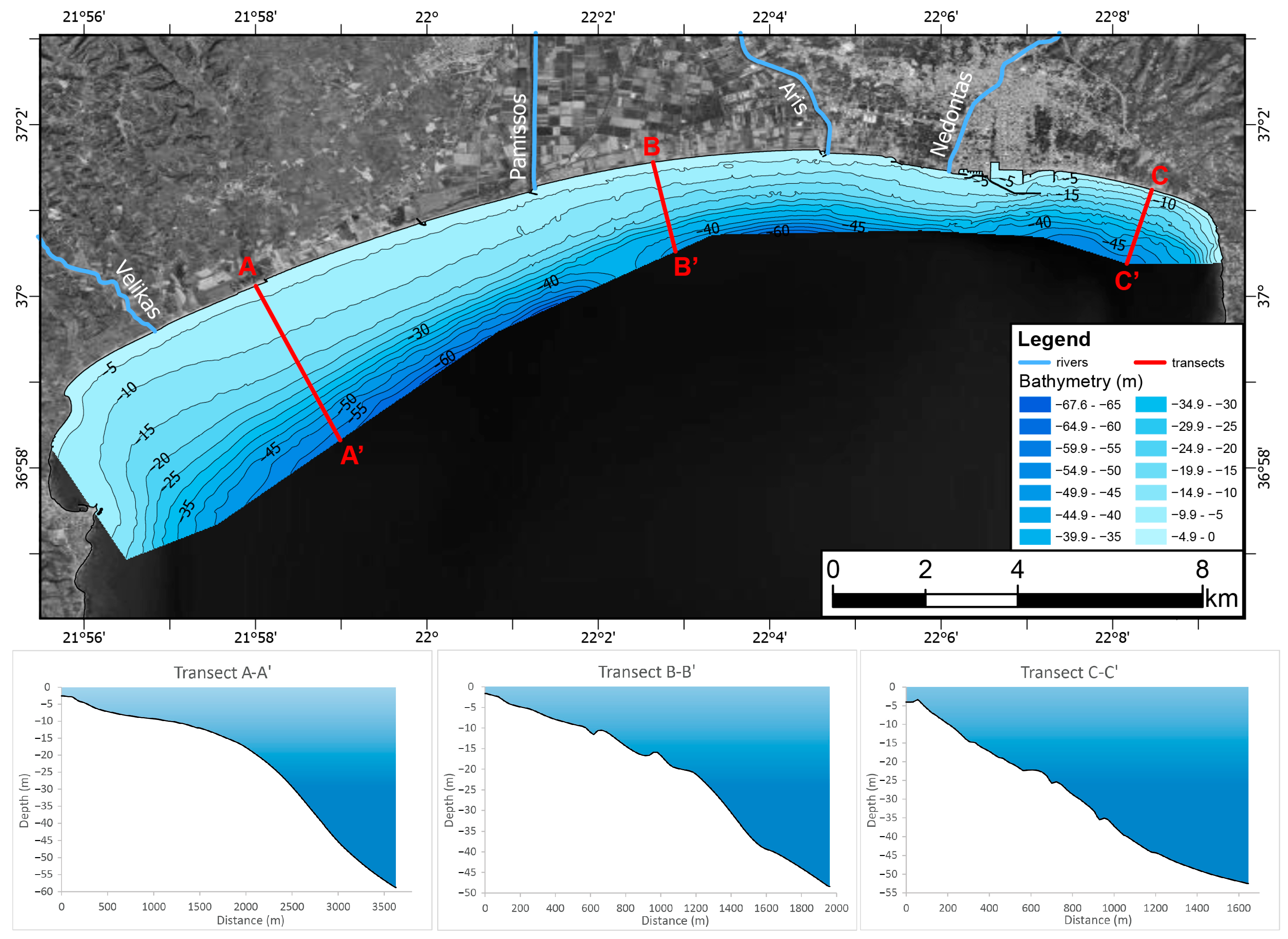
2. Study Area
3. Data Collection and Analysis
3.1. Data Collection
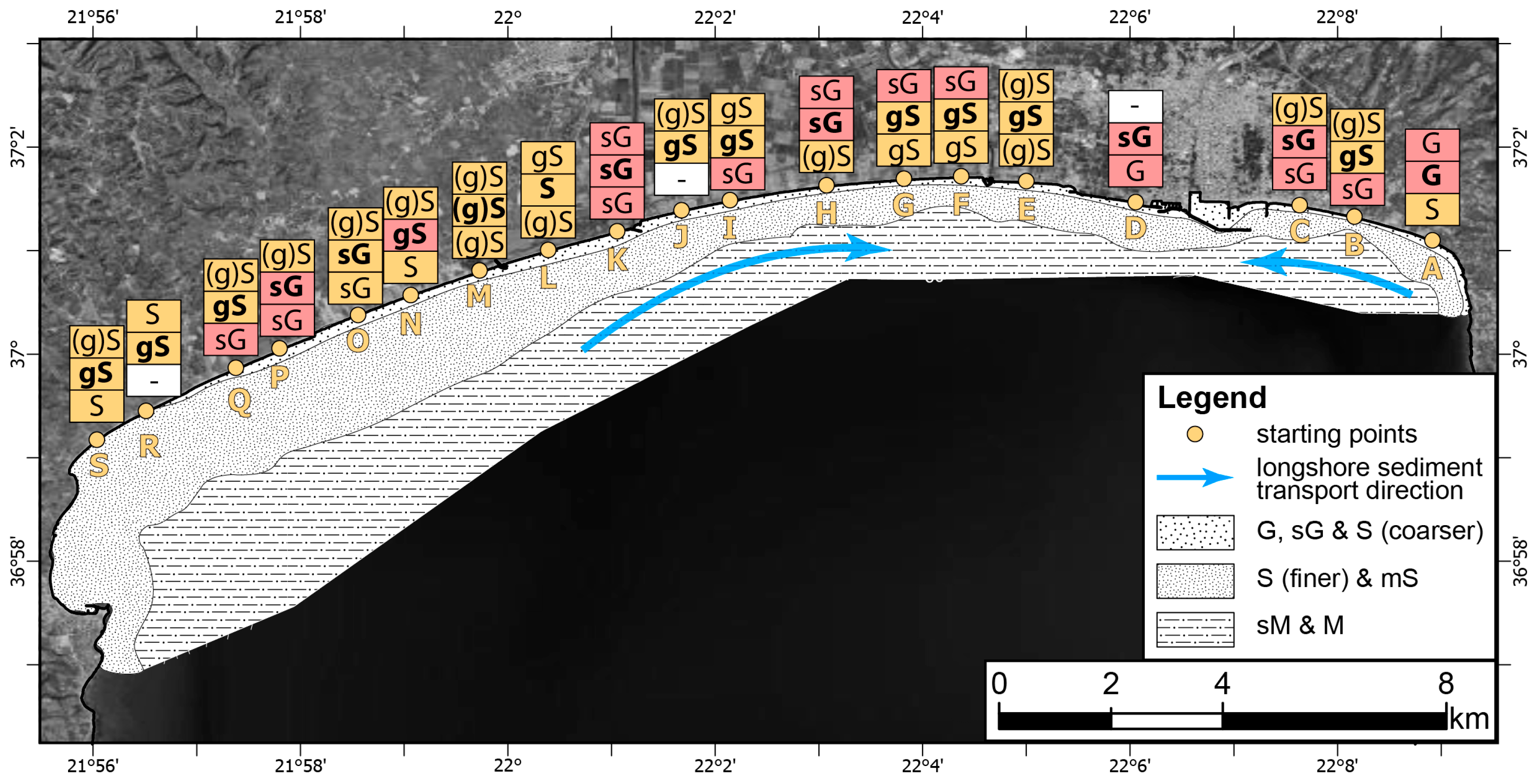
3.1.1. Morphological Characteristics
3.1.2. Shoreline Position
3.1.3. Wave Data
3.2. Data Analysis
3.2.1. Grain Size Analysis
3.2.2. Shoreline Spatial Changes
3.2.3. Elaboration of Wave Data
3.2.4. Beach Retreat Due Storm Surge and Sea Level Rise
4. Results
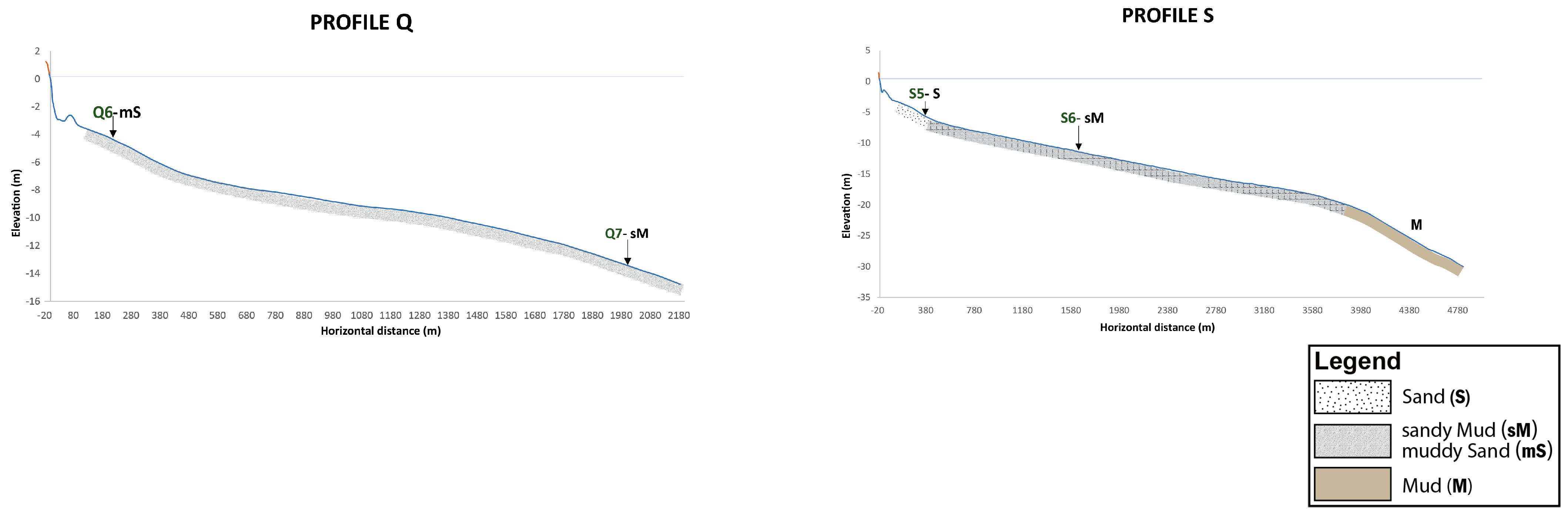
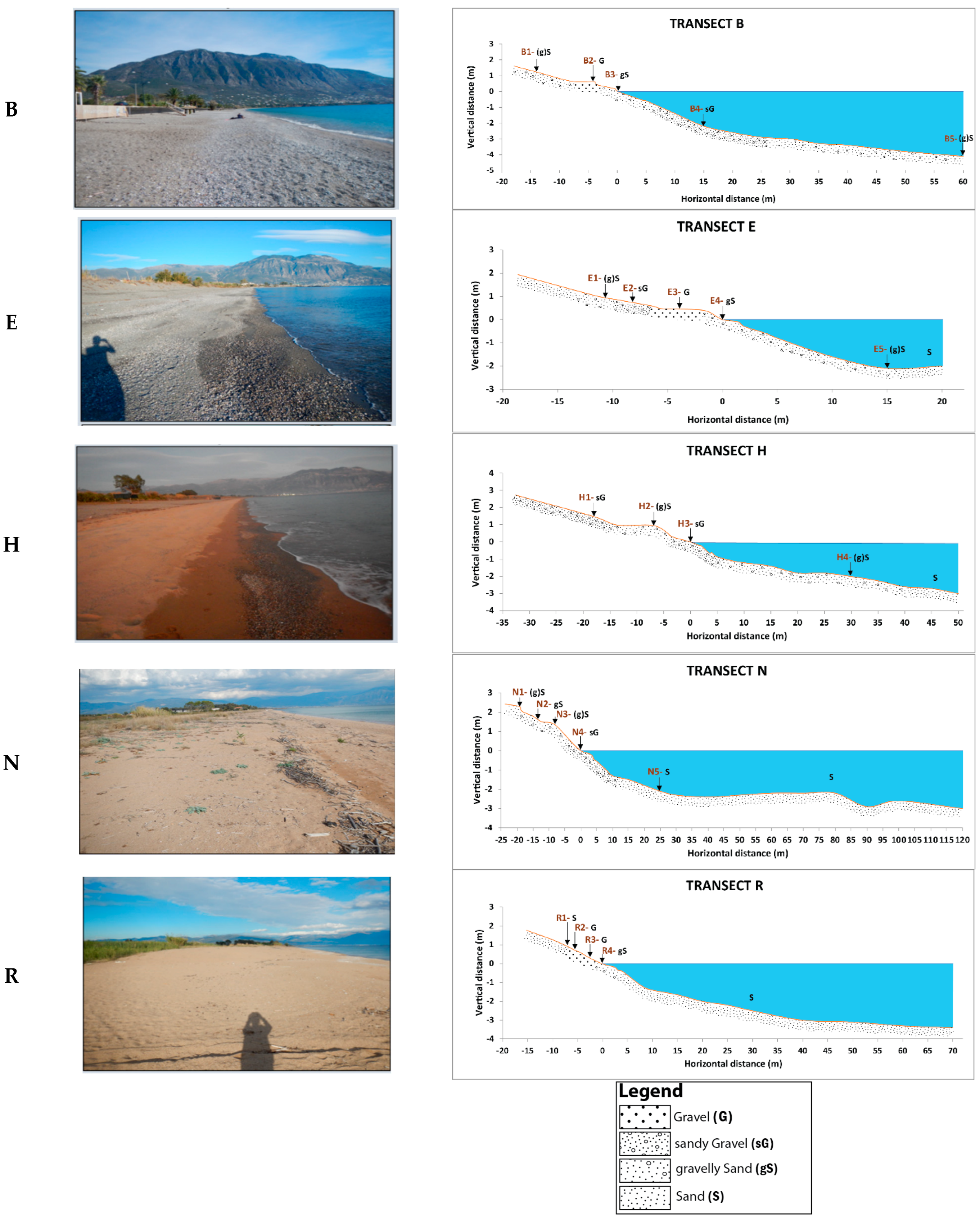
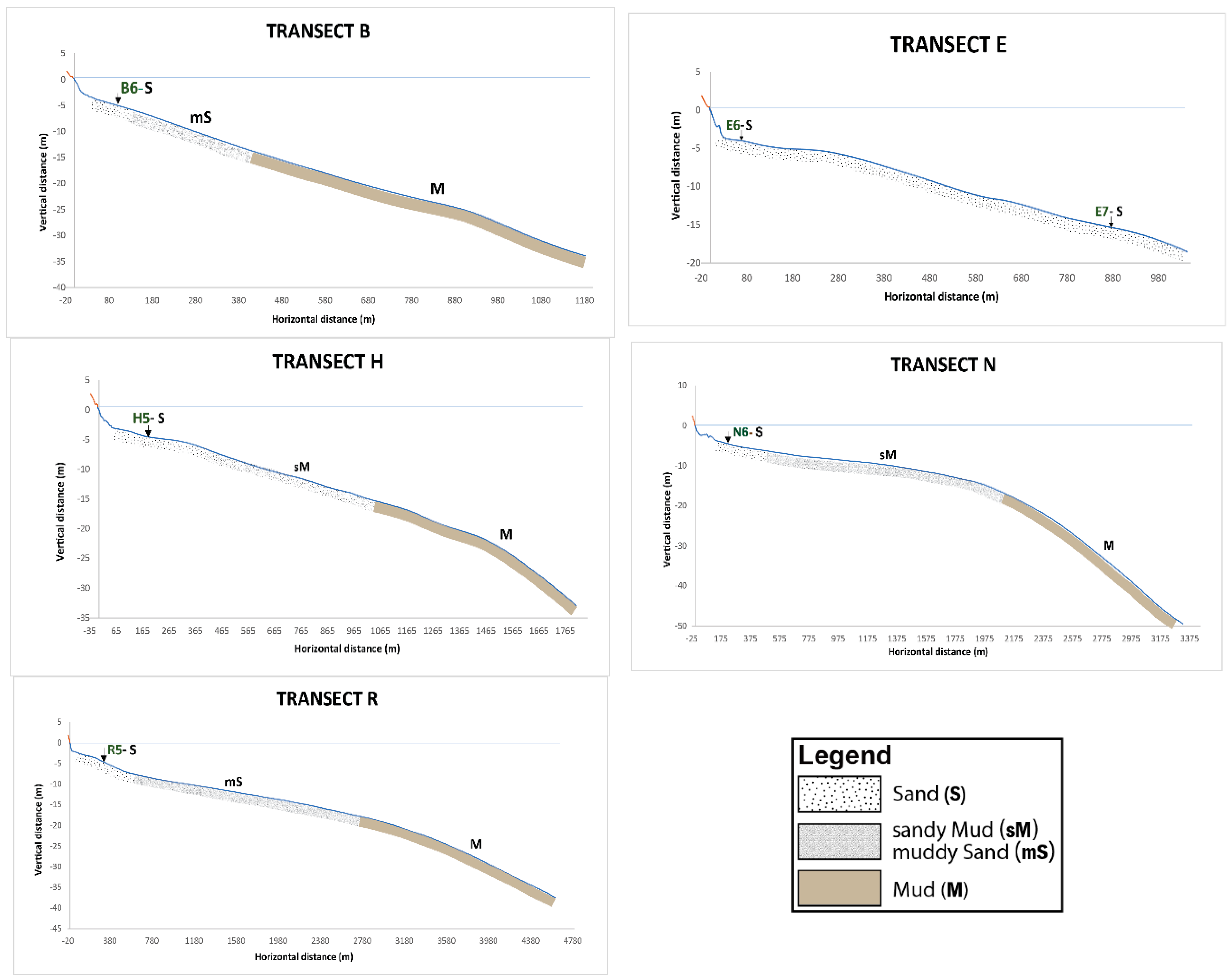
4.1. Beach Material and Morphology
4.2. Hydrodynamics/Morphodynamics
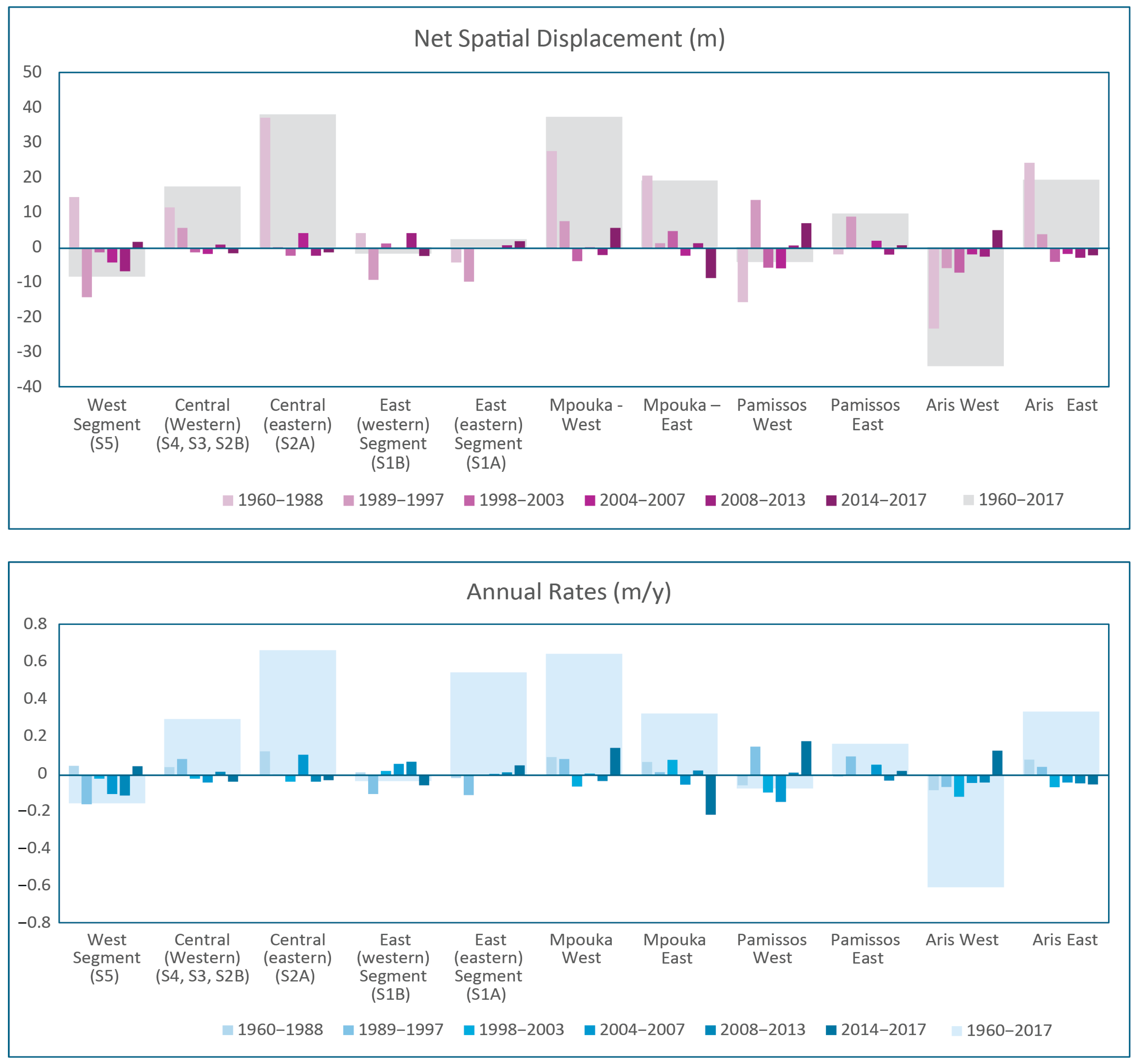
4.3. Shoreline Displacement
4.3.1. Past 60 Years (1960–2017)
4.3.2. Future Trend
5. Discussion
5.1. Morphodynamic Characteristics
5.2. Beach Retreat Due to Storm Surge
5.3. Shoreline Evolution
5.3.1. Past Period (1960–2017)
5.3.2. Future Retreat Due to Climate Change
6. Synopsis and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| C = (m/s) | (A1) | ||
| L = (m) | (A2) | ||
| d > 0.5 Lo (deep waters) | (a) | (A3) | |
| 0.5 Lo > d > 0.05 Lo (intermediate waters) | (b) | ||
| d < 0.05 Lo (shallow waters) | (c) | ||
| Rmax = 1.3·[(0.92·m·Hs0.7·Lo0.3) + (0.5·(1.28 + 3·m·Hs)] (m) | (A4) | ||
| hc = (2.28·He) − 68.5·(He2/(9.81·Te)2) (m) | (A5) | ||
| Hb = (−0.57 m2 + 0.31·m + 0.58)·Lo (Ho/Lo)0.83 (m) | (A6) | ||
| γb = 1.1·ξb0.167(m) | (A7) | ||
| ξ = m/(H/Lo)0.5 & ξb = m/(Hb/Lo)0.5 | (A8) | ||
| Ω = Hb/Tp·ws | (A9) | ||
| D ≤ 0.1 mm | (m/s) | (a) | (A10) |
| 0.1 < D < 1 mm | (m/s) | (b) | |
| D ≥ 1 mm | (m/s) | (c) | |
| where (D) is the grain diameter (diameter of the sieve holes), (s) the specific gravity (ρs/ρw: sediment density/seawater density) (s≌2.65) and (v) the kinematic viscosity (≌10−6 m2/s) | |||
| Qt,i = (kg/s) | (A11) | ||
| Cb/Co = αb/ao (m/s) when Cb = (g* db)0.5 | (A12) | ||
| (m) when, and A’ = 2.25 (ws2/g)1/3 | (A13) | ||
| where db is the breaking depth of the 0.137% highest incoming H(1/3) waves, Wb is the horizontal distance of the point of the breaking depth from the shoreline, mo is the beach face slope and ws the settling velocity of the beachface material (D50) | |||
| (m) | (A14) | ||
| where (a) is the sea level rise, (dC) is the maximum depth of bottom sediment mobilization for the 0.137% of the H(1/3) waves approaching annually, (Wh) is the horizontal distance of (dC) from the shoreline, and (B) is the height of the berm (in practice the upper beach limit). | |||
Appendix B
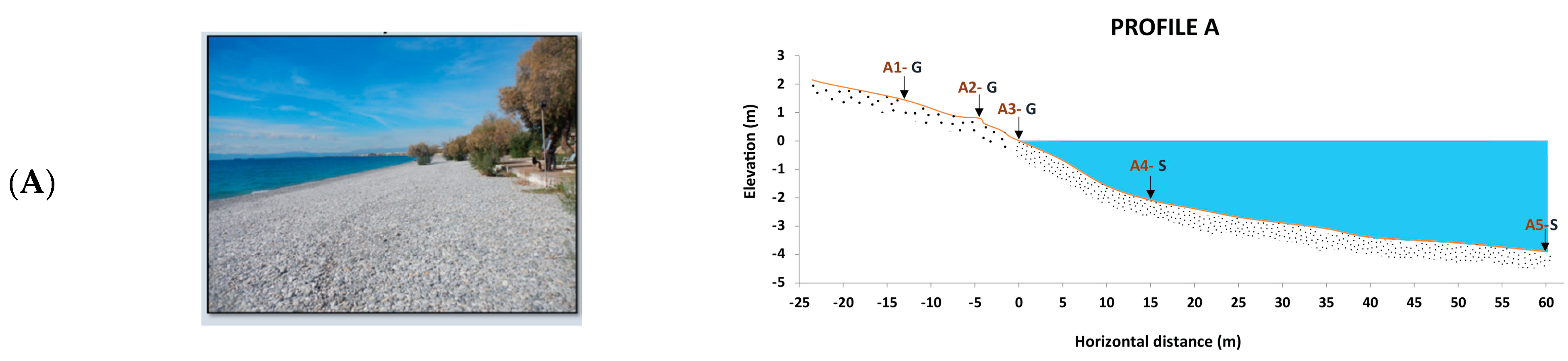
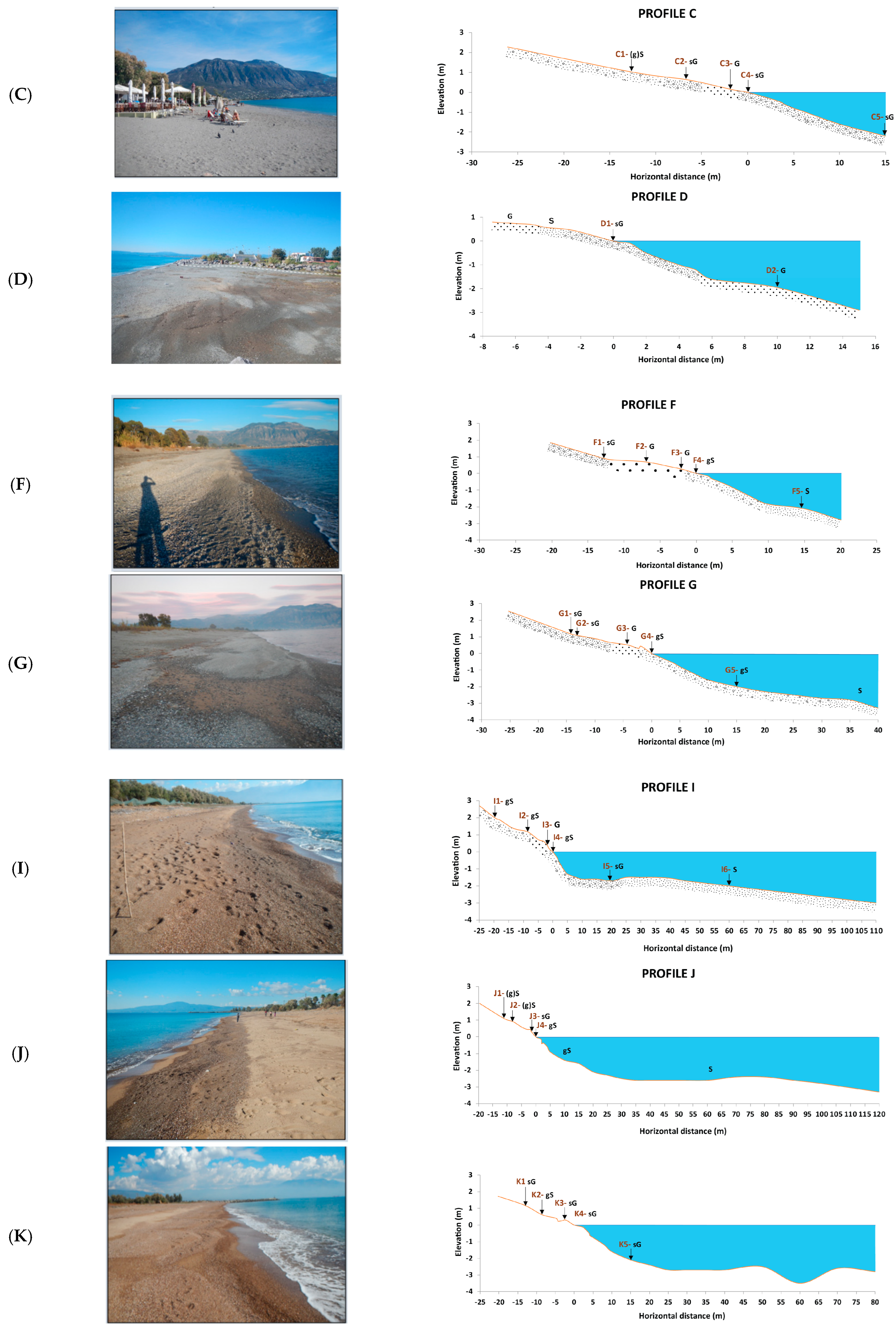
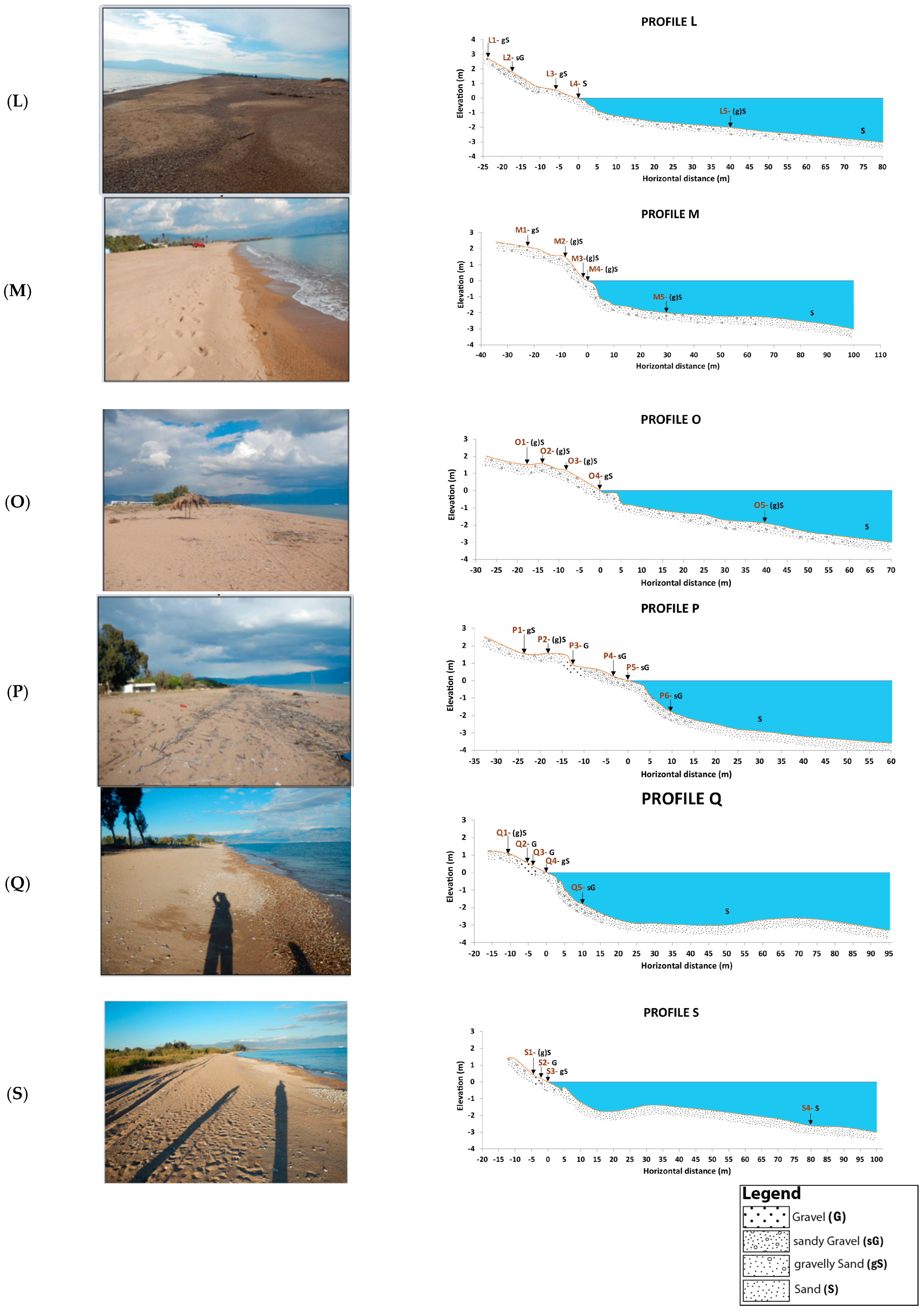
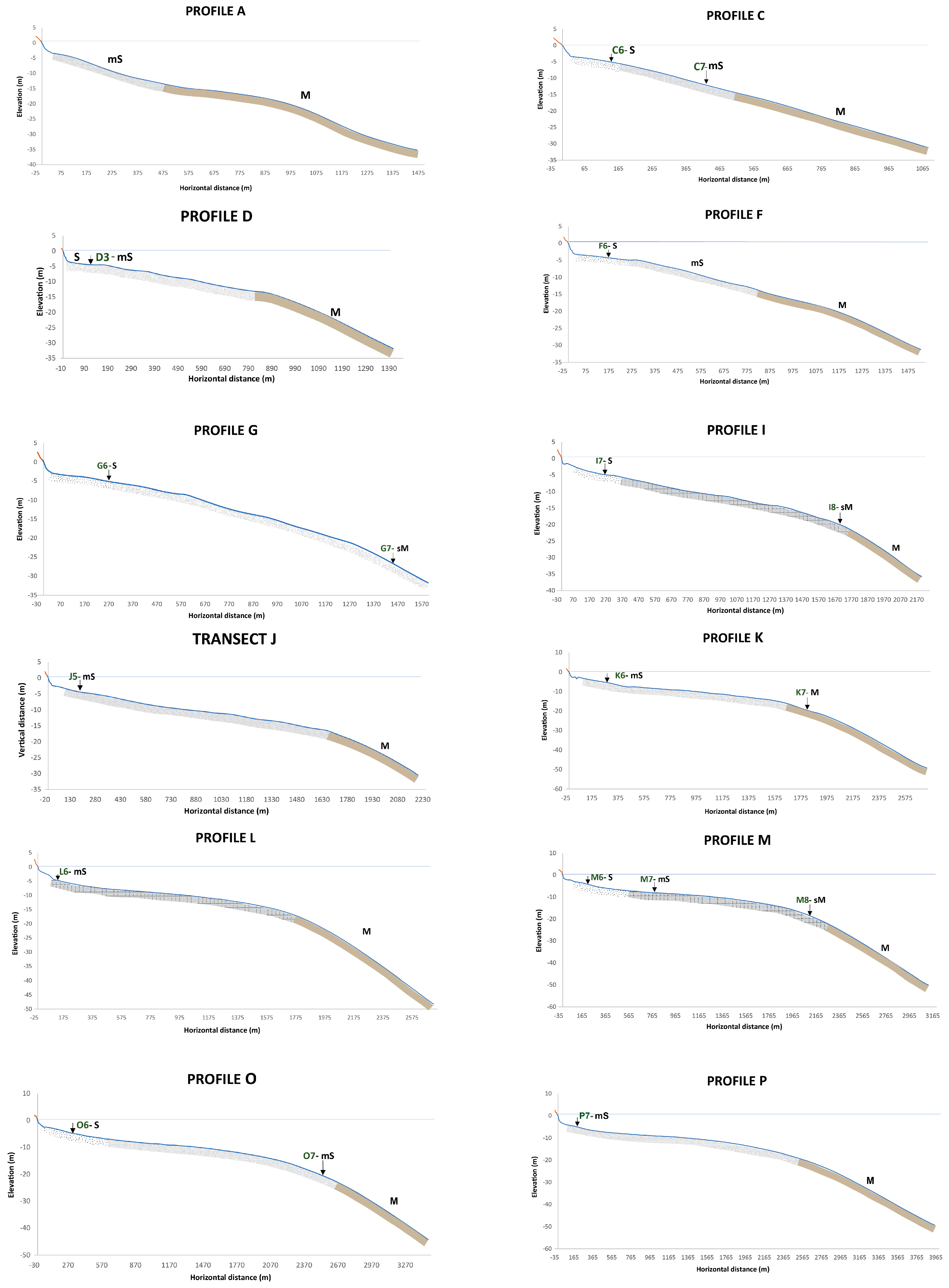
| Landward Zone | Subaerial Beach | Beach Face | Subaqueous Beach | ||||||
|---|---|---|---|---|---|---|---|---|---|
| B (m) | W (m) | GS-B | mo (%) | GS-bf | Bars (Depth/Distance) | Near-Shore Sl (%) | Off-Shore SL (%) | ||
| A | Hotel | 2.2 | 23.6 | Gravels | 16 | G | 2.5/20, 3/35; 3.5/47 | 2.2 | 3.3 |
| B | Pedestrian road | 1.6 | 17.8 | Gravels | 15 | gS | 2.7/27; 3/40; 5/920/? | 2.4 | 2.8 |
| C | Pedestrian road | 2.3 | 26.0 | Mixed | 13 | sG | --- | 2.6 | 2.8 |
| D | River mouth | 0.8 | 7.4 | Mixed (gravely) | 21 | sG | 2/10; 4.5/190; 7/330 | 1.5 | 2.5 |
| E | Low dunes | 1.9 | 18.6 | Mixed (gravely) | 19 | gS | 2/25; 3,5/75; 4.5/220 | 1.7 | 2.5 |
| F | Low dunes | 1.8 | 20.2 | Mixed (gravely) | 11 | gS | 2/15; 4.5/260 | 1.5 | 2.8 |
| G | Low dunes | 2.6 | 25.3 | Mixed (gravely) | 17 | sG | 2.7/35; 4.5/18; 0 7/600 | 1.7 | 3.3 |
| H | Agricultural land | 2.7 | 32.6 | Mixed | 15 | sG | 1.4/15; 1.8/30; 2.7/45; 4/150; 5/330 | 1.25 | 3.3 |
| I | Agricultural land | 2.7 | 24.9 | Mixed (sandy) | 20 | gS | 1.5/25–40; 5/315 | 1.3 | 2.5 |
| J | Low dunes | 2.0 | 19.7 | Mixed (sandy) | 20 | gS | 1.5/15; 2.4/75; 5/320 | 0.8 | 2.5 |
| K | Low dunes | 1.7 | 20.3 | Mixed (gravely) | 13 | sG | 2.5/50; 2.7/72; 5/300 | 0.7 | 2.25 |
| L | Alluvial plain | 2.8 | 24.0 | Mixed (sandy) | 12 | S | 0.6/4; 3/30 | 0.65 | 3.0 |
| M | Alluvial plain | 2.4 | 34.5 | Mixed (sandy) | 19 | (g)S | 1.6/15; 2.2/60; 3.3/130 | 0.6 | 2.7 |
| N | Alluvial plain | 2.4 | 23.8 | Mixed (sandy) | 15 | sG | 1.5/15; 2.2/80; 2.9/100 | 1.0 | 2.5 |
| O | Low dunes | 2.0 | 27.5 | Mixed (sandy) | 11 | gS | 1.5/22; 1.9/40; 3/65; 5/130 | 0.5 | 2.5 |
| P | Low dunes | 2.5 | 3.7 | Mixed (sandy) | 8 | sG | 2.5/20; 2.9/30; 5/210 | 0.35 | 1.25 |
| Q | Alluvial plain | 1.2 | 16.2 | Mixed (sandy) | 14 | gS | 1.8/10; 2.8/30–35; 2.7/65–75 | 0.5 | 0.7 |
| R | Alluvial plain | 1.8 | 15.2 | Mixed (sandy) | 16 | gS | 1.6/15; 2.2/25; 3/50 | 0.6 | 1.25 |
| S | Alluvial plain | 1.4 | 12.5 | Mixed (sandy) | 11 | gS | 0.5/6; 1.5/30–35; 2.6/90 | 0.4 | 1.25 |
Appendix C
| Elevation (±m) | Distance (m) | Grain Size | σΙ | |||||
|---|---|---|---|---|---|---|---|---|
| Texture | Mz (Φ) | D50 (mm) | Type | (φ) | Sorting | |||
| A1 | 1.5 | −13.2 | G | −5.18 | 28.895 | P | 0.55 | m.s |
| A2 | 0.8 | −4.5 | G | −3.35 | 13.420 | P | 0.84 | m.s |
| A3 | 0.0 | 0.0 | G | −2.68 | 7.053 | P | 0.93 | m.s |
| A4 | −2.1 | 15.0 | S | 2.99 | 0.128 | f.S | 0.63 | m.s |
| A5 | −3.9 | 60.0 | S | 3.50 | 0.088 | v.f.S | 0.48 | w.s |
| Β1 | 1.2 | −14.0 | (g)S | 0.55 | 0.693 | G | 1.05 | m.s |
| Β2 | 0.6 | −4.1 | G | −1.90 | 3.713 | G | 0.73 | m.s |
| Β3 | 0.0 | 0.0 | gS | −0.42 | 1.393 | v.c.S | 1.19 | p.s |
| Β4 | −2.2 | 15.0 | sG | 0.59 | 0.271 | c.S | 2.66 | v.p.s |
| Β5 | −4.1 | 58.0 | (g)S | 2.72 | 0.160 | f.S | 0.70 | m.w.s |
| Β6 | −5.1 | 85.0 | S | 3.20 | 0.095 | v.f.S | 0.68 | m.s |
| C1 | 1.0 | −12.5 | (g)S | 0.81 | 0.592 | c.S | 1.20 | p.s |
| C2 | 0.6 | −6.7 | sG | −1.19 | 1.906 | G. | 1.12 | p.s |
| C3 | 0.2 | −1.8 | G | −1.87 | 3.992 | G | 0.83 | m.s |
| C4 | 0.0 | 0.0 | sG | −1.14 | 2.216 | G | 0.81 | m.s |
| C5 | −2.2 | 15.0 | sG | 0.69 | 0.227 | c.S | 2.76 | v.p.s |
| C6 | −4.7 | 160.0 | S | 3.40 | 0.093 | v.f.S | 0.60 | m.s |
| C7 | −11.0 | 425.0 | mS | 5.21 | 0.071 | mS | 2.60 | v.p.s |
| D1 | 0.0 | 0.0 | sG | −0.84 | 1.715 | v.c.S | 0.78 | m.s |
| D2 | −2.0 | 10.0 | G | −2.39 | 5.730 | P | 1.34 | p.s |
| D3 | −4.3 | 115.0 | S | 3.34 | 0.093 | v.f.S | 0.80 | m.s |
| E1 | 0.9 | −11.6 | (g)S | 0.96 | 0.520 | c.S | 1.02 | p.s |
| E2 | 0.7 | −9.6 | sG | −1.31 | 4.953 | G | 1.79 | p.s |
| E3 | 0.45 | −3.8 | G | −2.10 | 4.651 | P | 0.68 | m.w.s |
| E4 | 0.0 | 0.0 | gS | 0.53 | 0.980 | c.S | 1.45 | p.s |
| E5 | −2.1 | 15.0 | (g)S | 2.44 | 0.179 | f.S | 0.76 | m.s |
| E6 | −4.2 | 80.0 | S | 3.45 | −0.445 | v.f.S | 0.57 | m.s |
| E7 | 15.4 | 890.0 | S | 3.33 | 0.095 | v.f.S | 1.48 | p.s |
| F1 | 1.1 | −12.8 | sG | −0.01 | 0.647 | v.c.S | 2.01 | p.s |
| F2 | 0.7 | −7.0 | G | −2.43 | 5.402 | P | 0.82 | m.s |
| F3 | 0.3 | −2.0 | G | −2.17 | 5.036 | P | 0.76 | m.s |
| F4 | 0.0 | 0.0 | gS | 0.59 | 0.776 | c.S | 1.43 | p.s |
| F5 | −2.2 | 15.0 | S | 2.93 | 0.134 | f.S | 0.64 | m.s |
| F6 | −4.3 | 175.0 | S | 3.29 | 0.096 | v.f.S | 0.70 | m.s |
| G1 | 1.2 | −14.5 | sG | −0.27 | 0.941 | v.c.S | 2.02 | v.p.s |
| G2 | 1.0 | −13.3 | sG | −1.52 | 0.392 | G | 2.14 | v.p.s |
| G3 | 0.5 | −4.2 | G | −2.08 | 4.503 | P | 0.64 | m.s |
| G4 | 0.0 | 0.0 | gS | 0.22 | 1.109 | c.S | 1.82 | p.s |
| G5 | −1.9 | 15.0 | gS | 0.90 | 0.176 | c.S | 2.76 | v.p.s |
| G6 | 4.9 | 270.0 | S | 3.38 | 0.093 | v.f.S | 0.65 | m.s |
| G7 | −26.4 | 1450.0 | sM | 6.80 | 0.022 | f.Z | 2.84 | v.p.s |
| H1 | 1.4 | −18.1 | sG | −0.74 | 2.463 | v.c.S | 1.75 | p.s |
| H2 | 0.9 | −6.9 | (g)S | 1.83 | 0.295 | G | 0.74 | m.s |
| H3 | 0.0 | 0.0 | sG | −0.14 | 1.692 | v.c.S | 1.80 | p.s |
| H4 | −2.2 | 32.0 | (g)S | 2.11 | 0.221 | f.S | 0.73 | m.s |
| H5 | −4.4 | 175.0 | S | 3.27 | 0.097 | v.f.S | 0.71 | m.s |
| I1 | 2.1 | −19.7 | gS | 0.67 | 0.607 | c.S | 0.97 | m.s |
| I2 | 1.2 | −8.5 | gS | −0.77 | 1.569 | v.c.S | 0.76 | m.s |
| I3 | 0.4 | −1.8 | G | −1.91 | 3.590 | v.c.S | 0.61 | m.s |
| I4 | 0.0 | 0.0 | gS | −0.28 | 1.281 | v.c.S | 0.71 | m.s |
| I5 | −1.4 | 4.8 | sG | −1.28 | 2.487 | G | 1.17 | p.s |
| I6 | −2.2 | 20.0 | S | 1.90 | 0.266 | m.S | 0.75 | m.s |
| I7 | −4.8 | 60.0 | S | 3.24 | 0.098 | v.f.S | 0.74 | m.s |
| I8 | −19.6 | 270.0 | sM | 6.75 | 0.023 | m.Z | 2.90 | v.p.s |
| J1 | 1.2 | −11.1 | (g)S | 0.76 | 0.627 | c.S | 0.75 | m.s |
| J2 | 0.9 | −8.1 | (g)S | 1.54 | 0.345 | G | 0.53 | m.s |
| J3 | 0.4 | −1.8 | sG | −0.85 | 3.562 | v.c.S | 2.00 | p.s |
| J4 | 0.0 | 0.0 | gS | 0.31 | 0.808 | c.S | 1.73 | p.s |
| J5 | −5.1 | 220.0 | mS | 3.29 | 0.097 | v.f.S | 1.75 | p.s |
| K1 | 1.2 | −13.2 | sG | 0.07 | 0.941 | c.S | 1.85 | p.s |
| K2 | 0.6 | −8.6 | gS | 1.07 | 0.246 | m.S | 1.84 | p.s |
| K3 | 0.3 | −2.6 | sG | −0.61 | 2.762 | v.c.S | 1.88 | p.s |
| K4 | 0.0 | 0.0 | sG | −0.26 | 2.102 | v.c.S | 2.09 | v.p.s |
| K5 | −1.9 | 12.0 | sG | 0.55 | 0.362 | c.S | 2.24 | v.p.s |
| K6 | −4.4 | 325.0 | mS | 5.82 | 0.079 | m.Z | 3.40 | v.p.s |
| K7 | −19.4 | 1850.0 | mS | 6.91 | 0.017 | m.Z | 2.84 | v.p.s |
| L1 | 1.4 | −14.5 | gS | 0.07 | 1.143 | c.S | 1.32 | p.s |
| L2 | 1.1 | −12.2 | sG | 0.01 | 1.519 | c.S | 1.66 | p.s |
| L3 | 0.4 | −4.6 | gS | 1.44 | 0.229 | m.S | 1.47 | p.s |
| L4 | 0.0 | 0.0 | S | 1.91 | 0.253 | m.S | 0.71 | m.s |
| L5 | −2.2 | 40.0 | (g)S | 2.31 | 0.190 | f.S | 0.71 | m.s |
| L6 | −4.9 | 1875.0 | mS | 5.99 | 0.069 | m.Z | 3.37 | v.p.s |
| M1 | 2.4 | 34.0 | gS | 0.00 | 1.081 | v.c.S | 0.87 | m.s |
| M2 | 1.8 | −8.3 | (g)S | 1.06 | 0.411 | m.S | 1.03 | p.s |
| M3 | 0.6 | −4.2 | (g)S | 1.44 | 0.365 | m.S | 0.71 | m.s |
| M4 | 0.0 | 0.0 | (g)S | 0.89 | 0.509 | c.S | 0.87 | m.s |
| M5 | −2.1 | 30.0 | (g)S | 2.11 | 0.217 | f.S | 0.71 | m.s |
| M6 | −4.2 | 200.0 | S | 2.95 | 0.130 | f.S | 0.71 | m.s |
| M7 | −8.1 | 780.0 | mS | 3.59 | 0.088 | v. f.S | 1.62 | p.s |
| M8 | −18.7 | 2100.0 | sM | 6.53 | 0.028 | m.Z | 3.14 | p.s |
| N1 | 2.5 | −20.2 | (g)S | 1.00 | 0.469 | c.S | 0.85 | m.s |
| N2 | 1.8 | −12.7 | gS | 1.03 | 0.394 | m.S | 1.37 | p.s |
| N3 | 1.5 | −8.8 | (g)S | 1.76 | 0.310 | m.S | 0.76 | m.s |
| N4 | 0.0 | 0.0 | sG | −0.20 | 1.187 | v.c.S | 2.24 | v.p.s |
| N5 | −2.1 | 25.0 | S | 2.15 | 0.212 | f.S | 0.71 | m.s |
| N6 | −4.7 | 190.0 | S | 6.04 | 0.080 | m.Z | 3.38 | v.p.s |
| O1 | 1.6 | −14.0 | (g)S | 1.16 | 0.429 | m.S | 1.02 | p.s |
| O2 | 1.2 | −8.5 | (g)S | 1.78 | 0.307 | m.S | 0.71 | m.s |
| O3 | 0.0 | 0.0 | gS | 0.88 | 0.441 | c.S | 1.40 | p.s |
| O4 | 2.1 | 45.0 | (g)S | 2.09 | 0.219 | f.S | 0.69 | m.w.s |
| O5 | −4.6 | 310.0 | S | 3.08 | 0.111 | v.f.S | 0.72 | p.s |
| O6 | −20.5 | 2600.0 | mS | 5.29 | 0.066 | m.Z | 2.60 | v.p.s |
| P1 | 1.6 | −24.2 | gS | 0.97 | 0.484 | c.S | 1.14 | p.s |
| P2 | 1.6 | −18.1 | (g)S | 1.06 | 0.461 | m.S | 0.71 | p.s |
| P3 | 1.2 | −12.9 | G | −2.45 | 5.451 | P | 0.72 | m.s |
| P4 | 0.4 | −4.5 | sG | −1.02 | 1.702 | G | 1.06 | p.s |
| P5 | 0.0 | 0.0 | sG | −0.57 | 1.535 | v.c.S | 0.93 | m.s |
| P6 | −1.8 | 10.0 | sG | −0.40 | 0.846 | v.c.S | 2.08 | v.p.s |
| P7 | −5.1 | 170.0 | mS | 3.54 | 0.086 | v.f.S | 0.71 | m.s |
| Q1 | 1.2 | −12.5 | (g)S | 0.45 | 0.720 | c.S | 0.76 | m.s |
| Q2 | 0.9 | −7.4 | G | −1.62 | 2.989 | G | 0.79 | m.s |
| Q3 | 0.4 | −3.9 | G | −2.16 | 5.214 | P | 1.41 | p.s |
| Q4 | 0.0 | 0.0 | gS | −0.23 | 1.234 | v.c.S | 0.74 | m.s |
| Q5 | −1.8 | 10.0 | sG | −1.94 | 3.887 | G | 1.72 | p.s |
| Q6 | 5.15 | 210.0 | mS | 5.64 | 0.020 | m.Z | 3.48 | v.p.s |
| Q7 | −13.1 | 2060.0 | sM | 6.01 | 0.015 | m.Z | 3.15 | v.p.s |
| R1 | 1.1 | −8.1 | S | 1.37 | 0.410 | m.S | 0.96 | m.s |
| R2 | 0.7 | −5.5 | G | −2.29 | 4.711 | m.S | 1.10 | p.s |
| R3 | 0.3 | −2.5 | G | −2.47 | 5.524 | P | 0.50 | w.s |
| R4 | 0.0 | 0.0 | gS | 0.64 | 0.727 | m.S | 1.63 | m.s |
| R5 | −4.8 | 380.0 | S | 3.34 | 0.099 | c.S | 0.71 | m.s |
| S1 | 0.5 | −4.5 | (g)S | 1.12 | 0.453 | P | 0.86 | m.s |
| S2 | 0.2 | −2.2 | G | −2.81 | 7.215 | c.S | 0.83 | p.s |
| S3 | 0.0 | 0.0 | gS | 0.13 | 0.696 | f.S | 1.60 | m.s |
| S4 | −2.5 | 80.0 | S | 2.50 | 0.175 | f.S | 0.87 | m.s |
| S5 | −4.7 | 390.0 | sM | 3.33 | 0.095 | v.f.S | 0.64 | v.w.s |
| S6 | −11.5 | 1670.0 | M | 7.71 | 0.005 | f.Z | 3.03 | v.p.s |
Appendix D
| Time Period | West Segment (S5); DSAS Sections: (A1–A59) | Central (Western) (S4, S3, S2B); DSAS Sections: A60–A285 | Central (Eastern) (S2A); DSAS Sections: A286–A328 | East (Western) Segment (S1B) DSAS Sections: B1–B26 | East (Eastern) Segment (S1A) DSAS Sections: B26–B54 | Mpouka—West. DSAS Section: A139–A141 | Mpouka—East. DSAS Section: A142–145 | Pamissos—West. DSAS Section: A182–A185 | Pamissos—East. DSAS Section: A186–A190 | Aris—West. DSAS Section: A284–A286 | Aris—East. DSAS Section: A287–A290 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1960–1988 | NSD | +15.0 | +12.0 | +38.0 | +4.5 | −4.0 | +28.3 | +21.2 | −15.5 | −1.6 | −23.1 | +24.9 |
| Rat. | +0.53 | +0.45 | +1.31 | +0.16 | −0.14 | +1.00 | +0.73 | −0.53 | −0.06 | −0.80 | +0.86 | |
| 1989–1997 | NSD | −14.0 | +6.00 | +0.50 | −9.00 | −9.50 | +8.00 | +1.60 | +14.1 | 9.3 | −5.60 | +4.20 |
| Rat. | −1.56 | +0.89 | +0.06 | −1.00 | −1.06 | 0.89 | +0.18 | +1.57 | +1.03 | −0.62 | +0.47 | |
| 1998–2003 | NSD | −1.0 | −1.00 | −2.00 | +1.50 | +0.20 | −3.60 | +5.10 | −5.5 | 0.3 | −6.90 | −3.80 |
| Rat. | −0.17 | −0.17 | −0.33 | +0.25 | +0.03 | −0.60 | +0.85 | −0.92 | +0.05 | −1.15 | −0.63 | |
| 2004–2007 | NSD | −4.00 | −1.50 | +4.50 | 2.50 | +0.30 | +0.40 | −2.0 | −5.70 | +2.3 | −1.60 | −1.50 |
| Rat. | −1.00 | −0.38 | +1.13 | +0.63 | +0.08 | +0.10 | −0.50 | −1.43 | +0.58 | −0.40 | −0.38 | |
| 2008–2013 | NSD | −6.50 | +1.2 | −2.00 | 4.50 | +1.00 | −1.80 | +1.6 | +0.9 | −1.7 | −2.30 | −2.60 |
| Rat. | −1.08 | +0.20 | −0.33 | 0.75 | +0.17 | −0.30 | 0.27 | +0.15 | −0.28 | −0.38 | −0.43 | |
| 2014–2017 | NSD | +2.00 | −1.30 | −1.00 | −2.10 | +2.20 | +6.00 | −8.50 | +7.40 | +1.00 | +5.40 | −1.90 |
| Rat. | +0.50 | −0.33 | −0.25 | −0.53 | 0.55 | +1.50 | −2.13 | +1.85 | +0.25 | +1.35 | −0.48 | |
| 1960–2017 | NSD | −8.5 | 17.3 | +38.0 | −1.90 | +2.20 | +37.3 | +19.0 | −4.30 | +9.6 | −34.1 | +19.3 |
| Rat. | −0.15 | +0.30 | +0.67 | −0.03 | +0.55 | +0.65 | +0.33 | −0.07 | +0.17 | −0.60 | +0.34 |
References
- López, M.; López, I.; Aragonés, L.; Serra, J.C.; Esteban, V. The Erosion on the East Coast of Spain: Wear of Particles, Mineral Composition, Carbonates and Posidonia oceanica. Sci. Total Environ. 2016, 572, 487–497. [Google Scholar] [CrossRef]
- Zuo, L.; Roelvink, D.; Lu, Y.; Li, S. On Incipient Motion of Silt-Sand under Combined Action of Waves and Currents. Appl. Ocean Res. 2017, 69, 116–125. [Google Scholar] [CrossRef]
- Boretto, G.M.; Rouzaut, S.; Cioccale, M.; Gordillo, S.; Benitez, Y. Dinámica Costera y Antropización En Playas Uruguayas. Un Análisis Integrado Para Su Conservación. Rev. Mex. Cienc. Geol. 2018, 35, 291–306. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy Coastlines under Threat of Erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Phillips, J.D. Environmental Gradients and Complexity in Coastal Landscape Response to Sea Level Rise. Catena 2018, 169, 107–118. [Google Scholar] [CrossRef]
- Di Paola, G.; Aucelli, P.P.C.; Benassai, G.; Rodríguez, G. Coastal vulnerability to wave storms of Sele littoral plain (southern Italy). Nat. Hazards 2014, 71, 1795–1819. [Google Scholar] [CrossRef]
- Bush, D.M.; Young, R. Coastal features and processes. In Geological Monitoring; Young, R., Norby, L., Eds.; Geological Society of America: Boulder, CO, USA, 2009; pp. 47–67. [Google Scholar]
- Mestanza-Ramón, C.; Pranzini, E.; Anfuso, G.; Botero, C.M.; Chica-Ruiz, J.A.; Mooser, A. An attempt to characterize the “3S” (Sea, Sun, and Sand) parameters: Application to the Galapagos Islands and continental Ecuadorian beaches. Sustainability 2020, 12, 3468. [Google Scholar] [CrossRef]
- Phillips, M.R.; Jones, A.L. Erosion and tourism infrastructure in the coastal zone: Problems, consequences and management. Tour. Manag. 2006, 27, 517–524. [Google Scholar] [CrossRef]
- Luijendijk, A.; de Vries, S. Global beach database. In Sandy Beach Morphodynamics; Elsevier: Amsterdam, The Netherlands, 2020; pp. 641–658. [Google Scholar]
- Bozzeda, F.; Ortega, L.; Costa, L.L.; Fanini, L.; Barboza, C.A.; McLachlan, A.; Defeo, O. Global patterns in sandy beach erosion: Unraveling the roles of anthropogenic, climatic and morphodynamic factors. Front. Mar. Sci. 2023, 10, 1270490. [Google Scholar] [CrossRef]
- Monioudi, I.N.; Karditsa, A.; Chatzipavlis, A.; Alexandrakis, G.; Andreadis, O.P.; Velegrakis, A.F.; Marinos, E. Assessment of vulnerability of the eastern Cretan beaches (Greece) to sea level rise. Reg. Environ. Chang. 2016, 16, 1951–1962. [Google Scholar] [CrossRef]
- Poulos, S.; Karditsa, K. Socio-Economic Assessment of the Impact of the Anticipated Sea Level Rise on Peloponnese Coast (Eastern Mediterranean). SSRN 2023. [Google Scholar] [CrossRef]
- Karditsa, A.; Niavis, S.; Paramana, T.; Monioudi, I.; Poulos, S.; Hatzaki, M. Is the insular coastal tourism of western Greece at risk due to climate induced sea level rise? Ocean Coast. Manag. 2024, 251, 107088. [Google Scholar] [CrossRef]
- Velegrakis, A.F.; Monioudi, I.; Tzoraki, O.; Vousdoukas, M.I.; Tragou, E.; Hasiotis, T.; Andreadis, O. Coastal Hazards and Related Impacts in Greece. In The Geography of Greece: Managing Crises and Building Resilience; Springer International Publishing: Cham, Switzerland, 2024; pp. 353–370. [Google Scholar]
- Cheston, E.M. An Overview and Analysis of the Consistency Requirement Under the Coastal Zone Management Act. Univ. Balt. J. Environ. Law 2002, 10, 135. [Google Scholar]
- Garten, L. The coastal zone management act: A mixed success. Consilience 2016, 16, 1–13. [Google Scholar]
- Haslett, S. Coastal Systems; Routledge: Oxfordshire, UK, 2008. [Google Scholar]
- Fountoulis, I.; Mariolakos, I.; Ladas, I. Quaternary basin sedimentation and geodynamics in SW Peloponnese (Greece) and late-stage uplift of Taygetos Mt. Boll. Geofis. Teor. Appl. 2014, 55, 303–324. [Google Scholar]
- Mariolakos, I.; Fountoulis, I.; Kranis, H. Paleoseismic events recorded in Pleistocene sediments in the area of Kalamata (Peloponnesos, Greece). J. Geodyn. 1996, 24, 241–247. [Google Scholar] [CrossRef]
- Mariolakos, I.; Fountoulis, I.; Logos, E.; Lozios, S. Surface faulting caused by the Kalamata, Greece earthquake of 13 September 1986. Tectonophysics 1989, 163, 197–203. [Google Scholar] [CrossRef]
- Mariolakos, H.; Fountoulis, I. Neotectonic macro-folds in the area of Filiatron (Western Messinia, Peloponnese). Bull. Hellenic Geol. Soc. 1991, XXV, 19–38. (In Greek) [Google Scholar]
- Pavlakis, P.; Papanikolaou, D.; Chronis, G.; Lykoussis, B.; Anagnostou, E. Geological structure of inner Messiniakos Gulf. Bull. Geol. Soc. Greece 1989, 23, 333–347. [Google Scholar]
- Soukissian, T.; Hatzinaki, M.; Korres, G.; Papadopoulos, A.; Kallos, G.; Anadranistakis, E. Wind and Wave Atlas of the Hellenic Seas; Hellenic Centre for Marine Research Publications: Athens, Greece, 2007. [Google Scholar]
- Tsimplis, M.N. Tidal oscillations in the Aegean and Ionian Seas. Estuar. Coast. Shelf Sci. 1994, 39, 201–208. [Google Scholar] [CrossRef]
- Sannino, G.; Carillo, A.; Pisacane, G.; Naranjo, C. On the relevance of tidal forcing in modelling the Mediterranean thermohaline circulation. Prog. Oceanogr. 2015, 134, 304–329. [Google Scholar] [CrossRef]
- Ravdas, M.; Zacharioudaki, A.; Korres, G. Implementation and validation of a new operational wave forecasting system of the Mediterranean Monitoring and Forecasting Centre in the framework of the Copernicus Marine Environment Monitoring Service. Nat. Hazards Earth Syst. Sci. 2018, 18, 2675–2695. [Google Scholar] [CrossRef]
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill Publishing Company: Austin, TX, USA, 1974. [Google Scholar]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.1 User Guide; Open-File Rep. 2021–1091; U.S. Geological Survey: Reston, VA, USA, 2021.
- Poulos, S.E.; Lesioti, S.; Karditsa, A. Insights to estimate the largest 1/3, 1/10, 1/100 of offshore wave heights and periods under fetch-limited conditions in the central Aegean Sea. Water 2025, 17, 1499. [Google Scholar] [CrossRef]
- Bretschneider, C.L. The Ash Wednesday East Coast Storm, March 5–8, 1962: A hindcast of events, causes, and effects. In Coastal Engineering 1964; ASCE: Reston, VA, USA, 1964; pp. 617–659. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures, 2nd ed.; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Conlin, M.P.; Wilson, G.; Bond, H.; Ardağ, D.; Arnowil, C. Predicting wave runup on composite beaches. Coast. Eng. 2025, 199, 104743. [Google Scholar] [CrossRef]
- Hallemeier, R.J. A profile zonation for seasonal sand beaches from wave climate. Coast. Eng. 1981, 4, 253–277. [Google Scholar] [CrossRef]
- Rattanapitikon, W.; Shibayama, T. Breaking wave formulas for breaking depth and orbital-to-phase velocity ratio. Coast. Eng. J. 2006, 48, 395–416. [Google Scholar] [CrossRef]
- Kraus, N.C.; Larson, M. Prediction of initial profile adjustment of nourished beaches to wave action. In Proceedings of the 1988 National Conference on Beach Preservation Technology, Gainesville, FL, USA, 23–25 March 1988; Florida Shore & Beach Preservation Association: Tallahassee, FL, USA; pp. 125–137. [Google Scholar]
- Gourlay, M.R.; Meulen, T. Beach and Dune Erosion Tests (I). Deltares (WL); Delft Hydraulics Laboratory: Delft, The Netherlands, 1968. [Google Scholar]
- van Rijn, L.C. Sediment Transport by Currents and Waves; Rep. H461; Delft Hydraulics: Delft, The Netherlands, 1989. [Google Scholar]
- Kamphuis, J.W. Closure to “Alongshore Sediment Transport Rate”. J. Waterw. Port Coastal Ocean Eng. 1993, 119, 346–349. [Google Scholar] [CrossRef]
- Kriebel, D.L.; Dean, R.G. Convolution method for time-dependent beach-profile response. J. Waterw. Port Coastal Ocean Eng. 1993, 119, 204–226. [Google Scholar] [CrossRef]
- Bruun, P. Sea Level Rise: A Cause of Shore Erosion. J. Waterw. Harb. Div. 1962, 9, 117–130. [Google Scholar] [CrossRef]
- Allan, R.P.; Arias, P.A.; Berger, S.; Canadell, J.G.; Cassou, C.; Chen, D.; Cherchi, A.; Connors, S.L.; Coppola, E.; Cruz, F.A.; et al. Intergovernmental Panel on Climate Change (IPCC). Summary for Policy-Makers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023; pp. 3–32. [Google Scholar]
- Krestenitis, Y.; Makris, C.; Androulidakis, Y.; Kombiadou, K.; Baltikas, V. Storm Surge Simulations in the Greek Coastal Zone Under Climate Change. Available online: https://www.researchgate.net/publication/283089485 (accessed on 22 June 2025).
- Stiros, S.; Kontogianni, V. Modelling of the 1986 Kalamata (SW Greece) Earthquake Faulting Using Geodetic Data. J. Appl. Geod. 2008, 2, 179–185. [Google Scholar] [CrossRef]
- Papazachos, B.; Kiratzi, A.; Karacostas, B.; Panagiotopoulos, D.; Scordilis, E.; Mountrakis, D.M. Surface Fault Traces, Fault Plane Solution and Spatial Distribution of the Aftershocks of the September 13, 1986 Earthquake of Kalamata (Southern Greece). Pure Appl. Geophys. 1988, 126, 55–68. [Google Scholar] [CrossRef]
- Lambeck, K. Sea-Level Change and Shore-Line Evolution in Aegean Greece since Upper Palaeolithic Time. Antiquity 1996, 70, 588–611. [Google Scholar] [CrossRef]
- Lambeck, K.; Purcell, A. Sea-Level Change in the Mediterranean Sea since the LGM: Model Predictions for Tectonically Stable Areas. Quat. Sci. Rev. 2005, 24, 1969–1988. [Google Scholar] [CrossRef]
- Poulos, S.E.; Ghionis, G.; Maroukian, H. Sea-Level Rise Trends in the Attico–Cycladic Region (Aegean Sea) during the Last 5000 Years. Geomorphology 2009, 107, 10–17. [Google Scholar] [CrossRef]
- Gamvroudis, C.; Nikolaidis, N.P.; Tzoraki, O.; Papadoulakis, V.; Karalemas, N. Water and Sediment Transport Modeling of a Large Temporary River Basin in Greece. Sci. Total Environ. 2015, 508, 354–365. [Google Scholar] [CrossRef] [PubMed]
- de Swart, R.L.; Ribas, F.; Simarro, G.; Guillén, J.; Calvete, D. The Role of Bathymetry and Directional Wave Conditions on Observed Crescentic Bar Dynamics. Earth Surf. Process. Landf. 2021, 46, 3252–3270. [Google Scholar] [CrossRef]
- Southgate, H.N.; Wijnberg, K.M.; Larson, M.; Capobianco, M.; Jansen, H. Analysis of Field Data of Coastal Morphological Evolution over Yearly and Decadal Timescales. Part 2: Non-Linear Techniques. J. Coastal Res. 2003, 19, 776–789. [Google Scholar]
- Koumpou, S.V.; Petrakis, S.; Karditsa, K.; Kapsimalis, V.; Poulos, S.E. Near-Shore Hydrodynamic Processes Related to Shoreline Retreat due to Sea Level Rise Induced by Climate Change, along the Northern Coast of Messiniakos Gulf (Ionian Sea). In Proceedings of the Marine and Inland Waters Research Symposium 2022, Porto Heli, Greece, 16–20 September 2022; pp. 57–62. [Google Scholar]
- Carter, R.W.G. Coastal Environments: An Introduction to the Physical, Ecological and Cultural Systems of Coastlines; Academic Press: London, UK, 1988. [Google Scholar]
- Komar, P.D. Beach Processes and Sedimentation, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]

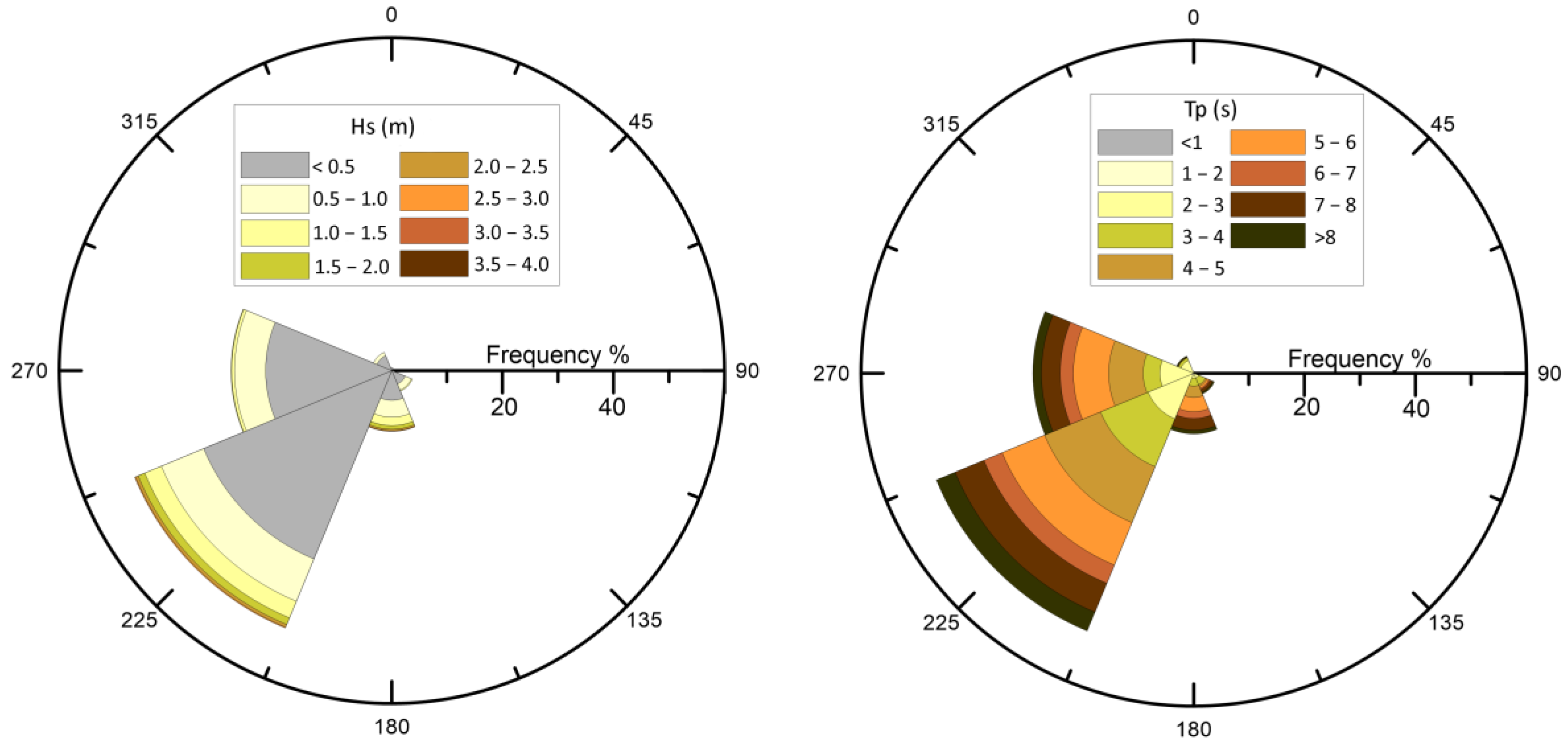


| ° | H | Tp | Dir | Ts | Hm | Tm | f (%) | L/2 | L/20 |
|---|---|---|---|---|---|---|---|---|---|
| (1/3) | 0.62 | 5.26 | 173.23 | 4.99 | 0.39 | 4.47 | 12.87 | 21.58 | 2.16 |
| (1/10) | 2.00 | 7.39 | 179.01 | 7.02 | 1.25 | 6.28 | 3.86 | 42.60 | 4.26 |
| (1/100) | 4.22 | 8.36 | 177.46 | 7.94 | 2.64 | 7.11 | 0.39 | 54.51 | 5.45 |
| (1/3)ext | 3.12 | 8.72 | 168.82 | 8.28 | 1.95 | 7.54 | 0.137 | 59.31 | 5.93 |
| Ω | Rmax (m) | hc | |
|---|---|---|---|
| S1 | 0.45 | 1.97 | 7.02 |
| S2 | 0.82 | 2.40 | |
| S3 | 0.80 | 1.65 | |
| S4 | 0.76 | 1.36 | |
| S5 | 0.80 | 1.27 |
| ° | Hb | ξb | γb | db | ab | |
|---|---|---|---|---|---|---|
| T1 | (1/3) | 0.78 | 1.30 | 1.15 | 0.68 | −5.07 |
| (1/10) | 2.20 | 0.06 | 0.69 | 3.18 | −5.01 | |
| (1/100) | 4.28 | 0.05 | 0.67 | 6.39 | −6.06 | |
| T2 | (1/3) | 0.79 | 1.63 | 1.19 | 0.66 | −2.66 |
| (1/10) | 2.29 | 0.61 | 1.01 | 2.26 | −1.34 | |
| (1/100) | 4.29 | 0.09 | 0.73 | 5.88 | −1.93 | |
| T3 | (1/3) | 0.78 | 1.04 | 1.11 | 0.70 | 3.98 |
| (1/10) | 2.23 | 0.19 | 0.83 | 2.68 | 3.00 | |
| (1/100) | 4.32 | 0.15 | 0.80 | 5.38 | 3.63 | |
| T4 | (1/3) | 0.77 | 0.82 | 1.06 | 0.72 | 8.20 |
| (1/10) | 2.21 | 0.09 | 0.74 | 2.98 | 8.66 | |
| (1/100) | 4.29 | 0.08 | 0.72 | 5.99 | 10.48 | |
| T5 | (1/3) | 0.77 | 0.75 | 1.05 | 0.73 | 11.22 |
| (1/10) | 2.20 | 0.06 | 0.69 | 3.18 | 13.12 | |
| (1/100) | 4.28 | 0.05 | 0.67 | 6.39 | 15.88 |
| S1 (B) | S2 (E) | S3 (H) | S4 (N) | S5 (R) | |
|---|---|---|---|---|---|
| Qt,i (103 t/y) | −34.23 | −24.460 | 25.25 | 31.12 | 36.10 |
| Qt,m (103 t/y) | −55.79 | −48.01 | 41.16 | 50.72 | 58.84 |
| BL/SSL | 0.30/1 | 0.07/1 | 0.07/1 | 0.25/1 | 0.33/1 |
| S1 (B) | S2 (E) | S3 (H) | S4 (N) | S5 (R) | |
|---|---|---|---|---|---|
| Storm Surge = 0.70 | 1.30 | 4.50 | 3.40 | 3.70 | 4.60 |
| Storm Surge = 0.35 | 0.60 | 2.10 | 1.06 | 1.70 | 2.10 |
| db (m) | 4.90 | 3.50 | 4.10 | 4.60 | 4.90 |
| wb (m) | 46.68 | 50.17 | 64.73 | 73.01 | 84.30 |
| mo (%) | 0.14 | 0.18 | 0.12 | 0.12 | 0.11 |
| D50 (mm) | 3.55 | 1.10 | 1.10 | 1.20 | 1.10 |
| wS (m/s) | 0.23 | 0.12 | 0.12 | 0.13 | 0.12 |
| An | 0.40 | 0.26 | 0.26 | 0.27 | 0.26 |
| SLR * | S1 (B) | S2 (E) | S3 (H) | S4 (N) | S5 (R) |
|---|---|---|---|---|---|
| 0.43 | 9.6 | 19.3 | 20.4 | 27.9 | 32.4 |
| 0.52 | 11.6 | 23.37 | 24.6 | 33.7 | 39.2 |
| 0.63 | 14.0 | 28.3 | 29.8 | 40.9 | 47.5 |
| 0.73 | 16.2 | 32.8 | 34.6 | 47.4 | 55.1 |
| 0.82 | 18.2 | 36.9 | 38.8 | 53.2 | 61.9 |
| Berm (B) | 2.0 | 1.9 | 2.5 | 2.25 | 1.75 |
| hc (1/3)max | 7.0 | 7.0 | 7.0 | 7.0 | 7.0 |
| Wh | 200 | 400 | 450 | 600 | 660 |
| 1960–1988 | 1989–1997 | 1998–2017 | 1960–2017 | |
|---|---|---|---|---|
| West Segment (S5); DSAS sections: (A1–A59) | +0.52 | −1.56 | −0.33 | −0.15 |
| Central (western) Segment (S4, S3, S2B); DSAS sections: A60–A285 | +0.45 | +0.89 | −0.09 | +0.30 |
| Central (eastern) Segment (S2A); DSAS sections: A286–A328 | +1.31 | +0.06 | −0.02 | +0.67 |
| East (western) Segment (S1B); DSAS sections: B1–B27 | +0.16 | −1.00 | +0.22 | −0.03 |
| East (eastern) Segment (S1A); DSAS sections: B28–B54 | −0.14 | −1.06 | +0.13 | +0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poulos, S.E.; Petrakis, S.; Karditsa, A.; Koumpou, S.-V.; Kapsimalis, V. Factors Controlling the Formation and Evolution of the Beach Zone in a Semi-Enclosed Tideless Embayment: The Case of the North Coast of the Messiniakos Gulf (Eastern Mediterranean). J. Mar. Sci. Eng. 2025, 13, 1810. https://doi.org/10.3390/jmse13091810
Poulos SE, Petrakis S, Karditsa A, Koumpou S-V, Kapsimalis V. Factors Controlling the Formation and Evolution of the Beach Zone in a Semi-Enclosed Tideless Embayment: The Case of the North Coast of the Messiniakos Gulf (Eastern Mediterranean). Journal of Marine Science and Engineering. 2025; 13(9):1810. https://doi.org/10.3390/jmse13091810
Chicago/Turabian StylePoulos, Serafeim E., Stelios Petrakis, Aikaterini Karditsa, Sylvia-Vasiliki Koumpou, and Vasileios Kapsimalis. 2025. "Factors Controlling the Formation and Evolution of the Beach Zone in a Semi-Enclosed Tideless Embayment: The Case of the North Coast of the Messiniakos Gulf (Eastern Mediterranean)" Journal of Marine Science and Engineering 13, no. 9: 1810. https://doi.org/10.3390/jmse13091810
APA StylePoulos, S. E., Petrakis, S., Karditsa, A., Koumpou, S.-V., & Kapsimalis, V. (2025). Factors Controlling the Formation and Evolution of the Beach Zone in a Semi-Enclosed Tideless Embayment: The Case of the North Coast of the Messiniakos Gulf (Eastern Mediterranean). Journal of Marine Science and Engineering, 13(9), 1810. https://doi.org/10.3390/jmse13091810










