Adaptive Fuzzy Sliding-Mode Control for Ship Path Tracking Based on a Fixed-Time Disturbance Observer
Abstract
1. Introduction
2. Mathematical Model
2.1. Path Tracking Error Modeling
2.2. Ship Motion Model
3. Controller Design
3.1. Adaptive Fuzzy Sliding-Mode Controller
- IF ( is NB) and ( is NB), then ( is VL).
- IF ( is NB) and ( is NS), then ( is VL).
- 25.
- IF ( is PB) and ( is PB), then ( is VL).
3.2. FTDO Design
3.3. Stability Analysis of the Closed-Loop System
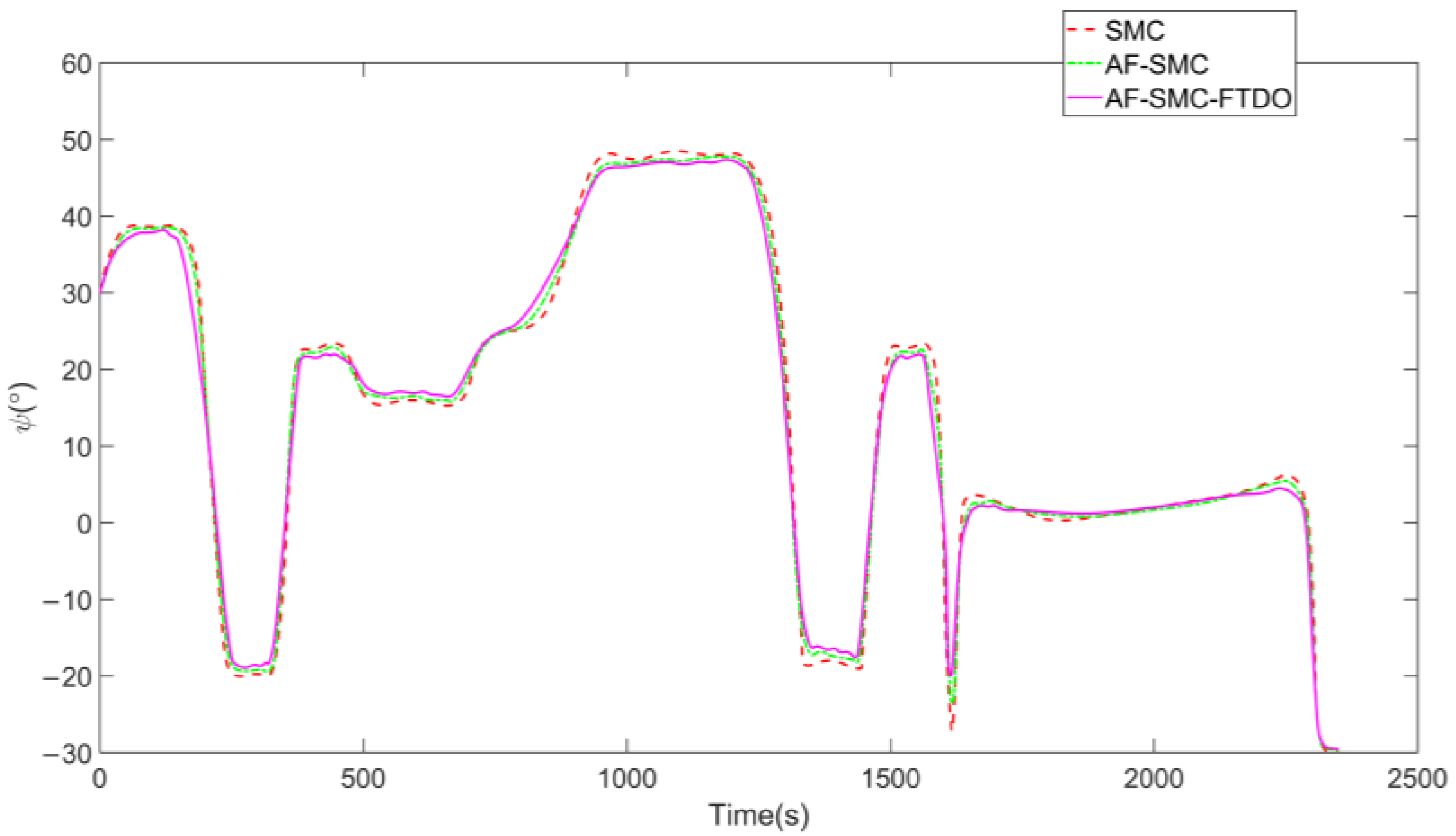
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF-SMC | Adaptive fuzzy sliding-mode control |
| FTDO | Fixed-time disturbance observer |
| ISM | Integral sliding mode |
| L | Large |
| M | Medium |
| NB | Negative big |
| NS | Negative small |
| PB | Positive big |
| PS | Positive small |
| S | Small |
| VL | Very large |
| VS | Very small |
| Z | Zero |
References
- Wu, J.; Peng, H.; Ohtsu, K.; Kitagawa, G.; Itoh, T. Ship’s tracking control based on nonlinear time series model. Appl. Ocean Res. 2012, 36, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Bu, R. Trajectory tracking of under-actuated ships based on optimal sliding mode control with state observer. Ocean Eng. 2021, 233, 109186. [Google Scholar] [CrossRef]
- Liu, H.; Sun, N.; Ren, G. Finite-time fast nonsingular terminal sliding mode path-following control for underactuated marine surface vehicles with input saturation. Ocean Eng. 2022, 262, 112327. [Google Scholar] [CrossRef]
- Li, R.; Jia, B.; Fan, S.; Pan, X. A novel active disturbance rejection control with hyperbolic tangent function for path following of underactuated marine surface ships. Meas. Control 2020, 53, 1579–1588. [Google Scholar] [CrossRef]
- Li, Z.; Li, R.; Bu, R. Path following of under-actuated ships based on model predictive control with state observer. J. Mar. Sci. Technol. 2021, 26, 408–418. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Bu, R. Sliding mode adaptive control for ship path following with sideslip angle observer. Ocean Eng. 2022, 251, 111106. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Cao, T.; Bu, R. Active disturbance rejection control for ship path following with Euler method. Ocean Eng. 2022, 247, 110516. [Google Scholar] [CrossRef]
- Yue, J.; Liu, L.; Peng, Z.; Wang, D.; Li, T. Data-driven adaptive extended state observer design for autonomous surface vehicles with unknown input gains based on concurrent learning. Neurocomputing 2022, 467, 337–347. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, S.; Huang, J.; Zhang, W. Dynamic Event-Triggered Path-Following Control of Underactuated Surface Vehicle With the Experiment Verification. IEEE Trans. Veh. Technol. 2022, 71, 10415–10425. [Google Scholar] [CrossRef]
- Lakhekar, G.V.; Waghmare, L.M. Robust self-organising fuzzy sliding mode-based path-following control for autonomous underwater vehicles. J. Mar. Eng. Technol. 2023, 22, 131–152. [Google Scholar] [CrossRef]
- Su, Y.; Wan, L.; Zhang, D.; Huang, F. An improved adaptive integral line-of-sight guidance law for unmanned surface vehicles with uncertainties. Appl. Ocean Res. 2021, 108, 102488. [Google Scholar] [CrossRef]
- Wan, L.; Su, Y.; Zhang, H.; Shi, B.; AbouOmar, M.S. An improved integral light-of-sight guidance law for path following of unmanned surface vehicles. Ocean Eng. 2020, 205, 107302. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, H.; Wang, C. High-Gain Observer-Based Line-of-Sight Guidance for Adaptive Neural Path Following Control of Underactuated Marine Surface Vessels. IEEE Access 2019, 7, 26088–26101. [Google Scholar] [CrossRef]
- Xiao, C.; Zhong, L.; Jianqiang, Z.; Dechao, Z.; Jiao, D. Adaptive sliding-mode path following control system of the underactuated USV under the influence of ocean currents. J. Syst. Eng. Electron. 2018, 29, 1271–1283. [Google Scholar] [CrossRef]
- Yan, Y.; Yu, S.; Sun, C. Event-triggered sliding mode tracking control of autonomous surface vehicles. J. Franklin Inst. 2021, 358, 4393–4409. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Gao, S.; Han, X.; Ma, D. Global fast terminal sliding mode control for path following of ultra large underactuated ship based on predictive LOS guidance. Ocean Eng. 2023, 285, 115387. [Google Scholar] [CrossRef]
- Yan, Y.; Zhao, X.; Yu, S.; Wang, C. Barrier function-based adaptive neural network sliding mode control of autonomous surface vehicles. Ocean Eng. 2021, 238, 109684. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, C.; Li, J.; Zhang, X. Improved composite learning path-following control for the underactuated cable-laying ship via the double layers logical guidance. Ocean Eng. 2020, 207, 107342. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Jin, X.; Liu, C. Robust Adaptive Neural Control for Wing-Sail-Assisted Vehicle via the Multiport Event-Triggered Approach. IEEE Trans. Cybern. 2022, 52, 12916–12928. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y.; Wang, N.; Guedes Soares, C. Data-driven sideslip observer-based adaptive sliding-mode path-following control of underactuated marine vessels. Ocean Eng. 2020, 197, 106910. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Bu, R. Radial Basis Function Neural Network Sliding Mode Control for Ship Path Following Based on Position Prediction. J. Mar. Sci. Eng. 2021, 9, 1055. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, C.; Liu, Y. Barrier Lyapunov Function-based adaptive prescribed-time extended state observers design for unmanned surface vehicles subject to unknown disturbances. Ocean Eng. 2023, 270, 113671. [Google Scholar] [CrossRef]


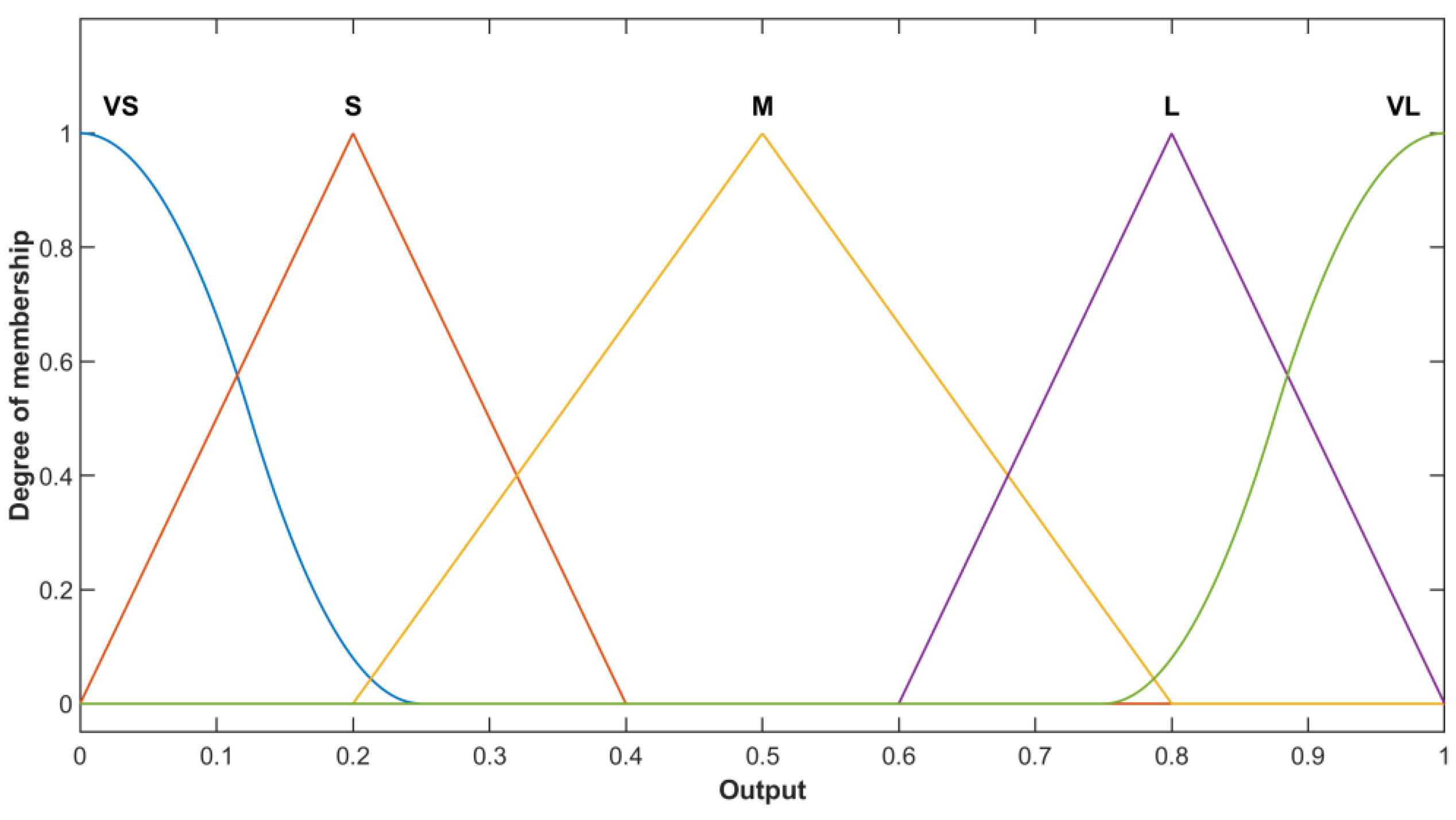








| NB | NS | Z | PS | PB | |
|---|---|---|---|---|---|
| NB | VL | VL | L | L | M |
| NS | VL | L | M | S | S |
| Z | L | M | VS | M | L |
| PS | S | S | M | L | VL |
| PB | M | L | L | VL | VL |
| Ship Parameters | Value | Unit |
|---|---|---|
| Full-load draft | 20.5 | m |
| Full-load displacement | 396,167 | t |
| Ship length L | 361.9 | m |
| Ship beam B | 65 | m |
| Block coefficient | 0.8323 | |
| Frontal windage area | 2962.1 | m2 |
| Lateral windage area | 1031.94 | m2 |
| Propeller diameter | 14.3 | m |
| Propeller pitch | 11.375 | m |
| Rudder area | 68.8 | m2 |
| Rudder aspect ratio | 5.375 | \ |
| Designed propeller rotational speed | 50 | n/min |
| Turning lag index T | 1142 | \ |
| Turning ability index K | 0.09 | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Bao, C.; Guo, R. Adaptive Fuzzy Sliding-Mode Control for Ship Path Tracking Based on a Fixed-Time Disturbance Observer. J. Mar. Sci. Eng. 2025, 13, 1788. https://doi.org/10.3390/jmse13091788
Li Y, Bao C, Guo R. Adaptive Fuzzy Sliding-Mode Control for Ship Path Tracking Based on a Fixed-Time Disturbance Observer. Journal of Marine Science and Engineering. 2025; 13(9):1788. https://doi.org/10.3390/jmse13091788
Chicago/Turabian StyleLi, Yibu, Changchun Bao, and Rui Guo. 2025. "Adaptive Fuzzy Sliding-Mode Control for Ship Path Tracking Based on a Fixed-Time Disturbance Observer" Journal of Marine Science and Engineering 13, no. 9: 1788. https://doi.org/10.3390/jmse13091788
APA StyleLi, Y., Bao, C., & Guo, R. (2025). Adaptive Fuzzy Sliding-Mode Control for Ship Path Tracking Based on a Fixed-Time Disturbance Observer. Journal of Marine Science and Engineering, 13(9), 1788. https://doi.org/10.3390/jmse13091788





