Abstract
This paper examines the effect of irregular bathymetry on the holographic reconstruction of the sound field generated by a moving source in shallow water. In this scenario, acoustic waves propagate along the path between the source and receiver. Spatial inhomogeneities in the waveguide, resulting from the complex bottom topography, cause the notable horizontal refraction of acoustic modes. The study focuses on how this horizontal refraction affects the structure of the interferogram and the hologram corresponding to the moving source. This investigation is carried out through numerical simulations that incorporate ray refraction due to irregularities in the waveguide. The interferogram, representing the received sound intensity in the frequency-time domain, and the hologram, obtained via a two-dimensional Fourier transform of the interferogram, are analyzed in the presence of spatial variability caused by non-uniform bathymetry. A key finding is that, despite these irregularities, the hologram retains sufficient structural information to extract and reconstruct source parameters (e.g., range, velocity). The paper also provides a quantitative estimate of the reconstruction error associated with this approach.
1. Introduction
In recent years, interferometric signal processing (ISP) has attracted increased scientific attention within the field of underwater acoustics. ISP exploits the stable features of interference patterns generated by broadband acoustic fields in shallow-water waveguides [1,2]. Comprehensive discussions of the theoretical foundations and methodological aspects of ISP can be found in seminal works [3,4,5]. Numerous studies have demonstrated the practical applications of ISP. For instance, in [6,7], ISP algorithms are used to determine waveguide-invariant parameters. The approach in [8] illustrates the use of ISP in processing weak signals, achieving performance improvements via array beamforming techniques. In [9], ISP is applied to classify seabed types using acoustic emissions from passing ships. The authors of [10] introduce a method for estimating the range to a source in shallow-water conditions based on ISP analysis. A range-independent invariant estimation framework utilizing ISP principles is described in [11]. Additionally, the work in [12] interprets interference fringe structures in terms of eigenray or eigenbeam arrival times. Finally, adaptations of ISP for deep-water passive sonar applications are reported in [13,14], highlighting the method’s flexibility for diverse underwater acoustic scenarios.
Among the various techniques in interferometric signal processing (ISP), holographic signal processing (HSP) is a particularly promising direction, as discussed in [15,16,17]. The essential physical concepts and mathematical framework for creating holograms were first formulated in [15]. In the HSP methodology, a quasi-coherent summation of the sound intensity in the joint frequency-time domain yields an interferogram , cf. [16,17]. To investigate the spatial distribution of the accumulated intensity, a two-dimensional Fourier transform (2D-FT) is then performed on . The outcome of this transformation, known as the Fourier hologram (or simply the hologram), is expressed as . Here, represents the redistribution of the acoustic energy from into distinct, localized focal regions that emerge as a consequence of modal interference patterns. In essence, a hologram is a variant of sound field focusing [18] that is implemented in the Fourier space using a single receiver.
In the early stages of developing the HSP method [15,16,17] and its verification [19], it was generally assumed that the properties of the acoustic waveguide remained unchanged in space and time. However, in reality, acoustic signals often propagate through waveguides with significant inhomogeneities. In shallow-water environments, this variability often results from hydrodynamic disturbances generated by internal waves. The first experimental study of HSP applied to a stationary source under realistic environmental conditions was reported in [20,21]. The study showed that hydrodynamic perturbations distorted the interferogram and expanded the focal regions observed in the reconstructed hologram . When inhomogeneities are present, the hologram can be presented as the sum of two components: one is produced by the unperturbed waveguide, and the other is associated with the perturbations.
This decomposition was used in [20,21] to interpret the measurements obtained during the SWARM’95 experiment [22,23]. During SWARM’95, the dominant source of waveguide variability was intense internal waves (IIWs) [23,24,25,26], a common hydrodynamic phenomenon in the ocean [24,25,26]. The experiment utilized two distinct acoustic propagation paths, both of which were generated by the same source and received by two vertically oriented arrays located in different positions. The first path was aligned at a small angle to the IIW wavefront; in this geometry, IIWs produce strong horizontal refraction of acoustic rays. The second path was perpendicular to the IIW wavefront so that the internal waves traveled along the propagation path from the source to the receiver. Under these conditions, horizontal refraction was absent, but the substantial redistribution of acoustic energy occurred between modes, i.e., mode coupling. The effects of IIWs have been discussed in our prior works [27,28,29].
In addition to internal waves, an important factor contributing to the spatial inhomogeneity of a shallow-water waveguide is the bottom relief, or irregularities in the bathymetry. The properties of these irregularities vary depending on the region being studied. Nevertheless, general patterns characteristic of many shallow-water areas across the world’s oceans exist. Experimental observations [30,31,32,33,34,35,36,37] indicate that the seabed on the continental shelf is generally smooth, with deviations from the average depth not exceeding tens of meters vertically. At the same time, the range of bottom relief variations is extensive [32,33,34,35], with horizontal scales spanning from a few centimeters to hundreds of kilometers. This structure of bathymetric irregularities, similar to that of internal waves, leads to significant acoustic effects associated with horizontal refraction and mode coupling. Therefore, the effects of irregular bathymetry on hologram formation from a moving source in shallow water are an important factor in the robustness of the HSP method and should be researched.
The aim of this paper is to study the effects of irregular bathymetry on holographic sound field reconstruction generated by a moving source in a shallow-water environment. Spatial inhomogeneities introduced by the complex bottom topography along the acoustic propagation path between the source and receiver cause the pronounced horizontal refraction of acoustic modes. This refraction alters the spatial–temporal structure of the received field, which can degrade the performance of holographic processing techniques. We conduct our analysis through high-fidelity numerical simulations that explicitly model the refraction of acoustic modes induced by the non-uniform bathymetric features of the waveguide. Within this framework, we examine the interferogram, which is defined as the distribution of received sound intensity in the joint frequency-time domain, and its corresponding hologram. The hologram is obtained via the two-dimensional Fourier transform of the interferogram. The study focuses on how spatial variability from the irregular seabed modifies the fine- and large-scale features of these representations. A key finding is that, despite the significant distortions introduced by horizontal refraction, the hologram retains a coherent and interpretable structure, containing sufficient information for the reliable extraction and reconstruction of key source parameters, including the range and velocity. This finding demonstrates that the holographic method is resilient to the effects of complex bathymetry and remains a viable approach to characterizing sources in realistic shallow-water conditions. The paper also provides a quantitative evaluation of the reconstruction error, offering practical insights into accuracy limits under varying degrees of bottom irregularity.
The paper consists of five sections. Section 1, the introduction, describes the current state of the problem under consideration. Section 2 presents a three-dimensional model of a shallow-water waveguide in the presence of bottom irregularities. Three cases of spatial dependence of are considered. These cases are as follows: a waveguide with regular bathymetry (Section 2.1); a littoral wedge waveguide (Section 2.2); and a canyon waveguide (Section 2.3). Section 3 describes the mathematical models of the interferogram and the hologram of a moving source in a shallow-water waveguide with an irregular bottom. Section 3 is organized into six distinct subsections, each addressing a specific aspect of the sound field in a shallow-water waveguide with irregular bathymetry. Section 3.1 introduces the theoretical framework for modeling the sound field in such a waveguide, employing the combined approach of vertical modes and horizontal ray approximations. This subsection outlines how these two methods interact to describe three-dimensional sound propagation in a complex underwater environment. Section 3.2 develops the Sturm–Liouville eigenvalue and eigenfunction problem, incorporating boundary conditions that model a free surface at the top and a solid or lossy bottom at the base of the waveguide. The solution to this problem yields a set of vertical modes that form the basis for subsequent acoustic field calculations. Section 3.3 shifts the focus to the mode ray description in the horizontal plane. Here, we derive the eikonal equation (which governs phase evolution) and the transport equation (which describes amplitude variation) for mode rays traveling through a waveguide whose bottom topography varies spatially. These equations form the foundation for predicting how sound energy is refracted, focused, or dispersed by bathymetric irregularities. Section 3.4 addresses an alternative, yet complementary, representation: the parabolic mode equations in the horizontal plane. This formulation efficiently simulates horizontal sound propagation over large distances, especially in environments where the slope and curvature of the bathymetry are significant. Section 3.5 presents the methodology for constructing a sound field interferogram in a waveguide with irregular bathymetry. The interferogram is a visualization tool that reveals patterns of constructive and destructive interference between modes, offering insights into the spatial structure of the acoustic field. Finally, Section 3.6 presents the formation and analysis of the sound field hologram for the same complex waveguide environment. This technique enables the reconstruction of the three-dimensional structure of the acoustic field, offering a deeper understanding of how bathymetric features impact wave propagation.
Section 4 considers the numerical modeling results for different cases of waveguide bathymetry. This section is divided into three subsections, each of which focuses on a particular scenario of acoustic wave propagation involving stationary or moving sound sources in various waveguide environments. Section 4.1 considers the regular waveguide. Section 4.1.1 examines the sound field generated by a stationary source in a waveguide with regular bathymetry, where the seabed topography is uniform and does not vary significantly with the horizontal position. This subsection outlines the theoretical formulation and provides representative results illustrating how sound propagates in this idealized environment. Section 4.1.2 extends the analysis to the sound field of a moving source in the same regular-bathymetry waveguide. Here, the influence of source motion on the spatial and temporal characteristics of the acoustic field is examined, including effects such as frequency shifts, beam pattern distortion, and the evolution of the interference structure. Section 4.2 considers the littoral wedge waveguide. Section 4.2.1 turns to a littoral wedge waveguide configuration and investigates the sound field produced by a stationary source. In this environment, the seabed rises toward the shoreline, creating a wedge-shaped bathymetry that introduces complex modal coupling, refraction, and energy redistribution effects. Section 4.2.2 considers the case of a moving source in a littoral wedge waveguide, emphasizing how the combination of source motion and sloping bathymetry modifies acoustic propagation. It places special focus on changes in mode excitation, shifting interference fringes, and potential shadow zones that may form due to the wedge geometry. Section 4.3 considers the canyon-type waveguide. Section 4.3.1 explores the sound field of a stationary source in a canyon-shaped waveguide where the seabed features a deep, narrow depression. The analysis examines how such a topographic feature traps, channels, or scatters sound energy, resulting in different spatial field patterns compared to those of regular bathymetry. Finally, Section 4.3.2 investigates the sound field generated by a moving source in a canyon waveguide. This scenario combines the effects of the source’s motion with the canyon’s strong topographic influence, revealing unique propagation behaviors, such as enhanced mode conversion, directional energy focusing, and localized acoustic hotspots. The main findings of the paper are summarized in Section 5.
2. Waveguide Model with Irregular Bathymetry
In this section, we present the three-dimensional model of the shallow-water waveguide with irregular bathymetry that was used in our study (see Figure 1).
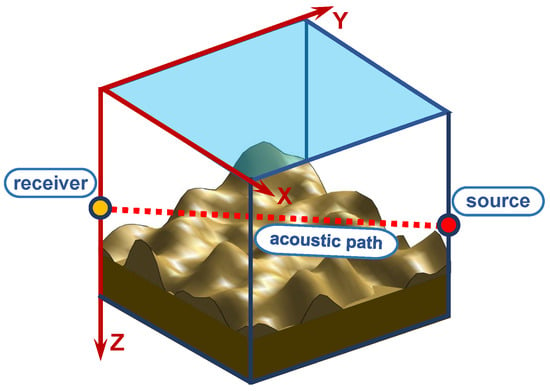
Figure 1.
Model of a shallow-water waveguide with irregular bathymetry.
The shallow-water waveguide is defined in a Cartesian coordinate system , where the x and y axes lie in the horizontal plane and the z axis points downward from the free surface at . The waveguide is modeled as a water layer with a spatially and temporally varying sound speed and density . Here, denotes the horizontal position vector. The water column is bounded above by the free surface at and below by the sea bottom at .
The seabed’s density and refractive index are given by and , respectively [38,39], where is the attenuation factor, defined as . In this expression, represents the bottom loss coefficient. is the acoustic velocity in the bottom layer, and f is the sound frequency.
The spatial variation of the bathymetry can be expressed as follows:
where describes general relief, and accounts for the meso- and microrelief of irregular bathymetry. The characteristics of bottom irregularities depend on the specific study area. However, some general features are typical of many shallow-water regions of the world’s oceans. According to the results of experimental studies [30,31,32,33,34,35,36,37], the seabed surface on the continental shelf is relatively smooth, with deviations from the mean seabed level not exceeding several tens of meters.
At the same time, the spectrum of bottom irregularities is very broad [33,34,35,36,37]—the linear dimensions range from centimeters to hundreds of kilometers. The entire spectrum can be divided into three parts: general relief, mesorelief, and microrelief. The general relief, which characterizes the main geomorphological features (ridges, plains, depressions, etc.), has dimensions of approximately to m. The mesorelief includes relief features stretching from approximately to m. The microrelief (formed by ripples, stones, hummocks, etc.) has spatial scales of approximately to m. According to this classification, the first large-scale component of the seabed relief corresponds to regular changes in waveguide parameters depending on the frequency. The other two components, mesorelief and microrelief, correspond to random changes.
In our paper, we will analyze the influence of the source hologram structure on the spatial variation of the bathymetry associated with the general relief . We will assume that the mesorelief and the microrelief are absent: . Thus, we will suppose that
Let us perform a comparative analysis of the spatial dependence of in three cases (see Figure 2). The cases are a waveguide with regular bathymetry (Figure 2a), a littoral wedge waveguide (Figure 2b), and a canyon waveguide (Figure 2c).
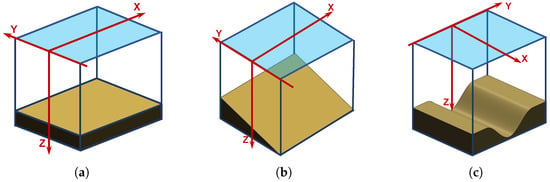
Figure 2.
Models of shallow-water waveguides: (a) regular waveguide; (b) littoral wedge waveguide; (c) canyon waveguide.
2.1. The Regular Waveguide
Consider the regular waveguide model (Figure 2a). In this model, the waveguide is shallow and uniform in depth across its entire horizontal extent, with no variation in the seabed elevation. This highly idealized representation is a standard benchmark in underwater acoustics because it provides a controlled environment in which the influence of environmental parameters, such as spatial variations in the sound speed profile of the water column, can be examined independently of changes in seabed topography. By eliminating bottom relief as a factor, one can focus on fundamental propagation mechanisms, validate analytical models, and compare numerical methods under consistent conditions.
According to the general model (Figure 2a) of a shallow-water waveguide, we use the Cartesian coordinate system , where the x and y axes lie in the horizontal plane, and the z axis points downward from the free surface at . The seabed is described by the depth function . In the case of a regular waveguide model, the depth is assumed to be constant in both the x and y directions:
Regular waveguide parameters:
- is the reference depth of the waveguide (in meters).
This configuration creates a waveguide through which acoustic modes can propagate without experiencing horizontal refraction or mode coupling due to bottom relief. The uniform bathymetry ensures translational isotropy in all horizontal directions.
2.2. The Littoral Wedge Waveguide
Consider the littoral wedge waveguide (see Figure 2b). The littoral wedge model describes a waveguide in shallow water in which the water depth changes linearly in one horizontal direction. This simplified yet representative configuration is a useful approximation of real-world nearshore environments, including continental shelves, gently sloping seabeds, tidal flats, and coastal approaches. In these settings, the seafloor gradually inclines, either descending toward deeper offshore waters or rising toward the shoreline. The model provides a convenient framework for investigating sound propagation in coastal zones, where depth variations strongly influence acoustic properties, alter underwater wave paths and speeds, and affect their interactions with the seabed and free surface. The littoral wedge model captures the essential geometric features of sloping-bottom environments, enabling researchers to analyze complex shallow-water acoustics in a more tractable and controlled manner.
We use the same Cartesian coordinate system (Figure 2b), where the x and y axes lie in the horizontal plane and the z axis points downward from the free surface at . The seabed is described by the depth function . In this case, the littoral wedge is assumed to vary only in the y direction:
Littoral wedge waveguide parameters:
- is the reference depth of the waveguide at (in meters).
- is the slope coefficient (meters in the vertical direction, per meter in the horizontal direction). For , the depth decreases as y increases; for , the depth increases as y increases; for , the depth remains constant as y changes.
- is the slope angle of the seabed plane () relative to the horizontal plane (radians).
In the case of a littoral wedge waveguide, the geometry supports the development of a guided acoustic environment. In this environment, modal propagation is subject to either pronounced horizontal refraction or mode coupling arising from bottom relief. The gradual seabed slope characteristic of the wedge profile induces the horizontal refraction of acoustic modes when they propagate at small angles relative to the x axis. Conversely, when propagation occurs at small angles relative to the y axis, mode coupling within the acoustic field becomes the dominant effect. These bathymetric irregularities give rise to substantial anisotropy in the acoustic propagation environment with distinct directional dependencies in sound energy transport.
2.3. The Canyon Waveguide
Consider the canyon waveguide model (see Figure 2c). This model describes a shallow-water acoustic environment featuring a pronounced, localized seabed depression, such as a trench or submarine canyon. This distinctive yet representative configuration is a useful approximation of the bathymetric conditions commonly found in the real world along continental margins, at fjord entrances, and near underwater escarpments. In these settings, the seafloor includes steeply sloping sidewalls and a narrow, elongated axis, which together create a confined acoustic channel.
These features can significantly impact the propagation of underwater sound by modifying the modal structure, trapping acoustic energy within the canyon boundaries, guiding sound waves along the canyon axis, and focusing beams through refractive effects. The model provides a practical framework for studying acoustic processes in complex coastal and shelf-edge environments where abrupt depth changes greatly impact wave speeds, transmission losses, and mode coupling. By capturing the essential geometric characteristics of submarine canyons, the canyon waveguide model allows researchers to study the interaction between topography and sound in a more manageable and controlled environment.
As before, we consider a Cartesian coordinate system (Figure 2c), where the x and y axes define the horizontal plane and the z axis points downward from the free surface at . The seabed profile is represented by the depth function . For the canyon waveguide model, the bathymetry includes a localized depression in the y direction. The canyon axis is oriented along the x direction. The mathematical model of the canyon waveguide bathymetry has the following form:
Canyon waveguide parameters:
- is the reference depth of the waveguide (in meters);
- is the canyon depth (in meters);
- is the canyon’s half-width (in meters).
In the case of a canyon waveguide, the seabed features a pronounced depression with steep sidewalls that form a natural acoustic channel. This configuration creates a complex shallow-water acoustic environment in which modal propagation is influenced by horizontal refraction and intermodal coupling driven by abrupt bathymetric variations. When acoustic waves propagate along the canyon’s axis—typically oriented in the x direction—the steep lateral gradients in depth can refract energy toward the canyon’s centerline, effectively trapping and guiding it over long distances. Conversely, when propagation is oriented across the canyon (i.e., in the y direction), the strong transverse bathymetric variation promotes significant mode coupling and energy redistribution between modes. This highly non-uniform bathymetry induces pronounced anisotropy in the acoustic propagation characteristics, resulting in direction-dependent transmission loss, altered modal dispersion properties, and the spatial focusing or defocusing of acoustic beams. Capturing these effects, the canyon waveguide model provides a powerful framework for investigating the interplay between the complex topography and underwater sound in continental shelf environments.
A summary of the three cases of the shallow-water waveguide models—regular waveguide, littoral wedge, and canyon—is presented in Table 1.

Table 1.
Models of shallow-water waveguides.
3. Interferogram and Hologram in Presence of Irregular Bathymetry
This section presents a model of the source interferogram and hologram within a shallow-water waveguide featuring irregular bathymetry. It is divided into six parts. Section 3.1 describes the sound field model in a waveguide with irregular bathymetry using the framework of vertical modes and the approximation of horizontal rays. Section 3.2 formulates the Sturm–Liouville eigenvalue and eigenfunction problem with boundary conditions representing a free surface and a bottom in a shallow-water waveguide. This problem is used to determine the vertical modes. Section 3.3 derives the eikonal and transport equations for mode rays in the horizontal plane for a waveguide with irregular bathymetry. Section 3.4 considers the mode parabolic equations in the horizontal plane for the same waveguide environment. Section 3.5 presents the sound field interferogram in a waveguide with irregular bathymetry. Finally, Section 3.6 analyzes the sound field hologram in a waveguide with irregular bathymetry.
Our work is based on the computational modeling of acoustic wave propagation in three-dimensional (3D) shallow-water waveguides with spatially varying properties. Variations in the medium, particularly those caused by irregularities in the seabed topography, can substantially modify the sound field through mechanisms such as refraction and scattering. Accurate broadband simulations at low frequencies in such complex 3D settings require considerable computational resources, often making it necessary to apply advanced numerical algorithms together with high-performance computing systems to achieve physically realistic predictions. There are five main categories of numerical techniques for modeling sound propagation in inhomogeneous shallow-water environments [40]: (1) three-dimensional Helmholtz equation (3DHE) methods [41,42,43]; (2) three-dimensional parabolic equation (3DPE) methods [44,45,46,47,48,49,50]; (3) three-dimensional ray-based (3DR) methods [51,52]; (4) vertical mode combined with two-dimensional modal parabolic equation (VMMPE) methods [53,54,55]; (5) vertical mode combined with horizontal ray (VMHR) methods [56,57].
In the present study, we examine low-frequency acoustic fields within two narrow frequency bands (100–140 Hz) in a shallow-water environment. Spatial inhomogeneities in this environment are attributed to bathymetric irregularities aligned along the propagation path from the source to the receiver. These variations in the seabed cause pronounced horizontal refraction effects. Of the five categories of numerical approaches described, the VMHR and VMMPE frameworks are the most appropriate for our problem. These methods are well suited for simulating the propagation of low-frequency waves in shallow-water settings affected by the seabed topography because they rigorously account for boundary conditions and effectively capture the physical processes associated with horizontal refraction.
In contrast, 3DR models are optimized for high-frequency applications and cannot adequately resolve modal behavior in shallow-water, low-frequency conditions. While 3DHE and 3DPE models can yield highly accurate solutions, they are too computationally expensive for the fully three-dimensional problem considered here. The VMHR and VMMPE approaches, on the other hand, strike an efficient balance between physical realism and numerical feasibility, enabling the accurate modeling of horizontal refraction phenomena. Consequently, these methods are adopted as the primary computational tools for simulating sound propagation under the influence of along-acoustic-path bathymetric irregularities in this work.
It should be noted that the influence of ocean waveguide bathymetric irregularities on acoustic field propagation has been investigated for several decades by numerous authors (see, e.g., [58,59,60,61,62,63,64,65,66,67,68,69]). However, none of these studies has considered the influence of irregular bathymetry on the holographic processing of hydroacoustic signals. Our work addresses this gap. The objective of the present study is to analyze how bathymetric irregularities affect the structure of the source hologram and the estimation of its parameters.
3.1. Sound Field
Within the frameworks of the VMHR and VMMPE approaches, the complex acoustic field in a shallow waveguide, influenced by bathymetric irregularities and described by Equations (1)–(5), can be expressed as follows, cf. [38,39]:
Here, denotes the horizontal position vector of the source, represents the amplitude of the m-th mode, and denotes the vertical structure (mode shape) of the corresponding acoustic mode in a waveguide unaffected by bathymetric irregularities.
3.2. Vertical Modes
For each mode, the complex horizontal wavenumber is expressed as
where and denote its real and imaginary components, respectively. The summation is carried out over M, the total number of propagating modes included in the model. Consequently, the acoustic pressure field p is a function of the angular frequency . The modal eigenfunctions and their corresponding complex wavenumbers are determined by solving a Sturm–Liouville boundary value problem with a free surface condition at the top and a bottom boundary condition at , as described in [38,39]:
3.3. Mode Rays in Horizontal Plane
The dependence determines the distribution of the modal amplitude in the horizontal plane [56,57]:
Within the ray approximation, can be represented as follows:
Here, and are determined by the eikonal and transport equations
where . Here, is the horizontal wavenumber of the mode for the reference depth . As seen from Equation (11), a significant drawback of the ray approach is the problem of accounting for multiple rays arriving at the observation point.
3.4. Mode Parabolic Equations in Horizontal Plane
The distribution of the modal amplitude is better suited for numerical calculations of the sound field and is represented within the framework of the parabolic approximation as [44,45]
where , under the assumption , satisfies the equation
where denotes the horizontal refractive index of the m-th acoustic mode in the waveguide in presence of the bathymetric irregularities Here, is the horizontal wavenumber of the mode for the reference depth . The numerical solution of Equation (14) is performed using the “Split Step Fourier” (SSF) algorithm [44,45]:
Here, is the fast Fourier transformation, denotes the inverse fast Fourier transformation, is the operator in the Fourier space of wavenumbers , and is the operator in the space of coordinates in the horizontal plane. To specify the initial conditions in the calculations using the scheme in Equation (15), it was assumed that the source, located at the point with coordinates , emits a field in the Fourier space described by the expression . The parameter defines the modal amplitude and depends on the mode value at the source depth. The parameter characterizes the range of initial beam angles taken into account in the calculation. The angle is measured from the x axis.
3.5. Interferogram
Within the VMHR and VMMPE frameworks—see Equation (6)—the interferogram for a moving source in the frequency-time domain can be expressed as [16,17]
where . The term represents the partial interferogram resulting from the interaction between the m-th and n-th modes. The quantity denotes the amplitude of the m-th mode,
with as the initial position of the source at , t as the current time, and v as the source velocity. The superscript “∗” indicates complex conjugation. The restriction ensures that the mean (auto-term) component is excluded from .
3.6. Hologram
In this part of the study, we analyze the holographic representation of an acoustic source in motion and take into account the effects of horizontal refraction due to bathymetric irregularities. A 2D-FT is applied to the interferogram given by Equation (16) in joint frequency-time space to extract the holographic information. The result is the hologram in the form [16,17]
where denotes the time delay, and is the angular frequency variable in the hologram domain. The function represents the contribution from the interference between modes m and n. Frequency integration is performed over the interval to . Here, is the signal bandwidth, is the reference (central) frequency, and corresponds to the total observation time. If the modal amplitudes and the source spectrum vary slowly with the frequency compared to the rapid oscillations of , the partial hologram in Equation (13) can be recast in the compact form [16,17]
where denotes the phase of the partial hologram :
As Equation (19) shows, the hologram is concentrated in two regions of the plane that are symmetric with respect to the origin (see Figure 3). This symmetry stems from the relation . When the radial velocity is negative (), corresponding to a trajectory angle , the hologram appears in quadrants I and III of the plane (Figure 3a). When the radial velocity is zero (), meaning that the source-receiver distance remains unchanged, the hologram lies along the axis (Figure 3b). A positive radial velocity (), associated with a trajectory angle , places the hologram in quadrants II and IV (Figure 3c).
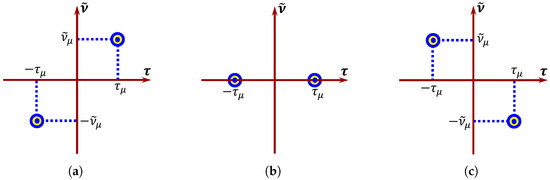
Figure 3.
The structure of the partial hologram for three different source motion scenarios: (a) the source approaches the receiver; (b) the source–receiver distance remains fixed; (c) the source recedes from the receiver.
These spatial patterns allow us to determine from the hologram whether the source is approaching or receding from the receiver. For the focal spot, the expressions for the radial velocity and initial source range are given by the following equations [16,17]:
where
Consider the angular distribution of the spectral density of the hologram :
The function has a maximum value at if the source is present. The criterion for source detection is .
4. Numerical Simulation Results
This section presents the results of the numerical modeling of the interferogram and the hologram for a broadband acoustic source in a shallow-water waveguide with irregular bathymetry. In the simulated scenarios, the irregularities on the bottom are aligned along the acoustic propagation path from the source to the receiver. This results in pronounced horizontal refraction. The analysis considers how such bathymetric features influence the interferogram and hologram of the acoustic field for two different source configurations. The first configuration corresponds to a fixed source-receiver geometry (i.e., a stationary source), while the second involves a moving source that propagates over irregular bathymetry. For the latter, three types of waveguide geometry are examined: regular bathymetry, a littoral wedge, and a submarine canyon. To enable a direct comparison of the effects of the bathymetry across all scenarios, the initial simulation parameters are identical in each case.
Section 4 is divided into three subsections, each addressing a specific combination of waveguide geometry and source motion. Section 4.1 considers the regular waveguide. Section 4.1.1 presents the results for a stationary source, and Section 4.1.2 analyzes the corresponding case with a moving source. Section 4.2 considers the littoral wedge waveguide. Section 4.2.1 reports the results for a stationary source, and Section 4.2.2 examines the effects of source motion in the same bathymetric environment. Section 4.3 considers the canyon-type waveguide. Section 4.3.1 provides the results for a stationary source, and Section 4.3.2 discusses modifications to the acoustic field and hologram structure for a moving source. This organization enables a systematic comparison of stationary and moving source scenarios across three distinct bathymetric settings and supports a consistent assessment of how the bottom topography influences the interferogram and the hologram.
4.1. Regular Waveguide
Consider the regular waveguide model (Figure 4). In this configuration, the waveguide is characterized by a shallow, horizontally uniform water column with a constant depth and invariant seabed elevation. This idealized setting has long been used as a benchmark in underwater acoustics because it provides a simplified yet rigorous framework for isolating the effects of specific environmental parameters.
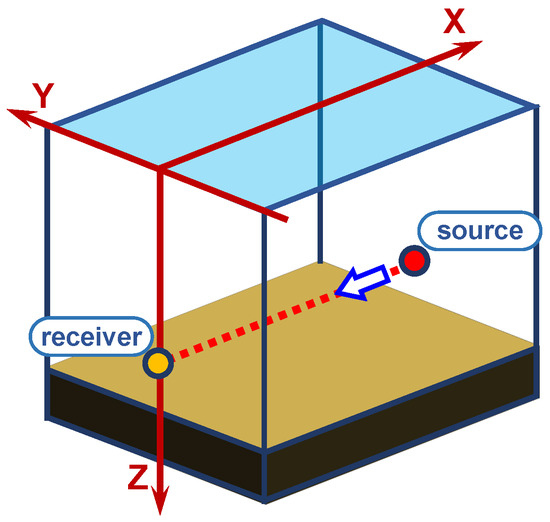
Figure 4.
Model of a shallow-water waveguide. Regular bathymetry.
The regular waveguide removes bathymetric variability as a factor, allowing researchers to investigate fundamental propagation mechanisms, assess the influence of water column properties (e.g., sound-speed profiles), and conduct systematic sensitivity studies. Its controlled geometry also facilitates the validation of theoretical formulations and serves as a reference case for the intercomparison of numerical models, enabling consistency checks across different computational approaches. Thus, the regular waveguide plays a critical role in establishing a baseline understanding and ensuring the reliability of more complex simulations in realistic ocean environments. Furthermore, it is often used to study broadband propagation and dispersion effects, offering a baseline scenario to evaluate the temporal and frequency-dependent behavior of acoustic signals in shallow water.
For this geometry, we have
where is the reference depth of the regular waveguide. The parameters of the regular waveguide used in the numerical simulation are presented in Table 2.

Table 2.
Shallow-water waveguide parameters. Regular waveguide.
4.1.1. Non-Moving Source ( m/s)
Source coordinates: km, m, m. Receiver coordinates: , m. The source is stationary (velocity m/s). The horizontal distance between the source and the receiver is km. Bearing . Frequency range Hz. Observation time s, realization duration s, time interval s. Number of modes . The values of the propagation constants and group velocities , , for a regular waveguide with depth m are given in Table 3. As can be seen, m−1 and (m/s)−1.

Table 3.
Sound field mode parameters (–140 Hz). Waveguide depth m.
Figure 5 illustrates the horizontal structure of the acoustic field modes in a regular shallow-water waveguide for a stationary source ( m/s). Figure 5a–c show the horizontal ray trajectories for the first, second, and third modes, respectively. Figure 5d–f present the corresponding normalized horizontal amplitude distributions, where the color scale (0 to 1) indicates the relative amplitude. Red dots mark the positions of the source (left) and receiver (right), which are separated by 10 km along the x axis. A regular waveguide for sound propagation represents an isotropic propagation medium in the horizontal plane. Therefore, as illustrated in Figure 5, the ray structure and amplitude distribution correspond to the rectilinear propagation of sound waves from the source to the receiver.
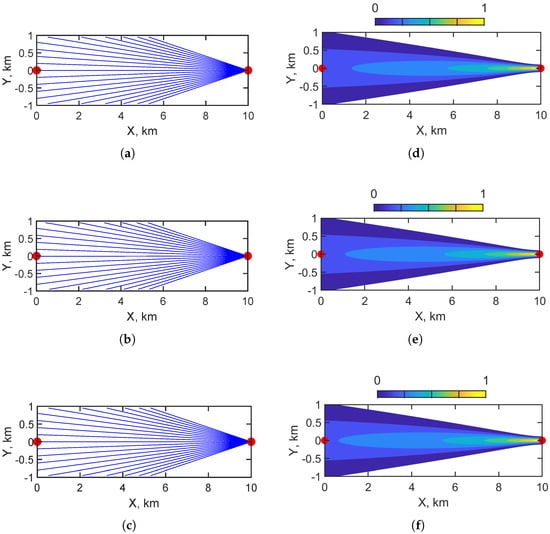
Figure 5.
Horizontal structures of sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Regular waveguide. Non-moving source ( m/s). The red dots indicate the source’s position () and the receiver’s position ().
Figure 6 presents the results of the HSP method for a stationary acoustic source in a regular waveguide. Figure 6a shows the interferogram , where the spectral content in the band remains stable throughout the observation interval, reflecting the absence of variations due to source motion. Figure 6b displays the hologram . As can be seen, the focal spots in the hologram domain for a stationary source are located along the axis. Figure 6c illustrates the function , which exhibits a sharp, well-defined peak at , indicating the stationary nature of the source.
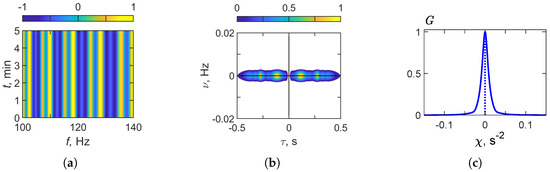
Figure 6.
Results of holographic signal processing: (a) , (b) , (c) . Regular waveguide. Non-moving source ( m/s). Frequency band: Hz.
Table 4 summarizes the numerical results of holographic signal processing for the frequency band . An analysis of the HSP results (see Figure 5) indicates that the rate of frequency variation of the interferogram is approximately . The focal point coordinates in hologram are and . The extremum point of is found to be , which is consistent with the case of a stationary source. The reconstructed source characteristics obtained from the holographic processing parameters are as follows: velocity and range . The error in the reconstructed source values amounts to for the velocity and for the range.

Table 4.
Numerical results of holographic signal processing. Source parameters.
4.1.2. Moving Source ( m/s)
In this section, we present the results of holographic processing obtained through numerical modeling when the source moves within a regular waveguide. The parameters of the regular waveguide used in the numerical simulation are presented in Table 2. The numerical experiment was conducted under the following conditions. The source was located at the coordinates km, m, m, and the receiver was positioned at , m. The source propagated toward the receiver along the line , moving from 10 km to km with a constant velocity of m/s. The initial horizontal separation between the source and receiver was km, with a bearing of . The acoustic signal was analyzed within the frequency band Hz. The observation interval was s, with a realization length of s and a temporal shift between realizations of s. The field was represented using modes. For a regular waveguide with a depth m, the corresponding propagation constants and group velocities are summarized in Table 3.
Figure 7 illustrates the horizontal structure of the acoustic field modes in a regular shallow-water waveguide for a moving source ( m/s). Figure 7a–c show the horizontal ray trajectories for the first, second, and third modes, respectively, as the source moves toward the receiver. Figure 7d–f present the corresponding normalized horizontal amplitude distributions, where the color scale (0 to 1) indicates the relative amplitude. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position (). In the case of a moving source, the regular waveguide represents an isotropic propagation medium in the horizontal plane. The overall structure of the rays and amplitudes continues to reflect rectilinear propagation from the source to the receiver.
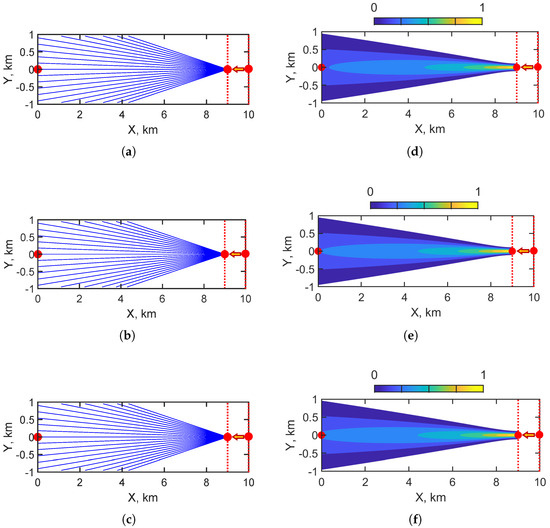
Figure 7.
Horizontal structures of sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Red dots indicate the source and receiver. Regular waveguide. Moving source ( m/s). Source moved from 10 km to km. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position ().
Figure 8 presents the HSP results for a moving acoustic source in a regular waveguide ( m/s). Figure 8a shows the interferogram , where the spectral content in the band Hz exhibits slanted interference fringes. These tilted structures reflect the temporal frequency variations caused by the motion of the source. Figure 8b displays the hologram . Unlike the stationary case, the focal spots are shifted from the axis and aligned along a non-zero frequency , corresponding to the source’s motion toward the receiver. Figure 8c illustrates the function , which has a pronounced maximum at , thereby confirming the non-stationary nature of the source.
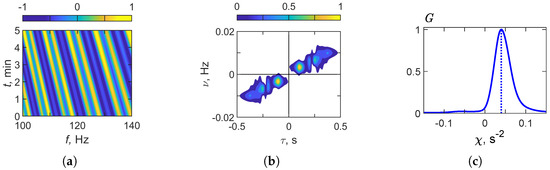
Figure 8.
Results of the holographic signal processing: (a) , (b) , (c) . Regular waveguide. Moving source ( m/s). Frequency band: = 100–140 Hz.
Table 5 presents the interferogram and hologram structure parameters used to estimate the source characteristics in the frequency band = 100–140 Hz. An analysis of the HSP results (see Figure 8) shows that the rate of frequency variation in the interferogram is approximately , reflecting the effects of source motion. The focal point coordinates in the hologram are determined as s and Hz. The extremum of the function is obtained at s−2, which corresponds to a non-stationary source. The reconstructed source parameters derived from these values are as follows: velocity m/s and range km. The error of the reconstructed source values amounts to for the velocity and for the range.

Table 5.
Interferogram and hologram structure parameters. Estimation of the source parameters.
4.2. Littoral Wedge Waveguide
Consider the littoral wedge waveguide (see Figure 9). The littoral wedge model represents a shallow-water acoustic environment in which the depth changes linearly along one horizontal axis. Despite its simplified formulation, this configuration is a useful and widely adopted model of realistic nearshore conditions, including continental shelves, gently sloping seabeds, tidal flats, and coastal approaches. In these environments, the bathymetry gradually inclines, either deepening toward the open ocean or shoaling toward the coastline.
Figure 9.
Model of a shallow-water waveguide. Littoral wedge.
This representation offers a mathematically tractable and physically meaningful framework for analyzing sound propagation in coastal waters, where variations in the seafloor exert a dominant influence on acoustic field characteristics. Specifically, gradual depth changes modify propagation paths, affect group and phase velocities, and alter reflection and refraction processes at the seabed and free surface. The littoral wedge model retains the essential geometric features of sloping-bottom topographies while avoiding the complexity of fully irregular bathymetries. This enables systematic investigations of shallow-water acoustic phenomena under controlled and reproducible conditions. Thus, it offers valuable insights into real-world applications of underwater acoustics.
In this case, we have
where is the reference depth, and is the slope coefficient. The parameters of the littoral wedge used in the numerical simulation are presented in Table 6.

Table 6.
Shallow-water waveguide parameters. Littoral wedge waveguide.
4.2.1. Non-Moving Source ( m/s)
Source coordinates: km, m, m. Receiver coordinates: , m. The source is stationary (velocity m/s). The horizontal distance between the source and the receiver is km. Bearing . Frequency range Hz. Observation time s, realization duration s, time interval s. Number of modes . The values of the propagation constants and group velocities , , for a littoral wedge waveguide are given in Table 7, Table 8 and Table 9. Table 7 corresponds to depth m, m−1 and (m/s)−1. Table 8 corresponds to depth m, m−1, and (m/s)−1. Table 9 corresponds to depth m, m−1, and (m/s)−1.

Table 7.
Sound field mode parameters (–140 Hz). Waveguide depth m.

Table 8.
Sound field mode parameters (–140 Hz). Waveguide depth m.

Table 9.
Sound field mode parameters (–140 Hz). Waveguide depth m.
Figure 10 illustrates the horizontal structures of the acoustic field modes in a littoral wedge waveguide for a stationary source ( m/s) located at km. Figure 10a–c show the horizontal ray trajectories corresponding to the first, second, and third modes, respectively. Figure 10d–f present the associated normalized horizontal amplitude distributions, where the color scale (0 to 1) indicates the relative amplitude. The red dots mark the positions of the source (right) and the receiver (left) along the x axis. Unlike in a regular waveguide, the presence of sloping bathymetry in a wedge environment leads to the horizontal refraction of acoustic modes. This is evident in the curvature of the ray paths and the asymmetry of the amplitude distributions.
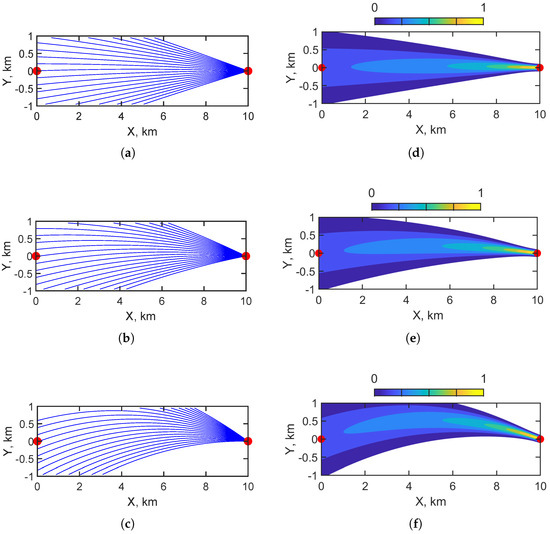
Figure 10.
Horizontal structures of the sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Littoral wedge waveguide. Non-moving source ( m/s). The red dots indicate the source’s position () and the receiver’s position ().
Figure 11 presents the results of the HSP method for a stationary acoustic source in a littoral wedge waveguide. Figure 11a shows the interferogram , where the spectral content in the band remains stable throughout the observation interval, consistent with the absence of source motion. Figure 11b displays the hologram . The focal spots in the hologram domain are aligned along the axis, indicating the stationary nature of the source. Figure 11c illustrates the function , which has a sharp, well-defined maximum at . This confirms the absence of motion and validates the stability of the reconstructed parameters in the wedge environment.
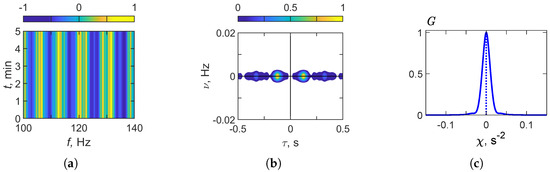
Figure 11.
Results of holographic signal processing: (a) , (b) , (c) . Littoral wedge waveguide. Non-moving source ( m/s). Frequency band: = 100–140 Hz.
Table 10 summarizes the interferogram and hologram structure parameters obtained from HSP in the frequency band = 100–140 Hz. An analysis of the results (see Figure 11) shows that the rate of frequency variation in the interferogram is approximately s−2, indicating the absence of frequency modulation. The focal point coordinates in the hologram are determined as s and Hz. The extremum of the function is found at s−2, which is consistent with the case of a stationary source. The reconstructed source parameters derived from these values are as follows: velocity m/s and range km. The error of the reconstructed estimates is for the velocity and approximately for the range, confirming the accuracy and robustness of holographic processing in the littoral wedge waveguide for a stationary source.

Table 10.
Interferogram and hologram structure parameters. Estimation of the source parameters.
4.2.2. Moving Source ( m/s)
In this section, we present the results of holographic processing obtained through numerical modeling for the case of a source moving in a littoral wedge waveguide. The parameters of the wedge-shaped environment used in the simulations are summarized in Table 2. The numerical experiment was carried out under the following conditions. The source was initially located at coordinates km, m, m, while the receiver was positioned at , m. The source propagated toward the receiver along the line , moving from km to km with a constant velocity of m/s. The initial horizontal separation between the source and the receiver was km, with a bearing of . The acoustic signal was analyzed within the frequency band f = 100–140 Hz. The observation interval was s, with a realization length of s and a temporal shift between realizations of s. The field was represented using modes. The corresponding propagation constants and group velocities are provided in Table 7, Table 8 and Table 9.
Figure 12 illustrates the horizontal structures of the acoustic field modes in a littoral wedge waveguide for a moving source ( m/s). Figure 12a–c display the horizontal ray trajectories for the first, second, and third modes, respectively, as the source moves toward the receiver. Figure 12d–f show the corresponding normalized horizontal amplitude distributions, with the color scale (0 to 1) indicating the relative amplitude. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position (). In the case of a moving source in a wedge-shaped environment, horizontal propagation becomes range-dependent due to varying depths. The structure of the rays and amplitudes reflects the influence of the sloping bathymetry on the distribution of modal energy and the source’s approach to the receiver.
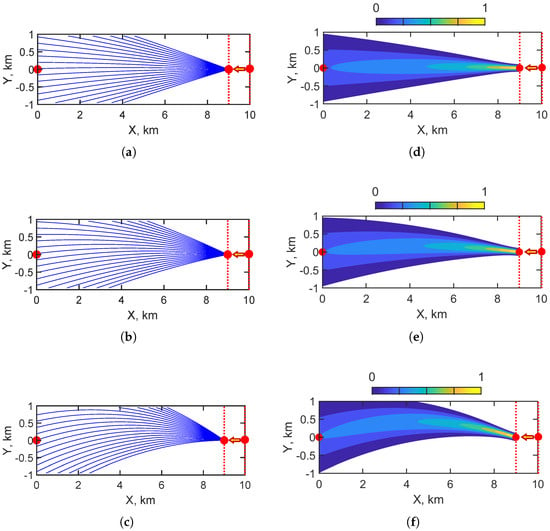
Figure 12.
Horizontal structures of sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Red dots indicate the source and the receiver. Littoral wedge waveguide. Moving source ( m/s). Source moved from 10 km to km. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position ().
Figure 13 presents the results of holographic signal processing for a moving source in a littoral wedge waveguide ( m/s). Figure 13a shows the interferogram within the frequency band 100–140 Hz, where inclined interference fringes are observed. These oblique patterns indicate frequency-time modulation induced by the source motion. Figure 13b depicts the hologram , where the focal regions are displaced from the axis and distributed along a non-zero frequency , consistent with a source approaching the receiver. Finally, Figure 13c illustrates the function , which exhibits a distinct peak at , thereby confirming the non-stationary dynamics of the source.
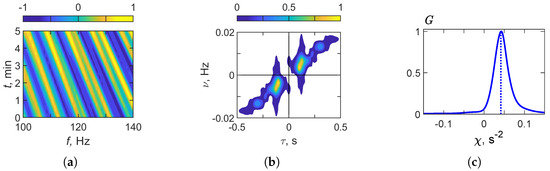
Figure 13.
Results of holographic signal processing: (a) , (b) , (c) . Littoral wedge waveguide. Moving source ( m/s). Frequency band: = 100–140 Hz.
Table 11 summarizes the interferogram and hologram structure parameters derived from holographic signal processing in the frequency band = 100–140 Hz. As shown in Figure 13, the frequency variation rate in the interferogram is estimated to be approximately s−2, indicating noticeable frequency modulation caused by the moving source. The focal spot coordinates in the hologram are determined to be s and Hz. The function exhibits a pronounced maximum at s−2, further confirming the non-stationary nature of the source. Based on these results, the reconstructed source parameters are velocity m/s and range km. The error in the reconstructed estimates is for the velocity and approximately for the range, confirming the accuracy and robustness of holographic processing in the littoral wedge waveguide for a moving source.

Table 11.
Interferogram and hologram structure parameters. Estimation of the source parameters.
4.3. Canyon Waveguide
Consider the canyon waveguide (see Figure 14). This model represents an oceanic environment characterized by a sharp depression with steeply sloping sides and a relatively narrow cross-section. Although idealized, this configuration captures the essential features of submarine canyons, which are prominent topographic features that connect shallow continental shelves to deeper ocean basins. These environments are of particular interest in underwater acoustics because of their strong influence on sound propagation, scattering, and trapping mechanisms.
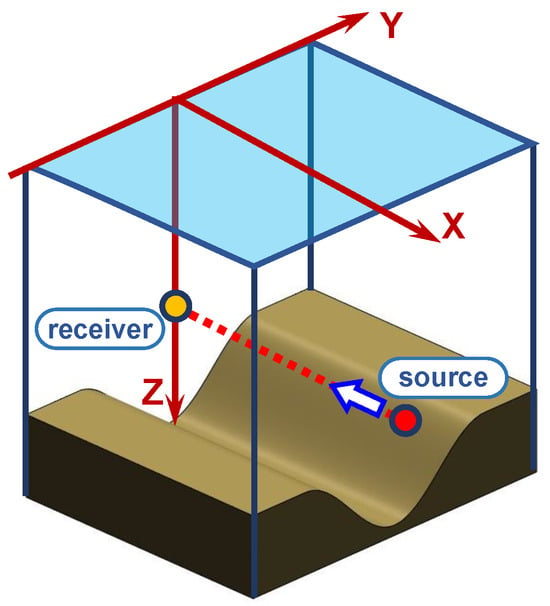
Figure 14.
Model of shallow-water waveguide. Canyon.
The canyon’s geometry significantly modifies the acoustic field characteristics. Steep bathymetric gradients, in particular, induce mode coupling, generate shadowing effects, and enhance multipath propagation. The canyon walls can also act as acoustic waveguides, channeling energy along the axis of the depression while altering the reflection and refraction conditions compared to flat-bottomed or wedge-like topographies. These effects make the canyon waveguide a useful model for analyzing the complex interactions between the bathymetric structure and acoustic propagation.
The mathematical model of the canyon waveguide bathymetry has the following form:
where is the reference depth, is the canyon depth, and is the canyon half-width. The parameters of the littoral wedge used in the numerical simulation are presented in Table 12.

Table 12.
Shallow-water waveguide parameters. Littoral wedge waveguide.
4.3.1. Non-Moving Source ( m/s)
Source coordinates: km, m, m. Receiver coordinates: , m. The source is stationary (velocity m/s). The horizontal distance between the source and the receiver is km. Bearing . Frequency range f = 100–140 Hz. Observation time s, realization duration s, time interval s. Number of modes . The values of the propagation constants and group velocities , , for a littoral wedge waveguide are given in Table 13 and Table 14. Table 13 corresponds to depth m, m−1, and (m/s)−1. Table 14 corresponds to depth m, m−1, and (m/s)−1.

Table 13.
Sound field mode parameters ( = 100–140 Hz). Waveguide depth m.

Table 14.
Sound field mode parameters ( = 100–140 Hz). Waveguide depth m.
Figure 15 shows the horizontal structures of the acoustic field modes in a canyon waveguide for a stationary source ( m/s) positioned at km. Figure 15a–c display the horizontal ray trajectories for the first, second, and third modes, respectively. Figure 15d–f present the corresponding normalized horizontal amplitude distributions, with the color scale ranging from 0 to 1 indicating the relative amplitude. The source and receiver positions are marked by red dots on the x axis. Unlike the wedge geometry, the canyon topography produces strong horizontal refraction and mode confinement. This is evident in the bending of the ray paths and the localized concentration of acoustic energy within the canyon region.
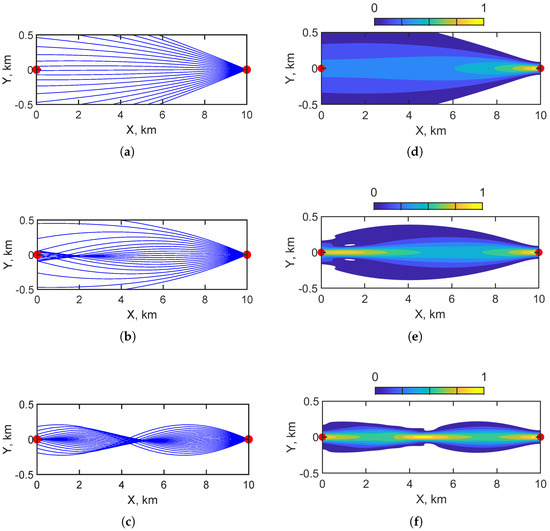
Figure 15.
Horizontal structures of sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Canyon waveguide. Non-moving source ( m/s). The red dots indicate the source’s position () and the receiver’s position ().
Figure 16 presents the results of holographic signal processing for a stationary acoustic source in a canyon waveguide. Figure 16a shows the interferogram , in which the spectral content within the 100–140 Hz frequency band remains constant over time. This indicates the absence of frequency modulation due to source motion. Figure 16b depicts the hologram , in which the focal spots are concentrated along the axis, consistent with a stationary source. Figure 16c shows the function , which has a clear peak at . This confirms that the source is not moving and validates the stability of the reconstructed parameters in the canyon environment.
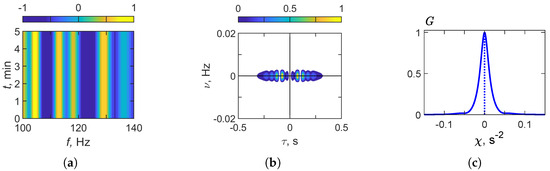
Figure 16.
Results of holographic signal processing: (a) , (b) , (c) . Canyon waveguide. Non-moving source ( m/s). Frequency band: = 100–140 Hz.
Table 15 summarizes the interferogram and hologram structure parameters obtained from holographic signal processing in the frequency band . The analysis of the results (see Figure 16) shows that the frequency variation rate in the interferogram is , confirming the absence of modulation effects associated with source motion. The focal spot coordinates in the hologram are found to be and . The function reaches its maximum at , which is consistent with the stationary nature of the source. The reconstructed parameters derived from these values are as follows: velocity and range . The error of the reconstructed estimates is for the velocity and approximately for the range, confirming the accuracy and robustness of holographic processing in the canyon waveguide for a stationary source.

Table 15.
Interferogram and hologram structure parameters. Estimation of source parameters.
4.3.2. Moving Source ( m/s)
In this section, we present the results of holographic processing obtained through numerical modeling for the case of a source located in a canyon waveguide. The parameters of the canyon environment used in the simulations are summarized in Table 2. The numerical experiment was conducted under the following conditions. The source was positioned at coordinates km, m, m, while the receiver was positioned at , m. The source was moving ( m/s) at a horizontal initial distance of km from the receiver, with a bearing angle of . The acoustic signal was analyzed in the frequency band f = 100–140 Hz. The observation interval was s, with a realization length of s and a temporal shift between realizations of s. The acoustic field was represented using modes. The corresponding propagation constants and group velocities are provided in Table 13 and Table 14.
Figure 17 illustrates the horizontal structure of the acoustic field modes in a canyon waveguide for a moving source (, m/s). Figure 17a–c show the horizontal ray trajectories of the first, second, and third modes, respectively, as the source moves toward the receiver. Figure 17d–f display the corresponding normalized horizontal amplitude distributions, with the color scale (0 to 1) representing the relative amplitude. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position (). In the canyon environment, horizontal propagation exhibits pronounced range dependence due to steep bathymetric gradients. Both the ray structures and amplitude patterns reveal strong refraction and confinement effects that influence the modal energy distribution as the source approaches the receiver.
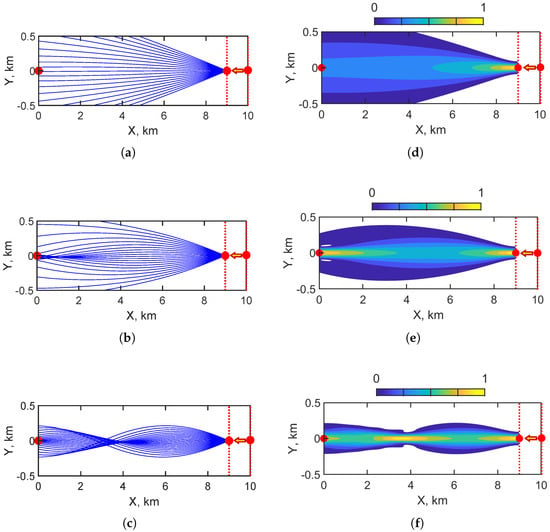
Figure 17.
Horizontal structures of sound field modes: (a) horizontal rays of first mode; (b) horizontal rays of second mode; (c) horizontal rays of third mode; (d) amplitude distribution of first mode; (e) amplitude distribution of second mode; (f) amplitude distribution of third mode. Red dots indicate the source and receiver. Canyon waveguide. Moving source ( m/s). Source moved from 10 km to km. The red dots indicate the source’s instantaneous positions—the initial () and the final ()—as well as the receiver’s position ().
Figure 18 presents the results of holographic signal processing for a moving source in a canyon waveguide ( m/s). Figure 18a shows the interferogram in the frequency band Hz, where the slanted interference fringes clearly reflect the frequency-time modulation produced by the source motion. Figure 18b displays the hologram , in which the focal spots are shifted away from the axis and aligned along a non-zero frequency , consistent with the source approaching the receiver. Figure 18c illustrates the function , which has a pronounced maximum at , thereby confirming the non-stationary character of the source in the canyon environment.
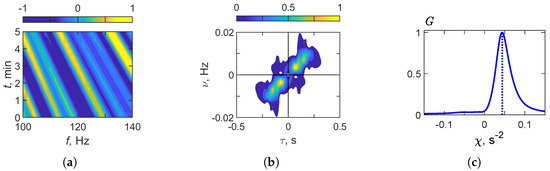
Figure 18.
Results of holographic signal processing: (a) , (b) , (c) . Canyon waveguide. Moving source ( m/s). Frequency band: = 100–140 Hz.
Table 16 summarizes the interferogram and hologram structure parameters obtained from holographic signal processing in the frequency band Hz. Figure 18 shows that the frequency variation rate in the interferogram is , reflecting the modulation induced by the source motion. The focal spot coordinates in the hologram are identified as and . The function reaches its maximum at , thereby confirming the non-stationary character of the source. Based on these results, the reconstructed source parameters are as follows: velocity and range . The error of the reconstructed estimates is for the velocity and approximately for the range, confirming the accuracy and robustness of holographic processing in the canyon waveguide for a stationary source.

Table 16.
Interferogram and hologram structure parameters. Estimation of source parameters.
5. Conclusions
This study examined the impact of irregular bathymetry on the HSP of a moving acoustic source in a shallow-water waveguide. Using the VMHR and VMMPE approaches, we developed a source hologram model that accounts for horizontal refraction caused by irregular bathymetry. A comparative analysis of the holographic processing results was carried out based on this approach for three types of waveguides: regular, littoral wedge, and canyon. This analysis enables a systematic comparison of their influences on interferograms, holograms, and reconstructed source parameters.
The results lead to the following key conclusions.
- Robustness of Interferogram and Hologram Structure Under Irregular Bathymetry.
Despite the significant distortion of the acoustic field’s structure in the horizontal plane caused by horizontal refraction due to bathymetric variability, the interferogram and hologram retain the structural features observed in a regular waveguide. This stability ensures the preservation of the key information necessary for reconstructing source parameters, including the range and velocity.
- Accuracy of Source Parameter Reconstruction.
Quantitative estimates show that the range of the acoustic source can be reconstructed with an error of about 10%. For a regular waveguide, the error in the velocity and range is 0% and 4% for a stationary source and 7% and 2% for a moving source, respectively. For a littoral wedge waveguide, the reconstruction errors are 0% in the velocity and 7% in the range for a stationary source and 13% and 2%, respectively, for a moving source. In a canyon waveguide, the estimation errors amount to 0% and 5% for the velocity and range in the stationary case and 8% and 17% in the moving case. These levels of accuracy are sufficient for practical underwater monitoring applications.
- Effectiveness of HSP Method.
Comparing different waveguide types (regular, littoral wedge, and canyon) shows that bathymetric irregularities lead to only a minor increase in reconstruction errors relative to a regular waveguide. These results confirm the robustness of the holographic signal processing method and its ability to provide reliable results in realistic, shallow-water conditions with an irregular bottom topography.
These findings substantially extend the applicability of holographic methods in underwater acoustics, demonstrating their potential for practical use in real-world scenarios with irregular and complex bathymetries. Furthermore, the approach’s ability to provide stable parameter estimates that are closely aligned with actual physical values underscores its relevance for theoretical studies and operational tasks in ocean monitoring and surveillance.
6. Future Works
In previous studies, we examined the sound field interferograms and holograms of a moving source in the presence of internal waves inducing horizontal refraction and mode coupling [28,29]. The primary focus of the present study was the influence of bottom relief, which causes significant horizontal refraction. It is important to note that other environmental factors also contribute to variability in the acoustic field under shallow-water conditions. Future research will extend the analysis in several directions.
Surface wave influence. We will investigate how surface gravity waves influence interferogram and hologram stability, as well as the accuracy of the reconstructed source parameters. Surface wave-induced fluctuations are expected to introduce additional distortions in the interferogram, which may affect hologram focusing.
Combined variability scenarios. Future simulations will consider environments in which internal waves, bathymetric irregularities, and surface waves act simultaneously. This will provide a more realistic assessment of the robustness of holographic processing under operational conditions.
Addressing these aspects will enable subsequent studies to provide a comprehensive understanding of the stability limits of holographic signal processing in complex ocean environments, advancing its potential for operational applications in ocean acoustics.
Author Contributions
Supervision and project administration, M.E. and S.P.; conceptualization and methodology, V.K. and S.P.; software, S.T., A.P. and N.L.; validation, M.E. and V.K.; formal analysis, M.E. and S.P.; writing—original draft preparation, M.E. and S.P.; writing—review and editing, M.E. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant from the Russian Science Foundation, № 23-61-10024, https://rscf.ru/project/23-61-10024/ (accessed on 6 August 2025).
Data Availability Statement
Data derived from public-domain resource [22,23]. All other parameters used are clearly mentioned in the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HSP | holographic signal processing |
| ISP | interferometric signal processing |
| 3DHE | 3D Helmholtz equation |
| 3DPE | 3D parabolic equation |
| 3DR | 3D ray-based |
| VMMPE | vertical mode and 2D modal parabolic equation |
| VCMHR | vertical coupled mode with horizontal ray |
| IIW | intense internal wave |
| 2D | two-dimensional |
| 3D | three-dimensional |
| 1D-FT | one-dimensional Fourier transform |
| 2D-FT | two-dimensional Fourier transform |
References
- Weston, D.; Stevens, K. Interference of wide-band sound in shallow water. J. Sound Vib. 1972, 21, 57–64. [Google Scholar] [CrossRef]
- Chuprov, S.D.; Brekhovskikh, L.M. Interference structure of a sound field in a layered ocean. Ocean Acoust. Curr. State. 1982, 71–91. [Google Scholar]
- Ianniello, J. Recent developments in sonar signal processing. IEEE Signal Proc. Magazine 1998, 15, 27–40. [Google Scholar]
- Thode, A.M. Source ranging with minimal environmental information using a virtual receiver and waveguide invariant theory. J. Acoust. Soc. Am. 2000, 108, 1582–1594. [Google Scholar] [CrossRef]
- Kuperman, W.A.; D’Spain, G.L. Ocean Acoustic Interference Phenomena and Signal Processing; American Institute of Physics: College Park, MD, USA, 2002; Volume 621. [Google Scholar]
- Rouseff, D.; Spindel, R.C. Modeling the waveguide invariant as a distribution. AIP Conf. Proc. Am. Inst. Phys. 2002, 621, 137–150. [Google Scholar]
- Baggeroer, A.B. Estimation of the distribution of the interference invariant with seismic streamers. AIP Conf. Proc. Am. Inst. Phys. 2002, 621, 151–170. [Google Scholar]
- Yang, T. Beam intensity striations and applications. J. Acoust. Soc. Am. 2003, 113, 1342–1352. [Google Scholar] [CrossRef] [PubMed]
- Heaney, K.D. Rapid geoacoustic characterization using a surface ship of opportunity. IEEE J. Oceanic Engrg. 2004, 29, 88–99. [Google Scholar] [CrossRef]
- Cockrell, K.L.; Schmidt, H. Robust passive range estimation using the waveguide invariant. J. Acoust. Soc. Am. 2010, 127, 2780–2789. [Google Scholar] [CrossRef]
- Rouseff, D.; Zurk, L.M. Striation-based beam forming for estimating the waveguide invariant with passive sonar. J. Acoust. Soc. Am. Express Lett. 2011, 130, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Harrison, C.H. The relation between the waveguide invariant, multipath impulse response, and ray cycles. J. Acoust. Soc. Am. 2011, 129, 2863–2877. [Google Scholar] [CrossRef]
- Emmetiere, R.; Bonnel, J.; Gehant, M.; Cristol, X.; Chonavel, T. Understanding deep-water striation patterns and predicting the waveguide invariant as a distribution depending on range and depth. J. Acoust. Soc. Am. 2018, 143, 3444–3454. [Google Scholar] [CrossRef]
- Emmetiere, R.; Bonnel, J.; Cristol, X.; Gehant, M.; Chonavel, T. Passive source depth discrimination in deep-water. IEEE J. Select. Topics Signal Process. 2019, 13, 185–197. [Google Scholar] [CrossRef]
- Kuznetsov, G.N.; Kuzkin, V.M.; Pereselkov, S.A. Spectrogram and localization of a sound source in a shallow sea. Acoust. Phys. 2017, 63, 449–461. [Google Scholar] [CrossRef]
- Pereselkov, S.A.; Kuz’kin, V.M. Interferometric processing of hydroacoustic signals for the purpose of source localization. J. Acoust. Soc. Am. 2022, 151, 666–676. [Google Scholar] [CrossRef] [PubMed]
- Ehrhardt, M.; Pereselkov, S.A.; Kuz’kin, V.M.; Kaznacheev, I.; Rybyanets, P. Experimental observation and theoretical analysis of the low-frequency source interferogram and hologram in shallow water. J. Sound Vibr. 2023, 544, 117388. [Google Scholar] [CrossRef]
- Pereselkov, S.; Kuz’kin, V.; Ehrhardt, M.; Tkachenko, S.; Rybyanets, P.; Ladykin, N. Use of interference patterns to control sound field focusing in shallow water. J. Mar. Sci. Eng. 2023, 11, 559. [Google Scholar] [CrossRef]
- Pereselkov, S.; Kuz’kin, V.; Ehrhardt, M.; Matvienko, Y.; Tkachenko, S.; Rybyanets, P. The formation of 2D holograms of a noise source and bearing estimation by a vector scalar receiver in the high-frequency band. J. Mar. Sci. Eng. 2024, 12, 704. [Google Scholar] [CrossRef]
- Kuz’kin, V.M.; Pereselkov, S.A.; Zvyagin, V.G.; Malykhin, A.Y.; Prosovetskiy, D.Y. Intense internal waves and their manifestation in interference patters of received signals on oceanic shelf. Phys. Wave Phenom. 2018, 26, 160–167. [Google Scholar] [CrossRef]
- Badiey, M.; Kuz’kin, V.M.; Lyakhov, G.A.; Pereselkov, S.A.; Prosovetskiy, D.Y.; Tkachenko, S.A. Intense internal waves and their manifestation in the interference patterns of received signals on oceanic shelf. Part II. Phys. Wave Phenom. 2019, 27, 313–319. [Google Scholar] [CrossRef]
- Badiey, M.; SWARM’95 group. Cruise Report. Ocean Acoustic Experiments in Support of Shallow Water Acoustic Remote Measurements (SWARM); University of Delaware: Newark, DE, USA, 1995; p. 72. [Google Scholar]
- Apel, J.R.; Badiey, M.; Chiu, C.-S.; Finette, S.; Headrick, R.H.; Kemp, J.; Lynch, J.F.; Newhall, A.E.; Orr, M.H.; Pasewark, B.H.; et al. An overview of the SWARM 1995 shallow-water internal wave acoustic scattering experiment. IEEE J. Ocean. Engrg. 1997, 22, 465–500. [Google Scholar] [CrossRef]
- Serebryany, A.N. Manifestation of the properties of solitons in internal waves on the shelf. Izv. Acad. Sci. USSR Phys. Atmos. Ocean 1993, 29, 285–293. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Do internal solitons exist in the ocean? Rev. Geophys. 1989, 27, 293–310. [Google Scholar] [CrossRef]
- Konyaev, K.V.; Sabinin, K.D. Waves Inside the Ocean; Gidromet: St. Petersburg, Russia, 1992; 271p. [Google Scholar]
- Katsnelson, B.G.; Pereselkov, S.A. Low-frequency horizontal acoustic refraction caused by internal wave solitons in a shallow sea. Acoust. Phys. 2000, 46, 684–691. [Google Scholar] [CrossRef]
- Pereselkov, S.; Kuz’kin, V.; Ehrhardt, M.; Tkachenko, S.; Rybyanets, P.; Ladykin, N. Three-Dimensional Modeling of Sound Field Holograms of a Moving Source in the Presence of Internal Waves Causing Horizontal Refraction. J. Mar. Sci. Eng. 2023, 11, 1922. [Google Scholar] [CrossRef]
- Pereselkov, S.; Kuz’kin, V.; Ehrhardt, M.; Tkachenko, S.; Pereselkov, A.; Ladykin, N. Influence of Intense Internal Waves Traveling Along an Acoustic Path on Source Holographic Reconstruction in Shallow Water. J. Mar. Sci. Eng. 2025, 13, 1409. [Google Scholar] [CrossRef]
- Harris, P.T.; Baker, E.K. (Eds.) Seafloor Geomorphology as Benthic Habitat: GeoHab Atlas of Seafloor Geomorphic Features and Benthic Habitats; Elsevier: Amsterdam, The Netherlands, 2012; 936p. [Google Scholar]
- Micallef, A.; Krastel, S.; Savini, A. (Eds.) Submarine Geomorphology; Springer: Berlin/Heidelberg, Germany, 2018; 636p. [Google Scholar]
- Chiocci, F.L.; Ridente, D. Seafloor Mapping Along Continental Shelves: Research and Applications; Springer: Berlin/Heidelberg, Germany, 2015; 276p. [Google Scholar]
- Lecours, V.; Dolan, M.F.J.; Micallef, A.; Lucieer, V.L. (Eds.) Marine Geomorphometry: Geomorphometry Concepts and Applications to Marine Environments; MDPI: Basel, Switzerland, 2020; 222p. [Google Scholar]
- GEBCO Compilation Group. The GEBCO_2023 Grid—Global Bathymetric Data Set. GEBCO. 2023. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 8 August 2025).
- Ashley, G.M. Classification of large-scale subaqueous bedforms: A new look at an old problem. J. Sediment. Res. 1990, 60, 160–172. [Google Scholar] [CrossRef]
- Kuperman, W.A.; Ingenito, F. (Eds.) Acoustics of the Ocean Bottom; Hemisphere Publishing Corporation: Washington, DC, USA, 1980; 454p. [Google Scholar]
- Hamilton, E. (Ed.) Acoustics of Marine Sediments; Springer/Plenum Press: New York, NY, USA, 1970; 498p. [Google Scholar]
- Brekhovskikh, L.M.; Lysanov, Y.P. Fundamentals of Ocean Acoustics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H.; Tolstoy, A. Computational Ocean Acoustics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lin, Y.-T.; Porter, M.B.; Sturm, F.; Isakson, M.J.; Chiu, C.-S. Introduction to the special issue on three-dimensional underwater acoustics. J. Acoust. Soc. Am. 2019, 146, 1855–1857. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, L.; Wang, W.; Wang, Y.; Ma, S.; Cheng, X.; Xiao, W. A three-dimensional finite difference model for ocean acoustic propagation and benchmarking for topographic effects. J. Acoust. Soc. Am. 2021, 150, 1140–1156. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Liu, W.; Yang, C.; Qin, J.; Ma, S.; Wang, X. Application of a Spectral Method to Simulate Quasi-Three-Dimensional Underwater Acoustic Fields. J. Sound Vibr. 2023, 545, 117421. [Google Scholar] [CrossRef]
- Larsson, E.; Abrahamsson, L. Helmholtz and parabolic equation solutions to a benchmark problem in ocean acoustics. J. Acoust. Soc. Am. 2003, 113, 2446–2454. [Google Scholar] [CrossRef]
- Smith, K.B.; Tappert, F.D. UMPE: The University of Miami Parabolic Equation Model; Version 1.1 “MPL Technical Memorandum 432”; Rosenstiel School of Marine and Atmospheric Science, University of Miami: Coral Gables, FL, USA, 1993; p. 96. [Google Scholar]
- Tappert, F.D. The parabolic approximation method. In Wave Propagation and Underwater Acoustics; Lecture Notes in Physics; Keller, J.B., Papadakis, J.S., Eds.; Springer: New York, NY, USA, 1977; Chapter 5; Volume 70, pp. 224–287. [Google Scholar]
- Lin, Y.-T. Three-dimensional boundary fitted parabolic-equation model of underwater sound propagation. J. Acoust. Soc. Am. 2019, 146, 2058–2067. [Google Scholar] [CrossRef]
- Heaney, K.D.; Campbell, R.L. Three-dimensional parabolic equation modeling of mesoscale eddy deflection. J. Acoust. Soc. Am. 2016, 139, 918–926. [Google Scholar] [CrossRef]
- Ivansson, S. Local accuracy of cross-term corrections of three-dimensional parabolic-equation models. J. Acoust. Soc. Am. 2019, 146, 2030–2040. [Google Scholar] [CrossRef]
- Lee, K.; Seong, W.; Na, Y. Three-dimensional Cartesian parabolic equation model with higher-order cross-terms using operator splitting, rational filtering, and split-step Padé algorithm. J. Acoust. Soc. Am. 2019, 146, 2030–2040. [Google Scholar] [CrossRef]
- Lee, K.; Seong, W.; Na, Y. Split-step Padé solver for three dimensional Cartesian acoustic parabolic equation in stair-step representation of ocean environment. J. Acoust. Soc. Am. 2019, 146, 2050–2057. [Google Scholar] [CrossRef]
- Porter, M.B. Beam tracing for two- and three-dimensional problems in ocean acoustics. J. Acoust. Soc. Am. 2019, 146, 2016–2029. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.B. Bellhop3d User Guide; Heat, Light, and Sound Research, Inc.: La Jolla, CA, USA, 2016. [Google Scholar]
- Collins, M.D. The adiabatic mode parabolic equation. J. Acoust. Soc. Am. 1993, 94, 2269–2278. [Google Scholar] [CrossRef]
- Trofimov, M.Y.; Kozitskiy, S.; Zakharenko, A. A mode parabolic equation method in the case of the resonant mode interaction. Wave Motion 2015, 58, 42–52. [Google Scholar] [CrossRef]
- Petrov, P.S.; Sturm, F. An explicit analytical solution for sound propagation in a three-dimensional penetrable wedge with small apex angle. J. Acoust. Soc. Am. 2016, 139, 1343–1352. [Google Scholar] [CrossRef]
- Kohler, W.; Papanicolaou, G.C. Wave propagation in a randomly inhomogeneous ocean. In Wave Propagation and Underwater Acoustics; Keller, J.B., Papadakis, J.S., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1977; Volume 70, pp. 153–223. [Google Scholar]
- Weinberg, H.; Burridge, R. Horizontal ray-theory for ocean acoustics. J. Acoust. Soc. Am. 1974, 55, 63–79. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A. Sound propagation in a wedge-shaped ocean with a penetrable bottom. J. Acoust. Soc. Am. 1980, 67, 1564–1566. [Google Scholar] [CrossRef]
- Buckingham, M. Theory of three-dimensional acoustic propagation in a wedgelike ocean with a penetrable bottom. J. Acoust. Soc. Am. 1987, 82, 198–210. [Google Scholar] [CrossRef]
- Deane, G.; Buckingham, M. An analysis of the three-dimensional sound field in a penetrable wedge with a stratified fluid or elastic basement. J. Acoust. Soc. Am. 1993, 93, 1319–1328. [Google Scholar] [CrossRef]
- Fawcett, J. Modeling three-dimensional propagation in an oceanic wedge using parabolic equation methods. J. Acoust. Soc. Am. 1993, 93, 2627–2632. [Google Scholar] [CrossRef]
- Westwood, E. Broadband modeling of the three-dimensional penetrable wedge. J. Acoust. Soc. Am. 1992, 92, 2212–2222. [Google Scholar] [CrossRef]
- Sturm, F. Examination of signal dispersion in a 3-D wedge-shaped waveguide using 3DWAPE. Acta Acust. united Ac. 2002, 88, 714–717. [Google Scholar]
- Sturm, F.; Fawcett, J. Numerical Simulation of the Effects of the Bathymetry on Underwater Sound Propagation Using Three-Dimensional Parabolic Equation Models; Technical Report SM-342; SACLANT Undersea Research Centre: La Spezia, Italy, 1993. [Google Scholar]
- Sturm, F.; Kampanis, N. Accurate treatment of a general sloping interface in a finite-element 3-D narrow-angle PE model. J. Comput. Acoust. 2007, 15, 285–318. [Google Scholar] [CrossRef]
- Sturm, F. Numerical study of broadband sound pulse propagation in three-dimensional shallow water waveguides. J. Acoust. Soc. Am. 2005, 117, 1058–1079. [Google Scholar] [CrossRef]
- Ballard, M.S.; Sagers, J.D. Measurements and modeling of acoustic propagation in a scale model canyon. J. Acoust. Soc. Am. 2019, 146, 1858–1866. [Google Scholar] [CrossRef]
- Barclay, D.L.; Barclay, D.R.; Lin, Y.T. Three-dimensional ambient noise modeling in a submarine canyon. J. Acoust. Soc. Am. 2019, 146, 1956–1967. [Google Scholar] [CrossRef] [PubMed]
- DeCourcy, B.J.; Lin, Y.T. Spatial and temporal variation of three-dimensional ship noise coherence in a submarine canyon. J. Acoust. Soc. Am. 2023, 153, 1042–1051. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).