The Numerical Evaluation of Hydrate Saturation in Marine Sediment During the Injection Process of Self-Heat Generating Fluid
Abstract
1. Introduction
2. Materials and Methods
2.1. Defining Two Stages in Reservoir Energy Stimulation
2.2. Simulation Tool Introduction
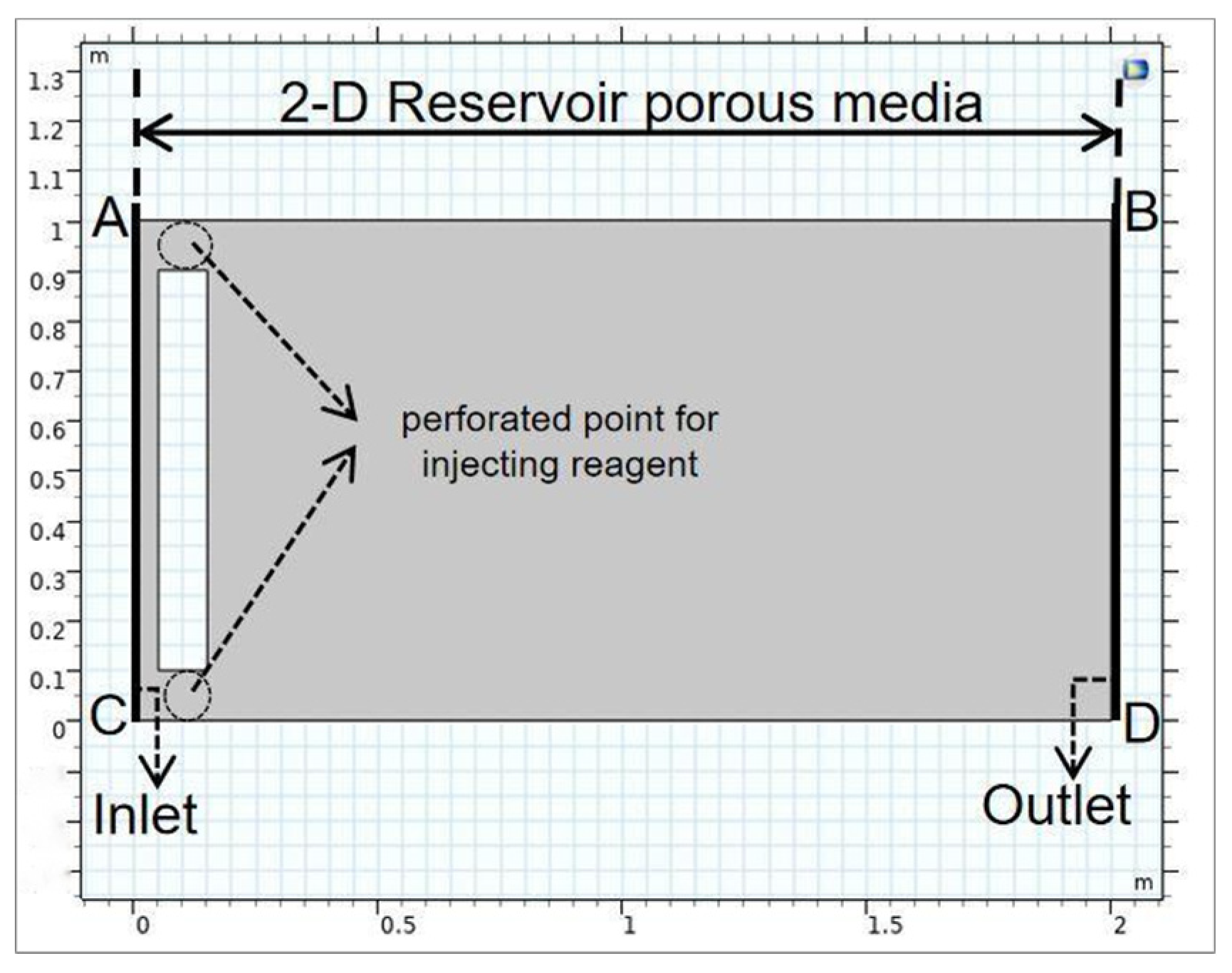
2.3. Model Construction
2.4. Model of Reactive Chemical Flow Stage (Stage 1)
- Momentum conservation equation
- Heat transfer equation at hydrate interface
- Mass conservation equation
2.5. Model of Non-Reactive Flow Stage (Stage 2)
- Momentum conservation equation
2.6. Boundary Condition and Key Parameters Descriptions
2.6.1. Boundary Condition Description
2.6.2. Key Parameters Description
- (1)
- The explanation for the heat capacity
- (2)
- The explanation for the velocity of reagent and water
- (3)
- Phase transition latent heat
2.7. Mesh Configuration, Convergence Criteria and Solver Settings
2.7.1. Convergence Criteria
2.7.2. Solver Settings
2.7.3. Mesh Configuration
3. Results and Discussions
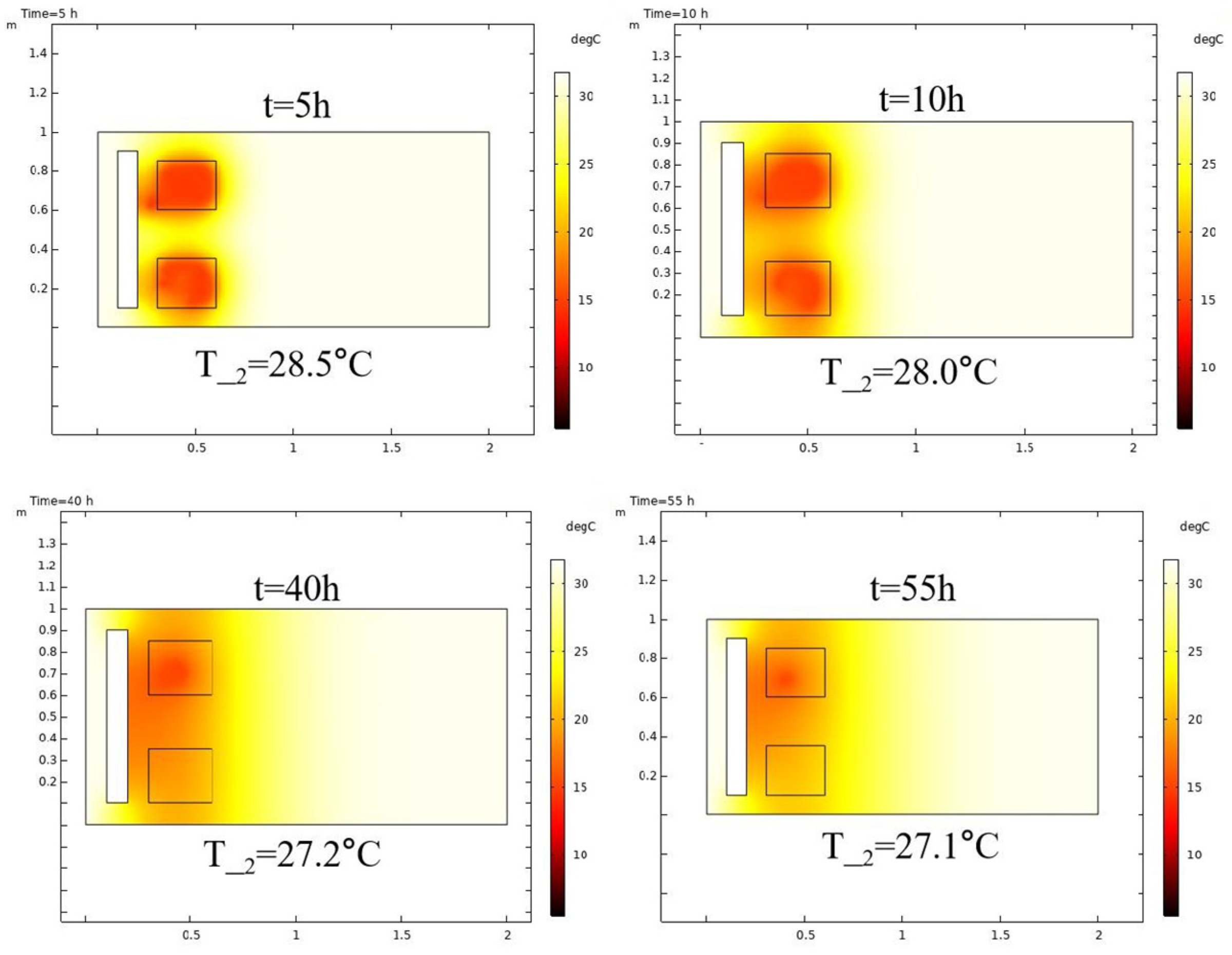
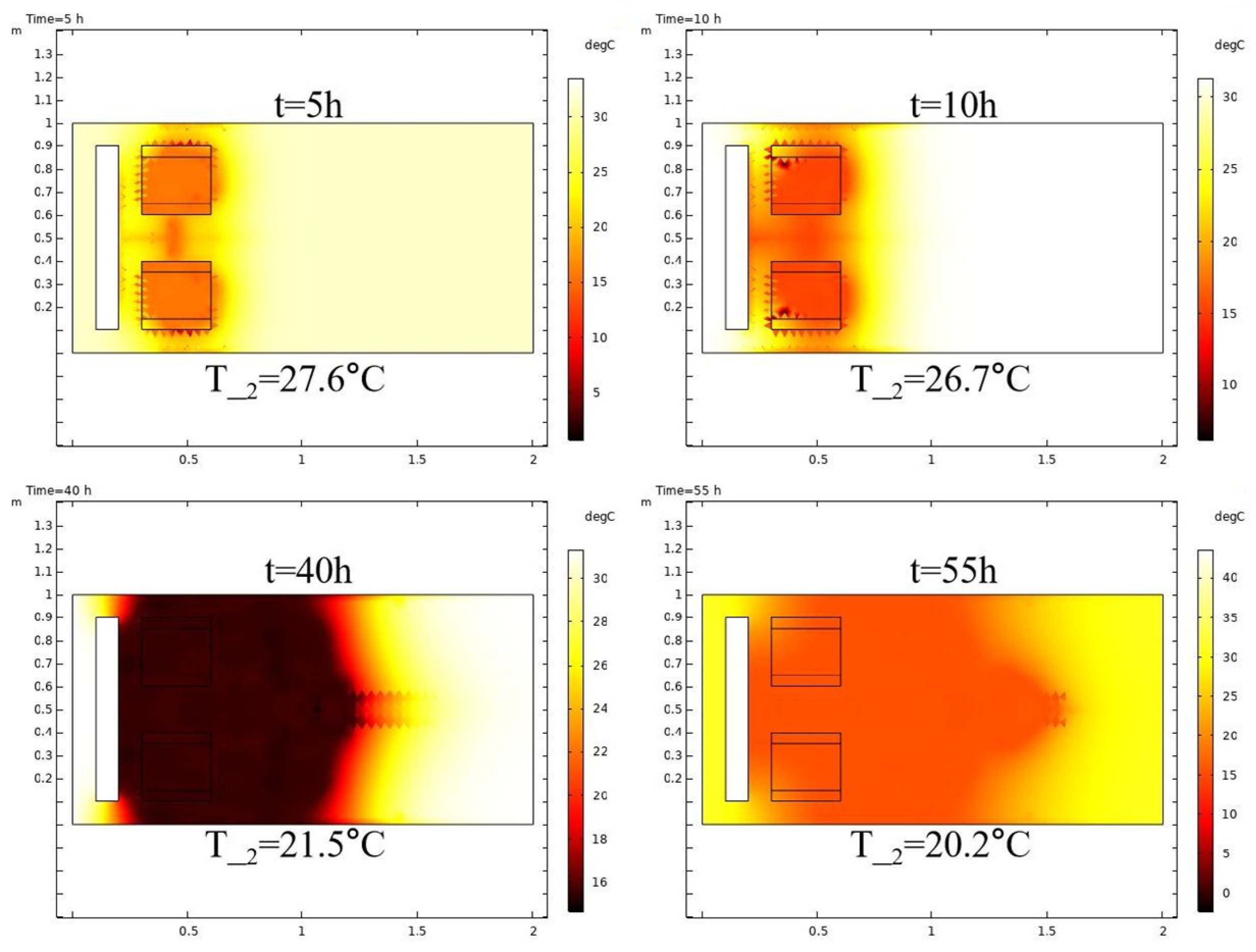
3.1. Base Case
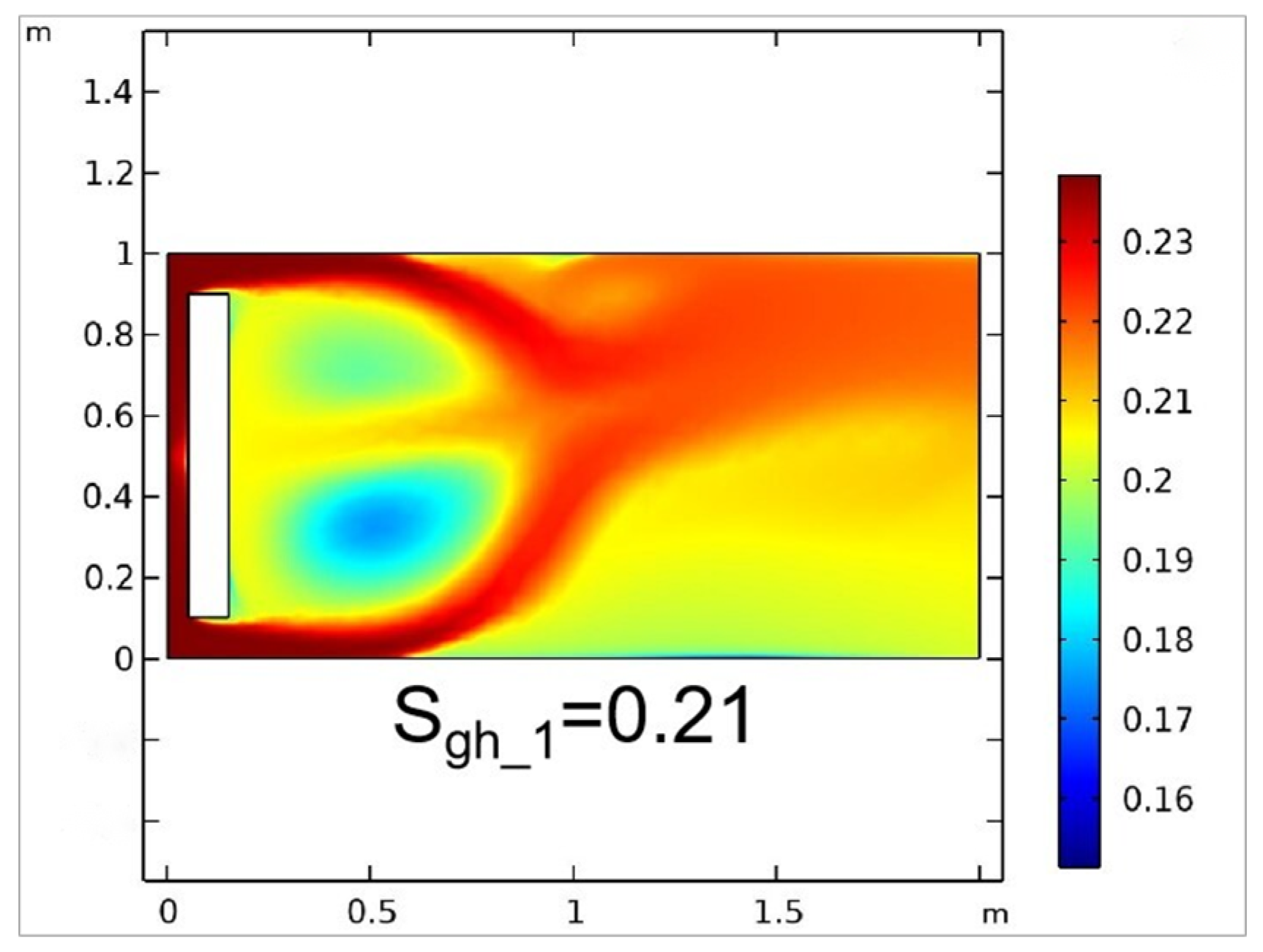
3.1.1. Reactive Chemical Flow Stage (Stage 1)
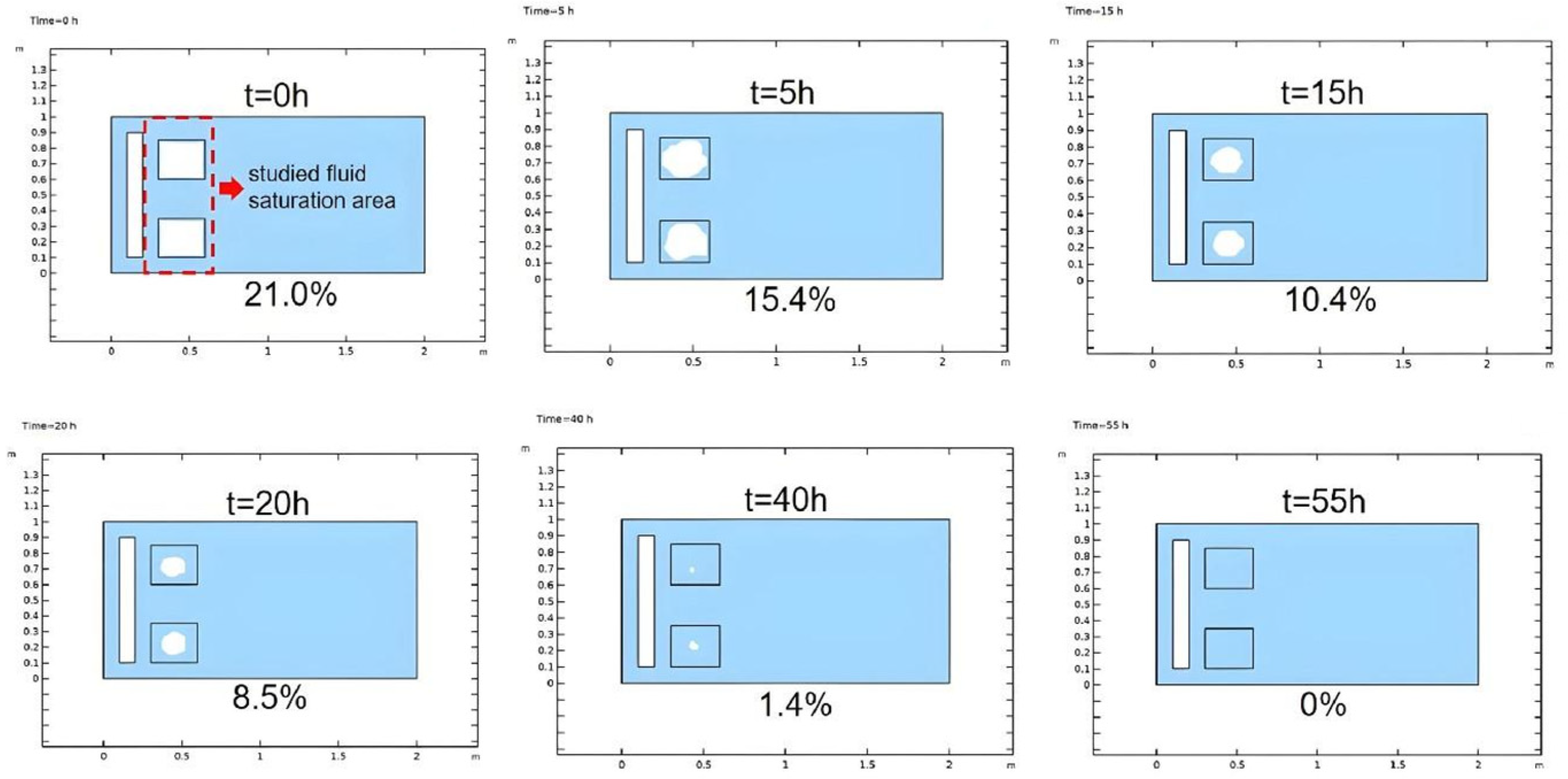
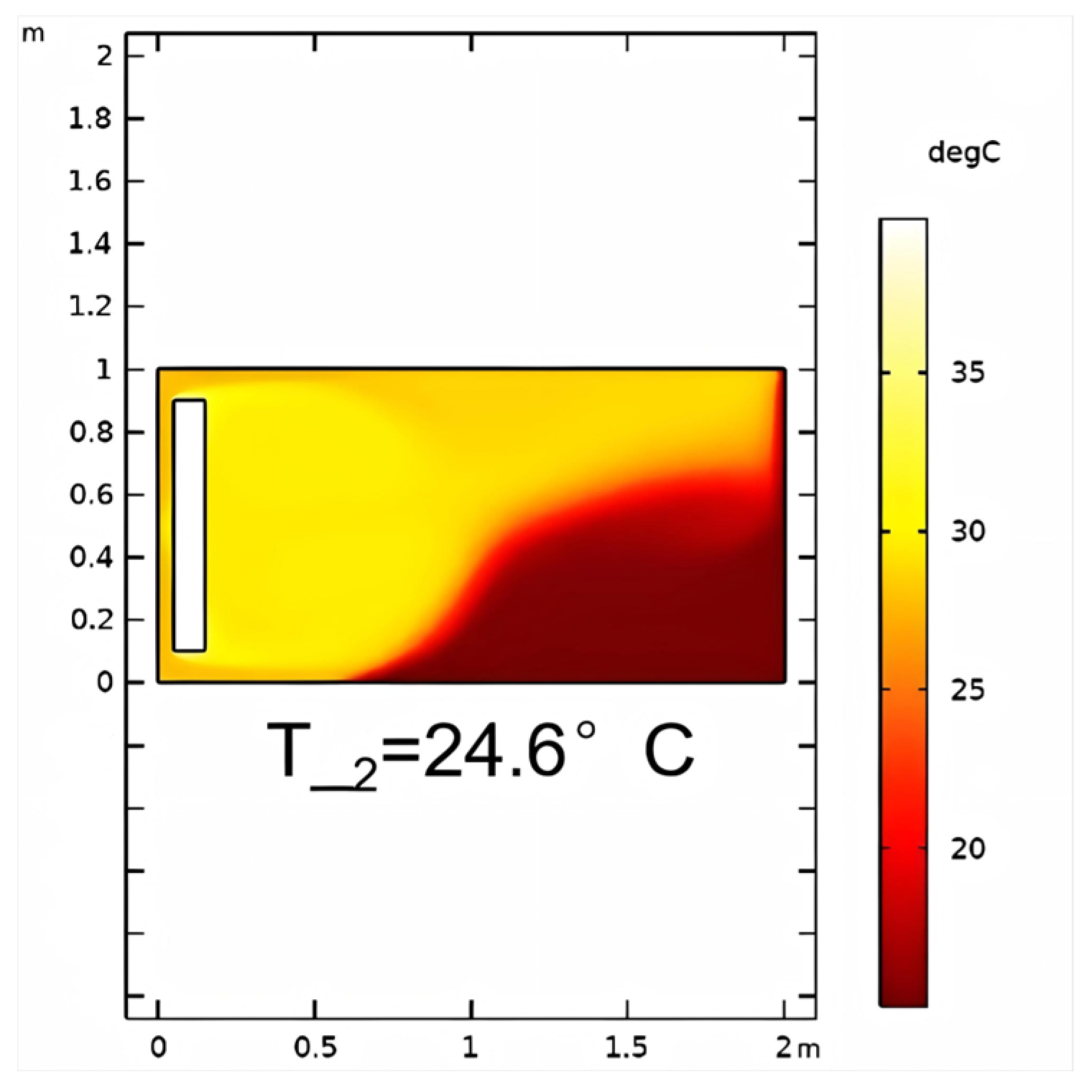
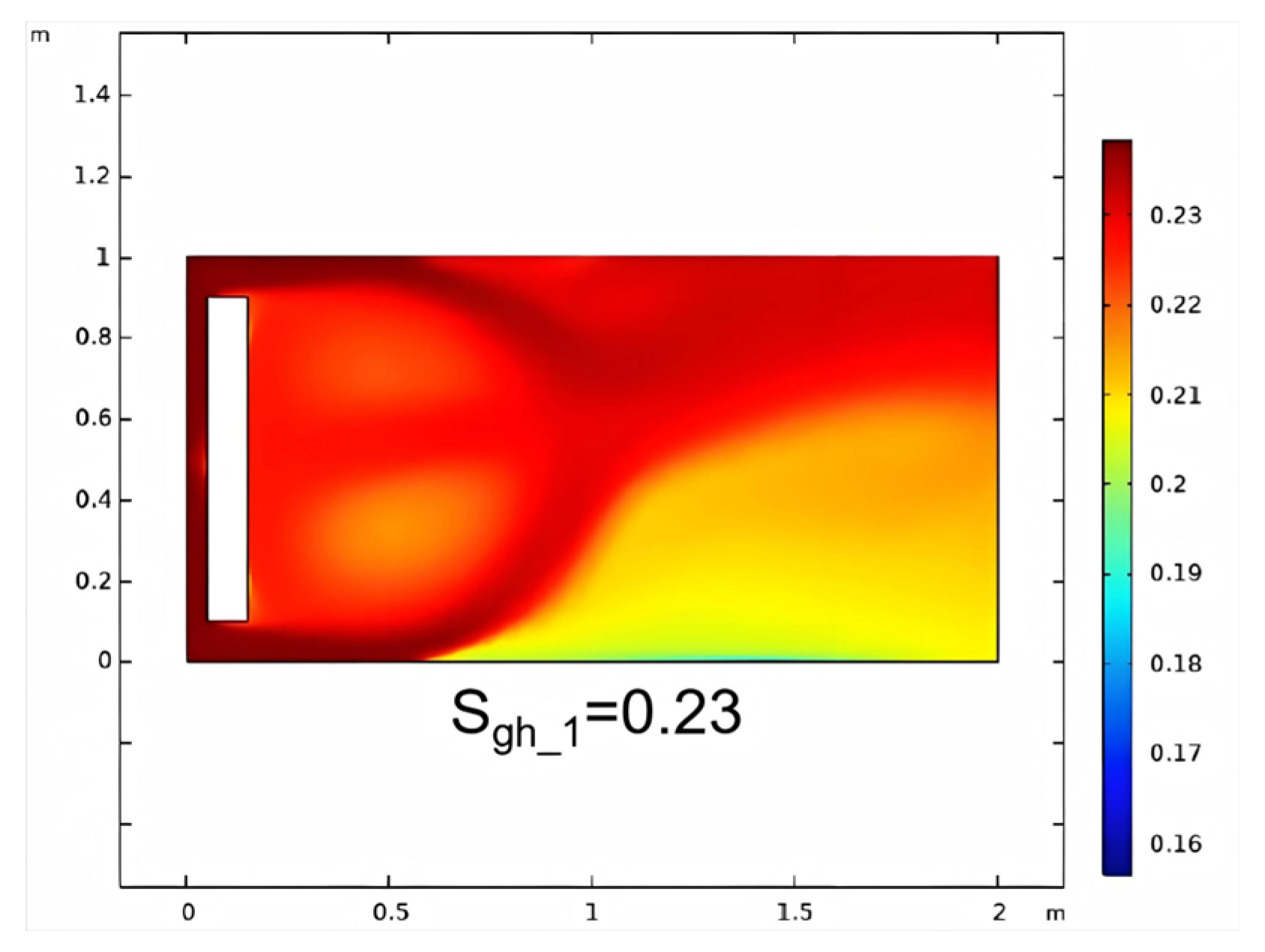
3.1.2. Non-Reactive Flow Stage (Stage 2)
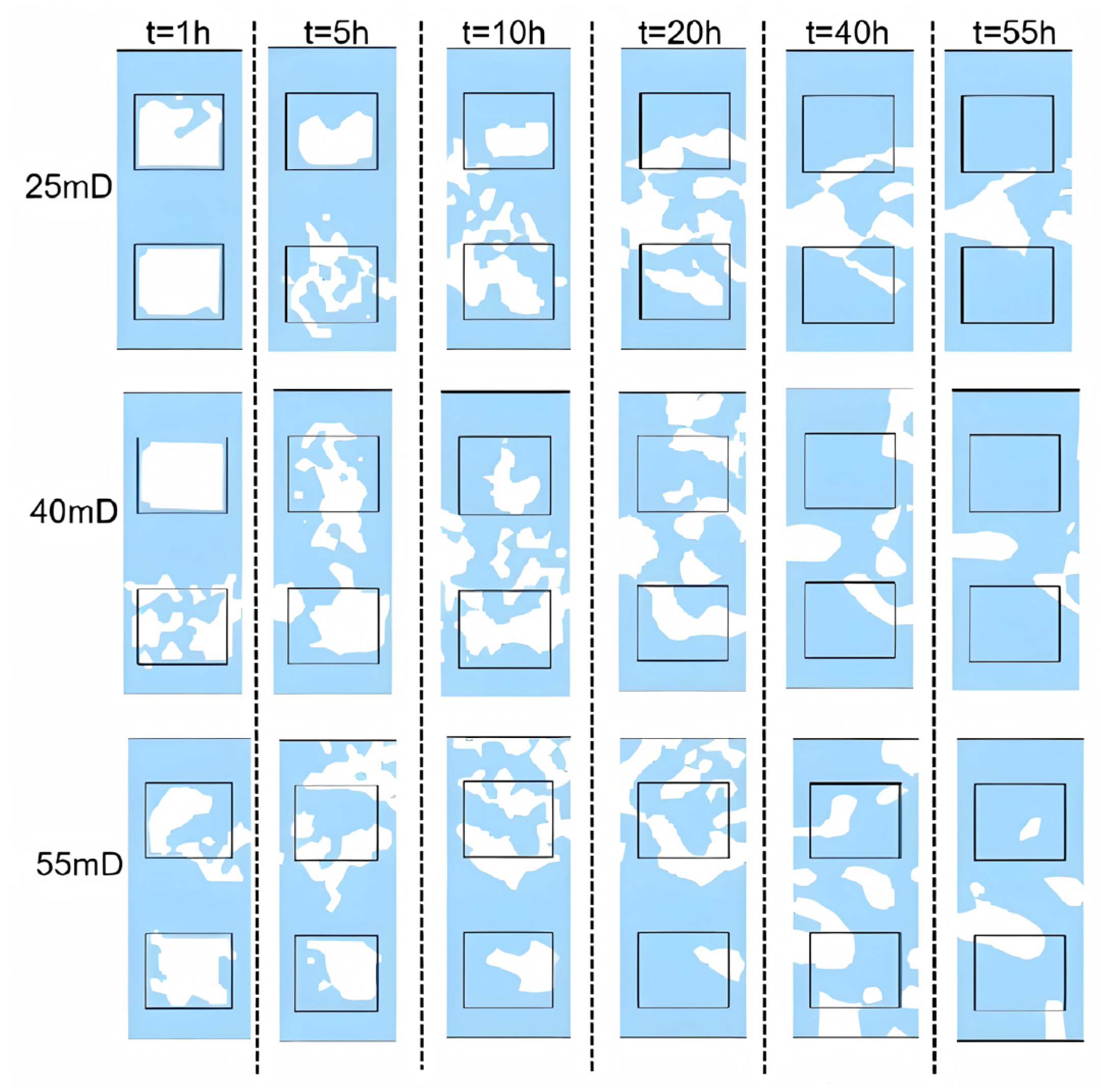
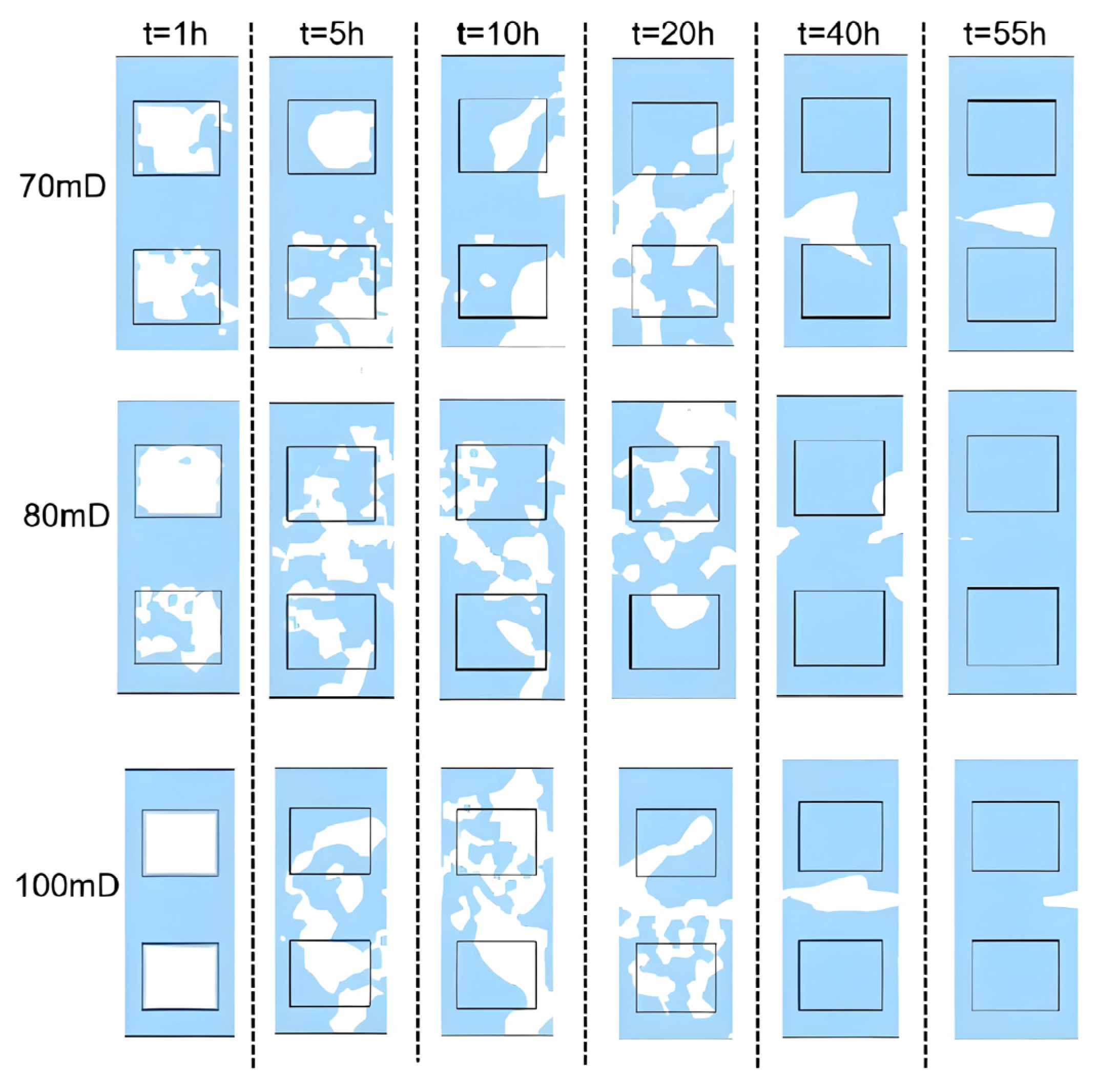
3.2. Sensitivity Analysis
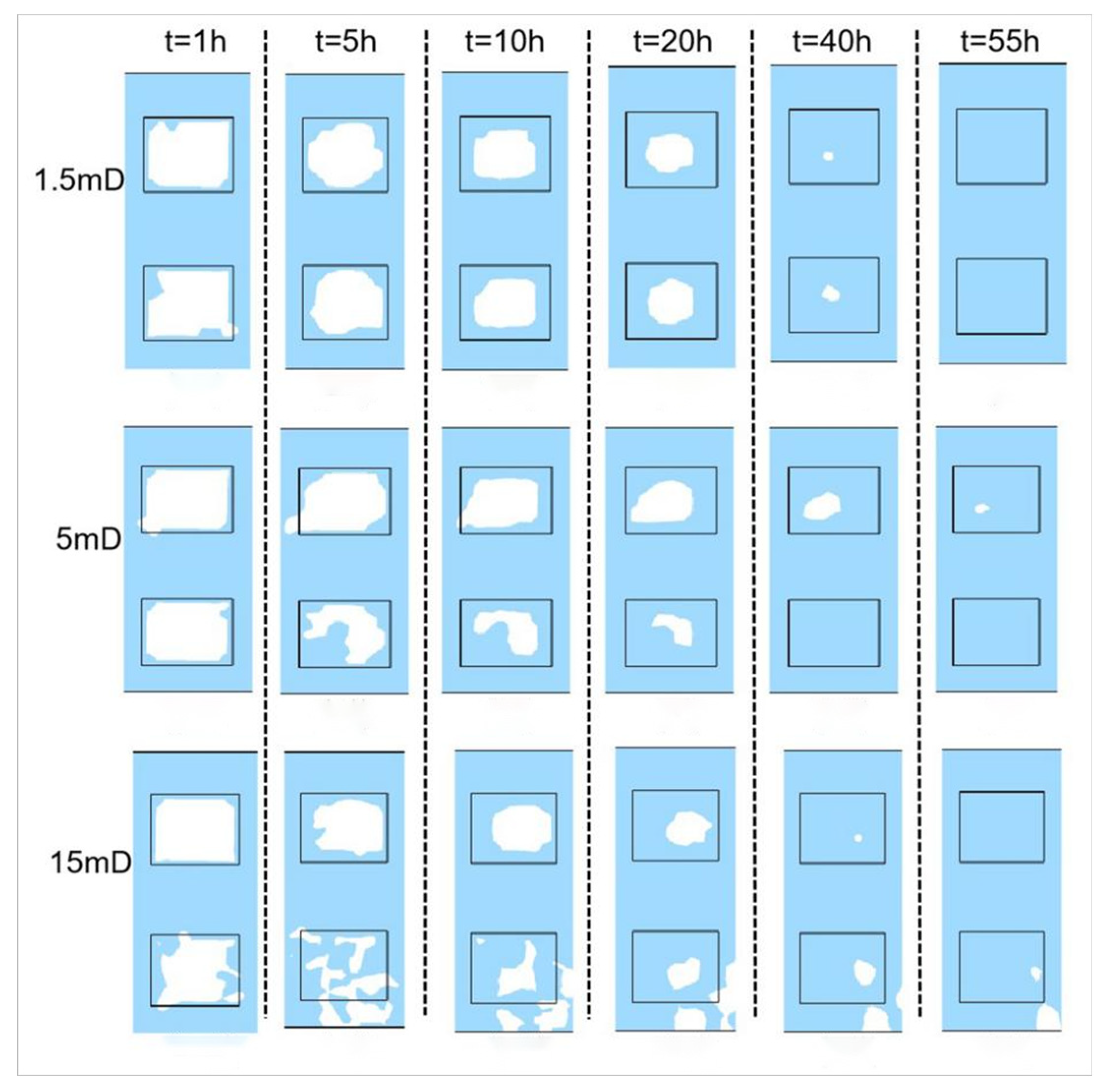
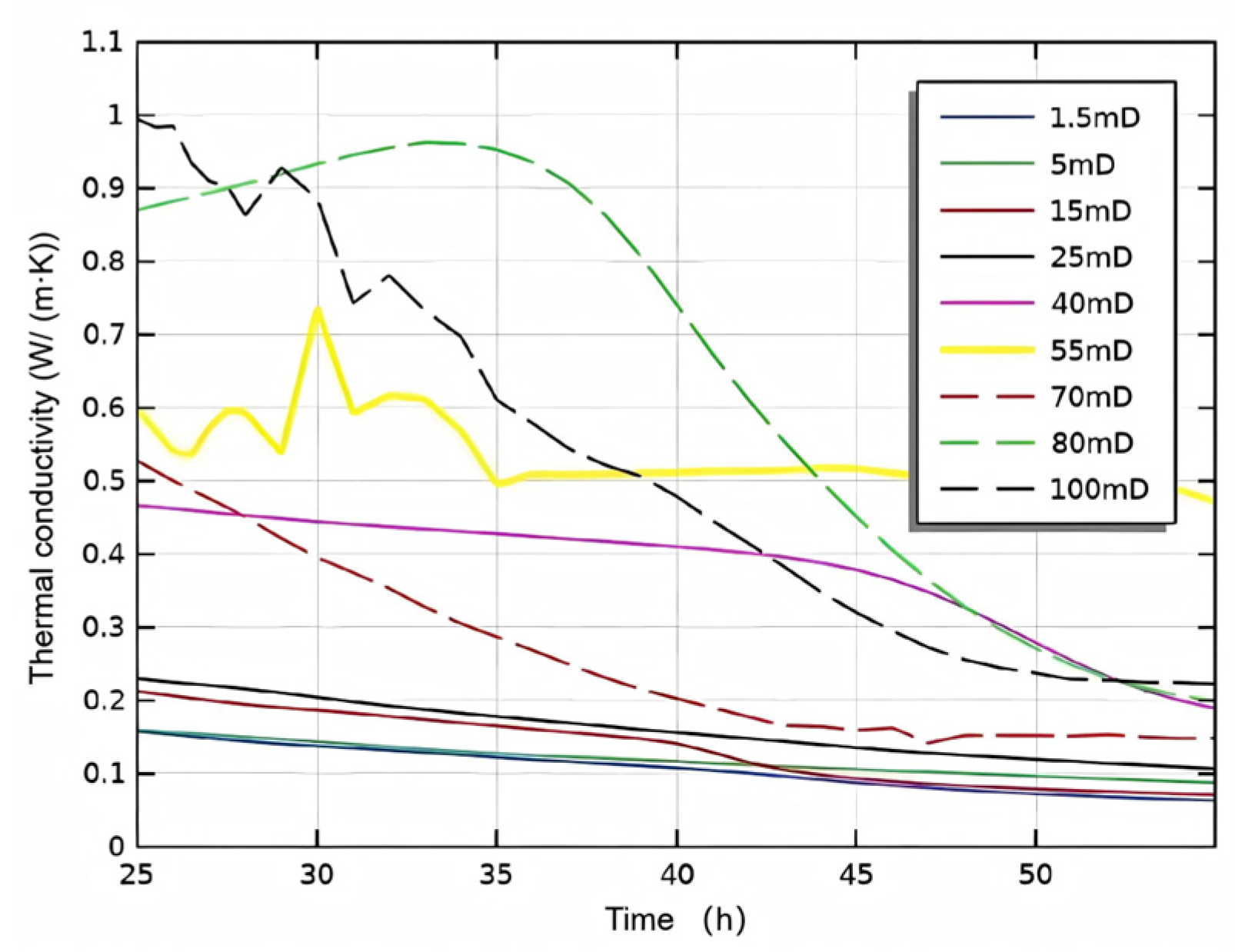
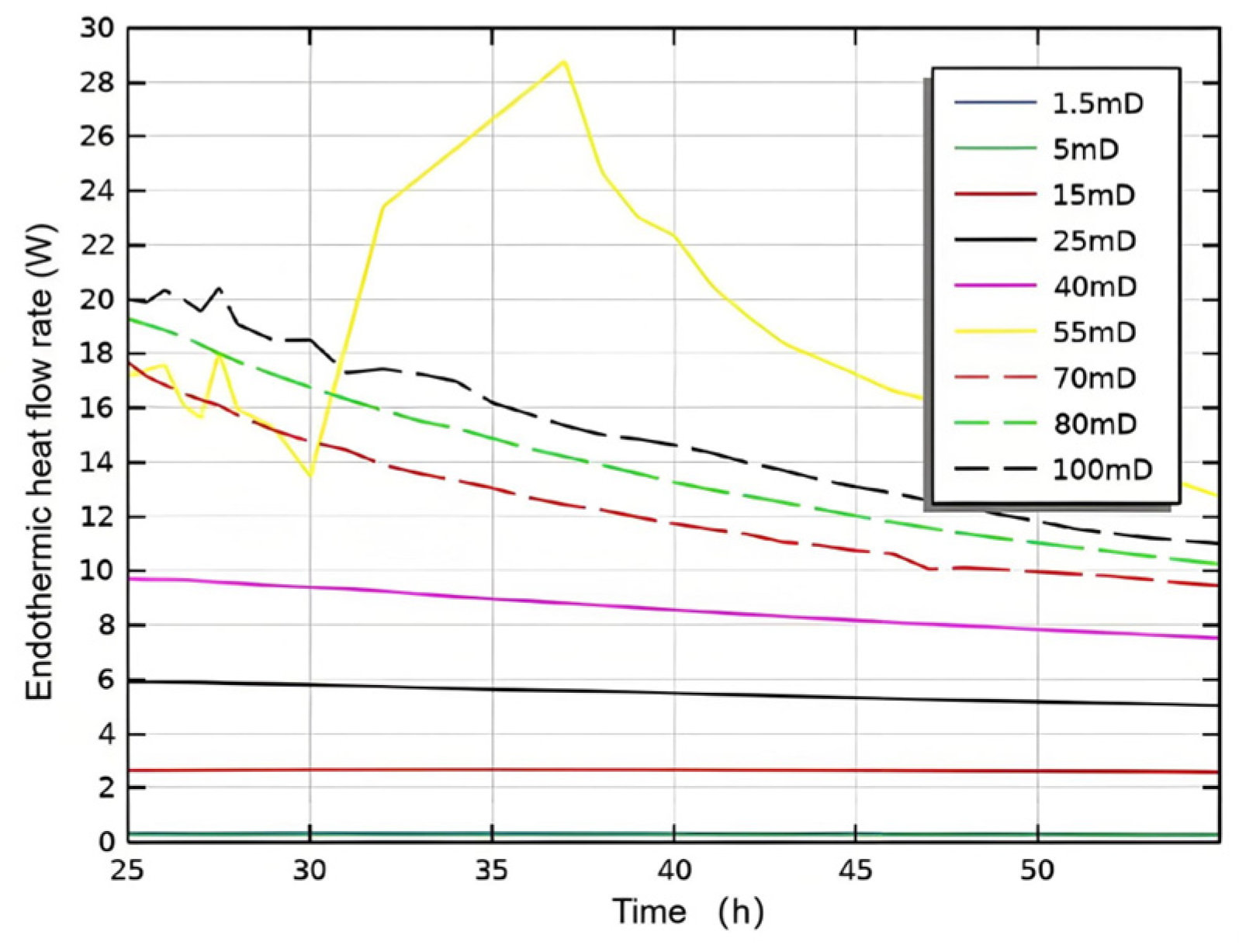
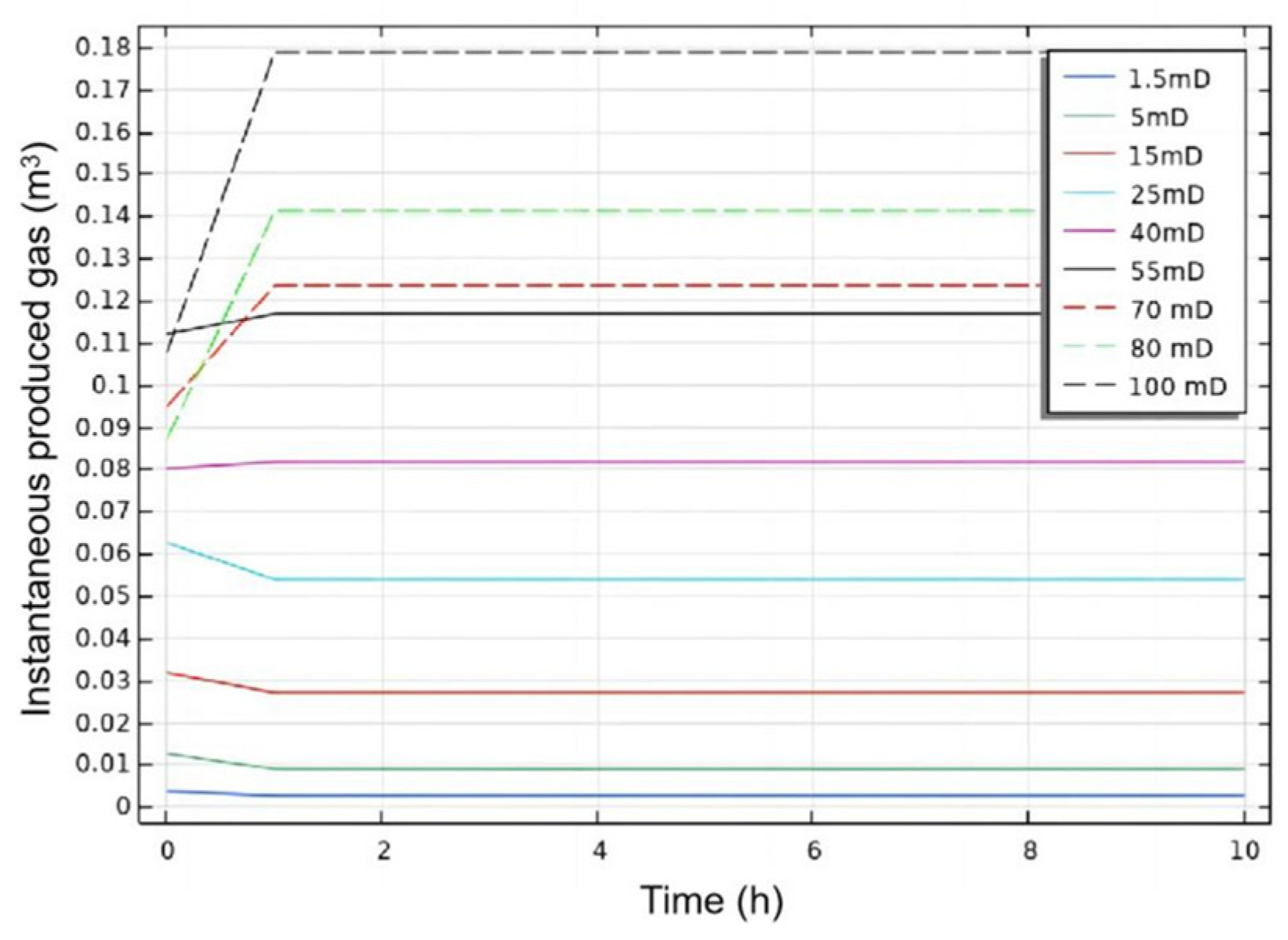
3.2.1. Initial Absolute Permeability
- Permeability Study: Non-Reactive Flow Stage (Stage 2)
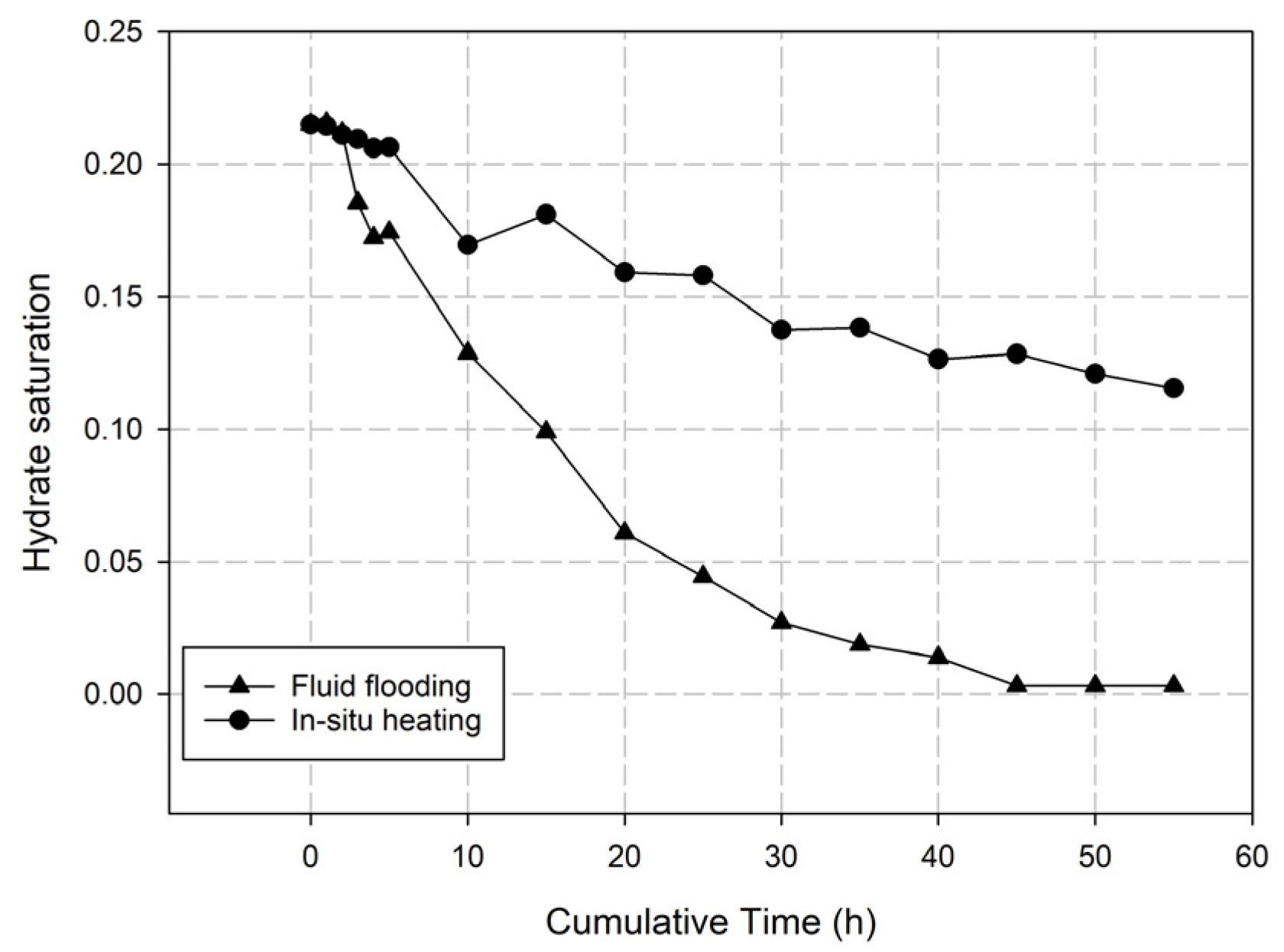
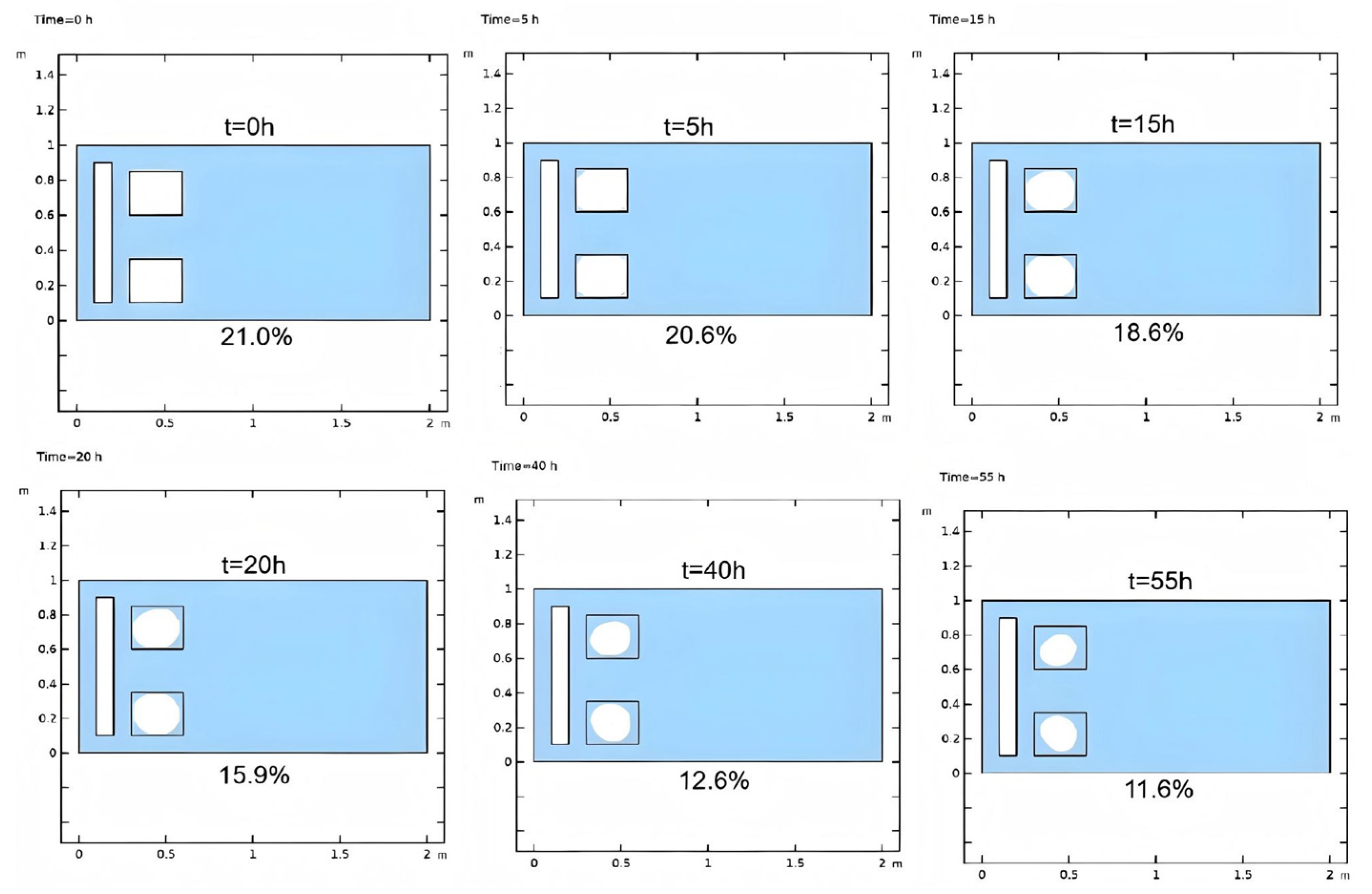
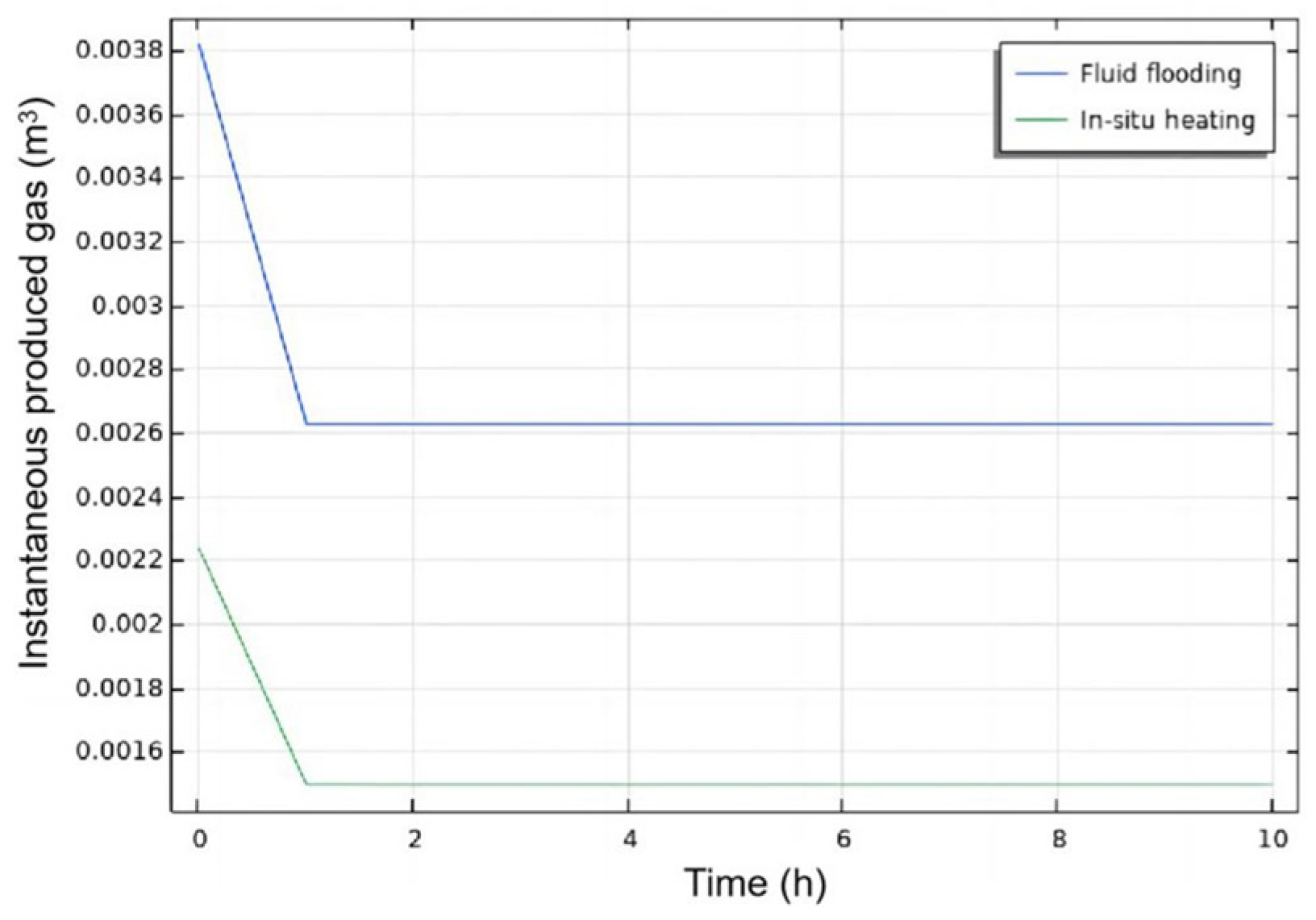
3.2.2. Injection Mode
- Injection Mode Study: Reactive Chemical Flow Stage (Stage 1)
- Injection Mode Study: Non-Reactive Flow Stage (Stage 2)
3.3. Post-Injection Gas Production Potential
3.4. Numerical Model Validation
3.4.1. The Experimental Case Selection
3.4.2. The Validation Process
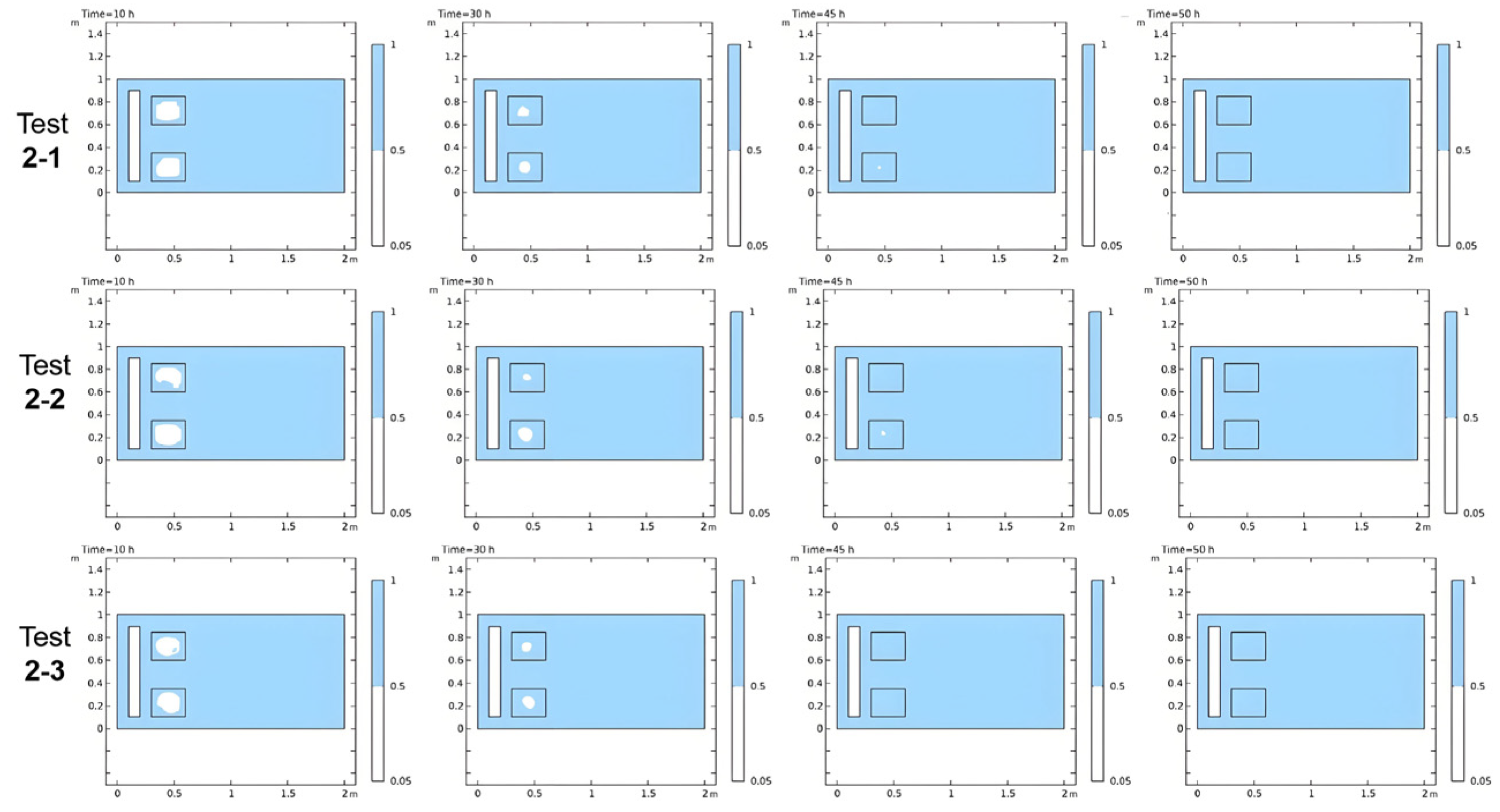
3.5. Numerical Stability Validation
3.6. Comparative Analysis with Prior Studies
3.6.1. Enhancing the Permeability-Secondary Hydrates Response Mechanism Study
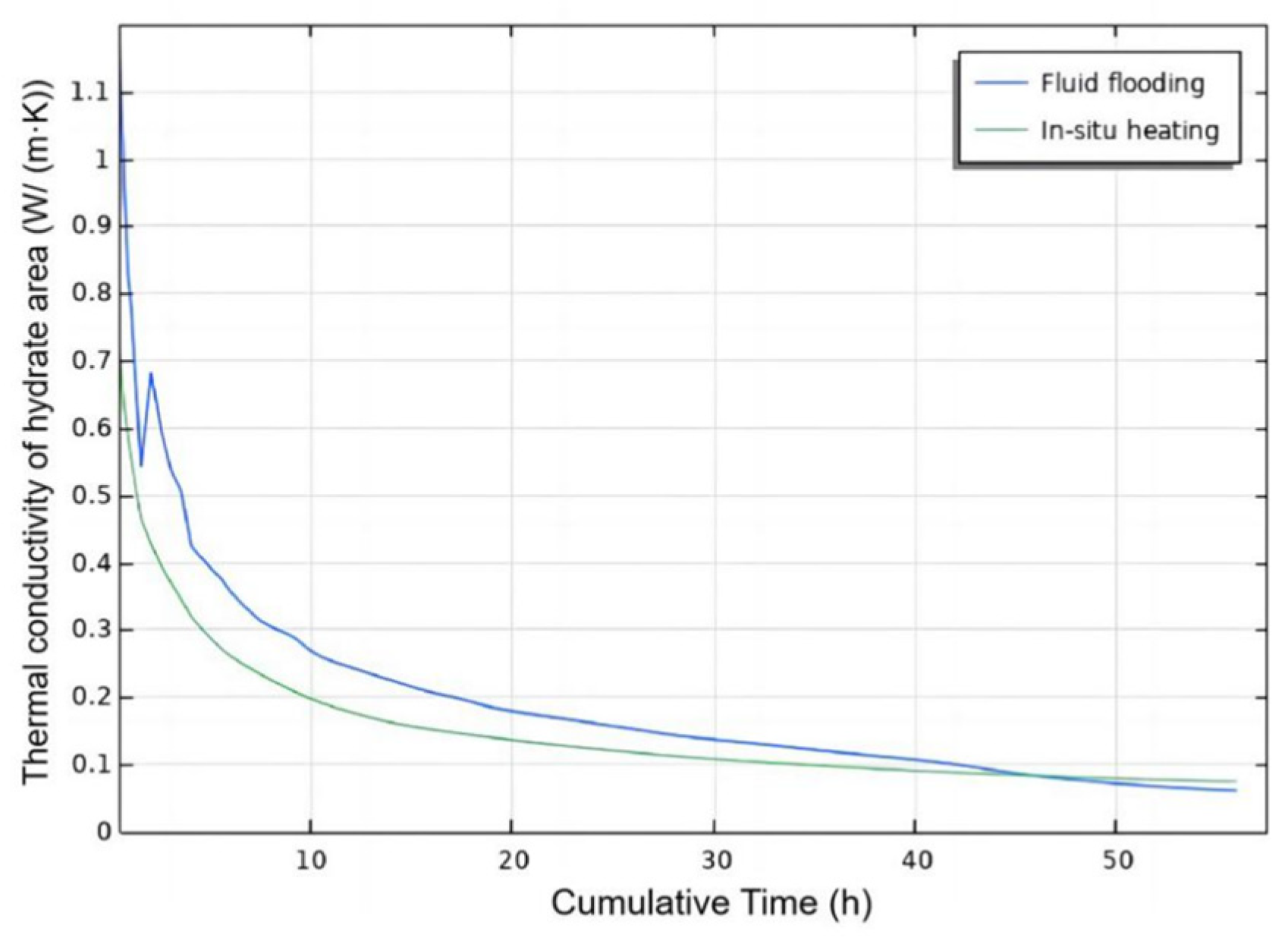
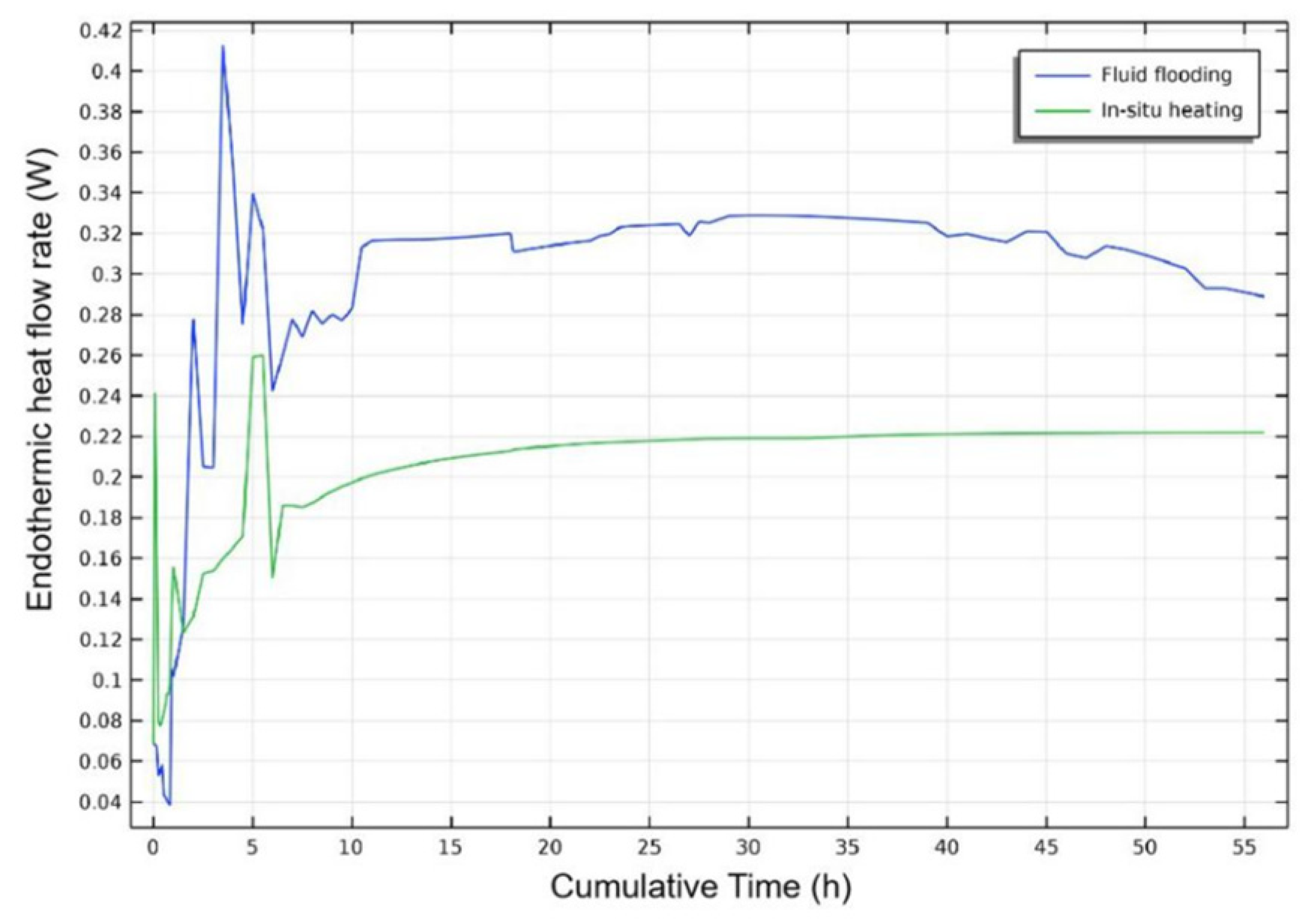
3.6.2. Complementing Existing Research on Heat Transfer Mechanisms
3.6.3. Synergistic Findings in Formation Heating Modes with Other Studies
3.7. Evaluation of Self-Heat System’s Impact on Methane Hydrate Decomposition: Quantitative Heat Release and Chemical Product Effects
3.7.1. Energy Efficiency Analysis: Self-Heat System Driven CH4 Hydrate Decomposition
3.7.2. NaNO2/NH4Cl Heating Effect and Hydrate Dissociation Performance
3.7.3. Quantity Comparison Between Reaction-Generated N2 and Hydrate-Dissociated CH4
3.7.4. The NaCl Effect and Crystallization Tendency
3.8. Recommendations for Field Application
3.8.1. Permeability-Graded Design for Secondary Hydrate Control
- (1)
- Prioritize low-permeability reservoirs (K < 15 mD)
- (2)
- For reservoirs with permeability of 15–55 mD
- (3)
- Avoid high-risk permeability zones (55–70 mD)
3.8.2. Field Operation Optimization: Thermal Front Dynamic Control
3.8.3. Field Operation Optimization: Real-Time Monitoring and Feedback Control
3.9. Limitations and Future Work Directions
3.9.1. The Assumption of Isotropic and Homogeneous Porous Media
- (1)
- The reason for the simplification
- (2)
- Potential implications for the results
- (3)
- Current offset strategies
- (4)
- Future plans
3.9.2. Hydrate Saturation-Geomechanical Assumption
- (1)
- The rationality of geomechanical effects simplification
- (2)
- Field Application Risks and Mitigation Strategies Analysis
3.9.3. Operational Parameter Limitations in Sensitivity Analysis
3.9.4. Validation Scope Limitation and Future Plans
- (1)
- Validation scale limitation
- (2)
- Lab and field saturation validation plans
3.9.5. Limitation of Phase-Specific Hydrate Regeneration Modeling
4. Conclusions
- (1)
- The stimulation process involving self-heating fluid injection into hydrate-bearing marine sediment is conceptualized as the reactive chemical flow stage (Stage 1), followed by the non-reactive flow stage (Stage 2). A near-wellbore 2D three-phase reservoir model is constructed to perform numerical simulations for both stages. In the base case, reservoir temperature rises from 13.0 °C to 29.3 °C with a 47.5% hydrate saturation reduction in Stage 1, followed by full dissociation in Stage 2. The evolution of hydrate saturation and reservoir temperature demonstrates that the self-heat fluid method provides a viable approach for effectively enhancing hydrate decomposition in the thermal stimulation process.
- (2)
- During the self-heating fluid injection process, variations in reservoir permeability critically affect thermal conductivity and heat flow rate in hydrate-bearing zones, resulting in non-uniform temperature distributions and hydrate saturation patterns within marine porous media. In low-permeability reservoirs (K < 15 mD), complete hydrate dissociation occurs during Stage 2, without secondary hydrate formation, whereas in the 15–55 mD permeability range, a dual-phase behavior is observed—initial hydrate regeneration in early-to-mid Stage 2 followed by secondary decomposition until the end of Stage 2. To minimize secondary hydrate formation, the self-heating fluid method should be applied only in reservoirs with permeability below 15 mD, while its use is strongly discouraged in the 55–70 mD range due to significant secondary hydrate generation.
- (3)
- Fluid flooding injection exhibits robust heat generation within the hydrate reservoir, evidenced by Stage 1 reservoir temperature analysis and Stage 2 hydrate saturation monitoring. This injection mode outperforms in situ heating mode by enhancing hydrate dissociation efficiency during the injection process of self-heat generating fluid, yielding higher post-injection gas recovery potential.
- (4)
- For the research domain of secondary hydrate formation suppression, by comparing with other research, this investigation supplements and extends the preceding studies on hydrate decomposition mechanisms: it concurrently demonstrates the regulatory influence of reservoir intrinsic permeability in secondary hydrate dynamics through thermodynamic and fluid dynamic analyses, corroborated by prior large-scale reservoir research. The study further suggests that integrating self-heat fluid flooding with huff-puff in situ heating could potentially establish a macro-convection + micro-reaction composite thermal transfer modality, thereby optimizing decomposition efficacy while alleviating secondary hydrate risks in 55–70 mD reservoirs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, R.P.; Xia, Y.Q.; Wang, Z.F.; Li, Q.P.; Lv, X.; Leng, S.D.; Zhang, L.X.; Zhang, Y.; Xiao, B.; Yang, S.X.; et al. Long-Term Numerical Simulation of a Joint Production of Gas Hydrate and Underlying Shallow Gas Through Dual Horizontal Wells in the South China Sea. Appl. Energy 2022, 320, 119235. [Google Scholar] [CrossRef]
- Liang, H.; Duan, Y.G.; Pei, J.; Wei, N. Study on Hydrate Phase Equilibrium Diagram of Methane Containing System Based on Thermodynamic Model. Front. Energy Res. 2021, 9, 743296. [Google Scholar] [CrossRef]
- Ye, J.L.; Qin, X.W.; Xie, W.W.; Lu, H.L.; Ma, B.J.; Qiu, H.J.; Liang, J.Q.; Lu, J.A.; Kuang, Z.G.; Lu, C.; et al. The Second Natural Gas Hydrate Production Test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Wang, L.Y.; Dou, M.Y.; Wang, Y.; Xu, Y.L.; Li, Y.; Chen, Y.; Li, L.S. A Review of the Effect of Porous Media on Gas Hydrate Formation. ACS Omega 2022, 7, 33666–33679. [Google Scholar] [CrossRef]
- Xiao, C.W.; Li, X.S.; Li, G.; Yu, Y.S.; Lv, Q.N.; Yu, Y.; Weng, Y.F.; Liu, J.W.; Yu, J.X. Kinetic Studies of the Secondary Hydrate Formation in Porous Media Based on Experiments in a Cubic Hydrate Simulator and a New Kinetic Model. Fuel 2024, 358, 130168. [Google Scholar] [CrossRef]
- Ma, X.L.; Sun, Y.H.; Liu, B.C.; Guo, W.; Jia, R.; Li, B.; Li, S.L. Numerical Study of Depressurization and Hot Water Injection for Gas Hydrate Production in China’s First Offshore Test Site. J. Nat. Gas Sci. Eng. 2020, 83, 103530. [Google Scholar] [CrossRef]
- Wu, N.Y.; Li, Y.L.; Wan, Y.Z.; Sun, J.Y.; Huang, L.; Mao, P.X. Prospect of Marine Natural Gas Hydrate Stimulation Theory and Technology System. Nat. Gas Ind. B 2021, 8, 173–187. [Google Scholar] [CrossRef]
- Wu, H.Z.; Zhang, X.; Yang, Z.H.; Liu, D. Numerical Simulation on Depressurization Extraction of Natural Gas Hydrate Based on a Coupled Thermal-Hydraulic-Chemical Model. Energy Rep. 2022, 8, 269–278. [Google Scholar] [CrossRef]
- Qin, X.W.; Lu, C.; Wang, P.K.; Liang, Q.Y. Hydrate Phase Transition and Seepage Mechanism during Natural Gas Hydrates Production Tests in the South China Sea: A Review and Prospect. China Geol. 2022, 5, 201–217. [Google Scholar] [CrossRef]
- Pan, D.B.; Ma, X.L.; Chen, C.; Zhong, X.P. Numerical Analysis of Hydrate Exploitation Performances of Depressurization Combined with Thermal Fluid Injection in Marine Hydrate Reservoir with Impermeable Boundary. Gas Sci. Eng. 2023, 110, 204894. [Google Scholar] [CrossRef]
- Mao, M.; Yan, K.; Li, X.; Chen, Z.; Wang, Y.; Feng, J.; Chen, C. Review of Heat Transfer Characteristics of Natural Gas Hydrate. Energies 2024, 17, 717. [Google Scholar] [CrossRef]
- Yu, Q.N.; Tang, H.M.; Li, C.L.; Chen, Z.J.; Zhang, K.; Yu, Y.; Liang, S. Numerical Simulation of Natural-Gas-Hydrate Decomposition in Process of Heat-Injection Production. Processes 2023, 11, 2349. [Google Scholar] [CrossRef]
- Han, S.; Deng, X.J.; Li, W.C.; Yu, L.; Guan, L.F. A Study on the Coupling Mechanism of Hydrate Dissociation-Seepage-Heat Transfer Induced by Suction Anchor Installation in Marine Sediments. Ocean Eng. 2023, 288, 116083. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.H.; Xin, G.; Yao, W.; Gao, D.Z.; Chen, L.T.; Sun, B.J. Theoretical Analysis and Numerical Simulation of Multi-Fields Coupled Variation During Deepwater Hydrate-Bearing Reservoir Exploitation. Int. Conf. Comput. Exp. Eng. Sci. 2019, 21, 88–89. [Google Scholar] [CrossRef]
- Shen, S.; Li, Y.H.; Sun, X.; Wang, L.; Song, Y.C. Stress Behavior of Hydrate-bearing Sands with Changing Temperature and Hydrate Saturation. J. Nat. Gas Sci. Eng. 2022, 98, 104389. [Google Scholar] [CrossRef]
- Chen, B.B.; Sun, H.R.; Zheng, J.J.; Yang, M.J. New Insights on Water-Gas Flow and Hydrate Decomposition Behaviors in Natural Gas Hydrates Deposits with Various Saturations. Appl. Energy 2020, 259, 114185. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zhang, X.H.; Lu, X.B.; Nie, X.Y. Laboratory Study on Physical and Mechanical Properties of Hydrate Sediment Samples. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Republic of Korea, 15–20 June 2014; p. ISOPE-I-14-098. [Google Scholar]
- Li, Q.C.; Cheng, Y.F.; Zhang, H.W.; Yan, C.L.; Liu, Y.W. Simulating the Effect of Hydrate Dissociation on Wellhead Stability during Oil and Gas Development in Deepwater. J. Ocean Univ. China 2018, 17, 35–45. [Google Scholar] [CrossRef]
- Wu, S.T.; Zhou, X.B.; Lu, J.S.; Liang, D.Q.; Li, D.L. Experimental Study on CH4 Hydrate Dissociation by the Injection of Hot Water, Brine, and Ionic Liquids. J. Mar. Sci. Eng. 2023, 11, 713. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, X.H.; Zhao, C.; Zhang, J.; Bondarenko, V.; Dreus, A.; Liang, J.Q.; Li, X.Y.; Zhu, J.L.; Wang, P.F.; et al. Decomposition Characteristics of Methane Hydrate in Porous Media under Continuous and Intermittent Microwave Heating. Fuel 2023, 332, 126230. [Google Scholar] [CrossRef]
- Hou, J.X.; Zhao, E.M.; Ji, Y.K. Numerical Simulation of Gas Production from Class III Hydrate Reservoirs Using Low-Frequency Electric Heating-Assisted Depressurization with Horizontal Wells. Fuel 2024, 357, 129906. [Google Scholar] [CrossRef]
- Wei, N.; Pei, J.; Li, H.T.; Sun, W.T.; Xue, J. Application of In-Situ Heat Generation Plugging Removal Agents in Removing Gas Hydrate: A Numerical Study. Fuel 2022, 323, 124397. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, Z.B.; Li, S.D.; Li, X.; Lu, C. Numerical Evaluation of Gas Hydrate Production Performance of the Depressurization and Backfilling with an In Situ Supplemental Heat Method. ACS Omega 2021, 6, 12274–12286. [Google Scholar] [CrossRef]
- Ping, X.L.; Han, G.Q.; Zhang, J.Q.; Chang, J.H.; Cen, X.Q.; Tang, H. Study on the Flow Behavior of Wellbore Fluids of a Natural Gas Hydrate Well with the Combined Depressurization and Heat Injection Method. Processes 2023, 11, 1625. [Google Scholar] [CrossRef]
- Ahmadpanah, S.J.; Manteghian, M.; Ganji, H. Effect of Cyclopentane and Sodium Chloride on the Formation Kinetics of Natural Gas Hydrate in Different Operating Conditions. J. Nat. Gas Sci. Eng. 2022, 99, 104417. [Google Scholar] [CrossRef]
- Wang, J.T.; Shao, Z.H.; Bai, Y.J.; He, G.L.; Wang, X.D.; Liu, L.; Liao, B.; Sun, X.H.; Lv, K.H.; Sun, J.S. Fabrication and Property Evaluation of Calcium-Oxide-Loaded Microcapsules during Supplemental Heat-Based Exploitation of Natural Gas Hydrates. RSC Adv. 2023, 13, 7212–7221. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, Y.Y.; Luo, Y.J.; Liang, Y.P.; Li, B. Analysis of Hydrate Exploitation by a New In-Situ Heat Generation Method with Chemical Reagents Based on Heat Utilization. J. Clean. Prod. 2020, 249, 119399. [Google Scholar] [CrossRef]
- Chibura, P.E.; Zhang, W.; Luo, A.J.; Wang, J.J. A Review on Gas Hydrate Production Feasibility for Permafrost and Marine Hydrates. J. Nat. Gas Sci. Eng. 2022, 100, 104441. [Google Scholar] [CrossRef]
- Wu, T.W.; Wan, K.; Li, X.S.; Wang, Y.; Chen, Z.Y. Heat Utilization Efficiency Analysis of Gas Production from Hydrate Reservoir by Depressurization in Conjunction with Heat Stimulation. Energy 2023, 263, 125625. [Google Scholar] [CrossRef]
- Ren, L.L.; Jiang, M.; Wang, L.B.; Zhu, Y.J.; Li, Z.; Sun, C.Y.; Chen, G.J. Gas Hydrate Exploitation and Carbon Dioxide Sequestration under Maintaining the Stiffness of Hydrate-Bearing Sediments. Energy 2020, 194, 116869. [Google Scholar] [CrossRef]
- Xiao, C.W.; Li, X.S.; Li, G.; Yu, Y.; Weng, Y.F.; Lv, Q.N.; Yu, J.X. Key Factors Controlling the Kinetics of Secondary Hydrate Formation in the Porous Media. Gas Sci. Eng. 2023, 110, 204911. [Google Scholar] [CrossRef]
- Liao, T.; Yuan, L.; Li, W.; Kan, J.Y.; Luo, W.; Xiong, X.Q.; Li, N. One-Dimensional Numerical Simulation on Removal of CO2 Hydrate Blockage around Wellbore by N2 Injection. Processess 2024, 12, 204. [Google Scholar] [CrossRef]
- Wang, Y.N.; Sun, Z.X.; Li, Q.P.; Lv, X.; Ge, Y. A Thermal Chemical Reaction System for Natural Gas Hydrates Exploitation. Front. Energy Res. 2022, 9, 804498. [Google Scholar] [CrossRef]
- Li, Q.P.; Lv, X.; Pang, W.X.; Yao, H.Y.; Ge, Y.; Wang, J.A. Numerical Simulation of the Effect of Porous Media Permeability on the Decomposition Characteristics of Natural Gas Hydrate at the Core Scale. Energy Fuels 2021, 35, 5843–5852. [Google Scholar] [CrossRef]
- Vikram, V.; David, L.; Samardeep, S.; Sharma, A.; Ranjith, P.G. Sensitivity Analysis of Methane Hydrate Bearing Class 3 Reservoirs during Thermal Injection. J. Pet. Sci. Eng. 2020, 195, 107575. [Google Scholar] [CrossRef]
- Liang, Y.P.; Liu, S.; Zhao, W.T.; Li, B.; Wan, Q.C.; Li, G. Effects of Vertical Center Well and Side Well on Hydrate Exploitation by Depressurization and Combination Method with Wellbore Heating. J. Nat. Gas Sci. Eng. 2018, 55, 154–164. [Google Scholar] [CrossRef]
- Li, J.F.; Ye, J.L.; Qin, X.W.; Qiu, H.J.; Wu, N.Y.; Lu, H.L.; Xie, W.W.; Lu, J.A.; Peng, F.; Xu, Z.Q.; et al. The First Offshore Natural Gas Hydrate Production Test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Falser, S.; Uchida, S.; Palmer, A.C.; Soga, K.; Tan, T.S. Increased Gas Production from Hydrates by Combining Depressurization with Heating of the Wellbore. Energy Fuels 2012, 26, 6259–6267. [Google Scholar] [CrossRef]
- Sun, X.; Luo, H.; Soga, K. A Coupled Thermal-Hydraulic-Mechanical-Chemical (THMC) Model for Methane Hydrate Bearing Sediments Using Comsol Multiphysics. J. Zhejiang Univ.-Sci. A 2018, 8, 600–623. [Google Scholar] [CrossRef]
- Comsol Search. All Research Results About Products, COMSOL Blog, and Application Gallery, etc. Available online: https://www.comsol.com/search/ (accessed on 12 May 2022).
- Datta, A.K. Porous Media Approaches to Studying Simultaneous Heat and Mass Transfer in Food Processes. I: Problem Formulations. J. Food Eng. 2007, 80, 80–95. [Google Scholar] [CrossRef]
- Zhao, Z.W. Thermodynamic Analysis for the Gas Production from Gas Hydrate by Heating. China Min. Mag. 2013, 8, 125–128. (In Chinese) [Google Scholar]
- Kou, X.; Feng, J.C.; Li, X.S.; Wang, Y.; Chen, Z.Y. Visualization of Interactions between Depressurization-Induced Hydrate Decomposition and Heat/Mass Transfer. Energy 2022, 239, 122230. [Google Scholar] [CrossRef]
- Kou, X.; Wang, Y.; Li, X.S.; Zhang, Y.; Chen, Z.Y. Influence of Heat Conduction and Heat Convection on Hydrate Dissociation by Depressurization in a Pilot-Scale Hydrate Simulator. Appl. Energy 2019, 251, 113405. [Google Scholar] [CrossRef]
- Li, G.; Moridis, G.J.; Zhang, K.N.; Li, X.S. The Use of Huff and Puff Method in a Single Horizontal Well in Gas Production from Marine Gas Hydrate Deposits in the Shenhu Area of South China Sea. J. Pet. Sci. Eng. 2011, 77, 49–68. [Google Scholar] [CrossRef]
- Malagar, B.R.; Lijith, K.P.; Singh, D.N. Formation & Dissociation of Methane Gas Hydrates in Sediments: A Critical Review. J. Nat. Gas Sci. Eng. 2019, 65, 168–184. [Google Scholar] [CrossRef]
- Wei, W.N.; Li, B.; Li, G.; Zhang, T.T.; Wan, Q.C.; Zhou, J.H. Investigating Optimal Thermal-Assisted Depressurization Regimes for Enhanced Methane Hydrate Dissolution in a Multiple Well System. Energy Fuels 2023, 37, 15795–15807. [Google Scholar] [CrossRef]
- Zhang, Y.Y. Experimental Study on Gas Production from Hydrate Reservoir Using Self-Heating System Injection Method. Master’s Thesis, Chongqing University, Chongqing, China, 2019. (In Chinese). [Google Scholar]
- Wang, Z.Q.; Liu, S.Y.; Li, H.Y.; Li, S.X.; Xu, J.C.; Wang, X.P. A Numerical Simulation Study of Methane Hydrate Reformation During the Dissociation Process Induced by Depressurization. Fuel 2022, 313, 122983. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, Z.Y.; Chen, L.Q.; Li, H.; Zhang, J.B.; Yang, H.M. Effects of Hydrate Saturation and Sand-Filling Content on Hydrate Exploitation Using In-Situ Heat Supply with Chemical Reagents. Lect. Notes Civ. Eng. 2024, 472, 568–589. [Google Scholar] [CrossRef]
- Yu, T.; Chen, B.B.; Jiang, L.L.; Zhang, L.X.; Yang, L.; Yang, M.J.; Song, Y.C.; Abudula, A. Feasibility Evaluation of a New Approach of Seawater Flooding for Offshore Natural Gas Hydrate Exploitation. Energy Fuels 2023, 37, 4349–4364. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Q.; Zhang, Q.; Wang, Y.F.; Wang, Y.F.; Wang, Y.F. Numerical Simulations of Combined Brine Flooding With Electrical Heating–Assisted Depressurization for Exploitation of Natural Gas Hydrate in the Shenhu Area of the South China Sea. Front. Earth Sci. 2022, 10, 843521. [Google Scholar] [CrossRef]
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Mok, J.H.; Choi, W.J.; Seo, Y.W. The Dual-Functional Roles of N2 Gas for the Exploitation of Natural Gas Hydrates: An Inhibitor for Dissociation and an External Guest for Replacement. Energy 2021, 232, 121054. [Google Scholar] [CrossRef]
- Wei, N.; Zheng, H.R.; Guo, B.Y.; Hu, H.Y.; Li, C. Acceleration Mechanism of Methane Hydrate Dissociation in Inorganic Salt Solutions: Experimental and Molecular Dynamics Study. Geoenergy Sci. Eng. 2025, 252, 213913. [Google Scholar] [CrossRef]
- Xing, Q.Z.; Wan, L.; Zhang, J.Y.; Zhang, S.F.; Cui, X.Y. Experimental Study of Methane Hydrate Decomposition Kinetics in NaCl, KCl, and PVP Solutions. ACS Omega 2025, 10, 22647–22656. [Google Scholar] [CrossRef]
- Zeng, H.P.; Zhang, Y.; Zhang, L.; Chen, Z.Y.; Li, X.S. Effects of the NaCl Concentration and Montmorillonite Content on Formation Kinetics of Methane Hydrate. J. Mar. Sci. Eng. 2022, 10, 548. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Moridis, G.; Linga, P. On the Importance of Phase Saturation Heterogeneity in the Analysis of Laboratory Studies of Hydrate Dissociation. Appl. Energy 2019, 255, 113861. [Google Scholar] [CrossRef]
- Li, R.R.; Han, Z.H.; Zhang, L.Q.; Zhou, J.; Wang, S. Effect of Hydrate Saturation on Permeability Anisotropy for Hydrate-Bearing Turbidite Sediments Based on Pore-Scale Seepage Simulation. J. Mar. Sci. Eng. 2024, 12, 1079. [Google Scholar] [CrossRef]
- Chen, H.; Du, H.; Shi, B.; Shan, W.C.; Hou, J.Q. Mechanical Properties and Strength Criterion of Clayey Sand Reservoirs During Natural Gas Hydrate Extraction. Energy 2021, 242, 122526. [Google Scholar] [CrossRef]
- Wang, Y.H.; Wu, P.; Huang, L.; Song, Y.C.; Li, Y.H. Stress-Induced Permeability Evolution Mechanism of Hydrate-Bearing Sediments from Pore-Scale Perspective. Energy 2025, 319, 134977. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, H.N.; Jiang, M.J. A Mechanistic Model for Porosity and Permeability in Deformable Hydrate-Bearing Sediments with Various Hydrate Growth Patterns. Acta Geotech. 2023, 19, 1–26. [Google Scholar] [CrossRef]
- Shang, Y.H.; Lei, G.; Tang, J.D.; Qu, J.T.; Ning, F.L. Permeability of Marine Gas Hydrate-Bearing Sediments Considering Effective Stress and Particle Size Distribution: A Theoretical Model. SSRN J. 2024. preprint. [Google Scholar] [CrossRef]
- Lei, G.; Qu, J.T.; Zhao, Y.J.; Wu, Q.; Liu, T.L. Permeability Behavior of Hydrate-Bearing Clayey-Silty Sediments During Creeping. J. Rock Mech. Geotech. Eng. 2024, 17, 2492–2510. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Shen, K.X.; Wang, Y.S.; Wu, J.; Liu, P.L.; Du, J.; Huang, Q.S.; Chen, C. Consolidation-Acidizing Experiments on Methane Natural Gas Sediment Skeleton. Front. Energy Res. 2024, 12, 1332495. [Google Scholar] [CrossRef]








| Parameters | Physical Meaning | Values |
|---|---|---|
| d [m] | Reservoir length (Figure 1, AB and CD) | 2.00 |
| b [m] | Reservoir width (Figure 1, AC and BD) | 1.00 |
| kpor [mD] | Reservoir initial absolute permeability | 1.50 |
| Reservoir porosity | 0.33 | |
| Sghi | Initial hydrate saturation | 0.40 |
| Swi | Initial water saturation | 0.55 |
| Sgi | Initial gas saturation | 0.05 |
| Mgh [g/mol] | Hydrate molar mass | 119.50 |
| Mm [g/mol] | Methane molar mass | 16 |
| Mw [g/mol] | Water molar mass | 18 |
| Parameters | Physical Meaning | Related Equation | Values |
|---|---|---|---|
| ρc [kg/m3] | Chemical reagent fluid density | Momentum conservation equation | 1.0 × 103 |
| VC [m/s] | Chemical reagent fluid velocity | 0.19 | |
| μc [Pa·s] | Chemical reagent fluid dynamic viscosity | 1.0 × 10−3 | |
| g [m/s2] | Force per unit volume of fluid | 9.80 | |
| ρG [kg/m3] | Hydrate density | Heat transfer equation | 0.91 |
| CG [J/(kg·K)] | Hydrate heat capacity | 1600 | |
| kG [W/(m·K)] | Hydrate thermal conductivity | 0.62 | |
| uG [m/s] | Hydrate velocity | 0 | |
| qG [W/m2] | Heat flux by conduction | −kG∇T | |
| QG [W/m3] | External heat source for hydrate | 0 | |
| Di [m2/s] | The diffusion coefficient of injected fluid molecules in porous media | Mass conservation equation | 1 × 10−9 |
| Parameters | Physical Meaning | Related Equation | Values |
|---|---|---|---|
| Cw [J/(kg·K)] | Water heat capacity | Heat transfer equation | 1600 |
| kw [W/(m·K)] | Water thermal conductivity | 0.62 | |
| Lpc [J/kg] | Latent heat for phase change | 43,500 | |
| Qh [W/m3] | External heat source | 0 | |
| ρw [kg/m3] | Water dynamic density | Darcy’s law equation | 1 × 103 |
| uw [m/s] | Water velocity | 1.96 × 10−8 | |
| μw [Pa·s] | Water dynamic viscosity | 1.0 × 10−3 | |
| Qm [W/m3] | Water mass increase due to hydrate phase change | Based on simulation process |
| Stage | Parameters | Physical Meaning | Values |
|---|---|---|---|
| Stage 1 | VC [m/s] | AB and CD boundary velocity of chemical reagent fluid | 0 |
| T1_ave [K] | Formation ambient temperature | 286.2 | |
| c_initial [mol/m3] | Initial chemical reagent fluid concentration in the reservoir | 0 | |
| c_inlet [mol/m3] | Initial chemical reagent fluid concentration at AC inlet boundary | 2000 | |
| Stage 2 | P_inlet [MPa] | Injected pressure for chemical reagent fluid | 20 |
| P_outlet [MPa] | Outlet pressure for chemical reagent fluid | 5 | |
| T2_ave [K] | Average formation temperature at the beginning of Stage 2 (by the end of Stage 1) | 303.8 (base case) | |
| T2_gh [K] | Hydrate temperature before phase change | 278.7 |
| Stages | Test Number | Grid Element Number | Maximum Grid Size | Minimum Grid Size | Maximum Element Growth Rate | Curvature Factor | Simulated Saturation |
|---|---|---|---|---|---|---|---|
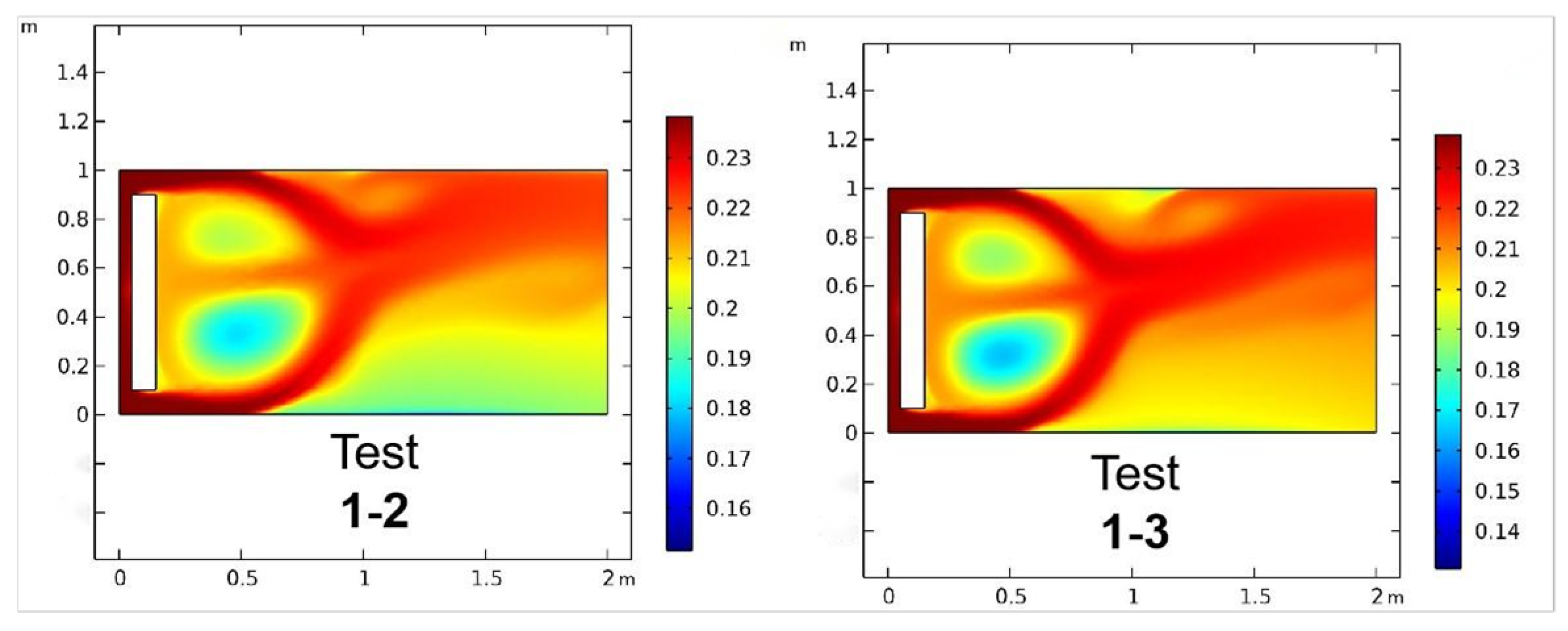
| Stage 1 | Test 1-1 | 3195 | 0.067 m | 0.003 m | 1.20 | 0.40 | 0.2111 |
| Test 1-2 | 3597 | 0.055 m | 0.002 m | 1.20 | 0.40 | 0.2133 | |
| Test 1-3 | 5420 | 0.045 m | 0.002 m | 1.15 | 0.30 | 0.2106 | |
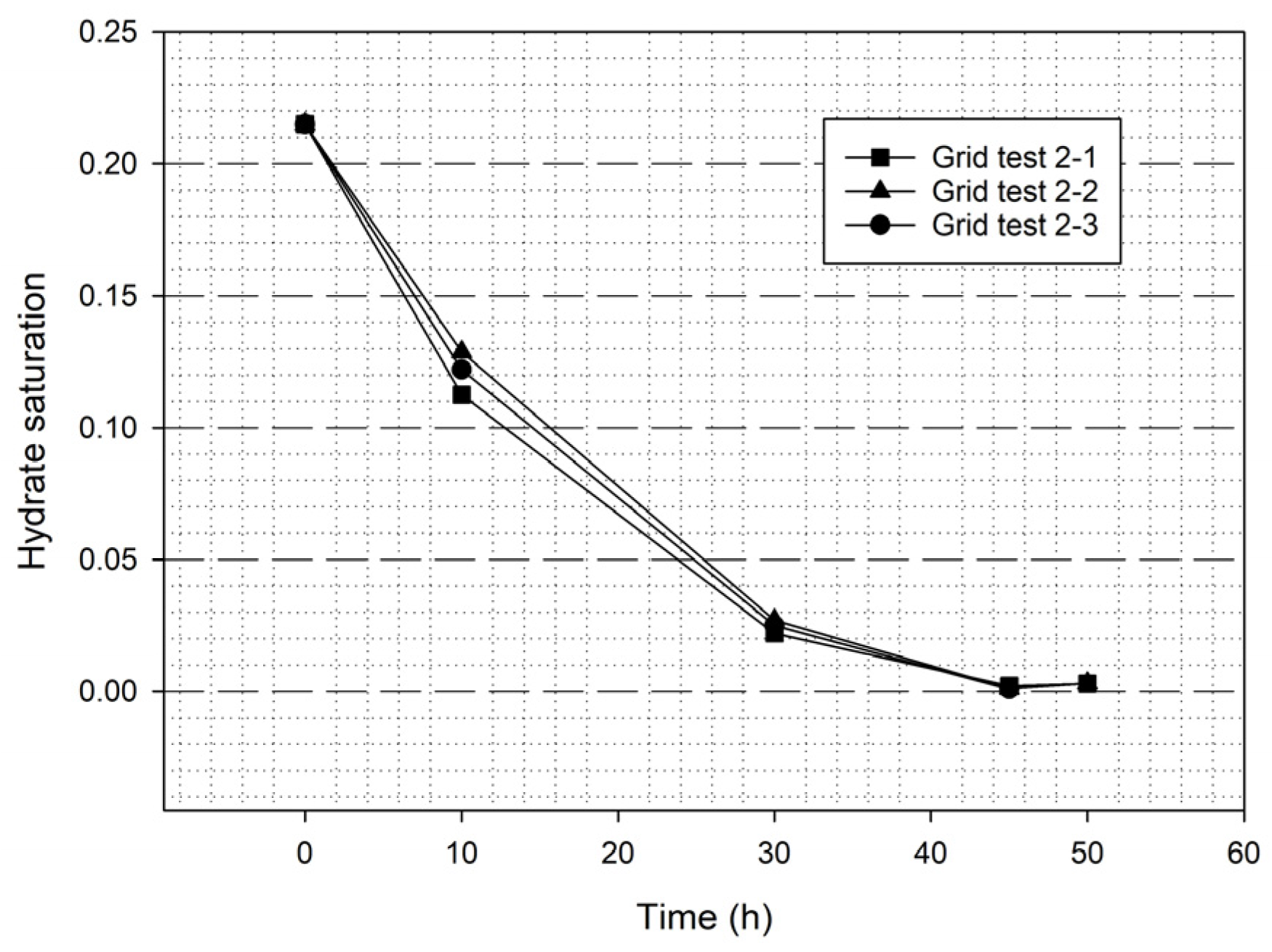
| Stage 2 | Test 2-1 | 3210 | 0.040 m | 1.5 × 10−4 | 1.20 | 0.25 | Please see Section 3.5 |
| Test 2-2 | 5774 | 0.030 m | 1.5 × 10−4 | 1.10 | 0.20 | ||
| Test 2-3 | 7998 | 0.025 m | 4.0 × 10−5 | 1.10 | 0.20 |
| Physical Parameters | Unit | 5.0% + 7.0% | 5.5% + 7.0% | 6.0% + 7.0% | 6.5% + 7.0% | 7.0% + 7.0% |
|---|---|---|---|---|---|---|
| Heat release | KJ | 241.0 | 265.1 | 289.2 | 313.3 | 337.40 |
| Decomposable CH4 hydrate molar number | mol | 4.38 | 4.82 | 5.26 | 5.70 | 6.13 |
| Generated N2 | mol | 0.73 | 0.80 | 0.87 | 0.94 | 1.01 |
| Generated NaCl | mol/L | 0.74 | 0.82 | 0.89 | 0.97 | 1.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Shen, K.; Yu, Y.; Wang, Y.; Zhou, J.; Zeng, J. The Numerical Evaluation of Hydrate Saturation in Marine Sediment During the Injection Process of Self-Heat Generating Fluid. J. Mar. Sci. Eng. 2025, 13, 1772. https://doi.org/10.3390/jmse13091772
Zhang K, Shen K, Yu Y, Wang Y, Zhou J, Zeng J. The Numerical Evaluation of Hydrate Saturation in Marine Sediment During the Injection Process of Self-Heat Generating Fluid. Journal of Marine Science and Engineering. 2025; 13(9):1772. https://doi.org/10.3390/jmse13091772
Chicago/Turabian StyleZhang, Kewei, Kaixiang Shen, Yanjiang Yu, Yingsheng Wang, Jiawei Zhou, and Jing Zeng. 2025. "The Numerical Evaluation of Hydrate Saturation in Marine Sediment During the Injection Process of Self-Heat Generating Fluid" Journal of Marine Science and Engineering 13, no. 9: 1772. https://doi.org/10.3390/jmse13091772
APA StyleZhang, K., Shen, K., Yu, Y., Wang, Y., Zhou, J., & Zeng, J. (2025). The Numerical Evaluation of Hydrate Saturation in Marine Sediment During the Injection Process of Self-Heat Generating Fluid. Journal of Marine Science and Engineering, 13(9), 1772. https://doi.org/10.3390/jmse13091772






