Structural Response and Volume Change Characteristics of Tuna Cages Equipped with External Egg Collection Nets
Abstract
1. Introduction
2. Materials and Methods
2.1. Fish Cage System Modeling
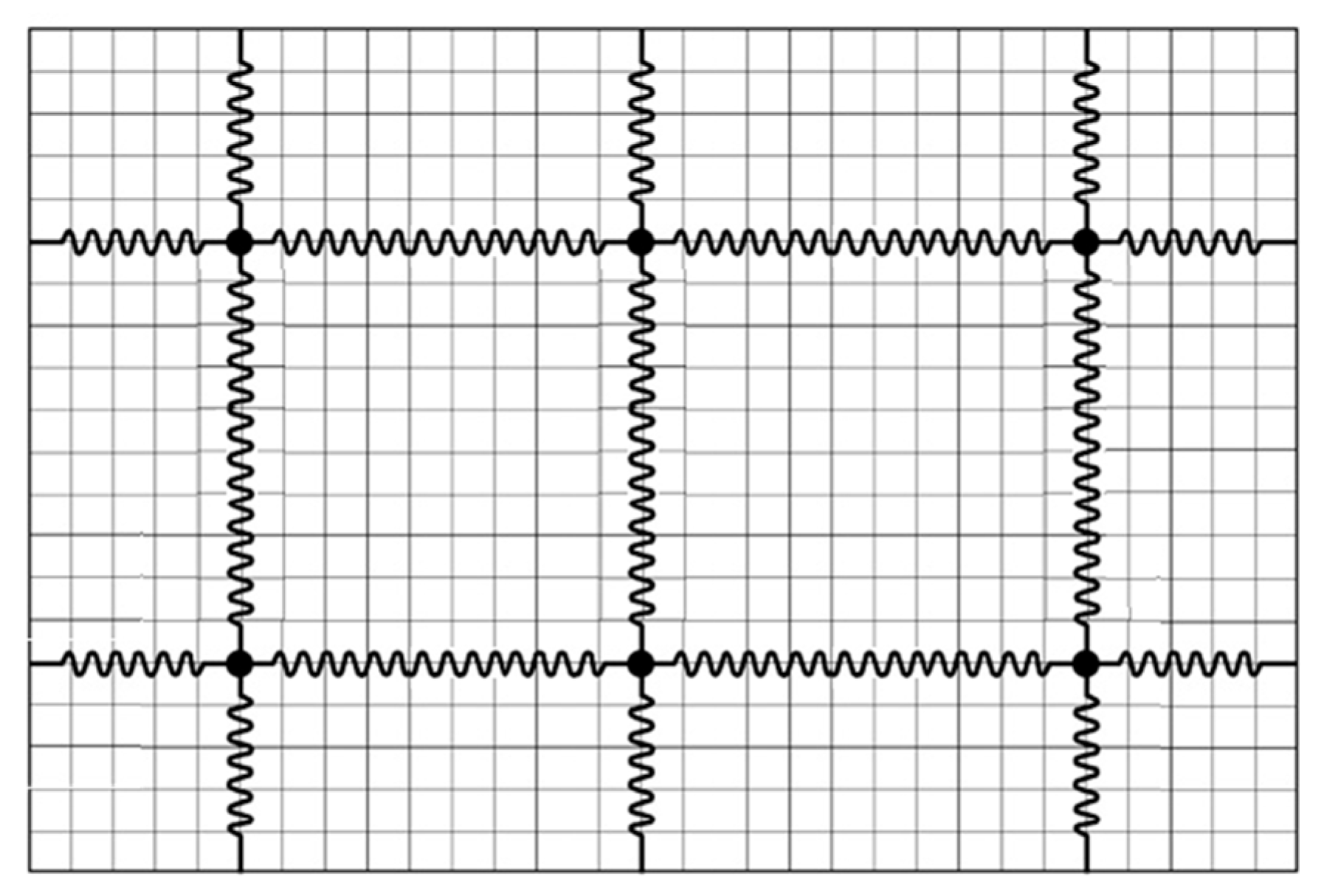
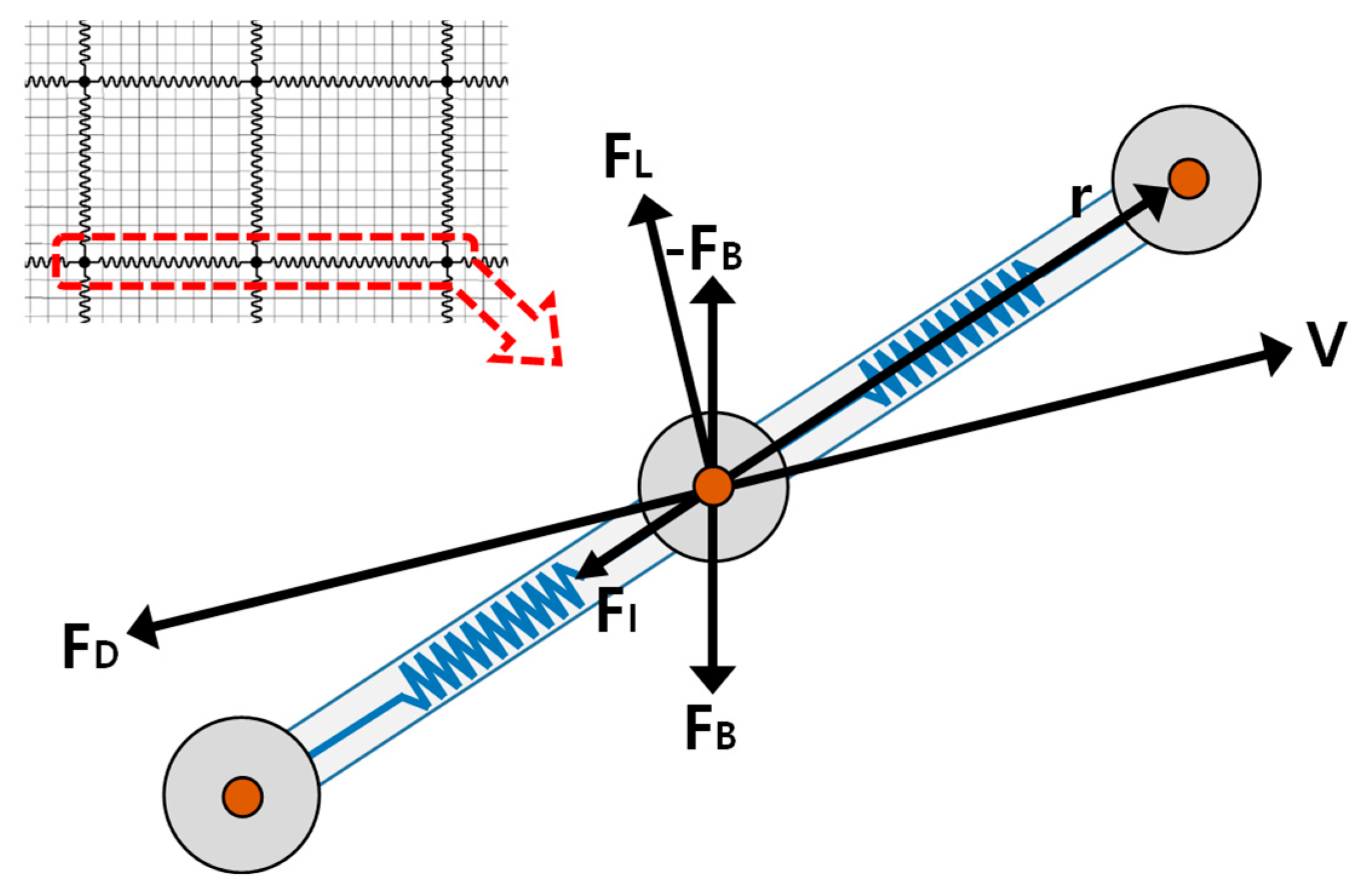
2.2. Modeling Method for Net-to-Net Interaction
2.3. Estimation of Volume Reduction in the Cage Net
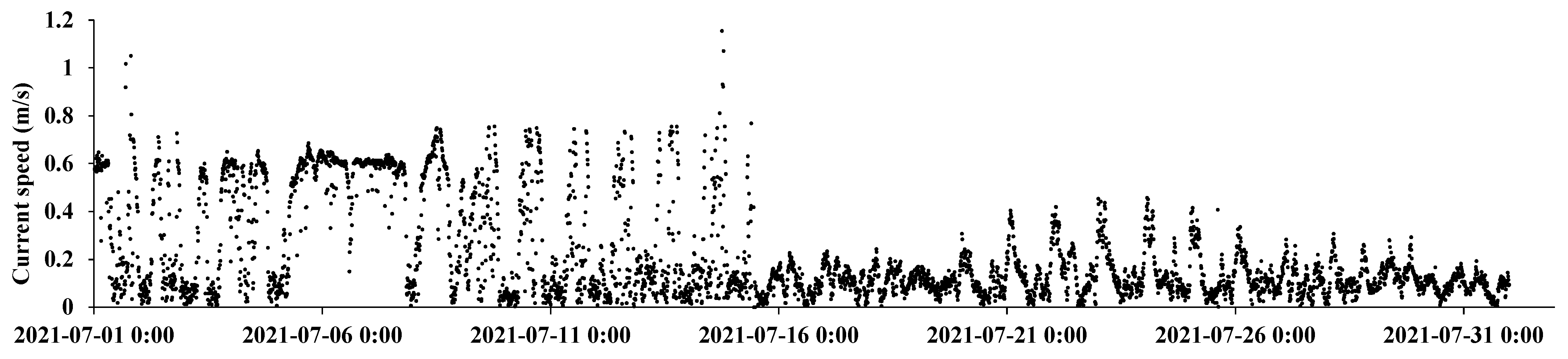
2.4. Simulation Conditions
3. Results and Discussion
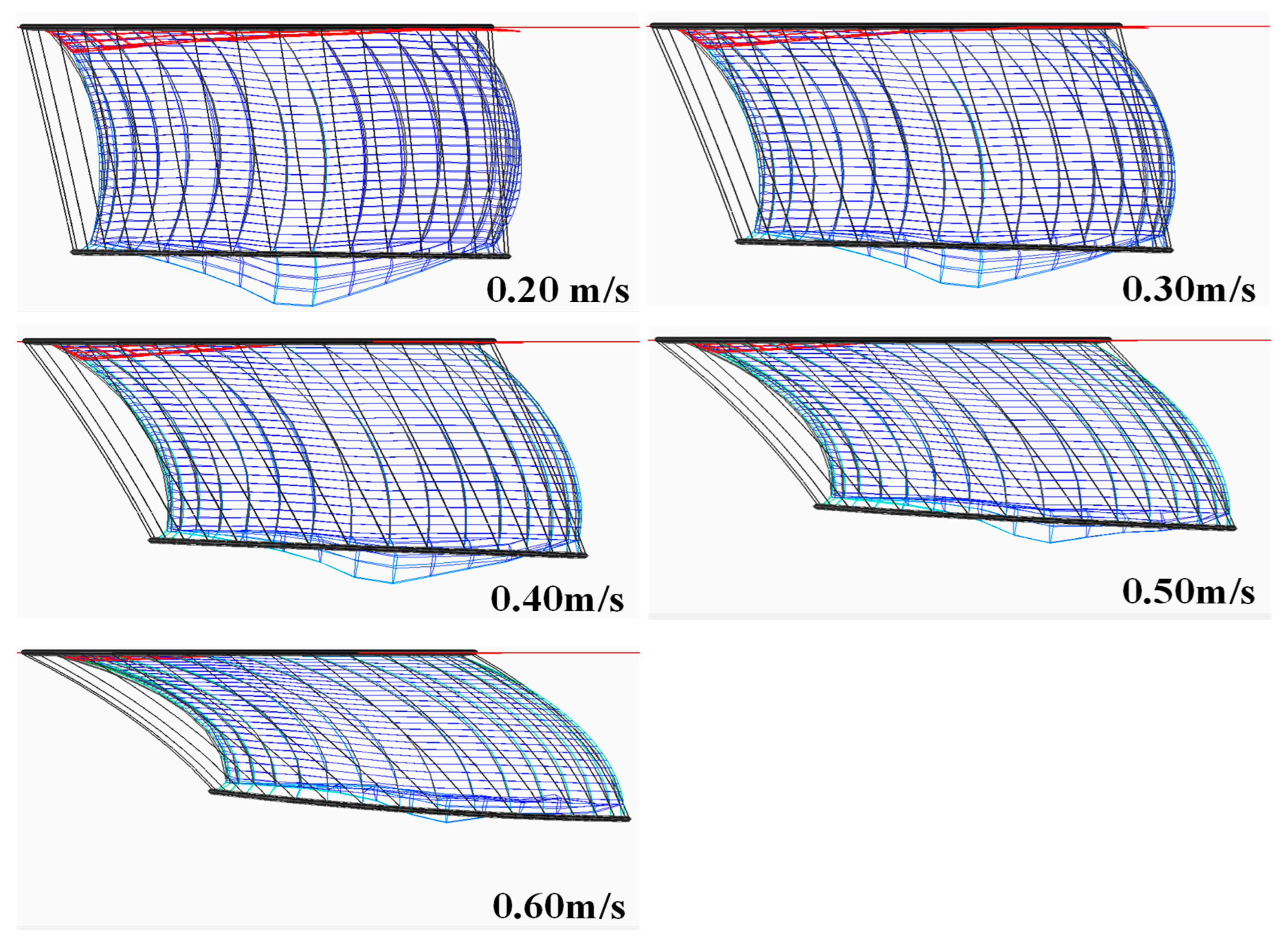
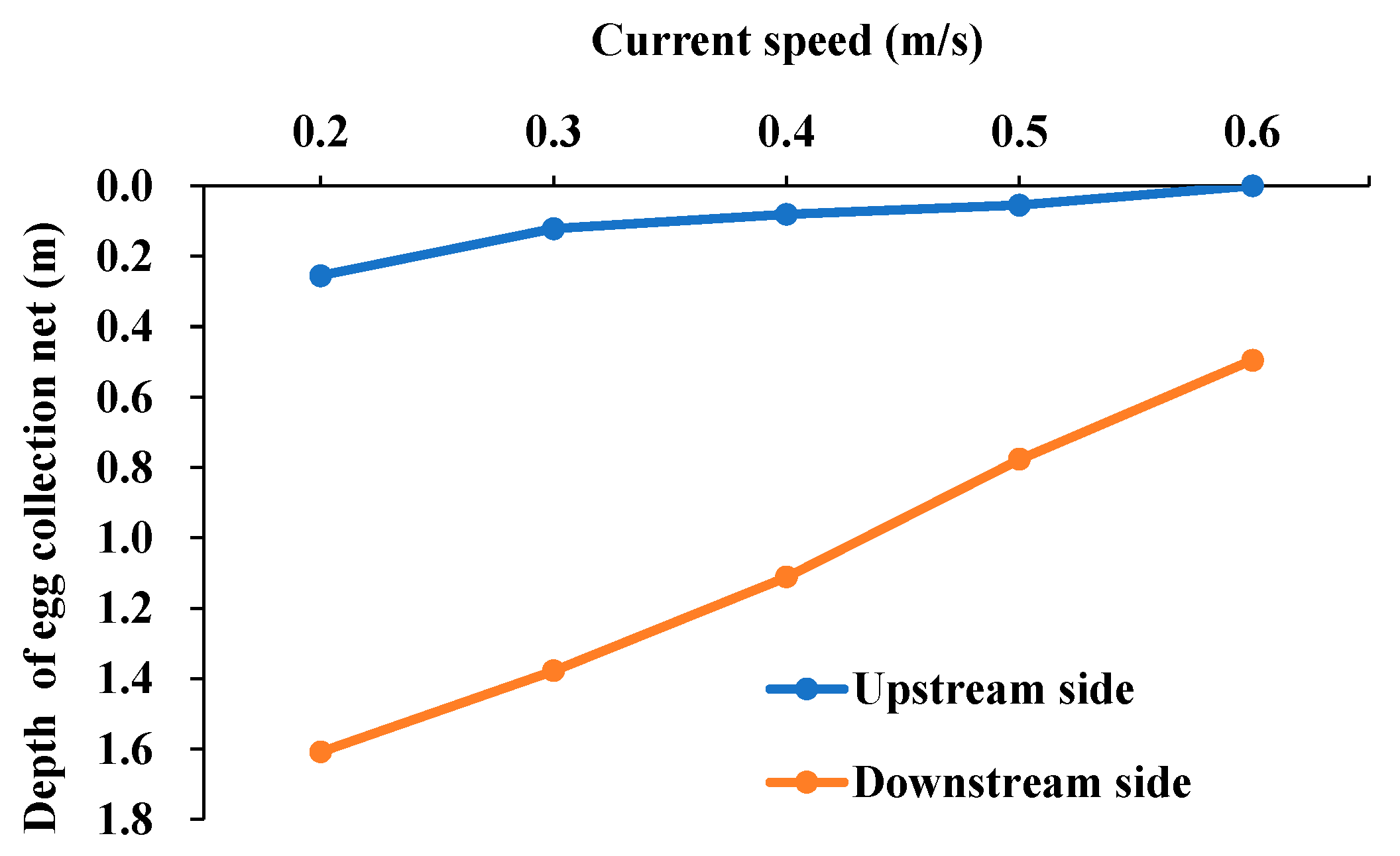
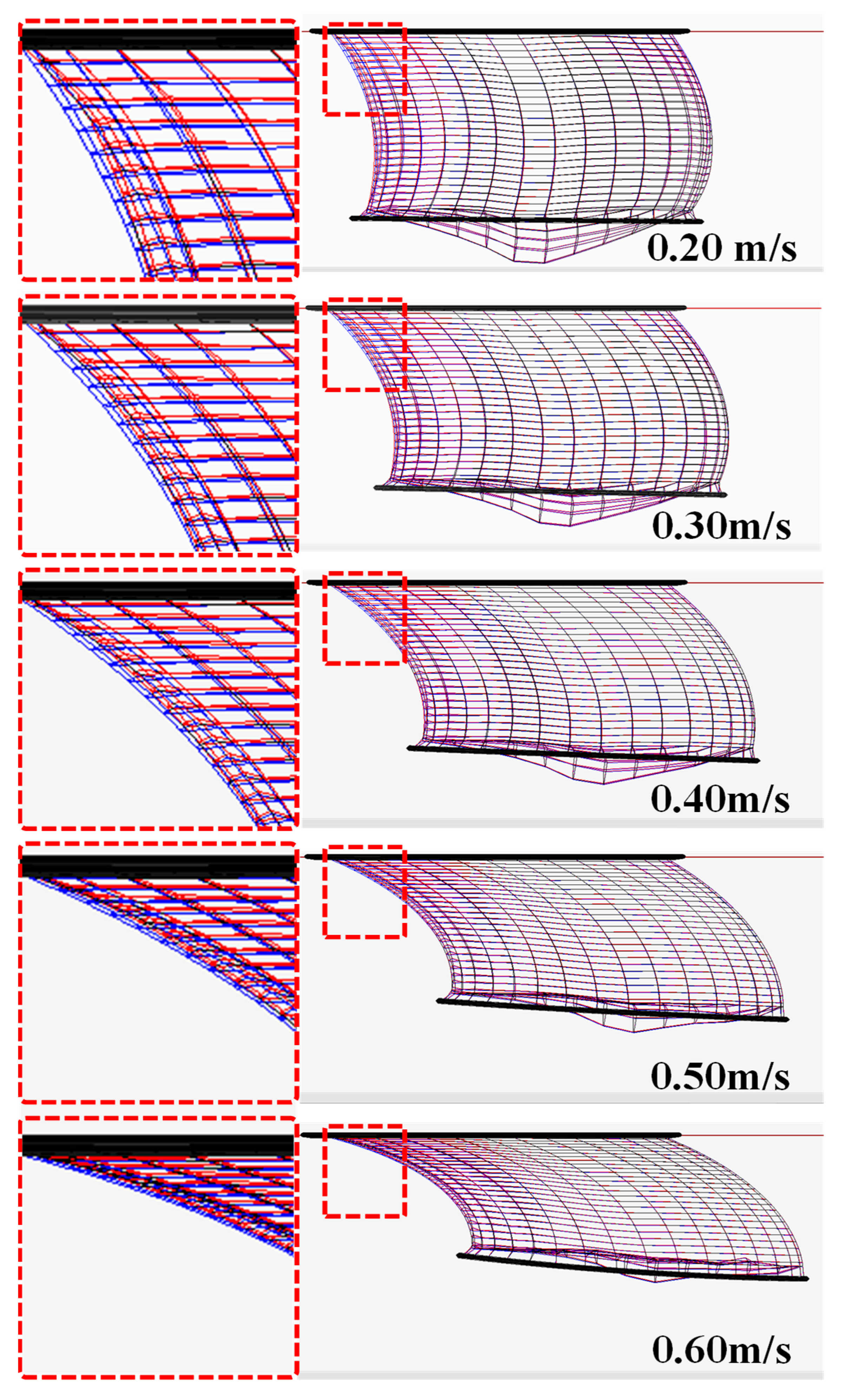
3.1. Behavior of the Net Cage and Egg Collection Net Under Various Current Speeds
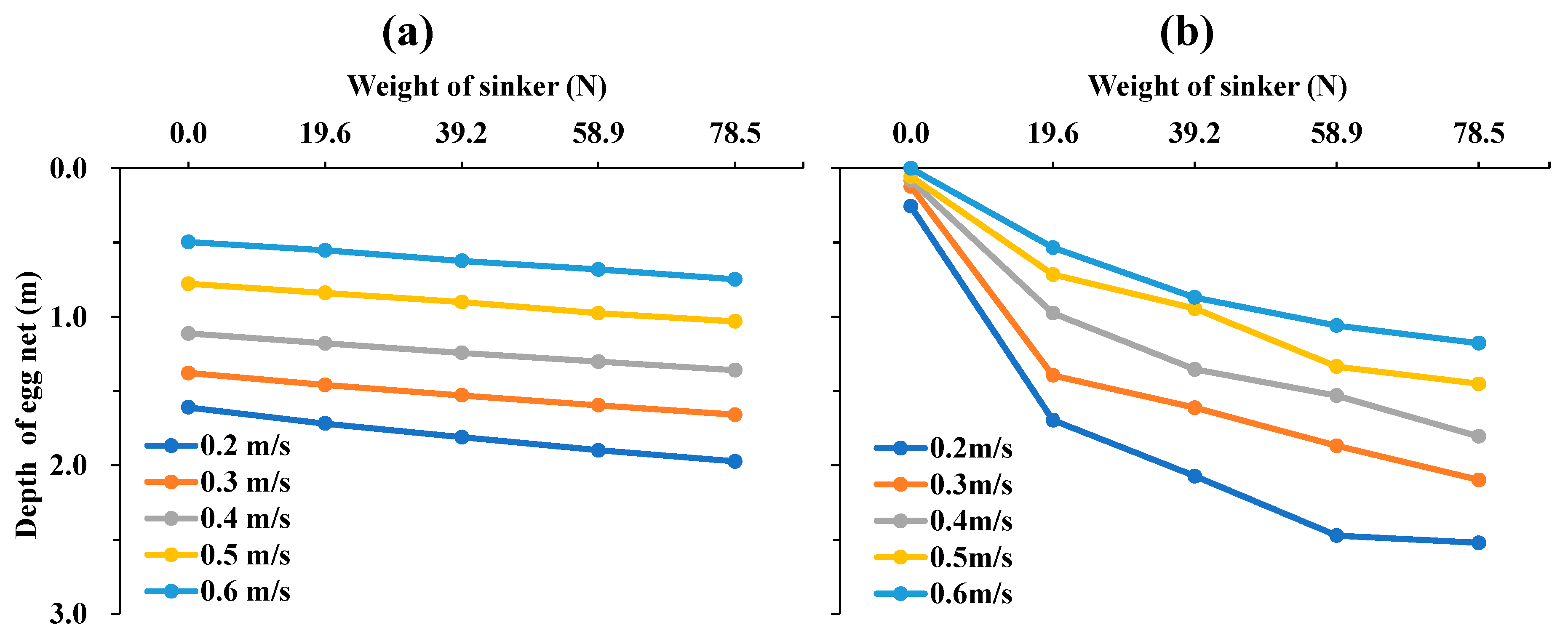
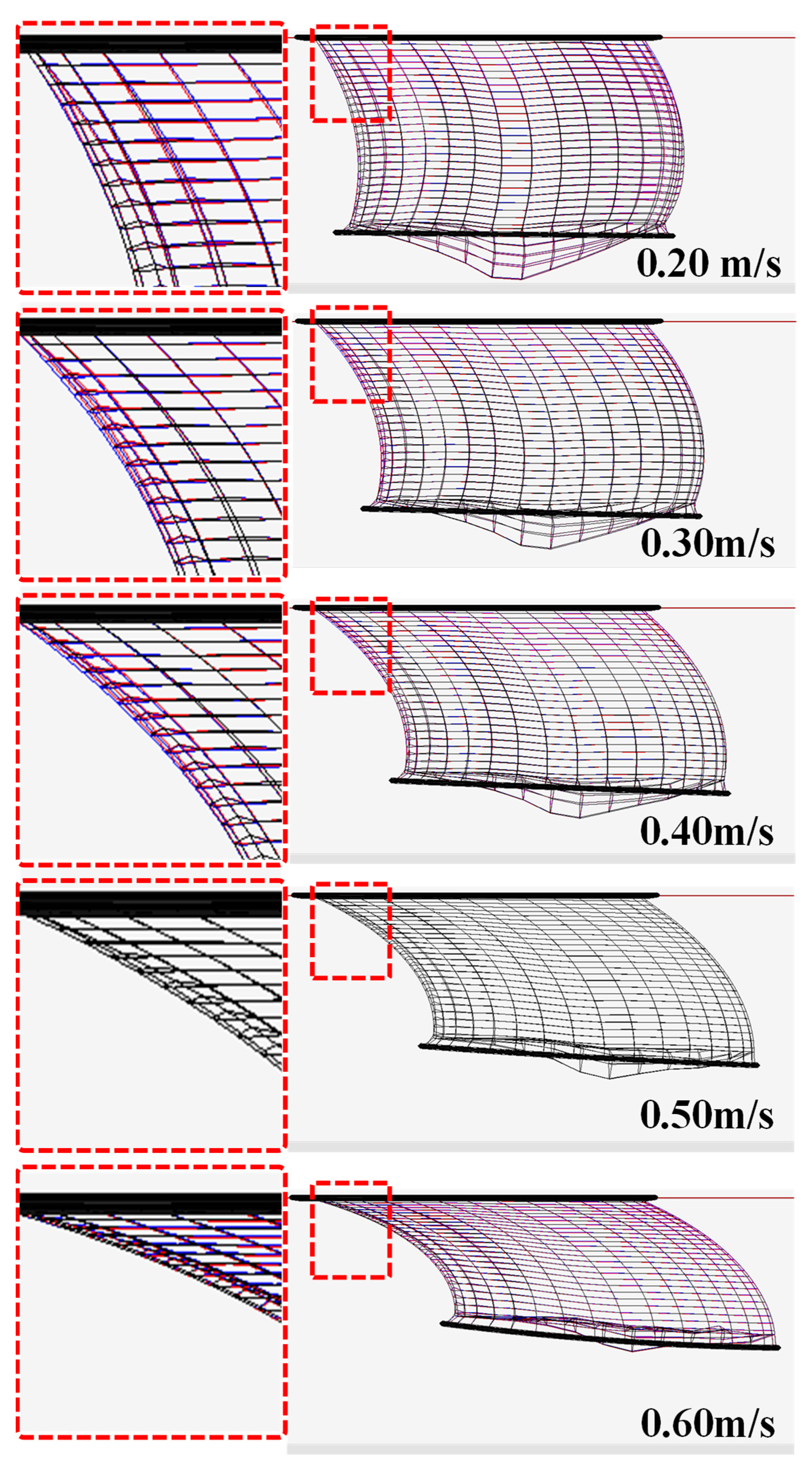
3.2. Behavior of the Egg Collection Net Based on Sinker Weight
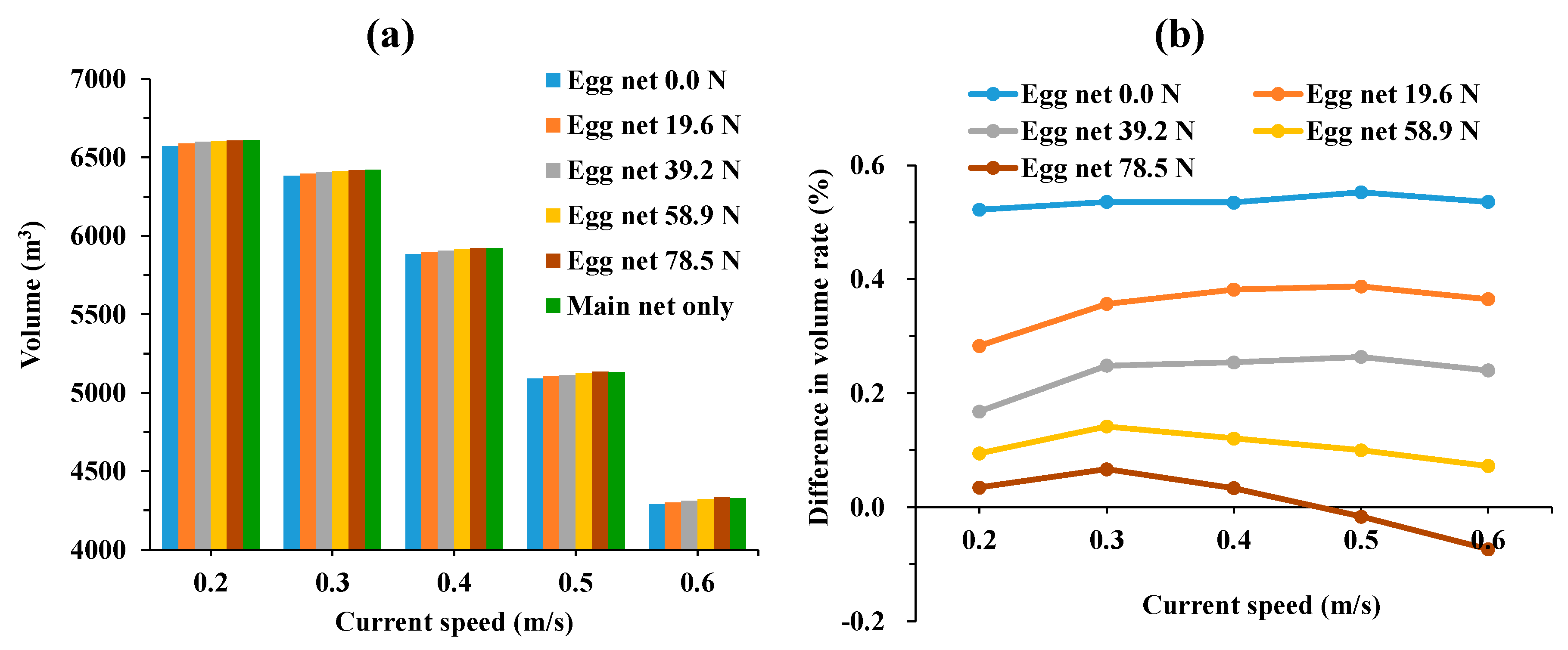
3.3. Impact of Egg Collection Net Installation on Cage Net Volume
4. Conclusions
- Egg collection net behavior: The upstream egg collection net was displaced downstream, overlapping with the cage net, and the extent of deflection increased with current speed. The downstream egg collection net experienced pronounced uplift, with its lower edge approaching the water surface under low-flow conditions.
- Effect of sinker weight: Additional sinker weight had negligible influence on the geometry of the cage net but effectively reduced uplift in the downstream egg collection net. The upstream egg collection net showed minimal sensitivity to weight.
- Depth variation: The depth of the upstream egg collection net’s lower edge increased linearly with sinker weight and decreased linearly with current speed, while the downstream net exhibited logarithmic depth growth with weight and linear reduction with current. The optimal sinker weight to minimize egg collection net deflection was 78.5 N/m.
- Cage volume impact: Cage volume reductions due to egg collection nets were minimal (0.01–0.54%) and decreased further as sinker weight increased from 0.0 to 78.5 N. Importantly, the overall shape of the cage net remained largely unaffected.
- Volume ratio dynamics: The difference in volume ratio between cages with and without egg collection nets showed a quadratic relationship with current speed and consistently decreased with increasing sinker weight.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masuma, S.; Takebe, T.; Sakakura, Y. A review of the broodstock management and larviculture of the Pacific northern bluefin tuna in Japan. Aquaculture 2011, 315, 2–8. [Google Scholar] [CrossRef]
- Shin, A.; Yoon, S.C.; Lee, S.I.; Park, H.W.; Kim, S. The relationship between fishing characteristics of Pacific bluefin tuna (Thunnus orientalis) and ocean conditions around Jeju Island. Fish Aquat. Sci. 2018, 21, 1. [Google Scholar] [CrossRef]
- Kim, J.-G.; Kim, J.-G. Changes in Climate Factors and Catches of Fisheries in the Republic of Korea over the Three Decades. Water 2023, 15, 1952. [Google Scholar] [CrossRef]
- Park, J.-W.; Kim, J.-H.; JI, S.C.; Ryu, Y.-W.; Cho, J.-H. The reproductive potential of Pacific bluefin tuna (Thunnus orientalis) farmed in sea cages in South Korea. J. World Aquac. Soc. 2023, 54, 1497–1512. [Google Scholar] [CrossRef]
- De La Gandara, F.; Mylonas, C.; Coves, D.; Ortega, A.; Bridges, C.R.; Belmonte, R.A.; Vassallo-Agius, R.; Papandroulakis, N.; Rosenfeld, H.; Tandler, A.; et al. Seedling production of Atlantic bluefin tuna (ABFT) Thunnus thynnus. The selfdott project. In Proceedings of the Joint International Symposium of Kinki University and Setouchi Town on the 40th Anniversary of Pacific Bluefin Tuna Aquaculture, Towards the Sustainable Aquaculture of Bluefin Tuna, Amami, Japan, 15–16 October 2010; pp. 69–73. [Google Scholar]
- De Metrio, G.; Bridges, C.R.; Mylonas, C.C.; Caggiano, M.; Deflorio, M.; Santamaria, N.; Zupa, R.; Pousis, C.; Vassallo-Agius, R.; Gordin, H.; et al. Spawning induction and large-scale collection of fertilized eggs in captive Atlantic bluefin tuna (Thunnus thynnus L.) and the first larval rearing efforts. J. Appl. Ichthyol. 2010, 26, 596–599. [Google Scholar] [CrossRef]
- Bi, C.-W.; Zhao, Y.-P.; Dong, G.-H.; Zheng, Y.-N.; Gui, F.-K. A numerical analysis on the hydrodynamic characteristics of net cages using coupled fluid–structure interaction model. Aquac. Eng. 2014, 59, 1–12. [Google Scholar] [CrossRef]
- Li, L.; Fu, S.; Xu, Y.; Wang, J.; Yang, J. Dynamic responses of floating fish cage in waves and current. Ocean Eng. 2013, 72, 297–303. [Google Scholar] [CrossRef]
- Zhao, Y.; Guan, C.; Bi, C.; Liu, H.; Cui, Y. Experimental investigations on hydrodynamic responses of a semi-submersible offshore fish farm in waves. J. Mar. Sci. Eng. 2019, 7, 238. [Google Scholar] [CrossRef]
- Chen, H. Modelling of Floating Fish Cage Dynamics with Computational Fluid Dynamics. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 23 December 2016. Available online: https://orbit.dtu.dk/files/162637176/Thesis_HaoChen_002_pdf (accessed on 19 July 2025).
- Shainee, M.; DeCew, J.; Leira, B.J.; Ellingsen, H.; Fredheim, A. Numerical simulation of a self-submersible SPM cage system in regular waves with following currents. Aquac. Eng. 2013, 54, 29–37. [Google Scholar] [CrossRef]
- Cha, B.J.; Lee, C.W.; Lee, J.H.; Kim, H.Y. Hydrodynamic simulation of midwater trawl system behavior. J. Korean Soc. Fish. Ocean Technol. 2002, 38, 164–171. [Google Scholar]
- Lee, C.W.; Kim, Y.B.; Lee, G.H.; Choe, M.Y.; Lee, M.K.; Koo, K.Y. Dynamic simulation of a fish cage system subjected to currents and waves. Ocean Eng. 2008, 35, 1521–1532. [Google Scholar] [CrossRef]
- Lee, G.H.; Cha, B.J.; Kim, H.Y. A study on the minimization of mooring load in fish-cage mooring systems with a damping buoy. J. Mar. Sci. Eng. 2020, 8, 814. [Google Scholar] [CrossRef]
- Lee, M.K.; Lee, C.W. Dynamic analysis of a cage affected by the current. J. Korean Soc. Fish Ocean Technol. 2004, 40, 214–224. [Google Scholar][Green Version]
- Kim, T.H. Design of Fish Aquaculture Cage; Jeonnam University: Yeosu, Republic of Korea, 2009; pp. 98–99. [Google Scholar]
- Shi, Y. A New Penalty Stiffness Treatment for Master-Slave Contact Surfaces. Master’s Thesis, McMaster University, Hamilton, ON, Canada, September 2001. Available online: https://macsphere.mcmaster.ca/bitstream/11375/25261/1/shi_yihai_2001Sep_masters.pdf (accessed on 16 April 2025).
- Corral, E.; Moreno, R.G.; García, M.J.G.; González, M.I. Nonlinear phenomena of contact in multibody systems dynamics: A review. Nonlinear Dyn. 2021, 104, 1269–1295. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tang, H.-J.; Liu, J.-Y. Dynamical analysis of net cage structures for marine aquaculture: Numerical simulation and model testing. Aquac. Eng. 2006, 35, 258–270. [Google Scholar] [CrossRef]
- Korea Hydrographic and Oceanographic Agency. Available online: https://www.khoa.go.kr/oceangrid/gis/category/reference/distribution.do (accessed on 15 February 2025).
- Rousseeuw, P.J.; Croux, C. Alternatives to the Median Absolute Deviation. J. Am. Stat. Assoc. 1993, 88, 1273–1283. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, H.; Shi, W.; Bi, C.; Li, X. Numerical Study on Internal and External Flow Fields of the UHMWPE Cage. J. Mar. Sci. Eng. 2023, 11, 1881. [Google Scholar] [CrossRef]
- Xu, T.-J.; Dong, G.-H.; Zhao, Y.-P.; Li, Y.-C.; Gui, F.-K. Numerical investigation of the hydrodynamic behaviors of multiple net cages in waves. Aquac. Eng. 2012, 48, 6–18. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Bi, C.-W.; Chen, C.-P.; Li, Y.-C.; Dong, G.-H. Experimental study on flow velocity and mooring loads for multiple net cages in steady current. Aquac. Eng. 2015, 67, 24–31. [Google Scholar] [CrossRef]
- Liu, Z.; Soares, C.G. Uncertainty Assessment of the Remaining Volume of an Offshore Gravity Fish Cage. J. Mar. Sci. Eng. 2024, 12, 289. [Google Scholar] [CrossRef]
- Ji, J.; Zhou, L.; Liu, B.; Soares, C.G. Experimental and numerical study on the flow field of a bottom-supported net cage with double-layer fishing nets. Ocean Eng. 2025, 319, 120228. [Google Scholar] [CrossRef]
- Cardiff, P.; Karač, A.; Ivanković, A. Development of a finite volume contact solver based on the penalty method. Comput. Mater. Sci. 2012, 64, 283–284. [Google Scholar] [CrossRef]
- Zang, M.; Gao, W.; Lei, Z. A contact algorithm for 3D discrete and finite element contact problems based on penalty function method. Comput. Mech. 2011, 48, 541–550. [Google Scholar] [CrossRef]

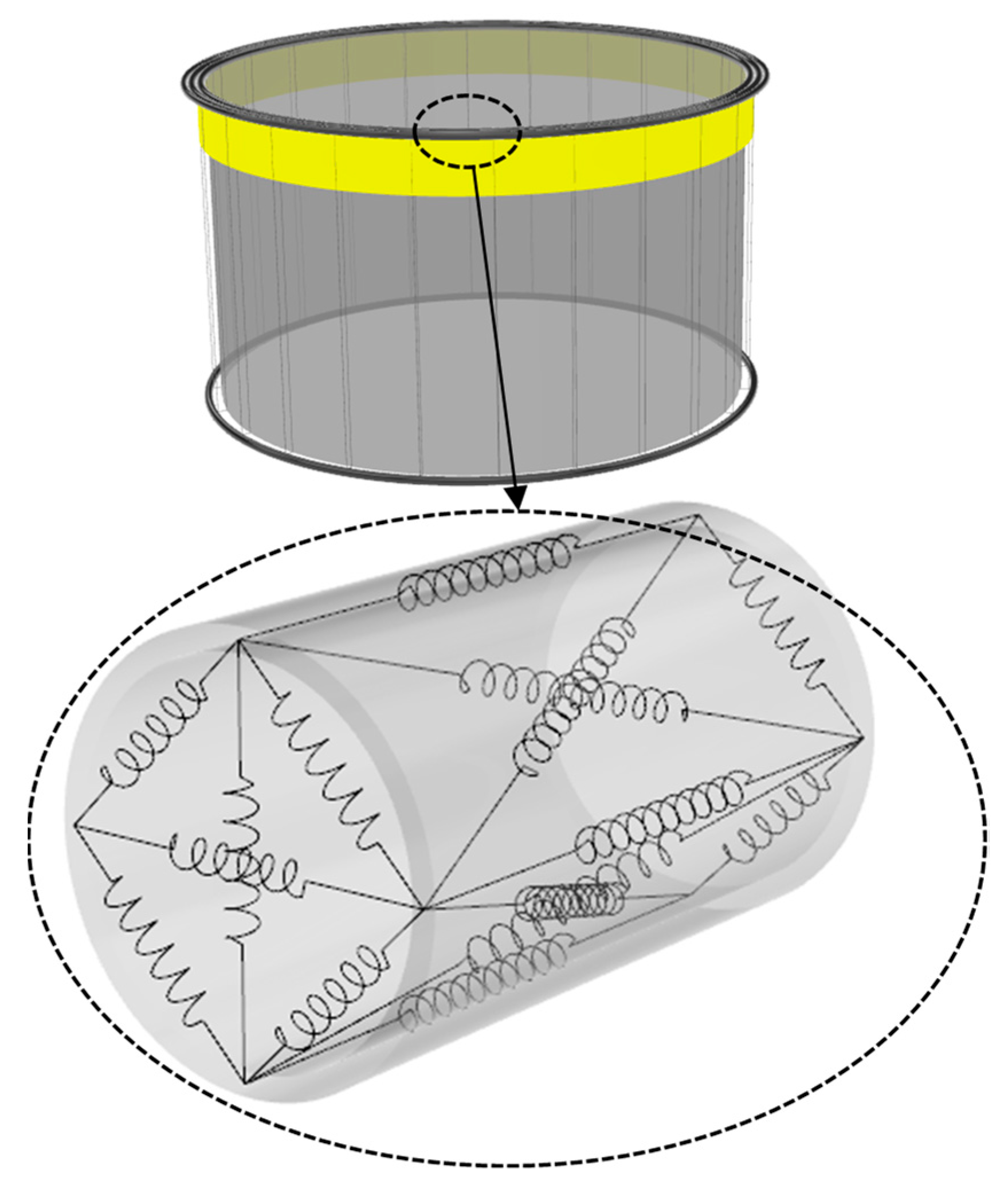
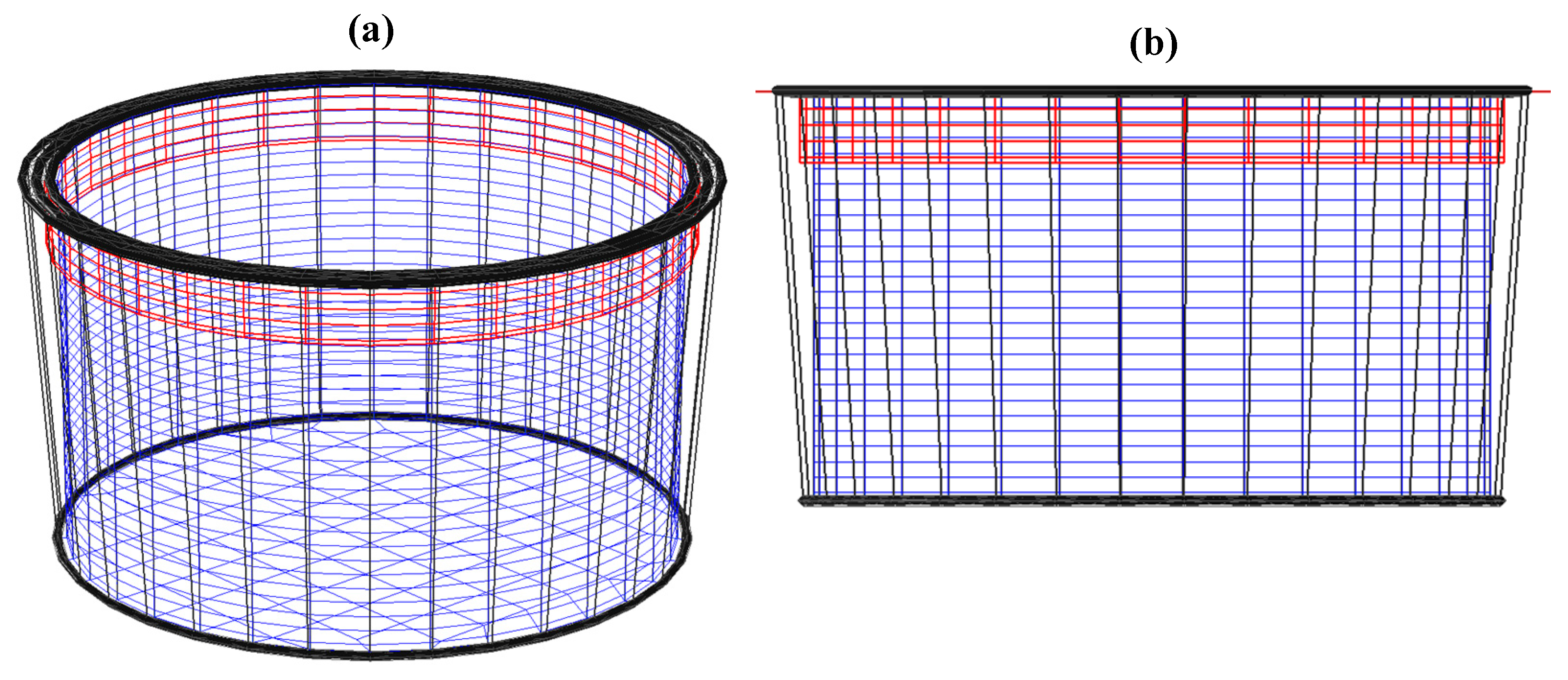

| Parameter | Size | Material Properties |
|---|---|---|
| Upper rim | ||
| Inner rim | ⌀400 mm, dia. 25.4 m, 22.5 T | HDPE |
| Middle rim | ⌀400 mm, dia. 26.5 m, 22.5 T | HDPE |
| Outer rim | ⌀315 mm, dia. 27.6 m, 18.0 T | HDPE |
| Lower rim | ⌀50 mm, dia. 26.0 m, W a 18,482 N | Steel |
| Side rope | ⌀30 mm × 24 line | PE |
| Lacing rope | ⌀24 mm × 24 line | PE |
| Sinker | 245.3 N × 2 ea | Iron |
| Body net | ⌀4 mm, mesh size 35.35 mm | PE (SG b = 0.94) |
| dia. 25.0 m, height 15.0 m | ||
| Solidity ratio 0.2135 | ||
| Egg collection net | ⌀353 µm, mesh size 818 µm | PET (SG b = 1.47) |
| dia. 25.8 m, height 2.6 m | ||
| Solidity ratio 0.6768 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.-H.; Kwon, I.; Ji, S.-C. Structural Response and Volume Change Characteristics of Tuna Cages Equipped with External Egg Collection Nets. J. Mar. Sci. Eng. 2025, 13, 1762. https://doi.org/10.3390/jmse13091762
Lee G-H, Kwon I, Ji S-C. Structural Response and Volume Change Characteristics of Tuna Cages Equipped with External Egg Collection Nets. Journal of Marine Science and Engineering. 2025; 13(9):1762. https://doi.org/10.3390/jmse13091762
Chicago/Turabian StyleLee, Gun-Ho, Inyeong Kwon, and Seung-Cheol Ji. 2025. "Structural Response and Volume Change Characteristics of Tuna Cages Equipped with External Egg Collection Nets" Journal of Marine Science and Engineering 13, no. 9: 1762. https://doi.org/10.3390/jmse13091762
APA StyleLee, G.-H., Kwon, I., & Ji, S.-C. (2025). Structural Response and Volume Change Characteristics of Tuna Cages Equipped with External Egg Collection Nets. Journal of Marine Science and Engineering, 13(9), 1762. https://doi.org/10.3390/jmse13091762






