Design of an Experimental Teaching Platform for Flow-Around Structures and AI-Driven Modeling in Marine Engineering
Abstract
1. Introduction
- We establish, in an instructional setting, a synchronized data schema coupling circumferential surface pressure measurements with three-component force records (Fx, Fy, and Fz). This integration enables validation that links local pressure coefficients to a drag (force) decomposition pathway and sharpens students’ quantitative understanding of boundary-layer separation effects.
- We design a lightweight ANN prediction framework that fuses physically interpretable descriptors (e.g., Reynolds number, angle of attack, and immersion depth) with data-driven inference, thereby articulating a pedagogical pathway for data–model–physics triadic synergy consistent with emerging trends in intelligent fluid mechanics [18,19,20].
2. Overall Platform Architecture
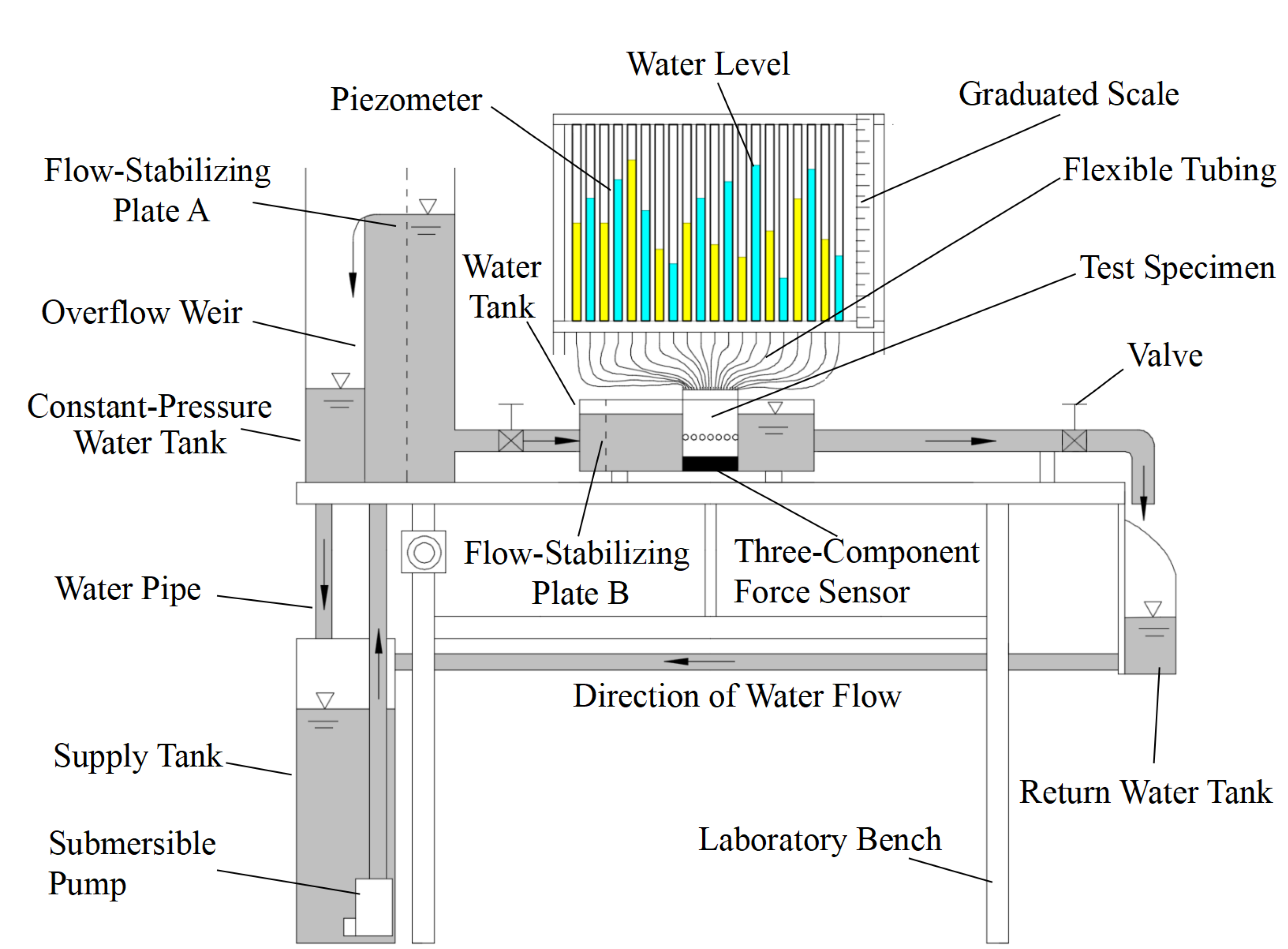
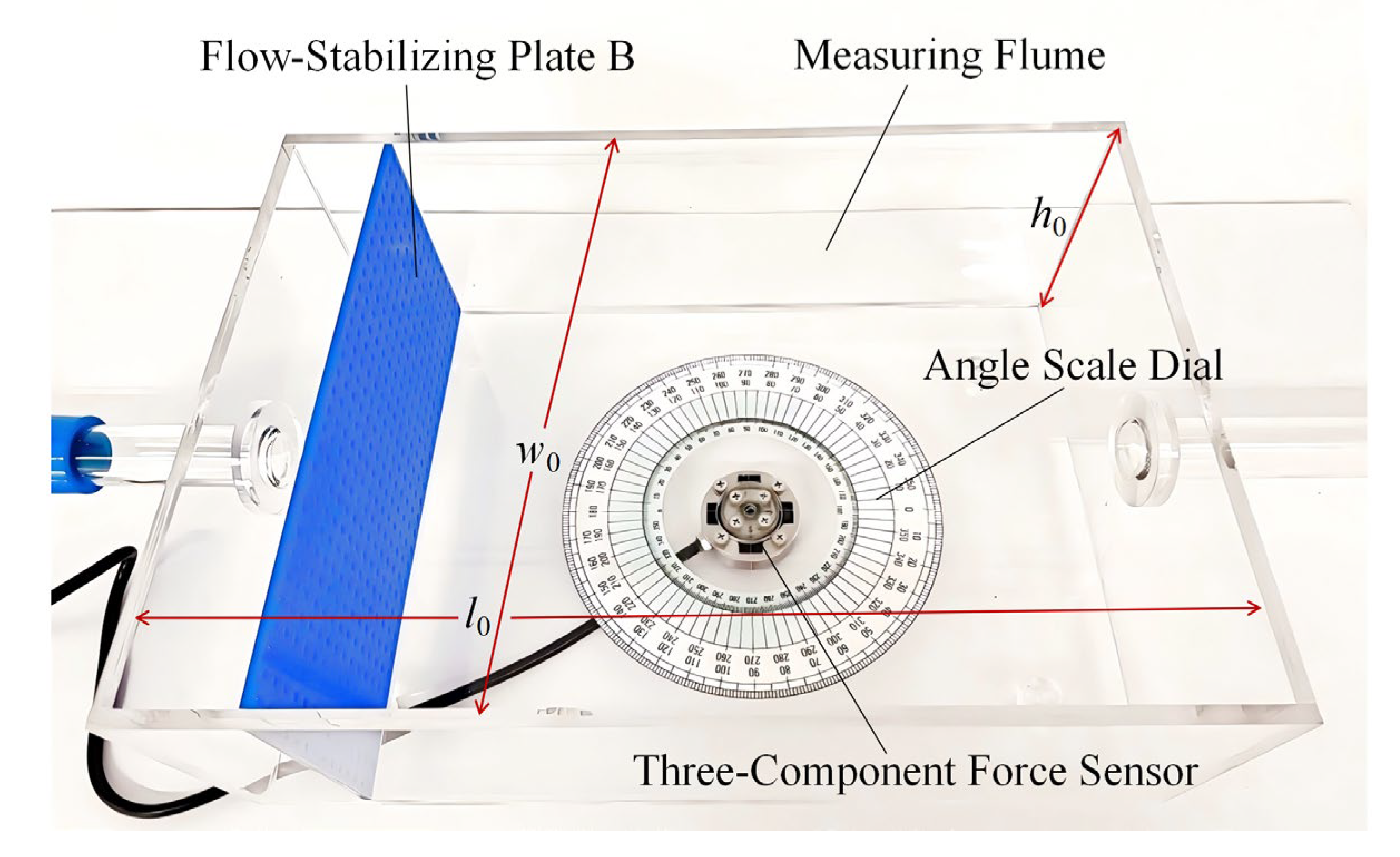
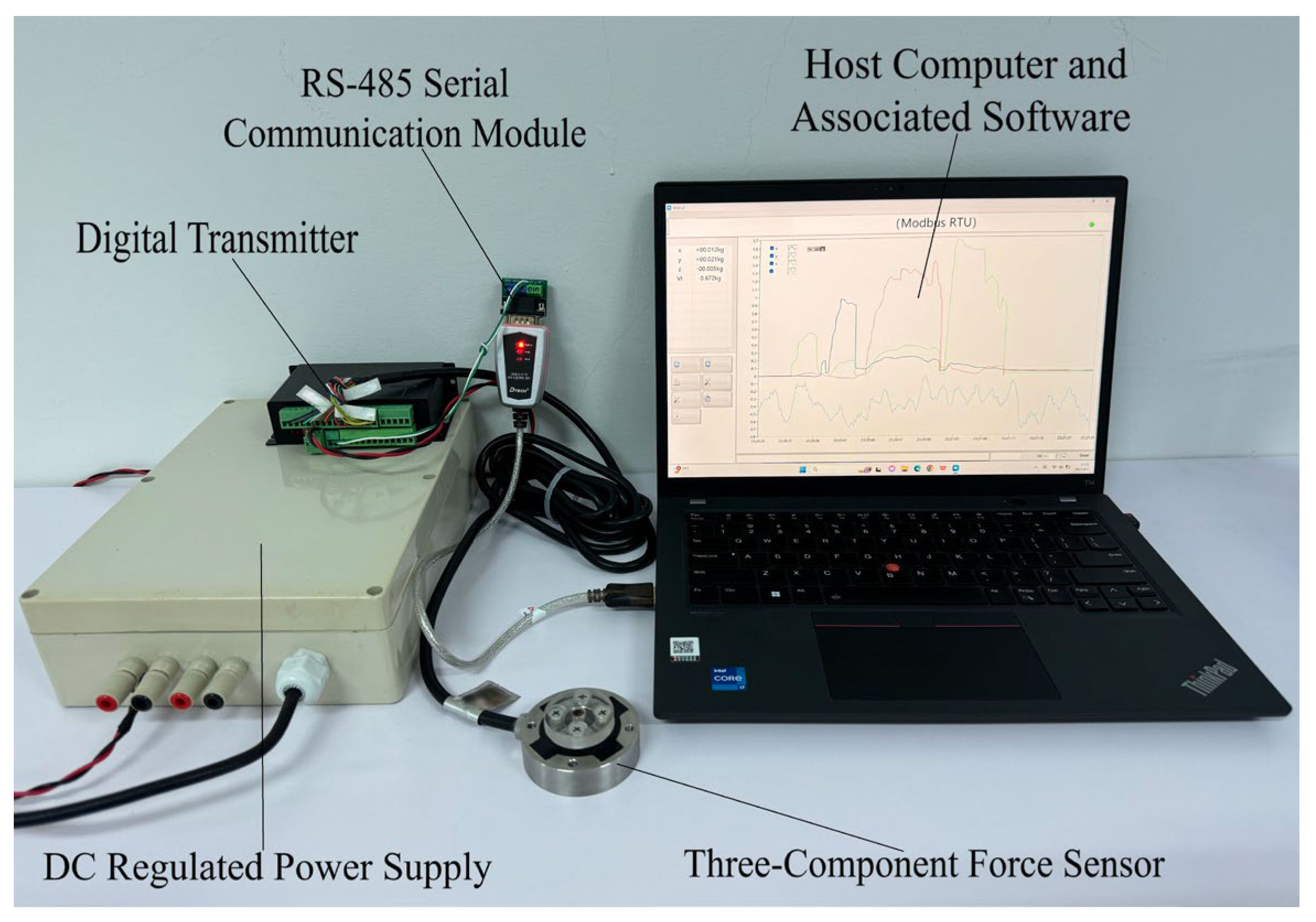
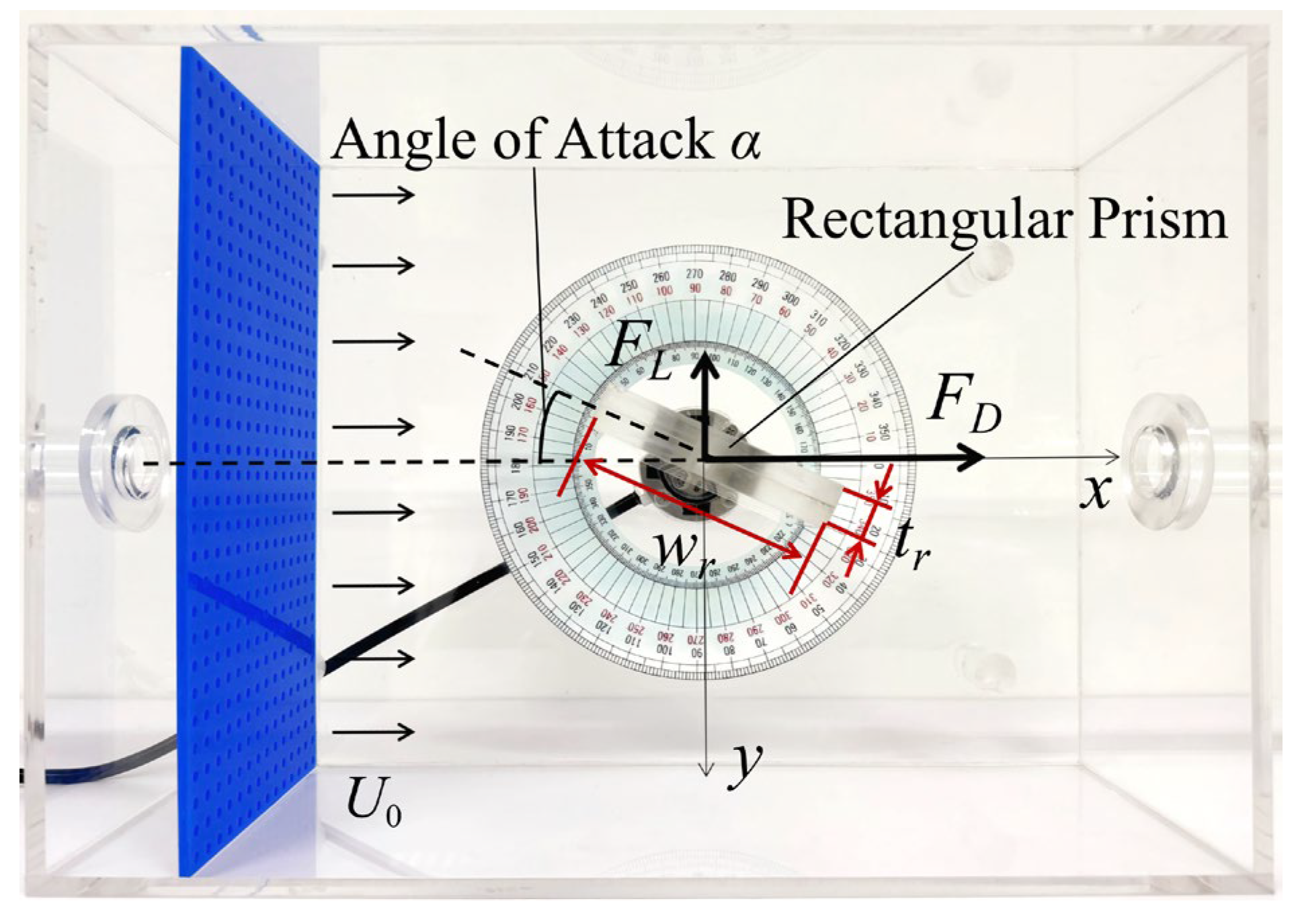
2.1. Design of the Experimental Apparatus
2.2. Experimental Procedure
3. Methodology
3.1. Surface Pressure Distribution: Theory and Experiment
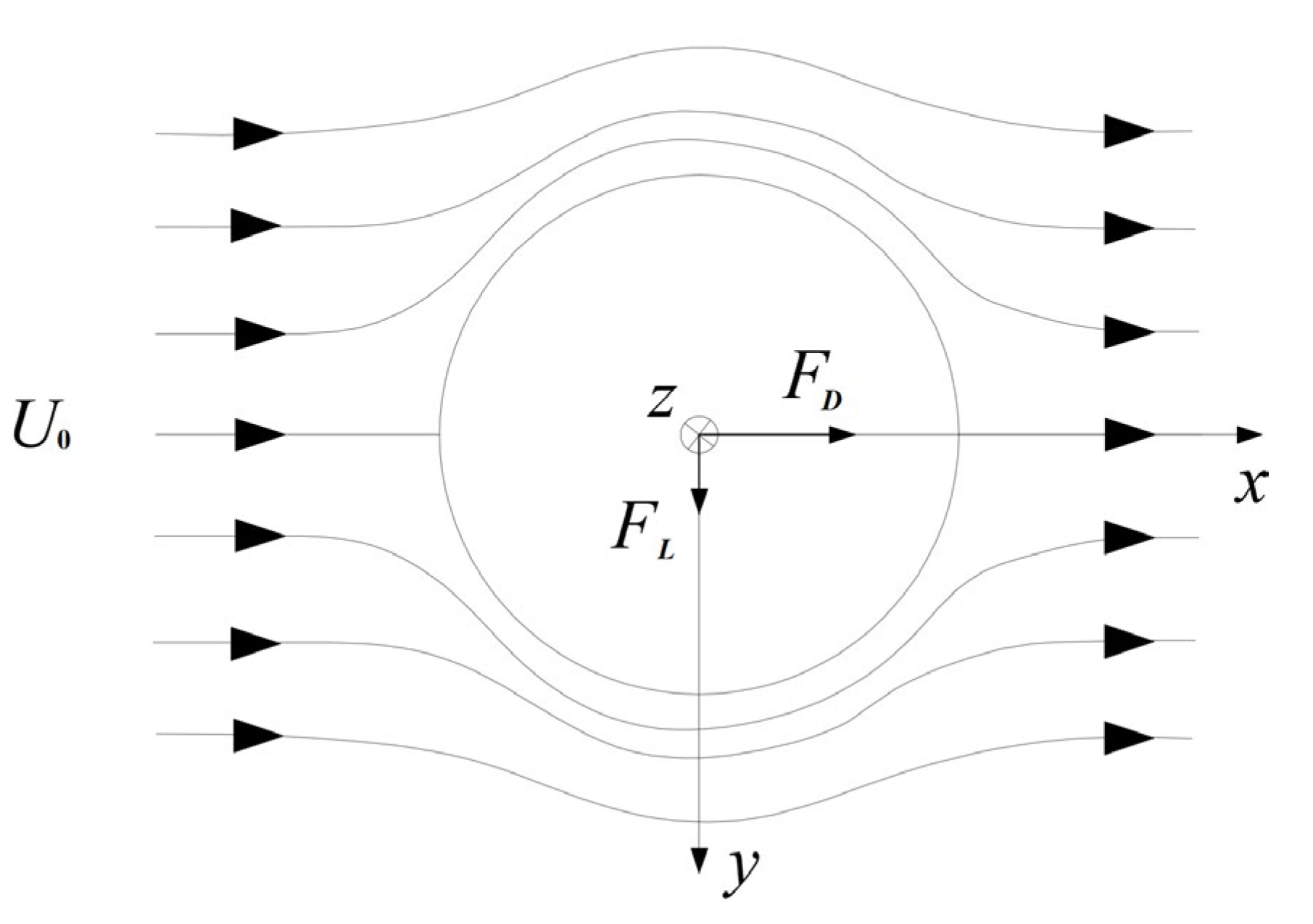
3.2. Theoretical and Experimental Analysis of Drag and Lift
3.3. AI and Data-Driven Modeling Approach
4. Results
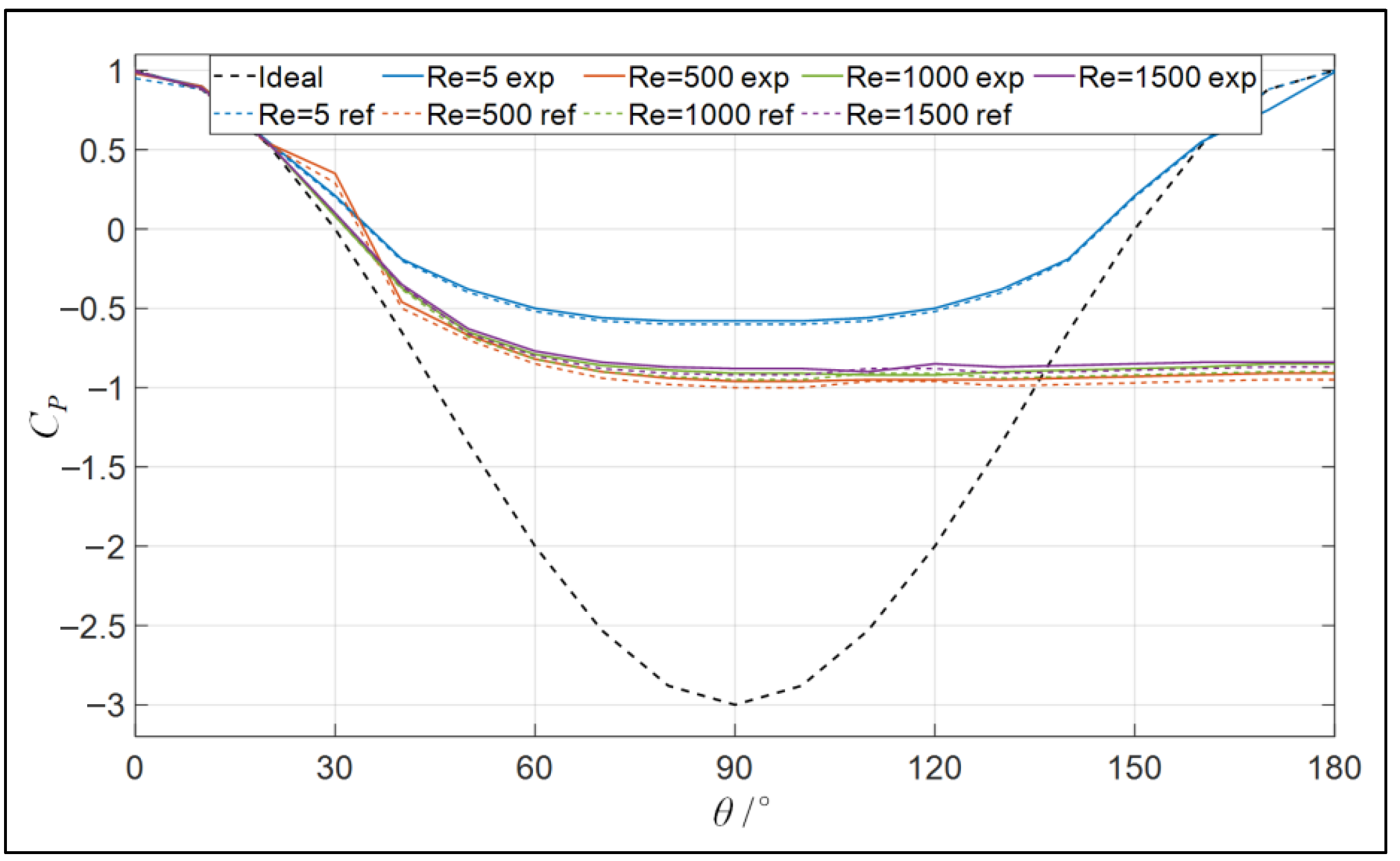
4.1. Surface Pressure Distribution
4.2. Drag Measurement
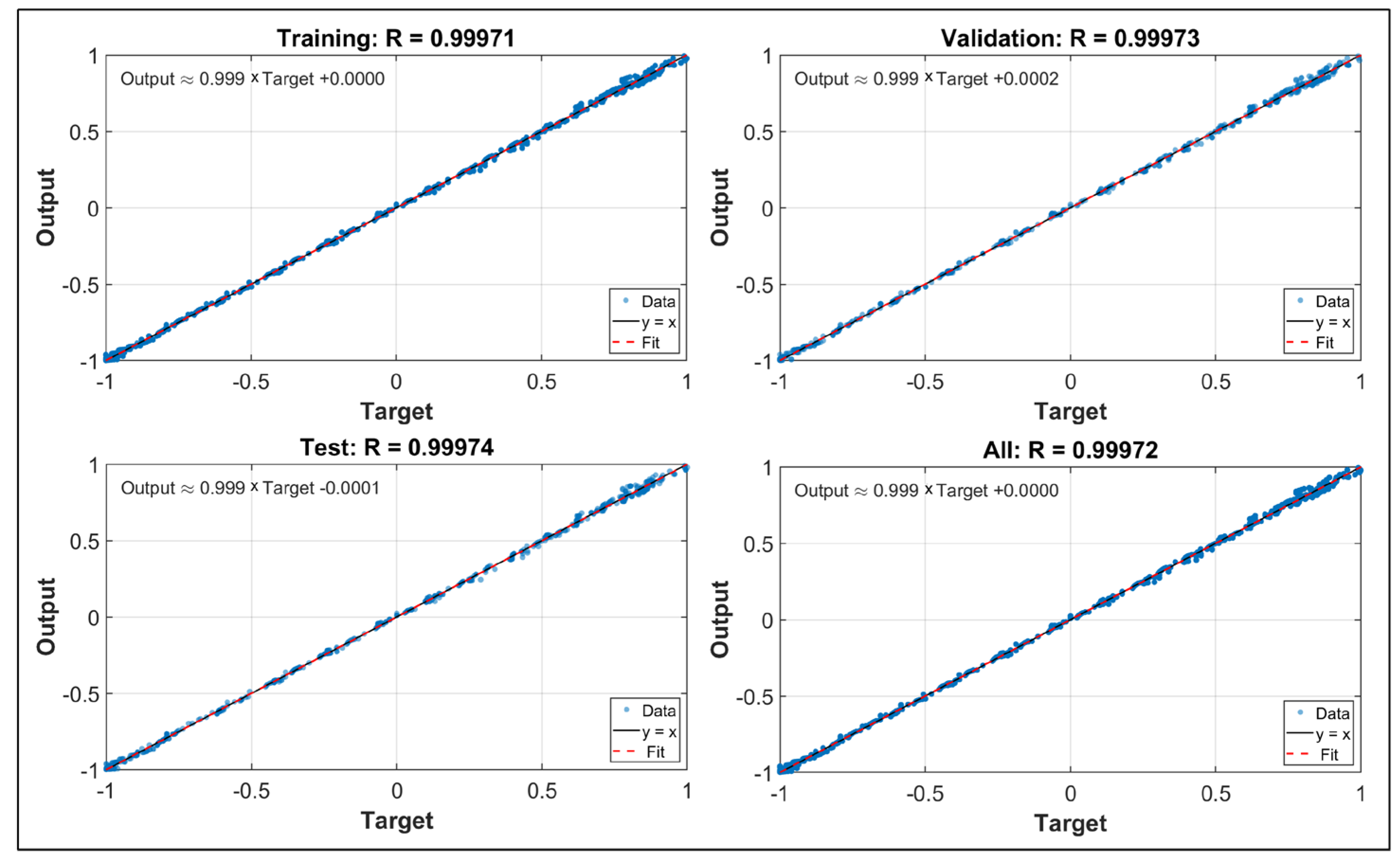
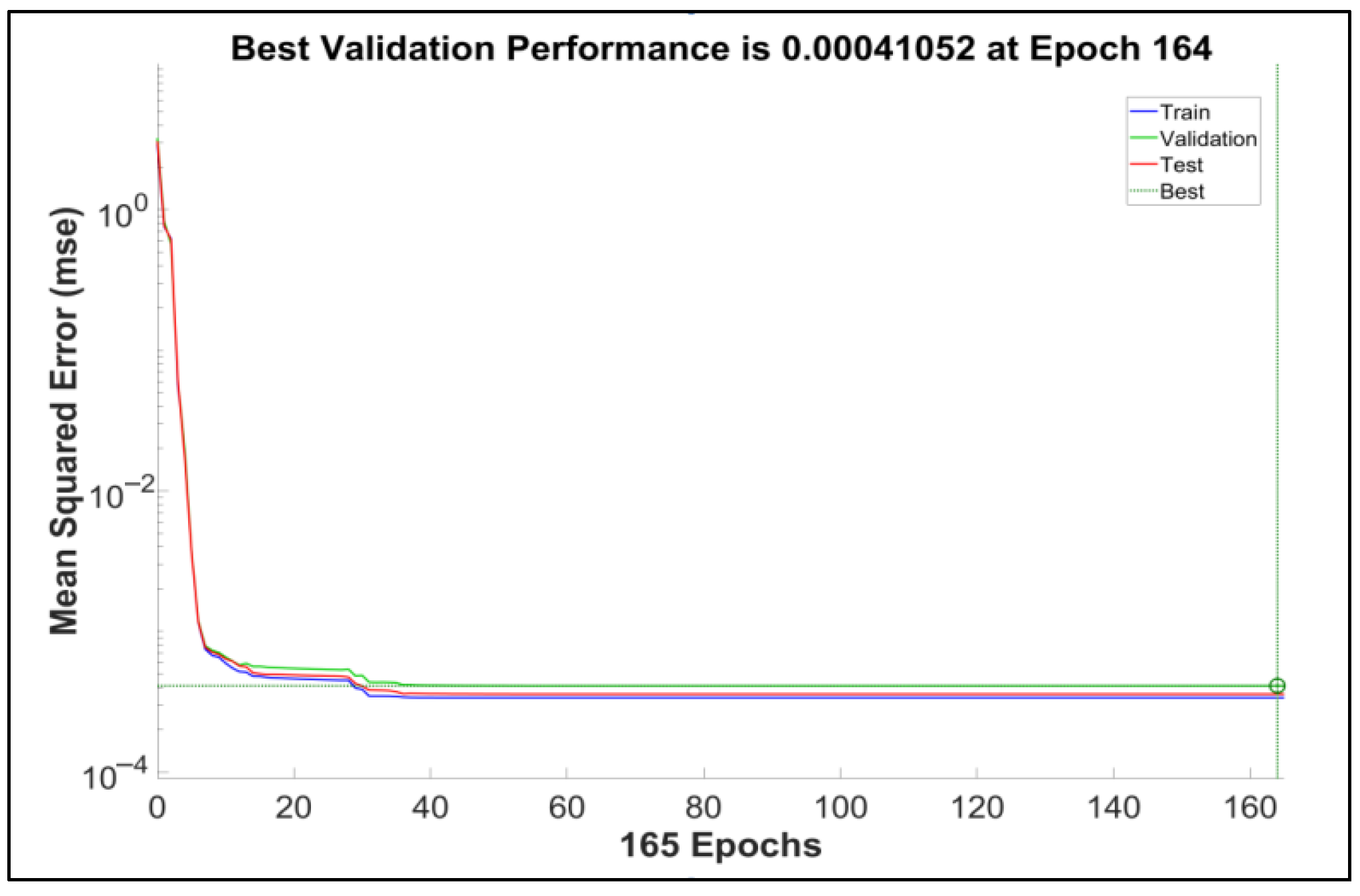
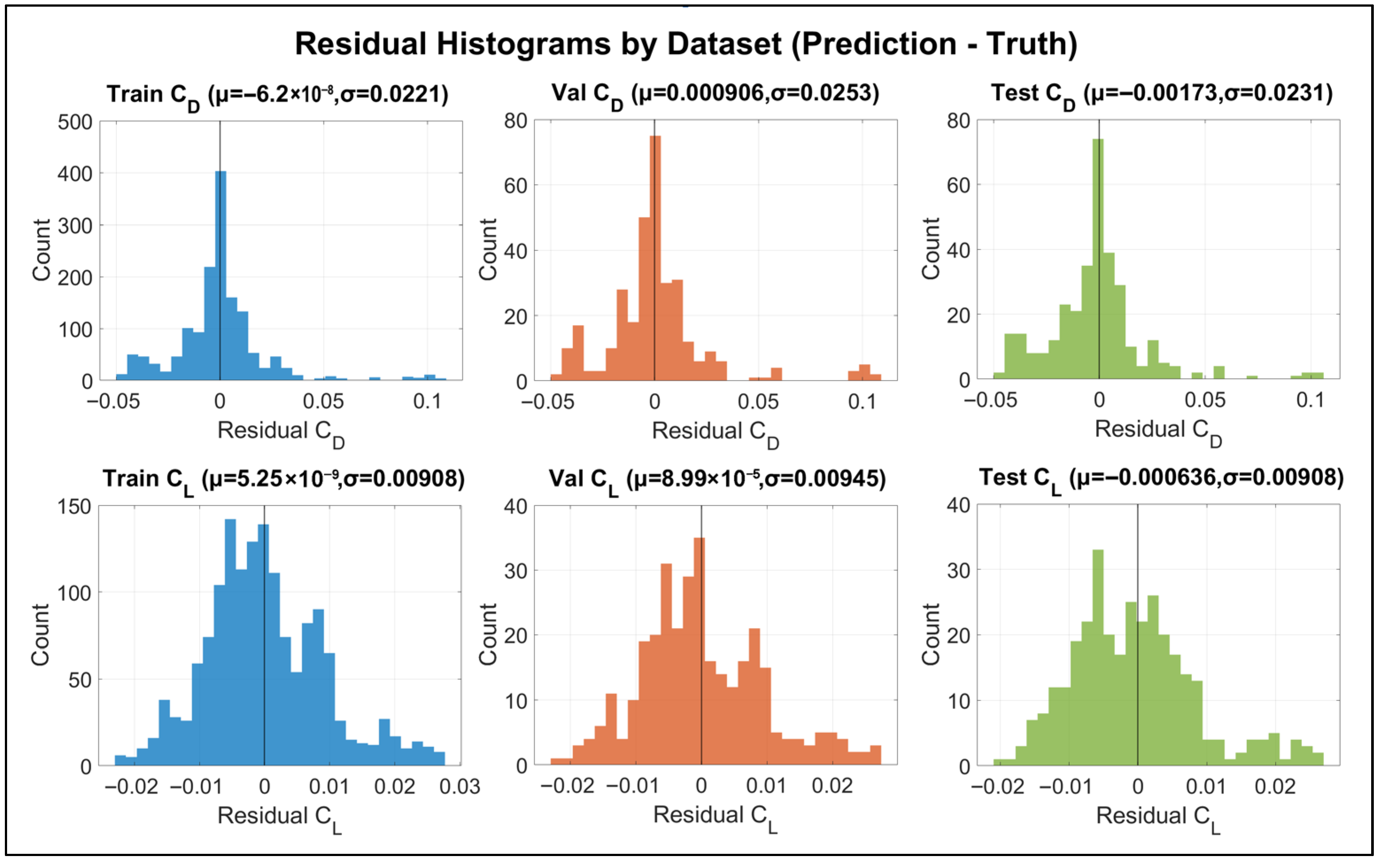
4.3. Development and Performance Evaluation of the Predictive Model
4.4. Sources of Uncertainty and Limitations
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zdravkovich, M.M. Flow Around Circular Cylinders. Vol. 1: Fundamentals; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Roshko, A. On the drag and shedding frequency of two-dimensional bluff bodies. NACA Rep. 1954, 1191. [Google Scholar]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Norberg, C. An experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J. Fluid Mech. 1994, 258, 287–316. [Google Scholar] [CrossRef]
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Sánchez Martín, J.; Vázquez Rodríguez, S.; García Cubero, M.T. FLUID-LABVIR: A hybrid virtual laboratory platform for fluid mechanics engineering education. Educ. Chem. Eng. 2021, 36, 123–134. [Google Scholar]
- Freeman, S.; Eddy, S.L.; McDonough, M.; Smith, M.K.; Okoroafor, N.; Jordt, H.; Wenderoth, M.P. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef]
- Prince, M. Does active learning work? A review of the research. J. Eng. Educ. 2004, 93, 223–231. [Google Scholar] [CrossRef]
- Lu, G.D.; Li, T.Y. Reflections on Pathways for the Construction and Development of Emerging Engineering Education. Res. High. Eng. Educ. 2017, 3, 20–26. [Google Scholar]
- Zhong, D.H. Connotations and Action Framework for Building Emerging Engineering Education. Res. High. Eng. Educ. 2017, 3, 1–6. [Google Scholar]
- Rowley, C.W.; Dawson, S.T.M. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds stress modeling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Wang, J.-X.; Wu, J.-L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancy. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Guo, X.; Li, W.; Iorio, F. Convolutional neural networks for steady flow approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’16), San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 481–490. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Y.; Guo, C.Y.; Wang, C.; Sun, C. Experimental teaching platform for an oscillating rotating cylinder based on the Magnus effect. Exp. Technol. Manag. 2020, 37, 54–57. [Google Scholar] [CrossRef]
- Guo, C.Y.; Zhang, H.R.; Han, Y.; Kuai, Y.F.; Li, R.X.; Gao, Y. Design of a high-fidelity flow field measurement experimental teaching platform based on SPIV technology. Mech. Pract. 2025, 47, 416–425. [Google Scholar]
- Vinuesa, R.; Brunton, S.L.; McKeon, B.J. The transformative potential of machine learning for experiments in fluid mechanics. Nat. Rev. Phys. 2023, 5, 536–545. [Google Scholar] [CrossRef]
- Vijaya Kumar, S.D.; Lo, M.; Karuppanan, S.; Ovinis, M. Empirical failure pressure prediction equations for pipelines with longitudinal interacting corrosion defects based on artificial neural network. J. Mar. Sci. Eng. 2022, 10, 764. [Google Scholar] [CrossRef]
- González-Díaz, R.; Gutiérrez-Naranjo, A.M.; Paluzo-Hidalgo, E. Two-hidden-layer feedforward neural networks are universal approximators: A constructive approach. arXiv 2019, arXiv:1907.11457. Available online: https://arxiv.org/abs/1907.11457 (accessed on 14 August 2025).
- Anderson, J.D. Fundamentals of Aerodynamics, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]



| Re | FD/N | Deviation/% | |
|---|---|---|---|
| Reference | Test | ||
| 200 | 2.83 × 10−5 | 2.54 × 10−5 | −10.25 |
| 400 | 1.11 × 10−4 | 1.19 × 10−4 | +7.21 |
| 600 | 2.46 × 10−4 | 2.56 × 10−4 | +4.07 |
| 800 | 4.30 × 10−4 | 4.64 × 10−4 | +7.91 |
| 1000 | 6.60 × 10−4 | 6.41 × 10−4 | −2.88 |
| 1200 | 1.28 × 10−3 | 1.36 × 10−3 | +6.25 |
| Index | Hidden Neurons | R2 |
|---|---|---|
| 1 | 5 | 0.9623 |
| 2 | 6 | 0.9654 |
| 3 | 7 | 0.9712 |
| 4 | 8 | 0.9827 |
| 5 | 9 | 0.9997 |
| 6 | 10 | 0.9977 |
| 7 | 11 | 0.9934 |
| 8 | 12 | 0.9931 |
| Re | α/° | H/cm | CD | Deviation/% | CL | Deviation/% | ||
|---|---|---|---|---|---|---|---|---|
| Exp. | Equation | Exp. | Equation | |||||
| 50 | 6 | 6 | 0.123 | 0.126 | 2.439 | 0.197 | 0.205 | 3.850 |
| 50 | 45 | 10 | 1.304 | 1.33 | 1.994 | 0.799 | 0.812 | 1.627 |
| 50 | 72 | 11 | 1.895 | 2.02 | 6.596 | 0.564 | 0.592 | 4.965 |
| 50 | 87 | 9 | 2.237 | 2.258 | 0.939 | 0.118 | 0.125 | 6.383 |
| 100 | 3 | 5 | 0.092 | 0.098 | 6.522 | 0.133 | 0.142 | 6.383 |
| 100 | 39 | 8 | 1.092 | 1.125 | 3.022 | 0.658 | 0.69 | 4.863 |
| 100 | 75 | 9 | 1.892 | 1.92 | 1.480 | 0.404 | 0.421 | 4.156 |
| 150 | 9 | 6 | 0.107 | 0.113 | 5.607 | 0.179 | 0.188 | 5.263 |
| 150 | 51 | 7 | 1.292 | 1.372 | 6.192 | 0.827 | 0.866 | 4.691 |
| 150 | 69 | 11 | 1.892 | 1.905 | 0.687 | 0.625 | 0.656 | 4.943 |
| 200 | 3 | 8 | 0.087 | 0.09 | 3.448 | 0.120 | 0.123 | 2.227 |
| 200 | 48 | 10 | 1.202 | 1.278 | 6.323 | 0.799 | 0.838 | 4.881 |
| 200 | 84 | 6 | 2.052 | 2.14 | 4.288 | 0.357 | 0.374 | 4.703 |
| 250 | 6 | 7 | 0.107 | 0.109 | 1.869 | 0.196 | 0.204 | 4.337 |
| 250 | 69 | 5 | 1.883 | 1.886 | 0.159 | 0.631 | 0.661 | 4.798 |
| 300 | 3 | 5 | 0.081 | 0.083 | 2.469 | 0.099 | 0.103 | 4.357 |
| 300 | 6 | 8 | 0.107 | 0.108 | 0.935 | 0.196 | 0.204 | 4.337 |
| 300 | 66 | 6 | 1.799 | 1.801 | 0.111 | 0.724 | 0.735 | 1.547 |
| 350 | 57 | 7 | 1.519 | 1.537 | 1.185 | 0.921 | 0.923 | 0.195 |
| 350 | 72 | 10 | 1.941 | 1.953 | 0.618 | 0.552 | 0.585 | 6.021 |
| 400 | 6 | 7 | 0.092 | 0.098 | 6.522 | 0.196 | 0.204 | 4.337 |
| 400 | 36 | 9 | 0.992 | 1.04 | 4.839 | 0.639 | 0.671 | 4.975 |
| 400 | 63 | 11 | 1.692 | 1.718 | 1.537 | 0.705 | 0.742 | 5.248 |
| 400 | 87 | 8 | 1.992 | 2.03 | 1.908 | 0.139 | 0.143 | 2.789 |
| 450 | 12 | 10 | 0.152 | 0.155 | 1.974 | 0.235 | 0.245 | 4.255 |
| 450 | 42 | 9 | 1.002 | 1.067 | 6.487 | 0.733 | 0.772 | 5.292 |
| 450 | 66 | 10 | 1.702 | 1.762 | 3.525 | 0.696 | 0.731 | 5.089 |
| 450 | 78 | 11 | 1.892 | 1.98 | 4.651 | 0.385 | 0.401 | 4.048 |
| 500 | 66 | 11 | 1.733 | 1.775 | 2.424 | 0.697 | 0.733 | 5.093 |
| 500 | 78 | 5 | 1.992 | 2.05 | 2.912 | 0.400 | 0.414 | 3.386 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhao, B.; Liang, X.; Lin, Q. Design of an Experimental Teaching Platform for Flow-Around Structures and AI-Driven Modeling in Marine Engineering. J. Mar. Sci. Eng. 2025, 13, 1761. https://doi.org/10.3390/jmse13091761
Zhao H, Zhao B, Liang X, Lin Q. Design of an Experimental Teaching Platform for Flow-Around Structures and AI-Driven Modeling in Marine Engineering. Journal of Marine Science and Engineering. 2025; 13(9):1761. https://doi.org/10.3390/jmse13091761
Chicago/Turabian StyleZhao, Hongyang, Bowen Zhao, Xu Liang, and Qianbin Lin. 2025. "Design of an Experimental Teaching Platform for Flow-Around Structures and AI-Driven Modeling in Marine Engineering" Journal of Marine Science and Engineering 13, no. 9: 1761. https://doi.org/10.3390/jmse13091761
APA StyleZhao, H., Zhao, B., Liang, X., & Lin, Q. (2025). Design of an Experimental Teaching Platform for Flow-Around Structures and AI-Driven Modeling in Marine Engineering. Journal of Marine Science and Engineering, 13(9), 1761. https://doi.org/10.3390/jmse13091761







