Power Estimation Method and Its Validation for Ships with Hybrid Contra Rotating Propeller
Abstract
1. Introduction
2. Methodology
2.1. Towing Tank Test Method
2.1.1. Propeller Open Water Tests
2.1.2. Resistance Test
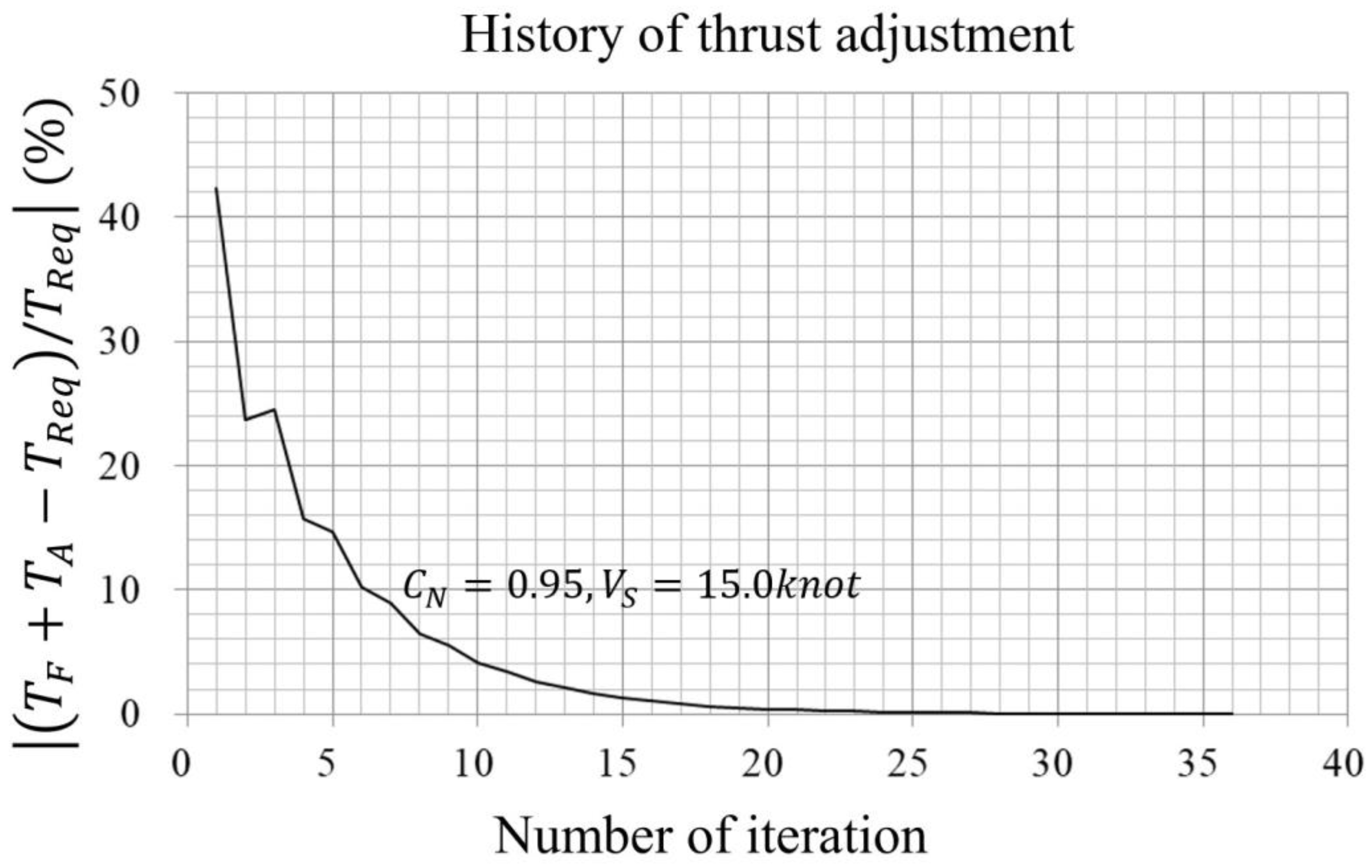
2.1.3. Self-Propulsion Test
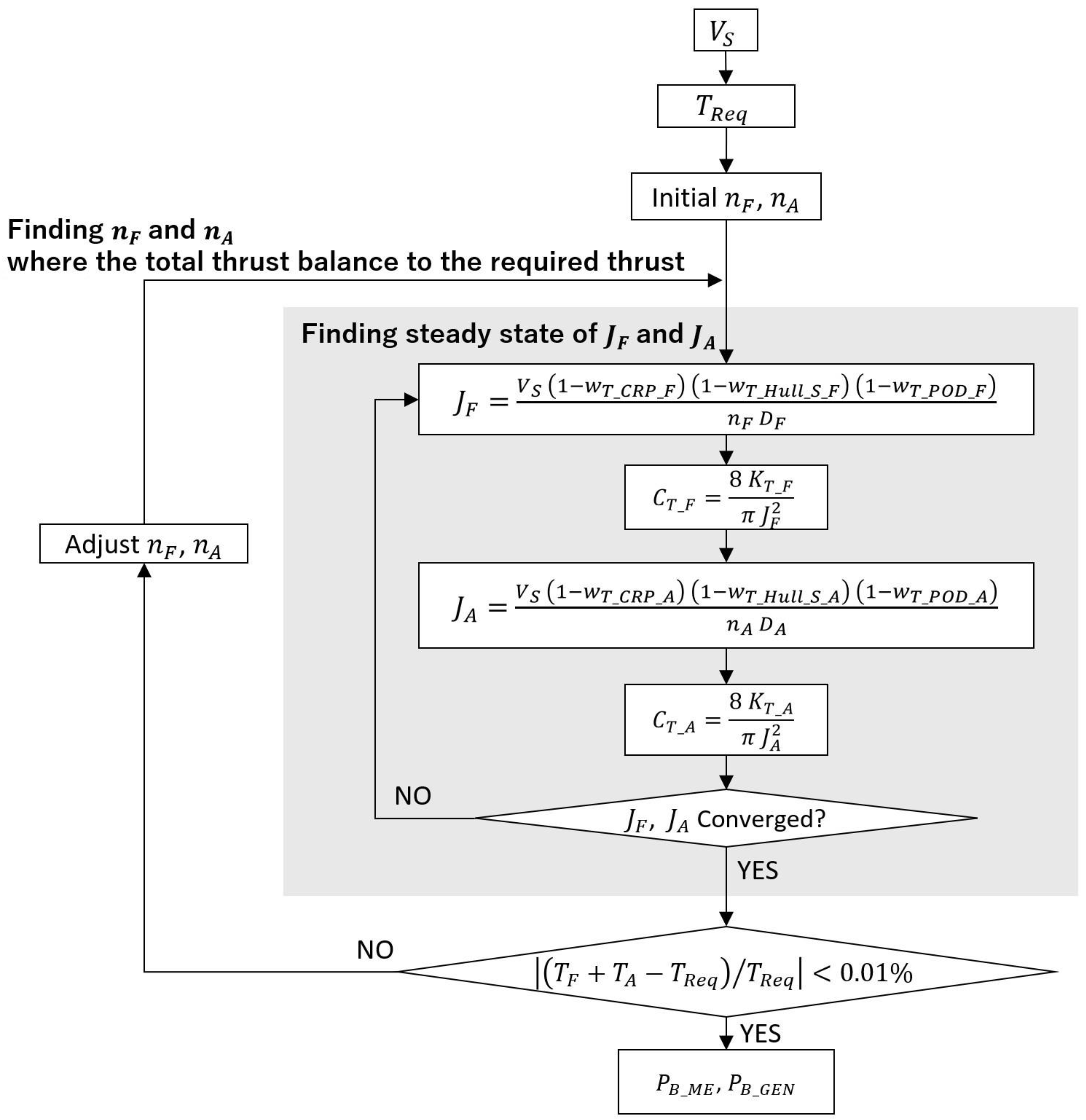
2.2. Powering Method
2.2.1. Required Thrust
2.2.2. Scaling for Wake Fraction of Hull
2.2.3. Propeller Rotational Speed
2.2.4. Output
3. Towing Tank Test Configurations, Results
3.1. Towing Tank Test Configulations
3.1.1. Test Facility
3.1.2. Fluid Parameters
3.1.3. Model Propellers
3.1.4. Model Ship
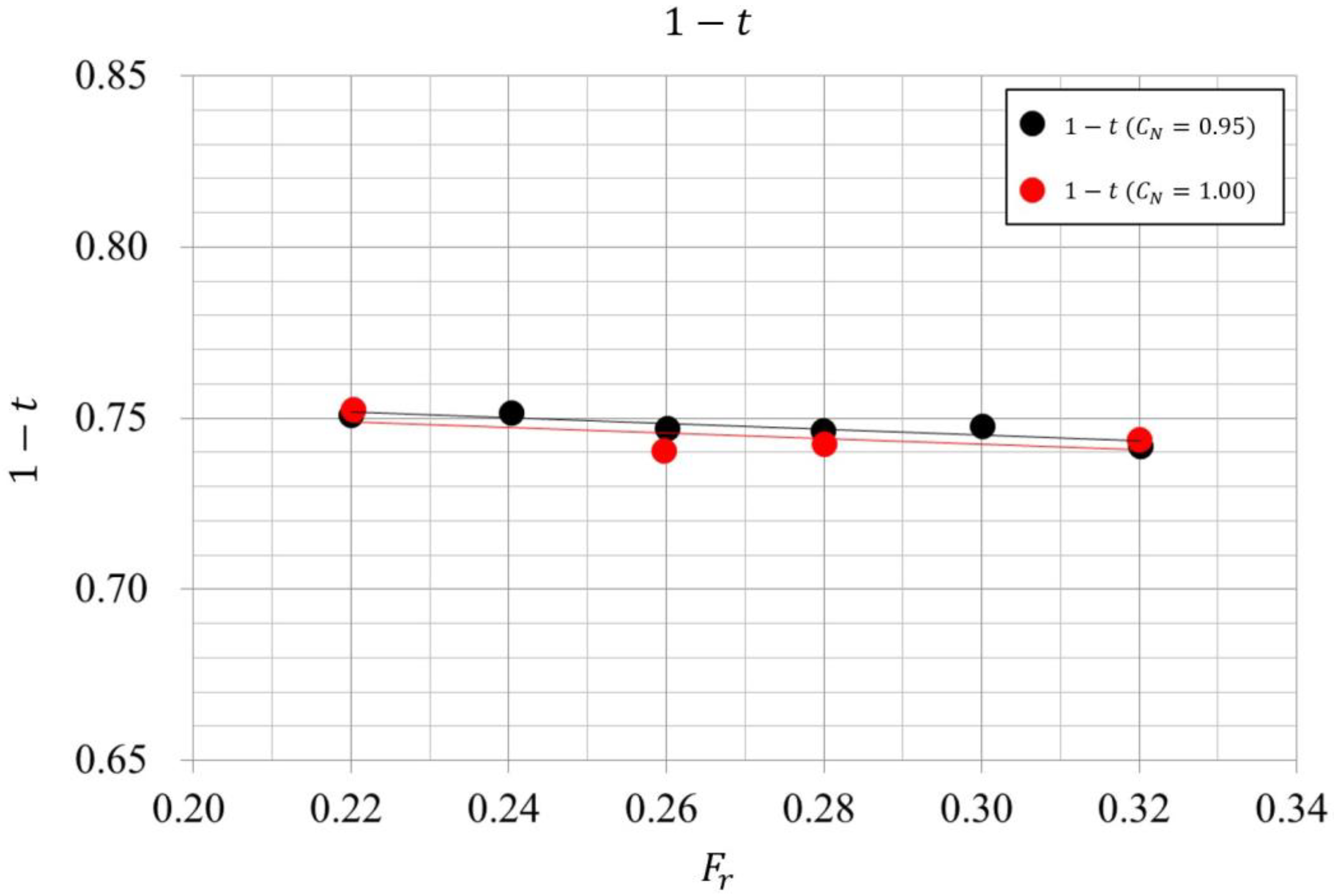
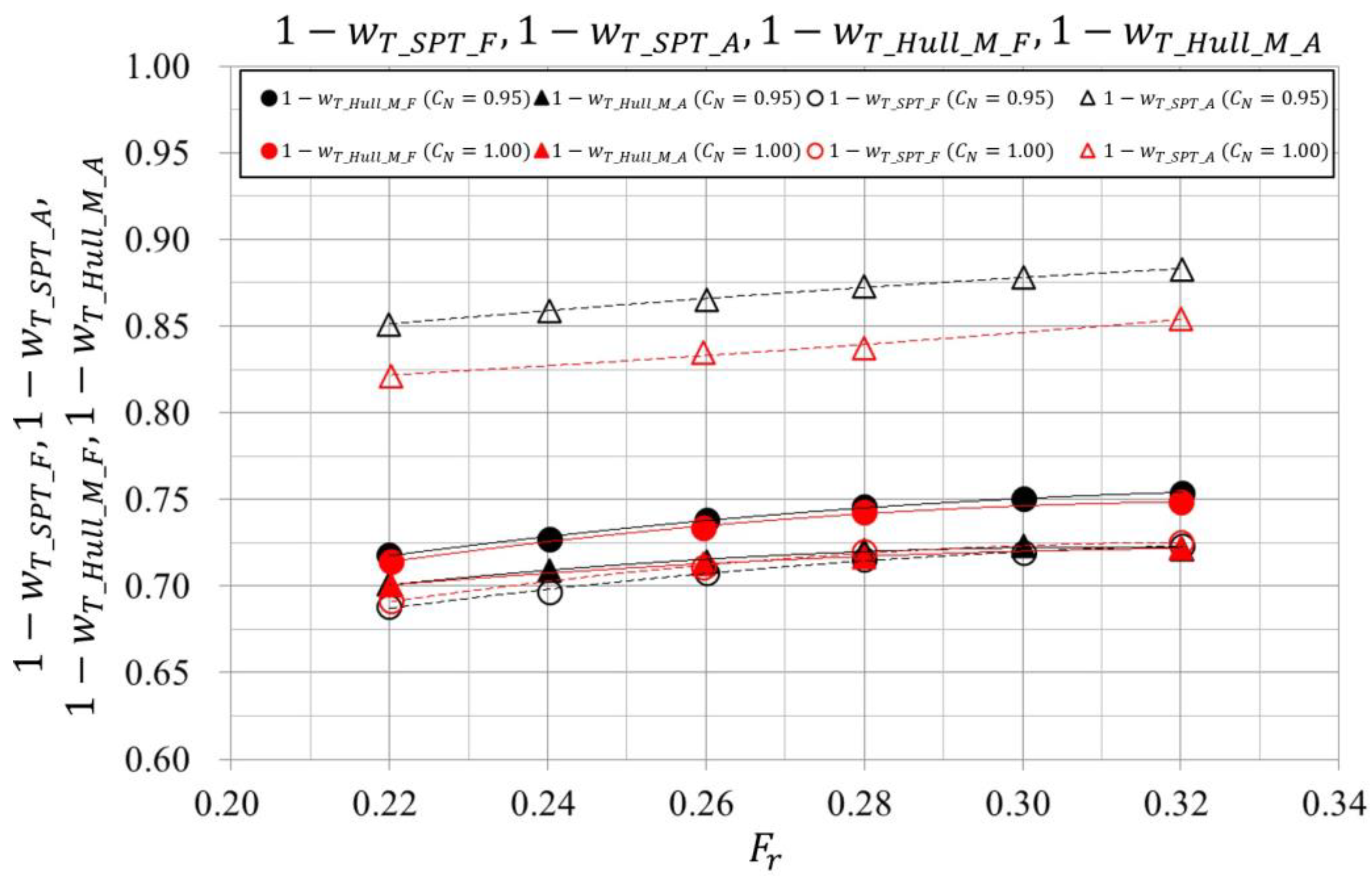
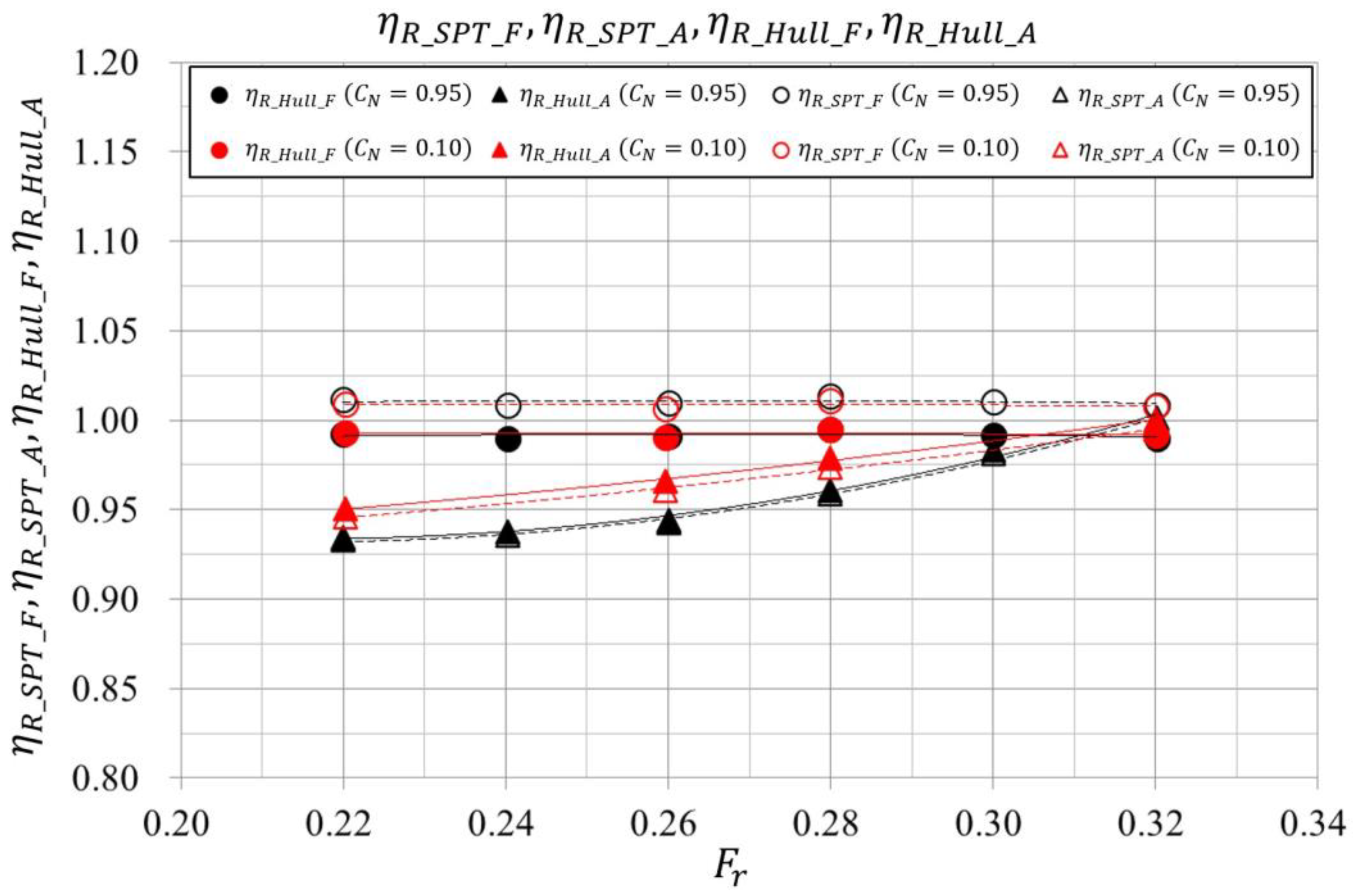
3.2. Towing Tank Test Results
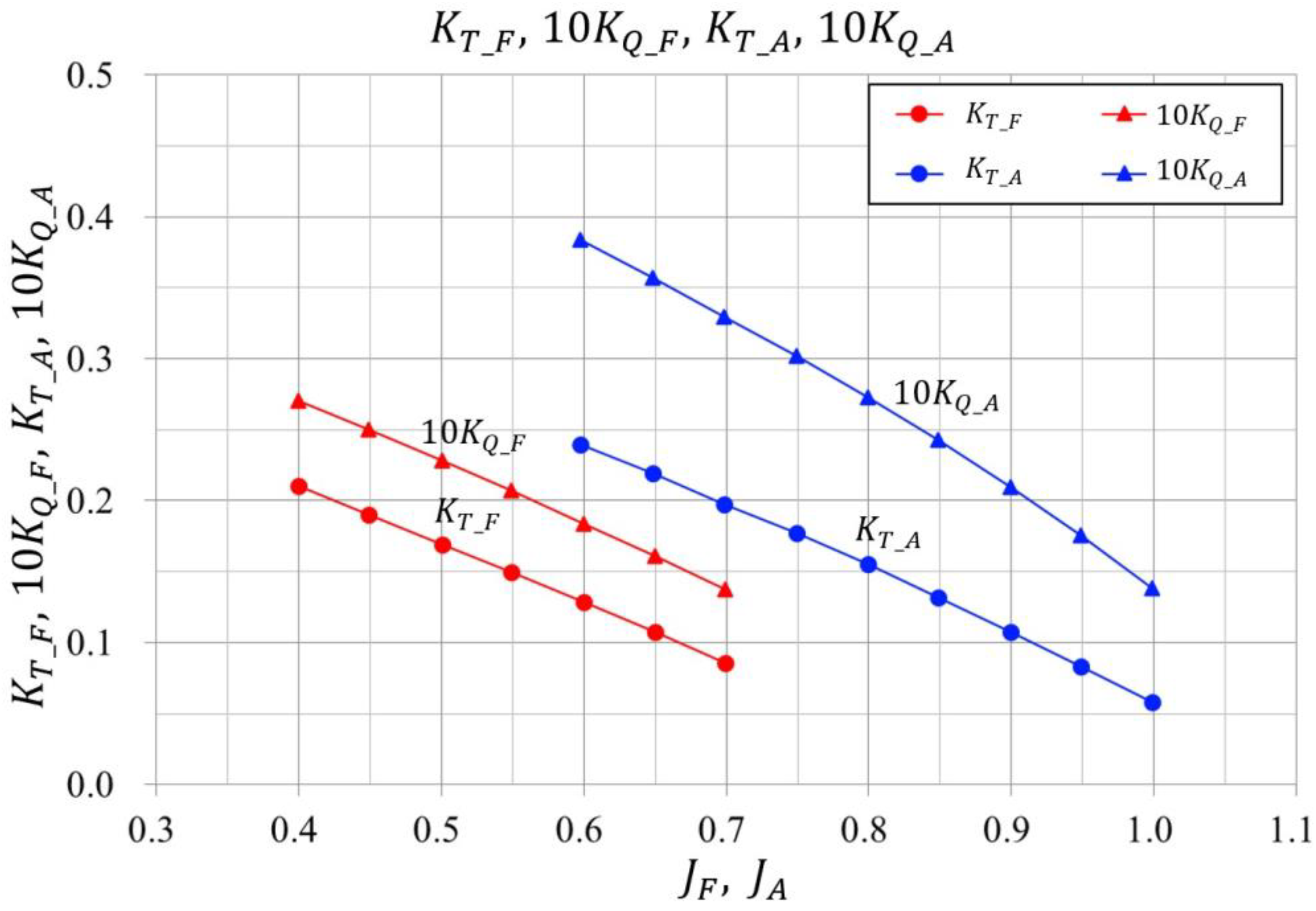
3.2.1. Propeller Open Water Test Result
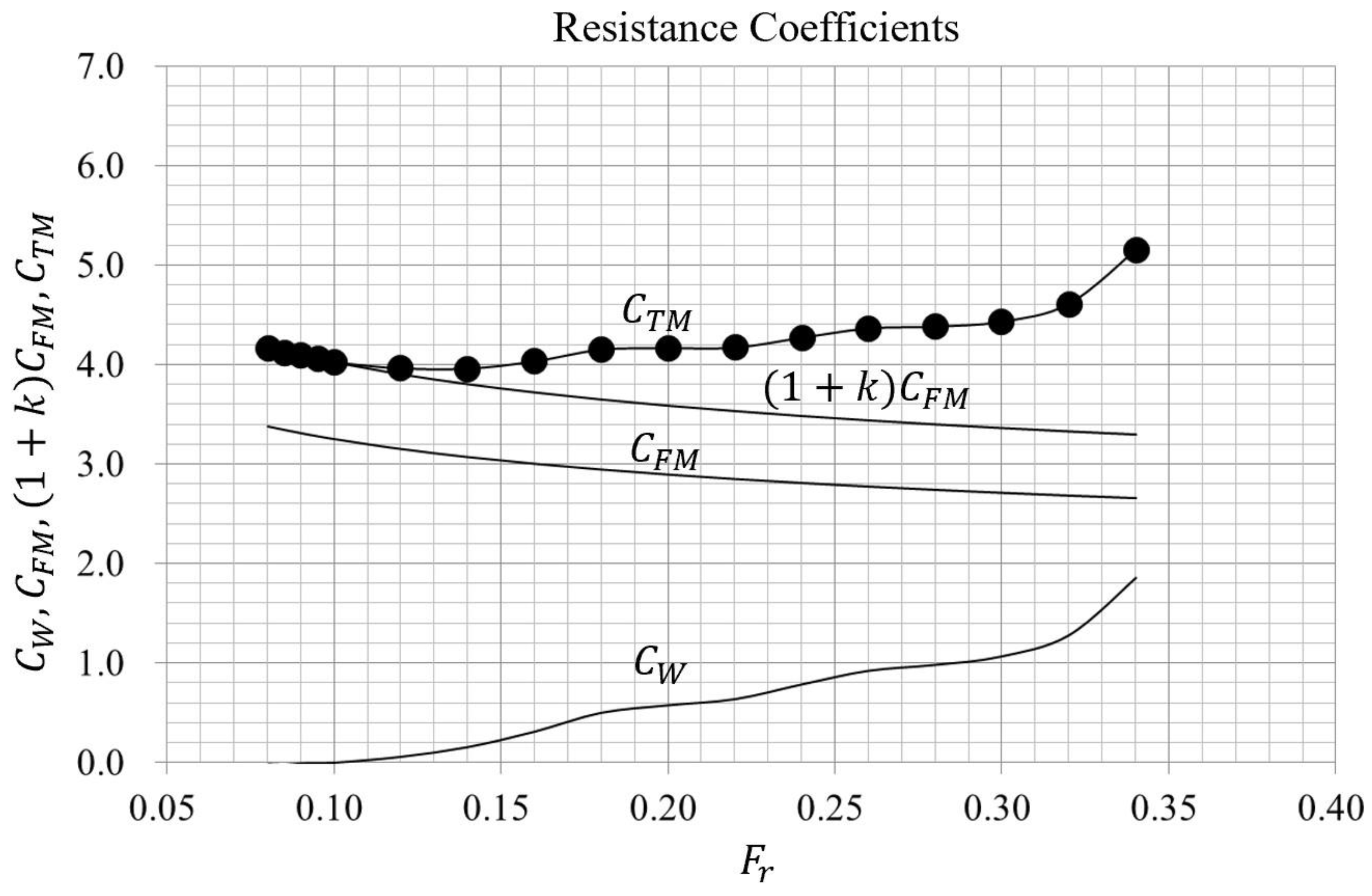
3.2.2. Resistance Test Result
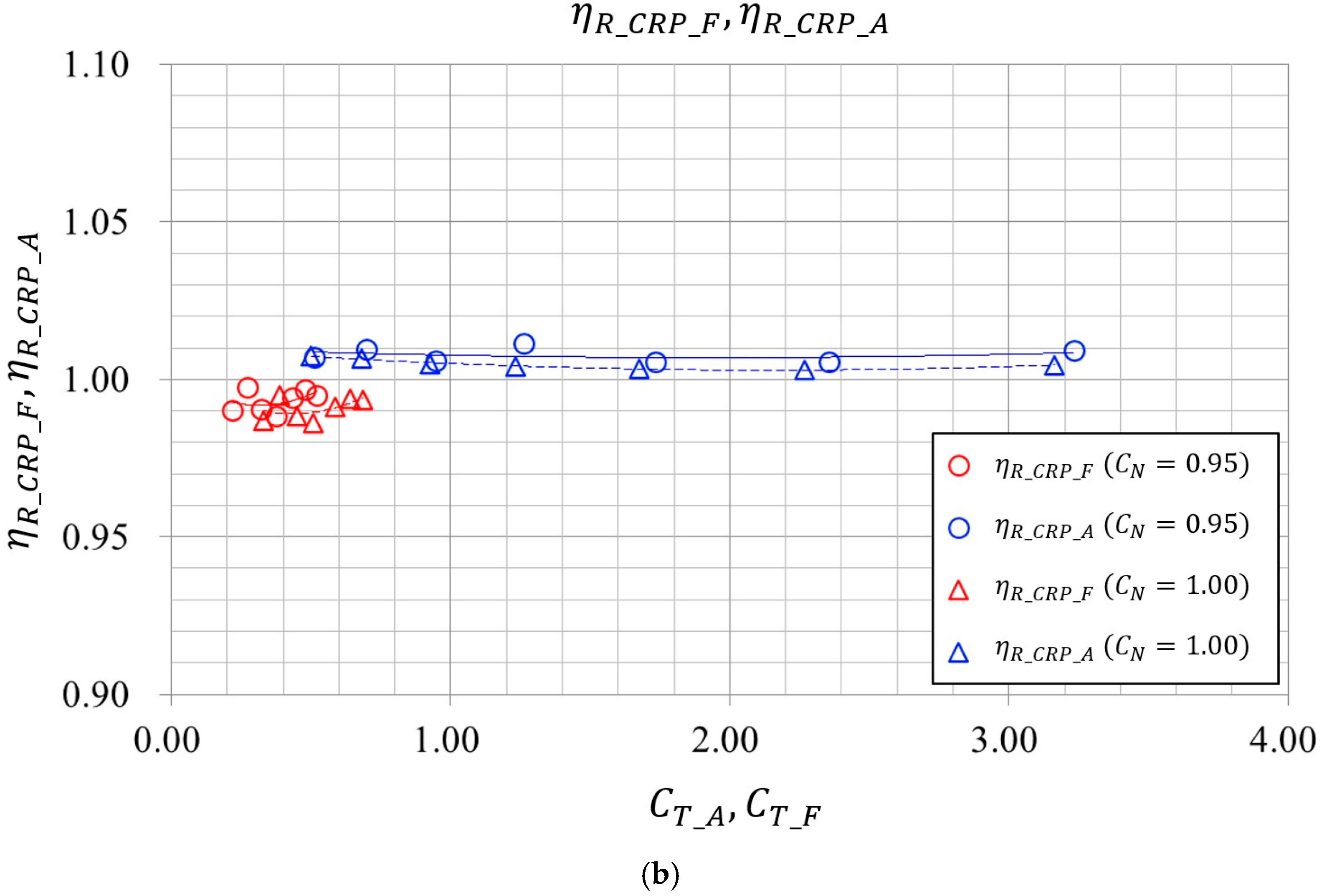
3.2.3. Self-Propulsion Test Result
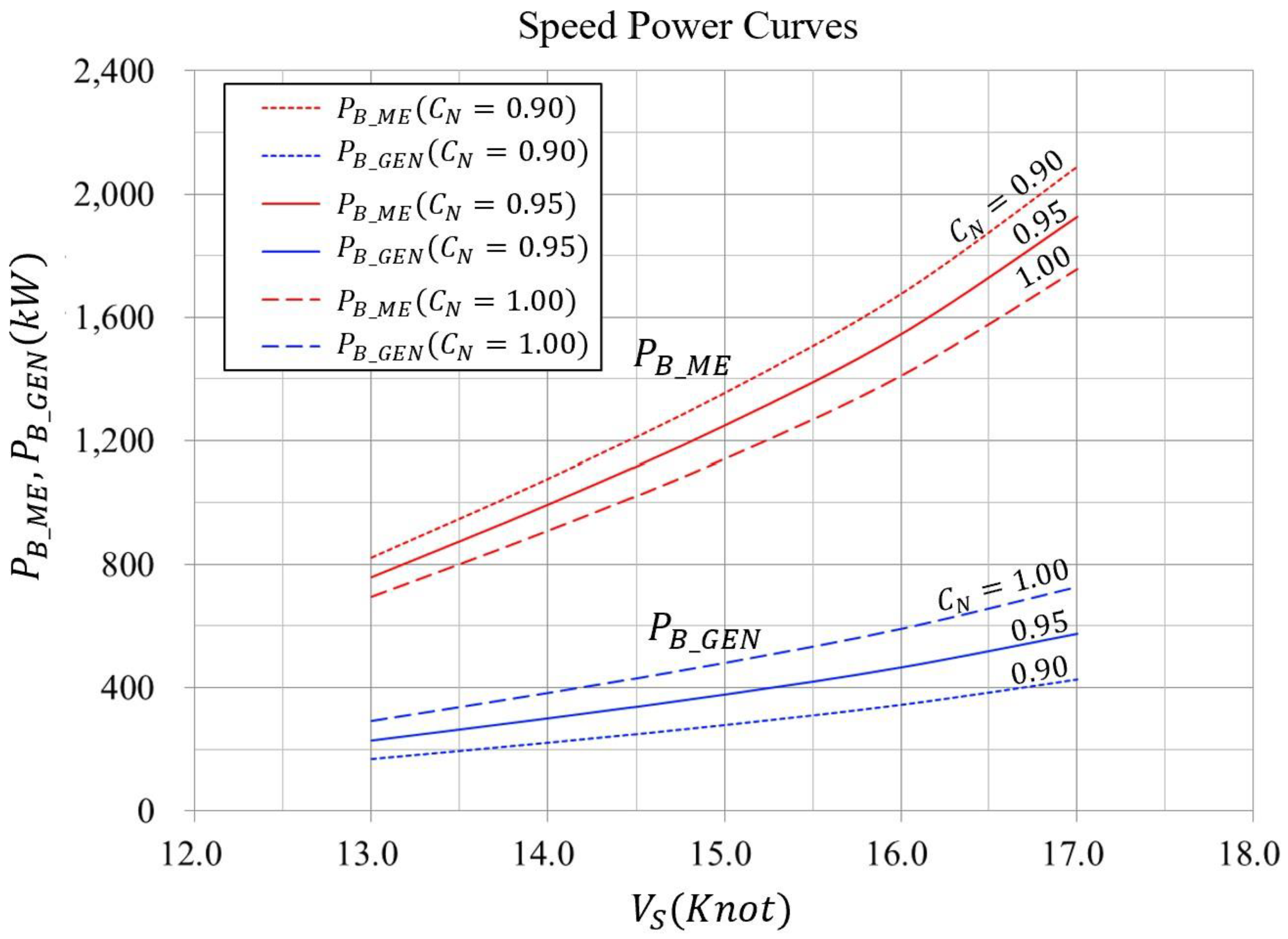
3.2.4. Estimated Speed Power Curves
4. Validation with Speed Trial in Actual Sea
4.1. Speed Trial at Constant Rotational Speed Ratio of Two Propellers
4.2. Rotational Speed Ratio Variation Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variable | Definition |
| Frictional resistance coefficient of a body in model scale | |
| Rotational speed ratio of two propellers | |
| Propeller loading factor | |
| Total resistance coefficient in model scale | |
| Wave making resistance coefficient | |
| Propeller diameter | |
| Towing force in self-propulsion test | |
| Froude Number | |
| Advance coefficient of propeller | |
| Three-dimensional form factor on flat plate friction | |
| Torque coefficient | |
| Thrust coefficient | |
| Rate of revolution | |
| Brake power | |
| Propeller torque | |
| Total resistance | |
| Thrust deduction fraction | |
| Propeller thrust | |
| Required thrust accounting for thrust deduction and total resistance | |
| Advance speed | |
| Thrust wake fraction | |
| Mechanical efficiency of transmission between engine and propeller | |
| Propeller efficiency in open water | |
| Relative rotative efficiency | |
| Mass density of water | |
| Subscript | Definition |
| The association with aft propeller | |
| The effect due to CRP interaction | |
| The association with fore propeller | |
| The effect due to Hull-Propeller interaction | |
| The association with model scale ship | |
| The effect due to POD-Propeller interaction | |
| The association with full scale ship | |
| The total effect due to CRP, POD and hull at self-propulsion test |
References
- IMO. 2023 IMO STRATEGY ON REDUCTION OF GHG EMISSION FROM SHIPS. Resolut. Mepc. 2023, 377, 2023. [Google Scholar]
- Soltani Motlagh, H.R.; Issa Zadeh, S.B.; Garay-Rondero, C.L. Towards International Maritime Organization Carbon Targets: A Multi-Criteria Decision-Making Analysis for Sustainable Container Shipping. Sustainability 2023, 15, 16834. [Google Scholar] [CrossRef]
- Issa-Zadeh, S.B.; Garay-Rondero, C.L. Maritime Pilotage and Sustainable Seaport: A Systematic Review. J. Mar. Sci. Eng. 2025, 13, 945. [Google Scholar] [CrossRef]
- Inukai, Y. Development of Electric Propulsion Vessels with Contra-Rotating Propeller. J. JIME 2011, 46, 26–32. [Google Scholar] [CrossRef][Green Version]
- Shimamoto, H.; Takeda, A.; Miyake, S. Tandem Hybrid CRP(Contra-Rotating-Propeller) System. J. JIME 2011, 46, 39–42. [Google Scholar] [CrossRef][Green Version]
- Nakamura, S.; Ohta, T.; Yonekura, K.; Sasajima, T.; Sakai, K. World’s First Contra-Rotating Propeller System Successfully Fitted to a Merchant Ship. In Proceedings of the Eleventh International Marine Propulsion Conference and Exhibition, Amsterdam, The Netherlands, 27–29 November 1989. [Google Scholar]
- SNishiyama; Sakamoto, Y.; Ishida, S.; Fujino, R.; Oshima, M. Development of Contrarotating-Propeller System for Juno-A 37,000-DWT Class Bullk Carrier. Trans. Soc. Nav. Archit. Mar. Eng. 1990, 98, 27–52. [Google Scholar][Green Version]
- Mewis, F. The Efficiency of Pod Propulsion. In Proceedings of the Twenty Second International Conference HADMAR 2001, Varna, Bulgaria, 1–4 October 2001. [Google Scholar]
- The First Hybrid CRP-POD Driven Fast ROPAX Ferry in the World. Available online: https://www.mhi.co.jp/technology/review/pdf/e416/e416338.pdf (accessed on 19 August 2025).
- Quereda, R.; Veikonheimo, T.; Pérez-Sobrino, M.; Ponce, J.; Sánchez-Caja, A.; Masip, J.; González-Adalid, J.; Uriarte, A.; Nijland, M.; Kokkila, K. Model testing and scaling for CRP POD. In Proceedings of the 10th International Conference on Hydrodynamics, St. Petersburg, Russia, 1–4 October 2012. [Google Scholar]
- Sánchez-Caja, A.; Pérez-Sobrino, M.; Quereda, R.; Nijland, M.; Veikonheimo, T.; González-Adalid, J.; Saisto, I.; Uriarte, A. Combination of Pod, CLT and CRP Propulsion for Improving Ship Efficiency: The TRIPOD project. In Proceedings of the Third International Symposium on Marine Propulsion Smp’13, Tasmania, Australia, 5–8 May 2013. [Google Scholar]
- Quereda, R.; Pérez-Sobrino, M.; González-Adalid, J.; Soriano, C. Conventional propeller in CRP-POD configuration. Tests an extrapolation. In Proceedings of the Fifth International Symposium on Marine Propulsors SMP’17, Espoo, Finland, 12–15 June 2017. [Google Scholar]
- van Manen, J.D.; Oosterveld, M.W.C. Model Tests on Contra-Rotating Propellers. In Proceedings of the Seventh ONR Symposium on Naval Hydrodynamics, Rome, Italy, 25–30 August 1968. [Google Scholar]
- Inukai, Y.; Ando, J. Full Scale Performance Prediction Method for a Ship with Contra Rotating Propellers. In Proceedings of the Fifth International Symposium on Marine Propulsion SMP’17, Espoo, Finland, 12–15 June 2017. [Google Scholar]
- Podded Propulsion Tests and Extrapolation. ITTC Recommended Procedure and Guidelines 7.5-02-03-01.3. 2021. Available online: https://www.ittc.info/media/10178/75-02-03-013-2.pdf (accessed on 19 August 2025).
- Sasaki, N.; Kuroda, M.; Fujisawa, J.; Imoto, T.; Sato, M. On the Model Tests and Design Method of Hybrid CRP Podded Propulsion System of a Feeder Container Ship. In Proceedings of the First International Symposium on Marine Propulsors Smp’09, Trondheim, Norway, 22–24 June 2009. [Google Scholar]
- Chang, B.J.; Go, S. Study on a procedure for propulsive performance prediction for CRP-POD systems. J. Mar. Sci. Technol. 2011, 16, 1–7. [Google Scholar] [CrossRef]
- Hybrid Contra-Rotating Shaft Pod Propulsors Model Test. ITTC Recommended Procedure and Guidelines 7.5-02-03-01.6. 2014. Available online: https://ittc.info/media/4072/75-02-03-016.pdf (accessed on 19 August 2025).
- Wakabayashi, T.; Katsui, T. Propeller Open-Water Test Method for Hybrid Contra Rotating Propeller. J. Mar. Sci. Eng. 2025, 13, 858. [Google Scholar] [CrossRef]
- Propulsion/Bollard Pull Test. ITTC Recommended Procedure and Guidelines 7.5-02-03-01.1. 2021. Available online: http://www.ittc.info/media/9607/75-02-03-011.pdf (accessed on 19 August 2025).
- Open Water Test. ITTC Recommended Procedure and Guidelines 7.5-02-03-02.1. 2021. Available online: https://www.ittc.info/media/9621/75-02-03-021.pdf (accessed on 19 August 2025).
- Resistance Test. ITTC Recommended Procedure and Guidelines 7.5-02-02-01.5. 2021. Available online: https://www.ittc.info/media/11780/75-02-02-01.pdf (accessed on 19 August 2025).
- 1978 ITTC Performance Prediction Method. ITTC Recommended Procedure and Guidelines 7.5-02-03-01.4. 2021. Available online: https://www.ittc.info/media/9872/75-02-03-014.pdf (accessed on 19 August 2025).
- Yazaki, A. A diagram to estimate the wake fraction for an actual ship from model tank test. In Proceedings of the 12th International Towing Tank Conference, Rome, Italy, 22–30 September 1969; p. 259. [Google Scholar]
- Tsu Ship Model Basin. Available online: https://ittc.info/media/5616/facilities-form-jmu-tsmb.pdf (accessed on 19 August 2025).
- Shoenherr, K.E. Resistance of flat surfaces moving through a fluid. Trans. Soc. Nav. Archit. Mar. Eng. 1932, 40, 279–313. [Google Scholar]
- Schuiling, B.; Kerkvliet, M.; Rijpkema, D. An Experimental Study on Visualisation and Passive Control of Model Propeller Boundary Layers. In Proceedings of the Eighth International Symposium on Marine Propulsion Smp’24, Berlin, Germany, 17–20 March 2024. [Google Scholar]
- Xiong, Y.; Zhang, K.; Wang, Z.-Z.; Qi, W.-J. Numerical and Experimental Studies on the Effect of Axial Spacing on Hydrodynamic Performance of the Hybrid CRP Pod Propulsion System. China Ocean. Eng. 2016, 30, 627–636. [Google Scholar] [CrossRef]
- Wang, Z.-Z.; Xiong, Y.; Wang, R.; Zhong, C.-H. A numerical investigation of the scale effect of hydro dynamic performance of the hybrid CRP pod propulsion system. Appl. Ocean. Res. 2016, 54, 26–38. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Zhou, X.-P.; Cheng, X.-K.; Li, Y.-L. A numerical study on the interaction between forward and aft propeller of hybrid CRP pod propulsion systems. Ocean. Eng. 2019, 186, 106084. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Cheng, X.-K.; Feng, L. Numerical investigation of the unsteady flow of a hybrid CRP pod propulsion system at behind-hull condition. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 918–927. [Google Scholar] [CrossRef]













| Length | 240 m |
| Width | 18 m |
| Depth | 8 m |
| Position | Fore | Aft |
|---|---|---|
| Diameter | 0.2800 m | 0.2221 m |
| Pitch Ratio | 0.7800 | 0.9600 |
| Expand Area Ratio | 0.5000 | 0.5000 |
| Number of Blades | 4 | 5 |
| Rotation direction | CW | CCW |
| Model Scale | Full Scale | |
|---|---|---|
| Length | 7.4667 m | 80.000 m |
| Breadth | 1.4000 m | 15.000 m |
| Depth | 0.7467 m | 8.000 m |
| Draft | 0.4667 m | 5.000 m |
| Displacement volume | 2.2989 m3 | 2827.49 m3 |
| Wetted surface area | 10.9125 m2 | 1252.72 m2 |
| Length | 77.000 m |
| L/B | 5.5000 |
| B/d | 3.1111 |
| Fore Propeller | Main engine driven CPP |
| Aft Propeller | Electric driven Podded FPP |
| Output | Error |
|---|---|
| M1 | −5.0% |
| M2 | −2.7% |
| M3 | −2.2% |
| M4 | −0.6% |
| M5 | −0.6% |
| Revolution Ratio | Power Distribution (Present Method) | Power Distribution (Sea Trial) |
|---|---|---|
| 0.92 | 0.81 | 0.83 |
| 0.96 | 0.75 | 0.78 |
| 0.99 | 0.71 | 0.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wakabayashi, T.; Katsui, T. Power Estimation Method and Its Validation for Ships with Hybrid Contra Rotating Propeller. J. Mar. Sci. Eng. 2025, 13, 1740. https://doi.org/10.3390/jmse13091740
Wakabayashi T, Katsui T. Power Estimation Method and Its Validation for Ships with Hybrid Contra Rotating Propeller. Journal of Marine Science and Engineering. 2025; 13(9):1740. https://doi.org/10.3390/jmse13091740
Chicago/Turabian StyleWakabayashi, Tomoki, and Tokihiro Katsui. 2025. "Power Estimation Method and Its Validation for Ships with Hybrid Contra Rotating Propeller" Journal of Marine Science and Engineering 13, no. 9: 1740. https://doi.org/10.3390/jmse13091740
APA StyleWakabayashi, T., & Katsui, T. (2025). Power Estimation Method and Its Validation for Ships with Hybrid Contra Rotating Propeller. Journal of Marine Science and Engineering, 13(9), 1740. https://doi.org/10.3390/jmse13091740






