A Discrete Particle Modeling Framework for Exploring the Evolution of Aeolian Sediment Transport on Moist Sand Surfaces
Abstract
1. Introduction
2. Methodology
2.1. Grain Motion Model
2.2. Liquid Bridge Model and Its Evolution Rule
2.3. Airflow Model
2.4. Simulation Set-Up
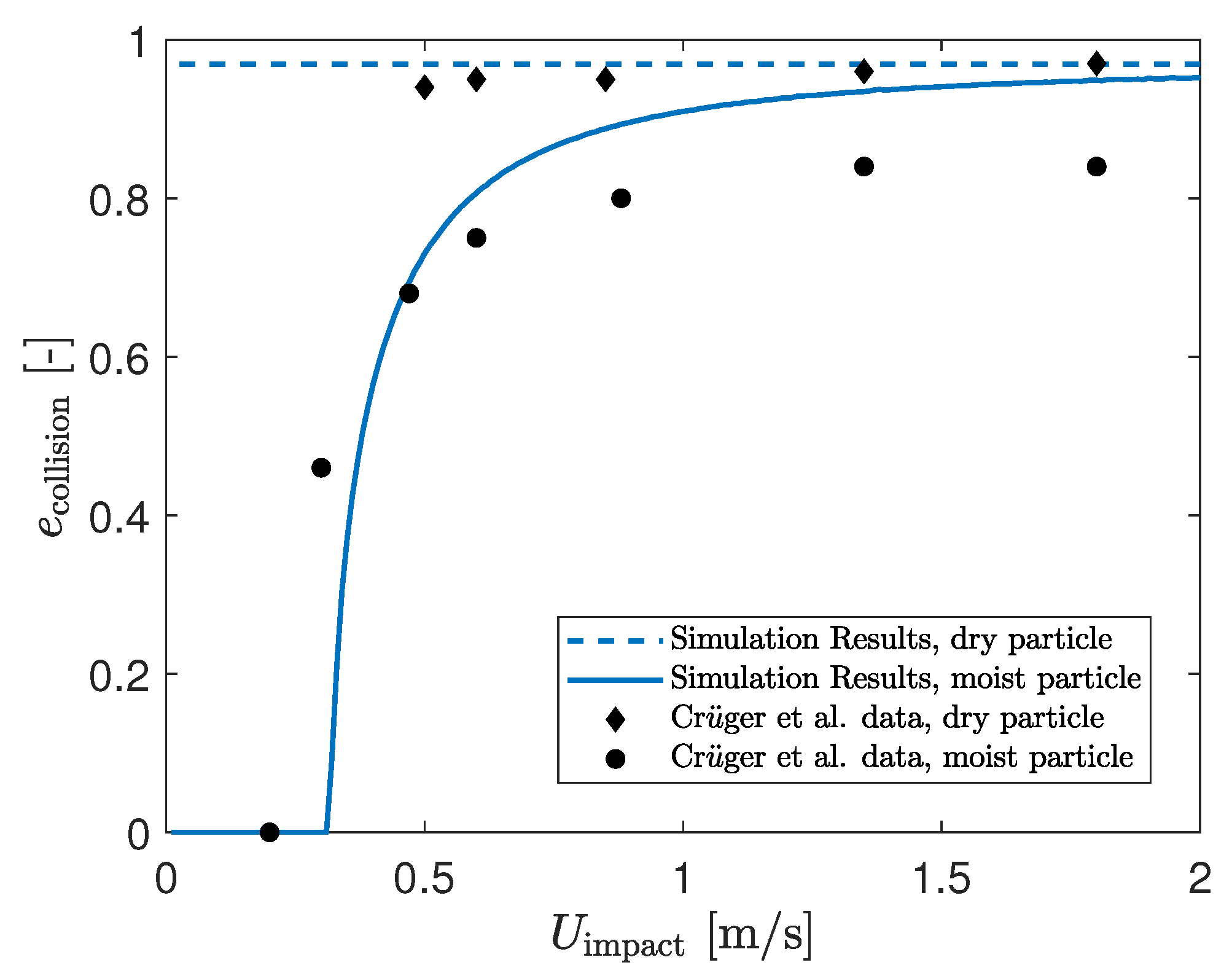
2.5. Validation of the Modeling Framework
Validation of the Transport Model at the Dry Limit
3. Results
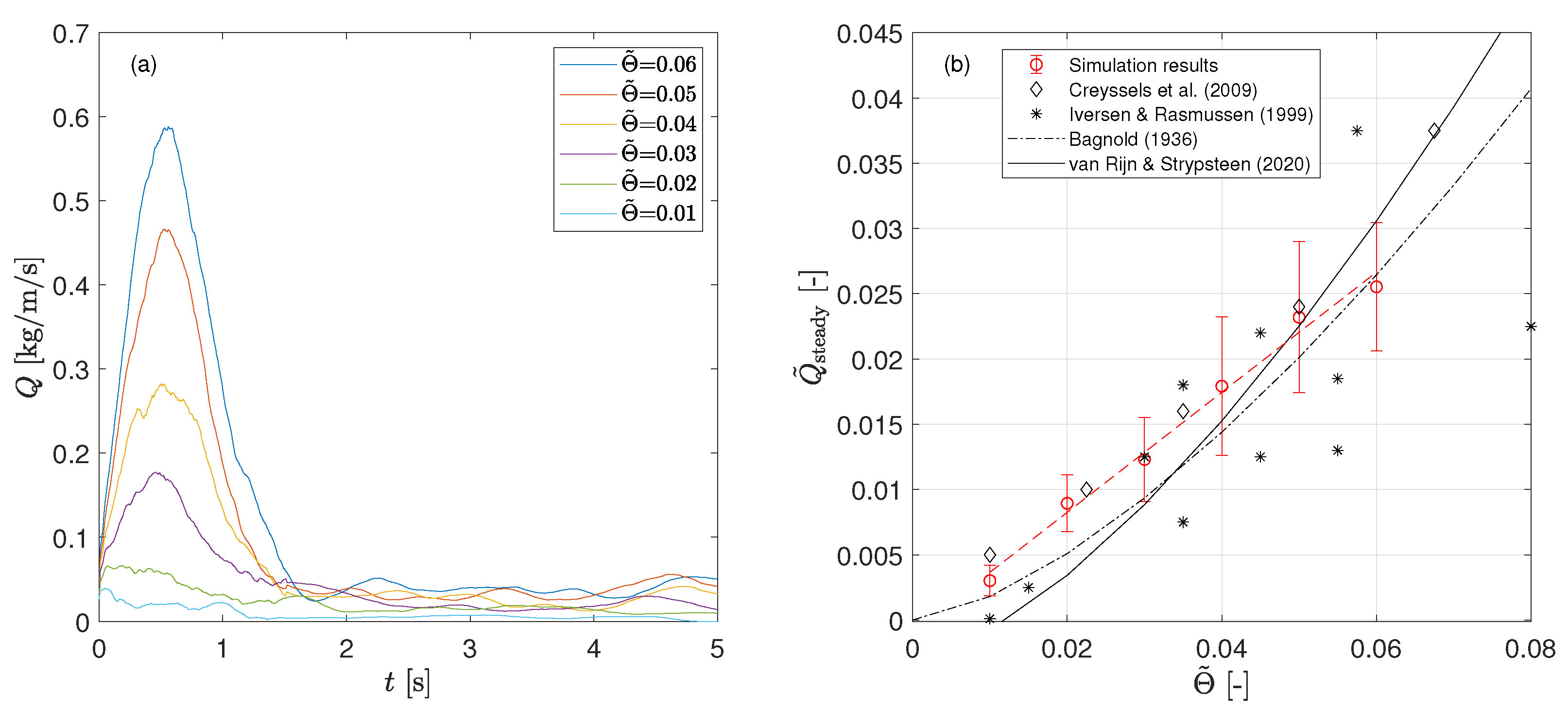
3.1. The Steady State of Transport
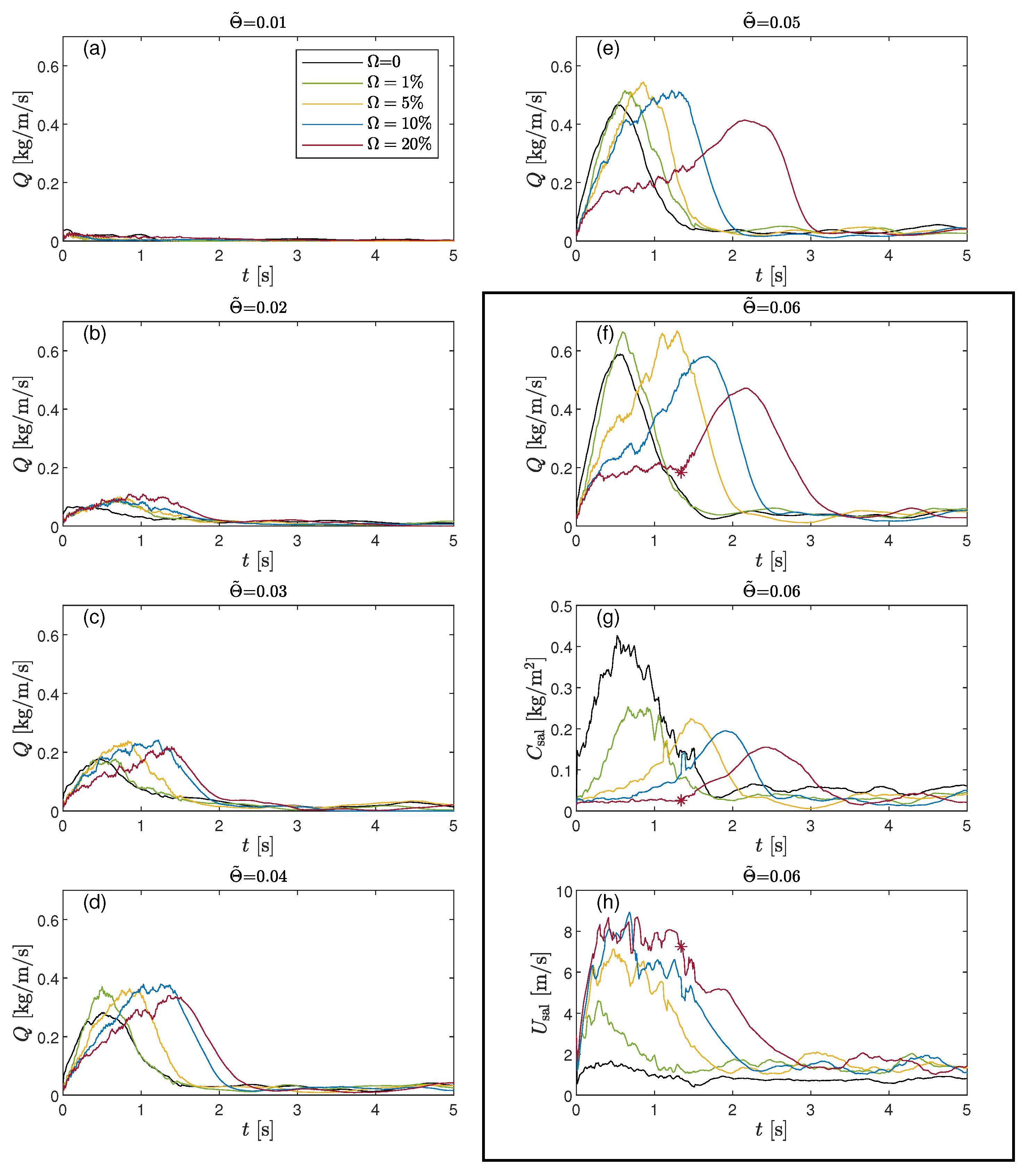
3.2. The Evolution of Transport
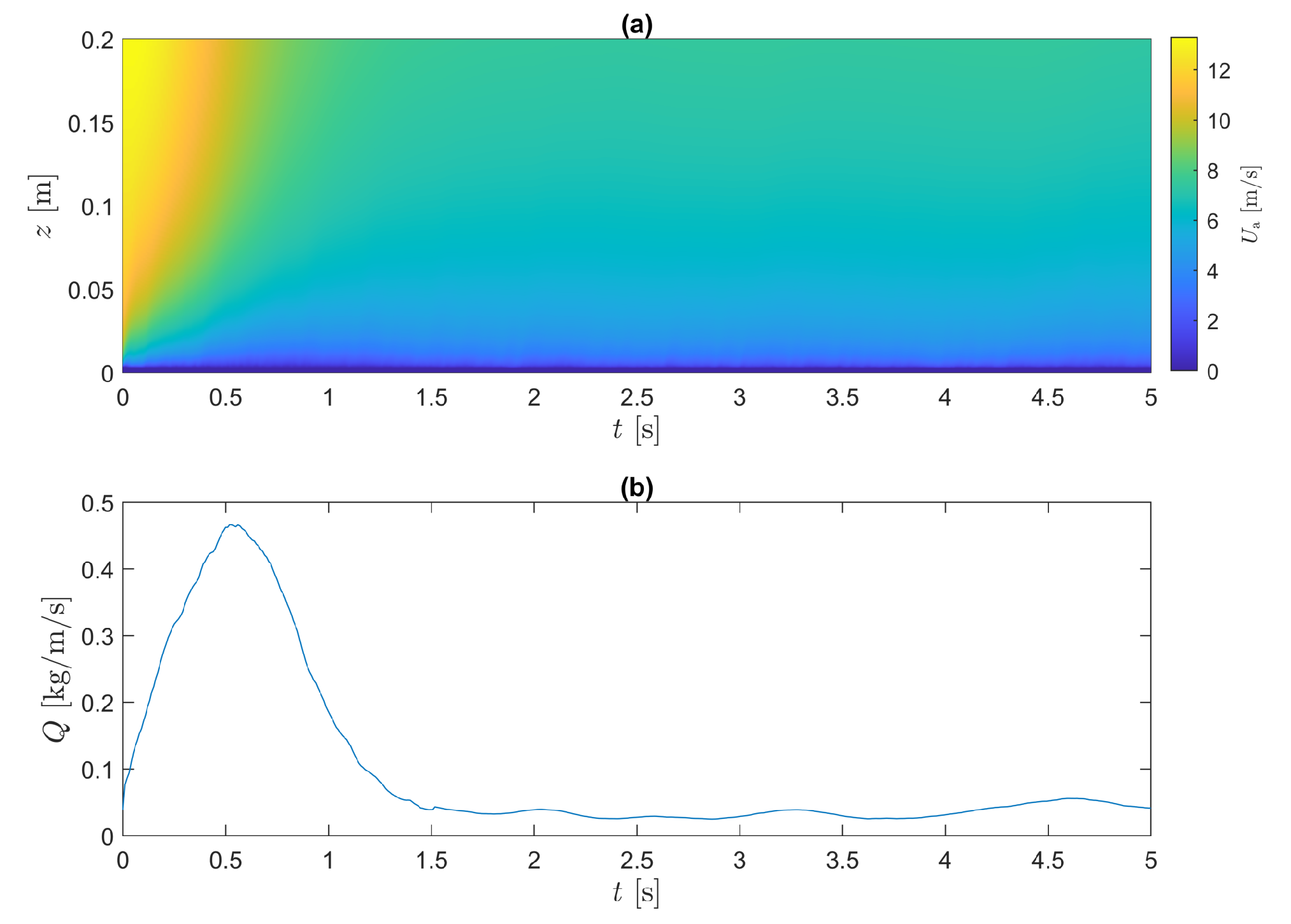
3.2.1. Temporal Evolution
3.2.2. Spatial Evolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Evolution of Wind Velocity Profile
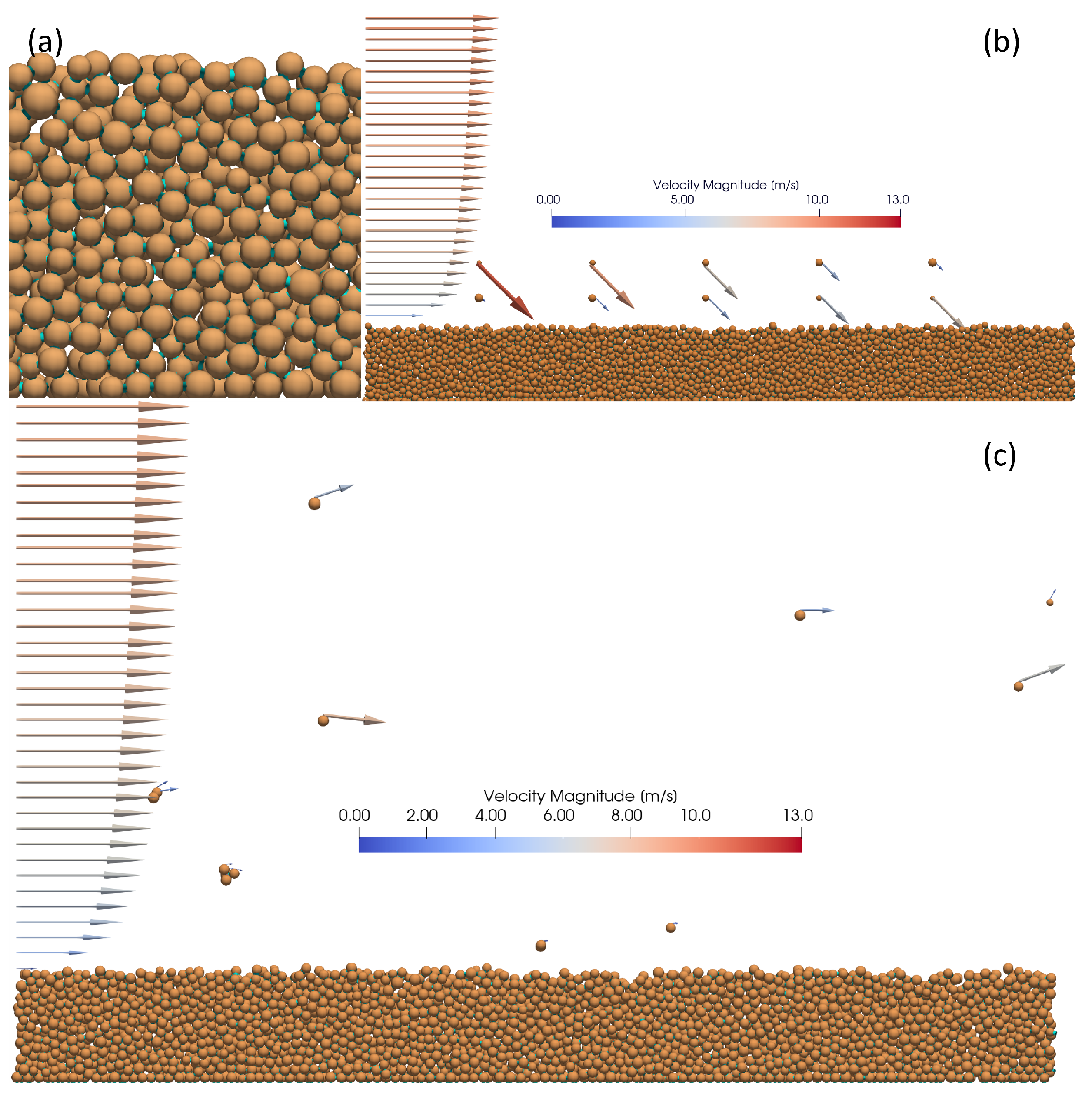
Appendix B. Direct Shear Test of the Moist Sediment Bed

Appendix C. An Overview of Different Initiation Conditions
| Number of Initiating Particles (Nip) | Particle ID | Position [m] | Velocity [m/s] | Diameter [mm] | ||
|---|---|---|---|---|---|---|
| 10 | 1 | 4 | 3.75 | 1 | −1 | 0.28 |
| 2 | 8 | 3.75 | 2 | −2 | 0.25 | |
| 3 | 12 | 3.75 | 3 | −3 | 0.22 | |
| 4 | 16 | 3.75 | 4 | −4 | 0.19 | |
| 5 | 20 | 3.75 | 5 | −5 | 0.16 | |
| 6 | 4 | 5 | 8 | −8 | 0.16 | |
| 7 | 8 | 5 | 6.4 | −6.4 | 0.19 | |
| 8 | 12 | 5 | 4.8 | −4.8 | 0.22 | |
| 9 | 16 | 5 | 3.2 | −3.2 | 0.25 | |
| 10 | 20 | 5 | 1.6 | −1.6 | 0.28 | |
| 5 | 1 | 4 | 3.9 | 2.10 | −2.10 | 0.27 |
| 2 | 8 | 4.1 | 3.34 | −3.34 | 0.24 | |
| 3 | 12 | 4.4 | 3.90 | −3.90 | 0.22 | |
| 4 | 16 | 4.6 | 3.44 | −3.44 | 0.24 | |
| 5 | 20 | 4.8 | 2.13 | −2.13 | 0.27 | |
| 1 | 1 | 12 | 4.4 | 2.92 | −2.92 | 0.25 |
Appendix D. An Estimation of Evaporation During Transport
Appendix D.1. Evaporation from the Bed
Appendix D.2. Evaporation on a Moist Saltating Particle

References
- Belly, P.Y. Sand movement by wind. In USACE Technical Memorandum 01; U.S. Army Corps of Engineers: Washington, DC, USA, 1964. [Google Scholar]
- McKenna-Neuman, C.; Nickling, W.G. A theoretical and wind tunnel investigation of the effect of capillary water on the entrainment of sediment by wind. Can. J. Soil Sci. 1989, 69, 79–96. [Google Scholar] [CrossRef]
- Neuman, C.M.; Scott, M.M. A wind tunnel study of the influence of pore water on aeolian sediment transport. J. Arid. Environ. 1998, 39, 403–419. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, X.; Wang, X. Wind initiation thresholds of the moistened sands. Geophys. Res. Lett. 2002, 29, 25-1–25-4. [Google Scholar] [CrossRef]
- Han, Q.; Qu, J.; Zhang, K.; Zu, R.; Niu, Q.; Liao, K. Wind tunnel investigation of the influence of surface moisture content on the entrainment and erosion of beach sand by wind using sands from tropical humid coastal southern China. Geomorphology 2009, 104, 230–237. [Google Scholar] [CrossRef]
- Davidson-Arnott, R.G.D.; Yang, Y.; Ollerhead, J.; Hesp, P.A.; Walker, I.J. The effects of surface moisture on aeolian sediment transport threshold and mass flux on a beach. Earth Surf. Processes Landforms J. Br. Geomorphol. Res. Group 2008, 33, 55–74. [Google Scholar] [CrossRef]
- Han, Q.; Qu, J.; Liao, K.; Zhu, S.; Zhang, K.; Zu, R.; Niu, Q. A wind tunnel study of aeolian sand transport on a wetted sand surface using sands from tropical humid coastal southern China. Environ. Earth Sci. 2011, 64, 1375–1385. [Google Scholar] [CrossRef]
- Rotnicka, J. Aeolian vertical mass flux profiles above dry and moist sandy beach surfaces. Geomorphology 2013, 187, 27–37. [Google Scholar] [CrossRef]
- Swann, C.; Lee, D.; Trimble, S.; Key, C. Aeolian sand transport over a wet, sandy beach. Aeolian Res. 2021, 51, 100712. [Google Scholar] [CrossRef]
- Davidson-Arnott, R.G.D.; Bauer, B.O. Aeolian sediment transport on a beach: Thresholds, intermittency, and high frequency variability. Geomorphology 2009, 105, 117–126. [Google Scholar] [CrossRef]
- Delgado-Fernandez, I.; Davidson-Arnott, R. Meso-scale aeolian sediment input to coastal dunes: The nature of aeolian transport events. Geomorphology 2011, 126, 217–232. [Google Scholar] [CrossRef]
- Bagnold, R. The Physics of Blown Sand and Desert Dunes; University of Arizona Press: Tucson, AZ, USA, 1941. [Google Scholar]
- Shao, Y.; Raupach, M. The overshoot and equilibration of saltation. J. Geophys. Res. Atmos. 1992, 97, 20559–20564. [Google Scholar] [CrossRef]
- Selmani, H.; Valance, A.; Ould El Moctar, A.; Dupont, P.; Zegadi, R. Aeolian sand transport in out-of-equilibrium regimes. Geophys. Res. Lett. 2018, 45, 1838–1844. [Google Scholar] [CrossRef]
- Delgado-Fernandez, I. A review of the application of the fetch effect to modelling sand supply to coastal foredunes. Aeolian Res. 2010, 2, 61–70. [Google Scholar] [CrossRef]
- Strypsteen, G.; Delgado-Fernandez, I.; Derijckere, J.; Rauwoens, P. Fetch-driven aeolian sediment transport on a sandy beach: A new study. Earth Surf. Processes Landforms 2024, 49, 1530–1543. [Google Scholar] [CrossRef]
- Haehnel, R.; Buck, N.; Song, A. Moisture effects on eolian particle entrainment. Environ. Fluid Mech. 2014, 14, 135–156. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Gladkyy, A.; Schwarze, R. Comparison of different capillary bridge models for application in the discrete element method. Granul. Matter 2014, 16, 911–920. [Google Scholar] [CrossRef]
- Carneiro, M.V.; Pähtz, T.; Herrmann, H.J. Jump at the onset of saltation. Phys. Rev. Lett. 2011, 107, 098001. [Google Scholar] [CrossRef]
- Durán, O.; Andreotti, B.; Claudin, P. Numerical simulation of turbulent sediment transport, from bed load to saltation. Phys. Fluids 2012, 24, 103306. [Google Scholar] [CrossRef]
- Pähtz, T.; Durán, O. The cessation threshold of nonsuspended sediment transport across aeolian and fluvial environments. J. Geophys. Res. Earth Surf. 2018, 123, 1638–1666. [Google Scholar] [CrossRef]
- Pähtz, T.; Omeradžić, A.; Carneiro, M.V.; Araújo, N.A.; Herrmann, H.J. Discrete element method simulations of the saturation of aeolian sand transport. Geophys. Res. Lett. 2015, 42, 2063–2070. [Google Scholar] [CrossRef]
- Comola, F.; Gaume, J.; Kok, J.F.; Lehning, M. Cohesion-induced enhancement of aeolian saltation. Geophys. Res. Lett. 2019, 46, 5566–5574. [Google Scholar] [CrossRef]
- Jia, S.; Wang, Z. Simulation of aerodynamic entrainment with interparticle cohesions based on discrete element method. Earth Surf. Processes Landforms 2021, 46, 1410–1418. [Google Scholar] [CrossRef]
- Dun, H.; Yue, P.; Huang, N.; Zhang, J. Discrete Element Simulation on Sand-Bed Collision Considering Surface Moisture Content. Processes 2021, 10, 52. [Google Scholar] [CrossRef]
- Ralaiarisoa, V.; Dupont, P.; El Moctar, A.O.; Naaim-Bouvet, F.; Oger, L.; Valance, A. Particle impact on a cohesive granular media. Phys. Rev. E 2022, 105, 054902. [Google Scholar] [CrossRef]
- Roy, S.; Luding, S.; Weinhart, T. Liquid redistribution in sheared wet granular media. Phys. Rev. E 2018, 98, 052906. [Google Scholar] [CrossRef]
- Weinhart, T.; Orefice, L.; Post, M.; van Schrojenstein Lantman, M.P.; Denissen, I.F.; Tunuguntla, D.R.; Tsang, J.; Cheng, H.; Shaheen, M.Y.; Shi, H.; et al. Fast, flexible particle simulations—An introduction to MercuryDPM. Comput. Phys. Commun. 2020, 249, 107129. [Google Scholar] [CrossRef]
- Thornton, A.R.; Plath, T.; Ostanin, I.; Götz, H.; Bisschop, J.W.; Hassan, M.; Roeplal, R.; Wang, X.; Pourandi, S.; Weinhart, T. Recent advances in MercuryDPM. Math. Comput. Sci. 2023, 17, 13. [Google Scholar] [CrossRef]
- Luding, S. Collisions & contacts between two particles. In Physics of Dry Granular Media; Springer: Berlin/Heidelberg, Germany, 1998; pp. 285–304. [Google Scholar]
- Wu, D.; Zhou, P.; Zhao, B.; Howes, T.; Wang, G. Liquid redistribution upon the liquid-bridge rupture between two unequal particles with a minimal energy method. Powder Technol. 2019, 354, 165–173. [Google Scholar] [CrossRef]
- Hagen, T.; Luding, S.; van der Meer, D.; Magnanimo, V.; Jarray, A. Liquid migration in flowing granular materials. EPJ Web Conf. 2021, 249, 09001. [Google Scholar] [CrossRef]
- Mani, R.; Kadau, D.; Or, D.; Herrmann, H.J. Fluid depletion in shear bands. Phys. Rev. Lett. 2012, 109, 248001. [Google Scholar] [CrossRef]
- Mani, R.; Kadau, D.; Herrmann, H.J. Liquid migration in sheared unsaturated granular media. Granul. Matter 2013, 15, 447–454. [Google Scholar] [CrossRef]
- Willett, C.D.; Adams, M.J.; Johnson, S.A.; Seville, J.P.K. Capillary bridges between two spherical bodies. Langmuir 2000, 16, 9396–9405. [Google Scholar] [CrossRef]
- Adams, M.; Perchard, V. The cohesive forces between particles with interstitial liquid. In Proceedings of the Institute of Chemical Engineering Symposium, Perth, Australia, 25–28 August 1985; Volume 91, pp. 147–160. [Google Scholar]
- Lian, G.; Thornton, C.; Adams, M.J. Discrete particle simulation of agglomerate impact coalescence. Chem. Eng. Sci. 1998, 53, 3381–3391. [Google Scholar] [CrossRef]
- Anand, A.; Curtis, J.S.; Wassgren, C.R.; Hancock, B.C.; Ketterhagen, W.R. Predicting discharge dynamics of wet cohesive particles from a rectangular hopper using the discrete element method (DEM). Chem. Eng. Sci. 2009, 64, 5268–5275. [Google Scholar] [CrossRef]
- Campmans, G.H.P.; Wijnberg, K.M. Modelling the vertical grain size sorting process in aeolian sediment transport using the discrete element method. Aeolian Res. 2022, 57, 100817. [Google Scholar] [CrossRef]
- Van Driest, E.R. On turbulent flow near a wall. J. Aeronaut. Sci. 1956, 23, 1007–1011. [Google Scholar] [CrossRef]
- He, Y.; Liu, J.; Cai, F.; Li, B.; Qi, H.; Zhao, S. Aeolian sand transport influenced by tide and beachface morphology. Geomorphology 2022, 396, 107987. [Google Scholar] [CrossRef]
- Jia, S.; Wang, Z. A new ejection model for aeolian splash. Catena 2022, 213, 106191. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Jia, S. Rheological sand bed generates non-rebounding particles. Sedimentology 2025, 72, 34–44. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X.; Wan, L. Influence of contact angle on soil–water characteristic curve with modified capillary rise method. Transp. Res. Rec. 2013, 2349, 32–40. [Google Scholar] [CrossRef]
- Richefeu, V.; El Youssoufi, M.S.; Radjai, F. Shear strength properties of wet granular materials. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 051304. [Google Scholar] [CrossRef] [PubMed]
- van Rijn, L.C. A fully predictive model for aeolian sand transport, part 2: Description and calibration of models and effect of moisture and coarse materials. Coast. Eng. 2022, 171, 104052. [Google Scholar] [CrossRef]
- Yang, R.; Zou, R.; Yu, A. Numerical study of the packing of wet coarse uniform spheres. AIChE J. 2003, 49, 1656–1666. [Google Scholar] [CrossRef]
- Davidson-Arnott, R.G.D.; MacQuarrie, K.; Aagaard, T. The effect of wind gusts, moisture content and fetch length on sand transport on a beach. Geomorphology 2005, 68, 115–129. [Google Scholar] [CrossRef]
- Wiggs, G.; Baird, A.J.; Atherton, R.J. The dynamic effects of moisture on the entrainment and transport of sand by wind. Geomorphology 2004, 59, 13–30. [Google Scholar] [CrossRef]
- Namikas, S.; Edwards, B.; Bitton, M.; Booth, J.; Zhu, Y. Temporal and spatial variabilities in the surface moisture content of a fine-grained beach. Geomorphology 2010, 114, 303–310. [Google Scholar] [CrossRef]
- Schmutz, P.P.; Namikas, S.L. Measurement and modeling of the spatiotemporal dynamics of beach surface moisture content. Aeolian Res. 2018, 34, 35–48. [Google Scholar] [CrossRef]
- Kok, J.F.; Parteli, E.J.; Michaels, T.I.; Karam, D.B. The physics of wind-blown sand and dust. Rep. Prog. Phys. 2012, 75, 106901. [Google Scholar] [CrossRef] [PubMed]
- Crüger, B.; Salikov, V.; Heinrich, S.; Antonyuk, S.; Sutkar, V.S.; Deen, N.G.; Kuipers, J. Coefficient of restitution for particles impacting on wet surfaces: An improved experimental approach. Particuology 2016, 25, 1–9. [Google Scholar] [CrossRef]
- Crüger, B.; Heinrich, S.; Antonyuk, S.; Deen, N.G.; Kuipers, J. Experimental study of oblique impact of particles on wet surfaces. Chem. Eng. Res. Des. 2016, 110, 209–219. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, C.Y. Discrete element analysis of normal elastic impact of wet particles. Powder Technol. 2020, 362, 628–634. [Google Scholar] [CrossRef]
- Darabi, P.; Pougatch, K.; Salcudean, M.; Grecov, D. A novel coalescence model for binary collision of identical wet particles. Chem. Eng. Sci. 2009, 64, 1868–1876. [Google Scholar] [CrossRef]
- Creyssels, M.; Dupont, P.; El Moctar, A.O.; Valance, A.; Cantat, I.; Jenkins, J.T.; Pasini, J.M.; Rasmussen, K.R. Saltating particles in a turbulent boundary layer: Experiment and theory. J. Fluid Mech. 2009, 625, 47–74. [Google Scholar] [CrossRef]
- Iversen, J.D.; Rasmussen, K.R. The effect of wind speed and bed slope on sand transport. Sedimentology 1999, 46, 723–731. [Google Scholar] [CrossRef]
- Bagnold, R.A. The movement of desert sand. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1936, 157, 594–620. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Strypsteen, G. A fully predictive model for aeolian sand transport. Coast. Eng. 2020, 156, 103600. [Google Scholar] [CrossRef]
- O’Brien, P.; Neuman, C.M.K. Effect of the surface water content on dry saltation cloud dynamics: A wind tunnel simulation with particle tracking velocimetry. Earth Surf. Processes Landforms 2023, 48, 3103–3114. [Google Scholar] [CrossRef]
- Gillette, D.A.; Herbert, G.; Stockton, P.H.; Owen, P. Causes of the fetch effect in wind erosion. Earth Surf. Processes Landforms 1996, 21, 641–659. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Zou, X.; Shen, Y.; Wang, R.; Wang, H. Field investigation of the fetch effect and essential conditions for saturated sand flow. Earth Surf. Processes Landforms 2022, 47, 2299–2309. [Google Scholar] [CrossRef]
- Pähtz, T.; Liu, Y.; Xia, Y.; Hu, P.; He, Z.; Tholen, K. Unified model of sediment transport threshold and rate across weak and intense subaqueous bedload, windblown sand, and windblown snow. J. Geophys. Res. Earth Surf. 2021, 126, e2020JF005859. [Google Scholar] [CrossRef]
- Pähtz, T.; Tholen, K. Aeolian sand transport: Scaling of mean saltation length and height and implications for mass flux scaling. Aeolian Res. 2021, 52, 100730. [Google Scholar] [CrossRef]
- Selmani, H.; Besnard, J.B.; Ould El Moctar, A.; Dupont, P.; Valance, A. Experimental study of particle impact on cohesive granular packing. Phys. Rev. E 2024, 110, 014901. [Google Scholar] [CrossRef]
- Schmutz, P.P. Investigation of Factors Controlling the Dynamics of Beach Surface Moisture Content; Louisiana State University and Agricultural & Mechanical College: Baton Rouge, LA, USA, 2014. [Google Scholar]
- Hallin, C.; van IJzendoorn, C.; Homberger, J.M.; de Vries, S. Simulating surface soil moisture on sandy beaches. Coast. Eng. 2023, 185, 104376. [Google Scholar] [CrossRef]
- Thornton, A.; Nguyen, Q.; Polman, H.; Bisschop, J.; Weinhart-Mejia, R.; Vesal, M.; Weinhart, T.; Post, M.; Ostanin, I. Simulating industrial scenarios: With the open-source software MercuryDPM. In Proceedings of the 8th International Conference on Particle-Based Methods, PARTICLES 2023, Milan, Italy, 9–11 October 2023. [Google Scholar]
- Kondo, J.; Saigusa, N.; Sato, T. A parameterization of evaporation from bare soil surfaces. J. Appl. Meteorol. Climatol. 1990, 29, 385–389. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Elsevier: Amsterdam, The Netherlands, 2006; Volume 92. [Google Scholar]
- Murray, F.W. On the computation of saturation vapor pressure. J. Appl. Meteorol. Climatol. 1967, 6, 203–204. [Google Scholar] [CrossRef]
- Camillo, P.; Gurney, R.; Schmugge, T. A soil and atmospheric boundary layer model for evapotranspiration and soil moisture studies. Water Resour. Res. 1983, 19, 371–380. [Google Scholar] [CrossRef]
- Tuijnman, J.T.; Donker, J.J.; Schwarz, C.S.; Ruessink, G. Consequences of a storm surge for aeolian sand transport on a low-gradient beach. J. Mar. Sci. Eng. 2020, 8, 584. [Google Scholar] [CrossRef]
- Williamson, R.E.; Threadgill, E.D. A simulation for the dynamics of evaporating spray droplets in agricultural spraying. Trans. ASAE [Am. Soc. Agric. Eng.] 1974, 17, 254–261. [Google Scholar] [CrossRef]
- Holterman, H. Kinetics and Evaporation of Water Drops in Sir; IMAG: Saratoga, CA, USA, 2003; Number 2003-12. [Google Scholar]
- Li, J.; Zhang, H.; Li, Z.; Du, M.; Chen, J.; Xiong, Y.; Zhang, H.; Cheng, Y. Wetting characteristic and flow behavior of silicate binder at various sand particle-particle interfaces: Fine or coarse, circular or angular particles. J. Mater. Res. Technol. 2023, 26, 7166–7181. [Google Scholar] [CrossRef]





| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Particle contact parameters | |||
| Particle density | kg/m3 | 2650 | |
| Normal stiffness | kg/s2 | 5000 | |
| Normal damping coefficient | kg/s | 4.7 | |
| Tangential stiffness | kg/s2 | 0.29 | |
| Tangential damping coefficient | kg/s | 0.29 | |
| Rolling stiffness | kg/s2 | 0.4 | |
| Rolling damping coefficient | kg/s | 0.4 | |
| Sliding friction coefficient | - | 0.5 | |
| Rolling friction coefficient | - | 0.5 | |
| Liquid parameters | |||
| Surface tension | kg/s2 | 0.0728 | |
| Contact angle | rad | ||
| Liquid dynamic viscosity | kg/m/s | 0.001 | |
| Air parameters | |||
| Air density | kg/m3 | 1.225 | |
| Air kinematic viscosity | m2/s | 1.46·10−5 | |
| Other parameters | |||
| Drag coefficient in the turbulent limit | - | 0.5 | |
| Critical particle Reynolds number | - | 24 | |
| Von Karman constant | - | 0.4 | |
| Mixing length scaling parameter | - | 7 | |
| Gravity acceleration | g | m/s2 | 9.81 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Mean particle diameter | mm | 0.25 | |
| Standard deviation of particle diameter | mm | 0.01 | |
| Cohesion number | - | 113 | |
| Moisture content of the bed | % | 0, 1, 5, 10, 20 | |
| Shields number | - | 0.01, 0.02, 0.03, 0.04, 0.05, 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Campmans, G.H.P.; Weinhart, T.; Thornton, A.R.; Wijnberg, K.M. A Discrete Particle Modeling Framework for Exploring the Evolution of Aeolian Sediment Transport on Moist Sand Surfaces. J. Mar. Sci. Eng. 2025, 13, 1733. https://doi.org/10.3390/jmse13091733
Wang X, Campmans GHP, Weinhart T, Thornton AR, Wijnberg KM. A Discrete Particle Modeling Framework for Exploring the Evolution of Aeolian Sediment Transport on Moist Sand Surfaces. Journal of Marine Science and Engineering. 2025; 13(9):1733. https://doi.org/10.3390/jmse13091733
Chicago/Turabian StyleWang, Xiuqi, Gerhardus H. P. Campmans, Thomas Weinhart, Anthony R. Thornton, and Kathelijne M. Wijnberg. 2025. "A Discrete Particle Modeling Framework for Exploring the Evolution of Aeolian Sediment Transport on Moist Sand Surfaces" Journal of Marine Science and Engineering 13, no. 9: 1733. https://doi.org/10.3390/jmse13091733
APA StyleWang, X., Campmans, G. H. P., Weinhart, T., Thornton, A. R., & Wijnberg, K. M. (2025). A Discrete Particle Modeling Framework for Exploring the Evolution of Aeolian Sediment Transport on Moist Sand Surfaces. Journal of Marine Science and Engineering, 13(9), 1733. https://doi.org/10.3390/jmse13091733








