Scour Characteristics and Bearing Capacity Response of MGB Hybrid Foundations in Offshore Wind Applications
Abstract
1. Introduction
2. Validation of the CFD-DEM Coupling Model
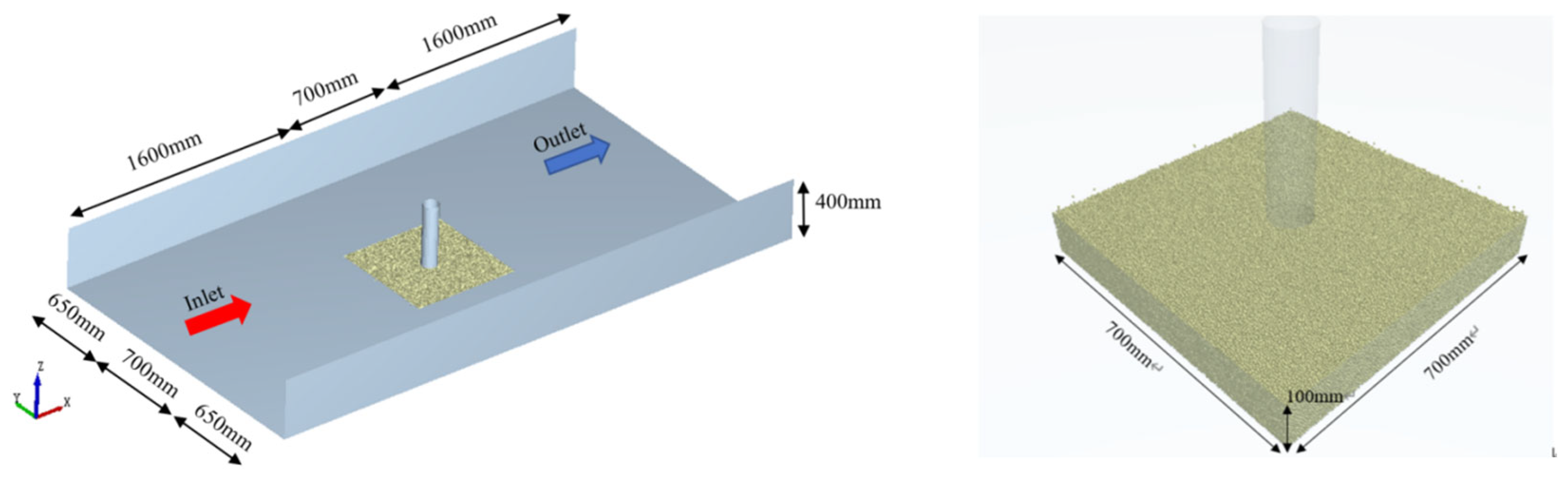
2.1. Model Fundamentals
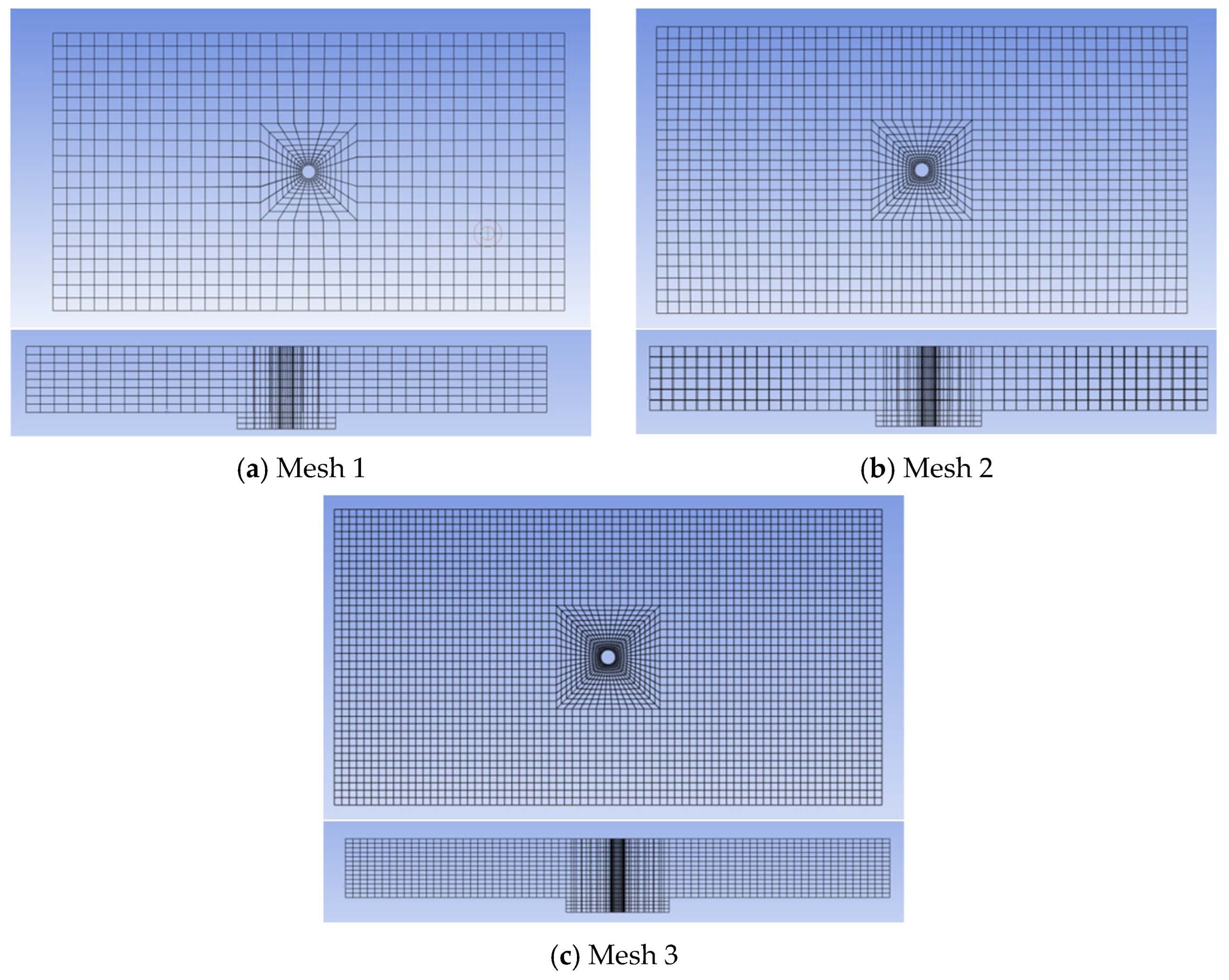
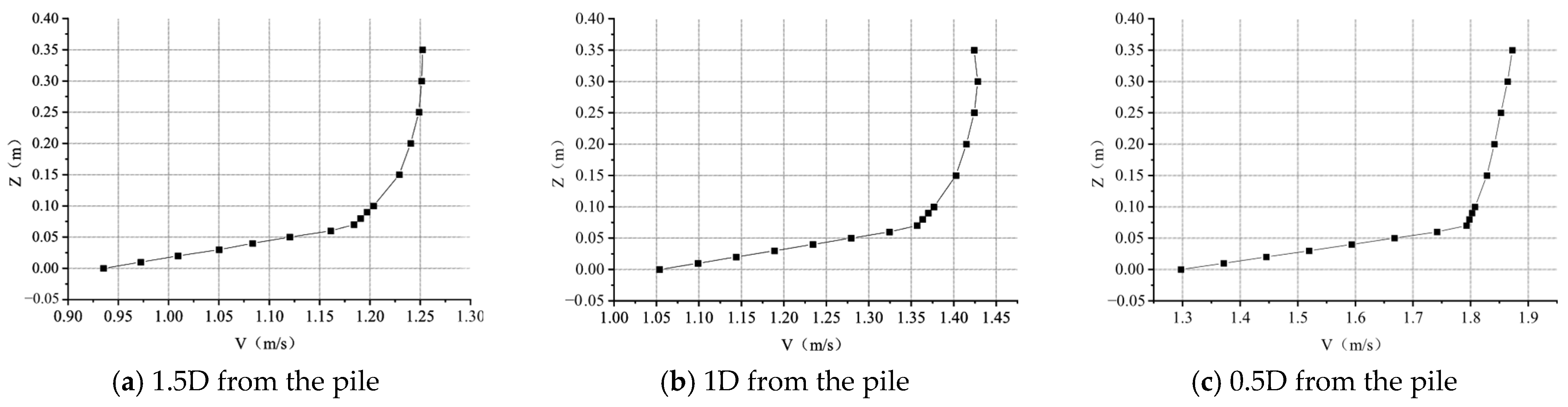
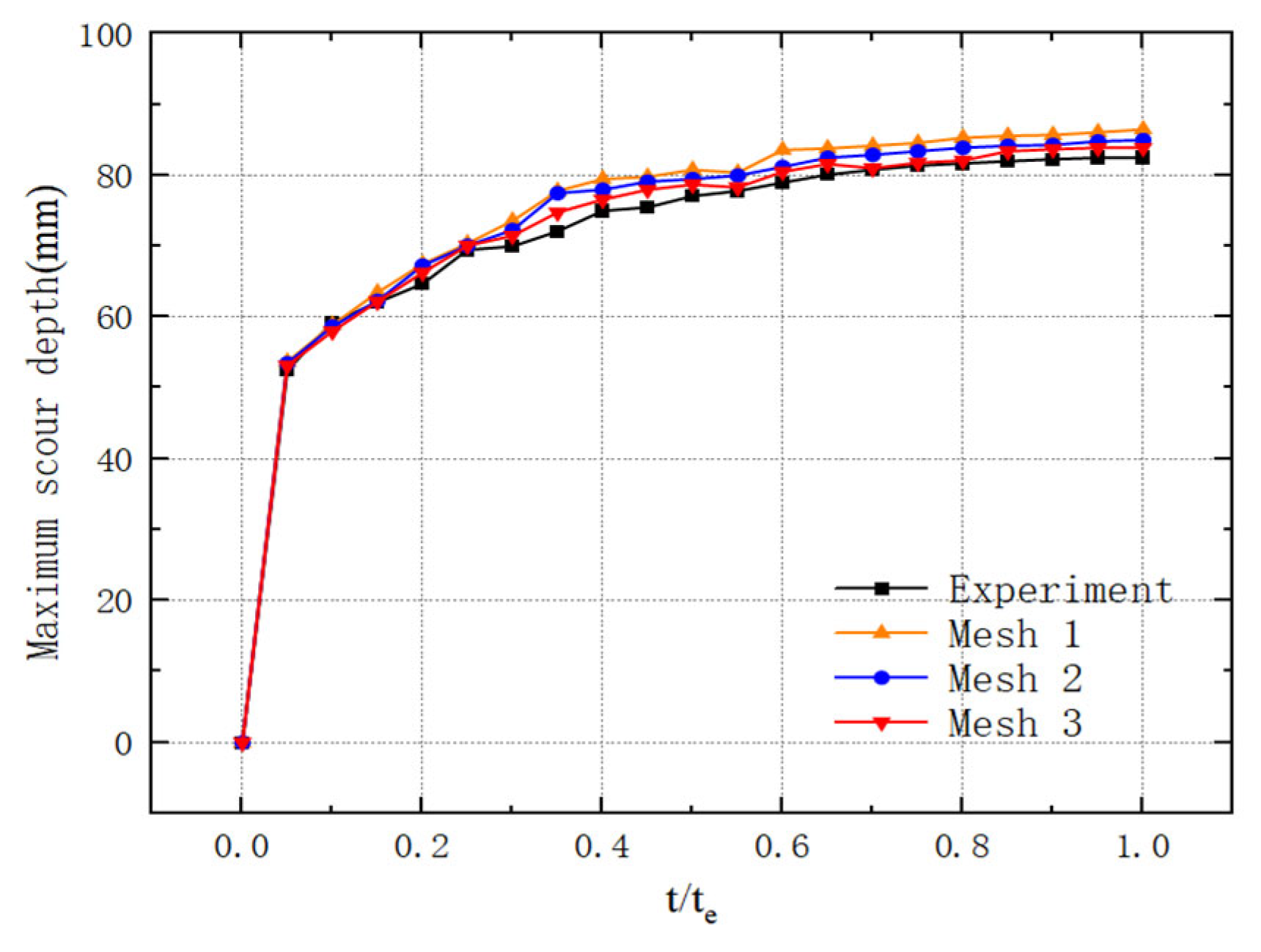
2.2. Model Validation
3. Scouring Characteristics Analysis of MGB Hybrid Foundations
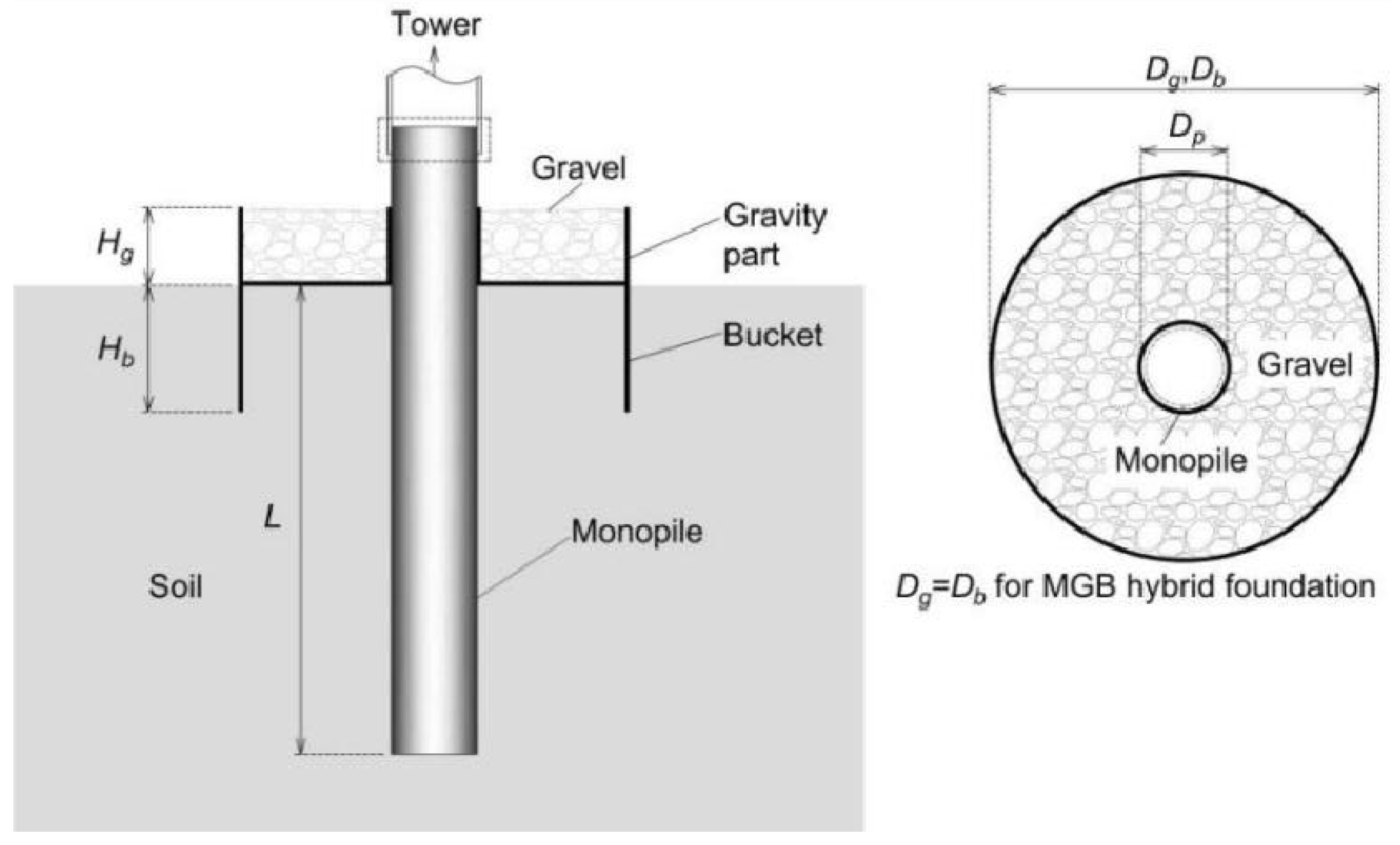
3.1. Model Development of the MGB Hybrid Foundation
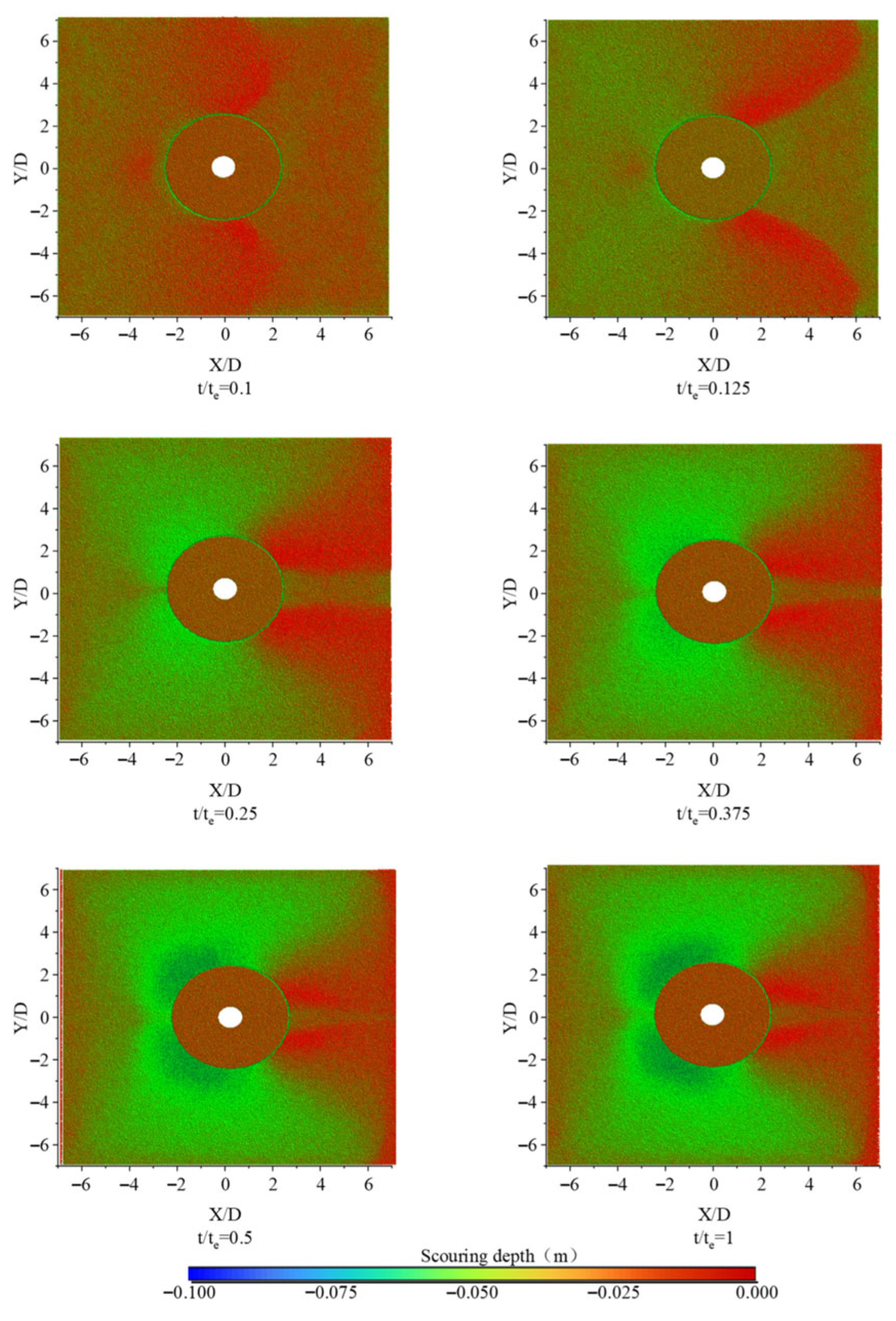
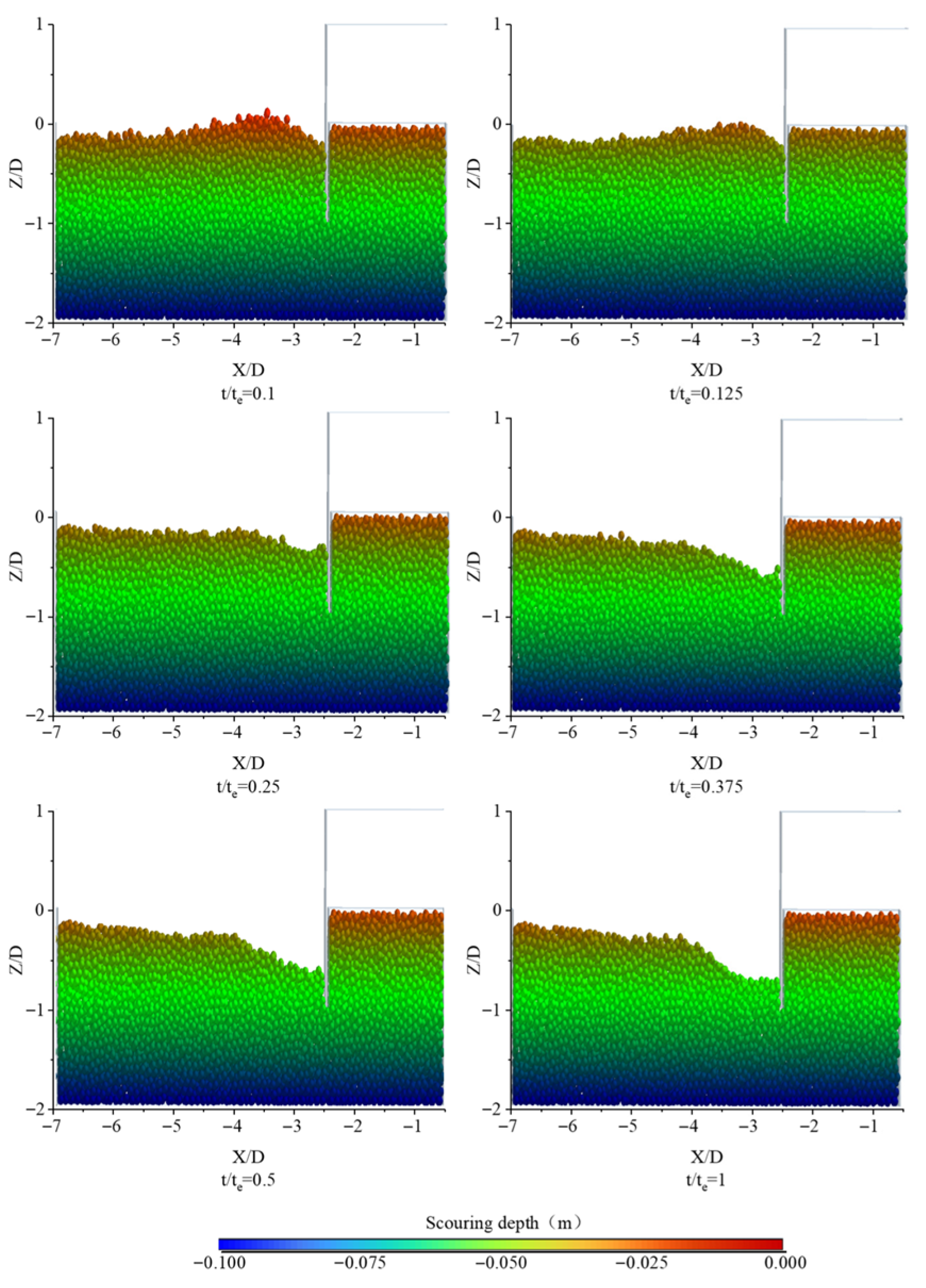
3.2. EDEM Analysis of Scouring Process in the Baseline Case
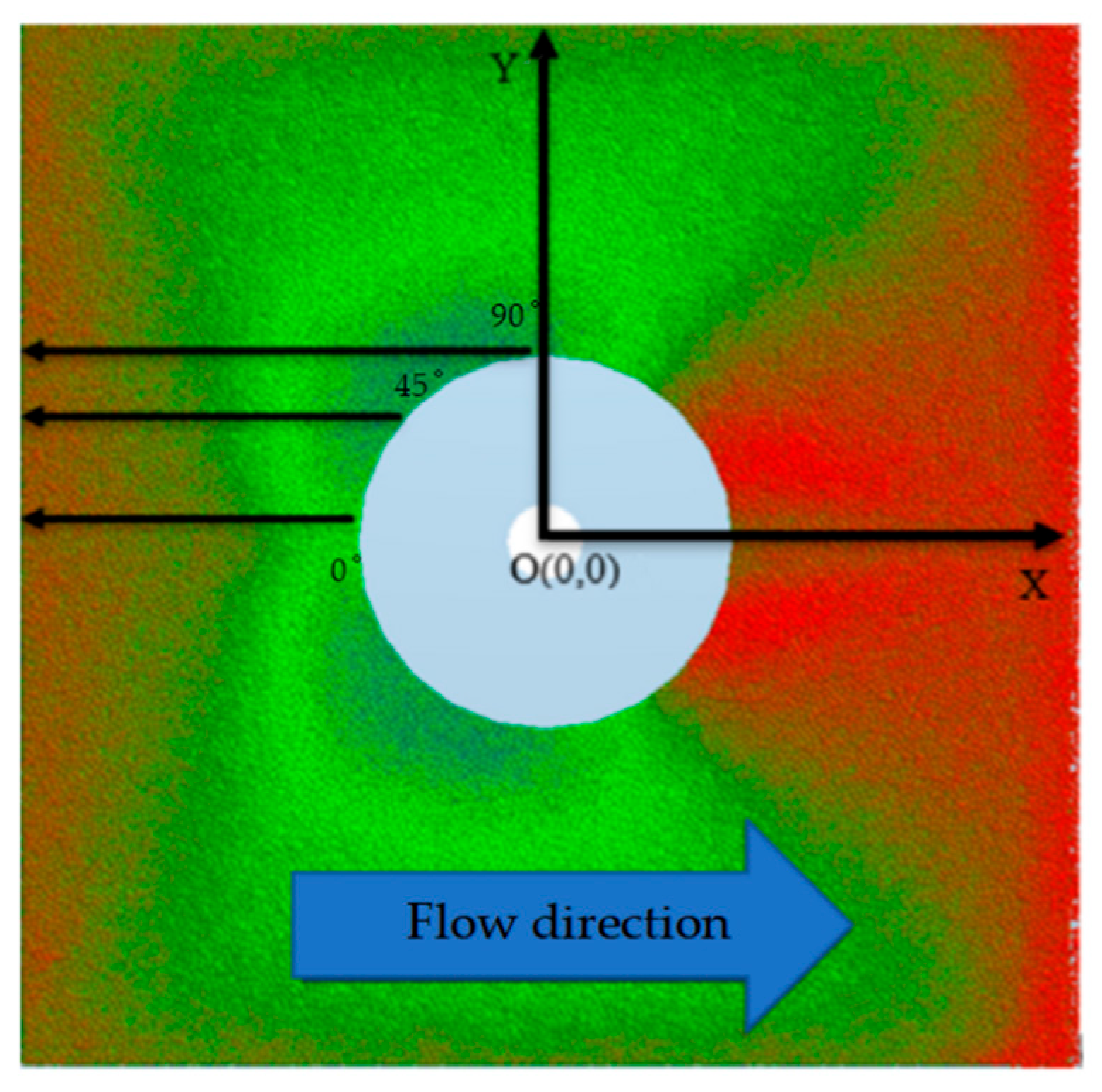
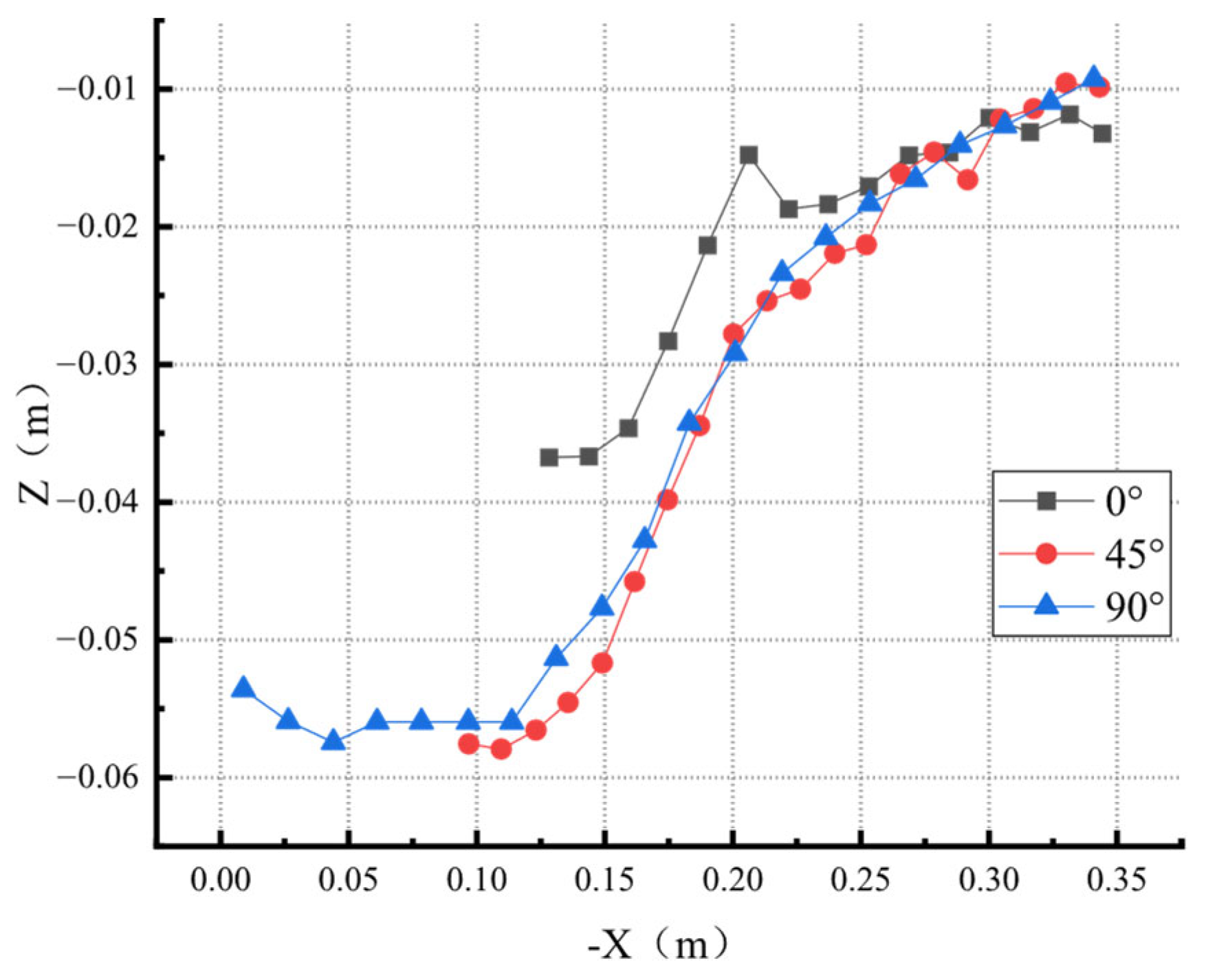
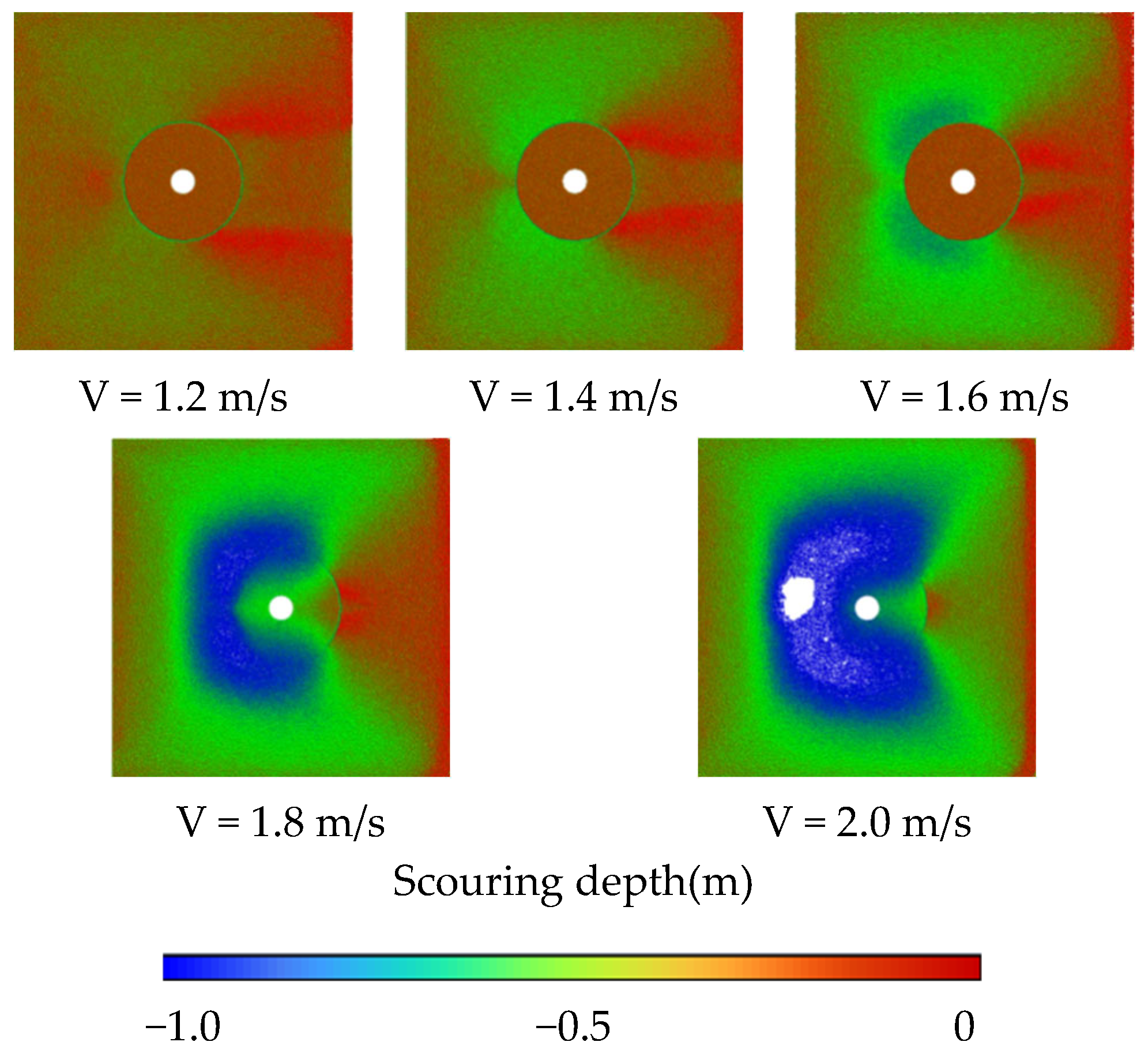
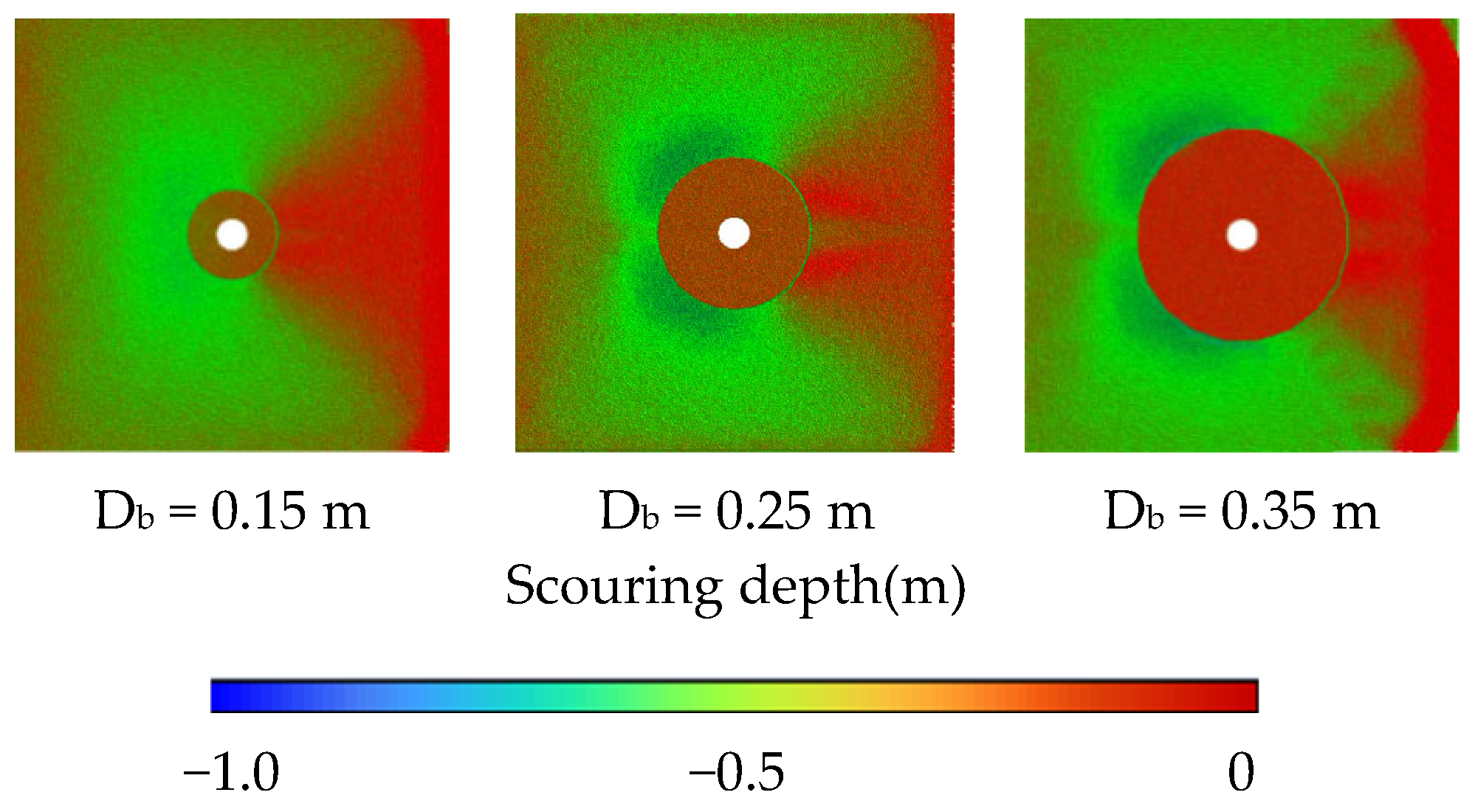
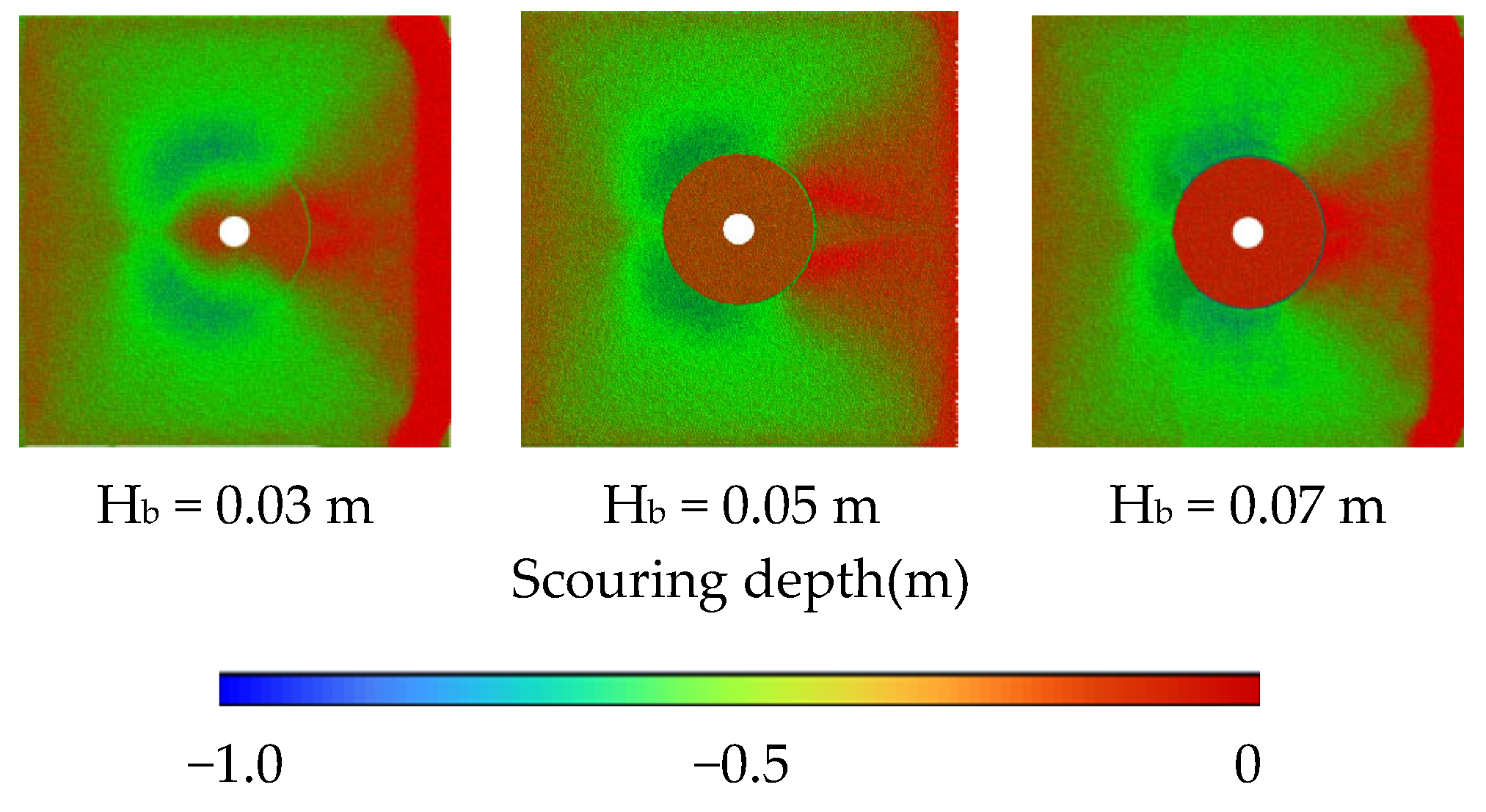
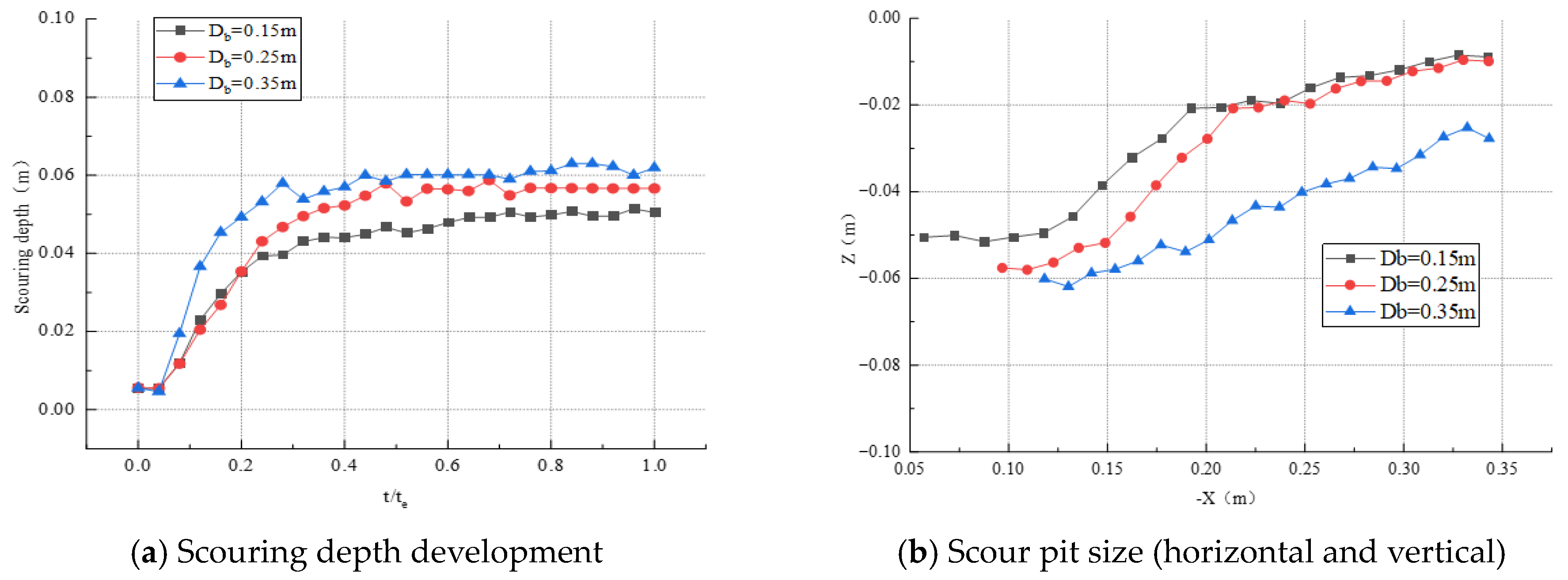
3.3. Scour Pit Profile Under Different Conditions
4. Finite Element Analysis of Ultimate Bearing Capacity for MGB Hybrid Foundations
4.1. Establishment of the Finite Element Model
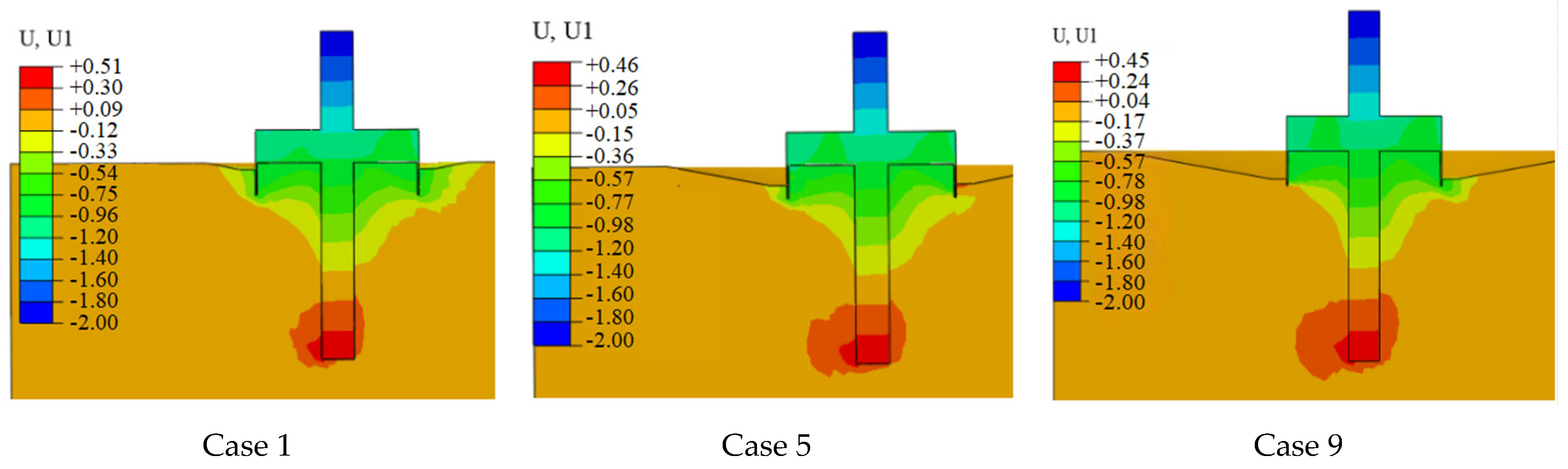
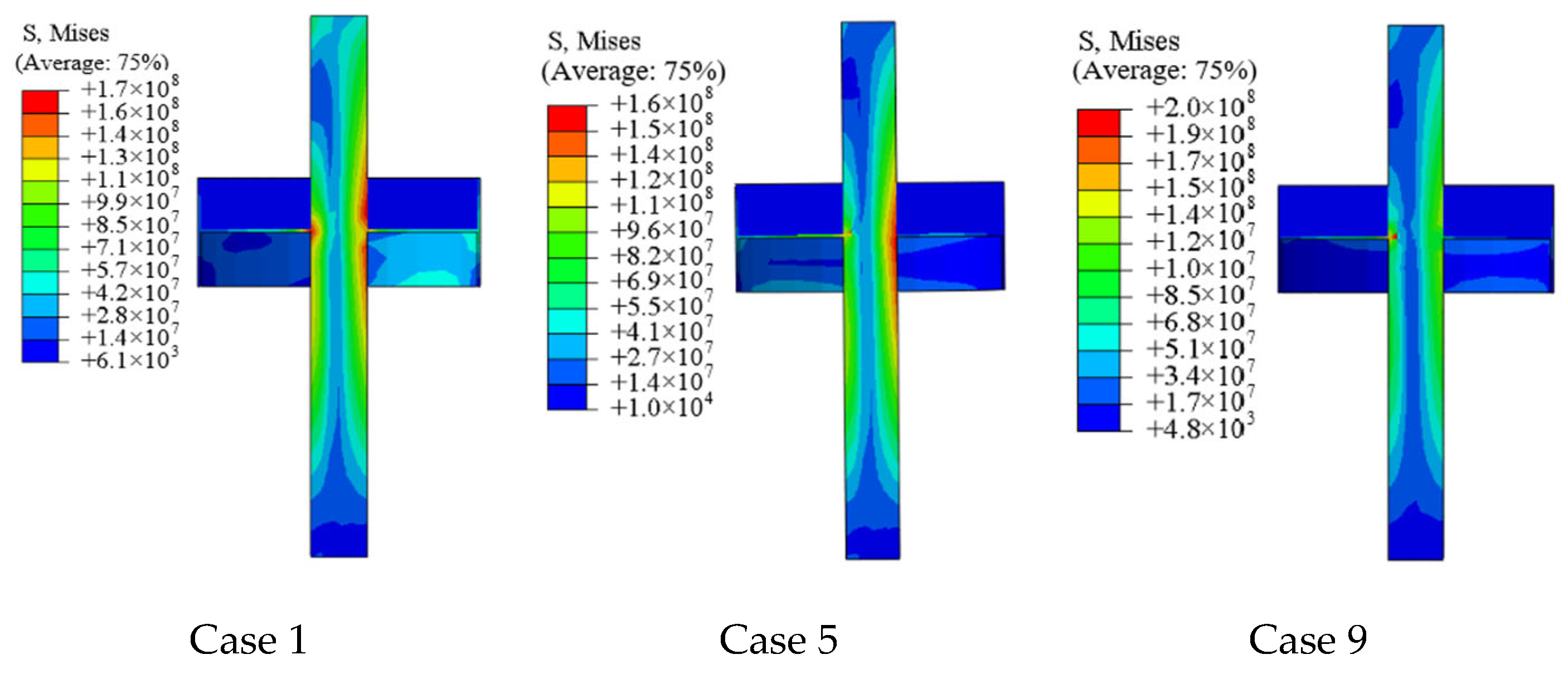
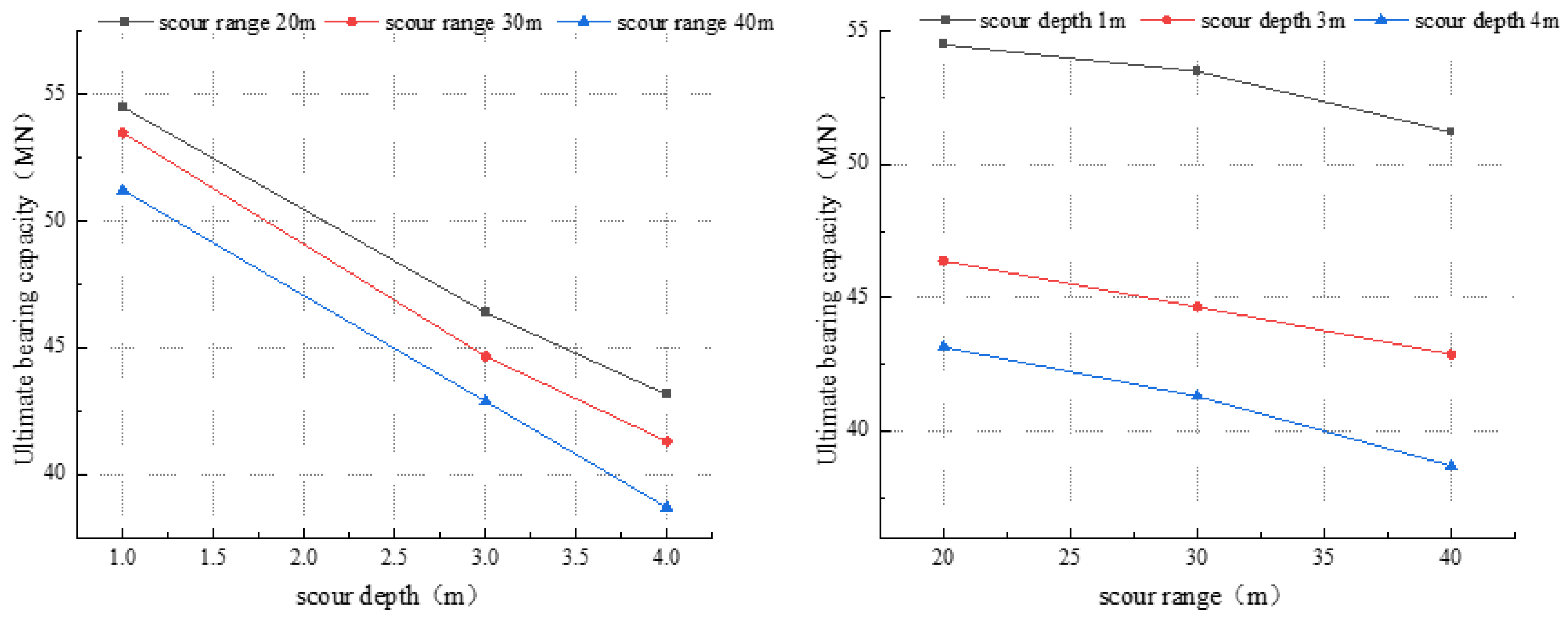
4.2. Foundation Bearing Characteristics Analysis
5. Conclusions and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gonzalez-Rodriguez, A.G. Review of Offshore Wind Farm Cost Components. Energy Sustain. Dev. 2017, 37, 10–19. [Google Scholar] [CrossRef]
- Jensen, K.S.; Petersen, S.J.; Pedersen, R.R. European Offshore Wind Engineering—Past, Present and Future. Proc. Inst. Civ. Eng.-Civ. Eng. 2018, 171, 159–165. [Google Scholar] [CrossRef]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of Offshore Wind Turbines: A Review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Lian, J. Review of Integrated Installation Technologies for Offshore Wind Turbines: Current Progress and Future Development Trends. Energy Convers. Manag. 2022, 255, 115319. [Google Scholar] [CrossRef]
- Li, X.; Zeng, X.; Wang, X. Feasibility Study of Monopile-Friction Wheel-Bucket Hybrid Foundation for Offshore Wind Turbine. Ocean Eng. 2020, 204, 107276. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M. Soil-Structure Interaction of a Laterally Loaded Hybrid Foundation for Offshore Wind Turbine. Ocean Eng. 2022, 263, 112197. [Google Scholar] [CrossRef]
- Li, X.; Zeng, X.; Yu, X.; Wang, X. Seismic Response of a Novel Hybrid Foundation for Offshore Wind Turbine by Geotechnical Centrifuge Modeling. Renew. Energy 2021, 172, 1404–1416. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Li, J. Lateral Response and Installation Recommendation of Hybrid Monopile Foundation for Offshore Wind Turbines under Combined Loadings. Ocean Eng. 2022, 257, 111637. [Google Scholar] [CrossRef]
- Zou, X.; Jiang, Y.; Wang, Y. Failure Mechanism of Single Pile-Friction Footing Hybrid Foundation under Combined V–H–M Loadings by PIV Experiments and FE Method. Ocean Eng. 2023, 280, 114461. [Google Scholar] [CrossRef]
- Qin, B.; Qu, R.; Yang, W.; Xie, Y. A Study on the Scour Surrounding the Fixed Foundation of an Offshore Wind Turbine under Complex Waves, Tidal Currents, and Pile Vibration Conditions. Energies 2024, 17, 1561. [Google Scholar] [CrossRef]
- Qin, B.; Xie, Y.; Yang, W.; Qu, R.; Geng, F. A Further Study on the Scour around the Monopile Foundation of Offshore Wind Turbines. Sustain. Energy Technol. Assess. 2023, 57, 103198. [Google Scholar] [CrossRef]
- Tang, Z.; Melville, B.; Shamseldin, A.; Guan, D.; Singhal, N.; Yao, Z. Experimental Study of Collar Protection for Local Scour Reduction around Offshore Wind Turbine Monopile Foundations. Coast. Eng. 2023, 183, 104324. [Google Scholar] [CrossRef]
- Wang, G.; Xu, S.; Zhang, Q.; Zhang, J. An Experimental Study of the Local Scour Protection Methods around the Monopile Foundation of Offshore Wind Turbines. Ocean Eng. 2023, 273, 113957. [Google Scholar] [CrossRef]
- Li, J.; Lian, J.; Guo, Y.; Dong, X.; Gao, Y. Experimental Study on Current-Induced Local Scour and Pre-Embedded Protective Measures of Multi-Bucket Jacket Foundation for Offshore Wind Turbines. Coast. Eng. 2025, 198, 104703. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Hou, D.; Guo, Y. On the Local Scour around a Jacket Foundation under Bidirectional Flow Loading. Ocean Eng. 2024, 310, 118772. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, J.; Zhang, Q.; Li, M.; Chen, T. Experimental Investigation of Local Scour Around A New Pile-Group Foundation for Offshore Wind Turbines in Bi-Directional Current. China Ocean Eng. 2018, 32, 737–745. [Google Scholar] [CrossRef]
- Mayall, R.O.; McAdam, R.A.; Whitehouse, R.J.S.; Burd, H.J.; Byrne, B.W.; Heald, S.G.; Sheil, B.B.; Slater, P.L. Flume Tank Testing of Offshore Wind Turbine Dynamics with Foundation Scour and Scour Protection. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04020033. [Google Scholar] [CrossRef]
- Barrie, A.; Wang, C.; Liang, F.; Qi, W. Experimental Investigation on the Mechanism of Local Scour around a Cylindrical Coastal Pile Foundation Considering Sloping Bed Conditions. Ocean Eng. 2024, 312, 119225. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Q.; Liang, J.; Liang, F.; Yu, X.B. Establishment and Implementation of an Artificial Intelligent Flume for Investigating Local Scour around Underwater Foundations. Transp. Geotech. 2024, 49, 101433. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Ngo, D.-V.; Lee, J.-H.; Kim, D.-H. Ultimate Limit State Scour Risk Assessment of a Pentapod Suction Bucket Support Structure for Offshore Wind Turbine. Energies 2022, 15, 2056. [Google Scholar] [CrossRef]
- Ma, H.; Chen, C. Scour Protection Assessment of Monopile Foundation Design for Offshore Wind Turbines. Ocean Eng. 2021, 231, 109083. [Google Scholar] [CrossRef]
- Menéndez-Vicente, C.; López-Querol, S.; Harris, J.M.; Tavouktsoglou, N.S. Numerical Study on the Stiffening Properties of Scour Protection around Monopiles for Offshore Wind Turbines. Eng. Geol. 2025, 345, 107835. [Google Scholar] [CrossRef]
- Menéndez-Vicente, C.; López-Querol, S.; Bhattacharya, S.; Simons, R. Numerical Study on the Effects of Scour on Monopile Foundations for Offshore Wind Turbines: The Case of Robin Rigg Wind Farm. Soil Dyn. Earthq. Eng. 2023, 167, 107803. [Google Scholar] [CrossRef]
- Li, J.; Guo, Y.; Lian, J.; Wang, H. Scour Effects on the Bearing Capacity of Multi-Bucket Jacket Foundation for Offshore Wind Turbines. Ocean Eng. 2022, 259, 111848. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, P.; Lv, Y.; Ding, H. Scour Effects on Bearing Capacity of Composite Bucket Foundation for Offshore Wind Turbines. Mar. Georesour. Geotechnol. 2020, 38, 223–237. [Google Scholar] [CrossRef]
- Ma, H.; Yang, J.; Chen, L. Effect of Scour on the Structural Response of an Offshore Wind Turbine Supported on Tripod Foundation. Appl. Ocean Res. 2018, 73, 179–189. [Google Scholar] [CrossRef]
- Jiang, W.; Lin, C.; Sun, M. Seismic Responses of Monopile-Supported Offshore Wind Turbines in Soft Clays under Scoured Conditions. Soil Dyn. Earthq. Eng. 2021, 142, 106549. [Google Scholar] [CrossRef]
- Al-Hammadi, M.; Simons, R.R. Local Scour Mechanism around Dynamically Active Marine Structures in Noncohesive Sediments and Unidirectional Current. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019026. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.; Hu, Z.; Ma, H. Microscopic Investigation of Shape Effect on Local Scour around the Monopile Using CFD-DEM. Comput. Geotech. 2025, 177, 106872. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, S.; Li, B. Numerical Investigation of Local Scour around Twin Piles under Steady Current Using CFD-DEM Coupling Method. Comput. Geotech. 2023, 164, 105805. [Google Scholar] [CrossRef]
- Zhang, N.; Yu, B.; Yin, S.; Guo, C.; Zhang, J.; Kong, F.; Zhai, W.; Qiu, G. Numerical Investigation of Local Scour Protection around the Foundation of an Offshore Wind Turbine. J. Mar. Sci. Eng. 2024, 12, 692. [Google Scholar] [CrossRef]
- Hu, R.; Lu, Y.; Zhao, Z.; Leng, H.; Liu, H. Local Scour Characteristics around Offshore Wind-Turbine Foundations under Nonlinear Waves and Currents. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 032084. [Google Scholar] [CrossRef]
- Zou, X.; Cao, X.; Zhou, C.; Zhou, M.; Zhang, X. Experimental Study on the Bearing Capacity of Large-Diameter Monopile in Sand under Water Flow Condition. Ocean Eng. 2021, 224, 108708. [Google Scholar] [CrossRef]
- Zou, X.; Chen, S.; Tu, X.; Yang, Z. Effects of Local Scouring on Load-Bearing Behaviors of Monopile–Friction Wheel Hybrid Foundations on Sandy Deposit Soil under Lateral Loading. Int. J. Geomech. 2024, 24, 04024085. [Google Scholar] [CrossRef]
- Cho, Y.-J. Scour Controlling Effect of Hybrid Mono-Pile as a Substructure of Offshore Wind Turbine: A Numerical Study. J. Mar. Sci. Eng. 2020, 8, 637. [Google Scholar] [CrossRef]
- Xu, Y. Experimental Investigation of Scour Around Vertical Piles in Steady Currents; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Wang, D.; Wang, Y.; Yang, B.; Zhang, W.; Lancaster, N. Statistical Analysis of Sand Grain/Bed Collision Process Recorded by High-Speed Digital Camera. Sedimentology 2008, 55, 461–470. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Zang, Z. Experimental and Numerical Investigation of Local Scour around a Submerged Vertical Circular Cylinder in Steady Currents. Coast. Eng. 2010, 57, 709–721. [Google Scholar] [CrossRef]





















| Parameter Name | Parameter Value |
|---|---|
| Particle diameter d (mm) | 5 |
| Poisson’s ratio v | 0.35 |
| Density ρp (kg/m3) | 2670 |
| Shear modulus G (Pa) | 5 × 106 |
| Coefficient of restitution e | 0.45 |
| Static friction coefficient μs | 0.65 |
| Rolling friction coefficient μr | 0.01 |
| Time step (s) | 5 × 10−5 |
| Data saving interval (s) | 0.05 |
| Parameter Name | Parameter Value |
|---|---|
| Flow velocity (m/s) | 1.6 |
| Outlet relative pressure (Pa) | 0 |
| Fluid density ρf (kg/m3) | 1000 |
| Dynamic viscosity ν (Pa·s) | 1 × 10−3 |
| Absolute convergence residual | 1 × 10−3 |
| Maximum iteration steps | 500 |
| Time step (s) | 5 × 10−3 |
| Total simulation steps | 10,000 |
| Parameter | VID3 Experiment | CFD-DEM |
|---|---|---|
| Pile diameter D (m) | 0.1 | 0.1 |
| Flow velocity V (m/s) | 0.286 | 1.6 |
| Water depth h (m) | 0.4 | 0.4 |
| Median sediment diameter d50 (mm) | 0.29 | 5 |
| Shields number θ | 0.036 | 0.050 |
| Critical Shields number θcr | 0.038 | 0.053 |
| Dimensionless θ/θcr | 0.955 | 0.955 |
| Parameter | D = 0.05 | D = 0.10 | D = 0.15 |
|---|---|---|---|
| Inflow velocity V1 (m/s) | 1.5 | 1.6 | 1.8 |
| Flow velocity V (m/s) | 1.072847679 | 1.161306509 | 1.230174593 |
| Calibration coefficient C1 | 1.304938276 | 1.377758574 | 1.463206938 |
| Calibration coefficient C2 | 1.141327318 | 1.235432457 | 1.308696376 |
| Simulation Cases | Monopile Diameter Dp/(m) | Bucket Diameter Db/(m) | Gravity Wheel Height Hg/(m) | Bucket Height Hb/(m) | Flow Velocity V/(m/s) | Water Depth h (m) |
|---|---|---|---|---|---|---|
| 1 | 0.05 | 0.25 | 0.05 | 0.05 | 1.6 | 0.4 |
| 2 | 0.05 | 0.25 | 0.05 | 0.05 | 1.2 | 0.4 |
| 3 | 0.05 | 0.25 | 0.05 | 0.05 | 1.4 | 0.4 |
| 4 | 0.05 | 0.25 | 0.05 | 0.05 | 1.8 | 0.4 |
| 5 | 0.05 | 0.25 | 0.05 | 0.05 | 2.0 | 0.4 |
| 6 | 0.05 | 0. 15 | 0.05 | 0.05 | 1.6 | 0.4 |
| 7 | 0.05 | 0.35 | 0.05 | 0.05 | 1.6 | 0.4 |
| 8 | 0.05 | 0.25 | 0.05 | 0.03 | 1.6 | 0.4 |
| 9 | 0.05 | 0.25 | 0.05 | 0.07 | 1.6 | 0.4 |
| Simulation Cases | H1 (m) | H2 (m) | H3 (m) |
|---|---|---|---|
| 1 | 1 | 20 | 2.5 |
| 2 | 1 | 30 | 2.5 |
| 3 | 1 | 40 | 2.5 |
| 4 | 3 | 20 | 2.5 |
| 5 | 3 | 30 | 2.5 |
| 6 | 3 | 40 | 2.5 |
| 7 | 4 | 20 | 2.5 |
| 8 | 4 | 30 | 2.5 |
| 9 | 4 | 40 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, B.; Wang, C. Scour Characteristics and Bearing Capacity Response of MGB Hybrid Foundations in Offshore Wind Applications. J. Mar. Sci. Eng. 2025, 13, 1726. https://doi.org/10.3390/jmse13091726
Li X, Zhang B, Wang C. Scour Characteristics and Bearing Capacity Response of MGB Hybrid Foundations in Offshore Wind Applications. Journal of Marine Science and Engineering. 2025; 13(9):1726. https://doi.org/10.3390/jmse13091726
Chicago/Turabian StyleLi, Xinyao, Baofang Zhang, and Chen Wang. 2025. "Scour Characteristics and Bearing Capacity Response of MGB Hybrid Foundations in Offshore Wind Applications" Journal of Marine Science and Engineering 13, no. 9: 1726. https://doi.org/10.3390/jmse13091726
APA StyleLi, X., Zhang, B., & Wang, C. (2025). Scour Characteristics and Bearing Capacity Response of MGB Hybrid Foundations in Offshore Wind Applications. Journal of Marine Science and Engineering, 13(9), 1726. https://doi.org/10.3390/jmse13091726






