Multi-Branch Towed Array System: Systematic Analysis of Modeling Methods, Environmental Responses and Mechanical Properties in Fracture Analysis
Abstract
1. Introduction
2. Cable Discrete Theory and Modeling Basics
2.1. Model Building
2.2. Control Equations for Towing Cable Motion
- (1)
- Tension in general the strain of the cable , the stress–strain relationship can be elastically treated.where: is the unit tangent vector in the direction of the cable length; E is the modulus of elasticity. The same reason can be obtained taking into account the tension and compression elastic properties of the towing cable is different, in this paper the towing cable under pressure (strain is negative) when the modulus of elasticity is taken as an approximation for the tensile 1/10.
- (2)
- Buoyancy and gravity , the buoyancy and gravity of node can be expressed aswhere is the acceleration of gravity.
- (3)
- Fluid resistance The dragline resistance is divided into tangential and normal directions and can be expressed after accounting for the effect of cable strain as followswhere: is the velocity vector of the node; is the diameter of the cable; , are the normal and tangential drag coefficients, respectively.
2.3. Mechanical Equations for Towing Cables
2.4. Other Common Types of Discrete Methods for Towing Cables
2.4.1. Cosserat Rod Model
2.4.2. Semicontinuous Model
2.4.3. Lumped Mass Method
2.4.4. Formulation of Absolute Nodal Coordinates Model
2.4.5. Finite Difference Method
2.4.6. The Theoretical Basis and Research Context of the Discrete Method of Towing Cables
2.4.7. Nonlinear Beam Model
3. Dynamic Response in Different Engineering Situations
3.1. Dynamical Response to the Action of Wave and Current
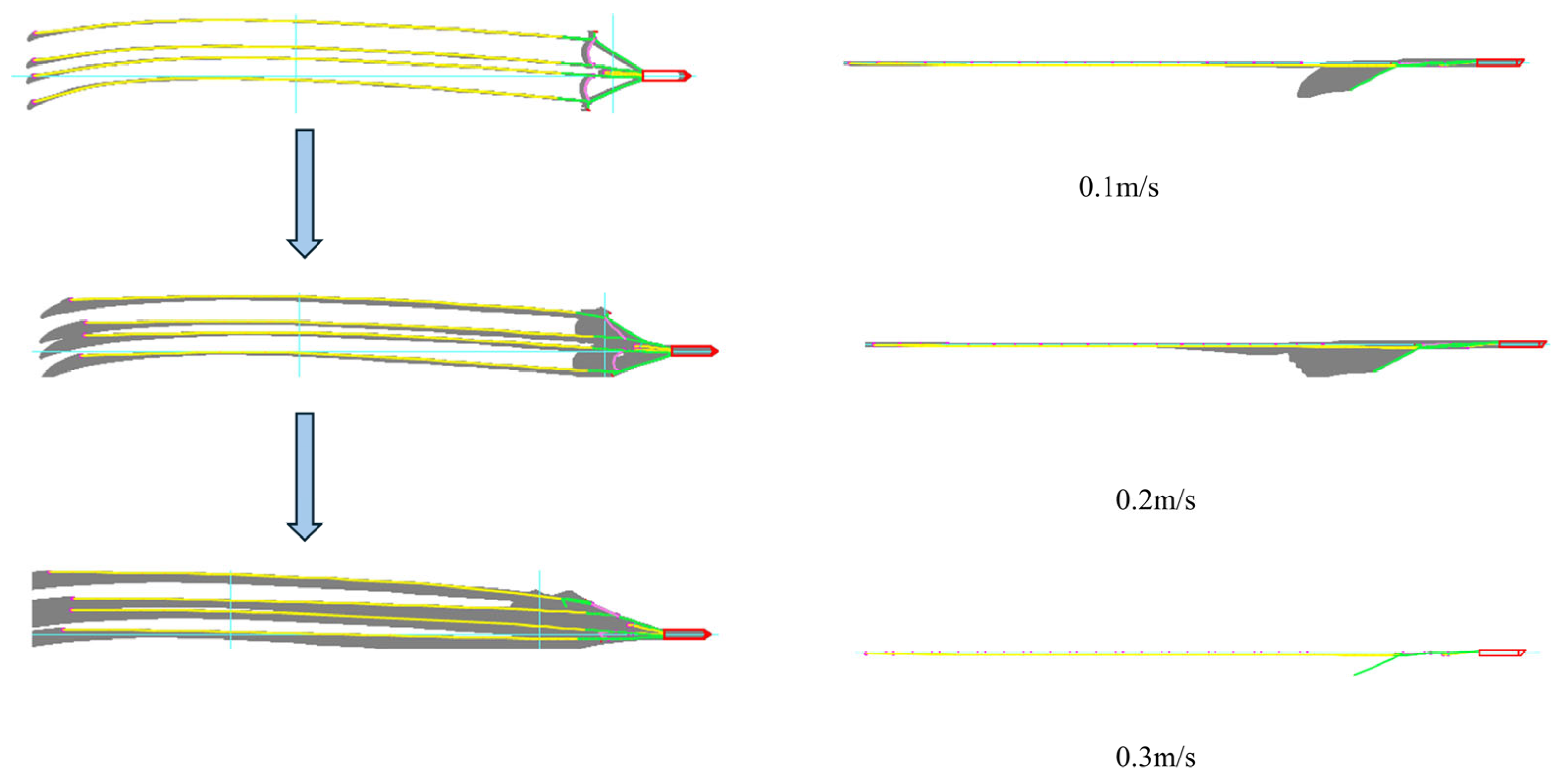
3.1.1. Dynamic Response of the Port Side Guide Cable During Failure Fracture Under Countercurrent Action
3.1.2. Dynamic Response of a Double Outboard Guide Cable During Failure Fracture Under Countercurrent Action
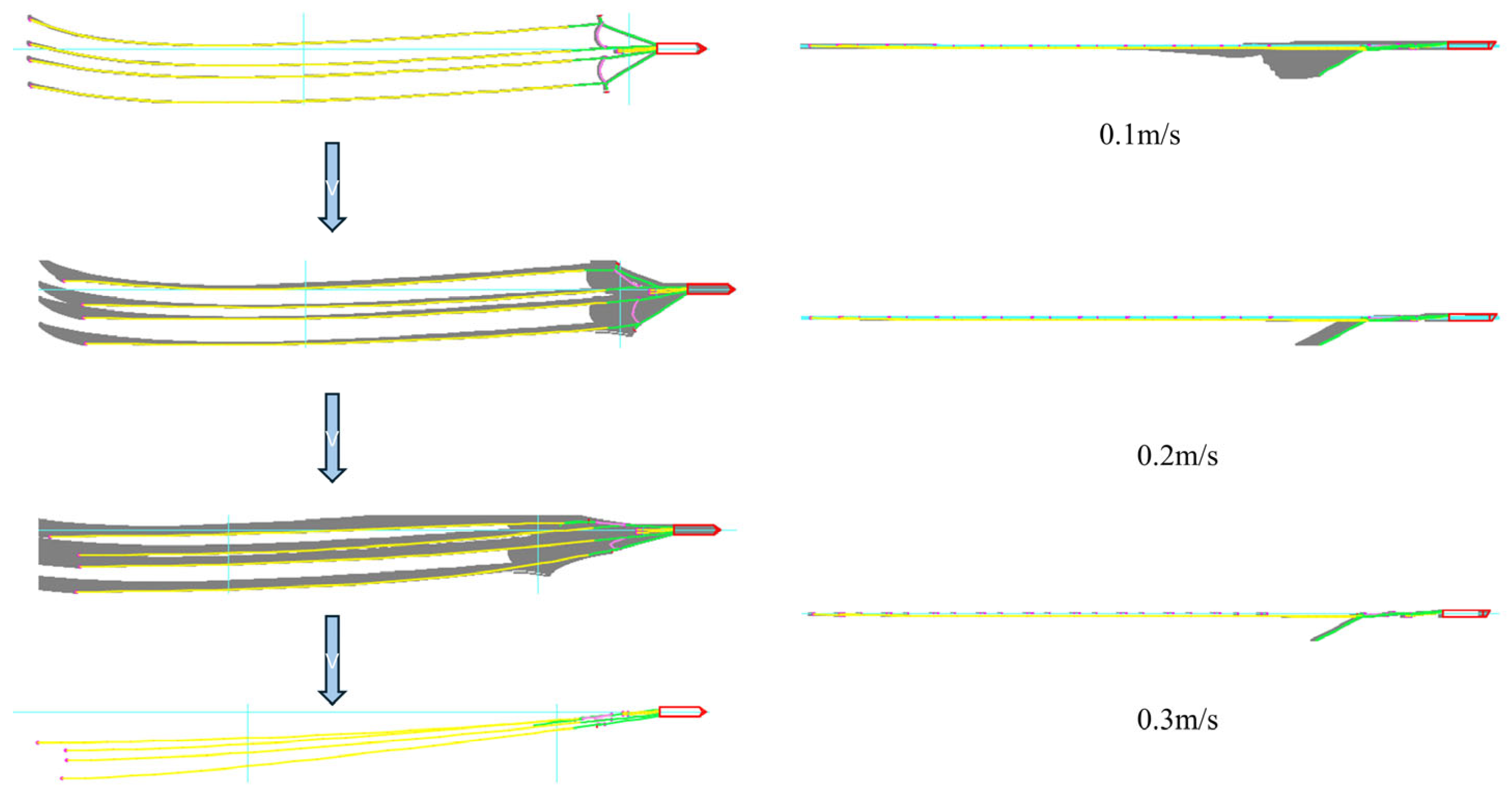
3.1.3. Dynamic Response of the Port Side Guide Cable During Failure Fracture Under Downstream Action
3.1.4. Dynamic Response of a Double Outboard Guide Cable During Failure Fracture Under Downstream Action
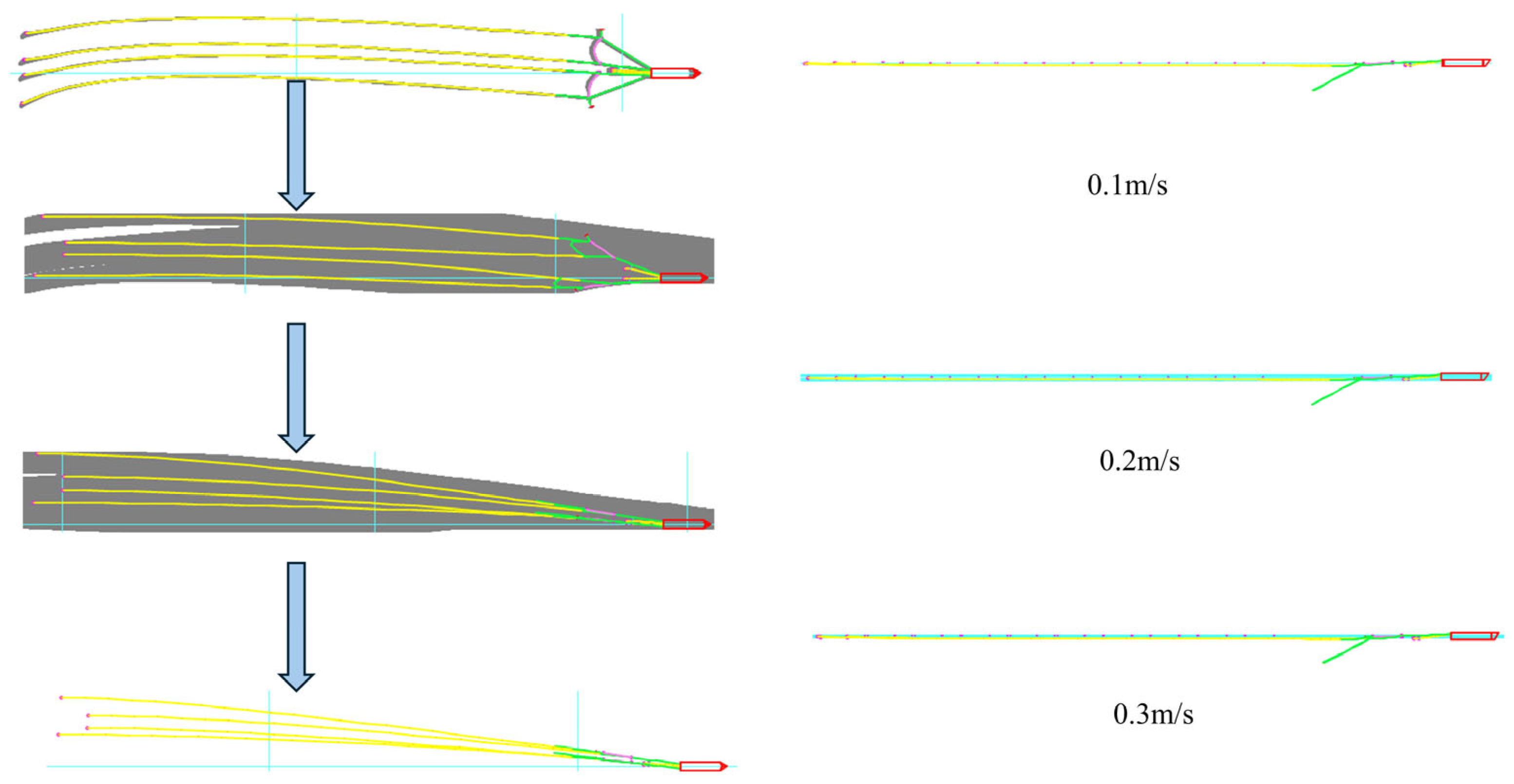
3.1.5. Dynamic Response to Failure Breakage of Port Side Guide Cable Under Cross Current (90°, 270°)
3.1.6. Dynamical Response of a Double Outboard Guide Cable During Failure Fracture Under Cross-Currents
3.2. Dynamic Response to Wave Action
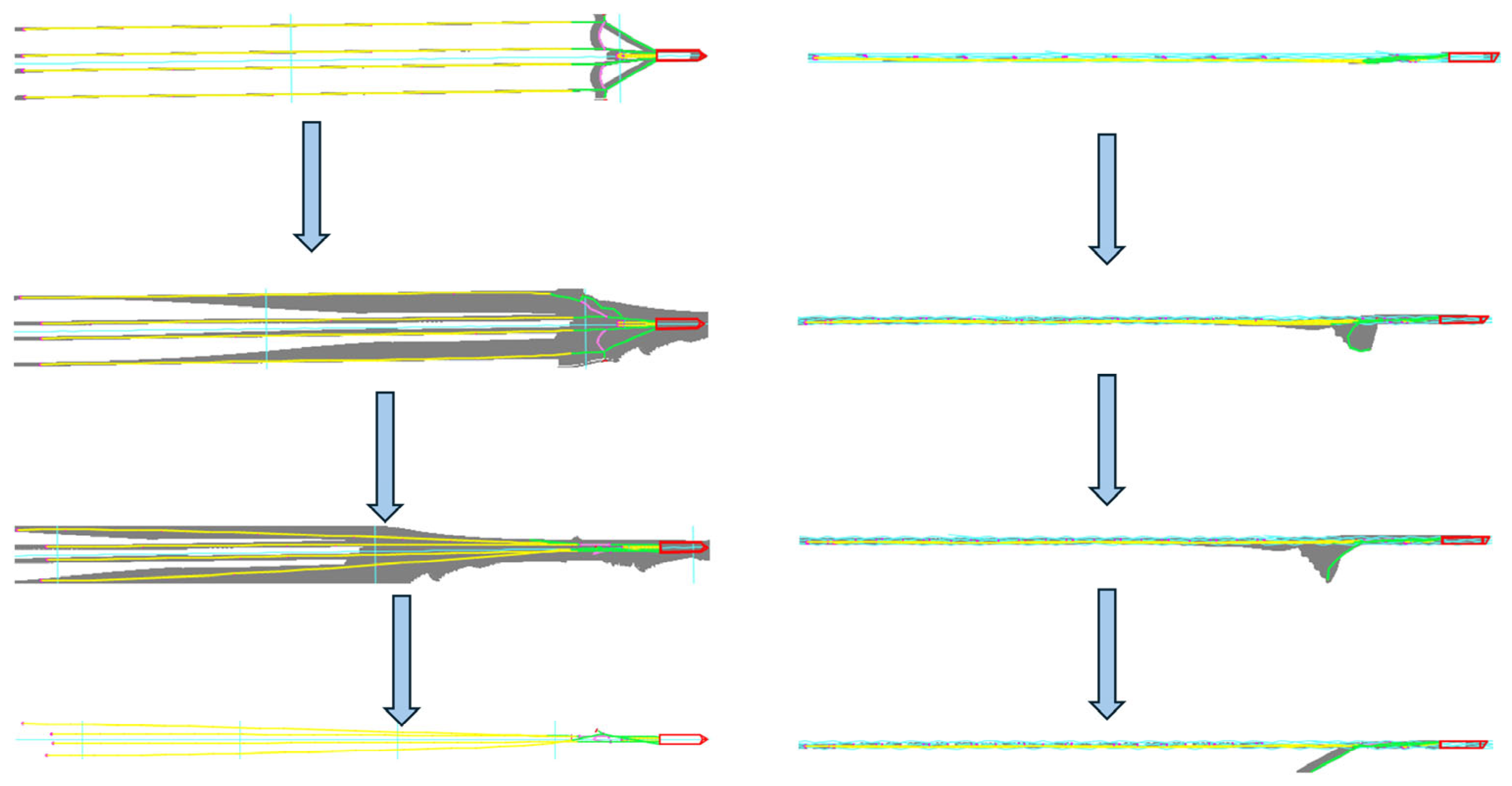
3.2.1. Dynamic Response of the Port Side Guide Cable During Failure Breakage Under Counter Wave Action
3.2.2. Dynamic Response of a Double Outboard Guide Cable During Failure Breakage Under Counter-Wave Action
3.2.3. Dynamic Response of an Outboard Guide Cable During Failure Breakage Under Downwash Action
3.2.4. Dynamic Response of the Port Side Guide Cable in Case of Failure Breakage Under Cross-Wave Action (90°, 270°)
3.2.5. Dynamic Response of a Double Outboard Guide Cable During Failure Breakage Under Cross-Wave Action
4. Analysis of Influencing Factors and Mechanical Properties
4.1. Factors Affecting the Deployment of Multi-Branch Towing Systems
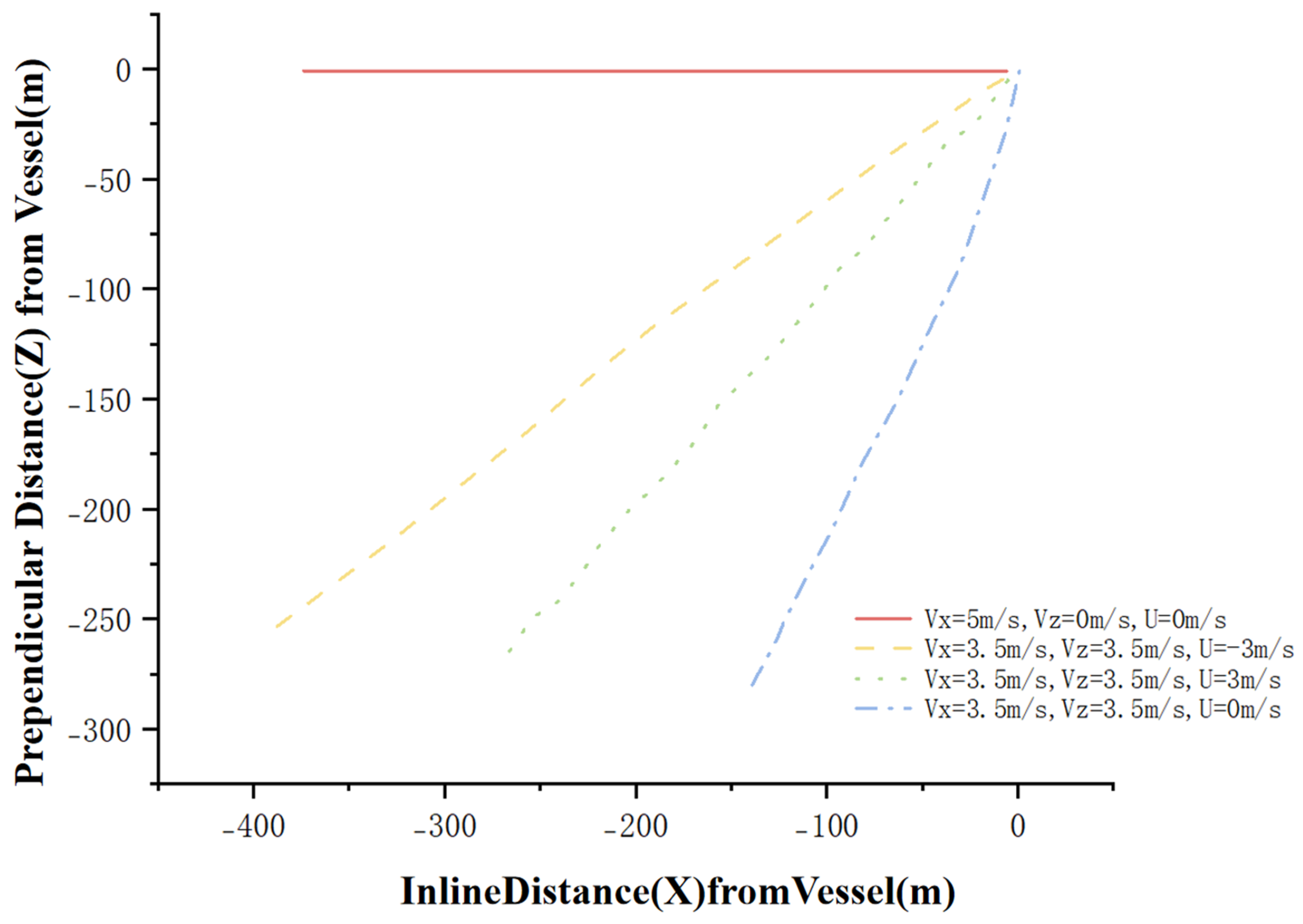
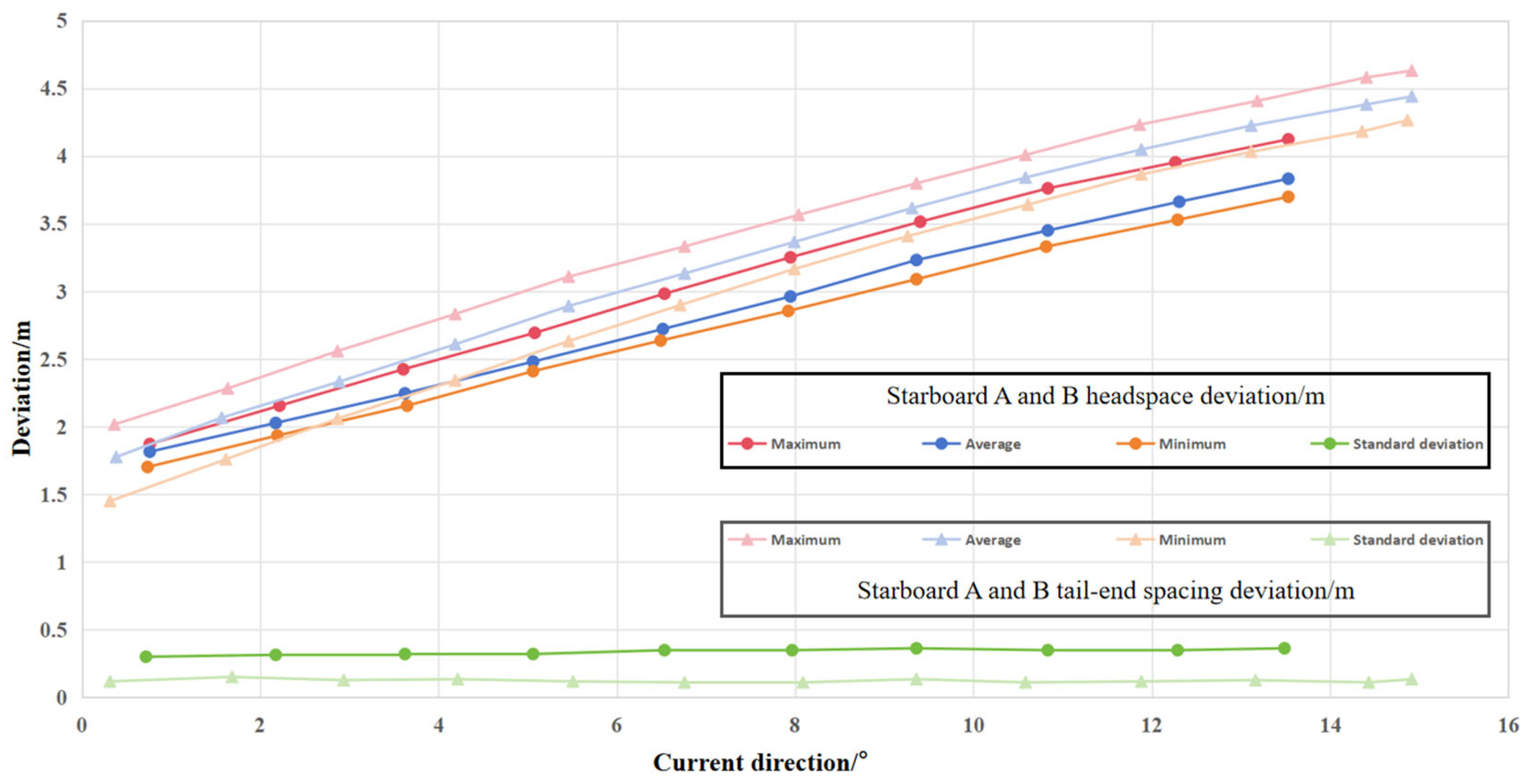
4.1.1. Current Velocity and Direction
4.1.2. Wave Parameters
- Wave direction
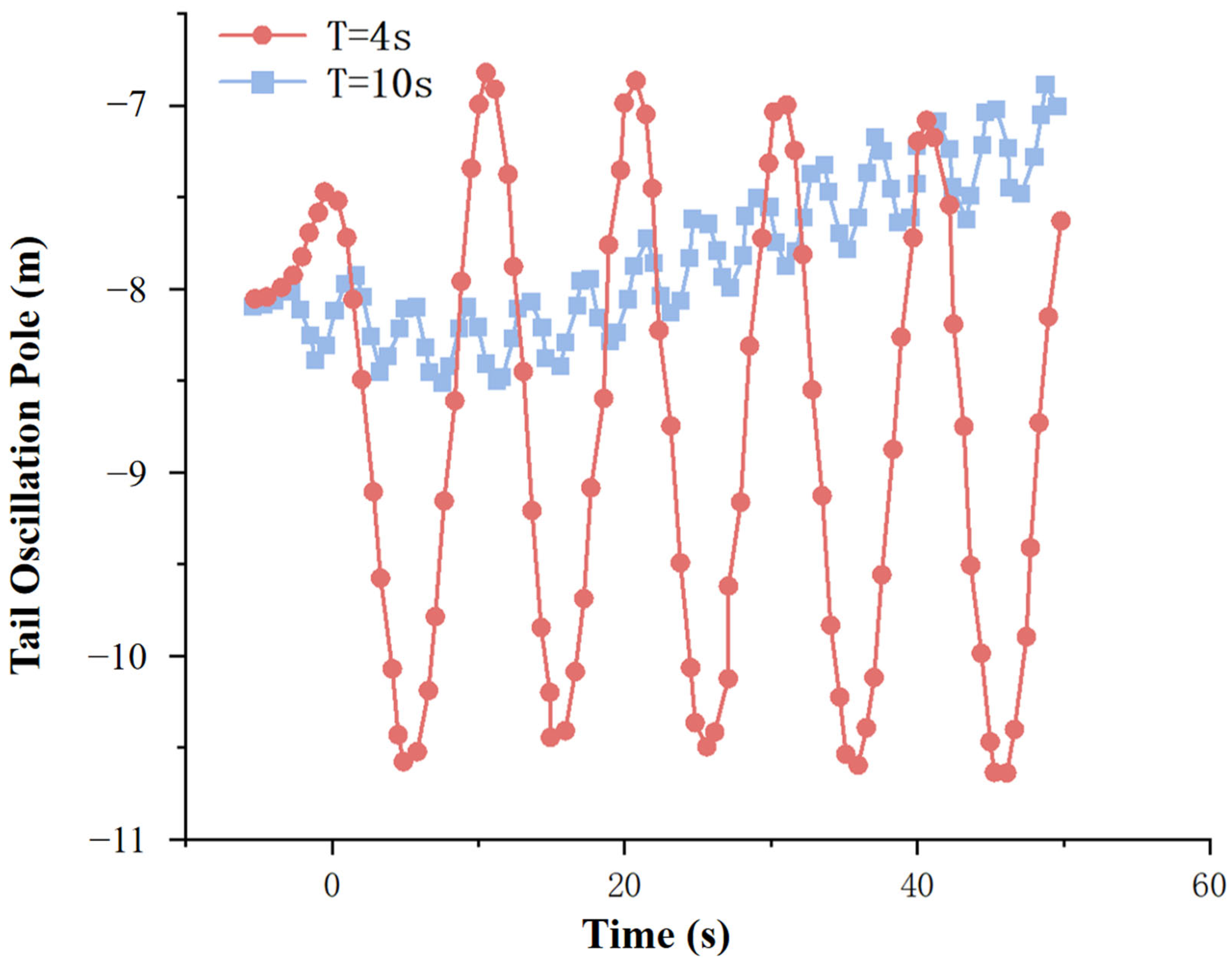
- Wave period
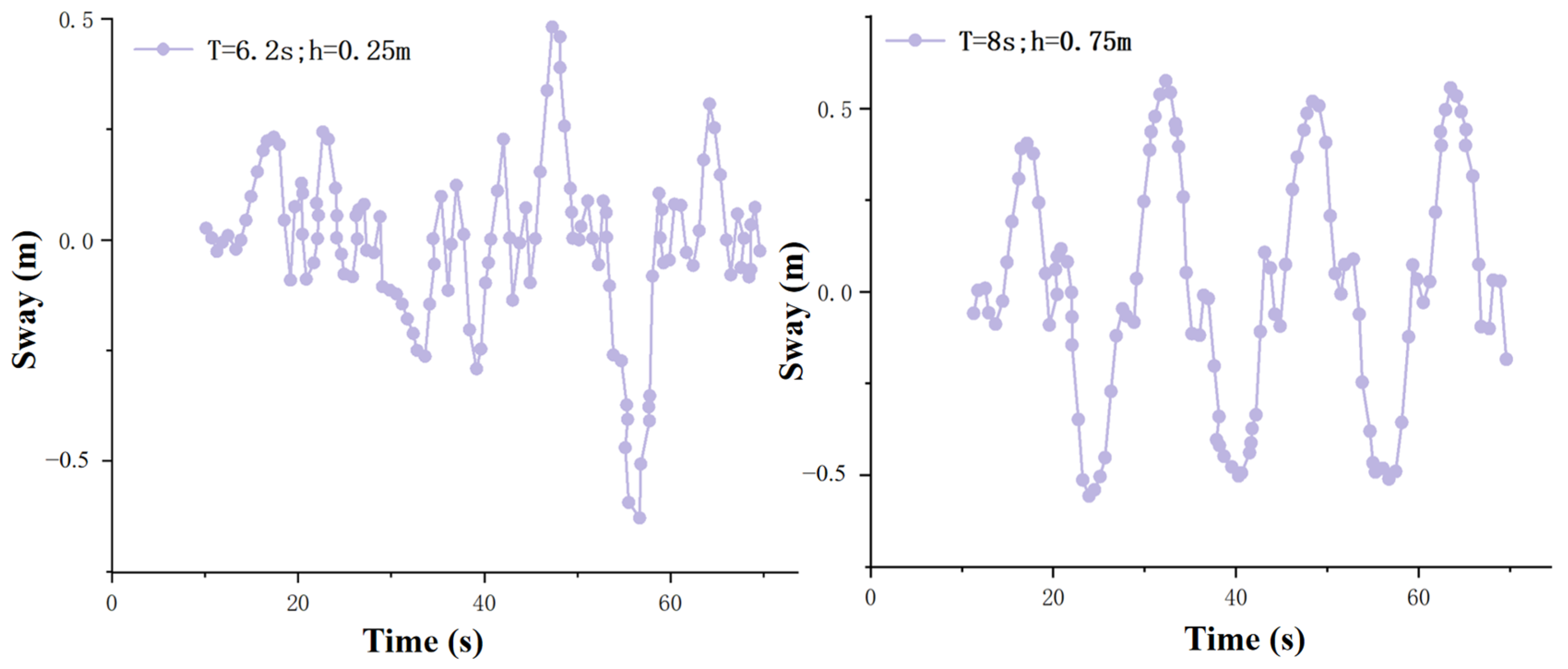
- Waveform height
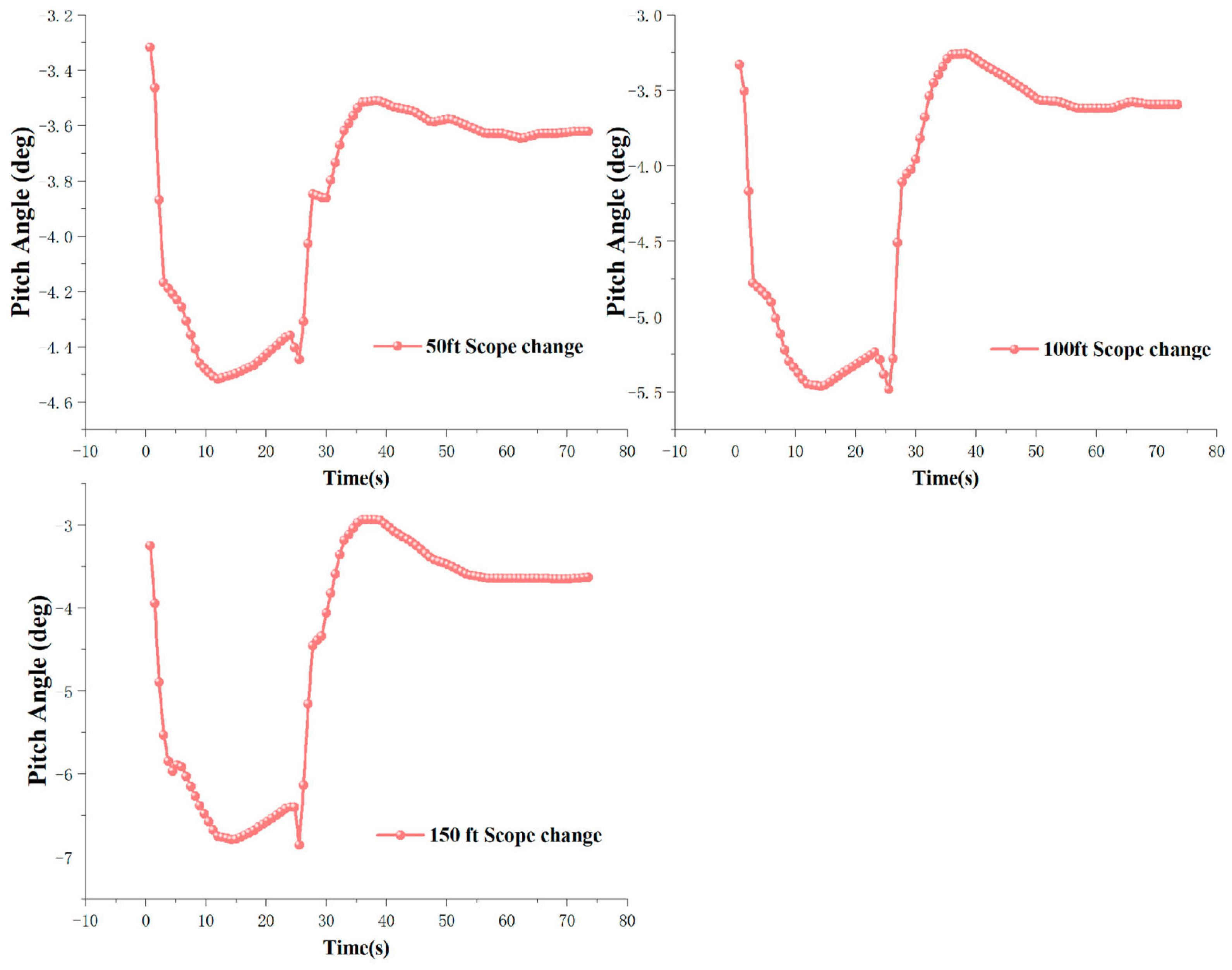
4.1.3. Cable Length
4.2. Trawl Recovery Characteristics (Analogy Analysis)
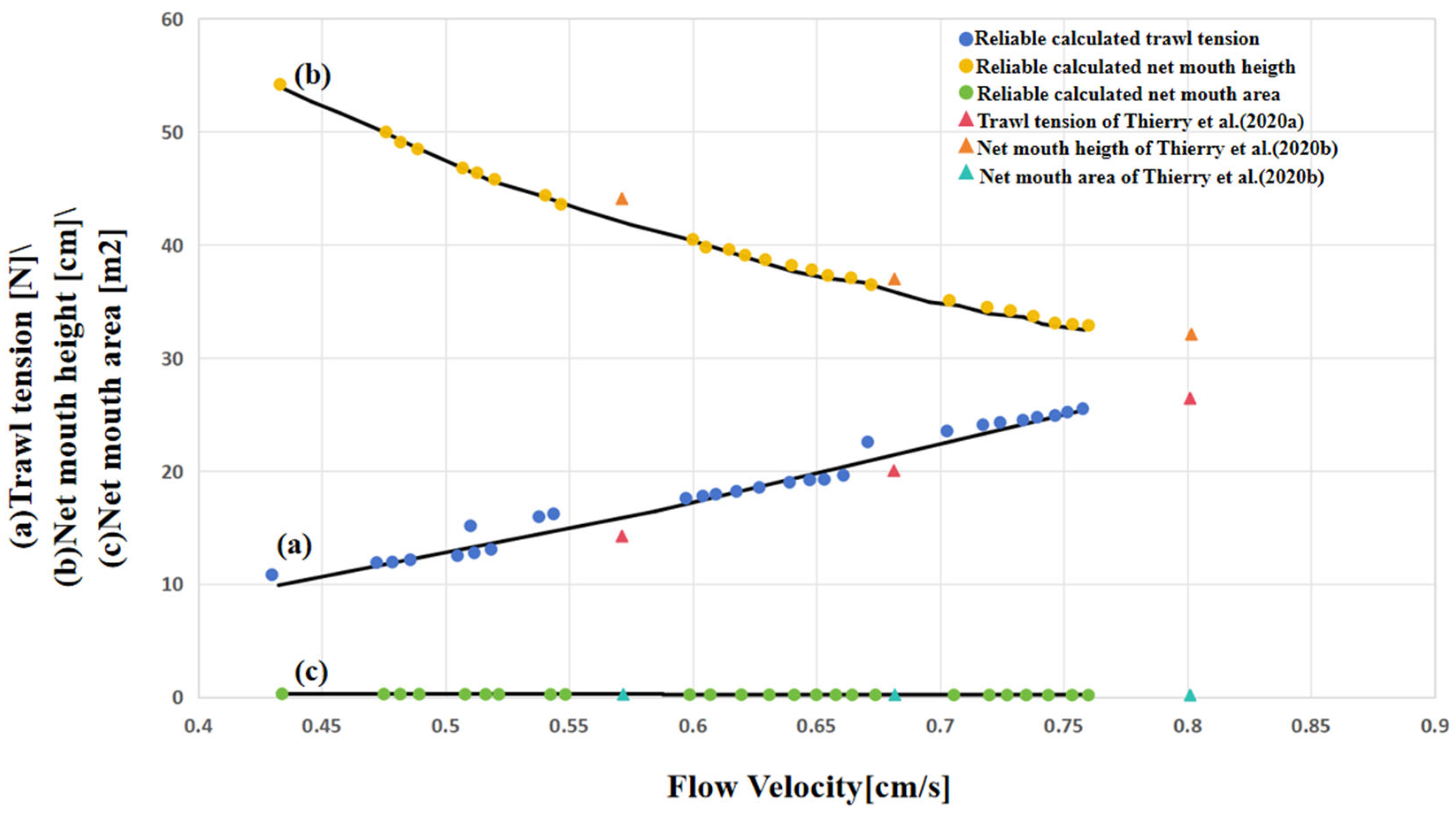
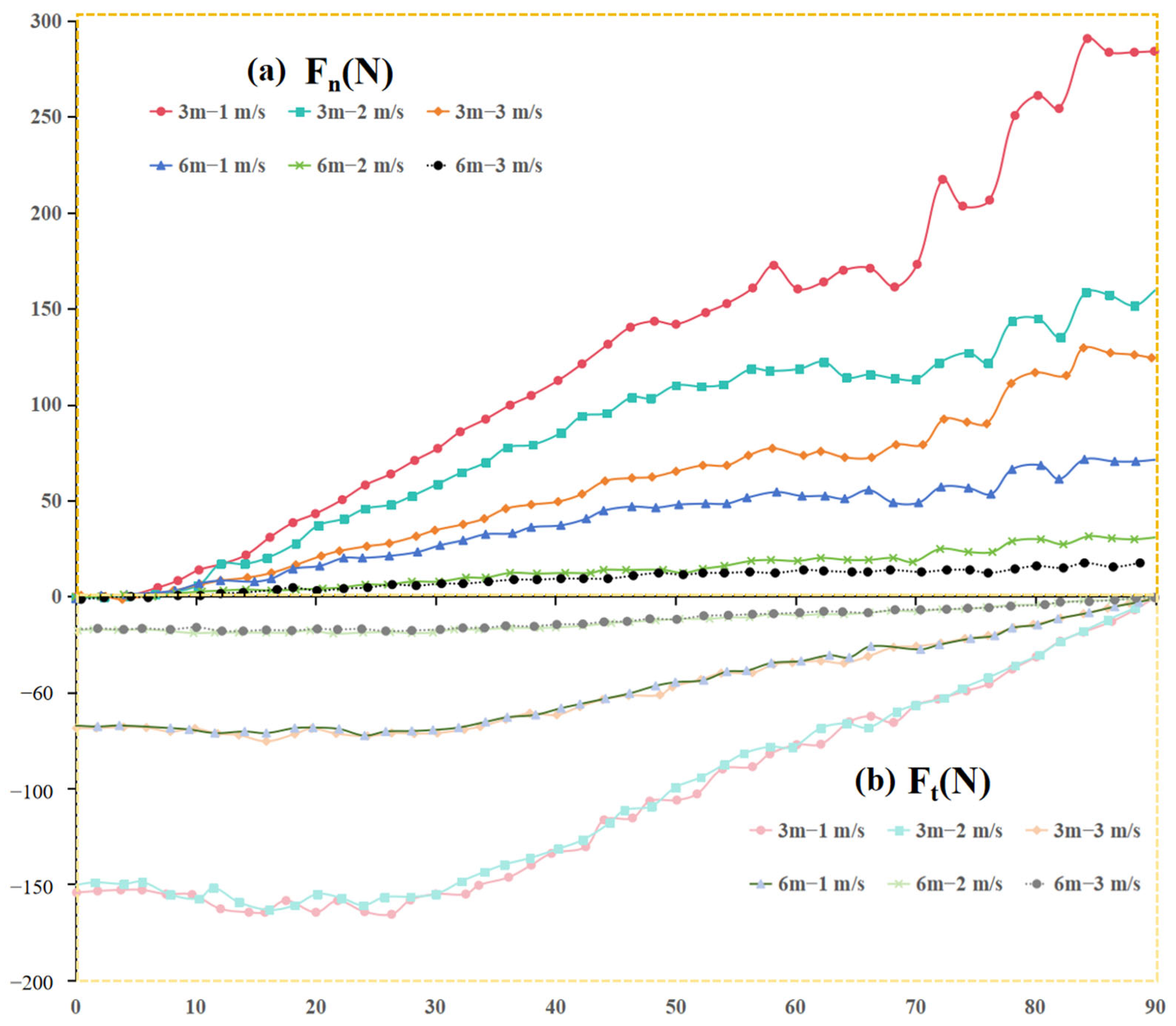
4.2.1. Effects of Different Current Velocities and Current Directions
4.2.2. Effects of Waves on Trawling
4.2.3. Impact of Tow Length
4.3. Mechanical Response Analysis of Towing Cable
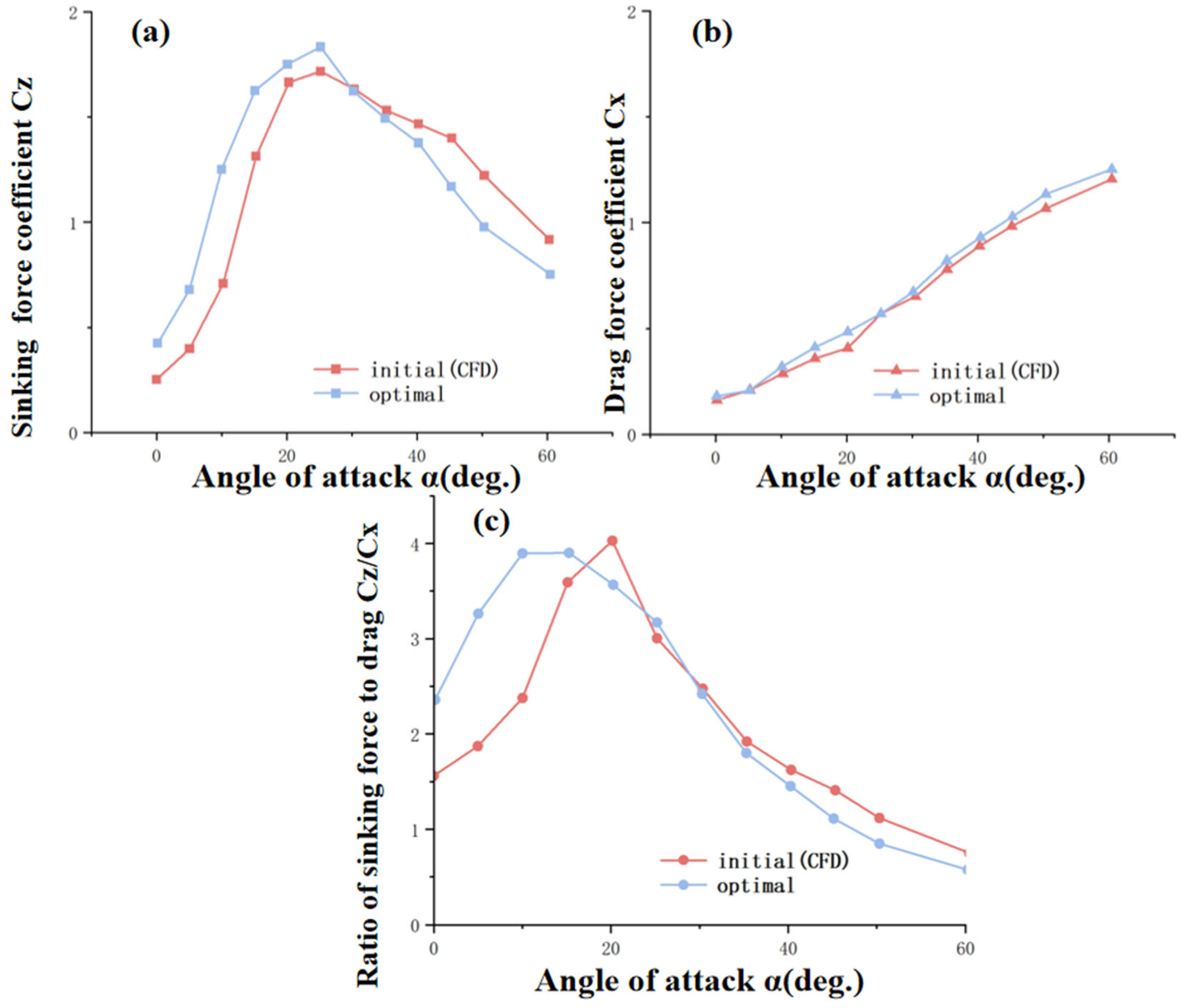
4.3.1. Munk Coefficient
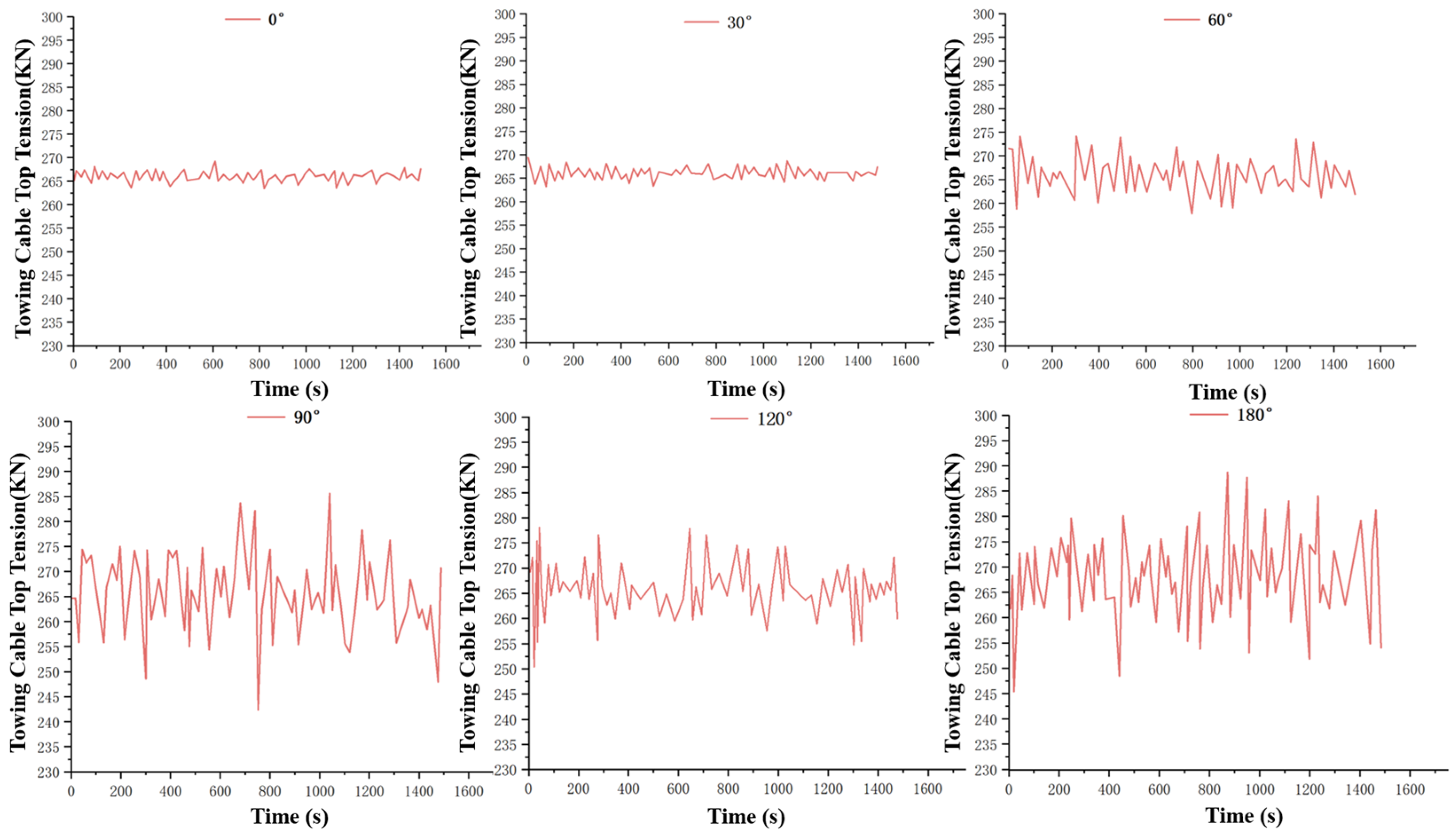
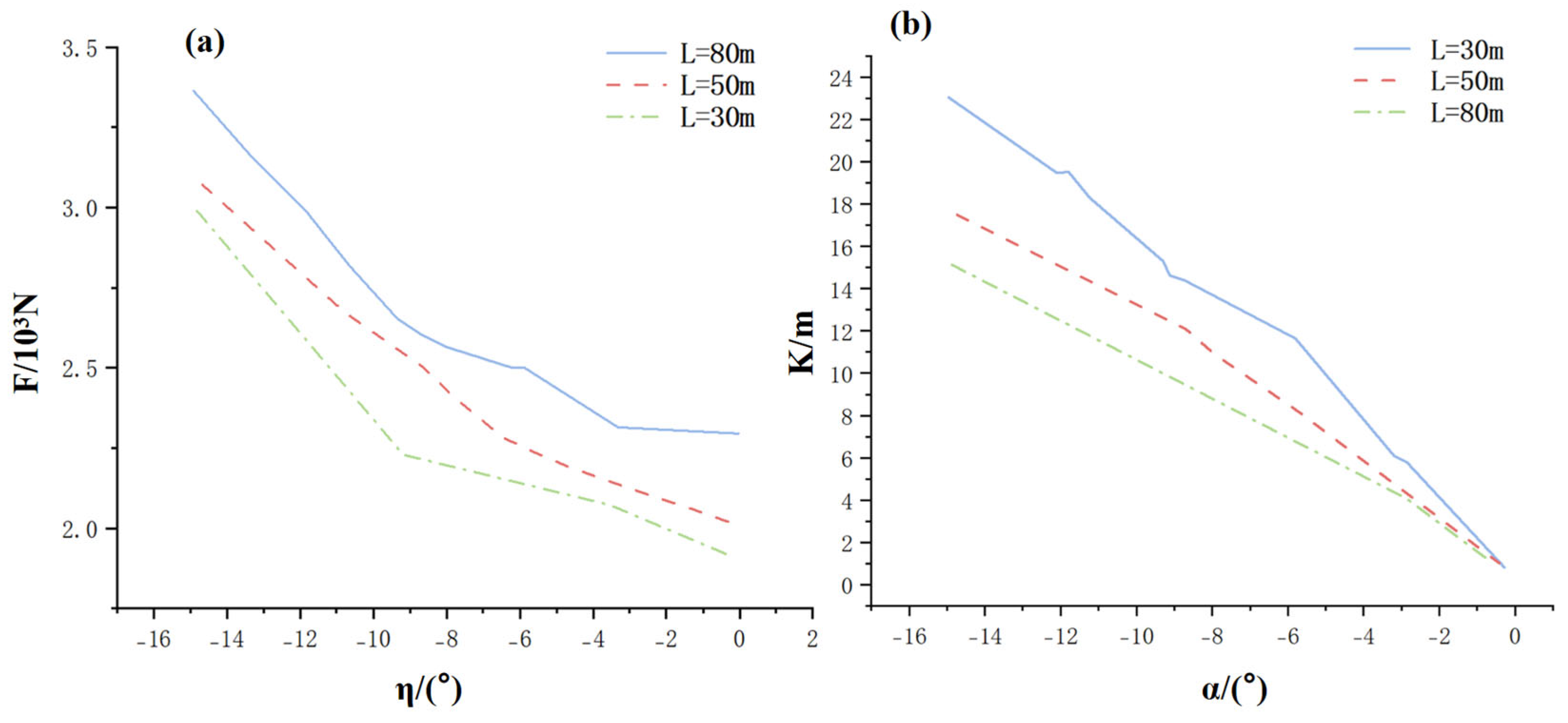
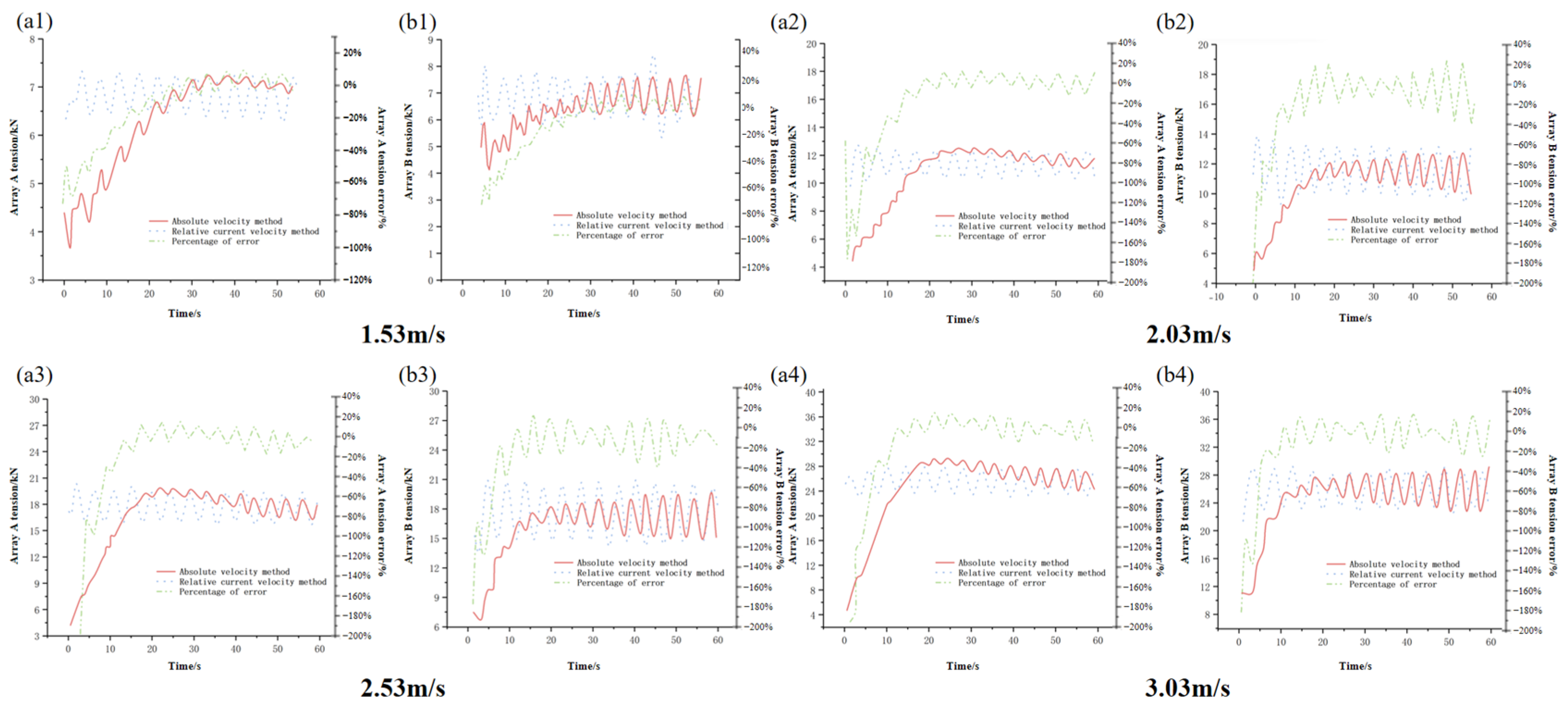
4.3.2. Different Towing Speeds and Towing Angles
5. Limitations and Prospects
5.1. Challenges in the Field of Multi-Branch Towed Line Array
5.1.1. Stability Challenges in Complex Marine Environments
5.1.2. Formation and Mechanical Response Problems Caused by Fracture of the Guide Cable
5.1.3. Complex Factors Affecting Towing System Unfolding and Retracting
5.1.4. Dilemma of Real-Time Monitoring and Safe Operation in Engineering Practice
5.2. Future Perspectives in the Field of Multi-Branch Towed Arrays System
5.2.1. Optimize System Design to Enhance Environmental Adaptability
5.2.2. Deepen the Fracture Mechanical Response Research and Monitoring Technology
5.2.3. Expanding Multidisciplinary Cross-Research and Application Scenarios
5.2.4. Promote the Application of Intelligent and Digital Technology
Funding
Conflicts of Interest
References
- Kim, Y.; Hong, J. The tacotron-based signal synthesis method for active sonar. Sensors 2022, 23, 28. [Google Scholar] [CrossRef]
- Huanghuang, J.; Wang, H.; Zhuang, Z. A new simple method to design degaussing coils using magnetic dipoles. J. Mar. Sci. Eng. 2022, 10, 1495. [Google Scholar] [CrossRef]
- Barger, J. Ira Dyer and the BBN Applied Research Division. J. Acoust. Soc. Am. 2017, 141 (Suppl. S5), 3652. [Google Scholar] [CrossRef]
- Chu, X.; Zhao, F.; Wang, Z.; Qian, Y.; Yang, G. Acoustic wave propagation in depth-evolving sound-speed field using the lattice Boltzmann method. Phys. Fluids 2024, 36, 0222202. [Google Scholar] [CrossRef]
- McCartney, I. The archaeology of second world war U-boat losses in the english channel and its impact on the historical record. Mar. Mirror 2020, 106, 62–81. [Google Scholar] [CrossRef]
- Gaber, M.; El-Banna, S.H.; El-Dabah, M. Intelligent Energy Management System for an all-electric ship based on adaptive neuro-fuzzy inference system. Energy Rep. 2021, 7, 7989–7998. [Google Scholar] [CrossRef]
- Liao, S.; Xiao, W.; Wang, Y. Optimization of route planning based on active towed array sonar for underwater search and rescue. Ocean Eng. 2025, 330, 121249. [Google Scholar] [CrossRef]
- Popper, A.N.; Halvorsen, M.B.; Miller, D.; Smith, M.E.; Song, J.; Wysocki, L.E.; Hastings, M.C.; Kane, A.S.; Stein, P. Effects of surveillance towed array sensor system (SURTASS) low frequency active sonar on fish. J. Acoust. Soc. Am. 2005, 117 (Suppl. S4), 2440. [Google Scholar] [CrossRef]
- An, S.; Lee, K.; Seong, W. Optimization of deployment depth for active towed array sonar (ATAS) using simulated annealing. J. Acoust. Soc. Am. 2018, 144 (Suppl. S3), 1770. [Google Scholar] [CrossRef]
- Ambatt, S.K. Fault Detection and Prognostic Health Monitoring of Towed Array Sonars. Def. Sci. J. 2022, 72, 495–503. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhao, B.; Ma, Y.; Si, K. Exploring subsea dynamics: A comprehensive review of underwater pipelines and cables. Phys. Fluids 2024, 36, 0231898. [Google Scholar] [CrossRef]
- Eleftherakis, D.; Vicen-Bueno, R. Sensors to increase the security of underwater communication cables: A review of underwater monitoring sensors. Sensors 2020, 20, 737. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Pei, Y.; Liu, C.; Zhang, L.; Luo, X.; Liu, K.; Li, W. A robust array geometry inversion method for a deep-towed multichannel seismic system with a complex seafloor. Front. Mar. Sci. 2023, 10, 1283061. [Google Scholar] [CrossRef]
- Mayer, L.A. Frontiers in seafloor mapping and visualization. Mar. Geophys. Res. 2006, 27, 7–17. [Google Scholar] [CrossRef]
- Karl, H.A.; Schwab, W.C.; Wright, A.S.C.; Drake, D.E.; Chin, J.L.; Danforth, W.W.; Ueber, E. Acoustic mapping as an environmental management tool: I. Detection of barrels of low-level radioactive waste, Gulf of the Farallones National Marine Sanctuary, California. Ocean Coast. Manag. 1994, 22, 201–227. [Google Scholar] [CrossRef]
- Mizuno, K.; Tabeta, S.; Matsumoto, Y.; Sakamoto, S.; Sugimoto, Y.; Ogawa, T.; Sugimoto, K.; Jimenez, L.A.; Terayama, K.; Fukami, H.; et al. Development of a towed optical camera array system (SSS: Speedy Sea Scanner) for sea environmental monitoring. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- von Benda-Beckmann, A.M.; Beerens, S.P.; Van Ijsselmuide, S.P. Effect of towed array stability on instantaneous localization of marine mammals. J. Acoust. Soc. Am. 2013, 134, 2409–2417. [Google Scholar] [CrossRef]
- Thode, A. Tracking sperm whale (Physeter macrocephalus) dive profiles using a towed passive acoustic array. J. Acoust. Soc. Am. 2004, 116, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Birin, I.; Maglić, L. Analysis of seismic methods used for subsea hydrocarbon exploration. J. Marit. Transp. Sci. 2020, 58, 77–89. [Google Scholar] [CrossRef]
- Dosso, S.E.; Riedel, M. Array element localization for towed marine seismic arrays. J. Acoust. Soc. Am. 2001, 110, 955–966. [Google Scholar] [CrossRef]
- Bjørnø, L. Developments in sonar and array technologies. In Proceedings of the 2011 IEEE Symposium on Underwater Technology and Workshop on Scientific Use of Submarine Cables and Related Technologies, Tokyo, Japan, 5–8 April 2011; IEEE: New York, NY, USA, 2011. [Google Scholar]
- Ødegård, Ø.; Sørensen, A.J.; Hansen, R.E.; Ludvigsen, M. A new method for underwater archaeological surveying using sensors and unmanned platforms. IFAC-PapersOnLine 2016, 49, 486–493. [Google Scholar] [CrossRef]
- Chi, C.; Pallayil, V.; Chitre, M. Design of an adaptive noise canceller for improving performance of an autonomous underwater vehicle-towed linear array. Ocean Eng. 2020, 202, 106886. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, Z.; Li, Y.; Xu, W. Fast estimation of direction of arrival based on sparse Bayesian learning for towed array sonar during manoeuvring. IET Radar Sonar Navig. 2023, 17, 1079–1087. [Google Scholar] [CrossRef]
- Yang, T.C.; Yoo, K.; Fialkowski, L.T. Subbottom profiling using a ship towed line array and geoacoustic inversion. J. Acoust. Soc. Am. 2007, 122, 3338–3352. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Z.; Li, Y.; Xu, W. Towing operation methods of offshore integrated meteorological mast for offshore wind farms. J. Mar. Sci. Eng. 2019, 7, 100. [Google Scholar] [CrossRef]
- Nair, B.M.; Kumar, A.; Bahl, R. Left–right ambiguity resolution methods for closely spaced arrays. IEEE J. Ocean. Eng. 2022, 47, 445–456. [Google Scholar] [CrossRef]
- He, Z.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Philbin, S.P.; Kennedy, D.A. Diagnostic framework and health check tool for engineering and technology projects. J. Ind. Eng. Manag. 2014, 7, 1145–1166. [Google Scholar] [CrossRef]
- Mishra, M.; Lourenço, P.B.; Ramana, G.V. Structural health monitoring of civil engineering structures by using the internet of things: A review. J. Build. Eng. 2022, 48, 103954. [Google Scholar] [CrossRef]
- Das, S.; Saha, P.; Satapathy, S.C.; Jena, J.J. Social group optimization algorithm for civil engineering structural health monitoring. Eng. Optim. 2021, 53, 1651–1670. [Google Scholar] [CrossRef]
- Li, Y.; Li, B.; Ji, J.; Kalhori, H. Advanced fault diagnosis and health monitoring techniques for complex engineering systems. Sensors 2022, 22, 10002. [Google Scholar] [CrossRef] [PubMed]
- Bao, Y.; Chen, Z.; Wei, S.; Xu, Y.; Tang, Z.; Li, H. The state of the art of data science and engineering in structural health monitoring. Engineering 2019, 5, 234–242. [Google Scholar] [CrossRef]
- Zhou, C.; Jia, Z.; Song, S.; Luo, S.; Zhang, X.; Zhang, X.; Pei, X.; Xu, Z. Application of FBG sensor in health monitoring of engineering building structure: A review. Sens. Rev. 2025, 45, 129–145. [Google Scholar] [CrossRef]
- Kumar, P.; Kota, S.R. Machine learning models in structural engineering research and a secured framework for structural health monitoring. Multimed. Tools Appl. 2024, 83, 7721–7759. [Google Scholar] [CrossRef]
- Li, X.; Zhu, X.; Sun, M.; Qu, Y.; Liu, K.; Pei, Y.; Choi, J.H. Surrogate model-based optimization of drogue dimensions and towing operations to straighten deep-towed nonuniform arrays. Ocean Eng. 2024, 299, 117321. [Google Scholar] [CrossRef]
- Yang, S.; Ren, H.; Zhu, X. Dynamic modeling of cable deployment/retrieval based on ALE-ANCF and adaptive step-size integrator. Ocean Eng. 2024, 309, 118517. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, X.; Ren, H. Dynamic analysis of a deep-towed seismic system based on a flexible multi-body dynamics frame. Ocean Eng. 2023, 279, 114587. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, X.; Ren, H. A two-dimensional σ-transform based finite element method for nonlinear water waves. Ocean Eng. 2024, 308, 118299. [Google Scholar] [CrossRef]
- Qin, H.; Yu, S.; Li, P. Dynamic response of floating collar and cage under waves and current. Ocean Eng. 2020, 205, 107330. [Google Scholar] [CrossRef]
- Chen, L.; Jeng, D.-S. Study on the seabed response around a dumbbell cofferdam under combined wave and current loading. Ocean Eng. 2022, 256, 111456. [Google Scholar] [CrossRef]
- Lou, S.; Chen, M.; Ma, G.; Liu, S.; Zhong, G. Laboratory study of the effect of vertically varying vegetation density on waves, currents and wave-current interactions. Appl. Ocean Res. 2018, 79, 74–87. [Google Scholar] [CrossRef]
- Gazi, A.H.; Purkayastha, S.; Afzal, M.S. The equilibrium scour depth around a pier under the action of collinear waves and current. J. Mar. Sci. Eng. 2020, 8, 36. [Google Scholar] [CrossRef]
- McCord, M.R.; Lee, Y.-K.; Lo, H.K. Ship routing through altimetry-derived ocean currents. Transp. Sci. 1999, 33, 49–67. [Google Scholar] [CrossRef]
- Shu, Y.; Han, B.; Song, L.; Yan, T.; Gan, L.; Zhu, Y.; Zheng, C. Analyzing the spatio-temporal correlation between tide and shipping behavior at estuarine port for energy-saving purposes. Appl. Energy 2024, 367, 123382. [Google Scholar] [CrossRef]
- Arkhangel’skii, E.A.; Boiko, A.V.; Prokof’ev, V.V. Distinctive Features of Using the Propulsor of the Underwater Sail Type and the Direct-Flow Wave Propulsor on a Semisubmerged Catamaran. Fluid Dyn. 2024, 59, 1017–1027. [Google Scholar] [CrossRef]
- Wang, P.; Wang, F.; Chen, Z. Investigation on aerodynamic performance of luxury cruise ship. Ocean Eng. 2020, 213, 107790. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, H.; Deng, C.; Zhang, J.; Chen, J.; Chang, Z. Propulsion and energy extraction performance of wave-powered mechanism considering wave and current. Renew. Energy 2024, 237, 121518. [Google Scholar] [CrossRef]
- Liao, L.; Li, J.; Chen, M.; An, R. Effects of hydraulic cues in barrier environments on fish navigation downstream of dams. J. Environ. Manag. 2024, 365, 121495. [Google Scholar] [CrossRef]
- Geng, Y.; Guo, M.; Guo, H.; Chen, H. Safety range in bridge areas based on the influence of cross flow on ship navigation. Ocean Eng. 2023, 281, 114649. [Google Scholar] [CrossRef]
- Ahmed, F.; Xiang, X.; Wang, H.; Zhang, J.; Xiang, G.; Yang, S. Nonlinear dynamics of novel flight-style autonomous underwater vehicle with bow wings, Part I: ASE and CFD based estimations of hydrodynamic coefficients, Part II: Nonlinear dynamic modeling and experimental validations. Appl. Ocean Res. 2023, 141, 103739. [Google Scholar] [CrossRef]
- Shi, Y.; Gao, S.; Pan, G.; Quan, X. RANS/LES investigation on the performance of air film fusion around a vertically launched underwater vehicle. Ocean Eng. 2022, 266, 112880. [Google Scholar] [CrossRef]
- Marley, M.; Skjetne, R.; Gil, M.; Krata, P. Four degree-of-freedom hydrodynamic maneuvering model of a small azipod-actuated ship with application to onboard decision support systems. IEEE Access 2023, 11, 58596–58609. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, Y.; Zhang, Y.; Ma, Y.; Zhu, K.; Zeng, S. A Comprehensive Review of an Underwater Towing Cable Array: A Discussion on the Dynamic Characteristics of the Towing Cable Array During the Outspread Process. J. Mar. Sci. Eng. 2024, 12, 1880. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, D.; Zhu, K.; Zhang, T. Dynamic analysis of umbilical cable under interference with riser. Ships Offshore Struct. 2018, 13, 809–821. [Google Scholar] [CrossRef]
- Guo, Y.; Li, P.; Qin, H.; Jiang, Z. Research on the Influence of Seabed on the Hydrodynamic Performance of the Underwater Vehicle. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Shanghai, China, 6–10 June 2022; ISOPE: Mountain View, CA, USA, 2022. [Google Scholar]
- Asmael, M.; Memarzadeh, A. A review on recent achievements and challenges in electrochemical machining of tungsten carbide. Arch. Adv. Eng. Sci. 2024, 2, 1–23. [Google Scholar] [CrossRef]
- Thorleifson, J.M.; Davies, T.C.; Black, M.R.; Hopkin, D.A.; Verrall, R.I.; Pope, A.; Monteith, I.; Den Hertog, V.; Butler, B. The Theseus autonomous underwater vehicle. A Canadian success story. In Proceedings of the Oceans’ 97. MTS/IEEE Conference Proceedings, Halifax, NS, Canada, 6–9 October 1997; IEEE: New York, NY, USA, 1997; Volume 2. [Google Scholar]
- Blintsov, V.S.; Trunin, K.S.; Tarełko, W. Determination of additional tension in towed streamer cable triggered by collision with underwater moving object. Pol. Marit. Res. 2020, 2, 58–68. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Yuan, X. Simulation of Recycling Cable in Underwater Towed System. In Proceedings of the 1st International Conference on Mechanical Engineering and Material Science (MEMS 2012), Shanghai, China, 28–30 December 2012; Atlantis Press: Amsterdam, The Netherlands, 2012. [Google Scholar][Green Version]
- Ivanovskaya, A.V.; Bogatyreva, E.V.; Rybak, A.T. Simulation of the cable part of the load-lifting device drive, represented as a rod system. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 1001, No. 1. [Google Scholar][Green Version]
- Wang, F.; Tu, W.; Deng, D.; Wu, X. Dynamic effect research of cable-lead-in rod on towed system. J. Shanghai Jiaotong Univ. Sci. 2019, 24, 745–753. [Google Scholar] [CrossRef]
- Yan, J.; Xue, X.; Cui, L.; Ding, S.; Gu, W.; Le, F. Analysis of dynamic behavior of spray boom under step excitation. Appl. Sci. 2021, 11, 10129. [Google Scholar] [CrossRef]
- Menting, J.G.; Yang, Y.; Chan, S.J.; Phillips, N.B.; Smith, B.J.; Whittaker, J.; Wickramasinghe, N.P.; Whittaker, L.J.; Pandyarajan, V.; Wan, Z.L.; et al. Protective hinge in insulin opens to enable its receptor engagement. Proc. Natl. Acad. Sci. USA 2014, 111, E3395–E3404. [Google Scholar] [CrossRef] [PubMed]
- Chai, Y.; Zhong, W.; Yang, C.; Shi, X.; Zhao, Q. Restitution coefficient of various particles based on acoustic technology. J. Phys. Conf. Ser. 2023, 2557, 012057. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Sun, J.; Zhang, Y.; Zhu, K.; Jiang, H. Influence of different static equilibrium calculation methods on the dynamic response of marine cables during the releasing process: Review and a case study. J. Mar. Sci. Eng. 2023, 11, 764. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhu, K. Mechanical characteristics analysis of horizontal lifting of subsea pipeline with different burial depths. Front. Earth Sci. 2022, 10, 1011291. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhu, K. Dynamic Analysis of Pipeline Lifting Operations for Different Current Velocities and Wave Heights. Fluid Dyn. Mater. Process. 2023, 19, 603–617. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhu, K. Dynamic analysis of the umbilical cable pull-in operation through J-tube under different wave directions. Ocean Eng. 2023, 280, 114838. [Google Scholar] [CrossRef]
- Lan, T.; Wang, Y.; Qiu, L.; Liu, G. Array shape estimation based on tug vehicle noise for towed linear array sonar during turning. Ocean Eng. 2024, 303, 117554. [Google Scholar] [CrossRef]
- Liu, J.; Gao, S.; Nian, R.; He, B.; Yan, T. Study on hydrodynamic characteristics and depth control of the towed sensors array system. Mar. Struct. 2023, 92, 103504. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhu, K.; Jiang, H. Dynamic analysis of towed cable with variable length during turning maneuvers. Sci. Rep. 2023, 13, 3525. [Google Scholar] [CrossRef]
- Antony, T.; Adithya, P.V.; Madhusoodanan, K.N.; Kumar, K.R. Miniature fiber optic towed array for AUV applications. In Proceedings of the Global Oceans 2020: Singapore–US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Park, S.H.; Lee, S.J.; Lee, S. Experimental investigation of towing-and course-stability of a FPSO towed by a tug-boat with lateral motion. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 12–23. [Google Scholar] [CrossRef]
- Yang, X.; Sheng, S.; Wu, J.; Yue, W. Numerical analysis of dynamic behaviors of underwater towed system with hydrofoil manipulations. Ocean Eng. 2024, 310, 118791. [Google Scholar] [CrossRef]
- Feng, H.; Sun, W.; Tang, G.; Wang, J.J. Study on a novel two-part underwater towed system for near-surface towed vehicle test. Ocean Eng. 2022, 255, 111440. [Google Scholar] [CrossRef]
- Wu, J.; Ye, J.; Yang, C.; Chen, Y.; Tian, H.; Xiong, X. Experimental study on a controllable underwater towed system. Ocean Eng. 2005, 32, 1803–1817. [Google Scholar] [CrossRef]
- Yang, X.; Wu, J.; Xu, S. Study on dynamic response of underwater towed system in ship propeller wakes using a new hydrodynamic model. Ocean Eng. 2022, 265, 112599. [Google Scholar] [CrossRef]
- Eggenberger, K.; Christie, P.; Vassallo, M.; Özbek, A.; Muyzert, E.; van Manen, D.J.; Kragh, E. Fidelity and repeatability of wave fields reconstructed from multicomponent streamer data. Geophys. Prospect. 2014, 62, 994–1008. [Google Scholar] [CrossRef]
- Deng, R.; Luo, F.; Ren, H.; Mo, X.; Wu, T. Experimental research for the influence of stern towing force on a planing hull in the towed system. Ocean Eng. 2022, 259, 111849. [Google Scholar] [CrossRef]
- Zhang, P.; Peng, Y.; Ding, H.; Hu, R.; Shi, J. Numerical analysis of offshore integrated meteorological mast for wind farms during wet towing transportation. Ocean Eng. 2019, 188, 106271. [Google Scholar] [CrossRef]
- Kragh, E.; Laws, R. Rough seas and statistical deconvolution. In Proceedings of the 63rd EAGE Conference & Exhibition, Amsterdam, The Netherlands, 11–15 June 2001; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2001. [Google Scholar]
- Westin, C. Framework for a physics-based digital twin of a towed cable-body system. Ocean Eng. 2025, 328, 121025. [Google Scholar] [CrossRef]
- Chagnaud, B.P.; Brücker, C.; Hofmann, M.H.; Bleckmann, H. Measuring flow velocity and flow direction by spatial and temporal analysis of flow fluctuations. J. Neurosci. 2008, 28, 4479–4487. [Google Scholar] [CrossRef]
- Constantin, A.; Johnson, R.S. Steady large-scale ocean flows in spherical coordinates. Oceanography 2018, 31, 42–50. [Google Scholar] [CrossRef]
- Gharib, M.R.; Heydari, A.; Kolahi, M.R.S. Modeling and analysis of static and dynamic behavior of marine towed cable-array system based on the vessel motion. Adv. Mech. Eng. 2024, 16, 16878132231220353. [Google Scholar] [CrossRef]
- Cahill, B.; Lewis, T. Wave periods and the calculation of wave power. In Proceedings of the 2nd Marine Energy Technology Symposium (METS2014), Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
- Steele, K.; Teng, C.-C.; Wang, D.J.O.E. Wave direction measurements using pitch-roll buoys. Ocean Eng. 1992, 19, 349–375. [Google Scholar] [CrossRef]
- Lauria, A.; Loprieno, P.; Rizzo, F.; Severini, A.; Foti, D.; Leone, E.; Francone, A.; Tomasicchio, G.R. On the effects of wind and operating conditions on mooring line tensions for floating offshore wind turbine. Appl. Ocean. Res. 2024, 152, 104197. [Google Scholar] [CrossRef]
- Tang, Z.H.; Zhu, K.; Bao, X. Study on the tension of the towing section and the vibration extreme value of the tail rope segment in the multi-branch towing line array system. J. Ningbo Univ. (Sci. Eng.) 2016, 29, 127–132. (In Chinese) [Google Scholar]
- Kamali, R.; Danial, K. Investigation of dynamic behavior of a towed underwater vehicle at Persian Gulf. In Proceedings of the 24th Annual International Conference on Mechanical Engineering—ISME, Yazd, Iran, 26–28 April 2016. [Google Scholar]
- Grosenbaugh, M.A. Transient behavior of towed cable systems during ship turning maneuvers. Ocean Eng. 2007, 34, 1532–1542. [Google Scholar] [CrossRef]
- Chen, S. The Research for Motion Response Analysis of Towed Linear Array Sonar. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. (In Chinese). [Google Scholar]
- Zhang, Y. Numerical Study on the Nonlinear Hydrodynamic Characteristics of Towed Linear Array Sonar. Master’s Thesis, Ningbo University, Ningbo, China, 2015. (In Chinese). [Google Scholar]
- Mudie, J.D.; Ivers, W.D. Simulation studies of the response of deeply towed vehicle to various towing ship maneuvers. Ocean Eng. 1975, 3, 37–46. [Google Scholar] [CrossRef]
- Kamman, J.W.; Huston, R.L. Modeling of variable length towed and tethered cable systems. J. Guid. Control Dyn. 1999, 22, 602–608. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G. Parameters influence on maneuvered towed cable system dynamics. Appl. Ocean Res. 2015, 49, 27–41. [Google Scholar] [CrossRef]
- Li, C.; Ai, Y.; Yu, H.; Jiang, X.; Song, W.; Wang, M. Lake experimental study on depth determination and deployment performance of underwater towing system. J. Harbin Eng. Univ. 2022, 43, 62–68. (In Chinese) [Google Scholar]
- Grosenbaugh, M.A. Dynamic Behavior of Towed Cable Systems During Ship Turning Maneuvers; Woods Hole Oceanographic Institution: Woods Hole, MA, USA, 2005. [Google Scholar]
- Pipchenko, A.; Tsymbal, N. Development of Mathematical Algorithms for the Seismic Research Vessel Maneuvering Simulator. In Proceedings of the INSLC. Available online: https://www.researchgate.net/profile/Oleksandr-Pipchenko/publication/336798657_Development_of_Mathematical_Algorithms_for_the_Seismic_Research_Vessel_Maneuvering_Simulator/links/5ec29f52A6FDCC90D67E2FC7/Development-of-Mathematical-Algorithms-for-the-Seismic-Research-Vessel-Maneuvering-Simulator.pdf (accessed on 5 May 2024).
- Obligado, M.; Bourgoin, M. An experimental investigation of the equilibrium and stability of long towed cable systems. New J. Phys. 2013, 15, 043019. [Google Scholar] [CrossRef]
- Konosu, S.; Yamaguchi, K.; Hayashi, T. Studies on Flavor Components in Boiled Crabs-1, Amino Acids and Related Compounds in the Extracts. Bull. Jpn. Soc. Sci. Flsheries 1978, 44, 505–510. [Google Scholar] [CrossRef]
- Engås, A.; Godø, O.R.; Jørgensen, T. A comparison between vessel and trawl tracks as observed by the ITI trawl instrumentation. Fish. Res. 2000, 45, 297–301. [Google Scholar] [CrossRef]
- Maina, I.; Kavadas, S.; Damalas, D.; Pantazi, M.; Katsanevakis, S. Dynamics of trawling effort in the Aegean Sea: Investigating the potential of Vessel Monitoring System (VMS) data. ICES J. Mar. Sci. 2018, 75, 2265–2275. [Google Scholar] [CrossRef]
- Preciado, I.; Arroyo, N.L.; González-Irusta, J.M.; López-López, L.; Punzón, A.; Muñoz, I.; Serrano, A. Small-scale spatial variations of trawling impact on food web structure. Ecol. Indic. 2019, 98, 442–452. [Google Scholar] [CrossRef]
- Nyatchouba Nsangue, B.T.; Tang, H.; Liu, W.; Xu, L.; Hu, F. Turbulent flow interacting with flexible trawl net structure including simulation catch in flume tank. Sci. Rep. 2023, 13, 6249. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Thierry, N.N.; Achille, N.P.; Mouangue, R.; Xu, L.; Hu, F.; Mbangue, E. Coupled dynamics of the moving Antarctic krill trawl structure and its hydrodynamics behavior using various catch sizes and door spreads based on wavelet-based and Fourier analysis. J. Fluids Struct. 2024, 124, 104037. [Google Scholar] [CrossRef]
- Balash, C.; Sterling, D.; Binns, J.; Thomas, G.; Bose, N. Drag characterisation of prawn-trawl bodies. Ocean. Eng. 2016, 113, 18–23. [Google Scholar] [CrossRef]
- Srivastava, S.K.; Ganapathy, C. Experimental investigations on loop manoeuvre of underwater towed cable-array system. Ocean. Eng. 1998, 25, 85–102. [Google Scholar] [CrossRef]
- Zhou, C. Research on Transient Electromagnetic Positioning Method of Underwater Towed Array Source for Moving Small Target on the Seabed. J. Phys. Conf. Ser. 2023, 2651, 012131. [Google Scholar] [CrossRef]
- Poli, V.; Litti, L.; Lavagnolo, M.C. Microplastic pollution in the North-east Atlantic Ocean surface water: How the sampling approach influences the extent of the issue. Sci. Total Environ. 2024, 947, 174561. [Google Scholar] [CrossRef]
- Russo, E.; Monti, M.A.; Mangano, M.C.; Raffaetà, A.; Sarà, G.; Silvestri, C.; Pranovi, F. Temporal and spatial patterns of trawl fishing activities in the Adriatic Sea (Central Mediterranean Sea, GSA17). Ocean. Coast. Manag. 2020, 192, 105231. [Google Scholar] [CrossRef]
- Van Denderen, P.D.; Plaza-Morlote, M.; Vaz, S.; Wijnhoven, S.; Borja, A.; Fernandez-Arcaya, U.; González-Irusta, J.M.; Hansen, J.L.; Katsiaras, N.; Pierucci, A.; et al. Complementarity and sensitivity of benthic state indicators to bottom-trawl fishing disturbance. Ecol. Appl. 2024, 34, e3050. [Google Scholar] [CrossRef]
- Du, R.; Sun, X.; Lin, H.; Pan, Z. Assessment of manta trawling and two newly-developed surface water microplastic monitoring techniques in the open sea. Sci. Total Environ. 2022, 842, 156803. [Google Scholar] [CrossRef]
- Thierry, N.N.; Tang, H.; Achille, N.P.; Xu, L.; Hu, F. Unsteady turbulent flow developing inside and around different parts of fluttering trawl net in flume tank. J. Fluids Struct. 2022, 108, 103451. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, F.; Wan, R.; Wang, Y.; Guo, S.; Yan, H.; Zhou, C. Hydrodynamic characteristics of frustum-type depressor for sampling midwater trawl. Ocean. Eng. 2024, 295, 117009. [Google Scholar] [CrossRef]
- Thierry, N.N.; Tang, H.; Liuxiong, X.; You, X.; Hu, F.; Achile, N.P.; Kindong, R. Hydrodynamic performance of bottom trawls with different materials, mesh sizes, and twine thicknesses. Fish. Res. 2020, 221, 105403. [Google Scholar] [CrossRef]
- Thierry, N.N.; Tang, H.; Achile, N.P.; Xu, L.; Hu, F.; You, X. Comparative study on the full-scale prediction performance of four trawl nets used in the coastal bottom trawl fishery by flume tank experimental investigation. Appl. Ocean. Res. 2020, 95, 102022. [Google Scholar] [CrossRef]
- Leonte, D.; Veraart, A.E. Simulation methods and error analysis for trawl processes and ambit fields. Math. Comput. Simul. 2024, 215, 518–542. [Google Scholar] [CrossRef]
- Grahovac, D.; Leonenko, N.N.; Taqqu, M.S. Intermittency of trawl processes. Stat. Probab. Lett. 2018, 137, 235–242. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, J.; Shi, Y.; Hong, F.; Jiang, G.; Huang, H.; Zhao, J. HiTrip: Historical trajectory interpolation for trawlers via deep learning on multi-source data. Ocean. Eng. 2024, 292, 116588. [Google Scholar] [CrossRef]
- Loiseau, J.F.; Batina, J.; Noël, F.; Peyrous, R. Hydrodynamical simulation of the electric wind generated by successive streamers in a point-to-plane reactor. J. Phys. D Appl. Phys. 2002, 35, 1020. [Google Scholar] [CrossRef]
- Haugen, J.; Imsland, L. Optimization-based motion planning for trawling. J. Mar. Sci. Technol. 2019, 24, 984–995. [Google Scholar] [CrossRef]
- Nsangue, B.T.; Tang, H.; Xu, L.; Hu, F.; Dong, S.; Achille, N.P.; Zou, B. Comparison between physical model testing and numerical simulation using two-way fluid-structure interaction approach of new trawl design for coastal bottom trawl net. Ocean. Eng. 2021, 233, 109112. [Google Scholar] [CrossRef]
- Nsangue, B.T.; Tang, H.; Mouangue, R.; Liu, W.; Pandong, A.N.; Xu, L.; Hu, F.; Tcham, L. Non-linear dynamic behavior of T0 and T90 mesopelagic trawls based on the Hilbert–Huang transform. Mar. Struct. 2025, 100, 103727. [Google Scholar] [CrossRef]
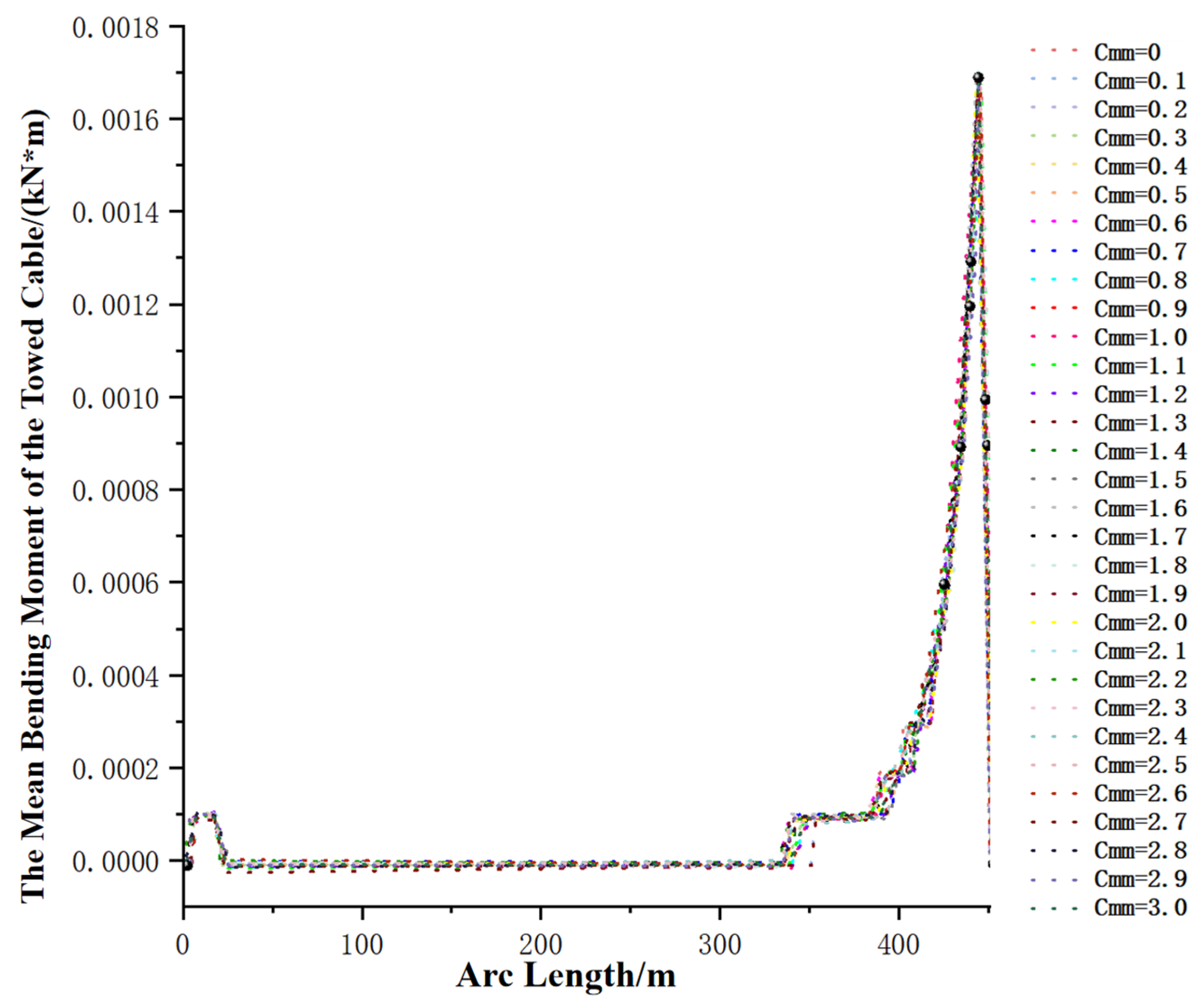
- Zhang, D.; Zhao, B.; Zhu, K. Hydrodynamic response of ocean-towed cable-array system under different munk moment coefficients. Sustainability 2022, 14, 1932. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Xie, Y.; Zhang, Y.; Liang, Z.; Zhu, K.; Zhang, S. Dynamic configuration simulation of multi-branches towed array system. Mar. Struct. 2025, 103, 103819. [Google Scholar] [CrossRef]

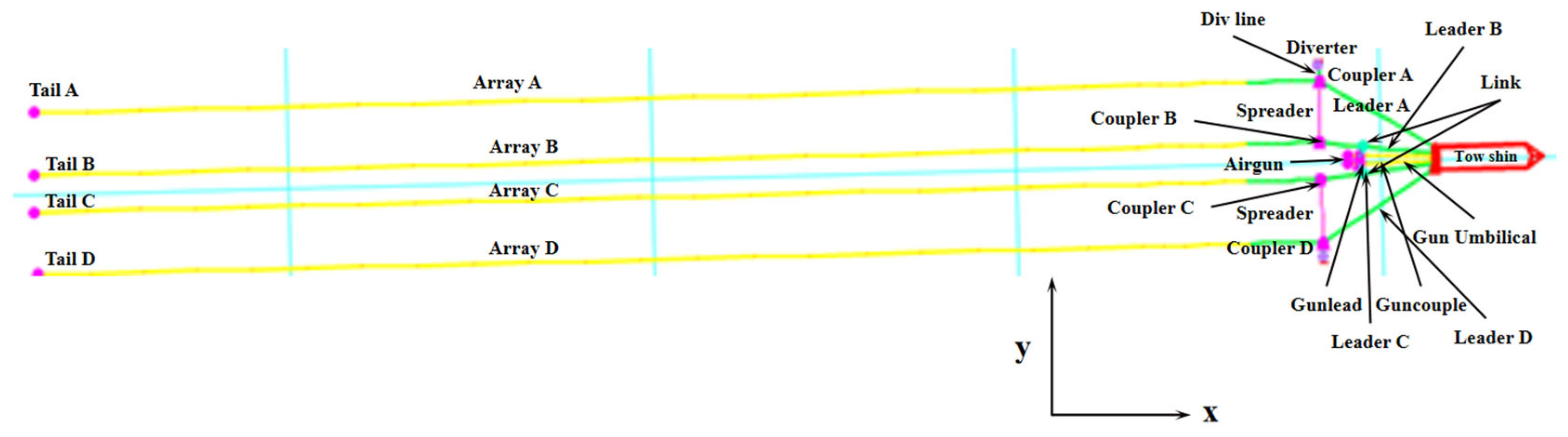
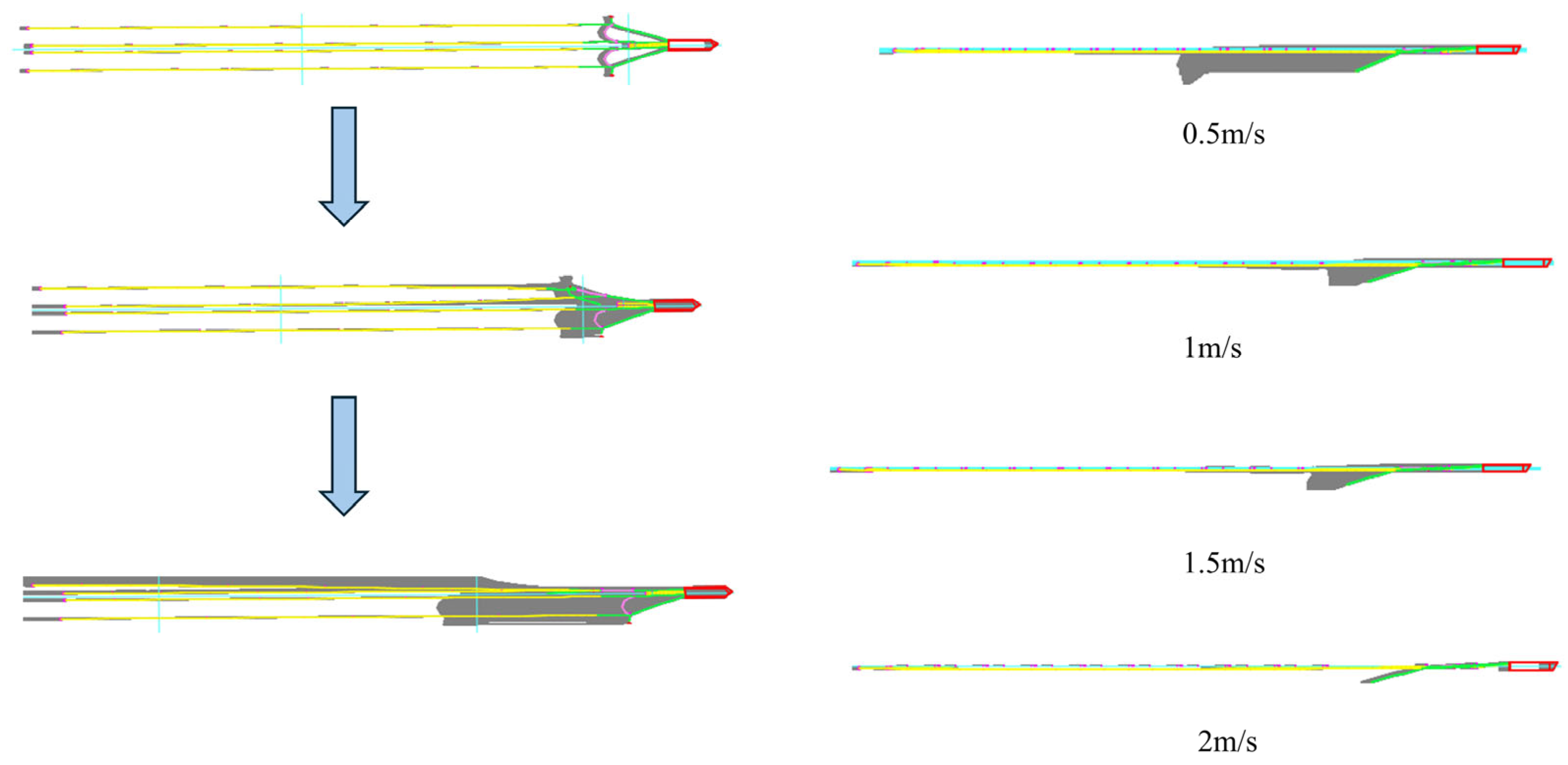

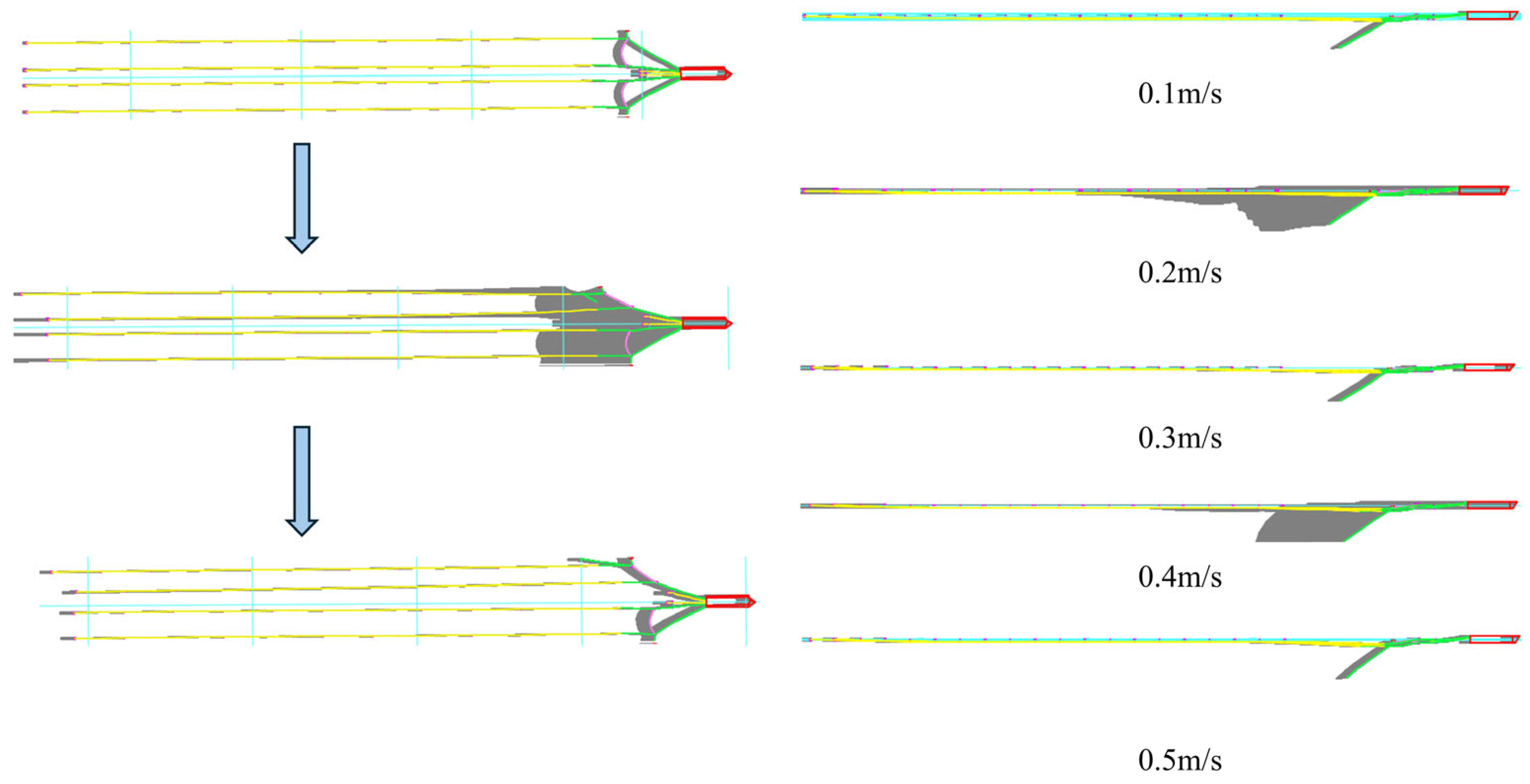
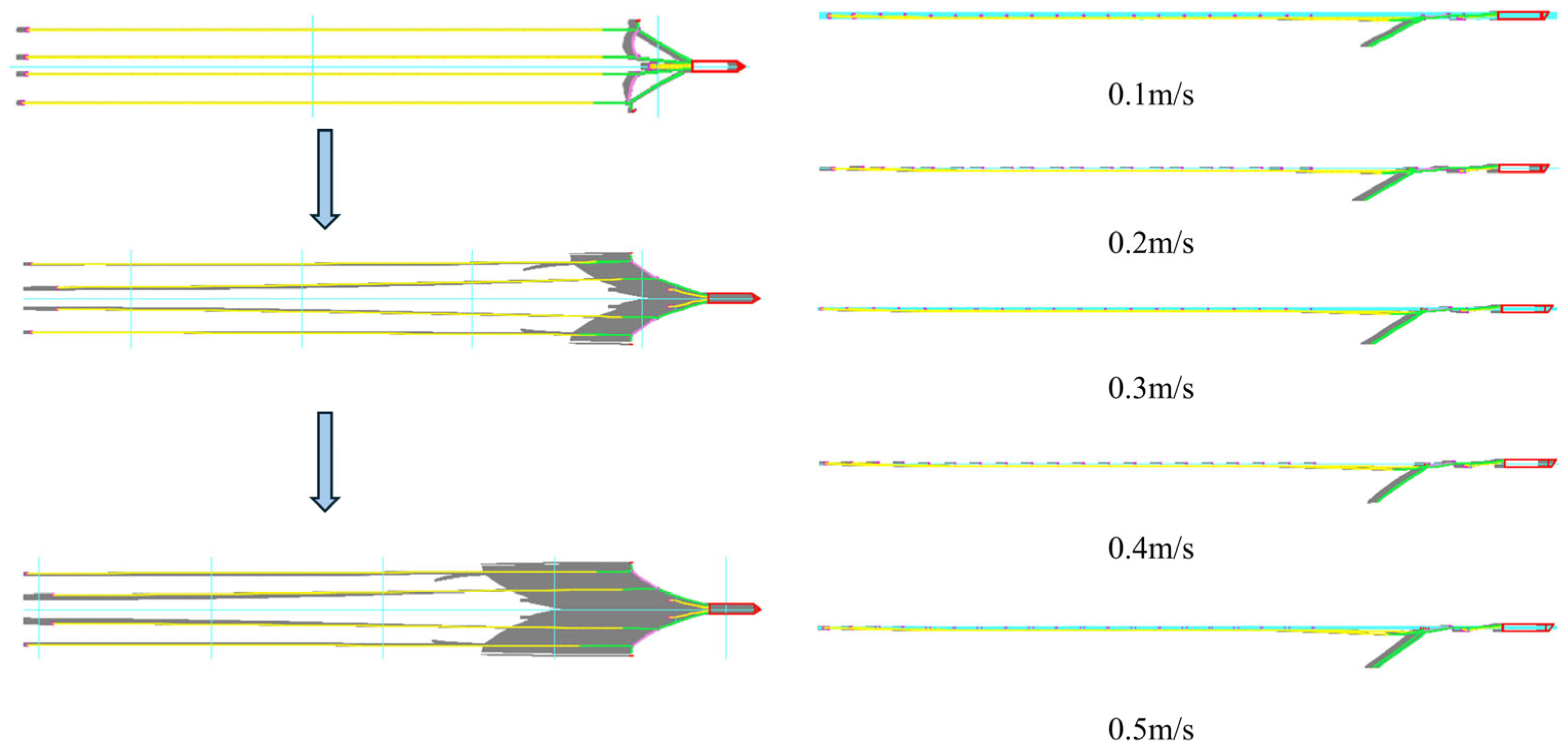

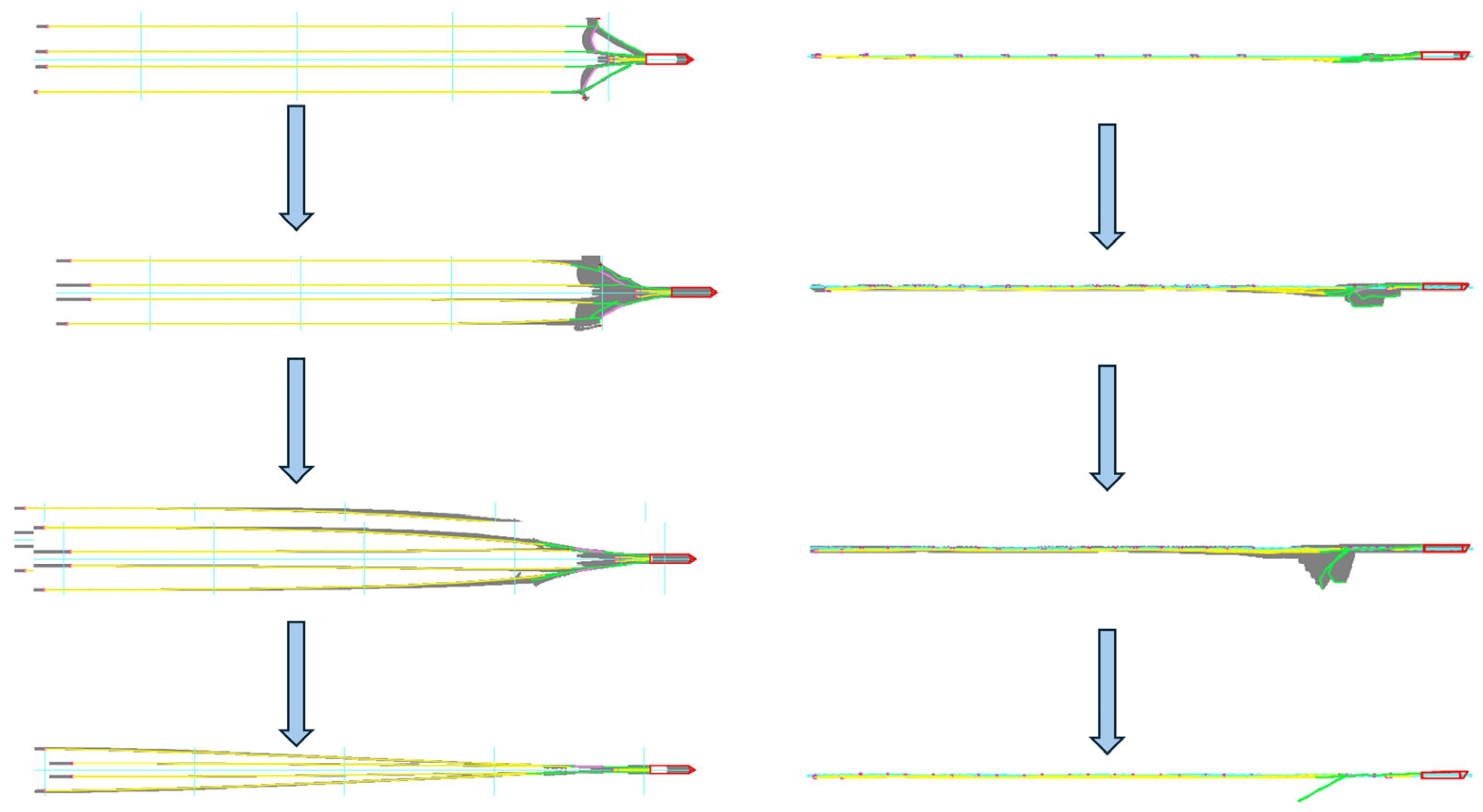
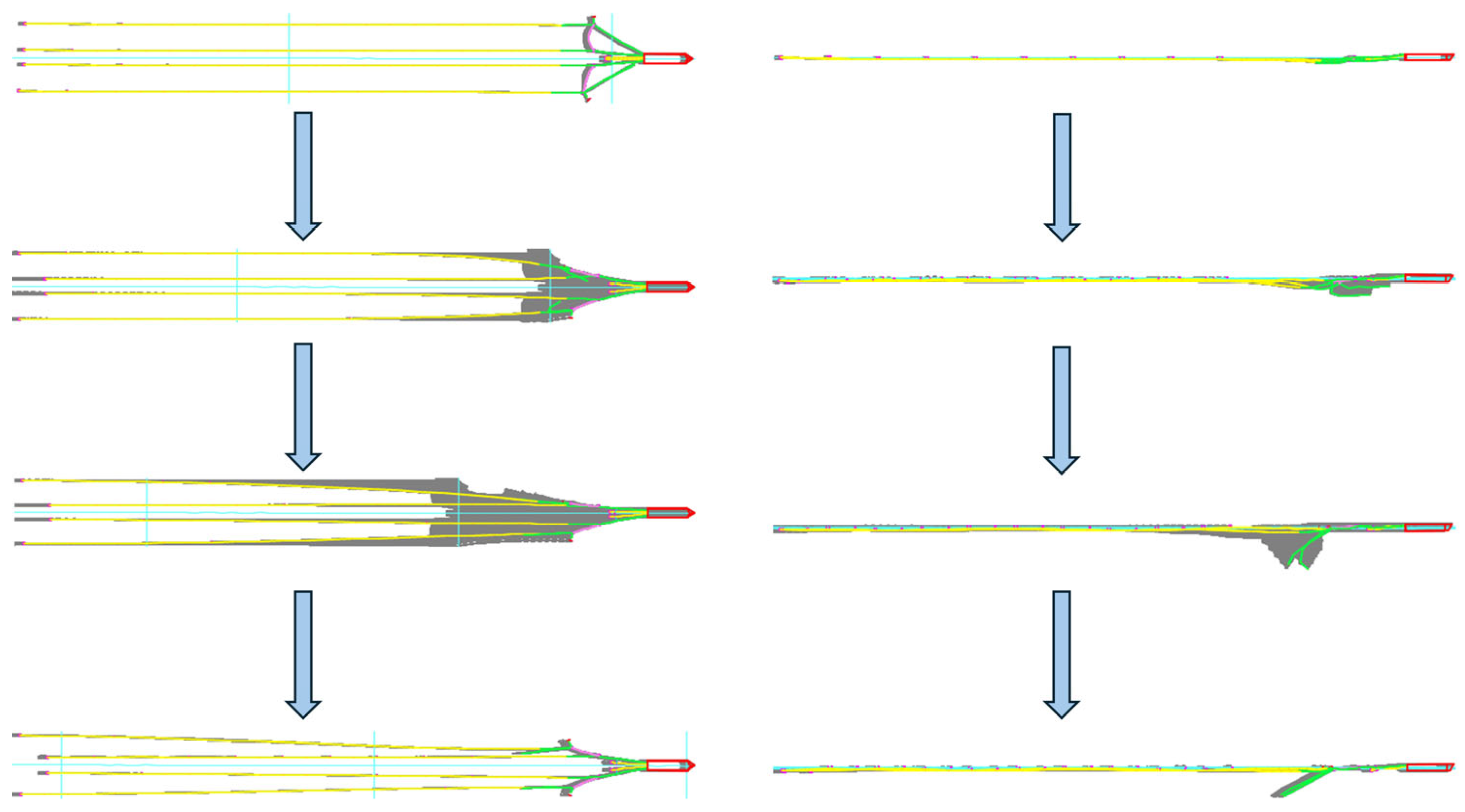
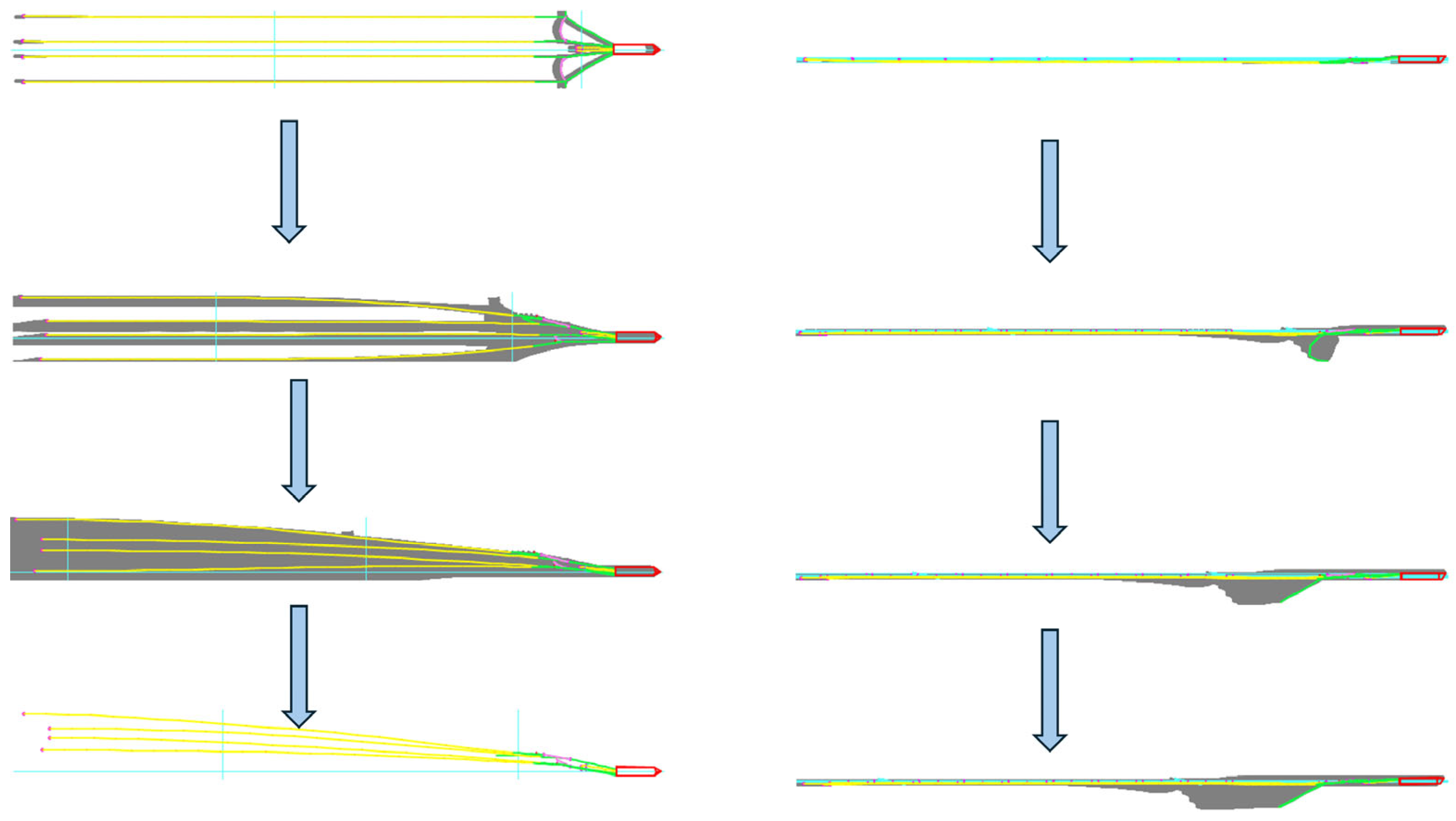
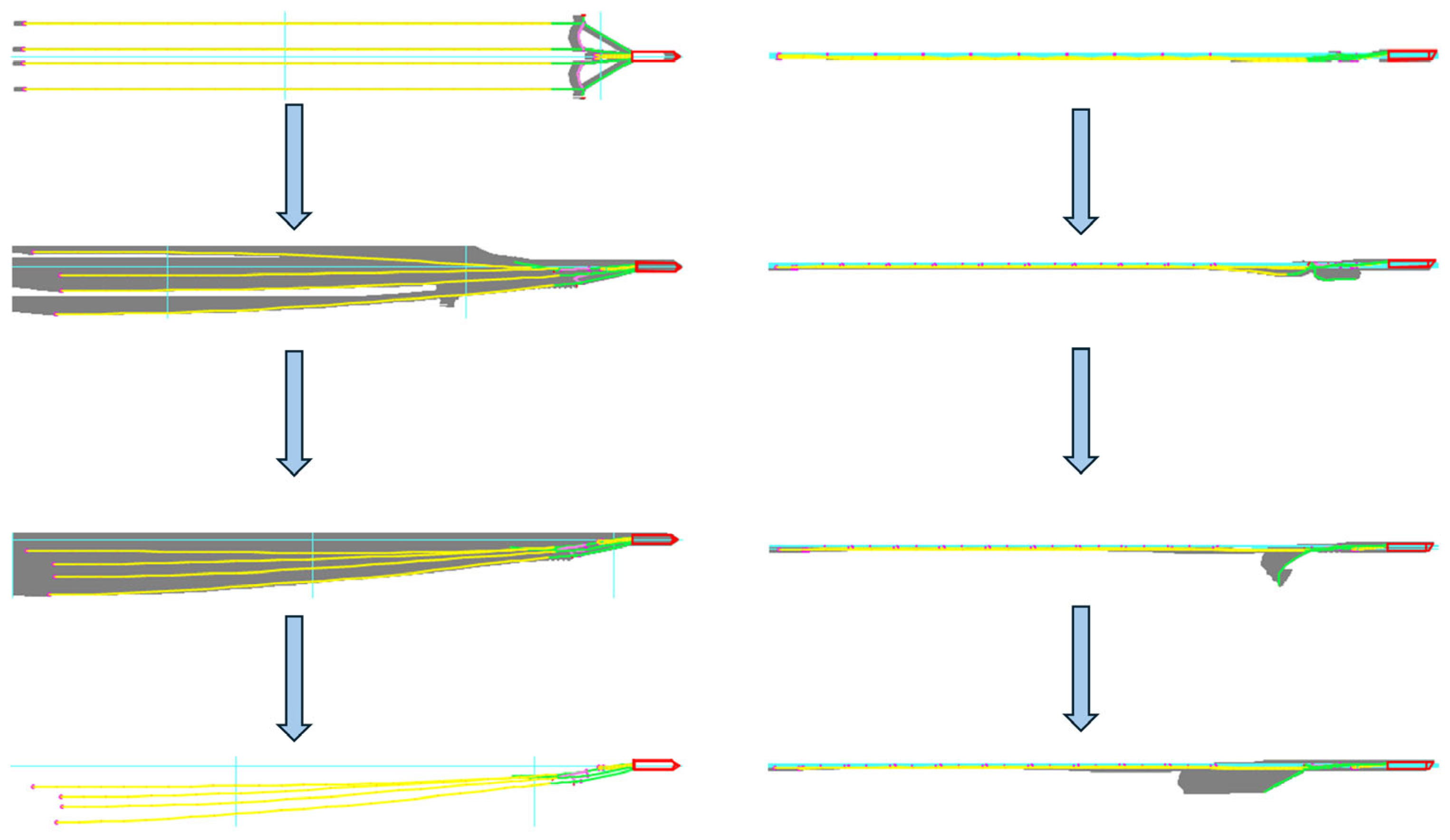
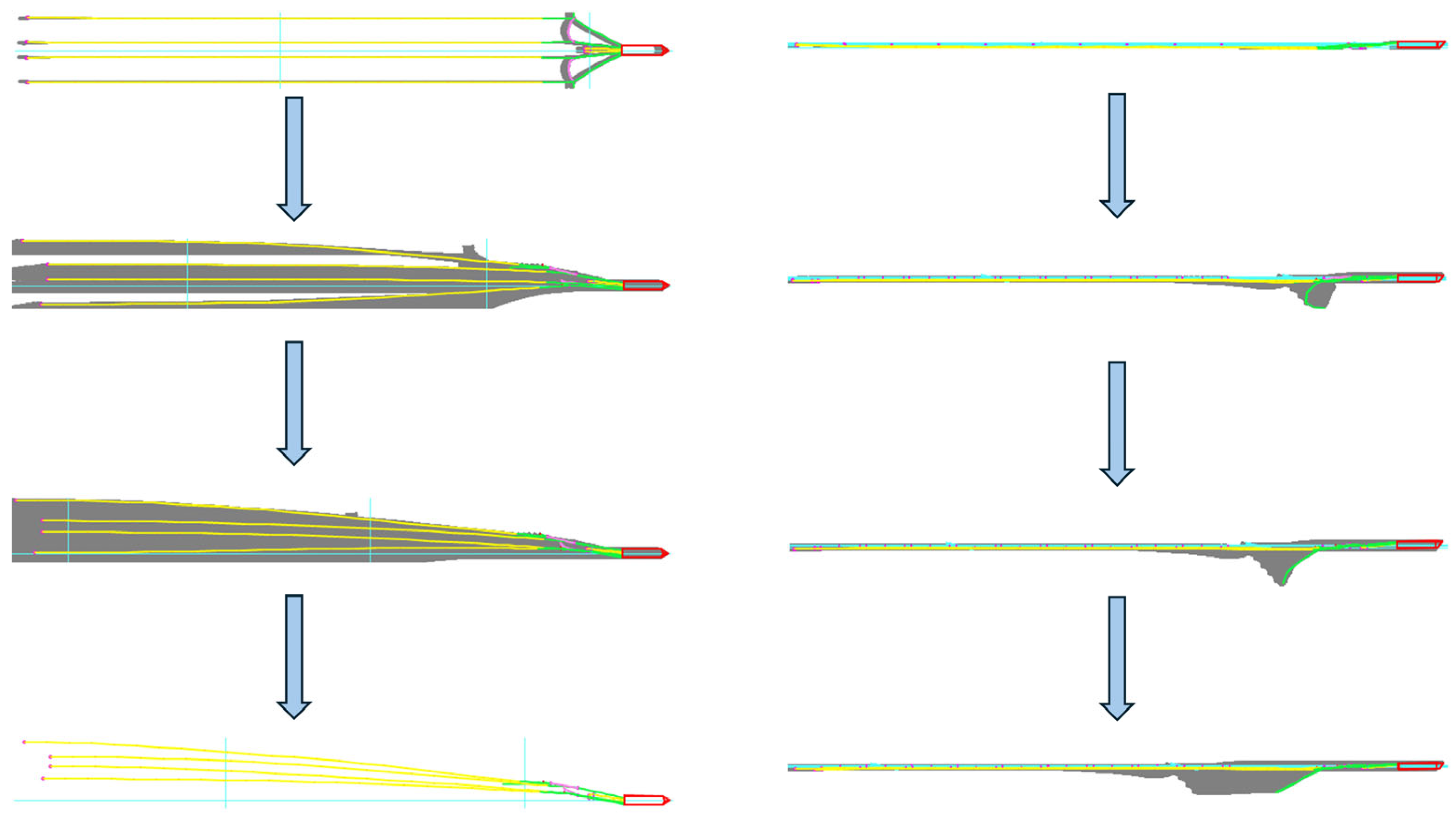
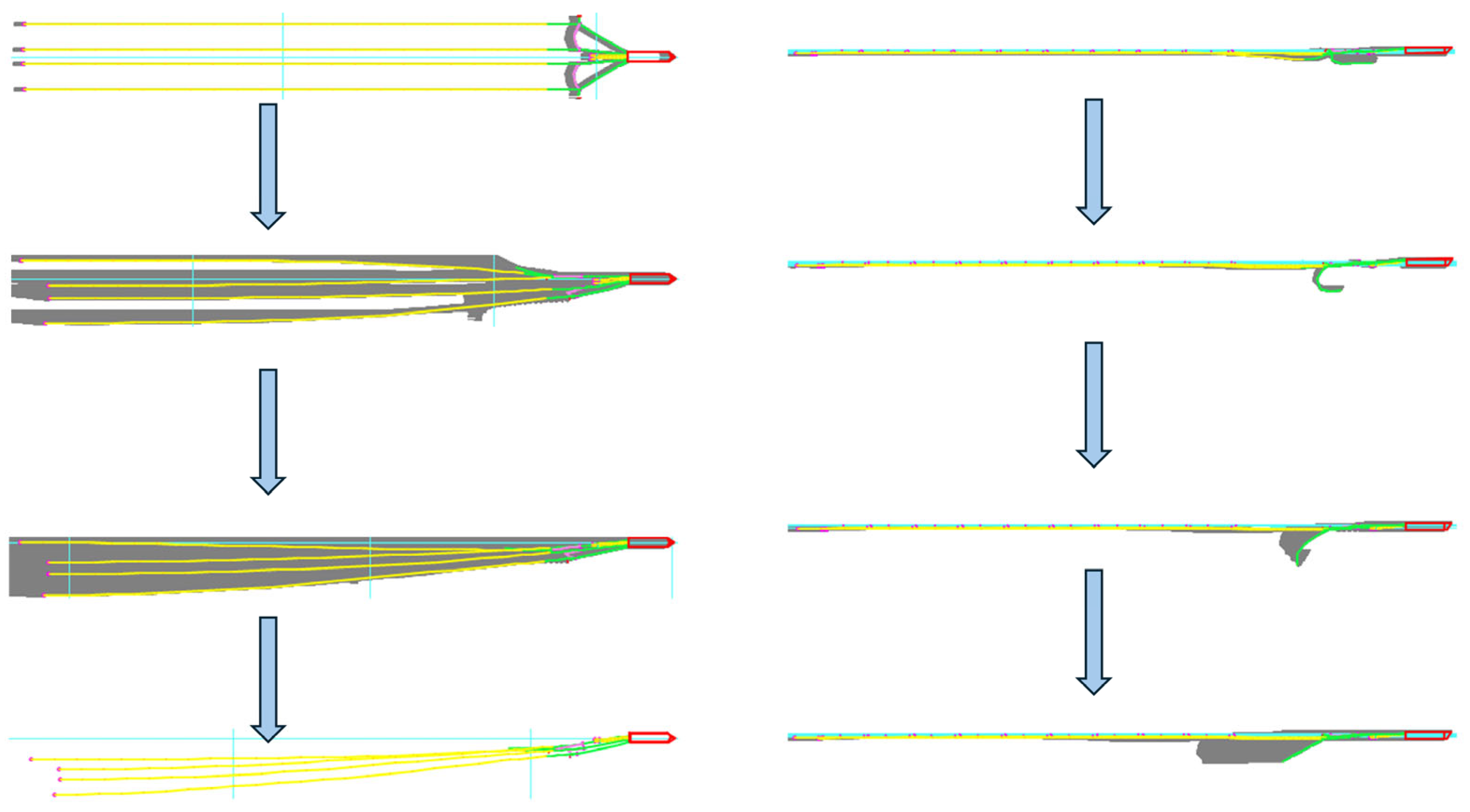
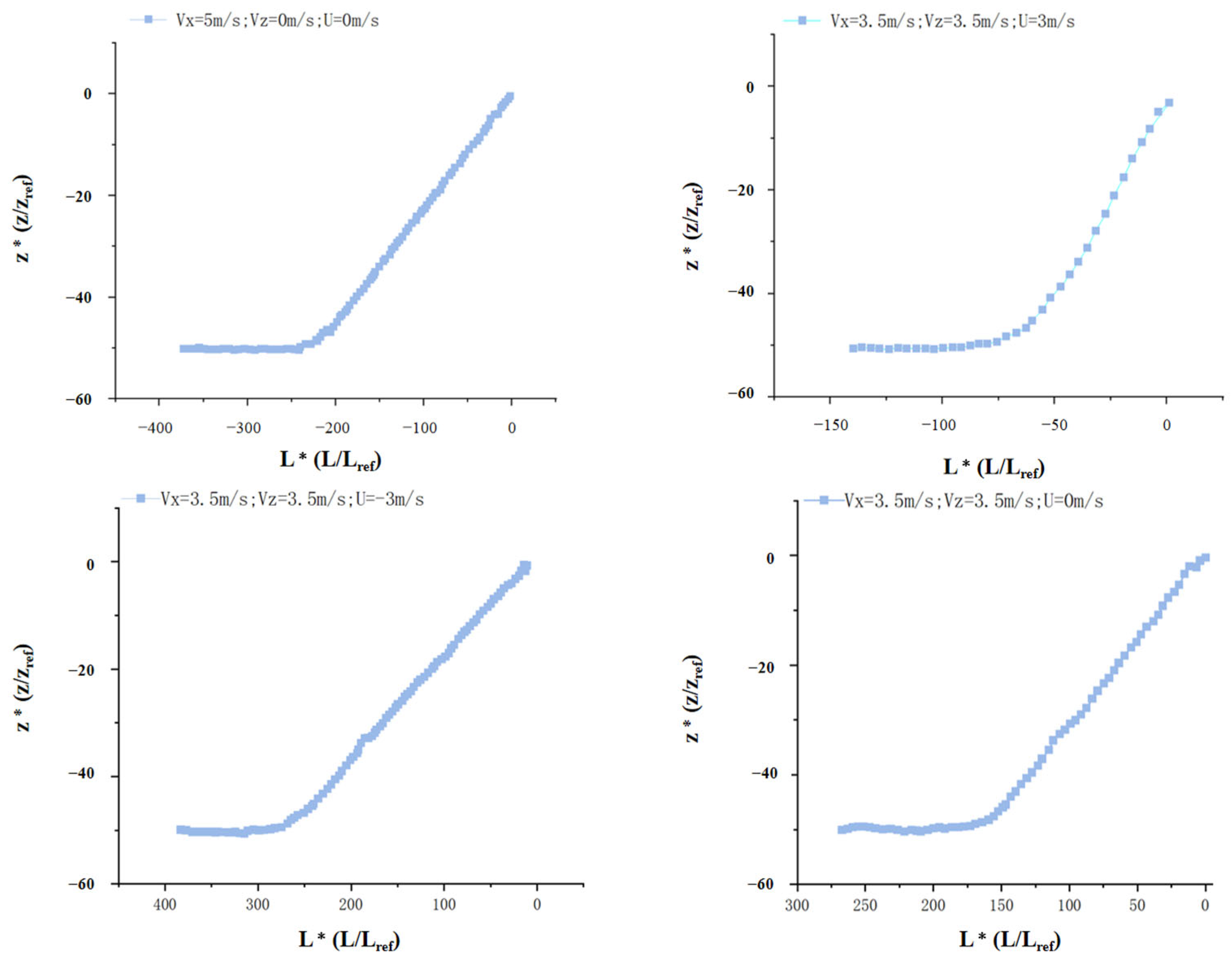

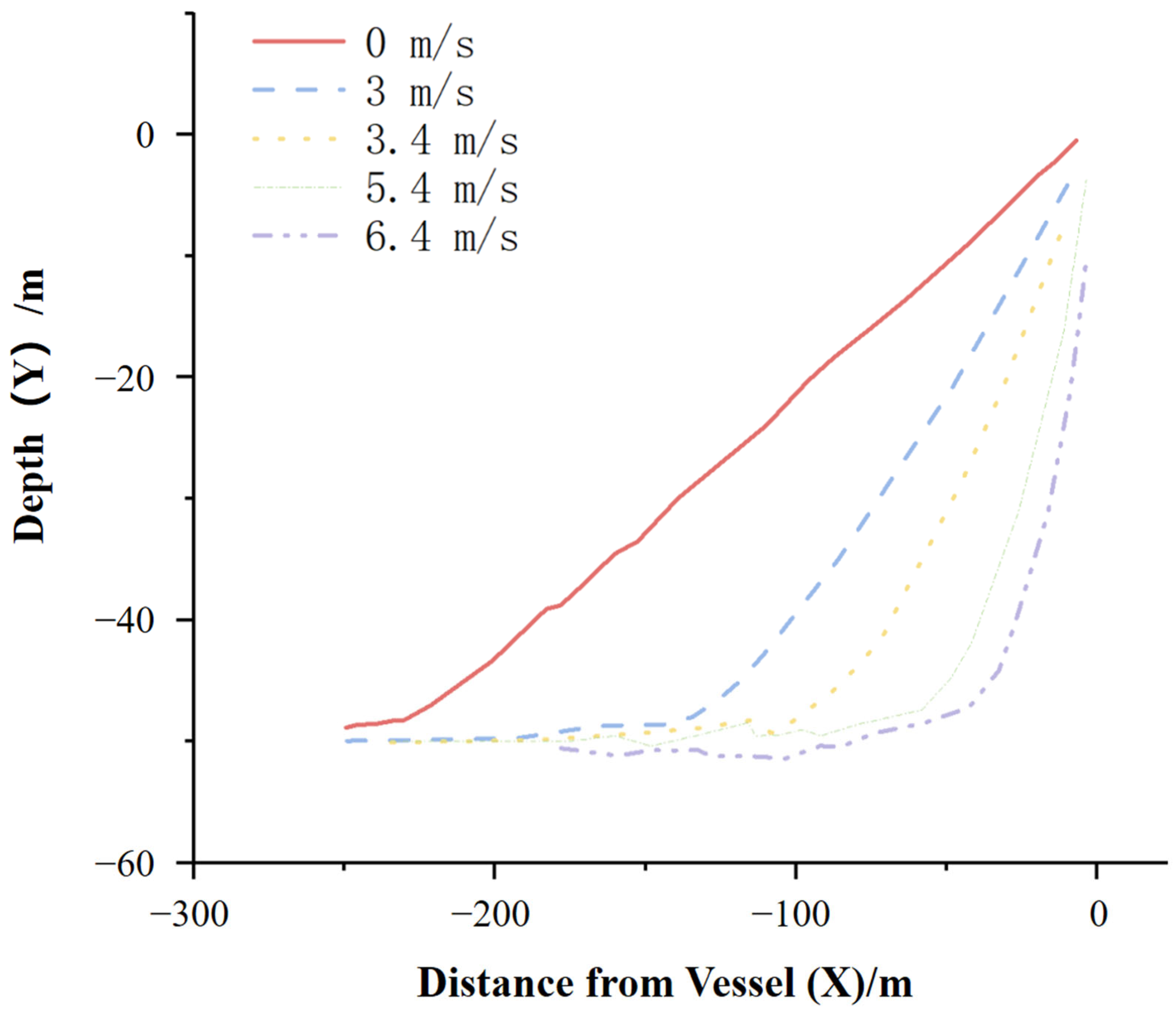

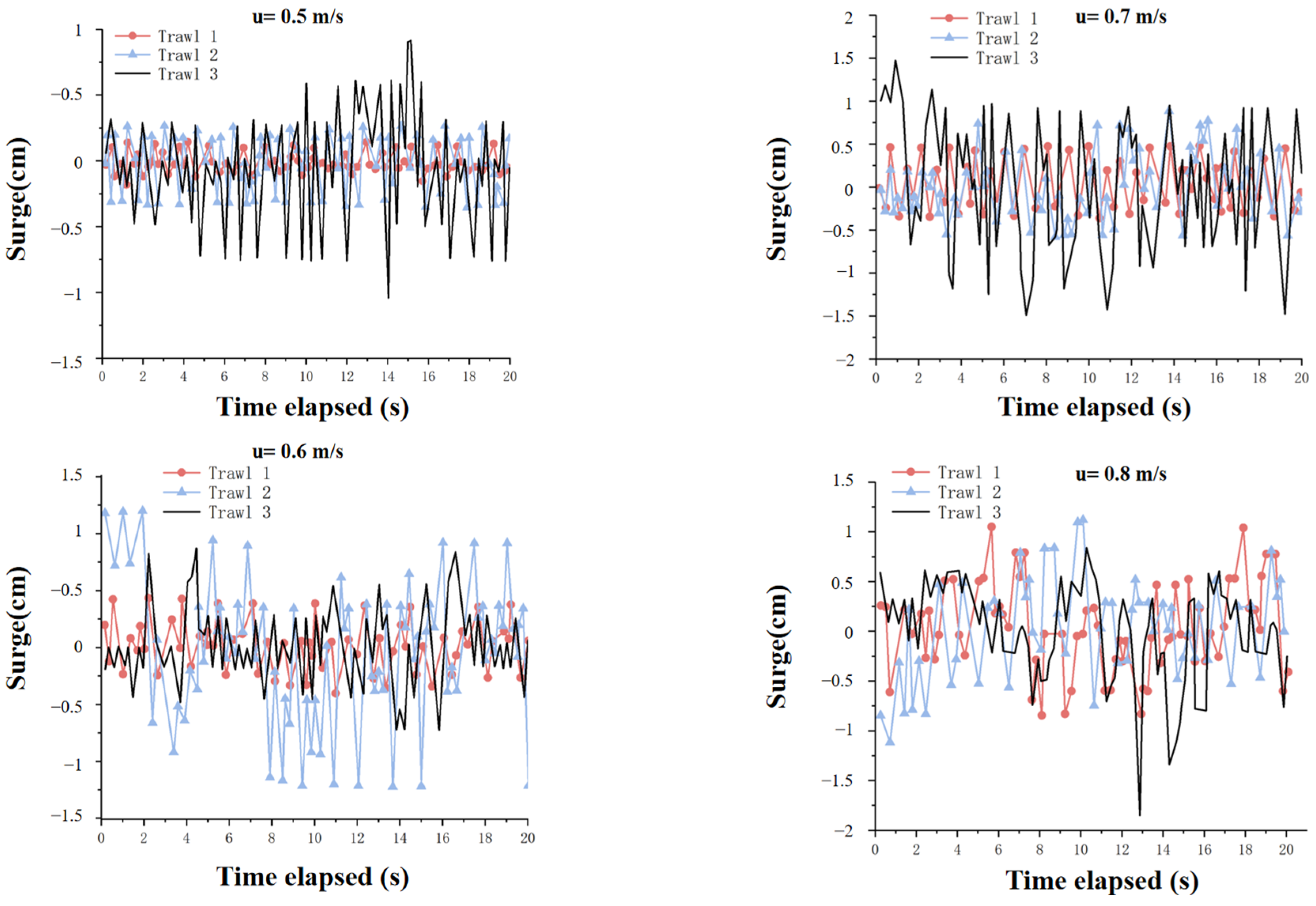
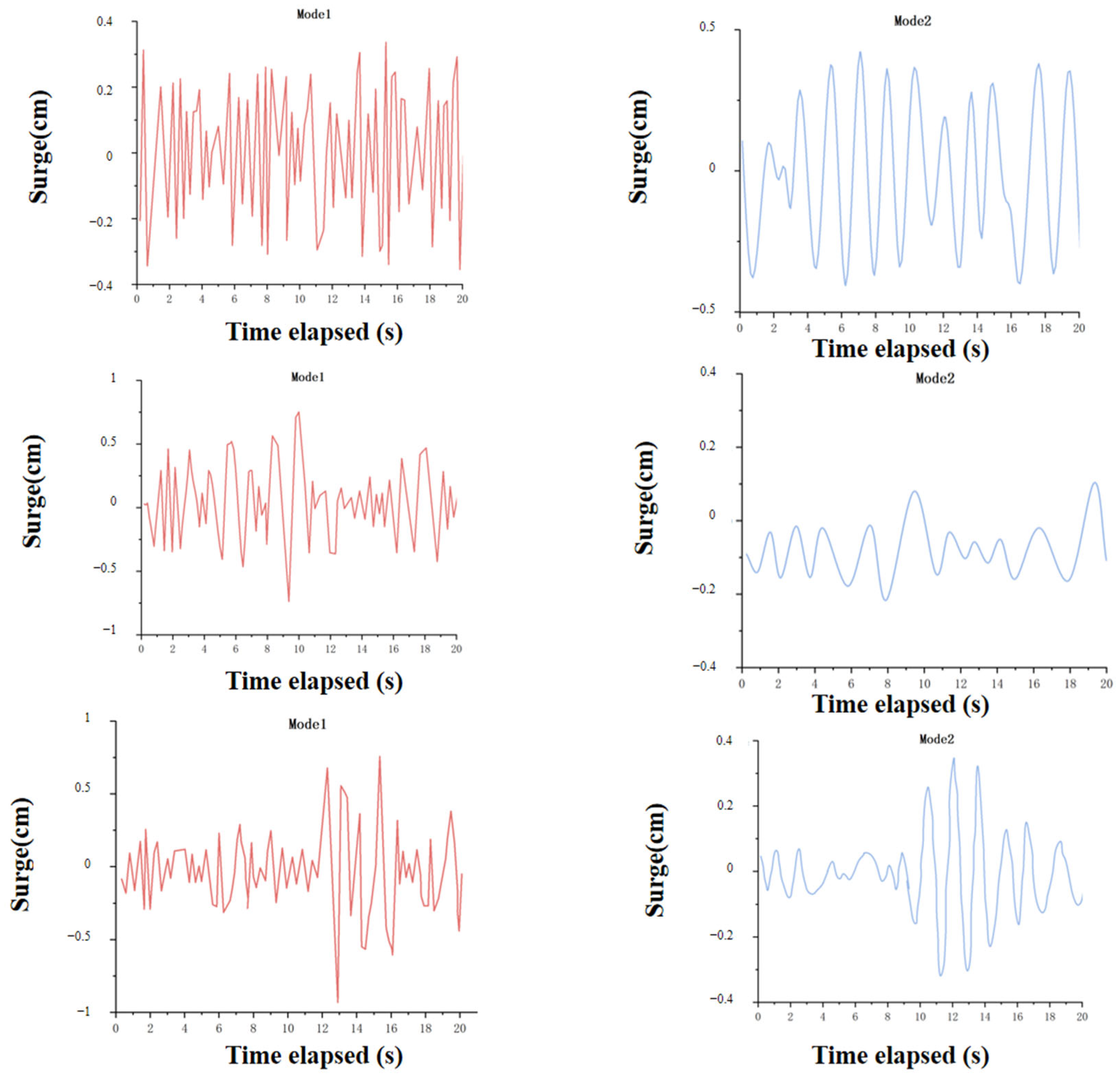
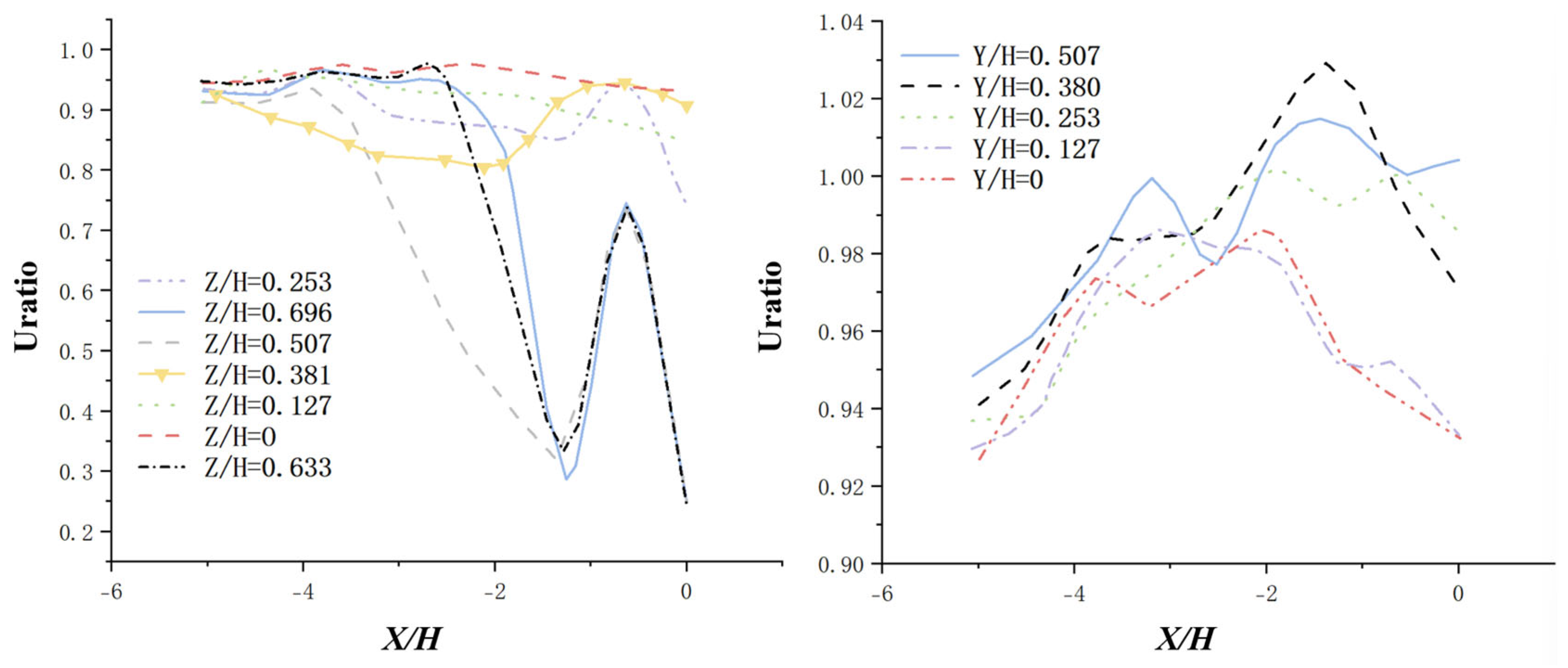
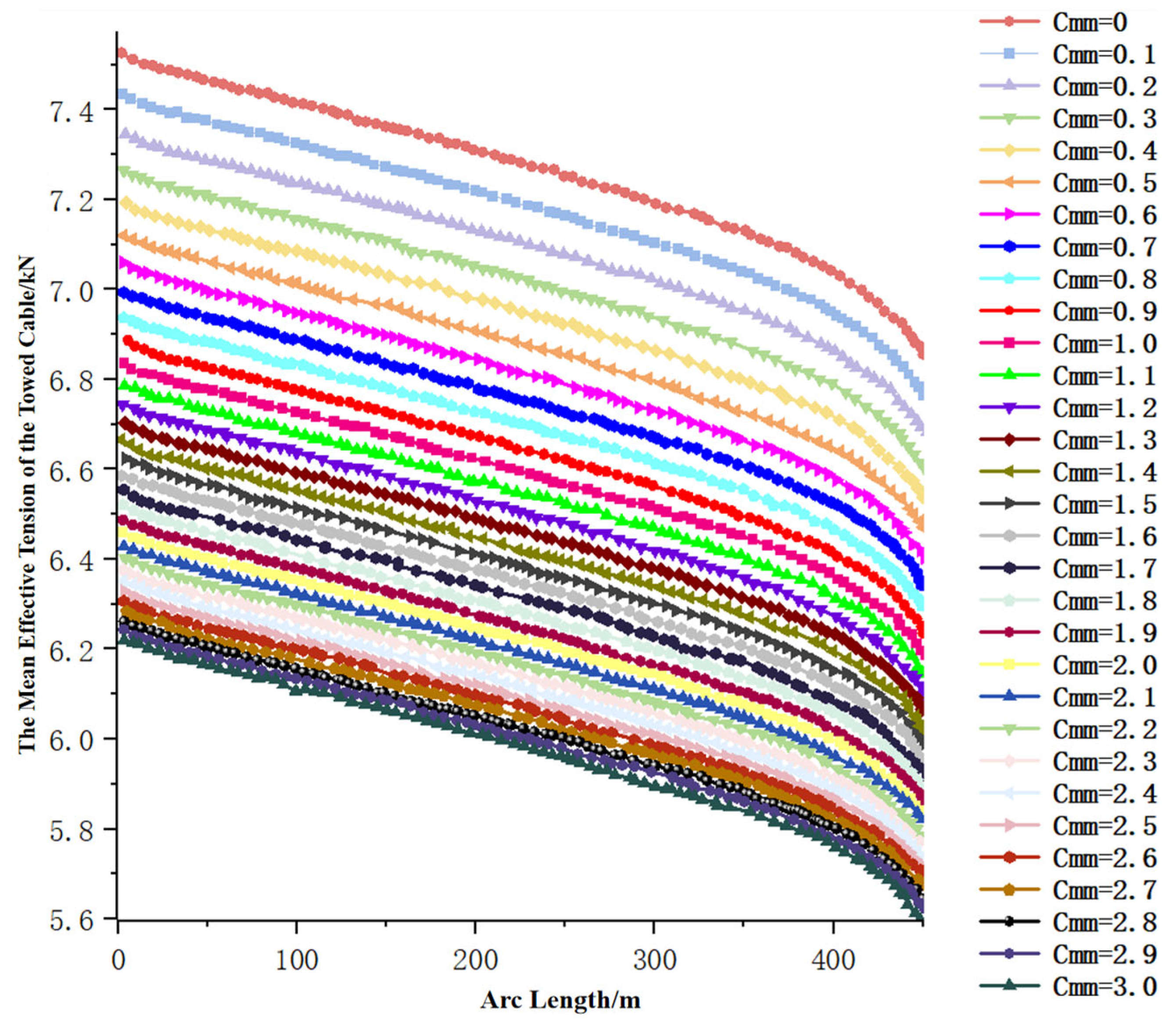

| Simulation Methods | Features of the Methodology | Scope of Application |
|---|---|---|
| Cosserat rod model | Translation and rotational degrees of freedom are included to accurately characterize geometric nonlinearity and derive complexity | It is suitable for the dynamic analysis of one-dimensional flexible rod systems with fine simulation geometric nonlinearity and torsional effect |
| Semicontinuous model | Continuously distributed parameters are used between discrete nodes to adapt to small deformation and linear elastic scenarios | Analysis of linear elastic scenarios such as static/quasi-static bending and deflection of cables with composite structures |
| Lumped mass method | Discrete point centralized mass simplified system, efficient but ignoring the moment of inertia | It is used for rapid simulation analysis under dynamic response and complex environmental loads of marine towing systems |
| Formulation of absolute nodal coordinates model | Describing the flexible body by the position of the node, high-precision processing of large deformation and complex contact, high cost | It is suitable for the analysis of geometric nonlinearity and complex contact problems of large deformed flexible bodies |
| Finite difference method | Discrete cables are grids, and the differential equations are used to approximate the derivative, and the principle is simple but the adaptability is narrow | Research on the basic dynamic properties of simple boundary and linear problems (such as vibration and verification theoretical solutions) |
| Elastic rod mode | Based on Hooke’s law, consider linear elastic deformation, relatively simple in dealing with small-scale, slow-varying deformation of rods, assume small displacements and linear stress–strain relations | Suitable for preliminary analysis of linear elastic deformation of rods in static or low-frequency dynamic cases, like small-deflection bending of simple elastic support rods |
| Nonlinear beam model | Account for large displacements, large rotations, and nonlinear material behavior (e.g., geometric nonlinearity from large deformations, material nonlinearity like elasto-plasticity). Incorporate effects like shear deformation, warping for more accurate complex scenario representation | Applied to analyze large-deformation, high-load nonlinear responses of beams, such as in structural collapse simulation, flexible structural dynamics under extreme loads, where geometric and material nonlinearities are prominent |
| L/m | Line Type | |
|---|---|---|
| Leader A/Leader D | 120 | Lead-in |
| Leader B/Leader C | 80 | Lead-in |
| Array A/Array D | 170 | Lead-in(70 m) + Streamer(100 m) |
| Array B/Array C | 170 | Lead-in(70 m) + streamer(100 m) |
| Div line | 13 | Lead-in |
| Spreader | 60 | Warp |
| Gun umbilical | 70 | Gun umb |
| Gunlead | 10 | Gun umb |
| Diverter Ballast | 2 | Diverter base |
| d/m | ρc/kg × m−1 | EA/kN | EI/kN × m2 | Cdτ | Cdn | Cdb | Caτ | Can | Cab | |
|---|---|---|---|---|---|---|---|---|---|---|
| Streamer | 0.08 | 5.2 | 2000 | 0.02 | 0 | 1.5 | 1.5 | 0 | 1.0 | 1.0 |
| Lead-in | 0.05 | 5.9 | 5000 | 0.02 | 0.01 | 1.5 | 1.5 | 0 | 1.0 | 1.0 |
| Warp | 0.025 | 0.74 | 2500 | 0 | 0.01 | 1.5 | 1.5 | 0 | 1.0 | 1.0 |
| Gun umb | 0.05 | 5.9 | 6000 | 0.04 | 0.01 | 1.5 | 1.5 | 0 | 1.0 | 1.0 |
| Diverter base | 0.2 | 300 | 1 | 0 | 0 | 1.2 | 1.2 | 0 | 1.0 | 1.0 |
| Environmental Conditions | The Changing Trend of the Minimum Spacing | Risk Threshold (Current Velocity/Wave Height) | Engineering Suggestions |
|---|---|---|---|
| Countercurrent (single break) | As the current velocity↑ → the spacing ↓ | Current velocity > 1.5 m/s (spacing < 5 m) | When flowing against the current, control the current velocity to be ≤ 1.2 m/s, or increase the strength of the mooring line. |
| Downstream (single break) | As the current velocity ↑, the spacing first ↓ and then stabilizes | Current velocity = 0.2 m/s (minimum spacing value) | When flowing downstream, avoid the current velocity range of 0.15–0.25 m/s to prevent resonance. |
| Cross –current (single break) | As the current velocity ↑ → the spacing drops abruptly | Current velocity > 0.2 m/s (spacing < 4 m) | When the cross-current velocity is ≤ 0.15 m/s, or add a transverse limit frame. |
| Against the waves (single break) | Wave height ↑ → Spacing fluctuation ↑ | Wave height > 0.6 m (Fluctuation > 30%) | When sailing against the waves, the wave height should be ≤ 0.5 m, or optimize the elastic support of the towing cable. |
| Stratified current (single break) | When the upper-layer ocean current accelerates, the distance decreases sharply; when the lower-layer ocean current accelerates, the distance decreases slowly. | The upper current velocity > 1.2 m/s (spacing < 3 m) | Avoid the towing cable from crossing the upper high-speed current area, or add a lateral limiter in the middle and lower part of the mooring cable. |
| Horizontal shear current (single fracture) | Shear strength (ΔUy) ↑→ Nonlinear decrease in spacing | ΔUy > 0.5 m/s (spacing < 2.5 m) | Detect the intensity of the lateral ocean current shear before operation. When ΔUy exceeds the threshold, reduce the speed of the tugboat to 1.5 m/s. |
| Head-on waves (single mooring line breakage) | Wave height ↑ → Spacing fluctuation ↑; Wavelength ↑ → Spacing fluctuation first ↓ then ↑ | Wave height > 1.5 m (fluctuation > 50%); wavelength < 15 m/λ > 45 m | When operating against the waves, control the wave height to be ≤ 1.2 m and the wavelength to be 25–35 m; when the wave height is 1.2–1.5 m, shorten the operation duration to within 2 h. |
| Following the waves (single mooring line breakage) | As the wave height increases ↑, the spacing first remains stable and then decreases suddenly; as the wavelength increases ↑, the stability of the spacing increases ↑ | Wave height > 2.0 m (spacing < 3 m); Wavelength < 20 m | The maximum allowable wave height for following-wave operation is 2.0 m. It is preferred to choose the sea condition with λ > 25 m. Equip elastic lateral supports to reduce vibration. |
| Cross waves (single mooring line breakage) | As wave height ↑ → the spacing decreases abruptly in a non-linear manner; as wavelength ↑ → the spacing offset ↑ | Wave height > 1.0 m (spacing < 4 m); Wavelength > 40 m | For cross-wave operation, the wave height is ≤0.8 m and the wavelength is 25–35 m; when the threshold is exceeded, the lateral limit frame is activated. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Yang, K.; Zeng, S.; Yang, K.; Zhang, D.; Zhu, K. Multi-Branch Towed Array System: Systematic Analysis of Modeling Methods, Environmental Responses and Mechanical Properties in Fracture Analysis. J. Mar. Sci. Eng. 2025, 13, 1697. https://doi.org/10.3390/jmse13091697
Yan J, Yang K, Zeng S, Yang K, Zhang D, Zhu K. Multi-Branch Towed Array System: Systematic Analysis of Modeling Methods, Environmental Responses and Mechanical Properties in Fracture Analysis. Journal of Marine Science and Engineering. 2025; 13(9):1697. https://doi.org/10.3390/jmse13091697
Chicago/Turabian StyleYan, Jin, Kefan Yang, Shengqing Zeng, Keqi Yang, Dapeng Zhang, and Keqiang Zhu. 2025. "Multi-Branch Towed Array System: Systematic Analysis of Modeling Methods, Environmental Responses and Mechanical Properties in Fracture Analysis" Journal of Marine Science and Engineering 13, no. 9: 1697. https://doi.org/10.3390/jmse13091697
APA StyleYan, J., Yang, K., Zeng, S., Yang, K., Zhang, D., & Zhu, K. (2025). Multi-Branch Towed Array System: Systematic Analysis of Modeling Methods, Environmental Responses and Mechanical Properties in Fracture Analysis. Journal of Marine Science and Engineering, 13(9), 1697. https://doi.org/10.3390/jmse13091697






