Synchronization Control for AUVs via Optimal-Sliding-Mode Adaptive Dynamic Programming with Actuator Saturation and Performance Constraints in Dynamic Recovery
Abstract
1. Introduction
- Compared with the conventional ADP method of designing the value function directly in terms of the system state or tracking error, we use the sliding-mode function as the design benchmark of the value function. By embedding the dynamic characteristics of the sliding-mode function into the construction of the value function, the joint optimization of the state error and its derivatives is achieved, which speeds up the control response of the system.
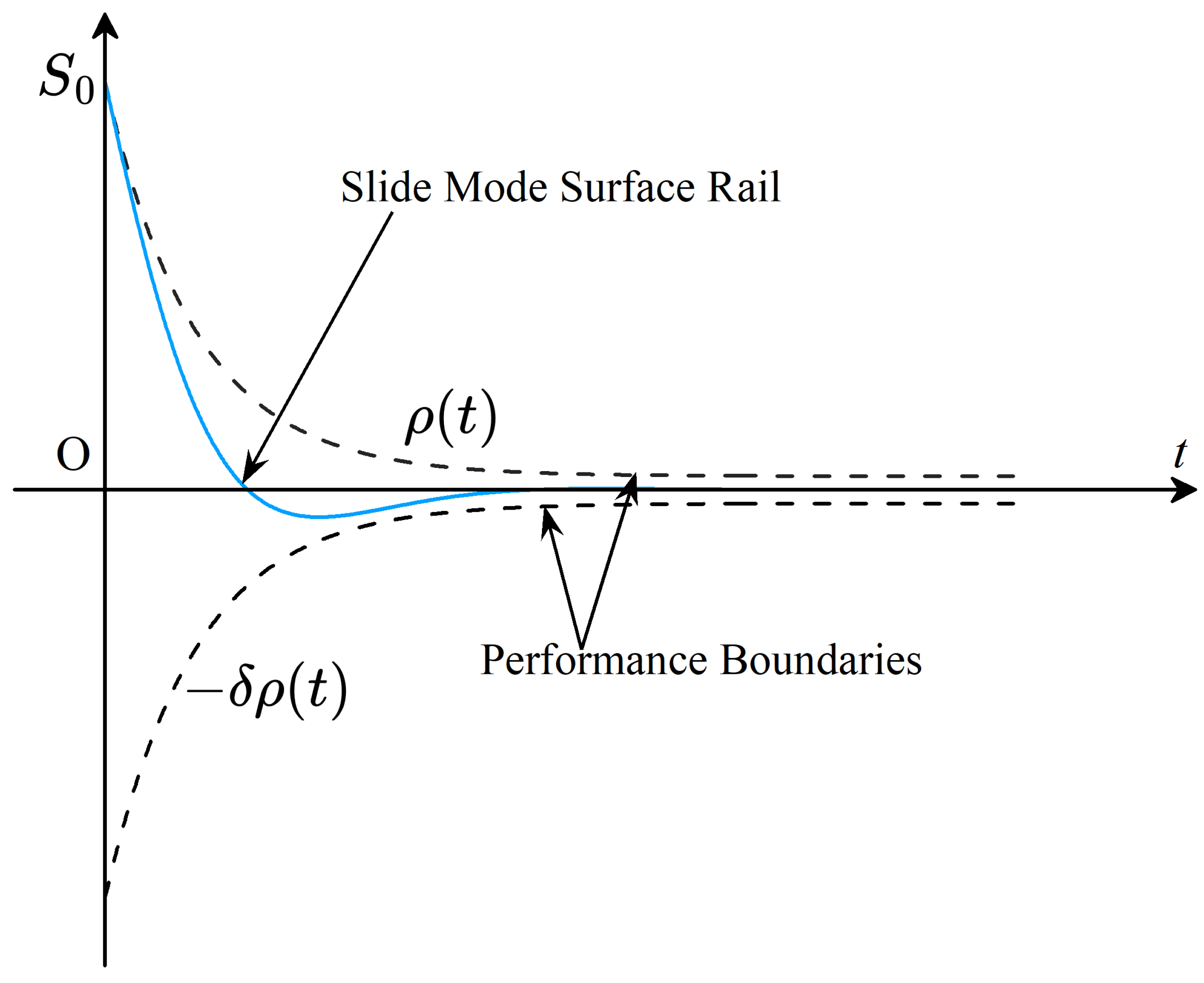
- Compared with conventional prescribed performance control (PPC), where constraints are imposed directly on the error, we use the dynamic sliding-mode function as the direct object of performance mapping. By designing a time-varying power function to constrain the evolutionary trajectory of the sliding-mode surface and simultaneously regulating the amplitude change rate and convergence phase of the sliding-mode surface, we enable the system to maintain the prescribed dynamic qualities under the constrained control force.
- Compared with the conventional quadratic value function method, we introduce the tanh function to design the nonquadratic value function, which maps the control inputs to the value function space so that the optimization process avoids the risk of input overshoot, does not need to design an additional anti-saturation compensator, and avoids the phase loss problem caused by saturation compensation lag.
2. Problem Formulation
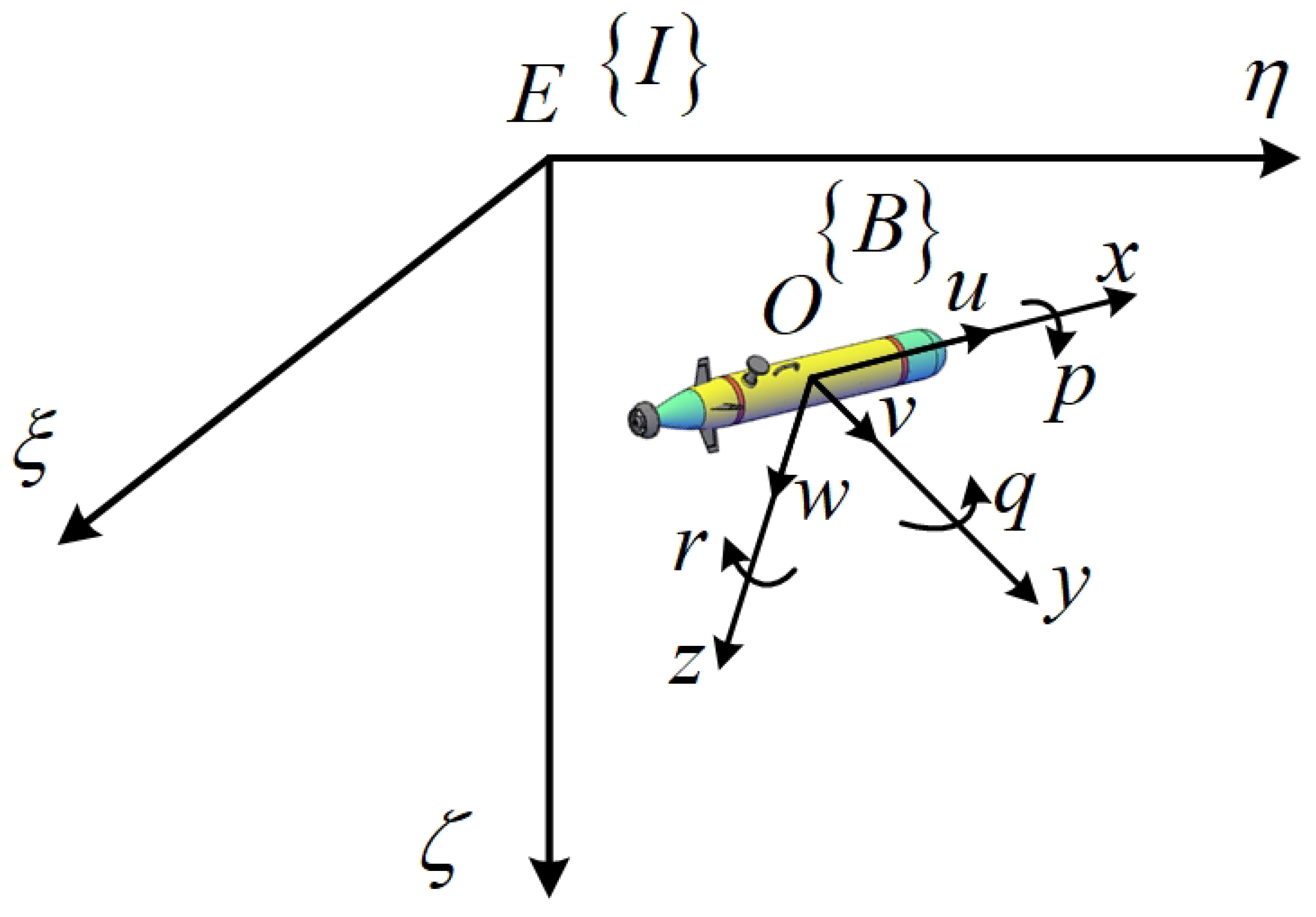
2.1. Coordinate System and AUV Model
2.2. Master–Slave Synchronization Framework and Error Model
3. Controller Design and Stability Analysis
3.1. Single-Critic Network ADP Controller
3.2. Optimal Sliding-Mode ADP (OSM-ADP) Controller Design
3.3. Stability Analysis
4. Simulation Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alghamdi, R.; Dahrouj, H.; Al-Naffouri, T.Y.; Alouini, M.S. Toward immersive underwater cloud-enabled networks: Prospects and challenges. IEEE BITS Inf. Theory Mag. 2023, 3, 54–66. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, D.; Pang, W.; Zhang, Y. A survey of underwater search for multi-target using Multi-AUV: Task allocation, path planning, and formation control. Ocean Eng. 2023, 278, 114393. [Google Scholar] [CrossRef]
- Sarda, E.I.; Dhanak, M.R. A USV-based automated launch and recovery system for AUVs. IEEE J. Ocean. Eng. 2016, 42, 37–55. [Google Scholar] [CrossRef]
- Sarda, E.I.; Dhanak, M.R. Launch and recovery of an autonomous underwater vehicle from a station-keeping unmanned surface vehicle. IEEE J. Ocean. Eng. 2018, 44, 290–299. [Google Scholar] [CrossRef]
- Szczotka, M. AUV launch & recovery handling simulation on a rough sea. Ocean Eng. 2022, 246, 110509. [Google Scholar] [CrossRef]
- Yazdani, A.M.; Sammut, K.; Yakimenko, O.; Lammas, A. A survey of underwater docking guidance systems. Robot. Auton. Syst. 2020, 124, 103382. [Google Scholar] [CrossRef]
- Zimmerman, R.; D’Spain, G.; Chadwell, C.D. Decreasing the radiated acoustic and vibration noise of a mid-size AUV. IEEE J. Ocean. Eng. 2005, 30, 179–187. [Google Scholar] [CrossRef]
- Fukasawa, T.; Noguchi, T.; Kawasaki, T.; Baino, M. “MARINE BIRD”, a new experimental AUV with underwater docking and recharging system. In Proceedings of the Oceans 2003. Celebrating the Past… Teaming Toward the Future (IEEE Cat. No. 03CH37492), San Diego, CA, USA, 22–26 September 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 2195–2200. [Google Scholar]
- Kawasaki, T.; Noguchi, T.; Fukasawa, T.; Hayashi, S.; Shibata, Y.; Limori, T.; Okaya, N.; Fukui, K.; Kinoshita, M. “Marine Bird”, a new experimental AUV-results of docking and electric power supply tests in sea trials. In Proceedings of the Oceans’ 04 MTS/IEEE Techno-Ocean’04 (IEEE Cat. No. 04CH37600), Kobe, Japan, 9–12 November 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 1738–1744. [Google Scholar]
- Allen, B.; Austin, T.; Forrester, N.; Goldsborough, R.; Kukulya, A.; Packard, G.; Purcell, M.; Stokey, R. Autonomous docking demonstrations with enhanced REMUS technology. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–6. [Google Scholar]
- Palomeras, N.; Ridao, P.; Ribas, D.; Vallicrosa, G. Autonomous I-AUV docking for fixed-base manipulation. IFAC Proc. Vol. 2014, 47, 12160–12165. [Google Scholar] [CrossRef]
- Palomeras, N.; Vallicrosa, G.; Mallios, A.; Bosch, J.; Vidal, E.; Hurtos, N.; Carreras, M.; Ridao, P. AUV homing and docking for remote operations. Ocean Eng. 2018, 154, 106–120. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, J.; Li, Y.; An, L.; Wang, Y. AUV Dynamic Docking Based on Longitudinal Safety Speed. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 80–84. [Google Scholar]
- Yan, Z.; Xu, D.; Chen, T.; Zhou, J.; Wei, S.; Wang, Y. Modeling, strategy and control of UUV for autonomous underwater docking recovery to moving platform. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4807–4812. [Google Scholar]
- Yan, Z.; Hao, B.; Liu, Y.; Hou, S. Movement Control in Recovering UUV Based on Two-Stage Discrete T-S Fuzzy Model. Discret. Dyn. Nat. Soc. 2014, 2014, 362787. [Google Scholar] [CrossRef]
- Xu, J.; Wang, M.; Zhang, G. Trajectory tracking control of an underactuated unmanned underwater vehicle synchronously following mother submarine without velocity measurement. Adv. Mech. Eng. 2015, 7, 1687814015595340. [Google Scholar] [CrossRef]
- Du, X.; Wu, W.; Zhang, W.; Hu, S. Research on UUV recovery active disturbance rejection control based on LMNN compensation. Int. J. Control. Autom. Syst. 2021, 19, 2569–2582. [Google Scholar] [CrossRef]
- Zhang, W.; Han, P.; Liu, Y.; Zhang, Y.; Wu, W.; Wang, Q. Design of an improved adaptive slide controller in UUV dynamic base recovery. Ocean Eng. 2023, 285, 115266. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, W.; Du, X.; Li, Z.; Wang, Q. Homing tracking control of autonomous underwater vehicle based on adaptive integral event-triggered nonlinear model predictive control. Ocean Eng. 2023, 277, 114243. [Google Scholar] [CrossRef]
- Deptula, P.; Bell, Z.I.; Zegers, F.M.; Licitra, R.A.; Dixon, W.E. Approximate optimal influence over an agent through an uncertain interaction dynamic. Automatica 2021, 134, 109913. [Google Scholar] [CrossRef]
- Huang, M.; Gao, W.; Jiang, Z.P. Connected cruise control with delayed feedback and disturbance: An adaptive dynamic programming approach. Int. J. Adapt. Control Signal Process. 2019, 33, 356–370. [Google Scholar] [CrossRef]
- Li, C.; Ding, J.; Lewis, F.L.; Chai, T. A novel adaptive dynamic programming based on tracking error for nonlinear discrete-time systems. Automatica 2021, 129, 109687. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Liu, Y.; Li, K. Self-learning-based optimal tracking control of an unmanned surface vehicle with pose and velocity constraints. Int. J. Robust Nonlinear Control 2022, 32, 2950–2968. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Zhang, X. Data-driven performance-prescribed reinforcement learning control of an unmanned surface vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5456–5467. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Zhao, H.; Ahn, C.K. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3034–3045. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Yang, C.; Zhang, X. Reinforcement learning-based finite-time tracking control of an unknown unmanned surface vehicle with input constraints. Neurocomputing 2022, 484, 26–37. [Google Scholar] [CrossRef]
- Che, G.; Yu, Z. Neural-network estimators based fault-tolerant tracking control for AUV via ADP with rudders faults and ocean current disturbance. Neurocomputing 2020, 411, 442–454. [Google Scholar] [CrossRef]
- Yang, X.; He, H. Adaptive critic designs for optimal control of uncertain nonlinear systems with unmatched interconnections. Neural Netw. 2018, 105, 142–153. [Google Scholar] [CrossRef]
- Che, G. Single critic network based fault-tolerant tracking control for underactuated AUV with actuator fault. Ocean Eng. 2022, 254, 111380. [Google Scholar] [CrossRef]
- Chen, F.; Zhou, X. Adaptive dynamic programming based tracking control for switched unmanned underwater vehicle systems. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1576–1580. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Abu-Khalaf, M.; Lewis, F.L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica 2005, 41, 779–791. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, X. Adaptive output feedback tracking control of stochastic nonlinear systems with dynamic uncertainties. Int. J. Robust Nonlinear Control 2015, 25, 1282–1300. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]

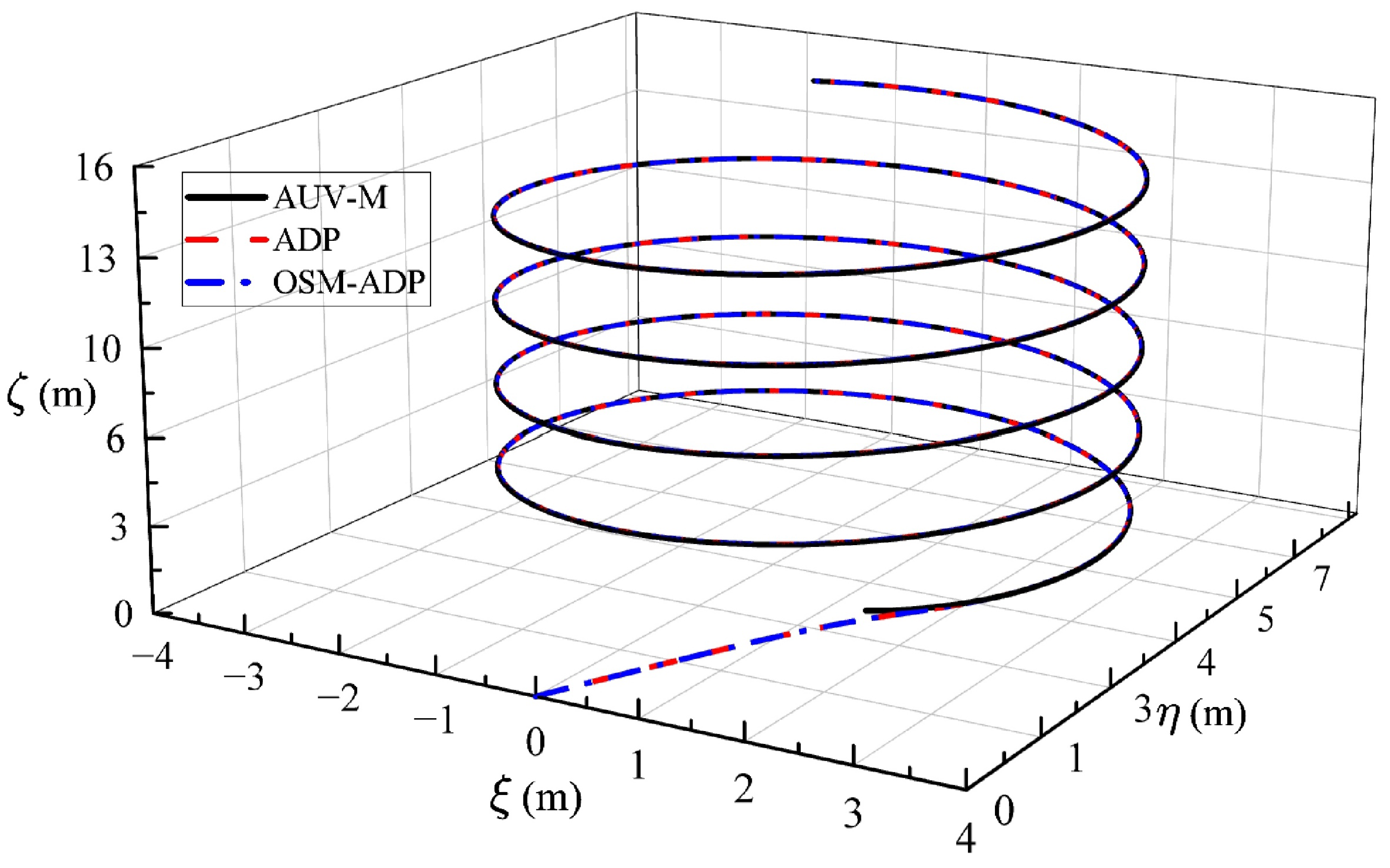
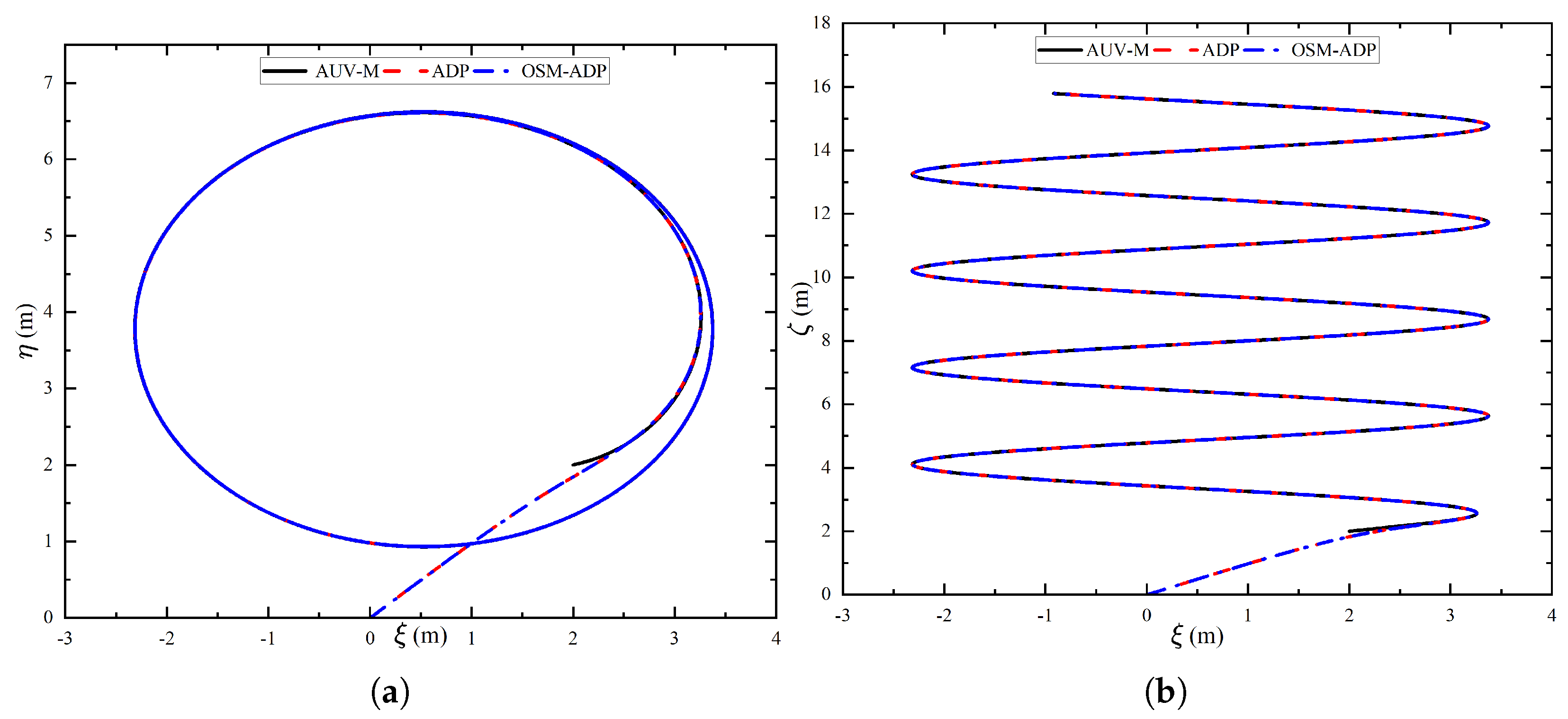

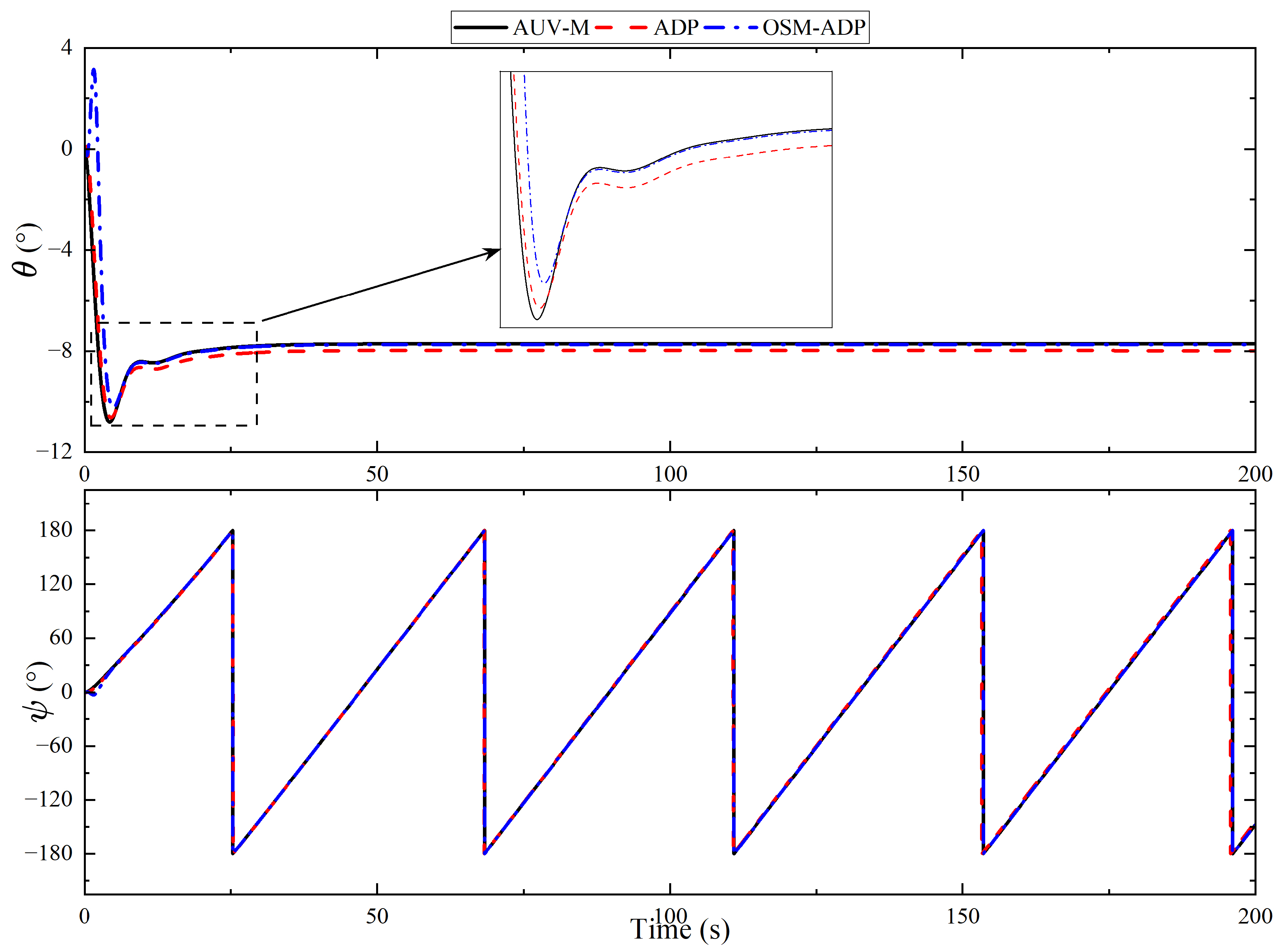
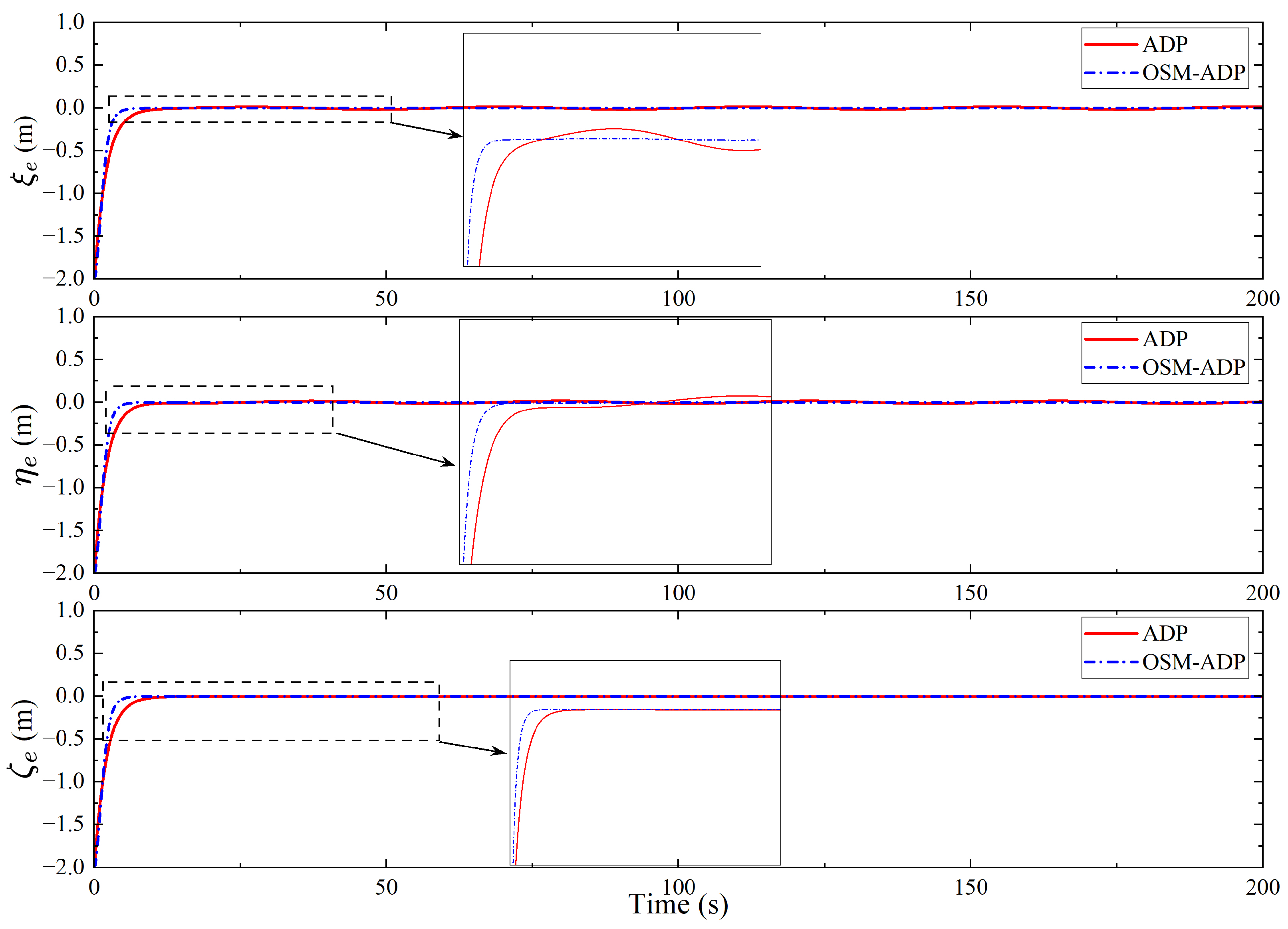
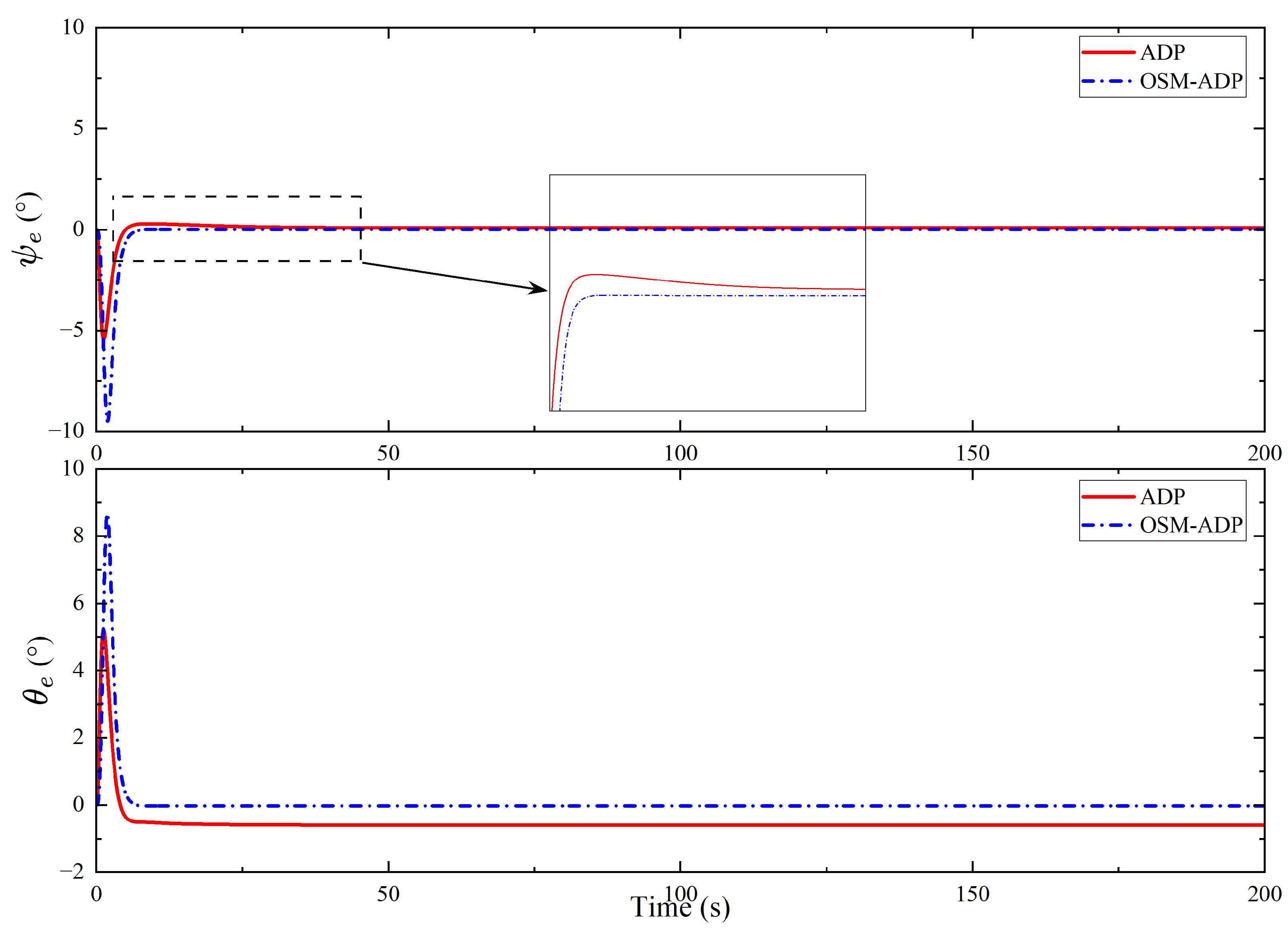
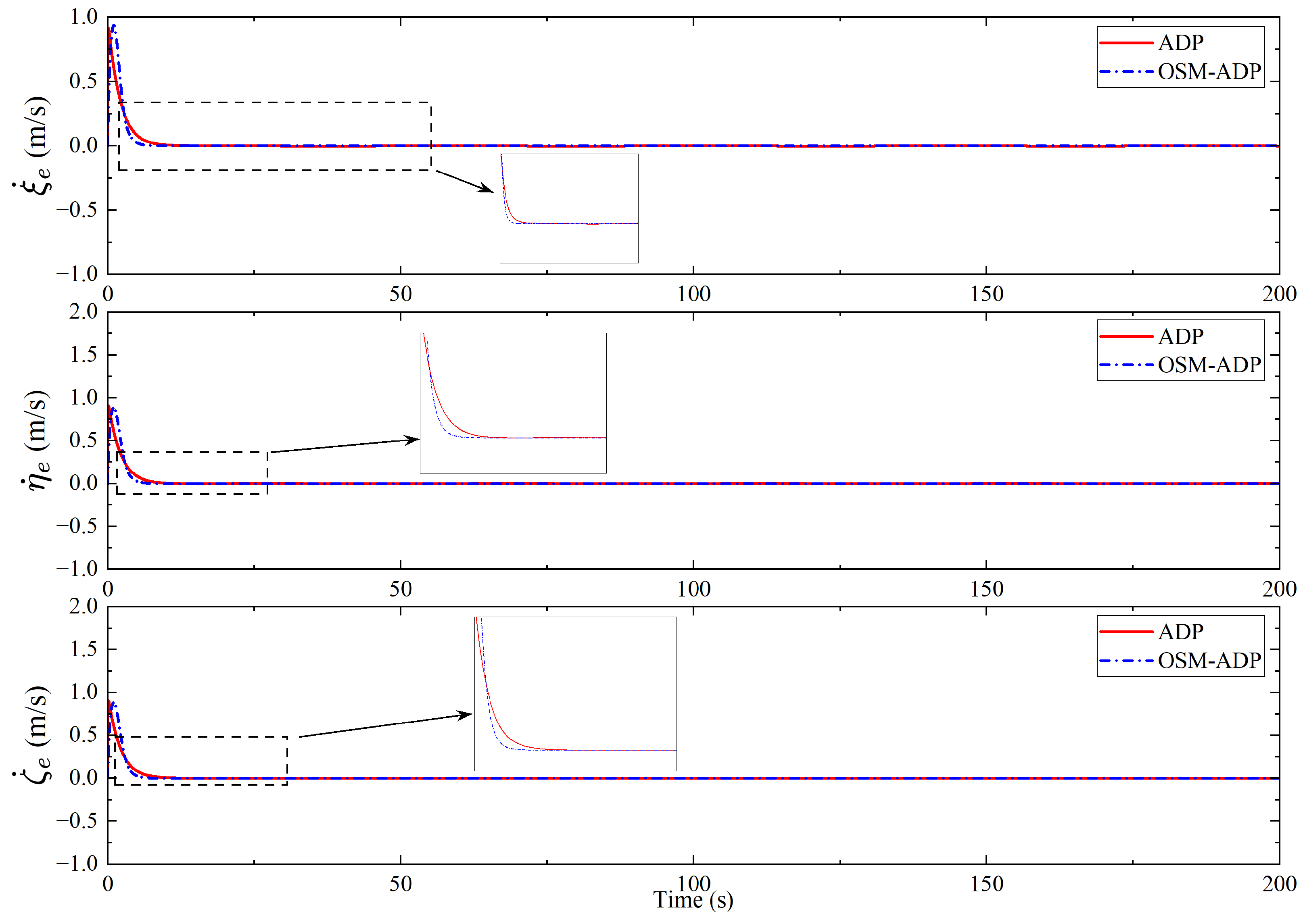
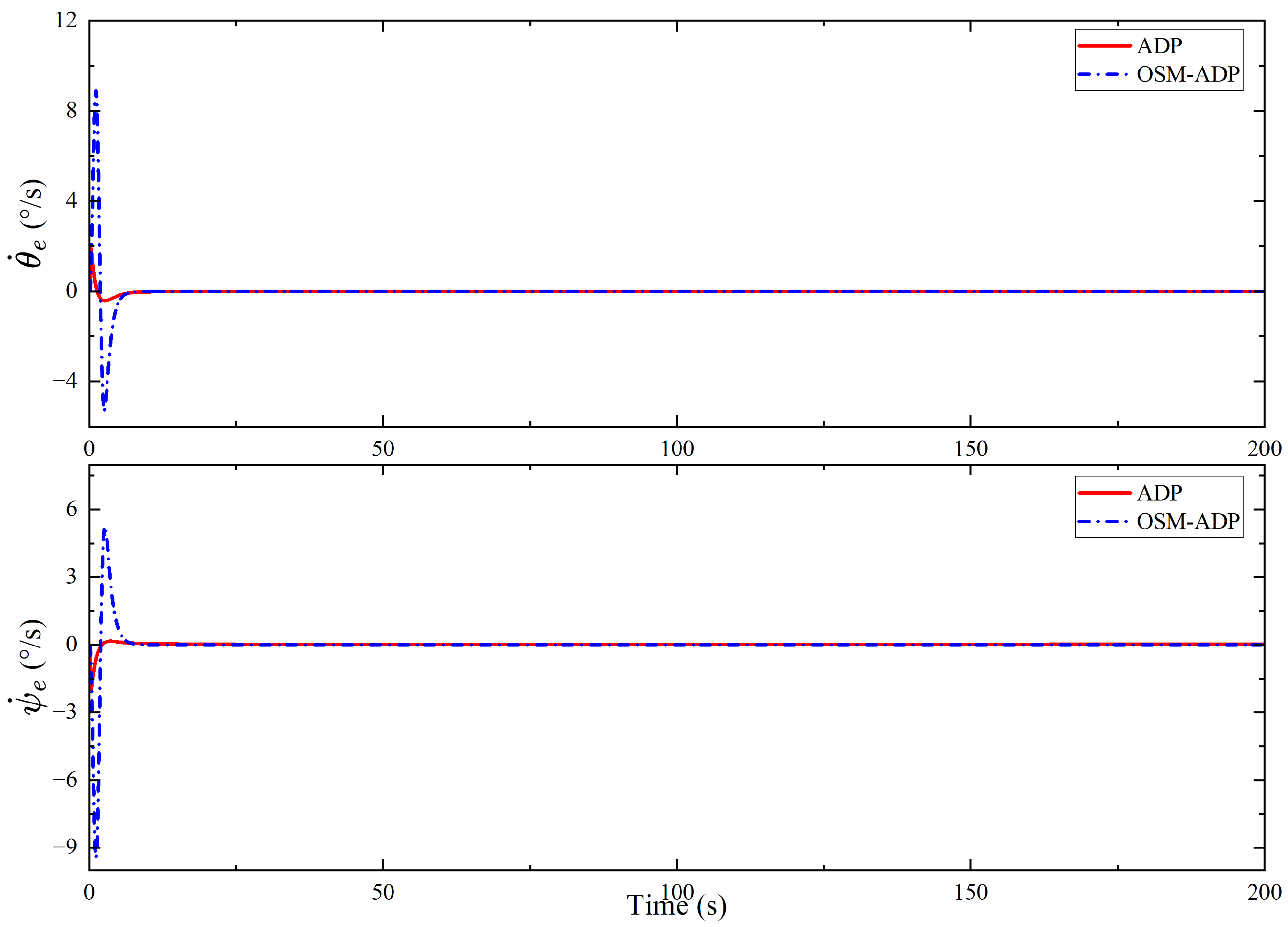
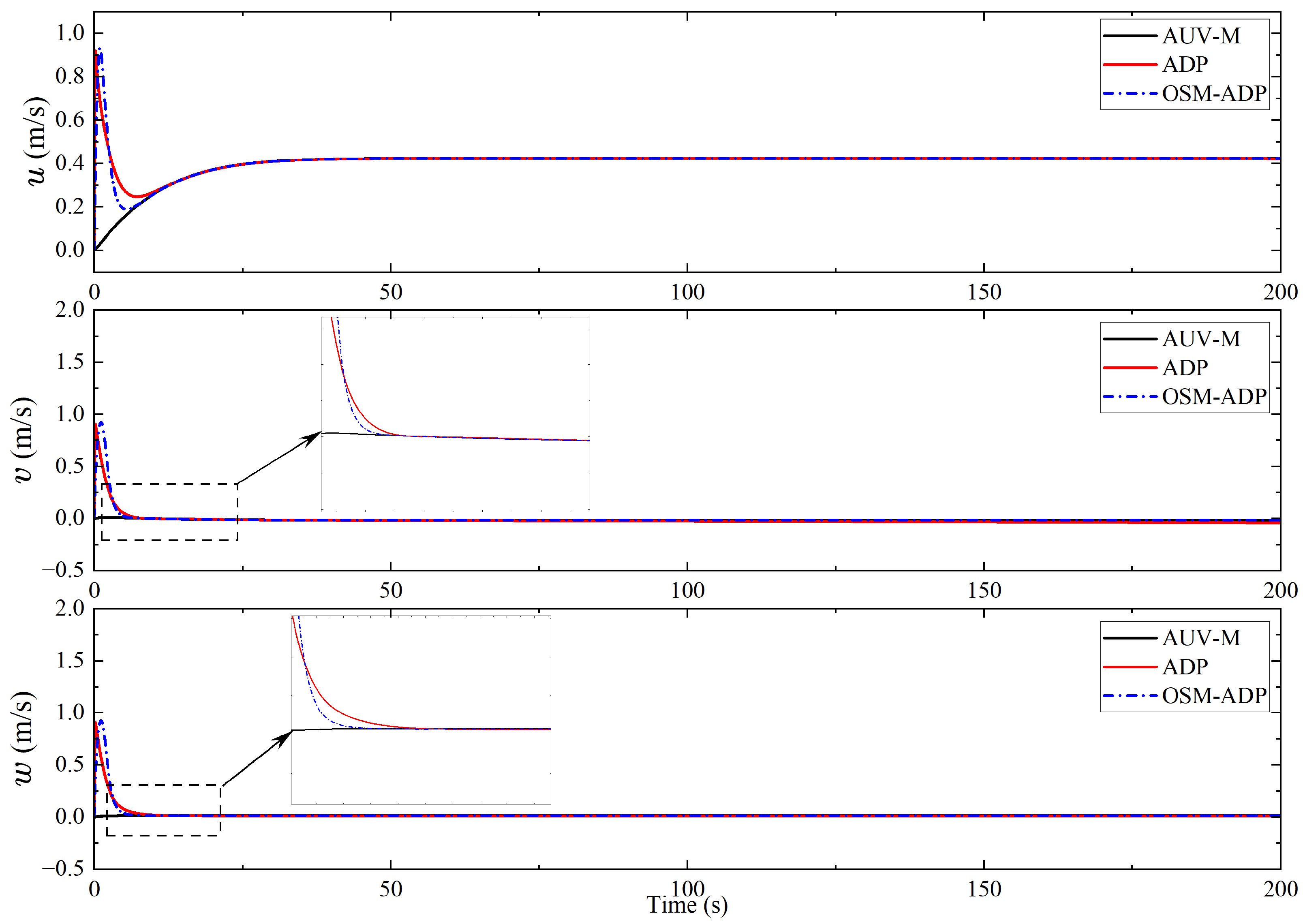
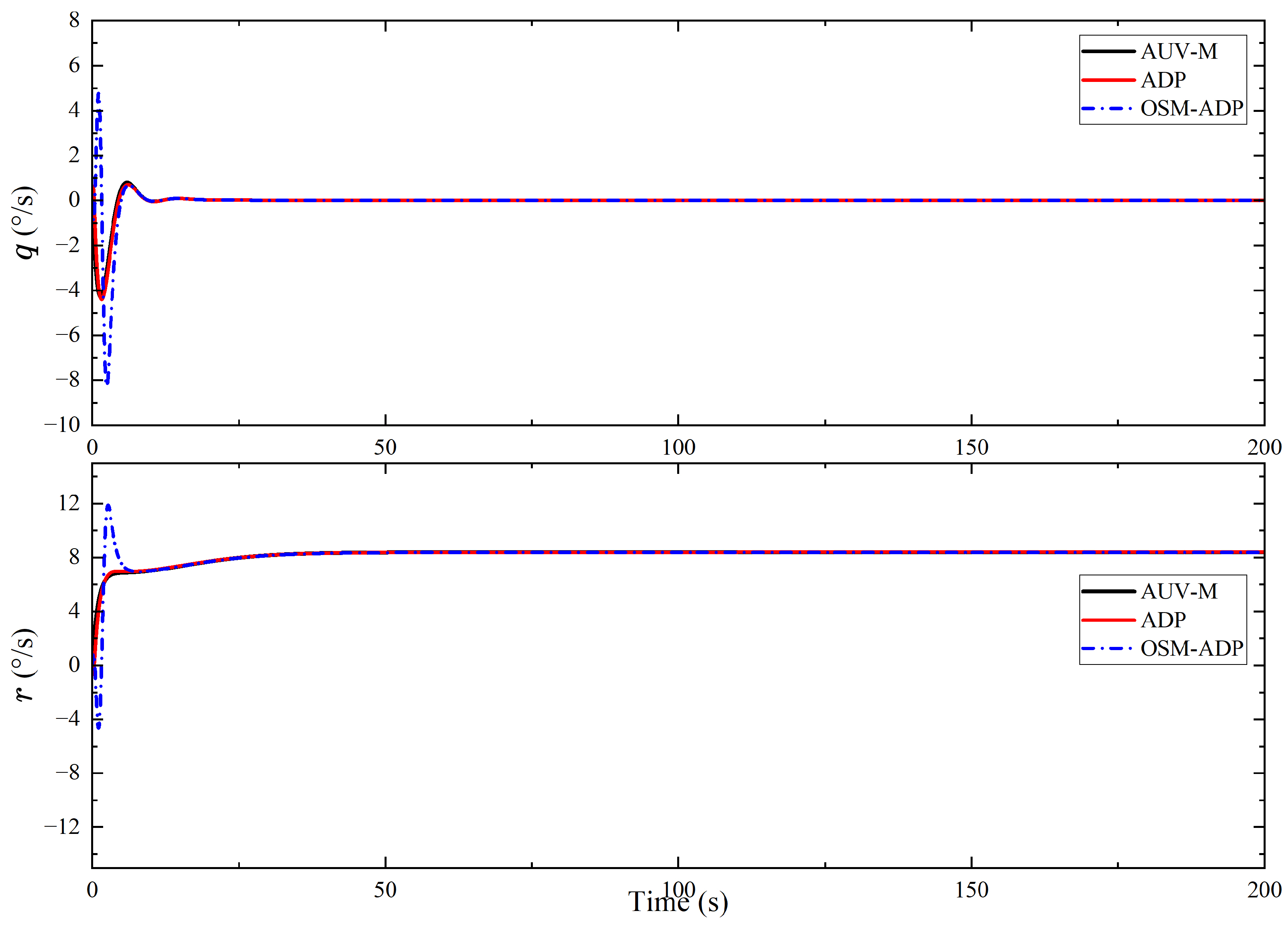


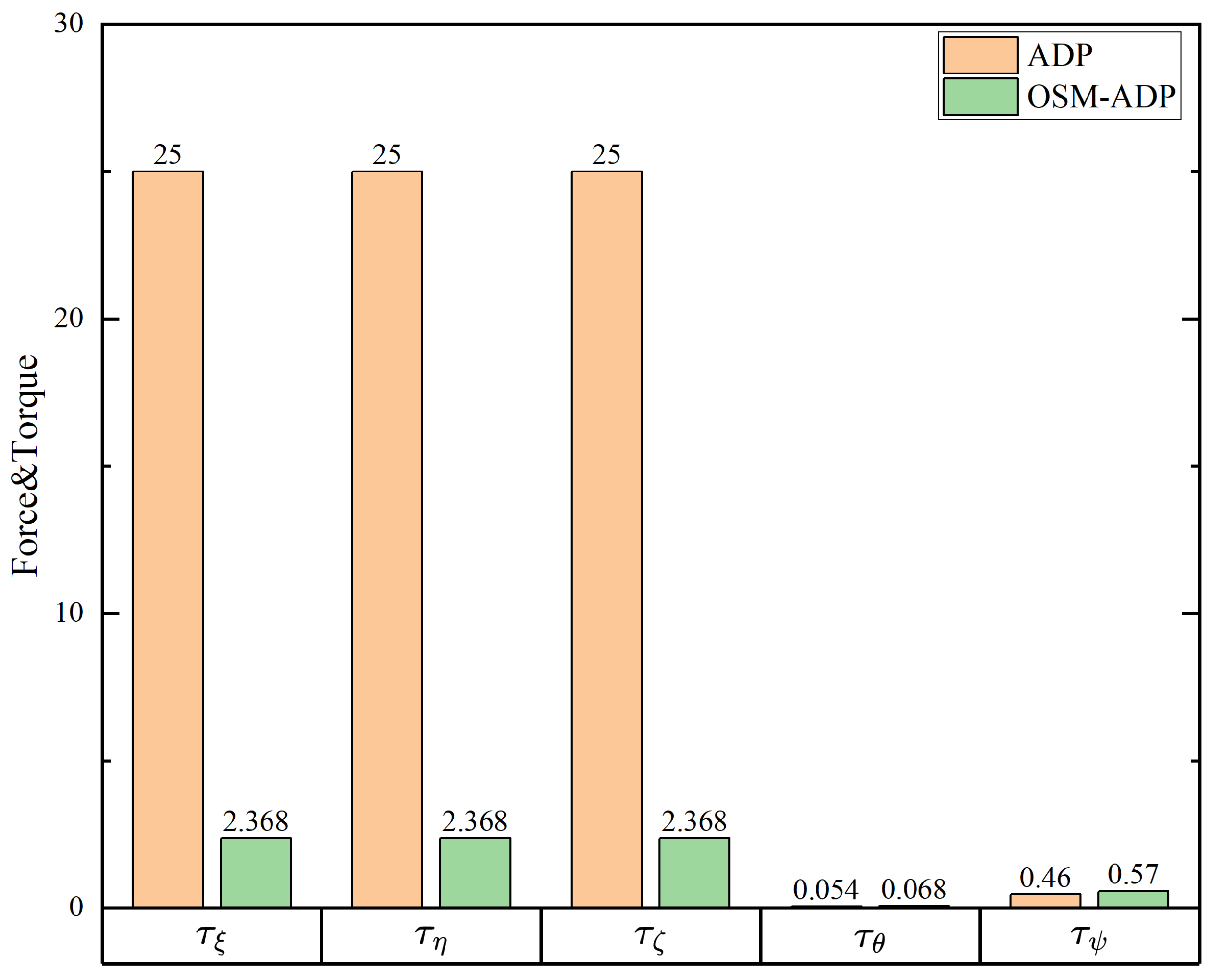
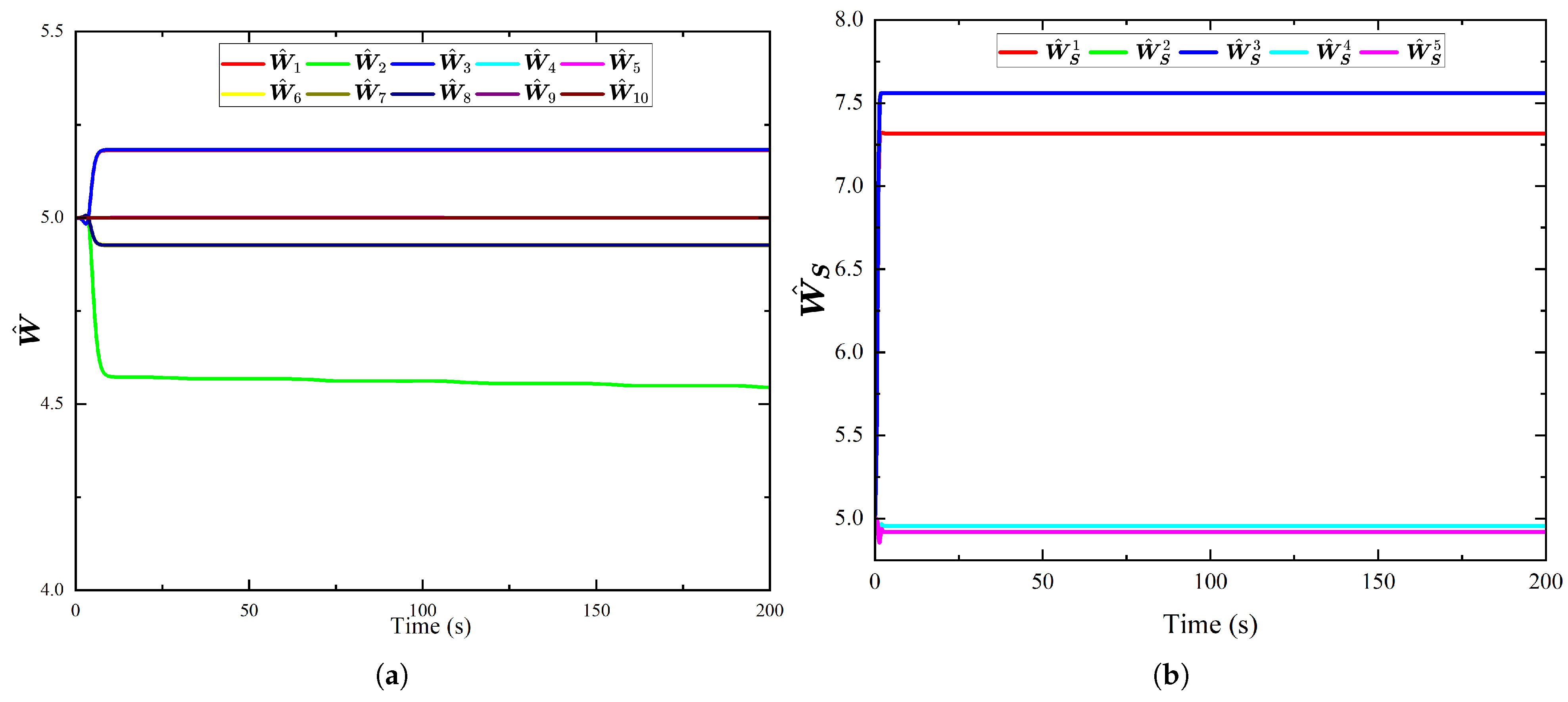
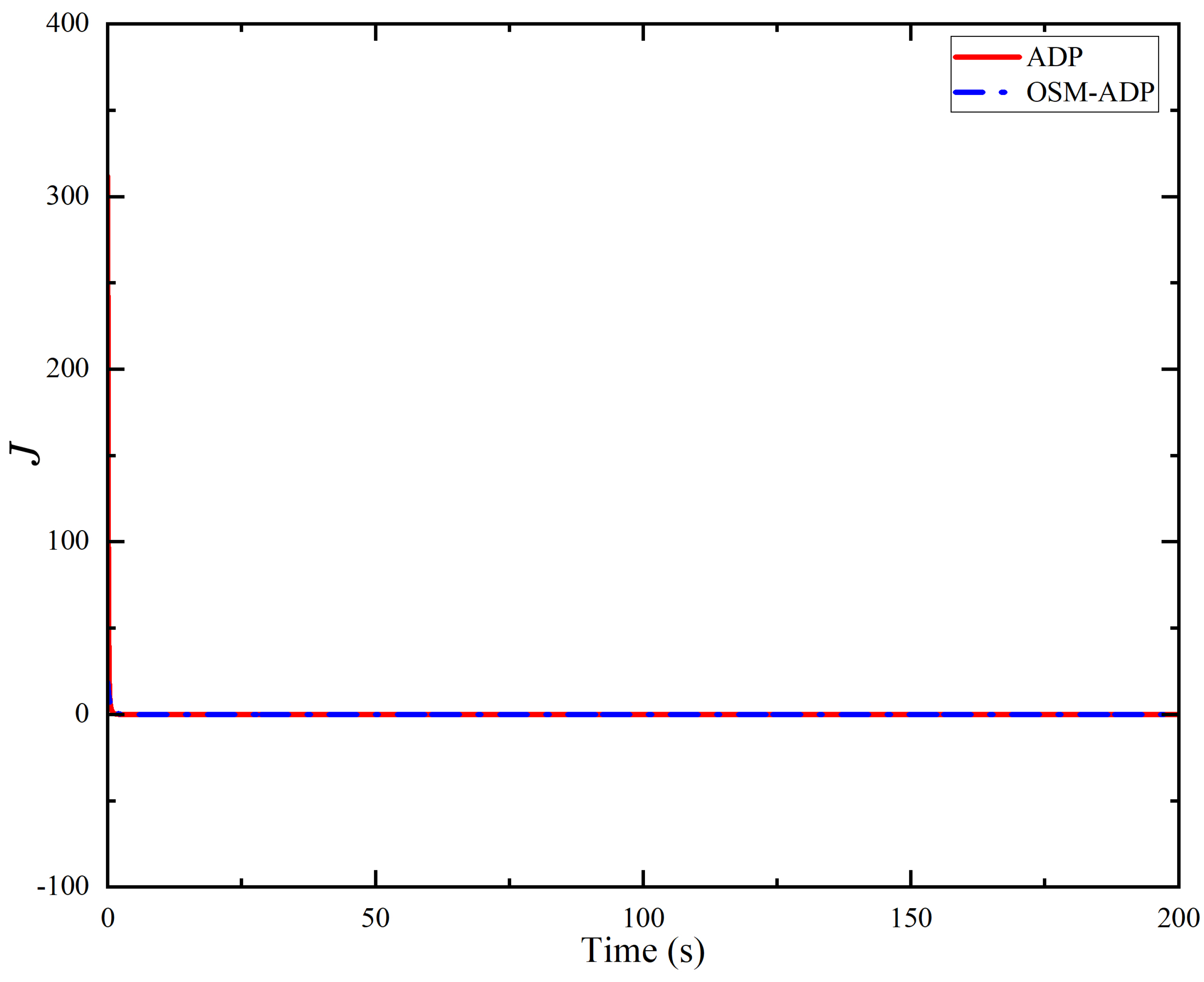

| Methods | Initial Value | Final Values |
|---|---|---|
| ADP | 312 | 0.043 |
| OSM-ADP | 18.9 | 0.041 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, P.; Xiong, Z.; Wu, W.; Sun, Y.; Gao, F. Synchronization Control for AUVs via Optimal-Sliding-Mode Adaptive Dynamic Programming with Actuator Saturation and Performance Constraints in Dynamic Recovery. J. Mar. Sci. Eng. 2025, 13, 1687. https://doi.org/10.3390/jmse13091687
Chai P, Xiong Z, Wu W, Sun Y, Gao F. Synchronization Control for AUVs via Optimal-Sliding-Mode Adaptive Dynamic Programming with Actuator Saturation and Performance Constraints in Dynamic Recovery. Journal of Marine Science and Engineering. 2025; 13(9):1687. https://doi.org/10.3390/jmse13091687
Chicago/Turabian StyleChai, Puxin, Zhenyu Xiong, Wenhua Wu, Yushan Sun, and Fukui Gao. 2025. "Synchronization Control for AUVs via Optimal-Sliding-Mode Adaptive Dynamic Programming with Actuator Saturation and Performance Constraints in Dynamic Recovery" Journal of Marine Science and Engineering 13, no. 9: 1687. https://doi.org/10.3390/jmse13091687
APA StyleChai, P., Xiong, Z., Wu, W., Sun, Y., & Gao, F. (2025). Synchronization Control for AUVs via Optimal-Sliding-Mode Adaptive Dynamic Programming with Actuator Saturation and Performance Constraints in Dynamic Recovery. Journal of Marine Science and Engineering, 13(9), 1687. https://doi.org/10.3390/jmse13091687






