A Nonlinear Filter Based on Fast Unscented Transformation with Lie Group State Representation for SINS/DVL Integration
Abstract
1. Introduction
1.1. Research Background and Key Challenges
1.2. Innovative Approach and Technical Contributions
1.3. Paper Organization Overview
2. Preliminary Knowledge
3. Theoretical Derivation
3.1. UKF Based on Lie Group State Representation
- Initialization State Variables: The initialization procedure establishes the state variables as , are composed of initial attitude , velocity , and position . Initial biases incorporate gyroscope bias and accelerometer bias , with their nominal values derived from sensor prior information. The state error covariance matrix and noise covariance matrix are initialized based on prior knowledge of initial alignment errors and sensor random noise characteristics. The error state vector for the proposed nonlinear filtering algorithm is defined as Equation (18).
- 2.
- Propagation Navigation State: The state propagation follows the time-difference Equations (1)–(3), (7), and (9), with numerical implementation employing a single-sample inertial navigation algorithm for nonlinear propagation to enhance computational efficiency.
- 3.
- Generation of Sigma Points: Sigma point generation applies the unscented transform to the posterior state estimate and its covariance :
- 4.
- Sigma Point Propagation and Perturbed State Update: Sigma points are propagated through two approaches: retraction and nonlinear propagation. The left and right invariant errors are processed through similar operations, with the right-invariant error defined as Equation (21).
- 5.
- Error Variable Update: The error variable between the perturbed update state and the nominal navigation state is computed via inverse retraction. The right-invariant error is expressed as Equation (25).
- 6.
- Computation of Predicted Mean and Covariance : The predicted mean of the error state variable is given by Equation (27).
- 7.
- Measurement Update: The measurement sigma points are first computed for the SINS/DVL integrated navigation system. Since the DVL provides velocity measurements , the measurement equation is expressed as Equation (29).
3.2. Fast Unscented Kalman Filter Based on Lie Group State Representation
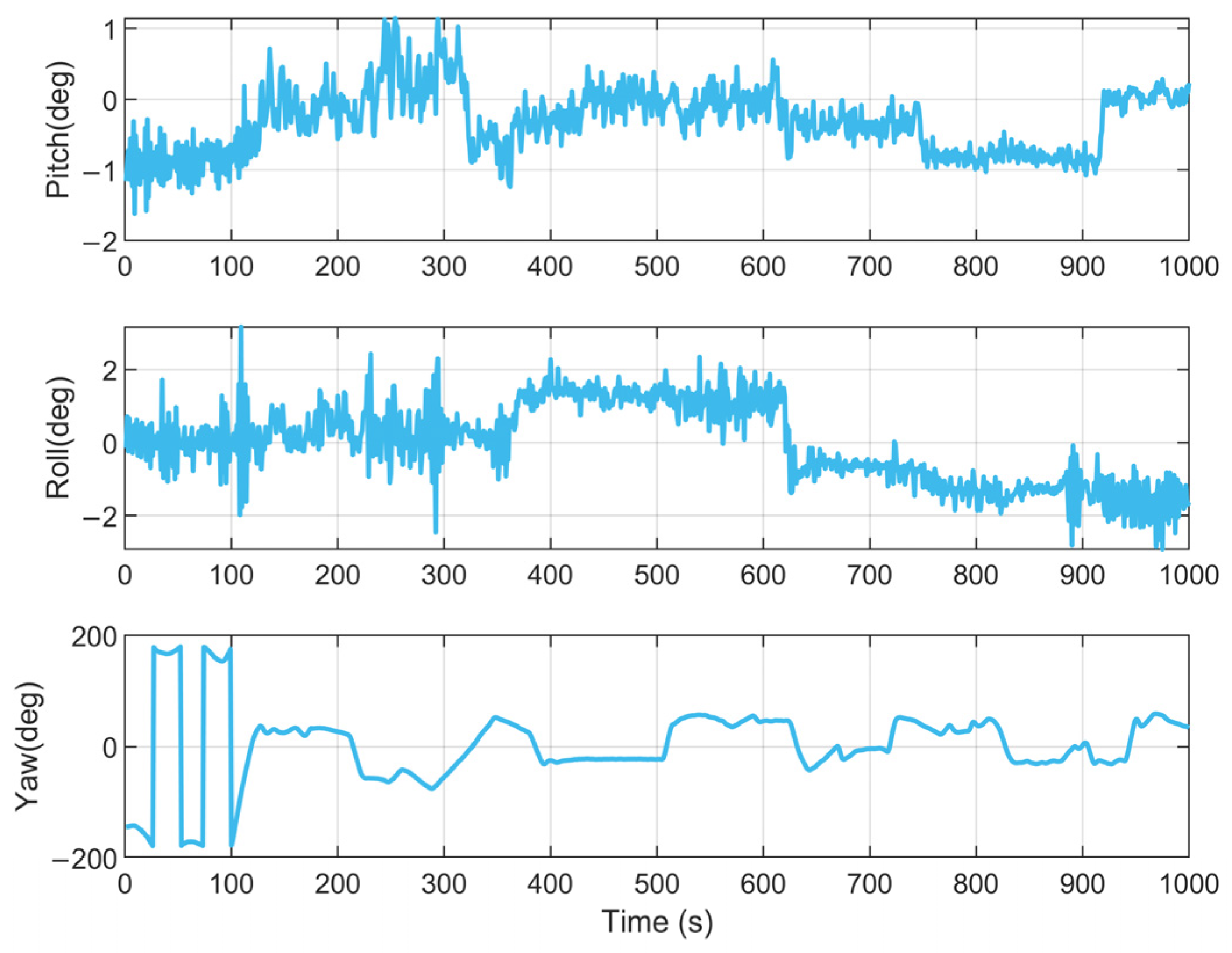
4. Experimental Verification
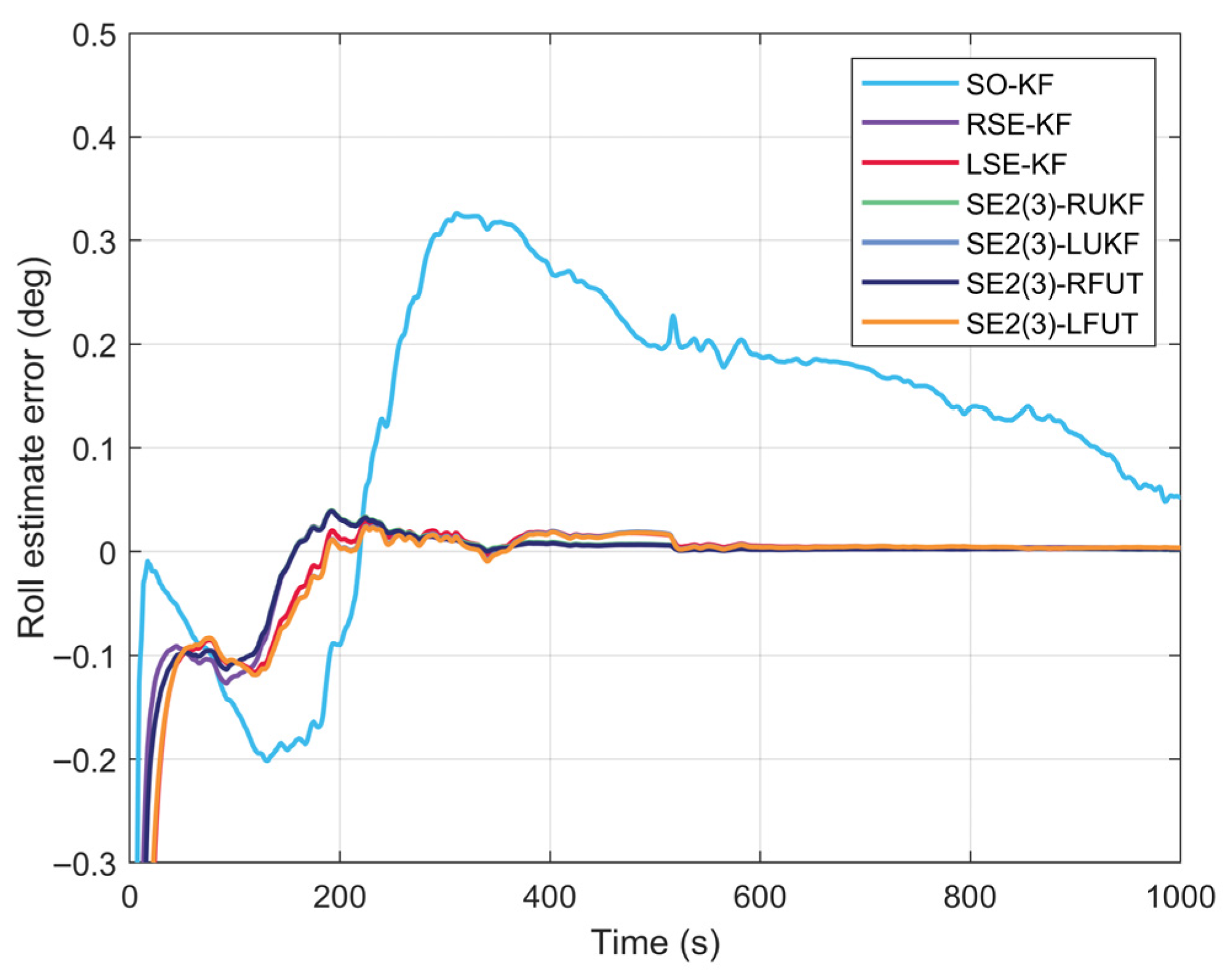
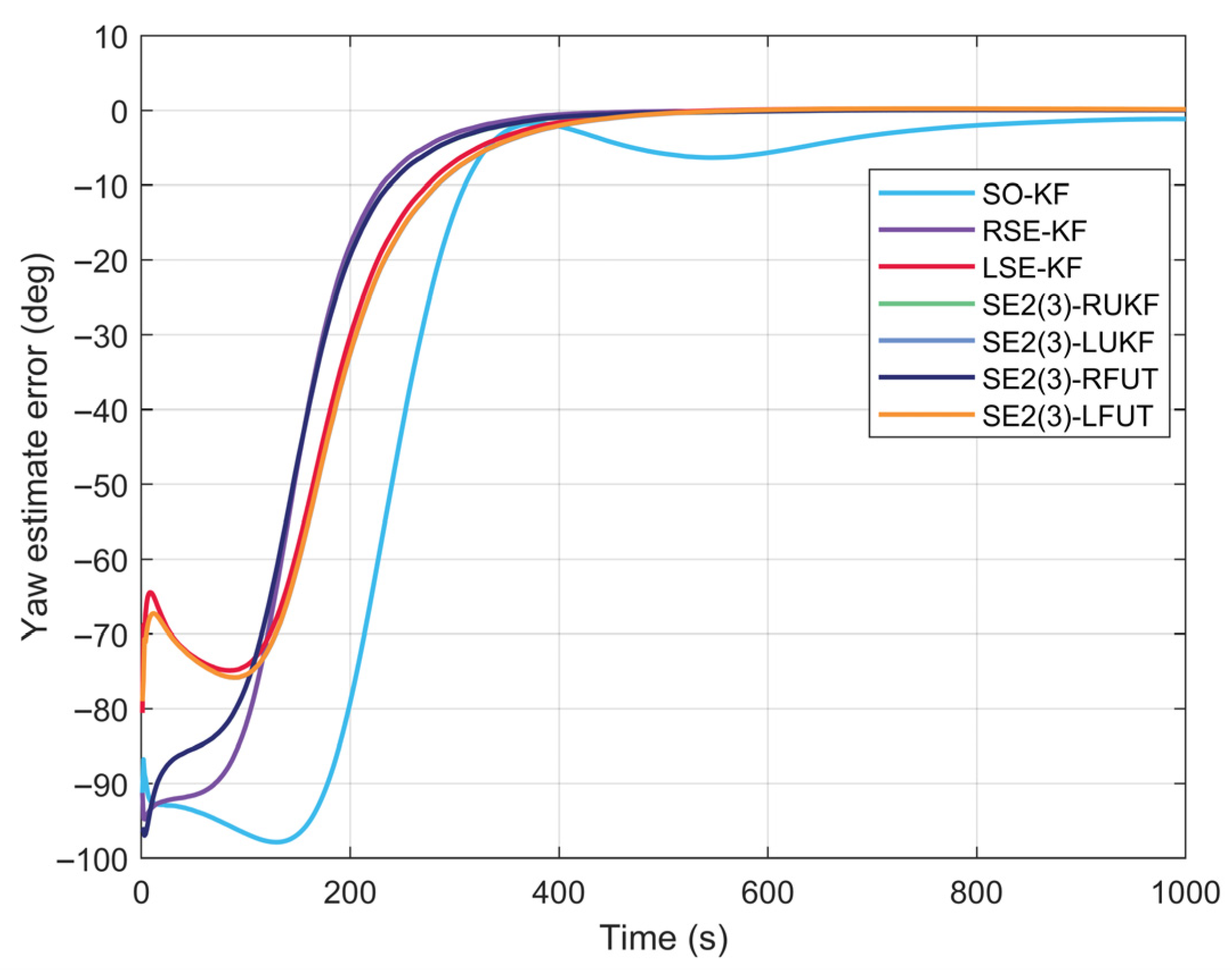
4.1. Performance Evaluation of Large Misalignment Initial Alignment Under Various Conditions
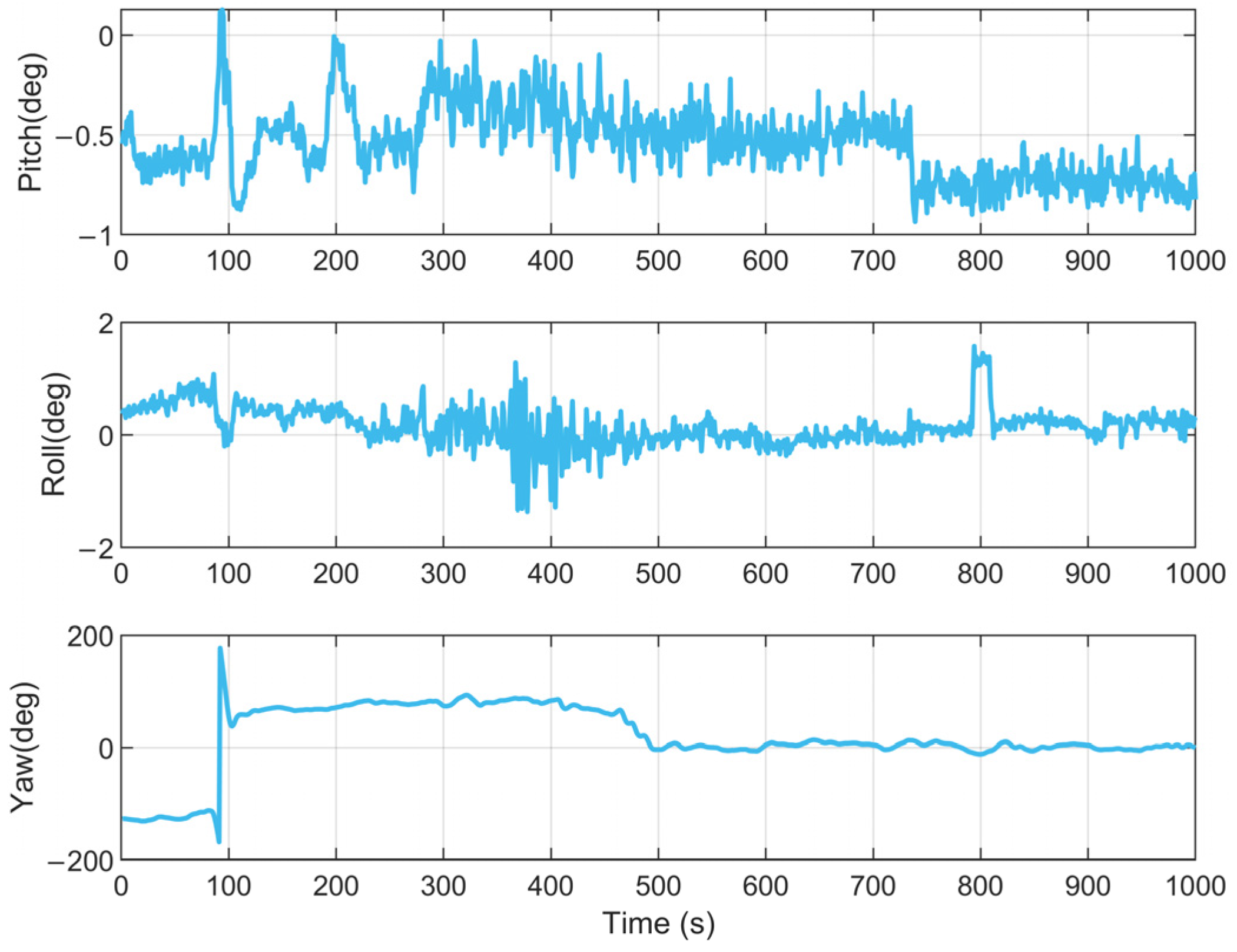
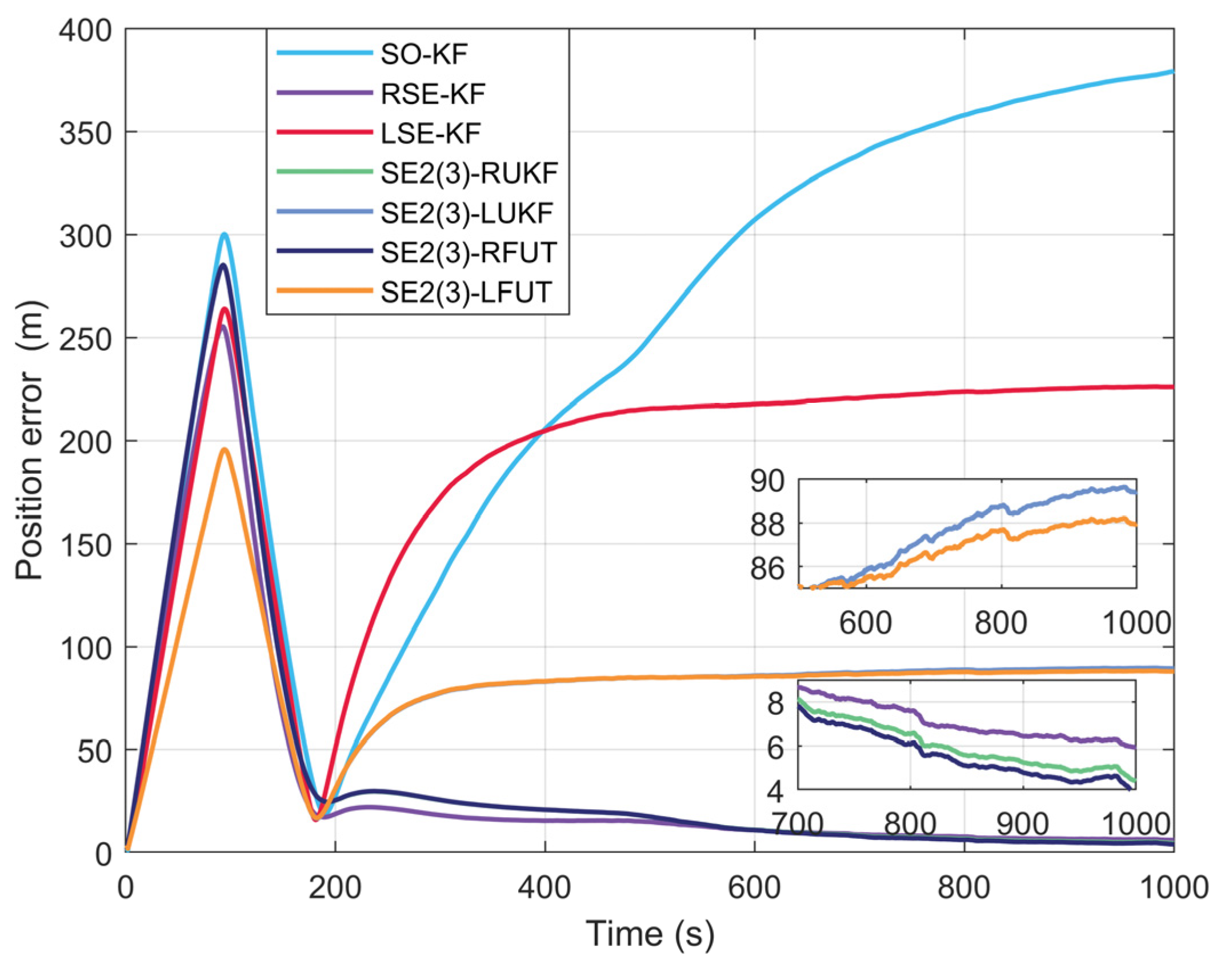
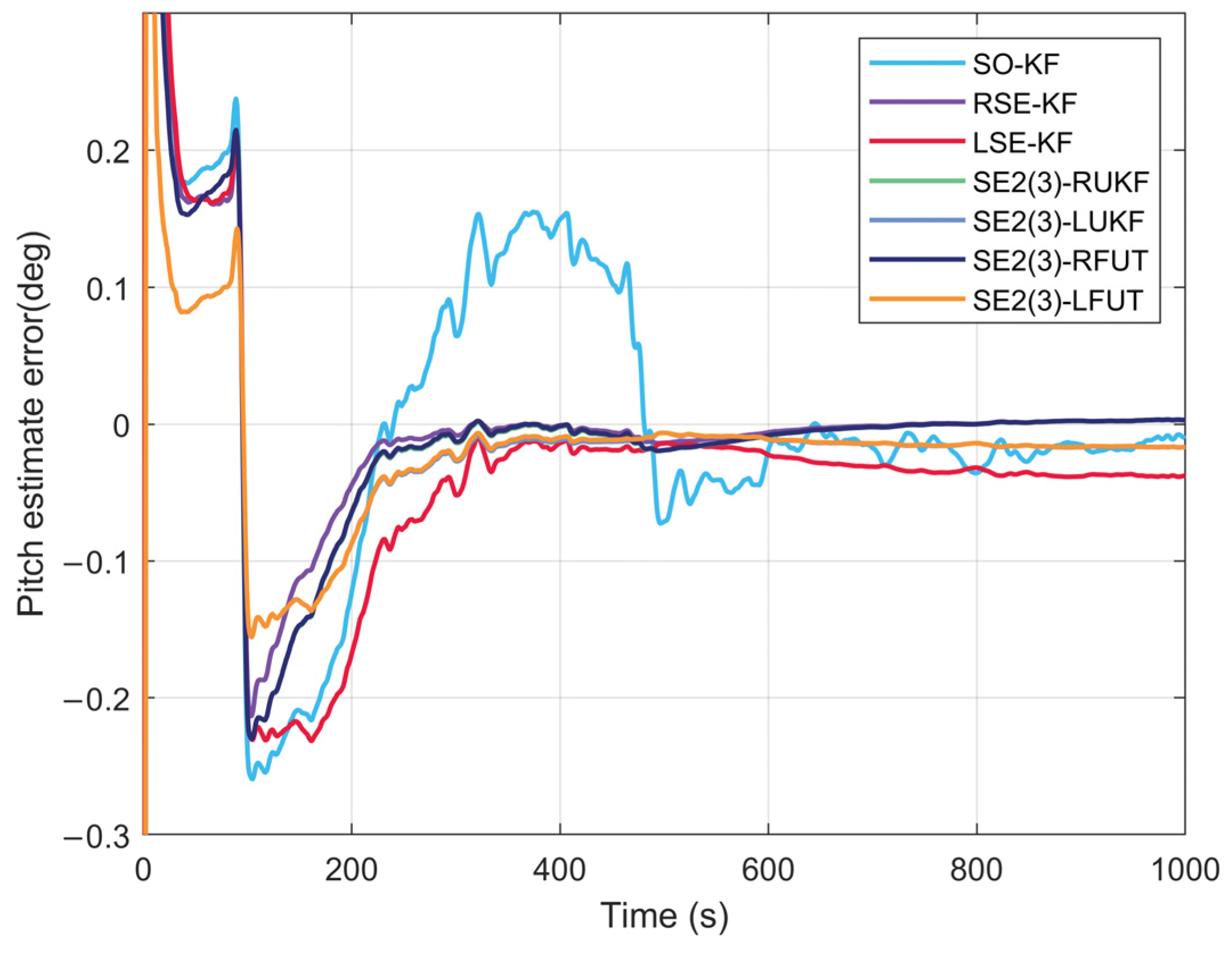
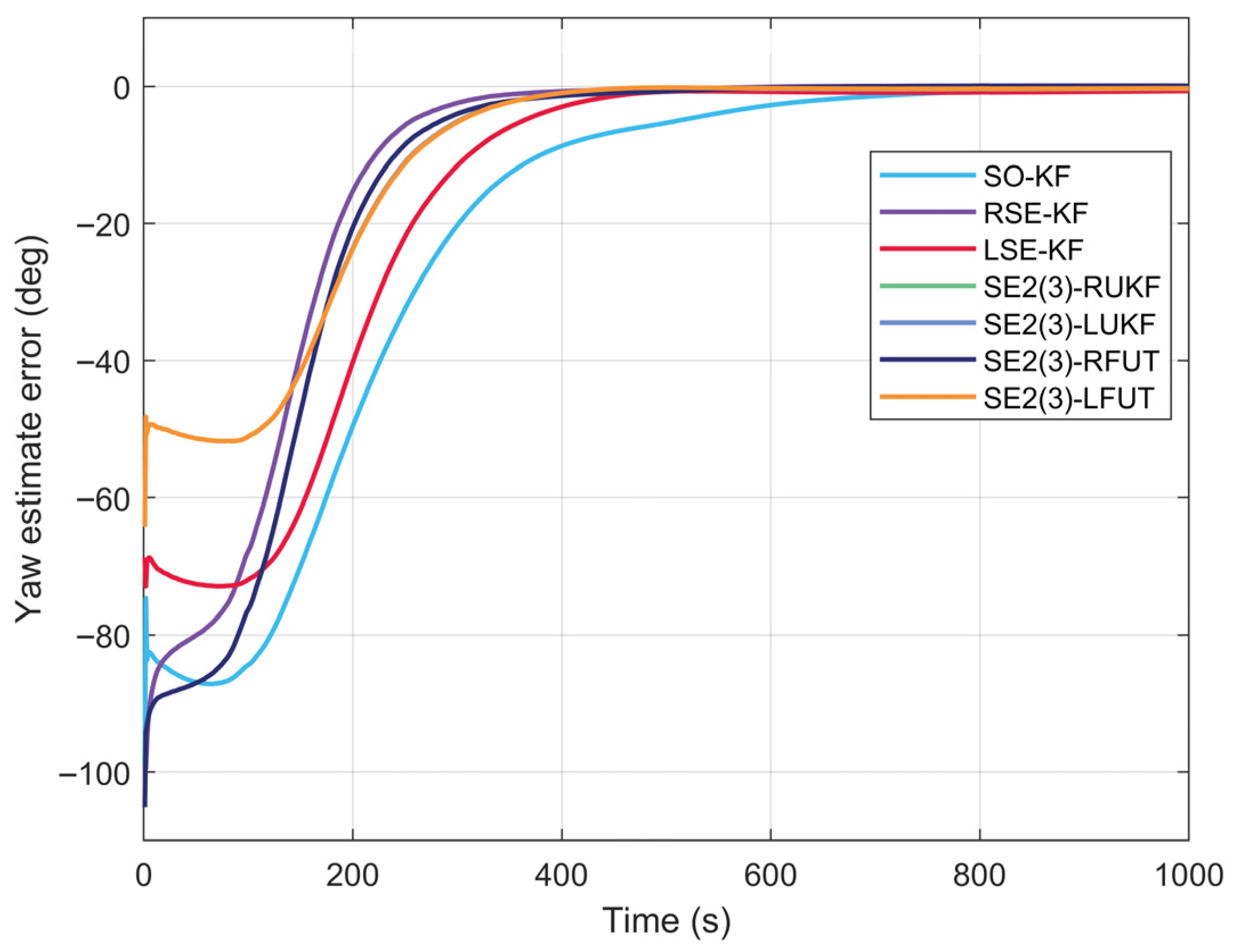
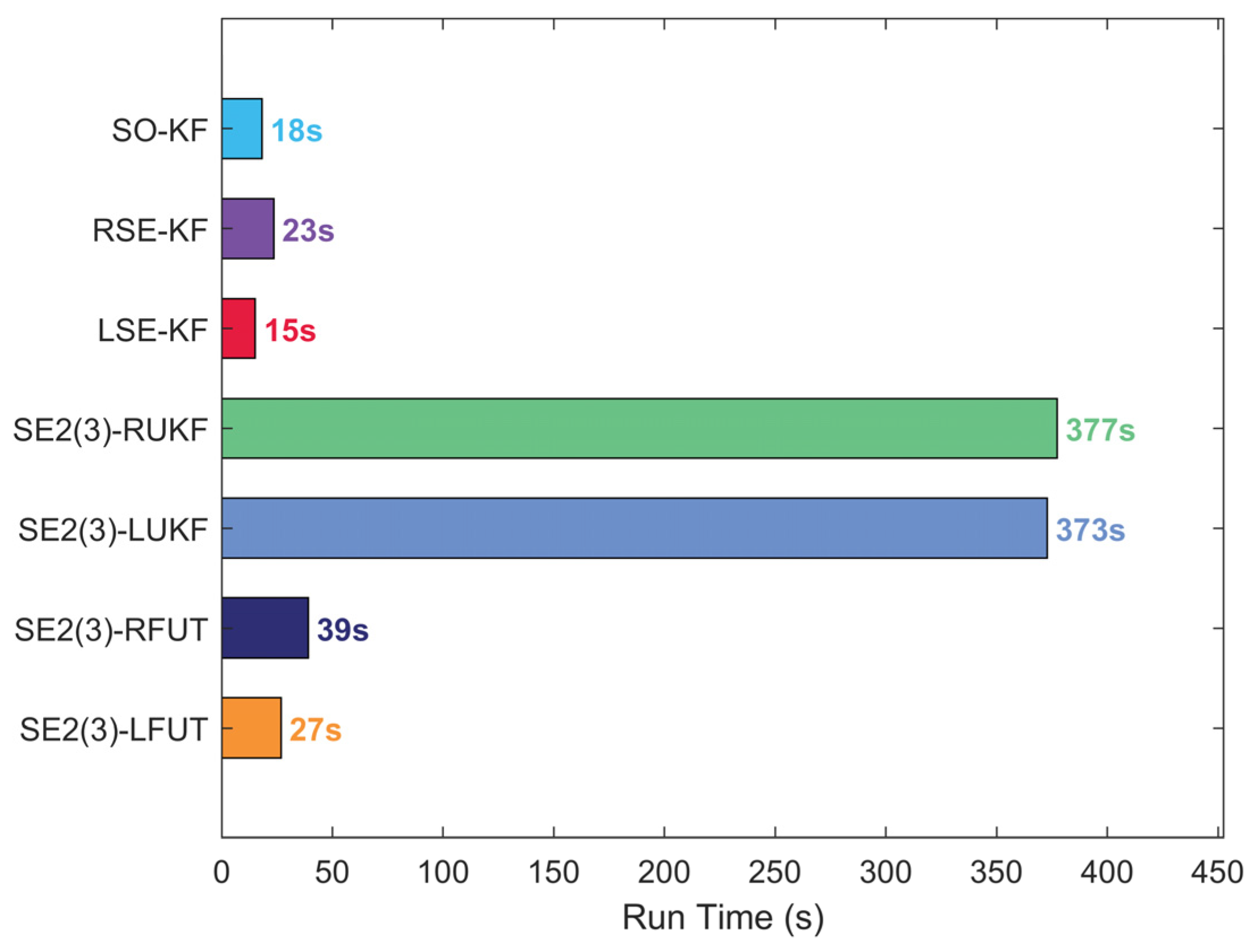
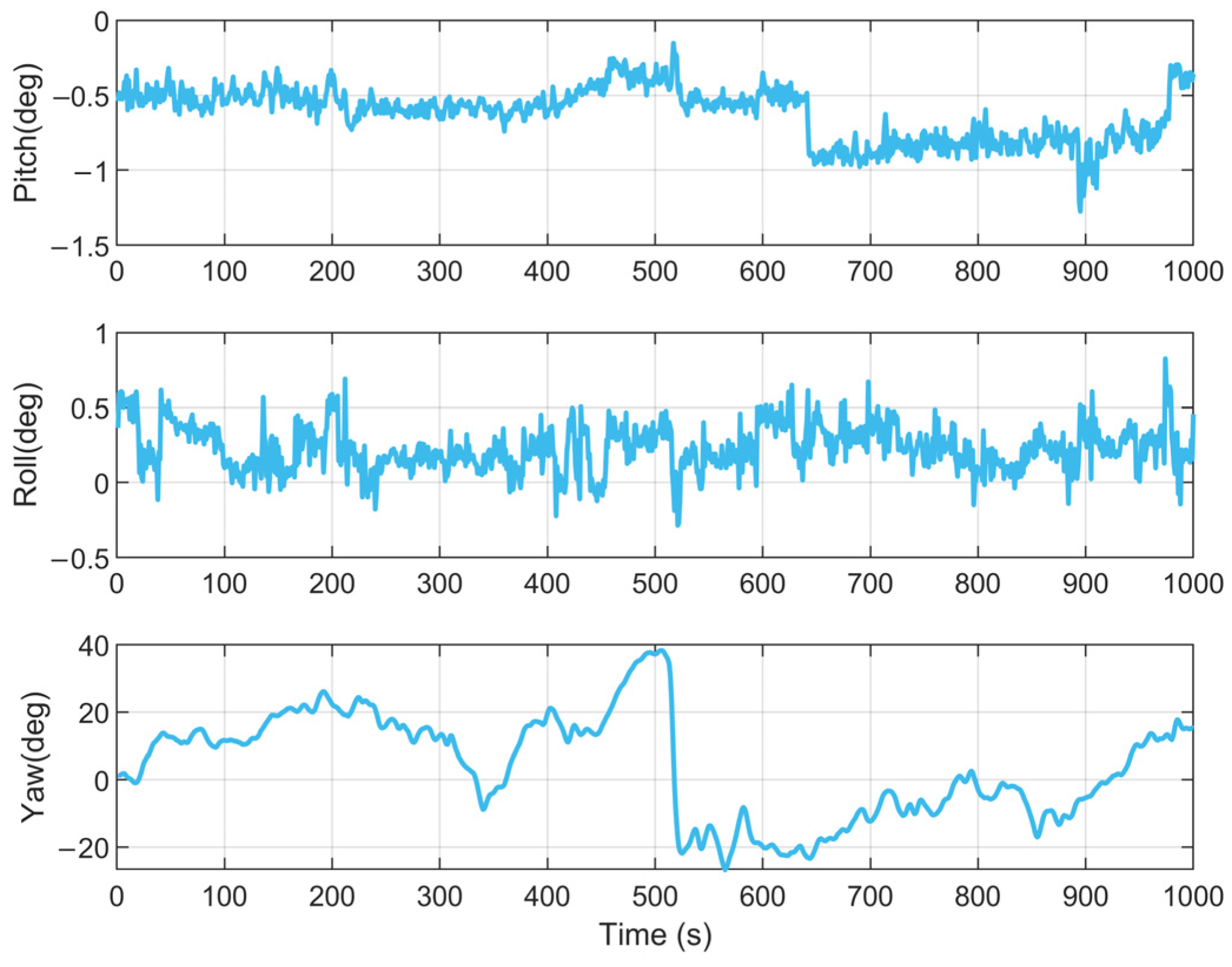
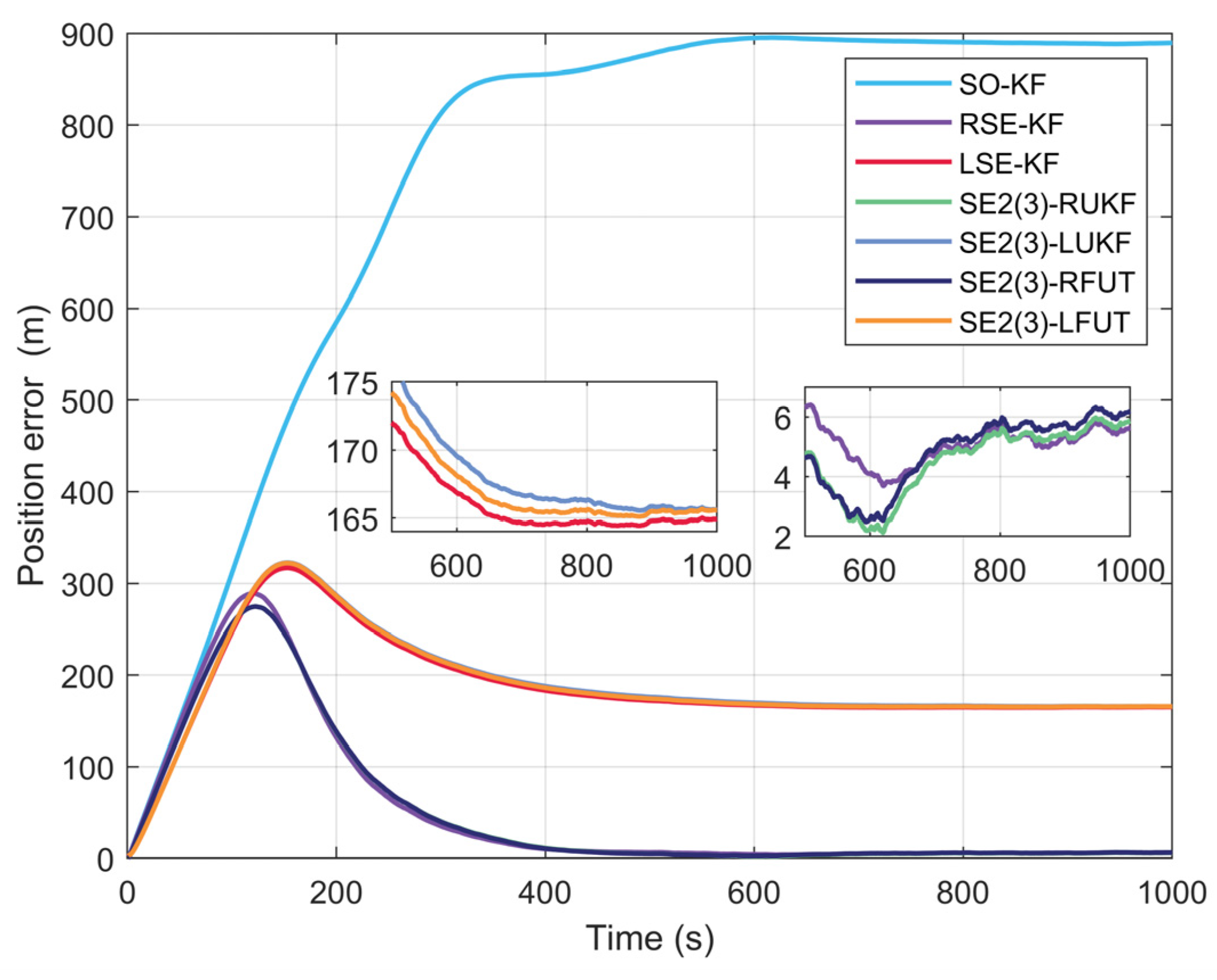
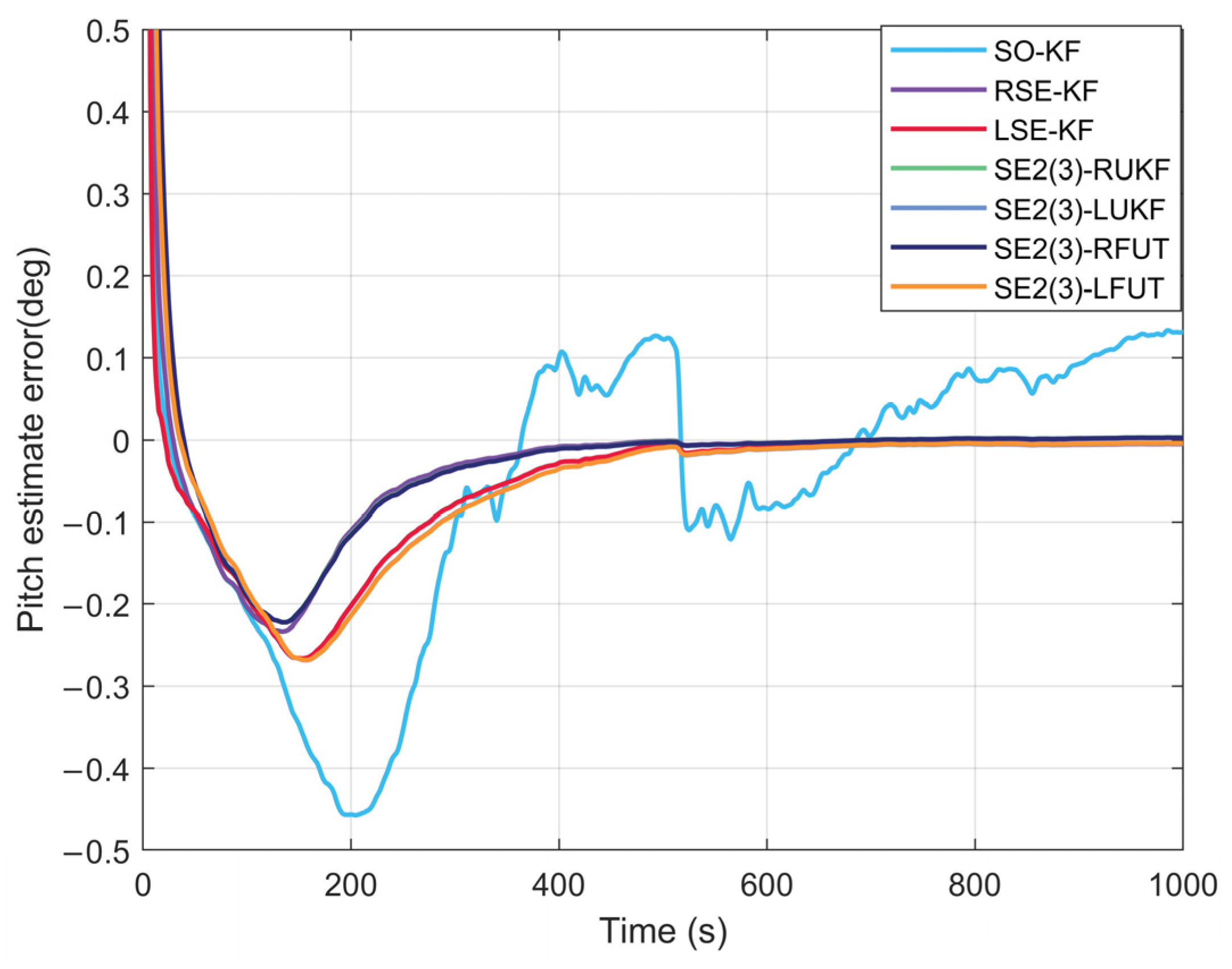
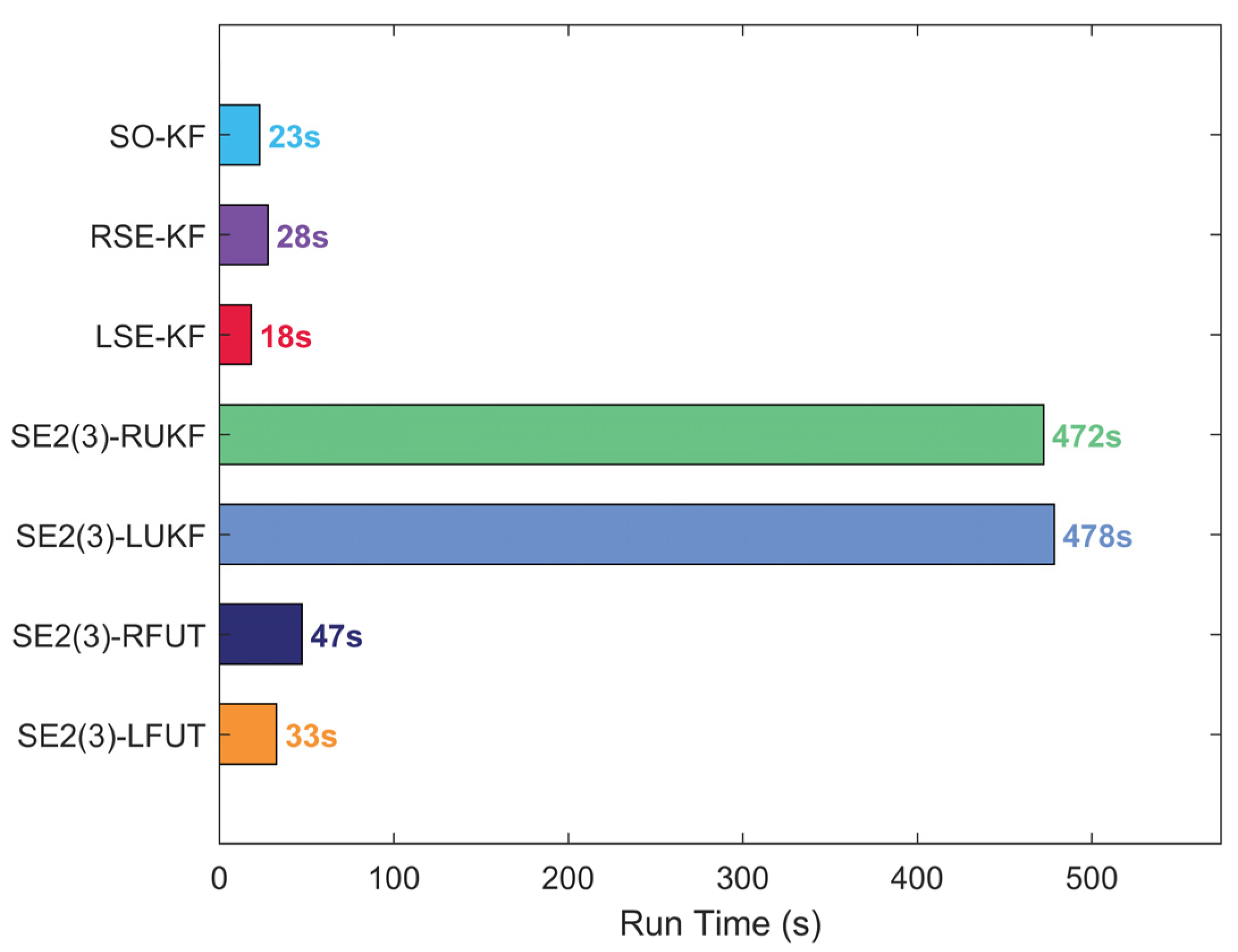
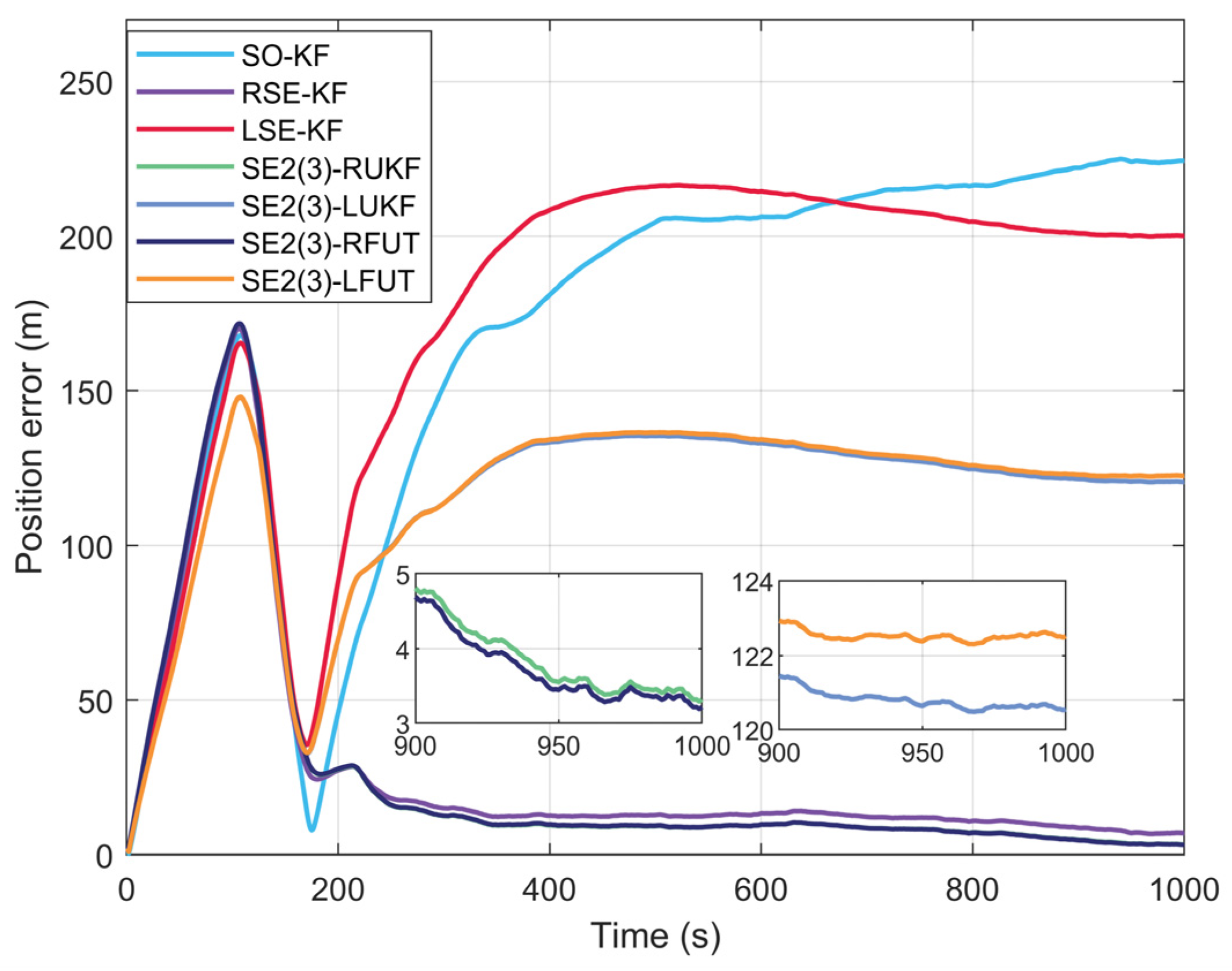
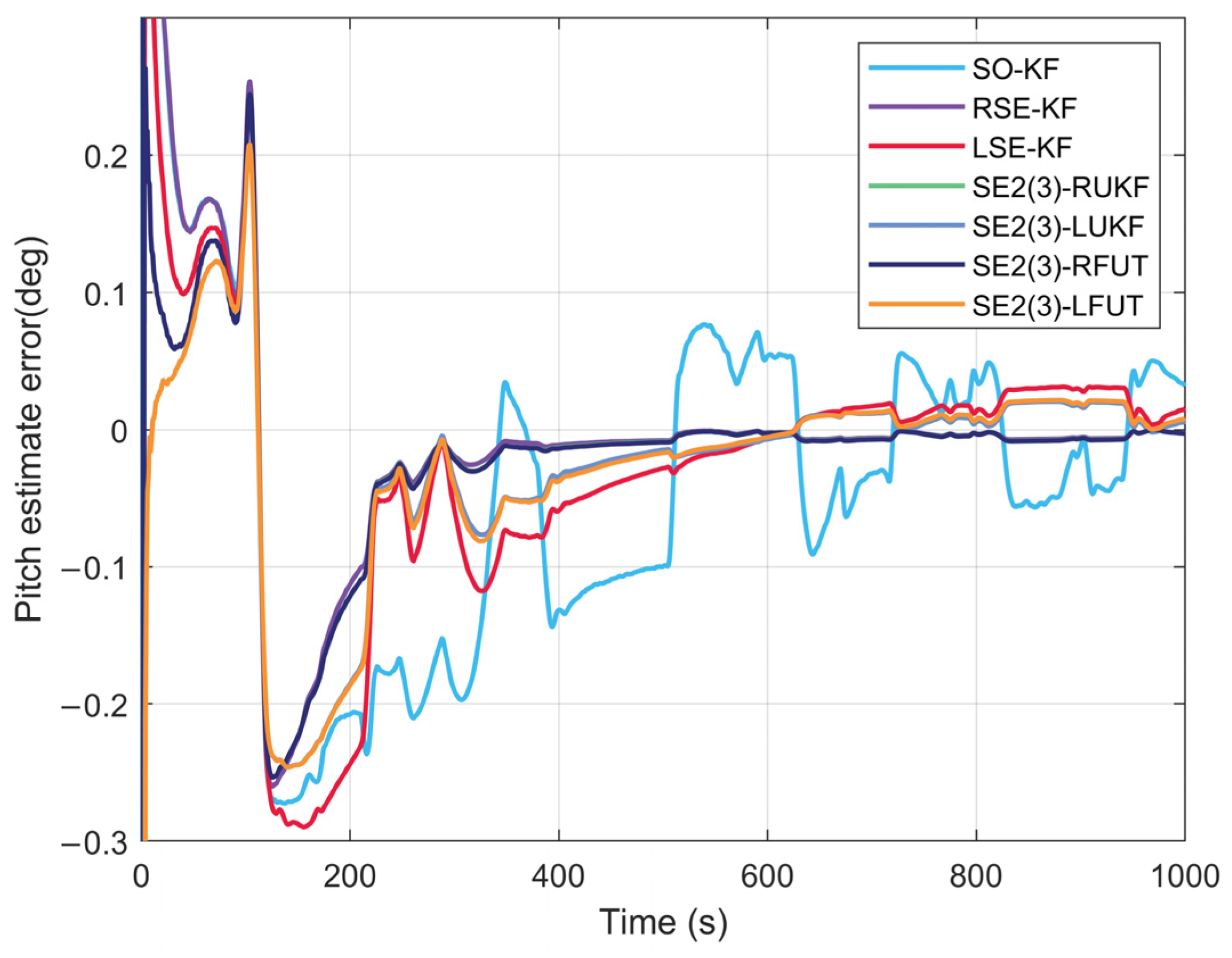
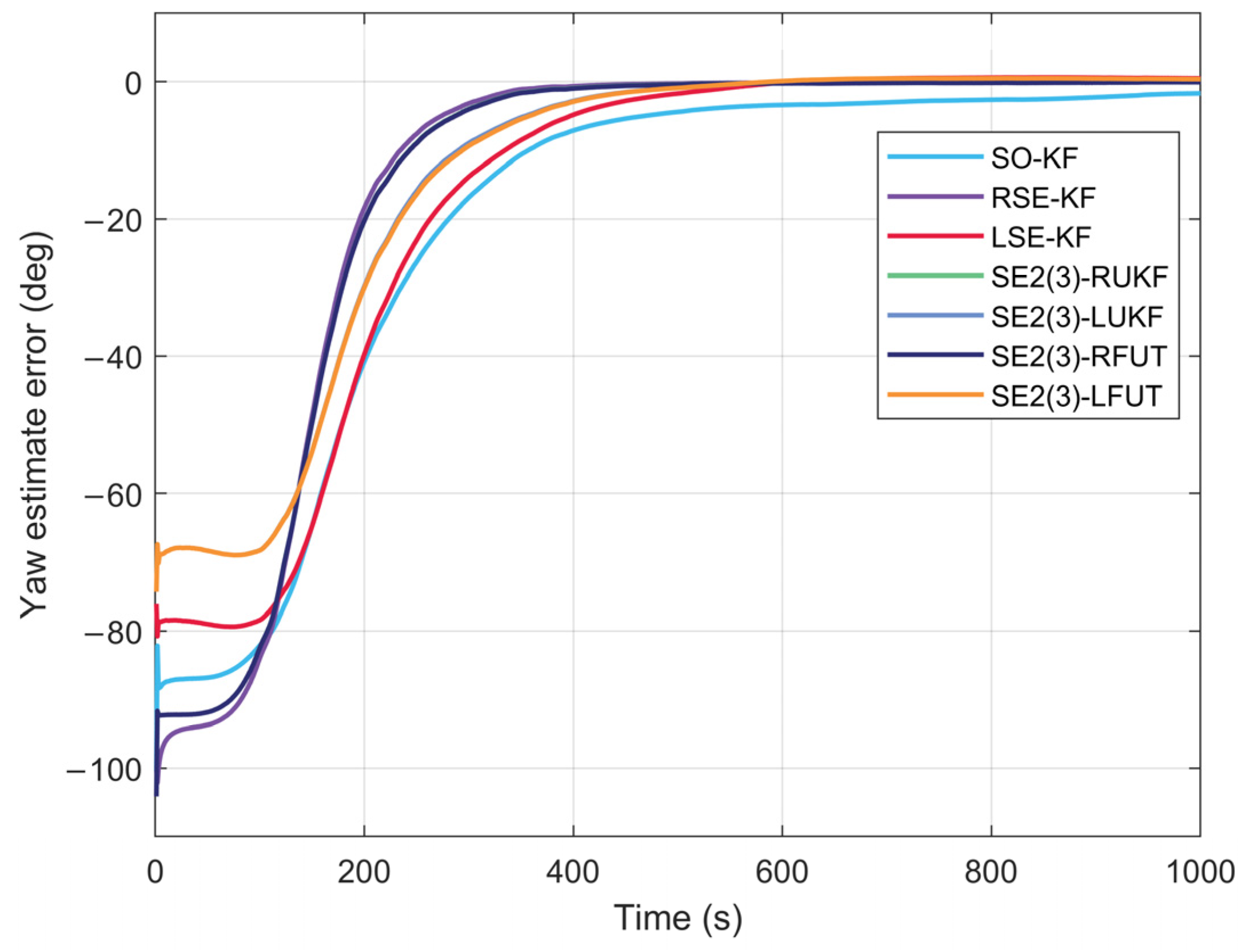
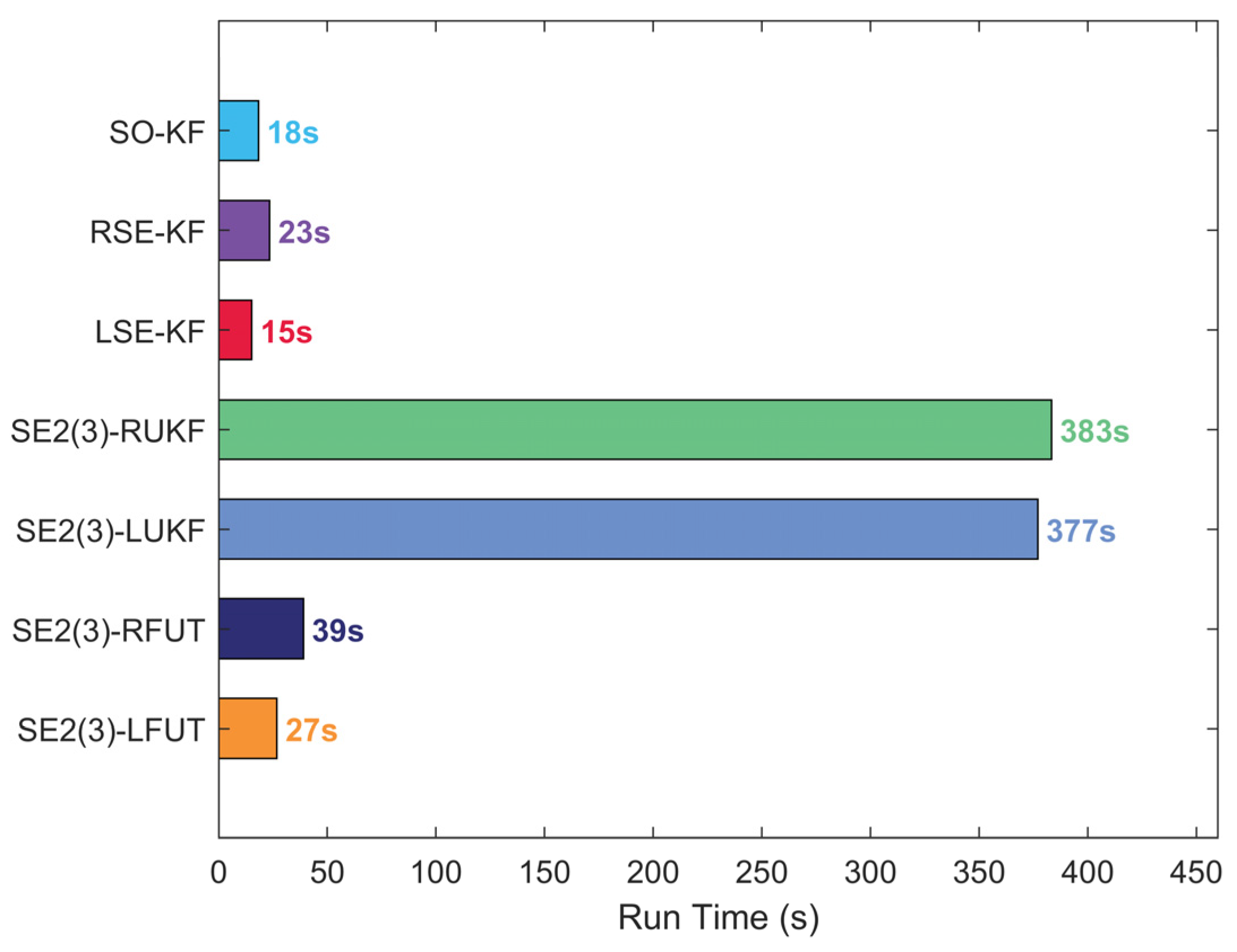
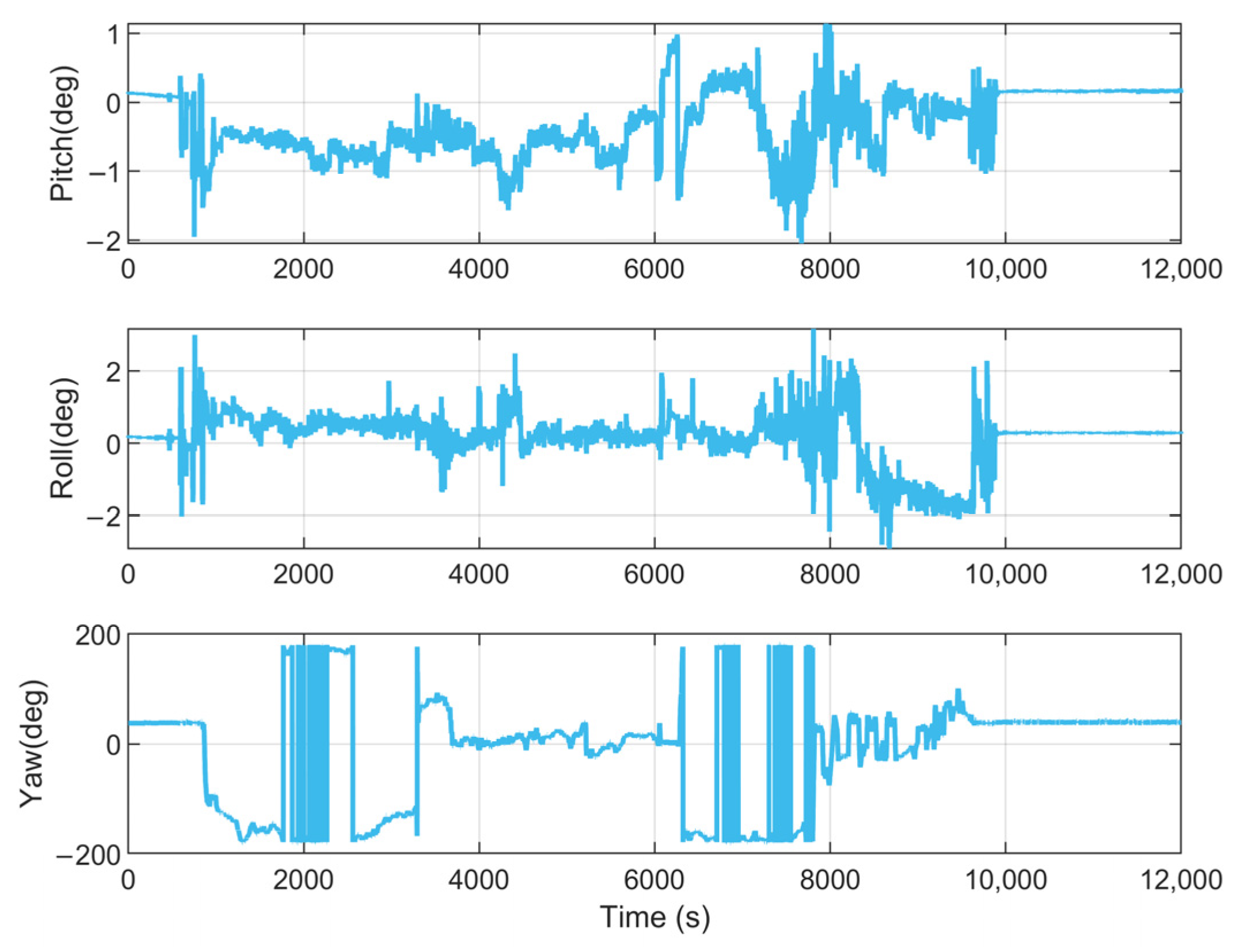
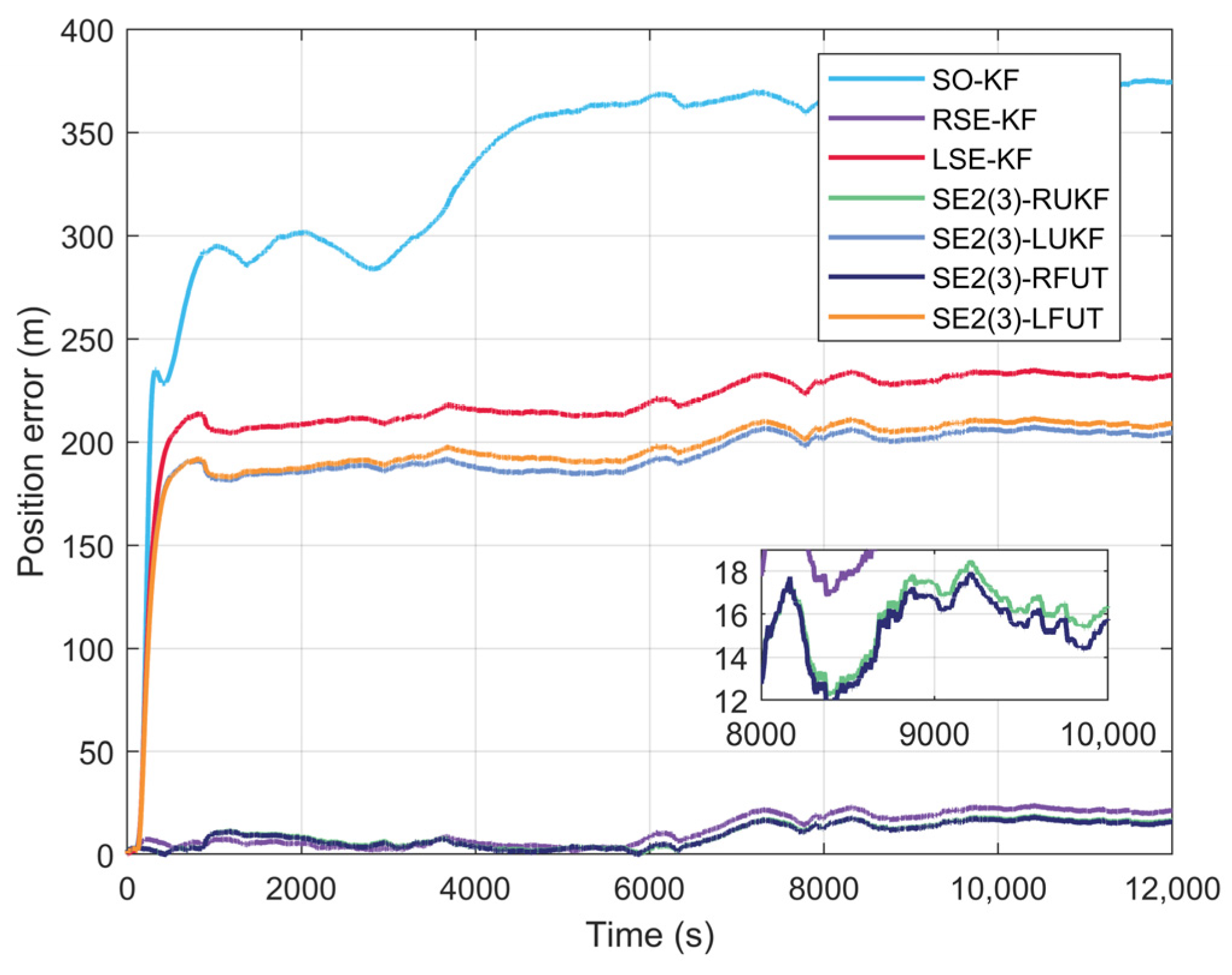
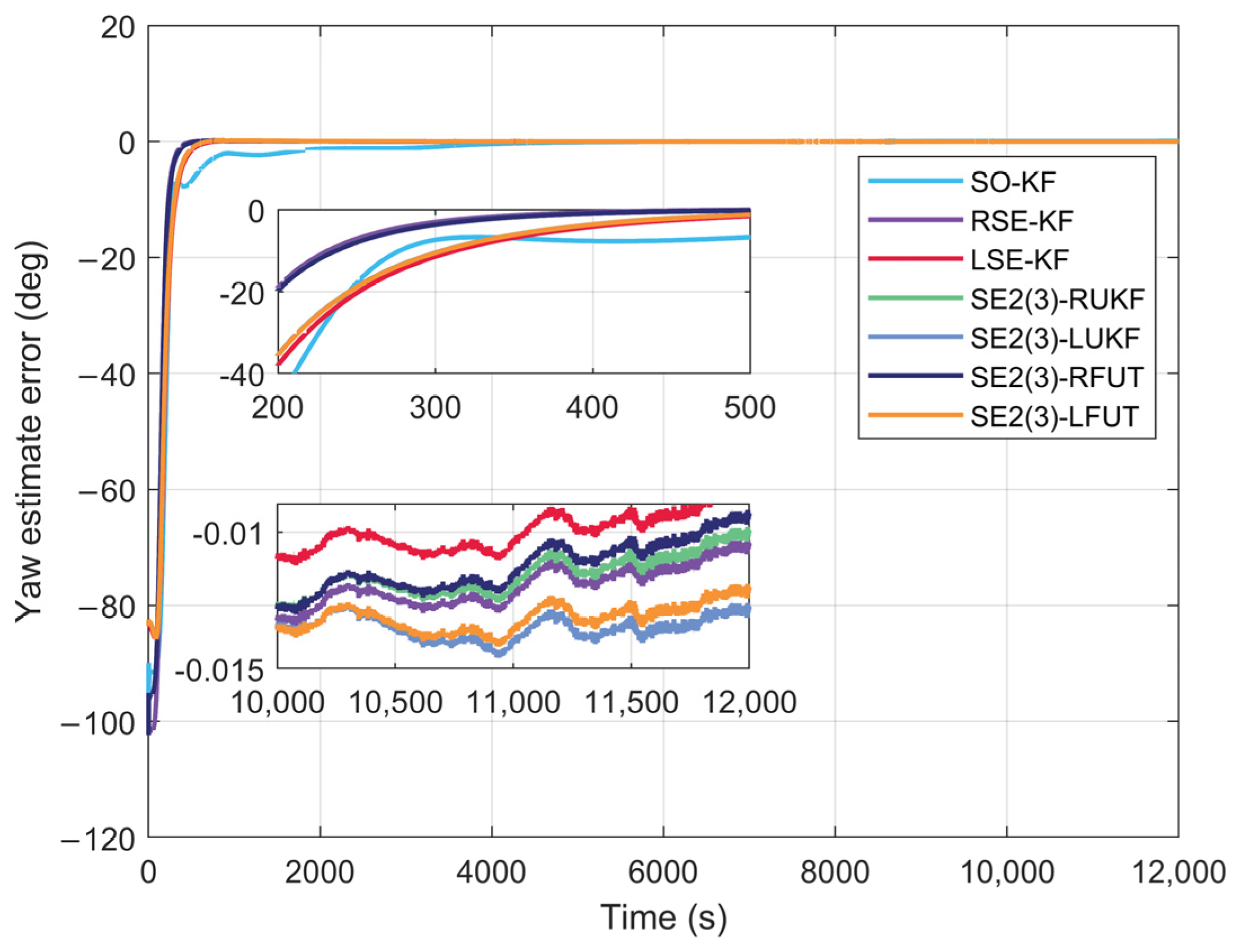
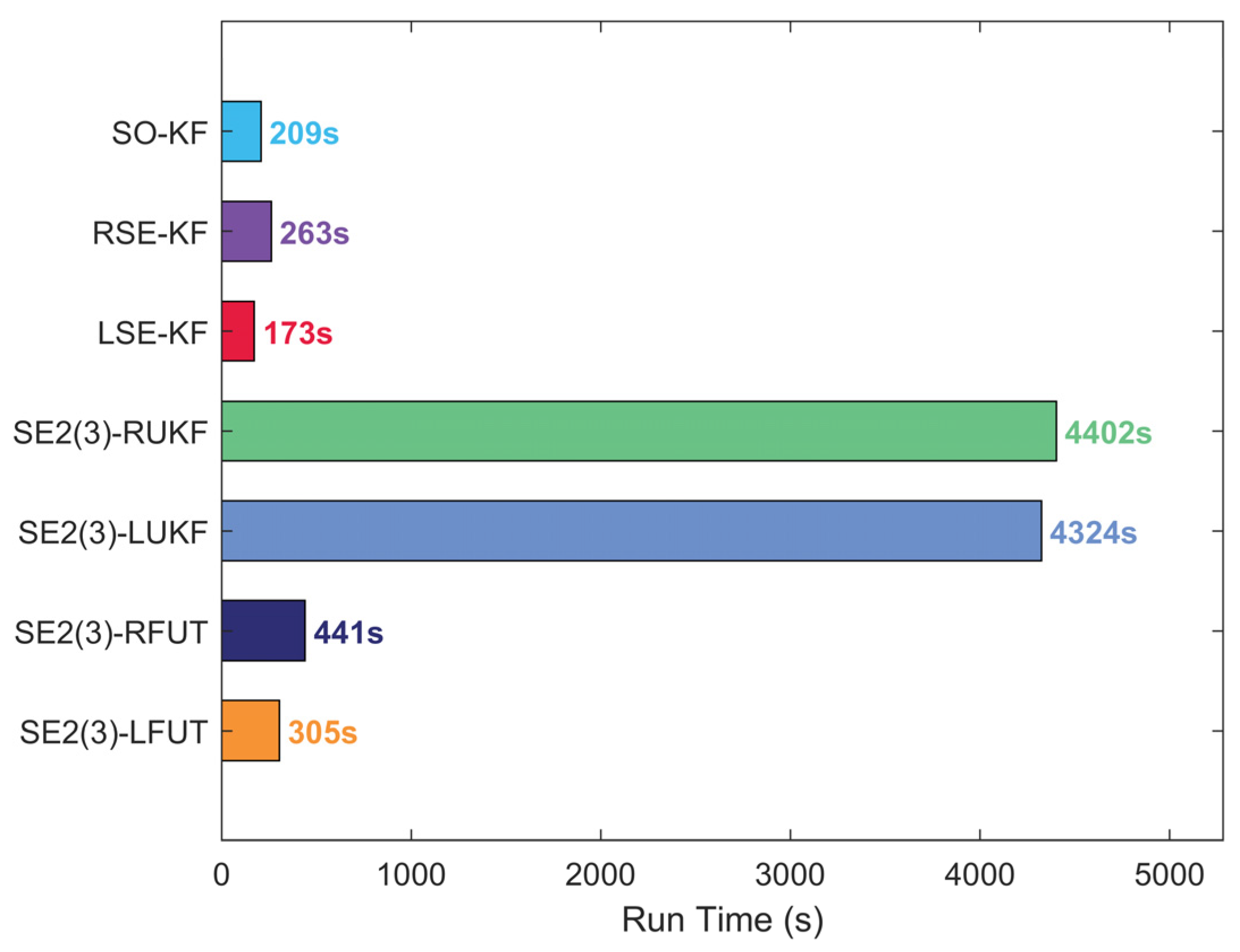
4.2. Long-Duration Navigation Performance Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. SO-KF State-Space Model
Appendix B. RSE-KF State-Space Model
Appendix C. LSE-KF State-Space Model
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Chen, K.-Y.; Huang, N.-Y.; Su, W.; Cheng, E. An Underwater Concealed Navigation and Positioning Method Based on SINS and LBL. J. Unmanned Undersea Syst. 2022, 30, 37–43. [Google Scholar]
- Liu, K.-R. Research on Deep-Sea Ultra-Short Baseline Positioning Algorithm Based on Underwater Acoustic Ultra-Wideband Signal. Ph.D. Thesis, Hainan University, Haikou, China, 2020. [Google Scholar]
- Li, W.-J.; Wang, Z.-J.; Sun, Z.; Zhang, S.-M. Sound Velocity Correction Method for Ultra-Short Baseline Based on Depth Constraint. J. Navig. Position. 2022, 10, 40–45. [Google Scholar]
- Wang, B.; Liu, J.-Y.; Liu, P.-J. Overview of SINS/DVL Integrated Navigation Technology. J. Navig. Position. 2020, 8, 1–6+22. [Google Scholar] [CrossRef]
- Zhao, J.-B.; Ge, X.-Y.; Feng, X.-L.; Zhou, H.-K. Survey of Underwater SINS/DVL Integrated Navigation Technology. J. Unmanned Undersea Syst. 2018, 26, 2–9. [Google Scholar]
- Zhu, Z. Research on Underwater SINS/DVL Integrated Navigation Technology. Master’s Thesis, China Three Gorges University, Yichang, China, 2024. [Google Scholar] [CrossRef]
- Lu, D.-H.; Song, S.-L.; Wang, J.; Cai, Y.-X.; Shen, H.-H. Development Review of Underwater SINS/DVL Integrated Navigation Technology. Control Theory Appl. 2022, 39, 1159–1170. [Google Scholar]
- Barrau, A.; Bonnabel, S. Intrinsic Filtering on SO(3) with Discrete-Time Observations. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 3255–3260. [Google Scholar] [CrossRef]
- Bonnabel, S.; Martin, P.; Salaün, E. Invariant Extended Kalman Filter: Theory and Application to a Velocity-Aided Attitude Estimation Problem. In Proceedings of the 48h IEEE Conference on Decision and Control, Shanghai, China, 15–18 December 2009; pp. 1297–1304. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Invariant Filtering for Pose EKF-SLAM Aided by an IMU. In Proceedings of the 2015 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 2133–2138. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. An EKF-SLAM Algorithm with Consistency Properties. arXiv 2015, arXiv:1510.06263. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Alignment Method for an Inertial Unit. U.S. Patent 15/037,653, 6 October 2016. [Google Scholar]
- Barrau, A.; Bonnabel, S. The Invariant Extended Kalman Filter as a Stable Observer. IEEE Trans. Autom. Control 2017, 62, 1797–1812. [Google Scholar] [CrossRef]
- Brossard, M.; Bonnabel, S.; Barrau, A. Invariant Kalman Filtering for Visual Inertial SLAM. In Proceedings of the 2018 21st International Conference on Information Fusion, Cambridge, UK, 10–13 July 2018; pp. 2021–2028. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. A Mathematical Framework for IMU Error Propagation with Applications to Pre-integration. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 5732–5738. [Google Scholar] [CrossRef]
- Barrau, A. Non-linear State Error Based Extended Kalman Filters with Applications to Navigation. Ph.D. Thesis, Department of Automatic, Mines ParisTech, Paris, France, 2015. [Google Scholar]
- Chang, L.; Di, J.; Qin, F. Inertial-based Integration with Transformed INS Mechanization in Earth Frame. IEEE/ASME Trans. Mechatron. 2022, 27, 1738–1749. [Google Scholar] [CrossRef]
- Chang, L.; Bian, Q.; Zuo, Y.; Zhou, Q. SINS/GNSS-integrated Navigation Based on Group Affine SINS Mechanization in Local-level Frame. IEEE/ASME Trans. Mechatron. 2023, 28, 2471–2482. [Google Scholar] [CrossRef]
- Chang, L.; Tang, H.; Hu, G.; Xu, J. SINS/DVL Linear Initial Alignment Based on Lie Group SE3(3). IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7203–7217. [Google Scholar] [CrossRef]
- Chang, L.; Luo, Y. Log-linear Error State Model Derivation Without Approximation for INS. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2029–2035. [Google Scholar] [CrossRef]
- Du, S.; Huang, Y.; Lin, B.; Qian, J.; Zhang, Y. A Lie Group Manifold-Based Nonlinear Estimation Algorithm and Its Application to Low-Accuracy SINS/GNSS Integrated Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1002927. [Google Scholar] [CrossRef]
- Chirikjian, G.S. Stochastic Models, Information Theory, and Lie Groups: Analytic Methods and Modern Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Solà, J.; Deray, J.; Atchuthan, D. A Micro Lie Theory for State Estimation in Robotics. arXiv 2018, arXiv:1812.01537. [Google Scholar]
- Hartley, R.; Ghaffari, M.; Eustice, R.M.; Grizzle, J.W. Contact Aided Invariant Extended Kalman Filtering for Robot State Estimation. Int. J. Robot. Res. 2020, 39, 402–430. [Google Scholar] [CrossRef]
- Mao, J.; Lian, J.; Hu, X. Strapdown Inertial Navigation Algorithms Based on Lie Group. J. Navigat. 2017, 70, 165–183. [Google Scholar] [CrossRef]
- Tang, H.; Xu, J.; Chang, L.; Shi, W.; He, H. Invariant Error-based Integrated Solution for SINS/DVL in Earth Frame: Extension and Comparison. IEEE Trans. Instrum. Meas. 2023, 72, 9500617. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, W.-A.; Tang, J.; Sun, H.; Shi, L. A Nonlinear Filter for Pose Estimation Based on Fast Unscented Transform on Lie Groups. IEEE Robot. Autom. Lett. 2024, 9, 10431–10438. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, C.; You, S.; Hu, J.; Liu, J. SE2(3) Based Extended Kalman Filtering and Smoothing Framework for Inertial-integrated Navigation. arXiv 2021, arXiv:2102.12897. [Google Scholar]
- Chen, X.; Liu, S.; Liu, R.W.; Wu, H.; Han, B.; Zhao, J. Quantifying Arctic Oil Spilling Event Risk by Integrating an Analytic Network Process and Fuzzy Comprehensive Evaluation Model. Ocean Coast. Manag. 2022, 228, 106326. [Google Scholar] [CrossRef]





| Sensor | Index | Parameter | |
|---|---|---|---|
| SINS | Gyroscope | dynamic range | |
| drift bias | |||
| random noise | |||
| Accelerometer | dynamic range | ||
| Drift bias | |||
| random noise | |||
| Date Update rate | |||
| DVL | Scale factor error | ||
| DVL random noise | |||
| Date update rate | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; He, F.; Chang, L. A Nonlinear Filter Based on Fast Unscented Transformation with Lie Group State Representation for SINS/DVL Integration. J. Mar. Sci. Eng. 2025, 13, 1682. https://doi.org/10.3390/jmse13091682
Li P, He F, Chang L. A Nonlinear Filter Based on Fast Unscented Transformation with Lie Group State Representation for SINS/DVL Integration. Journal of Marine Science and Engineering. 2025; 13(9):1682. https://doi.org/10.3390/jmse13091682
Chicago/Turabian StyleLi, Pinglan, Fang He, and Lubin Chang. 2025. "A Nonlinear Filter Based on Fast Unscented Transformation with Lie Group State Representation for SINS/DVL Integration" Journal of Marine Science and Engineering 13, no. 9: 1682. https://doi.org/10.3390/jmse13091682
APA StyleLi, P., He, F., & Chang, L. (2025). A Nonlinear Filter Based on Fast Unscented Transformation with Lie Group State Representation for SINS/DVL Integration. Journal of Marine Science and Engineering, 13(9), 1682. https://doi.org/10.3390/jmse13091682






