The Extremal Value Analysis of Sea Level in the Gulf of Cádiz and Alborán Sea: A New Methodology and the Resilience of Critical Infrastructures

Abstract

Rising sea levels and increasing storm wave heights are two clear indicators of climate change affecting coastal environments worldwide. Coastal cities and infrastructure are particularly vulnerable to these hazards, highlighting the need for accurate predictions and effective adaptation and resilience strategies to protect human lives and economic activities. This study focuses on the Andalusia coast of southern Spain, from Cádiz to Almería, analyzing twelve years of sea level and wave height records using an Extreme Value Analysis. A key challenge lies in selecting the most suitable statistical distribution for long-term predictions. To address this, we propose a modified application of the Cramér–Rao Lower Bound and compare it with the Akaike Information Criteria and the Bayesian Information Criteria. Our results indicate that sea level extremes generally follow a Gumbel distribution, while wave height extremes align more closely with the Fisher–Tippett I distribution. Additionally, a high-resolution digital elevation model of the Navantia Puerto Real shipyard, generated with LiDAR scanning, was used to identify flood-prone areas and assess potential operational impacts. This approach allows for the development of practical recommendations for enhancing infrastructure resilience. The main contribution of this work includes the estimation of extreme regimes for sea level and wave stations, a novel and more efficient application of the Cramér–Rao Lower Bound, a comparative analysis with Bayesian criteria, and providing recommendations to improve the resilience of shipyard operations.

1. Introduction

Coastal systems worldwide face significant threats from erosion and flooding caused by storm surges and rising sea levels [1]. These hazards are projected to intensify in the coming decades as a consequence of climate change [2,3,4,5], posing severe risks to ecosystems, urban settlements, infrastructure, and economic activities [6].

The maritime economy depends on a range of activities that manage and protect the ocean. Rising sea levels and increasingly intense meteorological events are direct consequences of climate change [5]. From an oceanographic perspective, these phenomena result in higher wind waves occurring over a rising sea level. Coastal areas are the most vulnerable and stressed by this combination of factors. Collaborative efforts are urgent among governments, academia, and social and economic stakeholders to develop adaptation and resilience strategies that safeguard and promote the sustainable use of coastal regions.

On one hand, ports are among the most critical infrastructures exposed to these hazards. Ports serve as major hubs for international trade and are particularly sensitive to extreme water levels, which can compromise docking operations, flood protective barriers, and damage equipment [7,8,9,10]. Notable adaptation initiatives have been developed for New York [11,12] and London [13], while in Spain, the Port Authority of the Balearic Islands has led pioneering efforts [14]. Undoubtedly, there are numerous policy challenges associated with implementing effective resilience strategies in the port sector and the maritime industry [15,16].

On the other hand, shipyards are equally strategic, supporting ship construction, repair, and maintenance. Often located in low-lying coastal zones, they are highly vulnerable to sea level rise and storm-induced flooding. The Navantia shipyard in Puerto Real (Cádiz) is one of the most important shipbuilding facilities in southern Spain. Spanning more than one million square meters, it has the capacity to construct large bulk carriers (up to one million deadweight tons) in a privileged location. It is equipped with Europe’s widest dry dock (500 m long and 100 m wide), cranes capable of lifting 600 tons (190 m high), highly specialized workshops, and a robust surrounding industry (see [17] and https://www.navantia.es/ accesed on 1 July 2025). Nevertheless, the entire site contains a high concentration of critical infrastructure and is exposed to risks from storm surges, high tides, and long-term sea level rise.

The Extreme Value Analysis (EVA) is a fundamental tool for estimating long-term maximum sea levels and wave heights, aiding in the design of coastal defenses and adaptation strategies. According to [18], EVA was originally introduced by Fisher and Tippett in 1928 [19], with subsequent contributions from Fréchet [20] and Gumbel [21]. Fréchet established two of the probability density functions used in EVA, and Gumbel advanced the field by codifying and systematizing EVA methods. Three main distributions are typically considered in EVA: Fisher–Tippett I, Fisher–Tippett II (Fréchet), and Gumbel. These will be detailed in Section 3.1.

Beyond the mathematical assessments of goodness of fit, two open questions remain. The first concerns identifying the most appropriate distribution for long-term projections, and the second relates to the physical reliability of estimating the parameters of extreme value distributions for a given model. Although some criteria exist to evaluate whether parameter estimates are plausible, the theoretical and numerical complexities involved are substantial. Among these, the three most easily implemented criteria are the Cramér–Rao Lower Bound (CRLB), the Akaike Information Criterion, and the Bayesian Information Criterion (BIC).

The CRLB was initially derived by [22], with its proof detailed in [23]; it was also independently obtained by [20,24]. The theorem states that if the estimation error of a parameter in a model attains its CRLB, then the estimator exists and can be both unbiased and of minimum variance. Conversely, if this bound is not met, the estimator is unreliable, and the model may be physically implausible despite the mathematical validity of the solution. Deriving the CRLB for model parameters provides an important link between statistical estimation and physical or engineering principles. The correct application of the CRLB involves computing the norm of the difference between the variance of the estimators and their respective CRLBs. The AIC was derived by Akaike [25], and it has been applied in many fields with many recommendations [26,27]. The BIC was derived by Schwarz [28], with the same applications as the AIC. While the AIC and BIC test the feasibility of a whole model, the CRLB tests every parameter. However, the AIC and BIC can always be computed, but not all models support a CRLB [29].

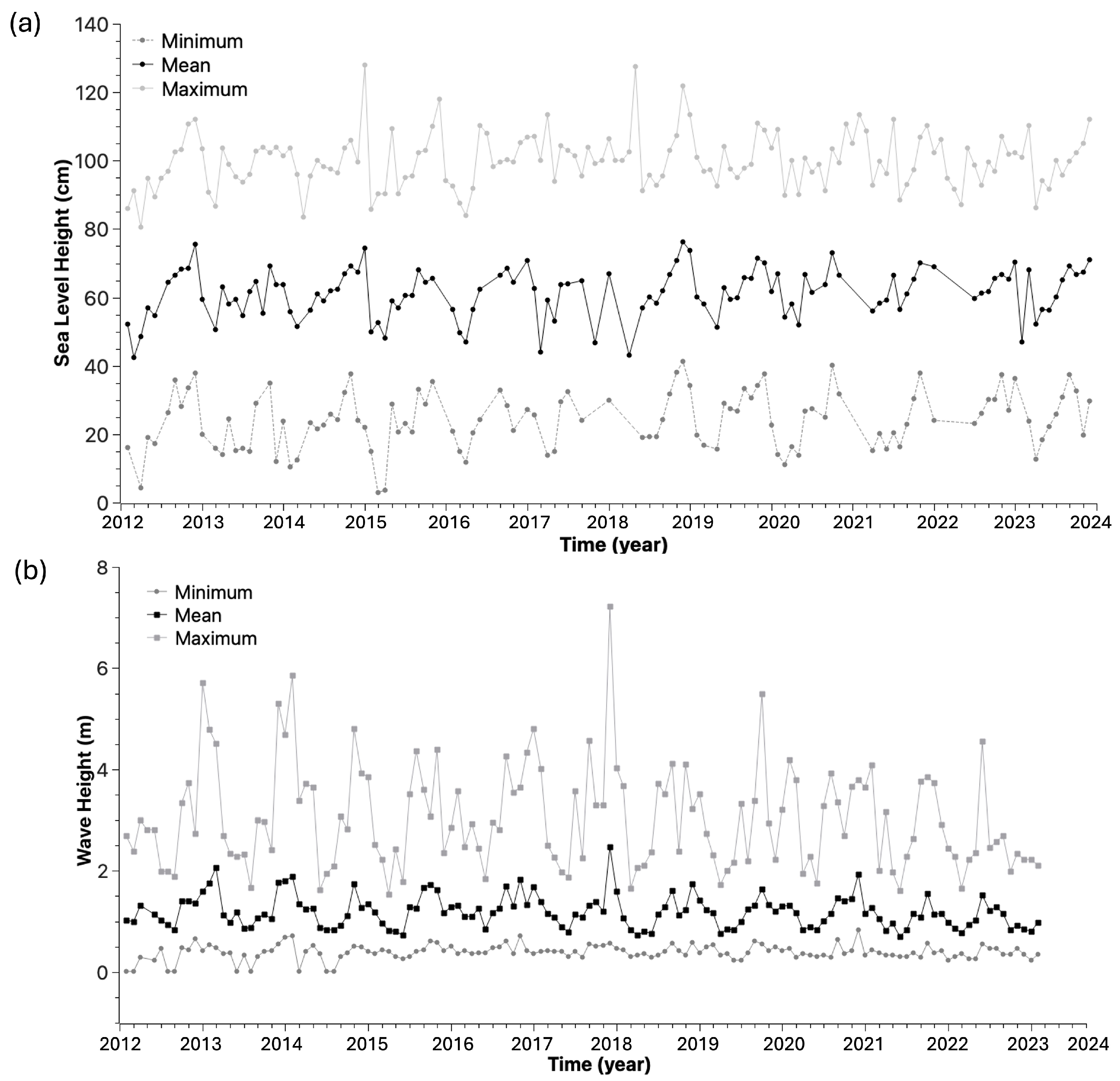
This study investigates the risk of sea level rise and extreme waves affecting ports and shipyards along the Gulf of Cádiz and the Alborán Sea on the Spanish coasts, focusing on the return periods of 10, 25, 50, 75, and 100 years. We analyze time series sea level stations in Cádiz, Tarifa, Málaga, and Almería, as well as data from offshore wave buoys (Figure 1). The sea level station at Cádiz port is operated by the Instituto Español de Oceanografía, and the other stations are managed by Puertos del Estado.

After conducting the EVA and computing the associated risk levels, the results were mapped onto a high-resolution digital elevation model developed by the authors using a 3D LiDAR scanner for the Navantia Puerto Real, the most significant shipyard in southern Spain. This model highlights the most vulnerable areas to flooding caused by sea level rise and storm surges, enabling the proposal of countermeasures aimed at extending the operational life of the shipyard in the face of rising sea levels.

The main contributions and findings of this study include: (i) the Extreme Value Analysis of sea level and wave heights; (ii) the derivation and computation of the CRLB, AIC, and BIC for the relevant models and parameters; (iii) the prediction of extreme values for different return periods based on physically plausible extreme value distributions; and (iv) the identification of potentially flooded areas within the Navantia Puerto Real shipyard, along with strategic recommendations for risk mitigation.

2. Study Area and Data

2.1. Study Area

The study area comprises the southern Spanish coastline along the Gulf of Cádiz and the Alborán Sea, extending from Cádiz to Almería (Figure 1). This region includes several major urban centers such as Cádiz, Málaga, and Almería, as well as highly developed tourist destinations like Benalmádena and Marbella, which experience significant seasonal population fluctuations [30,31]. The area also hosts two of Spain’s busiest ports: Algeciras—located near the Tarifa sea level station—and Málaga, both of which support large-scale commercial shipping operations. Additionally, the Navantia shipyard near Cádiz city is one of the most important industrial facilities in the region, specializing in ship construction and repairs.

The coastal morphology is strongly influenced by tidal and wind-driven processes. The Strait of Gibraltar acts as a natural hydrodynamic barrier, creating distinct tidal regimes in the study area. In the Gulf of Cádiz, tidal ranges reach approximately 2 m, decreasing to around 1 m at Tarifa, and less than 0.5 m near Almería in the Mediterranean Sea [32].

Wave dynamics are primarily controlled by fetch length and wind intensity. Persistent easterly and westerly winds generate significant swells in both the Gulf of Cádiz and the Alborán Sea. Offshore buoys of Wave Analysis and Numerical Assessments (WANA nodes, or WN) indicate that Cádiz is predominantly exposed to northeastward swells, while the Almería station experiences westward swells due to its more sheltered Mediterranean setting.

This combination of high population density, intense maritime activity, and increasing sea levels and wave extremes makes the region particularly vulnerable to coastal flooding and storm impacts, highlighting the need for accurate hazard assessments and resilient infrastructure planning.

2.2. Data Sets

Two main sources of oceanographic data were used in this study: an hourly time series of the sea level taken in the ports of Cádiz, Tarifa, Málaga, and Almería and wave heights from the wave nodes in the Gulf of Cádiz and Alborán Sea (Figure 1). The hourly time series of wave height and sea level data were kindly provided by Puertos del Estado (Official web: http://www.puertos.es, accessed 28 January 2025), except for the Cádiz station, which was obtained from Instituto Hidrográfico de la Marina (Official web: http://armada.defensa.gob.es, accessed 28 January 2025) and Instituto Español de Oceanografía (Official web: https://www.ieo.es/es/, accessed 28 January 2025).

Their geographic coordinates and the length of the corresponding time series in months are shown in

Table 1. (a): Geographical coordinates, initial and ending date, and number of months for the sea level stations. SLS stands for sea level station. (b): Geographical coordinates, initial and ending date, depth of installation, and number of available months for the wave nodes (WN).

Notation	Station	Latitude (Deg)	Longitude (Deg)	Initial Date	Ending Date	Depth (m)	N
(a)
SLS-T	Tarifa	36.01 N	5.60 W	1 January 2012	1 December 2023		144
SLS-M	Málaga	36.71 N	4.42 W	1 January 2012	1 December 2023		144
SLS-A	Almería	36.83 N	2.48 W	1 January 2012	1 December 2023		144
SLS-C	Cádiz	36.54 N	6.31 W	1 January 1967	1 December 2023		692
(b)
WN-AM	Almería	36.57 N	2.24 W	1 January 2012	1 December 2023	536	144
WN-M	Málaga	36.67 N	4.42 W	1 January 2012	1 December 2023	15	144
WN-A	Alborán	36.27 N	5.03 W	1 January 1997	1 December 2006	530	108
WN-C	Cádiz	36.49 N	6.96 W	1 January 2012	1 December 2023	450	144

a for the sea level stations and Table 1b for the wave nodes. Data series lengths vary by station. The Cádiz sea level station provides the longest record, spanning more than 50 years (1967–2023), while the other stations offer consistent 12-year datasets (2012–2023). Wave height records from the wave buoys cover periods ranging from 9 to 12 years, depending on the site. All measurements are referenced to the Spanish National Geodetic Network.

Figure 2 illustrates the time series of maximum monthly values for the sea level at the Málaga port (Figure 2a) and wave height at the Cádiz wave node (Figure 2b). In both cases, black lines represent the monthly mean values, and light gray lines represent the monthly maxima and dark gray the monthly minimum. The almost 8 m height wave (Figure 2b) corresponds to a very harsh sea storm in winter 2017.

2.3. LiDAR Digital Elevation Model

A high-resolution digital elevation model of the Navantia Puerto Real shipyard was obtained using a LiGrip H120 mobile LiDAR scanner by Green Valley International. This device is equipped with Simultaneous Localization and Mapping (SLAM) technology, a 360° field-of-view camera, and a scanning rate of 320,000 points per second, with an effective range of up to 120 m and a vertical accuracy of ±1 cm.

Data collection was performed on-site by walking through the facility in 10–15 min intervals with the scanner carried in a backpack configuration, supported by external batteries. Measurements were directly georeferenced using multiple GNSS constellations such as GPS, BDS, GLONASS, Galileo, and QZSS (product specifications: https://www.greenvalleyintl.com/LiGripH120/, accessed 13 February 2025). Post-processing of the point cloud was carried out using the proprietary software provided with the scanner to remove noise and refine the model. The resulting DEM, referenced to the Spanish National Geodetic Network and mean sea level, provides detailed topographic information for assessing flood-prone areas within the shipyard. Topographic survey validation was not performed, but the LiDAR data resolution is sufficient for preliminary flood risk analysis.

3. Numerical Methods

3.1. Extreme Value Distributions

According to [33], the three distributions typically used for Extreme Value Analysis (EVA) in Physical Oceanography and Coastal Engineering are as follows: Fisher–Tippett I (FTI), Fisher–Tippett II (also known as Fréchet, FTII), and the upper Gumbel distribution (G or Type III). These distributions describe the statistical behavior of extreme values for a given data set. The FTI is expressed as follows:

$$p\left(X\right)=Exp\left(-Exp\left({\displaystyle \frac{X-\epsilon }{\theta }}\right)\right)$$

(1)

where ε is called the location parameter, and θ is called the scale parameter.

The FTII is given by the following:

$$p\left(X\right)=Exp\left({-\left({\displaystyle \frac{X}{\theta }}\right)}^{-\alpha }\right)$$

(2)

where α is called the shape parameter.

Finally, the G distribution is expressed as follows:

$$p\left(X\right)=1-Exp\left(-{\left({\displaystyle \frac{X-\epsilon }{\theta }}\right)}^{\alpha }\right)$$

(3)

In all cases, $X$ represents the variable of interest (sea level or wave height), and $p\left(X\right)$ is the cumulative probability, read as $p\left(X\right)<\mathrm{x}$. There is no need to solve non-linear fitting problems, as the three equations above can be easily reduced to a straight-line form by taking the natural logarithm twice, as follows:

$$X=X; Y=ln (-ln (1-p\left(X\right)\left)\right)$$

(4)

$$X=ln\left(X\right); Y=ln(-ln(1-p\left(X\right)\left)\right)$$

(5)

where Equation (4) is the transformation of variables for the FTI (Equation (1)) and Equation (5)) is for the FTII (Equation (2)) and Type III (Equation (3)). The inverse transformation requires taking the exponentials and equations twice. These distributions are often referred to as “double exponential” functions. Although there are several formulations and methods for the fitting of the EVA distributions [34], the authors have used the usual method in coastal engineering.

The EVA procedure involves the following steps [35]: (i) isolate the monthly maximum values of the time series, obtaining N values; (ii) sort these values in decreasing order; (iii) assign a probability using the Gumbel formula, n/(N + 1), n being the ordinal; (iv) transform the variables according to Equation (4) or Equation (5) and perform a linear fit; and (iv) select a turnover time, and compute the sea level or wave height by inverting the transformations of Equation (4) or Equation (5).

3.2. Statistical Criteria for Model Election

Choosing the most appropriate distribution for EVA is not straightforward. Several statistical criteria are used to assess whether the parameter estimates are physically meaningful and which model provides the best fit. This study employs three criteria: the Cramér–Rao Lower Bound (CRLB), the Akaike Information Criterion (AIC), and the Bayesian Information Criterion (BIC).

3.2.1. The Cramér–Rao Lower Bound

Following [22,23,24,29], parameter estimation is a common challenge in applied sciences. Typically, one has a data set and a theoretical model. The data follows a usually unknown probability density function, and it is assumed that the residuals are Gaussian.

Ideally, parameter estimators should be MVU (Minimum Variance Unbiased) but achieving this is often difficult. A practical alternative is to compute the minimum possible variance that an estimator can have while remaining reliable. Several methods exist for this purpose, one of which is the Cramér–Rao Lower Bound (CRLB). The CRLB provides the theoretical minimum variance that any unbiased estimator can achieve. If an estimator has a variance lower than the CRLB, it implies that the estimator is either non-existent or physically impossible, even if the mathematical result appears excellent.

For a simple linear model subject to white noise:

$$y\left(n\right)=A+B·x\left(n\right)+w\left(n\right),n=0,\dots ,N-1$$

(6)

where $w\left(n\right)$ is Gaussian white noise, with the variance ${\sigma }_w^2$ assumed known. The likelihood function of the residuals is as follows:

$$p\left(\underset{\_}{y};\underset{\_}{\theta }\right)={\displaystyle \frac{1}{{\left(2\pi {\sigma }^2\right)}^{N/2}}}Exp\left(-{\displaystyle \frac{1}{{\sigma }^2}}{\sum }_{n=0}^{N-1}{\left(y\left(n\right)-A-B·x\left(n\right)\right)}^2\right)$$

(7)

where $\underset{\_}{\theta }=(A,B)$ is the vector of the model parameter, and $\underset{\_}{y}$ is the data vector. The Fisher information matrix is given by the following:

$$I\left(\underset{\_}{\theta }\right)=-E\left[{\displaystyle \frac{{\partial }^2\ln p\left(\underset{\_}{y};\underset{\_}{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right]={\displaystyle \frac{N}{{\sigma }^2}}\left(\begin{array}{cc}1& \overline{x}\\ \overline{x}& \sum x_n^2\end{array}\right)$$

(8)

where E[·] denotes the mathematical expectation, and the overline indicates the average value.

According to the Cramér–Rao theorem, the variance satisfies $var(\underset{\_}{\widehat{\theta }})\ge {\displaystyle \frac{1}{I\left(\underset{\_}{\theta }\right)}}$. Inverting the Fisher information matrix gives

$$I^{-1}\left(\underset{\_}{\theta }\right)={\displaystyle \frac{{\sigma }^2}{N·∆}}\left(\begin{array}{cc}1& \sum x\\ \sum x& \sum x_n^2\end{array}\right)$$

(9)

with $∆=\overline{\sum x_n^2}-(\sum x{)}^2$. The CRLB for the estimators of the intercept A and the slope B are the diagonal elements:

$$var(\widehat{A})\ge {\displaystyle \frac{{\sigma }^2}{N·∆}}$$

(10)

$$var(\widehat{B})\ge {\displaystyle \frac{{\sigma }^2}{N}}·{\displaystyle \frac{\sum x^2}{∆}}$$

(11)

Therefore, for the linear model in Equation (6), and following the Cramér–Rao theorem [28], the variances of the estimators for parameters A and B must be greater than or equal to the corresponding lower bounds in Equations (10) and (11) to be physically meaningful.

Some additional considerations are necessary. Least squares estimation is commonly used, but models that do not meet the CRLB should be interpreted with caution. If Equations (10) and (11) are not satisfied, the CRLB does not apply. However, the estimators may still be of minimum variance and unbiased [29], and the model should be used with care. If multiple models are tested and one shows a significantly higher correlation or determination coefficient than the others, computing the CRLB may not be necessary.

3.2.2. The Akaike and the Bayesian Information Criterion

Two popular statistical criteria for selecting the best model among several candidates are also based on the principle of Maximum Likelihood: the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Both begin with a functional model, linear or not. In this study, the model becomes linear after the variable transformation described in Equations (4) and (5). The likelihood function is constructed as Equation (7), assuming Gaussian residuals, and its natural logarithm is then computed. The expressions of the AIC and BIC for the linear model of Equation (6) are [35]

$$AIC=2k+2·\mathrm{l}\mathrm{n} \left(L\right)$$

(12)

$$BIC=k·ln\left(n\right)+2·ln \left(L\right)$$

(13)

where k is the number of parameters in the model, n is the number of data points, and L is the maximized value of the likelihood function. The difference between AIC and BIC lies in how each criterion penalizes model complexity and sample size. The best model is the one with the lowest AIC or BIC value. In the case of the linear model of Equation (6), it turns out that $L={\sigma }^2$ [34].

4. Results and Discussion

4.1. Extreme Value Analysis of Monthly Maxima

The time series of sea level and wave height measurements were processed following the methodology described in Section 3.1. The resulting parameter estimates for the three probability density functions (PDFs)—Fisher–Tippett I (FTI), Fisher–Tippett II (FTII), and Gumbel (G)—are summarized in

Table 2. Results of the EVA. Sea level station name, extreme PDF, correlation (R), estimation of the intercept, standard deviation of the intercept estimation, slope, and standard deviation of the slope estimation are reported. The intercept is always dimensionless, while the slope is expressed in units of 1/m or 1/cm, depending on the units of the observable for FTI. For FTII and G, the slope is expressed in 1/ln(m) or 1/ln(cm), again depending on the units of the observable. The corresponding standard deviations have the same units as their associated estimators.

Station	PDF	R	Intercept	σ Intercept	Slope	σ Slope
SLS-A	FTI	0.9830	−9.7664	0.1648	0.1549	0.0020
	FTII	0.9637	−41.685	0.9928	10.0750	0.2366
	G	0.9806	−43.552	0.7295	10.2510	0.1739
SLS-M	FTI	0.9927	−13.411	0.1435	0.1333	0.0014
	FTII	0.9860	−65.041	0.9300	14.1130	0.2000
	G	0.9579	−64.300	1.6025	13.7110	0.3447
SLA-T	FTI	0.9900	−20.048	0.2467	0.1402	0.0017
	FTII	0.9848	−102.490	1.5254	20.6560	0.3057
	G	0.9584	−100.850	2.5060	20.1020	0.5023
SLS-C	FTI	0.9910	−29.877	0.1466	8.1130	0.0382
	FTII	0.9870	−40.984	0.2348	31.4220	0.1748
	G	0.9587	−4.8231	0.2900	1.2895	0.0804

and

Table 3. Results of the EVA. WANA node name, extreme PDF, correlation (R), estimation of the intercept, standard deviation of the intercept estimation, slope, and standard deviation of the slope estimation are reported. The intercept is dimensionless, while the slope is expressed in units of 1/m or 1/cm, depending on the units of the observable for FTI. For FTII and G, the slope is expressed in 1/ln(m) or 1/ln(cm), again depending on the units of the observable. The corresponding standard deviations have the same units as their associated estimators.

Station	PDF	R	Intercept	σ Intercept	Slope	σ Slope
WN-AB	FTI	0.9599	−1.7733	0.0583	0.74694	0.0166
	FTII	0.9909	−2.5346	0.0345	2.9612	0.0307
	G	0.9067	−3.4031	0.1081	2.7096	0.0961
WN-A	FTI	0.9846	−3.2409	0.0621	0.67463	0.0105
	FTII	0.9821	−6.3396	0.1177	4.0951	0.0688
	G	0.9564	−7.2855	0.1826	3.9879	0.1068
WN-C	FTI	0.9945	−2.8859	0.0346	0.66297	0.0063
	FTII	0.9777	−5.0303	0.1108	3.5153	0.0681
	G	0.9587	−6.0472	0.1500	3.4472	0.0922
WN-M	FTI	0.9974	−10.3380	0.0685	1.9755	0.0123
	FTII	0.9921	−18.3900	0.2054	11.135	0.1204
	G	0.9432	−18.5830	0.5453	10.586	0.3197

for sea level stations (SLS) and WANA nodes (WN), respectively. Across all locations, correlation coefficients are high (typically above 0.95), and the standard errors of parameter estimates are one to three orders of magnitude smaller than the parameter values themselves. At first glance, this suggests that all three distributions could provide reliable models for predicting extreme values.

However, a closer examination reveals inconsistencies that make model selection non-trivial. For example, at the Almería sea level station, correlations are 0.9830 (FTI), 0.9637 (FTII), and 0.9806 (G). Based on correlation alone, the FTI or Gumbel distributions might appear preferable. Yet, when considering parameter errors and their physical plausibility, FTII could be equally valid. This highlights the need for more robust selection criteria beyond linear fit quality.

Similarly, for wave height data (Table 3), several stations yield very high correlations for multiple distributions with low deviation. This complicates the decision of which model to adopt for long-term risk projections.

The questions raised earlier remain pertinent: should the analyst automatically select the distribution with the highest correlation? Or could an alternative criterion be more appropriate? In this context, it is essential to consider practical tools for deciding which distribution should be used to compute long-term risk levels. The CRLB, the AIC, and the BIC play a key role here.

4.2. Application of Selection Criteria to Sea Level Data

The Cramér–Rao Lower Bound (CRLB) for the parameters of the linear model in Equation (6) was derived in Section 3.2, along with the AIC and the BIC for the same model. The model was adapted by treating the x-data as a numerical variable, following the EVA methodology. The application of the CRLB, AIC, and BIC is straightforward once the relevant quantities in Equations (10)–(13) are properly identified. Specifically, N represents the number of data pairs in each analysis; the white noise variance ${\sigma }^2$ corresponds to the variance of the residuals obtained from the linear fit; and the variance of the estimators is calculated by squaring their standard deviations, as listed in Table 2.

The CRLBs for the parameters of all regressions, along with the AIC and BIC values across the three sea level distributions, are presented in

Table 4. CRLB for the EVA of maximum sea level. “Station” refers to the sea level station, “N” is the number of data (months), and PDF indicates the type of distribution. ${\sigma }^2$ is the variance of the residuals from the regressions. ${\sigma }_A^2$ is the variance of the intercept, and “CRLB(A)” is the Cramér–Rao Lower Bound for the estimator of the intercept. ${\sigma }_B^2$ is the variance of the slope, and “CRLB(B)” is the Cramér–Rao Lower Bound for the slope. The column ||${\sigma }_B^2$-CRLB(B)|| shows the absolute difference, and the AIC and BIC columns report the values of the corresponding criteria, assuming two model parameters. An asterisk (*) marks the distributions that satisfy the corresponding criterion.

Station	N	PDF	${\mathit{\sigma }}^2$	${\mathit{\sigma }}_{\mathit{A}}^2$	CRLB[A]	${\mathit{\sigma }}_{\mathit{B}}^2$	CRLB[B]	||(${\mathit{\sigma }}_{\mathit{B}}^2$-CRLB[B])||	AIC	BIC
SLA-A	141	FTI	0.226	0.0271	3.72 × 10−9	6.02 × 10−6	0.0024	0.0024	−205.70	−204.22
		FTII	0.329	0.9856	5.43 × 10−9	0.0560	0.0035 *	0.0525	−152.75 *	−150.14 *
		G	0.242	0.5321	3.99 × 10−9	0.0302	0.0025 *	0.0277	−196.05	−194.37
SLS_M	144	FTI	0.149	0.0206	6.53 × 10−10	1.25 × 10−5	0.0010	0.0010	−270.15	−264.21
		FTII	0.205	0.8648	8.99 × 10−10	1.71 × 10−5	0.0014	0.0013	−224.20	−218.26
		G	0.354	2.5680	1.56 × 10−9	2.96 × 10−5	0.0025	0.0025	−145.54 *	−139.60 *
SLS-T	144	FTI	0.0609	0.0275	3.89 × 10−10	1.62 × 10−5	0.0012	0.0011	−398.75	−392.81
		FTII	2.3268	0.0275	4.79 × 10−10	1.99 × 10−5	0.0015	0.0015	125.62 *	131.56 *
		G	6.2800	0.0275	7.88 × 10−10	3.27 × 10−5	0.0025	0.0025	268.58	274.52
SLS-C	144	FTI	0.0972	0.0012	3.13 × 10−8	0.0012	2.97 × 10−4 *	0.0009	−331.96	−326.02
		FTII	0.115	0.0123	6.31 × 10−8	0.0024	5.98 × 10−4 *	0.0018	−307.45	−301.51
		G	0.469	0.0225	8.53 × 10−8	0.0032	8.09 × 10−4 *	0.0312	−105.03 *	−99.09 *

. These results clearly show that the optimal distribution is not always the one with the highest correlation (see Table 2). The CRLB highlights that an estimator, while mathematically valid, may not be physically feasible, and the AIC and BIC evaluate the overall quality of the model, not just the fit.

For Almería, both FTII and Gumbel distributions satisfy the CRLB, but only FTII achieves lower AIC and BIC values, suggesting it as the most appropriate choice despite its slightly lower correlation coefficient. For Málaga, none of the distributions fully meet the CRLB conditions (Table 4). Nevertheless, the coefficient of variation, also referenced in Table 2, exhibits the smallest coefficient of variation and lowest AIC and BIC values aligning with both criteria. A similar situation occurs at the Tarifa station with FTII. Conversely, at the Cádiz station, all three distributions conform to the CRLB, making it impossible to select a definitive best fit based solely on this criterion, but the BIC and AIC point to Gumbel as the preferred model.

These results demonstrate that selecting the distribution with the highest correlation coefficient may lead to physically implausible or suboptimal predictions. Incorporating the CRLB, AIC, and BIC improves the reliability of model selection, although some ambiguity may remain when the criteria are inconsistent.

4.3. Application to Wind Waves Data

The same procedure was applied to wave height data from the WANA nodes. Now the values for the computation of the CRLB, AIC, and BIC are taken from Table 3, and the results are presented in

Table 5. CRLB for the EVA of maximum wave heights. “Station” refers to the sea level station; “N” is the number of data points (months); “PDF” indicates the type; ${\sigma }_A^2$ is the variance of the intercept; and “CRLB(A)” is the Cramér–Rao Lower Bound for the estimator of the intercept. ${\sigma }_B^2$ is the variance of the slope, and “CRLB(B)” is the Cramér–Rao Lower Bound for the slope. The column ||${\sigma }_B^2$-CRLB(B)||shows the absolute difference, and the AIC and BIC columns report the values of the corresponding criteria, assuming two model parameters. An asterisk (*) marks the distributions that satisfy the corresponding criterion.

Station	N	PDF	${\mathit{\sigma }}^2$	${\mathit{\sigma }}_{\mathit{A}}^2$	CRLB[A]	${\mathit{\sigma }}_{\mathit{B}}^2$	CRLB[B]	||(${\mathit{\sigma }}_{\mathit{B}}^2$-CRLB[B])||	AIC	BIC
WN-AB	174	FTI	0.347	0.0034	1.51 × 10−6	2.77 × 10−4	0.0032	0.0029	−180.17	−173.85
		FTII	0.167	0.0012	7.25 × 10−7	9.42 × 10−4	0.0016	0.0007	−307.42	−301.10
		G	0.522	0.0117	2.27 × 10−6	0.0092	0.0049 *	0.0043	−109.11 *	−102.80 *
WN-A	132	FTI	0.215	0.0039	3.25 × 10−7	1.10 × 10−4	0.0015	0.0014	−198.90	−193.13
		FTII	0.231	0.0139	3.50 × 10−7	0.0047	0.0016 *	0.0031	−189.42	−183.66
		G	0.359	0.0334	5.43 × 10−7	0.0114	0.0025 *	0.0089	−131.22 *	−124.46 *
WN-C	125	FTI	0.128	0.0012	2.35 × 10−7	3.94 × 10−5	8.95 × 10−4	0.0009	−252.97	−247.31
		FTII	0.258	0.0123	4.74 × 10−7	0.0046	0.0018 *	0.0028	−165.35	−159.69
		G	0.349	0.0225	6.42 × 10−7	0.0085	0.0024 *	0.0061	−127.58 *	−121.93 *
WN-M	138	FTI	0.0893	0.0047	1.46 × 10−7	1.52 × 10−4	6.24 × 10−4 *	0.0005	−329.84	−323.98
		FTII	0.154	0.0422	2.53 × 10−7	0.0145	0.0011 *	0.0134	−254.17	−248.32
		G	0.409	0.2974	6.72 × 10−7	0.1022	0.0029 *	0.0993	−119.38 *	−113.52 *

similarly to the above.

In several cases, more than one distribution meets the CRLB, making the choice ambiguous. However, FTI generally provides the smallest difference between the variance of slope estimators and their CRLB, suggesting it as the most physically robust distribution.

Interestingly, in some cases, Gumbel distributions produce unrealistic extrapolated values despite having high correlations. This reinforces the importance of evaluating physical plausibility, not just statistical fit.

4.4. Predicted Extreme Sea Levels

The CRLB cannot be applied as usual, as in [29], for comparison with the AIC and BIC. While AIC and BIC focus on the model, the CRLB is on each parameter. In this study, the authors propose evaluating the CRLB by considering the distance for the most sensitive parameter, the slope, defined as ||(${\sigma }_B^2$-CRLB[B])||. The preferred distribution is the one with the largest value of this difference. For sea level data, the largest deviation from the CRLB is observed for the Gumbel distribution at the Málaga, Tarifa, and Cádiz stations and for the FTII distribution at Almería. Based on the results in Table 4, which indicate whether each distribution satisfies the CRLB condition, it is evident that selecting an inappropriate distribution can lead to significantly erroneous predictions. According to the AIC and BIC, FTII is selected for Almería and Tarifa, while Gumbel is selected for Málaga and Cádiz.

The computation of risk levels across all distributions provides valuable insight into the consequences of choosing an unsuitable model.

Table 6. Predicted extreme sea levels (cm) for return periods of 10, 25, 50, 75, and 100 years at the different sea level stations.

Station	Period of Return	FTI	FTII	G
SNS-A	10	77.12	53.62	127.13
	25	78.51	52.55	141.42
	50	79.42	51.86	153.28
	75	79.90	51.49	160.66
	100	80.23	51.24	166.11
SNS-M	10	117.35	89.80	154.24
	25	113.66	88.69	164.93
	50	114.52	87.98	173.50
	75	114.98	87.60	178.71
	100	115.29	87.34	182.50
SNS-T	10	154.16	132.41	191.50
	25	156.41	131.28	200.45
	50	156.23	130.57	207.49
	75	156.67	130.18	211.7
	100	156.97	129.92	214.78
SNS-C	10	387.56	350.60	103.13
	25	389.72	348.65	50.58
	50	391.14	347.38	29.53
	75	391.89	346.70	21.56
	100	392.40	346.84	17.24

presents the predicted extreme values for the return periods of 10, 25, 50, 75, and 100 years for sea level. For example, if the FTII distribution is selected for the Almería station (Table 6), it yields nearly flat estimates of approximately 52 cm. The FTI distribution produces similarly flat results, whereas the Gumbel distribution provides more realistic increasing estimates and is therefore the most appropriate. Likewise, at Málaga, both FTI and FTII predict decreasing extreme values, while Gumbel offers more plausible projections. Tarifa shows a similar behavior, while at Cádiz, the FTI distribution produces the best estimates.

It is noteworthy that the AIC and BIC criteria provide correct model selection for Málaga and Cádiz, while the CRLB favors Gumbel for Málaga, Tarifa, and Cádiz. For Almería, none of the criteria correctly identifies the most appropriate distribution, highlighting the limitations of existing selection methods.

4.5. Predicted Extreme Wave Heights

The same criteria were applied to the predictions of extreme wave heights at the WANA nodes (

Table 7. Predicted extreme wave heights (cm) for return periods of 10, 25, 50, 75, and 100 years at the WANA nodes.

Station	Period of Return	FTI	FTII	G
WN-AB	10	447.06	138.69	103.13
	25	470.51	130.73	50.58
	50	485.86	125.76	29.53
	75	494.09	123.18	21.56
	100	499.64	121.47	17.24
WN-A	10	712.52	320.81	2062.20
	25	739.48	307.38	2596.51
	50	755.48	298.89	3090.06
	75	764.59	294.44	3421.01
	100	770.73	291.48	3677.04
WN-C	10	671.51	267.91	2314.61
	25	697.92	254.89	3021.58
	50	715.22	246.71	3695.43
	75	724.49	242.44	4157.02
	100	730.74	239.60	4519.01
WN-M	10	602.58	453.09	909.10
	25	611.45	446.02	991.53
	50	617.25	441.45	1058.71
	75	620.36	439.02	1100.07
	100	622.46	437.39	1130.39

). For example, at the Alborán station (located between Málaga and Tarifa), Table 5 suggests that the Gumbel distribution should be chosen. However, the extreme value predictions presented in Table 7 are inconsistent, indicating that the FTI distribution provides more realist results. This demonstrates that the criterion based on the minimum difference ||(${\sigma }_B^2$-CRLB[B])|| is more reliable than the approaches outlined in Equations (10) and (11).

Our analysis shows that the most appropriate distribution is the one that minimizes this difference. This behavior is observed consistently for the FTI distribution across all WN stations (Table 5). Once again, computing the risk levels for all distributions and return periods proves to be essential for understanding the potential consequences of selecting an unsuitable model. The exact reason why these inconsistencies arise remains unclear and constitutes an important subject for future research.

4.6. Potential Flooded Areas: An Application on Navantia Puerto Real

The authors used a LiDAR 3D scanner to build a digital elevation model (DEM) of the Navantia Puerto Real shipyard. Height data were referenced to the Spanish National Geodetic Network and subsequently to the mean sea level.

Figure 3a shows a modified panoramic Google Maps image highlighting (1) the 500 m long and 100 m wide dry dock equipped with two heavy-duty overhead cranes of 190 m in height; (2) the historical area containing the oldest facilities, including a museum that preserves valuable cultural and industrial heritage; and (3) the auxiliary workshops located along the dock. Figure 3b presents the plan view of the shipyard.

Considering that (i) the inverted barometer effect—caused by a difference of approximately 40 mb in atmospheric pressure—can generate an increase of about 40 cm in the water column [36]; (ii) the highest recorded wave height in nearby ports is approximately 1.80 m [37]; and (iii) spring tides can reach up to 3 m [38], adding these contributions to the predicted sea levels from Table 6 allows for the estimation of potential flood levels. 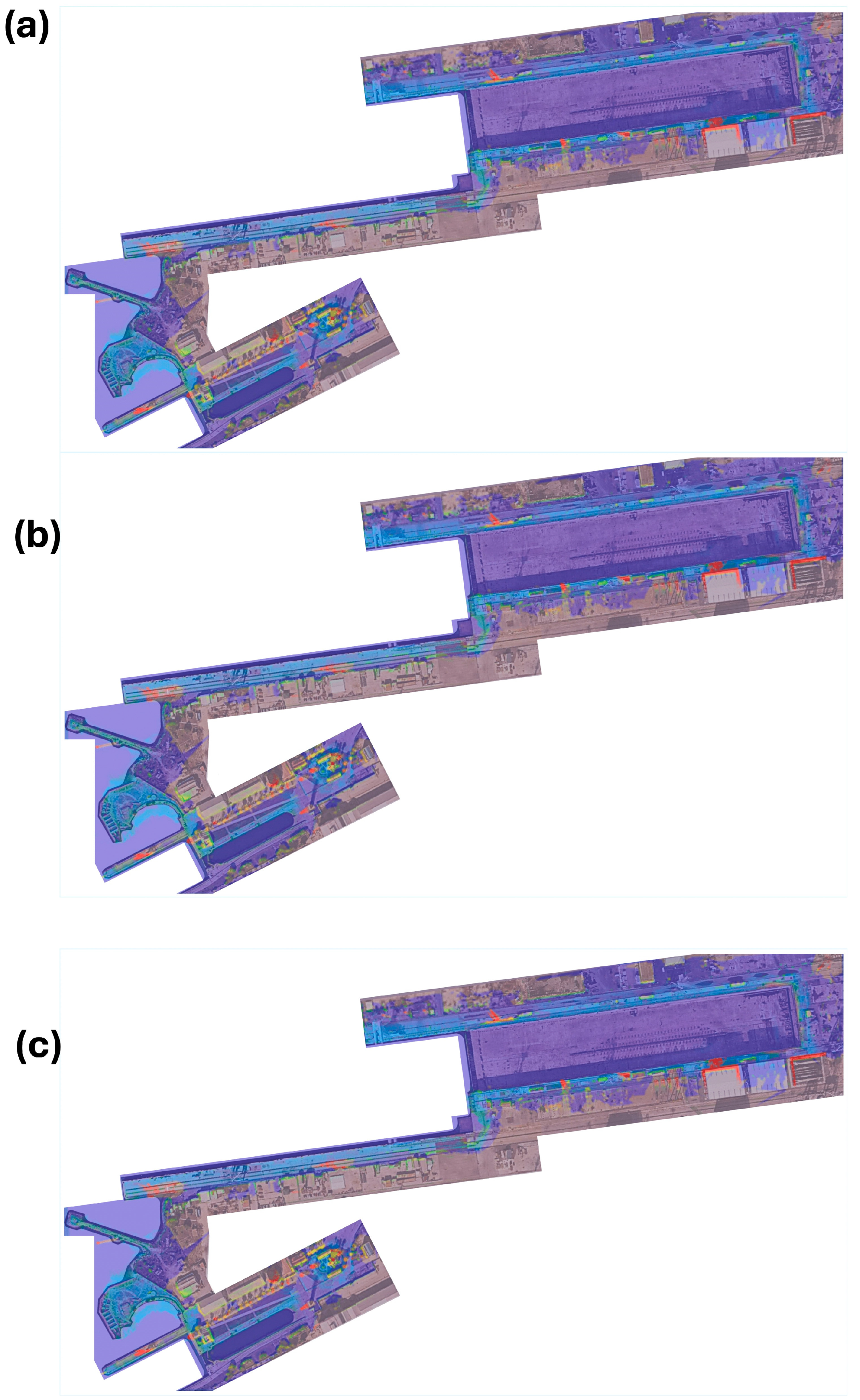Figure 4 illustrates the resulting flooded areas for return periods of 10, 25, and 75 years.

From an operational perspective, the most affected area is the dry dock and its surroundings, where specialized workshops and module assembly facilities are concentrated (Areas 1 and 3, Figure 3 and Figure 4). Flooding in these areas would likely occur within the first 10 years (Figure 4a). Over time, sea level rise would expand the flooded area to approximately 23% of the shipyard’s total surface, also affecting the historical area, which holds significant technological heritage.

To ensure the continuity of shipyard operations in the coming decades, several mitigation measures are proposed. While relocating the entire facility to a non-flood-prone site would eliminate long-term risks, this solution is economically and logistically unfeasible and could lead to client losses. A more practical approach involves the construction of perimeter flood protection walls set back slightly from the pier edge (e.g., 0.2 m). The proposed walls would be approximately 0.5 m high and of similar width, allowing for pedestrian seating while resting on the dock wall and incorporating waterproofing to minimize leaks.

Additionally, a stormwater collection pool should be built to capture overtopping waves, rainfall, or seepage. The pool should be designed to handle a flow rate of at least 60 mm of rainfall over one hour, with reinforced concrete walls and a depth not exceeding 3 m to avoid siphoning risks. A pumping system would discharge collected water back to the sea, powered by the electrical grid with an emergency generator as backup. The cost of constructing the wall, including waterproofing, is estimated at approximately EUR 110 per linear meter. For the pool and pumping system, the estimated cost is about EUR 23,000 per hectare (EUR 15,000 for construction, EUR 5000 for the pump, and EUR 3000 for the generator).

Finally, elevating critical installations, such as generators and electrical systems, to at least + 1.50 m above the current ground level using structural platforms is recommended. This measure is relatively inexpensive given Navantia’s consolidated turnover of approximately EUR 1528 million in 2024 (with ~EUR 584 M from shipbuilding, ~EUR 553 M from repairs, and ~EUR 248 M from offshore wind projects). Considering that mitigation costs are projected to represent only 10–20% of annual profits, the proposed measures are economically feasible while ensuring long-term operational resilience.

5. Conclusions

The long-term analysis of oceanographic variables, such as sea level and wave heights, is a complex task typically addressed through EVA. Several extreme value distributions must be considered, and linear fits often produce very high correlation coefficients and small parameter estimation errors. However, selecting the most appropriate distribution for predicting extremes requires scientific and engineering judgment rather than relying solely on statistical fit quality.

The main contributions of this work can be summarized as follows: (1) The study demonstrates that the distribution with the highest correlation coefficient is not necessarily the most suitable for extreme value predictions; (2) an additional statistical tool is needed to support the automatic identification of the most appropriate extreme value distribution. In this study, the Cramér–Rao Lower Bound (CRLB), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC) have been evaluated; (3) applying the Cramér–Rao Lower Bound (CRLB) in its traditional form does not always lead to conclusive results; instead, the distance between the variance of the estimators and the CRLB threshold offers more insight; (4) discrepancies were observed between the CRLB and the well-established AIC and BIC criteria, indicating that none of them can yet be considered a fully robust method for selecting the optimal distribution; and (5) the methodological analysis of the digital elevation model of the Navantia Puerto Real shipyard has identified its most vulnerable areas, supporting the development of a practical resilience plan. Rather than relocating the entire facility, constructing a flood protection wall with a water collection pool and pumping system appears to be the most feasible solution.

Finally, future work will extend the digital elevation model to include ports, small shipyards, and beaches along the southern Spanish coast (Andalusia), aiming to provide comprehensive risk assessments for rising sea levels and extreme wave events in the region.