Arctic Wave Climate Including Marginal Ice Zone and Future Climate Scenario
Abstract
1. Introduction
2. Methodology
2.1. Study Area
2.2. Models and Data
2.2.1. Winds
2.2.2. Waves
2.2.3. Wave-Ice Interaction Models
2.2.4. Sea Ice
2.2.5. Kappa Statistic
2.2.6. Extreme Value Analysis of Wave Climate Time Series (EVA)
2.2.7. Climate Change and Variability in Extreme Value Analysis
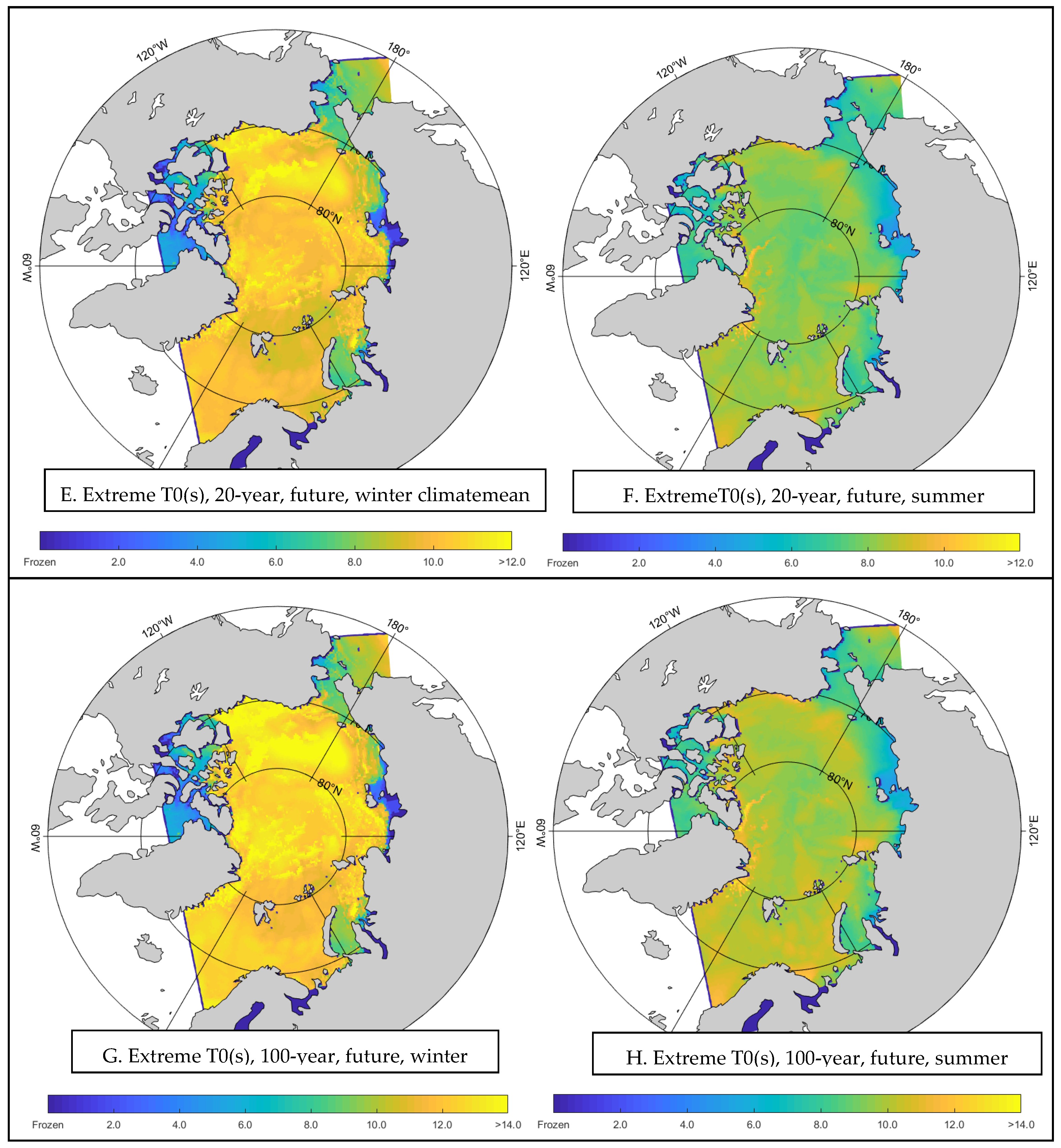
3. Results
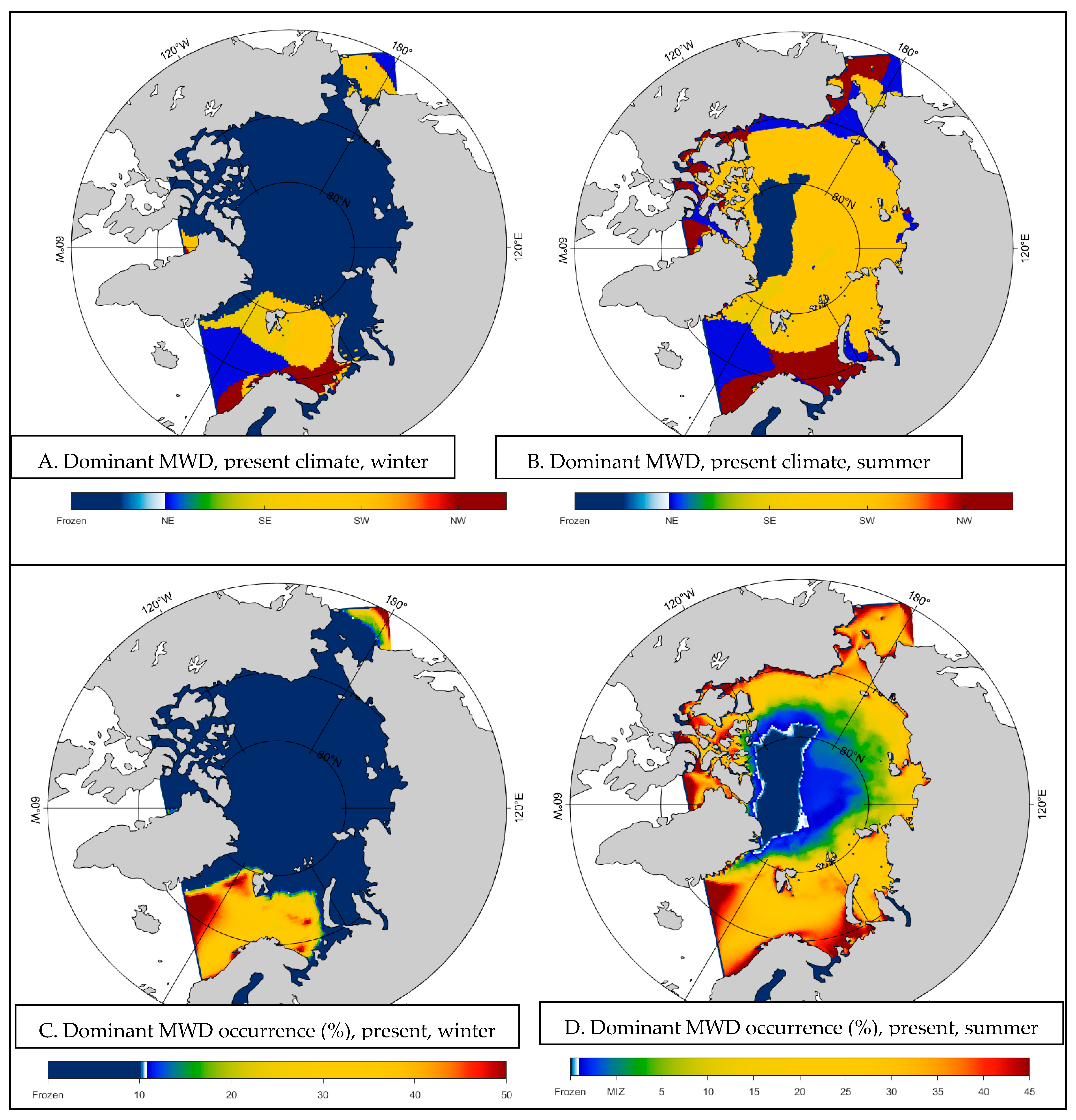
3.1. Spatial-Temporal Similarities Between Models for Wave—Ice Interactions
3.2. Wave Regime Assessment
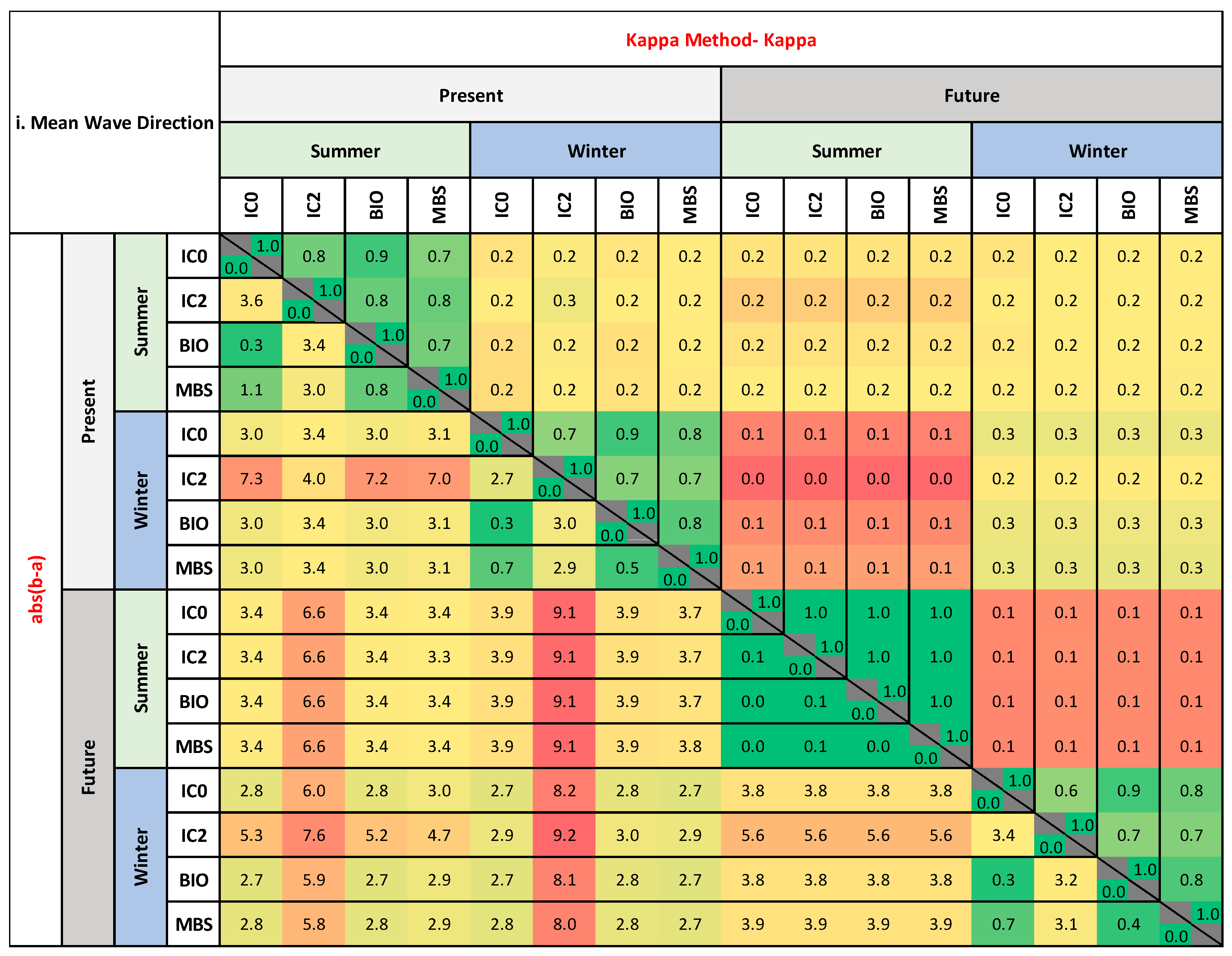
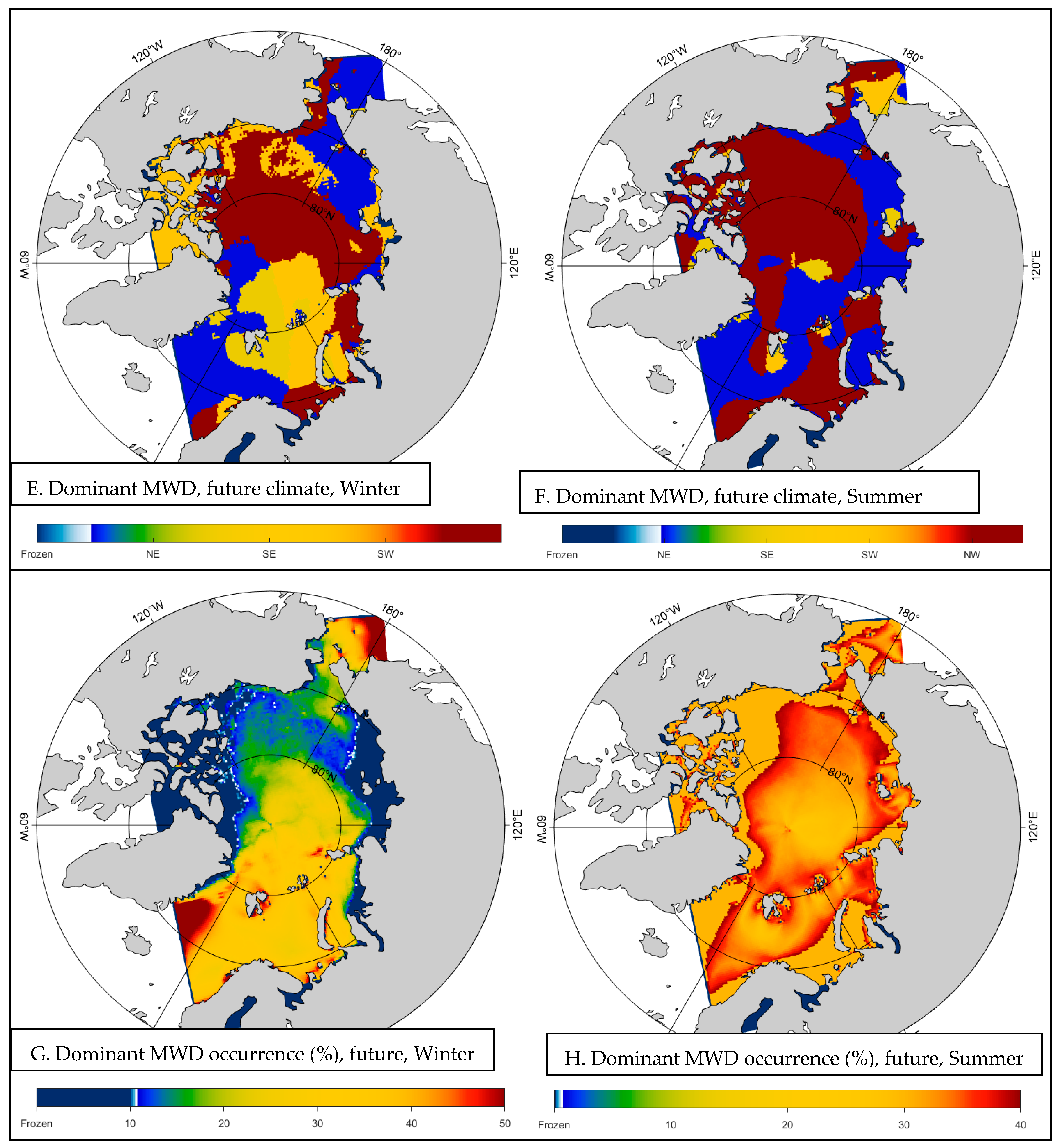
3.2.1. Mean Wave Direction Analysis
- Winter Season
- 2.
- Summer Season
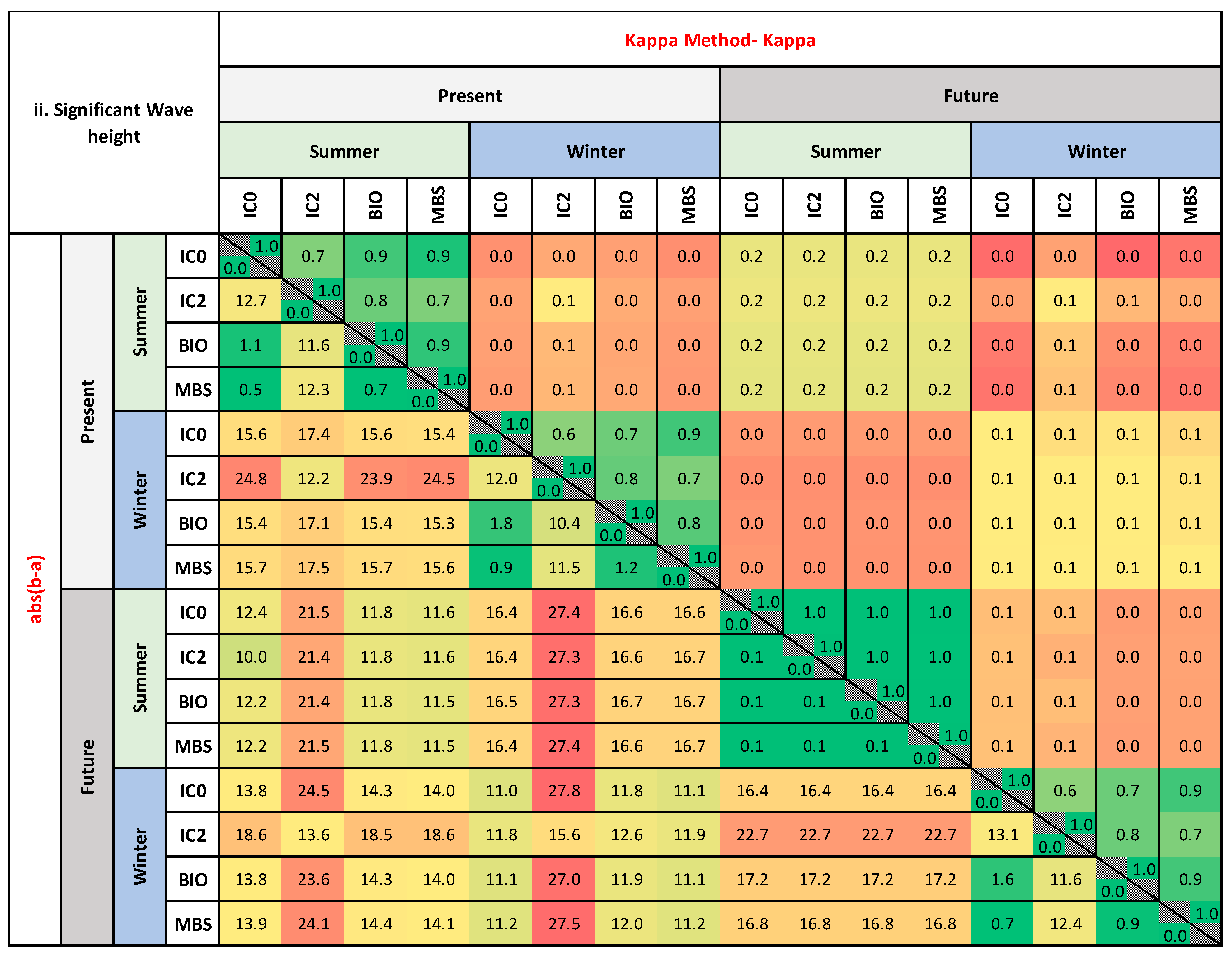
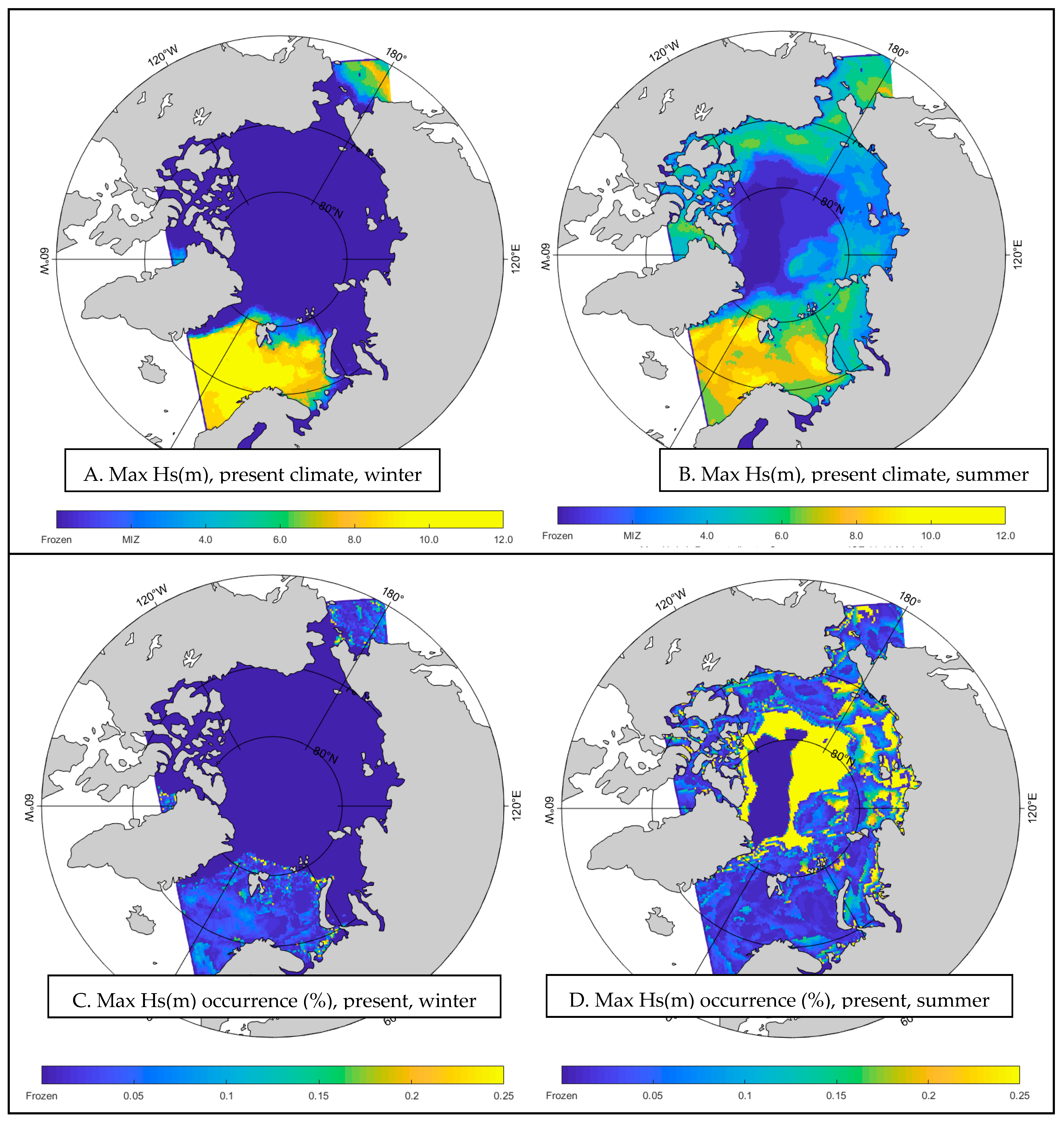
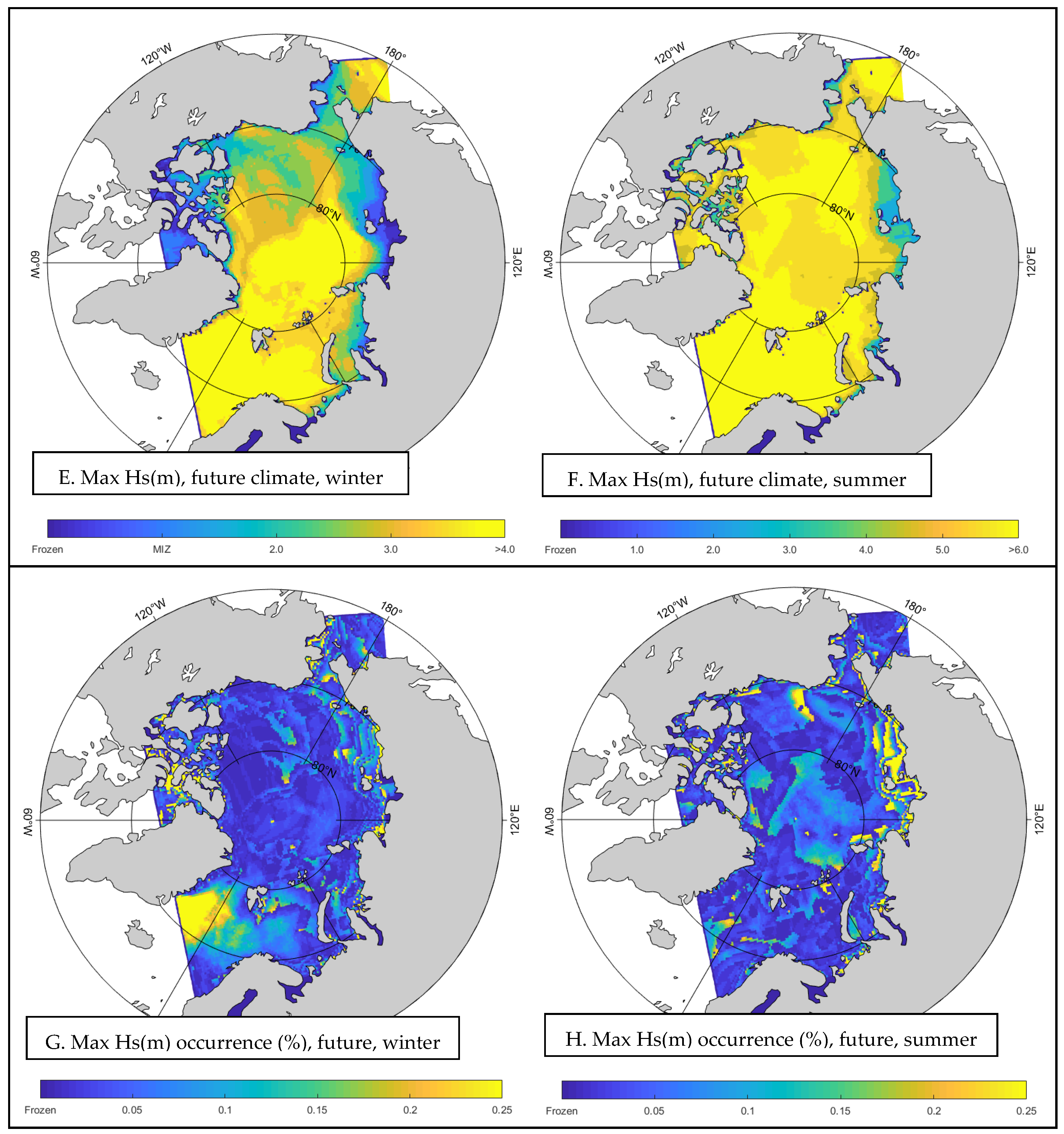
3.2.2. Significant Wave Height Analysis
- Winter Season
- 2.
- Winter Season
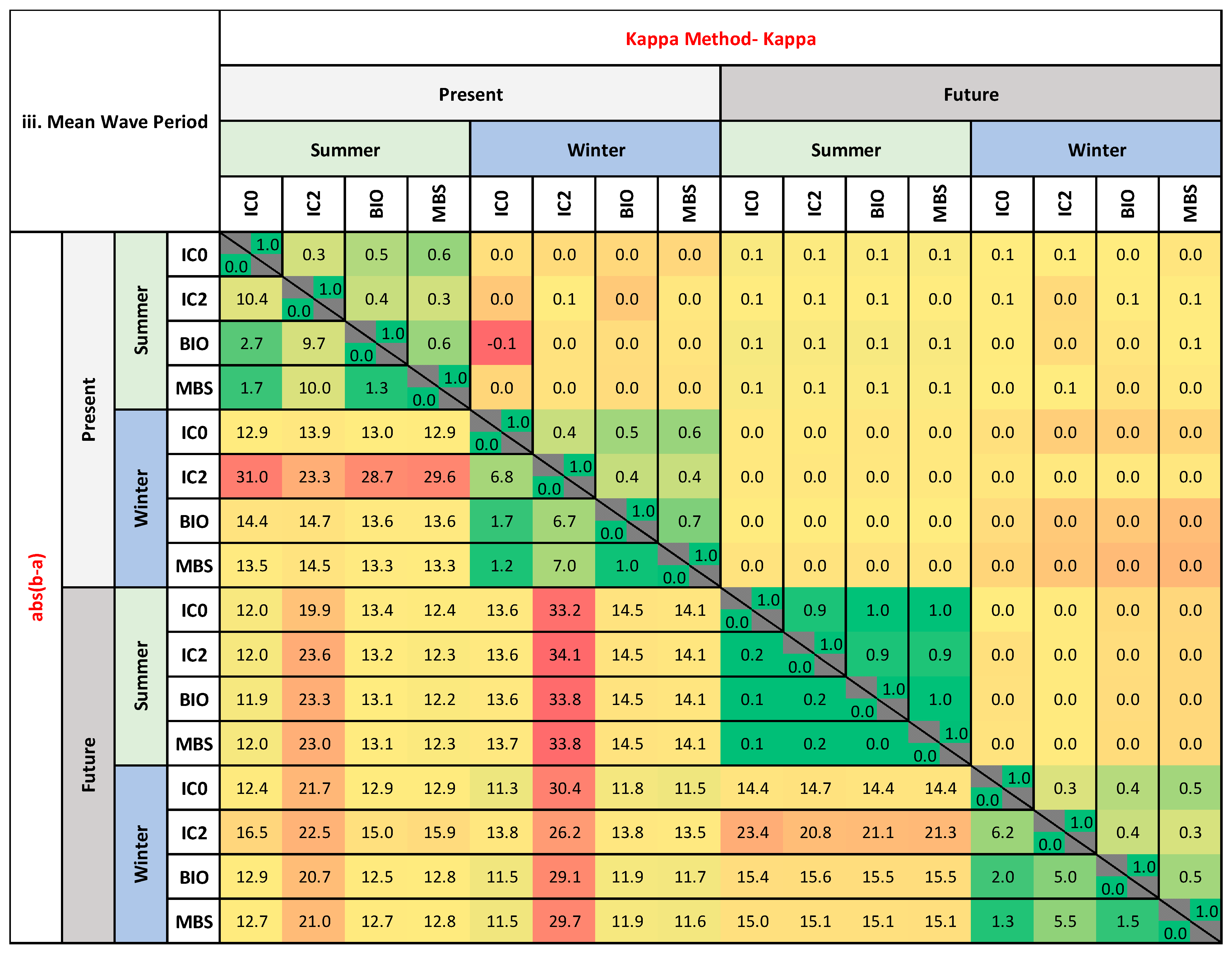
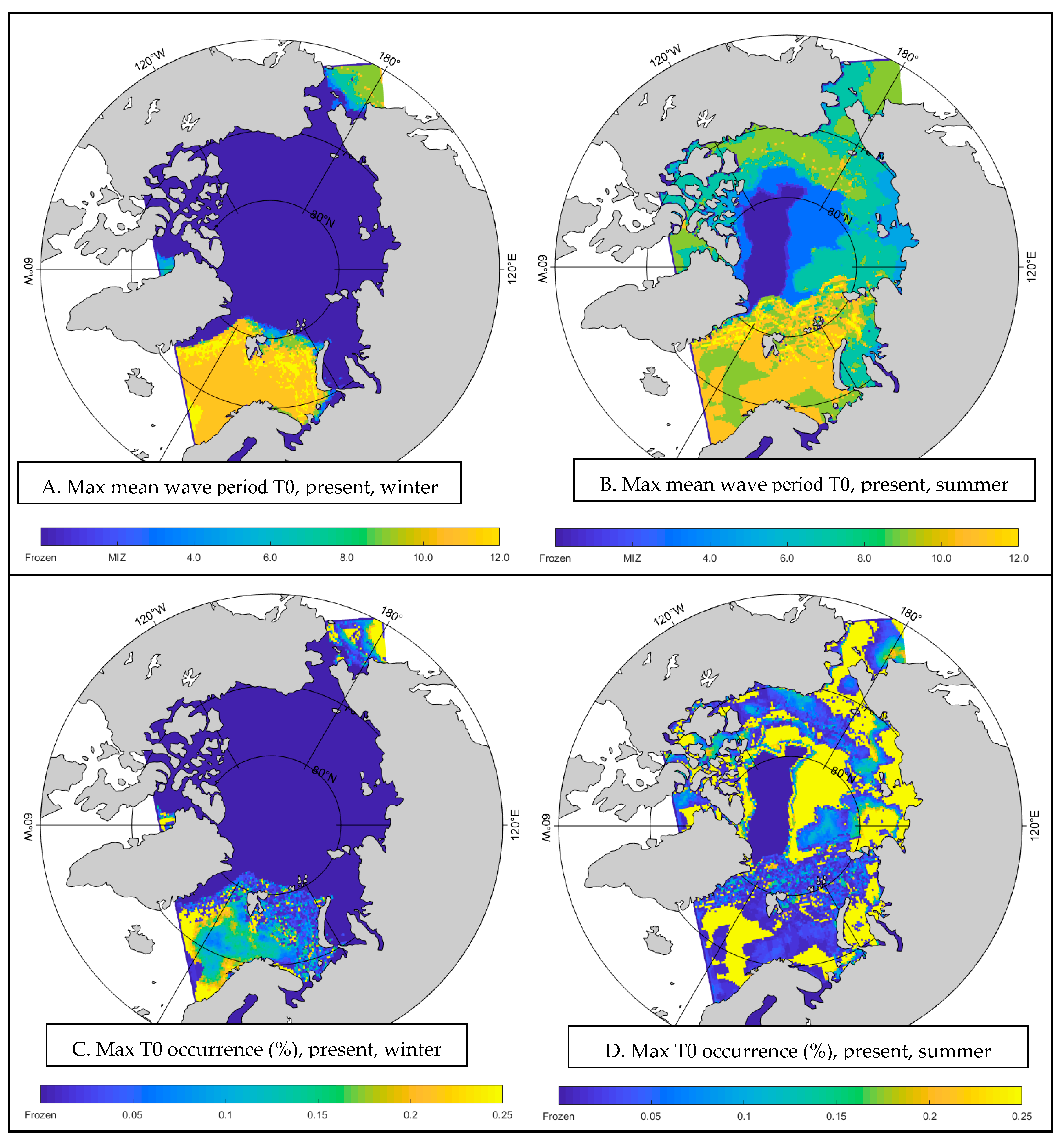
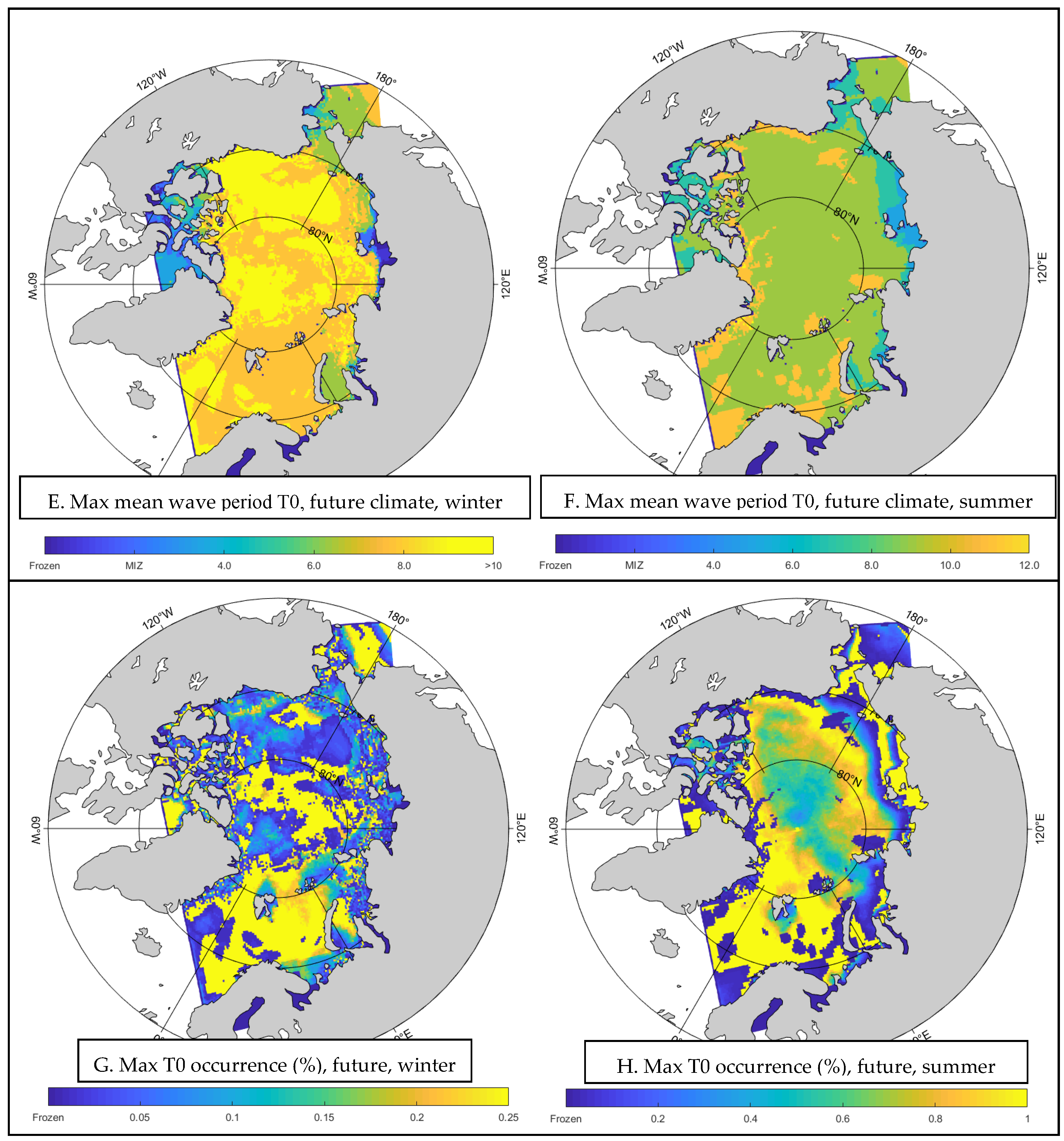
3.2.3. Mean Wave Period Analysis
- Winter Season
- 2.
- Summer Season
3.3. Extreme Value Analysis (EVA) in Hydrodynamic Ocean Modeling
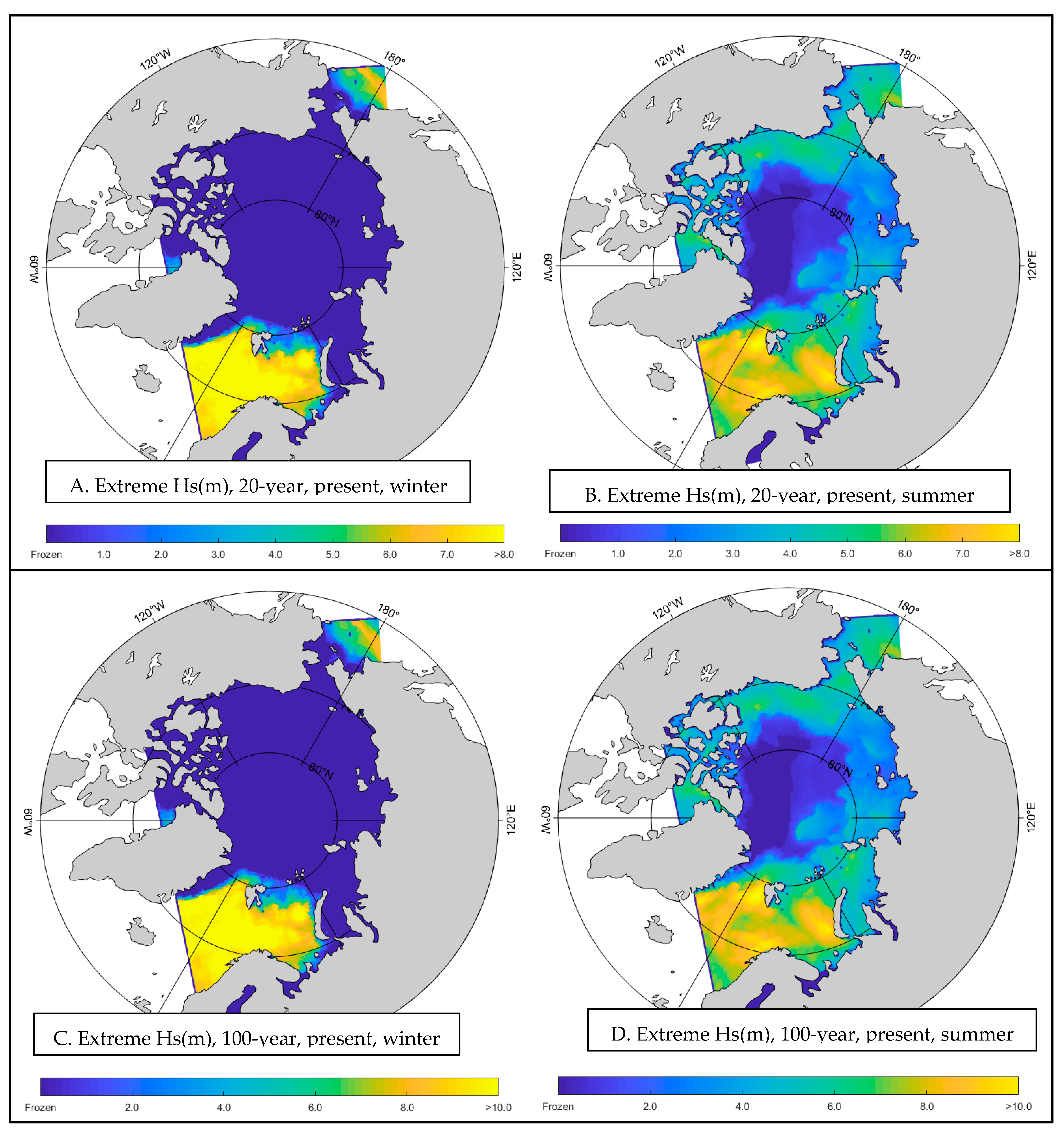
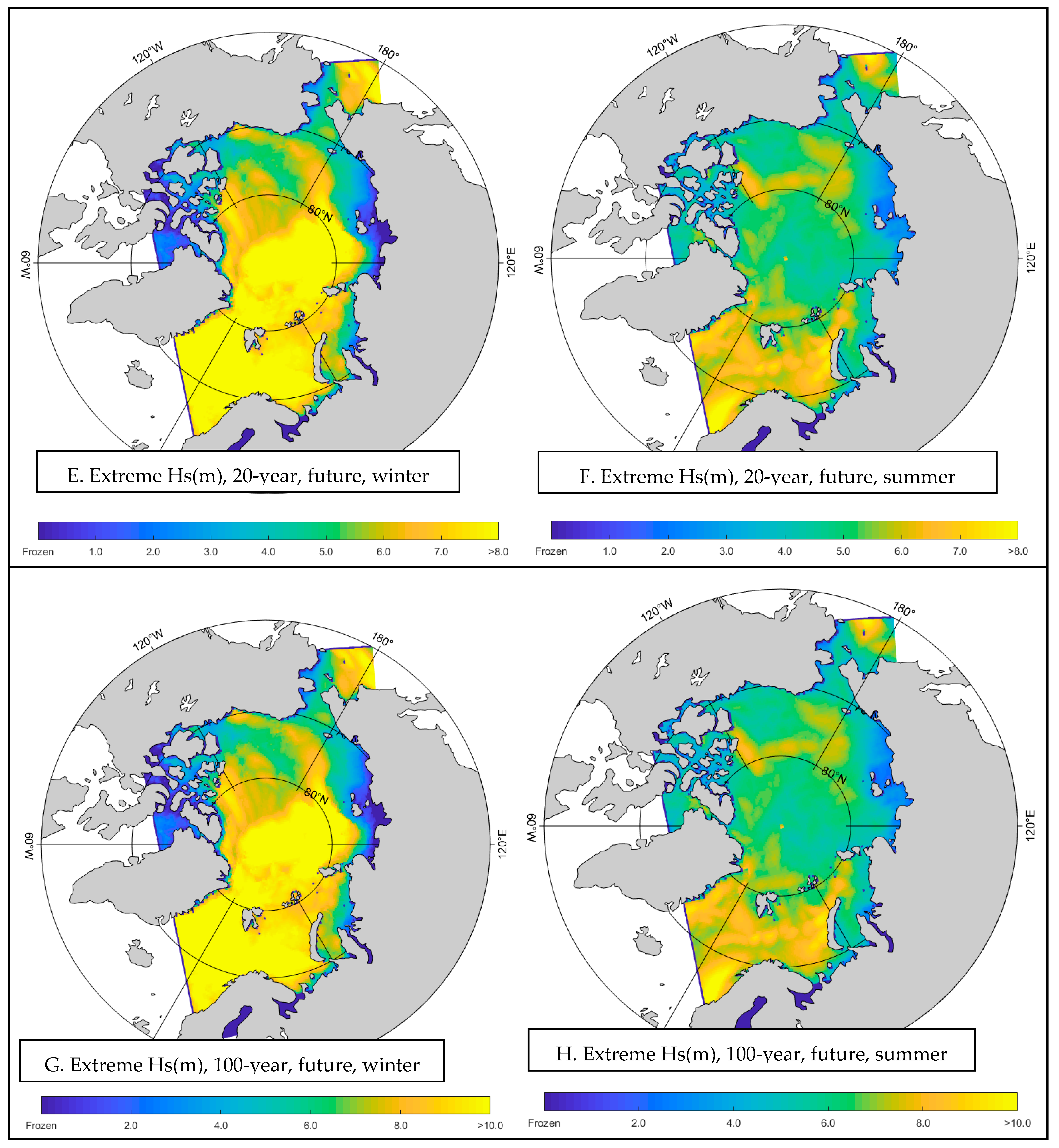
- Extremal Analysis for Significant Wave Heights
- 2.
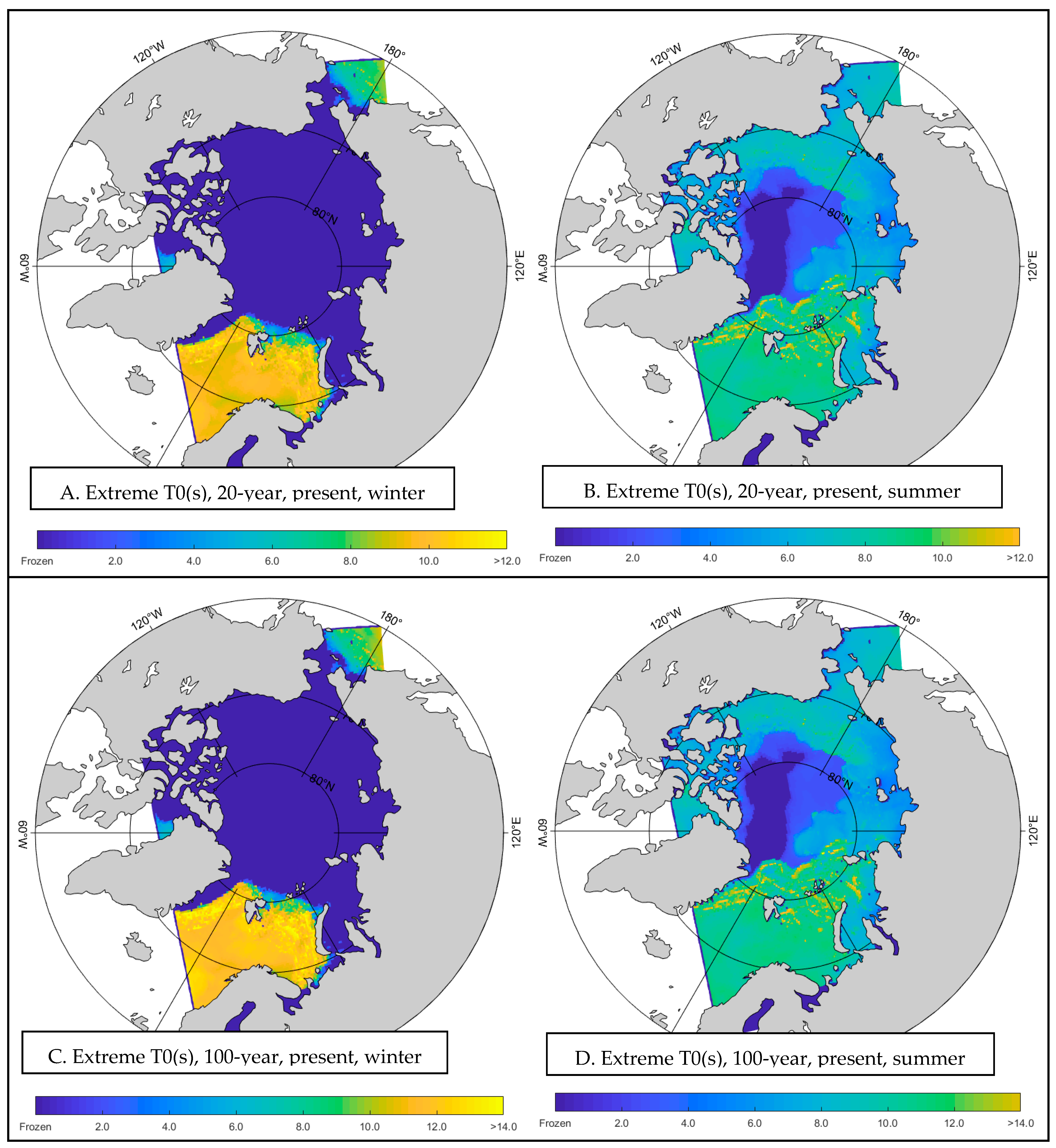
- Extreme Wave Period Values Under Different Conditions
4. Concluding Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Beer, M.; Quek, S.T. Long-term performance assessment and design of offshore structures. Comput. Struct. 2015, 154, 101–115. [Google Scholar] [CrossRef]
- Khon, V.C.; Mokhov, I.I.; Pogarskiy, F.A.; Babanin, A.; Dethloff, K.; Rinke, A.; Matthes, H. Wave heights in the 21st century Arctic Ocean simulated with a regional climate model. Geophys. Res. Lett. 2014, 41, 2956–2961. [Google Scholar] [CrossRef]
- Casas-Prat, M.; Wang, X.L. Projections of extreme ocean waves in the Arctic and potential implications for coastal inundation and erosion. J. Geophys. Res. Ocean. 2020, 125, e2019JC015745. [Google Scholar] [CrossRef]
- Meylan, M.H.; Perrie, W.; Toulany, B.; Hu, Y.; Casey, M.P. On the Three-dimensional Scattering of Waves by Flexible Marginal Ice Floes. J. Geophys. Res. 2020, 125, e2019JC015868. [Google Scholar] [CrossRef]
- Perrie, W.; Hu, Y. Air-ice-ocean momentum exchange. Part 1: Energy transfer between waves and ice floes. J. Phys. Oceanogr. 1996, 26, 1705–1720. [Google Scholar] [CrossRef]
- Perrie, W.; Meylan, M.; Toulany, B.; Casey, M. Modelling Wave-Ice Interactions in Three-Dimensions in the Marginal Ice Zone. Philos. Trans. R. Soc. A 2022, 380, 20210263. [Google Scholar] [CrossRef]
- Perrie, W.; Meylan, M.; Toulany, B.; Casey, M.; Hu, Y. Modelling Wave-Ice Interactions in Three-Dimensions in the Marginal Ice Zone of the Beaufort Sea. In Proceedings of the 105th Annual AMS Meeting 2025, New Orleans, LA, USA, 12–16 January 2025; Volume 105, p. 450201. [Google Scholar]
- Moreno-Ibáñez, M. Polar low research: Recent developments and promising courses of research. Front. Earth Sci. 2024, 12, 1368179. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: Singapore, 2010. [Google Scholar]
- Jonathan, P.; Ewans, K. Statistical modelling of extreme ocean environments for marine design: A review. Ocean. Eng. 2013, 62, 91–109. [Google Scholar] [CrossRef]
- Long, Z.; Perrie, W. Changes in Ocean Temperatures in the Barents Sea in the Twenty-First Century. J. Clim. 2017, 30, 5901–5921. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. A description of a three dimensional coastal ocean circulation model. In Three-Dimensional Coastal Ocean Models; Heaps, N.S., Ed.; American Geophysical Union: Slidell, LA, USA, 1987; pp. 1–16. [Google Scholar]
- Hibler, W.D., III. Adynamic thermodynamic sea ice model. J. Phys. Ocean. 1979, 9, 815–864. [Google Scholar] [CrossRef]
- Long, Z.; Perrie, W. Impacts of climate change on fresh water content and sea surface height in the Beaufort Sea. Ocean. Model. 2013, 71, 127–139. [Google Scholar] [CrossRef]
- Long, Z.; Perrie, W. Scenario changes of Atlantic water in the Arctic Ocean. J. Clim. 2015, 28, 5523–5548. [Google Scholar] [CrossRef]
- Zhang, M.; Perrie, W.; Long, Z. Dynamical Downscaling of the Arctic Climate with a Focus on Polar Cyclone Climatology. Atmos.-Ocean. 2017, 57, 41–60. [Google Scholar] [CrossRef]
- Zhang, M.; Perrie, W.; Long, Z. Future changes in the winter Beaufort High under warming climate scenarios. Geophys. Res. Lett. 2024, 51, e2024GL110317. [Google Scholar] [CrossRef]
- Meucci, A.; Young, I.R.; Hemer, M.; Trenham, C.; Watterson, I.G. 140 Years of Global Ocean Wind-Wave Climate Derived from CMIP6 ACCESS-CM2 and EC-Earth3 GCMs: Global Trends, Regional Changes, and Future Projections. J. Clim. 2023, 36, 1605–1631. [Google Scholar] [CrossRef]
- Zhang, M.; Perrie, W.; Long, Z. Impacts of climate change on Arctic winter cyclones. JGR–Atmos. 2025, 129, e2024JD041503. [Google Scholar] [CrossRef]
- WW3DG–The WAVEWATCH III® Development Group. User Manual and System Documentation of WAVEWATCH III® Version 5.16 (Tech. Note No. 329); NOAA/NWS/NCEP/MMAB: College Park, MD, USA, 2016; p. +Appendices.
- Ardhuin, F.; Pogers, E.; Babanin, A.V.; Filipot, J.-F.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.-M.; Aouf, L.; et al. Semi-empirical dissipation source functions for wind-wave models: Part I, definition, calibration and validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Rascle, N.; Ardhuin, F. A global wave parameter database for geophysical applications. Part 2: Model validation with improved source term parameterization. Ocean Model. 2013, 70, 174–188. [Google Scholar] [CrossRef]
- Ardhuin, F.; Collard, F.; Chapron, B.; Girard-Ardhuin, F.; Guitton, G.; Mouche, A.; Stopa, J.E. Estimates of ocean wave heights and attenuation in sea ice using the SAR wave mode on Sentinel-1A. Geophys. Res. Lett. 2015, 42, 2317–2325. [Google Scholar] [CrossRef]
- Wada, A.; Kunii, M. The role of ocean-atmosphere interaction in Typhoon Sinlaku (2008) using a regional coupled data assimilation system. J. Geophys. Res. Ocean. 2017, 122, 3675–3695. [Google Scholar] [CrossRef]
- Masson, D.; LeBlond, P.H. Spectral evolution of wind-generated surface gravity waves in a dispersed ice field. J. Fluid Mech. 1989, 202, 111–136. [Google Scholar] [CrossRef]
- Meylan, M.H.; Masson, D. A linear Boltzmann equation to model wave scattering in the marginal ice zone. Ocean Model 2006, 11, A17–A27. [Google Scholar] [CrossRef]
- Liu, A.K.; Mollo-Christensen, E. Wave propagation in a solid ice pack. J. Phys. Ocean. 1988, 18, 1702–1712. [Google Scholar] [CrossRef]
- Rogers, W.E.; Meylan, M.H.; Kohout, A.L. Estimates of spectral wave attenuation in Antarctic sea ice, using model/data inversion. Cold Reg. Sci. Technol. 2021, 182, 103198. [Google Scholar] [CrossRef]
- Meylan, M.H.; Bennetts, L. Three-dimensional time-domain scattering of waves in the marginal ice zone. Phil. Trans. R. Soc. A 2018, 376, 20170334. [Google Scholar] [CrossRef]
- Meylan, M.H.; Squire, V.A.; Fox, C. Towards realism in modeling ocean wave behavior in marginal ice zones. J. Geo-Phys. Res. 1997, 102, 22981–22991. [Google Scholar] [CrossRef]
- Hibler, W.D., III. Modeling a variable thickness sea ice cover. Mon. Weather Rev. 1980, 108, 1943–1973. [Google Scholar] [CrossRef]
- Monserud, R.A.; Leemans, R. Comparing global vegetation maps with the Kappa statistic. Ecol. Model. 1992, 62, 275–293. [Google Scholar] [CrossRef]
- Pérez, J.; Díaz, J.; Garcia-Martin, J.; Tabuenca, B. Systematic literature reviews in software engineering—Enhancement of the study selection process using Cohen’s Kappa statistic. J. Syst. Softw. 2020, 168, 110657. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, M. Kappa statistic for clustered physician–patients polytomous data. Comput. Stat. Data Anal. 2015, 87, 3–17. [Google Scholar] [CrossRef]
- Bulteau, T.; Lecacheux, S.; Lerma, A.N.; Paris, F. Spatial extreme value analysis of significant wave heights along the French coast. In Proceedings of the International Short Conference on Advances in Extreme Value Analysis and Application to Natural Hazards: EVAN2013, Siegen, Germany, 18 September 2013; p. hal-00857627. [Google Scholar]
- Dey, D.K.; Yan, J. Extreme Value Modeling and Risk Analysis: Methods and Applications; Chapman Hall Press: London, UK, 2020; 540p, ISBN 9780367737399. [Google Scholar]
- Menéndez, M.; Méndez, F.J.; Losada, I.J.; Graham, N.E. Variability of extreme wave heights in the northeast Pacific Ocean based on buoy measurements. Geophys. Res. Lett. 2008, 35, L22607. [Google Scholar] [CrossRef]
- Challenor, P.G.; Wimmer, W.; Ashton, I. Climate Change and Extreme Wave Heights in the North Atlantic; Special Publication; European Space Agency: Paris, France, 2005; Volume 572, pp. 1253–1257. [Google Scholar]
- Chini, N.; Stansby, P.; Leake, J.; Wolf, J.; Roberts-Jones, J.; Lowe, J. The impact of sea level rise and climate change on inshore wave climate: A case study for East Anglia (UK). Coast. Eng. 2010, 57, 973–984. [Google Scholar] [CrossRef]
- Mori, N.; Yasuda, T.; Mase, H.; Tom, T.; Oku, Y. Projection of extreme wave climate change under global warming. Hydrol. Res. Lett. 2010, 4, 15–19. [Google Scholar] [CrossRef]
- Young, I.R.; Vinoth, J.; Zieger, S.; Babanin, A.V. Investigation of trends in extreme value wave height and wind speed. J. Geophys. Res. 2012, 117, C00J06. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R.; Zwiers, F.W.; Zhang, X.; Feng, Y. Detection of external influence on trends of atmospheric storminess and ocean wave heights. Clim. Dyn. 2008, 32, 189–203. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef]
- Parker, C.L.; Mooney, P.A.; Webster, M.A.; Boisvert, L.N. The influence of recent and future climate change on spring Arctic cyclones. Nat. Commun. 2022, 13, 6514. [Google Scholar] [CrossRef] [PubMed]
- Timmermans, M.; Marshall, J. Understanding Arctic Ocean circulation: A review of ocean dynamics in a changing climate. J. Geophys. Res. 2020, 125, e2018JC014378. [Google Scholar] [CrossRef]
- Mioduszewski, J.; Vavrus, S.; Wang, M. Mioduszewski Vavrus Diminishing Arctic sea ice promotes stronger surface winds. J. Clim. 2018, 31, 8101–8119. [Google Scholar] [CrossRef]
- Ding, Q.; Schweiger, A.; Baxter, L. Nudging observed winds in the Arctic to quantify associated sea ice loss from 1979 to 2020. J. Clim. 2022, 35, 6797–6813. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goharnejad, H.; Perrie, W.; Toulany, B.; Zhang, M.; Long, Z.; Casey, M.; Meylan, M.H. Arctic Wave Climate Including Marginal Ice Zone and Future Climate Scenario. J. Mar. Sci. Eng. 2025, 13, 1562. https://doi.org/10.3390/jmse13081562
Goharnejad H, Perrie W, Toulany B, Zhang M, Long Z, Casey M, Meylan MH. Arctic Wave Climate Including Marginal Ice Zone and Future Climate Scenario. Journal of Marine Science and Engineering. 2025; 13(8):1562. https://doi.org/10.3390/jmse13081562
Chicago/Turabian StyleGoharnejad, Hamid, William Perrie, Bechara Toulany, Minghong Zhang, Zhenxia Long, Michael Casey, and Michael H. Meylan. 2025. "Arctic Wave Climate Including Marginal Ice Zone and Future Climate Scenario" Journal of Marine Science and Engineering 13, no. 8: 1562. https://doi.org/10.3390/jmse13081562
APA StyleGoharnejad, H., Perrie, W., Toulany, B., Zhang, M., Long, Z., Casey, M., & Meylan, M. H. (2025). Arctic Wave Climate Including Marginal Ice Zone and Future Climate Scenario. Journal of Marine Science and Engineering, 13(8), 1562. https://doi.org/10.3390/jmse13081562






