CFD Investigation on Effect of Ship–Helicopter Coupling Motions on Aerodynamic Flow Field and Rotor Loads
Abstract
1. Introduction
2. Numerical Model and Method Validation
2.1. Wave Model Formulation
2.2. Ship and Helicopter Models
2.3. Momentum Source Model
2.4. Verification and Validation (VV) Study
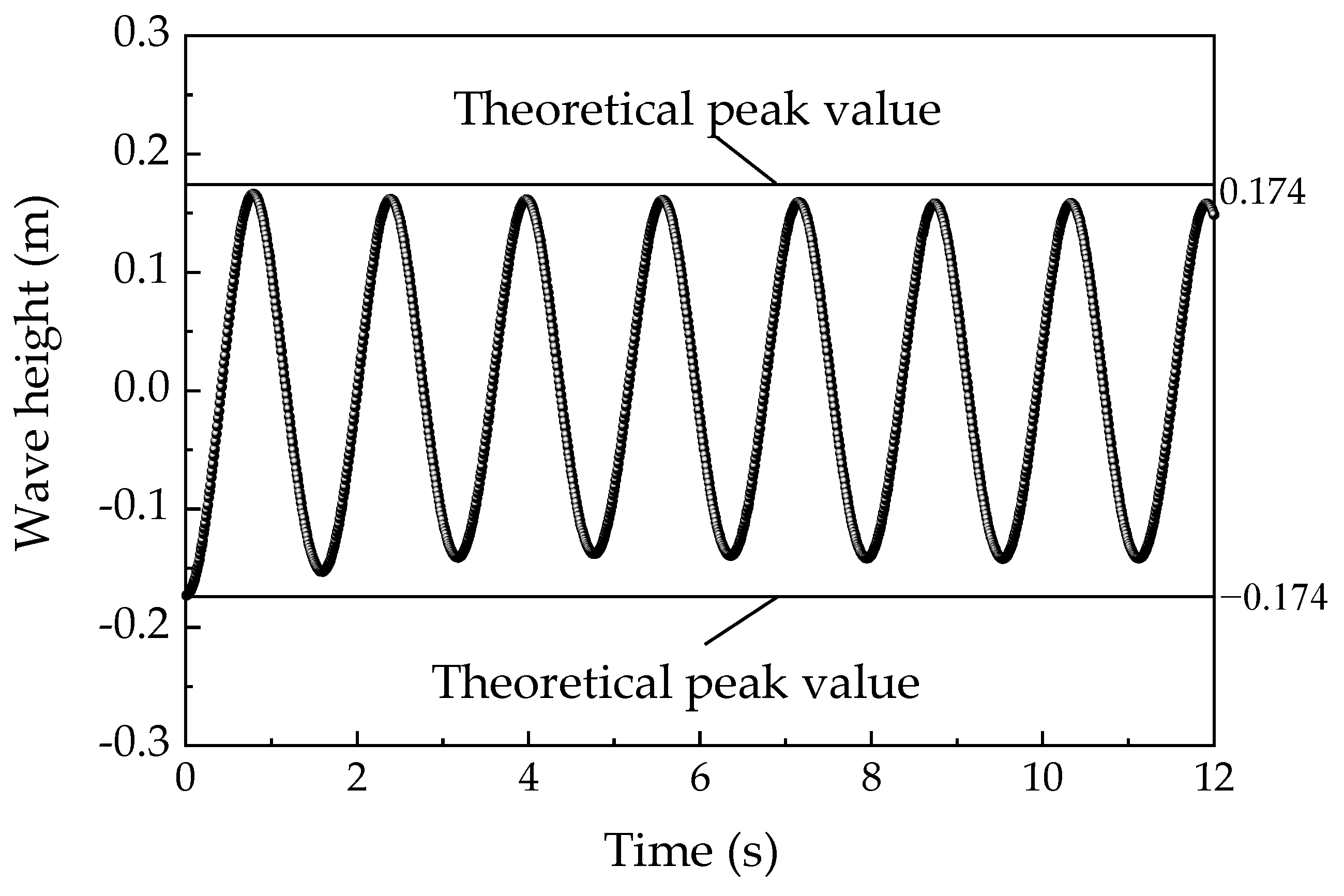
2.4.1. Verification of Numerical Wave Generation
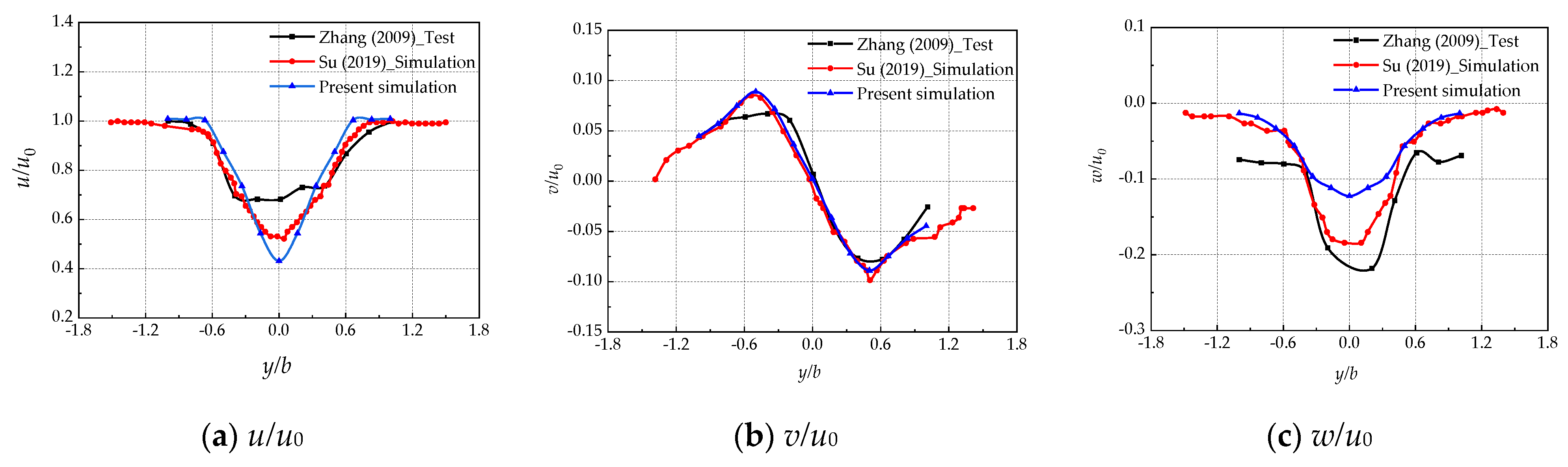
2.4.2. Ship-Wake Validation
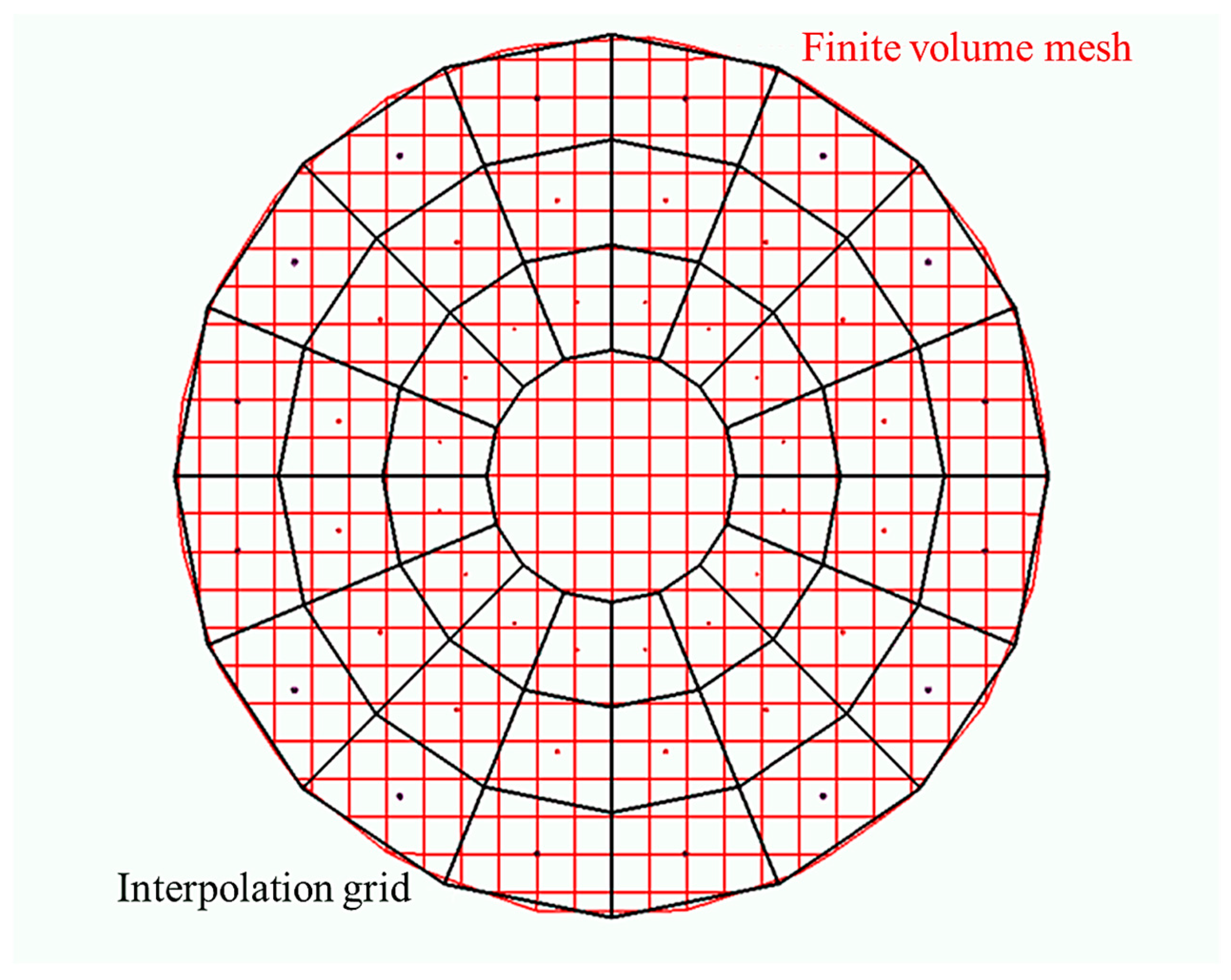
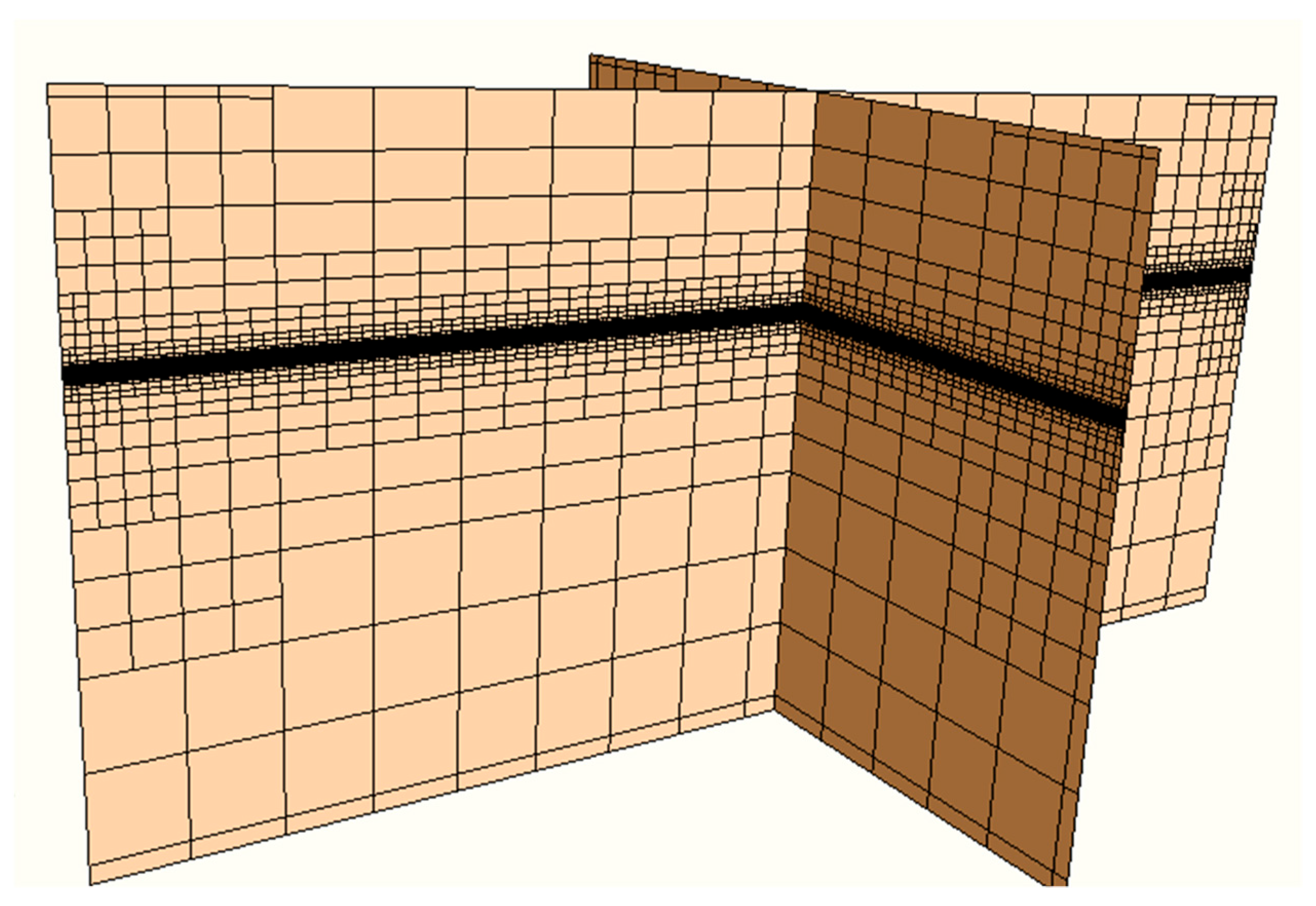
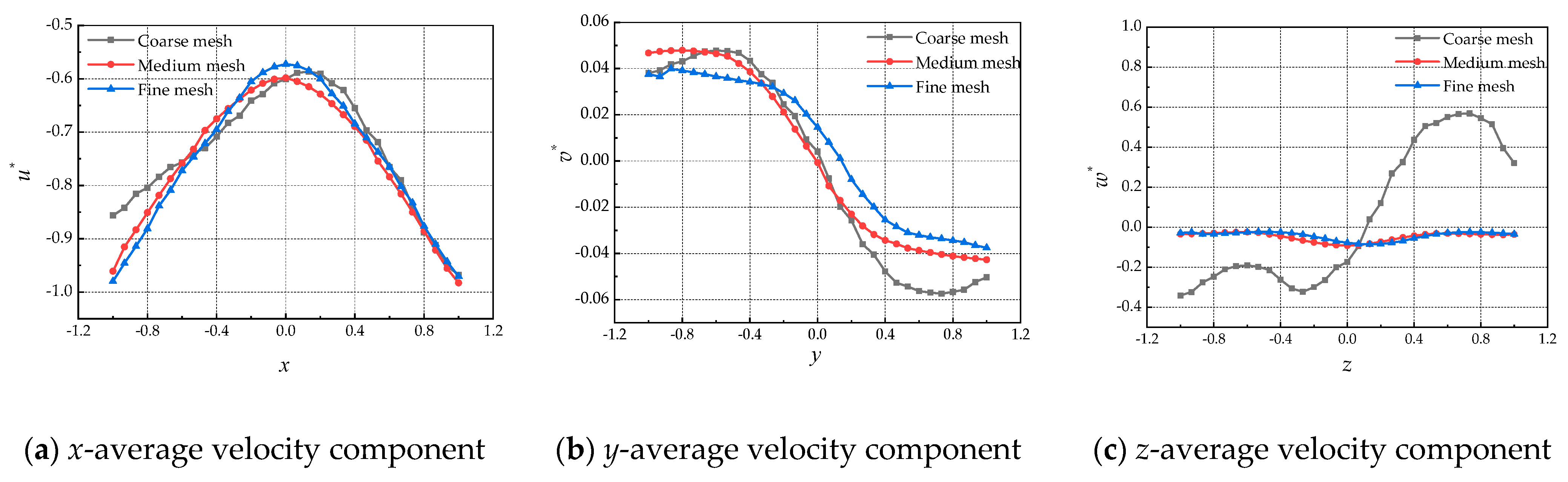
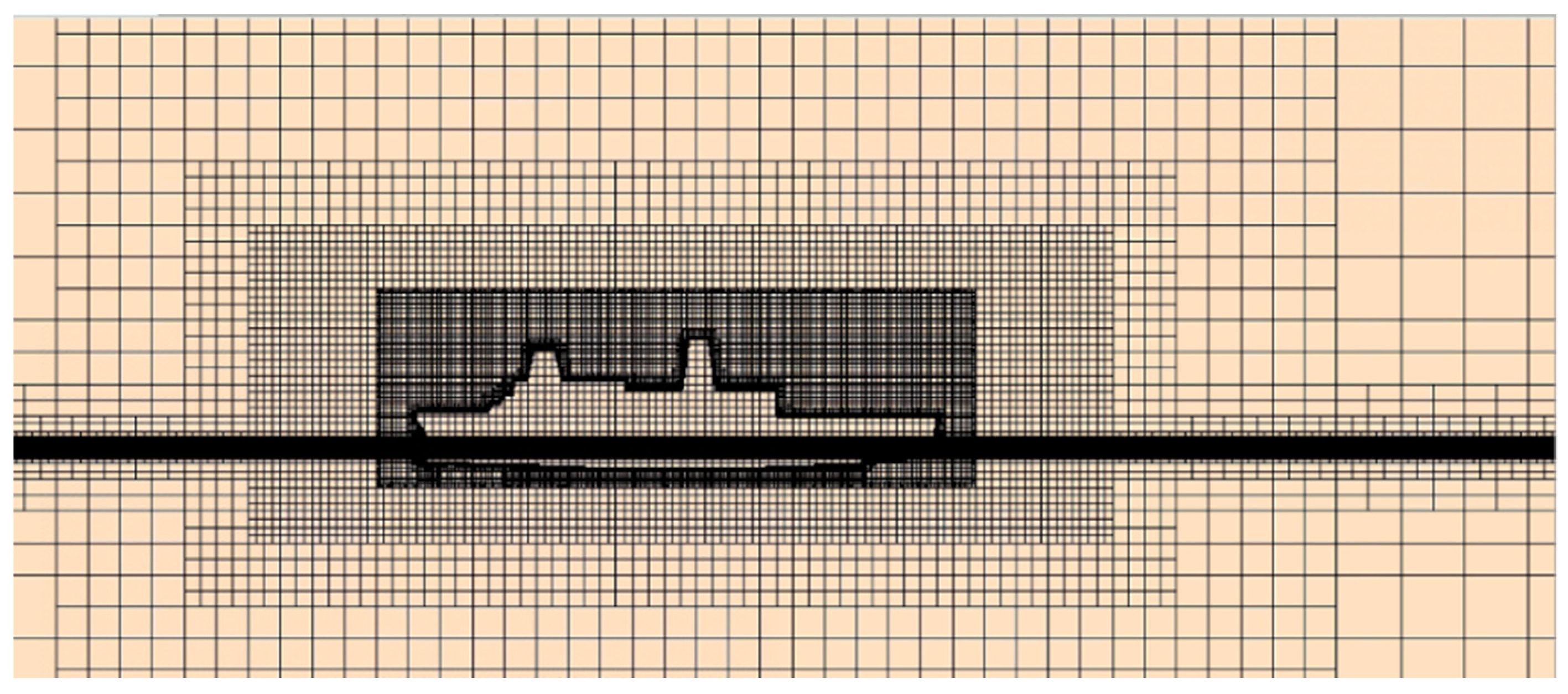
2.4.3. Grid Independence Analysis
3. Calculation Conditions and Physical Outputs
3.1. Seakeeping Analysis in Sea State 5
3.1.1. Calculation Conditions
3.1.2. Seakeeping Simulation
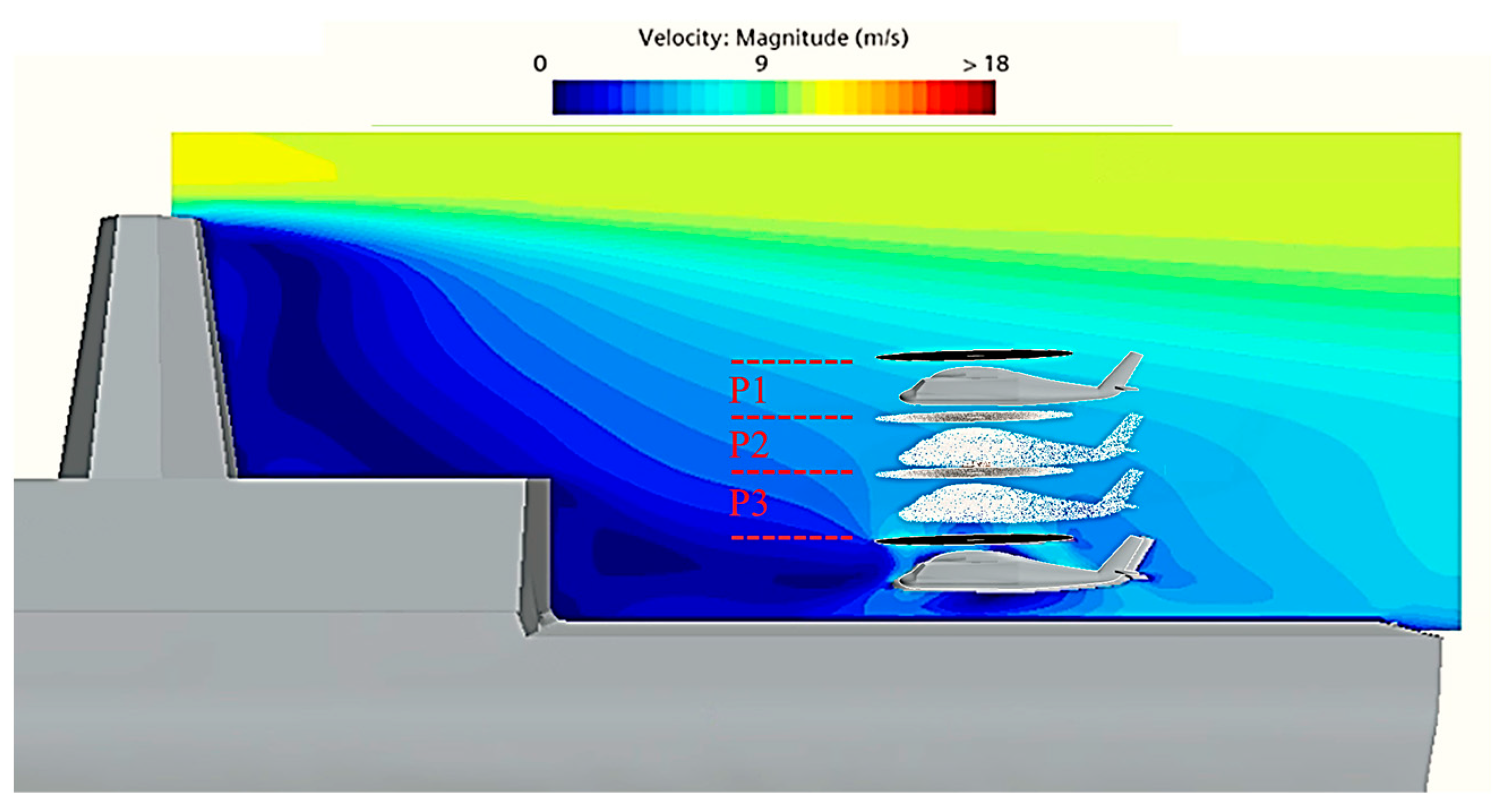
3.2. Case Configuration and Physical Outputs
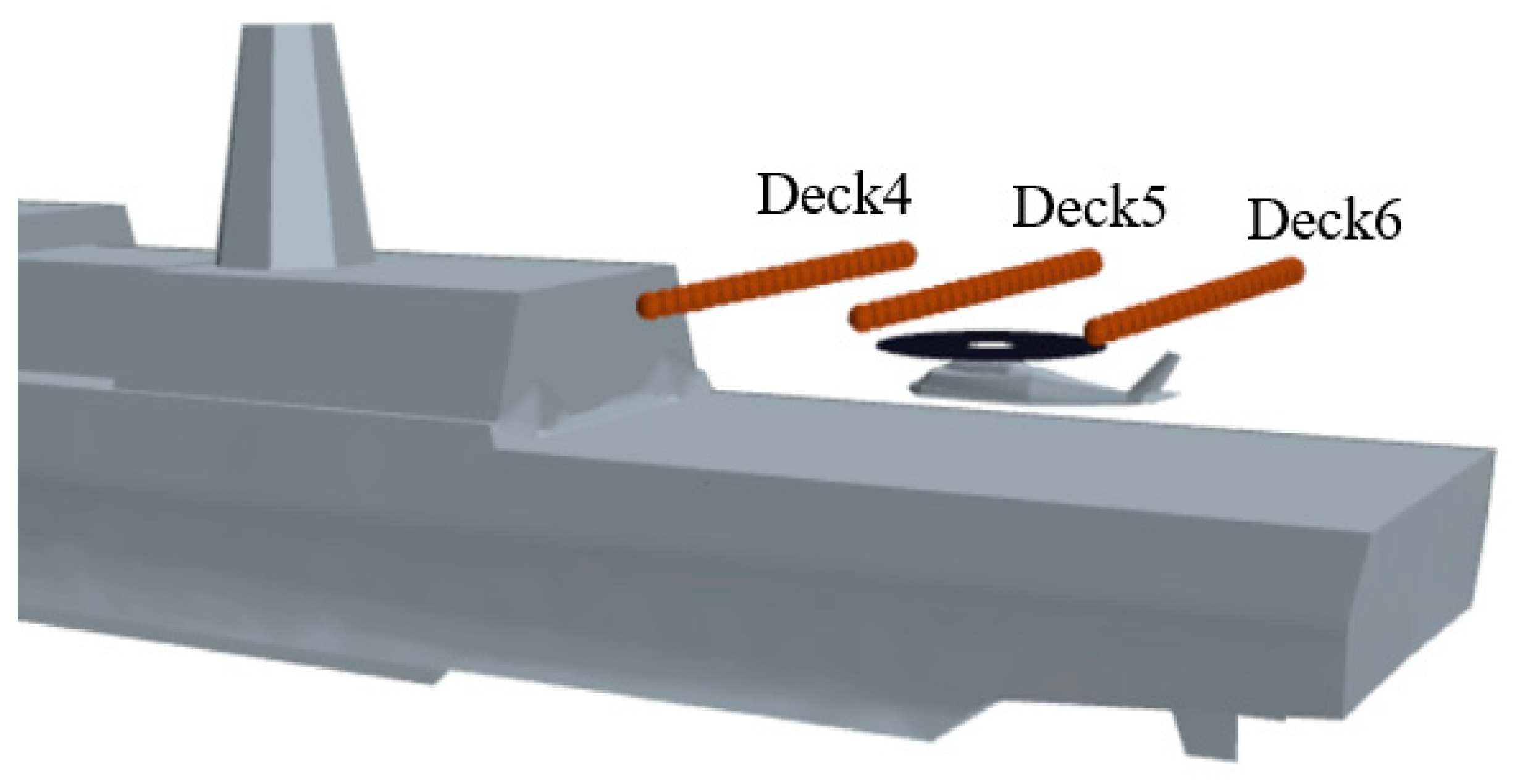
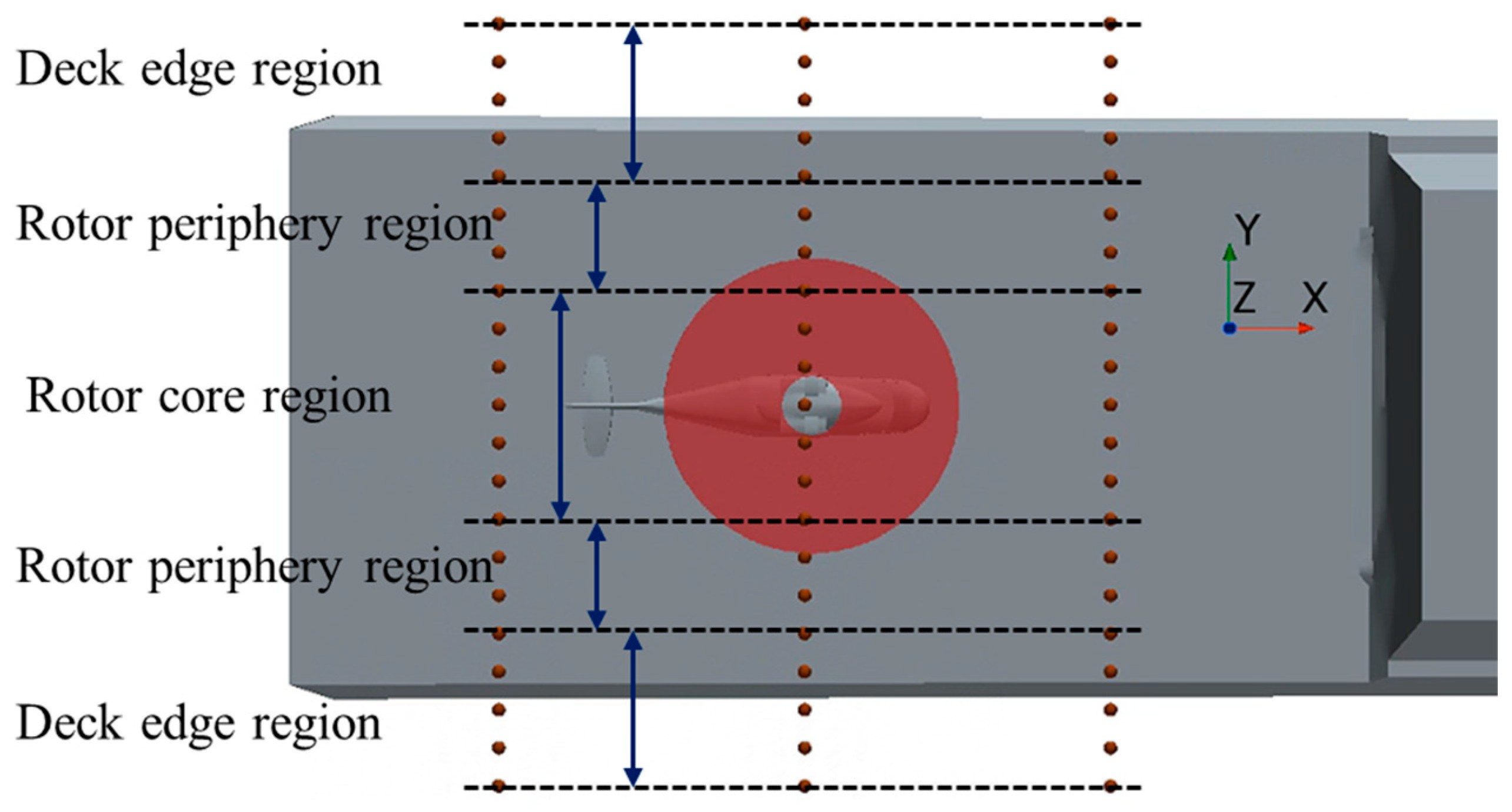
3.2.1. Case Setup
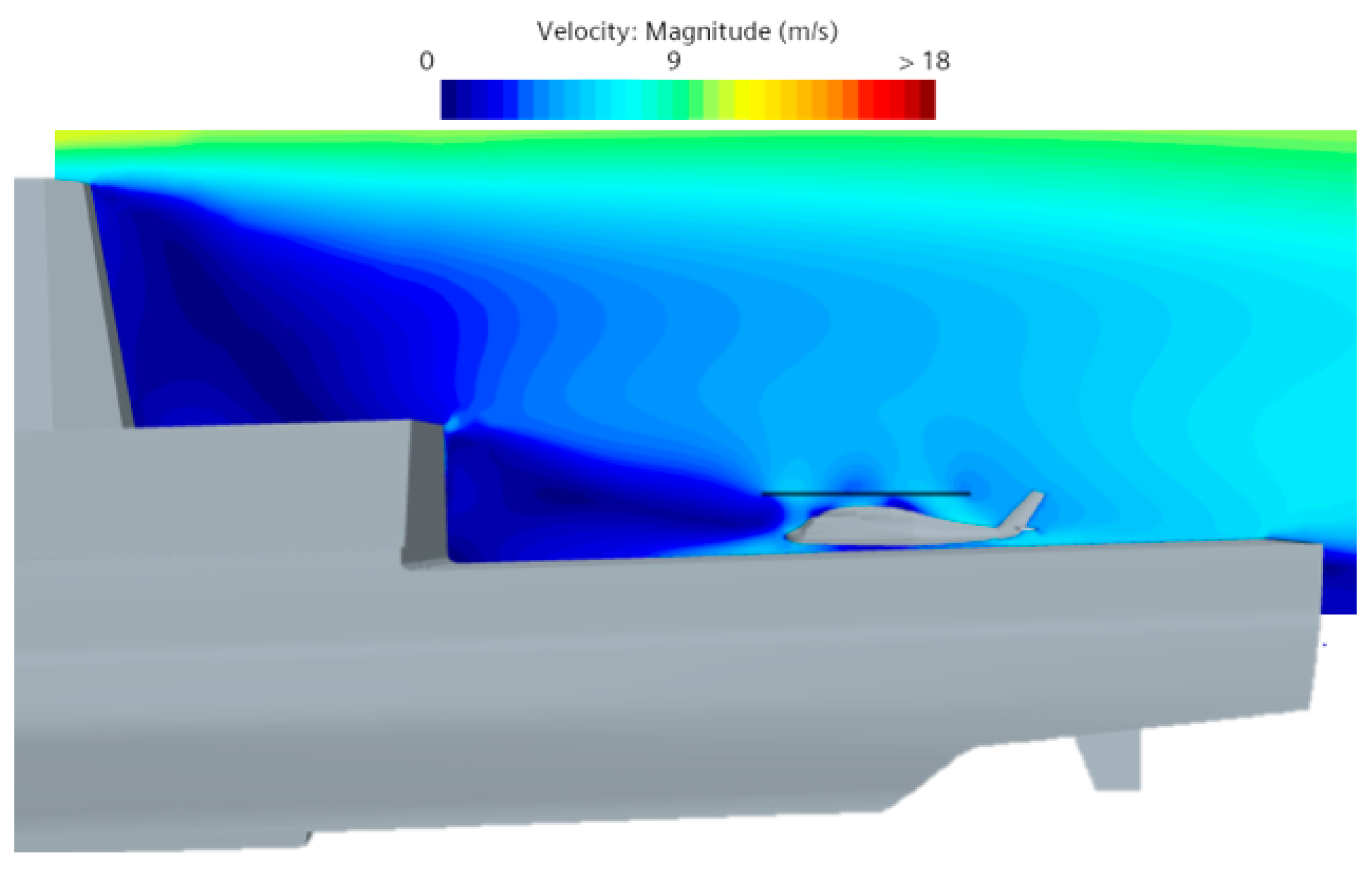
3.2.2. Coupled Flow Field Analysis
3.2.3. Dynamic Load Analysis of Shipborne Helicopter
4. Impact of SDOF Ship Motions on Coupled Flow Fields and Rotor Loads Under Sea State 5
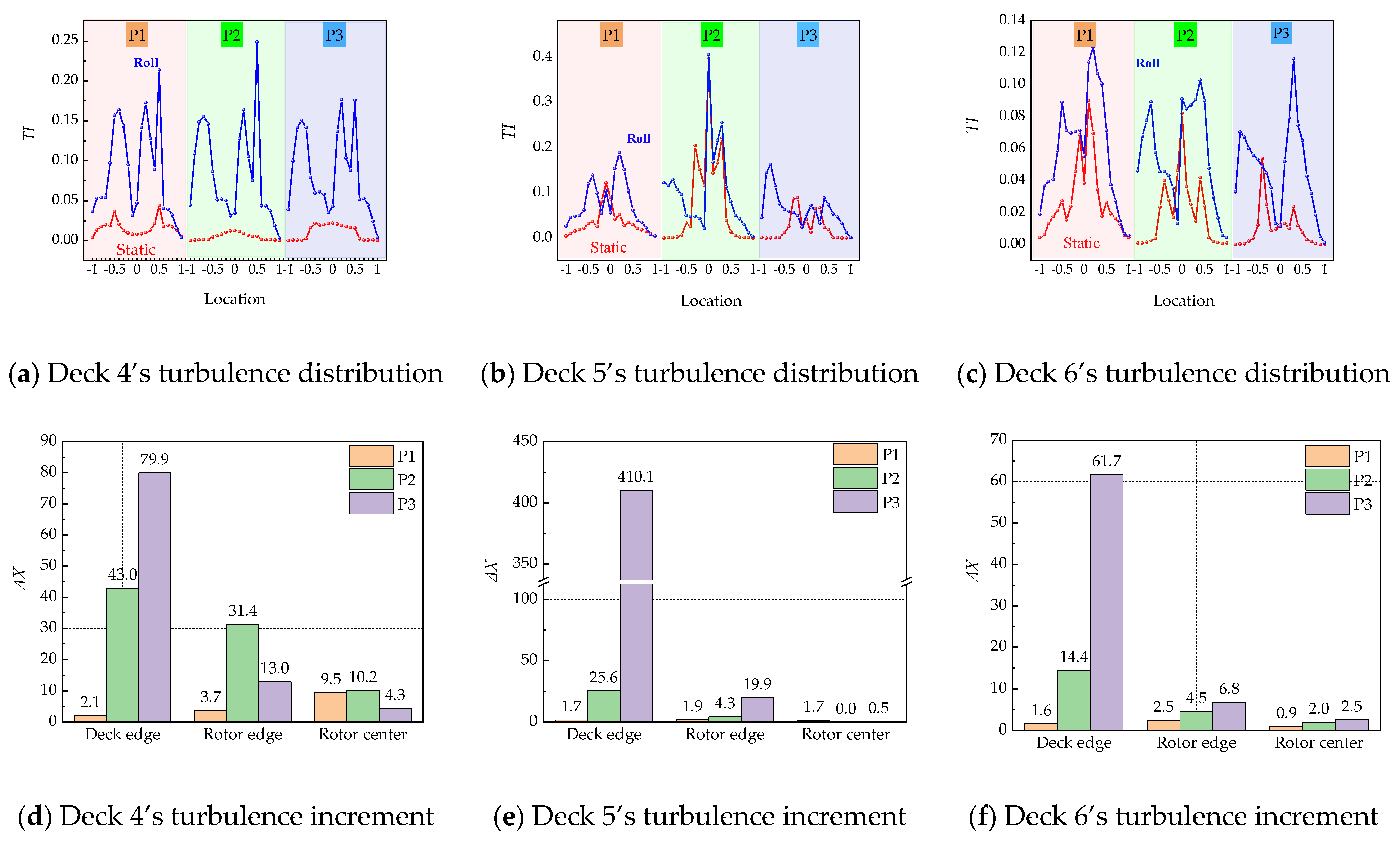
4.1. Influence of Ship Roll Motion
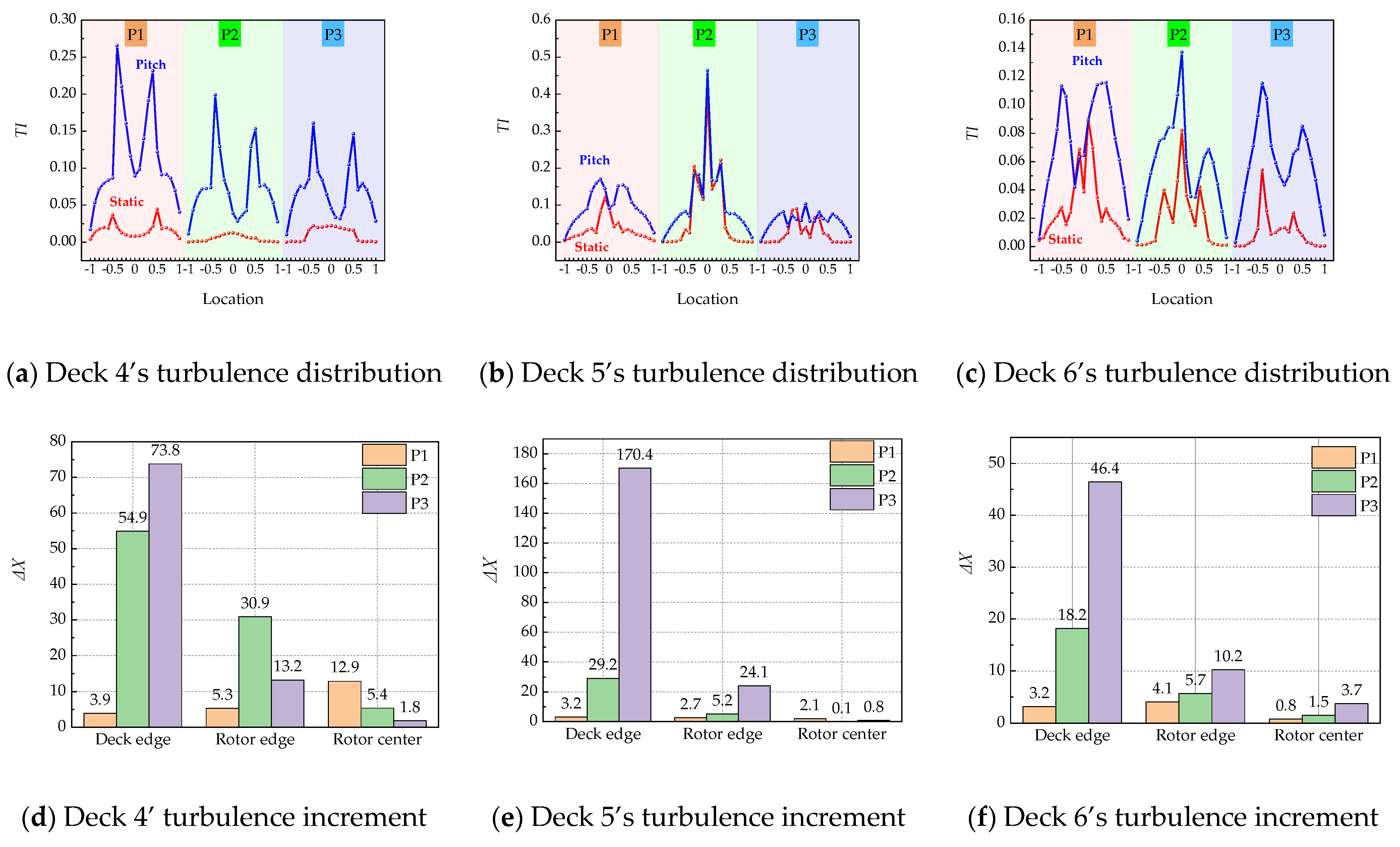
4.1.1. Impact on Coupled Flow Fields
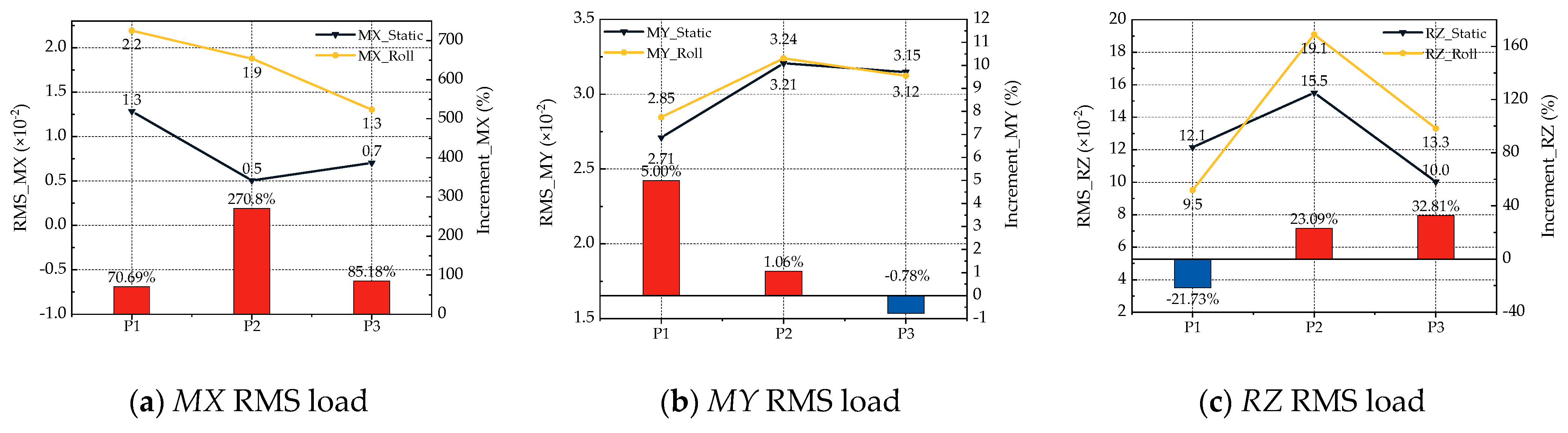
4.1.2. Impact of Roll Motion on Helicopter Dynamic Loads
4.2. Influence of Ship Pitching Motion
4.2.1. Effect of Pitching Motion on the Coupled Flow Field
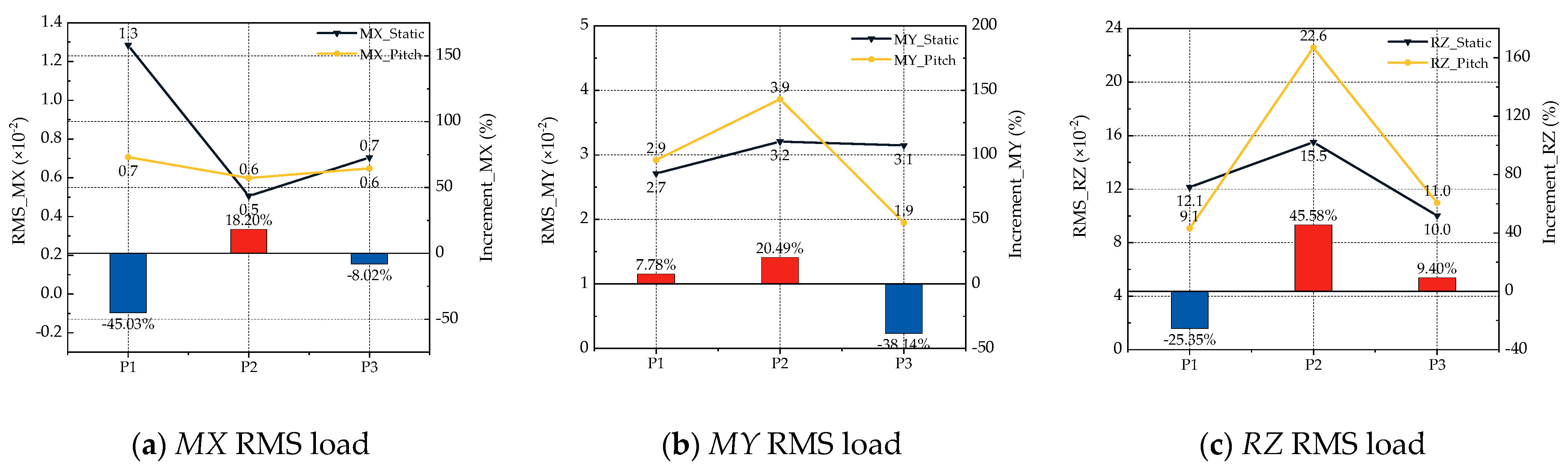
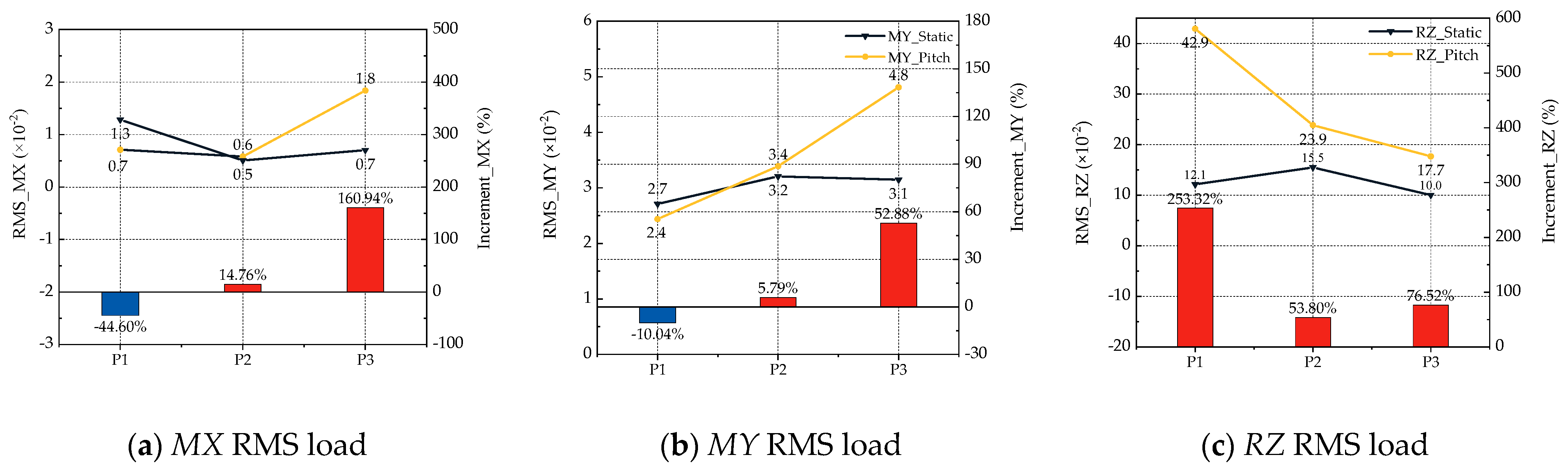
4.2.2. Influence of Pitch Motion on Shipborne Helicopter Dynamic Loads
4.3. Influence of Ship Heave Motion
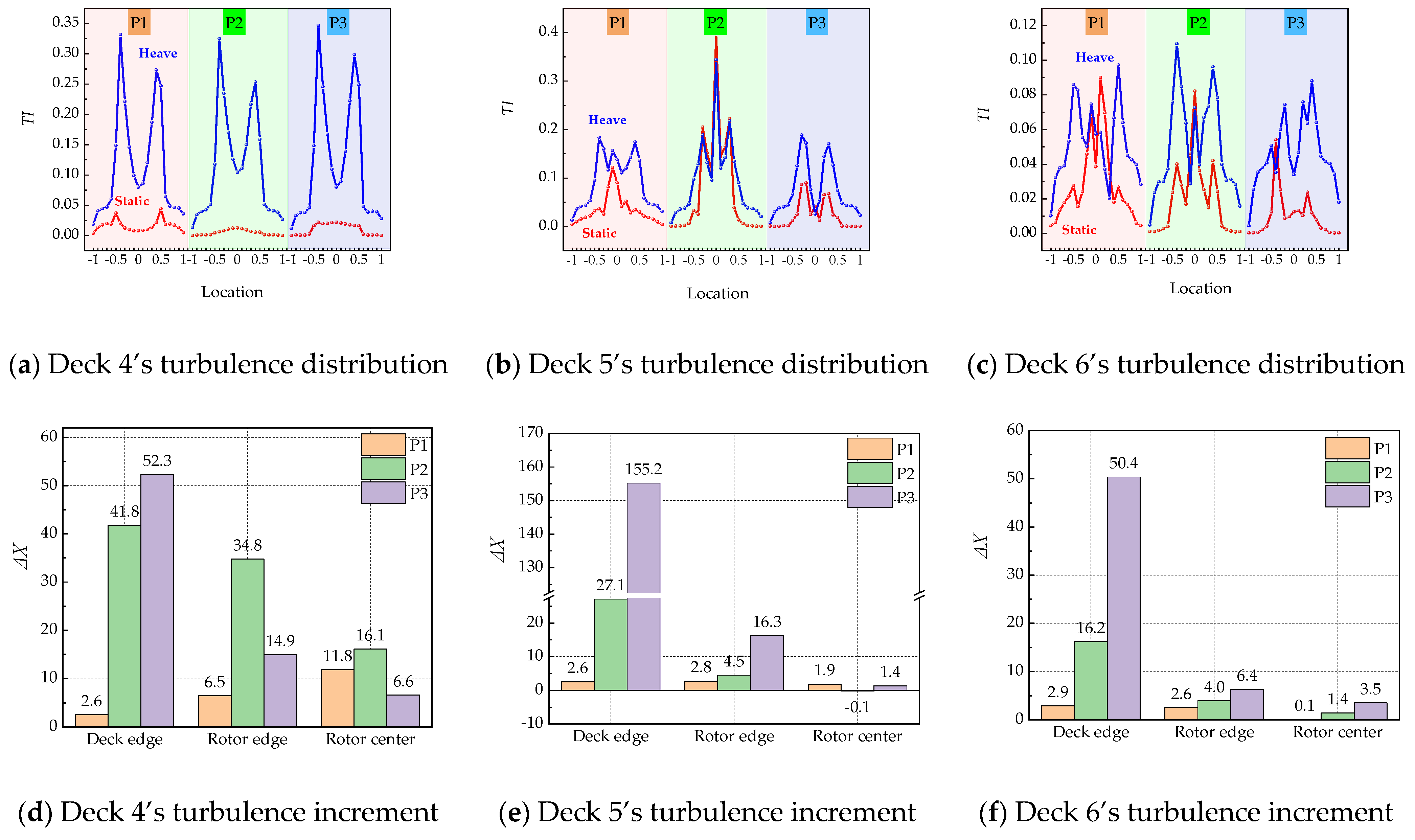
4.3.1. Effect of Heave Motion on the Coupled Flow Field
4.3.2. Influence of Heave Motion on Shipborne Helicopter Dynamic Loads
5. Impact of MDOF Ship Motions on Coupled Flow Fields and Rotor Loads Under Sea State 5
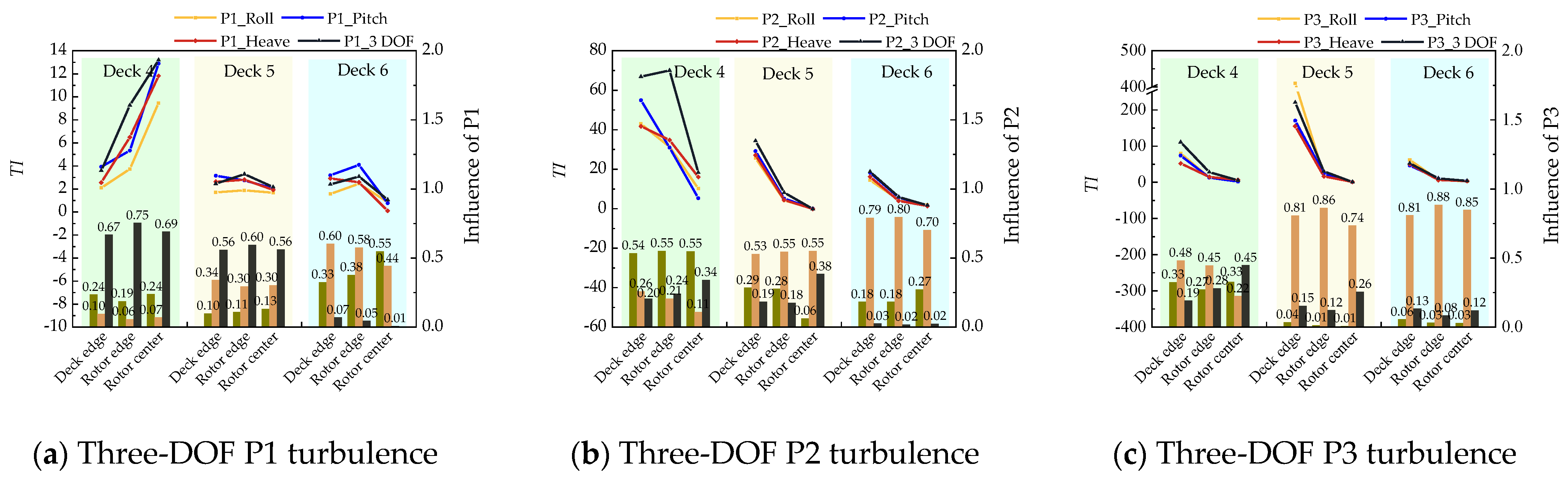
5.1. Coupling Index
5.1.1. Flow-Field Coupling Index
5.1.2. Load Coupling Index
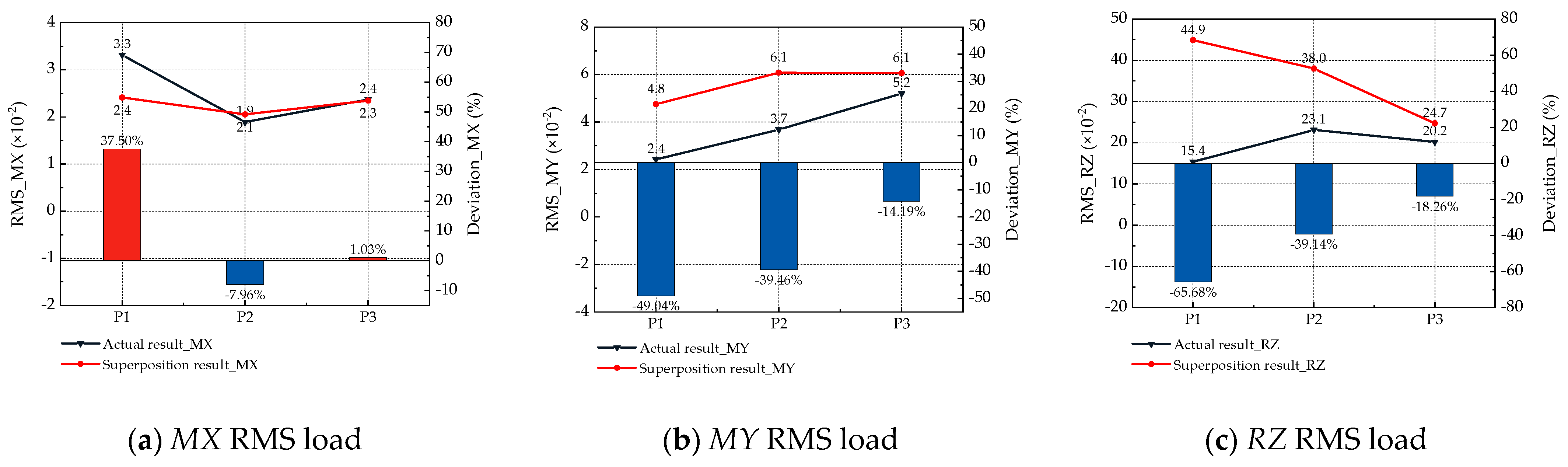
5.2. Influence of Coupled Motion on the Coupled Flow Field
5.3. Influence of Coupled Motion on Rotor Dynamic Loads
6. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, Z.L. Numerical Simulation of Coupled Interference Flow Field for Shipborne Aircraft and Ship in High Sea State. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Jeong, J.; Hussain, F. On the Identification of a Vortex. J. Fluid Mech. 1995, 332, 339–363. [Google Scholar] [CrossRef]
- Su, D.C.; Shi, Y.J.; Xu, G.H. Numerical study of the rotational direction effect on aerodynamic loading characteristics of shipborne helicopter rotor. Aeronaut. J. 2019, 123, 635–657. [Google Scholar] [CrossRef]
- Forrest, J.S.; Owen, I. An investigation of ship airwakes using Detached-Eddy Simulation. Comput. Fluids 2010, 39, 656–673. [Google Scholar] [CrossRef]
- Gu, Y.S.; Ming, X. Experimental Investigation on Flow Field Properties Around Aft-Deck of Destroyer. Acta Aeronaut. Astronaut. Sin. 2001, 06, 500–504. [Google Scholar]
- Lee, R.G.; Zan, S.J. Wind Tunnel Testing of a Helicopter Fuselage and Rotor in a Ship Airwake. In Proceedings of the 29th European Rotorcraft Forum, Friedrichshafen, Germany, 16–18 September 2003. [Google Scholar]
- Zan, S.J. Experimental Determination of Rotor Thrust in a Ship Airwake. J. Am. Helicopter Soc. 2002, 4, 100–108. [Google Scholar] [CrossRef]
- Czerwiec, R.; Plosky, S. LHA Airwake Wind Tunnel and CFD Comparison with and Without Bow Flap. In Proceedings of the 22nd Applied Aerodynamics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Zheng, Y.Y. Investigations on Active Flow Control Methods for Helicopter/Ship Dynamic-Interface Optimization. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. [Google Scholar]
- Lee, R.G.; Zan, S.J. Unsteady aerodynamic loading on a helicopter fuselage in a ship airwake. J. Am. Helicopter Soc. 2004, 2, 149–159. [Google Scholar] [CrossRef]
- Wu, S.Y. Study on the Influence of Dynamicsurface Moving Flow Field Underhelicopter/Ship Coupling. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Jaap, V.M.; Okko, J.B.; Jasper, V.V.; Joop, H.M.G. Computational ship airwake determination to support helicopter-ship dynamic interface assessment. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Choi, J.; Miklosovic, D.S. LES Simulations using the Moving Mesh Method with Comparison to Experimental Results for a Periodic Ship Airwake. In Proceedings of the AIAA Aviation Forum, Online, 15–19 June 2020. [Google Scholar]
- Chun, C.W.; Gao, S.; Sun, W.S. Analysis of Unmanned Helicopter Hovering in Ship Flow Field over Flight Deck. J. Nanjing Univ. Aeronaut. Astronaut. 1999, 6, 614–629. [Google Scholar]
- Shi, Y.; Su, D.; Xu, G. Numerical investigation of the influence of passive/active flow control on ship/helicopter dynamic interface. Aerosp. Sci. Technol. 2020, 106, 106205. [Google Scholar] [CrossRef]
- Linton, D.; Thornber, B. Quantifying uncertainty in turbulence resolving ship airwake simulations. Ocean. Eng. 2021, 229, 108983. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.B.; Zhao, N. Influence of Ship Motion on Flow Field over Modified Simple Frigate Shapes. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 521–534. [Google Scholar]
- Praveen, B.; Vijayakumar, R.; Singh, S.N. Flow characteristics on helodeck of a generic frigate ship model through experiment and CFD. Ocean. Eng. 2022, 250, 110912. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.B.; Zhao, N.; Deng, S.Q. Optimization of ship airwake on a simple frigate. J. Ship Mech. 2023, 27, 10–22. [Google Scholar]
- Dooley, G.; Martin, J.E.; Buchholz, J.H.J. Ship Airwakes in Waves and Motions and Effects on Helicopter Operation. Comput. Fluids 2020, 208, 104627. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, H.; Shuangji, Y.; Ni, T. Numerical investigation for coupled rotor/ship flowfield using two models based on the momentum source method. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1902–1918. [Google Scholar] [CrossRef]
- Cao, Y.; Qin, Y.; Tan, W.; Li, G. Numerical Simulation of Fully Coupled Flow-Field and Operational Limitation Envelopes of Helicopter-Ship Combinations. J. Mar. Sci. Eng. 2022, 10, 1455. [Google Scholar] [CrossRef]
- Lu, Y.; Chang, X.; Chuang, Z. Numerical investigation of the unsteady coupling airflow impact of a full-scale warship with a helicopter during shipboard landing. Eng. Appl. Comput. Fluid Mech. 2020, 14, 954–979. [Google Scholar] [CrossRef]
- Tezdogan, T.; Demirel, Y.K.; Kellett, P.; Khorasanchi, M.; Incecik, A.; Turan, O. Full-scale unsteady RANS CFD simulations of ship behaviour and performance in head seas due to slow steaming. Ocean. Eng. 2015, 97, 186–206. [Google Scholar] [CrossRef]
- Lakshmynarayanana, P.A.K.; Hirdaris, S. Comparison of nonlinear one- and two-way FFSI methods for the prediction of the symmetric response of a containership in waves. Ocean. Eng. 2020, 203, 107179. [Google Scholar] [CrossRef]
- CD-Adapco. UserguideSTAR-CCM+, version 9.0.2; CD-Adapco: Melville, NY, USA, 2014.
- Jiao, J.L.; Huang, S.X.; Tezdogan, T.; Terziev, M.; Soares, C.G. Slamming and green water loads on a ship sailing in regular waves predicted by a coupled CFD–FEA approach. Ocean. Eng. 2021, 241, 110107. [Google Scholar] [CrossRef]
- Querard, A.B.G.; Temarel, P.; Turnock, S.R. Influence of viscous effects on the hydrodynamics of ship-like sections undergoing symmetric and anti-symmetric motions, using RANS. In Proceedings of the ASME 27th Interna-tional Conference on Offshore Mechanics and Arctic Engineering (OMAE), Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Kim, S.P.; Lee, H.H. Fully nonlinear seakeeping analysis based on CFD simulations. In Proceedings of the 21st International Offshore and PolarEngineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Enger, S.; Peric, M.; Peric, R. Simulation of flow around KCS-hull. In Proceedings of the Gothenburg 2010-A Workshop on Numerical Ship Hydrodynamics, Gothenburg, Sweden, 8–10 December 2010. [Google Scholar]
- Shinoda, P.M.; Norman, T.R.; Jacklin, S.A.; Bernhard, A.P.F.; Haber, A. Investigation of a Full-Scale Wide Chord Blade Rotor System in the NASA Ames 40-by 80-Foot Wind Tunnel. In Report of Aeroflightdynamics Directorate (AMRDEC); NASA: Washington, DC, USA, 2004. [Google Scholar]
- Shinoda, P.M.; Yeo, H.; Itss, R.; Norman, T.R. Rotor Performance of a UH-60 Rotor System in the NASA Ames 80- by 120-Foot Wind Tunnel. In Report of US Army Aeroflightdynamics Directorate (AMCOM); NASA: Washington, DC, USA, 2004. [Google Scholar]
- Xiao, Z.Y. Investigation of Computational ModelingTechniques for Rotor Flowfields; China Aerodynamics Research and Development Center: Mianyang, China, 2007. [Google Scholar]
- William, G.B. Aerodynamic Characteristics of SC1095 and SC1094 R8 Airfoils; Report No.: NASA-TP 2003-212265; NASA: Washington, DC, USA, 2003.
- Lv, L.; Chen, Z.G. Parametric design method for multiple period stablenumerical wave-generation. Chin. J. Ship Res. 2022, 17, 99–107. [Google Scholar]
- Zhang, F.; Xu, H.; Ball, N. Numerical Simulation of Unsteady Flow Over SFS 2 Ship Model. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Guo, D.M.; Chen, Z.Y.; Duan, F. Dynamic Simulations of influence of ship rolling motion on aerodynamic flow field and helicopter loading under helicopter-ship coupling. In Proceedings of the ASME 2024 43nd International Conference on Ocean, Offshore and Arctic Engineering, Singapore, 9–14 June 2024. [Google Scholar]
- Yan, L. Key Technologies of Ship Motionsimulation Base on Sea State. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2008. [Google Scholar]
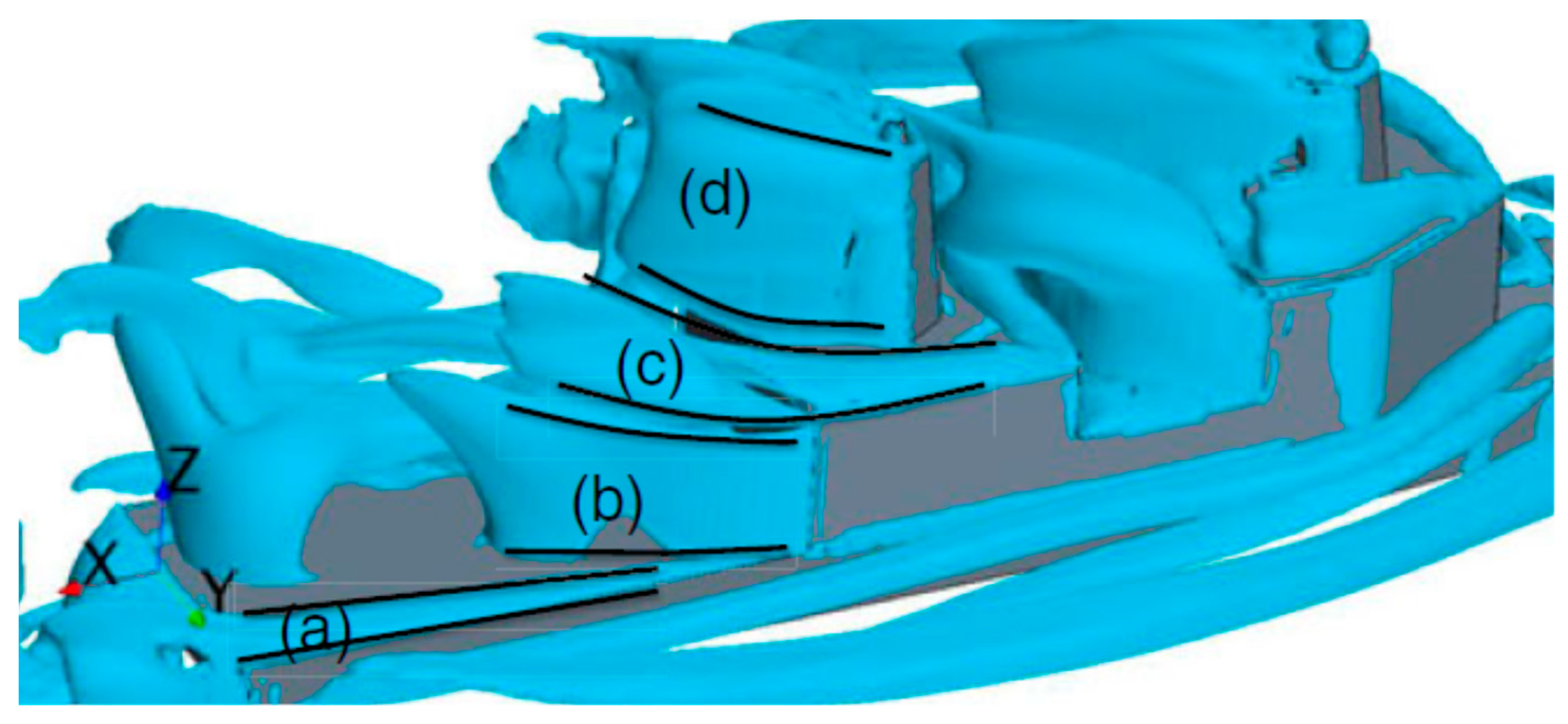
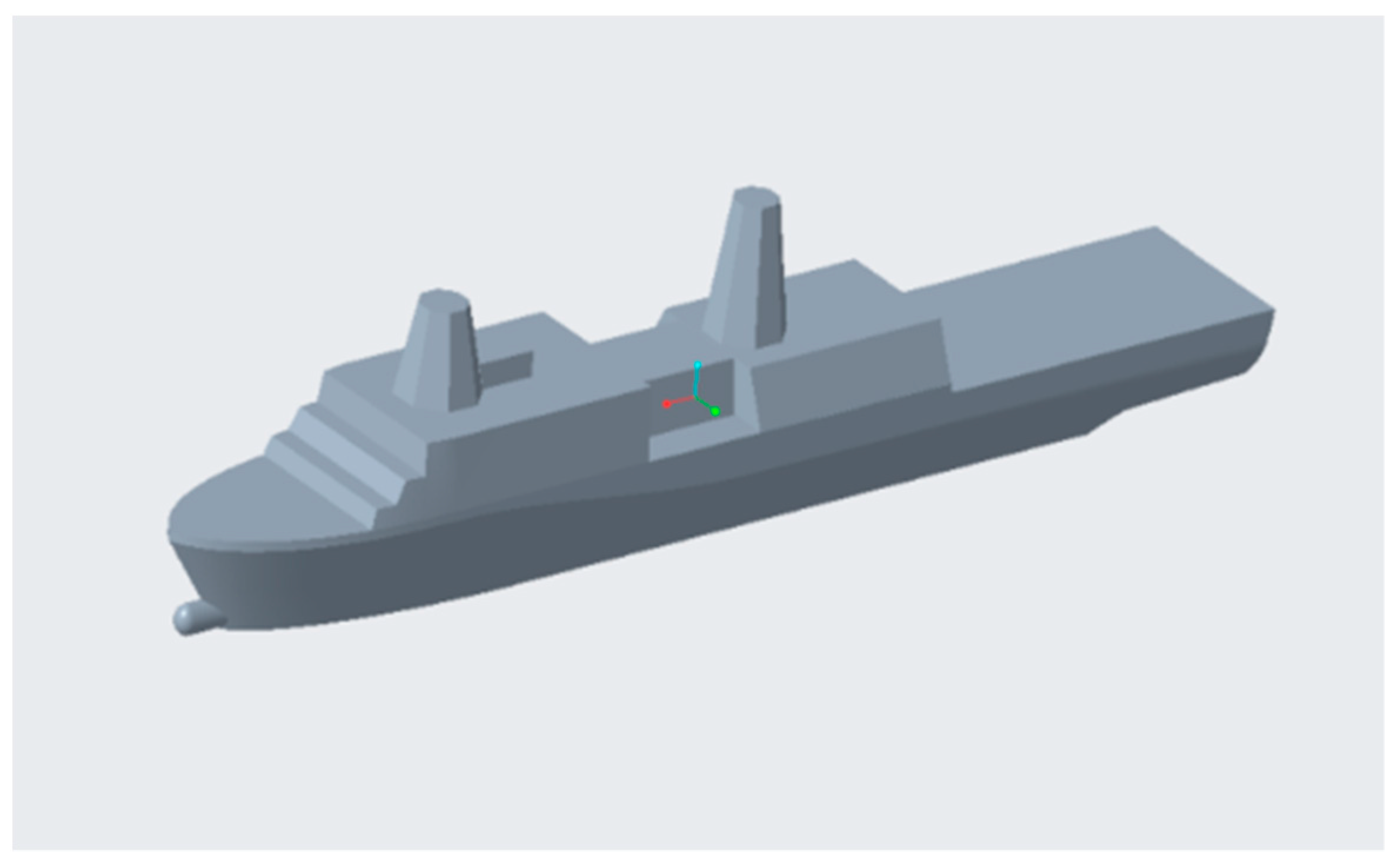








| Main Particular | Value |
|---|---|
| Length (L, m) | 208.5 |
| Beam (W, m) | 31.9 |
| Draft (D, m) | 7 |
| Displacement volume (m3) | 24,522 |
| Longitudinal COG (xg/L) | 0.469 |
| Transverse COG (yg/W) | 0.5 |
| Vertical COG (zg/L) | 0.208 |
| Ixx (kg·m2) | 1944.45 |
| Iyy (kg·m2) | 26,335.49 |
| Design speed (knot) | 22 |
| Parameter | Value |
|---|---|
| Fuselage length | 19.76 m |
| Overall height | 5.13 m |
| Number of main rotor blades | 4 |
| Main rotor diameter | 16.36 m |
| Main rotor chord length | 0.53 m |
| Main rotor tip sweep | 20° |
| Main rotor tip negative twist | 16° |
| Main rotor solidity | 0.083 |
| Main rotor tip speed | 221 m/s |
| Main rotor airfoil profiles | SC1094 R8, SC1095 |
| Coarse Mesh | Medium Mesh | Fine Mesh | |
|---|---|---|---|
| Minimum grid size | 0.042 m | 0.03 m | 0.02 m |
| Total grid count | 0.897 million | 2.129 million | 7 million |
| Ship surface Y+ | 35 | 35 | 35 |
| CFL | 1 | 1 | 1 |
| Total computation time | 21.2 h | 64.8 h | 240.9 h |
| Monitoring Line | Roll Average Influence | Pitch Average Influence | Heave Average Influence | |
|---|---|---|---|---|
| P1 | Deck 4 | 0.220 | 0.075 | 0.705 |
| Deck 5 | 0.114 | 0.313 | 0.573 | |
| Deck 6 | 0.418 | 0.541 | 0.041 | |
| Average influence | 0.251 | 0.310 | 0.439 | |
| P2 | Deck 4 | 0.546 | 0.192 | 0.262 |
| Deck 5 | 0.209 | 0.543 | 0.249 | |
| Deck 6 | 0.213 | 0.764 | 0.023 | |
| Average influence | 0.322 | 0.499 | 0.178 | |
| P3 | Deck 4 | 0.309 | 0.385 | 0.307 |
| Deck 5 | 0.019 | 0.803 | 0.178 | |
| Deck 6 | 0.040 | 0.847 | 0.113 | |
| Average influence | 0.122 | 0.678 | 0.199 |
| Coupling Index MX | Coupling Index MY | Coupling Index RZ | |
|---|---|---|---|
| P1 | 1.37 | 0.51 | 0.34 |
| P2 | 0.92 | 0.61 | 0.61 |
| P3 | 1.01 | 0.86 | 0.82 |
| Motion | Coupled Flow Field | Rotor Loads |
|---|---|---|
| Roll | Deck 4: Roll is the main influencing factor. Significant impact on TI at the deck edge and rotor edge. Deck 5: Rotor airflow is the main factor, but roll may affect the turbulence distribution. In phase P3, the turbulence intensity at the edge of the deck increases significantly. Deck 6: The numerical variation in TI is dominated by the rotor. | MX: Significant dynamic characteristics in P2. MY: Minimal impact from rolling motion, with only a 5% increase in P1. RZ: As the helicopter lands, the impact gradually intensifies, with a 32.81% increase in P3. Summary: MX > RZ > MY |
| Pitch | Deck 4: Motion mainly affects the rotor center in P1. Motion mainly affects the deck/rotor edge in P2 and P3. Deck 5–6: Influence on the coupled flow field is weak, especially in the rotor center. | MX: The MX component decreases during the early landing. MY: MY instability increases in the early landing phase, necessitating careful longitudinal pitch control. RZ: RZ reaches its peak in P2. |
| Heave | Overall, the impact on the deck edge increases with landing. Deck 4: Rotor center is most significantly affected in P1. Deck 5: Rotor edge region is most significantly affected in P3. Deck 6: Basically no effect on the rotor edge zone and rotor center zone. | MX: Lateral asymmetry in the rotor’s surrounding flow leads to a sharp 160.94% surge in MX in P3. MY: Attention should be paid to it in P3. RZ: RMS continues to increase with landing. Summary: MX > RZ > MY. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Liu, Y.; Ma, Y.; Chen, Z.; Zhao, W. CFD Investigation on Effect of Ship–Helicopter Coupling Motions on Aerodynamic Flow Field and Rotor Loads. J. Mar. Sci. Eng. 2025, 13, 1544. https://doi.org/10.3390/jmse13081544
Liu Z, Liu Y, Ma Y, Chen Z, Zhao W. CFD Investigation on Effect of Ship–Helicopter Coupling Motions on Aerodynamic Flow Field and Rotor Loads. Journal of Marine Science and Engineering. 2025; 13(8):1544. https://doi.org/10.3390/jmse13081544
Chicago/Turabian StyleLiu, Zhouyang, Yang Liu, Yingnan Ma, Zhanyang Chen, and Weidong Zhao. 2025. "CFD Investigation on Effect of Ship–Helicopter Coupling Motions on Aerodynamic Flow Field and Rotor Loads" Journal of Marine Science and Engineering 13, no. 8: 1544. https://doi.org/10.3390/jmse13081544
APA StyleLiu, Z., Liu, Y., Ma, Y., Chen, Z., & Zhao, W. (2025). CFD Investigation on Effect of Ship–Helicopter Coupling Motions on Aerodynamic Flow Field and Rotor Loads. Journal of Marine Science and Engineering, 13(8), 1544. https://doi.org/10.3390/jmse13081544