Intelligent Optimization of Waypoints on the Great Ellipse Routes for Arctic Navigation and Segmental Safety Assessment
Abstract
1. Introduction
1.1. Research Review
1.2. Innovations and Contributions
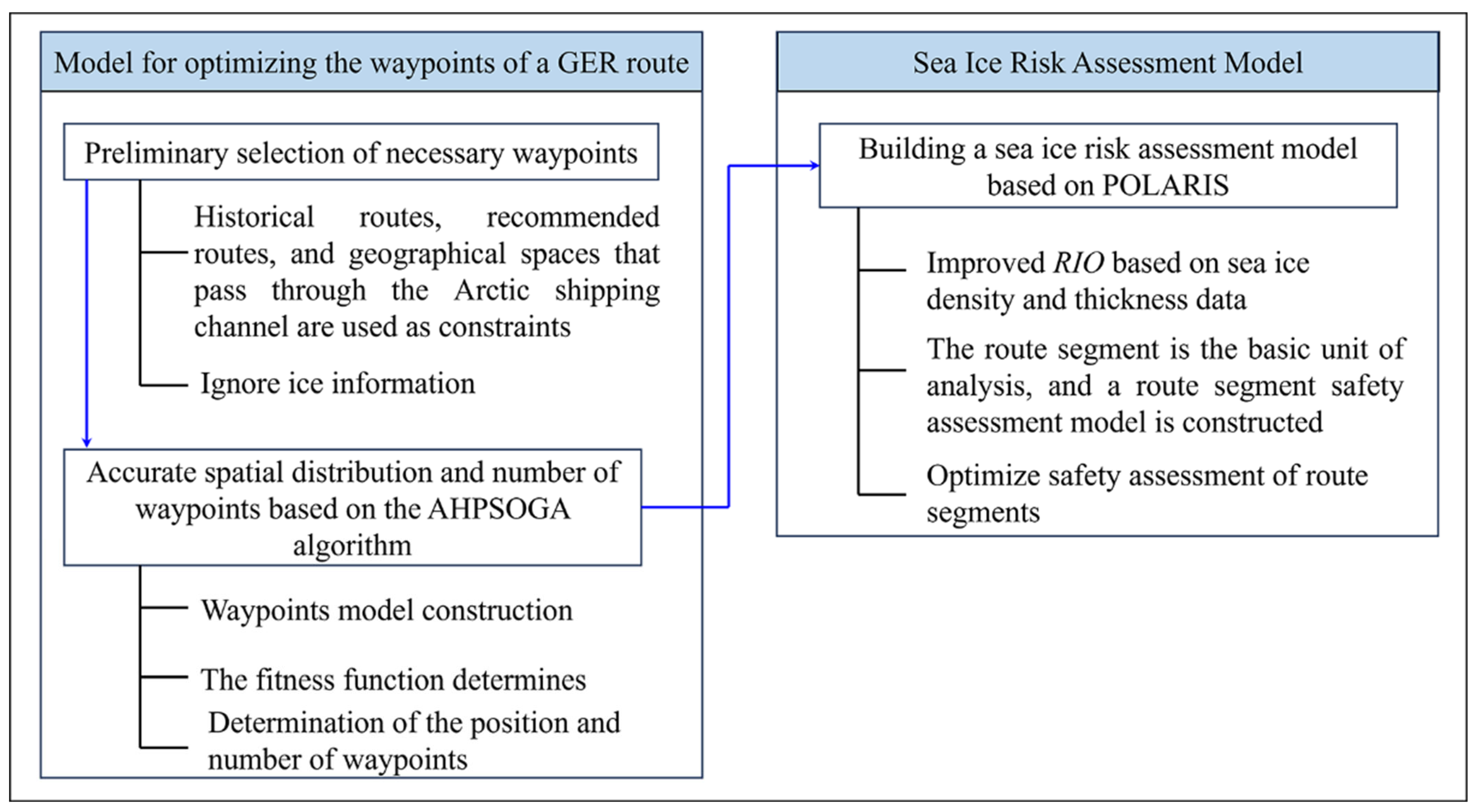
2. Methodology
2.1. Overview
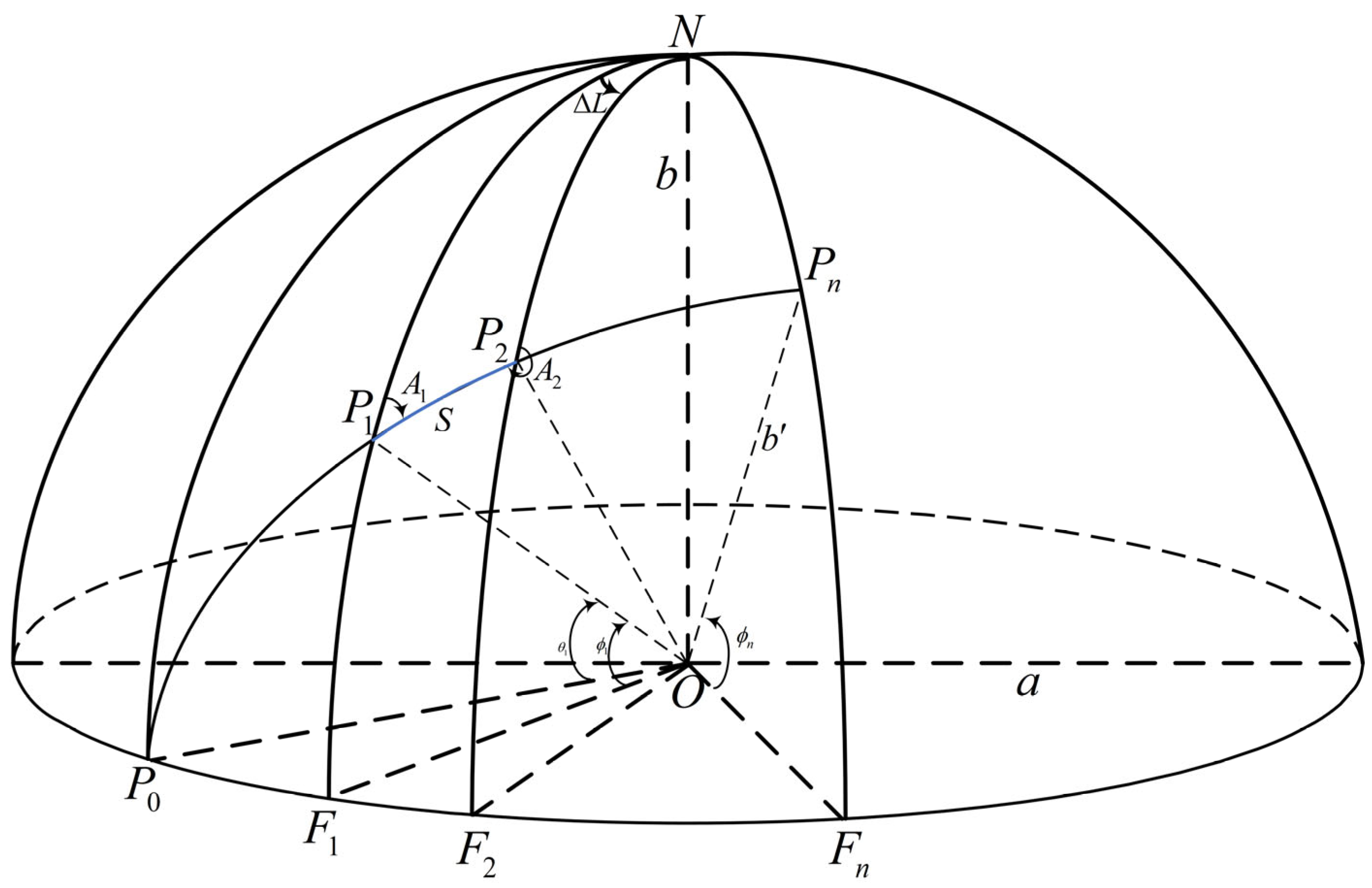
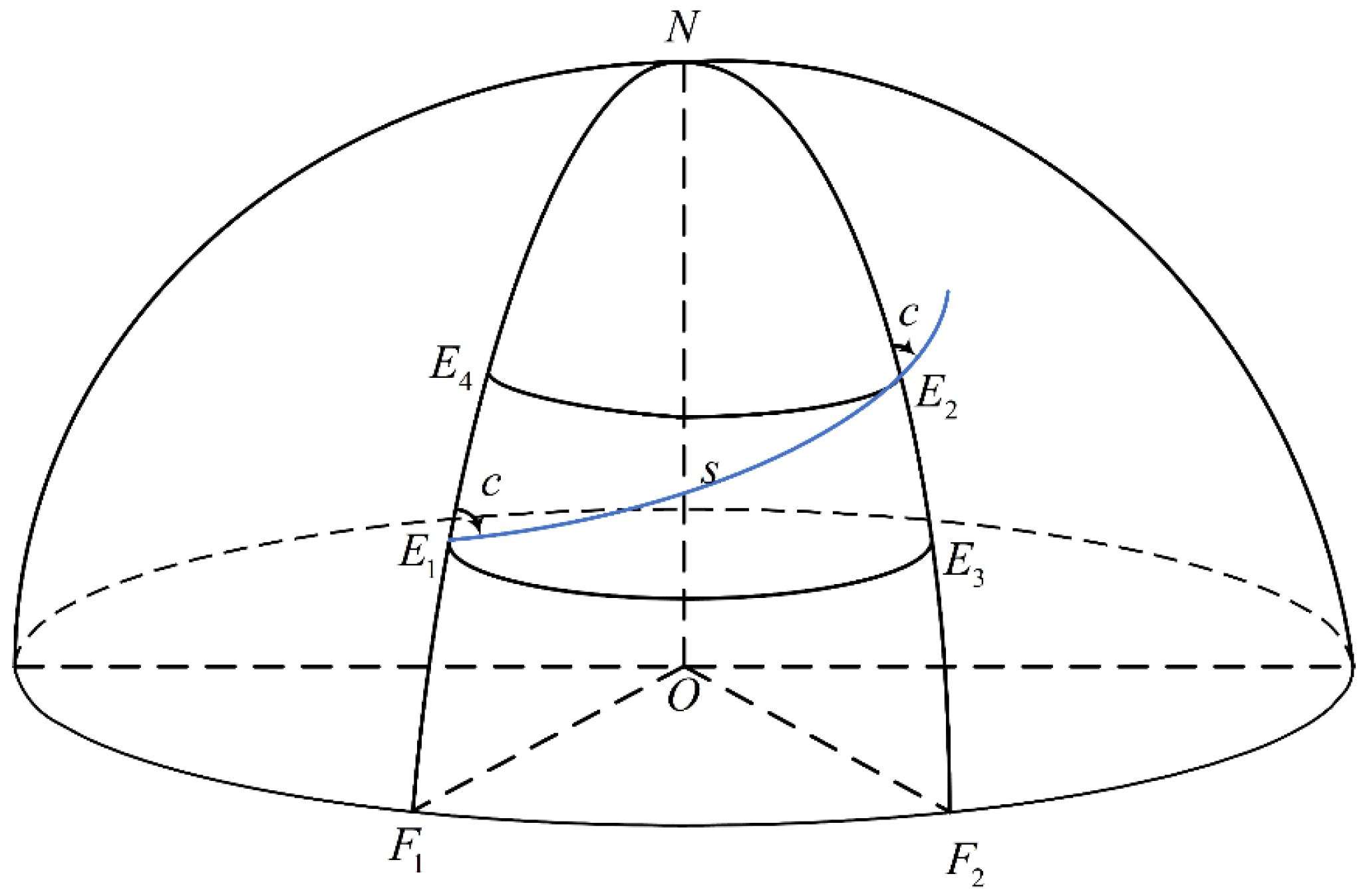
2.2. Great Ellipse Route-Related Formulae
2.2.1. Great Ellipse Route Distance
2.2.2. Rhumb Line Distance and Course
2.2.3. Coordinates of Waypoints
2.2.4. Distance Remaining Benefit for the GER
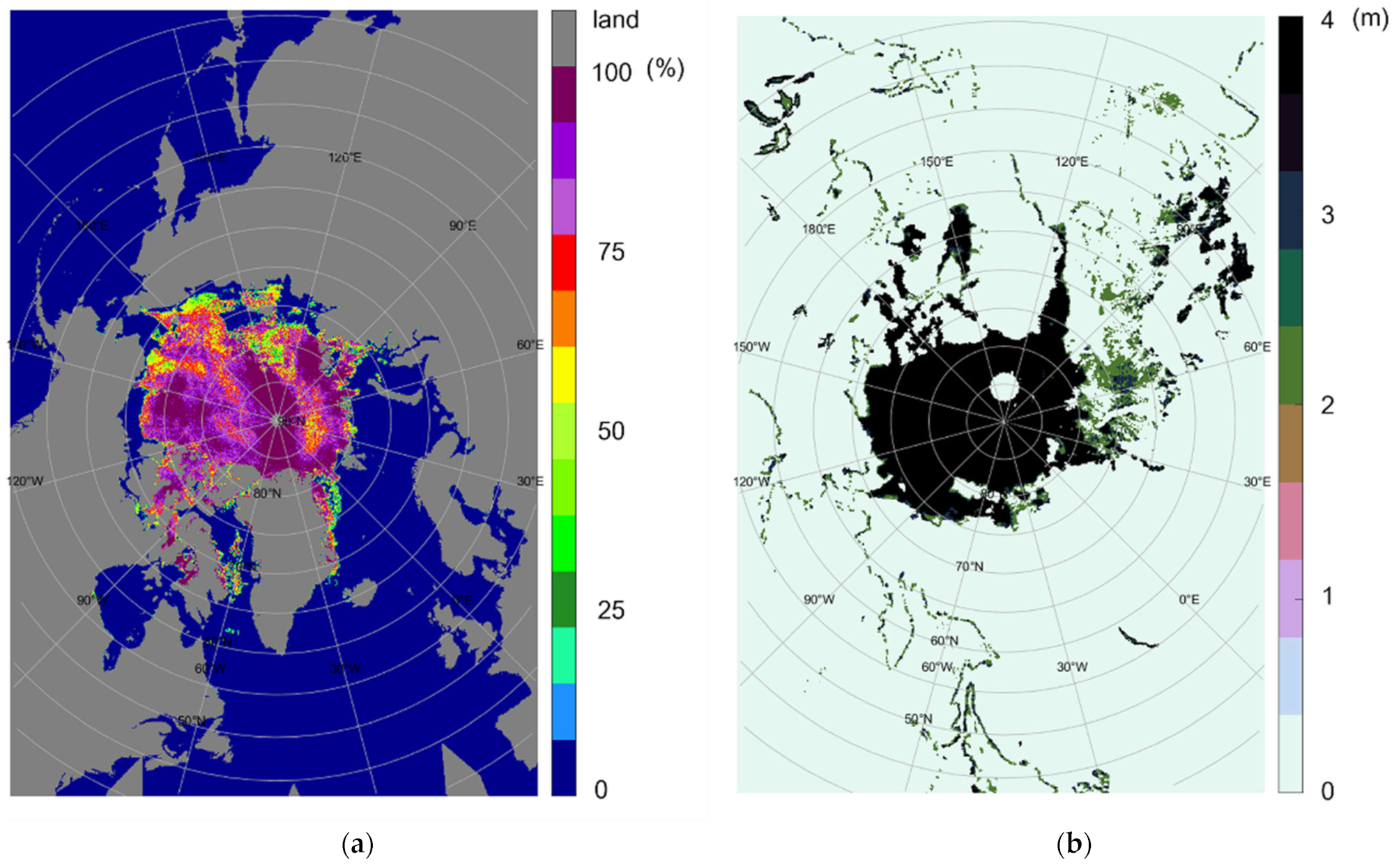
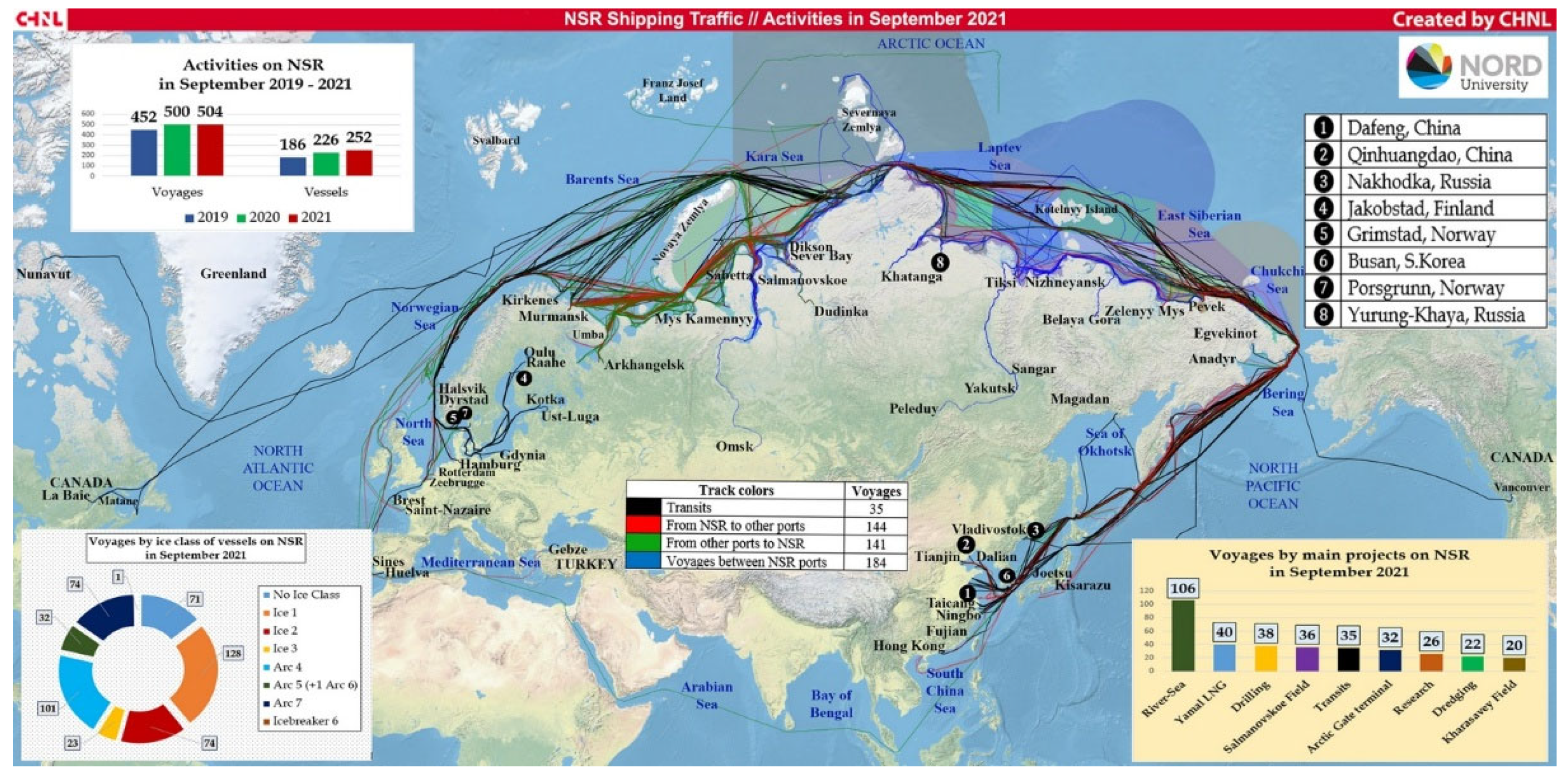
2.3. Research Area and Data Acquisition of Ice Conditions
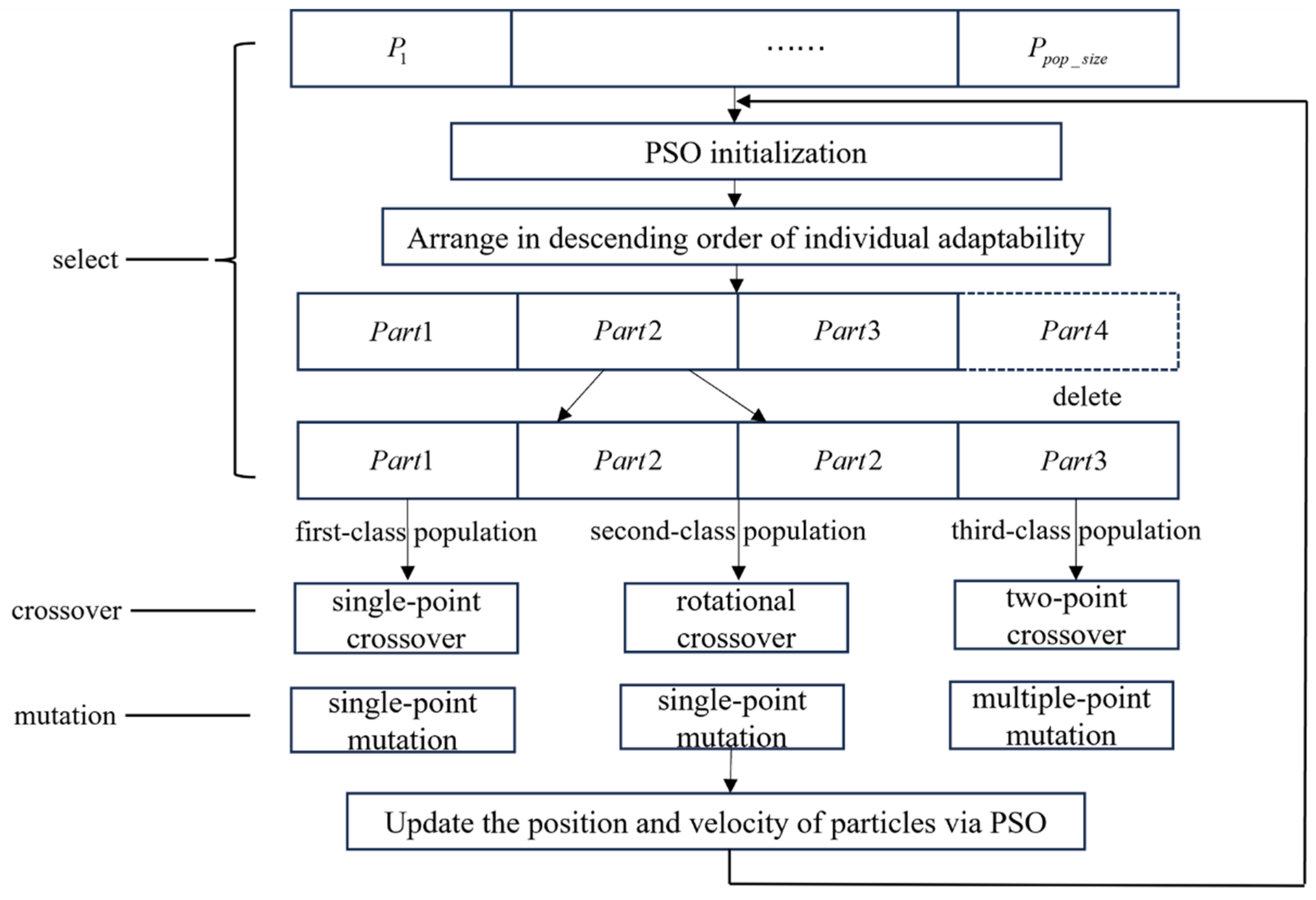
3. Model Optimization of Waypoints for the GER Based on the AHPSOGA Algorithm
3.1. Waypoint Model Construction
3.2. Definition of the Fitness Function
4. POLARIS-Based Sea Ice Risk Assessment Model
4.1. Preprocessing of Sea Ice Data
4.2. Sea Ice Risk Identification Model
4.2.1. RIO Calculation
4.2.2. Safety Assessment of Route Segments
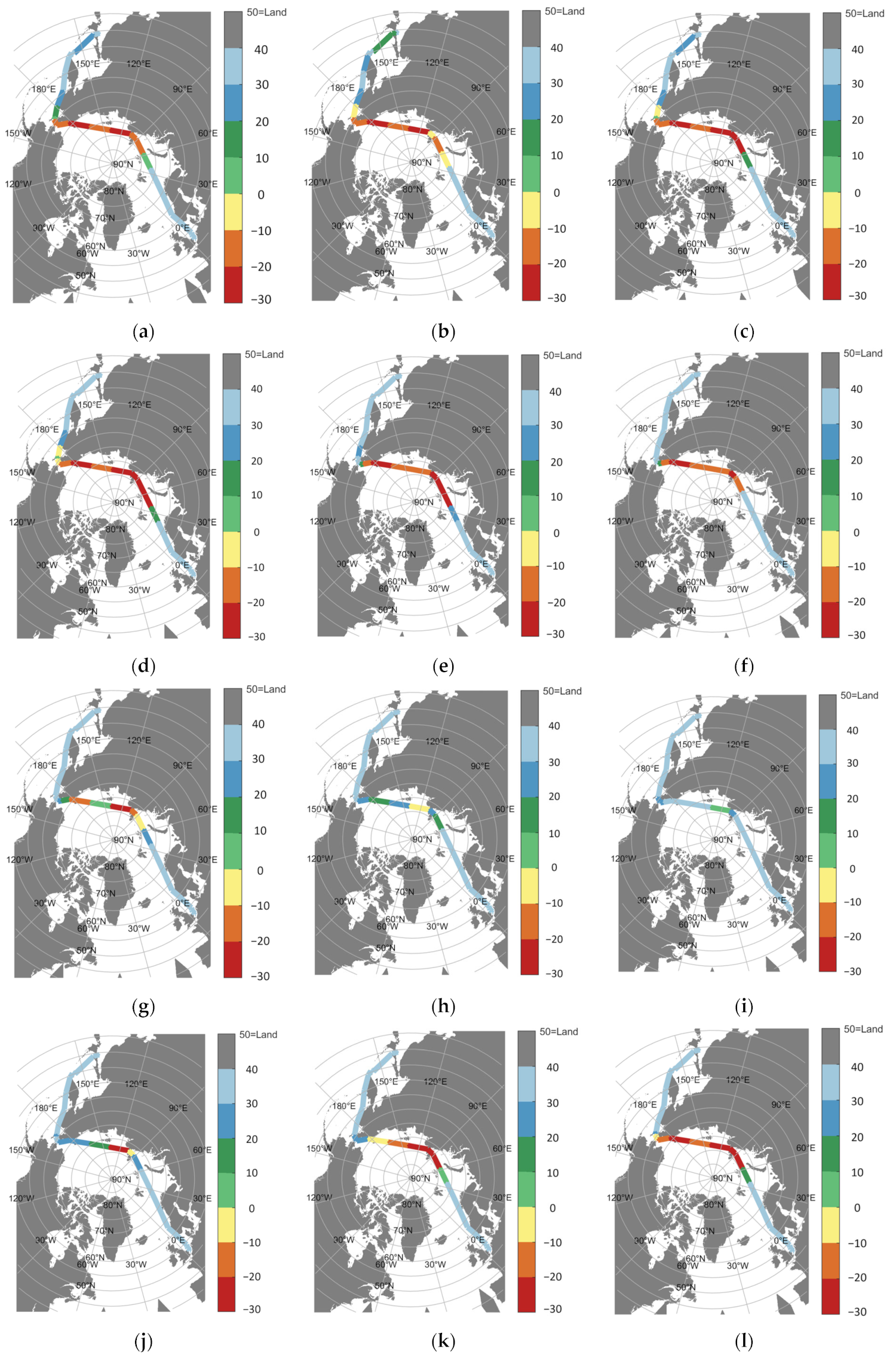
5. Experimental Results
5.1. Model Operation Analysis Based on the AHPSOGA Algorithm
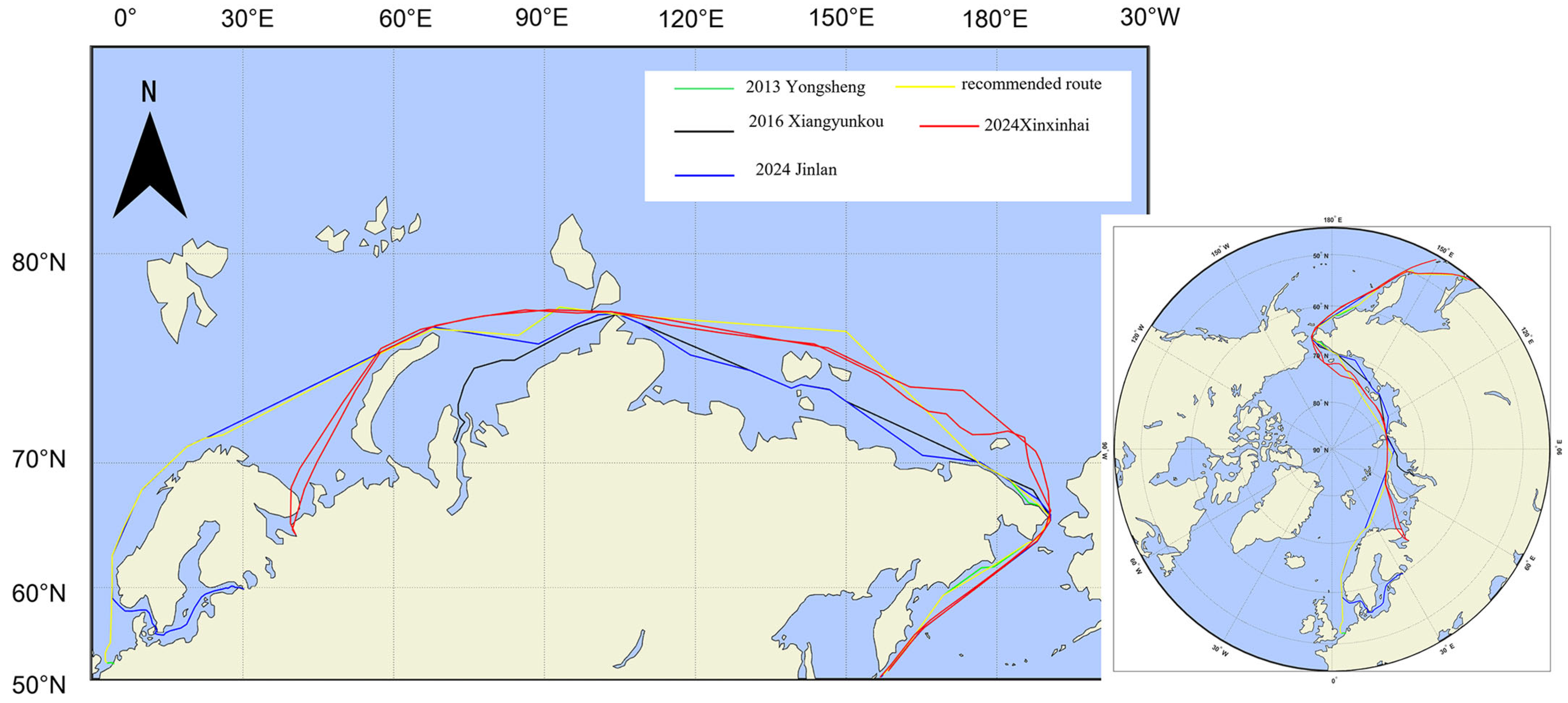
5.2. Comparative Analysis of the Optimization Model Based on the AHPSOGA Algorithm and the Conventional Methods Used in the Shipping Industry
5.3. Optimized Route Segment Safety Assessment
6. Discussion
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| ACO | Ant Colony Optimization |
| GCR | Great Circle Route |
| GER | Great Ellipse Route |
| POLARIS | Polar·Operational·Limits·Assessment Risk Index·System |
| RL | Rhumb Line |
| GNSS | Global Navigation Satellite System |
| AIS | Automatic Identification System |
| IMO | International Maritime Organization |
| WMO | World Meteorological Organization |
| RIO | Risk Index Outcome |
| IACS | International Association of Classification Societies |
Appendix A
| Algorithm A1: Adaptive Hybrid Particle Swarm Optimization-Genetic Algorithm |
| Initialization the relevant parameters Input PopSize, max_iter Calculate the theoretical distance of the GER Set the initial number of waypoints: n = 1 Initialize particle positions and velocities For iteration < max_iter: Calculate the fitness value of the particle and update the individual optimum and global optimum Calculate the adaptive crossover rate and mutation rate Calculate the adaptive inertia weight Descending order of adaptability Delete the 1/4 individuals with the worst fitness values Divide the remaining individuals into first-, second- and third-class populations according to the grouping strategy Duplicate the secondary population in the remaining individuals to form a new population The individuals in the third-class population perform a two-point crossover and multiple-point mutation operation The individuals in the secondary population perform a rotational crossover and single-point mutation operation The individuals in the primary population perform a single-point cross and single-point mutation operation Update the speed and position of the particles Judging whether the fitness value is optimal If the fitness value is not optimal update the individual optimum and global optimum and calculate the fitness value of the particle Else Judging whether the RB value is less than 12 If the RB value is not less than 12 n = n + 1 Else Output the position and number of waypoints End |
Appendix B
References
- Fu, S.; Yan, X.; Zhang, D.; Zhang, M. Risk influencing factors analysis of Arctic maritime transportation systems: A Chinese perspective. Marit. Policy Manag. 2018, 45, 439–455. [Google Scholar] [CrossRef]
- Bilge, T.A.; Fournier, N.; Mignac, D.; Hume-Wright, L.; Bertino, L.; Williams, T.; Tietsche, S. An Evaluation of the Performance of Sea Ice Thickness Forecasts to Support Arctic Marine Transport. J. Mar. Sci. Eng. 2022, 10, 265. [Google Scholar] [CrossRef]
- Shu, Y.; Cui, H.; Song, L.; Gan, L.; Xu, S.; Wu, J.; Zheng, C. Influence of sea ice on ship routes and speed along the Arctic Northeast Passage. Ocean. Coast Manag. 2024, 256, 107320. [Google Scholar] [CrossRef]
- Ma, L.; Qian, S.; Dong, H.; Fan, J.; Xu, J.; Cao, L.; Xu, S.; Li, X.; Cai, C.; Huang, Y.; et al. Navigability of Liquefied Natural Gas Carriers Along the Northern Sea Route. J. Mar. Sci. Eng. 2024, 12, 2166. [Google Scholar] [CrossRef]
- Zheng, Q.; Li, W.; Shao, Q.; Han, G.; Wang, X. A mid-and long-term arctic sea ice concentration prediction model based on deep learning technology. Remote Sens. 2022, 14, 2889. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, Y.; Lu, Y.; Yuan, L.; Li, F.; Li, R. A Dynamic Bayesian Network model for ship navigation risk in the Arctic Northeast Passage. Ocean Eng. 2024, 312, 119024. [Google Scholar] [CrossRef]
- Maritime Safety Administration of the People’s Republic of China. Arctic Navigation Guide (Northeast Passage); People’s Transportation Publishing House: Beijing, China, 2021.
- Wang, X.; Tang, Z.; Ji, C.; Guo, Z. Polar navigation method based on the great circle chart of the positive axis. Navig. China 2022, 45, 62–68. [Google Scholar]
- Hsieh, T.-H.; Meng, Q.; Han, B.; Wang, S.; Wu, X. Optimization of waypoints on the great circle route based on genetic algorithm and fuzzy logic. J. Mar. Sci. Eng. 2023, 11, 358. [Google Scholar] [CrossRef]
- Earle, M. Sphere to spheroid comparisons. J. Navig. 2006, 59, 491–496. [Google Scholar] [CrossRef]
- Ding, J. The Formula for Calculating the Great Ellipse Geographic Coordinate. Tianjin Naut. 1993, 41–43. [Google Scholar]
- Ding, J. On the relationship between the isometric route and the great ellipse. Tianjin Navig. 1994, 28–29. [Google Scholar]
- Earle, M. A vector solution for navigation on a great ellipse. J. Navig. 2000, 53, 473–481. [Google Scholar] [CrossRef]
- Earle, M. Vector solutions for azimuth. J. Navig. 2008, 61, 537–545. [Google Scholar] [CrossRef]
- Earle, M. Accurate harmonic series for inverse and direct solutions for the great ellipse. J. Navig. 2011, 64, 557–570. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Solutions to the direct and inverse navigation problems on the great ellipse. J. Geod. Sci. 2012, 2, 200–205. [Google Scholar] [CrossRef][Green Version]
- Liu, W.; Bian, H.; Wang, R.; Wen, C. Space vector method for great ellipse route design. Acta Geod. Cartogr. Sin. 2015, 44, 741–746. [Google Scholar]
- Fang, X. RNAV Route Design Based on Ellipsoid Model. Sci. Surv. Mapp. 2008, 33, 149–150. [Google Scholar]
- Li, H.; Wang, R. Great Elliptic Route method and its navigation parameter calculation. J. Nav. Univ. Eng. 2009, 21, 7–12. [Google Scholar]
- Jiao, C.; Wan, X.; Li, H.; Bian, S. Dynamic projection method of electronic navigational charts for polar navigation. J. Mar. Sci. Eng. 2024, 12, 577. [Google Scholar] [CrossRef]
- Bowditch, N. An epitome of navigation and nautical astronomy. In American Practical Navigator; US Government Printing Office: Washington, NW, USA, 1912. [Google Scholar]
- Holm, R.J. Great Circle Waypoints for Inertial Equipped Aircraft. Navig. J. Inst. Navig. 1972, 19, 191–194. [Google Scholar] [CrossRef]
- Keys, G. Practical Navigation by Calculator; Osprey Publishing: Oxford, UK, 1983. [Google Scholar]
- Chen, C.-L.; Hsieh, T.-H.; Hsu, T.-P. A novel approach to solve the great circle track based on rotation transformation. J. Mar. Sci. Technol. 2015, 23, 13–20. [Google Scholar]
- Hsu, T.-P.; Hsieh, T.-H. Evaluation and Execution of Great Elliptic Sailing. J. Navig. 2017, 70, 1023–1040. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Y.; Zhou, J.; Wu, H. Mini-Review of Unmanned Vehicle Route Planning Based on Ant Colony Algorithm. Autom. Mach. Learn. 2023, 4, 42–46. [Google Scholar] [CrossRef]
- Zhao, L.; Li, F.; Sun, D.; Zhao, Z. An improved ant colony algorithm based on Q-Learning for route planning of autonomous vehicle. Int. J. Comput. Commun. Control 2024, 19, 5382. [Google Scholar] [CrossRef]
- Heng, H.; Mohd, G.M.H.; Wan, R. Exploring the application of ant colony optimization in path planning for Unmanned Surface Vehicles. Ocean Eng. 2024, 311, 118738. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Perihan, P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Shi, K.; Huang, L.; Jiang, D.; Sun, Y.; Tong, X.; Xie, Y.; Fang, Z. Path planning optimization of intelligent vehicle based on improved genetic and ant colony hybrid algorithm. Front. Bioeng. Biotechnol. 2022, 10, 905983. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Zhang, Z.; Wang, H. Multicriteria ship route planning method based on improved particle swarm optimization–genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 357. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, C.; Yu, H.; Fei, H.; Li, D. Path planning of unmanned vehicles based on adaptive particle swarm optimization algorithm. Comput. Commun. 2024, 216, 112–129. [Google Scholar] [CrossRef]
- Tsou, M.-C.; Hsueh, C.-K. The Study of Ship Collision Avoidance Route Planning by Ant Colony Algorithm. J. Mar. Sci. Technol. Taiwan 2010, 18, 16. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, F.; Zhao, P.; Tong, X.; Huang, J.; Chen, K.; Zhang, H. Ship route planning based on particle swarm optimization. In Proceedings of the 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Jinzhou, China, 6–8 June 2019; pp. 211–215. [Google Scholar]
- Tong, B.; Hu, J. Path planning for ships navigating in ice areas based on an improved ant colony algorithm. Navig. China 2020, 43, 24–28. [Google Scholar]
- Zhang, C.; Zhang, D.; Zhang, M.; Zhang, J.; Mao, W. A three-dimensional ant colony algorithm for multi-objective ice routing of a ship in the Arctic area. Ocean Eng. 2022, 266, 113241. [Google Scholar] [CrossRef]
- Lee, H.-W.; Roh, M.-I.; Kim, K.-S. Ship route planning in Arctic Ocean based on POLARIS. Ocean Eng. 2021, 234, 109297. [Google Scholar] [CrossRef]
- Wang, L.; Scott, K.A.; Clausi, D.A. Sea ice concentration estimation during freeze-up from SAR imagery using a convolutional neural network. Remote Sens. 2017, 9, 408. [Google Scholar] [CrossRef]
- Choi, M.; De Silva, L.W.A.; Yamaguchi, H. Artificial neural network for the short-term prediction of arctic sea ice concentration. Remote Sens. 2019, 11, 1071. [Google Scholar] [CrossRef]
- Jiang, J.; He, S.; Jiang, H.; Chen, X.; Ji, S. Research on Sea Ice and Local Ice Load Monitoring System for Polar Cargo Vessels. J. Mar. Sci. Eng. 2025, 13, 808. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, J.; Wang, G.; Jiang, Y.; Sun, Y.; Zhao, H. STDNet: Spatio-Temporal Decompose Network for Predicting Arctic Sea Ice Concentration. Remote Sens. 2024, 16, 4534. [Google Scholar] [CrossRef]
- Huang, X.; Bian, S. A new solution to the length of the sectional ellipse arc in geodetic problems. Hydrogr. Surv. Charting 2007, 21–23. [Google Scholar]
- Zhang, X.; Jiao, C.; Li, H.; Bian, S.; Zhang, S. Analysis of three forms of meridian arc length positive and negative solution expressions. Mar. Surv. Mapp. 2023, 43, 70–76. [Google Scholar]
- Royal, N. Admiralty Manual of Navigation. In The Principles of Navigation, 10th ed.; Stationery Office Books: London, UK, 2008. [Google Scholar]
- Snyder, J. An equal-area map projection for polyhedral globes. Cartogr. Int. J. Geogr. Inf. Geovis. 1992, 29, 10–21. [Google Scholar] [CrossRef]
- Ma, L.; Qian, S.; Mou, X.; Fan, J.; Xu, J.; Cao, L.; Xu, B.; Yao, B.; Li, X.; Li, Y. Comparative Research on Vessel Navigability on the Northern Sea Route Based on the NSR Admission Criteria and POLARIS Methodology. J. Mar. Sci. Eng. 2025, 13, 1282. [Google Scholar] [CrossRef]
- An, L.; Ma, L.; Wang, H.; Zhang, H.-Y.; Li, Z.-H. Research on navigation risk of the Arctic Northeast Passage based on POLARIS. J. Navig. 2022, 75, 455–475. [Google Scholar] [CrossRef]
- Li, Z.; Ringsberg, J.W.; Rita, F. A voyage planning tool for ships sailing between Europe and Asia via the Arctic. Ships Offshore Struct. 2020, 15, S10–S19. [Google Scholar] [CrossRef]
- Xie, Z.; Xu, H.; Wang, S.; Han, B.; Wu, Z.; Liu, W. Sea-ice risk calculation for the Arctic shipping routes based on segmental safety assessment. Navig. China 2023, 46, 36–41, 58. [Google Scholar]
- Liu, C.; Zhou, Y.; Yang, Z.; Li, Y.; Li, T. Optimizing the scheduling scheme for NSR/SCR tramp vessel shipping between Asia and Europe. Ocean Eng. 2024, 304, 117747. [Google Scholar] [CrossRef]
- Li, Z.; Yao, C.; Zhu, X.; Gao, G.; Hu, S. A decision support model for ship navigation in Arctic waters based on dynamic risk assessment. Ocean Eng. 2022, 244, 110427. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, Y.; Xu, F.; Gan, L.; Lee, P.T.-W.; Yin, J.; Chen, J. Path planning for ships assisted by the icebreaker in ice-covered waters in the Northern Sea Route based on optimal control. Ocean Eng. 2023, 267, 113182. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Y.; Dai, W.; Li, J. Incremental route planning based on daily risk assessment for Arctic navigation. Ocean Eng. 2025, 320, 120294. [Google Scholar] [CrossRef]
- Zvyagina, T.; Zvyagin, P. A model of multi-objective route optimization for a vessel in drifting ice. Reliab. Eng. Syst. Saf. 2022, 218, 108147. [Google Scholar] [CrossRef]



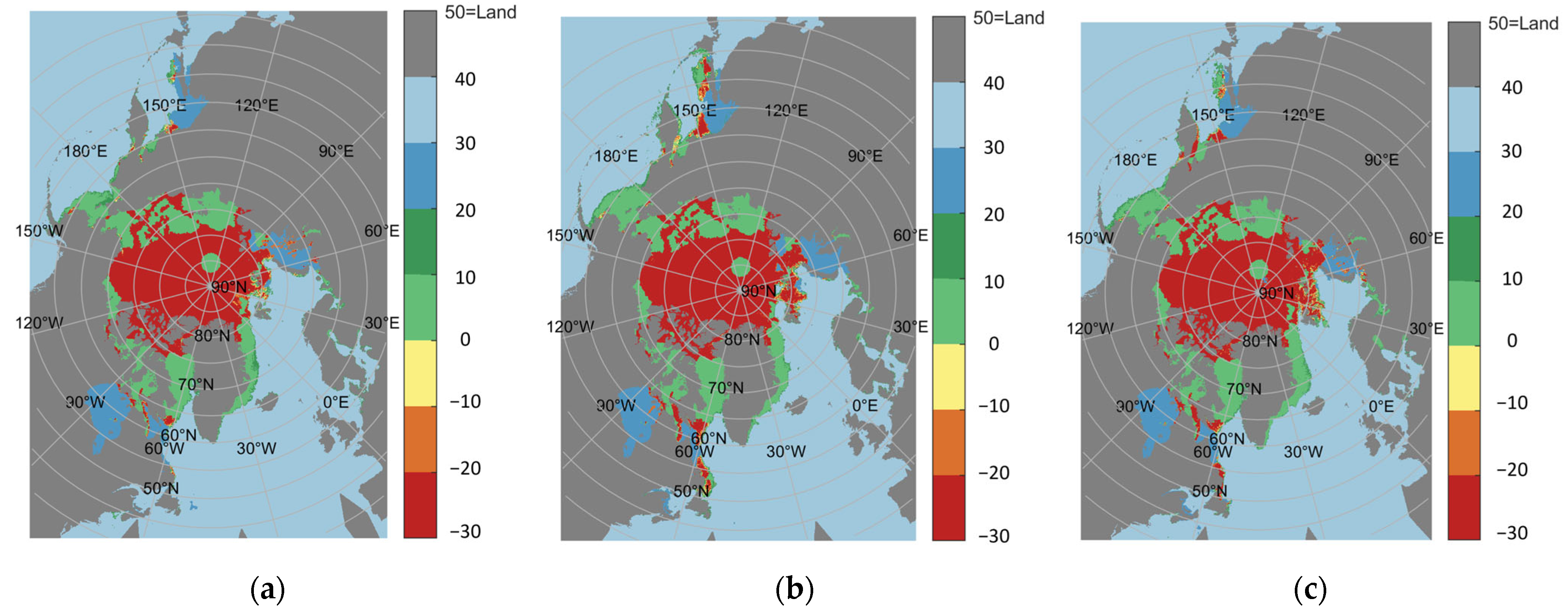
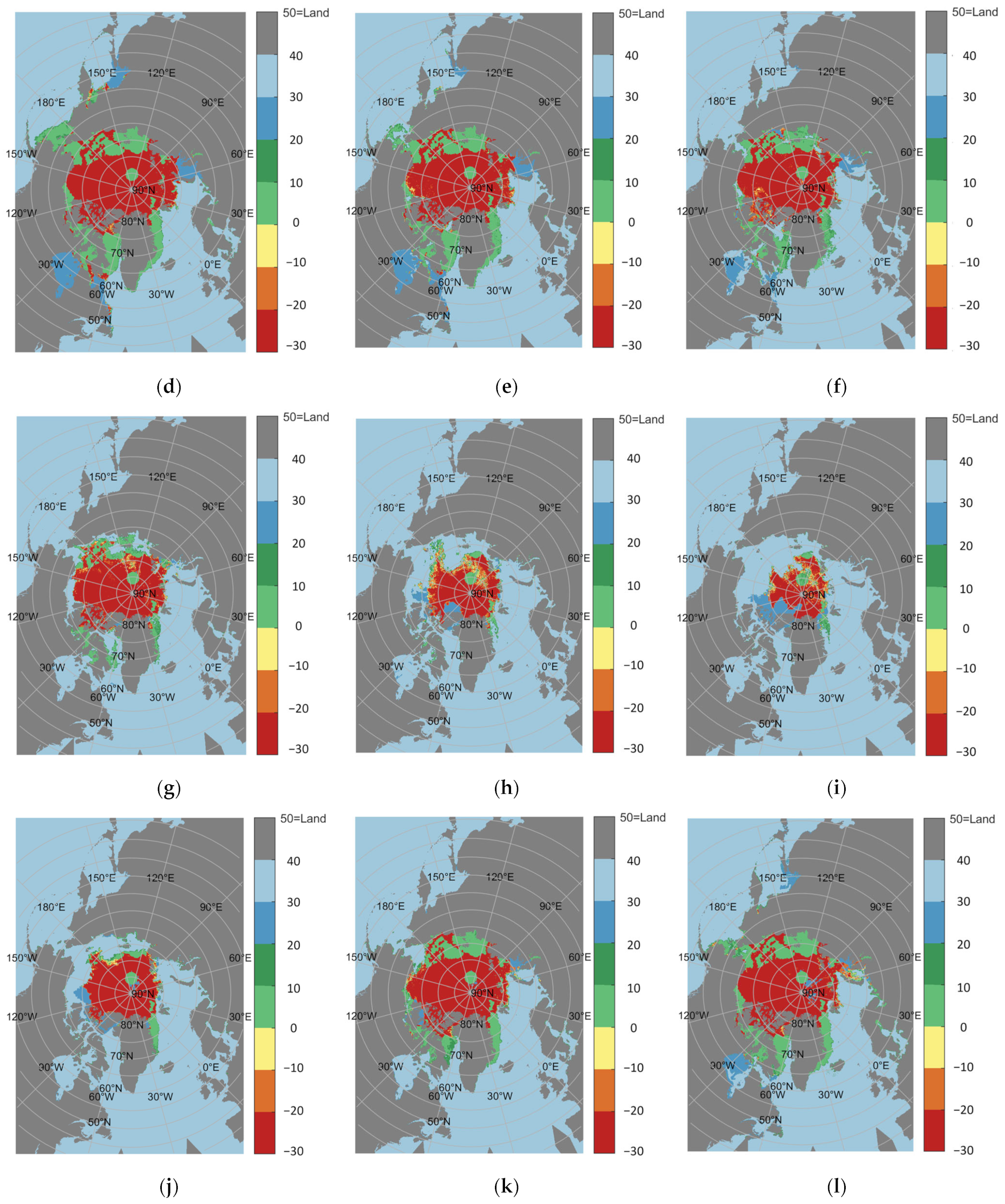


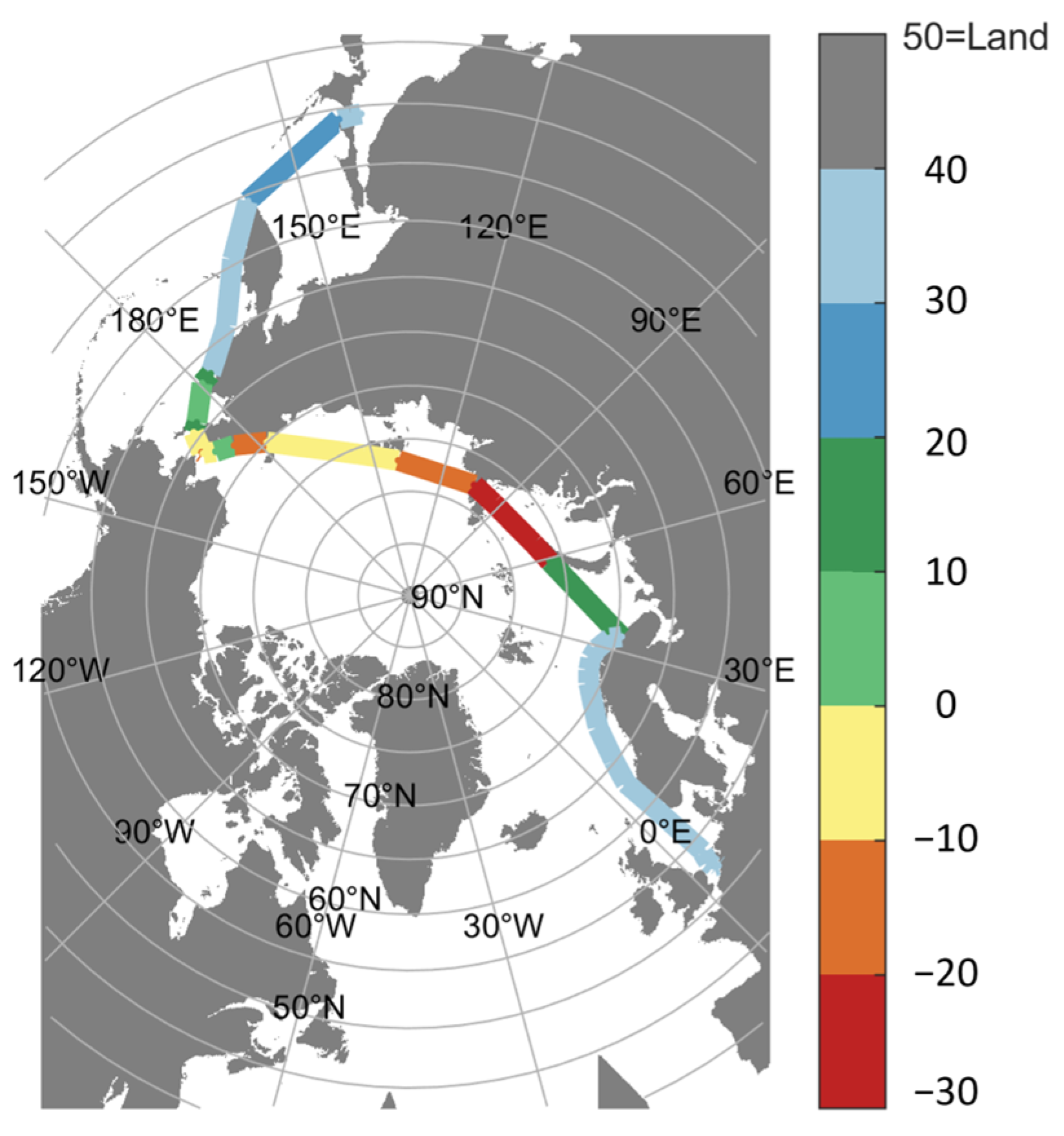
| , | , | , |
| , | , | , |
| Data Source | Variables | Spatial Resolution/km | Temporal Resolution | Matrix Size | Data Format | Website |
|---|---|---|---|---|---|---|
| University of Bremen, Bremen, Germany | density | 3.125 | daily average | 3584 × 2432 | .hdf | https://data.seaice.uni-bremen.de/amsr2/asi_daygrid_swath/ (accessed on 7 August 2025) |
| thickness | 12.5 | 896 × 608 | .nc | https://data.seaice.uni-bremen.de/smos/ (accessed on 7 August 2025) |
| Ice Class /cm | Ice Free0 |
New Ice |
Grey Ice |
Grey White Ice |
Thin First-Year Ice 1st Stage |
Thin First-Year Ice 2nd Stage |
Medium First-Year Ice 1st Stage |
Medium First-Year Ice 2nd Stage |
Thick First-Year Ice | Second-Year Ice |
Light Multi-Year Ice | Heavy Multi-Year Ice >250 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
| PC2 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 0 |
| PC3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 0 | −1 |
| PC4 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 1 | 0 | −1 | −2 |
| PC5 | 3 | 3 | 3 | 3 | 2 | 2 | 1 | 1 | 0 | −1 | −2 | −2 |
| PC6 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 0 | −1 | −2 | −3 | −3 |
| PC7 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | −1 | −2 | −3 | −3 | −3 |
| 1AS | 3 | 2 | 2 | 2 | 2 | 1 | 0 | −1 | −2 | −3 | −4 | −4 |
| 1A | 3 | 2 | 2 | 2 | 1 | 0 | −1 | −2 | −3 | −4 | −5 | −5 |
| 1B | 3 | 2 | 2 | 1 | 0 | −1 | −2 | −3 | −4 | −5 | −6 | −6 |
| 1C | 3 | 1 | 1 | 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 |
| PC1~PC7 | <PC7 | |
|---|---|---|
| normal sailing | normal sailing | |
| high-risk operation (speed limit) | special operation (change route) | |
| special operation (change route) | special operation (change route) |
| Number | Latitude | Longitude | Number | Latitude | Longitude |
|---|---|---|---|---|---|
| 1 | 8 | ||||
| 2 | 9 | ||||
| 3 | 10 | ||||
| 4 () | 11 | ||||
| 5 () | 12 | ||||
| 6 () | 13 | ||||
| 7 () |
| Parameter | Name | Value |
|---|---|---|
| maximum inertia weight | 0.9 | |
| minimum inertia weight | 0.4 | |
| cognitive factor | 1.5 | |
| social factor | 1.5 | |
| maximum crossover rate | 0.9 | |
| minimum crossover rate | 0.4 | |
| maximum mutation rate | 0.2 | |
| minimum mutation rate | 0.05 | |
| population size | 50 |
| Route Segment | Number of Waypoints | Number of Iterations | The Position of the Waypoints | RB/n Mile |
|---|---|---|---|---|
| 27 | 26.3506 | |||
| 40 | 11.7220 | |||
| 36 | 51.6626 | |||
| 49 | 23.1115 | |||
| 66 | 13.0156 | |||
| 68 | 8.3527 | |||
| Number | Recommended Route Waypoint Coordinates | Optimized Route Waypoint Coordinates | ||
|---|---|---|---|---|
| Latitude | Longitude | Latitude | Longitude | |
| 1 | ||||
| 2 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| Algorithm | Total Number of Iterations | Minimum Running Time/s | Average Running Time ± Standard Deviation/s |
|---|---|---|---|
| GA | 262 | 6.1284 | 7.5414 ± 0.61 |
| PSO | 271 | 6.5251 | 7.7669 ± 0.58 |
| AHPSOGA | 219 | 5.8746 | 6.6383 ± 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, C.; Liu, Z.; Hou, J.; Luo, J.; Wan, X. Intelligent Optimization of Waypoints on the Great Ellipse Routes for Arctic Navigation and Segmental Safety Assessment. J. Mar. Sci. Eng. 2025, 13, 1543. https://doi.org/10.3390/jmse13081543
Jiao C, Liu Z, Hou J, Luo J, Wan X. Intelligent Optimization of Waypoints on the Great Ellipse Routes for Arctic Navigation and Segmental Safety Assessment. Journal of Marine Science and Engineering. 2025; 13(8):1543. https://doi.org/10.3390/jmse13081543
Chicago/Turabian StyleJiao, Chenchen, Zhichen Liu, Jiaxin Hou, Jianan Luo, and Xiaoxia Wan. 2025. "Intelligent Optimization of Waypoints on the Great Ellipse Routes for Arctic Navigation and Segmental Safety Assessment" Journal of Marine Science and Engineering 13, no. 8: 1543. https://doi.org/10.3390/jmse13081543
APA StyleJiao, C., Liu, Z., Hou, J., Luo, J., & Wan, X. (2025). Intelligent Optimization of Waypoints on the Great Ellipse Routes for Arctic Navigation and Segmental Safety Assessment. Journal of Marine Science and Engineering, 13(8), 1543. https://doi.org/10.3390/jmse13081543







