Dynamic Behavior of a Rotationally Restrained Pipe Conveying Gas-Liquid Two-Phase Flow
Abstract
1. Introduction
2. Governing Equations and GITT Technique
2.1. Theoretical Model
2.1.1. Two-Phase Flow Model
2.1.2. Dimensionless Parameters
2.2. Integral Transform Solution
2.2.1. Auxiliary Eigenvalue Problem
2.2.2. Integral Transform Pair
2.2.3. The Main Governing Equation Transformation
2.3. Validation of GITT Calculations
3. Results and Discussion
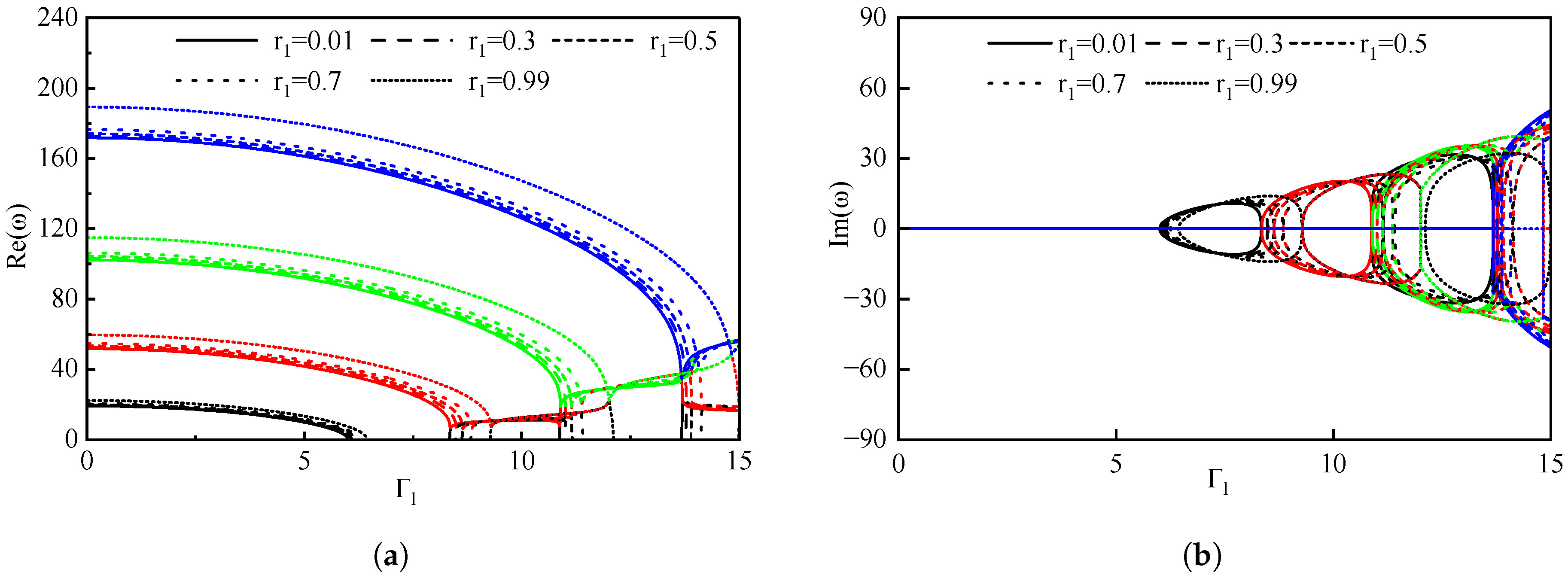
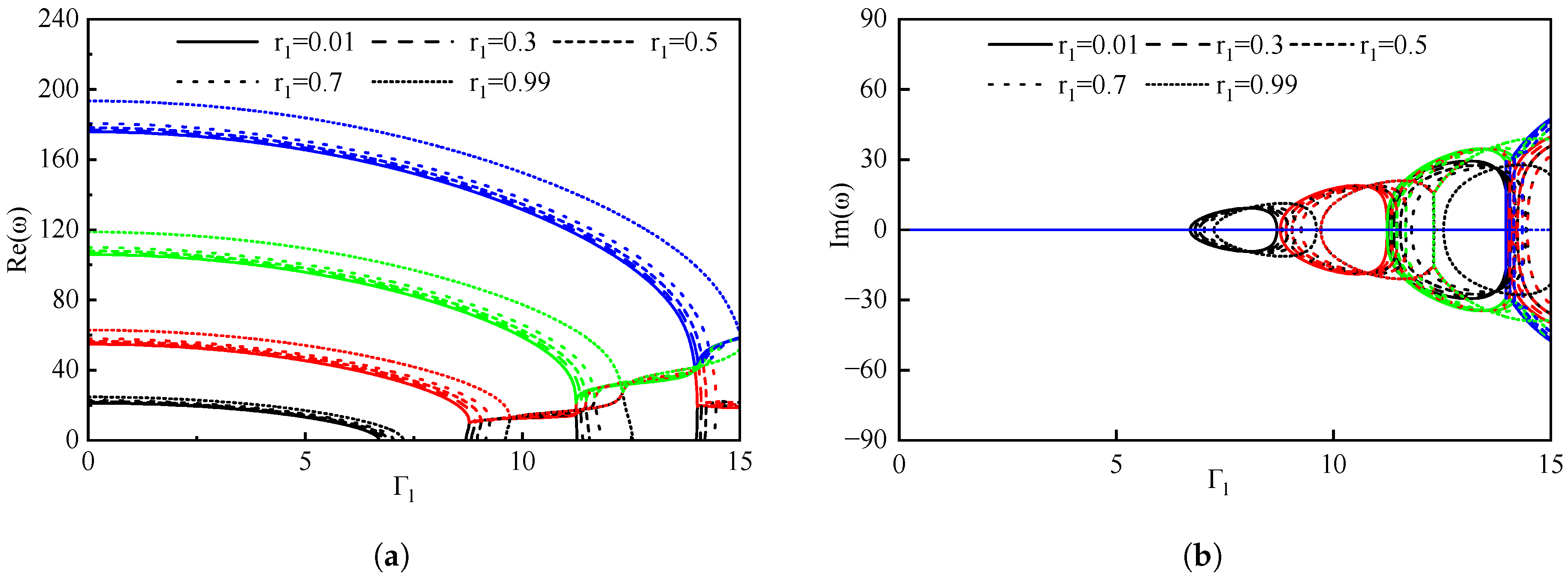
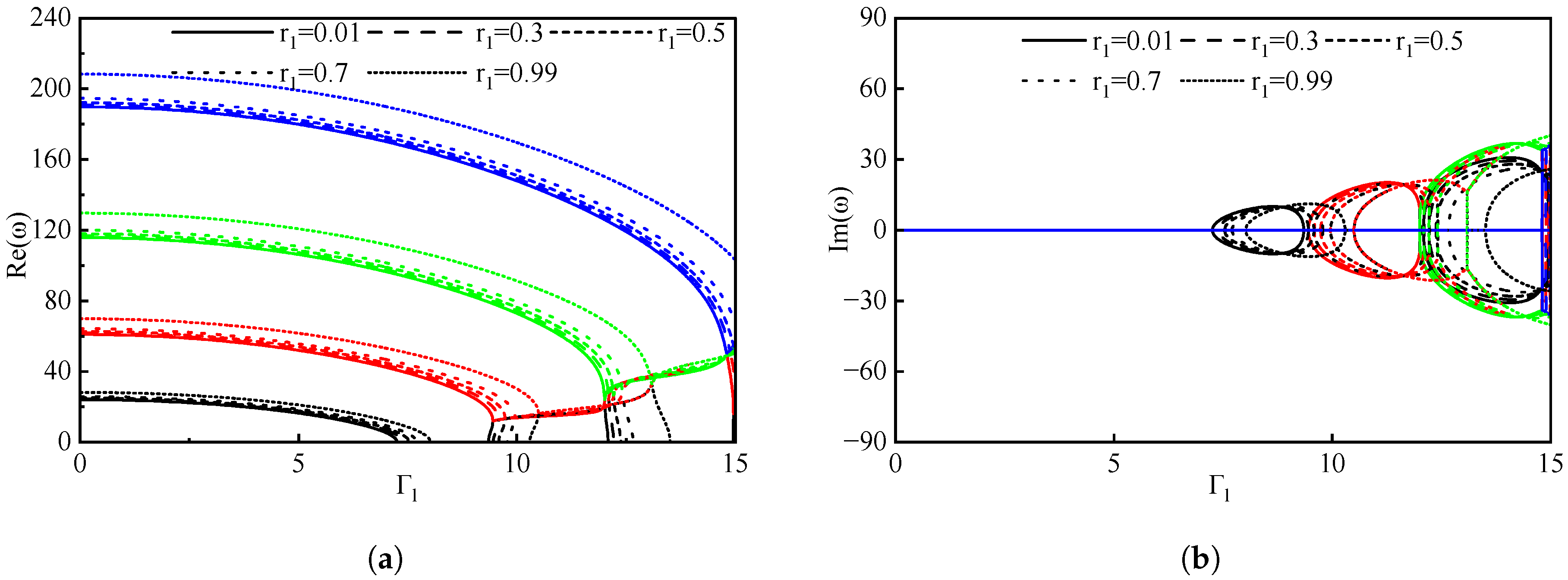
3.1. The Effects of the Gas Volume Fraction
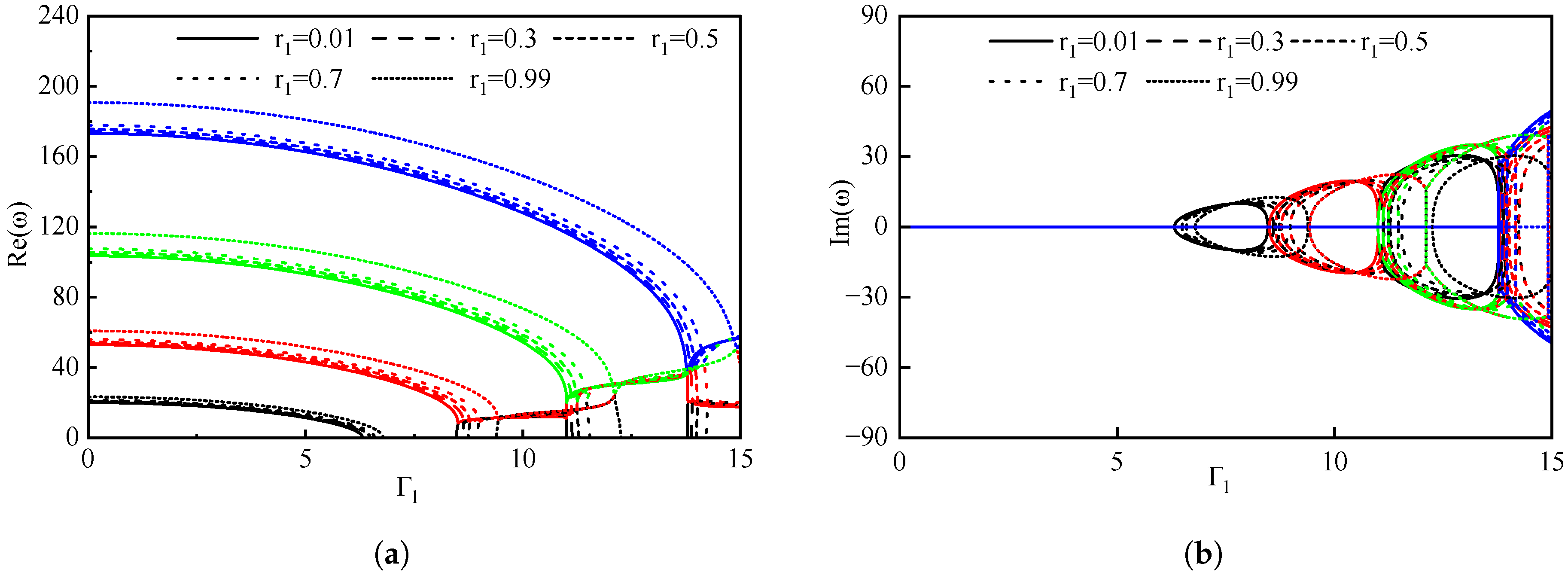
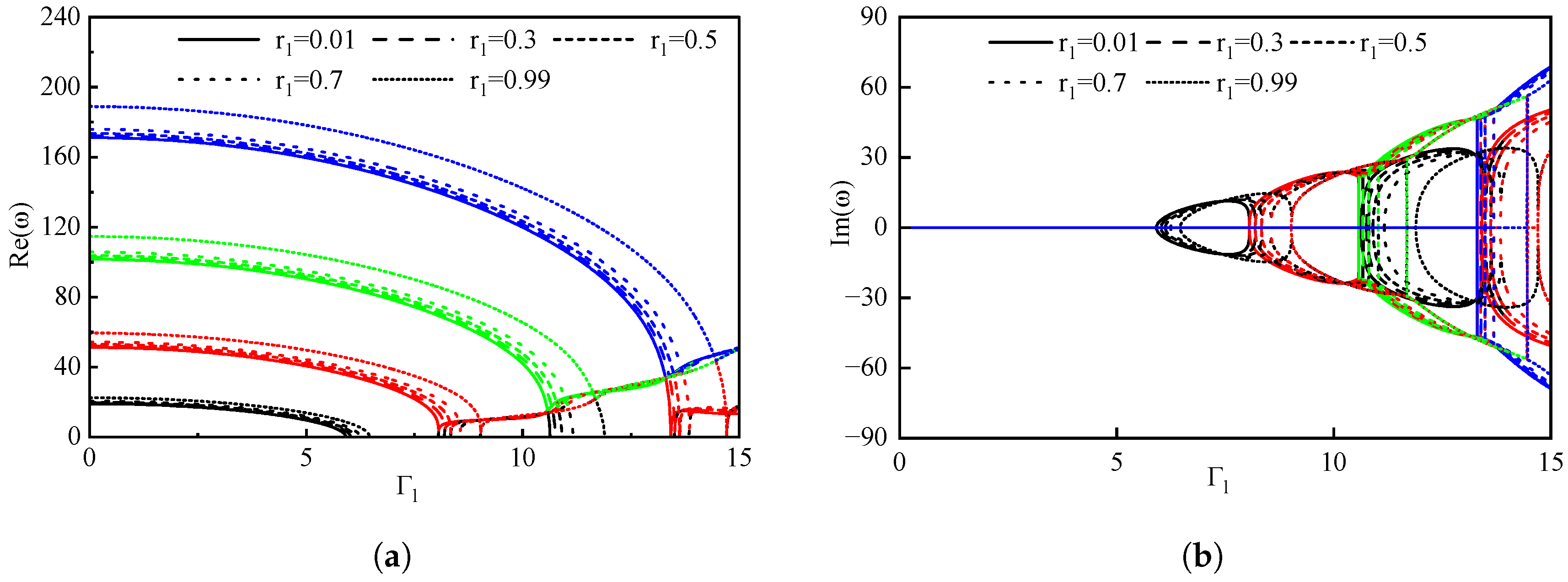
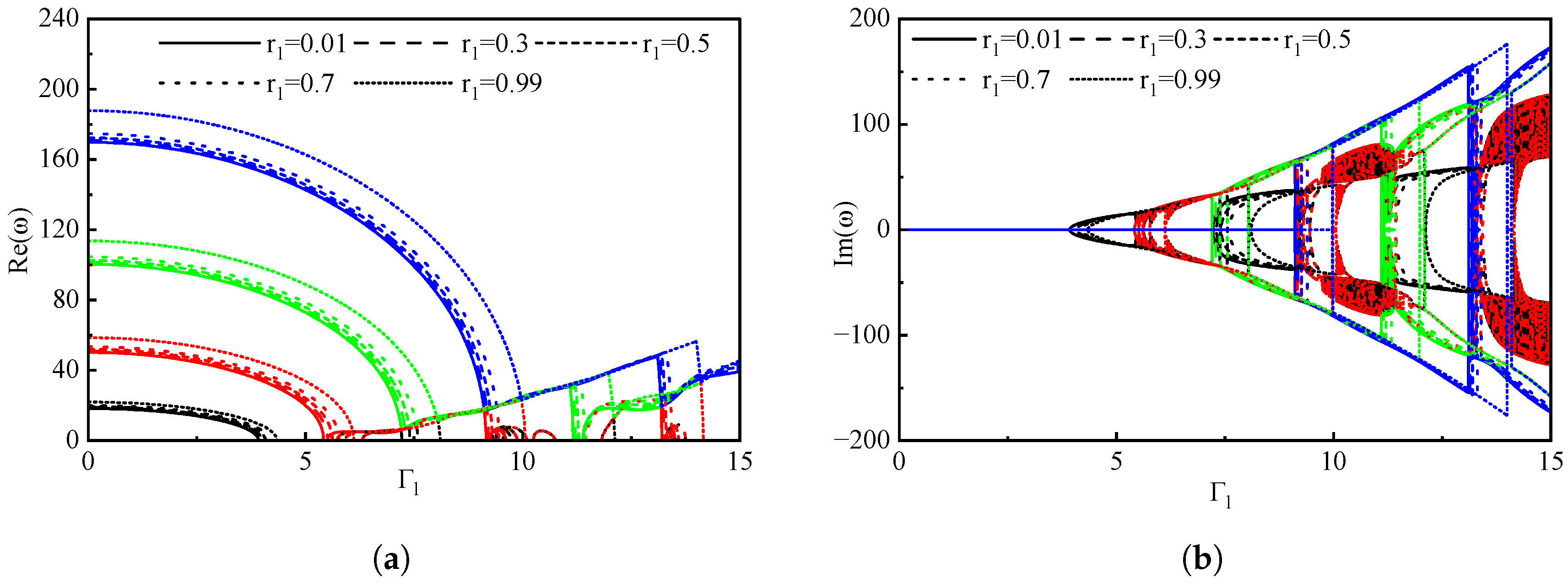
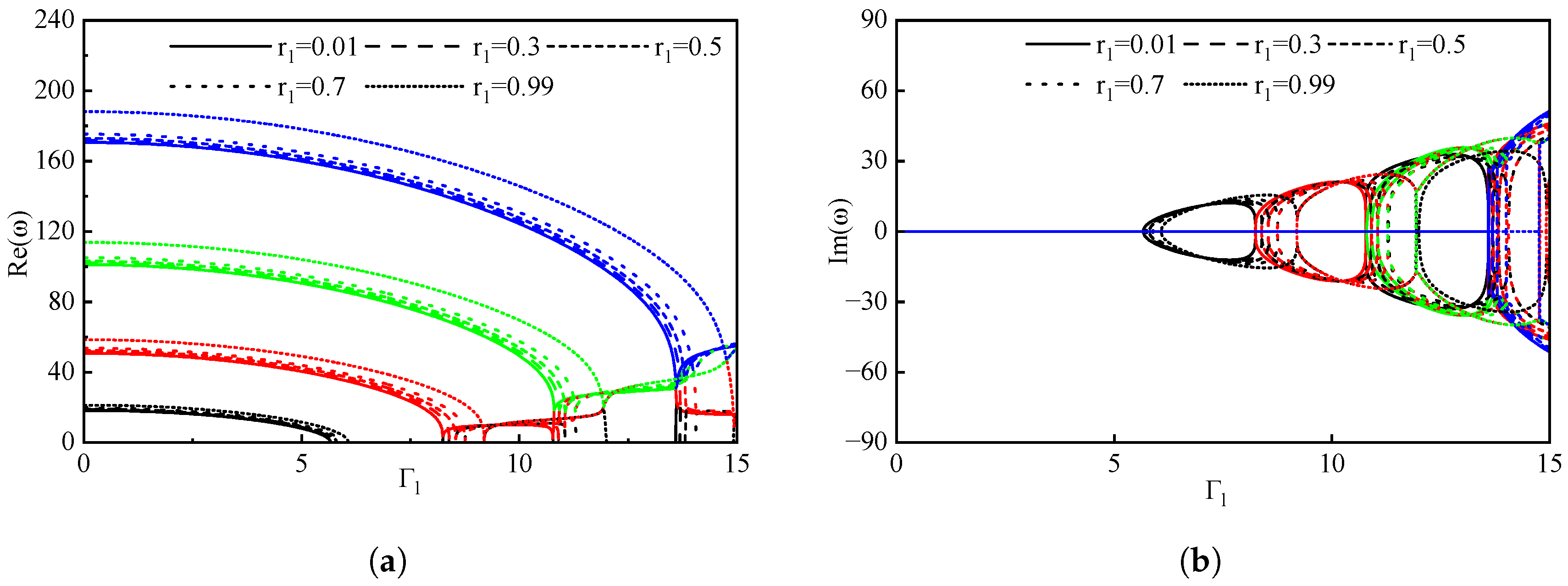
3.2. The Impact of Boundary Conditions on Pipes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Païdoussis, M.; Li, G. Pipes Conveying Fluid: A Model Dynamical Problem. J. Fluids Struct. 1993, 7, 137–204. [Google Scholar] [CrossRef]
- Li, T.; An, C.; Duan, M.; Huang, H.; Liang, W. Effect of the boundary conditions on the dynamic behaviours of subsea free-spanning pipelines. Int. J. Marit. Eng. 2018, 160 A2. [Google Scholar] [CrossRef]
- Wang, B.; Fu, G.; Wang, X.; Su, J.; Jiao, H.; Sun, B. Vibration analysis of a pipe conveying two-phase flow with improved drift-flow model. Appl. Ocean. Res. 2025, 161, 104647. [Google Scholar]
- Zhou, K.; Dai, H.; Wang, L.; Ni, Q.; Hagedorn, P. Modeling and nonlinear dynamics of cantilevered pipe with tapered free end concurrently subjected to axial internal and external flows. Mech. Syst. Signal Process. 2022, 169, 108794. [Google Scholar] [CrossRef]
- Ortega, A.; Rivera, A.; Larsen, C. Flexible riser response induced by combined slug flow and wave loads. In International Conference on Offshore Mechanics and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55379, p. V04BT04A008. [Google Scholar]
- Gu, J.; Duan, M. Integral transform solution for fluid force investigation of a flexible circular cylinder subject to vortex-induced vibrations. J. Mar. Sci. Technol. 2016, 21, 663–678. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, S.; Yang, D.; Huang, G. Numerical investigation on competitive mechanism between internal and external effects of submarine pipeline undergoing vortex-induced vibration. Ocean. Eng. 2022, 266, 112744. [Google Scholar] [CrossRef]
- Païdoussis, M. Pipes conveying fluid: A fertile dynamics problem. J. Fluids Struct. 2022, 114, 103664. [Google Scholar] [CrossRef]
- Païdoussis, M. Dynamics of cylindrical structures in axial flow: A review. J. Fluids Struct. 2021, 107, 103374. [Google Scholar] [CrossRef]
- An, C.; Duan, M.; Estefen, S.F.; Su, J. Structural and Thermal Analyses of Deepwater Pipes; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- An, C.; Su, J. Dynamic behavior of pipes conveying gas–liquid two-phase flow. Nucl. Eng. Des. 2021, 292, 204–212. [Google Scholar] [CrossRef]
- Yih, T.S.; Griffith, P. Unstayed Momentum Fluxes in Two-Phase Low and the Vibration of Nnclear Reactor Components; Massachusetts Institute of Technology, Engineering Projects Lab.: Cambridge, UK, 1968. [Google Scholar]
- Monette, C.; Pettigrew, M.J. Fluidelastic instability of flexible tubes subjected to two-phase internal flow. J. Fluids Struct. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Cargnelutti, M.F.; Belfroid, S.P.C.; Schiferli, W. Two-Phase flow-induced forces on bends in small scale tubes. J. Press. Vessel. Technol. 2010, 102, 041305. [Google Scholar] [CrossRef]
- Miwa, S.; Mori, M.; Hibiki, T. Two-phase flow induced vibration in piping systems. Prog. Nucl. Energy 2015, 78, 270–284. [Google Scholar] [CrossRef]
- Adegoke, A.S.; Oyediran, A.A. Natural frequencies, modes and critical velocities of top tensioned cantilever pipes conveying pressurized steady two-phase flow under thermal loading. Res. Eng. Struct. Mater. 2018, 4, 270–284. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Sotudeh-Gharebagh, R.; Zarghami, R.; Mostoufi, N. Dynamics of two-phase flow in vertical pipes. J. Fluids Struct. 2019, 87, 150–173. [Google Scholar] [CrossRef]
- Li, F.; An, C.; Duan, M.; Su, J. Combined damping model for dynamics and stability of a pipe conveying two-phase flow. Ocean. Eng. 2020, 195, 106683. [Google Scholar] [CrossRef]
- Fu, G.; Tuo, Y.; Su, J.; Wang, K.; Li, L.; Sun, B. Nonlinear dynamics of viscoelastic pipe conveying pulsating fluid subjected to base excitation. China Ocean. Eng. 2023, 37, 781–793. [Google Scholar] [CrossRef]
- Ortiz-Vidal, L.E.; Castillo, D.G.; Valverde, Q. Theoretical study on the dynamic behavior of pipes conveying gas-liquid flow. In Proceedings of the MATEC Web of Conferences, EDP Sciences, Sofia, Bulgaria, 21 September 2017; Volume 148, p. 01004. [Google Scholar]
- Lou, W.; Wang, Z.; Li, P.; Sun, X.; Sun, B.; Liu, Y.; Sun, D. Wellbore drift flow relation suitable for full flow pattern domain and full dip range. Pet. Explor. Dev. 2022, 49, 694–706. [Google Scholar] [CrossRef]
- Fu, G.; Wang, X.; Wang, B.; Su, J.; Wang, K.; Sun, B. Dynamic behavior of axially functionally graded pipe conveying gas–liquid two-phase flow. Appl. Ocean. Res. 2024, 142, 103827. [Google Scholar] [CrossRef]
- Ponte, P.J.V.; Ritto, T.G.; Deü, J.F. Dynamic analysis of a pipe conveying a two-phase fluid considering uncertainties in the flow parameters. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 626. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, B.; Zhao, X.; Chen, B.; Li, Y. Dynamic characteristics and stability of pipe-in-pipe system conveying two-phase flow in thermal environment. Appl. Ocean. Res. 2020, 103, 102333. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Q.; Wang, X.; Ullah, S.; Zhao, D.; Civalek, Ö.; Xue, C.; Qi, W. New exact analytical thermal buckling solutions of composite thin plates with all edges rotationally-restrained. Mech. Adv. Mater. Struct. 2020, 31, 3518–3530. [Google Scholar] [CrossRef]
- Chen, Q.; Qiao, P. Post-buckling behavior of imperfect laminated composite plates with rotationally-restrained edges. Compos. Struct. 2015, 125, 117–126. [Google Scholar] [CrossRef]
- Tang, X.; Guo, C.; Li, F.; Zhang, R.; Song, D.; Fu, P.; Liu, H. Thermal buckling analysis of rotationally-restrained orthotropic thin plates utilizing a two-dimensional improved Fourier series approach. Meccanica 2023, 58, 1443–1464. [Google Scholar] [CrossRef]
- Qiao, P.; Shan, L. Explicit local buckling analysis of rotationally restrained composite plates under biaxial loading. Int. J. Struct. Stab. Dyn. 2007, 7, 487–517. [Google Scholar] [CrossRef]
- Hu, W.; Han, S.; Deng, Z. Analyzing dynamic response of non-homogeneous string fixed at both ends. Int. J.-Non-Linear Mech. 2012, 47, 1111–1115. [Google Scholar] [CrossRef]
- Lee, J. Free vibration analysis of beams with non-ideal clamped boundary conditions. J. Mech. Sci. Technol. 2013, 27, 297–303. [Google Scholar] [CrossRef]
- Shahin, R.I.; Ahmed, M.; Yehia, S.A. Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions. Buildings 2023, 13, 2879. [Google Scholar] [CrossRef]
- Cheng, X.; Nie, J.; Zhao, L.; Shi, W. The thermal bend of RTP with one edge clamped and two edges simply supported and one edge free. Arch. Appl. Mech. 2015, 85, 287–302. [Google Scholar] [CrossRef]
- Jeong, J.; Lim, C.; Joeng, D.; Kook, S. A Study on the Dynamic Behavior of a Various Buried Pipeline. J. Earthq. Eng. Soc. Korea 2006, 10, 15–24. [Google Scholar] [CrossRef]
- Choi, H.S. Free spanning analysis of offshore pipelines. Ocean. Eng. 2001, 28, 1325–1338. [Google Scholar] [CrossRef]
- He, Y.; Duan, M.; Su, J. Bending of rectangular orthotropic plates with rotationally restrained and free edges: Generalized integral transform solutions. Eng. Struct. 2021, 247, 113129. [Google Scholar] [CrossRef]
- Zhou, J.; Chang, X.; Xiong, Z.; Li, Y. Stability and nonlinear vibration analysis of fluid-conveying composite pipes with elastic boundary conditions. Thin-Walled Struct. 2022, 179, 109597. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Wei, H.; Zhang, Z.; Yang, F.; Hu, H.; Hu, Y. Nonlinear dynamics of viscoelastic fluid-conveying pipe installed within uniform external cross flow by pipe clamps. Appl. Ocean. Res. 2023, 135, 103547. [Google Scholar] [CrossRef]
- Azliana, N.; Akmar, A.; Sallih, N.; Harith Irfan Ishak, M. Natural Frequency Analysis of Pipe with Different Boundary Conditions Using Analytical and Finite Element Method; Springer: Berlin/Heidelberg, Germany, 2022; pp. 559–570. [Google Scholar]
- Cotta, R.M. Benchmark results in computational heat and fluid flow: The integral transform method. Int. J. Heat Mass Transf. 1994, 37, 381–393. [Google Scholar] [CrossRef]
- Cotta, R.M.; Lisboa, K.M.; Curi, M.F.; Balabani, S.; Quaresma, J.N.N.; Perez-Guerrero, J.S.; Macêdo, E.N.; Amorim, N.S. A review of hybrid integral transform solutions in fluid flow problems with heat or mass transfer and under Navier–Stokes equations formulation. Numer. Heat Transf. Part Fundam. 2019, 76, 60–87. [Google Scholar] [CrossRef]
- Cotta, R.M.; Naveira-Cotta, C.P.; Knupp, D.C. Nonlinear eigenvalue problem in the integral transforms solution of convection-diffusion with nonlinear boundary conditions. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 767–789. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, L. Bending of rectangular orthotropic thin plates with rotationally restrained edges: A finite integral transform solution. Appl. Math. Model. 2017, 46, 48–62. [Google Scholar] [CrossRef]


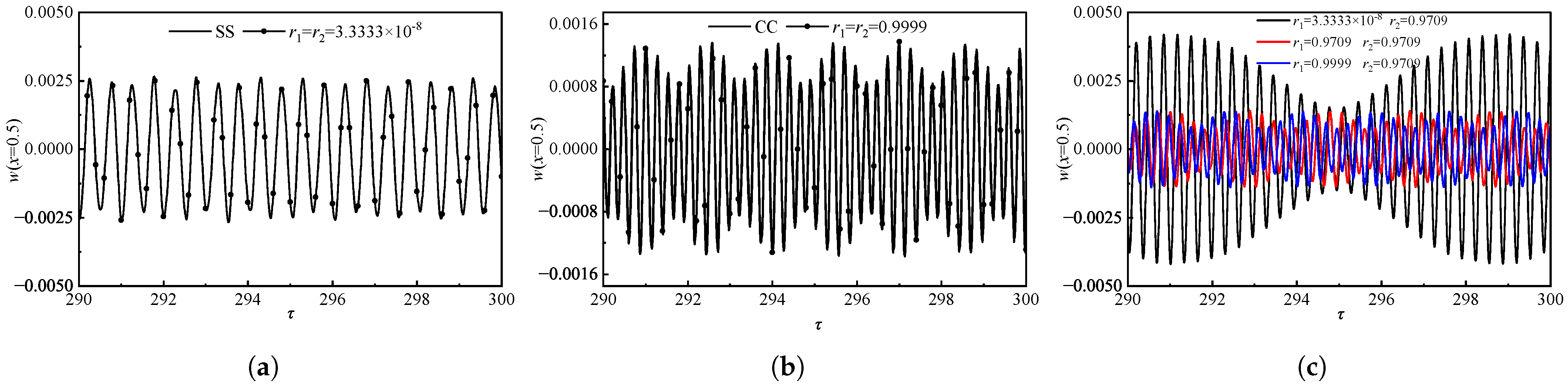
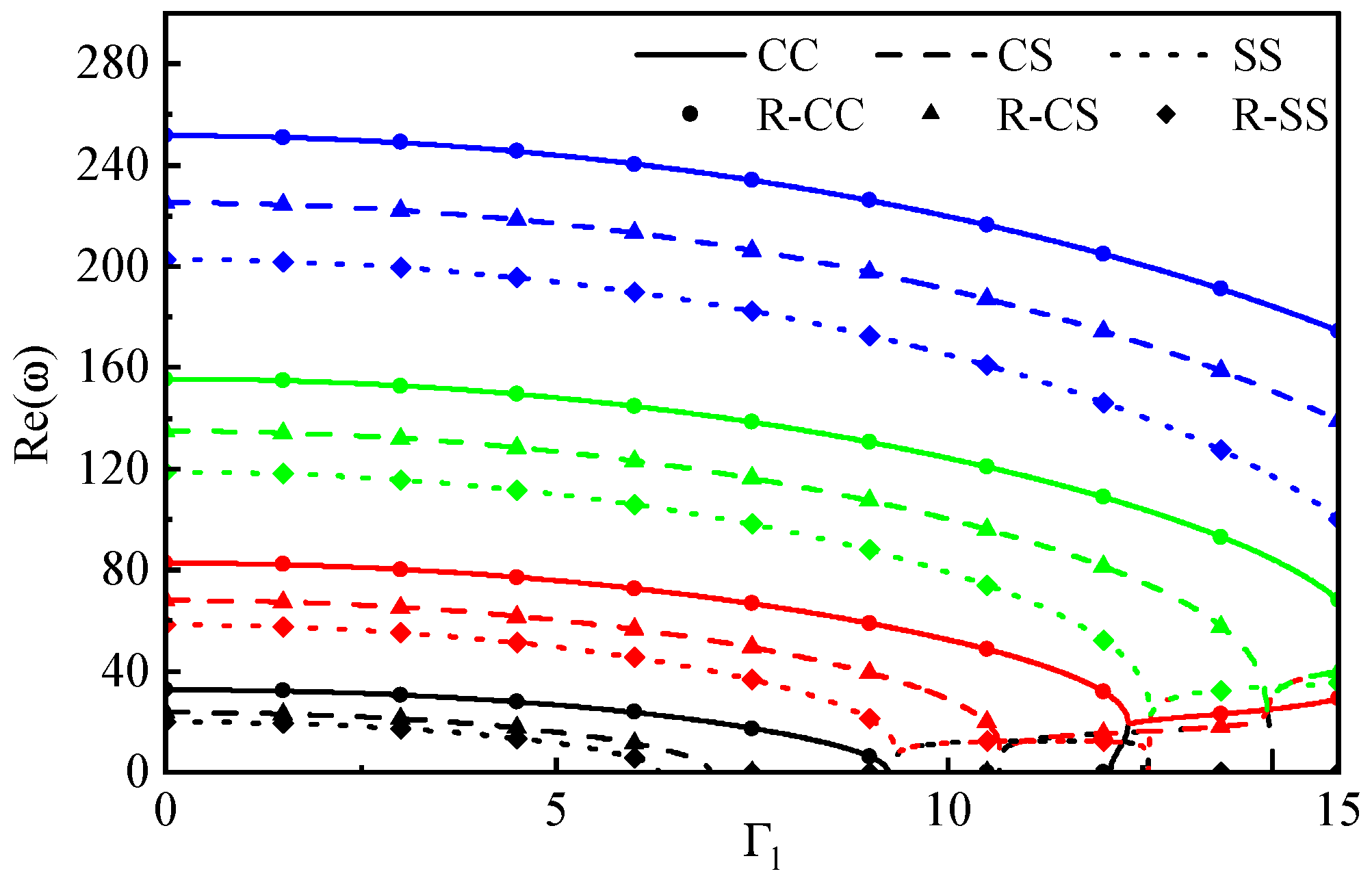
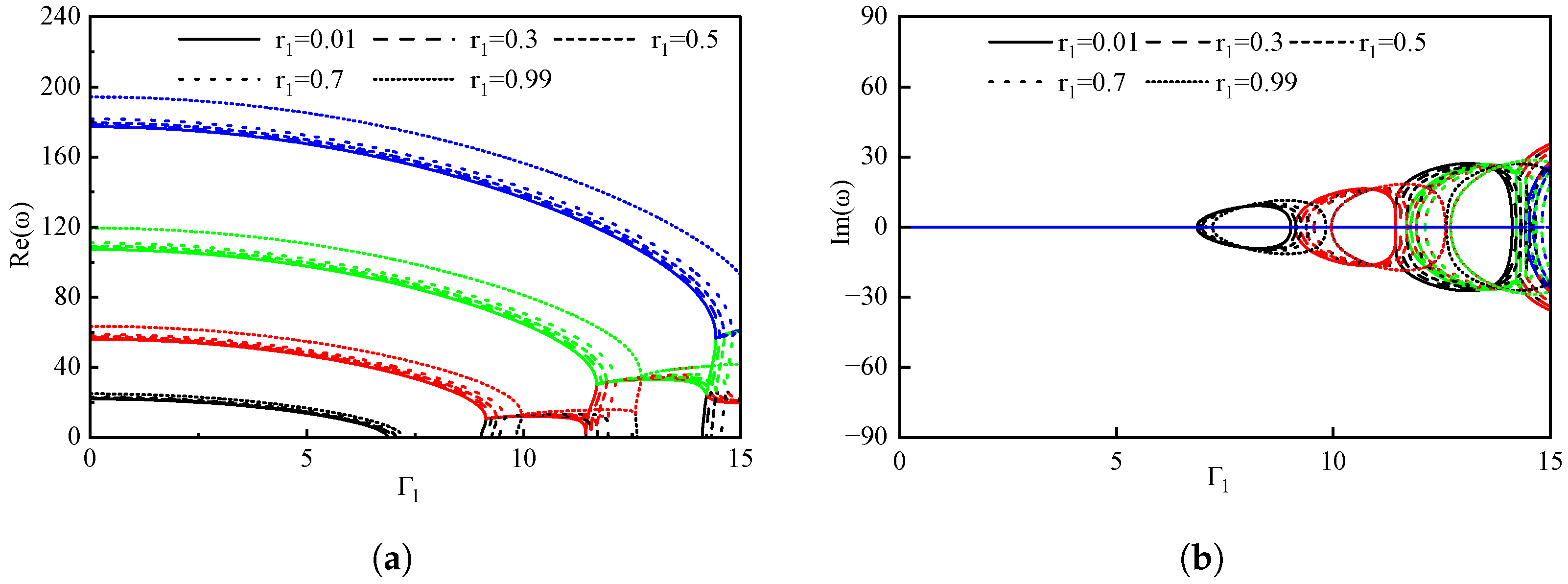
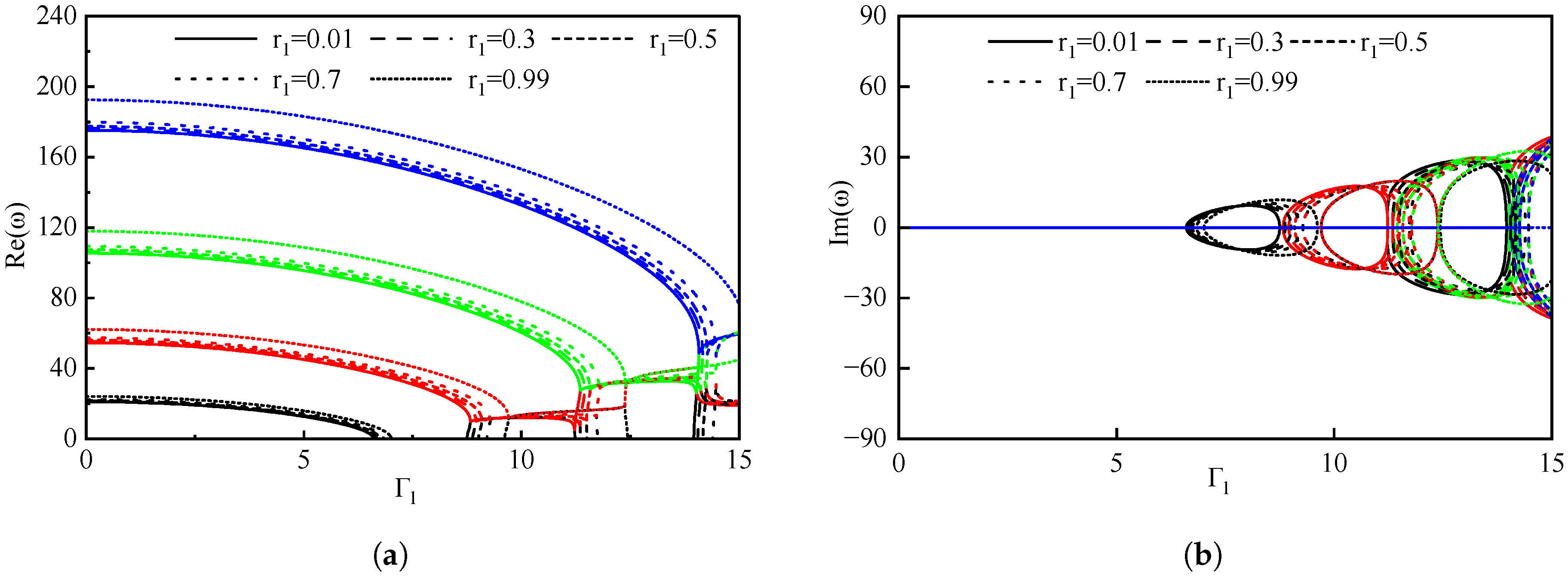

| Boundary Conditions | |||
|---|---|---|---|
| SS | 6.072 | 5.654 | 5.282 |
| , | 6.073 | 5.655 | 5.286 |
| (R-SS, , ) | |||
| , | 7.766 | 7.220 | 6.751 |
| (SR, , ) | |||
| , | 8.363 | 7.954 | 7.573 |
| (RR, , ) | |||
| , | 8.391 | 7.987 | 7.609 |
| (CR, , ) | |||
| , | 8.462 | 8.055 | 7.675 |
| (R-CC, , ) | |||
| CC | 8.463 | 8.055 | 7.675 |
| BC | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NW= | |||||||||||||
| 1st | SS | 14.293 | 14.293 | 14.293 | 14.293 | 12.478 | 12.477 | 12.477 | 12.477 | 11.004 | 11.004 | 11.004 | 11.004 |
| R-SS | 14.293 | 14.293 | 14.293 | 14.293 | 12.478 | 12.477 | 12.477 | 12.477 | 11.004 | 11.004 | 11.004 | 11.004 | |
| SR | 20.942 | 20.941 | 20.941 | 20.941 | 19.171 | 19.171 | 19.171 | 19.171 | 17.882 | 17.882 | 17.882 | 17.882 | |
| RR | 24.609 | 24.608 | 24.608 | 24.608 | 23.283 | 23.282 | 23.282 | 23.282 | 22.380 | 22.380 | 22.380 | 22.380 | |
| CR | 24.950 | 24.949 | 24.949 | 24.949 | 23.633 | 23.632 | 23.632 | 23.632 | 22.736 | 22.736 | 22.736 | 22.736 | |
| R-CC | 25.459 | 25.458 | 25.458 | 25.458 | 24.125 | 24.124 | 24.124 | 24.124 | 23.219 | 23.219 | 23.219 | 23.219 | |
| CC | 25.460 | 25.459 | 25.459 | 25.459 | 24.126 | 24.126 | 24.125 | 24.125 | 23.220 | 23.220 | 23.220 | 23.220 | |
| 2nd | SS | 47.200 | 47.200 | 47.195 | 47.194 | 44.308 | 44.305 | 44.304 | 44.304 | 42.112 | 42.110 | 42.110 | 42.110 |
| R-SS | 47.200 | 47.200 | 47.195 | 47.194 | 44.308 | 44.305 | 44.304 | 44.304 | 42.112 | 42.110 | 42.110 | 42.110 | |
| SR | 57.543 | 57.540 | 57.540 | 57.540 | 54.666 | 54.664 | 54.664 | 54.664 | 52.548 | 52.547 | 52.547 | 52.547 | |
| RR | 65.657 | 65.651 | 65.649 | 65.649 | 63.281 | 63.277 | 63.276 | 63.276 | 61.537 | 61.535 | 61.534 | 61.534 | |
| CR | 66.653 | 66.647 | 66.645 | 66.644 | 64.291 | 64.288 | 64.287 | 64.286 | 62.558 | 62.556 | 62.555 | 62.555 | |
| R-CC | 67.896 | 67.890 | 67.888 | 67.888 | 65.510 | 65.507 | 65.506 | 65.505 | 63.763 | 63.761 | 63.760 | 63.760 | |
| CC | 67.899 | 67.892 | 67.891 | 67.890 | 65.513 | 65.509 | 65.508 | 65.508 | 63.766 | 63.763 | 63.763 | 63.763 | |
| 3rd | SS | 97.896 | 97.877 | 97.874 | 97.872 | 94.428 | 94.418 | 94.414 | 94.414 | 91.881 | 91.876 | 91.875 | 91.874 |
| R-SS | 97.896 | 97.877 | 97.874 | 97.872 | 94.428 | 94.417 | 94.414 | 94.414 | 91.881 | 91.876 | 91.875 | 91.874 | |
| SR | 111.922 | 111.906 | 111.903 | 111.902 | 108.496 | 108.485 | 108.483 | 108.482 | 106.022 | 106.015 | 106.014 | 106.013 | |
| RR | 124.293 | 124.280 | 124.278 | 124.277 | 121.341 | 121.333 | 121.332 | 121.331 | 119.207 | 119.202 | 119.201 | 119.201 | |
| CR | 126.254 | 126.241 | 126.239 | 126.238 | 123.326 | 123.318 | 123.317 | 123.316 | 121.208 | 121.204 | 121.203 | 121.202 | |
| R-CC | 128.519 | 128.507 | 128.504 | 128.503 | 125.567 | 125.559 | 125.557 | 125.557 | 123.435 | 123.431 | 123.430 | 123.429 | |
| CC | 128.524 | 128.512 | 128.509 | 128.508 | 125.572 | 125.564 | 125.562 | 125.562 | 123.440 | 123.435 | 123.434 | 123.434 | |
| 4th | SS | 167.706 | 167.594 | 167.577 | 167.572 | 163.937 | 163.855 | 163.842 | 163.839 | 161.204 | 161.150 | 161.142 | 161.140 |
| R-SS | 167.706 | 167.594 | 167.578 | 167.572 | 163.938 | 163.855 | 163.842 | 163.839 | 161.204 | 161.150 | 161.142 | 161.140 | |
| SR | 185.273 | 185.171 | 185.157 | 185.153 | 181.557 | 181.481 | 181.471 | 181.468 | 178.890 | 178.841 | 178.834 | 178.833 | |
| RR | 201.603 | 201.489 | 201.473 | 201.469 | 198.291 | 198.210 | 198.199 | 198.196 | 195.908 | 195.856 | 195.849 | 195.848 | |
| CR | 204.818 | 204.702 | 204.686 | 204.682 | 201.535 | 201.453 | 201.442 | 201.440 | 199.172 | 199.120 | 199.113 | 199.111 | |
| R-CC | 208.381 | 208.265 | 208.249 | 208.245 | 205.074 | 204.992 | 204.981 | 204.979 | 202.697 | 202.646 | 202.639 | 202.637 | |
| CC | 208.389 | 208.273 | 208.257 | 208.253 | 205.082 | 205.000 | 204.989 | 204.987 | 202.705 | 202.654 | 202.647 | 202.645 | |
| 0.003 | 0.547 | 0.0657 | 0.0925 | 1.2 | 1000 1 |
| Character | Interpretation |
|---|---|
| the critical velocity for at which the 1st order instability of occurs in the pipe | |
| the critical velocity at which the pipe regains a stable state in the 1st order | |
| the critical velocity at which coupling flutter between the first and second orders emerges | |
| the critical velocity at which the coupling flutter between the first and second orders ceases | |
| the critical velocity at which coupling flutter between the second and third orders occurs | |
| the velocity at which coupling flutter between the first and second orders re-emerges | |
| the critical velocity associated with the coupling flutter between the third and fourth orders |
| = | ||||||
|---|---|---|---|---|---|---|
| 5.67 | 5.74 | 5.81 | 5.90 | 6.08 | ||
| 8.25 | 8.39 | 8.54 | 8.76 | 9.20 | ||
| 8.25 | 8.39 | 8.54 | 8.76 | 9.20 | ||
| 10.78 | 10.91 | 11.05 | 11.29 | 11.94 | ||
| 10.80 | 10.92 | 11.05 | 11.29 | 11.94 | ||
| 13.61 | 13.70 | 13.83 | 14.06 | 14.93 | ||
| 13.60 | 13.69 | 13.80 | 14.01 | 14.77 | ||
| 6.01 | 6.09 | 6.16 | 6.26 | 6.44 | ||
| 8.34 | 8.49 | 8.63 | 8.84 | 9.28 | ||
| 8.36 | 8.50 | 8.64 | 8.85 | 9.29 | ||
| 10.88 | 11.01 | 11.14 | 11.37 | 12.02 | ||
| 13.68 | 13.77 | 13.88 | 14.08 | 14.83 | ||
| 13.69 | 13.79 | 13.91 | 14.14 | 15.00 | ||
| 13.68 | 13.77 | 13.88 | 14.08 | 14.83 | ||
| 6.32 | 6.41 | 6.49 | 6.60 | 6.80 | ||
| 8.47 | 8.60 | 8.75 | 8.95 | 9.40 | ||
| 8.51 | 8.64 | 8.78 | 8.99 | 9.43 | ||
| 11.01 | 11.12 | 11.25 | 11.47 | 12.10 | ||
| 13.78 | 13.86 | 13.97 | 14.17 | 14.92 | ||
| 13.80 | 13.90 | 14.03 | 14.25 | - | ||
| 13.78 | 13.86 | 13.97 | 14.17 | 14.92 | ||
| 6.7 | 6.81 | 6.91 | 7.03 | 7.26 | ||
| 8.70 | 8.83 | 8.96 | 9.16 | 9.61 | ||
| 8.78 | 8.91 | 9.05 | 9.25 | 9.71 | ||
| 11.24 | 11.34 | 11.46 | 11.67 | 12.31 | ||
| 13.97 | 14.06 | 14.16 | 14.35 | - | ||
| 14.03 | 14.12 | 14.24 | 14.46 | - | ||
| 13.97 | 14.06 | 14.16 | 14.35 | - | ||
| 7.26 | 7.40 | 7.54 | 7.71 | 8.02 | ||
| 9.35 | 9.46 | 9.59 | 9.79 | 10.30 | ||
| 9.46 | 9.59 | 9.74 | 9.96 | 10.50 | ||
| 12.01 | 12.10 | 12.22 | 12.42 | 13.09 | ||
| 14.81 | 14.89 | 14.99 | - | - | ||
| 14.97 | - | - | - | - | ||
| 14.81 | 14.89 | 14.99 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, G.; Jiao, H.; Zhang, A.; Wang, X.; Wang, B.; Sun, B.; Su, J. Dynamic Behavior of a Rotationally Restrained Pipe Conveying Gas-Liquid Two-Phase Flow. J. Mar. Sci. Eng. 2025, 13, 1524. https://doi.org/10.3390/jmse13081524
Fu G, Jiao H, Zhang A, Wang X, Wang B, Sun B, Su J. Dynamic Behavior of a Rotationally Restrained Pipe Conveying Gas-Liquid Two-Phase Flow. Journal of Marine Science and Engineering. 2025; 13(8):1524. https://doi.org/10.3390/jmse13081524
Chicago/Turabian StyleFu, Guangming, Huilin Jiao, Aixia Zhang, Xiao Wang, Boying Wang, Baojiang Sun, and Jian Su. 2025. "Dynamic Behavior of a Rotationally Restrained Pipe Conveying Gas-Liquid Two-Phase Flow" Journal of Marine Science and Engineering 13, no. 8: 1524. https://doi.org/10.3390/jmse13081524
APA StyleFu, G., Jiao, H., Zhang, A., Wang, X., Wang, B., Sun, B., & Su, J. (2025). Dynamic Behavior of a Rotationally Restrained Pipe Conveying Gas-Liquid Two-Phase Flow. Journal of Marine Science and Engineering, 13(8), 1524. https://doi.org/10.3390/jmse13081524






